第十一章 卡方检验
合集下载
卡方检验
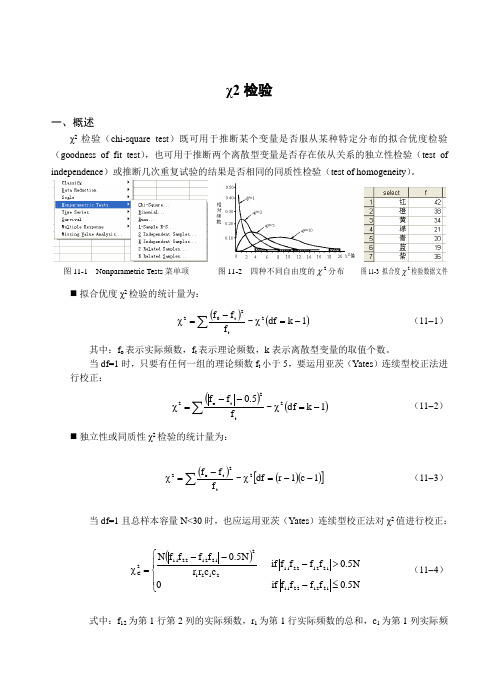
χ2检验一、概述χ2检验（chi-square test ）既可用于推断某个变量是否服从某种特定分布的拟合优度检验（goodness of fit test ），也可用于推断两个离散型变量是否存在依从关系的独立性检验（test of independence ）或推断几次重复试验的结果是否相同的同质性检验（test of homogeneity ）。
图11-1 Nonparametric Tests 菜单项 图11-2 四种不同自由度的2χ分布 图11-3 拟合度2χ检验数据文件⏹ 拟合优度χ2检验的统计量为：()()1k df ~f f f 2t2t 02-=χ-=χ∑（11-1）其中：f o 表示实际频数，f t 表示理论频数，k 表示离散型变量的取值个数。
当df=1时，只要有任何一组的理论频数f t 小于5，要运用亚茨（Yates ）连续型校正法进行校正：()()1k df ~f 5.0f f2t2t o2-=χ--=χ∑（11-2）⏹ 独立性或同质性χ2检验的统计量为：()()()[]1c 1r df ~f f f 2t2t o 2--=χ-=χ∑（11-3）当df=1且总样本容量N<30时，也应运用亚茨（Yates ）连续型校正法对χ2值进行校正：()⎪⎩⎪⎨⎧≤->---=χN5.0f f f f if 0N 5.0f f f f if c c r r N 5.0f f f f N 211222112112221121212211222112C （11-4）式中：f 12为第1行第2列的实际频数，r 1为第1行实际频数的总和，c 1为第1列实际频第十一章非参数检验151数的总和，其余类推。
因此，χ2值大于等于0，其大小随实际频数与理论频数之差的变化而变化。
二者之差越小，χ2值也越小，说明样本分布与假设的理论分布越一致；二者之差越大，χ2值也越大，说明样本分布与假设的理论分布越不一致。
第十一章卡方检验
第十一章卡方检验
2统计量的条件：Ｔ≥5
2
(AT)2 T
校正的2
2 (AT0.5)2
T
第十一章卡方检验
2检验的基本公式
2 (AT)2
T
❖ A—实际频数 ❖ T— 根据H0确定的理论频数
第十一章卡方检验
2检验基本思想
2值反映了样本实际频数与理论频数的符合程度。 如果原假设成立， 2值不会太大；反之，A若与T差 距大， 2值也大；当2值超出一定范围时，就有理
有效率 ％ 70.7 70.7
70.7
T a 8 7 0.7 % 0 5 6 .6 T b 8 0 2.3 % 9 2.4 3
T c 6 7 0.7 % 0 4.4 2 T d 6 2 0.3 % 9 1.6 7
第十一章卡方检验
四格表的理论频数由下式求得 ：
nn
T RC
RC
n
式中：TRC为第R 行C 列的理论频数， nR为相应的行合计， nC为相应的列合计。
➢ 四格表资料比较的是两种处理的效果。 ➢ 每种处理只产生两种相互对立的结果，如生与死，有
效与无效，患病与未患病，阳性与阴性，检出与未检 出，等等。
第十一章卡方检验
四格表资料的一般形式
处理组 A B
合计
发生数 a c
a+c
未发生数 合计
b
a+b
d
c+d
b+d
n=a+b+c
+d
第十一章卡方检验
例11-1 某医师为比较中药和西药治疗胃炎的疗效，随机 抽取140例胃炎患者分成中药组和西药组，结果中药组 治疗80例，有效64例，西药组治疗60例，有效35例， 问中药和西药治疗胃炎的效果是否相同？
第十一章 卡方检验
第一节 独立样本列联表的χ2检验
四格表资料： 1.完全随机设计的两样本率比较的χ2检验
2. 2 × 2列联表资料的χ2检验
3.R × C列联表资料的χ2检验
一、 χ2检验的基本思想
例11.1 某研究者欲比较甲、乙两药治疗小儿上消化 道出血的效果，将90名患儿随机分为两组，一组采 用甲药治疗，另一组采用乙药治疗，一个疗程后观 察结果，见下表。问两药治疗小儿上消化道出血的 有效率是否有差别？
Likelihood Ratio
10.338
1
.001
Fisher's Exact Test
.003
.002
Linear-by-Linear Association
9.761
1
.002
N of Valid Cases
90
a. Computed only for a 2x2 table
b. 0 cells (.0%) have expected count less than 5. The minimum expected count is 11. 50.
理论频数(theoretical frequency)
理论频数的计算方法： 在H0成立的情况下，即甲药治疗小儿上消化道出
血的有效率与乙药治疗小儿消化道出血的有效 率相同。 则理论上两种人群有相同的有效率74.44%，这时 计算出其相应的各个格子的理论频数。
(a) T11
(b) T12
(c) T21
(d) T22
其基本公式：
∑ χ2 = (A - T)2
T
2
0.5
0.4
0.3
纵高
理 解χ2值
0.2 0.1
统计学卡方检验
个体化干预
根据分析结果，为患者提供个体化的干预措施，提高生存质量。
06
卡方检验注意事项及局限 性讨论
样本量要求及抽样方法选择
样本量要求
卡方检验对样本量有一定的要求，通常建议每个单元格的期望频数不小于5，以确保检验结果的稳定性和可靠性 。当样本量不足时，可能会导致检验效能降低，增加第二类错误的概率。
抽样方法选择
在进行卡方检验时，应选择合适的抽样方法。简单随机抽样是最常用的方法，但在某些情况下，如分层抽样或整 群抽样可能更适合。选择合适的抽样方法有助于提高检验的准确性和可靠性。
期望频数过低时处理策略
合并类别
当某个单元格的期望频数过低时，可以考虑 合并相邻的类别，以增加期望频数。合并类 别时应注意保持类别的逻辑性和实际意义。
适用范围及条件
适用范围
卡方检验适用于多个分类变量之间的独立性或相关性检验，如医学、社会科学等领域的调查研究。
条件
使用卡方检验需要满足一些前提条件，如样本量足够大、每个单元格的期望频数不宜过小等。此外， 对于有序分类变量或存在空单元格的情况，需要采用相应的处理方法或选择其他适合的统计方法。
02
卡方检验方法
统计学卡方检验
目录
• 卡方检验基本概念 • 卡方检验方法 • 数据准备与预处理 • 卡方检验实施步骤 • 卡方检验在医学领域应用举例 • 卡方检验注意事项及局限性讨论
01
卡方检验基本概念
定义与原理
01
02
定义
原理
卡方检验是一种基于卡方分布的假设检验方法，用于推断两个或多个 分类变量之间是否独立或相关。
确定分组界限
在确定分组界限时，可以采用等距分组、等频分组或 基于数据分布的分组方法。选择合适的分组界限有助 于保持各组之间的均衡性，减少信息损失。
根据分析结果，为患者提供个体化的干预措施，提高生存质量。
06
卡方检验注意事项及局限 性讨论
样本量要求及抽样方法选择
样本量要求
卡方检验对样本量有一定的要求，通常建议每个单元格的期望频数不小于5，以确保检验结果的稳定性和可靠性 。当样本量不足时，可能会导致检验效能降低，增加第二类错误的概率。
抽样方法选择
在进行卡方检验时，应选择合适的抽样方法。简单随机抽样是最常用的方法，但在某些情况下，如分层抽样或整 群抽样可能更适合。选择合适的抽样方法有助于提高检验的准确性和可靠性。
期望频数过低时处理策略
合并类别
当某个单元格的期望频数过低时，可以考虑 合并相邻的类别，以增加期望频数。合并类 别时应注意保持类别的逻辑性和实际意义。
适用范围及条件
适用范围
卡方检验适用于多个分类变量之间的独立性或相关性检验，如医学、社会科学等领域的调查研究。
条件
使用卡方检验需要满足一些前提条件，如样本量足够大、每个单元格的期望频数不宜过小等。此外， 对于有序分类变量或存在空单元格的情况，需要采用相应的处理方法或选择其他适合的统计方法。
02
卡方检验方法
统计学卡方检验
目录
• 卡方检验基本概念 • 卡方检验方法 • 数据准备与预处理 • 卡方检验实施步骤 • 卡方检验在医学领域应用举例 • 卡方检验注意事项及局限性讨论
01
卡方检验基本概念
定义与原理
01
02
定义
原理
卡方检验是一种基于卡方分布的假设检验方法，用于推断两个或多个 分类变量之间是否独立或相关。
确定分组界限
在确定分组界限时，可以采用等距分组、等频分组或 基于数据分布的分组方法。选择合适的分组界限有助 于保持各组之间的均衡性，减少信息损失。
第11章 卡方检验
Pearson 2
1900 年 Karl Pearson 首 先 提 出 ， 故 又 称 Pearson 2
度量实际频数(A)与H0成立条件下理论频数(T)之
间吻合程度的指标
本例
2 ( A T ) 2 T
ad bc n ( A T )2 四格表 2 T a b c d a c b d
率或构成比的比较：比较两个或多个总体率或
构成比有无差别
频数分布的拟合优度检验 关联性分析/独立性检验 线性趋势检验
内容提要
概念和用途 基本思想和分析步骤 适用条件
2检验的应用
1.建立检验假设，确立检验水准
H0 : 血塞通 = 银杏达莫 合并 H1 : 血塞通 银杏达莫
3.83
4.67 5.53 …
5.35
6.35 7.34 …
7.23
8.38
8.56 10.64 12.59 15.03 16.81 18.55
9.80 12.02 14.07 16.62 18.48 20.28
9.52 11.03 13.36 15.51 18.17 20.09 21.95 … … … … … … …
1.建立检验假设，确立检验水准
H0：两种药有效率相同，即血塞通= 银杏达莫
H1：两种药有效率不同，即血塞通 银杏达莫
=0.05
2.选定检验方法，计算检验统计量
利用样本信息完成两总体率的比较，考虑选择2检验
2=5.004 ~ 2(1)
3.确定P值，作出统计推断
查2界值表，得0.02<P<0.05。按=0.05水准，拒绝H0，接受H1，差 别有统计学意义，可以认为两药治疗急性脑梗死的有效率不同，血塞 通较高。
第十一章 统计分析和调查报告
• 2、定序变量 • 3、定距或定比变量
第十三章 撰写研究报告
• 研究研究报告及其类型 • 研究报告是反映社会调查成果的一种书面 报告，它以文字、图表等形式将调查研究 的过程、方法和结果表现出来。其目的是 告诉有关读者，对于所研究的问题是如何 进行调查的，取得了哪些结果，这些结果 对于认识和解决这一问题有哪些理论意义 和实际意义等等
其它故事与发表情况
• 另外两种形式的故事叫做批判的故事（吸 引读者对社会问题的注意和重视）和形式 的故事（理论的表述）。 • 民族志写作惯例发生了变化。今天，被发 表的现实主义的故事越来越少，而印象主 义或坦白的故事则相对越来越多。 • 没有完美的理论，也没有完美的报告。
• 导言部分 • 普通调查报告的第一部分称作导言，它的主要任务是向读者简要地介绍 整个调查的有关背景。其中，最主要的内容包括调查的目的、调查的内 容、调查的对象、调查的时间、地点、调查的方法等等。导言的具体写 法有下列几种常见的方式。 • (1)直述式 • 即开门见山,平铺直述,直接把调查的目的,内容,对象,范围等一一写出.例 如: • 为了全面了解老年人的生活状况，加强老年人的社会保障工作，沈阳 师范大学社会学系于2003年2月至4月，在辽宁省沈阳市调查了300位老 年人的家庭与生活情况。下面是这次调查的方法及主要结果。 • (2)悬念式。 • 即先描述某种社会现象和社会问题，然后对这种社会现象和问题产生的 原因、它的影响等等提出一系列疑问，最后介绍调查的基本情况.例如: • 老年人丧偶是生活中十分普遍的现象，而老年人再婚，则是近年来出 现在我国社会中的一种新的社会现象。据有关部门统计，本市1980年再 婚老年夫妇为68对，1984年为116对，1988年为302对；1991年为： 495对；1994年为623对。促使老年人再婚比例提高的原因是什么?；社 会舆论对老年人再婚的评价如何?老年人再婚给他们的家庭及其生活带 来了哪些变化?；为了弄清这些问题，沈阳师范大学社会学系于今年3—5月，对沈阳市180对再婚老年夫妇进行了调查。
卡方检验算法范文
卡方检验算法范文卡方检验是一种用于确定两个类别变量之间是否存在显著关联的统计方法。
它基于观察值与期望值之间的差异来判断关联性。
在卡方检验中，我们将观察到的频数与预期的频数进行比较，以确定它们是否有显著的差异。
卡方检验的基本原理是假设零假设，即两个变量之间没有关联。
然后根据观察情况得到的频率表，计算出预期频率表。
最后，使用其中一种统计量来比较观察频率和预期频率。
卡方检验的步骤如下：1.构建频数表：根据研究问题，将两个类别变量的数据构建成一个二维频数表。
其中，行可以表示一个类别变量的不同取值，列可以表示另一个类别变量的不同取值。
然后将观察到的频数填入表格中。
例子：类别变量B类别变量AA1A2A3A4B1n11n12n13n14B2n21n22n23n24B3n31n32n33n342.计算预期频数：根据零假设，我们可以通过行和列的边际频数计算出期望频数。
每个单元的期望频数可以使用以下公式计算：期望频数=(行的边际频数*列的边际频数)/总频数例子：类别变量B类别变量AA1A2A3A4B1e11e12e13e14B2e21e22e23e24B3e31e32e33e34其中，eij表示第i行，第j列的预期频数。
3.计算卡方统计量：通过使用观察频数和预期频数，可以计算出卡方统计量，用于比较差异的程度。
卡方统计量的计算公式如下：χ²=Σ[(观察频数-预期频数)²/预期频数]其中，Σ表示对所有单元进行求和。
4.自由度和临界值：计算自由度和基于显著水平的临界值。
自由度的计算公式为：自由度=(行数-1)*(列数-1)临界值可以从卡方分布表中获取，根据给定的显著水平和自由度。
5.判断显著性：根据卡方统计量和临界值的比较，判断是否存在显著性差异。
如果卡方统计量大于临界值，则拒绝零假设，认为两个变量之间存在显著关联。
卡方检验的应用广泛，特别适用于两个分类变量之间的关联性分析。
它可以用于许多领域的研究和实践，例如医学、社会科学、市场研究等。
医学统计学(6) 卡方检验
•进一步的两两比较
•P<0.017才有 统计学意义！！
【例6】某中医院用三种治疗方法治疗413例糖尿病患者， 资料见表。为避免中医不同证型对疗效比较的影响，分 析3种疗法治疗的病人按3种中医分型的构成比有无差别？
SPSS软件操作
• 第1步：定义变量
• 第2步：输入 原始数据
• 第3步：定义频数 • 选择数据→加权个案 • 频数→加权个案（频 数变量）
CMH多维卡 方检验
• 第4步：x2检验（2） • 选择统计 量按钮 • 在交叉表： 统计量对 话框：勾 上卡方
• 第4步：x2检验（3） • 选择单元 格按钮 • 在交叉表： 单元显示 对话框： 勾上观察 值、百分 比：行、 列
• 第5步：结果解读（1）
• 结果解读：中西医组的治愈率为98.2%，西 医组的治愈率为74.0%。
【例4】某医师为研究乙肝免疫球蛋白预防胎儿宫内感 染HBV的效果，将33例HBsAg阳性孕妇随机分为预防 注射组和非预防组，结果见表。问两组新生儿的HBV总 体感染率有无差别？
• 第1步：定义变量
SPSS软件操作
• 第2步：输入 原始数据
• 第3步：定义频数 • 选择数据→加权个案 • 频数→加权个案（频 数变量）
医学统计学 （6 ）
《中华医学杂志》对来稿统计学处理的有关要求
卡方检验(chi-square test)
• χ2检验是现代统计学的创始人之一，英国人 Karl . Pearson于1900年提出的一种具有广 泛用途的统计方法。 • 可用于两个或多个率间的比较，计数资料 的关联度分析，拟合优度检验等等。
关联性分析
列联系数的意义 • |rp|<0.4，关联程度低 • 0.4≤|rp|<0.7，关联程度中等 • |rp|≥0.7，关联程度高
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
显著差异。下该结论犯错误的概率小于0.05。
【例】 在研究牛的毛色和角的有无两对相对 性状分离现象时 ，用黑色无角牛和红色有角牛杂 交 ，子二代出现黑色无角牛192头，黑色有角牛 78头，红色无角牛72头，红色有角牛18头，共 360头。试 问这两对性状是否符合孟德尔遗传规
律中9∶3∶3∶1的遗传比例？（ 0.05 ）
随机抽取60名学生，询问他们在高中是否需 要文理分科，赞成分科的39人，反对分科的21 人，问他们对分科的意见是否有显著差异？
( 0.05 )
上一张 下一张 主 页 退 出
检验步骤如下： （一）提出无效假设与备择假设 H0：他们对分科的意见无显著差异 H1：他们对分科的意见有显著差异 （二）确定自由度和统计公式 本例是二项分类，属性类别分类数k=2， 自由度df=k-1=2-1=1。
** fo-fe之差有正有负，但平方后将差异归于一个
方向，因此虽然2分布做双侧检验，但只有一
个临界值。
配合度检验
一、配合度检验的一般问题
1、配合度检验的意义
判断单一变量的实际观察的属性类别次数
分配是否符合已知属性类别次数分配理论或
学说的假设检验。
上一张 下一张 主 页 退 出
2、配合度检验的方法 下面结合实例说明配合度检验方法。
2分布的性质和特点
1. 分布的变量值始终为正
2. 分布的形状取决于其自由度n的大小，通常为不对称的 正偏分布，但随着自由度的增大逐渐趋于对称
3. 当 自 由 度 大 于 2 时 ， 期 望 为 ： E(2)=df， 方 差 为 ： D(2)=2df
4. 可 加 性 ： 若 U 和 V 为 两 个 独 立 的 2 分 布 随 机 变 量 ，
上一张 下一张 主 页 退 出
假设检验与2检验的区别
假设检验
数据为连续分布
2检验
数据为点计来的间断变量
数据来自的总体为正态分布 总体分布未知
对总体参数或几个参数之差 对总体分布的假设检验属
所进行的检验
df分布的非参数检验
3、 2 统计量（近似公式）
2 ( fo fe )2
fe
本质：表示实得次数与理论次数之间的差,则U+V这一不随同容机量变样本量的服抽从样分自布由度为
n1+n2的2分布
n=1
n=4
n=10
f (t)
n=20
O
2 (n)
t
2
2、检验方法：
（1） 2检验方法是处理一个因素或多项
分类的实际观察频数与理论频数分布是否 一致问题，或说有无差异问题。
（2）用来检验数据的总体分布和计数数 据的显著性检验。
（2）求理论次数（根据正态分布曲线面积）
fo 2
8
18
25
7
fe 2
14
28
14
2
（3）计算统计量 2 ( fo fe )2 fe
(2 2)2 (8 14)2 (7 2)2
2
14
2
27.29
（4）当自由度 df=K-1=5-1=4 时，
查 得 20.05（4） =9.49，则20.05（4） <2，
拒绝原假设。表明该该分布不服从正态分布。 下该结论犯错误的概率小于0.05。
列联表的独立性检验
一、独立性检验的意义 1、目的：研究两类变量之间的关联性和依存性问题。
**如果两个自变量是独立的无关联（ 2值不显著），
就意味着对一个变量来说，另一个自变量的多项 分类次数上的变化是在取样误差的范围之内，反 之，二变量之间存在关联或有交互作用。
上一张 下一张 主 页 退 出
检验步骤： （一）提出无效假设与备择假设 论H比0例：。实际观察次数之比符合9∶3∶3∶1的理 理H论1比：例实。际观察次数之比不符合9∶3∶3∶1的 （二）确定统计量 由于本例的属性类别分类数 k=4：自由 度
df=k-1=4-1=3，利用定义公式计算2。
（三）计算理论次数 依据各理论比例9:3:3:1计算理论次数：
从。
2
12
2 2
2 n
连续变量分布的吻合性检验
非连续变量分布形态的假设检验
【例】教师给学生的考试分数结果按五等 级评分，人数统计结果如下表，请检验
该分布是否服从正态分布。（ 0.05）
等级 不及格 及格 中等 良好 优秀 合计
人数 2
8
18 25 7 60
解（1）Ho：服从正态分布 H1：不服从正态分布
黑色无角牛的理论次数f1：360×9/16=202.5； 黑色有角牛的理论次数f2：360×3/16=67.5； 红色无角牛的理论次数f3：360×3/16=67.5； 红色有角牛的理论次数f4：360×1/16=22.5。
或 f4=360-202.5-67.5-67.5=22.5
上一张 下一张 主 页 退 出
上一张 下一张 主 页 退 出
总体分布的假设检验
目的：考察某个观测到的分布是否与理 论分布有差异。
分为： 连续变量的吻合性检验 非连续变量分布形态的假设检验
思想方法：
总体中抽出样本，
将样本的分布与所预
测的分布做比较，出
现的误差（即阴影）
之和的比例若进入危
机域，则总体不服从
预测分布，反之则服
2 检 验
2检验的原理
配合度检验 独立性检验
2检验的原理
一、 2统计量的意义
1、 2分布
设 x1 , x2 , , xn 是来自标准正态总体N (0 , 1) 的一 个样本，且相互独立，统计量
2 x12 x22 xn2 的分布服从自由度为n 的 2分布, 记为 2 ~ 2 (n) .
上一张 下一张 主 页 退 出
（三）计算理论次数 理论次数：fe1=fe2=60×1/2=30 （四）计算
2 ( fo fe )2 (39 30) 2 (21 30) 2 5.4
fe
30
30
(五)查临界2值，作出统计推断 当自由度 df=1 时， 查 得 20.05（1） =3.84， 计算的20.05（1） <2，表明学生对分科的意见有
（四）列表计算2
2 ( fo fe )2 =3.378 fe （五）查临界2值，作出统计推断
当df=3时，20.05(3)=7.81，因 2<2005(3) ，P>0.05，不能否定
H0 ，表明实际观察次数与理论次数差异不显著， 可以认为毛 色与角的有无两对性状杂 交 二 代 的 分 离 现 象 符 合 孟 德 尔 遗传规律中9∶3∶3∶1的遗传比例。
【例】 在研究牛的毛色和角的有无两对相对 性状分离现象时 ，用黑色无角牛和红色有角牛杂 交 ，子二代出现黑色无角牛192头，黑色有角牛 78头，红色无角牛72头，红色有角牛18头，共 360头。试 问这两对性状是否符合孟德尔遗传规
律中9∶3∶3∶1的遗传比例？（ 0.05 ）
随机抽取60名学生，询问他们在高中是否需 要文理分科，赞成分科的39人，反对分科的21 人，问他们对分科的意见是否有显著差异？
( 0.05 )
上一张 下一张 主 页 退 出
检验步骤如下： （一）提出无效假设与备择假设 H0：他们对分科的意见无显著差异 H1：他们对分科的意见有显著差异 （二）确定自由度和统计公式 本例是二项分类，属性类别分类数k=2， 自由度df=k-1=2-1=1。
** fo-fe之差有正有负，但平方后将差异归于一个
方向，因此虽然2分布做双侧检验，但只有一
个临界值。
配合度检验
一、配合度检验的一般问题
1、配合度检验的意义
判断单一变量的实际观察的属性类别次数
分配是否符合已知属性类别次数分配理论或
学说的假设检验。
上一张 下一张 主 页 退 出
2、配合度检验的方法 下面结合实例说明配合度检验方法。
2分布的性质和特点
1. 分布的变量值始终为正
2. 分布的形状取决于其自由度n的大小，通常为不对称的 正偏分布，但随着自由度的增大逐渐趋于对称
3. 当 自 由 度 大 于 2 时 ， 期 望 为 ： E(2)=df， 方 差 为 ： D(2)=2df
4. 可 加 性 ： 若 U 和 V 为 两 个 独 立 的 2 分 布 随 机 变 量 ，
上一张 下一张 主 页 退 出
假设检验与2检验的区别
假设检验
数据为连续分布
2检验
数据为点计来的间断变量
数据来自的总体为正态分布 总体分布未知
对总体参数或几个参数之差 对总体分布的假设检验属
所进行的检验
df分布的非参数检验
3、 2 统计量（近似公式）
2 ( fo fe )2
fe
本质：表示实得次数与理论次数之间的差,则U+V这一不随同容机量变样本量的服抽从样分自布由度为
n1+n2的2分布
n=1
n=4
n=10
f (t)
n=20
O
2 (n)
t
2
2、检验方法：
（1） 2检验方法是处理一个因素或多项
分类的实际观察频数与理论频数分布是否 一致问题，或说有无差异问题。
（2）用来检验数据的总体分布和计数数 据的显著性检验。
（2）求理论次数（根据正态分布曲线面积）
fo 2
8
18
25
7
fe 2
14
28
14
2
（3）计算统计量 2 ( fo fe )2 fe
(2 2)2 (8 14)2 (7 2)2
2
14
2
27.29
（4）当自由度 df=K-1=5-1=4 时，
查 得 20.05（4） =9.49，则20.05（4） <2，
拒绝原假设。表明该该分布不服从正态分布。 下该结论犯错误的概率小于0.05。
列联表的独立性检验
一、独立性检验的意义 1、目的：研究两类变量之间的关联性和依存性问题。
**如果两个自变量是独立的无关联（ 2值不显著），
就意味着对一个变量来说，另一个自变量的多项 分类次数上的变化是在取样误差的范围之内，反 之，二变量之间存在关联或有交互作用。
上一张 下一张 主 页 退 出
检验步骤： （一）提出无效假设与备择假设 论H比0例：。实际观察次数之比符合9∶3∶3∶1的理 理H论1比：例实。际观察次数之比不符合9∶3∶3∶1的 （二）确定统计量 由于本例的属性类别分类数 k=4：自由 度
df=k-1=4-1=3，利用定义公式计算2。
（三）计算理论次数 依据各理论比例9:3:3:1计算理论次数：
从。
2
12
2 2
2 n
连续变量分布的吻合性检验
非连续变量分布形态的假设检验
【例】教师给学生的考试分数结果按五等 级评分，人数统计结果如下表，请检验
该分布是否服从正态分布。（ 0.05）
等级 不及格 及格 中等 良好 优秀 合计
人数 2
8
18 25 7 60
解（1）Ho：服从正态分布 H1：不服从正态分布
黑色无角牛的理论次数f1：360×9/16=202.5； 黑色有角牛的理论次数f2：360×3/16=67.5； 红色无角牛的理论次数f3：360×3/16=67.5； 红色有角牛的理论次数f4：360×1/16=22.5。
或 f4=360-202.5-67.5-67.5=22.5
上一张 下一张 主 页 退 出
上一张 下一张 主 页 退 出
总体分布的假设检验
目的：考察某个观测到的分布是否与理 论分布有差异。
分为： 连续变量的吻合性检验 非连续变量分布形态的假设检验
思想方法：
总体中抽出样本，
将样本的分布与所预
测的分布做比较，出
现的误差（即阴影）
之和的比例若进入危
机域，则总体不服从
预测分布，反之则服
2 检 验
2检验的原理
配合度检验 独立性检验
2检验的原理
一、 2统计量的意义
1、 2分布
设 x1 , x2 , , xn 是来自标准正态总体N (0 , 1) 的一 个样本，且相互独立，统计量
2 x12 x22 xn2 的分布服从自由度为n 的 2分布, 记为 2 ~ 2 (n) .
上一张 下一张 主 页 退 出
（三）计算理论次数 理论次数：fe1=fe2=60×1/2=30 （四）计算
2 ( fo fe )2 (39 30) 2 (21 30) 2 5.4
fe
30
30
(五)查临界2值，作出统计推断 当自由度 df=1 时， 查 得 20.05（1） =3.84， 计算的20.05（1） <2，表明学生对分科的意见有
（四）列表计算2
2 ( fo fe )2 =3.378 fe （五）查临界2值，作出统计推断
当df=3时，20.05(3)=7.81，因 2<2005(3) ，P>0.05，不能否定
H0 ，表明实际观察次数与理论次数差异不显著， 可以认为毛 色与角的有无两对性状杂 交 二 代 的 分 离 现 象 符 合 孟 德 尔 遗传规律中9∶3∶3∶1的遗传比例。