2008年西北工业大学2029数值分析考博试题

2008年西北工业大学3097材料物理与化学专业综合二考博考研真题(回忆版)-考研真题资料

2008年西北工业大学3097材料物理与化学专业综合二考博试题（回忆版）
说明∶所有试题一律写在答题纸上
一、对于二维点阵，有①种布拉菲点阵、②种二维品系、③种二维点群、④种二维空间群。

（本题16分）
二、薄膜品体中有哪儿类缺陷?并举例说明。

（本题20分）
三、简述至少三种薄膜的表征方法.（本题20分）
四、比较现有几类透明导电薄膜的优缺点。

（本题16分）
五、计算题
1.在薄膜沉积过程中，取垂直基底表面且指向基底内部为坐标轴X的正方向，且坐标原点位于基底表面处。

若基底表面某种化学元素的浓度C，保持不变，并向无该成分的、无限厚的基底中扩散，即C=0（当t=0，0<X<∞）。

求扩散t时间后，基底内部任意位置x处扩散元素的浓度C（x，t）;
恒定，且初始时刻基底内部各处的扩散浓度相等且不为零，即2若表面浓度C
s
C=C
（当t=00<x<∞），则此种情况下的C（x，t）又将如何?（本题28分）s。

[考研类试卷]2008年工程硕士研究生学位课程(数值分析)真题试卷B.doc

[考研类试卷]2008年工程硕士研究生学位课程（数值分析）真题试卷B一、填空题请完成下列各题，在各题的空处填入恰当的答案。

1 为了使计算y=11+的乘除法运算次数尽量地少，应将该表达式改为_____．2 求方程x-f(x)=0根的牛顿迭代格式是_____3 设A=则‖A‖∞=_______4 解方程组的Jacobi迭代格式为______5 设f(x)=8x4+3x3-98x+1,则差商f[2，4，8，16，32]=______6 记h=(b-a)／n，x i=a+ih，0≤i≤n，则计算I(f)=的复化Simpson公式为______，代数精度为______7 用简单迭代法求非线性方程x-lnx=2在(2，+∞)内的根，要求精确至6位有效数字，并说明所用迭代格式为什么是收敛的．8 给定线性方程组 1)写出Gauss-Seidel迭代格式； 2)分析此迭代格式的收敛性．9 1)给定如下数据表：求f(x)的2次插值多项式L(x)；2)利用如下数据表：求f(x)的3次插值多项式H(x)．10 求a，b，使得达到最小，并求出此最小值．11 求系数A1，A2，A3，使得求积公式≈A1f(-1)+A2f(-1/3)+A3f(2/3)的代数精度尽可能高，并指出所达到的代数精度的次数．12 给定常微分方程初值问题取正整数n，并记h=(b-a)／n，x i=a十ih，0≤i≤n．1)分析如下求解公式的局部截断误差y i+1=y i+[f(x i+1,y i+1)+f(x i,y i)](A)2)分析如下求解公式的局部截断误差y i+1=y i+[3f(x i，y i)-f(x i-1，y i-1)]；(B)3)指出以上两个求解公式各是儿阶公式，并从局部截断误差的大小、显隐格式及单多步公式几方面作一个简单的比较．。

西北工业大学高等数学08-09(下)期中试题(new)

）
（A）（0，0）点不是 f ( x, y) 的极值点；
教务处印制共 6页第 2页
西北工业大学命题专用纸
（B）（0，0）点是 f ( x, y) 的极大值点；（C）（0，0）点是 f ( x, y) 的极小值点；（D）所给条件无法判断（0，0）点是否为 f ( x, y) 的极值点. 5. 如图，正方形 ( x, y ) | x | 1,| y | 1 被其对角线划分为四个区域 Dk (k 1, 2,3, 4) ， I k y cos xdxdy ，则 max I k (
6. 设 {2, 3,1} ， {1, 2,3} ， {2,1, 2} ，向量 x 满足 x , x ， prj x 14 ，则 x ___________________; 7. 设 f ( x) 为连续函数， F (t ) dy f ( x)dx ，则 F (2) __________;
上求一点，使得函数 f ( x, y, z) x 2 y 2 z 2 沿着点 A(1,1,1)到点 B(2,0,1)的方向导数具有最大值。
教务处印制
共 6页
第 6页
一、填空题(每小题 4 分, 共 40 分) 答案写在答题纸上, 写在题后无效. 1. lim (1 xy)
x 0 y 0 1 x y
_______ ；
y z 2. 设 z xf ( ,xy )，其中 f 具有连续导数，则 ______________ ； x x
3. 设函数 z z ( x, y ) 有方程 e xz ln _______________；
）
x 5 xy , ( x 4 y 4 0) 4 4 2. 设 f ( x, y ) x y ，则（ 0 , ( x 4 y 4 0)

西北工业大学自动控制原理2008考研试题

西北工业大学 2008 年硕士研究生入学考试试题
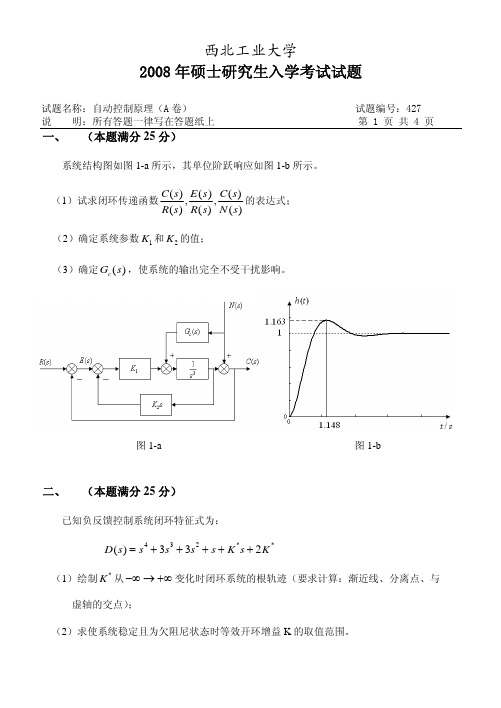
试题名称：自动控制原理（A 卷）说明：所有答题一律写在答题纸上试题编号：427 第 1 页共 4 页
一、
（本题满分 25 分）
系统结构图如图 1-a 所示，其单位阶跃响应如图 1-b 所示。（1）试求闭环传递函数
C ( s) E (s) C (s) , , 的表达式； R( s ) R( s ) N ( s )
% 0.16 0.4( M r 1) 100%
ts
2 1.5( M r 1) 2.5( M r 1) 2 c
1 sin
Mr
五、
（本题满分 25 分）
某离散系统结构图如图 3 所示，采样周期 T 0.2 秒，系统中的参数 K 5, 0.2 ，控制器 Gc ( z ) 的差分方程为 e2 ( k ) e2 ( k 1) e1 ( k ) （1）判断系统的稳定性；（2）求系统在 r (t ) t 作用下的稳态误差 ess 。
*
虚轴的交点）；（2）求使系统稳定且为欠阻尼状态时等效开环增益 K 的取值范围。
西北工业大学 2008 年硕士研究生入学考试试题
试题名称：自动控制原理（A 卷）说明：所有答题一律写在答题纸上试题编号：427 第 2 页共 4 页
三、
（本题满分 25 分）
某单位负反馈的最小相角系统，其开环对数幅频特性如图 2 所示。（1）写出系统的开环传递函数 G ( s ) 表达式；（2）求系统的截止频率 c 和相角裕度；（3）若在系统前向通道中串联一个纯延时环节 G ( s ) e 范围（ 0 ）。
图3
西北工业大学 2008 年硕士研究生入学考试试题

西北工业大学0708（一）理论力学试题a答案

西北工业大学考试试题（卷）2007－2008学年第1 学期开课学院六院课程理论力学（上）学时40R2. 命题教师和审题教师姓名应在试卷存档时填写。

共5页第1页a CP N BN AyN AxP西北工业大学命题专用纸西北工业大学命题专用纸x’y’图中v E 为滑块E 的绝对速度，v ED 为E 相对于D 的相对速度，由速度合成定理 v E ＝v D ＋v ED 得，23243cos /vv v v D E =⨯==β，4212sin v v v v E ED =⨯=⋅=β可以得到D 点的法向加速度a Dn 和切向加速度a Dt 的方向和大小以及E 相对于D 的法向相对加速度a EDn 的方向和大小，各加速度的方向见图所示。

b v b b v b OD a OCOCDn 16333169sin 222222=⨯=⋅=⋅=γωω bv b b v b OD a OC OC D 833833sin 2222=⨯=⋅=⋅=γαατbv b v b vDE va EDEDEDn 16116sin 2//2222=⨯===β 假设E 相对于D 的法向相对加速度a EDt 的方向以及E 的绝对加速度a E 方向如图所示。

由加速速度合成定理 a E ＝a Dn ＋a Dt ＋a EDn ＋a EDt由于E 水平运动，所以在垂直方向上的加速度分量等于零ββττcos )(sin )(⋅-=⋅+ED D n D ED n a a a a解得 bv a E D t 2432=所以， bv a a a a a ED DnD EDnE 2437sin )(cos )(2=⋅-+⋅+=ββττ。

西工大自主招生试题

2008西北工大自主招生高考测试数学试题（考试时间：120分钟，满分150分）第Ⅰ卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）：1．（理）若复数z 满足(34)25i i Z -=，则z 对应的点位于 ( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限（文）若:2,:(0p x q x ≥-≥，则p 是q 的（）A 、充分而不必要条件B 、必要而不充分条件C 、充要条件D 、既不充分也不必要条件 2．设集合{}2M |0x x x =->，}{N=|||2x x <，则A. R (C M )N =φB. R R (C M )N =C MC. R (C M )N =MD. R (C M )N =R 3．将4名实习老师分配到高一年级的3个班级实习，每班至少1名，则不同的分配方案有（）A ．6种B ．12种C ．24种D ．36种4．定义在R 上的函数f(x)满足f(x+2)=f(x)，当x ∈［1，3］,f(x)=2－|x －2|, 则下列结论中正确的是( ) A ．(sin )(cos)66f f ππ< B ．f(sin1)>f(cos1)C ．22(cos)(sin)33f f ππ< D ．f(cos2)>f(sin2)5．已知函数f(x)=2x -1x -1，若函数y=g(x)的图象与函数-1y f (x)+1=的图象关于直线y=x 对称，则g(3)的值为( )Ａ. 2 Ｂ. 3 Ｃ. 4 Ｄ. 76．Ｍ为△ABC 内一点，且1145A M AB AC =+ ，则△ABM 与△ABC 的面积之比为( ) Ａ.15Ｂ. 23 Ｃ. 25 Ｄ. 147．平面内有一长度为6的线段AB ，动点P 满足|PA|+|PB|=10，则|PA|的取值范围为( ) Ａ.［1，3］Ｂ.［2，8］Ｃ.［6，8］Ｄ.［3，5］ 8．在等差数列{a n }中，前n 项和n n S m=，前m 项和()m m S m n n=≠，则n m S +的值（） A ．大于4 B ．等于4 C ．小于4 D ．大于2小于4 9．在正三棱柱111ABC--A B C 中，若1BB =AB 2，则1C B 与1AB 所成角的大小为（）Ａ.15 Ｂ.75 Ｃ.90 Ｄ.60 10．（理）定义在R 上的连续函数f(x)，若x ≠0时，f(x)=1+x -131+x -1，则f(0)=( )Ａ.2 Ｂ.23 Ｃ.1 Ｄ.32（文）已知函数()3(24,x bf x x b -=≤≤是常数）过点(2,1)，则1212()[()]()F x fx fx --=-的值域为（） A.[2,5] B.[1,)+∞ C.[2,10] D.[2,3]11. 如果直线y=kx+1与圆22x +y +kx+m y-4=0 交于M 、N 两点，且M 、N 关于直线x-y=0对称，动点Ｐ（ａ，ｂ）在不等式组kx-y+20kx-m y 0y 0≥⎧⎪≤⎨⎪≥⎩表示的平面区域内部及边界上运动，则点Ａ（１，２）与点Ｐ连线的斜率取值范围是（） A ．[2,)+∞ Ｂ．(,2]-∞- Ｃ．[2,2]- Ｄ．(,2][2,)-∞-+∞12．（理）长为5,宽为4,高为3的长方体密闭容器内有一半径为1的小球，小球可在容器里任意运动，则容器内小球不能到达的空间的体积为( ) Ａ.22323π-B. 6πC.223π D.60π-（文）半径为r 的一个圆在一个长为7，宽为5的长方形（25r<）内任意滚动，则该圆滚不到的平面区域的面积为（）A.2(4)r π-B. 2(5)r π-C. 2(7)r π-D. 235r π-第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每小题4分，共16分）：13．已知()6211⎪⎭⎫ ⎝⎛++a ax x 的展开式中含4x 项的系数为30，则正实数a 的值为．14．等腰直角三角形的直角顶点A (1,0)，重心(2,0)G ，则三角形另两个顶点B 、C 的坐标为． 15．若20a a b >>>, log bb m a=、log aa n b=、log b p a =、log a q b =则把m 、n 、p 、q 从小到大的排列顺序是．16．已知函数f (x )满足：()()()f p q =f p f q +, (1)3,f =则：)7()8()4()5()6()3()3()4()2()1()2()1(2222f f f f f f f f f f f f +++++++= ．三、解答题（本大题共6小题，共74分。

西工大计算方法试题参考(完整版)

2002-2003第一学期一．计算及推导（5*8）1．已知* 3.141,x x π==，试确定*x 近似x 的有效数字位数。

2．有效数***1233.105,0.001,0.100x x x =-==，试确定***123x x x ++的相对误差限。

3．已知3()0.50.12f x x x =++，试计算差商[]0,1,2,3f 4．给出拟合三点(0,1),(1,0)A B ==和(1,1)C =的直线方程。

5．推导中矩形求积公式''31()()()()()224b aa b f x dx b a f f b a η+=-+-⎰ 6．试证明插值型求积公式()()nbi i ai f x dx A f x =≈∑⎰的代数精确度至少是n 次。

7．已知非线性方程()x f x =在区间[],a b内有一实根，试写出该实根的牛顿迭代公式。

8．用三角分解法求解线性方程组123121022331302x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦要用二次插值多项式计算(0.63891)f 的近似值，试选择合适的插值节点进行计算，并说明所选用节点依据。

（保留5位有效数字）（12分）三．已知方程ln 0x x +=在(0,1)内有一实根α（1）给出求该实根的一个迭代公式，试之对任意的初始近似0(0,1)x ∈迭代法都收敛，并证明其收敛性。

（2）00.5x =试用构造的迭代公式计算α的近似值n x ，要求3110n n x x ---≤。

四．设有方程组112233131232a x b a x b a x b ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦当参数a 满足什么条件时，雅可比方法对任意的初始向量都收敛。

写出与雅可比方法对应的高斯赛德尔迭代公式。

（12分）五．用欧拉预估校正法求解初值问题 '2 (00.2)(0)1x y y x y y ⎧=-≤≤⎪⎨⎪=⎩ 取h=0.1，小数点后保留5位。