三年级数学横式数字谜
三年级奥数横式数字谜
三年级奥数横式数字谜解这类问题时：第一步，要仔细审题；第二步，必须挑选突破口；第三步，实验求解。
灵活运用运算法则和整数的性质，仔细观察算式的特点，学会辨认出问题、分析问题。
研究和化解这类问题，有助于培育我们观测、分析、概括、推理小说等能力。
47；(4)36-150÷=96÷16。
练1代表什么数：(1)⨯9+6⨯=600÷2；(2)25⨯25-÷3=610。
基准2=6=，那么=。
例3在下列方框中填上适当的数，使等式成立：；(2)148÷=84。
练习3在下列方框中填上适当的数，使等式成立：(1)213÷=165；(2)÷9=305。
例4在下列等号左边的每两个数之间，添上加号或减号，也可以用括号，使算式成立。
12345=1练4在下面的式子里加之括号，并使等式设立。
(1)7⨯9+12÷3-2=23；(2)7⨯9+12÷3-2=75。
基准5迎上适度的加号或负号、乘号或除号，也可以用括号，并使下面的等式设立。
55555=10练5迎上适度的运算符号：加号或负号、乘号或除号，并使以下等式设立。
1234=1a+a+a+a则a+b=。
4、325⨯÷19=650=；2100÷(÷3)=70=。
5、把1～9分别插入下面九个圆圈中，并使等式设立。
===6=15应该是___________。
9、在等号左边适度的地方迎上括号，并使算式设立。
里，使等式成立，每个数字只能用一次。
10；(6)2⨯()=10。
11、把加号、减号、乘号、除号，分别填入下面等式中的圆圈内，使等式成立。
((9)=1212、把1，2，3，4，5，6使结果尽可能大，并求出结果。
×)=13、将1，2，3，4，5，6，7，8，9==14分别代表相同的三个数，并且1代表什么数：(1)⨯17+43=400；(2)(601+)⨯9=7209。
横(竖)式数字谜(一)
横（竖）式数字谜(一)在一个数学式子(横式或竖式)中擦去部分数字，或用字母、文字来代替部分数字的不完整的算式或竖式，叫做数字谜题目。
解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。
例如，求算式324+□=528中□所代表的数。
根据“加数=和-另一个加数”知，□=582-324＝258。
又如，求右竖式中字母A，B所代表的数字。
显然个位数相减时必须借位，所以，由12-B＝5知，B＝12-5＝7；由A-1＝3知，A＝3＋1＝4。
解数字谜问题既能增强数字运用能力，又能加深对运算的理解，还是培养和提高分析问题能力的有效方法。
这一讲介绍简单的算式(横式)数字谜的解法。
解横式数字谜，首先要熟知下面的运算规则：(1)一个加数+另一个加数=和；(2)被减数-减数=差；(3)被乘数×乘数=积；(4)被除数÷除数=商。
由它们推演还可以得到以下运算规则：由(1)，得和 - 一个加数=另一个加数；其次，要熟悉数字运算和拆分。
例如，8可用加法拆分为8＝0＋8＝1＋7＝2＋6＝3＋5＝4＋4；24可用乘法拆分为24＝1×24=2×12＝3×8＝4×6(两个数之积)=1×2×12＝2×2×6=…(三个数之积)=1×2×2×6＝2×2×2×3=…(四个数之积)例1下列算式中，□，○，△，☆，*各代表什么数？(1)□+5＝13-6；(2)28-○＝15＋7；(3)3×△=54；(4)☆÷3＝87；(5)56÷*＝7。
解：(1)由加法运算规则知，□=13-6-5＝2；(2)由减法运算规则知，○＝28-(15＋7)＝6；(3)由乘法运算规则知，△＝54÷3＝18；(4)由除法运算规则知，☆=87×3＝261；(5)由除法运算规则知，*＝56÷7＝8。
横式数字谜(三年级)
横式数字谜解横式数字谜，首先要熟知下面的运算规则：(1)一个加数+另一个加数=和；(2)被减数-减数=差；(3)被乘数×乘数=积；(4)被除数÷除数=商。
其次，要熟悉数字运算和拆分。
例如，8可用加法拆分为8＝0＋8＝1＋7＝2＋6＝3＋5＝4＋4；24可用乘法拆分为24＝1×24=2×12＝3×8＝4×6(两个数之积)24＝1×2×12＝2×2×6=…(三个数之积)24＝1×2×2×6＝2×2×2×3=…(四个数之积)例1下列算式中，□，○，△，☆，*各代表什么数？(1)□+5＝13-6 (2)28-○＝15＋7 (3)3×△=54(4)☆÷3＝87 (5)56÷*＝7例2 下列算式中，□，○，△，☆各代表什么数？(1)□+□+□=48；(2)○＋○＋6＝21-○；(3)5×△-18÷6＝12；(4)6×3-45÷☆＝13。
例3 (1)180是由哪四个不同的且大于1的数字相乘得到的？试把这四个数按从小到大的次序填在下式的□里:180=□×□×□×□。
(2)若数□，△满足□×△=48和□÷△=3，则□，△各等于多少？例4在等号左端的两个数中间添加上运算符号，使下列各式成立：(1)4 4 4 4＝24；(2)5 5 5 5 5=6。
分析：(1)因为4＋4＋4＋4＜24，所以必须填一个“×”。
4×4＝16，剩下的两个4只需凑成8，(2)因为5+1=6，等号左端有五个5，除一个5外，另外四个5凑成1，至少要有一个“÷”。
注：填运算符号的问题一般会有多个解。
这些填法都是通过对问题的综合观察、分析和试算得到的，如果只是盲目地“试算”，那么就可能走很多弯路。
小学三年级奥数--22横式数字谜
小学三年级奥数22横式数字谜本教程共30讲第22讲横式数字谜(二)第2讲我们初步介绍了简单的横式填数问题。
这一讲再继续介绍一些此类问题。
例1在下列各式的□里填上合适的数字：(1)237÷□□=□；(2)368÷□□=□□；(3)14×□□=3□8。
解：(1)将除法变为乘法，可以转化为“在237=□□×□中填入合适的数字”的问题。
因为 237＝237×1＝79×3，所以只有一种填法：(2)问题可以转化为“在368＝□□×□□中填入合适的数字”的问题。
因为368＝368×1＝184×2＝92×4＝46×8＝23×16，其中只有368＝23×16是两个两位数之积。
因而有如下两种填法：(3)由被乘数的个位数是4，积的个位数是8知，乘数的个位数只可能为2或7，再由被乘数的十位数是1，积的百位数是3知，乘数的十位数不能填大于3的数字。
所以乘数只可能是12，17，22，27，32或37。
经试算，符合题意的填法有两种：例2在下列各式的□里填上合适的数：(1)□÷32＝7……29；(2)480÷156＝□……12；(3)5367÷□＝83……55。
分析：根据有余数的除法(简称带余除法)知：被除数=不完全商×除数＋余数，被除数-余数=不完全商×除数。
上式说明，(被除数-余数)是不完全商或除数的倍数，并且有(被除数-余数)÷除数=不完全商，(被除数-余数)÷不完全商=除数。
由此分析，可以得到如下解法。
解：(1)由7×32＋29＝253，得到如下填法：(2)由(480-12)÷156＝3，得到如下填法：(3)由(5367-55)÷83＝64，得到如下填法：例3在下列各式的□里填入合适的数字，使等式成立：(1)□5□×23＝5□□2；(2)9□□4÷48=□0□。
word完整版本小学三年级数字数谜
数灯谜一、加减竖式谜例1在下边算式的空格中,各填入一个适合的数字,使算式建立.(1) □4□(2) □□ 4＋□8＋1□□□15□□□ 3(3)□0□6(4)1□5□－7□4□－□□9□67867例2下边每个汉字代表一个数字,同样的汉字代表同样的数字,不一样的汉字代表不一样的数字,这些汉字各代表哪些数字?(1)成都(2)助成都市助人＋爱成都市助人为1999＋乐于助人1993例3同样的汉字代表同样的数字，不一样的汉字代表不一样的数字，这些汉字各代表哪些数字?节童儿际国一六祝庆＋8 6 4 1 9 7 5 3 2庆贺六一国际小孩节二、乘法竖式谜例4 在下边算式的空格中,各填入一个适合的数字 ,使算式建立（1）□□8（2）□□9×□×□7921□52（３）437□(４)□□4×□×□□□□0052□2例5同样的汉字代表同样的数字，不一样的汉字代表不一样的数字，这些汉字各代表哪些数字? 数学俱乐部×３数学俱乐部１三、练习题1、在下边的空格中,各填入一个适合的数字,使式子建立.(1)□8□(2)□1＋□6□3＋□9□□□128□□9□(3)□□4（4）□001－□□－20□79□9□(5)□□８(6)□□9×□×□３１□２18322、下边的式子中同样的字母代表同样的数字 ,不一样的字母代表不一样的数字,式中的字母ABCD各代表哪些数字?A B C D×9D C B A3、在下边的式子里,6个小纸片各遮住了一个数字,问:被遮住的6个数字总和是多少?□□□＋□□□1 9 9 1。
三年级奥数_第11讲横式数字谜
名师堂学校讲义第^一讲年级：三姓名____________ 0横式数字谜一、教学目标：1、弄清横式数字谜式题的特点和常用的解答方法。
2、能熟练地运用四则运算中各部份之间的关系。
3、能灵活快速的解答这类式题。
二、重点：理解和掌握用四则运算中各部份关系解答这类题三、关键：解横式数字谜，首先要熟知下面的运算规则：(1) 一个加数+另一个加数二和；⑵被减数-减数二差；(3)被乘数x乘数二积；⑷被除数十除数二商。
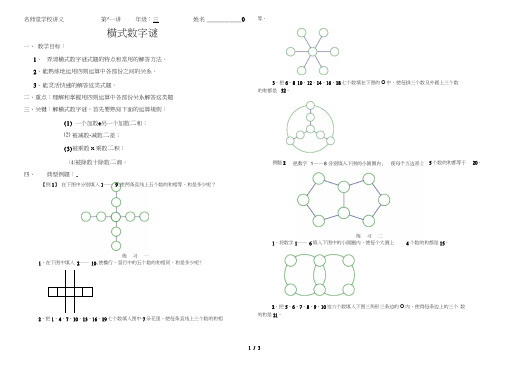
四、典型例题：.【例1】在下图中分别填入1―― 9,使两条直线上五个数的和相等，和是多少呢？等。
3，把6、8 10、12、14、16、18七个数填在下图的O中，使每排三个数及外圆上三个数的和都是32。
例题25个数的和都等于1，将数字1―― 6填入下图中的小圆圈内，使每个大圆上4个数的和都是15。
20。
1，在下图中填入2―― 10,使横行、竖行中的五个数的和相同。
和是多少呢?2，把1、4、7、10、13、16、19七个数填入图中7朵花里，使每条直线上三个数的和相2，把5、6、7、8、9、10这六个数填入下图三角形三条边的O内，使得每条边上的三个数的和是21。
1 / 3例题3在图中填入2―― 9,使每边3个数的和等于15。
练习三1，把1――8填入下图中，使每边3个数的和等于13。
3，把1―― 10这十个数填入下图中，使每个正方形顶点圆圈内四个数之和都相等，而且最大。
这个和是多少？例题4把1――8填入下图O内，使每边上三个数的和最大。
求最大的和是多少?3，把1――8这八个数，分别填入下图的各个□内，使得每一横行、每一竖行的三个数的和是13。
2，将1点的数字为1。
9这九个数填入下图中，使三角形每条边上四个数的和等于19,且有一个顶2 / 33 / 3习四把3―― 10填入下图O 中，使每边上三个数的和最大，求最大的和是多少?在图中各圆的空余部分分别填上1、 习五2、4、6，使每个圆中4个数的和是15。
把1――8填入下图O 中，使每边上三个数的和最小。
三年级 第四讲 横式数字谜
在下列（）中填上合适的数， 使等式成立
（1）156÷（ ）=8……4
除数=（被除数-余数）÷商
（3）（ ）÷9=30……5
被除数=除数×商+余数
下面算式中（）代表什么数 （1）29÷（ ）=（ ）……7
（2）215÷4=（ ）……3
（3）（
）÷8=40……7 )=5……6
（4）41÷(
由积的最高位是5可知因数的最高 位是2 可得：23×254=5842
在□内填上适当的数，使等式 成立
（1）4□×□3=1□□1 解：47×23 =1081
47×33 =1551
在□内填上适当的数，使等式 成立
（2）9□□4÷48=□0□ 解：9744÷48=203 9984÷48=208
在□里填上适当的数，使不等 式成立
在□里填上适当的数，使等式 成立
（1）326÷□=□□□…… □ 解：326÷3=108……2
（2）□×482= □□□
解：1×482=482 2×482=964
将1、2、3、4、5、6这六个数 字填入□，使等式成立，每个 数字只许用一次。
□ + □ =□ □×□=□ 解： 这几个数字里，能组成乘法 算式的是：2×3=6
在□内填上适当的数，使等式 成立
（1）4□×26=1□□8
解： 由积的个位是8可得：第一 个因数为43或48 43×26 =1118
48×26 =1248
所以，这两种情况都可以。
在□内填上适当的数，使等式 成立
（2）5□□2÷Βιβλιοθήκη 3=□5□解： 把题目可变为乘法算式：
23×□5□ = 5□□2
由积的个位2可知，因数的个位是4
剩下的1、4、5刚好可以组成 1+4=5 所以，等式为1+4=5 2×3=6
小学数学《横式数字谜》ppt
荷风送香气 竹露滴清响
例2在下列各式的□里填上合 适的数字:
77÷□=8……5 思路点拨：根据有余数的除
法可知：被除数=不完全 商×除数+余数，（被除 数－余数）÷不完全商= 除数。所以□=（77－5） ÷8=9.
解：77÷□9 =8……5
例3下列算式中○，△，☆，各代表一个数，求出 它们代表的数。
在1、2、3、4、5、6、7、8、9中，选择3个不同的数字可 以写出的乘法算式只有:①2×4=8; ②2×3=6.
如果选择第①个算式，剩下的1、3、5、6、7、9，这六个 数字无法凑成两道加法算式，所以这种情况不成立。
选择第②个算式，剩下的数字1、4、5、7、8、9，可以写 出另两道算式为：1+7=8；9－5=4
（1）○+○=58 （2）△+△－12=6 （3）9×☆+18÷3=42
灼灼荷花瑞 亭亭出水中
• 思路点拨：（1）根据原式可得 ○×2=18，想2个○是58，一 个○就是29，即2×29=58，所 以29+29=58.
• （2）根据原式可得△×2－ 12=6，把（△×2）看成一个数。 可知:
△×2=12+6即△×2=18，可知 △=9.
思路点拨：由第一个乘数的 个位数是4，积的个位数 是8值，第二个乘数的个 位数只可能成为2或7，再 由第一个乘数的十位数是 1，积的百位数是3，乘数 的十位数不能填大于3的 数字。所以第二个乘数只 可能是12,17,22,27,32或 37.经试算，符合题意的有 22和27.
14×□2 □2 =3□0 8,14×□2 □7 =3□7 8.
• □×□=□2=□□÷□
• 思路点拨:先看 □×□=□2，想乘积 是两位数，个位是2，
第02讲 横式数字谜(一)
第2讲横式数字谜小朋友们可能都猜过这样一个谜语，谜面是“空中码头”（打一城市名）。
谜底你还记得吗？记不得也没关系，想想“空中”指什么？“天”。
这个地名第1个字可能是天。
“码头”指什么呢？码头又称渡口，联系这个地名开头是“天”字，容易想到“天津”这个地名，而“津”正好又是“渡口”的意思。
这样谜底就出来了：天津。
数学当中也有这样的谜，它是由一些数字与算式构成的，称为算式谜。
日本人形象地称之为“虫食算”，即算式中一些数字被虫子咬去了。
要想猜出算式谜，也得先分析这些数字和算式构成的“谜面”，再运用一些推理方法打到“谜底”。
在一个数学式子(横式或竖式)中擦去部分数字，或用字母、文字来代替部分数字的不完整的算式或竖式，叫做数字谜题目。
解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。
例如，求算式324+□=528中□所代表的数。
根据“加数=和-另一个加数”知，□=582-324＝258。
又如，求右竖式中字母A，B所代表的数字。
显然个位数相减时必须借位，所以，由12-B＝5知，B＝12-5＝7；由A-1＝3知，A＝3＋1＝4。
解数字谜问题既能增强数字运用能力，又能加深对运算的理解，还是培养和提高分析问题能力的有效方法。
这一讲介绍简单的算式(横式)数字谜的解法。
解横式数字谜，首先要熟知下面的运算规则：(1)一个加数+另一个加数=和；(2)被减数-减数=差；(3)被乘数×乘数=积；(4)被除数÷除数=商。
由它们推演还可以得到以下运算规则：由(1)，得和 - 一个加数=另一个加数；其次，要熟悉数字运算和拆分。
例如，8可用加法拆分为8＝0＋8＝1＋7＝2＋6＝3＋5＝4＋4；24可用乘法拆分为24＝1×24=2×12＝3×8＝4×6(两个数之积)=1×2×12＝2×2×6=…(三个数之积)=1×2×2×6＝2×2×2×3=…(四个数之积)下列算式中，□，○，△，☆，*各代表什么数？(1)□+5＝13-6； (2)28-○＝15＋7；(3)3×△=54； (4)☆÷3＝87；(5)56÷*＝7。
小学数学横式数字谜知识点归纳！
小学数学横式数字谜知识点归纳！横式数字谜知识点归纳（一）1横式数字谜在一个数学式子(横式或竖式)中擦去部分数字，或用字母、文字来代替部分数字的不完整的算式或竖式，叫做数字谜题目。
解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。
例如，求算式324+□=528中□所代表的数。
根据“加数=和-另一个加数”知，□=582-324＝258。
又如，求右竖式中字母A，B所代表的数字。
显然个位数相减时必须借位，所以，由12-B＝5知，B＝12-5＝7；由A-1＝3知，A＝3＋1＝4。
解数字谜问题既能增强数字运用能力，又能加深对运算的理解，还是培养和提高分析问题能力的有效方法。
这一讲介绍简单的算式(横式)数字谜的解法。
解横式数字谜，首先要熟知下面的运算规则：(1)一个加数+另一个加数=和；(2)被减数-减数=差；(3)被乘数×乘数=积；(4)被除数÷除数=商。
由它们推演还可以得到以下运算规则：由(1)，得和-一个加数=另一个加数；其次，要熟悉数字运算和拆分。
例如，8可用加法拆分为8＝0＋8＝1＋7＝2＋6＝3＋5＝4＋4；24可用乘法拆分为24＝1×24=2×12＝3×8＝4×6(两个数之积)=1×2×12＝2×2×6=?(三个数之积)=1×2×2×6＝2×2×2×3=?(四个数之积)例1下列算式中，□，○，△，☆，*各代表什么数？(1)□+5＝13-6； (2)28-○＝15＋7；(3)3×△=54；(4)☆÷3＝87；(5)56÷*＝7。
解：(1)由加法运算规则知，□=13-6-5＝2；(2)由减法运算规则知，○＝28-(15＋7)＝6；(3)由乘法运算规则知，△＝54÷3＝18；(4)由除法运算规则知，☆=87×3＝261；(5)由除法运算规则知，*＝56÷7＝8。
第10讲 横式算式谜
知识要点：
•例1 求算式324+□=528中□所代表的数。
根据“加数=和-另一个加数”
□=582-324＝258。
•例2、求横式中字母A，B所代表的数字。
（1）12-B＝5（2）A来自1＝3。B=12-5=7
A=3+1=4
知识要点：
例3、在下列各式中，□，○，△各代表什么数？
150-□-□=□；
○×○＝○＋○；
在下列算式中 、 、 、 各代表一个数，求它们各自代表的数．
（1） ×9＋18－ ＝122 13 （3）4×9－ ÷2＝23 26
（2）(141－ )×8＝552 72
（4） ＋
26
－129÷3＝35－
练习3
在下列算式中 、 、 、 各代表一个数，求它们各自代表的数． （1） ×7－15－ ＝105 （2）(123－ )×9＝369 （3）7×6－ ÷2＝19 （4） ＋ ＋ －125÷5＝46＋
被减数＝_减__数__+__差__________________________
5__9_0－456＝234
小热身
2． 乘法口诀大比拼． （ 8 ）×9＝72
56÷（ 7 ）＝8
（ 48）÷6＝8
（ 7 ）×4＝28
49÷（ 7 ）＝7
小结：乘数＝__积__÷__另__一__个__乘__数___________________
（1） ＋ ＋ ＝138； 46
（2）134－ － － － ＝50 21
（3） （4）
＋ ＋6＝21－ ＋37＝ ＋ ＋
；5
＋
－26 21
练习2
在下列算式中， 、 、 、 （1） ＋ ＋ －25＝86 （2）85－ － ＋ ＝15 （3）102－ － ＝ ＋27
数字谜(磨刀篇)
数字谜(磨刀篇)
横式数字谜
(★★★★) (1997年小学数学奥林匹克决赛A 卷第3题) 下式中的“香港”、“中国”均代表一个两位自然数，那么香港＝______中国＝______。
(香港)2＋1997＝(中国)2＋1949
(★★)
在下列各等式的方框中填入恰当的数字，使等式成立，并且算式中的数字关于等号左右对称：
⑴12×23□＝□32×21； ⑵□3×6528＝8256×3□； ⑶24×2□1＝1□2×42。
例1
例2
例3
(★★★)(第五届小数报试题)
若用相同汉字表示相同数字，不同汉字表示不同数字，则在等式
学习好勤动脑×5＝勤动脑学习好×8
“学习好勤动脑”所表示的六位数最少是多少？
例4
(★★★★)
下面算式中的“国富”、“民富”、“强强”表示3个两位数，相同的汉字代表相同的数字，不同的汉字代表不同的数字，则“民、富、国、强”所表示的4个数的和是_______。
(国富＋民富)×强强＝2002
例5。
三年级奥数.计算综合.数字谜
第二讲乘除法数字谜一、基本概念数字谜定义:一般是指那些含有未知数字或未知运算符号的算式．填算符：指在一些数之间的适当地方填上适当的运算符号（包括括号），从而使这些数和运算符号构成的算式成为一个等式。
算符：指 +、-、×、÷、（）、[]、｛｝。
二、数字谜分类1、竖式谜2、横式谜3、填空谜4、幻方5、数阵三、解题技巧与方法竖式数字谜1、技巧（1）从首位或者末尾找突破口（突破口：指在做数字谜问题开始时的入口，一般在算式的首位或者末尾，可以确定其数字或者范围然后通过推理很快可以确定其值为后面的推理做好铺垫）；（2）要根据算式性质逐步缩小范围，并进行适当的估算逐步排除不符合的数字；（3）题目中涉及多个字母或汉字时，要注意用不同符号表示不同数字这一条件来排除若干可能性；（4）注意结合进位及退位来考虑；（5）数字谜中的文字，字母或其它符号，只取0~9中的某个数字。
（6）数字谜解出之后，最好验算一遍．2、数字迷加减法（1）个位数字分析法；（2）加减法中的进位与退位；（3）乘除法中的进位与退位；（4）奇偶性分析法。
横式数字谜解决巧填算符的基本方法（1）凑数法：根据所给的数，凑出一个与结果比较接近的数，再对算式中剩下的数字作适当的增加或减少，从而使等式成立。
（2）逆推法：常是从算式的最后一个数字开始，逐步向前推想，从而得到等式。
最值问题（1）横式转化为竖式数字谜，乘法转化为除法；（2）找突破口：末位和首位、进位和借位、个位数字、位数的差别等．（3）采用特殊分析方法：个位数字分析法、高位数字分析法、数字大小估算分析法、进位错位分析法、分解质因数法、奇偶分析法等．（4）除了数字谜问题常用的分析方法外，还会经常采用比较法，通过比较算式计算过程的各步骤，得到所求的最值的可能值，再验证能否取到这个最值．（5）数字谜问题往往综合了数字的整除特征、质数与合数、分解质因数、个位数字、余数、分数与小数互化、方程、估算、找规律等题型。
小学三年级 横式数字迷
教师：学生：日期：星期：时段：课题横式数字谜学习目标与分析学会解决简单横式数字谜问题，激发学习兴趣，锻炼思维学习重点教学重点掌握加减乘除运算规则及其变式教学难点数字的加减拆分、乘除拆分学习方法引导、启发、归纳学习内容与过程教师分批改一、数字谜：在一个数学式子(横式或竖式)中擦去部分数字，或用字母、文字来代替部分数字的不完整的算式或竖式，叫做数字谜题目。
解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。
例如，求算式324+□=528中□所代表的数。
根据“加数=和-另一个加数”知，□=582-324＝258。
又如，解数字谜问题既能增强数字运用能力，又能加深对运算的理解，还是培养和提高分析问题能力的有效方法。
这一讲介绍简单的算式(横式)数字谜的解法。
解横式数字谜，首先要熟知下面的运算规则：(1)一个加数+另一个加数=和；(2)被减数-减数=差；(3)被乘数×乘数=积；(4)被除数÷除数=商。
由它们推演还可以得到以下运算规则：由1.得和 - 个加数=另一个加数；由2.得减数+差=被减数，被减数-差=减数；由3.得积÷乘数=被乘数，积÷被乘数=乘数；由4.得商×除数=被除数，被除数÷商=除数。
其次，要熟悉数字运算和拆分。
例如，8可用加法拆分为8＝0＋8＝1＋7＝2＋6＝3＋5＝4＋4；24可用乘法拆分为24＝1×24=2×12＝3×8＝4×6(两个数之积)=1×2×12＝2×2×6=…(三个数之积)=1×2×2×6＝2×2×2×3=…(四个数之积)二、题型一：填数字例1下列算式中，□，○，△，☆，*各代表什么数？(1)□+5＝13-6；(2)28-○＝15＋7；(3)3×△=54；(4)☆÷3＝87；(5)56÷*＝7。
三年级数学谜语
三年级数学谜语一、数字类谜语。
1. 横看像把尺，竖看像根棒，年龄它最小，大哥它来当。
（谜底：1）- 解释：1在数字中是最小的正整数，但在计数顺序里排在最前面，就像大哥一样引领其他数字。
2. 像个蛋，不是蛋，说它圆，不太圆，说它没有它又有，成千上万连成串。
（谜底：0）- 解释：0的形状像蛋，它单独表示没有，但在多位数中是非常重要的组成部分，例如10、100等，成千上万的数都离不开它。
3. 五个兄弟，住在一起，名字不同，高矮不齐。
（谜底：手，手指代表数字1 - 5）- 解释：一只手有五个手指，就像五个兄弟，长短不一，而且可以分别用1 - 5来对应大拇指、食指、中指、无名指和小拇指。
二、运算符号类谜语。
1. 加一笔，增百倍；减一笔，少九成。
（谜底：十）- 解释：十加一笔变成千，是原来的百倍；十减一笔变成一，比原来少了九成（九成就是十分之九）。
2. 四去八进一。
（谜底：日或曰）- 解释：在汉字结构里，四去掉里面的八，再加上一横（进一）就变成了日或者曰。
从数学计算角度看，这是一种有趣的文字与数字关系的体现。
3. 左边九加九，右边九十九。
（谜底：柏）- 解释：九加九等于十八，木字可拆分为十和八；九十九是一百减一，百字减一就是白字，组合起来就是柏字。
这是将数学运算与汉字结构相结合的谜语。
三、数学概念类谜语。
1. 弯弯藤儿架上爬，串串珍珠上边发。
（谜底：葡萄，这里比喻算盘珠子，谜底与算盘相关，算盘是数学计算工具，体现了数学概念中的计算工具）- 解释：算盘的珠子就像串串珍珠，算盘架就像弯弯藤儿，算盘是以前常用的数学计算工具，通过这种形象的比喻来体现算盘这个数学概念。
2. 这个脑袋真正灵，忽闪忽闪眨眼睛，东南西北带着它，加减乘除不费劲。
（谜底：计算器）- 解释：计算器可以快速进行加减乘除运算，而且有显示屏就像会眨眼睛一样，人们在东南西北各个地方都可以方便地使用它进行数学计算。
横式数字谜
横式数字谜横式数字谜问题是指算式是横式形式，并且只给出了部分运算符号和数字，有些数字或运算符号“残缺”，只要我们根据运算法则，进行判断、推理，从而把“残缺”的算式补充完整。
解题步骤：第一步，要仔细审题；第二步，选择突破口；第三步，试验求解。
例1、下列算式中，□，○，△，☆，*各代表什么数？(1)□+5＝13－6；(2)28-○＝15＋7；(3)3×△=54；(4)☆÷3＝87；(5)56÷*＝7练1、下列算式中，□，○，△，☆各代表什么数？(1)□+□+□=48；(2)○＋○＋6＝21-○；(3)5×△-18÷6＝12；(4)6×3-45÷☆＝13例2、如果○＋□＝6，□＝○＋○，那么□－○＝？例3、（1）满足58＜12×□＜71的整数□等于几？(2)180是由哪四个不同的且大于1的数字相乘得到的？试把这四个数按从小到大的次序填在下式的方框中180=□×□×□×□。
(3)若数□，△满足□×△=48和□÷△=3，则□，△各等于多少？例4、在等号左端的两个数中间添加上运算符号，使下列各式成立：⑴4 4 4 4＝24；⑵5 5 5 5 5=6；⑶1 2 3 4 5＝1例5、在下列方框中填上适当的数，等式成立：（1）□÷5＝40......3；（2）148÷□＝8 (3)例6、在下列各题中，每一题的四个□中都填同一个数字，使式子成立：(1)□+□＞□×□；(2)□+□=□×□；(3)□+□＜□×□。
例7、将0，1，2，3，4，5，6七个数字分别填入下式的七个□里，使算式成立：□□÷□=□×□=□□。
例8、在下面的算式里，每个图形各表示什么数？○＋□=48○－□=12例9、将2、3、4、5、6、8、11、12这8个数填在图1的□中，使它们组成图1中的4个等式。
第二讲 横式数字谜
□-○=4-2=2。
随堂练习1
(1)□×9+6×□=600÷2
□ ×（ 9+6 ）=600÷2 □ ×15 =300 □ =300÷ 15 □=20 (2)25 × 25- □÷3 =610
25 × 25+ 610 =□÷3
625+610 =□÷3
Hale Waihona Puke 随堂练习4添上适当的运算符“+”“-”“×”“÷”，使以下等式 立
①1 2 3 4=1 1 × 2 + 3 - 4=1 ②4 4 4 4=2 4 ÷ 4 + 4 ÷ 4=2 4 -（4 + 4）÷ 4=2 4 × 4 ÷（4 + 4）=2
横式数字谜横式数字谜问题是指算式是横式的形式并且只给出了部分运算符号和数字有一些运算符号和数字残缺要我们根据运算法则进行判断推理从而把残缺的算式补充完整
第二讲
横式数字谜
横式数字谜
横式数字谜问题是指算式是横式的形 式,并且只给出了部分运算符号和数字,有一 些运算符号和数字“残缺”，要我们根据 运算法则，进行判断、推理，从而把“残 缺”的算式补充完整。 解决这类问题时：第一步要仔细审题； 第二步要选择突破口；第三步试验求解。
1235=□÷3
□ = 1235 × 3
□ =3705
例3，在下列□填上适当的数使，使
等式成立。 （1） □÷5=40……3 （2）148 ÷ □=8 …… 4
分析：可以根据有余数除法中,被除数=除数
×商+余数，可解题。
解：
（1）因为□=40 × 5+3=203，所以，
203 ÷5=40 …… 3
第11讲-横式数字谜(一)
横式数字谜(一)在一个数学式子(横式或竖式)中擦去部分数字，或用字母、文字来代替部分数字的不完整的算式或竖式，叫做数字谜题目。
解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。
解数字谜问题既能增强数字运用能力，又能加深对运算的理解，还是培养和提高分析问题能力的有效方法。
这一讲介绍简单的算式(横式)数字谜的解法。
解横式数字谜，首先要熟知下面的运算规则：(1)一个加数+另一个加数=和；(2)被减数-减数=差；(3)被乘数×乘数=积；(4)被除数÷除数=商。
由它们推演还可以得到以下运算规则：得和-一个加数=另一个加数；其次，要熟悉数字运算和拆分。
例如，8可用加法拆分为8＝0＋8＝1＋7＝2＋6＝3＋5＝4＋4；24可用乘法拆分为24＝1×24=2×12＝3×8＝4×6(两个数之积)=1×2×12＝2×2×6=…(三个数之积)=1×2×2×6＝2×2×2×3=…(四个数之积)例1，求算式324+□=528中□所代表的数是什么？例2 下列算式中，□，○，△，☆，*各代表什么数？(1)□+5＝13-6； (2)28-○＝15＋7； (3)3×△=54； (4)☆÷3＝7； (5)56÷*＝7。
例3下列算式中，□，○，△，☆各代表什么数？(1)□+□+□=48；(2)○＋○＋6＝21-○；(3)5×△-18÷6＝12；(4)6×3-45÷☆＝13。
例4 在等号左端的两个数中间添加上运算符号，使下列各式成立：(1)4 4 4 4＝24； (2)5 5 5 5 5=6。
例5 在下式的两数中间添上四则运算符号，使等式成立：8 2 3＝3 3。
练习21.在下列各式中，□分别代表什么数？□+16＝35； 47-□=12；□-3＝15；4×□=36；□÷4=5； 24÷□=4。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 例2 下列算式中，□，○，△， ☆各代表什么数？
• (1)□+□+□=48； • (2)○＋○＋6＝21-○； • (3)5×△-18÷6＝12； • (4)6×3-45÷☆＝13。
• 解：(1)□表示一个数，根据乘 法的意义知，
• □+□+□=□×3， • 故□=48÷3＝16。
• (2)先把左端(○＋○＋6)看成 一个数，就有
• 8＝0＋8＝1＋7＝2＋6＝3 ＋5＝4＋4；
• 24可用乘法拆分为
• 24＝1×24=2×12＝3×8 ＝4×6(两个数之积)
• =1×2×12＝ 2×2×6=…(三个数之积)
• =1×2×2×6＝ 2×2×2×3=…(四个数之积)
• 例1 下列算式中，□，○，△， ☆，*各代表什么数？
• (1)□+5＝13-6； (2)28-○＝15 ＋7；
• 若再限制拆分成四个“不同的” 数字的乘积，范围又缩小了。按从小 到大的次序排列只有下面一种：
• 180＝2×3×5×6。
• 所以填的四个数字依次为2，3， 5，6。
• (3)首先，由□÷△=3知，□＞△， 因此，在把48拆分为两数的乘积 时，有48＝48×1＝24×2＝ 16×3＝12×4＝8×6，
• (3)3×△=54； (4)☆÷3＝87；
• (5)56÷*＝7。
• 解：(1)由加法运算规则知， □=13-6-5＝2；
• (2)由减法运算规则知，○＝ 28-(15＋7)＝6；
• (3)由乘法运算规则知，△＝ 54÷3＝18；
• (4)由除法运算规则知， ☆=87×3＝261；
• (5)由除法运算规则知，*＝ 56÷7＝8。
• 由例4看出，填运算符号 的问题一般会有多个解。这些 填法都是通过对问题的综合观 察、分析和试算得到的，如果 只是盲目地“试算”，那么就 可能走很多弯路。
• 例5 在下式的两数中间添上四 则运算符号，使等式成立：
• 8 2 3＝3 3。 • 分析与解：首先考察右端“3
3”，它有四种填法： • 3+3＝6； 3-3＝0； • 3×3＝9； 3÷3=1。
• 再考察左端“8 2 3”，因 为只有一个奇数3，所以要想 得到奇数，3的前面只能填 “＋”或“-”，要想得到偶数， 3的前面只能填“×”。经试算， 只有两种符合题意的填法：
• 8-2＋3＝3×3；8÷2-3＝ 3÷3。
• 填运算符号可加深对四则 运算的理解和认识，也是培养 分析能力的好内容。
• 解横式数字谜，首先要熟 知下面的运算规则：
• (1)一个加数+另一个加数=和； • (2)被减数-减数=差； • (3)被乘数×乘数=积； • (4)被除数÷除数=商。
• 由它们推演还可以得到以 下运算规则：
• 由(1)，得 和-一个加数=另 一个加数；
• 其次，要熟悉数字运算和 拆分。例如，8可用加法拆分 为
• 第2讲 横式数字谜(一)
• 在一个数学式子(横式或竖式) 中擦去部分数字，或用字母、文 字来代替部分数字的不完整的算 式或竖式，叫做数字谜题目。解 数字谜题就是求出这些被擦去的 数或用字母、文字代替的数的数 值。
• 例如，求算式324+□=528中 □所代表的数。
• 根据“加数=和-另一个加数” 知，
•
• 练习2
• 1.在下列各式中，□分别 代表什么数？
• □+16＝35； 47-□=12； □-3＝15；
• =582-324＝258。
• 又如，求右竖式中字母A，B 所代表的数字。显然个位数相减 时必须借位，所以，由12-B＝5知， B＝12-5＝7；由A-1＝3知，A＝3 ＋1＝4。
• 解数字谜问题既能增强数 字运用能力，又能加深对运算 的理解，还是培养和提高分析 问题能力的有效方法。
• 这一讲介绍简单的算式(横 式)数字谜的解法。
• 其中，只有48＝12×4中， 12÷4=3，因此
• =12，△=4。
• 这道题还可以这样解：由 □÷△=3知，□=△×3。把 □×△=48中的□换成△×3， 就有
• (△×3)×△＝48，
• 于是得到△×△=48÷3＝16。 因为16＝4×4，所以△=4。再把 □=△×3中的△换成4，就有
• □=△×3=4×3=12。
• 4×4＋4＋4＝24；
• 4＋4×4＋4＝24；
• 4＋4＋4×4＝24。
• (2)因为5+1=6，等号左端有五 个5，除一个5外，另外四个5 凑成1，至少要有一个“÷”， 有如下填法：
• 5÷5+5-5+5＝6； • 5＋5÷5＋5-5＝6； • 5＋5×5÷5÷5=6； • 5＋5÷5×5÷5＝6。
• (○＋○＋6)＋○＝21， • ○×3＝21-6， • ○＝15÷3＝5。
• (3)把5×△，18÷6分别看成 一个数，得到
• 5×△=12＋18÷6， • 5×△=15， • △=15÷5＝3。
• (4)把6×3，45÷☆分别看成 一个数，得到
• 45÷☆＝6×3-13， • 45÷☆＝5， • ＝45÷5＝9。
• 这是一种“代换”的思想，它 在今后的数学学习中应用十分广泛。
• 下面，我们再结合例题讲 一类“填运算符号”问题。
• 例4 在等号左端的两个数中间 添加上运算符号，使下列各式 成立：
• (1)4 4 4 4＝24；
• (2)5 5 5 5 5=6。
• 解：(1)因为4＋4＋4＋4＜24，所 以必须填一个“×”。4×4＝16， 剩下的两个4只需凑成8，因此， 有如下一些填法：
• 58÷12＝4……10， 71÷12＝5……11，
• 并且□为整数，所以，只 有□=5才满足原式。
• (2)拆分180为四个整数的乘积 有很多种方法，如
• 180＝1×4×5×90＝ 1×2×3×30＝…
• 但拆分成四个“大于1”的 数字的乘积，范围就缩小了，
• 如180＝2×2×5×9＝2×3×5×6 ＝…
• 例3(1)满足58＜12×□＜71的 整数□等于几？
• (2)180是由哪四个不同的且大 于1的数字相乘得到的？试把 这四个数按从小到大的次序填 在下式的□里。
• 180=□×□×□×□。
• (3)若数□，△满足 • □×△=48和□÷△=3