圆切线的有关证明和计算
微专题十二 与圆的切线有关的计算与证明

微专题十二 与圆的切线有关的计算与证明[见学用《高分作业》PA48]类型一 与切线的性质有关的计算或证明【经典母题】如图Z12-1,⊙O 的切线PC 交直径AB 的延长线于点P ,C 为切点,若∠P =30°,⊙O 的半径为1,则PB 的长为__1__.图Z12-1 经典母题答图【解析】 如答图,连结OC .∵PC 为⊙O 的切线,∴∠PCO =90°,在Rt △OCP 中,∵OC =1,∠P =30°,∴OP =2OC =2,∴PB =OP -OB =2-1=1. 【思想方法】 (1)已知圆的切线,可得切线垂直于过切点的半径;(2)已知圆的切线,常作过切点的半径,得到切线与半径垂直.【中考变形】[2018·黄冈]如图Z12-2,AD 是⊙O 的直径,AB 为⊙O 的弦,OP ⊥AD ,OP 与AB 的延长线交于点P ,过B 点的切线交OP 于点C .(1)求证:∠CBP =∠D ;(2)若OA =2,AB =1,求线段BP 的长.图Z12-2 中考变形答图解:(1)证明:如答图,连结OB ,∵AD 是⊙O 的直径,∴∠ABD =90°,∴∠A +∠D =90°,∵BC 为切线,∴OB ⊥BC ,∴∠OBC =90°,∴∠OBA +∠CBP =90°,而OA =OB ,∴∠A =∠OBA ,∴∠CBP =∠D ;(2)∵OP ⊥AD ,∴∠POA =90°,∴∠P +∠A =90°,∵∠D +∠A =90°,∴∠P =∠D ,∴△AOP ∽△ABD ,∴AP AD =AO AB ,即1+BP 4=21,∴BP =7.【中考预测】[2018·白银]如图Z12-3,点O 是△ABC 的边AB 上一点,⊙O 与边AC 相切于点E ,与边BC ,AB 分别相交于点D ,F ,且DE =EF .(1)求证:∠C =90°;(2)当BC =3,sin A =35时,求AF 的长.图Z12-3 中考预测答图解:(1)证明:如答图,连结OE ,BE ,∵DE =EF ,∴DE ︵=EF ︵,∴∠OBE =∠DBE ,∵OE =OB ,∴∠OEB =∠OBE ,∴∠OEB =∠DBE ,∴OE ∥BC ,∵⊙O 与边AC 相切于点E ,∴OE ⊥AC ,∴BC ⊥AC ,∴∠C =90°;(2)在△ABC ,∠C =90°,BC =3,sin A =35,∴AB =5,设⊙O 的半径为r ,则AO =5-r ,在Rt △AOE 中,sin A =OE OA =r 5-r=35, ∴r =158,∴AF =5-2×158=54.类型之二 与切线的判定有关的计算或证明【经典母题】已知:如图Z12-4,A 是⊙O 外一点,AO 的延长线交⊙O 于点C ,点B 在圆上,且AB =BC ,∠A =30°,求证:直线AB 是⊙O 的切线.图Z12-4 经典母题答图证明:如答图,连结OB ,∵OB =OC ,AB =BC ,∠A =30°,∴∠OBC =∠C =∠A =30°,∴∠AOB =∠C +∠OBC =60°.∵∠ABO =180°-(∠AOB +∠A )=180°-(60°+30°)=90°,∴AB ⊥OB ,又∵OB 为⊙O 半径,∴AB 是⊙O 的切线. 【思想方法】 证明圆的切线常用两种方法“作半径,证垂直”或者“作垂直,证半径”.【中考变形】1.[2018·南充]如图Z12-5,C 是⊙O 上一点,点P 在直径AB 的延长线上,⊙O 的半径为3,PB =2,PC =4.(1)求证:PC 是⊙O 的切线;(2)求tan ∠CAB 的值.图Z12-5 中考变形1答图解:(1)证明:如答图,连结OC,BC,∵⊙O的半径为3,PB=2,∴OC=OB=3,OP=OB+PB=5,∵PC=4,∴OC2+PC2=OP2,∴△OCP是直角三角形,∴OC⊥PC,∴PC是⊙O的切线;(2)∵AB是直径,∴∠ACB=90°,∴∠ACO+∠OCB=90°,∵OC⊥PC,∴∠BCP+∠OCB=90°,∴∠BCP=∠ACO,∵OA=OC,∴∠A=∠ACO,∴∠A=∠BCP,在△PBC和△PCA中,∠BCP=∠A,∠P=∠P,∴△PBC∽△PCA,∴BCAC=PBPC=24=12,∴tan∠CAB=BCAC=12.2.[2018·郴州]如图Z12-6,已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.(1)求证:直线AD是⊙O的切线;(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.图Z12-6 中考变形2答图解:(1)证明:如答图,连结AO,∵∠AEC=30°,∴∠ABC=30°,∵AB=AD,∴∠D=∠ABC=30°,根据三角形的内角和定理得,∠BAD=120°,∵OA=OB,∴∠OAB=∠ABC=30°,∴∠OAD=∠BAD-∠OAB=90°,∴OA⊥AD,∵点A在⊙O上,∴直线AD是⊙O的切线;(2)∵∠AEC=30°,∴∠AOC=60°,∵BC⊥AE于M,∴AE=2AM,∠OMA=90°,在Rt△AOM中,AM=OA·sin∠AOM=4×sin60°=23,∴AE=2AM=4 3.【中考预测】如图Z12-7,AB是⊙O的直径,点C,D在⊙O上,∠A=2∠BCD,点E 在AB的延长线上,∠AED=∠ABC.(1)求证:DE与⊙O相切;(2)若BF=2,DF=10,求⊙O的半径.图Z12-7 中考预测答图解:(1)证明:如答图,连结OD.∵AB是⊙O的直径,∴∠ACB=90°,∴∠A+∠ABC=90°,∵∠BOD=2∠BCD,∠A=2∠BCD,∴∠BOD=∠A,∵∠AED=∠ABC,∴∠BOD+∠AED=90°,∴∠ODE=90°,即OD⊥DE,∴DE与⊙O相切;(2)如答图,连结BD,过点D作DH⊥BF于点H.∵DE与⊙O相切,∴∠ACD+∠BCD=∠ODB+∠BDE=90°,∵∠ACD=∠OBD,∠OBD=∠ODB,∴∠BDE=∠BCD,∵∠AED=∠ABC,∴∠AFC=∠DBF,∵∠AFC=∠DFB,∴△ACF与△FDB都是等腰三角形,∴FH=BH=12BF=1,∴HD=DF2-FH2=3,在Rt△ODH中,OH2+DH2=OD2,即(OD-1)2+32=OD2,∴OD=5.即⊙O的半径是5.。
圆中与切线有关的解题策略
圆中与切线有关的解题策略知识精解一、切线的三种判定方法:(1)和圆只有一公共点的直线是圆的切线;(2)圆心到直线的距离等于半径的直线是圆的切线;(3)经过半径外端且与半径垂直的直线是圆的切线;证题中常用后两种方法,且往往需要添加辅助线。
常见证明切线的方法(添加辅助线):(1)如果已知直线经过圆上一点,那么连结这点和圆心得到半径再证所作半径与这条直线垂直。
即“连半径,证_______”(2)如果已知条件中不知直线与圆是否有公共点,那么过圆心作直线的垂线段,再证明垂线段的长等于半径,即“作垂直,证_______”。
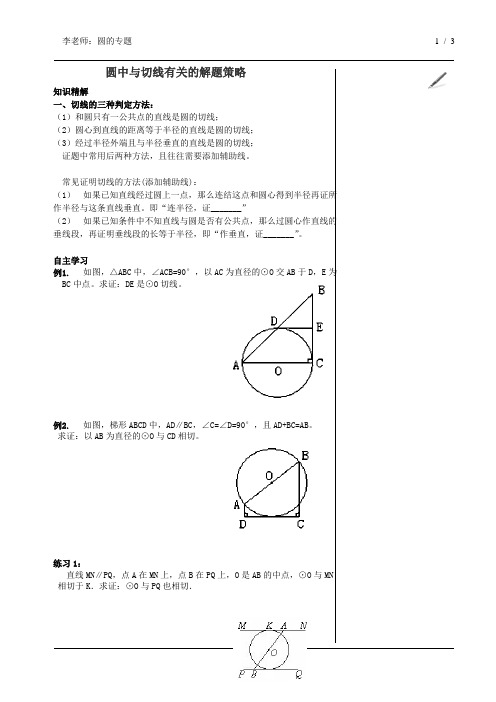
自主学习例1. 如图,△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于D,E为BC中点。
求证:DE是⊙O切线。
例2. 如图,梯形ABCD中,AD∥BC,∠C=∠D=90°,且AD+BC=AB。
求证:以AB为直径的⊙O与CD相切。
练习1:直线MN∥PQ,点A在MN上,点B在PQ上,O是AB的中点,⊙O与MN 相切于K.求证:⊙O与PQ也相切.练习2:已知△ABC 中,=∠90 C ,=AC BC ,,D E 分别是,AC BC 的中点,⊙O 是△DCE 的外接圆.求证:AB 是⊙O 的切线.练习3:已知:∠MAN=30°,O 为边AN 上一点,以O 为圆心、2为半径作⊙O ,交AN 于D 、E 两点,设AD=x ,⑴如图⑴当x 取何值时,⊙O 与AM 相切;⑵如图⑵当x 为何值时,⊙O 与AM 相交于B 、C 两点,且∠BOC=90°.二. 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等且这点和圆心连线平分两条切线的夹角。
如图,已知:P 是⊙O 外一点,PA 、PB 是⊙O 的切线,A 、B 为切点;结论:(1)PA____PB ; (2)OP______∠APB 。
由切线长定理,可以推得如下重要结论:(1)圆外切四边形的对边和相等;(2)圆的两条平行切线的切点连线是圆的______。
圆的切线定理

圆的切线定理定理表述设有一个圆和一条直线,当这条直线与圆相切时,直线与圆的切点之间的线段与半径垂直。
证明过程证明圆的切线定理的方法主要有两种:几何法和代数法。
几何法几何法是通过几何构造来证明定理。
我们可以通过以下步骤进行证明:1. 假设有一个圆和一条直线,直线与圆相切于点P。
2. 以圆心为起点,作一条半径OP。
3. 连接直线上的点P和圆心O,得到线段OP。
4. 利用三角形的性质,我们可以得出线段OP与直线的斜率相等。
5. 因为直线与圆相切,所以线段OP与半径OP垂直。
6. 因此,根据直线斜率的性质,直线与半径垂直。
通过以上步骤,我们证明了圆的切线与半径垂直。
代数法代数法是通过代数计算来证明定理。
我们可以使用坐标系的方法进行证明:1. 假设圆的方程为(x-a)^2 + (y-b)^2 = r^2,其中(a,b)为圆心坐标,r为半径。
2. 假设直线的方程为y = mx + c,其中m为直线的斜率,c为截距。
3. 将直线方程代入圆的方程,得到(x-a)^2 + (mx + c - b)^2 - r^2 = 0。
4. 根据圆的定义,当直线与圆相切时,该方程只有一个解。
5. 解方程得到一个二次方程,利用判别式判断方程有一个解的特性。
6. 通过计算判别式,可以得到切线方程有唯一解的条件。
7. 根据等式等式的性质,解方程得到的根与圆的切点相对应。
8. 证明了切线方程与圆的切点正交。
通过以上代数计算,我们证明了圆的切线与半径垂直。
应用和实例圆的切线定理在几何学和应用数学中有着广泛的应用。
它在解析几何的证明和问题求解中起着重要的作用。
例如,通过圆的切线定理,我们可以解决求直线与圆的切点坐标和切线方程的问题。
这对于工程学和物理学中的曲线研究非常有用。
另外,圆的切线定理在计算机图形学和计算机模拟中也被广泛应用。
通过计算机算法,我们可以快速计算出圆与直线的切点坐标,从而实现更精确的模拟效果。
总之,圆的切线定理是解析几何中重要的定理之一,它在几何学和应用数学中有着广泛的应用价值。
圆中与有关切线的问题

圆中与有关切线的问题基础知识:一、切线的定义:①与圆只有一个公共点的直线。
②若圆心到直线的距离与半径相等。
二、切线的性质:1、若L是圆的切线,则圆心到直线的距离等于半径。
2、圆的切线垂直过切点的半径。
3、推论:圆心、切点、垂直三、切线的判定:1、定义法:与圆只有一个公共点。
2、数量法:∵d=r ∴直线是圆的切线3、过半径的外端且与它垂直的直线。
方法:a、有明确的公共点,作半径,证垂直;b、无明确公共点,过圆心作垂直,证半径。
四、与切线有关的问题:1、切线长定理:a、切线长定义:b、切线长定理:过圆外一点引圆的两条切线,这两条切线相等,连接圆心与圆外的点平分两切线所成的角。
2、弦切角:a、弦切角的定义:b、弦切角定理(不能直接用)弦切角等于弦切角所夹弧所对的圆周角。
3、三角形的内切圆:a、定义:如果三角形的三边都与这个圆相切,则这个圆叫这个三角形的内切圆。
b、Rt△内切圆半径公式:Rt△内切圆半径等于两直角边的和与斜边的差的一半。
c、四边形内切圆:对边和相等。
d、公切线(长)五、常用辅助线:作半径。
能力测试:一、填空题。
1、直线L与半径为r的⊙O相交,且点O到直线L的距离为5,则r的取值范围是。
2、在射线OA上取一点P,使OP=4cm,以P为圆心作直径为4cm的圆,若⊙P与射线OB相交,则锐角∠AOB的取值范围是。
3、如图,CD是⊙O的直径,AE切⊙O于B,DC的延长线交AB于A,∠A=20°,则∠DBE=。
4、如图,AB为⊙O的直径,延长AB至D,使BD=OB,DC切⊙O于C,则AC:AD=。
5、如图,AB为⊙O的直径,C、D是⊙O的点,∠BAC=20°,⋂⋂=DCAD,DE是⊙O的切线,则∠EDC的度数为。
6、OA 、OB 是⊙O 的两条半径,BC 是⊙O 的切线,且∠AOB =84°,则∠ABC 的度数为 。
二、选择题。
1、下列命题中,错误的是( )A 、垂直于弦的直径平分这弦;B 、弦的垂直平分线过圆心;C 、垂直于切线的直线必过圆心;D 、经过圆心且垂直于切线的直线必过切点。
圆的切线证明方法归纳

圆的切线证明方法归纳切线是指与圆相切且与圆的半径垂直的直线。
在几何学中,圆的切线是一个重要的概念。
证明圆的切线有许多不同的方法,下面将介绍一些常见的证明方法。
1.垂直切线法:这是最常见的证明方法之一。
具体步骤如下:(1)假设圆的半径r,圆心O,切点A和切线上的一点T。
(2)连接OA,并且将OA延长到交切线于点T。
(3)根据勾股定理可得:OA^2 =OT^2 + AT^2。
(4)由于OT和AT都是切线的一部分,所以OT和AT都垂直于OA。
(5)根据垂直定理可知OT和AT平方和等于OA的平方,即OT^2 + AT^2 = OA^2。
(6)根据步骤4和5可得:AT^2 = OA^2 - OT^2。
(7)OT是半径,所以OT^2= r^2,代入上式得:AT^2 = OA^2 -r^2。
(8)AT是切线的一部分,所以AT > 0。
因此,OA^2 - r^2 > 0。
(9)根据正数平方根的性质,OA^2 - r^2的平方根存在。
(10)所以,根据步骤9,AT存在,即OT与切线上的一点T并非同一点。
(11)由于OT与圆的半径相交于点O,所以OT是与半径垂直的直线,即切线。
2.切线垂直与半径的证明:这种证明方法基于一个重要的定理:切线垂直于半径。
具体步骤如下:(1)假设圆的半径r,圆心O,切点A和切线上的一点T。
(2)连接OA和OT。
(3)由于AO是圆的半径,所以AO与圆心O的向量相等,即AO = OT。
(4)由于切线与圆相切,切点A是切线上的一点,所以OA与切线垂直。
(5)根据向量几何的性质可得,向量OA与向量OT垂直。
(6)根据定义,切线上的每一个点与圆心都构成一个向量,这个向量与向量OA垂直。
(7)所以,根据步骤6,切线与所有圆心上的向量都垂直,即切线垂直于半径。
3.外切圆的切线证明:这种证明方法适用于外切圆。
具体步骤如下:(1)假设有一个三角形ABC,其中AB和BC是两条直线段,角ABC是直角。
证明圆的切线的七种常用方法

证明圆的切线的七种常用方法类型1、有公共点:连半径,证垂直方法1、勾股定理逆定理法证垂直1.如图,⊙O的直径AB=12,点P是AB延长线上一点,且PB=4,点C是⊙O上一点,PC=8. 求证:PC是⊙O的切线.方法2、特殊角计算法证垂直2. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.(1)求证:P A是⊙O的切线;(2)若PD =5,求⊙O 的直径.方法3、等角代换法证垂直3.如图,在Rt△ABC中,∠C=90°,D为BC 的中点,以AC 为直径的⊙O交AB于点E . 求证:DE是⊙O 的切线.方法4、平行线性质法证垂直4.如图,已知四边形OABC的三个顶点A ,B ,C在以O为圆心的半圆上,过点C 作CD ⊥AB,分别交AB,AO 的延长线于点D,E,AE交半圆O于点F,连接CF,且∠E=30°,点B是︵AC的中点.(1)判断直线DE与半圆O的位置关系,并说明理由;(2)求证:CF=OC;(3)若⊙O的半径是6,求DC的长.AB POCACBPD OAEBDOCA O F ECDB方法5、全等三角形法证垂直5.如图,AB 是⊙O 的直径,点C ,D 在⊙O 上,且四边形AOCD 是平行四边形,过点D 作⊙O 的切线,交OC 的延长线于点F ,连接BF .求证:BF 是⊙O 的切线.类型2、无公共点:作垂直,证半径方法6、角平分线性质法证半径6.如图,在Rt △ABC 中,∠B =90°,∠BAC 的平分线交BC 于点D ,E 是AB 上一点,DE =DC ,以点D 为圆心,BD 长为半径作OD ,AB =5,EB =2. (1)求证:AC 是OD 的切线;(2)求线段AC 的长.方法7、全等三角形法证半径7.如图,四边形ABCD 中,∠A =∠ABC =90°,AD +BC =CD ,以AB 为直径作⊙O . 求证:⊙O 与边CD 相切.A OBCD F A B C D EA OB C D。
实用圆切线方程的证明

关于圆的切线方程及相关公式的证明一、点P(x 0,y 0)在圆上1、在圆的标准方程(x-a) 2+(y-b) 2=r 2上,则过点P(x 0,y 0)的切线方程为(x 0-a) (x-a) +(y 0-b) (y-b) =r 2或(x 0-a) (x-x 0) +(y 0-b) (y-y 0) =0证明:∵P(x 0,y 0)在圆上,(x 0-a) 2+(y 0-b) 2=r 2,圆心O(a,b),OP 的斜率ax by k --=00 ∴切线的斜率为k1-,切线方程)(0000x x b y ax y y ----=- 0))(())((0000=--+--y y b y x x a x ①(x 0-a) 2+(y 0-b) 2=r 2 ②①+②得出(x 0-a )(x -x 0+x 0-a)+(y 0-b)(y -y 0+y 0-b)= r 2 (x 0-a) (x -a) +(y 0-b) (y -b) =r 22、在圆的特殊方程x 2+y 2=r 2上,则过点P(x 0,y 0)的切线方程为x 0x + y 0y ==r 2(当a=0,b=0)3、在圆的一般方程x 2+y 2+Dx+Ey+F=0(D 2+E 2-4F >0)上,则过点P(x 0,y 0)的切线方程为x 0x + y 0y + D ×(2x x + )+ E ×(2y y + )+ F =0证明:x 2+y 2+Dx+Ey+F=0 化成圆的标准方程 44)2()2(2222FE D Ey Dx -+=+++∵P(x 0,y 0)在圆上,44)2()2(222020FE D Ey Dx -+=+++,OP 的斜率2200Dx Ey k ++=∴切线的斜率为k1-,切线方程)(220000x x E y Dx y y -++-=-0))(2())(2(0000=-++-+y y Ey x x Dx ①44)2()2(222020FE D Ey Dx -+=+++②①+②得出44)2)(2()2)(2(22000000FE D Ey y y Ey Dx x x Dx -+=++-++++-+4442)(42)(22200200FE D E y y E y y D x x D x x -+=++⨯++++⨯+x 0x + y 0y + D ×(2x x + )+ E ×(2y y + )+ F =0二、点P(x 1,y 1)在圆外1、切线长22121)()(r b y a x PA --+-= (标准方程(x-a) 2+(y-b) 2=r 2) 证明:用勾股定理。
2020中考数学 冲刺专题:圆切线的相关证明与计算
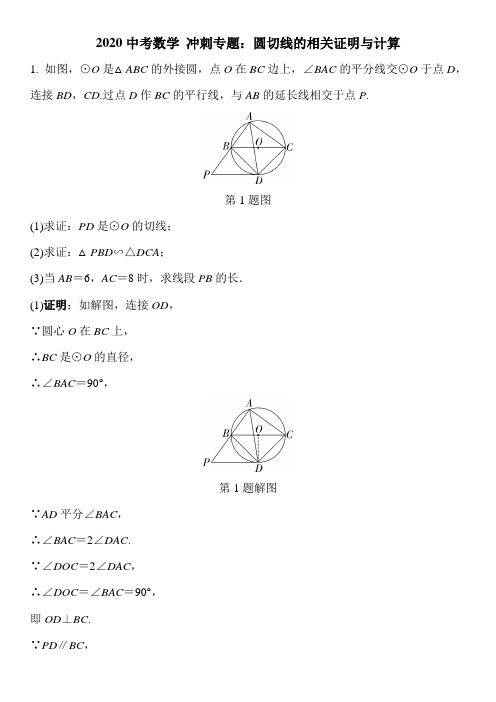
2020中考数学冲刺专题:圆切线的相关证明与计算1. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD.过点D作BC的平行线,与AB的延长线相交于点P.第1题图(1)求证:PD是⊙O的切线;(2)求证:△PBD∽△DCA;(3)当AB=6,AC=8时,求线段PB的长.(1)证明:如解图,连接OD,∵圆心O在BC上,∴BC是⊙O的直径,∴∠BAC=90°,第1题解图∵AD平分∠BAC,∴∠BAC=2∠DAC.∵∠DOC=2∠DAC,∴∠DOC=∠BAC=90°,即OD⊥BC.∵PD∥BC,∴OD ⊥PD .又∵OD 是⊙O 的半径, ∴PD 是⊙O 的切线; (2)证明:∵PD ∥BC , ∴∠P =∠ABC . 又∵∠ABC =∠ADC , ∴∠P =∠ADC .∵∠PBD +∠ABD =180°,∠ACD +∠ABD =180°, ∴∠PBD =∠ACD , ∴△PBD ∽△DCA ;(3)解:∵△ABC 是直角三角形, ∴BC 2=AB 2+AC 2=62+82=100, ∴BC =10.∵OD 垂直平分BC , ∴DB =DC .∵BC 是⊙O 的直径, ∴∠BDC =90°.∵在Rt △DBC 中,DB 2+DC 2=BC 2,即2DC 2=BC 2=100, ∴DC =DB =5 2. ∵△PBD ∽△DCA , ∴PB DC =BD CA ,∴PB =DC ·BD CA =52·528=254.2.如图,点A在⊙O上,点P是⊙O外一点,P A与⊙O相切于点A,连接OP交⊙O 于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.第2题图(1)求证:PB是⊙O的切线;(2)若PC=9,AB=63,求图中阴影部分的面积.(1)证明:连接OB,∵OP⊥AB,∴AC=BC,∴OP垂直平分AB,∴AP=BP,又∵OA=OB,OP=OP,第2题解图∴△APO≌△BPO(SSS),∵P A切⊙O于点A,∴AP⊥OA,∴∠P AO=90°,∴∠PBO=∠P AO=90°,∴OB ⊥BP , 又∵点B 在⊙O 上, ∴PB 与⊙O 相切于点B ;(2)解:∵OP ⊥AB ,OP 经过圆心O , ∴BC =12AB =33, ∵∠PBO =∠BCO =90°,∴∠PBC +∠OBC =∠OBC +∠BOC =90°, ∴∠PBC =∠BOC , ∵∠PCB =∠BCO =90°, ∴△PBC ∽△BOC , ∴BC OC =PC BC ,∴OC =BC ·BC PC =33×339=3, ∴在Rt △OCB 中,OB =OC 2+BC 2=6,tan ∠COB =BCOC =3,∴∠COB =60°,PB =OP ·sin60°=63,∴S △OPB =12PB ·BO =183,S 扇形DOB =6036360 g =6π,∴S 阴影=S △OPB -S 扇形DOB =183-6π.3.如图,AB 是⊙O 的直径,点C 、D 在⊙O 上,∠A =2∠BCD ,点E 在AB 的延长线上,∠AED =∠ABC . (1)求证:DE 与⊙O 相切;(2)若BF =2,DF =10,求⊙O 的半径.第3题图(1)证明:如解图,连接DO,∴∠BOD=2∠BCD=∠A,∵∠DEA=∠CBA,第3题解图∴∠DEA+∠DOE=∠CAB+∠CBA,∵∠ACB=90°,∴OD⊥DE,又∵OD为⊙O的半径,∴DE是⊙O的切线;(2)解:如解图,连接BD,可得△FBD∽△DBO,BD DF BF==,BO OD BD∴BD=DF10∴OB=5.4.如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长,交⊙O于点D、E,连接AD并延长,交BC于点F,连接BD、BE.第4题图(1)试判断∠CBD 与∠CEB 是否相等,并证明你的结论; (2)求证:BD BE =CDBC ;(3)若BC =2AB ,求tan ∠CDF 的值. (1)解:∠CBD =∠CEB ,证明如下: ∵AB 是⊙O 的直径,BC 切⊙O 于点B , ∴∠CBD =90°-∠OBD ,又∵DE 过⊙O 的圆心,∴∠DBE =90°,OB =OD , ∴∠CEB =90°-∠ODB ,∠ODB =∠OBD , ∴∠CBD =∠CEB ;(2)证明:∵在△CBD 和△CEB 中, ∵∠CBD =∠CEB ,∠C =∠C , ∴△CBD ∽△CEB ,∴BD BE =CD BC ; (3)解:∵BC =2AB ,OB =12AB , ∴在Rt △OBC 中,OC =32AB ,∴CD =OC -OD =AB ,∵DE 是⊙O 的直径, ∴∠DBE =90°,∵∠CDF =∠ADE =∠ABE =∠BED ,∴tan ∠CDF =tan ∠BED =BD BE =CD BC =AB 2AB =22.5.如图,在Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O 上,CE=CA,AB和CE的延长线交于点F.(1)求证:CE与⊙O相切;(2)若⊙O的半径为3,EF=4,求BD的长.第5题图(1)证明:如解图,连接OE,OC,第5题解图∵OA=OE,CE=CA,OC共用,∴△OEC≌△OAC(SSS),∴∠OEC=∠A=90°,∵OE是⊙O的半径,∴CE与⊙O相切;(2)解:在Rt△OEF中,OE=3,EF=4,∴OF=OE2+EF2=5,∴AF=8,在Rt△ACF中,设AC=x,则CF=CE+EF=x+4,∵AF2+AC2=CF2,∴82+x2=(x+4)2,解得x =6,则AC =6,在Rt △ABC 中,AB =6,AC =6, ∴BC =62,如解图,连接AD ,则AD ⊥BC , ∴BD =12BC =3 2.6.如图,在Rt △ABC 中,∠ACB =90°,以BC 为直径的⊙O 交AB 于点D ,点E 是AC 的中点,OE 交CD 于点F .(1)若∠BCD =36°,BC =10,求BD ︵的长; (2)判断直线DE 与⊙O 的位置关系,并说明理由.第6题图(1)解:如解图,连接OD ,∵∠BCD =36°, ∴∠BOD =2∠BCD =2×36°=72°, ∵BC 是⊙O 的直径,且BC =10, ∴l BD ︵=72π×5180=2π;第6题解图(2)解:DE 是⊙O 的切线.理由如下: ∵BC 是⊙O 的直径,∴∠ADC =180°-∠BDC =90°, 又∵点E 是线段AC 的中点, ∴DE =AE =EC =12AC , 在△DOE 与△COE 中, ∵⎩⎪⎨⎪⎧OD =OC OE =OE DE =CE , ∴△DOE ≌△COE , ∵∠ACB =90°,∴∠ODE =∠OCE =90°, ∵OD 是⊙O 的半径, ∴DE 是⊙O 的切线.7.如图,⊙O 的半径OC 垂直弦AB 于点H ,连接BC ,过点A 作弦AE ∥BC ,过点C 作CD ∥BA 交EA 延长线于点D ,延长CO 交AE 于点F . (1)求证:CD 为⊙O 的切线; (2)若BC =10,AB =16,求OF 的长.第7题图(1)证明:∵OC ⊥AB ,AB ∥CD , ∴OC ⊥DC , ∵OC 是⊙O 的半径, ∴CD 是⊙O 的切线; (2)解:如解图,连接BO .设OB =x ,∵AB =16,OC ⊥AB , ∴HA =BH =8, ∵BC =10,∴CH =6, ∴OH =x -6. 在Rt △BHO 中, ∵OH 2+BH 2=OB 2,∴(x -6)2+82=x 2,解得x =253, ∵CB ∥AE ,∴∠CBH =∠F AH , 在△CHB 和△FHA 中,⎩⎪⎨⎪⎧∠CBH =∠F AH ∠CHB =∠FHA BH =AH, ∴△CHB ≌△FHA ,∴CH =HF , ∴CF =2CH =12,∴OF =CF -OC =12-253=113.第7题解图8.如图,在Rt △ABC 中,∠ACB =90°,以BC 为直径的⊙O 交AB 于点D ,E 是AC 的中点,OE 交CD 于点F .(1)若∠BCD =36°,BC =10,求BD ︵的长;(2)判断直线DE 与⊙O 的位置关系,并说明理由;(3)求证:2CE 2=AB ·EF.第8题图(1)解:如解图,连接OD ,∵∠BCD =36°,∴∠BOD =2∠BCD =2×36°=72°, ∵BC 是⊙O 的直径,且BC =10,∴l BD ︵=72π×5180=2π.第8题解图(2)解:DE 是⊙O 的切线;理由如下:∵BC 是⊙O 的直径,∴∠ADC =∠BDC =90°,又∵点E 是线段AC 的中点,∴DE =AE =EC =12AC ,在△DOE 与△COE 中,∵⎩⎪⎨⎪⎧OD =OC OE =OE DE =CE,∴△DOE ≌△COE ; ∵∠ACB =90°,∴∠ODE =∠OCE =90°, ∵OD 是⊙O 的半径,∴DE 是⊙O 的切线;(3)证明:∵△DOE ≌△COE ,∴OE 是线段CD 的垂直平分线,DE =CE , ∴点F 是线段CD 的中点,∵点E 是线段AC 的中点,则EF =12AD ,在△ACD 与△ABC 中,⎩⎨⎧∠CAD =∠BAC ∠ADC =∠ACB, ∴△ACD ∽△ABC ,则AC AB =AD AC ,即AC 2=AB ·AD ,而AC =2CE ,AD =2EF , ∴(2CE )2=AB ·2EF ,即4CE 2=AB ·2EF ,∴2CE 2=AB ·EF .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆切线的有关证明和计算
已知:如图,在Rt ABC △中,90C ∠=,点O 在AB 上,以O 为圆心,OA 长为半径的圆与AC AB ,分别交于点D E ,,且CBD A ∠=∠. (1)判断直线BD 与O 的位置关系,并证明你的结论;
(2)若:8:5AD AO =,2BC =,求BD 的长.
解:(1)
(2)
已知:如图,在△ABC 中,AB=AC,AE 是角平分线,BM 平分∠ABC 交AE 于点M,经过
B,M 两点的⊙O 交BC 于点G,交AB 于点F,FB 恰为⊙O 的直径. (1)求证:AE 与⊙O 相切; (2)当BC=4,cosC=
1
3
时,求⊙O 的半径.
(1)通过平行找垂直。
如果以下几种题型
如图,已知△ABC ,以AB 为直径的⊙O 经过BC 的中点D ,DE ⊥AC 于E .
(1)求证:DE 是⊙O 的切线;
(2)若2
1
cos =
C , 6DE =, 求⊙O 的直径. 已知:如图,⊙O 为ΔABC 的外接圆,BC 为⊙O 的直径,作射线BF 使得BA 平分 ∠CBF ,过点A 作A
D ⊥BF 于D (1)求证:DA 为⊙O 的切线
(2)若BD=1,⊙O 的半径为2
5
,求tan ∠BAD
F
A
D
B O
C
(2)通过计算角的度数找垂直 如果以下题型
D C
O
A B
E
10.已知,A 是⊙O 上一点,半径的延长线与过点A 的直线交于B 点,OC=BC,AC=
2
1
OB 。
(1)求证:AB 是⊙O 的切线
(2)若∠ACD=45°,OC=2,求弦CD 的长 D O C A B
已知如图,点D 是⊙O 的直径延长线上一点,点B 在⊙O 上,且OA=AB=AD (1)求证:BD 是⊙O 的切线
(2)若点E 是劣弧BC 上一点,AE 与BC 相交于点F ,且BE=8,tan ∠BFA=
2
5
,求⊙O 的半径 B
F E D A O C
已知:如图,在⊿ABC 中,D 是AB 边上一点,⊙O 过 A,B,C 三点,∠DOC=2∠ACD=90° A (1)求证:直线AC 是⊙O 的切线; D (2)如果∠ACB=75°,⊙O 的半径为2,求BD 的长 B C O
(3)根据角与角的关系推导
已知:如图,AB 是O 的直径,BC 切O 于B ,AC 交O 于P ,D 为BC 边的中点,连结DP .
(1) DP 是O 的切线; (2) 若3cos 5
A
, O 的半径为5, 求DP 的长.
如图,D 是⊙O 的直径CA 延长线上一点,点 B 在⊙O 上, 且AB =AD =AO .
(1)求证:BD 是⊙O 的切线;
(2)若E 是劣弧BC 上一点,AE 与BC 相交于点F ,
B
A
O
B
F C
D
E
△BEF 的面积为8,且cos ∠BF A =3
2, 求△ACF 的面积.
如图,在△ABC ,AB =AC ,以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ,点F 在AC 的
延长线上,且∠CBF = 1
2
∠CAB .
(1)求证:直线BF 是⊙O 的切线; (2)若AB =5,sin ∠CBF =
5
5
,求BC 和BF 的长.
如图,AB 为⊙O 的直径,AB =4,点C 在⊙O 上, CF ⊥OC ,且CF =BF . (1)证明BF 是⊙O 的切线;
(2)设AC 与BF 的延长线交于点M ,若MC =6,求∠MCF 的大小.
二.在计算圆切线的有关线段时常用的方法有,三角函数值,勾股定理,三角形相似等,其中最通用的是三角形相似,如上面几题的第二问。
三.跟踪练习
1.已知:如图,AB 为⊙O 的直径,AB=AC ,BC 交⊙O 于点D ,延长CA 交⊙O 于点F ,连接DF ,作DE ⊥CF 于点E. (1)求证:DE 是⊙O 的切线 (2)若AB =10,cos ∠C=
5
4
,求EF 的长 C D
E B O A F
A F C O
B
M
2.已知:如图,AB 为⊙O 的直径,⊙O 过AC 的中点D,DE ⊥BC 于点E , (1)求证:DE 为⊙O 的切线 (2)若DE=2,tanC=2
1
,求⊙O 的直径 C
A D
O E
B
3.如图,已知⊙O 是⊿ABC 的外接圆,AB 是⊙O 的直径,D 是AB 延长线的一点,AE ⊥CD ,交DC 的延长线于E ,CF ⊥AB 于F,且CE=CF E (1)求证:DE 是的切线 C (2)若AB=6,BD=3,求AE 和BC 的长
A O F
B D
4.已知等边三角形ABC,以边BC 为直径的半圆与边AB,AC 分别交于点D ,点E,过点D 作DF ⊥AC ,垂足为点F 。
(1)判断DF 与⊙O 的位置关系,并证明你的结论
(2)过点F 作FH ⊥BC ,垂足为点H,若等边三角形ABC 的边长为4,求FH 的长 A F D E B O H C
.已知:如图,AB 为⊙O 的直径,弦AC ∥OD,BD 切⊙O 于点B ,连接CD (1)判断CD 和⊙O 的位置关系,并说明理由 (2)若AD=2,OD=6,求⊙O 的半径 A C O
B D
1. 如图,在矩形ABCD 中,点O 在对角AC 上,以OA 长为半径的⊙O 与AD 、AC 分
别交于点E 、F ,且DCE ACB ∠=∠。
(1)求证:CE 是⊙O 的切线;
(2)若4
3
tan =∠ACB ,7=AE ,求⊙O 的直径。
