冀教版数学六年级上册第1单元《圆和扇形》(扇形)知识梳理:圆和扇形
小学数学冀教版六年级上册《1.1圆和扇形》课件

3.由两条半径和圆上的一段曲线围成的图形叫 ( 扇形 )。
4.用圆规画一个半径为 5 厘米的圆,圆规两脚间 的距离是( 5厘米 ),如果画一个直径为 6 厘 米的圆,则圆规两脚间的距离是( 3厘米 )。
二、明辨是非。(判断对错)
1. 两端都在圆上的所有线段中,直径最长。(
在日常生活和学习中,我们经常用圆规画圆。
(1)把圆规的两脚 分开,定好两脚间的 距离(即半径)。
(2)把有针尖的一 只脚固定在一点(即 圆心)上。
(3)把装有铅笔尖的一 只脚旋转一周,就画出 一个圆。Βιβλιοθήκη 欣赏图案。 (1)(2)
(3)
(4)
用圆规和直尺等工具就能设计出这些图案。
右图中,圆上A、B两 点之间的部分叫做弧, 读作:弧AB。
冀教版数学 六年级上
圆和扇形
长方形
正方形 平行四边 形
梯形
三角形
直线图形
圆是平面上的一种曲线图形
圆
圆心 圆内
圆上 圆外
圆心 连接圆心和圆上任意一点的线段叫做半径。
直径 d 通过圆心并且两端都在圆上的线段叫做直径。
r
d• o r
d=r+r d=2r
r=
d 2
在同一个圆里,直径是半径的2倍,半径是直径的一半.
)
2. 在同一个圆内,两条半径就是一条直径。(
)
3. 通过圆心的线段叫做圆的直径。(
)
4. 一个圆至少对折3 次,就可以找到圆的圆心。(
)
5. 在正方形中画一个最大的圆,直径和正方形的边长相等。(
)
6. 圆在平面滚动时,圆心在一条直线上运动。(
六年级数学知识点 圆和扇形知识点_知识点总结

六年级数学知识点圆和扇形知识点_知识点总结圆和扇形是六年级数学中的重要知识点。
掌握圆和扇形的概念、性质以及相关计算方法对于解决与几何形体相关的问题尤为关键。
本文将对六年级数学中的圆和扇形知识点进行总结,帮助同学们更好地理解和掌握。
一、圆的概念圆是平面上一组距离中心点相等的点的集合。
其中,距离中心点相等的线段称为半径,中心点到圆上任意一点的距离称为半径。
圆上任意两点之间的线段称为弦。
二、圆的性质1. 圆的直径:通过圆心且在圆上的一条线段,其两个端点在圆上。
直径的长度是半径的两倍。
2. 圆的弧:两个端点在圆上的一条曲线。
3. 弧长:弧长是弧所对的圆心角所对应的圆周的长度。
如下图所示,弧AB所对应的圆周长度即为弧长。
4. 圆周角:以圆心为顶点的角。
任意两个在圆周上的点,以这两点为端点所得的圆心角都是一个圆周角。
三、扇形的概念扇形是由圆心、圆上的一个点和圆上的一条弧所确定的图形。
其中,圆心角是扇形的一条边所对应的圆心角。
四、扇形的性质1. 扇形的弧长:扇形的弧长是以圆心角所确定的扇形所对应的圆周的长度。
计算扇形的弧长使用的公式为:弧长 = (圆心角 / 360°) ×圆周长。
2. 扇形的面积:扇形的面积是以圆心角所确定的扇形所对应的圆的面积。
计算扇形的面积使用的公式为:面积 = (圆心角 / 360°) ×圆的面积。
五、圆和扇形的应用圆和扇形的概念和性质在实际中有广泛的应用。
以下是一些常见的应用情景:1. 钟面设计:钟面通常由多个扇形组成,掌握扇形的计算方法可以帮助我们设计出精美的钟表。
2. 构造轮胎:轮胎是由多个圆环组成的,掌握圆的性质可以帮助我们选择合适的尺寸和材料。
3. 日常生活中的圆物体:在生活中,我们经常会遇到圆形的物体,比如水杯、盘子等。
了解圆的概念和性质,可以帮助我们更好地理解和应用这些物体。
六、总结本文对六年级数学中的圆和扇形知识点进行了总结。
通过掌握圆和扇形的概念、性质以及应用,同学们可以更好地解决与几何形体相关的问题。
[冀教版数学六下]冀教版六年级数学上册第1单元圆和扇形教案及反思
![[冀教版数学六下]冀教版六年级数学上册第1单元圆和扇形教案及反思](https://img.taocdn.com/s3/m/461f88a0fe4733687e21aaf5.png)
[冀教版数学六下]冀教版六年级数学上册第1单元圆和扇形教案及反思第一单元圆和扇形一、教学内容说课的内容是小学数学冀教版六年级上册第一单元《圆的认识》的第一课时。
本课是空间与图形领域的内容,它既是一节起始课,同时也是后继学习的内容------圆周长、面积、扇形。
学生对圆并不陌生,但只是直观的认识,本课将进一步认识圆的特征及其内在联系,让学生深切体会圆与我们生活紧密相连。
二、教学目标根据我对教材的理解和学生的认知水平,设计如下教学目标1、知识与技能目标:组织学生通过画一画、折一折、观察体验圆的特征,认识圆的各部分名称,理解在同一个圆内直径与半径的关系;认识直径和半径的关系,能找出圆的对称轴。
2、过程与方法目标:在观察、操作、交流等活动中,经历认识圆的过程。
3、情感态度与价值观目标:对周围环境中与圆有关的事物有好奇心,发展初步的空间观念。
让学生养成在交流、合作中获1/ 12得新知的习惯。
教学重点:探索出圆各部分的名称、特征及关系。
教学难点:通过动手操作体会圆的特征。
6、教学关键:指导学生正确使用圆规,多进行实际操作练习。
学生分析:在小学阶段,学生的空间观念比较薄弱,动手操作能力比较低;本校处在城乡结合处,家庭辅导能力较低,学生接受能力较差;学生的学习水平差距较大,小组合作意识不强,鉴于以前学习长、正方形等是直线平面图形,而圆是曲线平面图形,估计学生在动手操作、合作探究方面会存在一些困难。
说教法学法:学生的学习过程是一个主动建构的过程,教师要激活学生的先前经验,激发学习热情,让学生在经历、体验和运用中真正感悟知识。
本节课我以学生亲自动手制作车轮为主线,在动手中引导学生认识圆的各部分名称,理解圆的特征,以及教学圆的画法时,有目的、有意识地安排了让学生画一画、指一指、比一比、量一量等动手实践活动,启发学生用眼观察,动脑思考,动口参加讨论,用耳去辨析同学们的答案。
教学中理应发挥学生的主体作用,淡化教师的主观影响,让学生自己在实践中产生问题意识,自己探究、尝试,修正错误,2/ 12总结规律,从而主动获取知识。
冀教版小学数学六年级上册第一单元 圆和扇形说课稿

第一单元 圆和扇形例1:在下面圆里的几条线段中,那一条是直径?观察比较这些线段的长度,你发现了什么?解析:此题考察了直径的定义。
解题关键是掌握直径的定义,即过圆心且两端都在圆上的线段是圆的直径。
据此即可找出直径;通过观察比较这些线段的长度可以发现:直径是连接圆上任意两点所成的线段中最长的一条。
答案:例2:你注意过吗?下水道的井盖都是圆形的。
你知道是为什么吗?解析:此题考查了,圆上任意一点到圆心的距离都相等。
根据这一特征井盖做成圆的,这样盖到下水道口比较密实,并且无论怎么翻转,井盖也不会掉到井内。
解答:因为在同圆中所有的半径都相等,所以这样的井盖盖到下水道口比较密实,并且无论怎么翻转,井盖也不会掉到井内。
例3:在正方形内画一个最大的圆。
解析:此题考察了圆的画法。
解题关键在正方形里找到最大圆的圆心和半径的长度。
圆心即正方形对角线的连线,半径即正方形边长的一半。
如图:解答:例4:在正方形里画一个最大圆,若圆的半径为2厘米,正方形的面积是多少?解析:此题考查了正方形与正方形内最大圆的的关系。
由图意可知正方形内最大的圆的半径是正方形边长的一半,即正方形的边长=半径×2,再根据正方形的面积=边长×边长,求出面积即可。
解答:(2×2)×(2×2)=16(平方厘米)例5:你能在下面的圆内画一个最大的正方形吗?解析:先确定出最大正方形的对角线即为最大圆的直径,先画出两条互相垂直的直径,在连接直径与圆的交点,即为所做的图形。
答案:点拨:圆的直径为正方形的对角线。
例6求长方形的面积。
解析:由图中可以看出长方形中的三个圆是等圆,即长方形的长与三个直径的长度相等,用长方形的长除以3既是圆的直径;长方形的宽与圆的直径相同。
根据长方形的面积公式=长×宽,即可求出长方形的面积。
解答:6×(6÷3)=12(平方厘米)答:长方形的面积是12平方厘米。
例7:画一个长4厘米,宽2.5厘米的长方形,在长方形内画一个最大的半圆, 这个半圆的半径是多少厘米?试着画一画。
冀教版六年级上册数学复习

冀教版六年级上册数学复习第一单元:圆和扇形1.圆的特点:易滚动,是轴对称图形,有无数条对称轴,所有对称轴都相交于圆中心的一点。
2.我们把圆中心的这一点叫做圆心,圆心用字母O来表示。
3.我们把通过圆心并且两端都在圆上的线段叫做直径,直径用字母d来表示,直径是圆上最长的线段。
4.我们把连接圆心和与圆上任意一点的线段叫做半径,半径一般用字母r来表示。
5.一个圆有无数条半径和直径。
6.同圆或等圆的直径是半径的2倍。
用字母表示d=2r或r=d÷2。
7.测量没有标出圆心的圆的直径的办法:1.在圆中画一个最大的正方形,画出正方形的对角线,找到圆心。
2.在圆的下方放一把直尺(紧贴圆的底部)再在直尺上方,圆的左右边分别放上两把三角板(紧贴圆)看直尺的刻度即可。
3.把圆的四个较长的地方向外延伸,画出一个正方形,画出正方的的对角线,找到圆心。
(和第一种方法相似,那个是在圆中画一个最大的正方形,这个是在正方形中画一个最大的圆。
)8.圆心决定圆的位置,半径决定圆的大小。
9.图案设计,只要有点想象力就ok了10.扇形都有一个角的顶点在圆心,扇形是由两条半径和圆上的一段曲线围成的。
(注意是一段曲线,绝对不会出现一个扇形的圆心角是360度的现象)二比和比例1.像1:3,3:1这样的表示方法,叫做比。
“:”是比号。
2.比表示两个数相除,两个数相除的结果,叫做比值,比由前项、比号、后项、比值组成。
3.比,分数,除法的不同,比表示一种关系,除法是运算,分数是值。
4.比的前项、后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
应用这个性质可以把比化成最简整数比。
5.表示两个比相等的式子叫做比例,组成比例的四个数叫做比例的项,两端的两项叫做比例的外项,中间的两项叫做比例的内项。
6.在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
7.如果把比例写成分数形式,等号的两端的分子和分母分别交叉相乘,它们的积相等。
冀教版数学知识点总结(六上)

六年级数学上册知识点总结第一单元圆和扇形一、圆的特征1、圆是平面内封闭曲线围成的平面图形。
2、圆的特征:外形美观,易滚动。
3、圆心o:圆中心的点叫做圆心.圆心一般用字母O表示.圆多次对折之后,折痕的相交于圆的中心即圆心。
圆心确定圆的位置。
半径r:连接圆心到圆上任意一点的线段叫做半径。
在同一个圆里,有无数条半径,且所有的半径都相等。
半径确定圆的大小。
直径d:通过圆心且两端都在圆上的线段叫做直径。
在同一个圆里,有无数条直径,且所有的直径都相等。
直径是圆内最长的线段。
同圆或等圆内直径是半径的2倍:d=2r 或 r=d÷24、等圆:半径相等的圆叫做等圆,等圆通过平移可以完全重合。
同心圆:圆心重合、半径不等的两个圆叫做同心圆。
5、圆是轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
折痕所在的直线叫做对称轴。
有一条对称轴的图形:半圆、扇形、等腰梯形、等腰三角形、角有二条对称轴的图形:长方形有三条对称轴的图形:等边三角形有四条对称轴的图形:正方形有无条对称轴的图形:圆,圆环6、画圆(1)圆规两脚间的距离是圆的半径。
(2)画圆步骤:定半径、定圆心、旋转一周。
二、扇形扇形是由两条半径和圆上的一段曲线围成的。
扇形都有一个角,角的顶点在圆心。
第二单元比和比例一、比1、比表示两个数相除。
两个数相除的结果叫做比值。
2、比式中,比号(∶)前面的数叫前项,比号后面的项叫做后项,比号相当于除号,比的前项除以后项的商叫做比值。
注:连比如:3:4:5 读作:3比4比53、比表示的是两个数的关系,可以用分数表示,写成分数的形式,读作几比几。
例:12∶20= 12÷20=0.6 12∶20读作:12比204、区分比和比值:比值是一个数,通常用分数表示,也可以是整数、小数。
比是一个式子,表示两个数的关系,可以写成比,也可以写成分数的形式。
5、比的基本性质:比的前项和后项同时乘以或除以相同的数(0除外),比值不变。
冀教版小学六年级上册数学 第一单元 圆和扇形 第1课时 圆的认识

· 圆心O 半径r 直径d
(教材P3 上面的T1)
1.用下面的方法可以测量出没有标出圆心的圆的直径。
同桌合作, 试一试。
(教材P3 上面的T2)
2.分别量出右面圆内几条线段的 长度。你发现了什么?
自己动手量一量。
发现:直径是两点都在圆上的最长的线段。
练一练
(教材P3 T1)
义务教育冀教版六年级上册
第一单元
第1课时
圆和扇形
圆的认识
情境导入
动物汽车设计大赛。
开始啦!
探究新知
你喜欢谁的设计? 说说喜欢的理由。
我们周围有很多物品的面是圆形的,如硬币的面、 钟表的面、圆桌的面、茶叶筒的上下面等。
你还能举出哪些物品的面是圆形的?
(1)用一个瓶盖或圆柱体在纸上描出一个圆并剪下来。
1.找出下面各圆的半径或直径并用字母表示。
直径d
半径r
半径r
(教材P3 T2)
2.按要求画出半径或直径,用字母表示并测量。
(1)画出一条半径。 (2)画出一条直径。
半径r
1.5cm
直径 d
2.5cm
(教材P3 T3)
3.你注意过吗?下水道的井盖都是圆形的。你知道这 是为什么吗?
小组讨论,全班交流。
课堂小结
通过这节课的学习,你有什么收获?
连接圆心和圆上任意一点的线段叫做半径。 半径一般用字母r来表示。
1.一个圆有多少条直径和多少条半径?它们有什么关系? 一个圆有无数条直径和半径。
同一个圆的直径 是半径的2倍。
· 圆心O 半径r 直径d
d=2r或r=
d 2
2.圆和我们以前学过的图形有什么不同?
长方形、正方形、三角形ຫໍສະໝຸດ 都是 由线段围成的图形;(2)将圆形纸片对折,打开;换个方向再对折,打开; 反复几次。你发现了什么?
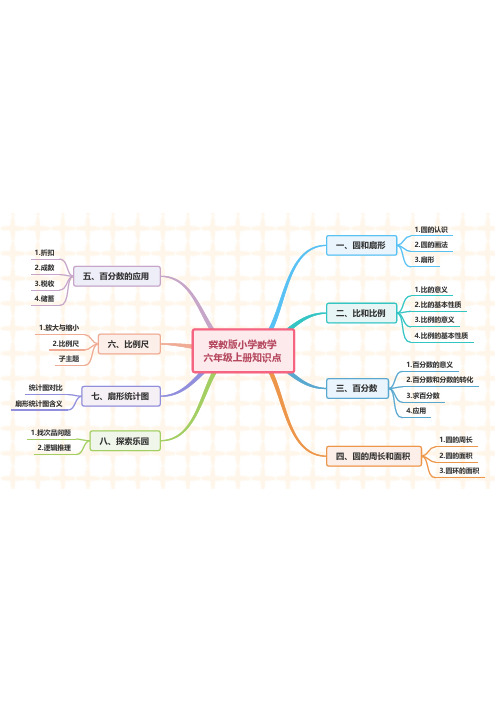
冀教版小学数学六年级上册1-8单元思维导图
把圆规的两脚分开,定好两脚间的距离(半径)
把有针尖的一只脚固定在一点(圆心)上。
把装有铅笔的一只脚旋转一周,就画出了一个圆。
圆是轴对称图形,直径所在的直线是对称轴
圆有无数条直径和半径
直径是圆内最长的线段
圆心决定圆的位置,半径决定圆的大小
同圆或等圆中,直径是半径的两倍
3.
比的前项和后项同时乘或者除以相同
的数(0除外)比值不变
求比值结果是一个数
化简比的结果是一个比
表示两个比相等的式子叫做比例
6:2=3:1
4.两个外项的积等于两个内项的积。
求比例中的未知项
找到总量和总份数
求出单个份数是多少
用乘法计算各部分量
根据比例的基本性质计算
百分数化分数分数化百分数去掉百分号
改写成分母为100的分数分数化小数
小数
单位
滚动法
绕绳法4.
周长
2.
2.圆环面积计算S=πR²-πr²S=π(
单位
原来的量
设方程解决应用题
2.
原价
2.
应纳税额
利息
按比例放大或缩小图形
图形各边的比例和角度都没变
图形的面积变了
比例尺
图上距离
实际距离
计算路线的长度
)条形统计图能够直观表达数量的多少
)折线统计图不仅能够表示数量多少,还能看到数量增减变化的多少)扇形统计图能清楚反映各部分与总数之间的关系
总量部分量
含义
方法不能平均分也要使多或少的那一份与其他只差
规律
对应次数+1
排除法
列表法
反证法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.同圆或等圆中半径和直径的关系:在同圆或等圆中,直径的长度是半径的2倍,可以表示为d=2r或r= 。
6.用圆规画圆的方法:
(1)把圆规的两脚分开,定好两脚间的距离(即半径);
(2)把有针尖的一只脚固定在一点(即圆心)上;
(3)把装有铅笔尖的一只脚旋转一周,就画出一个圆。
圆和扇形
知识模块
具体内容
要ห้องสมุดไป่ตู้提示
圆
1.圆的特征:圆是由曲线围成的封闭的图形,圆上任意一点到圆心的距离都相等。
2.圆的各部分名称:圆中心的一点叫做圆心,圆心一般用字母O表示;连结圆心上任意一点的线段叫做半径;半径一般用字母r表示;通过圆心并且两端都在圆上的线段叫做直径,直径一般用字母d表示。
3.圆心和半径的作用:圆心决定圆的位置,半径决定圆的大小。
1.在比较直径和半径的长度时,一定要考虑到附加条件,即在同圆或等圆中。
2.圆的大小由半径或直径决定。
图案设计
利用旋转、对称、平移的知识设计图案。
可以同时运用旋转、对称、平移设计图案。
扇形
1.扇形:由两条半径和圆上的一段曲线围成。
2.圆心角:顶点在圆心上,由两条半径组成的角叫做圆心角。
扇形是圆的一部分。
