第19届希望杯全国数学邀请赛初二第1试试题

合集下载

第19届希望杯全国数学邀请赛初二第1试试题

第19届希望杯全国数学邀请赛初二第1试试题一、选择题（每小题4分，满分40分）1．下列说法中正确的是（）A 、1的平方根和1的立方根相同B 、0的平方根和0的立方根相同C 、4的平方根是2±D 、8的立方根是2±2．若单项式x x b a 52-和x b a -3223的次数相同，则x 的整数值等于（）A 、1B 、-1C 、1±D 、1±以外的数3．若b a ,和b a +都是有理数，则（） A 、b a ,都是有理数 B 、b a ,都是无理数 C 、b a ,都是有理数或都是无理数 D 、b a ,中有理数和无理数各一个4．使不等式12>+x 成立的x 的值为（）A 、比-1大的数B 、比-3小的数C 、大于-1或小于-3的数D 、-2以外的数5．设e d c b a ,,,,只能从-3，-2，-1中取值，又22222,e d c b a y e d c b a x +-+-=+-+-=，则（）A 、x 的最大值比y 的最大值小B 、x 的最小值比y 的最小值小C 、x 的最大值比y 的最小值小D 、x 的最小值比y 的最大值大6．In the figure1, ABCD is a diamond, points E and F lie on its sides AB and BC respectively, such that CF BF BEAE=, and DEF ∆ is a regular triangle. Then BAD ∠ is equal to ( ) A 、400 B 、600 C 、800 D 、1000 （（英汉小词典：diamond 菱形；regular triangle 正三角形） 7．已知ABC ∆的三边长分别为c b a ,,，且a c b c b c a b a-++=+，则ABC ∆ 一定是（）A 、等边三角形B 、腰长为a 的等腰三角形C 、底边长为a 的等腰三角形D 、等腰直角三角形8．初二（1）班有48名同学，其中有男同学n 名，将他们编成1号、2号、…，n 号。

第19届希望杯数学邀请赛初二第二试试题

第十九届“希望杯”全国数学邀请赛初二第2试一、选择题(本大题共10小题，每小题4分，共40分.)以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题后面的圆括号内. 1.将数字“6”旋转180︒，得到数字9；将数字“9”旋转180︒，得数字6；那么将两位数“69” 旋转180︒，得到的数字是( )(A)69 (B)96 (C)66 (D)99【解析】选A . 2.关于x ，y 的方程组10210x ay bx y ++=⎧⎨-+=⎩，有无数组解，则a ，b 的值为( )(A)0a =，0b = (B)2a =-，1b = (C)2a =，1b =- (D)2a =，1b =【解析】选B .有无数组解，则要求1121a b ==-，故2a =-，1b =. 3.在平面直角坐标系内，有等腰三角形AOB ，O 是坐标原点，点A 的坐标是(a ，)b ，底边AB 的中线在1、3象限的角平分线上，则点B 的坐标是( )(A)(b ，)a (B)(a -，)b - (C)(a ，)b - (D)(a -，)b【解析】选A .底边上的中线即对称轴，可见AOB ∆以1、3象限的角平分线为对称轴，则A 、B 关于1、3象限的角平分线对称，从而可知B 的坐标.4.给出两列数：⑴ 1，3，5，7，…，2007；⑵ 1，6，11，16，…，2006，则同时出现在两列数中的数的个数是( )(A)201 (B)200 (C)199 (D)198【解析】选A .第1列数的第m 个数为21m a m =-，其中1004m ≤；第2列数的第n 个数为54n a n =-，其中402n ≤.同时出现在两列数中的数满足2154m n -=-，即235m n +=，当1m =，6，11， (1001)时n 取整数，这样m 共有201个，故选A .5.If one side of a triangle is 2 times of another side and it has the largest possible area ，then the ratio of its three sides is( )(A)123∶∶ (B)112∶∶ (C)132∶∶ (D)125∶∶(英汉小词典：possible 可能的；area 面积；ratio 比率，比值)【解析】选D .译文：如果三角形的一条边是另一条边的两倍，且其具有最大的面积，则三条边的比值为多少？由题意知，当此两边夹角为90︒时面积最大，若记两边分别为1和2，5，故选D .6.面值为10元、20元、50元的人民币(每种至少一张)共24张，合计1000元，那么其中面值为20元的人民币有( )张.(A)2或4 (B)4 (C)4或8 (D)2到46之间的任意偶数【解析】选B .记10元、20元、50元面值的人民币分别有a 张、b 张、c 张，则24a b c ++=，1020a b ++ 501000c =，由此条件可知2425100a b c a b c ++=⎧⎨++=⎩，消去c 可得4320a b +=，即4(5)3ab -=，当2a =时，4b =，此为唯一解.7.由1，2，3这三个数字组成四位数，在每个四位数中，这三个数字至少出现一次，这样的四位数有( )个.(A)33个 (B)36个 (C)37个 (D)39个【解析】选B .有四个数位，而仅有三个数字，故必有某一个数字出现了两次，记某个数字a 出现了两次，我们先将b 、c 排好，然后剩余的位置放下两个a 即可，这有43⨯种排法，而出现两次的数字可能是b 或c ，故所有情况共有43336⨯⨯=种.8.如图，矩形ABCD 的长9cm AD =，宽3cm AB =，将它折叠，使点D 与点B 重合，那么折叠后DE 的长和折痕EF 的长分别是( )(A)5cm，(B)5cm ，3cm (C)6cm(D)5cm ，4cm【解析】选A .记DE x =，则9AE x =-，由折叠的对称性可知DE BE =，即BE x =. 在Rt ABE ∆中，222AB AE BE +=，即2223(9)x x +-=，得5x =.连接BD 交EF 于点O ，由折叠的特点知BD EF ⊥，易知22310BD AB AD =+=，则31022BD BO ==. 而5BE =，故2210EO BE BO =-，从而210EF EO ==9.如图，函数4y mx m =-的图象分别交x 轴、y 轴于点M 、N ，线段MN 上两点A 、B 在x 轴上的垂足分别为1A 、1B ，若114OA OB +>，则1OA A ∆的面积1S 与1OB B ∆的面积2S 的大小关系是( )(A )12S S > (B )12S S = (C )12S S < (D )不确定的【解析】选C .对于直线4y mx m =-上的任意一点P ，记其横坐标为P x ，则其纵坐标4P P y mx m =-，其面积211(4)(4)222P P P P P P P m S x y x mx m x x ==-=-，故22121122(4)(4)2m S S x x x x ⎡⎤-=---⎣⎦221212()4()2m x x x x ⎡⎤=---⎣⎦[]1212()(4)2m x x x x =-+-. 注意到120x x -<，124x x +>，故120S S -<.10. 已知a 是方程3310x x +-=的一个实数根，则直线1y ax a =+-不经过( )(A )第1象限 (B )第2象限 (C )第3象限 (D )第4象限【解析】选D .实质是判断a 与0、a 与1的大小关系.注意到(0)(1)0f f ⋅<，故01a <<，从而选D .B 1yABMA 1NS 1S 2O二、填空题(本大题共l0小题，每小题4分，共40分.)11. 化简：7()3，得到 .【解析】填1.原式20082008100410042008200873(15)73()()()137(15)37+==⋅=+.12. 三位数3ab 的2倍等于8ab ，则3ab 等于 . 【解析】填374.视ab 为一个整体，则2(300)108ab ab +=+，即8592ab =，则74ab =，故3374ab =.13. 当2x >2121x x x x +---，得 . 【解析】填21x -221(1)211(11)11x x x x x x +--+-+-+-，221(1)211(11)11x x x x x x -----+--=-，2121(11)(11)21x x x x x x x +---=-+-=-14. 已知111()12f x x x x =--++，并且()0f a =，则a 等于 . 【解析】填2111()12f a a a a =--++111()12a a a =--++(1)1(1)2a a a a a +-=-++2112a a a =-++，从而必有22a a a +=+，即2a =15. If the sum of a 4-digit natural number and l 7，the difference between it and 72 are all squarenumbers ，then the 4-digit natural number is . (英汉小词典：4-digit natural number 四位自然数；difference 差；square number 完全平方数) 【解析】填2008.译文：若某个四位自然数与17的和，以及此四位自然数与72的差均为完全平方数，则此四位自然数是 .记此四位自然数为x ，则217x m +=，272x n -=，故2289m n -=，即()()891m n m n +-=⨯. 注意到m n m n +>-，故89m n +=，1m n -=，从而45m =，44n =，故2008x =.16. 将等腰三角形纸片ABC 的底边BC 折起，使点C 落在腰AB 上，这时纸片的不重合部分也是等腰三角形，则A ∠= . 【解析】填1807︒. 如图所示，C 点翻折之后的位置为'C ，记A x ∠=. 易知''AC CC =，故'ACC x ∠=，''2BCC BC C x ∠=∠=，3ACB x ∠=，而3ABC ACB x ∠=∠=，从而7180x =︒，解得1807x ︒=.17. 将100只乒乓球放在唧个盒子中，使得每个盒子中的乒乓球的个数都含有数字“8”，如当3n =时，箱子中的乒乓球的数目可以分别为8，8，84；若5n =时，有且只有两个箱子中的乒乓球个数相同，那么各箱子中的乒乓球的个数分别是 . 【解析】填8、8、18、28、38.考查球的个数最多的盒子其乒乓球个数的最大值是多少.因为有且仅有两个盒子的球的个数相同，故前四个盒子中球的总数的最小值为88182862+++=，则第五个盒子中最多有38个球.注意到“28”之后含有数字“8”的仅有“38”，即第五个盒子中球的个数不能比“38”小，故只能取“38”，从而五个盒子中球的个数只能是8、8、18、28、38.18. 已知一个有序数组(a ，b ，c ，)d ，现按下列方式重新写成数组1(a ，1b ，1c ，1)d ，使1a a b =+，1b b c =+，1c c d =+，1d d a =+，按照这个规律继续写出2(a ，2b ，2c ，2)d ，…，(n a ，n b ，n c ，)n d ，若1000<2000n n n na b c d a b c d+++<+++，则n = .【解析】填10.11112()a b c d a b c d +++=+++，2x3x2xxxC'CBA2222211112()2()a b c d a b c d a b c d +++=+++=+++， 3333322222()2()a b c d a b c d a b c d +++=+++=+++，…………2()n n n n n a b c d a b c d +++=+++.故100022000n <<，从而10n =.19. 如图，一束光线从点O 射出，照在经过A (1，0)、B (0，1)的镜面上的点D ，经AB 反射后，反射光线又照到竖立在y 轴位置的镜面．要使最后经y 轴再反射的光线恰好通过点A ，则点D的坐标是 .【解析】填(13，23).作点A 关于y 轴的对称点'A ，则'(1A -，0)；作点O 关于AB 的对称点'O ，则'(1O ，1). 连接''A O ，交AB 于点D ，此即所求的点.易知直线AB 的方程为1y x =-+，直线''A O 的方程为1122y x =+，则其交点为1(3D ，2)3.20. 某条直线公路上有1A ，2A ，…，11A 共11个车站，且212i i A A +≤km (1i =，2，3，…，9)，317i i A A +≥ km (1i =，2，3，…，8)，若11156A A =km ，则101127A A A A += km .【解析】填34.首先有233217125i i i i i i A A A A A A ++++=-≥-=.注意到111144771010111011()317A A A A A A A A A A A A =+++≥⨯+，即10115A A ≤，而235i i A A ++≥，故10115A A =.注意到811810101117A A A A A A =+≥，即81012A A ≥，而81012A A ≤，故81012A A =，进而可得1839A A =. y A BO O'A'y A B DEO而1814477878()217A A A A A A A A A A =++≥⨯+，则785A A ≤，而785A A ≥，故785A A =，进而可得5712A A =.同理，455A A =，2412A A =，125A A =. 故10112751251234A A A A +=+++=.三、解答题(本大题共3小题．共40分.) 要求：写出推算过程． 21. (本题满分10分)如图，在ABC ∆中，90ACB ∠=︒,10AC BC ==，CD 是射线，60BCF ∠=︒，点D 在AB 上，AF 、BE 分别垂直于CD (或延长线)于F 、E ，求EF 的长．【解析】由60BCE ∠=︒可知5CE =，由30ACF ∠=︒可知53FC =而EF FC EC =-，故535EF =.22. (本题满分15分)在直角坐标系中，ABC ∆满足：90C ∠=︒，2AC =，1BC =，点A 、 C 分别在x 轴、y 轴上，当A 点从原点开始在正x 轴上运动时，点 C 随着在正y 轴上运动．(1) 当A 在原点时，求原点O 到点B 的距离OB ； (2) 当OA OC =时，求原点O 到点B 的距离OB ；(3) 求原点O 到点B 的距离OB 的最大值，并确定此时图形应满足什么条件?【解析】 (1) 如图所示，5OB AB ==.60︒FABCD E y 21A BCEO y 21ABC DO(2) 过点O 作BC 的垂线，交BC 的延长线于点D ，如图所示.因为OA OC =，则45OCA ∠=︒，而90ACB ∠=︒，可知45OCD ∠=︒.易知2OA OC ==1DC DO ==，则2DB DC CB =+=，225OB DB DO =+=(3)取AC 的中点E ，连接BE 、OE ，则22BE BC CE =+1OE =. 而OB OE BE ≤+，故OB 的最大值为12+此时45OEA AEB ∠=∠=︒，而CE OE =，故122.52OCA OEA ∠=∠=︒.23. (本题满分15分)已知m ，n (m n >)是正整数．(1) 若3m 与3n 的末位数字相同，求m n +的最小值； (2) 若3m 与3n 的末两位数字都相同，求m n -的最小值．yx 21A B C EO y 21A BCE O【解析】 (1) 由题意得330(mod10)m n -≡，即3(31)0(mod10)n m n --≡，故31(mod10)m n -≡，从而4m n k -=，故(4)4241216m n k n n k n +=++=+≥⨯+⨯=.(2) 由题意得330(mod100)m n -≡，即3(31)0(mod100)n m n --≡，故31(mod100)m n -≡，从而4m n k -=，故811(mod100)k ≡，当5k =时5811(mod100)≡，此时m n -最小为20.。

小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

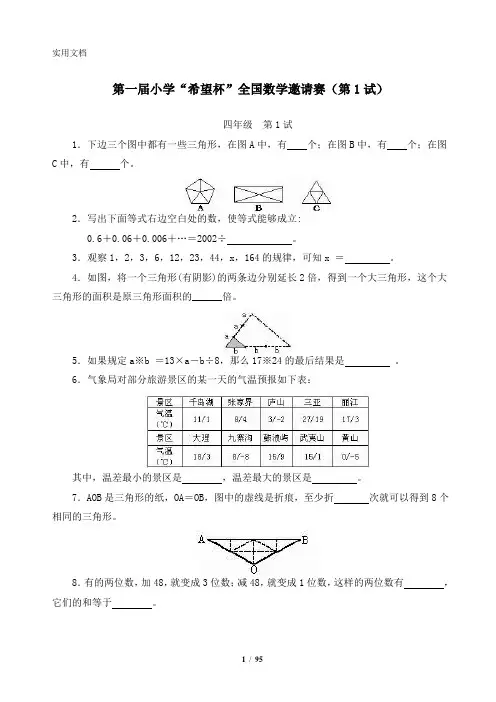
第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。

6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。

7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折次就可以得到8个相同的三角形。

8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有，它们的和等于。

9．甲、乙、丙、丁四个学习小组共有图书280本，班主任老师提议让四个组的书一样多，得到拥护，于是从甲调14本给乙，从乙调15本给丙，从丙调17本给丁，从丁调18本给甲。

这时四个组的书一样多。

这说明甲组原来有书本。

10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。

11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是，它比较小的数大。

12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距千米。

13．甲、乙、丙三人中只有1人会开汽车。

甲说：“我会开。

”乙说：“我不会开。

”丙说：“甲不会开。

”三人的话只有一句是真话。

会开车的是。

14．为了支援西部，1班班长小明和2班班长小光带了同样多的钱买了同一种书44本，钱全部用完，小明要了26本书，小光要了18本书。

回校后，小明补给小光28元。

小明、小光各带了元，每本书价元。

2018-2019年度第10届希望杯全国数学邀请赛初中二年级第1试试题(PDF版,含答案)

第１０届“希望杯”全国数学邀请赛试题初中二年级　第１试（１９９９年４月１８日）一、选择题１．下列各式中，正确的是（）（Ａ）（）１９２＝１３．（Ｂ）２槡１４＝１１２．（Ｃ）４＋９槡１６＝２＋３４．（Ｄ）１７２－７槡２＝１０．２．３０　１槡－槡３１与槡３０　＋槡３１的关系是（）（Ａ）相等．（Ｂ）互为相反数．（Ｃ）互为倒数．（Ｄ）互为负倒数．３．代数式π－３．１４１６３．１４１５－π的值（）（Ａ）是零．（Ｂ）在０与１之间．（Ｃ）在－１与０之间．（Ｄ）等于１或－１．４．某工厂到车站的路程为ｍ公里，现有一辆汽车从工厂到车站拉货，去时的速度为３ａ公里／小时，返回时的速度为２ａ公里／小时，那么这辆车往返一次的平均速度为（）（Ａ）５２ａ公里／小时．（Ｂ）２５ｍａ公里／小时．（Ｃ）７３ａ公里／小时．（Ｄ）１２５ａ公里／小时．５．两个数ａ，ｂ，且ａ＜ｂ，把ａ到ｂ的所有数记做［ａ，ｂ］，例如１到４的所有数记做［１，４］，如果５≤ｍ≤１５，２０≤ｎ≤３０，那么ｍｎ的一切值包含在（）内．（Ａ）［５，３０］．（Ｂ）１４，［］３４．（Ｃ）１６，［］２３．（Ｄ）１６，［］７８．６．ｘ，ｙ为实数，设ａ＝（－ｘ）槡２－ｘ，ｂ＝ｙ（－槡ｙ）２，ｃ＝３＋１４４－１２，则ａ，ｂ，ｃ的大小关系是（）（Ａ）ａ＜ｂ＜ｃ．（Ｂ）ｂ＜ａ＜ｃ．（Ｃ）ｂ＜ｃ＜ａ．（Ｄ）ａ＝ｂ＞ｃ．７．如果三角形的一个外角大于这个三角形的某两个内角的和的２倍，那么这个三角形一定是（）（Ａ）锐角三角形．　（Ｂ）钝角三角形．（Ｃ）直角三角形．　（Ｄ）直角或钝角三角形．８．在四边形ＡＢＣＤ中，若两条对角线ＡＣ＝ＢＤ且ＡＣ⊥ＢＤ，则这个四边形（）（Ａ）一定是正方形．图１（Ｂ）一定是菱形．（Ｃ）一定是平行四边形．（Ｄ）可能不是平行四边形．９．如图１，△ＡＢＣ中，ＡＢ＝ＡＣ，Ｄ、Ｅ、Ｆ分别在ＢＣ、ＡＣ、ＡＢ上，若ＢＤ＝ＣＥ，ＣＤ＝ＢＦ，则∠ＥＤＦ等于（）（Ａ）９０°－１２∠Ａ．（Ｂ）９０°－∠Ａ．（Ｃ）１８０°－∠Ａ．（Ｄ）１８０°－２∠Ａ．１０．如果三角形的重心在它的一条高线上，则这个三角形一定是（）（Ａ）等腰三角形．（Ｂ）直角三角形．（Ｃ）等边三角形．（Ｄ）等腰直角三角形．·６３·二、Ａ组填空题１１．分解因式：ｘｙ－１－ｘ＋ｙ＝．１２．计算：１０＋８　３＋槡槡槡２　２＝．１３．已知ｘ＝槡３－１，那么３－２ｘ２－４ｘｘ２＋２ｘ－１＝．１４．计算：槡１９９７（槡１９９７　－槡１９９９）（槡１９９７　－槡２００１）＋槡１９９９（槡１９９９　－槡２００１）（槡１９９９　－槡１９９７）＋槡２００１（槡２００１　－槡１９９７）（槡２００１　－槡１９９９）＝．１５．若ｘ３＋３ｘ２－３ｘ＋ｋ有一个因式是ｘ＋１，则ｋ＝．１６．给出四个自然数ａ，ｂ，ｃ，ｄ，其中每三个数之和分别是１８０，１９７，２０８，２２２，那么ａ，ｂ，ｃ，ｄ中最大的数的值是．１７．如果一个三角形的两条角平分线又是它的两条高线，那么这个三角形的形状是．图２１８．如图２，直线ｌ１∥ｌ２，△ＡＢＣ是直角三角形，∠Ａ＝９０°，∠ＡＢＦ＝２５°，则∠ＡＣＥ＝．１９．在纸上画一个正六边形，在六边形外画一条直线ｌ，从六个顶点分别向直线ｌ引垂线可以得到ｋ个不同的垂足，那么ｋ的值在３，４，５，６这四个数中不可能取得的是．２０．圆的内接矩形的周长与圆周长之比的最大值是．三、Ｂ组填空题２１．一个矩形的长为１５厘米，宽为８厘米，以矩形的四边中点为顶点的四边形的周长＝，面积＝．２２．实数ａ满足ａ＋ａ＝０且ａ≠－１，那么ａ－１ａ＋１＝或．２３．若实数ａ，ｂ满足（２ａ＋ｂ）２＋２ａ２－３２３　－槡ａ＝０，ａ＝，ｂ＝．２４．方程组ｘｙ＝９１槡ｘ＋１槡ｙ＝烅烄烆４３的解是或．２５．某班男女同学分别参加植树劳动，要求男女同学各种８行树，男同学种的树比女同学种的树多，如果每行都比预定的多种一棵树，那么男女同学种树的数目都超过１００棵；如果每行都比预定的少种一棵树，那么男女同学植树的数目都达不到１００棵．这样原来预定男同学种树棵；女同学种树棵．答·提示一、选择题题号１　２　３　４　５　６　７　８　９　１０答案Ｂ　Ｂ　Ｃ　Ｄ　Ｄ　Ｃ　Ｂ　Ｄ　Ａ　Ａ提示：１．２槡１４＝槡９４＝３２＝１１２．所以选（Ｂ）．２．因为１槡３０－槡３１＝槡３０　＋槡３１（槡３０　－槡３１）（槡３０　＋槡３１）＝－（槡３０　＋槡３１）选（Ｂ）．３．因为π＝３．１４１５９２…＜３．１４１６，所以π－３．１４１６３．１４１５－π＝３．１４１６－π３．１４１５－π＝１＋０．０００１３．１４１５－π＝１－０．０００１０．００００９…≈－１９选（Ｃ）．４．该车从工厂到车站所用时间ｔ１＝ｍ３ａ（小时），从车站返回工厂所用时间为ｔ２＝ｍ２ａ（小时）．所以往返一次的平均速度为·７３·ｖ＝２ｍｔ１＋ｔ２＝２ｍｍ３ａ＋ｍ２ａ＝１２５ａ（公里／小时）．选（Ｄ）．５．因为５≤ｍ≤１５，２０≤ｎ≤３０．所以当ｍ＝５，ｎ＝３０时，ｍｎ＝１６是ｍｎ中的最小值；当ｍ＝１５，ｎ＝２０时，ｍｎ＝３４（＜７８）是ｍｎ中的最大值．所以ｍｎ中的所有值都在１６，［］７８内．选（Ｄ）．６．　ａ＝（－ｘ）槡２－ｘ＝－ｘ－ｘ＝１．ｂ＝ｙ（－槡ｙ）２＝ｙ－ｙ＝－１．ｃ＝３＋１４４－１２＝１３１４．所以ｂ＜ｃ＜ａ．选（Ｃ）．７．不妨设三角形的三个内角为∠１、∠２、∠３，且∠１≤∠２≤∠３，则∠１的外角等于∠２＋∠３．由题意，它大于三角形两内角和的２倍．所以∠２＋∠３＞２（∠１＋∠２），所以∠３＞２∠１＋∠２，又因为∠１＋∠２＝１８０°－∠３，所以２∠３＞１８０°＋∠１，所以∠３＞９０°＋１２∠１．所以这个三角形一定是钝角三角形．选（Ｂ）．图３８．如图３，ＡＣ＝ＢＤ且ＡＣ⊥ＢＤ，这个四边形ＡＢＣＤ，既不是正方形、菱形，也不是平行四边形，选（Ｄ）．９．在△ＡＢＣ中，ＡＢ＝ＡＣ，所以△ＡＢＣ为等腰三角形．所以∠Ｂ＝∠Ｃ．又因为ＢＤ＝ＣＥ，ＣＤ＝ＢＦ，所以△ＢＤＦ≌△ＣＥＤ，∠ＢＤＦ＝∠ＣＥＤ．所以∠ＥＤＦ＝１８０°－（∠ＣＤＥ＋∠ＢＤＦ）＝１８０°－（∠ＣＤＥ＋∠ＣＥＤ）＝∠Ｃ．又∠Ｂ＝∠Ｃ＝１２（１８０°－∠Ａ）＝９０°－１２∠Ａ，所以∠ＥＤＦ＝９０°－１２∠Ａ．选（Ａ）．１０．不妨设△ＡＢＣ的重心Ｏ在ＢＣ边的高ＡＤ上，即ＡＤ⊥ＢＣ，又因为Ｏ为重心，所以ＡＤ又是ＢＣ的中线，即△ＡＢＣ是等腰三角形．选（Ａ）．二、Ａ组填空题题号１１　１２　１３　１４　１５答案（ｘ＋１）（ｙ－１）４＋槡２－１　０－５１６　１７　１８　１９　２０答案８９等边三角形６５°５槡２　２π 提示：１１．　ｘｙ－１－ｘ＋ｙ＝（ｘｙ＋ｙ）－（ｘ＋１）＝ｙ（ｘ＋１）－（ｘ＋１）＝（ｘ＋１）（ｙ－１）．１２．　１０＋８　３＋槡槡槡２　２＝１０＋８　２＋槡２　２＋槡槡１＝１０＋８（槡２＋１槡）＝１８＋槡槡８　２＝４２＋２×４×槡２＋（槡２）槡２＝４＋槡２．１３．因为ｘ　＝槡３－１，所以ｘ＋１　＝槡３，所以（ｘ＋１）２＝３．原式＝５－２（ｘ２＋２ｘ＋１）（ｘ２＋２ｘ＋１）－２＝５－２（ｘ＋１）２（ｘ＋１）２－２＝５－６３－２＝－１．·８３·１４．设槡１９９７＝ａ，槡１９９９＝ｂ，槡２００１＝ｃ，则原式＝ａ（ａ－ｂ）（ａ－ｃ）＋ｂ（ｂ－ｃ）（ｂ－ａ）＋　ｃｃ－ａｃ－ｂ＝－ａ（ｂ－ｃ）－ｂ（ｃ－ａ）－ｃ（ａ－ｂ）（ａ－ｂ）（ｂ－ｃ）（ｃ－ａ）＝－ａｂ＋ａｃ－ｂｃ＋ａｂ－ａｃ＋ｂｃ（ａ－ｂ）（ｂ－ｃ）（ｃ－ａ）＝０．１５．因为ｘ３＋３ｘ２－３ｘ＋ｋ有一个因式是ｘ＋１，所以　ｘ３＋３ｘ２－３ｘ＋ｋ＝ｘ３＋ｘ２＋２ｘ２＋２ｘ－５ｘ－５＋５＋ｋ＝ｘ２（ｘ＋１）＋２ｘ（ｘ＋１）－５（ｘ＋１）＋（ｋ＋５）＝（ｘ＋１）（ｘ２＋２ｘ－５）＋（ｋ＋５）．所以当ｋ＝－５时，原多项式有一个因式是ｘ＋１．１６．设ａ＜ｂ＜ｃ＜ｄ，则ａ＋ｂ＋ｃ＝１８０ａ＋ｂ＋ｄ＝１９７ａ＋ｃ＋ｄ＝２０８ｂ＋ｃ＋ｄ＝烅烄烆２２２①②③④①＋②＋③＋④得３（ａ＋ｂ＋ｃ＋ｄ）＝８０７，所以ａ＋ｂ＋ｃ＋ｄ＝２６９⑤⑤－①得ｄ＝８９；⑤－②得ｃ＝７２；⑤－③得ｂ＝６１；⑤－④得ａ＝４７．所以四个数中最大的数值是８９．图４１７．如图４，在△ＡＢＣ中，ＡＤ是∠ＢＡＣ的平分线，且ＡＤ又是ＢＣ边的高，所以△ＡＢＤ≌△ＡＣＤ，所以ＡＢ＝ＡＣ．同理，ＢＥ是∠ＡＢＣ的平分线，同时又是ＡＣ边的高，所以ＡＢ＝ＢＣ．所以ＡＢ＝ＡＣ＝ＢＣ，△ＡＢＣ为等边三角形．１８．因为ｌ１∥ｌ２，所以∠ＥＣＢ＋∠ＣＢＦ＝１８０°，由于△ＡＢＣ是直角三角形，∠Ａ＝９０°，所以∠ＡＣＢ＋∠ＡＢＣ＝９０°，所以　∠ＡＣＥ＝１８０°－（∠ＡＣＢ＋∠ＡＢＣ）－∠ＡＢＦ＝１８０°－９０°－２５°＝６５°．１９．正六边形ＡＢＣＤＥＦ的六个顶点向直线ｌ引垂线，不可能得到５个垂足．若恰好得到５个垂足，说明６个顶点中仅有两个顶点的垂足重合，其余各点的垂足不再重合．（１）若两个相邻顶点Ａ、Ｂ的垂足重合，因为ＡＢ∥ＤＥ，则Ｄ、Ｅ两顶点的垂足也重合，则上述假设不成立．（２）若两个对点Ａ、Ｄ的垂足重合，因为ＡＤ∥ＢＣ∥ＥＦ，所以Ｂ、Ｃ的垂足与Ｅ、Ｆ的垂足也分别重合，则上述假设也不成立．（３）若Ａ、Ｃ两点的垂足重合，因为ＡＣ∥ＤＦ，则Ｄ、Ｆ两点的垂足也重合，则上述假设不成立．综上所述，由６个顶点得到５个垂足是不可能的．２０．设矩形的长与宽分别为ａ、ｂ，则圆的直径为ａ２＋ｂ槡２．所以矩形周长＝２（ａ＋ｂ），圆周长＝πａ２＋ｂ槡２．所以（周长比）２＝４（ａ＋ｂ）２π２（ａ２＋ｂ２）．又（ａ－ｂ）２≥０，则ａ２＋ｂ２≥２ａｂ所以（ａ＋ｂ）２＝ａ２＋２ａｂ＋ｂ２≤２（ａ２＋ｂ２），所以（周长比）２＝４（ａ＋ｂ）２π２ａ２＋ｂ２≤８（ａ２＋ｂ２）π２ａ２＋ｂ２＝８π２，所以周长比≤槡２　２π，即周长比的最大值为槡２　２π．三、Ｂ组填空题题号２１　２２　２３　２４　２５答案３４；６０－１；１－４；８ｘ＝１ｙ＝｛９；ｘ＝９ｙ　＝｛１１０４；９６·９３·提示图５２１．如图５，矩形ＡＢＣＤ中．ＡＢ＝１５，ＢＣ＝８．连接ＡＣ，则ＡＣ＝ＡＢ２＋ＢＣ槡２＝１５２＋８槡２＝１７（厘米）．又　Ｅ，Ｆ，Ｇ，Ｈ分别为ＡＢ，ＢＣ，ＣＤ，ＡＤ的中点，则有ＥＦ瓛１２ＡＣ，ＨＧ瓛１２ＡＣ，ＦＧ瓛１２ＢＤ．ＥＨ瓛１２ＢＤ．所以四边形ＥＦＧＨ为菱形，其周长为４×ＥＦ＝２×１７＝３４（厘米）．ＳＥＦＧＨ＝１２ＳＡＢＣＤ＝１２×１５×８＝６０（平方厘米）．２２．因为ａ＋ａ＝０所以ａ＝－ａ．所以ａ≤０且ａ≠－１．当－１＜ａ≤０时，ａ－１ａ＋１＝－ａ－１ａ＋１＝－１；当ａ＜－１时，ａ－１ａ＋１＝－ａ－１－（ａ＋１）＝１．所以ａ－１ａ＋１＝－１（－１＜ａ≤０）　１（ａ＜－１｛）．２３．因为（２ａ＋ｂ）２＋２ａ２－３２３－槡ａ＝０，所以２ａ＋ｂ＝０２ａ２－３２＝０３－ａ＞烅烄烆０，解得ｂ＝－２ａａ＝±４ａ＜烅烄烆３，所以ａ＝－４，ｂ＝８．２４．由ｘｙ＝９１槡ｘ＋１槡ｙ＝烅烄烆４３①②将②的两边平方，得１ｘ＋２ｘ槡ｙ＋１ｙ＝１６９③由①得２ｘ槡ｙ＝２３，④③－２×④得　１ｘ－２ｘ槡ｙ＋１ｙ＝４９，所以１槡ｘ－１槡（）ｙ２＝４９，所以１槡ｘ－１槡ｙ＝±２３⑤由方程组１槡ｘ＋１槡ｙ＝４３１槡ｘ－１槡ｙ＝烅烄烆２３解得１槡ｘ＝１１槡ｙ＝烅烄烆１３所以ｘ＝１ｙ＝｛９．由方程组１槡ｘ＋１槡ｙ＝４３１槡ｘ－１槡ｙ＝－烅烄烆２３，解得１槡ｘ＝１３１槡ｙ＝烅烄烆１，所以ｘ＝９，ｙ＝１｛，所以原方程组的解是ｘ＝１ｙ　＝｛９或ｘ＝９ｙ　＝｛１．２５．设男同学每行种ｘ棵树，女同学每行种ｙ棵树，且ｘ＞ｙ．依题意有８（ｘ＋１）＞１００，８（ｘ－１）＜１００，８（ｙ＋１）＞１００，８（ｙ－１）＜烅烄烆１００①②③④由①得ｘ＞１１１２，由②得ｘ＜１３１２，所以１１１２＜ｘ＜１３１２．即ｘ＝１２或１３，同理１１１２＜ｙ＜１３１２，即ｙ＝１２或１３．又ｘ＞ｙ．所以ｘ＝１３，ｙ＝１２．所以男同学预定种树　８×１３＝１０４（棵）．女同学预定种树　８×１２＝９６（棵）．·０４·。

第19届希望杯初2第1试

第19届希望杯全国数学邀请赛试题·解答初中二年级第1试一、选择题以下每题的四个选项中，仅有一个是正确的，请将你认为是正确答案的英文字母填在每题后面的圆括号1．以下说法中正确的是（） A ．1的平方根和1的立方根相同B ．0的平方根和0的立方根相同C2± D ．8的立方根是2±2．若单项式52x xa b -和2233x a b -的次数相同，则x 的整数值等于（） A ．1 B ．1- C ．1± D ．1±以外的数3．若a b ，） A都是有理数B都是无理数C都是有理数或都是无理数D中有理数和无理数各有一个4．使不等式21x +>成立的x 的值是（）A ．比1-大的数B ．比3-小的数C ．大于1-或小于3-的数D ．2-以外的数5．设a ，b ，c ，d ，e 只能从3-，2-，1-中取值，又x a b c d e =-+-+，22222y a b c d e =-+-+，则（）A ．x 的最大值比y 的最大值小B ．x 的最小值比y 的最小值小C ．x 的最大值比y 的最小值小D ．x 的最小值比y 的最大值大 6．In the figure ，ABCD is a diamond ，pointsE andF lie on its sides AB and BC respectively ，such that AE BFBE CF=，and DEF △ is a regular triangle ．Then BAD ∠ is equal to ( ) A ．40 B ．60C ．80D ．1007．已知ABC △的三边的长分别为a ，b ，c ，且a a b cb c b c a++=+-，则ABC △一定是（）A ．等边三角形B ．腰长为a 的等腰三角形C ．底边长为a 的等腰三角形D ．等腰直角三角形8．初二⑴班有48名同学，其中有男同学n 名，将他们编成1号、2号、…、n 号．在寒假期间，1号给3名同学打过电话，2号给4名同学打过电话，3号给5名同学打过电话，……，n 号给全班一半同学打过电话，由此可知该班女同学的人数是（） A ．22 B ．24 C ．25 D ．26 9．使方程32200x y +=成立的正整数对()x y ，有（）A ．66个B ．33个C ．30个D ．18个10．一次函数y kx b =+的图像经过点()05A ，和点()40B ，，则在该图像和坐标轴围成的三角形内，横坐标和纵坐标都是正整数的点有（）A ．6个B ．7个C ．8个D ．9个B CD AEF二、A 组填空题11．已知a ，b ，c 都是正整数，并且2008abc =，则a b c ++的最小值是．12．若12320072008M =------ ，222222123420072008N =-+-++- ，则M 与N 的大小关系是．（填“>”、“<”或“=”）13．初二某班有49位同学，他们之间的年龄最多相差3岁，若按属相分组，那么人数最多的一组中至少有同学位．14．若实数a使等式131a a +=+-________a =．15．Let a be an integer and satisfy ()2212008a a +<<，then ______a =．BAPCBA16．如下左图，ABC △的面积是24，点D 是边BC 的中点，点E 是边AB 的一个三等分点，CE 交AD于点F ，则AEF △的面积是．17．如上右图，在ABC △中，5AB AC ==，P 是BC 边上点B ，C 外的任意一点，则2____AP PB PC +⋅=． 18．有一个运算程序，可以使：当0m n k ⊗=（k 为已知数）时，得()11m n k +⊗=-，()12m n k ⊗+=+．现在，已知112⊗=，那么20072007_________⊗=．19．用摄氏温度计测量，水的冰点是0℃，沸点是100℃．当用华氏温度计测量时，水的冰点是32F ，沸点是212F ，现在测量某温度，用摄氏温度计测得的温度是用华氏温度计测得的温度的5倍，那么，当用摄氏温度计测量时，该温度是 ℃．20．小华同学从运动场的A 点出发，向东走10米到达B 点，再向北走8米到达C 点，再向西走6米到达D 点，再向南走5米到达E 点，则E ，A 两点相距米．三、B 组填空题21．甲、乙两同学都想买同一本书，可是甲同学带的钱差7元，乙同学带的钱差6元，若两人带的钱合在一起买这本书则带剩1元，那么甲同学带了元，乙同学带了元．22．直角ABC △三边的长分别是x ，1x +和5，则ABC △的周长，ABC △的面积= ．23．如右图，边长为a 的正方形ABCD 和边长为b 的正方形BEFG 并排放在一起，1O 和2O 分别是两个正方形的中心，则阴影部分的面积= ，线段12O O 的长．24．若代数式33223x y x y axy +++含有因式x y -，则_____a =，在实数范围内将这个代数式分解因式，得33223x y x y axy +++= ． 25．如右图，I 是ABC △的内心，且CA AI BC +=．若80BAC ∠= ，则ABC ∠的大小是，AIB ∠ 的大小是．F EBIBAC解答一、选择题 1．B【解析】 1的平方根是1±，1的立方根是1，所以AC 不对；8的立方根是2，所以D 不对；只有0的平方根和立方根都是0，所以选B ．2．B【解析】由题意，知()523x x x +=+-当0x ≥时，则65x x =-，解得57x =，不合题意，舍去；当0x <时，则65x x -=-，解得1x =-，符合题意，所以选B ． 3．A【解析】 a ，b 都是有理数，所以a b -是有理数．12⎡⎤+⎣⎦是有理数，12⎡⎤=-⎣⎦是有理数．故选A ．4．C【解析】当2x =-时，不等式无解；当2x >-时，21x +>，1x >-，此时不等式解集为1x >-；当2x <-时，()21x -+>，3x <-．此时不等式解集为3x <-．所以1x >-或3x <-时，不等式成立．故选C5．A【解析】()13323x =-⨯+⨯=最大， ()33127x =-⨯+⨯=-最小； 931225y =⨯-⨯=最小，139215y =⨯-⨯=-最小．应选A ．6．B译文：图中，ABCD 是菱形，E ，F 是AB ，BC 上的点，满足AE BFBE CF=，且DEF △是正三角形，则BAD ∠的大小是（） A ．40 B ．60 C ．80D ．100【解析】如右图，由题意知BE CF =，在边AB 上取点K ，使AK BE =，连结DK ，BD ，易知AKD CFD △≌△，从而KD DF DE ==．故DKE △为等腰三角形，有D KE D EK ∠=∠，则DKA DEB △≌△，于是AD DB =，ADB △是等边三角形．、K B CDAE F所以60BAD ∠= ．选B7．B【解析】由已知，得()a b c b cbc b c a++=+-，去分母得()()()2b c ab ac a bc b c ++-=+，移项因式分解得()()20b c ab ac a bc ++--=．()()()0b c b a a c +--=．因为a ，b ，c 为三角形的边，所以0b c +>，得a b =或a c =．所以ABC △是以a 为一腰的等腰三角形．选B ．8．D【解析】由题意，n 号同学给()2n +名同学打过电话，所以2482n +=÷，22n =．所以女同学有482226-=（名）．选D ．9．B【解析】因为32200x y +=，x ，y 为正整数，所以200302xy -=>．所以2663x <．又因为x 为正偶数，所以x 可取2，4，6，…，66．共33个数．所以原方程的正整数解有33个．应选B ．10．A 【解析】如右图，将点()05，和()40，坐标分别代入y kx b =+得504b k b =⎧⎨=+⎩解得545k b ⎧=-⎪⎨⎪=⎩．所以一次函数解析式为554y x =-+．当1x =时，334y =，直线1x =在AOB △内有整点3个；当2x =时，122y =，直线2x =在AOB △内有整点2个；当3x =时，114y =，直线3x =在AOB △内有整点1个．选A ．二、A 组填空题11．257 【解析】 2008分解成24251⨯⨯时，24251257a b c ++=++=．这时a b c ++的值最小12．=【解析】 ()()()222222123420072008N =-++++-()()()()()()121234342007200820072008=+-++-+++- ()123420072008=-++++++M =所以M N =．13．13 【解析】由题意，按属相分组可以分成4组，若每组12人，那么还有1人没有进组，当他加入某一组后，该组至少有13人．14【解析】由已知((133a a +=+-+，即(24a +=+所以1a15．45-【解析】若0a ≥，则()221a a +>，与题意不符．所以0a <．因为()()2244200845-<<-，所以45a =-．16．2 【解析】如右图，连结BF ，设AEF S x =△，则2EFB S x =△．因为D 为BC 中点，所以3AFC AFB S S x ==△．所以4AEC S x =△．所以312ABC AEC S S x ==△△．所以112421212ABC x S ==⨯=△，即2AEF S =△．17．25【解析】如右图，过点A 作AD BC ⊥交BC 于点D ，因为AB AC =，所以ABC △是等腰三角形，D 是BC 的中点，BD CD =．所以222AP AD DP =+．所以()()22PB PC BD DP CD DP BD DP ⋅=+-=- 所以222222225AP PB PC AP BD DP BD AD AB +⋅=+-=+==18．2008 【解析】因为当m n k ⊗=（k 为已知数）时，()11m n k +⊗=-，()12m n k ⊗+=+，所以()()()11211m n k k +⊗+=+-=+．又112⊗=，所以200720072008⊗=． 19．20- 【解析】由题意，摄氏温度计从0到100度对应华氏温度计从32度到212度，它们的比值是100:1805:9=，即当摄氏温度计读数为x 度时，华氏温度计的读数为9325x ⎛⎫+ ⎪⎝⎭度．由题意，得95325x x ⎛⎫=+ ⎪⎝⎭，解得20x =-，所有用摄氏温度计测得的温度是20-℃．20．5 【解析】如右图，延长DE 交AB 于F ．在Rt AEF △中，853EF =-=（米），1064AF =-=（米），所以5AE （米）．三、B 组填空题21．7；8 【解析】设该书的单价为x 元，则甲同学带了()7x -元，乙同学带了()6x -元，依题意，有()()761x x x -+-=-，解得14x =元．所以甲同学带了7元钱，乙同学带了8元钱．CBAD PCBA10米5米8米6米F BEAC D22.12或30；6或30 【解析】因为1x x <+，所以x 不会是斜边长，当斜边长为5时，有()22125x x ++=，即2120x x +-=，得()()430x x +-= 因为40x +>，所以30x -=，3x =；当斜边长为1x +时，有()22251x x +=+，解得12x =．所以x 的值是3或12．所以直角三角形的三边分别为3，4，5或5，12，13．所以Rt ABC △的周长是12或30；面积是6或30． 23．14ab【解析】如图，1BO=，2BO =，12454590O BO ∠=+= ，所以1212111224O BO S BO BO ab =⋅⋅==△，12O O 24．5-；()()22x y x y x y -++【解析】设()()3322223x y x y axy x y x mxy ny +++=-++，则()()3223322331x x y axy y x m x y n m xy ny +++=+-+-- 所以131.m n m a n -=⎧⎪-=⎨⎪-=⎩，，所以4m =，1n =-．所以145a n m =-=--=-．原式()()224x y x xy y =-+-()()()())222224452x y xxy y y x y x y ⎡⎤=-++-⎣⎦⎡⎤=-+-⎢⎥⎣⎦()()()22x y x y x y =-++．25．40 ；120【解析】如右图，在BC 上取点D ，使CD AC =，连接DI ，已知CA AI BC +=，所以BD AI =．在ACI △和DCI △中，AC DC =，ACI DCI ∠=∠，CI 为公共边，所以ACI DCI △≌△．所以AI D I =．因为80BAC ∠= ，所以40CAI ∠= ，40CDI ∠= ．又CDI ∠是等腰BDI △的外角，所以1202DBI DIB CDI ∠=∠=∠= ．所以40ABC ∠= ．在AIB △中，40BAI ∠= ，20ABI ∠= ，所以()1802040120AIB ∠=-+=．B EFD 20o40o40o I BA C。

第十九届希望杯初中1、2年级第1、2试试题解析(命题人评析)

第19届 “希望杯”初中试题刍议2008年第19届全国“希望杯”数学邀请赛已经落下了帷幕。

作为数学爱好者总要回味今年的试题.，交流学习试题的体验。

“希望杯”初中试题的内容那样的基本，粗看平淡无奇，细品则另有醇美的风味.比如，初一1试题4. 正方形内有一点A ，到各边的距离分别为1，2，5，6，则正方形面积为（）（A ）33 （B ）36 （C ）48 （D ）49答案：选（D ）.由于A 在正方形内，所以A 到两组对边的距离之和相等，由于只有1+6=2+5，于是，正方形的边长只能为7，故面积是72=49（平方单位）.题目的设置将正方形的边长为7，以条件“正方形内有一点A ，到各边的距离分别为1，2，5，6”，将其巧妙地隐藏起来，等待解题者去发见。

接着又在初一2试中，进一步升华为试题9.平行四边形内一点到四条边的距离分别是1，2，3，4，那么，这样的平行四边形的面积最小是（）.（A ）21 （B ） 22 （C ） 24 （D ） 25.答案：选（A ）.如1图所设，a 和b 是平行四边形的两条边长，1h和2h 是平行四边形的两条高，则面积1212ah bh h h =≥⨯.从1，2，3，4共有3组组合可作为为1h 和2h ，其中1123 h ,=+=2347h =+= 时，1221h h ⨯=最小.本题巧妙地利用斜边大于直角边解决了最小值的问题. 拓广了前一个试题的内涵，足图1见命题者匠心独运. 对综合性的大题仔细品味，试题有如下特点. 一、题型基本，知识基本，技能基本，寓以新意有发展例1. 如图2，A 和B 两个小机器人，自甲处同时出发相背而行，绕直径为整数米的圆周上运动，15分钟内相遇7次，如果A 的速度每分钟增加6米，则A 和B 在15分钟内相遇9次，问圆周直径至多是多少米？至少是多少米？（取314.π=）分析：行程中的相遇问题，从小学开始就是重要的应用题型，属基本题型。

其中路程、时间与速度的关系是基本知识。

希望杯数学八年级竞赛真题及答案(1-23届)

1、第一届希望杯初二第1试试题2、第一届希望杯初二第2试试题3、第二届希望杯初二第1试试题4、第二届希望杯初二第2试试题5、第三届希望杯初二第1试试题6、第三届希望杯初二第2试试题7、第四届希望杯初二第1试试题8、第四届希望杯初二第2试试题9、第五届希望杯初二第1试试题10、第五届希望杯初二第2试试题11、第六届希望杯初二第1试试题12、第六届希望杯初二第2试试题13、第七届希望杯初二第1试试题14、第七届希望杯初二第2试试题15、第八届希望杯初二第1试试题16、第八届希望杯初二第2试试题17、第九届希望杯初二第1试试题18、第九届希望杯初二第2试试题19、第十届希望杯初二第1试试题20、第十届希望杯初二第2试试题21、第十一届希望杯初二第1试试题22、第十一届希望杯初二第2试试题23、第十二届希望杯初二第1试试题24、第十二届希望杯初二第2试试题25、第十三届希望杯初二第1试试题26、第十三届希望杯初二第2试试题27、第十四届希望杯初二第1试试题28、第十四届希望杯初二第2试试题28、第十五届希望杯初二第1试试题30、第十五届希望杯初二第2试试题31、第十六届希望杯初二第1试试题32、第十六届希望杯初二第2试试题33、第十七届希望杯初二第1试试题34、第十七届希望杯初二第2试试题35、第十八届希望杯初二第1试试题36、第十八届希望杯初二第2试试题37、第十九届希望杯初二第1试试题38、第十九届希望杯初二第2试试题39、第二十届希望杯初二第1试试题40、第二十届希望杯初二第2试试题41、第二十一届希望杯初二第1试试题42、第二十一届希望杯初二第2试试题43、第二十二届希望杯初二第1试试题44、第二十二届希望杯初二第2试试题45、第二十三届希望杯初二第1试试题46、第二十三届希望杯初二第2试试题希望杯第一届（1990年）初中二年级第一试试题一、选择题:（每题1分，共10分）1．一个角等于它的余角的5倍，那么这个角是 ( )A ．45°.B ．75°.C ．55°.D ．65°2．2的平方的平方根是 ( )A ．2.B ．2. C ．±2. D ．43．当x=1时，a 0x 10-a 1x 9+a 0x 8-a 1x 7-a 1x 6+a 1x 5-a 0x 4+a 1x 3-a 0x 2+a 1x 的值是( ) A ．0B ．a 0.C ．a 1D ．a 0-a 14. ΔABC,若AB=π27则下列式子成立的是( )A ．∠A ＞∠C ＞∠B;B ．∠C ＞∠B ＞∠A;C ．∠B ＞∠A ＞∠C;D ．∠C ＞∠A ＞∠B 5．平面上有4条直线，它们的交点最多有( ) A ．4个B ．5个.C ．6个.D ．76．725-的立方根是[ ] （A ）12-. （B ）21-.（C ）)12(-±. （D ）12+.7．把二次根式a a 1-⋅化为最简二次根式是[ ](A) a . (B)a -. (C) a --. (D) a -8．如图1在△ABC 中，AB=BC=CA ，且AD=BE=CF ，但D ，E ，F 不是AB ，BC ，CA 的中点．又AE ，BF ，CD 分别交于M ，N ，P ，如果把找出的三个全等三角形叫做一组全等三角形，那么从图中能找出全等三角形( ) A ．2组B ．3组.C ．4组D ．5组。

历年初中希望杯数学竞赛试题大全

历年初中希望杯数学竞赛试题大全 ][真诚为您服务试试题希望杯”全国数学邀请赛初二第2· 2009年第20届“次· 161· [4-30]★详细简介请参考下载页]· [竞赛 2试试题届“希望杯”全国数学邀请赛初一第年第· 200920 次· 153· [4-28]详细简介请参考下载页★]· [竞赛数学大赛初赛试卷（扫描版）届5“希望杯”年湖北省黄冈市第· 2009 · 76次· [4-17]★详细简介请参考下载页]· [竞赛试试题”全国数学邀请赛初二第1· 2009年第20届“希望杯次· 133· [4-7]对不起，尚无简介☆]竞赛· [ 试试题全国数学邀请赛初一第1届“希望杯”20· 2009年第· 122次· [4-7]详细简介请参考下载页★]· [竞赛全国数学邀请赛初二训练题”第十四届“希望杯·次· 44· [9-9]详细简介请参考下载页★]竞赛· [ 2试试题“希望杯”全国数学邀请赛初一第19· 2008年第届次· 203· [9-4]详细简介请参考下载页★]· [竞赛 1”“19· 2008年第届希望杯全国数学邀请赛初一第试试题次· 169· [9-4]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初二第219年第届“希望杯”· 2008 次· 156· [9-2]详细简介请参考下载页★]· [竞赛 1试试题希望杯”全国数学邀请赛初二第“· 2008年第19届· 146次· [9-2]详细简介请参考下载页★]竞赛· [ 2试试题”届“希望杯全国数学邀请赛初二第18· 2007年第· 101次· [9-2]详细简介请参考下载页★]竞赛· [ 1全国数学邀请赛初二第试试题”“18· 2007年第届希望杯次· 95· [9-2]详细简介请参考下载页★]竞赛· [ 试试题”全国数学邀请赛初二第2· 2006年第17届“希望杯次· 76· [9-2]详细简介请参考下载页★]竞赛· [ 1试试题“希望杯”全国数学邀请赛初二第届· 2006年第17 · 76次· [9-2]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初二第2希望杯· 2005年第16届“”次· 65· [9-1]详细简介请参考下载页★]· [竞赛 1试试题全国数学邀请赛初二第届· 2005年第16“希望杯”次· 52· [9-1]详细简介请参考下载页★]· [竞赛试试题全国数学邀请赛初二第希望杯”2· 2004年第15届“次· 47· [9-1]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初二第115届“希望杯”年第· 2004 次· 38· [9-1]详细简介请参考下载页★]· [竞赛 2试试题希望杯”全国数学邀请赛初二第届· 2003年第14“次· 30· [9-1]详细简介请参考下载页★]竞赛· [ 1试试题希望杯届“”全国数学邀请赛初二第年第· 200314 · 26次· [9-1]详细简介请参考下载页★]竞赛· [ 2试试题全国数学邀请赛初二第希望杯届年第· 200213“”· 31次· [9-1]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初二第1”年第13届“希望杯· 2002 次· 23· [9-1]详细简介请参考下载页★]竞赛· [ 2试试题“希望杯”全国数学邀请赛初二第· 2001年第12届· 17次· [9-1]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初二第112年第届“希望杯”· 2001 · 17次· [9-1]详细简介请参考下载页★]竞赛· [ 试试题2“届希望杯”全国数学邀请赛初二第11· 2000年第次· 15· [9-1]★详细简介请参考下载页]· [竞赛试试题”全国数学邀请赛初二第1“· 2000年第11届希望杯次· 15· [9-1]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初二第210届“希望杯”· 1999年第次· 13· [9-1]详细简介请参考下载页★]· [竞赛试试题1希望杯”全国数学邀请赛初二第· 1999年第10届“次· 15· [9-1]详细简介请参考下载页★]竞赛· [ 2试试题“希望杯”全国数学邀请赛初二第9· 1998年第届次· 11· [8-29]详细简介请参考下载页★]· [竞赛 1”“9· 1998年第届希望杯全国数学邀请赛初二第试试题次· 10· [8-29]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初二第28年第届“希望杯”· 1997 次· 13· [8-29]详细简介请参考下载页★]· [竞赛 1试试题希望杯”全国数学邀请赛初二第“· 1997年第8届· 10次· [8-29]详细简介请参考下载页★]竞赛· [ 2试试题”届“希望杯全国数学邀请赛初二第7· 1996年第· 11次· [8-29]详细简介请参考下载页★]竞赛· [ 1全国数学邀请赛初二第试试题”“7· 1996年第届希望杯次· 10· [8-29]详细简介请参考下载页★]· [竞赛试试题”希望杯全国数学邀请赛初二第2· 1995年第6届“次· 14· [8-29]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初二第16届“希望杯”· 1995年第次· 14· [8-29]★详细简介请参考下载页]· [竞赛 2试试题希望杯”全国数学邀请赛初二第5· 1994年第届“次· 12· [8-29]详细简介请参考下载页★]竞赛· [ 1试试题“届希望杯”全国数学邀请赛初二第· 1994年第5 · 12次· [8-29]（每一、选择题 :年第五届希望杯全国数学邀请赛1994 初中二年级第一试试题 [] Ax 1.303小题分，共分）使等式成立的的值是．是]· [竞赛试试题初二第2”年第4届“希望杯全国数学邀请赛· 1993 次· 9· [8-29]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初二第14届“希望杯”· 1993年第次· 10· [8-29]详细简介请参考下载页★]· [竞赛试试题2希望杯”全国数学邀请赛初二第· 1992年第3届“次· 11· [8-29]详细简介请参考下载页★]竞赛· [ 1试试题“希望杯”全国数学邀请赛初二第3· 1992年第届次· 9· [8-29]详细简介请参考下载页★]· [竞赛 2”“2· 1991年第届希望杯全国数学邀请赛初二第试试题· 14次· [8-28]详细简介请参考下载页★]· [竞赛试试题”全国数学邀请赛初二第1年第· 19912届“希望杯次· 12· [8-28]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初二第21届“希望杯”· 1990年第· 13次· [8-28]详细简介请参考下载页★]· [竞赛试试题”全国数学邀请赛初二第1希望杯· 1990年第1届“次· 11· [8-28]分，（每题1 ”全国数学邀请赛初二第一试一、选择题:“1990年第一届希望杯() 倍，那么这个角是 1．一个角等于它的余角的5分）共10]竞赛· [ 2试试题全国数学邀请赛初一第希望杯届年第· 200718“”· 94次· [8-28]详细简介请参考下载页★]竞赛· [ 试试题全国数学邀请赛初一第118届“希望杯”· 2007年第次· 42· [8-28]详细简介请参考下载页★]· [竞赛试试题”希望杯全国数学邀请赛初一第2· 2006年第17届“次· 41· [8-28]详细简介请参考下载页★]竞赛· [ 试试题1希望杯”全国数学邀请赛初一第“· 2006年第17届次· 43· [8-28]试第1全国数学邀请赛初一希望杯年第十七届2006“”……中考资源网，竞赛试题任你选！更多数学竞赛试题请点击。

第21届希望杯初二第1试试题及答案

第二十一届“希望杯”全国数学邀请赛初二第1试一、选择题（每小题4分，共40分．）以下每题的四个选项中，仅有一个是正确的，请将正确答案前的英文字母写在下面的表格内．1．下列图案都是由字母m 组合而成的，其中不是中心对称图形的是（）A ．B ．C ．D ．【解析】 B ．B 中5个”m ”分布在正五边形上，不是中心对称图形．2．若230a a ≥≥，则（）A 3a aB 3a aC ．1a ≥D ．01a <<【解析】 B ．∵23a a ≥≥0，∴01a ≤≤3a a320102009xx --x 的取值范围是（）A ．2010x ≤B ．2010x ，≤且2009x ≠±C ．2010x ≤且2009x ≠D ．2010x ，≤且2009x ≠-【解析】 B ．2010020090x x -⎧⎪⎨-≠⎪⎩≥，解得2010x ，≤且2009x ≠±． 4．正整数a b c ，，是等腰三角形三边的长，并且24a bc b ca +++=，则这样的三角形有（）A ．1个B ．2个C ．3个D ．4个【解析】 C ．()()124a bc b ca a b c +++=++=∵a b c +>，,,a b c 均为正整数，∴1a b c ++≥ 又12c +≥，∴1c +只能取2，3，4．若12c +=，即1c =，则12a b +=，于是6a b ==；若13c +=，即2c =，则8a b +=，于是4a b ==；若14c +=，即3c =，则6a b +=，于是3a b ==．综上，这样的三角形有3个．5．顺次连接一个凸四边形各边的中点，得到一个菱形，则这个四边形一定是（）A ．任意的四边形B ．两条对角线等长的四边形C ．矩形D ．平行四边形【解析】 B ．顺次连接一个凸四边形各边的中点得到的四边形，每组对边都等于对应对角线长的一半．因此若得到的四边形为菱形，则这个四边形一定是两条对角线等长的四边形．6．设p =a b c d ，，，是正实数，并且1a b c d +++=，则（）A ．5p >B ．5p <C ．4p <D ．5p =【解析】 A ．1a >=+，于是()()()()1111p a b c d >+++++++5=．7．Given a b c ，， satisfy c b a << and 0ac <，then which one is not sure to be correct in the following inequalities ？（） A ．b c a a>B ．0b ac->C ．22b ac c>D ．0a cac-< 【解析】 C ．∵a c >且0ac <，∴0a >，0c <∵b c >，0a >，∴b c a a >；∵b a <，0c <，∴0b ac ->； ∵a c >，0ac <，∴0a cac-<；因此只有C 不一定成立．8．某公司的员工分别住在A B C 、、三个小区，A 区住员工30人，B 区住员工15人，C 区住员工10人，三个小区在一条直线上，位置如图1所示，若公司的班车只设一个停靠点，为使所有员工步行到停靠点的路程总和最短，那么停靠点的位置应在（） A ．A 区 B ．B 区C ．C 区D ．A B C 、、区以外的一个位置【解析】 A ．以A 区为原点，从A 区往方向为正方向建立数轴，设停靠点的坐标为x ，那么所有员工步行到停靠点的路程总和为301510010300x x x +-+-，由绝对值函数的性质易知在0x =处，该函数值最小．9．ABC △的内角A 和B 都是锐角，CD 是高，若2AD AC DB BC ⎛⎫= ⎪⎝⎭，则ABC △是（）A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等腰三角形或直角三角形【解析】 D ．∵22AC AD BC BD =，∴cos cos ADAC A AC BD BC B BC==，又由正弦定理sin sin AC BBC A=， ∴cos sin cos sin A B B A=，于是sin2sin2A B =，∴A B =或90A B +=︒． 10．某人沿正在向下运动的自动扶梯从楼上走到楼下，用了24秒；若他站在自动扶梯上不动，从楼上到楼下要用56秒．若扶梯停止运动，他从楼上走到楼下要用（） A ．32秒B ．38秒C ．42秒D ．48秒【解析】 C ．设若扶梯停止运动，他从楼上走到楼下要用x 秒，则1112456x=+，解得42x =（秒）．图1二、A 组填空题（每小题4分，共40分．）11．四个多项式：①22a b -+；②22x y --；③22249x y z -；④4221625m n p -，其中不能用平方差公式分解的是_______________．（填写序号）【解析】 ②．①()()22a b b a b a -+=+-；③()()2224977x y z xy z xy z -=+-； ④()()4222216254545m n p m np m np -=+-．12．若111111a b c b c d===---，，，则a 与d 的大小关系是a _______d ．（填“>”、“=”或“<”）【解析】 =．1111111111111111111da d d d d d cd dd======--+----+----- 13．分式方程222510111x x x x ++=--+的解是x =______________．【解析】 2-．222510111x x x x ++=--+ ()()225110x x x +++-=22640x x ++= 2320x x ++=1x =-（舍去）或2x =-14．甲、乙两人从A 点同时同向出发沿400米的环形跑道跑步，过一段时间后，甲在跑道上离A 点200米处，而乙在离A 点不到100米处正向A 点跑去，若甲、乙两人的速度比是4：3，则此时乙至少跑了____________米．【解析】 750．假设甲的速度是4m ，乙的速度是3m ，题中所述情况是在开始跑步后t 时刻且此时甲、乙已经跑了1k 、2k 个整圈，则14400200m t k ⋅=⋅+，23400m t k x ⋅=⋅+（其中300400x <<）于是1240020040043k k x ++=，即()121234002004003004001504x k k k k =+-=-+ ∵300400x <<，∴123685k k <-<，因此12684k k -=．于是当12k =，21k =时，2k 最小，此时乙跑了400350750+=（米）．15．已知等腰三角形三边的长分别是421156x x x -+-，，，则它的周长是_____________．【解析】 12.3．421x x -=+时，1x =，此时三角形的三边长分别为2,2,9，矛盾；42156x x -=-时，1710x =，此时三角形的三边长分别为242724,,5105，周长为1231412.310x -==； 1156x x +=-时，2x =，此时三角形的三边长分别为6,3,3，矛盾．16．若29453737a b =-=-，，则336a ab b -+=______________．【解析】 8-．∵294523737a b +=--=-，∴2b a =-- 于是()()33336622a ab b a a a a -+=---+--()3321262a a a a =++-+()32326126128a a a a a a =++-+++8=-17．直线59544y x =-与x 轴、y 轴的交点分别为A B 、，则线段AB 上（包括端点A B 、）横坐标和纵坐标都是整数的点有_____________个．【解析】 5．59544y x =-即5495x y -=，于是y 必然整除5；另一方面()19,0A 、950,4B ⎛⎫-⎪⎝⎭，∴954y -≤≤0，于是y 的可能取值为20,15,10,5,0----对应的点均在线段AB 上．18．已知关于x 的不等式()2132343a x a x --->-的解是1x >-，则a =_______________．【解析】 0．原不等式⇔231124433a x a x -⎛⎫--> ⎪⎝⎭232114343a x a -⎛⎫⎛⎫⇔->- ⎪ ⎪⎝⎭⎝⎭()24131a x a ⇔+>-∴231141410a a a ⎧-=-⎪+⎨⎪+>⎩，解得43a =-（舍去）或0a =．19．当a 分别取2,1,0,1,2,3,,97--这100个数时，关于x 的分式方程212(1)1232a a x x x x +-=---+有解的概率是_______________．【解析】 4950．2112(1)1232a x x x x +-=---+()()()2221213232x a x a x x x x -+-+⇔=-+-+()2134320a x a x x ⎧+=+⎪⇔⎨-+≠⎪⎩ ∴当()1134a a +⋅=+和()1234a a +⋅=+以及()134a x a +=+无解时原方程无解，即2a =-和1a =-时原方程无解．因此方程有解的概率为4950．20．十位数2010888abc 能被11整除，则三位数abc 最大是______________．【解析】 990．()()218800811b a c k ++++-++++=，∴b a c --能整除11∴而9abc bc ≤，此时9b c --能整除11，∴三位数abc 最大是990．（注：能被11整数的自然数的特点是：奇数位上的数字和与偶数位上的数字和的差是11的整数倍）三、B 组填空题（每小题8分，共40分）21．一个矩形的长与宽是两个不相等的整数，它的周长与面积的数值相等，那么这个矩形的长与宽分别是______________和______________．【解析】 6，3．设长和宽分别为x 、y ，则()2x y xy +=，即()()224x y --= 因为x y ≠，∴24x -=，21y -=，于是长和宽分别为2和1．22．用[]x 表示不大于x 的最大整数，如[][]414253=-=-.，.．则方程[]6370x x -+=的解是______________或______________．【解析】 196x =-；83x =-． ∵[]673x x +=，而[]1x x x -<≤，∴()31673x x x -<+≤，解得10733x <-≤-．因此13677x -<+-≤，∴67x +的可能取值为12-和9-，解得196x =-和83x =-．经验证，这两个解均为原方程的解．23．As in figure 2，in a quadrilateral ABCD ，we have its diagonal AC bisects DAB ∠，and21910AB AD BC DC ====，，，then the distance from point C to line AB is______________，and the length of AC is________________．（英汉词典：quadrilateral 四边形：bisect 平分）Fig 22191010D C BAEDCBA【解析】 8；17．如图，过D 作AC 的垂线，交AB 于E ，连结CE ，则AD AE =，CD CE = 于是CEB △中，10CE CD BC ===，12BE AB AE =-=，因此容易算得等腰三角形△CEB 底边上的高为8．∴22218912642252892AC ⎛⎫=++⋅=+= ⎪⎝⎭，17AC =．24．如图3，Rt ABC △位于第一象限内，A 点的坐标为（1，1），两条直角边AB AC 、分别平行于x轴、y 轴，43AB AC ==，，若反比例函数(0)ky k x=≠的图象与Rt ABC △有交点，则k 的最大值是____________，最小值是______________．【解析】 36148；1．当反比例函数的图象过A 点时k 最小，为1；当反比例函数的图象与BC 相切时k 最大，此时∵()5,1B ，()1,4C ，直线BC 的方程为31944y x =-+∴方程2319044x x k -+-=的判别式3613016k -=，解得36148k =． 25．设011n A A A -，，，依次是面积为整数的正n 边形的n 个顶点，考虑由连续的若干个顶点连成的凸多边形，如四边形3446A A A A 、七边形2101234n n A A A A A A A --等，如果所有这样的凸多边形的面积之和是231，那么n 的最大值是_________________，此时正n 边形的面积是_____________．【解析】 23；1．设正n 边形的面积为n S ，则∵正n 边形的对角线共有()112n n -条，∴所有满足条件的凸边形共有()1n n -个，它们的面积之和为()112n n n S -⋅∴()146223711n n n S -==⋅⋅⋅ ∴711n n S =⎧⎨=⎩或231nn S =⎧⎨=⎩，于是n 的最大值是23，此时正n 边形的面积是1．第二十一届“希望杯”全国数学邀请赛答案第二第1试1．答案（1）选择题（2）A 组填空题（3）B 组填空题。

第21届希望杯全国数学邀请赛初二第一试试题 (1)

第二十一届“希望杯”全国数学邀请赛初二第1试2010年3月14日上午8：30~10：00一、选择题 (每小题4分，共40分) 以下每题的四个选项中，仅有一个是正确的，请将正确答案前的英文字母写在下面的表格内。

1. 下列图案都是由字母m 组合而成的，其中不是中心对称图形的是2. 若a 2≥a 3≥0，则 (A) a ≥3a (B) a ≤3a (C) a ≥1 (D) 0<a <1 。

3. 若代数式2009||2010--x x 有意义，则x 的取值范围是 (A) x ≤2010 (B) x ≤2010，且x ≠±2009 (C) x ≤2010，且x ≠2009 (D) x ≤2010，且x ≠ -20092 。

4. 正整数a ，b ，c 是等腰三角形三边的长，并且a +bc +b +ca =24，则这样的三角形有 (A) 1个(B) 2个 (C) 3个 (D) 4个。

5. 顺次连接一个凸四边形各边的中点，得到一个菱形，则这个四边形一定是 (A) 任意的四边形 (B) 两条对角线等长的四边形 (C) 矩形 (D) 平行四边形。

6. 设p =317+a +317+b +317+c +317+d ，其中a ，b ，c ，d 是正实数，并且a +b +c +d =1，则(A) p >5 (B) p <5 (C) p <4 (D) p =5 。

7. Given a ，b ，c satisfy c <b <a and ac <0，then which one is not sure to be correct in the followinginequalities ？ (A ) a b >a c (B ) c a b ->0 (C ) c b 2>c a 2 (D ) acc a -<0 。

(英汉词典：be sure to 确定；correct 正确的；inequality 不等式)8. 某公司的员工分别住在A 、B 、C 三个小区，A 区住员工30人，B 区住员工15人，C 区住员工10人，三个小区在一条直线上，位置如图所示。

第20届希望杯初二第1试试题及答案

初二年级第1试一、选择题（以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题后面的圆括号内．）1．在一次视力检查中，初二（1）班的50人中只有8人的视力达标，用扇形图表示视力检查结果，则表示视力达标的扇形的圆心角是（）A ．64.8︒B ．57.6︒C ．48︒D ．16︒2．如图1，点B 在反比例函数k y x=的图像上，从点B 分别作x 轴、y轴的垂线，垂足分别是A ，C ．若ABC △的面积是4，则反比例函数的解析式是（） A ．8y x =-B ．8y x =C ．4yx=-D ．4yx=3．如果22a ab b ++=，且b 是有理数，那么（）A ．a 是整数B ．a 是有理数C ．a 是无理数D ．a 可能是有理数，也可能是无理数4．复印纸的型号有01234A A A A A ，，，，等，它们有如下的关系：将上一个型号（例如3A ）的复印纸在长的方向对折后就得到两张下一个型号（得到4A ）的复印纸，且各种型号的复印纸的长与宽的比相等，那么这些型号的复印纸的长与宽的比约为（）A ．1.414:1B ．2:1C ．1:0.618D ．1.732:15．The number of integer solutions for the system of inequalities 2321x a x -⎧⎨->-⎩，≥0about x is图1yxO CBAjust 6，then the range of value for real number ais （）A ． 2.52a -<-≤B ． 2.52a --≤≤C ．54a -<-≤D ．54a --≤≤（英汉词典：integer solution 整数解，system of inequalities 不等式组，the range of value取值范围）6．若分式232x x --的值是负数，则x 的取值范围是（） A ．223x <<B ．23x >或2x <- C ．22x -<<且23x ≠D ．223x <<或2x <-7．在100到1000的整数中（含100和1000），既不是完全平方数，也不是完全立方数的数有（）A ．890个B ．884个C ．874个D ．864个8．如图2，在正方形ABC D中，E 是D C 的中点，点F 在BC 上，E AF D A E ∠=∠，则下列结论中正确的（）A ．EAF FAB∠=∠B ．13FC BC=C ．AF AE FC =+D ．AFBC FC=+9．计算：()()233211471147++-，结果等于（） A ．58B ．387C ．247D ．32710．已知在代数式2a bx cx ++中，a b c ，，都是整数，当3x =时，该式的值是2008；当7x =时，该式的值是2009，这样的代数式有（） A ．0个B ．1个C ．10个D ．无穷多个二、A 组填空题11．某地区有20000户居民，从中随机抽取200户，调查是否已安装电话，结果如右表所示，则该地区已安装电话的户数大约是________________．图2F E DCBA12．若2145212x x +-=-，则2645x x -+的值等于______________．13．不等式12x x->的最大整数解是_______________．14．已知m 是整数，以4521m m +-，，20m -这三个数作为同一个三角形三边的长，则这样的三角形有__________________个． 15．当x 依次取1，2，3，…，2009，11112342009 ，，，，时，代数式221xx+的值的和等于___________． 16．由一次函数22y x y x =+=-+，和x 轴围成的三角形与圆心在点(11)，、半径为1的圆构成的图形覆盖的面积等于_____________． 17．在R t ABC △中，90C ∠=︒，斜边AB上的高为h ，则两条直角边的和a b+与斜边及其高的和c h+的大小关系是a b +___________c h +.（填“）”、“〈”或“=”）18．Figure 3 is composed of squareABC Dand triangleBEC，where BEC ∠ is a right angle，Suppose the lengthof C Eis a ，and the length of BEis b ，then the distance between point Aand lineC Eequals to _______________．（英汉词典：be composed of 由……组成，right angle 直角，length 长度，distance 距离） 19．如图4，在ABC △中，A BB C>，BD 平分ABC ∠，若BD 将ABC△的周长分为4：3的两部分，则ABD △和D B C △的面积之比等于_____________．20．将n 个棋子放入10个盒子内，可以找到一种放法，使每个盒子内都有棋子，且这10个盒子内的棋子数都不相同．若将()1n +个棋子放入11个盒子内，却找不到一种放法，能够使每个盒子内都有棋子，并且这11个盒子内的棋子数都不相同．则整数n 的最大值等于_____________，最小值等于_______________. 三、B 组填空题EDCBAFigure 3图4D CBA21．如果自然数a 和()b a b >的和、差、积、商相加得27，那么a =______________，b=____________．（拟题：李国威上海市青浦区教师进修学院 201700）22．若a b c b cc aa b==+++，则223a b c a b c +++-=_____________或______________．23．若以x 为未知数的方程212(1)1232aa x xx x +-=---+无解，则a =__________或___________或________________．24．对于正整数k ，记直线111k yx k k =-+++与坐标轴所围成的直角三角形的面积为k S ，则kS =___________，1234S S S S +++=___________________．25．将1111234100，，，，这99个分数化成小数，则其中的有限小数有____________个，纯循环小数有________________个（纯循环小数，是从小数点后第一位开始循环的小数）参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 答案 BACAADCDBA提示1．周角为360︒，对应全体学生，则表示视力达标的扇形的圆心角为836057.650⨯︒=︒，选B ．2．点()B x y ，在第四象限，所以00x y ><，，且满足k y x=，即xy k =<，ABC△的面积12ABCS xy =，△由已知得1482xy xy ==，，则8k xy ==-，所以批比例函数的解析式是8y x =-，选A ．3．由题目条件得()()()()()22221312221212121bb b b b a b b b b ---+-===-++-=()2221232121b b b b +---，因为b 是有理数，则2321bb -和22121b b +-也都是有理数，而2是无理数，所以a 是无理数．选C ．4．设3A 型号的复印纸长为x ，宽为y ，对折后得到4A 型号的复印纸长为y ，宽为2x，由题意得2x y x y=，即222x y=，所以 :2:1 1.414:1x y =≈，选A5．译文：关于x 的不等式组20321x a x -⎧⎨->-⎩，≥的整数解恰好有6个，那么实数a 的取值范围是（）A ． 2.52a -<-≤B ． 2.52a --≤≤C ．54a -<-≤D ．32a -<-≤解解20x a -，≥得2x a ≥；解321x ->-，得2x <，所以不等式组的解是22a x <≤，由题意知不等式组恰好有6个整数解，所以这6个整数解应为 -4，-3，-2，-1，0，1，所以 524a -<-≤，解得 2.52a -<-≤，选A ．6．由题意，分式232x x --的值为负，则2x -和32x -异号．当320x ->，即23x >时，应当有202x x -<<，，解得22x -<<，又23x >，所以 223x <<；当320x -<，即23x <时，应当有202x x ->>，，解得2x >或2x <-，又23x <，所以2x <-．综上可知，x 的取值是范围是223x <<或2x <-，选D ．7．解法1 用()A n 表示不大于n 的非零自然数中既不是完全平方数也不是完全立方数的数的个数．由于36999104100010310004<<<=<<，，，所以 (99)99(942)88A =-+-=．由于3631100032100010310004<<=<<，，，所以 (1000)1000(31103)962A =-+-=故有(1000)(99)96288874A A -=-=．即在100到1000的整数中（含100和1000），既不是完全平方数也不是完全立方数的数有874个，选C ．解法2 因为2221001031100032=<<，，所以在100到1000之间的完全平方数有222210111231 ，，，，，共22个，又因为33341005100010<<=，，所以在100到1000之间的完全立方数有333356910 ，，，，共6个，其中3629327==即是完全平方米，也是完全立方数．所以，在100到1000的整数中（含100和1000），既不是完全平方数也不是完全立方数的数有901-22-6+1=874（个），选C ．8．如图5所示，从点E 作EG AF⊥，垂足为G ．在R t D AE △和R t G AE△中，AE AE DAE EAG=∠=∠，，所以 D AE G AE≅△△，所以AG AD BC EG ED EC====，，AEDAEG∠=∠．GABCDE F图5又在R t EFG △和R t EFC △中，EF EF EG EC ==，，所以 EFG EFC≅△△，FC GF FEG FEC =∠=∠，，所以 AF AG G F BC FC=+=+，D 选项正确．又AEAD BC>=，可知AFAE FC<+，C 选项错误．由AED AEG FEGFEC∠=∠∠=∠，，且这四个角之和等于180︒，所以 90AEF ∠=︒．令1AB =，在R t AFE △中，22254AE AD DE =+=，所以 225(1)4G F EF-=+， ①在R t EFC △中，222214EFEC FC FC=+=+ ②①+②，并由G FFC=得14FC =，故14FC BC =，B 选项错误．据此可知FAB DAE FAB EAF ∠≠∠∠≠∠，，A 选项错误．故选D ． 9．原式=()()3322227227272272+⨯++-⨯+=()()3322227272⎡⎤⎡⎤++-⎢⎥⎢⎥⎣⎦⎣⎦=()()337272++-=()()()()3232223737237273723722+⨯⨯+⨯⨯+-⨯⨯+⨯⨯-=277674387⨯+⨯=，选B ．10．当3x=时，392008a b c ++=， ①当7x =时，7492009a b c ++=． ② ②-①，得4401b c +=．当b c ，都是整数时，上式左边总为偶数，不可能等于1．所以不存在这样的代数式，选A ．二、A 组填空题题号 11 12 1314 1516 17 1819 20 答案 950073x =-2120082π42+<a b+4：364：55提示11．抽取的200户居民中，已经安装电话的有60+35=95（户），则该地区的20000户居民中，已经安装电话的大约有95200009500200⨯=（户） 12．因为2145212x x +-=-，所以 2211470x x --=，即23210x x --=，所以 ()22645232177x x x x -+=--+=． 13．由12x x->得21x x ->，即()121x ->，因为 120-<，所以()121 2.41412x <=-+≈--，所以原不等式的最大整数解是3x =-． 14．由450210200m m m +>->->，，，解得1202m <<，因为m 是整数，所以 119m ≤≤，又由“三角形两边之和大于第三边”得452120452021212045m m m m m m m m m ++->-⎧⎪++->-⎨⎪-+->+⎩，，，解得2272624.3m m m ⎧>⎪⎪>-⎨⎪⎪<⎩，，得222473m <<，因为m 是整数，所以只能取34，．当3m =时，三角形三边的长分别是17517，，；当4m=时，三角形三边的长分别是21716，，．故满足题意的三角形共有2个． 15．当a 为实数时，把x a =与1x a=分别代入代数式221xx+中，得到的两个值的和是222222211111111aaa aaaa+=+=++++，所以，若将11112320092342009x = ，，，，，，，，代入代数式221xx+中求值，得到的所有值的和是2008，又当1x =时，22112xx=+所以，得到的所有代数式的值的和等于120082．16．由一次函数22y x y x =+=-+，和x 轴可以确定三条直线，每两条直线相交于一点，共得三个点（0，2）（-2，0），（2，0），它们构成了一个三角形，这个三角形的面积为4．由于点（1，1）在直线2y x =-+上，所以圆的一半与三角图6yx（2，0）（1，1）（0，2）（0，0）（-2，0）形重叠，如图6所示．所以，所求图形的面积为21π4π1422+⨯⨯=+．17．因为ABC △是直角三角形，所以222a b c+=，又1122ABC S ab ch==△，所以 ab ch=则()()2222222222a b a ab b c ch c ch h c h +=++=+<++=+，所以 a b c h+<+18．译文：图3由正方形ABC D 和三角形BEC 构成，其中BEC ∠是直角，记C E 的长为a ，BE 的长为b ，则点A 到直线C E 的距离等于___________________．解如图7所示，从点A 作AF CE ⊥，交线段C E 于点F ，交线段BC 于点H ；从点B 作BGAF⊥交AF 于G ，则四边形B E F G 是矩形，G FBE b==．因为 90BAG BH A ∠=︒-∠，90BC E C H F∠=︒-∠，又BH A C H F∠=∠，所以 BAG BC E∠=∠．在R t ABG △与R t C BE △中，90BAG BCE AB CB AGB BEC ∠=∠=∠=∠=︒，，所以 ABG CBE AG CE a ≅==，△△，所以 AF AG G F a b===+19．如图8所示，作DE AB⊥于E ，D FBC⊥于F ．因为BD是ABC ∠的平分线，GHF图7ABCDEF EBDE AB DF BC⊥⊥，，所以 DE DF=，则11:::22ABD D BC S S A B D EB C D E A B B C ⎛⎫⎛⎫=⋅⋅= ⎪ ⎪⎝⎭⎝⎭△△又 ::ABD DBC S S AD CD=△△，所以:():()4:3ABD DBC S S AB AD BC CD =++=△△．20．由题意，将n 个棋子放入10个盒子中，可以找到一种放法，使每个盒子内都有棋子，且这10个盒子内的棋子数都不相同，按最少的放法，盒子内依次放入1，2，3，…，10个棋子，即至少需要1+2+3+…+10=55（个）棋子，所以55n ≥．同理，将1n +个棋子放入11个盒子内，找不到一种放法，使每个盒子内都有棋子，并且这11个盒子内的柜子数都不相同，则11231166n +<++++= ，即65n <．综上，得5565n ≤≤，取5564n ≤≤．三、B 组填空题题号 21 22 232425答案 6；2-5；14-2；32-；1-12(1)k k +；2514；39提示21．将两数a 和b 的和、差、积、商相加得27，因为27是整数，所以a 必是b 的整数倍，设a kb=（k 是整数），则有227kb b kb b kb k ++-++=，化简得2227kb kb k ++=，222(1)33271k b +=⨯=⨯，则 326k b a ===，，，或2700k b a ===，，（不符合题意，舍去）．所以 326k b a ===，，.22.令 a b ckb cc aa b===+++．当0a b c ++≠时，()122a b ck a b c ++==++，所以()12c a b =+，()()()()1222251332a b a b a b c a b ca b a b +++++==-+-+-⋅+．当0a b c ++=时，()c a b =-+，所以()()()()2221334a b a b a b c a b ca b a b +-+++==+-+++．23．当10x -≠且20x -≠时，将原方程去分母得()()()2121x a x a -+-=+，整理得 ()134a x a +=+，当1a≠-时，原方程的解为341a x a +=+．由于原方程无解，那么可能的情况是1a =-或求得的根是增根．当增根是1x =时，即 3411a a +=+，解得32a =-；当增根是2x =时，即 3421a a +=+，解得2a=-，所以a 的值为32-或-2或-1．24．直线111k yx k k =-+++与横轴的交点坐标为10k ⎛⎫⎪⎝⎭，，与纵轴的交点坐标为101k ⎛⎫ ⎪+⎝⎭，，所以该直线与坐标轴所围成的直角三角形的面积是()121k S k k =+，所以该直线与坐标轴所围成的直角三角形的面积是()()112321kS k n k k ==+ ，，，，．123411111212233445S S S S ⎛⎫+++=+++ ⎪⨯⨯⨯⨯⎝⎭=11111111122233445⎛⎫-+-+-+- ⎪⎝⎭=25．25．⑴若p 为正整数，且1p是有限小数，则p 可以写成25mn⋅（m n ，是自然数）的形式．其中若0n =，则22100m ≤≤，得123456m =，，，，，．即248163264p =，，，，，共6个；若1n =，则1220m ≤≤，得01234m =，，，，，即510204080p =，，，，共5个；若2n =，则124m ≤≤，得012m =，，，即25p =，50，100共3个；若3n ≥，则不存在合理的m 的值．所以可以化为有限小数的分数共有6+5+3=14（个）．（2）若p 为正整数，且1p是纯循环小数，则p 的质因数一定没有2或5．在2到100的整数中，质因数含有2的数有50个，质因数含有5的数有20个，质因数同时含有2和5的数有10个，所以从2到100这99个整数中，质因数中不含有2且不含有5的整数有99-50-20+10=39（个）。

第二十四届希望杯全国数学邀请赛初二试题(第1试)及答案

第二十四届“希望杯”全国数学邀请赛初二第1试试题2013年3月17日上午8：30至10：00一、选择题(每小题4分，共40分) 1．有下列五个等式： 13+=x y ①；1y22-=x ②；x y =③；||x y =④；x y =||⑤；其中，表示“y是x 的函数”的有( )A ．1个B ．2个C ．3个D ．4个2．点),7(m -和点),8(n -都在直线62--=x y 上，则m 和n 的大小关系是( ) A ．m>n B ．m<n C ．m=n D ．不能确定 3．下列命题中，正确的是( )A ．若0>a ，则aa 1> B ．若2a a >，则1>aC ．若10<<a ，则2a a >D ．若a a =||，则0>a 4．若定义运算“⊗”：a b b a =⊗，如82233==⊗，则213⊗等于( )A ．81B ．8C ．61D ．235．以下关于平行四边形的判定中，不正确的是( ) A ．两组对角分别相等的四边形是平行四边形； B ．两组对边分别相等的四边形是平行四边形； C ．对角线相等的四边形是平行四边形；D ．一组对边平行且相等的四边形是平行四边形；6．用一根长为a ，并且没有伸缩性的线围成面积为S 的等边三角形．在这个等边三角形内任取一点P ，则点P 到等边三角形三条边的距离之和为( )A ．aS 2 B ．aS 4 C ．aS 6 D ．aS 87．若199199<<-x ，且100-=x m 的值为整数，则m 的值为( ) A ．100个 B ．101个 C ．201个 D ．203个 8．已知32+=x ，且)86(148+=+y x x ，则y 的值是( )A ．10B ．15C ．20D ．309．If a right triangle has edge lengths b a -，a ，and b a + (a and b are both positive integers)，then the perimeter of the triangle might be ( ) A ．60 B ．70 C ．80 D ．9010．小王与小李约定下午3点在学校门口见面，他们在早上8点将自己的手表对准．小王于下午3点到达学校门口，可是小李还没有到，原来小李的手表比正确时间每小时慢4分钟．如果小李按他自己的手表在3点到达，则小王还需要等( )(正确时间) A ．26分钟 B ．28分钟 C ．30分钟 D ．32分钟二、A 组填空题(每小题4分，共40分) 11．若125512=+x ，则____________)2(2012=-+xx ．12．计算：___________1222222201120122013=------ ．13．用边长为1cm 的小正方形在桌面上摆放成如图1所示的塔状图形，则第n 次所摆图形的周长是______________cm(用关于n 的代数式表示)14．有两个函数b ax y +=和5+=cx y ，第1次第2次第3次图1学生甲求出它们图象的交点的正确坐标)2,3(-，学生乙因抄错c 而得出交点坐标⎪⎭⎫⎝⎛41,43，则函数b ax y +=的解析式是_____________；15．如图2，三个正比例函数的图象分别对应解析式：ax y =①，bx y =②，cx y =③，若将a ，b ，c 从小到大排列，则应当是_____________．16．如图3，在正方形ABCD 中，E 、G 、F 分别是AB 、AD 、BC 边上的点，若BE=2AE ，AG=1，BF=2，∠GEF=90°，则GF 的长是_______________．17．一个三角形的三条边的长分别是3，5，7，另一个三角形的三条边的长分别是3，23-x ，12-x ．若这两个三角形全等，则x 的值是___________．18．有甲、乙、丙三种商品，购甲3件，乙7件，丙1件，需3．15元；购甲4件，乙10件，丙1件，需4．20元．若购甲、乙、丙各1件，则需______________元．19．设a ，b 是实数，且a b b a -=+-+11111，则baa b +++++1111的值是____________． 20．将不大于20的正偶数分成两组，使得第一组中数的乘积能被第二组中数的乘积整除．则商的最小值是__________________．三、B 组填空题(每小题8分，共40分) 21．数学老师用10道题作为一次课堂练习，课代表将全班同学的答题情况绘制成条形统计图，如图4所示．观察此图可知，每位同学答对的题的个数组成的样本众数是______，中位数是_______．22．方程3||12||=+-x x 的解是__________或__________．23．若关于x 的方程234222+=-+-x x mx x 有增根，则_______=m 或________． 24．Let 20131=⎪⎭⎫ ⎝⎛+x y x ，x and y are both positive integers ，then the largest value ofy x + is ____________，the smallest value of y x + is _________．25．已知0=++c b a ，c b a ≥≥，0≠a ，则ac 的最大值是____________，最小值是___________．附加题(每小题10分，共20分) 1．A 商品的单价是50元，B 商品的单价是60元，几所学校各付款1220元购买这两种商品，任意2所学校购买的A 商品的数量都不同．则参加这次采购的学校最多有________所． 2．十进制数中，右边的数友比左边的数友大的数叫做上升数，如134，258．那么三位数中的上升数有_________个；在三位上升数中，3的倍数有___________个．F 图2 图3 答对题数5 图4答案：一、选择题(每小题4分，共40)二、A 组填空题(每小题4分，共40分)11．1- 12．1 13．4n 14．1+-=x y 15．c<a<b 16．10 17．3 18．1.05 19．3 20．7三、B 组填空题(每小题8分，共40分)21．8， 9 22．234=-=x x 或 23．46-或 24．2013，507 25．21-，2-附加题(每小题10分，共20分)1．4 2．84，30。

第19届希望杯全国数学邀请赛初二第1试试题