弓形计算
弓形面积的通用计算公式

弓形面积的通用计算公式
一、已知弓形的底为(2b)(b为半弦长)、高为h;
二、弓形半径公式:
R=(b2+h2) /(2h);
三、弓形面积的通用计算公式:
S=b(h-R)+R2arccos(1-h/R)(arccos为反余弦:0≤arccos(x)≤π)(劣弧弓形、优弧弓形,二者通用)
四、已知半径R和弧角θ(弧度)的弓形面积通用计算公式:
S=(1/2)R2(θ-sinθ)(劣弧弓形、优弧弓形,二者通用)
注意:(1) 弧角θ必需使用弧度单位。
(2) 若弧角θ单位为度,则计算公式为
S=(1/2)R2(θπ/180-sinθ)
(3) 电脑对sinθ默认的θ是弧度,若θ为度,则计算公式为
S=(1/2)R2[θπ/180-sin(θπ/180)]
五、已知半径R和弧角θ的求弓高H通用计算公式:
H=R[1-cos(θ/2)]=2R*sin2(θ/4)
六、已知半径R和弓高H的求弦长L通用计算公式:
L=2*√[H(2R-H)]
七、已知半径R和弧角θ的求弦长L通用计算公式:
L=2R*sin(θ/2)。
扇形、三角形、弓形、菱形公式[整理版]
![扇形、三角形、弓形、菱形公式[整理版]](https://img.taocdn.com/s3/m/b6f8b31d91c69ec3d5bbfd0a79563c1ec5dad70c.png)
常用面积公式面积公式扇形面积公式00在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积S=πR^2,所以圆心角为n°的扇形面积:00S=nπR²÷360 00比如:半径为1cm的圆,那么所对圆心角为135°的扇形的周长:00C=2R+nπR÷180 00=2×1+135×3.14×1÷180 00=2+2.355 00=4.355(cm)=43.55(mm) 00扇形的面积:00S=nπR²÷360 00=135×3.14×1×1÷360 00=1.1775(cm²)=117.75(mm²) 00扇形还有另一个面积公式00S=1/2lR 00其中l为弧长,R为半径00扇环面积00圆环周长:外圆的周长+内圆的周长(圆周率X(大直径+小直径)) 0圆环面积:外圆面积-内圆面积(圆周率X大半径的平方-圆周率X小半径的平方\圆周率X(大半径的平方-小半径的平方)) 00用字母表示:00S内+S外(∏R方)00S外—S内=∏(R方-r方)00还有第二种方法:00S=π[(R-r)×(R+r)] 00R=大圆半径00r=圆环宽度=大圆半径-小圆半径00还有一种方法:00已知圆环的外直径为D,圆环厚度(即外内半径之差)为d。
00d=R-r,00D-d=2R-(R-r)=R+r,00可由第一、二种方法推得S=π[(R-r)×(R+r)]=π(D-d)×d,0圆环面积S=π(D-d)×d 00这是根据外直径和圆环厚度(即外内半径之差)得出面积。
这两个数据在现实易于测量,适用于计算实物,例如圆钢管。
三角形面积公式00海伦公式00任意三角形的面积公式(海伦公式):S²=p(p-a)(p-b)(p-c), p=(a+b+c)/2, a.b.c为三角形三边。
扇形弓形面积计算公式(一)

扇形弓形面积计算公式(一)扇形弓形面积计算公式扇形面积计算公式扇形是圆形的一部分,计算扇形的面积需要知道圆的半径和扇形的弧度。
扇形面积计算公式如下:扇形面积 = (圆的半径 * 圆的半径 * 弧度) / 2其中,圆的半径是指从圆心到圆上任意一点的距离,弧度是扇形所对应的圆心角的弧度值(1弧度= 180/π度)。
例子假设有一个半径为5 cm的扇形,对应的圆心角为60°,则可以使用扇形面积计算公式来计算扇形的面积:圆的半径 = 5 cm弧度= 60° * π / 180° = π / 3 rad扇形面积= (5 cm * 5 cm * π / 3 rad) / 2= (25 cm² * π / 3 rad) / 2≈ cm²因此,该半径为5 cm,圆心角为60°的扇形的面积约为cm²。
弓形面积计算公式弓形是圆的一部分,同时含有一条弦线。
计算弓形的面积需要知道圆的半径和弓形的弧度,以及弦线的长度。
弓形面积计算公式如下: 弓形面积 = (圆的半径 * 圆的半径 * 弧度 - 弦线的长度 * 圆的半径 * ) / 2其中,圆的半径和弧度的含义与扇形相同,弦线的长度是弓形上两点所连成的线段的长度。
例子假设有一个半径为8 cm的弓形,对应的圆心角为90°,弦线的长度为10 cm,则可以使用弓形面积计算公式来计算弓形的面积: 圆的半径 = 8 cm弧度= 90° * π / 180° = π / 2 rad弦线的长度 = 10 cm弓形面积= (8 cm * 8 cm * π / 2 rad - 10 cm * 8 cm * ) / 2= (64 cm² * π / 2 rad - 40 cm²) / 2≈ cm²因此,该半径为8 cm,圆心角为90°,弦线长度为10 cm的弓形的面积约为cm²。
弓形导线结构尺寸的计算
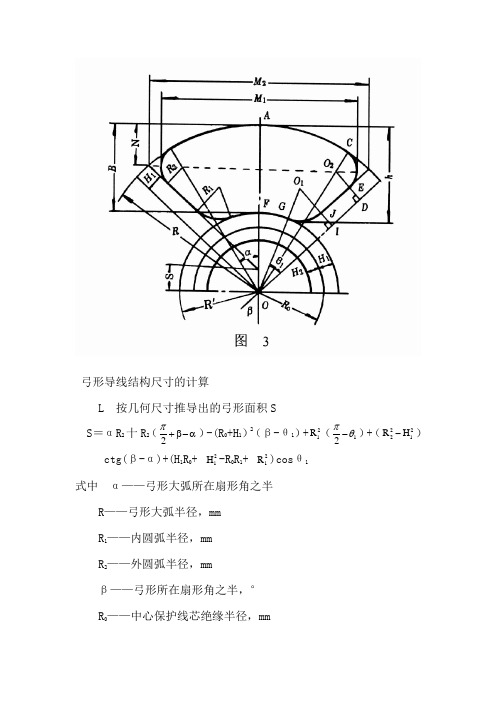
弓形导线结构尺寸的计算L 按几何尺寸推导出的弓形面积SS =αR 2十R 2(2π+β-α)-(R 0+H 1)2(β-θ1)+21R (12πθ-)+(2221R H -)ctg(β-α)+(H 1R 0+21H -R 0R 1+21R )cos θ1 式中 α——弓形大弧所在扇形角之半 R ——弓形大弧半径,mm R 1——内圆弧半径,mm R 2——外圆弧半径,mmβ——弓形所在扇形角之半,° R 0——中心保护线芯绝缘半径,mmH 1——弓形绝缘厚度,mmθ1——内圆弧的圆心所在直线与弓形绝缘后轮廓线的夹角° θ1=arcsin11011H +R R +H +R2弓形大弧半径R 12H +R R=sin(-)βα3弓形小弧半径R ’ R ’=R 0+H 1 (mm)4 内圆弧半径R1和外圆弧半径R2z R l =K 1R , (mm) R 2=K 2R , (mm)式中 K 1——系数取K l 为0.20 K 2——系数,取K 2为0.12 5 弓形厚度BB =R-R 0-H 1, (mm) 6 弓形高度hh =R-(R 0+H 1+R 1)× cos(β-θ1)+R1 7 弓形宽度M1M 1= 2[(R —θ1)sin α+R 2] 8弓形轮廓周长LL =2[αR 十R 2(2π+β-α)(R 2+H 1) ctg θ1+R 1(12πθ-)+(R 0+H 1)(β-θ1)] 9 弓形相当圆直径D D =L /π (mm)紧压模具的设计 上压模的宽度M 2和高度N (1)截面较大时 M 2=2(R-H 1ctg β)sin β N=R-21M Hctg 2sin β-β(2)截面较小时 M 2=2Rsin(β-arcsin1H R+δ)式中δ——上、下压模的间隙, 取δ=0.6mm 。
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
与弓形有关的计算公式

与弓形有关的计算公式
弓形(或称弧)是圆的一部分,它由圆周上的两点和这两点之间的圆弧组成。
与弓形有关的计算公式主要包括弓形的面积、弦长、圆心角等。
以下是一些基本的公式:
1.弓形面积公式:如果已知半径r 和圆心角θ(以弧度为单位),
则弓形的面积A 可以用以下公式计算:A = r² * θ / 2
2.弦长公式:如果已知半径r 和圆心角θ(以弧度为单位),则弦
长L 可以用以下公式计算:L = 2r * sin(θ / 2)
3.圆心角转换为度数:如果圆心角是以弧度为单位,要将其转换为度
数,可以使用以下公式:θ(度) = θ(弧度) * (180 / π)
4.扇形面积减去三角形面积得到弓形面积:如果有一个扇形,其圆心
角为θ,半径为r,则扇形面积S_sector 为:S_sector = π * r² * (θ / 2)
如果需要计算弓形面积,且知道包含该弓形的等腰三角形的底边即
弦长L,则该三角形面积S_triangle 为:S_triangle = r * L / 2 因此,弓形面积A_segment 可以通过扇形面积减去三角形面积得
到:A_segment = S_sector - S_triangle
请注意,上述公式中圆心角θ 应当用弧度表示;若使用角度,则需要对公式进行调整。
在使用这些公式时,确保角度单位一致,以避免计算错误。
求圆弓型的面积弧长及半径图文

求圆弓型面积、半径及弧长的图文说明一、 圆弓型的面积1、 已知条件:弦长 a ,矢高h2、求圆弓型的面积3、公式:①S=2/3ah ②S=1/2[Lr-a(r-h)]4、例题:例1:⑴已知条件:弦长a ,矢高h ,半径r ,弧长L,求圆弓型的面积S⑵计算:S=2÷3×11.31×2.2=16.59例1:⑴已知条件:弦长a=11.31,矢高h=2.2,半径r=8.3727,弧长L=12.42;求圆弓型的面积S 。
⑵计算:S=1/2[12.42*8.3727-11.31(8.3727-2.2)]=17.09二、圆弓型的弧长(一)1、已知条件:弦长a,矢高h,半径r, 求弧长L。
2、公式:L=[4/3ah+a(r-h)]/r3、例:已知条件:弦长a=11.31,矢高h=2.2,半径r=8.3727, 求弧长L。
答L=[4/3*11.31*2.2+11.31(8.3727-2.2)]/8.3727 =12.30(二) 1、已知条件:等腰三角形边长A,半径r。
2、求弧长L3、计算步骤:a= (A2+A2)的平方根sin∟O=(1/2a)/r 查三角函数表求得∟O的度数α。
L=[(2πr)/360]×2α。
4、例题:例1:⑴已知条件:等腰三角形边长A=8,半径r=8.3727。
⑵计算:a=√----(82+82) =11.3137sin∟O=(0.5*11.3137)/8.3727= 0.6756查三角函数表求得∟O的度数α=42.500L=[(2*3.1416*8.3727)/360]*2*42.5=12.42三、圆弓型的半径1、已知条件:弦长a,矢高h2、求圆弓型的半径3、公式:r=[(1/2a)2/h+h]/24、例:r=[(0.5*11.3137)2/2.2+2.2]/2=8.3727四、自动计算见《求圆弓型的面积、弧长及半径自动计算表》。
弓形半径公式

弓形半径公式弓形半径公式是在几何学中常用的计算弧线半径的公式。
它可以帮助我们计算出弧线上任意一点的曲率半径,从而更好地理解和分析曲线的性质和特点。
本文将详细介绍弓形半径公式的原理和应用。
一、弓形半径公式的原理弓形半径公式是通过对弧线进行微分来推导的。
在微积分中,我们知道曲线的曲率可以通过对曲线方程的二阶导数求解得到。
而曲率半径则是曲率的倒数,即曲率半径R=1/曲率。
对于弧线来说,弓形半径就是在弧线上任意一点处的曲率半径。
具体推导过程可以通过以下步骤完成:1. 假设有一条弧线的参数方程为x=f(t),y=g(t),其中t为参数。
2. 求出弧线的切向量T的表达式,即T=(dx/dt, dy/dt)。
3. 求出弧线的曲率k的表达式,即k=(dx/dt*dy^2/dx^3 - dy/dt*dx^2/dy^3)/(dx/dt^2+dy/dt^2)。
4. 根据曲率半径R=1/曲率,得到弓形半径公式R=(dx/dt^2+dy/dt^2)/(dx/dt*dy^2/dx^3 - dy/dt*dx^2/dy^3)。
二、弓形半径公式的应用弓形半径公式在现实生活中有着广泛的应用。
以下是几个常见的应用场景:1. 道路设计:在道路设计中,我们需要考虑道路的弯曲程度和转弯半径。
弓形半径公式可以帮助工程师计算出道路上每个弯道的曲率半径,从而确保车辆能够顺利转弯并保持稳定。
2. 轨道交通:对于高速铁路和地铁等轨道交通系统来说,保持列车行驶的平稳和安全是非常重要的。
弓形半径公式可以帮助工程师计算出轨道的曲率半径,以确保列车在曲线处的行驶稳定。
3. 建筑设计:在建筑设计中,我们常常需要设计曲线形状的建筑物,如拱桥、弧形天花板等。
弓形半径公式可以帮助设计师计算出这些曲线的曲率半径,从而确保建筑物的结构稳定和美观。
4. 机械工程:在机械工程中,弓形半径公式可以用于计算曲线表面的曲率半径,从而帮助工程师设计出更加精准和合理的机械零件。
总结:弓形半径公式是计算弧线曲率半径的常用公式,它在许多领域都有着广泛的应用。
弓形(弧形)面积全能公式计算表

弓形(弧形)面积全能公式计算表弓形(弧形)面积计算全能公式表静闲翡翠林于2014年6月27日创建2014年11月16日完善弧(弓)形面积==面积--扇形中的三角形面积弦心距==2√[半径2--(弦长÷2)2]弦心距==半径--矢高扇形中的三角形面积==2√[半径2--(弦长÷2)2]×半径÷2扇形面积==半径2×3.14÷360×弧对应圆心角周长==半径×2×3.14==直径×3.14弧与周长的%==弧÷周长×100弧对应圆心角==(弧÷周长×100)×360÷100弧对应圆心角==弧÷周长×360矢高==半径--弦心距说明:2√[……]:表示括号内的计算结果必须开二次方;弧两端点对应圆心的三角形就是扇形中的三角形(等腰);弦中点到圆心的距离,简称“弦心距”,也可叫“中位线”;弧中点到弦中点的距离,简称“矢高”;弧长、弦长、半径、矢高、中心角等可全部或部分从电子图中获取;以上计算公式可利用电子表格创建一个非常方便的功能计算表如下弓形(弧形)面积全能公式计算表部位名称弧长矢高弦长弦心距半径周长弧/ 周%中心角弧面积123456789计算式:2=5--4 6=5×2×3.14 7=1÷6×100 8=7×360÷100 8=1÷6×3604=5--√[52--(3÷2)2] 9=5×5×3.14÷360×8--3×(5--2)÷2 2居室台顶3.5910.3403.5084.3604.70029.51612.16643.7990.7912居厅台顶4.2660.4764.1214.2244.70029.51614.45352.0311.3213居厅台顶4.2640.3414.1906.2596.60041.44810.28837.0350.9593居室台顶6.9310.9376.7805.6636.60041.44816.72260.2003.675注:计算式中的黑体字是常数,其余数是计算列序的编号;。
