2012中考数学复习(37):相似三角形(一)
初三数学相似三角形典例及练习(含答案)

初三数学相似三角形(一)相似三角形是初中几何的一个重点,同时也是一个难点,本节复习的目标是:1。
理解线段的比、成比例线段的概念,会根据比例线段的有关概念和性质求线段的长或两线段的比,了解黄金分割.2. 会用平行线分线段成比例定理进行有关的计算、证明,会分线段成已知比。
3. 能熟练应用相似三角形的判定和性质解答有关的计算与证明题。
4. 能熟练运用相似三角形的有关概念解决实际问题本节的重点内容是相似三角形的判定定理和性质定理以及平行线分线段成比例定理。
本节的难点内容是利用判定定理证明两个三角形相似以及相似三角形性质的应用。
相似三角形是平面几何的主要内容之一,在中考试题中时常与四边形、圆的知识相结合构成高分值的综合题,题型常以填空、选择、简答或综合出现,分值一般在10%左右,有时也单独成题,形成创新与探索型试题;有利于培养学生的综合素质。
(二)重要知识点介绍: 1。
比例线段的有关概念: 在比例式::中,、叫外项,、叫内项,、叫前项,a b cda b c d a d b c a c ==() b 、d 叫后项,d 叫第四比例项,如果b=c ,那么b 叫做a 、d 的比例中项。
把线段AB 分成两条线段AC 和BC,使AC 2=AB ·BC ,叫做把线段AB 黄金分割,C 叫做线段AB 的黄金分割点。
2. 比例性质: ①基本性质:a b cdad bc =⇔= ②合比性质:±±a b c d a b b c d d=⇒= ③等比性质:……≠……a b c d m n b d n a c m b d n a b===+++⇒++++++=()03。
平行线分线段成比例定理:①定理:三条平行线截两条直线,所得的对应线段成比例,如图:l 1∥l 2∥l 3。
则,,,…AB BC DE EF AB AC DE DF BC AC EFDF===②推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。
人教版中考数学知识点复习资料-相似三角形
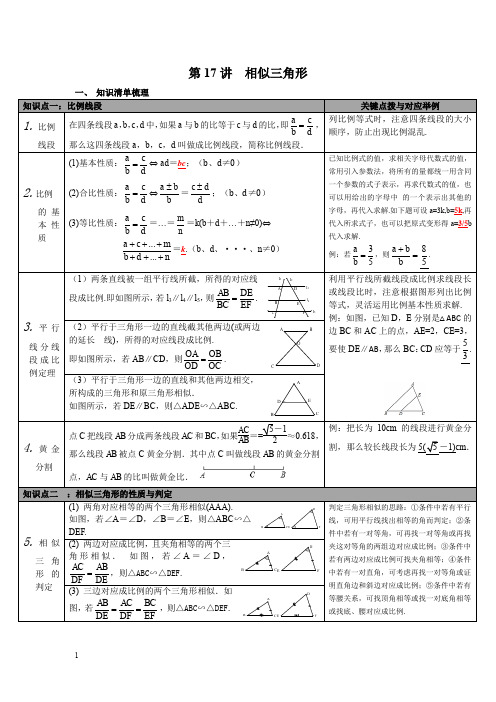
第17讲相似三角形一、知识清单梳理知识点一:比例线段关键点拨与对应举例1.比例线段在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即a cb d=,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.列比例等式时,注意四条线段的大小顺序,防止出现比例混乱.2.比例的基本性质(1)基本性质:a cb d=⇔ ad=bc;(b、d≠0)(2)合比性质:a cb d=⇔a bb±=c dd±;(b、d≠0)(3)等比性质:a cb d==…=mn=k(b+d+…+n≠0)⇔......a c mb d n++++++=k.(b、d、···、n≠0)已知比例式的值,求相关字母代数式的值,常用引入参数法,将所有的量都统一用含同一个参数的式子表示,再求代数式的值,也可以用给出的字母中的一个表示出其他的字母,再代入求解.如下题可设a=3k,b=5k,再代入所求式子,也可以把原式变形得a=3/5b代入求解.例:若35ab=,则a bb+=85.3.平行线分线段成比例定理(1)两条直线被一组平行线所截,所得的对应线段成比例.即如图所示,若l3∥l4∥l5,则AB DEBC EF=.利用平行线所截线段成比例求线段长或线段比时,注意根据图形列出比例等式,灵活运用比例基本性质求解.例:如图,已知D,E分别是△ABC的边BC和AC上的点,AE=2,CE=3,要使DE∥AB,那么BC:CD应等于53. (2)平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.即如图所示,若AB∥CD,则OA OBOD OC=.(3)平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.如图所示,若DE∥BC,则△ADE∽△ABC.4.黄金分割点C把线段AB分成两条线段AC和BC,如果ACAB==5-12≈0.618,那么线段AB被点C黄金分割.其中点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.例:把长为10cm的线段进行黄金分割,那么较长线段长为5(5-1)cm.知识点二:相似三角形的性质与判定5.相似三角形的判定(1) 两角对应相等的两个三角形相似(AAA).如图,若∠A=∠D,∠B=∠E,则△ABC∽△DEF.判定三角形相似的思路:①条件中若有平行线,可用平行线找出相等的角而判定;②条件中若有一对等角,可再找一对等角或再找夹这对等角的两组边对应成比例;③条件中若有两边对应成比例可找夹角相等;④条件中若有一对直角,可考虑再找一对等角或证明直角边和斜边对应成比例;⑤条件中若有等腰关系,可找顶角相等或找一对底角相等或找底、腰对应成比例.(2) 两边对应成比例,且夹角相等的两个三角形相似.如图,若∠A=∠D,AC ABDF DE=,则△ABC∽△DEF.(3) 三边对应成比例的两个三角形相似.如图,若AB AC BCDE DF EF==,则△ABC∽△DEF.FEDCBAl5l4l3l2l1ODCBAEDCBAFEDCBAFEDCBAFEDCBA6.相似三角形的性质(1)对应角相等,对应边成比例.(2)周长之比等于相似比,面积之比等于相似比的平方.(3)相似三角形对应高的比、对应角平分线的比和对应中线的比等于相似比.例:(1)已知△ABC∽△DEF,△ABC的周长为3,△DEF的周长为2,则△ABC与△DEF的面积之比为9:4.(2) 如图,DE∥BC,AF⊥BC,已知S△ADE:S△ABC=1:4,则AF:AG=1:2.7.相似三角形的基本模型(1)熟悉利用利用相似求解问题的基本图形,可以迅速找到解题思路,事半功倍. (2)证明等积式或者比例式的一般方法:经常把等积式化为比例式,把比例式的四条线段分别看做两个三角形的对应边.然后,通过证明这两个三角形相似,从而得出结果.。
中考数学专题之相似三角形题型篇

中考数学专题之相似三角形题型篇(附答案)题型1:相似的性质(★)例1:如图,在△ABC 中,DE△BC ,DE 分别与AB 、AC 相交于点D 、E ,若AD=4,DB=2,则DE△BC 的值为___________ 。
(★)例2:如图,王芳同学跳起来把一个排球打在离地2m 远的地上,然后反弹碰到墙上,如果她跳起击球时的高度是1.8m ,排球落地点离墙的距离是6m ,假设球一直沿直线运动,球能碰到墙面离地多高的地方?题型2:三角形相似的判定(★★)例1:如图2,点P 是ABC ∆的边AC 上一点,连结BP ,以下条件中,不能判定 ABP ∆∽ACB ∆的是( )A .AB AC AP AB = B .ABAC BP BC = C .C ABP ∠=∠ D .ABC APB ∠=∠(★★)例2:如图,小正方形的边长均为1,则图中三角形(阴影部分)与ABC ∆相似的是( )(★★)例3:如图3,D 、E 分别在边AB 、AC 上,且B ∠=∠=∠21,则图中相似三角形有( )A .1对B .2对C .3对D .4对题型3:三角形相似的应用(★★)例1: 某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的的矩形彩条,如图,在ABC Rt ∆中,cm AB cm AC C 50,30,90==︒=∠,仿效裁下宽为cm 1的矩形纸条321,,a a a ,……,若使得裁得的矩形纸条的长都不小于cm 5,则每张直角三角形彩纸能裁成的矩形纸条的总数是( )A .24B .25C .26D .27(★★)例2:美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165cm ,下半身长x 与身高l 的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )A .4cmB .6cmC .8cmD .10cm(★)例3:小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E 处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD =1.2m ,CE =0.8m ,CA =30m (点A E C 、、在同一直线上).已知小明的身高EF 是1.7m ,请你帮小明求出楼高AB (结果精确到0.1m ).(★)检测题1:已知⊿ABC 的三边长分别为2,6,2,⊿A ′B ′C ′的两边长分别是1和3,如果⊿ABC 与⊿A ′B ′C ′相似,那么⊿A ′B ′C ′的第三边长应该是( )A BD FA.2B.22C.26D.33 (★★)检测题2:若P 是Rt △ABC 的斜边BC 上异于B ,C 的一点,过点P 作直线截△ABC ,截得的三角形与原△ABC 相似,满足这样条件的直线共有( )A .1条B .2条C .3条D .4条(★★)检测题3:如图,若A 、B 、C 、P 、Q 、甲、乙、丙、丁都是方格纸中的格点,为使PQR ∆∽ABC ∆,则点R 应是甲、乙、丙、丁四点中的 。
中考数学几何专项——相似模型(相似三角形)

中考数学几何专项——相似模型(相似三角形)相似模型相似模型一:A字型特征:DE∥BC模型结论:根据A字型相似模型,可以得出以下结论:C∠B=∠XXXAC²=AD×AB相似模型二:X型特征:AC∥BD模型结论:根据X型相似模型,可以得出以下结论:AO×OB=OC×ODBOC∽△DOACAOC∽△DOB相似模型三:旋转相似特征:成比例线,段共端点模型结论:根据旋转相似模型,可以得出以下结论:BEF∽△BCDDEF∽△DABAEB∽△DEC相似模型四:三平行模型特征:AB∥EF∥CD模型结论:根据三平行模型,可以得出以下结论:ABE∽△CDF相似模型五:半角模型特征:90度,45度;120度,60度模型结论:根据半角模型,可以得出以下结论:ABN∽△MAN∽△MCAABD∽△CAE∽△CBA相似模型六:三角形内接矩形模型特征:矩形EFGH或正方形EFGH内接与三角形模型结论:根据三角形内接矩形模型,可以得出以下结论:ABC∽△EFH相似模型七:十字模型特征:正方形HDGB模型结论:根据十字模型,可以得出以下结论:若AF=BE,则AF⊥BE,且为长方形若AF⊥BE,则AF=BEBDBC平行四边形,且△GME∽△HNF,△MED≌△BFA。
下面给出几个几何问题。
1.在△ABC中,AB=AC,且有以下七个结论:①D为AC中点;②AE⊥BD;③BE:EC=2:1;④∠ADB=∠CDE;⑤∠AEB=∠CED;⑥∠BMC=135°;⑦BM:MC=2:1.求AC和CD的比值。
2.在平行四边形ABCD中,AB∥CD,线段BC,AD相交于点F,点E是线段AF上一点且满足∠BEF=∠C,其中AF=6,DF=3,CF=2,求AE的长度。
3.在Rt△ABD中,过点D作CD⊥BD,垂足为D,连接XXX于点E,过点E作EF⊥BD于点F,若AB=15,CD=10,求4.在□ABCD中,E为BC的中点,连接AE,AC,分别交BD于M,N,求5.在平行四边形ABCD中,AB∥CD,AD,BC相交于点E,过E作EF∥AB交BD于点F。
相似三角形-中考数学第一轮总复习课件(全国通用)

中考数学第一轮总复习典例精讲考点聚集查漏补缺拓展提升第四单元 三角形专题4.4 相似三角形知识点比例线段01相似三角形的性质与判定02相似三角形的应用03拓展训练04【例1】已知2x=3y(y≠0),则下面结论成立的是( ) A.x:y=3:2 B.x:3=2:y C.x:y=2:3 D.x:2=y:3A1.线段的比:在同一单位长度下,两条线段长度的比叫做两条线段的比;2.比例线段:对于四条线段a,b,c,d,若其中两条线段的比与另两条线段的比相等(a:b=c:d).我们就说这四条线段成比例,简称比例线段.3.比例的基本性质:4.更比定理:考点聚集ad=bc知识点一典例精讲比例线段1.已知 ,则 的值是____.2.人们认为最美人体的头顶至肚脐的长度与肚脐至足底之比是 .某人测得头顶至肚脐长约65cm,肚脐至足底长约102cm,为尽可能达到黄金比的美感效果,作为形象设计师的你,对于她的着装建议为穿一双( )cm的高跟鞋(精确到1cm) A.2 B.3 C.4 D.5B 知识点一强化训练比例线段知识点比例线段01相似三角形的性质与判定02相似三角形的应用03拓展训练04【例2】如图,已知△ABC中,∠BAC=90º,延长BA到点D,使AD=0.5AB,点E,F分别是边BC,AC的中点.求证:DF=BE 方法一:证△ADF≌△FEC(SAS)AFDBCE方法二:证△ADF∽△BCA方法三:连接AE,利用平行四边形证明知识点二典例精讲相似三角形的性质与判定1.如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( ) A.∠C=∠AED B.AB:AD=AC:AE C.∠B=∠D D.AB:AD=BC:DE2.如图,△ABC 中,∠A =78º,AB =4,AC =6.将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )DA 1CEBD2知识点二强化训练三角形相似的性质与判定CAC B78ºAC B78ºAAC B14DAC B 23CAC B 78ºB3.如图,在□ABCD中,连接AC,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,连接DF.若S △AEF =4,则S △ADF 的值为_____.4.如图,一束光线从点A(4,4)射出,经y轴上的点C的反射后,经过点B(1,0),则点C的坐标是( ) A.(0,0.5) B.(0,0.8) C.(0,1) D.(0,2)5.在□ABCD中,E是AD上的一点,且点E将AD分为2:3的两部分,连接BE,AC相交于F,则S △AEF :S △CBF =_______.AFE DCB10知识点二强化训练三角形相似的性质与判定B AyxC OB(1,0)知识点比例线段01相似三角形的性质与判定02相似三角形的应用03拓展训练04【例3】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=_____m.5.5 DAE BFC 知识点三典例精讲相似三角形的应用3.如图,△ABC是一张锐角三角形硬纸片,AD是边BC上的高BC=40cm,AD=30cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G,H分别在AC,AB上,AD与HG的交点为M.(1)求证:AM:AD=HG:BC;(2)求矩形EFGH的周长。
初三中考数学专题复习:二次函数综合题(相似三角形问题)含答案

中考数学专题复习:二次函数综合题(相似三角形问题)1.如图①,二次函数y =﹣x 2+bx +c 的图象与x 轴交于点A (﹣1,0)、B (3,0),与y 轴交于点C ,连接BC ,点P 是抛物线上一动点.(1)求二次函数的表达式.(2)当点P 不与点A 、B 重合时,作直线AP ,交直线BC 于点Q ,若①ABQ 的面积是①BPQ 面积的4倍,求点P 的横坐标.(3)如图①,当点P 在第一象限时,连接AP ,交线段BC 于点M ,以AM 为斜边向①ABM 外作等腰直角三角形AMN ,连接BN ,①ABN 的面积是否变化?如果不变,请求出①ABN 的面积;如果变化,请说明理由.2.如图,二次函数2314y x bx =++的图像经过点()8,3A ,交x 轴于点B ,C (点B 在点C 的左侧),与y 轴交于点D .(1)填空:b = ______;(2)点P 是第一象限内抛物线上一点,直线PO 交直线CD 于点Q ,过点P 作x 轴的垂线交直线CD 于点T ,若PQ QT =,求点P 的坐标;(3)在x 轴的正半轴上找一点E ,过点E 作AE 的垂线EF 交y 轴于F ,若AEF 与EFO △相似,求OE 的长.3.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得①CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.4.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.5.如图,在平面直角坐标系中,已知直线4y x =+与x 轴、y 轴分别相交于点A 和点C ,抛物线21y x kx k =++-的图象经过点A 和点C ,与x 轴的另一个交点是点B .(1)求出此抛物线的解析式; (2)求出点B 的坐标;(3)若在y 轴的负半轴上存在点D .能使得以A ,C ,D 为顶点的三角形与①ABC 相似,请求出点D 的坐标.6.如图1,已知抛物线23y ax bx =++经过点()1,5D ,且交x 轴于A ,B 两点,交y 轴于点C ,已知点()1,0A -,(),P m n 是抛物线在第一象限内的一个动点,PQ BC ⊥于点Q .(1)求抛物线的解析式;(2)当PQ =m 的值;(3)是否存在点P ,使BPQ 与BOC 相似?若存在,请求出P 点的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,直线y =12x +2与x 轴交于点A ,与y 轴交于点C .抛物线y =ax 2+bx +c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)求二次函数y=ax2+bx+c的表达式;(2)点P为线段AB上的动点,求AP+2PC的最小值;(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与①ABC 相似?若存在,求出点M的坐标;若不存在,请说明理由.8.如图,抛物线y=−x2+bx+c与x轴相交于A(−1,0),B(3,0)两点,与y轴交于点C,顶点为点D,抛物线的对称轴与BC相交于点E,与x轴相交于点F.(1)求抛物线的函数关系式;(2)连结DA,求sin A的值;(3)若点H线段BC上,BOC与BFH△相似,请直接写出点H的坐标.9.如图,抛物线y=1-2x2+bx+c与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =720S △ABC 时,求点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与①OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.10.如图,抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点C ,设抛物线的顶点为D .(1)求该抛物线的表达式与顶点D 的坐标; (2)试判断BCD △的形状,并说明理由;(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似?若存在,请求出点P 的坐标;若不存在,请说明理由.11.如图,抛物线y =ax 2﹣2ax ﹣3a (a ≠0)与x 轴交于点A ,B .与y 轴交于点C .连接AC ,BC .已知ABC 的面积为2.(1)求抛物线的解析式;(2)平行于x 轴的直线与抛物线从左到右依次交于P ,Q 两点.过P ,Q 向x 轴作垂线,垂足分别为G ,H .若四边形PGHQ 为正方形,求正方形的边长;(3)抛物线上是否存在一点N ,使得①BCN =①CAB ﹣①CBA ,若存在,请求出满足条件N 点的横坐标,若不存在请说明理由.12.如图,二次函数2y x bx c =-++的图像与x 轴交于点A (-1,0),B (2,0),与y 轴相交于点C .(1)求这个二次函数的解析式;(2)若点M 在此抛物线上,且在y 轴的右侧.①M 与y 轴相切,过点M 作MD ①y 轴,垂足为点D .以C ,D ,M 为顶点的三角形与①AOC 相似,求点M 的坐标及①M 的半径长.13.如图,在平面直角坐标系中,抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .若线段OA OB OC 、、的长满足2OC OA OB =⋅,则这样的抛物线称为“黄金”抛物线.如图,抛物线22(0)y ax bx a =++≠为“黄金”抛物线,其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB =(1)求抛物线的解析式;(2)若P 为AC 上方抛物线上的动点,过点P 作PD AC ⊥,垂足为D . ①求PD 的最大值;①连接PC ,当PCD 与ACO △相似时,求点P 的坐标.14.如图,在平面直角坐标系xOy 中,已知抛物线2y x bx c =++与x 轴交于点A 、B 两点,其中1,0A ,与y 轴交于点()0,3C .(1)求抛物线解析式;(2)如图1,过点B 作x 轴垂线,在该垂线上取点P ,使得①PBC 与①ABC 相似,请求出点P 坐标;(3)如图2,在线段OB 上取一点M ,连接CM ,请求出12CM BM +最小值.15.如图,抛物线y =ax 2+k (a >0,k <0)与x 轴交于A ,B 两点(点B 在点A 的右侧),其顶点为C ,点P 为线段OC 上一点,且PC =14OC .过点P 作DE ①AB ,分别交抛物线于D ,E 两点(点E 在点D 的右侧),连接OD ,DC .(1)直接写出A ,B ,C 三点的坐标;(用含a ,k 的式子表示) (2)猜想线段DE 与AB 之间的数量关系,并证明你的猜想;(3)若①ODC =90°,k =﹣4,求a 的值.16.如图,抛物线223y x bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,连接AC ,已知B (﹣1,0),且抛物线经过点D (2,﹣2).(1)求抛物线的表达式;(2)若点E 是抛物线上第四象限内的一点,且2ABES=,求点E 的坐标;(3)若点P 是y 轴上一点,以P ,A ,C 三点为顶点的三角形是等腰三角形,求P 点的坐标.17.如图,在直角坐标系xOy 中,抛物线y =ax 2+bx +2(a ≠0)与x 轴交于点A (﹣1,0)和B (4,0),与y 轴交于点C ,点P 是抛物线上的动点(不与点A ,B ,C 重合).(1)求抛物线的解析式;(2)当点P 在第一象限时,设①ACP 的面积为S 1,①ABP 的面积为S 2,当S 1=S 2时,求点P 的坐标; (3)过点O 作直线l ①BC ,点Q 是直线l 上的动点,当BQ ①PQ ,且①BPQ =①CAB 时,请直接写出点P 的坐标.18.如图,在平面直角坐标系xOy中,直线y=﹣x+3与两坐标轴交于A、B两点,抛物线y=x2+bx+c 过点A和点B,并与x轴交于另一点C,顶点为D.点E在对称轴右侧的抛物线上.(1)求抛物线的函数表达式和顶点D的坐标;(2)若点F在抛物线的对称轴上,且EF①x轴,若以点D,E,F为顶点的三角形与①ABD相似,求出此时点E的坐标;(3)若点P为坐标平面内一动点,满足tan①APB=3,请直接写出①P AB面积最大时点P的坐标及该三角形面积的最大值.19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴交于点C,且OC=2OB=6OA=6,点P是第一象限内抛物线上的动点.(1)求抛物线的解析式;(2)连接BC与OP,交于点D,当S△PCD:S△ODC的值最大时,求点P的坐标;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N.使①CMN=90°,且①CMN与①BOC 相似,若存在,请求出点M、点N的坐标.20.如图,抛物线y=x2+bx+12(b<0)与x轴交于A,B两点(A点在B点左侧),且OB=3OA.(1)请直接写出b=,A点的坐标是,B点的坐标是;(2)如图(1),D点从原点出发,向y轴正方向运动,速度为2个单位长度/秒,直线BD交抛物线于点E,若BE=5DE,求D点运动时间;(3)如图(2),F点是抛物线顶点,过点F作x轴平行线MN,点C是对称轴右侧的抛物线上的一定点,P 点在直线MN上运动.若恰好存在3个P点使得①P AC为直角三角形,请求出C点坐标,并直接写出P点的坐标.答案1.(1)y =﹣x 2+2x +3.(2)P 352或 (3)①ABN 的面积不变,为4.2.(1)2-(2)5⎛ ⎝⎭或5⎛ ⎝⎭(3)4或493.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)4.(1)抛物线L 1:223y x x =--,抛物线L 2:2y x 2x 3=-++;(2)435(,)39M 或(4,5)M -.5.(1)254y x x =++(2)点B 的坐标为(-1,0)(3)点D 的坐标是(0,-203) 6.(1)215322y x x =-++ (2)1或5(3)存在;P (53,529)7.(1)抛物线表达式为:213222y x x =--+;(2)AP +2PC 的最小值是4;(3)存在M(0,2)或(-3,2)或(2,-3)或(5,-18),使得以点A 、M 、N 为顶点的三角形与ABC 相似.8.(1)y =-x 2+2x +3(3)点H 的坐标为(1,2)或(2,1)9.(1)21382y x x =++ (2)P 1(1,10.5),P 2(7,4.5)(3)存在,(3,8)或(3,5或(3,11)30.(1)y =﹣x 2﹣2x +3,(﹣1,4);(2)直角三角形,理由见解析;(3)存在,(0,0)或(0,﹣13)或(-9,0)11.(1)y =﹣13x 2+23x +1(2)﹣6﹣(3)存在,5或11712.(1)22y x x =-++; (2)M 的坐标为(12,94),(32, 54 ),(3,-4),①M 的半径长为12或32或313.(1)213222y x x =--+(2)①PD ①P 坐标为(3,2)-或325()28,-14.(1)243y x x =-+(2)P 点坐标为()3,9或()3,215.(1)点A 、B 、C 的坐标分别为(、、(0,k ) (2)DE =12AB(3)a =1316.(1)224233y x x =--(2)E ,-1)(3)P 点的坐标(0,2)或(02)或(0,﹣2或(0,54)17.(1)213222y x x =-++ (2)点P 的坐标为(103,139)(3)点P 的坐标为(32,﹣2)或(32,﹣2)或(173,﹣509)18.(1)y =x 2﹣4x +3,(2,﹣1)(2)(5,8)或(73,89-)(3)①P AB ,此时P )19.(1)y =﹣2x 2+4x +6 (2)点P 的坐标为(32,152) (3)存在,M 、N 的坐标分别为(3,0)、(0,﹣32)或(94,398)、(0,38)或(1,8)、(0,172)或(74,558)、(0,838)20.(1)﹣8,(2,0),(6,0)(2)3秒或212秒 (3)C 点坐标为(143,﹣329),P 点的坐标为(103,﹣4)或(﹣103,﹣4)或(11027,﹣4)。
中考数学专题训练------相似三角形

一、比例1.第四比例项、比例中项、比例线段; 2.比例性质: (1)基本性质:bc ad d c b a =⇔= ac bc b b a =⇔=2(2)合比定理:ddc b b ad c b a ±=±⇒=(3)等比定理:)0.(≠+++=++++++⇒==n d b ba nd b m c a nm dc b a3.黄金分割:如图,若AB PB PA ⋅=2,则点P 为线段AB 的黄金分割点.结论:PA= AB . 4.平行线分线段成比例定理: 5.相似三角形:(1)定义:对应角相等,对应边成比例的两个三角形. (2)判定方法.(3)直角三角形判定方法. 6.相似三角形性质.(1)对应角相等,对应边成比例; (2)对应线段之比等于 ; (3)周长之比等于 ; (4)面积之比等于 . 7.相似三角形中的基本图形. (1)平行型:(A 型,X 型) (2)交错型:(3)旋转型: (4)母子三角形:二、例题解析:1.如果cm a 4=,cm b 6=,cm a 3=,则a ,b ,c 的第四比例项是 .如果3=a ,12=c ,则a 与c 的比例中项是 . 2.已知,542c b a ==,则=-+-+bc a b c a 22 .3.如图,在△ABC 中,DE ∥BC ,AD=3,BD=2,EC=1,则AC= . 4.如图,平行四边形ABCD 中,AE ∶EB=1∶2,若S △AEF =6,则S △CDF = .E DBACAED CBFEDCBA5.如图,△ABC 中,DE ∥BD ,AD ∶DB=2∶3,则S △ADE ∶S △ECB = .6.如图,Rt △ABC 中,∠ACB=Rt ∠,CD ⊥AB 于D .(1)若AC=4,BC=3,则AD= ,BD= ,CD= ;(2)若AB ∶BC=9∶1,则AD ∶BD= .7.如图,平行四边形ABCD 中,BC=18cm ,P 、Q 是三等分点,DP 延长线交BC 于E ,EQ 延长线交AD 于F ,则AF=_______.8.如图,在△ABC 中,AB>AC ,边AB 上取一点D ,边AC 上取一点E ,使AD=AE ,直线DE 和BC 的延长线交于点P . 求证:BP ∶CP=BD ∶CE .9.如图,CD 是Rt △ABC 的斜边上的高线,∠BAC 的平分线交BC ,CD 于E ,F . 求证:(1)△ACF ∽△ABE ;(2)AC ·AE= AF ·AB .FAB CD E a b cA BCDEABCDEABCDEABCDDA BCABCDED AB CE BA BEDAPBE DCAFBEDC AF QPCBAD10.如图,在平行四边形ABCD 中,过点B 作BE ⊥CD ,垂足为E ,连结AE ,F 为AE 上一点,且∠BFE=∠C . (1)求证:△ABF ∽△EAD ;(2)若AB=4,∠BAE=30°,求AE 的长; (3)在(1),(2)条件下,若AD=3,求BF 的长.11.如图,Rt △ABC 中,∠BAC=Rt ∠,AB=AC=2,点D 在BC 上运动(不能到点B ,C ),过D 作∠ADE=45°,DE 交AC 于E . (1)求证:△ABD ∽△DCE ;(2)设BD=x ,AE=y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围; (3)当△ADE 是等腰三角形时,求AE 的长.一、判断题:1.两个等边三角形一定相似( )2.两个相似三角形的面积之比为1∶4,则它们的周长之比为1∶2( ) 3.两个等腰三角形一定相似( )4.若一个三角形的两个角分别是400、1000,而另一个三角形是顶角为1000的等腰三角形,则这两个三角形相似( ) 二、填空题:1.如图,Rt △ABC 中,∠ACB =900,CD 是AB 边上的高,若AC =5cm ,CD =4cm ,则AD = cm ,AB = cm .2.如图,在平行四边形ABCD 中,E 是BC 延长线上一点,AE 交CD 于点F ,若AB =7cm ,CF =3cm ,则AD ∶CE = .FEDC B AB CE DA3.如图,矩形ABCD 中,E 是BC 上的点,AE ⊥DE ,BE =4,EC =1,则AB 的长为 . 4.CM 是△ABC 的中线,AB =12,AC =9,AC 上有一点N ,且∠ANM =∠B ,则CN = .NMCB AOFEDCBAFEDCBA5.梯形ABCD 的对角线AC 、BD 相交于点O ,过O 作EF 平行于底,与腰AD 、BC 相交于E 、F ,若DC =14,OF =8,AE =12,则DE = .6.如图,正方形ABCD 的面积为144cm 2,点F 在AD 上,点E 在AB 的延长线上,Rt △CEF 的面积为112.5cm 2,则BE 的长为 cm . 三、选择题: 1.已知21=ba ,则ba a +的值为( )(A )21 (B )32 (C )31 (D )432.如图,已知△ADE ∽△ACB ,且∠ADE=∠C ,则AD :AC=( ) (A )AE :AC (B )DE :BC (C )AE :BC (D )DE :ABABCDABCD EBF EDCABEDCABF3.D ,E 分别是△ABC 的边AB ,AC 上的点,DE ∥BC ,如果23=DBAD ,AE=15,那么EC 的长是( )(A ) 10 (B ) 22. 5 (C ) 25 (D ) 6 4.如图,△ABC 中,DE ∥BC ,DCE ADE S S ∆∆=2,则 ABCADE S S ∆∆=( )(A )41 (B )21 (C )32 (D )945.如图,DE 是三角形ABC 的中位线,△ADE 的面积为3cm 2,则梯形DBCE 的面积为( )A 、6cm2B 、9cm2C 、12cm 2D 、24cm2FE DCBA第5题 第6题 第8题6.如图,E 是平行四边形ABCD 的边AD 上的点,AE =21ED ,BE 交AC 于F ,则FCAF =( ) A 、21 B 、31 C 、32 D 、417.如图,△ABC 中,D 是AB 上的点,不能判定△ACD ∽△ABC 的是以下条件中的( )A 、∠ACD =∠B B 、∠ADC =∠ACB C 、AC 2=AD ·AB D 、AD ∶AC =CD ∶BC 8.如图FD ∥BC ,FB ∥AC ,53=BCFE ,则FBAD =( )A 、52 B 、53 C 、32 D 、859.梯形ABCD 的两腰AD 和BC 延长相交于点E ,若两底的长度分别为12和8,梯形ABCD 的面积等于90,则△DCE 的面积为( )A 、50B 、64C 、72D 、5010.如图,已知△ABC 的面积为4 cm 2,它的三条中位线组成△DEF ,△DEF 的三条中位线组成△MNP ,则△MNP 的面积等于( ) A 、161cm 2B 、81cm2C 、41cm2D 、1cm 2D FEC B AOD FECBA11.如图,E 是AC 的中点,C 是BD 的中点,则EDFE =( )A 、21 B 、31 C 、32 D 、4112.如图,平行四边形ABCD 中,E 是AB 的中点,F 在AD 上,且AF =21FD ,EF 交AC 于点O ,若AC =12,则AO =( )A 、4B 、3C 、2.4D 、213.如图,E 是矩形ABCD 的边CD 上的点,BE 交AC 于点O ,已知△COE 与△BOC 的面积分别为2和8,则四边形AOED 的面积为( )A 、16B 、32C 、38D 、40 14.如图,在梯形ABCD 中,AB ∥CD ,AB =3CD ,E 为对角线AC 的中点,直线BE 交AD 于点F ,则AF ∶FD 的值等于( )A 、2B 、35 C 、23 D 、115.如图,AD 是Rt △ABC 斜边上的高,DE ⊥DF ,且DE 和DF 分别交AB ,AC 于E ,F .求证:BDBE ADAF =.ABCDEABCDE ABCD EABCDEFECADBAEF OEDCBAE FDCBA16.如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC 修一座底面是矩形DEFG 的大楼,当这座大楼的地基面积最大时.这个矩形的长和宽各是多少?FG HMABCDE。
中考数学一轮复习专题解析—相似三角形

中考数学一轮复习专题解析—相似三角形复习目标1.了解相似图形和相似三角形的概念。
2.掌握三角形相似的判定方法和性质并学会运用。
考点梳理一、相似图形1.形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形.2.比例线段的相关概念如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nm b a =,或写成n m b a ::=. 注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位. 在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注意:(1)当两个比例式的每一项都对应相同,两个比例式才是同一比例式.(2)比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:ad c b =. 3. 比例的性质基本性质:(1)bc ad d c b a =⇔=::;(2)b a c b c c a ⋅=⇔=2::.注意:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.更比性质(交换比例的内项或外项):()()()a b c d a c d c b d b ad b c a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项 反比性质(把比的前项、后项交换):cd a b d c b a =⇒=. 合比性质:dd c b b a d c b a ±=±⇒=. 注意:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间 发生同样和差变化比例仍成立.如:⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a c c d a a b d c b a 等等. 等比性质: 如果)0(≠++++====n f d b n m f e d c b a ,那么b a n f d b m e c a =++++++++ . 注意:(1)此性质的证明运用了“设k 法” ,这种方法是有关比例计算,变形中一种常用方法.(2)应用等比性质时,要考虑到分母是否为零.(3)可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.4.比例线段的有关定理平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.推论:(1)平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.(2)平行于三角形一边并且和其它两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例.定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形第三边.5.黄金分割把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB 例1.如果0ab cd =≠,则下列正确的是( )A .::a c b d =B .::a d c b =C .::a b c d =D .::d c b a = 【答案】B【分析】根据比例的基本性质,列出比例式即可.【详解】解:∵0ab cd =≠,∵::a d c b =,故选:B .例2.两个相似多边形的一组对应边的长分别为6cm ,9cm ,那么它们的相似比为( )A .23B C .49 D .94【答案】A【分析】根据相似多边形的性质求解即可;【详解】两个相似多边形一组对应边的长分别为6cm ,9cm ,∵它们的相似比为:6293=.故选A .二、相似三角形的概念对应角相等,对应边成比例的三角形,叫做相似三角形.相似用符号“∵”表示,读作“相似于” .相似三角形对应边的比叫做相似比(或相似系数).相似三角形对应角相等,对应边成比例.注意:∵对应性:即两个三角形相似时,通常把表示对应顶点的字母写在对应位置上,这样写比较容易找到相似三角形的对应角和对应边.∵顺序性:相似三角形的相似比是有顺序的.∵两个三角形形状一样,但大小不一定一样.∵全等三角形是相似比为1的相似三角形.二者的区别在于全等要求对应边相等,而相似要求对应边成比例.三、相似三角形的等价关系(1)反身性:对于任一ABC ∆有ABC ∆∵ABC ∆.(2)对称性:若ABC ∆∵'''C B A ∆,则'''C B A ∆∵ABC ∆.(3)传递性:若ABC ∆∵C B A '∆'',且C B A '∆''∵C B A ''''''∆,则ABC ∆∵C B A ''''''∆.四、相似三角形的基本定理定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似.定理的基本图形:五、三角形相似的判定方法1、定义法:对应角相等,对应边成比例的两个三角形相似.2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似.3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.4、判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.6、判定直角三角形相似的方法:(1)以上各种判定均适用.(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学复习(37):相似三角形(一)
知识考点:
本节知识包括相似三角形的判定定理、三角形相似的判定及应用,这是中考必考内容。
掌握好相似三角形的基础知识尤为重要。
精典例题:
【例1】如图,点O 是△ABC 的两条角平分线的交点,过O 作AO 的垂线交AB 于D 。
求证:△OBD ∽△CBO 。
分析:此题不易得到边的比例关系,但O 点是三角形的角平分线的交点,有多对相等的角,故宜从角相等方面去考虑。
由角平分线及三角形内角和定理知:∠1+∠2+∠DAO =900,再由AO ⊥DO 可得∠5=∠1+∠2,而∠5=∠3+∠4,从而∠1+∠2=∠3+∠4,由∠1=∠3可得∠2=∠4,于是结论得证。
例1图
5
4
32
1
O
D C
B A
变式1图
O
E D
C
B
A
例2图
F
E
D
C
B
A
变式1:已知如图,在△ABC 中,AD =AE ,AO ⊥DE 于O ,DE 交AB 于D ,交AC 于E ,BO 平分∠ABC 。
求证:BC BD BO ⋅=2。
变式2:已知如图(同变式1图),在△ABC 中,O 为两内角平分线的交点,过点O 作直线交AB 于D ,交AC 于E ,且AD =AE 。
求证:(1)△BDO ∽△OEC ;(2)CE BD DO ⋅=2。
【例2】如图,在△ABC 中,∠BAC =900,AD ⊥BC 于D ,E 为AC 中点,DE 交BA 的延长线于F 。
求证:AB ∶AC =BF ∶DF 。
分析:由于△ABC 和△FBD 一个是直角三角形,一个是钝角三角形,不可能由这一对三角形相似直接找到对应边而得结论,势必要找“过渡”的线段或线段比,这种寻找“中间”搭桥的线段或线段比是重要的解题技巧。
证明:∵AB ⊥AC ,AD ⊥BC
∴Rt △ABD ∽Rt △CAD ,∠DAC =∠B
∴
AD
BD
AC AB =………① 又∵AD ⊥BC ,E 为AC 中点 ∴DE =AE ,∠DAE =∠ADE ∴∠B =∠ADE 又∵∠F =∠F
∴△FAD ∽△FDB ∴
DF
BF
AD BD =………②
由①②得
DF
BF
AC AB = 变式:本题条件、结论不变,而只改变图形的位置时,如下图所示,本题又该怎样证明呢?
例2变式图1
F
E
D C
B
A
例2变式图2
F
E
D
C
B
A
例3图
G
F
E D
C
B
A
【例3】如图,梯形ABCD 中,AD ∥BC ,BE ⊥CD 于E ,且BC =BD ,对角线AC 、BD 相交于G ,AC 、BE 相交于F 。
求证:FA FG FC ⋅=2。
分析:由于FG 、FA 、FC 三条线段在同一直线上,不能直接证明一对三角形相似而得结论。
根据题设条件易得BE 是DC 的垂直平分线,于是连结FD 得FD =FC ,再证△FDG ∽△FAD 即可。
探索与创新:
【问题一】如图,∠ACB =∠ADC =900,AC =6,AD =2。
问当AB 的长为多少时,这两个直角三角形相似? 略解:∵AC =6,AD =2 ∴CD =
222=-AD AC
要使这两个直角三角形相似,有两种情况: (1)当Rt △ABC ∽Rt △ACD 时,有
AC
AB
AD AC = ∴32
==
AD
AC AB (2)当Rt △ACB ∽Rt △CDA 时,有
AC
AB
CD AC = ∴232
==CD
AC AB 故当AB 的长为3或23时,这两个直角三角形相似。
【问题二】已知如图,正方形ABCD 的边长为1,P 是CD 边的中点,点Q 在线段BC 上,设BQ =k ,是否存在这样的实数k ,使得Q 、C 、P 为顶点的三角形与△ADP 相似,若存在,求出k 的值;若不存在,请说明理由。
略解:假设存在满足条件的实数k ,则在正方形ABCD 中,∠D =∠C =900,由Rt △
问题一图
D
C
B
A
ADP ∽Rt △QCP 或Rt △ADP ∽Rt △PCQ 得:
CP DP QC AD =或CQ
DP
PC AD =
由此解得:CQ =1或CQ =41,从而0=k 或4
3=k 故当0=k 或4
3
=
k 时,△ADP 与△QCP 。
跟踪训练: 一、填空题:
1、如图,在△ABC 中,P 是边AB 上一点,连结CP ,使△ACP ∽△ABC 的条件是 。
2、在直角坐标系中,已知A (-3,0)、B (0,-4)、C (0,1),过C 点作直线l 交x 轴于D ,使得以点D 、C 、O 为顶点的三角形与△AOB 相似,这样的直线有 条。
3、如图,在△ABC 中,∠C =900,AC =8,CB =6,在斜边AB 上取一点M ,使MB =CB ,过M 作MN ⊥AB 交AC 于N ,则MN = 。
第1题图
P
C
B A
第3题图
N
M C
B A
第5题图
E
D
C
B A
4、一个钢筋三角架长分别为20cm 、50 cm 、60 cm ,现要再做一个与其相似的钢筋三角架,而只有长为30 cm 和50 cm 的两根钢筋,要求以其中一根为一边,从另一根上截下两段(允许有余料)作为两边,则不同的载法有 种。
5、如图,在锐角△ABC 中,BD ⊥AC ,DE ⊥BC ,AB =14,AD =4,BE ∶EC =5∶1,则CD = 。
二、选择题:
1、下面两个三角形一定相似的是( )
A 、两个等腰三角形
B 、两个直角三角形
C 、两个钝角三角形
D 、两个等边三角形 2、如图,点
E 是平行四边形ABCD 的边CB 延长线上一点,
EA 分别交CD 、BD 的延长线于点F 、G ,则图中相似三角形共有( )
A 、3对
B 、4对
C 、5对
D 、6对
三、解答题: 1、如图,在Rt △ABC 中,∠B =900,AB =BE =EF =FC 。
求
问题二图
P
C
选择第2题图 F
G E
D C B A
证:△AEF ∽△CEA 。
解答第1题图
F E C
B
A
2、如图,在四边形ABCD 中,AB ⊥BC ,AD ⊥DC ,DE ⊥AC 于E ,交AB 于F 。
求证:△AFD ∽△ADB 。
解答第2题图
D
F
E
C
B
A
3、如图,在梯形ABCD 中,AB ∥CD ,∠D =900,AB =3,DC =7,AD =15,请你在AD 上找一点P ,使得以P 、A 、B 和以P 、D 、C 为顶点的两个三角形相似吗?若能,这样的P 点有几个?并求出AP 的长;若不能,请说明理由。
解答第3题图
P
4、在边长为1的正方形网格中有A 、B 、C 、D 、E 五个点,问△ABC 与△ADE 是否相似?为什么?由此,你还能找出图中相似的三角形吗?若能,请找出来,并说明理由。
解答第4题图
C
参考答案:
一、填空题:
1、∠ACP =∠B 或∠APC =∠ACB 或AB AP AC ⋅=2
;2、4条;3、3,5; 4、2种;5、6 二、选择题:DD 三、解答题:
1、设AB =BE =EF =FC =a ,∵∠B =900,∴AE =a 2 ∵
22==a a
EF AE ,222==a
a AE EC ∴
AE
EC
EF AE =且∠AEF =∠CEA ∴△AEF ∽△CEA
2、证△AED ∽△ADC ,△FAE ∽△CAB ,△FAD ∽△DAB
3、能,有三个,AP =4.5或
2
141
15± 4、△ABC ∽△ADE ,还有△ABD ∽△ACE 。
