Application_of_COMSOL_in_Image_ Processing
comsol等离子体放电二维模型

DC Glow DischargeIntroductionDC glow discharges in the low pressure regime have long been used for gas lasers and fluorescent lamps. DC discharges are attractive to study because the solution is time independent. This model shows how to use the DC Discharge interface to set up an analysis of a positive column. The discharge is sustained by emission of secondary electrons at the cathode.Model DefinitionThe DC discharge consists of two electrodes, one powered (the anode) and one grounded (the cathode). The positive column is coupled to an external circuit:Figure 1: Schematic of the DC discharge and external circuit.D O M A I NE Q U A T I O N SThe electron density and mean electron energy are computed by solving a pair of drift-diffusion equations for the electron density and mean electron energy.Convection of electrons due to fluid motion is neglected. For detailed information on electron transport see Theory for the Drift Diffusion Interface in the Plasma Module User’s Guide .where:Cathode AnodePlasma 1000 ΩV1 pF t ∂∂n e()∇n e μe E •()–D e ∇n e •–[]⋅+R e =t ∂∂n ε()∇n εμεE •()–D ε∇n ε•–[]E Γe ⋅+⋅+R ε=The electron source R e and the energy loss due to inelastic collisions R ε are defined later. The electron diffusivity, energy mobility and energy diffusivity are computed from the electron mobility using:The source coefficients in the above equations are determined by the plasma chemistry using rate coefficients. Suppose that there are M reactions which contribute to the growth or decay of electron density and P inelastic electron-neutral collisions. In general P >> M . In the case of rate coefficients, the electron source term is given by:where x j is the mole fraction of the target species for reaction j , k j is the rate coefficient for reaction j (m 3/s), and N n is the total neutral number density (1/m 3). For DC discharges it is better practice to use Townsend coefficients instead of rate coefficients to define reaction rates. Townsend coefficients provide a better description of what happens in the cathode fall region Ref 1. When Townsend coefficients are used, the electron source term is given by:where αj is the Townsend coefficient for reaction j (m 2) and Γe is the electron flux as defined above (1/(m 2·s)). Townsend coefficients can increase the stability of the numerical scheme when the electron flux is field driven as is the case with DCdischarges. The electron energy loss is obtained by summing the collisional energy loss over all reactions:where Δεj is the energy loss from reaction j (V). The rate coefficients may be computed from cross section data by the following integral:Γe μe E •()n e –D e ∇n e•–=D e μe T e =με,53--⎝⎭⎛⎫μe =D ε,μεT e =R e x j k j N n n ej 1=M∑=R e x j αj N n Γej 1=M∑=R εx j k j N n n e Δεjj 1=P∑=where γ = (2q /m e )1/2 (C 1/2/kg 1/2), m e is the electron mass (kg), ε is energy (V), σk is the collision cross section (m 2) and f is the electron energy distribution function. In this case a Maxwellian EEDF is assumed. When Townsend coefficients are used, the electron energy loss is taken as:For non-electron species, the following equation is solved for the mass fraction of each species. For detailed information on the transport of the non-electron species see Theory for the Heavy Species Transport Interface in the Plasma Module User’s Guide .The electrostatic field is computed using the following equation:The space charge density ρ is automatically computed based on the plasma chemistry specified in the model using the formula:For detailed information about electrostatics see Theory for the Electrostatics Interface in the Plasma Module User’s Guide .B O U N D A R YC O ND I T I O N SUnlike RF discharges, the mechanism for sustaining the discharge is emission ofsecondary electrons from the cathode. An electron is emitted from the cathode surface with a specified probability when struck by an ion. These electrons are then accelerated by the strong electric field close to the cathode where they acquire enough energy to initiate ionization. The net result is a rapid increase in the electron density close to the cathode in a region often known as the cathode fall or Crookes dark space .k k γεσk ε()f ε()εd 0∞⎰=R εx j αj N n Γe Δεjj 1=P∑=ρt∂∂w k ()ρu ∇⋅()w k +∇j k ⋅R k +=∇–ε0εr V ∇⋅ρ=ρq Z k n k k 1=N ∑n e –⎝⎭ ⎪ ⎪⎛⎫=Electrons are lost to the wall due to random motion within a few mean free paths of the wall and gained due to secondary emission effects, resulting in the following boundary condition for the electron flux:(1)and the electron energy flux:(2)The second term on the right-hand side of Equation 1 is the gain of electrons due to secondary emission effects, γp being the secondary emission coefficient. The second term in Equation 2 is the secondary emission energy flux, εp being the mean energy of the secondary electrons. For the heavy species, ions are lost to the wall due to surface reactions and the fact that the electric field is directed towards the wall:P L A S M A C H E M I S T R YArgon is one of the simplest mechanisms to implement at low pressures. The electronically excited states can be lumped into a single species which results in a chemical mechanism consisting of only 3 species and 7 reactions:TABLE 1: TABLE OF COLLISIONS AND REACTIONS MODELED REACTION FORMULA TYPE 1e+Ar=>e+Ar Elastic 02e+Ar=>e+Ars Excitation 11.53e+Ars=>e+Ar Superelastic -11.54e+Ar=>2e+Ar+Ionization 15.85e+Ars=>2e+Ar+Ionization 4.246Ars+Ars=>e+Ar+Ar+Penning ionization -7Ars+Ar=>Ar+Ar Metastable quenching-n –Γ⋅e 12--νe th ,n e ⎝⎭⎛⎫γp Γp n ⋅()p ∑–=n –Γ⋅ε56--νe th ,n ε⎝⎭⎛⎫εp γp Γp n ⋅()p ∑–=n –j k ⋅M w R k M w c k Z μk E n ⋅()Z k μk E n ⋅()0>[]+=Δε(eV)In a CCP reactor the electron density and density of excited species is relatively low so stepwise ionization is not as important as in high density discharges. In addition to volumetric reactions, the following surface reactions are implemented:TABLE 2: TABLE OF SURFACE REACTIONSREACTION FORMULA STICKING COEFFICIENT1Ars=>Ar12Ar+=>Ar1When a metastable argon atom makes contact with the wall, it reverts to the ground state argon atom with some probability (the sticking coefficient).Results and DiscussionThe electric potential, electron density and mean electron energy are all quantities of interest. Most of the variation in each of these quantities occurs along the axial length of the column. Figure 2 plots the electron density in the column. The electron density peaks in the region between the cathode fall and positive column. This region is sometimes referred to as Faraday dark space. The electron density also decreases rapidly in the radial direction. The is caused by diffusive loss of electrons to the outerwalls of the column where they accumulate a surface charge. The build up of negative charge leads to a positive potential in the center of the column with respect to the walls.Figure 2: Surface plot of electron density inside the column.In Figure 4 the electric potential is plotted along the axial length of the column. Notice that the potential profile is markedly different from the linear drop in potential which results in the absence of the plasma. The strong electric field in the cathode region can lead to high energy ion bombardment of the cathode. Heating of the cathode surfaceoccurs which may in turn lead to thermal electron emission where additional electrons are emitted from the cathode surface.Figure 3: Plot of electron “temperature” along the axial length of the positive column.Figure 4: Plot of the electric potential along the axial length of the positive column.Figure 6: Plot of the electron temperature along the axial length of the positive column.Figure 8: Plot of the number density of excited argon atoms.Figure 9: Plot of the number density of argon ions.Reference1. M.A. Lieberman and A.J. Lichtenberg, Principles of Plasma Discharges and Materials Processing, John Wiley & Sons, 2005.Application Library path: Plasma_Module/Direct_Current_Discharges/ positive_column_2dModeling InstructionsFrom the File menu, choose New.N E W1In the New window, click Model Wizard.M O D E L W I Z A R D1In the Model Wizard window, click 2D Axisymmetric.2In the Select physics tree, select Plasma>DC Discharge (dc).3Click Add.4Click Study.5In the Select study tree, select Preset Studies>Time Dependent.6Click Done.G E O M E T R Y1Rectangle 1 (r1)1On the Geometry toolbar, click Primitives and choose Rectangle.2In the Settings window for Rectangle, locate the Size and Shape section.3In the Width text field, type 0.05.4In the Height text field, type 0.4.Rectangle 2 (r2)1On the Geometry toolbar, click Primitives and choose Rectangle.2In the Settings window for Rectangle, locate the Size and Shape section.3In the Width text field, type 0.0375.4In the Height text field, type 6e-3.5Locate the Position section. In the z text field, type 0.01.Rectangle 3 (r3)1On the Geometry toolbar, click Primitives and choose Rectangle.2In the Settings window for Rectangle, locate the Size and Shape section.3In the Width text field, type 0.0375.4In the Height text field, type 6e-3.5Locate the Position section. In the z text field, type 0.384.Compose 1 (co1)1On the Geometry toolbar, click Booleans and Partitions and choose Compose. 2Select the object r1 only.3In the Settings window for Compose, locate the Compose section.4In the Set formula text field, type r1-r2-r3.Bézier Polygon 1 (b1)1On the Geometry toolbar, click Primitives and choose Bézier Polygon.2In the Settings window for Bézier Polygon, locate the Polygon Segments section. 3Find the Added segments subsection. Click Add Linear.4Find the Control points subsection. In row 1, set z to 0.02.5In row 2, set r to 0.0375.6In row 2, set z to 0.02.7Click the Build All Objects button.Mesh Control Edges 1 (mce1)1On the Geometry toolbar, click Virtual Operations and choose Mesh Control Edges. 2On the object fin, select Boundary 7 only.3On the Geometry toolbar, click Build All.D E F I N I T I O N SVariables 11On the Home toolbar, click Variables and choose Local Variables.2In the Settings window for Variables, locate the Variables section.3In the table, enter the following settings:Name Expression Unit DescriptionmueN1E25[1/(m*V*s)]1/(V·m·s)Reduced electron mobilityV0125[V]V Applied voltageWf5Work functionp00.5[torr]Pa Gas pressureExplicit 11On the Definitions toolbar, click Explicit.2In the Model Builder window, right-click Explicit 1 and choose Rename.3In the Rename Explicit dialog box, type Cathode in the New label text field.4Click OK.5In the Settings window for Explicit, locate the Input Entities section.6From the Geometric entity level list, choose Boundary.7Select Boundaries 3, 5, and 10 only.Explicit 21On the Definitions toolbar, click Explicit.2In the Model Builder window, right-click Explicit 2 and choose Rename.3In the Rename Explicit dialog box, type Anode in the New label text field.4Click OK.5In the Settings window for Explicit, locate the Input Entities section.6From the Geometric entity level list, choose Boundary.7Select Boundaries 6, 8, and 11 only.Explicit 31On the Definitions toolbar, click Explicit.2In the Model Builder window, right-click Explicit 3 and choose Rename.3In the Rename Explicit dialog box, type Walls in the New label text field.4Click OK.5In the Settings window for Explicit, locate the Input Entities section.6From the Geometric entity level list, choose Boundary.7Select Boundaries 2, 9, and 12 only.Explicit 41On the Definitions toolbar, click Explicit.2In the Model Builder window, right-click Explicit 4 and choose Rename.3In the Rename Explicit dialog box, type All Walls in the New label text field.4Click OK.5In the Settings window for Explicit, locate the Input Entities section.6From the Geometric entity level list, choose Boundary.7Select Boundaries 2, 3, 5, 6, and 8–12 only.Explicit 51On the Definitions toolbar, click Explicit.2In the Model Builder window, right-click Explicit 5 and choose Rename.3In the Rename Explicit dialog box, type Non Cathode Walls in the New label text field.4Click OK.5In the Settings window for Explicit, locate the Input Entities section.6From the Geometric entity level list, choose Boundary.7Select Boundaries 2, 6, 8, 9, 11, and 12 only.D C D I S C H A R G E(D C)Cross Section Import 11On the Physics toolbar, click Global and choose Cross Section Import.2In the Settings window for Cross Section Import, locate the Cross Section Import section.3Click Browse.4Browse to the application’s Application Library folder and double-click the file Ar_xsecs.txt.5In the Model Builder window, click DC Discharge (dc).6In the Settings window for DC Discharge, locate the Plasma Properties section.7Select the Use reduced electron transport properties check box.Plasma Model 11In the Model Builder window, under Component 1 (comp1)>DC Discharge (dc) click Plasma Model 1.2In the Settings window for Plasma Model, locate the Model Inputs section.3In the p A text field, type p0.4Locate the Electron Density and Energy section. In the μe N n text field, type mueN. You now change the way the source coefficients for electronic excitation and ionization are specified. By default, COMSOL computes rate coefficients based on the cross section data you supplied. For DC discharges, Townsend coefficients provide a more accurate description of the cathode fall region so they should be used. The Townsend coefficients are typically computed using the Boltzmann Equation, Two-Term Approximation interface.2: e+Ar=>e+Ars1In the Model Builder window, under Component 1 (comp1)>DC Discharge (dc) click 2: e+Ar=>e+Ars.2In the Settings window for Electron Impact Reaction, locate the Collision section.3From the Specify reaction using list, choose Use lookup table.4Locate the Source Coefficient Data section. From the Rate constant form list, choose Townsend coefficient.5Click Load from File.6Browse to the application’s Application Library folder and double-click the file town2.txt.4: e+Ar=>2e+Ar+1In the Model Builder window, under Component 1 (comp1)>DC Discharge (dc) click 4: e+Ar=>2e+Ar+.2In the Settings window for Electron Impact Reaction, locate the Collision section. 3From the Specify reaction using list, choose Use lookup table.4Locate the Source Coefficient Data section. From the Rate constant form list, choose Townsend coefficient.5Click Load from File.6Browse to the application’s Application Library folder and double-click the file town4.txt.Reaction 11On the Physics toolbar, click Domains and choose Reaction.2In the Settings window for Reaction, locate the Reaction Formula section.3In the Formula text field, type Ars+Ars=>e+Ar+Ar+.4Locate the Kinetics Expressions section. In the k f text field, type 3.734E8.Reaction 21On the Physics toolbar, click Domains and choose Reaction.2In the Settings window for Reaction, locate the Reaction Formula section.3In the Formula text field, type Ars+Ar=>Ar+Ar.4Locate the Kinetics Expressions section. In the k f text field, type 1807.When solving a reacting flow problem there always needs to be one species which is selected to fullfill the mass constraint. This should be taken as the species with the largest mass fraction.Species: Ar1In the Model Builder window, under Component 1 (comp1)>DC Discharge (dc) click Species: Ar.2In the Settings window for Species, locate the Species Formula section.3Select the From mass constraint check box.4Locate the General Parameters section. From the Preset species data list, choose Ar.Species: Ars1In the Model Builder window, under Component 1 (comp1)>DC Discharge (dc) click Species: Ars.2In the Settings window for Species, locate the General Parameters section.3From the Preset species data list, choose Ar.When solving a plasma problem the plasma must be initially charge neutral. COMSOL automatically computes the initial concentration of a selected ionic species such that the electroneutrality constraint is satisfied.Species: Ar+1In the Model Builder window, under Component 1 (comp1)>DC Discharge (dc) click Species: Ar+.2In the Settings window for Species, locate the Species Formula section.3Select the Initial value from electroneutrality constraint check box.4Locate the General Parameters section. From the Preset species data list, choose Ar.Wall 11On the Physics toolbar, click Boundaries and choose Wall.2In the Settings window for Wall, locate the Boundary Selection section.3From the Selection list, choose All Walls.Ground 11On the Physics toolbar, click Boundaries and choose Ground.2In the Settings window for Ground, locate the Boundary Selection section.3From the Selection list, choose Cathode.Metal Contact 11On the Physics toolbar, click Boundaries and choose Metal Contact.2In the Settings window for Metal Contact, locate the Boundary Selection section.3From the Selection list, choose Anode.4Locate the Terminal section. In the V0 text field, type V0.5Locate the Quick Circuit Settings section. From the Quick circuit type list, choose Series RC circuit.Dielectric Contact 11On the Physics toolbar, click Boundaries and choose Dielectric Contact.2In the Settings window for Dielectric Contact, locate the Boundary Selection section.3From the Selection list, choose Walls.Now you add a surface reaction which describes the neutralization of Argon ions on the electrode. Secondary emission of electrons is required to sustain the discharge, so you enter the emission coefficient and an estimate of the mean energy of the secondary electrons based on the ionization energy threshold and the work function of the surface.Surface Reaction 11On the Physics toolbar, click Boundaries and choose Surface Reaction.2In the Settings window for Surface Reaction, locate the Reaction Formula section. 3In the Formula text field, type Ar+=>Ar.4Locate the Boundary Selection section. From the Selection list, choose Cathode. Make the secondary emission coefficient 0.25 and set the mean energy of the secondary electrons to be the ionization energy (given by the expression dc.de_4) minus twice the work function of the electrode.5Locate the Secondary Emission Parameters section. In the γi text field, type 0.25.6In the εi text field, type dc.de_4-2*Wf.Surface Reaction 21On the Physics toolbar, click Boundaries and choose Surface Reaction.2In the Settings window for Surface Reaction, locate the Reaction Formula section. 3In the Formula text field, type Ar+=>Ar.4Locate the Boundary Selection section. From the Selection list, choose Non Cathode Walls.Surface Reaction 31On the Physics toolbar, click Boundaries and choose Surface Reaction.2In the Settings window for Surface Reaction, locate the Reaction Formula section. 3In the Formula text field, type Ars=>Ar.4Locate the Boundary Selection section. From the Selection list, choose All Walls.M E S H1Edge 11In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose More Operations>Edge.2Select Boundaries 3, 5, 6, 8, 10, 11, and 14 only.Size 11Right-click Component 1 (comp1)>Mesh 1>Edge 1 and choose Size.2In the Settings window for Size, locate the Element Size section.3From the Predefined list, choose Extremely fine.4Click the Custom button.5Locate the Element Size Parameters section. Select the Maximum element size check box.6In the associated text field, type 0.001.7Click the Zoom Extents button on the Graphics toolbar.Free Triangular 1In the Model Builder window, right-click Mesh 1 and choose Free Triangular.Size 11In the Model Builder window, under Component 1 (comp1)>Mesh 1 right-click Free Triangular 1 and choose Size.2In the Settings window for Size, locate the Element Size section.3From the Predefined list, choose Extra fine.Boundary Layer Properties1In the Model Builder window, right-click Mesh 1 and choose Boundary Layers.2In the Settings window for Boundary Layer Properties, locate the Boundary Selection section.3From the Selection list, choose All Walls.4Locate the Boundary Layer Properties section. In the Number of boundary layers text field, type 4.5Click the Build All button.S T U D Y1Step 1: Time Dependent1In the Model Builder window, expand the Study 1 node, then click Step 1: Time Dependent.2In the Settings window for Time Dependent, locate the Study Settings section.3In the Times text field, type 0.4Click Range.5In the Range dialog box, choose Number of values from the Entry method list.6In the Start text field, type -8.7In the Stop text field, type 0.8In the Number of values text field, type 21.9From the Function to apply to all values list, choose exp10.10Click Add.11On the Home toolbar, click Compute.R E S U L T SSelectionOn the Results toolbar, click Selection.Data Sets1In the Settings window for Selection, locate the Geometric Entity Selection section. 2From the Geometric entity level list, choose Boundary.3From the Selection list, choose All Walls.Cut Line 2D 1On the Results toolbar, click Cut Line 2D.Data Sets1In the Settings window for Cut Line 2D, locate the Line Data section.2In row Point 1, set z to 0.016.3In row Point 2, set r to 0.4In row Point 2, set z to 0.384.Mirror 2D 1On the Results toolbar, click More Data Sets and choose Mirror 2D.Electron Density (dc)1In the Model Builder window, under Results click Electron Density (dc).2In the Settings window for 2D Plot Group, locate the Data section.3From the Data set list, choose Mirror 2D 1.4On the Electron Density (dc) toolbar, click Plot.5Click the Zoom Extents button on the Graphics toolbar.Electron Temperature (dc)1In the Model Builder window, under Results click Electron Temperature (dc).2In the Settings window for 2D Plot Group, locate the Data section.3From the Data set list, choose Mirror 2D 1.4On the Electron Temperature (dc) toolbar, click Plot.5Click the Zoom Extents button on the Graphics toolbar.Electric Potential (dc)1In the Model Builder window, under Results click Electric Potential (dc).2In the Settings window for 2D Plot Group, locate the Data section.3From the Data set list, choose Mirror 2D 1.4On the Electric Potential (dc) toolbar, click Plot.5Click the Zoom Extents button on the Graphics toolbar.1D Plot Group 41On the Home toolbar, click Add Plot Group and choose 1D Plot Group.2In the Settings window for 1D Plot Group, locate the Data section.3From the Time selection list, choose Last.4Locate the Plot Settings section. Select the x-axis label check box.5In the associated text field, type Distance (x).6Select the y-axis label check box.7In the associated text field, type Electric Potential (V).8Locate the Data section. From the Data set list, choose Cut Line 2D 1.Line Graph 1On the 1D Plot Group 4 toolbar, click Line Graph.1D Plot Group 41In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the y-axis data section. From the menu, choose Model>Component 1>DC Discharge (Electrostatics)>Electric>V - Electric potential.2In the Model Builder window, click 1D Plot Group 4.3On the 1D Plot Group 4 toolbar, click Plot.4Click the Zoom Extents button on the Graphics toolbar.1D Plot Group 51On the Home toolbar, click Add Plot Group and choose 1D Plot Group.2In the Settings window for 1D Plot Group, locate the Data section.3From the Time selection list, choose Last.4Locate the Plot Settings section. Select the x-axis label check box.5In the associated text field, type Distance (x).6Select the y-axis label check box.7In the associated text field, type Electron Temperature (V).8Locate the Data section. From the Data set list, choose Cut Line 2D 1.Line Graph 1On the 1D Plot Group 5 toolbar, click Line Graph.1D Plot Group 51In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the y-axis data section. From the menu, choose Model>Component 1>DC Discharge (Drift Diffusion)>Electron energy density>dc.Te - Electron temperature.2On the 1D Plot Group 5 toolbar, click Plot.3Click the Zoom Extents button on the Graphics toolbar.1D Plot Group 61On the Home toolbar, click Add Plot Group and choose 1D Plot Group.2In the Settings window for 1D Plot Group, locate the Data section.3From the Time selection list, choose Last.4Locate the Plot Settings section. Select the x-axis label check box.5In the associated text field, type Distance (x).6Select the y-axis label check box.7In the associated text field, type Electron Density (1/m^3).8Locate the Data section. From the Data set list, choose Cut Line 2D 1.Line Graph 1On the 1D Plot Group 6 toolbar, click Line Graph.1D Plot Group 61In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the y-axis data section. From the menu, choose Model>Component 1>DC Discharge (Drift Diffusion)>Electron density>dc.ne - Electron density.2On the 1D Plot Group 6 toolbar, click Plot.3Click the Zoom Extents button on the Graphics toolbar.1D Plot Group 71On the Home toolbar, click Add Plot Group and choose 1D Plot Group.2In the Settings window for 1D Plot Group, locate the Data section.3From the Time selection list, choose Last.4Locate the Plot Settings section. Select the x-axis label check box.5In the associated text field, type Distance (x).6Select the y-axis label check box.7In the associated text field, type Excited Argon Density (1/m^3).8Locate the Data section. From the Data set list, choose Cut Line 2D 1.Line Graph 1On the 1D Plot Group 7 toolbar, click Line Graph.1D Plot Group 71In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the y-axis data section. From the menu, choose Model>Component 1>DC Discharge (Heavy Species Transport)>Number densities>dc.n_wArs - Number density.2On the 1D Plot Group 7 toolbar, click Plot.3Click the Zoom Extents button on the Graphics toolbar.1D Plot Group 81On the Home toolbar, click Add Plot Group and choose 1D Plot Group.2In the Settings window for 1D Plot Group, locate the Data section.3From the Time selection list, choose Last.4Locate the Plot Settings section. Select the x-axis label check box.5In the associated text field, type Distance (x).6Select the y-axis label check box.7In the associated text field, type Argon +1 Density (1/m^3).8Locate the Data section. From the Data set list, choose Cut Line 2D 1.Line Graph 1On the 1D Plot Group 8 toolbar, click Line Graph.1D Plot Group 81In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the y-axis data section. From the menu, choose Model>Component 1>DC Discharge (Heavy Species Transport)>Number densities>dc.n_wAr_1p - Number density.。
comsol4.3中文使用手册

应用领域 ..................................................................................................................................................................- 9 RF 模块........................................................................................................................................................................- 10 -
全国统一客户服务热线:400 888 5100 网址: 邮箱:info@ -1-
中仿科技公司 CnTech Co.,Ltd
精确描述真实世界
COMSOL 成立之初,一切的源动力就在于强调多物理仿真的重要性。只有从多物理的角度看待问题,仿真技术 才能保证数值结果的准确性,也就是与真实世界的一致性。工程师根据自己的经验,认为一些物理过程或许可以忽 略,或许另外的一些物理过程必须同时考虑,他们可以用多物理仿真的思想验证它,并且获得准确的结果。这就是 对真实世界的精确描述。
力学与传热分析................................................................................................................................................................................ - 16 传热模块.....................................................................................................................................................................- 16 -
Comsol有限元软件在大型水下目标声学仿真上的应用

第37卷第8期 计算机应用与软件Vol 37No.82020年8月 ComputerApplicationsandSoftwareAug.2020Comsol有限元软件在大型水下目标声学仿真上的应用周 烨 温 玮(海军航空大学 山东烟台264000)收稿日期:2019-06-24。
山东省重点研发计划项目(2016CYJS02A01)。
周烨,硕士生,主研领域:水声工程。
温玮,副教授。
摘 要 针对现有有限元分析软件在大型水下目标多物理场耦合问题处理上复杂度高、操作不便等问题,提出基于Comsol有限元仿真软件对于大型三维目标的仿真应用方案。
推导其特有的间断伽辽金算法在Lax Friedrichs通量下针对波动方程的空间离散方程,并结合非定长时间显式4阶龙格 库塔法计算水声目标仿真。
与解析解对比验证了Comsol求解水声目标在处理多物理场耦合问题的有效性。
仿真三维潜艇模型的水下散射声场。
通过和传统有限元方法对比,验证了该方法在计算大型目标声散射时的高效性,为Comsol在水声领域的应用提供了有效借鉴。
关键词 Comsol 间断伽辽金 Lax Friedrichs 声散射中图分类号 TP31 TB56 文献标志码 A DOI:10.3969/j.issn.1000 386x.2020.08.014APPLICATIONOFCOMSOLFINITEELEMENTSOFTWAREINACOUSTICSIMULATIONOFUNDERWATERTARGETZhouYe WenWei(NavalAirUniversity,Yantai264000,Shandong,China)Abstract Aimingatthehighcomplexityandinconvenientoperationoftheexistingfiniteelementanalysissoftwareindealingwiththemulti physicalfieldcouplingoflargeunderwaterobjects,weproposeasimulationapplicationschemeoflarge3DobjectsbasedonComsolfiniteelementsimulationsoftware.ThediscretespatialequationofthewaveequationunderLax Friedrichsfluxwasderived,andthe4 orderrunge kuttamethodwasusedtocalculatetheunderwateracoustictargetsimulation.ThecomparisonwiththeanalyticalsolutionverifiedtheeffectivenessofComsolinsolvingthemultiphysicscouplingproblemwhensolvingtheunderwateracoustictarget.Theunderwaterscatteringacousticfieldof3Dsubmarinemodelwassimulated.Theeffectivenessofthismethodincalculatingacousticscatteringoflargetargetsisverifiedbycomparisonwiththefinite differencemethod.ItprovidesaneffectivereferencefortheapplicationofComsolinthefieldofunderwateracoustic.Keywords Comsol Discontinuousgalerkin Lax Friedrichs Acousticscattering0 引 言在实际应用中,尤其是水下目标识别探测中,越来越多的场合涉及数值计算,目前有很多成熟的有限元计算软件,把复杂的仿真过程以很简洁的过程实现[1]。
COMSOL Multiphysics安装指南说明书

COMSOL Multiphysics安装指南C O M S O L M u l t i p h y s i c s安装指南© 1998–2021 COMSOL 版权所有受列于/patents的专利保护;您也可以参见 COMSOL Desktop“文件”菜单中的“帮助 >关于 COMSOL Multiphysics”,获取可能适用的美国专利的详细列表。
专利申请中。
本文档和本文所述的程序根据《COMSOL 软件许可协议》(/comsol-license-agreement)提供,且仅能按照许可协议的条款进行使用或复制。
COMSOL、COMSOL 徽标、COMSOL Multiphysics、COMSOL Desktop、COMSOL Compiler、COMSOL Server 和LiveLink 为COMSOL AB 的注册商标或商标。
所有其他商标均为其各自所有者的财产,COMSOL AB 及其子公司和产品不与上述商标所有者相关联,亦不由其担保、赞助或支持。
相关商标所有者的列表请参见/trademarks。
版本:COMSOL 6.0联系信息请访问“联系我们”页面/contact,以提交一般查询或搜索我们的联系地址和电话号码。
您也可以访问全球销售办事处页面/contact/offices,获取更多地址和联系信息。
如需联系技术支持,请访问 COMSOL Access 页面/support/case,创建并提交在线请求表单。
其他常用链接包括:•技术支持中心:/support•产品下载:/product-download•产品更新:/support/updates•COMSOL 博客:/blogs•用户论坛:/forum•活动:/events•COMSOL 视频中心:/videos•技术支持知识库:/support/knowledgebase文档编号:CM010002目录前言 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9安装介质选项 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9系统要求 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10先前安装版本 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11软件许可协议 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11许可证类型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11许可证管理工具 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14COMSOL Access . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15在 Windows 上安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16通过 Internet 安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16下载并安装 COMSOL 软件 . . . . . . . . . . . . . . . . . . . . . . . . . . . 19通过 USB 闪存驱动器安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . 20运行 COMSOL 安装程序 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20移除(卸载)COMSOL 安装程序 . . . . . . . . . . . . . . . . . . . . . 43安装软件更新 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44自动安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45产品更新和库更新 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46LiveLink™for Excel®安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . 47LiveLink™ for AutoCAD®安装. . . . . . . . . . . . . . . . . . . . . . . 47LiveLink™ for Inventor®安装 . . . . . . . . . . . . . . . . . . . . . . . . 48LiveLink™ for PTC® Creo® Parametric™安装 . . . . . . . . . 49LiveLink™for PTC® Pro/ENGINEER®:更改安装路径 . . 50| 3LiveLink™for Revit®安装 . . . . . . . . . . . . . . . . . . . . . . . . . . .51 LiveLink™for Solid Edge®安装 . . . . . . . . . . . . . . . . . . . . . .52 LiveLink™for SOLIDWORKS®安装 . . . . . . . . . . . . . . . . . . .53集群安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .54在 Windows 上安装许可证管理器 . . . . . . . . . . . . . . . . . . . .57什么是 FlexNet®许可证管理器? . . . . . . . . . . . . . . . . . . . . . .57 FlexNet®许可证管理器的系统要求 . . . . . . . . . . . . . . . . . . . . .58 FlexNet®许可证管理器软件组件 . . . . . . . . . . . . . . . . . . . . . . .58 FlexNet®许可证管理器文档 . . . . . . . . . . . . . . . . . . . . . . . . . . .59许可证文件和许可证特征 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .59安装许可证管理器 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .67启动许可证管理器 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .69确认许可证管理器正在运行 . . . . . . . . . . . . . . . . . . . . . . . . . . .70启动 COMSOL Multiphysics . . . . . . . . . . . . . . . . . . . . . . . . . . .71更改许可证 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .71在 IPV6 网络中使用 COMSOL . . . . . . . . . . . . . . . . . . . . . . . . .72许可证错误故障排除 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .72在 Windows 上运行 COMSOL Multiphysics . . . . . . . . . . . .73“开始”菜单中的 COMSOL Multiphysics 文件夹 . . . . . . . .73启动使用课堂许可证套装的 COMSOL Multiphysics . . . . . . .74手动创建桌面快捷方式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .75在客户端/服务器模式下运行 COMSOL Multiphysics . . . . . .76在批处理模式下运行 COMSOL Multiphysics . . . . . . . . . . . . .78多核设置 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .794 |在集群上运行 COMSOL Multiphysics . . . . . . . . . . . . . . . . . . 80在云上运行 COMSOL Multiphysics . . . . . . . . . . . . . . . . . . . . 82运行 COMSOL Multiphysics with MATLAB . . . . . . . . . . . . . 82运行 COMSOL Multiphysics with Simulink . . . . . . . . . . . . . . 83在 macOS 上安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84通过 Internet 安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84下载并安装 COMSOL 软件 . . . . . . . . . . . . . . . . . . . . . . . . . . . 87通过 USB 闪存驱动器安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . 88运行 COMSOL 安装程序 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89自动安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89移除(卸载)COMSOL 安装程序 . . . . . . . . . . . . . . . . . . . . . 89产品更新和案例库更新 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90更改 MATLAB®安装路径 . . . . . . . . . . . . . . . . . . . . . . . . . . . 90在 macOS 上安装许可证管理器 . . . . . . . . . . . . . . . . . . . . . 91 FlexNet 许可证管理器软件组件 . . . . . . . . . . . . . . . . . . . . . . . 91FlexNet 许可证管理器文档 . . . . . . . . . . . . . . . . . . . . . . . . . . . 91许可证文件 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92安装许可证管理器 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92启动许可证管理器 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94确认许可证管理器正在运行 . . . . . . . . . . . . . . . . . . . . . . . . . . 95启动 COMSOL Multiphysics . . . . . . . . . . . . . . . . . . . . . . . . . . 95更改许可证 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95在 IPV6 网络中使用 COMSOL . . . . . . . . . . . . . . . . . . . . . . . . 96许可证错误故障排除 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96| 5在 macOS 上运行 COMSOL Multiphysics . . . . . . . . . . . . . .97 COMSOL 应用程序 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .97从终端窗口运行 COMSOL Multiphysics . . . . . . . . . . . . . . . . .98运行课堂许可证套装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .98在客户端/服务器模式下运行 COMSOL Multiphysics . . . . . .98在批处理模式下运行 COMSOL Multiphysics . . . . . . . . . . . .100多核设置 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .101在集群上运行 COMSOL Multiphysics . . . . . . . . . . . . . . . . . .101在云上运行 COMSOL Multiphysics . . . . . . . . . . . . . . . . . . . .102在 Linux 上安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .103通过 Internet 安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .103下载并安装 COMSOL 软件 . . . . . . . . . . . . . . . . . . . . . . . . . .105从 DVD 安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .106通过 USB 闪存驱动器安装 . . . . . . . . . . . . . . . . . . . . . . . . . . .107运行 COMSOL 安装程序 . . . . . . . . . . . . . . . . . . . . . . . . . . . .107用于查看文档的 Web 浏览器 . . . . . . . . . . . . . . . . . . . . . . . . .108自动安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .109移除(卸载)COMSOL 安装程序 . . . . . . . . . . . . . . . . . . . . .109产品更新和案例库更新 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .109更改 MATLAB®安装路径 . . . . . . . . . . . . . . . . . . . . . . . . . . .110集群安装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .110在 Linux 上安装许可证管理器 . . . . . . . . . . . . . . . . . . . . .112 FlexNet 许可证管理器软件组件 . . . . . . . . . . . . . . . . . . . . . . .112 FlexNet 许可证管理器文档 . . . . . . . . . . . . . . . . . . . . . . . . . . .112 6 |许可证文件 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113安装许可证管理器 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113启动许可证管理器 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115确认许可证管理器正在运行 . . . . . . . . . . . . . . . . . . . . . . . . . 116启动 COMSOL Multiphysics . . . . . . . . . . . . . . . . . . . . . . . . . 116更改许可证 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117在 IPV6 网络中使用 COMSOL . . . . . . . . . . . . . . . . . . . . . . . 117许可证错误故障排除 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118在 Linux 上运行 COMSOL Multiphysics . . . . . . . . . . . . . 119运行 COMSOL Multiphysics . . . . . . . . . . . . . . . . . . . . . . . . . 119多核设置 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119在批处理模式下运行 COMSOL Multiphysics . . . . . . . . . . . 120在客户端/服务器模式下运行 COMSOL Multiphysics . . . . . 121运行课堂许可证套装 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122在集群上运行 COMSOL . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122在云上运行 COMSOL Multiphysics . . . . . . . . . . . . . . . . . . . 124运行 COMSOL Multiphysics with MATLAB . . . . . . . . . . . . 124运行 COMSOL Multiphysics with Simulink . . . . . . . . . . . . . 125 COMSOL 软件安全. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126 COMSOL Multiphysics 客户端/服务器安全 . . . . . . . . . . . . . 126App 和物理场开发器安全 . . . . . . . . . . . . . . . . . . . . . . . . . . . 128方法安全性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128COMSOL Server 安全 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129许可证错误故障排除 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130| 78 |前言欢迎您阅读《COMSOL Multiphysics 安装指南》,本书提供有关安装 COMSOL Multiphysics®及其附加产品的操作说明。
声学超结构在车内低频轰鸣声控制中的应用

2021年第4期【摘要】针对某款轿车在30km/h 匀速行驶过程中产生明显的低频轰鸣声问题,通过测试和分析,确定了车内35Hz 噪声峰值过高是引发该问题的直接原因,并判断出该频率峰值与尾门薄壁件振动密切相关。
基于局域共振原理,设计了具有轻量化、小型化特征的声学超结构,并完成了谐振单元构型的选择与带隙设计、整车布置规划及谐振单元排布与基体框架设计。
实车测试结果表明:贴附声学超结构后,前排和后排35Hz 车内噪声声压级分别降低了4.23dB(A)、5.77dB(A)。
主题词:声学超结构结构声控制局域共振车内低频轰鸣中图分类号:U461.1文献标识码:ADOI:10.19620/ki.1000-3703.20200952The Application of Acoustic Superstructure on Control of LowFrequency Roaring in VehicleTang Jiyou 1,Ding Weiping 1,Wu Yudong 1,Huang Haibo 1,Luo Deyang 2(1.Southwest Jiao Tong University,Chengdu 610031;2.SAIC GM Wuling Automobile Co.,Ltd.,Liuzhou 545000)【Abstract 】Obvious low-frequency roaring sound is produced by a car model during the constant speed of 30km/h.By testing and analysis,it is determined that the high peak of 35Hz noise inside the car is the direct cause of this problem,and it is judged that the peak frequency is closely related to the vibration of thin-wall parts of the tail door.Furthermore,based on the principle of local resonance,a lightweight and miniaturized acoustic superstructure is developed,which involves the selection of its resonant unit configuration,band-gap design,vehicle layout planning,resonant unitarrangement,matrix frame size design.The real vehicle test shows that after attaching the acoustic superstructure,the noise of 35Hz in the car is reduced by 4.23dB(A)and 5.77dB(A)respectively in the front and rear rows.Key words:Acoustic superstructure,Structural sound control,Local resonance,Low frequencyRoaring in vehicle唐吉有1丁渭平1吴昱东1黄海波1罗德洋2(1.西南交通大学,成都610031;2.上汽通用五菱汽车股份有限公司,柳州545000)*基金项目:国家自然科学基金项目(51775451)。
comsol错误提示及解决方法(可编辑修改word版)
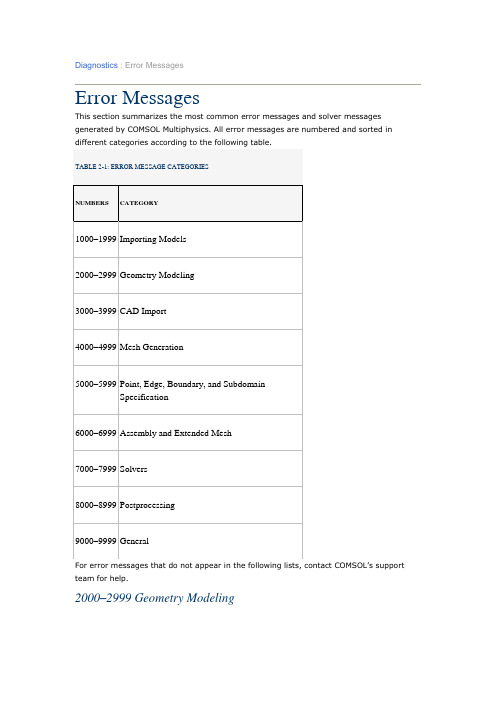
ERROR MESSAGE
EXPLANATION
6008
Circular variable dependency detected
A variable has been defined in terms of itself, possibly in a circular chain of expression variables. Make sure that variable definitions are sound. Be cautious with equation variables in equations.
Incorrect geometry for mapped mesh.
2190
Invalid radius or distance
Incorrect input parameters to fillet/chamfer.
2197
Operation resulted in empty geometry object
6063
Invalid degree of freedom name
The software does not recognize the name of a degree of freedom. Check the names of dependent variables that you have entered for the model. See also Error 7192.
2140
Singular extrusions not supported
Error in input parameters.
2141
Singular revolutions not supported
comsol多相流仿真流程

comsol多相流仿真流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!COMSOL 多相流仿真流程一、问题定义与模型建立阶段。
comsol application

Optical scattering and electric field enhancement from core–shell plasmonic nanostructuresA. Mejdoubi, M. Malki, M. Essone Mezeme, Z. Sekkat, M. Bousmina et al.Citation: J. Appl. Phys. 110, 103105 (2011); doi: 10.1063/1.3660774View online: /10.1063/1.3660774View Table of Contents: /resource/1/JAPIAU/v110/i10Published by the American Institute of Physics.Related ArticlesSealing SU-8 microfluidic channels using PDMSBiomicrofluidics 5, 046503 (2011)Waveguide superconducting single-photon detectors for integrated quantum photonic circuitsAppl. Phys. Lett. 99, 181110 (2011)GaN directional couplers for integrated quantum photonicsAppl. Phys. Lett. 99, 161119 (2011)Waveguide Fabry-Pérot microcavity arraysAppl. Phys. Lett. 99, 053119 (2011)1×12 Unequally spaced waveguide array for actively tuned optical phased array on a silicon nanomembrane Appl. Phys. Lett. 99, 051104 (2011)Additional information on J. Appl. Phys.Journal Homepage: /Journal Information: /about/about_the_journalTop downloads: /features/most_downloadedInformation for Authors: /authorsDownloaded 29 Dec 2011 to 162.105.41.73. Redistribution subject to AIP license or copyright; see /about/rights_and_permissionsOptical scattering and electric field enhancement from core–shell plasmonic nanostructuresA.Mejdoubi,1,2M.Malki,1,2,3M.Essone Mezeme,4Z.Sekkat,2,5M.Bousmina,6and C.Brosseau4,7,a)1Institute for Nanomaterials and Nanotechnology,Avenue de l’Arme´e Royale,Rabat,Morocco2Moroccan Foundation for Advanced Science and Innovation and Research(MAScIR),Rabat,Morocco3LMPHE,Faculte´des Sciences,Universite´Mohammed V Agdal,Rabat,Morocco4Universite´Europe´enne de Bretagne,Universite´de Brest,Lab-STICC,CS93837,6Avenue Le Gorgeu,Brest29238,France5Optics and Photonics Centre,Avenue de l’Arme´e Royale,Rabat,Morocco6Hassan II Academy of Science and Technology,Km4,Mohamed VI Avenue,Rabat10220,Morocco7De´partement de Physique,Universite´de Bretagne Occidentale,Brest,France(Received10June2011;accepted13October2011;published online23November2011)Three-dimensionalfinite-difference time-domain simulations are used to study the near-and far-field properties of plasmonic core–shell(CS)nanostructures of reduced symmetry.Special attention is given to silica core and gold shell nanoparticles by changing their geometry.For the simulated range of wavelengths(300–2100nm)our calculations of the scattering and absorption efficiencies imply strong polarization sensitivity and are highly dependent on the size and geometry of the CS nanostructures.Strong enhancements of the exciting electricfield associated with the excitations of nanoparticle plasmons are observed.The wavelength dependence of the scattering spectra and concentration of electromagneticfield in subwavelength volumes have a potential for biosensing and bioimaging.V C2011American Institute of Physics.[doi:10.1063/1.3660774]I.INTRODUCTIONPlasmonic excitation and the associated subwavelength light–matter interaction has opened new and fascinating ave-nues for research that originates from the observations and expectations of several unique properties of the interactions between waves and conduction electrons confined near metal/dielectric interfaces,including surface-enhanced Raman scattering,and mode localization(for reviews,see, e.g.,Refs.1–4).Transition to the nanoscale has lead to increased interest in many new problems including the local-ized surface plasmon resonances and increased localfield enhancement.3,4Whereas the properties can be understood partly as the result of the behaviors of the constituent materi-als under the electricfield excitation,in many cases the topo-logical features of the interfaces have been shown to play a critical role.For example,the superlens effect,in a self-similar chain of nanoparticles can be used to prepare a subwavelength scale energy localization in the narrow gap separating two neighboring nanoparticles,has been a subject of recent study,5,6invisibility dips occur in the scattering spectrum of a pair of metallic nanoparticles,which originates from a destructive interference between each surface plas-mon mode,7and metal nanoparticles,when placed on top of a high-index substrate,can efficiently couple light into the substrate.8The impact of localized multipole plasmons on the optical absorption and the energy loss of metallodielec-tric crystals were also addressed in Ref.9.As a result,the design of collective electromagnetic coupling and optimized interface engineering become essential strategies in guiding exploration of plasmonic nanostructures.Much of the recent searching for engineering nanoscale optical antennas for THz,near-field tissue imaging applica-tions has concentrated on plasmonic core–shell(CS)nano-structures.10A quintessential feature of nanoantenna structures is its ability to couple the energy of an electromag-netic excitation to a confined region of subwavelength size.11,12The high sensitivity of these nanostructures to the dielectric environment andfield polarization in the visible range are expected to be useful for biosensing applications.13 More specifically,the Au shell layer provides a relatively chemically inert surface layer that can be functionalized to enhance solubility in various media and promote biocompat-ibility while preserving the properties of the core phase.For tissue imaging applications,nanoantennas positioned in spe-cific locations,e.g.,near a tumor,can be used for directional energy guiding.Despite substantial development to investi-gate the shape anisotropy for topologically nontrivial struc-tures,many important questions are not yet answered. Of particular interest are the numerical simulations studies, e.g.,finite-difference time-domain(FDTD),discrete dipole approximation(DDA),and boundary element method (BEM),which provided important insights into the mecha-nisms that control the transport properties.14The literature on this subject is vast.The reader may wish to consult Ref.3 for a critical comparison of the computational efficiency and accuracy of the FDTD,DDA,and BEM approaches to simu-late absorption and scattering spectra.It is fair to say that the subject is still far from being ex-hausted and new effects continue to be uncovered.The pres-ent study is another contribution to this effort.We focus on aa)Electronic mail:brosseau@univ-brest.fr.0021-8979/2011/110(10)/103105/6/$30.00V C2011American Institute of Physics110,103105-1JOURNAL OF APPLIED PHYSICS110,103105(2011)simulation of the optical response of resonant plasmonic nanostructures.One route to investigating the electromag-netic interaction with nanostructures is through the FDTD method,which is ideally suited for this endeavor.Two recent developments inform the present work.First,in a recent pa-per,15the authors characterized the frequency dependence of the effective magnetic permeability and permittivity of reduced-symmetry CS nanostructures composed of a mag-netic core and a plasmonic shell with well-controlled dimen-sions for different geometries and polarizations.Changing the internal geometry of the nanostructure not only shifts the resonance frequencies,but can also strongly modify the rela-tive magnitudes of the electricfield enhancement,independ-ently of nanoparticle shape.Plasmonic CS nanostructures turn out to be particularly useful for biological applications, e.g.,see Ref.16.Second,advances in computing power and techniques now allow us to make full electromagnetic simu-lations of arbitrarily shaped nanoparticles allowing direct comparison with experiment.17The goal of the calculations was to investigate theeffects of geometric parameters of the CS nanostructures and excitation polarized parallel and perpendicular to the antenna axis on the scattering and absorption efficiencies.First,we demonstrate manipulation of the plasmonic resonance(PLR) as a function of the nanostructure’s size and shape,as well as the polarization of the incident electromagneticfield,which can be designed to lie within the biological window of high transmission in blood and tissue between700and1100nm. Second,the characteristics of the PLR and the polarization influence on the resonance depending of the geometry of the shell provide additional important information about the electricfield enhancement(EFE).Third,we have generated maps of EFE associated with resonances.We found nanolo-calized THzfields corresponding to large EFE up to three orders of magnitude higher in amplitude than the excitation opticalfield.These results address both fundamental and applied issues that can be promising in the perspective of developing optical nanoantennas for biosensing applications. II.METHODOLOGYTo motivate our approach,we begin by discussing the computational method performed in this study.First-principles calculations presented in this work were performed using the FDTD method implemented in the Lumerical FDTD Solutions simulation package.18The essential features of our model can be summarized as follows.We use a cubic cell with1200Â1200Â1200nm3dimensions for these sim-ulations.The system was discretized into uniform cubic Yee cells with a side equal to2nm,and a time step D t¼10À18s, which satisfies the Courant-Friedrich-Lewy stability crite-rion.19To absorb the outgoing radiation,the computational domain was surrounded by a region of many cells of per-fectly matched layers.See,e.g.,Ref.19for details of the cal-culational method,its numerical stability,and its accuracy assessment.The core–shell scatterer is illuminated with an incident plane wave,of amplitude E0,on the XZ plane. We use a Cartesian coordinate system(Fig.1)as a reference system using a total-field–scattered-field source(TFSF)to simulate a broadband(300–2100nm)plane wave pulse, which is launched in theÀY direction.20TFSF sources are used to separate the computation region into two distinct regions,i.e.,one that contains the totalfield(the sum of the incidentfield and the scatteredfield),whereas the second region contains only the scatteredfield.An expÀi x tðÞtime convention is assumed.As input,we used the intrinsic(relative)permittivity of the core(Si),e3,and the shell layer(Au),e2,respectively. We shall assume throughout that the homogeneous embed-ding medium(phase1)has dielectric properties that can be assimilated to water,i.e.,constant refractive index n¼1.33 in the THz range of frequencies.Note that the three-dimensional FDTD calculations are performed with the frequency-dependent empirical permittivity data tabulated in Palik21for Si and we used the values from the Johnson and Christy21tabulated data for the frequency-dependent permit-tivity of Au(see Ref.21for a review).As nanostructures decrease in size,the chargefluctuations are expected to become inherently quantum mechanical.However,because the thickness of the metallic shell is much larger than the Fermi wavelengthðe)k F%0:5nmÞ;quantum mechanical effects can be ignored and the physics described by our approach is entirely classical.It is informative to note that the mean free path of electrons in bulk Au%38nm)e: We have verified thatfinite-size correction has little effect on the analysis,and thus will be inconsequential for this range of frequencies.22,23To benchmark the accuracy of our method,we begin by considering the idealized case of a CS spherical structure with a Au nanoshell(Fig.1(a)).All computations below are done for the physical settings,core radius R and shell thick-ness e,which are achievable in the lab.Observe also that the values of e are smaller than the skin depth,which is%15nm in the range of k considered.An examination of the static (dipolar)polarizability a for a coated sphere,21a¼4p R32e2þe3ðÞe2Àe1ðÞþf e3Àe2ðÞ2e2þe1ðÞ2e1þe2ðÞe3þ2e2ðÞþ2f e2Àe1ðÞe3Àe2ðÞ; FIG.1.(Color online)Cross-sectional3D views of the CS nanostructures considered:(a)isotropic case;(b)and(c)refer to representative axially sym-metric CS nanostructures situations,where the shell of the CS nanostructures involves sharp edges and tips.In all simulations we concentrated on the visi-ble and near-infrared regions and assumed that the core and the shell layer are made of Si and Au,respectively.The nanostructures are supposed to be immersed in an aqueous solution.The origin is taken at the center of the spherical core.with f¼1Àe=RðÞ3being the fraction of the total particle volume occupied by the core phase,is of interest and leads to the corresponding cross sections for scattering,C sca¼8p33ka j j2/R6;and absorption,C abs¼2pffiffiffiffie1pkIm aðÞ/R3;where k denotes the free space light wavelength.The conver-gence of the FDTD code was checked by comparing the cal-culated real and imaginary components of the effective permittivity spectra withfinite-element(FE)calculations using the COMSOL MULTIPHYSICS code package24under the quasistatic approximation(Fig.2).In this long-wavelength limit,i.e.,R(k,the composite material can be replaced by an effective homogeneous medium e,such thatelectromagnetic modes propagate with angular frequency x given as a function of k by x¼2p cffiffie p=k,where c denotes the speed of light.The relative differences(not shown)are only%4%.To put our results in perspective,we have plotted our FDTD values of PLR wavelength over the whole R range with the values of the Fro¨hlich modes which are reached at the points where the denominator of a vanishes.21,25,26We observe,generally,a good agreement.As shown in Fig.3, the R-dependent PLR wavelength is a linear law(Fig.3), reflecting the expected trend previously considered by others.21,27–29The behavior is entirely consistent with the expectations based on FE calculations.These differences are reasonable because we must consider several percent of errors for the FDTD results.19III.RESULTS AND DISCUSSIONThe scattering C sca/G a,absorption C abs/G a,and extinc-tion(C scaþC abs)/G a efficiency spectra are shown in Fig.4 for different sizes of particles and shells,where G a¼p R2 FIG.2.(Color online)Effective dielectric spectra of the CS nanostructureshown in Fig.1(a)with Au shell thickness e¼5nm and Si spheres with radiiranging from15nm to40nm.The numbers in the inset indicate the radii Rof the particles considered.(a)Real part of the permittivity as a function ofwavelength.(b)Same as in(a)for the imaginary part of the permittivity.The Au and Si material dispersion parameters are taken from Ref.21.FIG. 3.(Color online)Comparison of the resonant mode wavelengthbetween the FDTD(squares),FE(circles),and analytic calculations(trian-gles)as extracted from the vanishing of the denominator of a.Here,e¼5nm.In the inset,we have plotted the differences(residuals)between the FDTDand FE simulations(squares)and the differences between the analytic calcula-tions and the FE simulations(triangles)vs R.FIG.4.(Color online)Scattering,absorption,and extinction efficiency forthe CS nanostructure(a)shown in Fig.1,where G a denotes the particlecross-sectional area projected onto a plane perpendicular to the incidentwave.To ease comparison we use the same color code for the spectra.Thegeometric parameters are:(a)R¼43.4nm and e¼13.4nm,(b)R¼45nmand e¼5nm,(c)R¼55nm and e¼10nm,(d)R¼60nm and e¼5nm,(e)R¼75nm and e¼10nm,and(f)R¼100nm and e¼10nm.The CS parti-cle was illuminated with polarization in the XZ plane.The Au and Si mate-rial dispersion parameters are taken from Ref.21.denotes the particle cross-section area projected onto a plane perpendicular to the incident wave.In the simulations shown in Fig.4,the spectra exhibit two pronounced broad resonan-ces(a lower wavelength resonance with highly asymmetric line shape and a more symmetric higher wavelength reso-nance.PLRs are identified by the maxima in the extinction cross section(Fig.4).Such bimodal resonant structure has been predicted to appear in the far-field optical properties of nanoshells.26,30It has also been recently pointed out31that many PLRs occur in CS ellipsoidal nanorods.More specifi-cally,the plasmon hybridization picture was proposed to describe the optical properties of nanoshells.30The basic idea is that the separate solid sphere and spherical cavity PLRs are coupled,or hybridized,producing a lower wave-length antisymmetric resonance and a higher symmetric res-onance.30A comparative analysis indicates that the peak wavelength and spectral bandwidth of the resonances dis-played in Fig.4can be tuned from the visible to the near-infrared regions by varying the CS aspect ratio e=R.14The analysis of the relative change in intensity across the PLR peak manifold cannot be understood as relating simply to the ratio e=R,1,25i.e.,the asymmetry of these modes can be attributed to phase retardation because of thefinite size of the nanostructure.30A detailed observation shows that the scattering efficiency(/kÀ4)is much smaller(larger)in magnitude compared to the absorption efficiency(/kÀ1)for the higher wavelength(lower wavelength)PLR.This is con-sistent with what has been found in previous boundary ele-ment method,FDTD,and discrete-dipole approximationcalculations.3,14As we are interested in the interplay between the effects of shape anisotropy,polarization of the excitation,and scat-tering efficiencies,the next step is to consider the lower sym-metry CS nanoantennnas with protruding tips shown in Figs. 1(b)and1(c).The cross-sectional areas are defined as G b¼ðR2Àr2Þðtan aÀaÞþp R2and G c¼p l2/8þlpÀ[b ÀpÀ0.5Âsin2b]R2,with b¼a sin(l/2R),respectively,for Figs.1(b)and1(c)nanostructures.The results are,respec-tively,shown in Figs.5and6,where the scattering,absorp-tion,and extinction efficiency spectra are plotted against wavelength for different polarization angles with respect to the Z axis.The asymmetry of the scattering and extinction peaks is noticeable.The scattering and extinction efficiencies generally decrease with larger polarization angle,providing a means for producing differently colored labels in,e.g.,an immunocytology assay.Each spectrum is,of course,unique unto itself but there are overall similarities with those dis-played in Fig.4,which one would like to explain.The lower wavelength resonant mode at wavelength%400nm is very comparable to that of the spherical nanoparticle and is insen-sitive to polarization as one might expect.The higher-wavelength resonant mode(hereinafter denoted sPLR)is very similar to the PLR of the isotropic case Fig.4(b)(which considers very similar values of R and e).Interestingly,we find that its characteristics are very sensitive to the rotation of the electricfield in the XZ plane.An additional resonance (denoted aPLR)appears at wavelength%600nm for nano-structure Fig.4(b)and at wavelength%800for nanostructure Fig.4(c).As can be appreciated in Figs.5and6,changes in the magnitude of the aPLR when the electricfield is rotated correlate to changes in the magnitude of the sPLR.Again this suggests that the aPLR is caused by the intra-particle plasmonic coupling of the low-symmetry tip andthe FIG.5.(Color online)(a)Absorption efficiency C abs/G b,where G b denotes the particle cross-sectional area projected onto a plane perpendicular to the incident wave.The nanostructure considered is shown in Fig.1(b)with geo-metrical parameters set to:R¼50nm,e¼5nm,d¼80nm,r0¼10nm,and 2a¼p=3.The numbers in the plots correspond to the polarization angles of the incident electricfield with respect to the Z axis.(b)Same as in(a)for the scattering efficiency C sca/G b spectrum.(c)Same as in(a)for the extinc-tion efficiency C ext/G b spectrum.The Au and Si material dispersion parame-ters are taken from Ref.21.FIG.6.(Color online)Same as in Fig.5for the nanostructure considered shown in Fig.1(c)with geometrical parameters set to:R¼45nm,e¼5nm, p¼54nm,and‘¼26nm.spherical part of the nanoshell resonance modes.32That the differences in the absorption,scattering,and therefore extinction efficiencies between spherical nanoshells (Fig.4)and CS nanostructures of reduced symmetry (Figs.5and 6)may be rationalized,in terms of the plasmon hybridization mechanism,remains a conjecture.On the experimental side,we stress that recent work by Zia et al .33further developed this conjecture to demonstrate that the PLR of Au nanostar-shaped particles results from the hybridization of plasmons associated with the core and the individual tips of the parti-cle.This nontrivial feature of nanostar structure shows itself through specific angular asymmetries in scattering processes.33The disappearance of the scattering and extinction peaks for the polarization perpendicular (h ¼90 )to the symmetry axis of the CS nanostructure is consistent with this interpretation.This comparative analysis indicates that the aPLR is sensitive to the details of the shell tip geometry of the nanoantenna,i.e.,rounded Fig.4(c)versus sharp Fig.4(b)edge.This naturally brings us to determine the magnitude and spatial distribution of electric field at resonance and off-resonance,i.e.,off-resonance wavelengths correspond to the maximum electric field magnitude conditions.We now address the visualization of the near-field distribution inside and outside the particle by two-dimensional diagrams and the role of shape anisotropy on EFE E 2=E 20map for the nano-structures of Fig.1,where E 0denotes the amplitude of the incident field is investigated further with a different type of simulation.The incident electric field is polarized along the long nanoantenna (Z)axis.Two planes are chosen for these plots,the XY plane and the XZ plane that is perpendicular to the polarization vector.Figure 7shows the values of the nanolocalized EFE at the nanostructure Fig.1(a)’s metallic surfaces when the incident electric field is polarized along the Z axis.Different points on the surface of the nanostruc-tures can have their maximum EFEs at different wave-lengths,i.e.,the wavelength is 417.2nm for the left panel corresponding to the maximum of extinction efficiency,whereas the wavelengths are 882.3nm for the top right map and 535nm for the bottom right map corresponding to the maximum of the electric field magnitude.For all tested wavelengths,the observed EFE in the vicinity of the par-ticles remains relatively small.For comparison,Figs.8and 9illustrate (for nanostructures Figs.1(b)and 1(c),respec-tively)the EFE maps that arise at resonance and off-resonance conditions.For resonance,the largest EFE is about 10.However,by changing the wavelength to off-resonance conditions,it is feasible to achieve EFEs larger than 103,suggesting that the EFEs are distributed over a large spectral range.26The typical distributions of the EFE in these cases show that the energy is extremely confined attheFIG.7.(Color online)Resonance (left panel)and off-resonance (right panel)normalized near-field electric field enhancement (EFE)E 2=E 20map for nanostructure (a)of Fig.1,where E 0denotes the amplitude of the inci-dent field,in the XY and XZ planes,R ¼45nm,and e ¼5nm.The incident electric field is oriented along the Z axis.The wavelength is 417.2nm for the left panel corresponding to the maximum of extinction efficiency,whereas the wavelengths are 882.3nm for the top right map and 535nm for the bottom right map corresponding to the maximum of the electric fieldmagnitude.FIG.8.(Color online)Same as in Fig.7for nanostructure (b)of Fig.1.The wavelength is 438.9nm for the left panel corresponding to the maximum of extinction efficiency,whereas the wavelengths are 736.4nm for the top right map and 598nm for the bottom right map corresponding to the maximum of the electric fieldmagnitude.FIG.9.(Color online)Same as in Fig.7for nanostructure (c)of Fig.1.The wavelength is 418.3nm for the left panel corresponding to the maximum of extinction efficiency,whereas the wavelengths are 788.5nm for the top right map and 832.7nm for the bottom right map corresponding to the maximum of the electric field magnitude.vicinity of the metal coating.What we wish to point out now is that the results in Figs.8and9show that,in the XZ plane, the exciting electricfield is enhanced by a factor that is larger than the Q factor of the resonant mode at wavelength %400nm,Q%4.25–34IV.SUMMARYIn summary,the systematic numerical simulation of the scattering and extinction spectra of several low-symmetry CS nanostructures with subwavelength dimensions suggest that the interrelation between nanoparticle size and polariza-tion of the excitation gives rise to complex resonance phe-nomena.In addition to providing a potential means to extract the wavelength dependence of the scattering and absorption behaviors at resonance,our results raise interesting theoreti-cal questions regarding the control of the light emission at the nanoscale,and the impact of geometry on the scattering and extinction of plasmonic CS nanoparticles having sharp corners.We showed that our composite plasmonic nano-structures demonstrate strong enhancements of the exciting electricfielding nonlocalized spots.The broader implication of this work is that advances in modeling the absorption of plasmonic CS nanoantennas pro-vides an effective means in the design of non-invasive high-resolution biosensors for the characterization and diagnostics of living tissue.33–361S.A.Maier,Plasmonics:Fundamentals and Applications(Springer,New York,2007).2G. C.Schatz and R.P.van Duyne,Electromagnetic Mechanism of Surface-Enhanced Spectroscopy,in Handbook of Vibrational Spectroscopy, edited by J.M.Chalmers and P.R.Griffiths(Wiley,Chichester,2002).3V.Myroshnychenko,J.Rodrı´guez-Ferna´ndez,I.Pastoriza-Santos,A.M. Funston,C.Novo,P.Mulvaney,L.M.Liz-Marza´n,and F.Javier Garcia de Abajo,Chem.Soc.Rev.37,1792(2008).4E.Ozbay,Science311,189(2006);P.Mulvaney,Langmuir12,788 (1996);E.Hutter and J.H.Fendler,Adv.Mater.16,1685(2004).5K.Li,M.I.Stockman,and D.J.Bergman,Phys.Rev.Lett.91,227402 (2003);K.Li,M.I.Stockman,and D.J.Bergman,Phys.Rev.Lett.91, 227402(2003).6M.Essone Mezeme,squellec,and C.Brosseau,“Design of magneto-plasmonic resonant nanoantennas for biosensing applications”(unpublished). 7A.Aubry,D.Y.Lei,S.A.Meir,and J.B.Pendry,Phys.Rev.Lett.105, 233901(2010).8P.Spineli,C.van Lare,E.Verhagen,and A.Polman,Opt.Express19, A303(2011).9J.M.Pitarke,F.J.Garcı´a-Vidal,and J.B.Pendry,Phys.Rev.B57,15261 (1998);J.M.Pitarke,F.J.Garcı´a-Vidal,and J.B.Pendry,Surf.Sci.433, 605(1999).10P.Bharadwaj,B.Deutsch,and L.Novotny,Adv.Opt.Photon.1,438 (2009);Y.Saito and P.Verma,Eur.Phys.J.Appl.Phys.46,20101 (2009);A.I.Denisyuk,G.Adamo,K.F.MacDonald,J.Edgar,M.D. Arnold,V.Myroshnychenko,M.J.Ford,F.Javier Garcia de Abajo,and N.I.Zheludev,Nano Lett.10,3250(2010).11P.Mu¨hlschlegel,H.-J.Eisler,O.J.F.Martin,D.W.Pohl,and B.Hecht, Science308,1607(2005).12A.Kinkhabwala,Z.F.Yu,S.H.Fan,Y.Avlasevich,K.Mullen,and W.E. Moerner,Nat.Photonics3,654(2009).13B.Rothenhausler and W.Knoll,Nature(London)332,615(1988);D.P. O’Neal,L.R.Hirsch,N.J.Halas,J.D.Payne,and J.L.West,Cancer Lett. 209,171(2004);B.Radt,T.A.Smith,and F.Caruso,Adv.Mater.16, 2184(2004);I.-H.El-Sayed,X.Huang,and M.A.El-Sayed,Nano Lett.5, 829(2005);Y.Lu,G.L.Liu,J.Kim,Y.X.Mejia,and L.P.Lee,ibid.5, 119(2005).14C.L.Nehl,H.W.Liao,and J.H.Hafner,Nano Lett.6,683(2006);F.Hao,C.L.Nehl,J.H.Hafner,and P.Nordlander,ibid.7,729(2007); W.Challener,I.Sendur,and C.Peng,Opt.Express11,3160(2003);L.M. Liz-Marza´n,Langmuir22,32(2006);F.Hao,C.L.Nehl,J.H.Hafner, and P.Nordlander,Nano Lett.7,729(2007);F.J.Garcia de Abajo and A.Howie,Phys.Rev.Lett.80,5180(1998).15M.Essone Mezeme,squellec,and C.Brosseau,J.Appl.Phys.109, 014302(2011).16J.Kim,S.Park,J.E.Lee,S.M.Jin,J.H.Lee,I.S.Lee,I.Yang,J.S. Kim,S.H.Kim,M.-H.Cho,and T.Hyeon,Angew.Chem.,Int.Ed.45, 7754(2006).17M.Essone Mezeme,squellec,and C.Brosseau,Phys.Rev.E81, 057602(2010);M.Essone Mezeme,squellec,and C.Brosseau, J.Appl.Phys.107,014701(2010);M.Essone Mezeme,squellec,and C.Brosseau,J.Phys.D42,135420(2009);C.Charnay,A.Lee,S.-Q. Man,C.E.Moran,C.Radloff,R.K.Bradley,and N.J.Halas,J.Phys. Chem.B107,7327(2003).18Commercial software package FDTD Solutions-Lumerical Inc.,see http:// .19A.Mejdoubi and C.Brosseau,J.Appl.Phys.99,063502(2006);A.Mej-doubi and C.Brosseau,Phys.Rev.B74,165424(2006);A.Taflove,Com-putational Electrodynamics:The Finite-Difference Time-Domain Method (Artech House,Norwood,1995).20See /fdtd_online_helpprevious_help/user_gui-de_tfsf-source.php for help and user guide.21C.F.Bohren and D.R.Huffman,Absorption and Scattering of Light by Small Particles(Wiley,New York,1983);E.D.Palik,Handbook of Opti-cal Constants of Solids(Academic,San Diego,1998);P.B.Johnson and R.W.Christy,Phys.Rev.B6,4370(1972).22J.Zuloaga,E.Prodan,and P.Nordlander,Nano Lett.9,887(2009);J.M. McMahon,S.K.Gray,and G.C.Schatz,Nano Lett.10,3473(2010).23R.Fuchs and F.Claro,Phys.Rev.B35,3722(1987).24COMSOL MULTIPHYSICS,version3.4,2007,see sol. com.25J.P.Kottman,O.J.F.Martin,D.R.Smith,and S.Schultz,Opt.Express6, 213(2000).26N.K.Grady,N.J.Halas,and P.Nordlander,Chem.Phys.Lett.399,167 (2004);A.Sihvola,Prog.Electromagn.Res.62,317(2006);Z.Jian and Z. Caili,J.Appl.Phys.100,026104(2006).27B.Yan,Y.Yang,and Y.Wang,J.Phys.Chem.B107,9159(2003).28S.Link and M.A.El-Sayed,J.Phys.Chem.B109,10531(2005).29E.S.Kooij and B.Poelsema,Phys.Chem.Chem.Phys.8,3349(2006). 30E.Prodan,C.Radloff,N.J.Halas,and P.Nordlander,Science302,419 (2003);H.Wang,D.W.Brandl,P.Nordlander,and N.J.Halas,Acc. Chem.Res.40,53(2007);F.Hao,C.L.Nehl,J.H.Hafner,and P.Nord-lander,Nano Lett.7,729(2007).31J.Zhu,J.Nanosci.Nanotechnol.7,1059(2007).32J.Kim,G.L.Liu,Y.Lu,and L.P.Lee,Opt.Express13,8332(2005).33R.Zia,J.A.Schuler,A.Chandran,and M.L.Brongersma,Mater.Today 9,20(2006).34T.Werne,M.Testorf,and U.Gibson,J.Opt.Soc.Am.23,2299(2006). 35B.Alberts et al.,Molecular Biology of the Cell(Garland,New York, 2008),4th ed;B.Hille,Ion Channels of Excitable Membranes(Sinauer Associates,Sunderland,MA,2001).36P.J.Hunter,W.W.Li,A.D.McCulloch,and D.Noble,Computer39,48 (2006).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1< p < 2
3、Implementation of PDE models in the COMOSL Multiphysics
Add Physics
Import the initial image
Draw the image domain Set the coefficient、 boundary and initial values Mesh
Add noise
Fig 2 original interferogram
Fig 3 noise interferogram
Fig 4 linear diffusion result
Fig 5 PM model result
Fig 6 TV model result
Coupled PDE model in image processing
1、Introduction
• Subject background
Fig 1 Experimental interferogram
• The interferogram from the Interferometric Synthetic Aperture Sonar (InSAS) has much noise because of the sonar shadow、water environment、under Sampling etc. The noise will make the following phase unwrapping become very difficult. So it is important for InSAS to denoise the interferogram effectively.
• 1、Introduction
• 2、PDE models in image processing • 3、Implementation of PDE models in the COMSOL Multiphysics • 4、Experimental results and data analysis • 5、Conclusion and outlook
2、PDE models in image processing
• 2.1 The general form of PDE in image processing
⎧ ∂u 2 t , x + F x , u t , x , ∇ u t , x , ∇ 在 ( 0, T ) × Ω上, ( ) ( ) ( ) ( x x u ( t , x ) ) = 0, ⎪ ∂t ⎪ ⎪ ∂u 在 ( 0, T ) × Ω上, ⎨ ( t , x ) |∂Ω = 0, ⎪ ∂n ⎪u ( 0, x ) = u0 ( x ) , 在Ω内, ⎪ ⎩ • Where Ω ⊂ R2is the image domain, ∂Ω is the boundary Ω of of is the initial F ∂Ω u n , is unit normal vector 0 ( x) ,
2 ⎧ ∂u ⎪ ∂t = ∇ ⋅ c ∇u ∇u , ⎪ ⎪ ∂u ⎨ |∂Ω = 0, ⎪ ∂n ⎪u ( 0, x ) = u0 ( x ) , ⎪ ⎩
(( ) )
在 ( 0,T ) × Ω内, 在 ( 0,T ) × ∂Ω上, 在Ω内,
• It is a an anisotropy diffusion equation. Where c ∇u is a diffusion function depended on the image gradient. P-M model can denoise and preserve edges well by defining the diffusion function suitably.
the edge function defined as gk (s) = 1 1 + s 2 k 2 . • It is a coupled PDE model, which can preserve the image edges well when the image gradient ∇u changes a lot.
5、Conclusion and outlook
• Conclusion
• This paper introduces the basic ideas and theoretical frame of image processing based on PDE, presents the idea of the application of COMSOL Multiphysics in image processing. • The simulated and real lake experimental interferogram was denoised by the PDE models which are implemented in the COMSOL Multiphysics.The experimental results indicate that COMSOL Multiphysics is able to provide a new finite element simulation platform for image processing.
Ideas of this paper
• PDE is an important tool in image processing. COMSOL Multiphysics builds the models based on PDE,it is easy to define and solve the coupled problem of any physical field. • However, it has not the image processing module so far. So the idea is that COMSOL Multiphysics can be a new platform for image processing.
image. It can denoise the interferogram, however, it can not preserve the edges of image.
PDE models in image processing
• 2.3 Perona-Malik model in image processing
(
)
• Where λ is the lagrange multiplier depended on noise level. The model can overcome the staircase effect as long as we choose the proper p .
1 λ p 2 min J p ( u ) = ∫ ∇u dxdy + ∫ u − u0 dxdy, u pΩ 2Ω
• Coupled PDE model in image processing
∇u ⎧ ∂ u = α g ( ∇ v ) ∇ u div ( ) + α∇( g k ( ∇v )) ⋅∇u − β (u − I ) ∇u k ⎪ t ∇u ⎪ ⎪ ∇v ) − b (v − u ) ⎨∂ t v = a (t )div( ∇v ⎪ ⎪u ( x, y, 0) = u ( x, y ), v( x, y, 0) = u ( x, y ) 0 0 ⎪ ⎩ • Where I , u0 ( x, y ) are all the original noise image, g k ( s ) is
2s
5s
Fig 8 experimental interferogram
Fig 9 2s Coupled model filter result
Fig 10 5s Coupled model filter result
Table 1 Data analysis of the denoising results Interferogram data Lake experiment interferogram Solve time 0s 2s 5s Residues 1834 36 12
(
)
Experimental results and analysis
• The interferogram obtained by the InSAS lake experiment is denoised by Coupled PDE model which is built on the COMSOL Multiphysics, the experimental results and data analysis is
2011年中国区用户年会
Application of COMSOL in Image Processing
Speaker:Wang Maolin Supervisor:Yue Jun Qingdao Technological University October 18, 2011,Beijing
The outline of the report
(
2age processing
• 2.4 TV model in image processing p−2 ⎧ ∂u 2 t , x = ∇ ⋅ ∇ u ∇ u + λ u − u , t ≥ 0, x = x , x ∈ R , ( ) ( ) ( ) 0 1 2 ⎪ ∂t ⎪ ⎪ ∂u 在 ( 0,T ) × ∂Ω上, ⎨ ( t , x ) |∂Ω = 0, ⎪ ∂n ⎪u ( 0, x ) = u0 ( x ), 在Ω内, ⎪ ⎩ • It is obtained by minimize the following function
