2019学年湖北省广水市九年级下学期第一次月考数学试卷【含答案及解析】
湖北初三初中数学月考试卷带答案解析

湖北初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、单选题1.下列方程是一元二次方程的是( ) A .B .C .D .2.如果关于x 的方程有实数根α、β,那么α+β的取值范围是( )A .α+β≥1B .α+β≤1C .α+β≥D .α+β≤3.若函数的图象与x 轴只有一个交点,那么m 的值为( ) A .0B .0或2C .2或-2D .0、2或-24.若二次函数的图象过点A (-1,y 1)、B(2,y 2)、C (5,y 3)三点,则y 1、y 2、y 3的大小关系是( ) A .y 1>y 2>y 3B .y 1>y 3>y 2C .y 2>y 1>y 3D .y 3>y 1>y 25.在平面直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( ) A .(4,-3) B .(-4,3) C .(0,-3) D .(0,3)6.若关于x 的一元二次方程(x -2)(x -3)=a 有实数根x 1、x 2,且x 1≠x 2,有下列结论:①x 1=2,x 2=3 ②a >-③二次函数的图象与x 轴交点坐标为(2,0),(3,0),其中正确的结论的个数是( ) A .0个B .1个C .2个D .3个7.如图,在⊙O 中,,∠AOB =50°,则∠ADC 的度数是( )A .50°B .40°C .30°D .25°8.如图,Rt △ABC 中,∠C =90°,AC =3cm ,BC =4cm ,则它的内切圆半径为( )A .1cmB .2cmC .3cmD .4cm9.在如图的网格图中,每个小正方形的边长均为1,△ABC 的三个顶点都是网格线的交点,已知B 、C 两点坐标分别为(-1,-1),(1,-2),将△ABC 绕点C 顺时针旋转90°,则A 点的对应点坐标为( )A. (4,1)B. (4,-1)C. (5,1)D. (5,-1) 10.如图,△AOB 为等腰三角形,顶点A 的坐标为(2,),底边OB 在x 轴上,将△AOB 绕点B 按顺时针方向旋转一定角度后得△A’O’B ,点A 的对应点A’在x 轴上,则点O’的坐标为( )A .B .C .D .二、填空题1.关于x 的一元二次方程的两实根分别为2和b ,则ab =____。
2019届九年级下学期第一次月考数学试题(附答案)(2)

2018~2019学年度第二学期第1次月度联考九 年 级 数 学 试 题(考试时间:120分钟,满分:150分)一.选择题 (每小题3分,共18分)1.抛物线y =x 2+3与y 轴的交点坐标为( ) A .(3,0)B .(0,3)C .(0,)D .(,0)2.在Rt △ABC 中,∠C =90°,如果AC =4,BC =3,那么∠A 的正切值为( ) A .B .C .D .3.有15位学生参加学校组织的“爱我中华”演讲比赛,比赛结束后根据每位学生的最后得分计算出平均数、中位数、众数、方差.如果修改规则:先去掉一个最高分,去掉一个最低分,再进行统计,则上述四个统计量中,一定不会发生变化的是( ) A .平均数B .中位数C .众数D .方差4.在一个不透明的盒子里有3个红球和若干个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到红球的概率是,则白球的个数是( ) A .3B .4C .6D .95.如图,∠APD =90°,AP =PB =BC =CD ,则下列结论成立的是( )A .△P AB ∽△PCA B .△ABC ∽△DBAC .△P AB ∽△PDAD .△ABC ∽△DCA6.如图,分别过点P i (i ,0)(i =1、2、…、n )作x 轴的垂线,交221x y =的图象于点A i ,交直线x y 21-=于点B i .则n n B A B A B A 1112111+++ 的值为( ) A .12+n nB .2C .)1(2+n nD .12+n第5题 第6题 第8题二.填空题( (每小题3分,共30分) 7.小明沿坡比为1:的山坡向上走了100米.那么他升高了 米.8.如图,四边形ABCD 内接于⊙O ,AB 为⊙O 的直径,C 为弧BD 的中点,若∠DAB =40°,则∠ADC = .9.某地区2017年投入教育经费2500万元,2019年计划投入教育经费3025万元.则2017年至2019年,该地区投入教育经费的年平均增长率为 .10.若一个扇形的半径是18cm ,且它的弧长是12πcm ,则此扇形的圆心角等于 °. 11.已知一组数据6,6,5,x ,1,请你给正整数x 一个值 ,使这组数据的众数为6,中位数为5.12.小丽同学今年在六次数学考试中的成绩分别是:117,118,120,116,118,119,则她这六次考试成绩的方差是 .13.随着北京申办冬奥会的成功,愈来愈多的同学开始关注我国的冰雪体育项目.小健从新闻中了解到:在2018年平昌冬奥会的短道速滑男子500米决赛中,中国选手武大靖以39秒584的成绩打破世界纪录,收获中国男子短道速滑队在冬奥会上的首枚金牌.同年11月12日,武大靖又以39秒505的成绩再破世界纪录.于是小健对同学们说:“2022年北京冬奥会上武大靖再获金牌的可能性大小是100%.”你认为小健的说法 (填“合理”或“不合理”),理由是 . 14.如图,双曲线xky =与抛物线y =ax 2+bx +c 交于点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),由图象可得不等式组c bx ax xk++20的解集为 .第14题 第15题 第16题15.如图,点G 为△ABC 的重心,连接AG 、BG 并延长,分别交BC 、AC 于点D 、E ,过点E 作EF ∥BC 交AD 于点F ,那么AF :AG = .16.如图,正方形ABCD 的对角线相交于点O ,正方形OEFG 的一边OG 经过点D ,且D是OG 的中点,OG =AB ,若正方形ABCD 固定,将正方形OEFG 绕O 点逆时针旋转α角,(0°<α<360°)得到正方形OE ′F ′G ′,当α= 度时,∠OAG ′=90°. 三.解答题(本大题共10小题,共102分)17.(12分)⑴计算:2cos60°+4sin60°•tan30°﹣6cos 245°.⑵已知:线段a 、b 、c ,且432cb a ==.a +b +c =27,求a ﹣b +c 的值.18.(8分)已知抛物线y =2x 2﹣4x ﹣6.⑴请用配方法求出顶点的坐标;⑵如果该抛物线沿x 轴向左平移m (m >0)个单位后经过原点,求m 的值.19.(8分)小明周末要乘坐公交车到植物园游玩,从地图上查找路线发现,几条线路都需要换乘一次.在出发站点可选择空调车A 、空调车B 、普通车a ,换乘站点可选择空调车C ,普通车b 、普通车c ,且均在同一站点换乘.空调车投币2元,普通车投币1元. ⑴求小明在出发站点乘坐空调车的概率; ⑵求小明到达植物园恰好花费3元公交费的概率.20.(8分)某校课程中心为了了解学生对开设的3D 打印、木工制作、机器人和电脑编程四门课程的喜爱程度,随机调查了部分学生,每人只能选一项最喜爱的课程.图①是四门课程最喜爱人数的扇形统计图,图②是四门课程男、女生最喜爱人数的条形统计图.⑴求图①中m 的值,补全图②中的条形统计图,标上相应的人数; ⑵若该校共有1800名学生,则该校最喜爱3D 打印课程的学生约有多少人?21.(10分)如图,已知直线AC 与⊙O 相交于点C ,直线AO 与⊙O 相交于D ,B 两点. 已知∠ACD =∠B .⑴求证:AC 是⊙O 的切线;⑵若AC=6,AD=4,求⊙O的半径;22.(10分)如图,一块材料的形状是锐角三角形ABC,边BC长120mm,高AD为80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.⑴图中与△ABC相似的三角形是,说明理由;⑵这个正方形零件的边长为多少?23.(10分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡AF 上的D处测得大树顶端B的仰角是30°,在地面上A处测得大树顶端B的仰角是45°.若坡角∠F AE=30°,AD=6m,求大树的高度.(结果保留整数,参考数据:≈1.73)24.(10分)如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴相交于原点O 和点B(4,0),点A(3,m)在抛物线上.⑴求抛物线的表达式,并写出它的对称轴;⑵求tan∠OAB的值.25.(12分)如图,在矩形ABCD中,AC为对角线,点P为BC边上一动点,连接AP,过点B作BQ⊥AP,垂足为Q,连接CQ.⑴证明:△ABP∽△BQP;⑵当点P为BC的中点时,若∠BAC=37°,求∠CQP的度数;⑶当点P运动到与点C重合时,延长BQ交CD于点F,若AQ=AD,则=.26.(14分)在平面直角坐标系中,已知二次函数y=ax2﹣2ax﹣3a(a>0)图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为D.⑴求点A,B的坐标;⑵若M为对称轴与x轴交点,且DM=2AM,①求二次函数解析式;②当t﹣2≤x≤t时,二次函数有最大值5,求t值;③若直线x=4与此抛物线交于点E,将抛物线在C,E之间的部分记为图象记为图象P(含C,E两点),将图象P沿直线x=4翻折,得到图象Q,又过点(10,﹣4)的直线y=kx+b与图象P,图象Q都相交,且只有两个交点,求b的取值范围.2018~2019学年度第二学期第1次月度联考九年级数学参考答案与试题解析一.选择题1.B.2.A.3.B.4.C.5.B.6.A.二.填空题7.50.8.110°.9.10%.10.120.11.2.12..13.不合理,2022年北京冬奥会上武大靖再获金牌属于随机事件.14.x2<x<x3.15.3:4.16.解:当α为锐角时,如图1所示:∵四边形ABCD是正方形,∴BC=AB,∠ABC=90°,OA=OD=AC,∴AC=AB,∵OG=AB,∴OG′=OG=AC=2AO,∵∠OAG′=90°,OA=OG′,∴∠AG′O=30°,∴∠AOG′=60°,∴∠DOG′=90°﹣60°=30°,即α=30°;当旋转到如图2所示位置,同理证得∠AG′O=30°,∴∠AOG′=60°,∴α=90°+60°=150°,综上所述:α的度数为30°或150°,故答案为:30°或150°.三.解答题17.(1)解:原式=2×+4××﹣6×()2=1+2﹣3 =0.(2)设===k,则a=2k,b=3k,c=4k,∵a+b+c=27,∴2k+3k+4k=27,∴k=3,∴a=6,b=9,c=12,∴a﹣b+c=6﹣9+12=9.18.解:(1)y=2x2﹣4x﹣6 =2(x2﹣2x)﹣6 =2(x﹣1)2﹣8,故该函数的顶点坐标为:(1,﹣8);(2)当y=0时,0=2(x﹣1)2﹣8,解得:x1=﹣1,x2=3,即图象与x轴的交点坐标为:(﹣1,0),(3,0),故该抛物线沿x轴向左平移3个单位后经过原点,即m=3.19.解:(1)∵在出发站点可选择空调车A、空调车B、普通车a,∴小明在出发站点乘坐空调车的概率为:;(2)如图所示:,一共有9种组合,只有Ab,Ac,Bb,Bc,aC组合恰好花费3元,故小明到达植物园恰好花费3元公交费的概率为:.20.解:(1)调查的人数为:(20+22)÷35%=120(人),∴机器人一项所占的百分比m%=×100%=30%,∴m=30,∵木工制作一项的人数为:15%×120=18(人),∴女生选择木工制作的人数为18﹣9=9(人),∵电脑编辑一项的人数为:20%×120=24(人),∴女生选择电脑编辑的人数为24﹣14=10(人),条形统计图如图所示:(2)1800×35%=630(人),答:该校最喜爱3D打印课程的学生约有630人.直接反映部分占总体的百分比大小.21.(1)证明:连接OC,∵OC=OB,∴∠BCO=∠B,∵DB是⊙O直径,∴∠DCB=90°,∴∠DCO+∠BCO=∠DCO+∠B=90°,∵∠ACD=∠B.∴∠DCO+∠ACD=∠ACO=90°,∴AC是⊙O的切线;(2)解:∵∠ACD=∠B,∵∠A=∠A,∴△ACD∽△ABC,∴=,∴62 =4×(4+DB),∴DB=5,∴⊙O的半径是.22.解:(Ⅰ)∵正方形EGHF,∴EF∥BC,∴△AEF∽△ABC,故答案为:△AEF;(Ⅱ)设EG=EF=x∵△AEF∽△ABC ∴=,∴=,∴x=48,∴正方形零件的边长为48mm.23.解:延长BD交AE于点G,作DH⊥AE于H,设BC=xm,由题意得,∠DGA=∠DAG=30°,∴DG=AD=6,∴DH=3,GH==3,∴GA=6,在Rt△BGC中,tan∠BGC=,∴CG==x,在Rt△BAC中,∠BAC=45°,∴AC=BC=x,由题意得,x﹣x=6,解得,x=≈14,答:大树的高度约为14m.24.解:(1)把点O(0,0),点B(4,0)分别代入y=﹣x2+bx+c得:,解得:,即抛物线的表达式为:y=﹣x2+4x,它的对称轴为:x=﹣=2,(2)把点A(3,m)代入y=﹣x2+4x得:m=﹣32+4×3=3,即点A的坐标为:(3,3),过点B作BD⊥OA,交OA于点D,过点A作AE⊥OB,交OB于点E,如下图所示,AE=3,OE=3,BE=4﹣3=1,OA==3,AB==,S△OAB=×OB×AE=×OA×BD,BD===2,AD==,tan∠OAB==2.25.(1)证明:∵四边形ABCD是矩形,∴∠ABP=90°,∵BQ⊥AP,∴∠BQP=∠ABP=90°,∵∠BPQ=∠APB,∴△ABP∽△BQP.(2)解:∵△ABP∽△BQP,∴=,∴PB2=PQ•P A,∵PB=PC,∴PC2=PQ•P A,∴=,∵∠CPQ=∠APC,∴△CPQ∽△APC,∴∠PQC=∠ACP,∵∠BAC=37°,∴∠ACB=90°﹣37°=53°,∴∠CQP=53°.(3)解:连接AF.∵∠D=∠AQF=90°,AF=AF,AD=AQ,∴Rt△ADF≌Rt△AQF(HL),∴DF=QF,设AD=AQ=BC=m,DF=FQ=x,FC=y,CQ=a,∵∠BCF=∠CQB=∠CQF=90°,∴∠BCQ+∠FCQ=90°,∠∠CBQ=90°,∴∠FCQ=∠CBQ,∴△BCQ∽△CFQ,∴=,∴=,∴=,∵CF∥AB,∴=,∴=,∴=,∴x2+xy﹣y2=0,∴x=y或y(舍弃),∴=,∴=.故答案为.26.解:(1)令y=0,即:ax2﹣2ax﹣3a=0,解得:x=﹣1或3,即点A、B的坐标分别为(﹣1,0)、(3,0),函数的对称轴x=﹣=1;(2)①DM=2AM=4,即点D的坐标为(1,﹣4),将点D的坐标代入二次函数表达式得:﹣4=a﹣2a﹣3a,解得:a=1,即函数的表达式为:y=x2﹣2x﹣3;②当x=t和x=t﹣2在对称轴右侧时,函数在x=t处,取得最大值,即:t2﹣2t﹣3=5,解得:t=﹣2或4(舍去t=﹣2),即t=4;同理当x=t和x=t﹣2在对称轴左侧或两侧时,解得:t=0,故:t值为0或4;③如下图所示,直线m、l、n都是直线y=kx+b与图象P、Q都相交,且只有两个交点的临界点,点E、R、C′坐标分别为(4,5)、(10,﹣4)、(8,﹣3),直线l的表达式:把点E、R的坐标代入直线y=kx+b得:,解得:,同理可得直线m的表达式为:y =﹣x﹣1,直线n的表达式为:y=﹣4,故:b的取值范围为:﹣1≤b≤11或b=﹣4.。
湖北初三初中数学月考试卷带答案解析

湖北初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.下列方程是一元二次方程的是()A.B.C.D.2.一元二次方程化成一般形式后,若a="2" ,则b,c的值是()A.b=3;c=5B.b=;c=5C.b=;c=D.b=3;c=3.抛物线的顶点在()A.第一象限B.第二象限C.x轴上D.y轴上4.用配方法解一元二次方程+8x+7=0,则方程可变形为()A.=9B.=9C.=16D.="57"5.方程(a≠0)有实数根,那么总成立的式子是()A.>0B.<0C.≥0D.≤06.二次函数,当k取不同的实数值时,图像顶点所在的直线是()A.B.x轴C.D.y轴7.下列方程中两根互为倒数有()A.0个B.1个C.2个D.3个8.把抛物线向右平移一个单位,再向上平移3个单位,得到抛物线的解析式为()A.B.C.D.9.在同一直角坐标系中,一次函数和二次函数的图像是()A.B.C.D.10.已知a,b为实数,,则代数式的值为()A.2B.3C.D.3或二、填空题1.方程:的解是。
2.已知方程的一根是1,.则另一根为,k的值为。
3.抛物线的对称轴是直线,顶点坐标为。
4.若关于x的一元二次方程的一个根是1,且a,b满足,则c= 。
5.关于x的方程有根为0,则a的值 .6.已知二次函数,若当x取,(≠)时,函数值相等,则当x取+时,函数值为 .7.若关于x的一元二次方程的两根为a,b,且满足,则m= .8.已知α,β是方程的两实根,则的值为 .三、解答题1.解方程(10分)(1)、(2)、(x+3)(x-6)=2.已知二次函数当x=时,有最大值,且当x=0时,y= ,求二次函数的解析式。
3.如图,抛物线与x轴交于A,B两点,与直线相交于B,C两点,连结A,C两点。
(1)写出直线BC的解析式(2)求△ABC的面积4.关于x的一元二次方程有实根.(1)求a的最大整数值;(2)当a取最大整数值时,①求出该方程的根;②求的值.5.关于x的方程有实数根.(1)求k的取值范围.(2)若是方程的两个实数根,且满足,求k.6.已知抛物线与y轴交于点C,与x轴交于A(,0),B(,0),(<)两点,顶点M的纵坐标为,若,是方程的两根,且。
湖北初三初中数学月考试卷带答案解析

湖北初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.下列计算正确的是 ( ) A .B .C .D .2.下列成语所描述的事件是必然事件的是 ( ) A .水中捞月 B .拔苗助长C .守株待兔D .瓮中捉鳖3.有六张背面相同的卡片, 其正面分别画有六个不同的几何图形, 如图, 现将这六张卡片背面朝上洗匀后随机摸取一张, 则摸出的卡片中的图形既是轴对称图形, 又是中心对称图形的概率为 ( )A .B .C .D .4.已知A (,y 1),B (2,y 2),C (-,y 3)是二次函数y=3(x -1)2+k 图象上三点,则y 1、y 2、y 3的大小关系为 ( ) A .y 1>y 2>y 3 B .y -2>y 1>y 3C .y 3>y 2>y 1D .y 2>y 3>y 15.已知实数x 满足(x 2-x )2-4(x 2-x )-12=0,则x 2-x=________ ( ) A .-2 B .6或-2 C .6D .36.如图, 15个外径为1m 的钢管以如图方式堆放, 为了防雨, 需要搭建防雨棚的高度最低应为_______m. ( )A .2+1B .C .5D .2+27.如图,△ABC 内接于⊙O ,∠B=60º,∠A=40º,半径OE ⊥AB ,连接CE ,则∠E=( )A .5ºB .10ºC .15ºD .20º8.如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是:()①DE是⊙O的切线;②直径AB长为20cm;③弦AC长为15cm;④C为弧AD的中点.A. ①②④B.①③④C. ①②D.②③二、填空题1.代数式中,字母x的取值范围是_____________.2.函数的图像与x轴交于A、B,顶点为M,则S△ABM =_________.3.若两圆的圆心距为5,半径分别是方程的两根,则这两圆的位置关系___________.4.若函数的部分图象如图所示,由图可知,关于x的方程的一根是3,则另一根为________.5.一个均匀的立方体骰子六个面上分别标有数1、2、3、4、5、6,连续两次掷骰子,朝上一面所标的数依次为m和n,则关于x的一元二次方程没有实数根的概率为__________.6.如图,矩形ABCD的周长是20,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68,那么矩形ABCD的面积是________.7.如图,⊙P与两坐标轴分别交于点A(-2、0)、B(-6、0)、C(0、-3)和点D,双曲线过点P,则k=_______.8.如图,二次函数的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴。
湖北初三初中数学月考试卷带答案解析
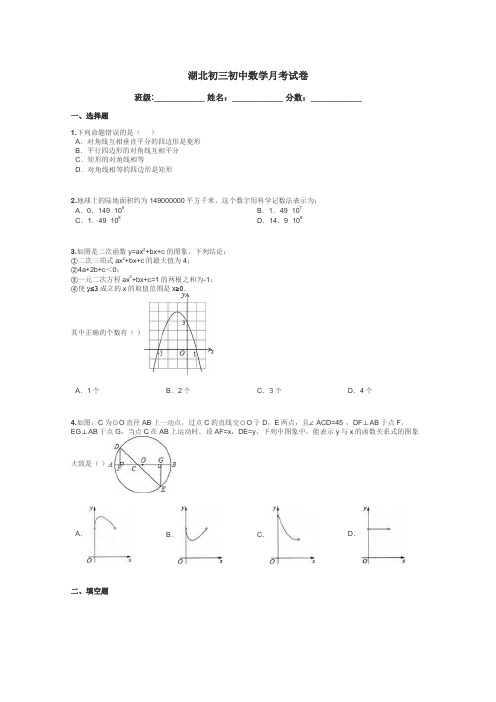
湖北初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.下列命题错误的是()A.对角线互相垂直平分的四边形是菱形B.平行四边形的对角线互相平分C.矩形的对角线相等D.对角线相等的四边形是矩形2.地球上的陆地面积约为149000000平方千米,这个数字用科学记数法表示为:A.0.149×106B.1.49×107C.1.49×108D.14.9×1083.如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为-1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数有()A.1个B.2个C.3个D.4个4.如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D,E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时.设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是()A.B.C.D.二、填空题1.小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有人.2.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为.3.已知关于x的一元二次方程x2+ax+b=0有一个非零根﹣b,则a﹣b的值为_________4.分解因式:a3﹣4a2+4a = _____________三、解答题1.如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)2.已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=OB.(1)求证:AB是⊙O的切线;(2)若∠ACD=45°,OC=2,求弦CD的长.四、单选题1.实数﹣17的相反数是()A.17B.C.﹣17D.﹣2.在初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是()A.平均数为160B.中位数为158C.众数为158D.方差为20.33.如图,AB 是⊙O 的直径,AB =15,AC =9,则tan ∠ADC = ( )A .B .C .D .4.如图所示的几何体的俯视图是( )A .B .C .D .五、判断题1.计算:2.先化简,再求值:,其中。
湖北初三初中数学月考试卷带答案解析

湖北初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是()A.凌晨4时气温最低为﹣3℃B.14时气温最高为8℃C.从0时至14时,气温随时间增长而上升D.从14时至24时,气温随时间增长而下降2.下列说法中正确的是()A.“任意画出一个等边三角形,它是轴对称图形”是随机事件B.“任意画出一个平行四边形,它是中心对称图形”是必然事件C.“概率为0.0001的事件”是不可能事件D.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次3.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为()A.50°B.80°C.100°D.130°二、解答题(12分)如图,在平面直角坐标系中,已知抛物线的对称轴为,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.(1)求抛物线的解析式;(2)填空:①用含m的式子表示点C,D的坐标:C(,),D(,);②当m= 时,△ACD的周长最小;(3)若△ACD为等腰三角形,求出所有符合条件的点P的坐标.三、填空题1.关于x的一元二次方程x2-2x=0有两个相等的实数根,则m的值为。
2.王经理到襄阳出差带回襄阳特产——孔明菜若干袋,分给朋友们品尝.如果每人分5袋,还余3袋;如果每人分6袋,还差3袋,则王经理带回孔明菜袋.3.如图,正方形ABCD的边长为2,对角线AC,BD相交于点0,E是OC的中点。
连接BE,过点A作AM⊥BE于点M交BD于点F则FM的长为.4.分解因式:a2-1=______________5.为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一组标杆、皮尺,设计了如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E同一直线上,此同学眼睛距地面1.6m标杆长为3.3 m且BC=1 m,CD=4 m,则ED=__________四、单选题1.-2的绝对值是()A.2B.-2C.D.2.中国人口众多、地大物博,仅领水面积就约为370 000 km2,将370 000这个数用科学记数法表示为()A.3.7×106B.3.7×105C.37×104D.3.7×1043.下列运算中正确的是()A.a3-a2=a B.a3·a4=a12C.a6÷a2=a3D.(-a2)3=-a64.如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点为位似中心,相似比为1∶3,在第一象限内把线段AB缩小得到线段CD,则C的坐标为()A.(2,1)B.(2,0)C.(3,3)D.(3,1)5.三角形ABC的三边长分别为6 cm、7.5 cm、9 cm,三角形DEF的一边长为4 cm.当三角形DEF的另两边长是下列哪一组时,这两个三角形相似()A.2 cm、3 cm B.4 cm、5 cm C.5 cm、6 cm D.6 cm、7 cm6.如图,以点A(1,)为圆心的⊙A交y轴正半轴于B、C两点,且,点D是⊙A上第一象限内的一点,连接OD、CD.若OD与⊙A相切,则CD的长为()A.B.C.D.五、判断题1.解方程:(x-3)2=2x(x-3)2.如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,求证:AD·AB=AE·AC3.如图,CD是⊙O的弦,AB是直径,CD⊥AB,垂足为P,求证:PC2=PA·PB4.“端午节”吃粽子是我国流传了上千年的习俗.某班学生在“端午节”前组织了一次综合实践活动,购买了一些材料制作爱心粽,每人从自己制作的粽子的个数,将制作粽子数量相同的学生分为一组,全班学生可分为A、B、C、D四个组,各组每人制作的粽子个数分别为4、5、6、7.根据下面不完整的统计图解答下列问题:(1) 请补全上面两统计图(2) 该班学生制作粽子个数的平均数是____________(3) 若全校2000名同学一起制作粽子,这次端午节全校同学共送给敬老院的老人__________个粽子5.如图,AB为⊙O的直径,ED切⊙O于点C,过点A作AF⊥ED于点F,交⊙O于点G,连接AC(1) 猜想线段AC、AB与AF之间的数量关系,并证明你的结论(2) 若CF=4,GF=2,求⊙O的半径6.在“六城”同创活动中,为努力把我市建成“国家园林城市”,绿化公司计划购买A、B、C三种绿化树共800株,用20辆货车一次运回,对我市城区新建道路进行绿化.按计划,20辆货车都要装运,每辆货车只能装运同一种绿化树,且必须装满.根据下表提供的信息,解答以下问题:绿化树品种A B C(1) 设装运A种绿化树的车辆数为x,装运B种绿化树的车辆数为y,求y与x之间的函数关系式(2) 如果装运每种绿化树的车辆数都不多于8辆,那么车辆的安排方案有几种?并写出每种安排方案(3) 若在“六城”同创活动中要求“厉行节约”办实事,则应采用(2)中的哪种安排方案?为什么?7.已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°(1) 如图1,当四边形ABCD和EFCG均为正方形时,连接BF①求证:△CAE∽△CBF②若BE=1,AE=2,求CE的长(2) 如图2,当四边形ABCD和EFCG均为矩形,且时.若BE=1,AE=2,CE=3,则k=__________湖北初三初中数学月考试卷答案及解析一、选择题1.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是()A.凌晨4时气温最低为﹣3℃B.14时气温最高为8℃C.从0时至14时,气温随时间增长而上升D.从14时至24时,气温随时间增长而下降【答案】C.【解析】A.∵由图象可知,在凌晨4点函数图象在最低点﹣3,∴凌晨4时气温最低为﹣3℃,故本选项正确;B.∵由图象可知,在14点函数图象在最高点8,∴14时气温最高为8℃,故本选项正确;C.∵由图象可知,从4时至14时,气温随时间增长而上上升,不是从0点,故本选项错误;D.∵由图象可知,14时至24时,气温随时间增长而下降,故本选项正确.故选C.【考点】函数的图象.2.下列说法中正确的是()A.“任意画出一个等边三角形,它是轴对称图形”是随机事件B.“任意画出一个平行四边形,它是中心对称图形”是必然事件C.“概率为0.0001的事件”是不可能事件D.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次【答案】B【解析】“任意画出一个等边三角形,它是轴对称图形”有可能是,也可能不是,因此是随机事件,故错误;“任意画出一个平行四边形,它是中心对称图形”是一定的,是必然事件,故正确;“概率为0.0001的事件”是可能发生的事件,因此错误;任意掷一枚质地均匀的硬币10次,正面向上的不一定是5次,故错误.故选B【考点】必然事件与随机事件3.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为()A.50°B.80°C.100°D.130°【答案】D【解析】首先根据圆周角与圆心角的关系,求出∠BAD的度数;然后根据圆内接四边形的对角互补,用180°减去∠BAD的度数,求出∠BCD的度数是多少即可.解:∵∠BOD=100°,∴∠BAD=100°÷2=50°,∴∠BCD=180°﹣∠BAD=180°﹣50°=130°故选:D.【考点】圆周角定理;圆内接四边形的性质.二、解答题(12分)如图,在平面直角坐标系中,已知抛物线的对称轴为,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.(1)求抛物线的解析式;(2)填空:①用含m 的式子表示点C ,D 的坐标:C ( , ),D ( , ); ②当m= 时,△ACD 的周长最小;(3)若△ACD 为等腰三角形,求出所有符合条件的点P 的坐标. 【答案】(1);(2)①C (m ,m ),D (2m ,0);②m=1; (3)P 1(1,),P 2(,),P 3(,).【解析】(1)由抛物线对称轴公式和经过点A (2,1)可得关于a ,b 的方程组,解方程组即可得到抛物线的解析式;(2)①设OA 所在的直线解析式为y=kx ,将点A (2,1)代入求得OA 所在的解析式为,因为PC ⊥x 轴,所以C 得横坐标与P 的横坐标相同,为m ,令x=m ,则y=,所以得出点C (m ,),又点O 、D 关于直线PB 的对称,所以由中点坐标公式可得点D 的横坐标为2m ,则点D 的坐标为(2m ,0); ②因为O 与D 关于直线PB 的对称,所以PB 垂直平分OD ,则CO=CD ,因为,△ACD 的周长=AC+CD+AD=AC+CO+AD=AO ,AO===,所以当AD 最小时,△ACD 的周长最小;根据垂线段最短,可知此时点D 与E 重合,其横坐标为2,故m=1.(3)由中垂线得出CD=OC ,再将OC 、AC 、AD 用m 表示,然后分三种情况讨论:①AC=CD ;②AC=AD ;③DA=DC .试题解析:(1)依题意,得:,解得:,∴;(2)①设OA 所在的直线解析式为,将点A (2,1)代入求得OA 所在的解析式为,∵PC ⊥x 轴,∴C 得横坐标与P 的横坐标相同,为m ,令x=m ,则y=,∴点C (m ,),又∵点O 、D 关于直线PB的对称,∴由中点坐标公式可得点D 的横坐标为2m ,∴点D 的坐标为(2m ,0);故答案为:C (m ,m ),D (2m ,0);②∵O 与D 关于直线PB 的对称,∴PB 垂直平分OD ,∴CO=CD ,∵△ACD 的周长=AC+CD+AD=AC+CO+AD=AO ,AO===,∴当AD 最小时,△ACD 的周长最小;根据垂线段最短,可知此时点D 与E 重合,其横坐标为2,故m=1; (3)依题意,得B (m ,0)在RT △OBC 中,==,∴OC= 又∵O ,D关于直线PC 对称,∴CD=OC=,在RT △AOE 中,OA===,∴AC=OA ﹣OC=,在RT △ADE 中,==, 分三种情况讨论:①若AC=CD ,即=,解得m=1,∴P (1,);②若AC=AD ,则有,即,解得m=0或.∵0<m <2,∴,∴P (,);③若DA=DC ,则有,即,解得或m=2,∵,0<m <2,∴,∴P(,);综上所述,当△ACD 为等腰三角形是,点P 的坐标分别为P 1(1,),P 2(,),P 3(,).【考点】1.二次函数综合题;2.等腰三角形的判定与性质;3.最值问题;4.分类讨论;5.综合题;6.压轴题.三、填空题1.关于x的一元二次方程x2-2x=0有两个相等的实数根,则m的值为。
19初三数学月考试卷答案(1)

初三年级数学试卷参考答案一、选择题(本大题共10小题,每小题3分,共30分.)1.C;2.B;3.B;4.A;5.D;6.A;7.B;8.A;9. D;10.A.二、填空题(本大题共8小题,每小题3分,共24分.)11.72°;12.3;13.22°;14.20π;15.65°;16.(-2,-1);17;18..三、解答题(本大题共10小题,共96分.)19.(本小题满分6分)解:连接AO,设OA=x.∴OA=10 (6)20.(本小题满分7分)解:连接OB,OC,∴OC=BC=4,∴直径=8 ································· 6+1 21.(本小题满分8分)证明:连接BD,取BD的中点O,连接OA,OC (1)∴A,B,C,D四个点在同一个圆上. (8)22.(本小题满分9分)解:设AE=x,∴AE=4,BD=9,CF=5. ····································· 3+3+3 23.(本小题满分8分)解:在Rt△COE中,CE=1,∴CD=2. (8)24.(本小题满分10分)(1)证明:连接OC,易证CD是⊙O的切线; (4)(2)解:AC=2. (10)25.(本小题满分10分)(1)解:连接OD,易得EC=2; (5)(2)解:S阴影=83π. (10)26.(本小题满分12分)(1)解:①连接CD,DF,得CD=EF=5; (6)②∵EF是直径,CD是弦,∴EF≥CD=5,∴EF最小=5. (10)(2)解:4.8. (12)27.(本小题满分12分)解:(1)180 ; (2)(2)当t=4或8时,∠POA=120°; (8)(3)当t=2,3,9,10,△POB为直角三角形. (12)28.(本小题满分14分)解:(1)答案不唯一,如:(4,3),(3,4); (4)(2)①连结MN,∵OM=ON=4,∴Rt△OMN是等腰直角三角形.过O作OA⊥MN于点A,∴点M,N关于直线OA对称.由圆的对称性可知,圆心P在直线OA上.∴圆心P所在直线为y=x. (10)②当MN为⊙P直径时,由等腰直角三角形性质,可知m-n=当点M,N重合时,即点M,N横纵坐标相等,所以m-n=0;∴m-n的取值范围是0<m-n≤ (14)。
湖北初三初中数学月考试卷带答案解析

湖北初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.下列成语所描述的事件是必然发生的是()。
A.水中捞月B.拔苗助长C.守株待兔D.瓮中捉鳖2.将如图所示的图案,绕其中心旋转n°时,与原图形重合,那么n的最小值是()A.60B.90C.120D.1803.方程的根是()A.B.C.D.4.如图:将半径为2cm的圆形纸片折叠后,圆弧恰好过圆心O,则折痕AB的长为()。
A.2cm B.cm C.2cm D.cm5.某班体育委员统计了全班45名同学一周的体育锻炼时间(单位:小时),并绘制了如图所示的折线统计图,下列说法中错误的是A.众数是9B.中位数是9C.平均数是9D.锻炼时间不低于9小时的有14人6.如图,是由若干个同样大小的立方体搭成的几何体的俯视图,小正方形中的数字表示该位置立方体的个数,则这个几何体的主视图是()=,则tanA+tanB=()7.在Rt△ABC中,∠C=90°,AB=4,S△ABCA.B.C.D.48.关于的方程有实数根,则整数的最大值是()A.6B.7C.8D.99.某中学初三(1)班对本班甲、乙两名学生10次数学测验的成绩进行统计,得到两组数据,其方差分别为,则下列判断正确的是A.甲比乙的成绩稳定B.乙比甲的成绩稳定C.甲、乙的成绩一样稳定D.无法确定哪一名同学的成绩更稳定,当时对应的函数值为,若10.已知二次函数,当时,对应的函数值为y1且时,则()A.B.C.D.y1、y2的大小关系不确定二、填空题1.函数的自变量的取值范围是____________________2.将一个底面半径为2,高为4的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图形面积为.3.是一个三位的自然数,已知,这个三位数是218;聪明的小亮在解决这种问题时,采取列成连减竖式的方法(见右图)确定要求的自然数,请你仿照小亮的作法,解决这种问题.如果是一个四位的自然数,且,那么,这个四位数是_____________.4.如图,直角三角形纸片ABC中,∠ACB=90°,AC=8,BC=6.折叠该纸片使点B与点C重合,折痕与AB、BC 的交点分别为D、E.将折叠后的图形沿直线AE剪开,原纸片被剪成三块,其中最小一块的面积等于.5.某校九年级三班在体育毕业考试中,全班所有学生得分情况如下表所示:人数段18分以下18-20分21-23分24-26分27-29分30分那么,随机地抽取1人,恰好是获得30分的学生的概率是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019学年湖北省广水市九年级下学期第一次月考数学
试卷【含答案及解析】
姓名___________ 班级____________ 分数__________
一、选择题
1. ﹣7的绝对值是().
A.﹣7 B.7 C.﹣ D.
2. 下列四个图形中,既是轴对称图形又是中心对称图形的是().
3. 据统计,我国2013年全年完成造林面积约6090000公顷.6090000用科学记数法可表示为()
A.6.09×106 B.6.09×104 C.609×104 D.60.9×105
4. 下列运算正确的是().
A.x2•x3=x6 B.x6÷x5=x C.(﹣x2)4=x6 D.x2+x3=x5
5. 函数y=中,自变量x的取值范围是().
A.x≠0 B.x≥2 C.x>2且x≠0 D.x≥2且x≠0
6. 如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB=().
A.1:4 B.2:3 C.1:3 D.1:2
7. 如图,圆锥体的高h=2cm,底面半径r=2cm,则圆锥体的全面积为()cm2.
A.4π B.8π C.12π D.(4+4)π
8. 如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为().
A.100米 B.50米 C.米 D.50米
9. 函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是().
10. 已知:在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC边于点F.点D为BC上一点,连接DE、DF.设点E到BC的距离为x,则△DEF的面积
S关于x的函数图象大致为().
二、填空题
11. 分解因式:8(a2+1)﹣16a= .
12. 当x=﹣1时,代数式÷+x的值是.
13. 计算:+(π﹣2)0﹣()﹣1= .
14. 如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2,则CD= .
15. 如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且
DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是(只填写序号).
16. 如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三
角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为 cm2.
三、解答题
17. 解不等式组(4分):,
18. (5分)广水市为了改善全市中、小学办学条件,计划集中采购一批电子白板和投影机.已知购买2块电子白板比购买3台投影机多4000元,购买4块电子白板和3台投影
机共需44000元.问购买一块电子白板和一台投影机各需要多少元?
19. (6分)长岭中心中学现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为①号选手和②号选手代表学校参加全镇汉字听写大赛.
(1)请用树状图或列表法列举出各种可能选派的结果;
(2)求恰好选派一男一女两位同学参赛的概率.
20. (6分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线,交BC于点E.
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
21. (8分)我市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.市实验中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:
(1)本次被调查的学生有名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图2中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
22. (8分)如图所示,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°相距20海里的C 处救生船,并通知救生船,遇险船在它的正东方向B处,现救生船沿着航线CB前往B处救援,若救生船的速度为20海里/时,请问:救生船到达B处大约需要多长时间?(结果精确到0.1小时:参考数据:sin38°≈0.62,cos38°≈0.79, sin22°≈0.37,cos22°≈0.93, sin37°≈0.60,cos37°≈0.80)
23. (9分)如图,A,P,B,C是⊙O上的四个点,∠APC=∠BPC=60°,过点A作⊙O的切线交BP的延长线于点D.
(1)求证:△ADP∽△BDA;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)若AD=2,PD=1,求线段BC的长.
24. (12分)长岭中心中学九年级数学兴趣小组经过市场调查,整理出某种商品在第x (1≤x≤90)天的售价与销量的相关信息如下表:
25. 时间x(天)1≤x<5050≤x≤90售价(元/件)x+4090每天销量(件)200﹣
2x<td><td><td>td
26. (14分)如图,平行四边形ABCD在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,4),抛物线经过点A和C.
(1)求抛物线的解析式.
(2)该抛物线的对称轴将平行四边形ABCO分成两部分,对称轴左侧部分的图形面积记为,右侧部分图形的面积记为,求与的比.
(3)在y轴上取一点D,坐标是(0,),将直线OC沿x轴平移到,点D关于直
线的对称点记为,当点正好在抛物线上时,求出此时点坐标并直接写出直线的函数解析式.
参考答案及解析
第1题【答案】
第2题【答案】
第3题【答案】
第4题【答案】
第5题【答案】
第6题【答案】
第7题【答案】
第8题【答案】
第9题【答案】
第10题【答案】
第11题【答案】
第12题【答案】
第13题【答案】
第14题【答案】
第15题【答案】
第16题【答案】
第17题【答案】
第18题【答案】
第19题【答案】
第20题【答案】
第21题【答案】
第22题【答案】
第23题【答案】。
