29.2 第1课时 几何体的三视图
29.2 第1课时 三视图

九年级数学下(RJ) 教学课件
投影与视图
29.2 三视图
第1课时 三视图
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.会从投影的角度理解视图的概念,明确视图与投影的关系; 2.会画简单几何体的三视图;(重点、难点)
导入新课
“横看成岭侧成峰,远近高低各不同.不识庐山真 面目,只缘身在此山中”你能说明是什么原因吗?
正面
左 视
图
俯视图
主视图
左视图
高
长
宽
宽 俯视图
三视图是主视图、俯视图、左视图的统称.它是从三个 方向分别表示物体形状的一种常用视图.
二 三视图的画法
典例精析 例1 画出图中基本几何体的三视图:
解:如图所示: 主视图 左视图
俯视图
主视图 左视图 俯视图
宽
归纳总结
三视图的具体画法为: 1.确定主视图的位置,画出主视图;
主视图
左视图
高
长
宽
宽 俯视图
2. 在主视图正下方画出俯视图,注意与主视图“长对正”;
3. 在主视图正右方画出左视图,注意与主视图“高平 齐”,与俯视图“宽相等”.
例2 画出如图所示的支架的三视图,其中支架 的两个台阶的高度和宽度相等. 解:下图是支架的三视图.
主
左
视
视
图
图
俯 视 图
练一练 1.画出图中的几何体的三视图.
当我们从某一方向观察一个物体时,所看到的图 形叫做物体的一个视图.视图也可以看作物体在 某一个方向的光线下的正投影,对于同一物体, 如果从不同方向观察,所得到的视图可能不同.
讲授新课
一 三视图的概念及关系
29.2三视图(第1课时)教案

1.确定主视图的位置,画出主视图;
2.在主视图正下方画出俯视图,注意与主视图“长对正”。
3.在主视图正右方画出左视图.注意与主视图“高平齐”,与俯视图“宽相等”.
解:
练习:
1、
2、你能画出下图1中几何体的三视图吗小明画出了它们的三种视图(图2),他画的对吗请你判断一下.
四、小结
1、画一个立体图形的三视图时要考虑从某一个方向看物体获得的平面图形的形状和大小,不要受到该方向的物体结构的干扰。
2、在画三视图时,三个三视图不要随意乱放,应做到俯视图在主视图的下方,左视图在主视图的右边,三个视图之间保持:长对正,高平齐,宽相等。
作业
设计
必做
教科书P116:1
选做
练习册
教学重点
从投影的角度加深对三视图的理解和会画简单的三视图
教学难点
对三视图概念理解的升华及正确画出三棱柱的三视图
教学准备
教师
多媒体课件
学生
“预习课文、学习袋、学习用具”
课堂教学程序设计
设计意图
(一)创设情境,引入新课
这个水平投影能完全反映这个物体的形状和大小吗?如不能,那么还需哪些投影面?
物体的正投影从一个方向反映了物体的形状和大小,为了全面地反映一个物体的形状和大小,我们常常再选择正面和侧面两个投影面,画出物体的正投影。
教学时间
课题
29.2三视图(一)
课型
新授课
教
学
目
标
知 识
和
能 力
1、会从 投影的角度理解视图的概念会画简单几何体的三视图
过 程
和
方 法
通过观察探究等活动使学生知道物体的三视图与正投影的相互关系及三视图中位 置关系、大小关系
初中人教版数学九年级下册29.2核心素养【教学课件】《三视图》

实 物
展 开 图
人民教育出版社 九年级 | 下册
• ⒉由三视图描述几何体(或实物原型),一
般步骤为: • ① 想象:根据各视图想象从各个方向看到 的几何体形状; • ② 定形:综合确定几何体(或实物原型) 的形状; • ③ 定大小位置:根据三个视图“长对正, 高平齐,宽相等”的关系,确定轮廓线的位 置,以及各个方向的尺寸.
27990 (mm2)
人民教育出版社 九年级 | 下册
练 习
由三视图想象实物形状:
(1) 实 物
(2)
实 物
人民教育出版社 九年级 | 下册
(3) 实 物
(4)
实 物
人民教育出版社 九年级 | 下册
练习
根据几何体的三视图画出它的表面展开图:
实 物
展 开 图
人民教育出版社 九年级 | 下册
一、创设问题,引入新课
问题1 :问题:横看成岭侧成峰,远近高低各不同.不识 庐山真面目,只缘身在此山中 ,你能说明是什么原因吗?
人民教育出版社 九年级 | 下册
二、创设情境,探究学习 问题2:你能指出这些图形分别从哪个角度观察得到的吗?
人民教别从哪个角度观察得到的吗?
(1)画三视图时,三视图的位置摆放有什么要求?
(2)画三视图时,三视图的大小有什么要求?
(3)为什么画三视图时要长对正,高平齐,宽相等?
(4)什么时候画实线,什么时候画虚线?
人民教育出版社 九年级 | 下册
问题4: 画出图所示的支架(一 种小零件)的三视图.
主 视 图
左 视 图
俯 视 图
人民教育出版社 九年级 | 下册
长对正, 可见实,
俯视图 主视图
左视图
人教版九年级数学下册-29.2 第1课时 三视图【数学专题教学设计】
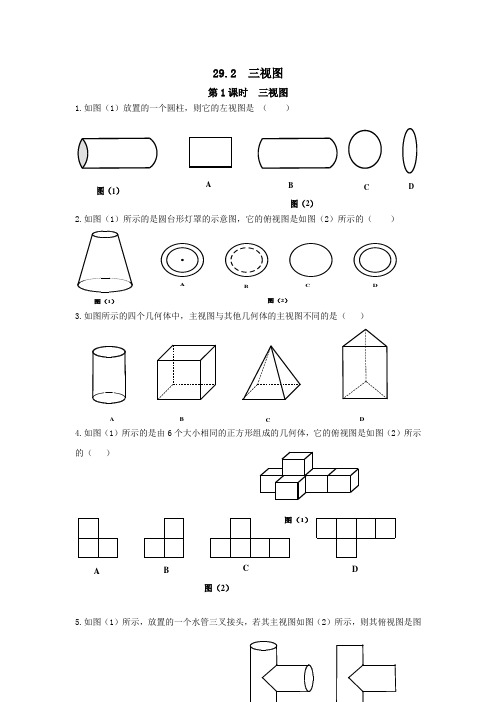
29.2 三视图第1课时三视图1.如图(1)放置的一个圆柱,则它的左视图是()2.如图(1)所示的是圆台形灯罩的示意图,它的俯视图是如图(2)所示的()3.如图所示的四个几何体中,主视图与其他几何体的主视图不同的是()4.如图(1)所示的是由6个大小相同的正方形组成的几何体,它的俯视图是如图(2)所示的()5.如图(1)所示,放置的一个水管三叉接头,若其主视图如图(2)所示,则其俯视图是图DCBA图(2)DCBA图(1)图(2)DCBA图(2)DCBA图(1)图(1)(3)所示的( )6.在水平的讲台上放置圆柱形水杯和长方形粉笔盒,如图(1)所示,则它的主视图是图(2)所示的( )7.沿圆柱体上面直径截去一部分的物体如图所示,画出它的三视图.考点综合专题:反比例函数与其他知识的综合◆类型一 反比例函数与一次函数的综合一、判断函数图象1.当k >0时,反比例函数y =kx和一次函数y =kx +2的图象大致是【方法3④】( )图(3)DCBA图(2)DCBA(第3题)二、求交点坐标或根据交点求取值范围2.(2017·自贡中考)一次函数y 1=k 1x +b 和反比例函数y 2=k 2x (k 1·k 2≠0)的图象如图所示.若y 1>y 2,则x 的取值范围是【方法3③】( )A .-2<x <0或x >1B .-2<x <1C .x <-2或x >1D .x <-2或0<x <1第2题图 第3题图 第5题图3.如图,直线y =-x +b 与反比例函数y =kx 的图象的一个交点为A (-1,2),则另一个交点B 的坐标为【方法3①】( )A .(-2,1)B .(2,1)吧C .(1,-2)D .(2,-1)4.若一次函数y =mx +6的图象与反比例函数y =nx 在第一象限的图象有公共点,则有( )A .mn ≥-9B .-9≤mn ≤0C .mn ≥-4D .-4≤mn ≤05.(2017·长沙中考)如图,点M 是函数y =3x 与y =kx 的图象在第一象限内的交点,OM=4,则k 的值为________.6.(2017·菏泽中考)直线y =kx (k >0)与双曲线y =6x 交于A (x 1,y 1)和B (x 2,y 2)两点,则3x 1y 2-9x 2y 1的值为________.【方法4】7.(2017·广安中考)如图,一次函数y =kx +b 的图象与反比例函数y =mx 的图象在第一象限交于点A (4,2),与y 轴的负半轴交于点B ,且OB =6.(1)求函数y =mx和y =kx +b 的解析式;(2)已知直线AB 与x 轴相交于点C ,在第一象限内,求反比例函数y =mx 的图象上一点P ,使得S △POC =9.◆类型二 反比例函数与二次函数的综合8.(2017·广州中考)当a ≠0时,函数y =ax 与y =-ax 2+a 在同一直角坐标系中的大致图象可能是( )9.★如图,在矩形OABC 中,OA =3,OC =2,F 是AB 上的一个动点(F 不与A ,B 重合),过点F 的反比例函数y =kx(x >0)的图象与BC 边交于点E .(1)当F 为AB 的中点时,求该函数的解析式;(2)当k 为何值时,△EF A 的面积最大,最大面积是多少?◆类型三 与三角形的综合10.位于第一象限的点E 在反比例函数y =kx 的图象上,点F 在x 轴的正半轴上,O 是坐标原点.若EO =EF ,△EOF 的面积等于2,则k 的值为( )A .4B .2C .1D .-211.(2017·包头中考)如图,一次函数y =x -1的图象与反比例函数y =2x 的图象在第一象限相交于点A ,与x 轴相交于点B ,点C 在y 轴上.若AC =BC ,则点C 的坐标为________.第11题图 第12题图 第13题图12.(2017·西宁中考)如图,点A 在双曲线y =3x(x >0)上,过点A 作AC ⊥x 轴,垂足为C ,OA 的垂直平分线交OC 于点B .当AC =1时,△ABC 的周长为________.13.(2017·贵港中考)如图,过C (2,1)作AC ∥x 轴,BC ∥y 轴,点A ,B 都在直线y =-x +6上.若双曲线y =kx(x >0)与△ABC 总有公共点,则k 的取值范围是________.14.(2017·苏州中考)如图,在△ABC 中,AC =BC ,AB ⊥x 轴,垂足为A .反比例函数y =k x (x >0)的图象经过点C ,交AB 于点D .已知AB =4,BC =52. (1)若OA =4,求k 的值;(2)连接OC ,若BD =BC ,求OC 的长.◆类型四 与特殊四边形的综合15.(2017·衢州中考)如图,在直角坐标系中,点A 在函数y =4x (x >0)的图象上,AB ⊥x轴于点B ,AB 的垂直平分线与y 轴交于点C ,与函数y =4x (x >0)的图象交于点D ,连接AC ,CB ,BD ,DA ,则四边形ACBD 的面积等于( )A .2B .2 3C .4D .43第15题图 第16题图16.(2016·齐齐哈尔中考)如图,已知点P (6,3),过点P 作PM ⊥x 轴于点M ,PN ⊥y 轴于点N ,反比例函数y =kx 的图象交PM 于点A ,交PN 于点B .若四边形OAPB 的面积为12,则k =________.17.(2016·泰安中考)如图,在平面直角坐标系中,正方形OABC 的顶点O 与坐标原点重合,点C 的坐标为(0,3),点A 在x 轴的负半轴上,点D 、M 分别在边AB 、OA 上,且AD =2DB ,AM =2MO ,一次函数y =kx +b 的图象过点D 和M ,反比例函数y =mx 的图象经过点D ,与BC 的交点为N .(1)求反比例函数和一次函数的解析式;(2)若点P 在直线DM 上,且使△OPM 的面积与四边形OMNC 的面积相等,求点P 的坐标.参考答案与解析 1.C 2.D 3.D4.A 解析:将y =mx +6代入y =n x 中,得mx +6=nx ,整理得mx 2+6x -n =0.∵两个图象有公共点,∴Δ=62+4mn ≥0,∴mn ≥-9.故选A.5.436.36 解析:由题可知点A (x 1,y 1),B (x 2,y 2)关于原点对称,∴x 1=-x 2,y 1=-y 2.把A (x 1,y 1)代入双曲线y =6x ,得x 1y 1=6,∴3x 1y 2-9x 2y 1=-3x 1y 1+9x 1y 1=6x 1y 1=36.故答案为36.7.解:(1)把点A (4,2)代入反比例函数y =mx,可得m =8,∴反比例函数解析式为y=8x .∵OB =6,∴B (0,-6),把点A (4,2),B (0,-6)代入一次函数y =kx +b ,可得⎩⎪⎨⎪⎧2=4k +b ,-6=b ,解得⎩⎪⎨⎪⎧k =2,b =-6,∴一次函数解析式为y =2x -6.(2)在y =2x -6中,令y =0,则x =3,即C (3,0),∴CO =3.设P ⎝⎛⎭⎫a ,8a ,则由S △POC =9,可得12×3×8a =9,解得a =43,∴P ⎝⎛⎭⎫43,6. 8.D9.解:(1)∵在矩形OABC 中,OA =3,OC =2,∴B 点坐标为(3,2).∵F 为AB 的中点,∴F 点坐标为(3,1).∵点F 在反比例函数y =kx (x >0)的图象上,∴k =3,∴该函数的解析式为y =3x(x >0).(2)由题意知E ,F 两点坐标分别为E ⎝⎛⎭⎫k 2,2,F ⎝⎛⎭⎫3,k 3,∴S △EF A =12AF ·BE =12×13k ×⎝⎛⎭⎫3-12k =12k -112k 2=-112(k 2-6k +9-9)=-112(k -3)2+34.当k =3时,S △EF A 有最大值,最大值为34. 10.B11.(0,2) 解析:由⎩⎪⎨⎪⎧y =x -1,y =2x ,解得⎩⎪⎨⎪⎧x =2,y =1,或⎩⎪⎨⎪⎧x =-1,y =-2,∴A (2,1),B (1,0).设C (0,m ),∵BC =AC ,∴AC 2=BC 2,即4+(m -1)2=1+m 2,∴m =2,故答案为(0,2).12.3+113.2≤k ≤9 解析:当反比例函数的图象过C 点时,把C 的坐标代入得k =2×1=2;把y =-x +6代入y =k x 得-x +6=kx ,x 2-6x +k =0,Δ=(-6)2-4k =36-4k .∵反比例函数y =kx 的图象与△ABC 有公共点,∴36-4k ≥0,解得k ≤9,即k 的取值范围是2≤k ≤9,故答案为2≤k ≤9.14.解:(1)如图,作CE ⊥AB ,垂足为E .作CF ⊥x 轴,垂足为F .∵AC =BC ,AB =4,∴AE =BE =2.在Rt △BCE 中,BC =52,BE =2,由勾股定理得CE =32.∵OA =4,∴OF =OA-CE =52,∴C 点的坐标为⎝⎛⎭⎫52,2.∵点C 在y =kx的图象上,∴k =5.(2)设A 点的坐标为(m ,0).∵BD =BC =52,∴AD =32,∴D ,C 两点的坐标分别为⎝⎛⎭⎫m ,32,⎝⎛⎭⎫m -32,2.∵点C ,D 都在y =k x 的图象上,∴32m =2⎝⎛⎭⎫m -32,解得m =6,∴C 点的坐标为⎝⎛⎭⎫92,2,∴OF =92,CF =2.在Rt △OFC 中,OC 2=OF 2+CF 2,∴OC =972.15.C16.6 解析:∵∠NOM =90°,PM ⊥x 轴,PN ⊥y 轴,∴四边形ONPM 是矩形.∵点P 的坐标为(6,3),∴PM =3,PN =6.∵A ,B 在反比例函数y =k x 上,∴S △NOB =S △OAM =k2.∵S四边形OAPB=S 矩形OMPN -S △OAM -S △NBO =12,∴6×3-12k -12k =12,解得k =6.17.解:(1)∵正方形OABC 的顶点C 的坐标为(0,3),∴OA =AB =BC =OC =3,∠OAB =∠B =∠BCO =90°.∵AD =2DB ,∴AD =23AB =2,∴D 点的坐标为(-3,2).把D 点的坐标代入y =m x 得m =-6,∴反比例函数的解析式为y =-6x .∵AM =2MO ,∴MO =13OA =1,∴M 点的坐标为(-1,0).把M 点与D 点的坐标代入y =kx +b 中得⎩⎪⎨⎪⎧-k +b =0,-3k +b =2,解得⎩⎪⎨⎪⎧k =-1,b =-1,则一次函数的解析式为y =-x -1. (2)把y =3代入y =-6x 得x =-2,∴N 点坐标为(-2,3),∴NC =2.设P 点坐标为(x ,y ).∵△OPM 的面积与四边形OMNC 的面积相等,∴12(OM +NC )·OC =12OM ·|y |,即|y |=9,解得y =±9.在y =-x -1中,当y =9时,x =-10;当y =-9时,x =8,则点P 的坐标为(-10,9)或(8,-9).考点综合专题:反比例函数与其他知识的综合◆类型一 反比例函数与一次函数的综合 一、判断函数图象1.当k >0时,反比例函数y =kx和一次函数y =kx +2的图象大致是【方法3④】( )二、求交点坐标或根据交点求取值范围2.(2017·自贡中考)一次函数y 1=k 1x +b 和反比例函数y 2=k 2x (k 1·k 2≠0)的图象如图所示.若y 1>y 2,则x 的取值范围是【方法3③】( )A .-2<x <0或x >1B .-2<x <1C .x <-2或x >1D .x <-2或0<x <1第2题图 第3题图 第5题图3.如图,直线y =-x +b 与反比例函数y =kx 的图象的一个交点为A (-1,2),则另一个交点B 的坐标为【方法3①】( )A .(-2,1)B .(2,1)吧C .(1,-2)D .(2,-1)4.若一次函数y =mx +6的图象与反比例函数y =nx 在第一象限的图象有公共点,则有( )A .mn ≥-9B .-9≤mn ≤0C .mn ≥-4D .-4≤mn ≤05.(2017·长沙中考)如图,点M 是函数y =3x 与y =kx 的图象在第一象限内的交点,OM=4,则k 的值为________.6.(2017·菏泽中考)直线y =kx (k >0)与双曲线y =6x 交于A (x 1,y 1)和B (x 2,y 2)两点,则3x 1y 2-9x 2y 1的值为________.【方法4】7.(2017·广安中考)如图,一次函数y =kx +b 的图象与反比例函数y =mx 的图象在第一象限交于点A (4,2),与y 轴的负半轴交于点B ,且OB =6.(1)求函数y =mx和y =kx +b 的解析式;(2)已知直线AB 与x 轴相交于点C ,在第一象限内,求反比例函数y =mx 的图象上一点P ,使得S △POC =9.◆类型二 反比例函数与二次函数的综合8.(2017·广州中考)当a ≠0时,函数y =ax 与y =-ax 2+a 在同一直角坐标系中的大致图象可能是( )9.★如图,在矩形OABC 中,OA =3,OC =2,F 是AB 上的一个动点(F 不与A ,B 重合),过点F 的反比例函数y =kx(x >0)的图象与BC 边交于点E .(1)当F 为AB 的中点时,求该函数的解析式;(2)当k 为何值时,△EF A 的面积最大,最大面积是多少?◆类型三 与三角形的综合10.位于第一象限的点E 在反比例函数y =kx 的图象上,点F 在x 轴的正半轴上,O 是坐标原点.若EO =EF ,△EOF 的面积等于2,则k 的值为( )A .4B .2C .1D .-211.(2017·包头中考)如图,一次函数y =x -1的图象与反比例函数y =2x 的图象在第一象限相交于点A ,与x 轴相交于点B ,点C 在y 轴上.若AC =BC ,则点C 的坐标为________.第11题图 第12题图 第13题图12.(2017·西宁中考)如图,点A 在双曲线y =3x(x >0)上,过点A 作AC ⊥x 轴,垂足为C ,OA 的垂直平分线交OC 于点B .当AC =1时,△ABC 的周长为________.13.(2017·贵港中考)如图,过C (2,1)作AC ∥x 轴,BC ∥y 轴,点A ,B 都在直线y =-x +6上.若双曲线y =kx(x >0)与△ABC 总有公共点,则k 的取值范围是________.14.(2017·苏州中考)如图,在△ABC 中,AC =BC ,AB ⊥x 轴,垂足为A .反比例函数y =k x (x >0)的图象经过点C ,交AB 于点D .已知AB =4,BC =52. (1)若OA =4,求k 的值;(2)连接OC ,若BD =BC ,求OC 的长.◆类型四 与特殊四边形的综合15.(2017·衢州中考)如图,在直角坐标系中,点A 在函数y =4x (x >0)的图象上,AB ⊥x轴于点B ,AB 的垂直平分线与y 轴交于点C ,与函数y =4x (x >0)的图象交于点D ,连接AC ,CB ,BD ,DA ,则四边形ACBD 的面积等于( )A .2B .2 3C .4D .43第15题图 第16题图16.(2016·齐齐哈尔中考)如图,已知点P (6,3),过点P 作PM ⊥x 轴于点M ,PN ⊥y 轴于点N ,反比例函数y =kx 的图象交PM 于点A ,交PN 于点B .若四边形OAPB 的面积为12,则k =________.17.(2016·泰安中考)如图,在平面直角坐标系中,正方形OABC 的顶点O 与坐标原点重合,点C 的坐标为(0,3),点A 在x 轴的负半轴上,点D 、M 分别在边AB 、OA 上,且AD =2DB ,AM =2MO ,一次函数y =kx +b 的图象过点D 和M ,反比例函数y =mx 的图象经过点D ,与BC 的交点为N .(1)求反比例函数和一次函数的解析式;(2)若点P 在直线DM 上,且使△OPM 的面积与四边形OMNC 的面积相等,求点P 的坐标.参考答案与解析 1.C 2.D 3.D4.A 解析:将y =mx +6代入y =n x 中,得mx +6=nx ,整理得mx 2+6x -n =0.∵两个图象有公共点,∴Δ=62+4mn ≥0,∴mn ≥-9.故选A.5.436.36 解析:由题可知点A (x 1,y 1),B (x 2,y 2)关于原点对称,∴x 1=-x 2,y 1=-y 2.把A (x 1,y 1)代入双曲线y =6x ,得x 1y 1=6,∴3x 1y 2-9x 2y 1=-3x 1y 1+9x 1y 1=6x 1y 1=36.故答案为36.7.解:(1)把点A (4,2)代入反比例函数y =mx,可得m =8,∴反比例函数解析式为y=8x .∵OB =6,∴B (0,-6),把点A (4,2),B (0,-6)代入一次函数y =kx +b ,可得⎩⎪⎨⎪⎧2=4k +b ,-6=b ,解得⎩⎪⎨⎪⎧k =2,b =-6,∴一次函数解析式为y =2x -6.(2)在y =2x -6中,令y =0,则x =3,即C (3,0),∴CO =3.设P ⎝⎛⎭⎫a ,8a ,则由S △POC =9,可得12×3×8a =9,解得a =43,∴P ⎝⎛⎭⎫43,6. 8.D9.解:(1)∵在矩形OABC 中,OA =3,OC =2,∴B 点坐标为(3,2).∵F 为AB 的中点,∴F 点坐标为(3,1).∵点F 在反比例函数y =kx (x >0)的图象上,∴k =3,∴该函数的解析式为y =3x(x >0).(2)由题意知E ,F 两点坐标分别为E ⎝⎛⎭⎫k 2,2,F ⎝⎛⎭⎫3,k 3,∴S △EF A =12AF ·BE =12×13k ×⎝⎛⎭⎫3-12k =12k -112k 2=-112(k 2-6k +9-9)=-112(k -3)2+34.当k =3时,S △EF A 有最大值,最大值为34. 10.B11.(0,2) 解析:由⎩⎪⎨⎪⎧y =x -1,y =2x ,解得⎩⎪⎨⎪⎧x =2,y =1,或⎩⎪⎨⎪⎧x =-1,y =-2,∴A (2,1),B (1,0).设C (0,m ),∵BC =AC ,∴AC 2=BC 2,即4+(m -1)2=1+m 2,∴m =2,故答案为(0,2).12.3+113.2≤k ≤9 解析:当反比例函数的图象过C 点时,把C 的坐标代入得k =2×1=2;把y =-x +6代入y =k x 得-x +6=kx ,x 2-6x +k =0,Δ=(-6)2-4k =36-4k .∵反比例函数y =kx 的图象与△ABC 有公共点,∴36-4k ≥0,解得k ≤9,即k 的取值范围是2≤k ≤9,故答案为2≤k ≤9.14.解:(1)如图,作CE ⊥AB ,垂足为E .作CF ⊥x 轴,垂足为F .∵AC =BC ,AB =4,∴AE =BE =2.在Rt △BCE 中,BC =52,BE =2,由勾股定理得CE =32.∵OA =4,∴OF =OA-CE =52,∴C 点的坐标为⎝⎛⎭⎫52,2.∵点C 在y =kx的图象上,∴k =5.(2)设A 点的坐标为(m ,0).∵BD =BC =52,∴AD =32,∴D ,C 两点的坐标分别为⎝⎛⎭⎫m ,32,⎝⎛⎭⎫m -32,2.∵点C ,D 都在y =k x 的图象上,∴32m =2⎝⎛⎭⎫m -32,解得m =6,∴C 点的坐标为⎝⎛⎭⎫92,2,∴OF =92,CF =2.在Rt △OFC 中,OC 2=OF 2+CF 2,∴OC =972.15.C16.6 解析:∵∠NOM =90°,PM ⊥x 轴,PN ⊥y 轴,∴四边形ONPM 是矩形.∵点P 的坐标为(6,3),∴PM =3,PN =6.∵A ,B 在反比例函数y =k x 上,∴S △NOB =S △OAM =k2.∵S四边形OAPB=S 矩形OMPN -S △OAM -S △NBO =12,∴6×3-12k -12k =12,解得k =6.17.解:(1)∵正方形OABC 的顶点C 的坐标为(0,3),∴OA =AB =BC =OC =3,∠OAB =∠B =∠BCO =90°.∵AD =2DB ,∴AD =23AB =2,∴D 点的坐标为(-3,2).把D 点的坐标代入y =m x 得m =-6,∴反比例函数的解析式为y =-6x .∵AM =2MO ,∴MO =13OA =1,∴M 点的坐标为(-1,0).把M 点与D 点的坐标代入y =kx +b 中得⎩⎪⎨⎪⎧-k +b =0,-3k +b =2,解得⎩⎪⎨⎪⎧k =-1,b =-1,则一次函数的解析式为y =-x -1. (2)把y =3代入y =-6x 得x =-2,∴N 点坐标为(-2,3),∴NC =2.设P 点坐标为(x ,y ).∵△OPM 的面积与四边形OMNC 的面积相等,∴12(OM +NC )·OC =12OM ·|y |,即|y |=9,解得y =±9.在y =-x -1中,当y =9时,x =-10;当y =-9时,x =8,则点P 的坐标为(-10,9)或(8,-9).。
人教版九年级下册第二十九章:29.2.1 三视图 优质课课件

高 高
左 视 图
长对正,高平齐,宽相等.
(3)线的虚实原则
俯视图
可见实,
遮挡虚.
宽
举例
长 高 长 长
高
主视图
高 宽
左视图
俯视图
长对正,
宽
高平齐, 宽相等.
例1 画出下图所示一些基本几何体的三视图.
1.确定主视图的位置,画出主视图; 2. 在主视图正下方画出俯视图,注意与主视图“长对正”; 3. 在主视图正右方画出左视图,注意与主视图“高平齐”, 与俯视图“宽相等”.
主 视 图
左 视 图
俯 视 图
练习2
画出几何体的三视图:
从正面看
主视图
左视图
俯视图
从正面看
小结
•
•• •
拓展
1、三视图: 主视图——从正面看到的图 左视图——从左面看到的图 俯视图——从上面看到的图 2、画物体的三视图时的原则?
•
1、习题29.2 第1、2、3题
2、单元评价练习
正面 侧面
俯视图
水平面
一个物体(例如一个长方体)在三个投影面内同时进行正投影, 在正面内得到的由前向后观察物体的视图,叫做主视图; 在水平面内得到的由上向下观察物体的视图,叫做俯视图
在侧面内得到由左向右观察物体的视图,叫做左视图.
画三视图时,要符合什么原则?
(1)位置原则 (2)大小原则
主 视 图 长 长 宽相等
三视图如图所示
圆 柱
球
主 视 图
左 视 图
主 视 图
左 视 图
俯 视 图
俯 视 图
三视图如图所示
四 棱 锥
主 视 图
左 视 图
级数学下册 29.2 三视图 第1课时 基本几何体的三视图课件 (新版)新人教版.ppt

3.常见几何体的三视图
4.在画几何体的三视图中,不但要画出几何体的外部轮廓线,还要画出几何体的内部 轮廓线,并且看得见的轮廓线要画成__实线__,看不见的轮廓线要画成__虚线 __.并 且为表示圆柱、圆锥等图形的对称性,还要加画_课时 基本几何体的三视图
1.三视图概念:对一个物体在三个投影面内进行正投影,在正面内得到的由前向后 观察物体的视图,叫做__主视图__;在水平面内得到的由上向下观察物体的视图,叫 做_俯视图 ;在侧面内得到的由左向右观察物体的视图,叫做__左视图__.__主视图__, __俯视图__,__左_ 视图_叫做物体的三视图. 2.画几何体三视图的方法:(1)先确定_主_ 视图__的位置,画出__主视图__;(2)在主视 图正下方画出__俯视图__,与主视图“长对正”;(3)在主视图正右方画出__左视图__, 与主视图“高平齐”,与俯视图“宽相等”.
人教版九年级数学下册第1课时(三视图的概念及画法)课件

知识点一:几何体的三视图
新知探究
我对们一用个三物个体互(例相如垂一直个的长平方面体作) 为在投三影个面投,影其面中内进行正投影, 正在对正着面我内们得的到平的面 由叫 前做 向正 后面 观, 察 下物方体的平视面图叫,做叫水 做平主面视,图; 右在边侧的面平内面得叫到做的侧 由面 左向. 右观察 物体的视图,叫做 左视图.
人教版数学九年级下册
第29章 投影与视图 29.2 三视图
第1课时 三视图的概念及画法
情景引入
你能说出上面左侧英汉词典三个图分别是从什么方向观察得 到的吗? 这三个图象就是今天要学习的三视图.
知识点一:几何体的三视图
当我们从某一方向观察一个物体时,所看到的平面图形 叫做物体的一个视图.
视图可以看作物体在某一方向光线下的正投影. 对于同一个物体, 如果从不同方向观察, 所得到的视图可能不同. 如图是英汉词典的三个 不同的视图.
左视图
做一做:由几个相同的小立方块搭成的几何体的俯视图如图 所示。方格中的数字表示该位置的小方块的个数.请画出这个 几何体的三视图。
1
3
2
同学们,再见!
•
9、 人的价值,在招收诱惑的一瞬间被决定 。21.4.321.4.3Saturday, April 03, 2021
•
10、低头要有勇气,抬头要有低气。12:30:2912:30:2912:304/3/2021 12:30:29 PM
球的三视图:
主视图
左视图
俯视图
圆柱的三视图:
主视图
左视图
俯视图
圆锥的三视图:
主视图
左视图
注意
点不要漏画哦!
俯视图
正三棱柱的三视图: 注意
第1课时几何体的三视图

第1课时几何体的三视图
2020/8/17
29.2 三视图
第1课时 几何体的三视图
学习目 标
1.了解视图的概念,明确视图与投影的关系. 2.理解三视图中主视图、左视图、俯视图的概念.明确三视图与我们从 三个方向看物体所得到的图象的联系与区别,会画立体图形的三视图. 3.画三视图时,要使主视图与俯视图的长对正,主视图与左视图的高平 齐,左视图与俯视图的宽相等.
跟踪训练2
(《名校课堂》29.2第1课时习题)一位美术老师在课堂上进行立体模型素描教 学时,把由圆锥与圆柱组成的几何体(如图所示,圆锥在圆柱上底面正中间放 置)摆在讲桌上,请你画出这个几何体的三视图.
解:如图.
巩固训 练
1.小明从正面观察如图所示的两个物体,看到的是( C )
2.左下图表示一个用于防震的L形包装泡沫塑料,当俯视这一物体时,看到的图 形形状是( B )
【分析】支架的形状是由两个大小不等的长方体构成的组合体,画三视图时要 注意这两个长方体的上下、前后位置关系. 【解答】如图是支架的三视图. 【点拨】对于由几种基本几何体组合而成的组合体,其各种视图可以分解为基 本几何体的视图再组合,画三视图时要注意各几何体的上、下、前、后、左、 右位置关系.
名校讲 坛
巩固训 练
3.如图,从不同方向看下面左图中的物体,下图中三个平面图形分别是从哪个 方向看到的?
正面 从 上 面看 从 前 面看 从 左 面看 4.如图是由5个大小相同的小正方体组合成的简单几何体.请在下面方格纸中 画出它的三个视图.
解:如图所示.
课堂小 结
1.画物体的三视图时,先确定主视图的位置,在主视图的右边画左视图, 在主视图的正下方画俯视图. 2.画物体的三视图时,看得见部分的轮廓线画成实线,看不见部分的轮 廓线画成虚线. 3.画简单组合体的三视图时,要把组合体分割成规则的几何图形.
