空间直线与平面的垂直关系
线面垂直、面面垂直的性质与判定定理

转化结论
CB
D β
E 证明:在平面β内过D作直线
A
DE ⊥AB
则CDE是二面角 - AB 的平面角
由 ⊥β 得CD ⊥ DE
又CD ⊥ AB, 且DE ∩ AB =D
所以直线CD⊥平面β
8
平面与平面垂直的性质定理:
两个平面垂直,则一个平面内垂直于交线 的直线与另一个平面垂直。
β
a l
A α
符号语言:
α
Aa
β
a⊥β
B
12
例3 , a , a ,判断a与位置关系
证明:设 I l
α a //
在α内作直线b⊥l
b
a
l
β
I bbll Nhomakorabeab 又a
线面垂直
a // b 性质
b
a //
a
面面垂直性质 13
变式:
思考:已知平面,,直线a,且 , AB, a //, a AB,试判断直线a与平面的位置关系。
2、会利用“转化思想”解决垂直问题
面面关系
线面关系
线线关系
空间问题平面化 面面平行
线面平行
线线平行
面面垂直
线面垂直
线线垂直
16
线l在平面α内,那么直线l与平面β的位
置关系有哪几种可能?
α l
β
平行
α
l
β
相交
α
l β
线在面内
6
知识探究:
思考2:黑板所在平面与地面所在平面垂 直,在黑板上是否存在直线与地面垂直? 若存在,怎样画线?
α
β
7
证明问题:
已知: , AB,CD ,且CD AB. 求证:CD
人教版高数必修二第6讲:空间中的垂直关系(教师版)

空间中的垂直关系____________________________________________________________________________________________________________________________________________________________________理解空间中三种垂直关系的定义;掌握空间中三种垂直关系判定及性质;用空间中三种垂直关系的定义、判定及性质解决垂直问题.一、直线与平面垂直1.如果两条直线相交于一点或经过平移后相交于一点,并且交角为直角,则称这两条直线互垂直.2.如果一条直线(AB)和一个平面(α)相交于点O,并且和这个平面内过点O的任何直线都垂直,我们就说这条直线和这个平面互相垂直,记作AB⊥α,直线叫做平面的垂线,平面叫做直线的垂面,交点叫做垂足.垂线上任一点到垂足间的线段,叫做这点到这个平面的垂线段.垂线段的长度叫做这点到平面的距离3.直线和平面垂直的判定4.(1)判定定理:如果一条直线和一个平面内的任何两条相交直线都垂直,那么这条直线垂直于这个平面.符号语言:l⊥a,l⊥b,a∩b=A,a⊂α,b⊂α⇒l⊥α,如图:(2)如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一个平面.符号语言:a∥b,a⊥α⇒b⊥α,如图:5.直线与平面垂直的性质(1)性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.符号语言:a⊥α,b⊥α⇒a∥b,如图:(2)一条直线垂直于一个平面,它就和平面内的任意一条直线垂直.符号语言:a⊥α,b⊂α⇒a⊥b,如图:6.设P是三角形ABC所在平面α外一点,O是P在α内的射影(1)若PA=PB=PC,则O为△ABC的外心.特别地当∠C=90°时,O为斜边AB中点.(2)若PA、PB、PC两两垂直,则O为△ABC的垂心.(3)若P到△ABC三边距离相等,则O为△ABC的内心.7.(1)过一点有且只有一条直线与已知平面垂直.(2)过一点有且只有一个平面与已知直线垂直.二、直线和平面平行1.平面与平面垂直的定义:如果两个相交平面的交线与第三个平面垂直,又这两个平面与第三个平面相交所得的两条交线互相垂直,就称这两个平面互相垂直.平面α、β互相垂直,记作α⊥β.2.两个平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.符号表示:a⊥α,a⊂β⇒α⊥β,如图:3.两个平面垂直的性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线,垂直于另一个平面.符号表示:α⊥β,α∩β=CD,BA⊂α,BA⊥CD,B为垂足⇒BA⊥β,如图:推论:如果两个平面垂直,那么过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内.类型一线面垂直例1:如图,直角△ABC所在平面外一点S,且SA=SB=SC,点D为斜边AC的中点.(1)求证:SD⊥平面ABC;(2)若AB=BC,求证:BD⊥平面SAC.解析:由于D是AC中点,SA=SC,∴SD是△SAC的高,连接BD,可证△SDB≌△SDA.由AB=BC,则Rt△ABC是等腰直角三角形,则BD⊥AC,利用线面垂直的判定定理即可得证.答案:(1)∵SA=SC,D为AC的中点,∴SD⊥AC.在Rt△ABC中,连接BD,则AD=DC=BD,又∵SB=SA,SD=SD,∴△ADS≌△BDS.∴SD⊥BD.又AC∩BD=D,∴SD⊥面ABC.(2)∵BA=BC,D为AC中点,∴BD⊥AC.又由(1)知SD⊥面ABC,∴SD⊥BD.于是BD垂直于平面SAC内的两条相交直线,∴BD⊥平面SAC.练习1:((2014·河南南阳一中高一月考)如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱P A⊥平面ABCD,E、F分别是AB、PC的中点,P A=AD.求证:EF⊥平面PCD.答案:如图,取PD的中点H,连接AH、HF.∴FH 12 CD,∴FH AE,∴四边形AEFH是平行四边形,∴AH∥EF. ∵底面ABCD是矩形,∴CD⊥AD.又∵PA⊥底面ABCD,∴PA ⊥CD ,PA ∩AD =A , ∴CD ⊥平面PAD .又∵AH ⊂平面PAD ,∴CD ⊥AH .又∵PA =AD ,∴AH ⊥PD ,PD ∩CD =D , ∴AH ⊥平面PCD ,又∵AH ∥EF ,∴EF ⊥平面PCD .练习2:如右图,在正方体1111ABCD A B C D -中,P 为1DD 的中点,O 为ABCD 的中心, 求证:1B O ⊥平面PAC 答案:连结111,,PO PB B D ,由正方体的性质可知,1,AC BD AC BB ⊥⊥,且1BD BB B =I ∴AC ⊥面11BDD B 又∵BO ⊂面11BDD B ∴1B O AC ⊥ 设AB a =,则11121,2,2OB OD a B D a PD PD a ===== ∵2222222222221113113,22424OB OB BB a a a OP PD DO a a a =+=+==+=+= 222222111119244PB B D PD a a a =+=+=∴2221OB PO PB += ∴1B O PO ⊥ ∵PO AC O =I∴1B O ⊥平面PAC练习3:在如右图,在空间四边形ABCD 中,,AB AD BC CD ==, 求证:AC BD ⊥答案:设E 为BD 的中点,连结,AE EC∵AB AD = ∴BD AE ⊥ 同理可证:BD EC ⊥又∵AE EC E =I ∴BD ⊥面AEC∵AE ⊂面AEC ∴BD AC ⊥例2:如图在△ABC 中,∠B =90°,SA ⊥平面ABC , 点A 在SB 和SC 上的射影分别是N 、M ,求证:MN ⊥SC .解析:根据直线平面垂直的性质,找到所求垂直的线段中的 一条与另一条所在的平面垂直,即可证明这两条线段互相垂直. 答案:证明:∵SA ⊥平面ABC , ∴SA ⊥BC ,又∠ABC =90°, ∴BC ⊥AB ,∴BC ⊥平面SAB , ∴AN ⊥BC ,又AN ⊥SB ,∴AN ⊥平面SBC ,E ABCDOP D 1C 1B 1A 1DCBA∴AN ⊥SC ,又AM ⊥SC , ∴SC ⊥平面AMN , ∴MN ⊥SC .练习1:如图,在正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为A 1D 、AC 上的点,且EF ⊥A 1D ,EF ⊥AC .求证:EF ∥BD 1. 答案:如图所示,连接A 1C 1、C 1D 、BD 、B 1D 1. 由于AC ∥A 1C 1,EF ⊥AC ,∴EF ⊥A 1C 1. 又EF ⊥A 1D ,A 1D ∩A 1C 1=A 1, ∴EF ⊥平面A 1C 1D . ∵BB 1⊥平面A 1B 1C 1D 1,A 1C 1⊂平面A 1B 1C 1D 1, ∴BB 1⊥A 1C 1.又∵四边形A 1B 1C 1D 1为正方形,∴A 1C 1⊥B 1D 1. ∵BB 1∩B 1D 1=B 1,∴A 1C 1⊥平面BB 1D 1D . 而BD 1⊂平面BB 1D 1D ,∴BD 1⊥A 1C 1. 同理,DC 1⊥BD 1,DC 1∩A 1C 1=C 1, ∴BD 1⊥平面A 1C 1D . 由①②可知EF ∥BD 1.练习2:在空间中,下列命题:①平行于同一条直线的两条直线平行;②垂直与同一直线的两条直线平行;③平行与同一平面的两条直线平行;④垂直于同一平面的两条直线平行.其中正确的由___. 答案:①④练习3:已知,,a b c 及平面β,则下列命题正确的是( )A 、////a a b b ββ⎫⇒⎬⊂⎭B 、a a b b ββ⊥⎫⇒⊥⎬⊥⎭C 、//a c a b b c ⊥⎫⇒⎬⊥⎭D 、//a a b b ββ⊂⎫⇒⎬⊂⎭ 答案:B例3:如图,在底面为直角梯形的四棱锥P -ABCD 中,AD ∥BC , ∠ABC =90°,PA ⊥平面ABCD ,PA =3,AD =2,AB =23,BC =6.求证:BD ⊥平面PAC .解析:通过计算得到直角,进而得到垂直. 答案:∵PA ⊥平面ABCD ,BD ⊂平面ABCD ,∴BD ⊥PA .∵∠BAD 和∠ABC 都是直角,∴tan ∠ABD =AD AB =33,tan ∠BAC =BCAB=3, ∴∠ABD =30°,∠BAC =60°.∴∠AEB =90°,即BD ⊥AC , 又PA ∩AC =A ,∴BD ⊥平面PAC .练习1:在正方体中ABCD -A 1B 1C 1D 1中,P 为DD 1的中点, O 为底面ABCD 的中心.求证:B 1O ⊥平面PAC . 答案:如图所示,连接AB 1、CB 1、B 1D 1、PB 1、PO .设AB =a ,则AB 1=CB 1=B 1D 1=2a ,AO =OC =22a , ∴B 1O ⊥AC .∵B 1O 2=OB 2+BB 21=⎝⎛⎭⎪⎫22a 2+a 2=32a 2,PB 21=PD 21+B 1D 21=⎝ ⎛⎭⎪⎫12a 2+(2a )2=94a 2,OP 2=PD 2+DO 2=⎝ ⎛⎭⎪⎫12a +⎝⎛⎭⎪⎫22a 2=34a 2,∴B 1O 2+OP 2=PB 21,∴B 1O ⊥OP . 又PO ∩AC =O ,∴B 1O ⊥平面PAC . 练习2:如图,若测得旗杆PO =4,P A =PB =5,OA =OB =3,则旗杆PO 和地面α的关系是________.答案:∵PO =4,OA =OB =3,P A =PB =5,∴PO 2+AO 2=P A 2,PO 2+OB 2=PB 2, ∴PO ⊥OA ,PO ⊥OB .又OA ∩OB =O ,∴PO ⊥平面AOB ,∴PO ⊥地面α.类型二平面与平面垂直例4:(2014·山东临沂高一期末测试)如图,在底面为正三角形的直三棱柱ABC -A 1B 1C 1中,点D 是BC 的中点,求证:平面AC 1D ⊥平面BCC 1B 1.解析:运用平面垂直的判定.答案:∵△ABC 为正三角形,D 为BC 的中点,∴AD ⊥BC .又∵CC 1⊥底面ABC ,AD ⊂平面ABC , ∴CC 1⊥AD .又BC ∩CC 1=C , ∴AD ⊥平面BCC 1B 1. 又AD ⊂平面AC 1D ,∴平面AC 1D ⊥平面BCC 1B 1.练习1:三棱锥S -ABC 中,∠BSC =90°,∠ASB =60°,∠ASC =60°,SA =SB =SC . 求证:平面ABC ⊥平面SBC .答案:解法一:取BC 的中点D ,连接AD 、SD .由题意知△ASB 与△ASC 是等边三角形,则AB =AC . ∴AD ⊥BC ,SD ⊥BC .令SA =a ,在△SBC 中,SD =22a , 又∵AD =AC 2-CD 2=22a ,∴AD 2+SD 2=SA 2. 即AD ⊥SD .又∵AD ⊥BC ,∴AD ⊥平面SBC . ∵AD ⊂平面ABC ,∴平面ABC ⊥平面SBC .解法二:∵SA =SB =SC =a , 又∵∠ASB =∠ASC =60°,∴△ASB 、△ASC 都是等边三角形. ∴AB =AC =a .作AD ⊥平面SBC 于点D ,∵AB =AC =AS ,∴D 为△SBC 的外心. 又∵△BSC 是以BC 为斜边的直角三角形, ∴D 为BC 的中点,故AD ⊂平面ABC . ∴平面ABC ⊥平面SBC .练习2:如右图,在四面体ABCD 中,2,BD a AB AD CB CD a =====.求证:平面ABD ⊥平面BCD . 答案:取BD 的中点E ,连结,AE EC∵AB AD = ∴AE BD ⊥同理CE BD ⊥ 在△ABD 中,12,2AB a BE BD a === ∴2222AE AB BE a =-=同理22CE a = 在△AEC 中,2,2AE CE a AC a ===∴222AC AE CE =+ ∴AE CE ⊥ ∵BD CE E =I ∴AE ⊥平面BCD ∵AE ⊂平面ABD ∴平面ABD ⊥平面BCD 练习3:空间四边形ABCD 中,若,AD BC BD AD ⊥⊥,那么有( ) A 、平面ABC ⊥平面ADC B 、平面ABC ⊥平面ADBC 、平面ABC ⊥平面DBCD 、平面ADC ⊥平面DBC 答案:D例5:已知P 是△ABC 所在平面外的一点,且P A ⊥平面ABC ,平面P AC ⊥平面PBC ,求证:BC ⊥AC .解析:已知条件是线面垂直和面面垂直,要证明两条直线垂直,应将两条直线中的一条放入一平面中,使另一条直线与该平面垂直,即由线面垂直得到线线垂直.在空间图形中,高一级的垂直关系蕴含着低一级的垂直关系,通过本题可以看到:面面垂直⇒线面垂直⇒线线垂直. 答案:如图,在平面P AC 内作AD ⊥PC 于点D ,∵平面P AC ⊥平面PBC ,AD ⊂平面P AC ,且AD ⊥PC , ∴AD ⊥平面PBC ,又BC ⊂平面PBC ,∴AD ⊥BC .∵P A ⊥平面ABC ,BC ⊂平面ABC , ∴P A ⊥BC ,∵AD ∩P A =A ,∴BC ⊥平面P AC , 又AC ⊂平面P AC ,∴BC ⊥AC .练习1:已知三棱锥P -ABC 中,侧面PAC 与底面ABC 垂直,PA =PB =PC . (1)求证:AB ⊥BC ;(2)若AB =BC ,过点A 作AF ⊥PB 于点F ,连接CF ,求证:平面PBD ⊥平面AFC .ABCDE答案:如图所示:(1)取AC的中点D,连接PD、BD,∵PA=PC,∴PD⊥AC,又平面PAC⊥平面ABC,且平面PAC∩平面ABC=AC,∴PD⊥平面ABC,D为垂足.∵PA=PB=PC,∴DA=DB=DC,∴AC为△ABC的外接圆的直径,故AB⊥BC.(2)∵PA=PC,AB=BC,PB=PB,∴△ABP≌△CBP.∵AF⊥PB,∴CF⊥PB,又AF∩CF=F,∴PB⊥平面AFC,又PB⊂平面PBD,∴平面PBD⊥平面AFC.练习2:已知平面P AB⊥平面ABC,平面P AC⊥平面ABC,如图所示.求证:P A⊥平面ABC.答案:如图所示,在平面ABC内任取一点D,作DF⊥AC于点F,作DG⊥AB于点G,∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,∴DF⊥平面PAC,又∵PA⊂平面PAC,∴PA⊥DF,同理可证:DG⊥PA,∵DF∩DG=D,且DF⊂平面ABC,DG⊂平面ABC,∴PA⊥平面ABC.1.一条直线和三角形的两边同时垂直,则这条直线和三角形的第三边的位置关系是() A.平行B.垂直C.相交不垂直D.不确定答案:B2.若一条直线l上有两个点到平面α的距离相等,则l与α的关系是()A.平行B.相交C.垂直D.不确定答案:D3.已知直线l⊥平面α,直线m⊂平面β,给出下列四个命题:①α∥β,l⊄β⇒l⊥m②α⊥β⇒l∥m③l∥m⇒α⊥β④l⊥m⇒α∥β其中正确的两个命题是()A.①②B.③④C.②④D.①③答案:D4.如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是()A .平面ABD ⊥平面ABCB .平面ADC ⊥平面BDC C .平面ABC ⊥平面BDCD .平面ADC ⊥平面ABC 答案:D5.若有直线m 、n 和平面α、β,下列四个命题中,正确的是()A .若m ∥α,n ∥α,则m ∥nB .若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC .若α⊥β,m ⊂α,则m ⊥βD .若α⊥β,m ⊥β,m ⊄α,则m ∥α 答案:D6.Rt △ABC 所在平面α外一点P 到直角顶点的距离为24,到两直角边的距离都是610,那么点P到平面α的距离等于__________.答案:12_________________________________________________________________________________ _________________________________________________________________________________基础巩固1.已知一平面平行于两条异面直线,一直线与两异面直线都垂直,那么这个平面与这条直线的位置关系是()A .平行B .垂直C .斜交D .不能确定 答案:B2.直线a ⊥直线b ,a ⊥平面β,则b 与β的位置关系是()A .b ⊥βB .b ∥βC .b ⊂βD .b ⊂β或b ∥β 答案:D 3.下列命题①⎭⎪⎬⎪⎫a ⊥αb ⊂α⇒a ⊥b ; ②⎭⎪⎬⎪⎫a ⊥αa ∥b ⇒b ⊥α; ③⎭⎪⎬⎪⎫a ⊥αb ∥α⇒a ⊥b; ④⎭⎪⎬⎪⎫a ⊥ba ⊥b b ⊂αc ⊂α⇒a ⊥α; ⑤⎭⎪⎬⎪⎫a ∥αa ⊥b ⇒b ⊥α; ⑥⎭⎪⎬⎪⎫a ⊥αb ⊥a ⇒b ∥α. 其中正确命题的个数是( ) A .3 B .4 C .5 D .6答案:A4..若平面α∥平面β,直线a⊂α,直线b⊂β,那么a、b的位置关系是()A.无公共点B.平行C.既不平行也不相交D.相交答案:A5.直线a与平面α内的两条直线都垂直,则a与α的位置关系是()A.垂直B.平行C.a在平面α内D.不确定答案:D6.若平面α⊥平面β,且平面α内的一条直线a垂直于平面β内的一条直线b,则() A.直线a必垂直于平面βB.直线b必垂直于平面αC.直线a不一定垂直于平面βD.过a的平面与过b的平面垂直答案:C7.长方体ABCD-A1B1C1D1中,MN在平面BCC1B1内,MN⊥BC于M,则MN与AB的位置关系为____________________.答案:MN⊥AB8.如图所示,已知正三棱柱ABC-A1B1C1的面对角线A1B⊥B1C,求证B1C⊥C1A.答案:如图所示,连接A1C,交AC1于点D,则点D是A1C的中点.取BC的中点N,连接AN、DN,则DN∥A1B.又A1B⊥B1C,∴B1C⊥DN.又△ABC是正三角形,∴AN⊥BC.又平面ABC⊥平面BB1C1C,平面ABCD∩平面BB1C1C=BC,AN⊂平面ABC,∴AN⊥平面BB1C1C.又B1C⊂平面BB1C1C,∴B1C⊥AN.又AN⊂平面AND,DN⊂平面AND,AN∩DN=N,∴B1C⊥平面AND.又C1A⊂平面AND,∴B1C⊥AC1.能力提升9.若两直线a与b异面,则过a且与b垂直的平面()A.有且只有一个B.至多有一个C.有无数多个D.一定不存在答案:B10.已知三棱锥S-ABC的各顶点都在一个半径为r的球面上,球心O在AB上,SO⊥底面ABC,AC=2r,则球的体积与三棱锥体积之比是()A.πB.2πC.3πD.4π答案:D11.(2014·浙江文,6)设m,n是两条不同的直线,α、β是两个不同的平面()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α答案:C12.已知平面ABC外一点P,且PH⊥平面ABC于H.给出下列4个命题:①若P A⊥BC,PB⊥AC,则H是△ABC的垂心;②若P A、PB、PC两两互相垂直,则H是△ABC的垂心;③若∠ABC=90°,H是AC的中点,则P A=PB=PC;④若P A=PB=PC,则H是△ABC的外心.其中正确命题的个数为()A.1 B.2C.3 D.4答案:D13.平面α的斜线AB交α于点B,过定点A的动直线l与AB垂直,且交α于点C,则动点C的轨迹为________.(填直线、圆、其它曲线)答案:直线14.如图所示,已知矩形ABCD中,AB=1,BC=a,P A⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a的值等于________.答案:215.如图所示,在四棱锥P-ABCD中,P A⊥底面ABCD.底面各边都相等,M是PC上的一动点,当点M满足________________时,平面MBD⊥平面PCD.(注:只要填写一个你认为正确的即可)答案:BM⊥PC(其它合理答案亦可)16.如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE,且CE=AC=2BD,M是AE的中点.(1)求证:DE=DA;(2)求证:平面BDM⊥平面ECA;(3)求证:平面DEA⊥平面ECA.答案:(1)取EC的中点F,连接DF.∵CE⊥平面ABC,∴CE⊥BC.易知DF∥BC,∴CE⊥DF.∵BD ∥CE ,∴BD ⊥平面ABC .在Rt △EFD 和Rt △DBA 中,EF =12CE =DB ,DF =BC =AB , ∴Rt △EFD ≌Rt △DBA .故DE =DA .(2)取AC 的中点N ,连接MN 、BN ,则MN CF . ∵BD CF ,∴MN BD ,∴N ∈平面BDM . ∵EC ⊥平面ABC ,∴EC ⊥BN .又∵AC ⊥BN ,EC ∩AC =C ,∴BN ⊥平面ECA . 又∵BN ⊂平面BDM ,∴平面BDM ⊥平面ECA .(3)∵DM ∥BN ,BN ⊥平面ECA ,∴DM ⊥平面ECA .又∵DM ⊂平面DEA ,∴平面DEA ⊥平面ECA .。
线线垂直、线面垂直、面面垂直的判定和性质

空间中的垂直关系1.线面垂直直线与平面垂直的判定定理:如果 ,那么这条直线垂直于这个平面。
推理模式:直线与平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线 。
2.面面垂直两个平面垂直的定义:相交成 的两个平面叫做互相垂直的平面。
两平面垂直的判定定理:(线面垂直⇒面面垂直)如果 ,那么这两个平面互相垂直。
推理模式:两平面垂直的性质定理:(面面垂直⇒线面垂直)若两个平面互相垂直,那么在一个平面内垂直于它们的 的直线垂直于另一个平面。
一般来说,线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为:线线垂直−−−→←−−−判定性质线面垂直−−−→←−−−判定性质面面垂直.这三者之间的关系非常密切,可以互相转化,从前面推出后面就是判定定理,而从后面推出前面就是性质定理.同学们应当学会灵活应用这些定理证明问题.在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,下面举例说明.例题:1.如图,AB 就是圆O 的直径,C 就是圆周上一点,PA ⊥平面ABC.(1)求证:平面PAC ⊥平面PBC;(2)若D 也就是圆周上一点,且与C 分居直径AB 的两侧,试写出图中所有互相垂直的各对平面.2、如图,棱柱111ABC A B C -的侧面11BCC B 就是菱形,11B C A B ⊥证明:平面1AB C ⊥平面11A BC3、如图所示,在长方体1111ABCD A B C D -中,AB=AD=1,AA 1=2,M 就是棱CC 1的中点 (Ⅰ)求异面直线A 1M 与C 1D 1所成的角的正切值;(Ⅱ)证明:平面ABM ⊥平面A 1B 1M 14、如图,AB 就是圆O的直径,C就是圆周上一点,PA ⊥平面ABC .若AE ⊥PC ,E为垂足,F就是PB 上任意一点,求证:平面AEF ⊥平面PBC .5、如图,直三棱柱ABC —A 1B 1C 1 中,AC =BC =1,∠ACB =90°,AA 1 =2,D 就是A 1B 1 中点.(1)求证C 1D ⊥平面A 1B ;(2)当点F 在BB 1 上什么位置时,会使得AB 1 ⊥平面C 1DF ?并证明您的结论6、S 就是△ABC 所在平面外一点,SA ⊥平面ABC,平面SAB⊥平面SBC,求证AB ⊥BC 、7、在四棱锥中,底面ABCD 就是正方形,侧面VAD 就是正三角形,平面VAD ⊥底面ABCD证明:AB ⊥平面VAD8、如图,平行四边形ABCD 中,60DAB ︒∠=,2,4AB AD ==,将CBD ∆沿BD 折起到EBD ∆的位置,使平面EDB ⊥平面ABD 、求证:AB DE ⊥VDC B A SAB9、如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD,AB=AD,∠BAD=60°,E 、F 分别就是AP 、AD 的中点求证:(1)直线EF ‖平面PCD;(2)平面BEF ⊥平面PAD10、如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,AB AS BC AB =⊥,、过A 作SB AF ⊥,垂足为F ,点G E ,分别就是棱SC SA ,的中点。
认识简单的空间几何平行与垂直的关系

认识简单的空间几何平行与垂直的关系平行与垂直是空间几何中常见的两种关系,它们在许多领域都有重要应用,包括建筑设计、工程测量、物体运动的研究等。
本文将介绍简单的空间几何中平行与垂直的概念及其相关性质,并通过实际例子加深理解。
一、平行的定义与性质在空间几何中,我们将两条直线或两个平面称为平行,当且仅当它们不相交,且永远保持相同的距离。
具体而言,对于两条直线l和m,如果它们在同一平面内,且没有交点,我们说l与m平行;对于两个平面α和β,如果它们没有交线,我们说α与β平行。
平行的性质如下:1. 平行线与平行线之间的距离在任意两点处相等;同理,平行平面与平行平面之间的距离也相等。
示例1:在一个矩形的平面上,有一条直线l与矩形的一条边平行,那么l与矩形的另一条边也平行。
2. 若一条直线与平行于它的直线相交,则两直线之间的夹角等于对应的内错角。
示例2:设有两条平行线l和m,l与m的夹角为θ,则与l平行且与m相交的另一条线n与l的夹角也为θ。
3. 若两个平面分别与第三个平面平行,则它们之间的夹角等于对应的内错角。
示例3:三个平面α、β和γ,其中α与β平行,β与γ平行,那么α与γ之间的夹角等于α与β之间的夹角。
二、垂直的定义与性质在空间几何中,两个直线或两个平面相互垂直,当且仅当它们的夹角为90度。
直线与平面相互垂直的情况,也包括直线在平面内垂直和直线与平面相交垂直两种情况。
垂直的性质如下:1. 两条平行线与同一直线相交,在相交点处的垂直线也是平行线。
示例4:设有两条平行线l和m,直线n与l相交于点A,那么n与m的交点与A之间的线段也是垂直于l和m的。
2. 两条直线垂直于同一平面,在该平面上的交线也是垂直于该平面。
示例5:在一个平面上,有一条直线l垂直于平面,直线m也垂直于该平面,那么m与l在平面上的交线也是垂直于该平面。
3. 若两个平面互相垂直,则它们的交线为直线,并且该直线垂直于这两个平面。
示例6:平面α与平面β垂直,平面β与平面γ垂直,那么平面α与平面γ的交线即为一条垂直于平面α和平面γ的直线。
空间内两直线垂直公式

空间内两直线垂直公式在三维几何中,垂直是两个直线或曲线所形成的角度为90度的关系。
而在二维几何中,垂直是两条直线所形成的角度为90度的关系。
在本文中,我们将讨论在空间内两直线垂直的条件和如何判断两直线是否垂直。
两直线垂直的条件:1.方向垂直:两条直线的方向向量的点积为0。
设直线L1的方向向量为a1,直线L2的方向向量为a2,则方向垂直的条件为a1·a2=0。
点积为0意味着两个向量之间的夹角为90度,即两条直线的方向垂直。
2.两个平面垂直:两条直线分别位于两个平面上,且两个平面垂直。
设平面P1的法线向量为n1,平面P2的法线向量为n2,则两个平面垂直的条件为n1·n2=0。
如果两个平面垂直,那么位于它们上面的直线也垂直。
3.直线与平面垂直:直线L位于平面P上,且直线L与平面P垂直。
设平面P的法线向量为n,直线L的方向向量为a,则直线与平面垂直的条件为n·a=0。
直线与平面垂直的意义是直线在平面上的投影为零。
判断两直线是否垂直的方法:1.方向向量法:判断两条直线的方向向量是否垂直。
如果两条直线的方向向量垂直,那么它们是垂直的。
2.位置向量法:判断一条直线上的一个点到另一条直线的距离是否为零。
设一条直线为L1,另一条直线为L2,直线L2上的一点为P2,直线L1上的一个点为P1、如果P1到P2的距离为零,那么两条直线是垂直的。
3.平面交点法:判断两个平面的交线与一条直线是否垂直。
如果两个平面的交线与一条直线垂直,那么这条直线位于两个平面上。
示例:1.判断直线L1:{(x,y,z),x-2=0,y+z=0}和直线L2:{(x,y,z),2x-y+z=1,3x-y-2z=0}是否垂直。
直线L1的方向向量为a1=(1,0,0),直线L2的方向向量为a2=(2,-1,-2)。
计算a1·a2=1*2+0*(-1)+0*(-2)=2,由于a1·a2不等于零,所以直线L1和直线L2不垂直。
第11讲 空间中垂直关系的判定与性质
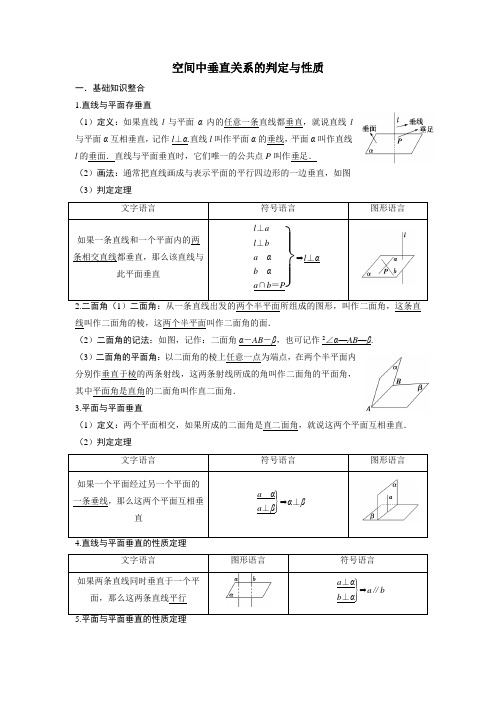
空间中垂直关系的判定与性质一.基础知识整合1.直线与平面存垂直(1)定义:如果直线l 与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直,记作l ⊥α.直线l 叫作平面α的垂线,平面α叫作直线l 的垂面.直线与平面垂直时,它们唯一的公共点P 叫作垂足.(2)画法:通常把直线画成与表示平面的平行四边形的一边垂直,如图(3)判定定理 ⎭⎪⎬⎪⎫l ⊥a l ⊥b a αb αa ∩b =P ⇒l ⊥α从一条直线出发的两个半平面所组成的图形,叫作二面角,这条直线叫作二面角的棱,这两个半平面叫作二面角的面.(2)二面角的记法:如图,记作:二面角α-AB -β,也可记作2∠α—AB —β.(3)二面角的平面角:以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角叫作二面角的平面角,其中平面角是直角的二面角叫作直二面角.3.平面与平面垂直(1)定义:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.(2)判定定理⎭⎪⎬⎪⎫a αa ⊥β⇒α⊥β符号语言⎭⎪⎬⎪⎫α⊥βα∩β=l a αa ⊥l ⇒a ⊥β 题型一:线面垂直的判定 例1:如图所示,在Rt △ABC 中,∠B =90°,且S 为所在平面外一点,满足SA =SB =SC .D为AC 的中点.求证:SD ⊥平面ABC .证明:∵在Rt △ABC 中,∠B =90°,且D 为AC 的中点,∴BD =AD =DC .又∵SA =SB =SC ,SD为公共边,∴△SBD ≌△SAD ≌△SCD , ∴∠SDB =∠SDA =∠SCD =90°,∴SD ⊥AD ,SD ⊥BD ,∵AD ∩BD =D ,∴SD ⊥平面ABC .变式训练1:如图,已知AB 是⊙O 的直径,C 是圆周上不同于A ,B 的点,P A ⊥⊙O 所在的平面,AF ⊥PC 于F ,求证:BC ⊥平面PAC .证明:因为AB 为⊙O 的直径,所以BC ⊥AC .因为P A ⊥平面ABC ,BC平面ABC ,所以P A ⊥BC .因为P A ∩AC =A ,所以BC ⊥平面P AC .题型二:面面垂直的判定例2:已知四面体ABCD 的棱长都相等,E ,F ,G ,H 分别为AB ,AC ,AD ,BC 的中点.求证:平面EHG ⊥平面FHG .证明:如图,取CD 的中点M ,连接HM ,MG ,FM ,则四边形MHEG为平行四边形.连接EM 交HG 于O ,连接FO .在△FHG 中,O 为HG的中点,且FH =FG ,所以 FO ⊥HG .同理可证FO ⊥EM .又HG ∩EM =O ,所以FO ⊥平面EHMG .又FO 平面FHG ,所以平面EHG ⊥平面FHG .变式训练2:如图,在空间四边形ABDC中,AB =BC ,CD =DA ,E 、F 、G 分别为CD 、DA 和对角线AC 的中点.:求证:平面BEF ⊥平面BDG .证明:∵AB =BC ,CD =AD ,G 是AC 的中点,∴BG ⊥AC ,DG ⊥AC ,又EF ∥AC ,∴EF ⊥BG ,EF ⊥DG .∴EF ⊥平面BGD .∵EF 平面BEF ,∴平面BDG ⊥平面BEF .题型三:垂直关系的综合应用例3:如图,在三棱锥P —ABC 中,P A ⊥底面ABC ,P A =AB ,∠BCA=90°.点D ,E 分别在棱PB ,PC 上,且DE ∥BC .(1)求证:BC ⊥平面P AC ;(2)是否存在点E 使得二面角A —DE —P 为直二面角?并说明理由.证明:(1)∵P A ⊥底面ABC ,∴P A ⊥BC .又∠BCA =90°,∴AC ⊥BC .又P A ∩AC =A ,∴BC ⊥平面P AC .(2)存在点E 使得二面角A —DE —P 为直二面角.由(1)知BC ⊥平面P AC ,又∵DE ∥BC ,∴DE ⊥平面P AC .又∵AE 平面P AC ,PE 平面P AC ,∴DE ⊥AE ,DE ⊥PE .∴∠AEP 为二面角A —DE —P 的平面角.又∵P A ⊥底面ABC ,∴P A ⊥AC .∴∠P AC =90°.∴在棱PC 上存在一点E ,使得AE ⊥PC .这时,∠AEP =90°.故存在点E 使得二面角A —DE —P 是直二面角.变式训练3:如图所示,P A ⊥平面ABC ,AC ⊥BC ,AB =2,BC =2,PB =6,求二面角P —BC —A 的大小.解:∵P A ⊥平面ABC ,BC 平面ABC ,∴P A ⊥BC .又AC ⊥BC ,P A ∩AC =A ,∴BC ⊥平面P AC .又PC 平面P AC ,∴BC ⊥PC .又BC ⊥AC ,∴∠PCA 为二面角P —BC —A 的平面角.在Rt △PBC 中,∵PB =6,BC =2,∴PC =2.在Rt △ABC 中,∵AB =2,BC =2,∴AC = 2.∴在Rt △P AC 中,cos ∠PCA =22,∴∠PCA=45°,即二面角P —BC —A 的大小为45°.题型四:线面垂直性质定理的应用例4:如图,在正方体ABCD -A 1B 1C 1D 1中,点E 、F 分别在A 1D 、AC 上,且EF ⊥A 1D ,EF ⊥AC .求证:EF ∥BD 1.证明:如图所示,连接AB 1、B 1C 、BD .∵DD 1⊥平面ABCD ,AC 平面ABCD .∴DD 1⊥AC .又∵AC ⊥BD ,且BD ∩DD 1=D ,∴AC ⊥平面BDD 1. ∵BD 1平面BDD 1,∴BD 1⊥AC .同理可证BD 1⊥B 1C .∴BD 1⊥平面AB 1C .∵EF ⊥A 1D ,A 1D ∥B 1C ,∴EF ⊥B 1C .又EF ⊥AC ,且AC ∩B 1C =C ,∴EF ⊥平面AB 1C ,∴EF ∥BD 1.变式训练3:如图,在正方体ABCD -A 1B 1C 1D 1中,点E 、F 分别在A 1D 、AC上,且EF ⊥A 1D ,EF ⊥AC .若G 是AB 的中点,则E 在A 1D 上什么位置时,能使EG ⊥平面AB1C?解:若EG⊥平面AB1C,因为BD1⊥平面AB1C,所以EG∥BD1.因为G为AB的中点,所以E为AD1的中点,即E为A1D的中点时,EG⊥平面AB1C.题型五:面面垂直性质定理的应用例5:已知平面P AB⊥平面ABC,平面P AC⊥平面ABC,求证:P A⊥平面ABC.证明:如图所示,在BC上任取一点D,作DF⊥AC于F,DG⊥AB于G,∵平面P AC⊥平面ABC,且平面P AC∩平面ABC=AC,∴DF⊥平面P AC,又∵P A平面P AC,∴DF⊥P A,同理DG⊥P A,又∵DF∩DG=D且DF平面ABC,DG平面ABC,∴P A⊥平面ABC.变式训练5:如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=22,M为BC的中点.求证:AM⊥PM.证明:如图连接AP.矩形ABCD中,AD⊥DC,BC⊥DC,又∵平面PDC⊥平面ABCD,平面PDC∩平面ABCD=DC,∴AD⊥平面PDC,BC⊥平面PDC,又∵PD平面PDC,PC平面PDC,∴AD⊥PD,BC⊥PC,在Rt△P AD和Rt△PMC中,易知AP2=AD2+PD2=(22)2+22=12,PM2=PC2+MC2=22+(2)2=6,又∵Rt△ABM中,AM2=AB2+BM2=22+(22)2=6,∴AP2=PM2+AM2,∴AM⊥PM.题型六:垂直关系的综合应用例6:如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,F A=FE,∠AEF=45°.(1)求证:EF⊥平面BCE;(2)设线段CD、AE的中点分别为P,M,求证:PM∥平面BCE.证明:(1)因为平面ABEF⊥平面ABCD,BC平面ABCD,BC⊥AB,平面ABEF∩平面ABCD =AB,所以BC⊥平面ABEF.所以BC⊥EF.因为△ABE为等腰直角三角形,AB=AE,所以∠AEB=45°.又因为∠AEF =45°,所以∠FEB =90°,即EF ⊥BE .因为BC 平面BCE ,BE 平面BCE ,BC ∩BE =B ,所以EF ⊥平面BCE .(2)取BE 的中点N ,连接CN ,MN ,则MN 綊12AB 綊PC ,所以PMNC 为平行四边形.所以PM ∥CN . 因为CN 在平面BCE 内,PM 不在平面BCE 内,所以PM ∥平面BCE .变式训练6:如图,四棱锥S -ABCD 中,SD ⊥平面ABCD ,AB ∥DC ,AD ⊥DC ,AB =AD=1,SD =2,BC ⊥BD ,E 为棱SB 上的一点,平面EDC ⊥平面SBC .(1)证明:DE ⊥平面SBC ;(2)证明:SE =2EB .证明:(1)连接BD ,∵SD ⊥平面ABCD ,故BC ⊥SD ,又∵BC ⊥BD ,BD ∩SD =D ,∴BC ⊥平面BDS ,∴BC ⊥DE . 作BK ⊥EC ,K 为垂足,因平面EDC⊥平面SBC ,故BK ⊥平面EDC ,BK ⊥DE . 又∵BK 平面SBC ,BC 平面SBC ,BK ∩BC =B ,∴DE ⊥平面SBC .(2)由(1)知DE ⊥SB ,DB =2AD = 2.∴SB =SD 2+DB 2=6,DE =SD ·DB SB =233,EB =DB 2-DE 2=63,SE =SB -EB =263,∴SE =2EB . 三.方法规律总结1.线面垂直的判定定理是证明线面垂直的主要方法,证明的关键是在平面内找到两条相交直线与已知直线垂直.2.在证明面面垂直时,一般方法是从一个平面内寻找另一个平面的垂线,若这样的直线图中不存在,则可通过作辅助线来解决(所作辅助线要有利于题目的证明),即由线面垂直证面面垂直.3.空间中线线、线面、面面之间的垂直关系可以相互转化,其转化关系如下:4.会用线面垂直的性质定理证明平行问题,用面面垂直的性质定理证明垂直问题.四:课后练习作业一、选择题1.设l、m为不同的直线,α为平面,且l⊥α,下列为假命题的是(B) A.若m⊥α,则m∥l B.若m⊥l,则m∥αC.若m∥α,则m⊥l D.若m∥l,则m⊥α【解析】A中,若l⊥α,m⊥α,则m∥l,所以A正确;B中,若l⊥α,m⊥l,则m∥α或mα,所以B错误;C中,若l⊥α,m∥α,则m⊥l,所以C正确;若l⊥α,m∥l,则m⊥α,所以D正确.2.在正方体ABCD—A1B1C1D1中,与AD1垂直的平面是(A)A.平面A1DCB1 B.平面DD1C1C C.平面A1B1C1D1D.平面A1DB【解析】连接A1D、B1C,由ABCD—A1B1C1D1为正方体可知,AD1⊥A1B1,AD1⊥A1D.故AD1⊥平面A1DCB1.3.如图,在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是(C)A.BC∥平面PDF B.DF⊥平面P AEC.平面PDF⊥平面ABC D.平面P AE⊥平面ABC【解析】由题意知BC∥DF,且BC⊥PE,BC⊥AE.∵PE∩AE=E,∴BC⊥平面P AE,∴BC∥平面PDF成立,DF⊥平面P AE成立,平面P AE⊥平面ABC也成立.4.设α、β是两个不同的平面,l是一条直线,以下命题正确的是(C) A.若l⊥α,α⊥β,则lβB.若l∥α,α∥β,则lβC.若l⊥α,α∥β,则l⊥βD.若l∥α,α⊥β,则l⊥β【解析】A错,可能l∥β;B错,可能l∥β;C正确;D错,不一定l⊥β.5.设平面α⊥平面β,且α∩β=l,直线aα,直线bβ,且a不与l垂直,b不与l垂直,那么a与b (B)A.可能垂直,不可能平行B.可能平行,不可能垂直C.可能垂直,也可能平行D.不可能垂直,也不可能平行【解析】当a,b都平行于l时,a与b平行,假设a与b垂直,如图所示,由于b与l不垂直,在b上任取一点A,过点A作b′⊥l,∵平面α⊥平面β,∴b′⊥平面α,从而b′⊥a,又由假设a⊥b易知a⊥平面β,从而a⊥l,这与已知a不与l垂直矛盾,∴假设不正确,a与b不可能垂直.6.空间四边形ABCD,若AB、AC、AD与平面BCD所成角相等,则A点在平面BCD的射影是△BCD的(A)A.外心B.内心C.重心D.垂心【解析】设A点在平面BCD内的射影为O.可知,△OAB≌△OAC≌△OAD.∴OB=OC=OD,∴点O为外心.7.下列说法中正确命题的个数为(B)①如果直线l与平面α内的无数条直线垂直,则l⊥α;②如果直线l不垂直于α,则α内没有与l垂直的直线;③如果一条直线与平面内的一条直线垂直,则该直线与此平面必相交;④如果一条直线和平面的一条垂线垂直,该直线必在这个平面内;⑤如果一条直线和一个平面垂直,该直线垂直于平面内的任一直线.A.0B.1C.2D.3【解析】如图(1)所示,l与α相交(不垂直),此时也有无数条直线与l垂直.故①②错误;如图(2)所示,l与α平行,此时平面内也存在无数条直线与l垂直,故③④错误;如图(3)所示,直线l与平面α的垂线m垂直,但l不在平面α内;由线面垂直的定义可知,⑤正确.8.如图,在正方形ABCD中,E、F分别为边BC,CD的中点,H是EF的中点,现沿AE、AF,EF把这个正方形折成一个几何体,使B、C、D三点重合于点G,则下列结论中成立的是(A)A.AG⊥平面EFG B.AH⊥平面EFGC.GF⊥平面AEF D.GH⊥平面AEF【解析】∵AG⊥GF,AG⊥GE,GF∩GE=G,∴AG⊥平面EFG.9.如图,在四边形ABCD中,AD∥BC,AB=AD,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列命题正确的是(B)A.平面ADC⊥平面BDCB.平面ABD⊥平面ABCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC【解析】在图①中,∵∠BAD=90°,AD=AB,∴∠ADB=∠ABD=45°.∵AD∥BC,∴∠DBC=45°.又∵∠BCD=45°.∴∠BDC=90°,即BD⊥CD.在图②中,此关系仍成立.∵平面ABD⊥平面BCD,∴CD⊥平面ABD.∵BA平面ADB,∴CD⊥AB.∵BA⊥AD,∴BA⊥平面ACD.∵BA平面ABC,∴平面ABC⊥平面ACD.10.如图,在正方体ABCD—A1B1C1D1中,点P在侧面BCC1B1上运动,并且总保持AP⊥BD1,则动点P在(A)A.线段B1C上B.线段BC1上C.BB1中点与CC1中点的连线上D.B1C1中点与BC中点的连线上【解析】连接AC,B1C,AB1,由线面垂直的判定可知BD1⊥平面AB1C.若AP平面AB1C,则AP⊥BD1.这样只要P在B1C上移动即可.二、填空题11.如图,在正方体ABCD—A1B1C1D1中,平面ACD1与平面BB1D1D的位置关系是________.垂直D⊥平面ABCD,AC平面【解析】∵ABCD是正方形,∴AC⊥BD.又∵DABCD,∴D1D⊥AC.∵D1D∩DB=D,∴AC⊥平面BB1D1D.∵AC平面ACD1,∴平面ACD1⊥平面BB1D1D.12.如图所示,已知P A⊥平面α,PB⊥平面β,垂足分别为A、B,α∩β=l,∠APB=50°,则二面角α-l-β的大小为________.130°【解析】如图,设平面P AB∩l=O,连接AO,BO,AB,∵P A⊥α,lα,∴P A⊥l.同理PB⊥l,而PB∩P A=P,∴l⊥平面P AB,∴l⊥AO,l⊥BO,∴∠AOB即为二面角α-l-β的平面角.结合图形知∠AOB+∠APB=180°,∴∠AOB=130°.13.如图,已知平面α⊥平面β,在α与β的交线l上,取线段AB=4,AC、BD分别在平面α和平面β内,它们都垂直于交线AB,并且AC=3 cm,BD=12 cm,则CD=______.13 cm【解析】连接BC.因为平面α⊥平面β,且α∩β=l,又因为BD平面β,且BD⊥l,所以BD⊥平面α.又∵BC平面α,∴BC⊥BD.所以△CBD也是直角三角形.在Rt △BAC 中,BC =32+42=5.在Rt △CBD 中,CD =52+122=13.所以CD 长为13 cm.14.α,β是两个不同的平面,m ,n 是平面α与β之外的两条不同直线,给出四个论断:①m ⊥n ;②α⊥β;③n ⊥β;④m ⊥α.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________.若①③④,则②(或若②③④,则①)【解析】利用面面垂直的判定,可知①③④⇒②为真;利用面面垂直的性质,可知②③④⇒①为真.15.如图平面ABC ⊥平面BDC ,∠BAC =∠BDC =90°,且AB =AC =a ,则AD =_______a【解析】如图所示,取BC 的中点E ,连接ED ,AE ,∵AB =AC ,∴AE ⊥BC ,∵平面ABC ⊥平面BDC .∴AE ⊥平面BDC ,∴AE ⊥ED .在Rt △ABC 和Rt △BCD 中,AE =ED =12BC =22a ,∴在Rt △AED 中,AD =AE 2+ED 2=a .三、解答题16.如图所示,AB 是圆O 的直径,P A 垂直于圆O 所在的平面,M 是圆周上任意一点,AN ⊥PM ,垂足为N .求证:AN ⊥平面PBM .证明:设圆O 所在的平面为α,∵P A ⊥α,且BM α,∴P A ⊥BM .又∵AB 为⊙O 的直径,点M 为圆周上一点,∴AM ⊥BM ,∵直线P A ∩AM =A ,∴BM ⊥平面P AM .又AN 平面P AM ,∴BM ⊥AN .这样,AN 与PM ,BM 两条相交直线垂直.故AN ⊥平面PBM .17.如图所示,过S 引三条长度相等但不共面的线段SA ,SB ,SC 且∠ASB =∠ASC =60°,∠BSC =90°.求证:平面ABC ⊥平面BSC .【证明】(法一)取BC 的中点D ,连接AD ,SD .∵∠ASB =∠ASC ,且SA =SB=AC ,∴AS =AB =AC .∴AD ⊥BC .又△ABS 是正三角形,△BSC 为等腰直角三角形,∴BD =SD .∴AD 2+SD 2=AD 2+BD 2=AB 2=AS 2.由勾股定理的逆定理,知AD ⊥SD .又∵SD ∩BC =D ,∴AD⊥平面BSC .又AD 平面ABC ,∴平面ABC ⊥平面BSC .(法二)同法一证得AD ⊥BC ,SD ⊥BC ,则∠ADS 即为二面角A —BC —S 的平面角.∵∠BSC =90°,令SA =1,则SD =22,AD =22,∴SD 2+AD 2=SA 2.∴∠ADS =90°.∴平面ABC ⊥平面BSC .18.如图,在三棱锥S -ABC 中,SA ⊥平面ABC ,AB ⊥BC ,DE 垂直平分SC ,分别交AC 、SC 于D 、E ,且SA =AB =a ,BC =2a .(1)求证:SC ⊥平面BDE ;(2)求平面BDE 与平面BDC 所成二面角的大小.(1)证明:∵SA ⊥平面ABC ,又AB 、AC 、BD 平面ABC ,∴SA ⊥AB ,SA ⊥AC ,SA ⊥BD ,∴SB =SA 2+AB 2=2a .∵BC =2a ,∴SB =BC .∵E 为SC 的中点,∴BE ⊥SC .又DE ⊥SC ,BE ∩DE =E ,∴SC ⊥平面BDE .(2)由(1)及BD 平面BDE ,得BD ⊥SC .又知BD ⊥SA ,∴BD ⊥平面SAC .∴BD ⊥AC 且BD ⊥DE .∴∠CDE 为平面BDE 与平面BDC 所成二面角的平面角.∵AB ⊥BC ,AC =AB 2+BC 2=3a .∴Rt △SAC中,tan ∠SCA =SA AC =33,∴∠SCA =30°.∴∠CDE =60°,即平面BDE 与平面BDC 所成二面角为60°.19.如图,已知三棱锥A BPC -中,AP PC ⊥,AC BC ⊥,M为AB 中点,D 为PB 中点,且PMB ∆为正三角形.(1)求证:DM APC ∥平面;(2)求证:ABC APC ⊥平面平面.证明:(1)∵M 为AB 中点,D 为PB 中点,∴MD //AP ,又MD不在平面APC 上,∴MD //平面APC.(2)∵△PMB 为正三角形,又D 为PB 中点. ∴MD ⊥PB .又由(1)知MD //A P , ∴AP ⊥PB . 又AP ⊥PC , 且PB ∩PC =P ,∴AP ⊥平面PBC , ∴AP ⊥BC , 又∵AC ⊥BC , 且AP ∩AC =A ∴BC ⊥平面APC , 又BC 在平面ABC 内,∴平面ABC ⊥平面APC .20.如图所示,在正方体ABCD -A 1B 1C 1D 1中,M 是AB 上一点,N 是A 1C 的中 点,MN ⊥平面A 1DC .求证:(1)MN ∥AD 1;(2)M 是AB 的中点.证明:(1)∵ADD 1A 1为正方形,∴AD 1⊥A 1D .又∵CD ⊥平面ADD 1A 1,AD 1平面ADD 1A 1,∴CD ⊥AD 1.∵A 1D ∩CD =D ,∴AD 1⊥平面A 1DC .又∵MN ⊥平面A 1DC ,∴MN ∥AD 1. MD B P C A(2)连接ON ,在△A 1DC 中,A 1O =OD ,A 1N =NC .∴ON 綊12CD 綊12AB ,∴ON ∥AM .又∵MN ∥OA ,∴四边形AMNO 为平行四边形,∴ON =AM .∵ON =12AB ,∴AM =12AB ,∴M 是AB 的中点. 21.如图所示,P 是四边形ABCD 所在平面外一点,ABCD 是∠DAB =60°且边长为a 的菱形,侧面P AD 为正三角形,其所在平面垂直于底面ABCD .(1)若G 为AD 边的中点,求证:BG ⊥平面P AD ;(2)求证:AD ⊥PB .证明:(1)连接PG ,BD .由题知△P AD 为正三角形,G 是AD 的中点,∴PG ⊥AD .又平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,PG 平面P AD ,∴PG ⊥平面ABCD ,∴PG ⊥BG .又∵四边形ABCD 是菱形且∠DAB =60°,∴△ABD 是正三角形,∴BG ⊥AD .又AD 平面P AD ,PG 平面P AD ,且AD ∩PG =G ,∴BG ⊥平面P AD .(2)由(1)可知BG ⊥AD ,PG ⊥AD .又BG 平面PBG ,PG 平面PBG ,且BG ∩PG =G ,AD ⊥平面PBG ,∴AD ⊥PB .。
第3章 3.4~3.5 直线与平面的垂直关系 平面的法向量 Word版含解析

3.4~3.5直线与平面的垂直关系__平面的法向量[读教材·填要点]1.射影(1)过空间任意一点P作平面α的垂线与α相交于点P0,则P0称为点P在平面α内的射影.(2)预先给定平面α,空间任何一个图形的每一个点P在平面α上都有一个射影P0,所有这些P0在平面α上组成一个图形,称为这个空间图形在平面α上的射影.2.三垂线定理及其逆定理(1)三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.(2)三垂线定理的逆定理:在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直.3.平面的法向量与平面α垂直的非零向量称为α的法向量.[小问题·大思维]1.平面的法向量是唯一的吗?若不唯一,平面的法向量之间的关系是怎样的?提示:平面的法向量不是唯一的,平面的不同法向量是共线的.2.若直线l的一个方向向量为(1,1,1),向量(1,-1,0)及向量(0,1,-1)都与平面α平行,则l与α有怎样的位置关系?提示:∵(1,1,1)·(0,1,-1)=0,(1,1,1)·(1,-1,0)=0,而向量(1,-1,0)与向量(0,1,-1)不平行,∴l⊥α.利用判定定理用向量法证明线面垂直在正方体ABCD-A1B1C1D1中,E,F分别为BB1,D1B1的中点,求证:EF⊥平面B1AC.[自主解答] 设正方体的棱长为2,建立如图所示的直角坐标系,则A (2,0,0),C (0,2,0),B 1(2,2,2),E (2,2,1),F (1,1,2).EF ―→=(-1,-1,1),AB 1―→=(0,2,2),AC ―→=(-2,2,0). ∴EF ―→·AB 1―→=(-1,-1,1)·(0,2,2)=0, EF ―→·AC ―→=(-1,-1,1)·(-2,2,0)=0, ∴EF ⊥AB 1,EF ⊥AC .又AB 1∩AC =A , ∴EF ⊥平面B 1AC .利用判定定理,即通过证明向量数量积为0来验证直线的方向向量与平面内两条相交直线的方向向量垂直.1.已知长方体ABCD -A 1B 1C 1D 1中,AD =AA 1,AB =2AD ,点E 是线段C 1D 1的中点,求证:DE ⊥平面EBC .证明:建立如图所示的空间直角坐标系D -xyz ,设AD =1,则AA 1=1,AB =2,则可得D (0,0,0),E (0,1,1),B (1,2,0),C (0,2,0),DE ―→=(0,1,1),EB ―→=(1,1,-1), EC ―→=(0,1,-1), 因为DE ―→·EB ―→=1-1=0, DE ―→·EC ―→=1-1=0, 所以DE ⊥EB ,DE ⊥EC ,又EB ∩EC =E ,所以DE ⊥平面EBC .求平面的法向量在正方体ABCD -A 1B 1C 1D 1中,棱长为a ,G ,E ,F 分别为AA 1,AB ,BC 的中点,试建立适当的空间直角坐标系,求平面GEF 的法向量.[自主解答] 以D 点为坐标原点,建立如图所示的空间直角坐标系.则G ⎝⎛⎭⎫a ,0,12a ,E ⎝⎛⎭⎫a ,12a ,0,F ⎝⎛⎭⎫12a ,a ,0, ∴GE ―→=⎝⎛⎭⎫0,12a ,-12a , GF ―→=⎝⎛⎭⎫-12a ,a ,-12a . 设平面GEF 的法向量n =(x ,y ,z ),则 ⎩⎪⎨⎪⎧n ·GE ―→=0,n ·GF ―→=0,即⎩⎨⎧12ay -12az =0,-12ax +ay -12az =0.令y =z =1,则x =1,∴平面GEF 的一个法向量为(1,1,1).本例条件不变,求平面A 1EFC 1的法向量. 解:A 1(a,0,a ),E ⎝⎛⎭⎫a ,12a ,0,F ⎝⎛⎭⎫12a ,a ,0, ∴A 1E ―→=⎝⎛⎭⎫0,12a ,-a ,A 1F ―→=⎝⎛⎭⎫-12a ,a ,-a . 设平面A 1EFC 1的法向量为n =(x ,y ,z ),则 ⎩⎪⎨⎪⎧n ·A 1E ―→=0,n ·A 1F ―→=0,即⎩⎨⎧12ay -az =0,-12ax +ay -az =0.令y =2,z =1,则x =2.∴平面A 1EFC 1的一个法向量为(2,2,1).求平面法向量的一般步骤为: (1)设出平面的法向量为n =(x ,y ,z );(2)找出(求出)平面的两个不共线的向量的坐标a =(a 1,a 2,a 3),b =(b 1,b 2,b 3);(3)根据法向量的定义建立关于x ,y ,z 的方程组⎩⎪⎨⎪⎧n ·a =0,n ·b =0;(4)解方程组,取其中的一个解作为法向量,由于一个平面的法向量有无数多个,故可在方程组解中取一个最简单的作为平面的法向量.2.已知△ABC 的三个顶点的坐标分别为A (1,2,3),B (2,0,-1),C (3,-2,0),试求出平面ABC 的一个法向量.解:设平面ABC 的法向量为n =(x ,y ,z ). ∵A (1,2,3),B (2,0,-1),C (3,-2,0), ∴AB ―→=(1,-2,-4),AC ―→=(2,-4,-3), 由题设得: ⎩⎪⎨⎪⎧n ·AB ―→=0,n ·AC ―→=0,即⎩⎪⎨⎪⎧ x -2y -4z =0,2x -4y -3z =0,解得⎩⎪⎨⎪⎧x =2y ,z =0,取y =1,则x =2.故平面ABC 的一个法向量为n =(2,1,0).利用法向量证明线面垂直如图所示,正方体ABCD -A 1B 1C 1D 1中,M ,N 分别为AB ,B 1C 的中点.试用向量法判断MN 与平面A 1BD 的位置关系.[自主解答] 设正方体的棱长为1,以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系D -xyz .则B (1,1,0),A 1(1,0,1), M ⎝⎛⎭⎫1,12,0,N ⎝⎛⎭⎫12,1,12, ∴DA 1―→=(1,0,1),DB ―→=(1,1,0), MN ―→=⎝⎛⎭⎫-12,12,12.设平面A 1BD 的一个法向量为n 0=(x ,y ,z ), 则⎩⎪⎨⎪⎧DA 1―→·n 0=0, DB ―→·n 0=0,即⎩⎪⎨⎪⎧x +z =0,x +y =0. 取x =1,则y =z =-1, ∴n 0=(1,-1,-1). ∴n 0=-2MN ―→,即n 0∥MN ―→. ∴MN ⊥平面A 1BD .利用法向量证明线面垂直,即通过证明直线的方向向量与平面的法向量平行来证明线面垂直.解决此类问题的关键是正确求解平面的法向量.3.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 为棱BB 1的中点,在棱DD 1上是否存在点P ,使MD ⊥平面PAC?解:如图,建立空间直角坐标系,则 A (1,0,0),C (0,1,0),D (0,0,0), M ⎝⎛⎭⎫1,1,12,假设存在P (0,0,x )满足条件, 则PA ―→=(1,0,-x ),AC ―→=(-1,1,0). 设平面PAC 的法向量为n =(x 1,y 1,z 1), 则由⎩⎪⎨⎪⎧PA ―→·n =0, AC ―→·n =0,得⎩⎪⎨⎪⎧x 1-xz 1=0,-x 1+y 1=0.令x 1=1得y 1=1,z 1=1x ,即n =⎝⎛⎭⎫1,1,1x , 由题意MD ―→∥n ,由MD ―→=⎝⎛⎭⎫-1,-1,-12得x =2, ∵正方体棱长为1,且2>1,∴棱DD 1上不存在点P ,使MD ⊥平面PAC .解题高手 妙解题 什么是智慧,智慧就是简单、高效、不走弯路如图在正方体ABCD -A 1B 1C 1D 1中,E 为BB 1的中点,F 为CD 的中点,G 为AB 的中点.求证:平面ADE ⊥平面A 1FG .[巧思] 利用空间向量证明面面垂直通常可以有两个途径,一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直;二是直接求解两个平面的法向量,证明两个法向量垂直,从而得到两个平面垂直.[妙解] 法一:以D 为原点,DA ,DC ,DD 1所在的直线分别为x ,y ,z 轴建立空间直角坐标系D -xyz ,设正方体棱长为1.∴D (0,0,0),E ⎝⎛⎭⎫1,1,12,A (1,0,0),A 1(1,0,1),G ⎝⎛⎭⎫1,12,0,F ⎝⎛⎭⎫0,12,0. ∴AE ―→=⎝⎛⎭⎫0,1,12, A 1G ―→=⎝⎛⎭⎫0,12,-1,GF ―→=(-1,0,0). ∴AE ―→·A 1G ―→=0+12-12=0,AE ―→·GF ―→=0+0+0=0.∴AE ―→⊥A 1G ―→,AE ―→⊥GF ―→, 即AE ⊥A 1G ,AE ⊥GF , 又A 1G ∩GF =G , ∴AE ⊥平面A 1GF . ∵AE ⊂平面ADE ,∴平面ADE ⊥平面A 1GF . 法二:建立坐标系如法一.设平面AED 的法向量为n =(x 1,y 1,z 1). 平面A 1GF 的法向量为m =(x 2,y 2,z 2). 则n ⊥AE ―→,n ⊥AD ―→, ∴⎩⎨⎧n ·AE ―→=y 1+12z 1=0,n ·AD ―→=-x 1=0,取z 1=2,则n =(0,-1,2). 由m ⊥A 1G ―→,m ⊥GF ―→得 ⎩⎨⎧m ·A 1G ―→=12y 2-z 2=0,m ·GF ―→=-x 2=0,取z 2=1,则m =(0,2,1). ∵m ·n =0-2+2=0,∴m ⊥n . ∴平面ADE ⊥平面A 1GF .1.给定下列命题:①若n 1,n 2分别是平面α,β的法向量,则n 1∥n 2⇔α∥β;②若n 1,n 2分别是平面α,β的法向量,则α∥β⇔n 1·n 2=0;③若n 是平面α的法向量,且向量a 与平面α共面,则a ·n =0;④若两个平面的法向量不垂直,则这两个平面一定不垂直.其中正确命题的个数是( )A .1B .2C .3D .4解析:①③④正确,②中由α∥β⇒n 1∥n 2. 答案:C2.若直线l 的方向向量为a =(-1,0,2),平面α的法向量为n =(-2,0,4),则( ) A .l ∥α B .l ⊥α C .l ⊂αD .l 与α斜交解析:∵a =(-1,0,2),n =(-2,0,4), ∴n =2a ,即a ∥n . ∴l ⊥α. 答案:B3.若平面α,β的法向量分别为(-1,2,4),(x ,-1,-2),且α⊥β,则x 的值为( ) A .10 B .-10 C.12D .-12解析:∵α⊥β,∴α,β的法向量也垂直, 即(-1,2,4)·(x ,-1,-2)=0. ∴-x -2-8=0.∴x =-10. 答案:B4.设平面α与向量a =(-1,2,-4)垂直,平面β与向量b =(2,3,1)垂直,则平面α与β的位置关系是________.解析:由已知,a ,b 分别是平面α,β的法向量. ∵a ·b =-2+6-4=0, ∴a ⊥b ,∴α⊥β. 答案:垂直5.已知点P 是平行四边形ABCD 所在的平面外一点,如果AB ―→=(2,-1,-4),AD ―→=(4,2,0),AP ―→=(-1,2,-1).对于结论:①AP ⊥AB ;②AP ⊥AD ;③AP ―→是平面ABCD 的法向量;④AP ―→∥BD ―→.其中正确的是________.解析:AB ―→·AP ―→=-2-2+4=0,∴AP ⊥AB ,①正确;AP ―→·AD ―→=-4+4=0,∴AP ⊥AD ,②正确;且AP ―→是平面ABCD 的法向量;∴③正确,④错误.答案:①②③6.如图,在四棱锥P -ABCD 中,底面ABCD 是矩形,PA ⊥平面ABCD ,AP =AB =2,BC =22,E ,F 分别是AD ,PC 的中点.证明:PC ⊥平面BEF .证明:如图,以A 为坐标原点,AB ,AD ,AP 所在直线分别为x ,y ,z 轴建立空间直角坐标系.∵AP =AB =2,BC =AD =22,四边形ABCD 是矩形. 则A (0,0,0),B (2,0,0),C (2,22,0),D (0,22,0),P (0,0,2). 又E ,F 分别是AD ,PC 的中点, ∴E (0,2,0),F (1,2,1).∴PC ―→=(2,22,-2),BF ―→=(-1,2,1),EF ―→=(1,0,1). ∴PC ―→·BF ―→=-2+4-2=0,PC ―→·EF ―→=2+0-2=0. ∴PC ―→⊥BF ―→,PC ―→⊥EF ―→. ∴PC ⊥BF ,PC ⊥EF . 又BF ∩EF =F , ∴PC ⊥平面BEF .一、选择题1.若平面α,β的法向量分别为u =(2,-3,5),v =(-3,1,-4),则( ) A .α∥β B .α⊥β C .α,β相交但不垂直D .以上均不正确解析:∵-32≠1-3≠-45且u ·v ≠0,∴α,β相交但不垂直. 答案:C2.若直线l 的方向向量为ν=(2,2,2),向量m =(1,-1,0)及n =(0,1,-1)都与平面α平行,则( )A .l ⊥αB .l ∥αC .l ⊂αD .l 与α相交但不垂直解析:因为ν·m =2-2+0=0,ν·n =0+2-2=0,所以ν⊥m ,且ν⊥n ,又m 与n 不平行,所以ν⊥α,即l ⊥α.答案:A3.设A 是空间一定点,n 为空间内任一非零向量,满足条件AM ―→·n =0的点M 构成的图形是( )A .圆B .直线C .平面D .线段解析:M 构成的图形是经过点A ,且以n 为法向量的平面. 答案:C4.已知平面α内有一个点A (2,-1,2),它的一个法向量为n =(3,1,2),则下列点P 中,在平面α内的是( )A .(1,-1,1) B.⎝⎛⎭⎫1,3,32 C.⎝⎛⎭⎫1,-3,32 D.⎝⎛⎭⎫-1,3,-32 解析:要判断点P 是否在平面内,只需判断向量PA ―→与平面的法向量n 是否垂直,即PA ―→·n 是否为0即可,因此,要对各个选项进行逐个检验.对于选项A ,PA ―→=(1,0,1),则PA ―→·n =(1,0,1)·(3,1,2)=5≠0,故排除A ;对于选项B ,PA ―→=⎝⎛⎭⎫1,-4,12,则PA ―→·n =⎝⎛⎭⎫1,-4,12·(3,1,2)=0.同理,选项C 、D 也不符合要求,故选B.答案:B 二、填空题5.若直线l 的方向向量为(2,1,m ),平面α的法向量为⎝⎛⎭⎫1,12,2,且l ⊥α,则m =________.解析:∵l ⊥α,∴直线l 的方向向量平行于平面α的法向量.∴21=112=m 2,∴m =4. 答案:46.已知a =(0,1,1),b =(1,1,0),c =(1,0,1)分别是平面α,β,γ的法向量,则α,β,γ三个平面中互相垂直的有________对.解析:∵a ·b =(0,1,1)·(1,1,0)=1≠0,a ·c =(0,1,1)·(1,0,1)=1≠0,b ·c =(1,1,0)·(1,0,1)=1≠0.∴a ,b ,c 中任意两个都不垂直,即α,β,γ中任意两个都不垂直.答案:07.平面α,β的法向量分别为m =(1,2,-2),n =(-2,-4,k ),若α⊥β,则k 等于________.解析:由α⊥β知,m ·n =0.∴-2-8-2k =0,解得k =-5.答案:-58.如图所示,在直三棱柱ABC -A 1B 1C 1中,底面是以∠ABC 为直角的等腰三角形,AC =2a ,BB 1=3a ,D 是A 1C 1的中点,点E 在棱AA 1上,要使CE ⊥面B 1DE ,则AE =________.解析:建立如图所示的空间直角坐标系,则B 1(0,0,3a ),C (0,2a,0),D ⎝⎛⎭⎫2a 2,2a 2,3 a , 设E (2a,0,z )(0≤z ≤3a ),则CE ―→=()2a ,-2a ,z , B 1E ―→=(2a,0,z -3a ),B 1D ―→=⎝⎛⎭⎫2a 2,2a 2,0.又CE ―→·B 1D ―→=a 2-a 2+0=0,故由题意得2a 2+z 2-3az =0,解得z =a 或2a .故AE =a 或2a .答案:a 或2a三、解答题9.如图,正三棱柱ABC -A 1B 1C 1的所有棱长都为2,D 为CC 1中点.求证:AB 1⊥平面A 1BD .证明:取BC 中点O ,B 1C 1中点O 1,以O 为原点,OB ―→,OO 1―→,OA―→的方向为x 轴、y 轴、z 轴的正方向建立如图所示的空间直角坐标系,则B (1,0,0),D (-1,1,0),A 1(0,2, 3),A (0,0,3),B 1(1,2,0),∴AB 1―→=(1,2,-3),BD ―→=(-2,1,0),BA 1―→=(-1,2,3).∵AB 1―→·BD ―→=-2+2+0=0,AB 1―→·BA 1―→=-1+4-3=0,∴AB 1―→⊥BD ―→,AB 1―→⊥BA 1―→.即AB 1⊥BD ,AB 1⊥BA 1.又BD ∩BA 1=B ,∴AB 1⊥平面A 1BD .10.如图,正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点.(1)证明:平面AED ⊥平面A 1FD 1;(2)在AE 上求一点M ,使得A 1M ⊥平面DAE .解:(1)证明:建立如图所示的空间直角坐标系D - xyz ,不妨设正方体的棱长为2,则A (2,0,0),E (2,2,1),F (0,1,0),A 1(2,0,2),D 1(0,0,2).设平面AED 的法向量为n 1=(x 1,y 1,z 1),则⎩⎪⎨⎪⎧ n 1·DA ―→=(x 1,y 1,z 1)·(2,0,0)=0,n 1·DE ―→=(x 1,y 1,z 1)·(2,2,1)=0. ∴2x 1=0,2x 1+2y 1+z 1=0. 令y 1=1,得n 1=(0,1,-2). 同理可得平面A 1FD 1的法向量n 2=(0,2,1). 因为n 1·n 2=0,所以平面AED ⊥平面A 1FD 1.(2)由于点M 在AE 上,所以可设 AM ―→=λ·AE ―→=λ·(0,2,1)=(0,2λ,λ),可得M (2,2λ,λ),于是A 1M ―→=(0,2λ,λ-2).要使A 1M ⊥平面DAE ,需A 1M ⊥AE ,所以A 1M ―→·AE ―→=(0,2λ,λ-2)·(0,2,1)=5λ-2=0, 得λ=25.故当AM =25AE 时,A 1M ⊥平面DAE .。
空间直线平面的垂直

空间直线平面的垂直
在空间中,如果一条直线和一个平面内的任何一条直线都垂直,我们就说这条直线和这个平面互相垂直,直线叫做平面的垂线,平面叫做直线的垂面,平面的垂线和平面一定相交,交点叫垂足。
直线与平面垂直的判定定理为:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
此外,如果两个平面互相垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
直线与平面垂直是空间中一种重要的位置关系,在实际应用中有着广泛的应用。
如在建筑、工程、几何等领域中,常常需要判断直线与平面是否垂直。
