镜像法1(中文)
对偶原理、镜像原理(中文)

�
� l E � dl Im
jB � dS
S
S
前B述�边dS界条m件也必须加以修正 , 但仅涉及电场
强度的切向分量和磁场强度的法向分量, 即
en E2 E1 J mS
en B2 B1 mS
式中JmS (r) 为表面磁流密度;mS(r) 为表面磁荷密度 ;en
由媒质①指2向1,, 媒21 et质e②n E,2Jtm如S E下1t 图BB所12nn 示。
解 对于无限大的理想导电平面,垂直电流元
的镜像为正像。因此,上半空间的场强等于长度为 2l 的电流元产生的辐射场,即
E
j
Z0 I lsin r
e jkr
可见,场强振幅提高一倍。
接地的电流元仅向上半空间辐射,计算辐射功率 时仅需沿上半球面进行积分, 即
Pr
2π
d
π
2 Sr 2 sin
d
160π2 I 2
设时变电流元 Il 位于无限大的理想导电平 面附近,且垂直于该平面,如下图所示。
Il
,
Il
, ,
I'l'
引入的镜像源必须保持原有的边界条件。
正弦时变电流与时变电荷的关系为 I 。j时q 变电
流元的电荷积累在电流元的两端,上端电荷
端电q 荷I ,如下左图q 所 示I。
j
j
,下
镜像电流元为 I l ,且令I I ,l l
电磁场方程如下:
He J j Ee Ee j He
Be 0
De
H m j Em
Em J m j H m Bm m
Dm 0
He Jm Em Jm j H m Bm m
镜像法原理

镜像法原理镜像法,又称镜像原理,是物理学中的一种重要原理,它在光学、电磁学、流体力学等领域都有着广泛的应用。
镜像法的基本原理是通过假想一个镜像,来简化问题的求解,从而使得问题的求解变得更加容易和直观。
镜像法的应用可以大大简化问题的求解过程,提高问题的解决效率。
下面我们将详细介绍镜像法的原理及其在不同领域的应用。
首先,我们来介绍镜像法在光学中的应用。
在光学中,镜像法被广泛应用于光学成像问题的求解。
例如,在平面镜成像问题中,我们可以通过假想一个虚拟的物体,将实际物体和虚拟物体关于镜面的位置进行对称,从而得到虚拟物体的像的位置。
这样一来,我们就可以利用镜像法来简化平面镜成像问题的求解过程,大大提高问题的求解效率。
其次,镜像法在电磁学中也有着重要的应用。
在电磁学中,镜像法被广泛应用于求解导体表面的电场分布问题。
通过假想一个虚拟的镜像电荷,将实际电荷和虚拟电荷关于导体表面进行对称,从而得到虚拟电荷在导体表面的电场分布。
这样一来,我们就可以利用镜像法来简化导体表面的电场分布问题的求解过程,提高问题的解决效率。
此外,镜像法还在流体力学中有着重要的应用。
在流体力学中,镜像法被广泛应用于求解流体与固体边界的流动问题。
通过假想一个虚拟的镜像流体,将实际流体和虚拟流体关于固体边界进行对称,从而得到虚拟流体在固体边界的流动情况。
这样一来,我们就可以利用镜像法来简化流体与固体边界的流动问题的求解过程,提高问题的解决效率。
总的来说,镜像法是一种非常重要的物理原理,它在光学、电磁学、流体力学等领域都有着广泛的应用。
通过假想一个镜像,镜像法可以简化问题的求解过程,提高问题的解决效率。
因此,掌握镜像法的原理及其在不同领域的应用对于物理学和工程学领域的学习和研究都具有着重要的意义。
希望本文的介绍能够帮助大家更好地理解镜像法的原理及其应用。
第十三讲:镜像法

3.5镜像法1、了解镜像法的基本思想及理论依据;2、了解镜像法的替代要求;3、能运用镜像法求解某些形状简单的界面情况下的电场分布。
重点:1)镜像法的基本原理,2)像电荷的位置和大小的确定; 难点:根据界面情况设定像电荷位置。
讲授法 2学时3.5镜像法一、镜像法的基本思想和理论依据如果在所考虑的区域边界是导体或介质界面,则界面会产生感应电荷或极化电 荷,它们将对区域的场分布产生影响,但这些电荷分布事先并不知道,如何求解场分 布?能否将 感Q 、极Q 用场空间以外的区域的假想电荷来代替呢?若能,则就可以把 原来的边值问题的求解转化为均匀无界空间中的问题来求解。
1、镜像法的基本思想将边界对场的影响用边界外部虚设的像电荷代替。
2、镜像法的理论基础 唯一性定理、迭加原理 3、镜像法的替代要求1)像电荷必须放在研究的场域外,否则将改变研究区域的电荷分布。
2)像电荷和原来电荷共同产生的定解问题的边界条件和原来的一致。
3) 有限个像电荷。
像电荷无限多时,一般无意义。
但有时也可以求近似解。
二、镜像法的具体应用 1、接地导体平面的镜像例题1、接地无限大平面导体板附近有一点电荷,其电量为q ,距板为h 处,求空间 中的势分布。
解:1) 0z 的空间所以,0ϕ=。
✓ 方程与边界条件()2,,q x y z h ϕδε∇=-- (1)0R ϕ→∞= (2) 00z ϕ== (3) ✓ 求镜像为了满足方程(1),假想的电荷'q 必须在下半空间内,这样才能使原方程不变。
由于导体是等势体,'q 必须在q 的正下方(距导体面高度设为'h ),否则电场线不会 垂直于导体表面。
引入'q 后,边界条件(2)自然成立,由边界条件(3)有:'00z ϕ===上式对任意的(),x y 均成立,因而有:'h h =,'q q =-。
这样得到下半空间的势为:(),,x y z ϕ=讨论:1)感应电荷分布:()()3/23/222222022S z q h q hzx y h h ϕρεππρ=∂=-=-=-∂+++感应电荷: ()3/2022222in S S Sq hq dS d d q h ρρπρρπρρπρ∞∞===-=-+⎰⎰⎰ 2)导体板不接地,需要给出什么条件才能确定空间的电势?此时,下半空间的 势还为零吗?3)介质中极化电荷的分布? 4)如何计算q 受到的电场力? 推广:1)、线电荷对无限大接地导体平面的镜像;(注意电位零点的选择)x2) 0z >的空间2)、点电荷对相交半无限大接地导体平面的镜像;(垂直、夹角为n απ=) 2、导体球面的镜像例题2、点电荷q 位于一个半径为a 的接地导体球外,与球心距离为()d d a >, 求空 间各点的电位。
镜像法
p v R
则区域2中任一点的电位为:
2
q q
4π 2 R
q q
2
2
在分界面(R = R′= R″)上,应满足电位的边界条件:
1
1
设想用镜像电荷 代替界面上极化 电荷的作用,并 使镜像电荷和点 电荷共同作用, 满足界面上的边
界条件。
当待求区域为介质1所在区域时,在边界之外设一镜像电荷 q′
介质1中任一点的电位为:
1
q q
4π1R 4π1R
电磁场
第3章 静电场及其边值问题的解法
当待求区域为介质2所在区域时,
* 此时要保证z=0平面边界条件不变,即应为零电位。
q q 4R 4R
故对z=0平面上任意点有R R R0 :
于是,
q 4
1 R
1 R
q 4
q q 0 4 R0
1
x2 y2 (z h)2
电位的法向导数
n
s
f2 s
一、二类边界条件的 线性组合,即
n
s2
f4 s
电磁场
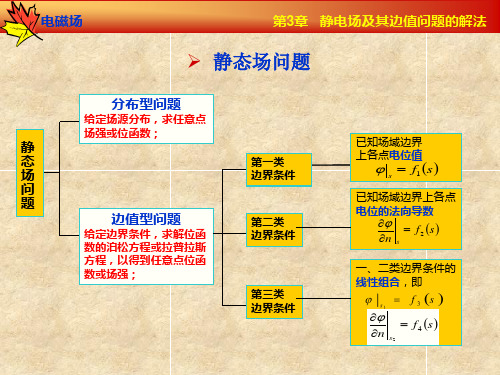
一、静电场边值问题及其分类
第3章 静电场及其边值问题的解法
1. 边值问题的分类----根据场域边界条件的不同
狄利克雷问题:给定整个场域边界上的电位函数值 s f1s
(第一类)
聂曼问题:给定待求位函数在边界上的法向导数值 (第二类)
U0
O
ax
第3章 静电场及其边值问题的解法
镜像法

/jp2007/02/wlkc/htm/c_4_p_4.htm§4.4 镜像法镜像法是求解电磁场的一种特殊方法,特别适用于边界面较规则(如平面、球面和柱面等)情况下,点源或线源产生的静态场的计算问题。
例如当一点电荷q 位于一导体附近时,该导体将处于点电荷q产生的静电场中,在导体表面上会产生感应电荷,则空间的电场应为该感应电荷产生的电场和点电荷q产生的电场的叠加。
一般情况下,在空间电场未确定之前,导体表面的感应电荷分布是不知道的,因此直接求解该空间的电场是困难的。
然而,在一定条件下,可以用一个或多个位于待求场域边界以外虚设的等效电荷来代替导体表面上感应电荷的作用,且保持原有边界上边界条件不变,则根据惟一性定理,空间电场可由原来的电荷q和所有等效电荷产生的电场叠加得到。
这些等效电荷称为镜像电荷,这种求解方法称为镜像法。
可见,惟一性定理是镜像法的理论依据。
在镜像法应用中应注意以下几点:(1)镜像电荷位于待求场域边界之外。
(2)将有边界的不均匀空间处理为无限大均匀空间,该均匀空间中媒质特性与待求场域中一致。
(3)实际电荷(或电流)和镜像电荷(或电流)共同作用保持原边界上的边界条件不变。
4.4.1 点电荷对无限大接地导体平面的镜像zqdx设在自由空间有一点电荷位于无限大接地导体平面上方,且与导体平面的距离为d 。
如图4.2(a)所示上半空间的电位分布和电场强度计算可用镜像法解决。
待求场域为0z >空间,边界为0z =的无限大导体平面,边界条件为在边界上电位为零,即(,,)0x y z φ= (4.29)设想将无限大平面导体撤去,整个空间为自由空间。
在原边界之外放置一镜像电荷'q ,当'q q =-,且'q 和q 相对于0z =边界对称时,如图4.2(b)所示。
点电荷q 和镜像电荷'q 在边界上产生的电位满足式(4.29)所示的边界条件。
根据镜像法原理,在0z >空间的电位为点电荷q 和镜像电荷'q 所产生的电位叠加,即1/21/2222222011{}4()()qx y z d x y z d φπε=-⎡⎤⎡⎤++-+++⎣⎦⎣⎦(4.30)上半空间任一点的电场强度为E φ=-∇电场强度E 的三个分量分别为3/23/22222220{}4()()x qxxE x y z d x y z d πε=-⎡⎤⎡⎤++-+++⎣⎦⎣⎦(4.31a)3/23/22222220{}4()()y qyyE x y z d x y z d πε=-⎡⎤⎡⎤++-+++⎣⎦⎣⎦(4.31b)3/23/22222220{}4()()z qz dz dE x y z d x y z d πε-+=-⎡⎤⎡⎤++-+++⎣⎦⎣⎦(4.31c)可见,在导体表面0z =处,0x y E E ==,只有z E 存在,即导体表面上法向电场存在。
大学电磁场与电磁波第二章2.8镜像法

E
=
q 4πε0
1 (r2
er
−
R dr12
er1
+
R dr2 2
er2
)
不接地导体球面上的正负感应电荷的 绝对值等于镜像电荷 q′吗? 为什么?
图2.8.7 点电荷位于不接地导体球附近的场图
补充题: 试确定用镜像法求解下列问题时,其镜像电荷的个数,大小与位置?
图2.8.8 点电荷对导体球面的镜像
=
qh
(h
2
1 + x2 )1/
2
∞
0
= −q
2. 导体球面镜像 设在点电荷附近有一接地导体球,求导体球外空间的电位及电场分布。
1) 边值问题:
∇2ϕ = 0 (除q点外的导体球外空间)
ϕ =0 r →∞
ϕ
=0
导球面
2) 设镜像电荷 − q′位于球内,球面上任一点电位为
ϕp
=q
4πε
r
− q' = 0
2
sin
θ
=
q'' 4πε2r
2
sin
θ
q + q' = q'' ε1 ε1 ε2 q − q'= q''
q' = ε1 − ε 2 q ε1 +ε2
和
q' ' = 2ε2 q ε1 +ε2
•ε1中的电场是由q与q' 共同产生,其有效区在上半空间,q'是等效替代极化电荷的
影响。
•ε 2中的电场是由 q'决' 定,其有效区在下半空间,q''是等效替代自由电荷与极化电荷
镜像法的原理及应用实例

镜像法的原理及应用实例1. 什么是镜像法?镜像法是一种分析问题和解决问题的方法,它借助于类比和比较的手段来帮助我们更好地理解问题的本质和寻找解决方案。
镜像法的基本思路是将问题或者事物转化为类似的模型或者情境,从而找到解决问题的方法或者规律。
2. 镜像法的原理镜像法的原理可以概括为以下几点:2.1 类比思维类比是镜像法的核心思维方式,它通过将问题或者事物与其他类似的模型或情境进行比较,以引出新的见解和解决思路。
通过类比思维,我们可以扩大思维的广度,提取共性和相似之处,从而更好地理解问题和找到解决方案。
2.2 转化思维镜像法的另一个重要原理是转化思维,即将问题或者事物转化为其他形式或者模型来进行分析和解决。
通过转化思维,我们可以摆脱原有的框架和限制,以新的视角来审视问题,发现不同的解决方案。
2.3 反向思维反向思维是镜像法的又一重要原理,它通过对问题进行反向思考,找到与常规思维相反的解决方案。
反向思维可以打破固有的思维局限,以不同的角度来看待问题,从而找到更加创新和有效的解决方案。
3. 镜像法的应用实例镜像法在各个领域都有着广泛的应用,接下来将为您介绍几个典型的应用实例。
3.1 创新设计在设计领域,我们经常会遇到需要解决新颖问题的情况。
镜像法可以帮助设计师通过类比和转化思维,从其他领域或者事物中找到灵感来源,创造出新的设计理念和方案。
3.2 问题解决在解决问题的过程中,我们常常会遇到难以解决或者复杂的问题。
镜像法可以帮助我们通过类比和反向思维,找到新的解决方案。
例如,如何解决一个复杂的算法问题,我们可以将其转化为其他领域的问题,然后采用类似的方法解决。
3.3 决策支持在决策过程中,我们需要全面分析和权衡各种因素。
镜像法可以帮助我们通过类比,比较不同方案的优劣,并找到最有效的解决方案。
通过镜像法,我们可以更好地理解和把握决策的关键因素。
4. 总结镜像法是一种重要的思维方法,它通过类比和转化的方式帮助我们更好地理解问题和寻找解决方案。
镜像法-高中物理竞赛讲义

与
是相似三角形,即
,于是球外任意一点的电位为
(4.4.3.6)
采用球坐标,取原点为球心 O 点,z 轴与 轴重合,则球外任一点
处
有
(4.4.3.7)
这样可求得电场 的分量为
(4.4.3.8)
r=a 时球面上的感应电荷密度1)
(1)点电荷对不接地、净电荷为零的导体球的镜像。 (2)点电荷对不接地、净电荷不为零的导体球的镜像。 (3)接地球形空腔内电荷的镜像
《镜像法》4,15
平行导线间单位长度电容: (4.4.2.10)
其中
小天线的镜像
与地面的小天线,长度为 l ,离地高度为 h 。 用位于地面下方 h 处的镜像小天线代替地面上的感应电荷,边界条件 维持不变。 与自由空间的天线比较,当天线离平面很近时,若天线与平面平行, 辐射功率为零,若天线与平面垂直,辐射功率增强。若天线与平面倾斜放置,则 辐射功率的变化与倾斜角度有关。具体辐射功率的计算请参看天线辐射(超链), 此处仅给出思路和结论。
点电荷对相交接地平面的镜像
条件:两相交接地平面夹角为 镜像电荷:2n-1 个。
,n=1,2,3…
若两相交接地平面夹角不满足上述条件,则镜像电荷为无
穷多个。
点电荷对介质平面的镜像
图 4.4.5 点电荷对相交接地地面 的镜像
1 区和 2 区为不同介质,求解时要分区域考虑。
求解区 1 的场:在区 2 置镜像电荷 。求解区 2 的场:在区 1 置镜
像
与地面平行的均匀双线传输线, 半径为 a,离地高度为 h,导线间距离为 d,导线一带正电荷+ ,导线二带负电荷-
。
用位于地面下方 h 处的镜像双 导线代替地面上的感应电荷,边界条件维
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这些等效电荷通常处于原电荷的镜像位置,因此 称 为镜像电荷,而这种方法称为镜像法。
依据:惟一性定理。等效电荷的引入不能改变原 来的边界条件。
关键:确定镜像电荷的大小及其位置。 局限性:仅仅对于某些特殊的边界以及特殊的电 荷分布才有可能确定其镜像电荷。
(1)点电荷与无限大的导体平面
以一个镜像点电荷q代替边界的影响,使整个空间变 成
均匀的介电常数为的空间,则空间任一点P的电位
由q及q'共同产生,即
+ q q'
中= r 无限r'大导体平面的电位为零
电场线与等位面的分布特性与电偶极子的上半部分 完全相同。
电场线
等位线
体
* 根据电荷守恒定律,镜像点电荷的电荷量应该等 于 导体表面上感应电荷的总电荷量。 * 上述等效性仅对于导体平面的上半空间成立,因 为 在上半空间中,源及边界条件未变。
对于半无限大导体平面形成的劈形边界也可应用镜 像法。但是为了保证这种劈形边界的电位为零,必须 引 入几个镜像电荷。
例如,夹角为n的导电劈需引入5个镜像电荷。
/g e :/ g
㊀/
/㊀ /㊉
兀 仅当这种导体劈的夹角等于 的整数分之一时,
才可求出其镜像电荷。 为什么?
位于无限大的导体平面附近的线电荷,根据叠加 原理得知,同样可以应用镜像法求解。
.P/
•Pl
「Pl
