1_7梯度算子
用sobel算子计算梯度例题

用sobel算子计算梯度例题Sobel算子是一种简单而常用的边缘检测算法,可以用于计算图像灰度值的一阶差分,从而得到图像领域的梯度。
Sobel算子基于离散卷积操作,对图像的每个像素点应用一个3x3的卷积核,计算其在x和y方向上的梯度,最终得到梯度幅值和方向。
下面是一个使用Sobel算子计算梯度的例题。
假设我们有一个灰度图像,如下所示:```23 44 56 34 1240 41 65 21 1719 32 43 71 2926 38 79 74 3653 31 68 25 47```我们首先需要定义两个Sobel卷积核,一个用于计算x方向上的梯度,另一个用于计算y方向上的梯度。
这两个卷积核如下所示:```Sx = [[-1, 0, 1],[-2, 0, 2],[-1, 0, 1]]Sy = [[-1, -2, -1],[ 0, 0, 0],[ 1, 2, 1]]```接下来,我们将这两个卷积核分别应用于原始图像,计算每个像素点在x和y方向上的梯度。
对于x方向上的梯度,我们通过将Sx卷积核与原始图像进行离散卷积操作,得到如下结果:```-34 -34 -77 -51 22-30 -24 -135 -50 3214 -9 -106 -17 4219 -41 -85 -59 1322 -37 -57 9 50```对于y方向上的梯度,我们通过将Sy卷积核与原始图像进行离散卷积操作,得到如下结果:```-95 -132 -9 37 -1225 82 -120 -57 -64-58 -56 -43 -7 2811 -6 36 35 -222 -7 41 42 5```接下来,我们可以使用计算得到的梯度值来得到梯度幅值。
梯度幅值可以简单地通过计算每个像素点在x和y方向上梯度值的模来得到。
```104 150 86 65 2252 102 144 72 5364 59 113 74 5029 43 95 84 1531 43 71 44 52```最后,我们还可以计算梯度方向,通过计算每个像素点在x和y方向上梯度值的反正切来得到。
roberts梯度算子的matlab程序

在机器学习和图像处理领域,Roberts梯度算子是一种常用的边缘检测算法。
它可以帮助我们在图像中快速准确地找到边缘位置,对于图像分割和特征提取等任务非常有用。
在本文中,我将重点介绍Roberts梯度算子的matlab程序,以及它在图像处理中的应用。
1. Roberts梯度算子的原理Roberts梯度算子是一种基于差分的边缘检测方法,它利用了图像中像素点的灰度值之间的变化来检测边缘。
具体来说,Roberts算子使用了两个3x3的卷积核:$$\begin{bmatrix}1 & 0 & 0\\0 & -1 & 0\\0 & 0 & 0\end{bmatrix}和\begin{bmatrix}0 & 1 & 0\\-1 & 0 & 0\\0 & 0 & 0\end{bmatrix}$$分别对图像进行卷积运算,然后将它们的平方和再开方得到边缘检测结果。
这种方法可以很好地捕捉到图像灰度值的变化,从而找到图像中的边缘。
2. Roberts梯度算子的matlab程序下面是一个简单的Roberts梯度算子的matlab程序示例:```matlabfunction [edge_image] = roberts_edge_detection(image)[m, n] = size(image);edge_image = zeros(m, n);for i = 1 : m - 1for j = 1 : n - 1% 对图像进行卷积运算edge_image(i, j) = abs(image(i, j) - image(i+1, j+1)) + abs(image(i, j+1) - image(i+1, j));endendend```这段matlab代码实现了对图像的Roberts边缘检测。
首先读入图像,然后对每个像素点进行Roberts算子的卷积运算,最后得到一个边缘图像。
【计算机应用】_梯度算子_期刊发文热词逐年推荐_20140728
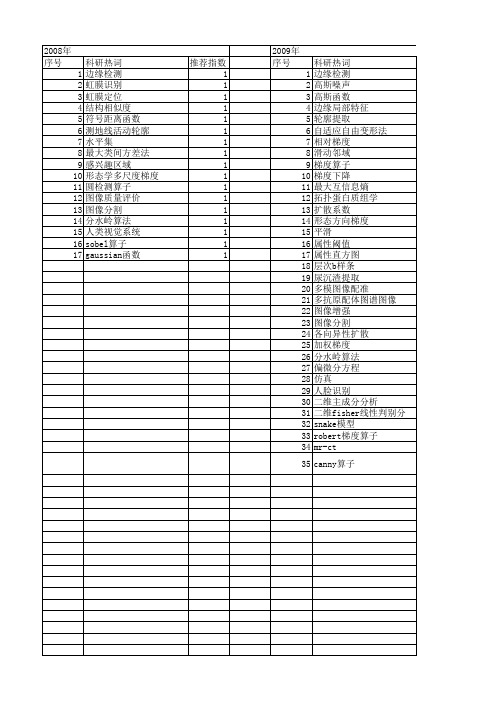
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
科研热词 边缘检测 高斯噪声 高斯函数 边缘局部特征 轮廓提取 自适应自由变形法 相对梯度 滑动邻域 梯度算子 梯度下降 最大互信息熵 拓扑蛋白质组学 扩散系数 形态方向梯度 平滑 属性阈值 属性直方图 层次b样条 尿沉渣提取 多模图像配准 多抗原配体图谱图像 图像增强 图像分割 各向异性扩散 加权梯度 分水岭算法 偏微分方程 仿真 人脸识别 二维主成分分析 二维fisher线性判别分析 snake模型 robert梯度算子 mr-ct canny算子
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
科研热词 推荐指数 边缘检测 3 最大类间方差法 2 非整数步长 1 边缘连接 1 边缘宽度细化 1 行人检测 1 自适应阈值 1 背景建模 1 羊毛细度测量 1 纹理分析 1 码书 1 电容层析成像 1 灰度调整因子 1 灰度共生矩阵 1 梯度算子 1 梯度方向直方图 1 梯度因子 1 梯度信息 1 标准偏差 1 斜坡模型 1 数学形态学 1 支持向量机 1 拉格朗日插值 1 异质扩散 1 局部能量 1 多尺度检测 1 图像重建 1 图像融合 1 图像分块 1 图像二值化 1 前景分割 1 偏微分方程 1 visual basic 1 sobel算子 1 riemann-liouville分数阶微分 1 canny算子 1 bernsen法 1
罗伯特交叉梯度算子例题

罗伯特交叉梯度算子例题罗伯特交叉梯度算子是一种经典的边缘检测算子,它可以帮助我们在图像中检测出边缘的位置。
这个算子是由罗伯特·C·加德(Robert C. Roberts)于1973年提出的,它利用了图像中相邻像素之间的差异来识别边缘。
为了更好地理解罗伯特交叉梯度算子的原理,我们可以通过一个简单的例题来说明。
假设我们有一个3x3的图像矩阵如下:1 2 3。
4 5 6。
7 8 9。
我们可以使用罗伯特交叉梯度算子来计算每个像素点的边缘强度。
具体地,我们可以使用以下两个3x3的卷积核(也称为罗伯特算子)来进行卷积操作:Gx = [[1, 0, 0], [0, -1, 0], [0, 0, 0]]Gy = [[0, 1, 0], [-1, 0, 0], [0, 0, 0]]其中,Gx是用来检测水平边缘的卷积核,Gy是用来检测垂直边缘的卷积核。
我们分别将这两个卷积核与原始图像进行卷积操作,得到水平方向和垂直方向的边缘强度。
对于上述的3x3图像矩阵,我们可以计算出每个像素点的水平和垂直边缘强度。
例如,对于像素点(2,2)处的像素值5,我们可以使用以下公式来计算水平和垂直边缘强度:水平边缘强度,Gx = (6-4) = 2。
垂直边缘强度,Gy = (2-8) = -6。
通过计算所有像素点的水平和垂直边缘强度,我们可以得到整个图像的边缘信息。
一般来说,我们可以将水平和垂直边缘强度进行合并,得到最终的边缘强度。
在实际应用中,我们可以设定一个阈值来筛选出边缘强度大于阈值的像素点,从而得到图像的边缘信息。
总的来说,罗伯特交叉梯度算子通过计算图像中相邻像素之间的差异来检测边缘,它是一种简单而有效的边缘检测算子。
在实际应用中,它常常被用于计算机视觉和图像处理领域,用来帮助识别图像中的边缘信息。
梯度算子公式

梯度算子公式梯度算子公式在图像处理中起着重要的作用。
它被广泛应用于图像边缘检测、特征提取和图像增强等领域。
本文将对梯度算子公式进行详细介绍,并且讨论其在图像处理中的应用。
在图像处理中,梯度算子公式用于计算图像中每个像素点的梯度值。
梯度指的是函数在某一点上的变化率,可以看作是函数在该点上的导数。
对于二维图像,梯度算子公式可以表示为:G(x, y) = sqrt((Gx(x, y))^2 + (Gy(x, y))^2)其中,Gx(x, y)和Gy(x, y)分别表示图像在x和y方向上的梯度值。
梯度算子公式的计算是通过对图像进行卷积操作来实现的。
常用的梯度算子有Sobel算子、Prewitt算子和Roberts算子等。
Sobel算子是一种常用的梯度算子,它可以检测图像中的边缘。
Sobel算子的计算公式如下:Gx = [-1 0 1; -2 0 2; -1 0 1] * AGy = [-1 -2 -1; 0 0 0; 1 2 1] * A其中,A表示原始图像,Gx和Gy分别表示图像在x和y方向上的梯度值。
在计算过程中,首先将原始图像与Sobel算子进行卷积操作,然后将卷积结果分别与Gx和Gy相乘得到最终的梯度值。
Prewitt算子也是一种常用的梯度算子,它与Sobel算子类似,可以用于边缘检测。
Prewitt算子的计算公式如下:Gx = [-1 0 1; -1 0 1; -1 0 1] * AGy = [-1 -1 -1; 0 0 0; 1 1 1] * ARoberts算子是一种简单但有效的梯度算子,它可以用于图像边缘检测。
Roberts算子的计算公式如下:Gx = [1 0; 0 -1] * AGy = [0 1; -1 0] * A除了边缘检测,梯度算子公式还可以用于图像特征提取。
通过计算图像的梯度值,可以获取图像中的纹理、形状等特征信息。
梯度算子可以用于图像的角点检测、轮廓提取和目标定位等应用中。
边缘检测与梯度算子

边缘检测与梯度算⼦边缘检测边缘是指图象中灰度发⽣急剧变化的区域。
图象的变化情况可以⽤灰度分布的梯度来反映,给定连续图象f(x,y),其在边缘法线⽅向上取得局部最⼤值。
图象中⼀点的边缘被定义为⼀个⽮量,模为当前点最⼈的⽅向导数,⽅向为该⾓度代表的⽅向。
通常我们只考虑其模,⽽不关⼼⽅向。
梯度算⼦(⼀)梯度算⼦可分为3类:1、使⽤差分近似图像函数导数的算⼦。
有些是具有旋转不变性的(如:),因此只需要⼀个卷积掩模来计算。
其它近似的算⼦使⽤⼏个掩模。
2、基于图像函数⼆阶导数过零点的算⼦(如:M arr—Hild reth或Canny边缘检测算⼦。
3、试图将图像函数与边缘的参数模型相匹配的箅⼦。
(⼆)第⼀类梯度算⼦(Laplace)算⼦通常使⽤3×3的掩模,有时也使⽤强调中⼼象素或其邻接性的(这种近似不再具有旋转不变性)。
拉普拉斯算⼦的缺点:它对图像中的某些边缘产⽣双重响应。
图像锐化(shapeening)图像锐化的⽬的是图像的边缘更陡峭、清晰。
的输出图像f是根据下式从输⼊图像g得到的:f(i,j)=g(i,j)-c s(i,j),其中c是反映锐化程度的正系数,s(i,j)是图像函数锐化程度的度量,⽤梯度箅⼦来计算,Laplacian箅⼦常被⽤于这⼀⽬的。
Prewitt边缘检测算⼦Sobel边缘检测算⼦(三)第⼆类梯度算⼦--⼆阶导数过零点算⼦根据图象边缘处的⼀阶微分(梯度)应该是极值点的事实,图象边缘处的⼆阶微分应为零,确定过零点的位置要⽐确定极值点容易得多也⽐较精确。
右侧是Lena的过零点检测结果。
为抑制噪声,可先作平滑滤波然后再作⼆次微分,通常采⽤⾼斯函数作平滑滤波,故有LoG(Laplacian of Gaussian)算⼦。
⾼斯-拉普拉斯(LoG,Laplacian of Gaussian)算⼦。
噪声点对边缘检测有较⼤的影响,效果更好的边缘检测器是⾼斯-拉普拉斯(Lo G)算⼦。
它把⾼斯平滑滤波器和拉普拉斯滤波器结合起来,先平滑掉噪声,再进⾏,所以效果更好。
梯度算子的名词解释

梯度算子的名词解释梯度算子,是一种在图像处理和计算机视觉领域中广泛使用的数学工具。
它被用来表示图像中每个像素点的强度变化情况,从而为进一步的图像处理提供了重要的信息。
一、梯度的概念梯度可以理解为一个向量,它包含了某个函数在每个点上的变化率和变化方向。
在图像处理中,梯度表示了图像中像素强度的改变情况。
以二维图像为例,对于图像中的某个像素点,梯度可以用一个二维向量表示。
这个向量的方向指向像素点周围变化最快的方向,大小表示强度变化的大小。
通常情况下,我们用灰度图像进行处理,所以梯度向量的大小可以近似表示图像中的边缘强度。
二、梯度算子的引入为了计算图像中的梯度,人们引入了不同的算子和滤波器。
这些算子可以对图像进行卷积操作,从而得到图像中每个像素点的梯度信息。
常用的梯度算子有Sobel算子、Prewitt算子和Laplacian算子等。
1. Sobel算子Sobel算子是一种线性滤波器,它分别在水平和垂直方向上计算梯度。
在计算过程中,Sobel算子采用了一个3x3的卷积核。
对于水平方向梯度,卷积核的权重为[-1, 0, 1; -2, 0, 2; -1, 0, 1],而对于垂直方向梯度,卷积核的权重为[-1, -2, -1; 0, 0, 0; 1, 2, 1]。
通过卷积操作,Sobel算子可以分别计算出水平和垂直方向上的梯度信息,从而得到整个图像的梯度。
2. Prewitt算子Prewitt算子是另一种用于计算图像梯度的算子。
它也采用了3x3的卷积核,但其权重分布不同于Sobel算子。
Prewitt算子在水平和垂直方向上的卷积核权重分别为[-1, 0, 1; -1, 0, 1; -1, 0, 1]和[-1, -1, -1; 0, 0, 0; 1, 1, 1]。
类似于Sobel算子,Prewitt 算子可以得到图像中的水平和垂直方向上的梯度信息。
3. Laplacian算子与Sobel算子和Prewitt算子不同,Laplacian算子是一种二阶的梯度算子,它能够更好地检测图像中的边缘。
梯度算子运算法则

梯度算子运算法则
在数值计算中,梯度算子运算法则对实现的准确性有着至关重要的作用。
梯度算子,也称做梯度操作或者率运算符,是一种求极值的方法。
它用来指示变量在哪个方向上的变化最快,也可以用来代表该函数随着其变量改变的速度。
梯度算子有多种不同的形式,但是其核心思想是一致的:一阶偏导数(即一阶梯度)提供了某个特定变量的梯度,这个梯度表示了该函数关于它的变量的变化程度。
在这里,我们将讨论梯度算子运算法则的基本概念和实际操作。
首先,让我们来了解梯度算子的基本概念。
梯度算子是求取局部函数极值的一种数值估计方法,它利用了函数导数对指定变量的导数值来估计极值。
梯度算子可以在没有解析解的情况下,通过数值计算而得到一阶偏导数,从而求得变量的极值,比如求函数最大值或最小值。
梯度算子的具体运算法则主要分为三步:一是计算一阶偏导数;二是确定增量;三是根据增量迭代求解。
对于一般的函数y=f(x) 上的梯度算子,首先要计算函数的一阶偏导数∂f/∂x,以获取当前变量x 的梯度;然后确定一个增量,得到增量后x 的变化量为Δx ;最后,在x 上增加增量Δx 后求函数的新值,即y1 = f(x + Δx)。
上述三步实现的是梯度算子运算的基本原理,梯度算子的多元变量求解过程则比较复杂,但基本思想是一致的。
在多元变量
的求解中,采用同样的梯度算子的运算法则:先求多元变量的梯度,然后确定增量,再根据增量迭代求解。
最后,梯度算子运算是一种有效且精确的求极值方法。
然而,使用这种数值比值计算法可能引入一些错误,比如误差传递,取样误差等等。
因此,在使用梯度算子计算极值时,要注意避免这些错误的产生,以确保计算的精确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这里我们把 ∇ 看成一个新的算符,这是一个标量算符。由于经常出现在物理学
2
中,因而它被赋予一个名称,即 Laplace 算符:
∂2 ∂2 ∂2 ∇ = ∂i∂i = 2 + + ∂x1 ∂x2 2 ∂x32
2
(20)
由于 Laplace 算符是一个标量算符,就可以用它来对一个矢量进行运算——这意 味着对在直角坐标系的每一个分量进行同一种运算:
∇ ≡ ( ∂1 , ∂ 2 , ∂ 3 )
或者
(7)
ˆi ∂ i ∇=x
那当然就意味着其分量
(8)
∇i = ∂i
(9)
顺便提一句,在有关张量的现代处理中,我们正是把 ∂ i 这样的微分算符看作矢 量基的。
第 2 页,共 7 页
当 ∇ 作用在标量函数或者矢量场上, 就是我们所熟悉的梯度、 散度以及旋度:
∂x1 、∂φ ∂x2 和 ∂φ ∂x3 。由于有这三种微商,而我们又知道要
形成一个矢量需要三个数量,也许这三个微商就是一个矢量的分量?! 当然,一般并非任何三个数量都能构成为一个矢量的。只有当我们旋转坐标 系,各个分量按照正确的方式变换时,这才成立。所以需要分析坐标系旋转时, 这些微商是如何变换的。为此,我们采用一个新坐标系 xi′ 系中,微商变为 ∂φ ′ 式法则,有
因此,体积元为
gθθ = r 2 ,
g =r
(A4)
dV = gdrdθ dz = rdrdθ dz
而
(A5)
∂f 1 ∂f ˆ ∂f ˆ+ ˆ θ+ z r ∂r r ∂θ ∂z 1 ∂ ⎛ ∂f ⎞ 1 ∂ 2 f ∂ 2 f 2 ∇ f = + ⎜r ⎟+ r ∂r ⎝ ∂r ⎠ r 2 ∂θ 2 ∂z 2 K 1 ∂ 1 ∂A ∂A ∇⋅ A = ( rAr ) + θ + z ∂z r ∂r r ∂θ K ⎛ 1 ∂Az ∂Aθ ⎞ ⎛ ∂Ar ∂Az ˆ+⎜ ∇× A = ⎜ − − ⎟r ∂ ∂ ∂ ∂r θ r z z ⎝ ⎠ ⎝ ∇f =
i
(15)
1 = ε ijk ( ∂ i ∂ j Ak − ∂ i ∂ j Ak ) ≡ 0 2
第一个式子说明任一标量场的梯度是无旋场, 而第二个则是说任一矢量场的旋度 是无散场(或无源场) 。 现在我将不加证明地陈述两个物理学中非常有用的数学定理。在一个物理问 题中,我们经常会发现某一个矢量场的旋度为零,而我们注意到,一个梯度的旋 度为零,于是,肯定有可能本来就是某一个标量的梯度,这样它的旋度才必然等 于零。第一个定理是讲:
梯度算子
首先我想谈谈场这个在物理学中非常基本的概念。我们所说的场是指取决于 空间位置的一个量。最可能简单的一种物理场是标量场,所谓标量场,是指每点 仅有一个单独数量——一个标量——所标志的那种场。 当然这个数量还可随时间 而变,不过眼下我们还无需为此操心。我们将只谈论在某一特定时刻,场看来是 个什么样子。作为标量场的一个例子,你可以考虑一块固体材料,其中某些地方 受热而另一些地方受冷,使得该物体的温度以一种复杂方式逐点改变。于是温度 将是从某个迪卡尔坐标系上量得的代表空间每一位置的函数。 可见温度是一标量 场。另一个常见的例子则是势场。 还有一种场叫做矢量场, 意义也十分简单。 就是在空间每一点给出一个矢量, 这个矢量逐点变化。作为一个例子,可考虑一个旋转物体。在每点上物体中原子 的速度便是位置函数的矢量。作为第二个例子,考虑在一块材料中的热流。如果 某处的温度高于另一处的,热量就会从较热处流至较冷处。在材料中的不同位置 热量将朝不同的方向流动,这一热流就是一个矢量场。 当然,类似的,你也可以给张量场下个定义。 当场随时间变化时,可通过给出场对时间的微商来加以描述。我们希望也按 同样办法来描述场对空间的变化, 因为对于例如或者相邻两点之间的温度或者势 能关系我们是感兴趣的。值得注意的是,对任一标量场,例如 φ ,其可能的微商 有三个: ∂φ
因而 (22)
K K K (23) ∇ × (∇ × A ) = ∇ (∇ ⋅ A) − ∇ 2 A K 而这里出现的 ∇ ( ∇ ⋅ A ) 也就是我们仅剩的还未考虑的一个组合, 不过是偶尔会
出现的一种矢量场罢了,对它没什么特别需要注意的。 把上面的结论放在一起:
∇ ⋅ ( ∇φ ) = ∇ 2φ = scalar field ∇ × ( ∇φ ) = 0 K ∇ ( ∇ ⋅ A ) = vector field K ∇ ⋅ (∇ × A) = 0 K K K ∇ × ( ∇ × A ) = ∇ ( ∇ ⋅ A ) − ∇ 2 A = vector field K K 2 A A ∇ ⋅ ∇ = ∇ = vector field ( )
如果 就有一个 使得
当散度为零时,还有一个类似定理:
K ∇× A = 0 K A = ∇ψ
K ∇⋅B = 0 K A K K B = ∇× A
ψ
(16)
如果 就有一个 使得
(17)
在检查由两个算符的可能结合中,我们已经找出了其中有两种结合总是等于 零的。现在看看那些不等于零的。考虑(14)所列的第一结合,
K
K
K
K = ∂f ∂r ,在分析力学部分我们会
比较多的采用这个记法, 其好处在下面这样一个简单的例子中可见一斑。 设 粒子位矢 r 的函数,而 r 本身又是某个变量 q 的函数,现在我们要求 微商,根据链式法则,有
f
是
K
K
f
对q 的
df ∂f dx i = dq ∂xi dq
而采用这里的写法,我们就可以将上式写为
∂ 2φ ∂ 2φ ∂ 2φ ∇ ⋅ ( ∇φ ) = ∂ i ( ∂ iφ ) = ∂ i ∂ iφ = 2 + + ∂x1 ∂x2 2 ∂x32
∇ ⋅ ( ∇φ ) = ∇ ⋅ ∇φ = ( ∇ ⋅ ∇ )φ = ∇ 2φ
第 4 页,共 7 页
(18)
因此在这个式子中我们没必要保留那个括号,所以,在不引起混乱的情况下写成 (19)
∂f ˆi = K grad φ = ∇φ = ( ∂ iφ ) x ∂r K K div A = ∇ ⋅ A = ∂ i Ai K K ˆi curl A = ∇ × A = ( ε ijk ∂ j Ak ) x
(10)
值得注意的是,上面的式子中顺序是很重要的,例如 ∇ ⋅ A 是矢量场 A 的散度, 它是一个标量;而 A ⋅ ∇ 并非一个数值,它仍然是某种算符。另外,这里我还写 出了标量场梯度的另一种表示方法,即 ∇φ
(11)
K df ∂f dr = K⋅ dq ∂r dq
(12)
这在涉及质点组问题时会带来较大的方便。 利用式(10)给出的这些结合,就可以按照一种方便的方式——一种并不依赖 于任一特定坐标系的普遍方式——来写出关于场的空间变化。 作为对矢量微分算 符 ∇ 应用的一个例子,我在这里把 Maxwell 方程写出来:
例如,对于柱坐标系有
K 1 ∂ ⎛ g ⎞ Ai ⎟ ∇⋅ A = ⎜ ⎟ g g ∂ui ⎜ ⎝ i ⎠ 1 ∂ ⎛ g ∂f ⎞ ∇2 f = ⎜ ⎟ ⎟ ∂ g u g ∂ui ⎜ i ⎠ ⎝ i
(A2)
ds 2 = dr 2 + r 2 dθ 2 + dz 2
即
(A3)
g rr = g zz = 1,
∂Ar ⎞ ˆ 1⎛ ∂ ⎟θ + ⎜ ( rAθ ) − ∂θ r ⎝ ∂r ⎠
⎞ ˆ ⎟z ⎠
(A6)
第 6 页,共 7 页
而对于球坐标系,则有
ds 2 = dr 2 + r 2 dθ 2 + r 2 sin 2 θ dϕ 2
即
(A7)
g rr = 1,
因此,体积元为
gθθ = r 2 ,
gϕϕ = r 2 sin 2 θ ,
∂x j ∂x′ = λkj k = λkjδ ik = λij ∂xi′ ∂xi′
将它代入式(1),我们就得到了
(3)
∂φ ∂φ = λij ∂xi′ ∂x j
这个式子说明
(4)
( ∂φ
∂x1 , ∂φ ∂x2 , ∂φ ∂x3 ) 是一个矢量。
上面的论证与我们究竟是在对哪一个标量场进行微分是没有关系的。既然不 管我们对之进行微分的是什么,那些变换公式都相同,那就可以略去 φ 而由一个 算符方程式来代替式(4):
K ∇ ⋅ E = ρ, K ∇ ⋅ B = 0,
K K ∂B ∇× E = − ∂t K K ∂E K ∇× B = +J ∂t
(13)
迄今为止,我们只有场的一阶变化。当然我们本来也可以考虑二阶微商,这 有以下几种可能的结合式:
∇ ⋅ ( ∇φ ) ,
∇ × ( ∇φ ) ,
K ∇ (∇ ⋅ A) ,
= λij x j ,在这个坐标
∂xi′ = ∂φ ∂xi′ ,这是因为 ∂φ ′ ∂xi′ 是一个标量。利用链
∂φ ∂x j ∂φ 页
(1)
为了得到 ∂x j
∂xi′ 这个系数,我们写出坐标变换的反变换 ′ x j = λkj xk
(2)
并将其两边对 xi′ 求导数,得
∂ ∂ = λij ∂xi′ ∂x j
在很多参考书上也将 ∂
(5)
∂xi 用 ∂ i 来表示,即 ∂ i ≡ ∂ ∂xi 。这样的记号写起来更
加简单,而且在复杂的场合也不容易出错。而目前,我们则可以利用它将上面的 变换关系可以写得好看一些
∂′ i = λij ∂ j
(6)
由于这些微分算符本身就已如同一个矢量的分量那样进行变换,我们便可以 称之为一个矢量算符的分量,通常用符号 ∇ 来表示这个矢量算符,即可以写成
K ∇ ⋅ (∇ × A ) ,
K ∇ × (∇ × A )
