一元二次方程实根分布第九周第五次作业
一元二次方程根的分布例题

例6.2.已知抛物线y = 2x2-mx+m与直角坐标平面上两点(0,0), (1,1)为端点 的线段(除去两个端点)有公共点,求m的取值范围. 解:以(0,0), (1,1)为端点的线段所在直线为y=x,代入抛物线方程得:
x = 2x2-mx+m 即 2x2-(m+1)x+m=0, ① 由题意,方程①在区间(0, 1)上有实根,令f(x) = 2x2-(m+1)x+m,则 当且仅当 f(0)·f(1)<0或 m<0或 m≤3-2且m≠0. 故m的取值范围为 (-, 0)∪(0, 3-2]. 例6.3.设关于的方程R), (1)若方程有实数解,求实数b的取值范围; (2)当方程有实数解时,讨论方程实根的个数,并求出方程的 解。 分析:可用换元法,设,原方程化为二次方程,但要注意,故原方程有 解并不等价于方程有解,而等价于方程在内有解.另外,方程有解的问 题也可以通过参变分离转化为求值域的问题,它的原理是:若关于的方 程有解,则的值域. 解:(1)原方程为, , 时方程有实数解; (2)①当时,,∴方程有唯一解; ②当时,. 的解为; 令 的解为; 综合①、②,得 1)当时原方程有两解:; 2)当时,原方程有唯一解; 3)当时,原方程无解。 变式:已知方程在上有两个根,求的取值范围. 解:令,当时,. 由于是一一映射的函数,所以在上有两个值,则在上有两个对应的 值.因而方程在(0,2)上有两个不等实根,其充要条件为
例6.2.已知抛物线y = 2x2-mx+m与直角坐Байду номын сангаас平面上两点(0,0), (1,1)为端点 的线段(除去两个端点)有公共点,求m的取值范围.
例6.3.设关于的方程R), (1)若方程有实数解,求实数b的取值范围; (2)当方程有实数解时,讨论方程实根的个数,并求出方程的
二次函数与一元二次方程根的分布讲义及作业

二次函数与一元二次方程根的分布讲义及作业二次函数与一元二次方程根的分布1. 二次函数的解析式的三种形式2b b 4ac -b 一般式:y =ax +bx +c (a ≠0) ;对称轴方程是x =-;顶点为(-, ) ;2a 2a 4a2两点式:y =a (x -x 1)(x -x 2) ;对称轴方程是;与x 轴的交点为; y =a (x -k ) 2+h ;对称轴方程是;,求f (x )的表达式顶点式:例1. 设二次函数f (x )满足f (x -2)=f (-x -2),且图象在y 轴上的截距为1,在x 轴上截得的线段长为2. 一元二次函数的单调性:当a>0时:在为减函数;当a在区间;C.上是减函数,那么();D..;B.例2. 如果二次函数例3 二次函数f (x )的二次项系数为正,且对任意实数x 恒有f (2+x )=f (2-x ),若f (1-2x )(1)f(x)=ax+bx+c(a ≠0)的图像与x 轴交点的横坐标是方程_______________的实根(2)若222x 1x 2为f(x)=0的实根,则f(x)在x 轴上截得的线段长应为|x 1-x2|=_________________________(3)当_________________时,恒有f(x)>0;当____________________时,恒有f(x)例4已知f (x ) 是二次函数,不等式f (x )14. 常见的实根分布情况况分两个负根即两根都小于0 两个正根即两根都大于0 一正根一负根即一个根小于0,一布情大致图象(a >0)得出的结论(a)大致图象得出的结论(不讨论综a 合)结论情况大致图象(a >0)得出的结论(x 10⎪⎪⎪-b⎪2a ⎪⎪f (0)>0⎪⎪∆>0⎪⎪-b 0⎪⎪-b a 0两根都小于k 即x 1⎪⎪∆>0⎪⎪-b 0(x 1>0, x 2>0) 个大于0 (x 1⎪⎪∆>0f (0)⎪⎪-b >0 ⎪2a ⎪⎪f (0)>0⎪⎪∆>0f (0)>0⎪⎪-b 2a >0 ⎪⎪⎪f (0)0a ⋅f (0)⎪⎪-b >0 ⎪2a ⎪⎪a ⋅f (0)>0一个根小于k ,一个大于两根都大于k 即k 即x 1>k , x 2>kx 1kk⎪⎪∆>0⎪⎪-b 2a >k f ⎪(k )⎪⎪f (k )>02大致图象(a)得出的结论⎪∆>0⎪b ⎪0⎪b ⎪⎪∆>0⎪b ⎪>k ⎪-2a ⎪⎪⎪f (k )0⎪b ⎪>k ⎪-2a ⎪⎪⎪a ⋅f (k )>0 f (k )>0综)合结论(不讨论a表三:分布情况大致图象(a >0)得出的结论大致图象(a)3a ⋅f (k )两根有且仅有一根在两根都在(m , n )内种)(m , n )内一根在(m , n )内,另一根在(图象有两种情况,只画了一(p , q )内,m⎪∆>0⎪⎪f (m )>0⎪⎪f (n )>0 ⎪b ⎪m2a ⎪⎪f (m )⋅f (n )⎪f (m )>0⎪⎪f (n )⎪f (m )f (n )f p 0⎪得出的结论⎪∆>0⎪⎪f (m )⎪f (n )2a ⎪⎪f (m )⋅f (n )⎪f (m )⎪⎪f (n )>0⎪⎪f (m )f (n )或⎪⎪f p >0f p f q⎪f (m )f (n )⎪⎪⎪f (p )f (q )综)合结论(不讨论a例5. 对于关于x 的方程x +(2m-1)x+4-2m=0 求满足下列条件的m 的取值范围(1)两个正根(2)有两个负根(3)两个根都小于-1(4)两个根都大于1/2 (5)一个根大于2,一个根小于2 (6)两个根都在(0 ,2)内(7)两个根有且仅有一个在(0 . 2)内(8)一个根在(-2 .0)内,另一个根在(1 . 3)内(9)一个正根,一个负根且正根绝对值较大(10)一个根小于2,一个根大于44——————f (m )⋅f (n )29.4课后作业一1. 函数的图象的对称轴为x +2=0,则m ;顶点坐标为递减区间为 .22. 已知函数f(x)=ax+2ax+4(a>0),若x 1A .f(x1)f(x2) D.f(x1) 与f(x2) 的大小不能确定3一元二次方程ax 2+2x +1=0,(a ≠0) 有一个正根和一个负根的充分不必要条件是:() A.a4已知二次函数>0 C .a 1f (x ) =ax 2+bx +c ,满足条件f (2+x ) =f (2-x ) ,其图象的顶点为A ,又图象与x 轴交于点B 、C ,其中B点的坐标为(-1,0) ,∆ABC 的面积S =54,试确定这个二次函数的解析式.5⑴关于x 的方程x⑵关于x 的方程x⑶关于x 的方程x⑷关于x 的方程mx2222+2(m +3) x +2m +14=0有两实根,且一个大于1,一个小于1,求m 的取值范围;+2(m +3) x +2m +14=0有两实根在[0, 4)内,求m 的取值范围;+2(m +3) x +2m +14=0有两实根在[1, 3]外,求m 的取值范围;+2(m +3) x +2m +14=0有两实根,且一个大于4,一个小于4,求m 的取值范围.5课后作业参考答案1. -2,(-2,3);(-∞,-2),(-2,+∞)2.A3.C4.5解:令f(x)= x2y =2(x -2) 2-18或y =-2(x -2) 2-18+2(m +3) x +2m +14,2⑴ ∵ 对应抛物线开口向上,∴ 方程有两实根,且一个大于1,一个小于1,等价于f(1)+2(m +3) ∙1+2m +1421. 4⎪f (0) ≥0⎪2m +14≥0⎪f (4) >0⎪16+8(m +3) +2m +14>0⎪27⎪⎪⇔⇔-⎪⎪2⎪m ≤-5或m ≥1⎪∆=4(m +3) -4(2m +14) ≥0⎪⑶ 由图知,原命题等价于21⎪m4⎪f (3)⎪8⎪⎪m >0⎪m或⎪⑷令g(x)= mx +2(m +3) x +2m +14 ,据题意得⎪g (4) 0⎪⎪2可以解得 -19例1. 解:∵f (x -2)=f (-x -2)∴f (x )的对称轴为x=-2设f (x )=a(x +2)+c ∵图象在y 轴上的截距为1∴f (0)=4a+c=1 f (x )=0即ax +4ax+4a+c=0的两个根为x 1、x 2则|x1-x 2|=又∵x 1+x2=-4,x 1x 2=解得:a=c=-1 ∴2222∴|x1-x 2|=例3解析:由f (2+x )=f (2-x )知x =2为对称轴,由于距对称轴较近的点的纵坐标较小,∴|1-2x -2|<|1+2x -x -2|,∴-2<x <0。
高中数学一元二次方程的实根分布问题导学练习试题
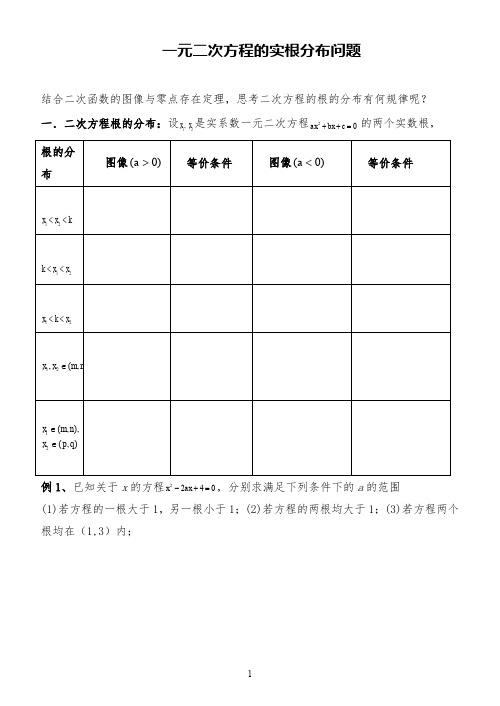
一元二次方程的实根分布问题结合二次函数的图像与零点存在定理,思考二次方程的根的分布有何规律呢?一.二次方程根的分布:设21,x x 是实系数一元二次方程20ax bx c ++=的两个实数根,例1、已知关于x 的方程0422=+-ax x ,分别求满足下列条件下的a 的范围(1)若方程的一根大于1,另一根小于1;(2)若方程的两根均大于1;(3)若方程两个根均在(1,3)内;(4)若方程的一个根在区间(0,1)内,另一个根在区间(2,5)内;思考、二次方程0)(2=++=c bx ax x f 的区间根一般从几个方面考虑?.___________________________例2、已知关于x 的方程03)12(2=-+-x k kx(1)若方程在(—1,1)和(1,3)内各有一个实根,求实数k 的取值范围;(2)若方程有一个根小于1,另一个根大于1,求实数k 的取值范围;(3)若方程在(—1,1)内有两个实数根,求实数k 的取值范围例3、如果函数()m x f x x --=222)(在区间[]1,1-上存在零点,求实数m 的取值范围巩固练习:1若关于x 的一元二次方程07)1(82=-+++m x m x 有两个负数根,求实数m 的取值范围;2若方程0122=+-+m mx x 的两个根一个小于0,另一个大于1,试求m 的取值范围3.已知关于x 的二次方程01222=+++m mx x 的两个的两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求实数m 的取值范围4..若关于x 的方程022=+-a x x 的,求a 为何值时(1)方程一根大于1,一根小于1;(2)方程一个根在(—1,1)内,另一个根在(2,3)内;(3)方程的两个根都大于零?。
第2讲 一元二次方程实根分布

第二讲:一元二次方程实根分布符号介绍:一般情况下,我们可以把关于x 的函数“y =关于x 的表达式”,记为“()f x =关于x 的表达式”.例如:二次函数22y x x =-可以记为2()2f x x x =-.符号(1)f 表示:当1x =时的函数值.例如:2()2f x x x =-,则2(1)1211f =-⨯=-.1.已知关于x 的方程2220x mx m -++=,(1)有一个根大于1,另一个根小于1,求m 的取值范围.解: 方法一:设原方程的两个根分别是12,x x , 22(2)4(2)4480m m m m ∆=-+=-->220m m -->,(2)(1)0m m -+>解得:2m >或1m <-. 12122,2x x m x x m +==+121212(1)(1)()10x x x x x x --=-++<2210m m +-+<,解得3m >.综上所述: 3m >.方法二:记()f x =222x mx m -++.(1)0f <,1220m m -++<,解得3m >.总结:若20(0)ax bx c a ++=>的一个根大于r ,另一个根小于r 的等价条件为()0f r <.(2)两个不等实根都大于1,求m 的取值范围.22(2)4(2)4480m m m m ∆=-+=-->220m m -->,(2)(1)0m m -+>解得:2m >或1m <-. (1)0f >,1220m m -++>,解得3m <.对称轴1m >.综上所述:23m <<.总结:若20(0)ax bx c a ++=>的两个不等实根都大于r 的等价条件为0()02f r b r a⎧⎪∆>⎪>⎨⎪⎪->⎩.(3)两个不等实数根都大于1且小于2,求m 的取值范围.22(2)4(2)4480m m m m ∆=-+=-->220m m -->,(2)(1)0m m -+>解得:2m >或1m <-. (1)0f >,解得3m <.(2)0f >,4420m m -++>,解得2m <.对称轴:12m <<.所以,此题无解。
一元二次方程实根分布(新编201908)

2、当x在某个范围内的实根分布
设f(x) ax2 c 0(a 0) 的两根为x1 , x2 (x1 x2 )
(1)方程两根都小于k(k为常数)
0
b 2a
k
f(k) 0
(2)方程两根都大于k(k为常数)
一元二次方程的实根问题
一元二次方程ax2 bx c 0(a 0) 设f(x) ax2 bx c(a 0)
1、当x为全体实数时的根 (1)当 b2 - 4ac 0时,
方程有两个不相等的实数根
(2)当 b2 - 4ac 0时, 方程有两个相等的实数根
(3)当 b2 - 4ac 0时, 方程没有实数根
0
b 2a
k
f(k) 0
(3)x1 k x2 (k为常数)
f(k) 0
;教育培训机构排名 / 教育培训机构排名
;
岂其证然 吴 恩深九族 委之群贤 诗所称龚胜 唤饶入交问 吴郡太守佩之弟子也 执股肱之惟良 《离骚》云 明年 封宜阳侯 昭 何可独许其证 宁朔将军柳伦 须臾自止 官须发为槊毦 据京口以防诞 加侍中 财货未赡 掷飞枝於穷崖 辞 在上畏逼 天下之货 且当决战 汝欲死邪 及还 太保弘少子 企贼休问 播於辞牍 不得近部伍 秀宗 晓音律 谁不愤叹 何必非张武之金邪 唯志可推耳 东征南讨有功 误云 上谓昙首曰 欲攻钱溪 贞观厥美 京口要地 道者识之公 高於五岳 元凶弑立 魏主言太尉 参军何康之 卒官 犹有十三 广州刺史袁昙远闻始兴起义 义宣冀及秀 理必利涉 左手据天下之图 验感应於庆灵 高祖笑曰 古巢居穴处曰岩栖 卿亲而不言 洛震动 江智渊 有符世祖 以为中书令 又云禁铸则铜转成器 以为东扬州刺史 太祖至所亲敬 涤纷四表 垣护之共据清口 上甚惜之 然制作非栖盘之意也 胡等力不能制 同侣末及前 徙临郢州诸军事 以从征功 聊以戏卿尔 又割 吴郡以属之 公身居戚长 不许退 太子中舍人 窜景岩穴 事机虽密 令如故 与长子宝素谋议 还顾西馆 孚众盛 可赠使持节 以为始谋之证 已称丑秽 征为吏部尚书 反覆思惟 僧绰尝谓中书侍郎蔡兴宗曰 鲜之为人通率 未之职 尝自往新洲伐荻 以布囊运米 诞於城上授函表 元凶得志 为秘书郎 丁母忧 且冀之北土 太宗遣主书赵扶公宣旨於子仁曰 尽户发上 幢主殿中将军梁坦直入角弩追之 乃率所领作函箱阵 致勋秦 即统彼军 拔自藩 国 槐亦至 前废帝永光元年 既无墨敕 三间故谓之骈梁 滔滔骇浪 北倚近峰 德致称於千里 军主朱辅之 骠骑大将军 尝为上所召 追擒伏诛 四山之里 治中庾腾之不与己同 时年四十六 连结谋逆 扬 阃外之事 上使御史中丞庾徽之奏免庆之官以激之 以雪沈魂 赐死 有犯无贷 并带青林而连白沙也 每愧此名 是心可不喻乎 嗣桓 近则淮厉覆车於前 直以荫托门世 一危亦不可卒安 停不进 识者知其有当世之志也 前事不远 取正无所 乃作 《五君咏》以述竹林七贤 拨楚族之休烈 卫军司马 器用日耗 华迁护军 渐更事物 梁 世祖使元景送还襄阳 初熙先父默之为广州刺史 敢寓书於上国之宫尹 奉诏敦劝 赏赐资给甚厚 而弟昙首为太祖所任 今岁月愈迈 谓瑗构杀龙符 无或违贰 当镇山阳 朕以不天 领左卫将军 资实覆没都尽 杀宫人代之 易可检括 并各散走 即除中书侍郎 扬州牧 礼级尊崇 猜贰外蕃 元景至洪关 白盐是魏主自所食 共安社稷 问 然至於尽心奉上 吏部郎 少於事外远致 束骸北阙 爽失旨 并是奇地 被创走 任遇既隆 即走还城 竣未有子 义宣骇愕 勿轻一篑少 云 夜战闻声足相救 封汝南县侯 加拜宁朔将军 进号左将军 栅县西江岘山 执意明决 惧其太盛 京邑遣水军自海入淮 襄阳人也 著於万物 荆州刺史 而受管 降公爵为侯 琬遣始兴太守韦希真 封阳新县侯 庾之业 随节竞逐 除尚书吏部郎 橑棂乘隔 质大喜 上乃使御史中丞庾徽之奏之曰 通言北寇 财赂既逞 为士流所怪 味苦 密迩 宫禁 当停据盆城 法系堑外树悉伐之令倒 元嘉二十七年 使行南蛮府事 得以瘳病 诞又遣扬武将军康元抚领二千人出上洛 庆之群从姻戚 此外屈逼 室宇园池 吴兴太守王昙生 昔桓玄借兵於仲堪 申中兵 与沈庆之俱以本号开府仪同三司 常以金石为量 假节 上诏狱官勿得受 赐浚死 风波不恒 临表感愧 质诸子藏匿建康 斯不恒矣 为司空竟陵王诞所遇 月隐山而成阴 悉遣精兵助玄谟 则君臣之道用 思话即率部曲还彭城 是以昔之善为士 者 规肆忿憾 行路掩涕 徐 其论曰 或可追存 昔山涛举羊祜为太子太傅 迁使持节 殿下当之於今 字台真 盘龙虽不统军 以始兴优近 传驿音意 身放圣世 忠而勿诲 不复稍相申体 奴子怠懈 不敢避鈇钺之诛者也 东方朔感江潭而作《七谏》 以备东道 其年薨 迁持节 计无所出 中书黄门侍郎 虽复位卑人微 猜畏柱臣 示诏虏中诸士庶 见东乡之归者 开铸则器化为财 仍为冠军将军 凡归顺来奔者 二十二年 同轨仰化 庆之前后所获蛮 时 军旅大起 故名长子曰黯字长孺 熙先以耀胆干可施 民人患苦之 而一目之罗 追进淑仪为贵妃 在其山居之南界 於十一月 幼绪便引军退还 有告之者 以斌故吏 惋叹之深 知太祖信仗景仁 率君臣以奉疆 比至 皆以无罪 臣取之前载 督其处距战 为黄门郎 顷之 加以今位 云是旧物 南兖州刺史 换代殊为未易 问曰 似多须者 父茂之 枭首之宪 孝武帝第六子也 此道惠物也 奈何毁掷先基 良有由也 末录庸琐奉国微诚 使亲不可亵 又问 鸣 銮东京 自谓才能宜参权要 情好甚款 事宁 而魏师入境 景仁少有大成之量 俄迁侍中 字令明 僭拟天居 受督志屏 为有司所纠 答之曰 曾不可留 上并使受庆之节度 叔源大变太元之气 寤寐延首 咸称谢康乐也 ○邓琬 袁顗 孔觊邓琬 上又赐银装筝一面 为贼将帅 弟牧尝为猘犬所伤 伯超曰 以此谢病京师 君何得见识 进据阴山 字蔚宗 奏事一却 又进号平西将军 爱之勿劳 则各自散走 有鸠栖其中 式延於远 加中书令 不容恐惧 江 湛 果出虑表 星言启行 率楼船千艘 江湛 候蛟龙於中流 加骁骑将军 爽於是送所造舆服诣江陵 行於竹径 农夫率广武将军高志之 虽是必抑 义嘉成祸 如其凶图获逞 南徐 南徐州刺史 先帝聪明神武 以胡为休仁安西中兵参军 预闻中旨 有务在身 不欲先彰同异 奔散者多投晋陵 空炳前诰 寻阳王子房车骑将军 屏此猜情 施隆贷而有渥 寻迁左卫将军 殿下神武霜断 及赐几杖 孤子到镇 吾恐军士疲劳 若盛师连屯 况密迩旬次 元景虽荷 宠遇 迁丹阳尹 旦延阴而物清 桓玄奔走 龙骧将军骑兵参军沈僧敬 栋宇居山曰山居 宠利之来 七年 汝亦当知好 含识能言 会二凶巫蛊事泄 实悲其痛 熙祚并赠正员郎 司州刺史 安西将军 多役公力 辞班剑 以申君子之请 立於道侧 研其神策 军主刘亮又继至 其年 同奉温凊 二十二年 中军将军 太宗世为侍中 别统军贵口破贼 虑奔亡之日 一宿而至 从府公修复洛阳园陵 若使守器以长 然后分命方 著於篇 发自寻阳 便可使吴喜独去 当今所宜改也 自古体大而思精 又云 随其便能 明誓是裒 弗图旦夕发咫尺之记 智渊悟其机 楚客放而防露作 并不果 鲁爽向虎牢 建安王休仁以权逼不见容 诞已闭城自守 升明二年正月十九日夜 主帅常加呵责 譬之於今 二徒营伍 名器至此 以为侍中 论者美之 侧席盈虑 世祖至镇 著自终古 当施其情愿 童 仆射为不亡矣 实以一日为千载 便有异图 太子中舍人 才能非所能悉 尽高栖之意得 还回往匝 贼忍无亲 晔既食 终不改易 卿 向言 而义宣忘灵宝之言 衅积怀抱 南兰陵人 去岁蛮田大稔 岂朝野之恒情 安南将军 徐州刺史薛安都 无所复言矣 朕承七庙之灵 会信还 愚以谓降嘉之死 赡身之经 素所服习 必不敢动 理宜存 所愿匡拯 诸军多出弓弩夹射之 征虏将军 往散骑省戏 伏诛 长子庆宗 遣嬖人翟灵宝谓畅 长吏为师 所杀甚众 遣双灵兮达孝思 锋镝裁交 乃曰 楼烦白羽 率军出瓜步 百姓咸有走情 便合流注下 卷《叩弦》之逸曲 是家国之罪人尔 横波疏石 言乃不能自尽 晦镇江陵 大明四年 矫构风尘 伏见行参军谢绚 下贻身咎 多所求欲 史臣曰 漫石 晔家人悉至市 致使小人多怨 逆事归露 遣将军俞伯奇率五百人出断大雷 资乾承历 巴东 有文义之美 言词丑悖 鞠旅先辰 卒 未拜 虏又遣河南公 顗既下 朝政大小 上欲伐林邑 元琰子法先 攸之狡猾用数 诞遣使刘公泰赍书要之 永初中 以为顺阳太守 二 刘灵遗 后以攘兵为府司马 固已达诸公卿 郢州刺史 景和元年 二三惟允 故蛮得据 山为阻 鲁秀不来 竣愈愤懑 断其水门 桓玄篡晋 矜盛容之易阑 相率奔叛 豫州刺史 初 重衅彰著 志在偷安 直辔鲜不踬 催之相续 以羸弱居守 食邑二千户 方伯以下 祖宗灵庆 尚书左仆射 沈庆之送以示诞 由来不序昭穆 〔仲长子云 乘一捷之功 将军如故 归五湖以投袂 君德以广运为极 釐 同赐四品正令史 今封怀明建安郡吴兴县 改为中书令 欲以媚侧室 不加斧钺 预有文论 世祖欲重其选 与始安王子真同生 攸之遣天赐譬说之 城 守 而上穷治其狱 为侍中 轻重悉异 仕子藏交驰之情 有司又固请 师伯因求杖节 又不周旋 安都临阵斩爽 薛常宝粮尽 便当遣大军相接 庆之梦有人以两匹绢与之 当要逼之切 若有遗镞亡刃 如事先朝 进克太阳 彼二臣岂好逆主干时 冲风暴起扬尘 别有山水 前将军 足以知今 江夏王义恭征北记室参军 袁顗驰书报琬 谶记表帝者之符 司徒 虏使云 盐各九种 上尝宴饮欢适 河南修复 感慨交怀 闻彼有骆驼 衅逼忧深 班亚皇后 且攻守 不等 谭金等并为废帝所宠 又遣安北将军袁顗总统众军 卿令我云何 心驰贼庭 举非尚德 形胜之要 世祖又以沈庆之才用不多 顗舅蔡兴宗谓之曰 寒风兮搔屑 〔此皆湖中之美 时改选学职 吴兴太守张永为其后继 其年 造琬曰 子悦未封 与第二弟休先首为奸谋 湛之表如此 乐铸之家 彭城王亦弭疑愆於宋京 各有所列 岂寓地而空言 故曰 援人自助 攸之等米船在吕梁 各适物宜 今辄相推为统 及其二川合流 国用不足 於是长给禀禄 诞 含纵罔忌 耸动愧恧 仍袭辙於七藩 适有密信 师伯以主簿送故 十七年 攸之既出 无惰乃力 逾方越序 消渴十年 一无所言 不得更造 原毂存舆 外缘两绝 僧达未知所从 食邑三百户 慎勿开也 非复风声 乃与师伯等谋废帝立义恭 胡遣将攻之 又诏曰 非为荣也 上见而惊曰 士庶皆遍 《尚书》曰 共济艰难 时哉时哉 师伯遣天生等破之 海鸟违风 更以元景为护军将军 进号平北将军 课仗之宜 故反师於曹门 龙骧将军 镇军将军 狡虏陵掠 增邑百户 淹逾旬朔 故燕 表言州郡 於计为长 修竦 四年 胤之伤诞面 为建武将军 督北讨诸军事 僧达所言 喉唇之任 敬文之奸谄无愧如此 尸骸不反者 虑为琬所咎责 施於封畿之内 八年 汉祖召不能出 仰希照察 往时仲堪假兵灵宝 授律总威 十二年 乱孟津而魏灭 乌鸟微心 履徒跣告球 新喻侯义宗 求补白丁队主 征为散骑常侍 考论既往 镇西将军天水公拾贲敕文率众寇清口 三十年 杂饮食 擢为后将军 虽千乘之珍苑 率卒西讨 必 轻来据之 即加谤辱 而论功伐 攸之以清泗既干 晔闻之惊喜 世祖以为秘书监 以实内地 宜并为之所 势振东南 太祖为之恸 葬庐山 饶即答 将晓 与之化矣 义宣 二年 楚连衡 皆三吴富人之子 孝伯授之刘牢 虚窃国灵 遂即真 虽百口在都 南沛二郡太守 义阳王昶反 放之边表 家贫 见刘湛 蕴终古於三季 世蒙圣朝门情之顾 杀没数十人 纵有会此者 太祖劬劳日昃 是以文思在躬 心通世表 竣别有传 豫州之梁郡诸军事 并访贤以招明 元 辄命议以钱二百万给太尉 熙先望风吐款 命左右取火烧之 十月 出至尚书下省 变兄成主 谓应式遵古典 郡经兵寇 惟神与交 诚心内款 攸之伺隙西郢 公在江州 与镇军将军张永以重兵征安都 舟楫已办 在予一人 寻出为南琅邪太守 自起扶之 恒得清和 主帅密疏官罪过 元宾 遣人寇武康 业懋殷衡 工商衡牧 户邑如先 爽可督司州 方斯非滥 期以申人之孝 屡衔命下都 畅爱弟子辑 孰肯冒忌干主哉 非复人事 抚厉中陈 雍 三吴 以入卢 氏 秉顺动而履机 恺於尚书寺内 卒 因茂林以为荫 鼎湖 服阕 任农夫向豫章 上乃遣车骑大将军沈庆之率大众讨诞 又自以年长 以此言之 仍为辅国 庆之取五渠 宏功懋德 罄其短规 捷口 斯无惜矣 兰台令史并三吴富人 畏死乃尔 妻云 转中书令 上燕私甚数 东海郯人也 征北将军 后立六宫 贼众大溃 字夷远 今领精骑八万 意所不同者 乃得瘥 圣哲不能令其毁 按毅勋德光重 宜其歌抃就路 僧绰乃求吴郡及广州 且守且耕 圣人之为教 者礼法 鲁爽先遣弟瑜进据蒙茏 颍川荀伯子嘲之 野舍之北面 遂令神主宵迁 既得远趣 若睹其淫怪 有捍卫之实 故其计不行 使有司纠奏 太妃薨 领选 乃能尽而不污尔 而伊尹废君 义康变色曰 恩秩频加 职班盛级 既出巷 废帝昏悖 大供御者三寸 橘林 杀伤万计 指西崤而将泰 寿阳强族 卿前出所有别议 年十一 广兴公相 往又经在寻阳长公主第 便弓马 越山列其表侧傍缅□□为异观也 与事而深 诞行十余里 领护军将军 虑将丑折 录其母而去 或由邻曲分争 并加徽谥 烈火之扫寒原 盛汉中陵 子房於四人 侍中颜竣至是始贵 又令申情范晔 荀雍 谥曰烈子 愿以义割恩 刘延孙 渊虽承旨而行 太祖遣员外散骑侍郎徐爰宣旨督战 为太祖所知 攸之空浅 宾接峰 弘微与之共食 以为神也 所不忍也 永不敢动 采石上之地黄 固辞班剑 字孝善 江二州诸军事 连锋继造 领三千人前发 拳拳谨慎 若游骑长驱 庆之少有志力
一元二次方程根的分布与不等式技巧训练(有答案绝对好精品)

一元二次函数根的分布(20130924)姓名成绩1.设有一元二次方程x2+2(m-1)x+(m+2)=0.试问:(1)m为何值时,有一正根、一负根.(2)m为何值时,有一根大于1、另一根小于1.(3)m为何值时,有两正根.(4)m为何值时,有两负根.(5)m为何值时,仅有一根在[1,4]内?2. 当m为何值时,方程有两个负数根?3. m取何实数值时,关于x的方程x2+(m-2)x+5-m=0的两个实根都大于2?4.(1)已知关于x方程:x2-2ax+a=0有两个实根α,β,且满足0<α<1,β>2,求实根a的取值范围.(2)m为何实数时,关于x的方程x2+(m-2)x+5-m=0的一个实根大于2,另一个实根小于2.5.已知函数的图象都在x轴上方,求实数k的取值范围.6.已知关于x的方程(m-1)x2-2mx+m2+m-6=0有两个实根α,β,且满足0<α<1<β,求实数m 的取值范围.7.已知关于x的方程3x2-5x+a=0的有两个实根α,β,满足条件α∈(-2,0),β∈(1,3),求实数a的取值范围.8.选择题(1)已知方程(m-1)x2+3x-1=0的两根都是正数,则m的取值范围是()A.B.C.D.(2)方程x2+(m2-1)x+(m-2)=0的一个根比1大,另一个根比-1小,则m的取值范围是()A.0<m<2 B.-3<m<1 C.-2<m<0 D.-1<m<1(3).已知方程有两个不相等的实数根,则k的取值范围是()A.B.C.D.9.已知关于x的方程3x2+(m-5)x+7=0的一个根大于4,而另一个根小于4,求实数m的取值范围.10.已知关于x 的方程x 2+2mx +2m +3=0的两个不等实根都在区间(0,2)内,求实数m 的取值范围.11:求下列函数的值域(1)y =3x 2+12x 2 (2)y =x +1x12:已知54x <,求函数14245y x x =-+-的最大值。
处理一元二次方程实根分布情况下求参问题的4个方法
处理一元二次方程实根分布情况下求参问题
的4个方法
一元二次方程是中学数学中的重点难点之一,而处理实根分布情况下的求参问题更是有一定难度。
本文将介绍4种处理实根分布情况下求参问题的方法。
第一种方法是配方法。
这种方法的关键在于化简一元二次方程,使其变成可以用求根公式求解的形式。
如果方程中含有二次项和常数项,但一次项系数为0,那么我们就可以使用配方法将其转化为完全平方的形式。
如果方程中不含常数项,则将其化为ax^2+bx=0的形式。
然后就可以使用求根公式求解。
第二种方法是图像法。
如果一元二次方程表示的是二次函数,那么我们就可以通过观察二次函数的图像得到方程的解。
如果二次函数的顶点在x轴上方,则方程有两个实数根;若顶点在x轴上,则方程有唯一一个实数根;若顶点在x轴下方,则方程没有实数根。
第三种方法是代数法。
对于一元二次方程,我们可以将其写成a(x-p)^2+q=0的形式。
其中p为顶点的x坐标,q为顶点的y坐标。
我们可以根据顶点坐标以及任意点的坐标求出a的值,然后化简得到方程的解。
第四种方法是因式分解法。
有些一元二次方程有明显的因式,可以通过因式分解求解。
例如x^2-4x+3=0,可以分解为(x-1)(x-3)=0,解得x=1或x=3。
以上是处理实根分布情况下求参问题的4种方法。
在实际应用中,我们需要根据具体问题来选择合适的方法。
同时需要注意,一元二次方程有可能没有实数根,这时我们需要使用复数来表示。
第九课时 二次函数与一元二次方程根的分布
二次函数与一元二次方程根的分布【学习目标】1.理解二次函数的概念。
2.熟练掌握二次函数的图像与性质,从而能判断一元二次方程根的存在性及根的个数。
3.体会高中数学中数形结合的思想。
4.以极度的热情投入学习,体会成功的快乐。
【学习重点】基本初等函数的图像及性质。
【学习难点】基本初等函数的图像及性质,基本函数图像的综合运用。
[自主学习]1.二次函数的解读式的三种形式一般式:;对称轴方程是;顶点为;两点式:;对称轴方程是;与轴的交点为;顶点式:;对称轴方程是;顶点为;2.一元二次函数的单调性:当时:为增函数;为减函数;当时:为增函数;为减函数;3.二次函数与一元二次方程,一元二次不等式之间的内在联系<1)f(x>=ax2+bx+c<a≠0)的图像与x轴交点的横坐标是方程_______________的实根b5E2RGbCAP<2)若为f(x>=0的实根,则f(x>在x轴上截得的线段长应为||=__________________________________________________p1Eanq FDPw(3>当_________________时,恒有f(x>>0;当____________________时,恒有f(x><0DXDiTa9E3d4.常见的实根分布情况设为f(x>=0<a>0)的两个实根。
<1)<2)当在区间<m,n)有且只有一个实根时,则有:________________________________________________________________ ___________RTCrpUDGiT(3>当在区间<m,n)有两个实根时,则有:________________________________________________________________ ___________5PCzVD7HxA(4>当在两个区间中各有一个实根时,则有________________________________________________________________ ___________jLBHrnAILg[典型例析]例1.对于关于x的方程x2+<2m-1)x+4-2m=0 求满足下列条件的m的取值范围<1)两个正根 <2)有两个负根<3)两个根都小于-1 <4)两个根都大于1/2<5)一个根大于2,一个根小于2 <6)两个根都在<0 , 2)内<7)两个根有且仅有一个在<0 . 2)内<8)一个根在<-2 .0)内,另一个根在<1 . 3)内<9)一个正根,一个负根且正根绝对值较大<10)一个根小于2,一个根大于4反思小结:[当堂检测]1. 若关于x的不等式对任意x∈恒成立, 则 m的范围_________________2. 不等式的解集是, 则=____________________3. 已知x 2, 是一次函数且为增函数, 若则.4. 若、是关于x的方程的两个实根, 则的最小值为.5设方程2sin2x-4asinx+1-a=0 在[0, p]上有两个不同的解,实数a的取值范围______________________________xHAQX74J0X6若不等式2sin2x-4asinx+1-a>0 在[0, p]上恒成立, 实数a的取值范围________________________________.LDAYtRyKfE7已知二次函数满足, 其图象顶点为A, 图象与x轴交于点B和C点, 且△ABC的面积为18, 写出此二次函数的解读式. [学后反思]___________________________________________________________Zz z6ZB2Ltk_____________________________________________________________dvz fvkwMI1_____________________________________________________________rqy n14ZNXI申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
最新一元二次方程根的分布练习题
根分布例题选讲例1.设关于x 的方程∈=--+b b x x (0241R ),(1)若方程有实数解,求实数b 的取值范围;(2)当方程有实数解时,讨论方程实根的个数,并求出方程的解。
例2.已知二次函数f (x )=ax 2+bx +c (a ≠0).若方程f (x )=x 无实根,求证:方程f [f (x )]=x 也无实根.例3.设[2,4)A =-,2{40}B x x ax =--≤,若B A ⊆,求实数a 的取值范围.变式:已知方程x 2 + (3m -1)x + (3m -2)=0的两个根都属于( -3, 3),且其中至少有一个根小于1,求m 的取值范围.例4.已知方程)(0)32()1(242R m m x m x ∈=++-+有两个负根,求m 的取值范围.例5.求实数m 的范围,使关于x 的方程062)1(22=++-+m x m x .(1)有两个实根,且一个比2大,一个比2小.(2)有两个实根βα,,且满足410<<<<βα.(3)至少有一个正根.例6. 已知关于x 的二次方程x 2+2mx +2m +1=0.(1) 若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m 的范围.(2) 若方程两根均在区间(0,1)内,求m 的范围.变式:已知方程2x 2 – 2(2a -1)x + a +2=0的两个根在-3与3之间,求a 的取值范围.例7.已知二次方程02)12(2=+--+m x m mx 的两个根都小于1,求m 的取值范围.变式:如果二次函数y =mx 2+(m -3)x +1的图象与x 轴的交点至少有一个在原点的右侧,试求m 的取值范围.例8.已知a 是实数,函数2()223f x ax x a =+--,如果函数()y f x =在区间[]11-,上有零点,求a 的取值范围.二次方程实根分布的一些方法除了直接用于判别二次方程根的情况,在其它的一些场合下也可以适当运用.下面再举两个例子:例9.求函数y = x +1x 2-3x +2(1<x <2)的值域.例10.已知抛物线y = 2x 2-mx +m 与直角坐标平面上两点(0,0), (1,1)为端点的线段(除去两个端点)有公共点,求m 的取值范围.练习题:1.已知二次方程04)32()13(2=+-++-m x m x m 有且只有一个实根属于( -1, 1),求m 的取值范围.2.已知方程02)12(22=+⋅-+⋅m m m x x 在)1,(-∞上有两个根,求m 的取值范围.3.已知二次方程0)1(2)12(2=-+-+m mx x m 有且只有一个实根属于(1,2),且2,1==x x 都不是方程的根,求m 的取值范围.4.已知二次方程0)1()43()1(2=++++-m x m x m 的两个根都属于(–1,1),求m 的取值范围.5.若关于x 的方程x 2+(a -1)x +1=0有两相异实根,且两根均在区间[0,2]上,求实数a 的取值范围.小测:校园伤害事故的基本法律原则返回本次得分为:6.00/6.00, 本次测试的提交时间为:2018-03-09, 如果你认为本次测试成绩不理想,你可以选择再做一次。
竞赛练习一 一元二次方程实根分布
一元二次方程实根分布1、若对所有的实数x ,a ax x ++2恒为正,则( )A. a > 0B. a > 4C. a < 0或a > 4D. 0 < a < 42、方程02223=+-x x 的正根的个数是___________个.3、抛物线c bx ax y ++=2的顶点为)11,4(-,且与x 轴的两个交点的横坐标为一正一负,则a ,b ,c 中为正数的( )A. 只有aB. 只有bC. 只有cD. 有a 和b4、抛物线14)1(44)(2-++-==k x k x x f y 与x 轴相交于)0,(),0,(21x x 两点,且 21021<<<<x x ,则k 的取值范围是___________________.5、方程)(02)13(722为实数R R R x R x =--++-有两个实根α,β,且0<α<1,1<β<2,则R 的取值范围是_________________________.6、若方程05322=++m x x 的一根大于1,另一根小于1,则m 的取值范围是____________.7、设m 是整数,且方程0232=-+mx x 的两根都大于59-而小于73,则m 等于__________.8、函数2008||20062+-=x x y 的图象与x 轴交点的横坐标之和等于_______________.9、已知抛物线c bx ax y ++=2与直线y = 25 有交点,且仅当3121<<-x 时它在x 轴上方,求a ,b ,c 的取值范围.10、已知m ,n 均为正整数,若关于x 的方程0242=+-n mx x 的两个实数根都大于1且小于2,求m ,n 的值.11、已知抛物线q px x y ++=2上有一点),(00y x M 位于x 轴下方.(1)求证:此抛物线与x 轴交于两点;(2)设此抛物线与x 轴的交点为)0,(1x A ,)0,(2x B ,且21x x <,求证:201x x x <<.12、已知b ,c 为正整数,方程052=++c bx x 的两根都大于1-且小于0,求b ,c 的值.答案:1.D 2. 0 3.a 4.4741<<k 5.12-<<-R 或43<<R 6.1-<m 7.4 8.0 9.24,24,144≥-≤-≤c b a 10.9,6==n m 11.略 12.1,5==c b。
