圆内接多边形练习题

合集下载

83九年级下册第三章第八节圆内接正多边形课后作业

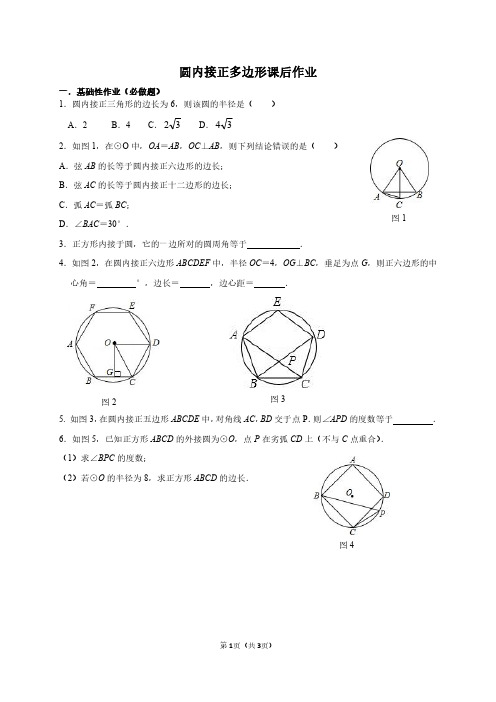
圆内接正多边形课后作业一．基础性作业（必做题）1．圆内接正三角形的边长为6，则该圆的半径是（）A ．2B ．4C ．32D ．342．如图1，在⊙O 中，OA ＝AB ，OC ⊥AB ，则下列结论错误的是（）A ．弦AB 的长等于圆内接正六边形的边长；B ．弦AC 的长等于圆内接正十二边形的边长；C ．弧AC ＝弧BC ；D ．∠BAC ＝30°．3．正方形内接于圆，它的一边所对的圆周角等于．4．如图2，在圆内接正六边形ABCDEF 中，半径OC ＝4，OG ⊥BC ，垂足为点G ，则正六边形的中心角＝°，边长＝，边心距＝．5.如图3，在圆内接正五边形ABCDE 中，对角线AC ，BD 交于点P ．则∠APD 的度数等于．6．如图5，已知正方形ABCD 的外接圆为⊙O ，点P 在劣弧CD 上（不与C 点重合）．（1）求∠BPC 的度数；（2）若⊙O 的半径为8，求正方形ABCD 的边长．图1图2图4图3二、拓展性作业（选做题）1．如图5，请用直尺和圆规确定已知圆的圆心，并作出此圆的内接正六边形ABCDEF ；（保留作图痕迹，不写作法）2．我国魏晋时期的数学家刘徽首创“割圆术”，利用圆的内接正多边形来确定圆周率．若设⊙O 的半径为R ，圆内接正n 边形的边长、面积分别为a n ，S n ，圆内接正2n 边形边长、面积分别为a 2n ，S 2n ．刘徽用以下公式求出a 2n 和S 2n ．22222))21(()21(n n n a R R a a --+=，R na n 21S n 2=．如图6，若⊙O 的半径为1，则⊙O 的内接正八边形AEBFCGDH 的面积为．图5图63．【探索发现】小迪同学在学习圆的内接正多边形时，发现：如图7，若P是圆内接正三角形ABC 的外接圆的弧BC上任一点，则∠APB＝60°，在PA上截取PM＝PC．连接MC，可证明△MCP 是（填“等腰”“等边”或“直角”）三角形，从而得到PC＝MC，再进一步证明△PBC ≌，得到PB＝MA，可证得：PB+PC＝PA．【拓展应用】小迪同学对以上推理进行类比研究，发现：如图8，若P是圆内接正四边形ABCD 的外接圆的弧BC上任一点，则∠APB＝∠APD＝°，分别过点B、D作BM⊥AP于M、DN⊥AP于N．【猜想证明】分别过点B，D作BM⊥AP于M，DN⊥AP于N．请写出PB、PD与PA之间的数量关系，并说明理由．图7图8。

九年级数学圆内接正多边形专题练习(含解析)

C．连接 AD，则 AD 分别平分∠EAC 与∠EDC D．图中一共能画出 3 条对称轴
答案：B 解析：解答： A.∵多边形 ABCDEF 是正六边形， ∴△ACE 是等边三角形，故本选项正确； B.∵△ACE 是等边三角形，∴是轴对称图形，不是中心对称图形，故本选项错误； C.∵△ACE 是等边三角形，∴连接 AD，则 AD 分别平分∠EAC 与∠EDC，故本选项正确； D.∵△ACE 是等边三角形，∴图中一共能画 3 条对称轴，故本选项正确．故选 B．分析：根据正多边形的性质和轴对称图形与中心对称图形的定义解答．
C．18
D．36
答案：C
解析：解答：连接正六边形的中心与各个顶点，得到六个等边三角形，
等边三角形的边长是 2 ，高为 3，
因而等边三角形的面积是 3 ，
∴正六边形的面积=18 ，故选 C．分析：解题的关键要记住正六边形的特点，它被半径分成六个全等的等边三角形．
12.已知某个正多边形的内切圆的半径是（）
∴△OAB 是等边三角形， ∴OB=AB=24cm，
∴ 60 ´ 24 = 8 180
故选 B 分析：连接 OA、OB，得出等边三角形 AOB，求出 OB 长和∠AOB 度数，根据弧长公式求
出即可．
10.若一个正六边形的半径为 2，则它的边心距等于（）
A．2 B．1 C．
D．2
答案：C 解析：解答：已知正六边形的半径为 2，则正六边形 ABCDEF 的外接圆半径为 2，如图：
连接 OA，作 OM⊥AB 于点 M，得到∠AOM=30°，
则 OM=OA•cos30°= ．
则正六边形的边心距是．
故选 C．分析：根据正六边形的边长与外接圆的半径相等，构建直角三角形，利用直角三角形的边角关系即可求出．

圆内接正多边形练习北师大版九年级数学下册

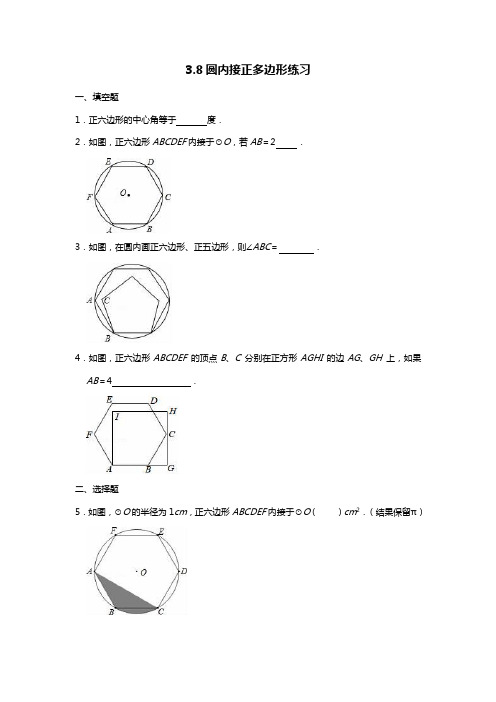
3.8圆内接正多边形练习一、填空题1．正六边形的中心角等于度．2．如图，正六边形ABCDEF内接于⊙O，若AB＝2 ．3．如图，在圆内画正六边形、正五边形，则∠ABC＝．4．如图，正六边形ABCDEF的顶点B、C分别在正方形AGHI的边AG、GH上，如果AB＝4 ．二、选择题5．如图，⊙O的半径为1cm，正六边形ABCDEF内接于⊙O（）cm2．（结果保留π）A．B．C．D．6．如图，正六边形ABCDEF是半径为2的圆的内接六边形，则图中阴影部分的面积是（）A．B．C．D．7．已知等边三角形的内切圆半径，外接圆半径和高的比是（）A．1：2：B．2：3：4 C．1：：2 D．1：2：3 8．如图，正方形ABCD和正△AEF都内接于⊙O，EF与BC、CD分别相交于点G、H，则（）A．B．C．D．29．蜂巢的构造非常美丽、科学，如图是由7个形状、大小完全相同的正六边形组成的网络，正六边形的顶点称为格点，则△ABC是直角三角形的个数有（）A．4个B．6个C．8个D．10个10．先作半径为的第一个圆的外切正六边形，接着作上述外切正六边形的外接圆，…，则按以上规律作出的第8个外切正六边形的边长为（）A．B．C．D．11．如图，有一圆内接正八边形ABCDEFGH，若△ADE的面积为10（）A．40 B．50 C．60 D．80 12．如图，正六边形的顶点在矩形的各条边上，若阴影部分的面积为3（）A．B．6 C．9 D．12 13．如图，正六边形ABCDEF内接于⊙O，若直线PA与⊙O相切于点A（）A．30°B．40°C．45°D．60°14．正方形的边长为2，则正方形外接圆的半径是（）A．1 B．C．D．2 15．如图，正八边形ABCDEFGH内接于⊙O，则∠ADB的度数为（）A．45°B．25°C．22.5°D．20°16．如图，正五边形ABCDE的边长为2，连接AC、AD、BE，连接DF，给出下列结论：①∠FDG＝18°；③（S四边形CDEF）2＝9+2；④DF2﹣DG2＝7﹣2．其中结论正确的个数是（）A．1 B．2 C．3 D．4三、解答题17．如图，正三角形ABC内接于⊙O，若AB＝cm，求⊙O的半径．18．如图是由边长为2的六个等边三角形组成的正六边形，建立适当的直角坐标系，写出正六边形各顶点的坐标．19．如图，⊙O的周长等于8πcm，正六边形ABCDEF内接于⊙O．（1）求圆心O到AF的距离；（2）求正六边形ABCDEF的面积．20．如图正方形ABCD内接于⊙O，E为CD任意一点，连接DE、AE．（1）求∠AED的度数．（2）如图2，过点B作BF∥DE交⊙O于点F，连接AF，AF＝1，AE＝4，求DE的长度．21．如图，四边形ABCD是⊙O的内接正方形，若正方形的面积等于4，求⊙O的面积．。

九年级数学下册圆内接正多边形同步测试

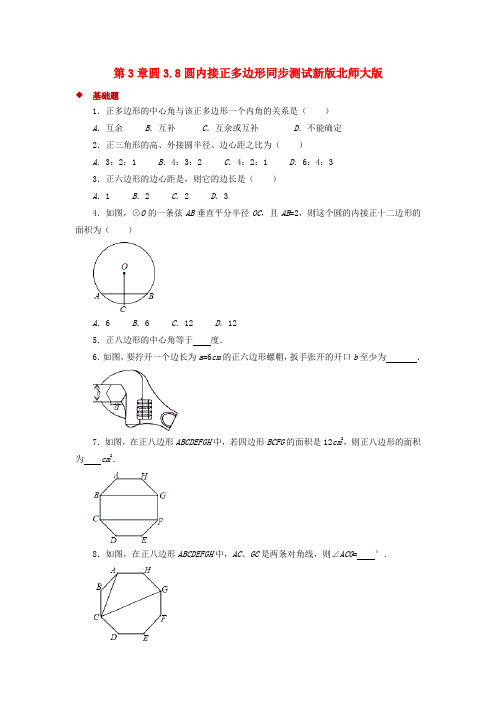
第3章圆3.8圆内接正多边形同步测试新版北师大版◆基础题1．正多边形的中心角与该正多边形一个内角的关系是（）A．互余B．互补C．互余或互补D．不能确定2．正三角形的高、外接圆半径、边心距之比为（）A．3：2：1 B．4：3：2 C．4：2：1 D．6：4：33．正六边形的边心距是，则它的边长是（）A．1 B．2 C．2 D．34．如图，⊙O的一条弦AB垂直平分半径OC，且AB=2，则这个圆的内接正十二边形的面积为（）A．6 B．6 C．12 D．125．正八边形的中心角等于度．6．如图，要拧开一个边长为a=6cm的正六边形螺帽，扳手张开的开口b至少为．7．如图，在正八边形ABCDEFGH中，若四边形BCFG的面积是12cm2，则正八边形的面积为cm2．8．如图，在正八边形ABCDEFGH中，AC、GC是两条对角线，则∠ACG= °．9．如图，正三角形ABC内接于⊙O，若AB=2cm，求⊙O的半径．10．如图，点G，H分别是正六边形ABCDEF的边BC，CD上的点，且BG=CH，AG交BH 于点P．（1）求证：△ABG≌△BCH；（2）求∠APH的度数．◆能力题1．如图，由7个形状，大小完全相同的正六边形组成的网格，正六边形的顶点称为格点，已知每个正六边形的边长为1，△ABC的顶点都在格点上，则△ABC的面积是（）A．B．2 C．D．32．若一个正多边形的中心角等于其内角，则这个正多边形的边数为（）A．3 B．4 C．5 D．63．古代数学家祖冲之和他的儿子根据刘徽的“割圆术”（用圆内接正多边形的周长代替圆周长），来计算圆周率π的近似值．他从正六边形算起，一直算到正24576边形，将圆周率精确到小数后七位，在世界上领先一千多年．根据这个办法，由圆内接正六边形算得的圆周率π的近似值是（）A．2.9 B．3 C．3.1 D．3.144．如果正n边形的中心角为2α，边长为5，那么它的边心距为．（用锐角α的三角比表示）5．如图，AB，AC分别为⊙O的内接正六边形，内接正方形的一边，BC是圆内接n边形的一边，则n等于．6．如图，P、Q分别是⊙O的内接正五边形的边AB、BC上的点，BP=CQ，则∠POQ= ．7．如图，⊙O半径为4cm，其内接正六边形ABCDEF，点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，连接PB，QE，PE，BQ．设运动时间为t（s）．（1）求证：四边形PEQB为平行四边形；（2）填空：①当t= s时，四边形PBQE为菱形；②当t= s时，四边形PBQE为矩形．8．（1）如图1，在圆内接正六边形ABCDEF中，半径OC=4，求正六边形的边长．（2）如图2，在△ABC中，AB=13，BC=10，BC边上的中线AD=12．求证：AB=AC．◆提升题1．如图，在正五边形ABCDE中，连接AC、AD、CE，CE交AD于点F，连接BF，下列说法不正确的是（）A．△CDF的周长等于AD+CD B．FC平分∠BFDC．AC2+BF2=4CD2D．DE2=EF•CE2．如图，有一圆内接正八边形ABCDEFGH，若△ADE的面积为10，则正八边形ABCDEFGH 的面积为何（）A．40 B．50 C．60 D．80【答案】A3．小刚在纸上画了一个面积为6分米2的正六边形，然后连接相隔一点的两点得到如图所示的对称图案，他发现中间也出现了一个正六边形，则中间的正六边形的面积是分米2．4．阅读下面材料：对于平面图形A，如果存在一个圆，使图形A上的任意一点到圆心的距离都不大于这个圆的半径，则称图形A被这个圆所覆盖．对于平面图形A，如果存在两个或两个以上的圆，使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径，则称图形A被这些圆所覆盖．例如：图中①的三角形被一个圆覆盖，②中的四边形被两个圆所覆盖．已知长宽分别为2cm，1cm的矩形被两个半径都为r的圆所覆盖，则r的最小值是cm．5．如图正方形ABCD内接于⊙O，E为CD任意一点，连接DE、AE．（1）求∠AED的度数．（2）如图2，过点B作BF∥DE交⊙O于点F，连接AF，AF=1，AE=4，求DE的长度．6．教材的《课题学习》要求同学们用一张正三角形纸片折叠成正六边形，小明同学按照如下步骤折叠：请你根据小明同学的折叠方法，回答以下问题：（1）如果设正三角形ABC的边长为a，那么CO= （用含a的式子表示）；（2）根据折叠性质可以知道△CDE的形状为三角形；（3）请同学们利用（1）、（2）的结论，证明六边形KHGFED是一个六边形．答案和解析◆基础题1．【答案】B解：设正多边形的边数为n，则正多边形的中心角为，正多边形的一个外角等于，所以正多边形的中心角等于正多边形的一个外角，而正多边形的一个外角与该正多边形相邻的一个内角的互补，所以正多边形的中心角与该正多边形一个内角互补．2．【答案】A解：如图，△ABC是等边三角形，AD是高．点O是其外接圆的圆心，由等边三角形的三线合一得点O在AD上，并且点O还是它的内切圆的圆心．∵AD⊥BC，∠1=∠4=30°，∴BO=2OD，而OA=OB，∴AD=3OD，∴AD：OA：OD=3：2：1．3．【答案】B解：∵正六边形的边心距为，∴OB=，AB=OA，∵OA2=AB2+OB2，∴OA2=（OA）2+（）2，解得OA=2．4．【答案】C解：如图，连接OA；取的中点D，连接AD、CD、OD；过点D作DE⊥OC于点E；∵OF=OA，且∠OFA=90°，∴∠OAF=30°，∠AOC=60°，∠AOD=∠COD=30°；∵圆的内接正十二边形的中心角==30°，∴AD、DC为该圆的内接正十二边形的两边；∵OC⊥AB，且AB=2，∴AF=；在△AOF中，由勾股定理得：；在△ODE中，∵∠EOD=30°，∴DE=OD=1，，∴这个圆的内接正十二边形的面积为12．5．【答案】45解：正八边形的中心角等于360°÷8=45°．6．【答案】6cm解：设正多边形的中心是O，其一边是AB，∴∠AOB=∠BOC=60°，∴OA=OB=AB=OC=BC，∴四边形ABCO是菱形，∵AB=6cm，∠AOB=60°，∴cos∠BAC=，∴AM=6×=3（cm），∵OA=OC，且∠AOB=∠BOC，∴AM=MC=AC，∴AC=2AM=6（cm）．7．【答案】24解：连接HE，AD，在正八边形ABCDEFGH中，可得：HE⊥BG于点M，AD⊥BG于点N，∵正八边形每个内角为：=135°，∴∠HGM =45°，∴MH =MG ，设MH =MG =x ，则HG =AH =AB =GF =x ，∴BG ×GF =2（+1）x 2=12，∴四边形ABGH 面积=（AH +BG ）×HM =（+1）x 2=6，∴正八边形的面积为：6×2+12=24（cm 2）．8．【答案】45°解：设正八边形ABCDEFGH 的外接圆为⊙O ；∵正八边形ABCDEFGH 的各边相等，∴圆周长，∴的度数为=90°，∴圆周角∠ACG =．9．解：过点O 作OD ⊥BC 于点D ，连接BO ，∵正三角形ABC 内接于⊙O ，∴点O 即是三角形内心也是外心，∴∠OBD =30°，BD =CD =BC =AB =，∴cos 30°=，解得：BO =2，即⊙O 的半径为2cm ．10．（1）证明：∵在正六边形ABCDEF 中，AB =BC ，∠ABC =∠C =120°，在△ABG 与△BCH 中120AB BC ABC C BG CH =⎧⎪∠=∠=︒⎨⎪=⎩，∴△ABG ≌△BCH ；（2）解：由（1）知：△ABG ≌△BCH ，∴∠BAG =∠HBC ，∴∠BPG =∠ABG =120°，∴∠APH =∠BPG =120°．◆ 能力题1．【答案】B解：延长AB ，然后作出过点C 与格点所在的直线，一定交于格点E ．正六边形的边长为1，则半径是1，则CE =4，中间间隔一个顶点的两个顶点之间的距离是，则△BCE 的边EC 上的高是，△ACE 边EC 上的高是，则S △ABC =S △AEC ﹣S △BEC =×4×（﹣）=2．2．【答案】B解：360°÷n =．故这个正多边形的边数为4．3．【答案】B解：由题意n =6时，π≈=3．4．【答案】解：如图所示：∵正n 边形的中心角为2α，边长为5，∵边心距OD =．5．【答案】12解：连接AO ，BO ，CO ．∵AB 、AC 分别为⊙O 的内接正六边形、内接正方形的一边，∴∠AOB ==60°，∠AOC ==90°，∴∠BOC =30°，∴n ==12．6．【答案】72°解：连接OA 、OB 、OC ，∵五边形ABCDE 是⊙O 的内接正五边形，∴∠AOB =∠BOC =72°，∵OA =OB ，OB =OC ，∴∠OBA =∠OCB =54°，在△OBP 和△OCQ 中，OB OC OBP OCQ BP CQ =⎧⎪∠=∠⎨⎪=⎩，∴△OBP ≌△OCQ ，∴∠BOP =∠COQ ，∵∠AOB =∠AOP +∠BOP ，∠BOC =∠BOQ +∠QOC ，∴∠BOP =∠QOC ，∵∠POQ =∠BOP +∠BOQ ，∠BOC =∠BOQ +∠QOC ，∴∠POQ =∠BOC =72°．7．（1）证明：∵正六边形ABCDEF内接于⊙O，∴AB=BC=CD=DE=EF=FA，∠A=∠ABC=∠C=∠D=∠DEF=∠F，∵点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，∴AP=DQ=t，PF=QC=4﹣t，在△ABP和△DEQ中，AB DE A D AP DQ=⎧⎪∠=∠⎨⎪=⎩，∴△ABP≌△DEQ（SAS），∴BP=EQ，同理可证PE=QB，∴四边形PEQB是平行四边形．（2）解：①当PA=PF，QC=QD时，四边形PBEQ是菱形时，此时t=2s．②当t=0时，∠EPF=∠PEF=30°，∴∠BPE=120°﹣30°=90°，∴此时四边形PBQE是矩形．当t=4时，同法可知∠BPE=90°，此时四边形PBQE是矩形．综上所述，t=0s或4s时，四边形PBQE是矩形．8．（1）解：连接OD，如图所示：∵六边形ABCDEF是圆O的内接正六边形，∴∠O==60°，∵OC=OD，∴△OCD是等边三角形，∴CD=OC=4，即正六边形的边长为4；（2）证明：∵AD是△ABC的中线，∴BD=CD=BC=5，∵AB=13，AD=12，∴BD2+AD2=52+122=169=132=AB2，∴△ABD是直角三角形，AD⊥BC，又∵BD=CD，∴AB=AC．◆提升题1．【答案】B解：∵五边形ABCDE是正五边形，∴AB=BC=CD=DE=AE，BA∥CE，AD∥BC，AC∥DE，AC=AD=CE，∴四边形ABCF是菱形，∴CF=AF，∴△CDF的周长等于CF+DF+CD，即△CDF的周长等于AD+CD，故A选项正确；∵四边形ABCF是菱形，∴AC⊥BF，设AC与BF交于点O，由勾股定理得OB2+OC2=BC2，∴AC2+BF2=（2OC）2+（2OB）2=4OC2+4OB2=4BC2，∴AC2+BF2=4CD2．故C选项正确；由正五边形的性质得，△ADE≌△CDE，∴∠DCE=∠EDF，∴△CDE∽△DFE，∴，∴DE2=EF •CE，故D选项正确．2．【答案】A解：取AE中点I，则点I为圆的圆心，圆内接正八边形ABCDEFGH是由8个与△IDE全等的三角形构成．易得△IDE的面积为5，则圆内接正八边形ABCDEFGH为8×5=40．3．【答案】2解：设O是原正六边形的中心，连接AO，FO，MO，设FO与AE交于点Q，AO与BE交于P，∵一个面积为6分米2的正六边形，连接相隔一点的两顶点得到如图所示的对称图案，∴∠AOF=×360°=60°，S△AOF=×6=1（分米2），∴△OAF是等边三角形，∵AB=AF，∴OA⊥BF，∴AP=OP，∴AM=OM，同理：OF⊥AE，OQ=FQ，∴OM=FM，∴点M是△AOF的外心，∴S△OAM=S△AOF=（分米2），∴S△OPM=S△OAM=（分米2），∴中间的正六边形的面积是：12×S△OPM=2（分米2）．4．【答案】解：如图：矩形ABCD中AB=1，BC=2，则覆盖ABCD的两个圆与矩形交于E、F两点，由对称性知E、F分别是AD和BC的中点，则四边形ABFE、EFCD是两个边长为1的正方形，所以圆的半径r=，两圆心距=1．5．解：（1）如图1中，连接OA、OD．∵四边形ABCD是正方形，∴∠AOD=90°，∴∠AED=∠AOD=45°．（2）如图2中，连接CF、CE、CA，作DH⊥AE于H．∵BF∥DE，AB∥CD，∴∠ABF=∠CDE，∵∠CFA=∠AEC=90°，∴∠DEC=∠AFB=135°，∵CD=AB，∴△CDE≌△ABF，∴AF=CE=1，∴AC=，∴AD=AC=，∵∠DHE=90°，∴∠HDE=∠HED=45°，∴DH=HE，设DH=EH=x，在Rt△ADH中，∵AD2=AH2+DH2，∴=（4﹣x）2+x2，解得x=或，∴DE=DH=或．6．解：（1）∵正三角形ABC的边长为a，由折叠的性质可知，点O是三角形的重心，∴CO=a；（2）△CDE为等边三角形；（3）由（2）知△CDE为等边三角形，∴CD=CE=DE=CO÷cos30°=a，∠ADE=∠BED=120°，同理可得，AH=AK=KH=a，BG=BF=GF=a，∠CKH=∠BHK=120°，∵AB=BC=AC=a，∴DE=DK=KH=HG=GF=FE=a，∠ADE=∠BED=∠CKH=∠BHK=∠CFG=∠AGF=120°，∴六边形KHGFED是一个正六边形．3.8圆内接正多边形一、选择题1.下列说法正确的是（） A.各边相等的多边形是正多边形 B.各角相等的多边形是正多边形C.各边相等的圆内接多边形是正多边形D.各角相等的圆内接多边形是正多边形2.（2013•天津）正六边形的边心距与边长之比为（） A ．：3 B ．：2 C ． 1：2 D ．：23.(2013山东滨州)若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为 ( )A ．6，32B ．32，3C ．6，3D ．62，324. 如图所示，正六边形ABCDEF 内接于⊙O ，则∠ADB 的度数是（）．A ．60°B ．45°C ．30°D ．22．5°5.半径相等的圆的内接正三角形，正方形，正六边形的边长的比为（） A.1:2:3 B.3:2:1C.3:2:1D.1:2:36. 圆内接正五边形ABCDE 中，对角线AC 和BD 相交于点P ，则∠APB 的度数是（）． A ．36° B ．60° C ．72° D ．108°7.（2013•自贡）如图，点O 是正六边形的对称中心，如果用一副三角板的角，借助点O （使该角的顶点落在点O 处），把这个正六边形的面积n 等分，那么n 的所有可能取值的个数是（）A.4B.5C.6D.78.如图，△PQR 是⊙O 的内接正三角形，四边形ABCD 是⊙O 的内接正方形，BC ∥QR ，则∠AOQ 的度数是（） A.60° B.65°C.72°D.75°二、填空题9.一个正n 边形的边长为a ，面积为S ，则它的边心距为__________.第4题第6题第7题第8题10.正多边形的一个中心角为36度,那么这个正多边形的一个内角等于__________度.11.若正六边形的面积是243cm2，则这个正六边形的边长是__________.12.已知正六边形的边心距为3，则它的周长是_______.13.点M、N分别是正八边形相邻的边AB、BC上的点，且AM=BN，点O是正八边形的中心，则∠MON=_____________.14.边长为a的正三角形的边心距、半径（外接圆的半径）和高之比为_________________.15.要用圆形铁片截出边长为4cm的正方形铁片，则选用的圆形铁片的直径最小要__________cm.16.若正多边形的边心距与边长的比为1:2，则这个正多边形的边数是__________.17.一个正三角形和一个正六边形的周长相等，则它们的面积比为__________.18.(2013•徐州)如图，在正八边形ABCDEFGH中，四边形BCFG的面积为20cm2，则正八边形的面积为________cm2.三、解答题19.比较正五边形与正六边形，可以发现它们的相同点与不同点.正五边形正六边形例如它们的一个相同点：正五边形的各边相等，正六边形的各边也相等.它们的一个不同点：正五边形不是中心对称图形，正六边形是中心对称图形.请你再写出它们的两个相同点和不同点.相同点：（1）____________________________________________________________________;（2）___________________________________________________________________. 不同点：（1）____________________________________________________________________;（2）____________________________________________________________________.20.已知，如图，正六边形ABCDEF的边长为6cm，求这个正六边形的外接圆半径R、边心距r6、面积S6.第13题第18题第20题21.如图，⊙O 的半径为2，⊙O 的内接一个正多边形，边心距为1，求它的中心角、边长、面积.22.已知⊙O 和⊙O 上的一点A.（1）作⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ；（2）在（1）题的作图中，如果点E 在弧AD 上，求证：DE 是⊙O 内接正十二边形的一边.23.如图1、图2、图3、…、图n ，M 、N 分别是⊙O 的内接正三角形ABC 、正方形ABCD 、正五边形ABCDE 、…、正n 边形ABCDE…的边AB 、BC 上的点，且BM=CN ，连结OM 、ON.(1)求图1中∠MON 的度数；(2)图2中∠MON 的度数是_________，图3中∠MON 的度数是_________； (3)试探究∠MON 的度数与正n 边形边数n 的关系(直接写出答案).第21题第22题3.8圆内接正多边形知识要点基础练知识点1正多边形与圆1.以下说法正确的是(C)A.每个内角都是120°的六边形一定是正六边形B.正n边形的对称轴不一定有n条C.正n边形的每一个外角度数等于它的中心角度数D.正多边形一定既是轴对称图形,又是中心对称图形2.小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为(B)A.2 3 cmB.4 3 cmC.6 3 cmD.8 3 cm3.如图所示,正六边形ABCDEF内接于☉O,则∠ADB的度数是(C)A.60°B.45°C.30°D.22.5°知识点2正多边形的性质4.同圆的内接正三角形与内接正方形的边长的比是(A)A. 6 2B. 3 4C. 6 3D. 4 3【变式拓展】以半径为1的圆内接正三角形、正方形、正六边形的边长为三边作三角形,则(B)A.这个三角形是等腰三角形B.这个三角形是直角三角形C.这个三角形是锐角三角形D.不能构成三角形5.如图,在☉O中,OA=AB,OC⊥AB,则下列结论正确的是(D)①弦AB的长等于圆内接正六边形的边长;②弦AC的长等于圆内接正十二边形的边长;③AA=AA ;④∠BAC=30°.A.①②④B.①③④C.②③④D.①②③6.(贵阳中考)如图,正六边形ABCDEF内接于☉O,☉O的半径为6,则这个正六边形的边心距OM的长为 3 3 .7.图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图2,AE是☉O的直径,用直尺和圆规作☉O的内接正八边形ABCDEFGH.(不写作法,保留作图痕迹)解:如图所示,八边形ABCDEFGH即为所求.综合能力提升练8.正六边形的两条平行边之间的距离为1,则它的边长为(D)A. 3 6B. 3 4C. 2 3 3D. 3 39.(连云港中考)如图所示,一动点从半径为2的☉O上的A0点出发,沿着射线A0O方向运动到☉O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到☉O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到☉O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到☉O上的点A4处;…按此规律运动到点A2019处,则点A2019与点A0间的距离是(C) A.4 B.2 3C.2D.010.张萌取三个如图1所示的面积为4 cm2的钝角三角形按如图2所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为(C)A.12 cm2B.20 cm2C.24 cm2D.32 cm211.如图,正六边形ABCDEF中,AB=4,P是ED的中点,连接AP,则AP的长为 (C)A.4 3B.8C.2 13D.2 1112.(株洲中考)如图,正五边形ABCDE和正三角形AMN都是☉O的内接多边形,则∠BOM= 48°.13.如图,若干个全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需7个五边形.14.如图,已知☉O和☉O上的一点A.(1)作☉O的内接正方形ABCD和内接正六边形AEFCGH;(2)在(1)题的作图中,如果点E在AA上,求证:DE是☉O的内接正十二边形的一边.解:(1)作法:①作直径AC;②作直径BD⊥AC;③依次连接A,B,C,D四点,四边形ABCD即为☉O的内接正方形;④分别以A,C为圆心,OA长为半径作弧,交☉O于点E,H,F,G;⑤顺次连接A,E,F,C,G,H各点,六边形AEFCGH即为☉O的内接正六边形.(2)连接OE,DE.∵∠AOD= 360° 4 =90°,∠AOE= 360° 6 =60°,∴∠DOE=∠AOD-∠AOE=30°,∴DE为☉O的内接正十二边形的一边.拓展探究突破练15.如图1,2,3,4分别是☉O的内接正三角形、正四边形、正五边形、正n边形,点M,N分别从点B,C开始以相同的速度在☉O上逆时针运动.(1)求图1中∠APN的度数;(2)图2中,∠APN的度数是90°,图3中,∠APN的度数是108°;(3)试探索∠APN的度数与正多边形边数n的关系.解:(1)∵点M,N分别从点B,C开始以相同的速度在☉O上逆时针运动,∴AA=AA ,则∠BAM=∠CBN,∴∠APN=∠ABP+∠BAM=∠ABP+∠CBN=∠ABC=60°.(2)提示:在题图2中,∵点M,N分别从点B,C开始以相同的速度在☉O上逆时针运动,∴AA=AA ,∴∠BAM=∠CBN.又∵∠APN=∠ABN+∠BAM,∴∠APN=∠ABN+∠CBN,即∠APN=∠ABC.∵四边形ABCD是正四边形,∴∠ABC=90°,∴∠APN=90°.同理可得:在题图3中,∠APN=108°.(3)由(1)(2)可知,∠APN=它所在的正多边形的内角度数,由多边形内角和公式可知:正多边形的内角度数为 (A-2)×180°A (n≥3,且n为整数), ∴∠APN= (A-2)×180°A.。

2021-2022学年北师大版九年级数学下册《3-8圆内接正多边形》同步测试题(附答案)

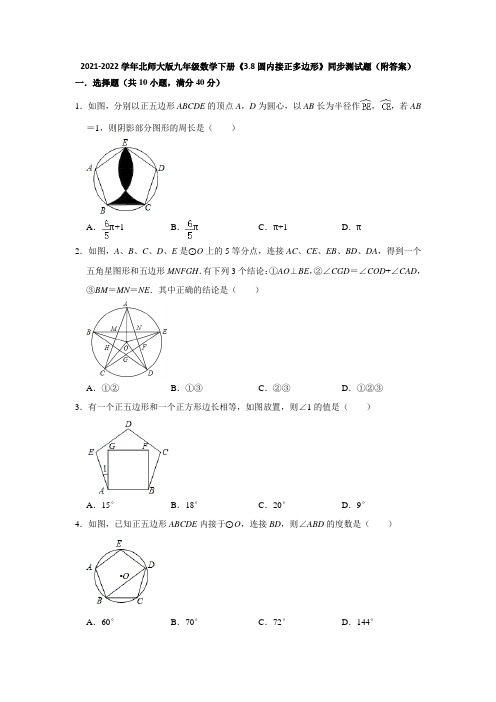
2021-2022学年北师大版九年级数学下册《3.8圆内接正多边形》同步测试题（附答案）一．选择题（共10小题，满分40分）1．如图，分别以正五边形ABCDE的顶点A，D为圆心，以AB长为半径作，，若AB ＝1，则阴影部分图形的周长是（）A．π+1B．πC．π+1D．π2．如图，A、B、C、D、E是⊙O上的5等分点，连接AC、CE、EB、BD、DA，得到一个五角星图形和五边形MNFGH．有下列3个结论：①AO⊥BE，②∠CGD＝∠COD+∠CAD，③BM＝MN＝NE．其中正确的结论是（）A．①②B．①③C．②③D．①②③3．有一个正五边形和一个正方形边长相等，如图放置，则∠1的值是（）A．15°B．18°C．20°D．9°4．如图，已知正五边形ABCDE内接于⊙O，连接BD，则∠ABD的度数是（）A．60°B．70°C．72°D．144°5．如图，正五边形ABCDE内接于⊙O，P为上的一点（点P不与点D重合），则∠CPD 的度数为（）A．30°B．36°C．60°D．72°6．如图，点M、N分别是正五边形ABCDE的两边AB、BC上的点．且AM＝BN，点O是正五边形的中心，则∠MON的度数是（）A．45度B．60度C．72度D．90度7．一个正五边形和一个正六边形按如图方式摆放，它们都有一边在直线l上，且有一个公共顶点O，则∠AOB的度数是（）A．83°B．84°C．85°D．94°8．如图，边长为3的正五边形ABCDE，顶点A、B在半径为3的圆上，其他各点在圆内，将正五边形ABCDE绕点A逆时针旋转，当点E第一次落在圆上时，则点C转过的度数为（）A．12°B．16°C．20°D．24°9．边长相等的正五边形与正六边形按如图所示拼接在一起，则∠ABO的度数为（）A．24°B．48°C．60°D．72°10．如图，若干个全等的正五边形排成环状，图中所示的是前3个正五边形，要完成这一圆环还需正五边形的个数为（）A．10B．9C．8D．7二．填空题（共10小题，满分40分）11．如图，正五边形ABCDE内接于⊙O，F是CD弧的中点，则∠CBF的度数为．12．如图，正五边形形ABCDE的边长为2，分别以点C、D为圆心，CD长为半径画弧，两弧交于点F，则的长为．（结果保留π）13．已知正五边形ABCDE内接于⊙O，连接BD，则∠ABD的度数是．14．阅读下列材料：问题：如图1，正方形ABCD内有一点P，P A＝，PB＝，PC＝1，求∠BPC的度数．小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连接PP′．请你参考小明同学的思路，解决下列问题：（1）图2中∠BPC的度数为；（2）如图3，若在正六边形ABCDEF内有一点P，且P A＝2，PB＝4，PC＝2，则∠BPC的度数为，正六边形ABCDEF的边长为．15．如图，⊙O经过正五边形OABCD的顶点A，D，点E在优弧AD上，则∠E等于度．16．如图，五边形ABCDE是⊙O的内接正五边形，AF是⊙O的直径，则∠BDF的度数是°．17．如图，点M、N分别是正五边形ABCDE的两边AB、BC上的点．且AM＝BN，点O是正五边形的中心，则∠MON的度数是度．18．如图，正五边形ABCDE和正三角形AMN都是⊙O的内接多边形，则∠BOM＝．19．如图，正五边形ABCDE内接于⊙O，连接对角线AC，AD，则下列结论：①BC∥AD；②∠BAE＝3∠CAD；③△BAC≌△EAD；④AC＝2CD．其中判断正确的是．（填序号）20．如图，正三角形AMN与正五边形ABCDE内接于⊙O，则∠BOM的度数是．三．解答题（共4小题，满分40分）21．O是边长为a的正多边形的中心，将一块半径足够长，圆心角为α的扇形纸板的圆心放在O点处，并将纸板绕O点旋转．（1）若正多边形为正三角形，扇形的圆心角α＝120°，请你通过观察或测量，填空：①如图1，正三角形ABC的边被扇形纸板覆盖部分的总长度为；②如图2，正三角形ABC的边被扇形纸板覆盖部分的总长度为；（2）若正多边形为正方形，扇形的圆心角α＝90°时，①如图3，正方形ABCD的边被扇形纸板覆盖部分的总长度为；②如图4，正方形ABCD的边被扇形纸板覆盖部分的总长度为多少？并给予证明；（3）若正多边形为正五边形，如图5，当扇形纸板的圆心角α为时，正五边形的边被扇形纸板覆盖部分的总长度仍为定值a．（4）一般地，将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形的中心O点处，并将纸板绕O点旋转．当扇形纸板的圆心角为时，正n边形的边被扇形纸板覆盖部分的总长度为定值a．22．如图，正五边形ABCDE中，点F、G分别是BC、CD的中点，AF与BG相交于H．（1）求证：△ABF≌△BCG；（2）求∠AHG的度数．23．比较正五边形与正六边形，可以发现它们的相同点和不同点．例如：它们的一个相同点：正五边形的各边相等，正六边形的各边也相等．它们的一个不同点：正五边形不是中心对称图形，正六边形是中心对称图形．请你再写出它们的两个相同点和不同点：相同点：①；②．不同点：①；②．24．如图，分别是正方形、正五边形和正六边形，（1）试分别计算这三种正多边形的相邻两条对角线的夹角的度数；（2）探究正n边形相邻两条对角线的夹角满足的规律．参考答案一．选择题（共10小题，满分40分）1．解：∵五边形ABCDE为正五边形，AB＝1，∴AB＝BC＝CD＝DE＝EA＝1，∠A＝∠D＝108°，∴的长＝的长＝＝π，∴阴影部分图形的周长＝的长+的长+BC＝π+1．故选：A．2．解：∵A、B、C、D、E是⊙O上的5等分点，∴＝，∴AO⊥BE，故①正确；∵A、B、C、D、E是⊙O上的5等分点，∴的度数＝＝72°，∴∠COD＝72°，∵∠COD＝2∠CAD，∴∠CAD＝36°；连接CD∵A、B、C、D、E是⊙O上的5等分点，∴＝＝＝，∴∠BDC＝∠DCE＝∠CAD＝36°，∴∠CGD＝108°，∴∠CGD＝∠COD+∠CAD，故②正确；连接AB，AE，∴∠MBA＝∠MAB＝36°，∴AM＝BM，∵∠MAN＝36°，∠ANM＝∠DAE+∠AEB＝72°，∴AM≠MN，∴BM≠MN③错误！则∠BAM＝∠ABM＝∠EAN＝∠AEN＝36°，∵AB＝AE，∴△ABM≌△AEN（ASA），∴BM＝EN＝AM＝AN，∵∠MAN＝36°，∴AM≠MN，∴③错误．故选：A．3．解：正五边形的内角的度数是×（5﹣2）×180°＝108°，正方形的内角是90°，则∠1＝108°﹣90°＝18°．故选：B．4．解：∵五边形ABCDE为正五边形，∴∠ABC＝∠C＝＝108°，∵CD＝CB，∴∠CBD＝＝36°，∴∠ABD＝∠ABC﹣∠CBD＝72°，故选：C．5．解：如图，连接OC，OD．∵ABCDE是正五边形，∴∠COD＝＝72°，∴∠CPD＝∠COD＝36°，故选：B．6．解：连接OA、OB、OC，∠AOB＝＝72°，∵∠AOB＝∠BOC，OA＝OB，OB＝OC，∴∠OAB＝∠OBC，在△AOM和△BON中，，∴△AOM≌△BON（SAS）∴∠BON＝∠AOM，∴∠MON＝∠AOB＝72°，故选：C．7．解：由题意：∠AOE＝108°，∠BOF＝120°，∠OEF＝72°，∠OFE＝60°，∴∠EOF＝180°﹣72°﹣60°＝48°，∴∠AOB＝360°﹣108°﹣48°﹣120°＝84°，故选：B．8．解：设点E第一次落在圆上时的对应点为E′，连接OA、OB、OE′，如图，∵五边形ABCDE为正五边形，∴∠EAB＝108°，∵正五边形ABCDE绕点A逆时针旋转，点E第一次落在圆上E′点，∴AE＝AE′＝3，∵OA＝AB＝OB＝OE′＝3，∴△OAE′、△OAB都为等边三角形，∴∠OAB＝∠OAE′＝60°，∴∠E′AB＝120°，∴∠EAE′＝12°，∴当点E第一次落在圆上时，则点C转过的度数为12°．故选：A．9．解：由题意得：正六边形的每个内角都等于120°，正五边形的每个内角都等于108°，∴∠BOA＝360°﹣120°﹣108°＝132°，∵AO＝BO，∴∠ABO＝∠OAB＝＝24°故选：A．10．解：∵五边形的内角和为（5﹣2）•180°＝540°，∴正五边形的每一个内角为540°÷5＝108°，如图，延长正五边形的两边相交于点O，则∠1＝360°﹣108°×3＝360°﹣324°＝36°，360°÷36°＝10，∵已经有3个五边形，∴10﹣3＝7，即完成这一圆环还需7个五边形．故选：D．二．填空题（共10小题，满分40分）11．解：设圆心为O，连接OC，OD，BD，∵五边形ABCDE为正五边形，∴∠O＝＝72°，∴∠CBD＝O＝36°，∵F是的中点，∴∠CBF＝∠DBF＝CBD＝18°，故答案为：18°．12．解：连接CF，DF，则△CFD是等边三角形，∴∠FCD＝60°，∵在正五边形ABCDE中，∠BCD＝108°，∴∠BCF＝48°，∴的长＝＝π，故答案为：π．13．解：∵五边形ABCDE为正五边形，∴∠ABC＝∠C＝＝108°，∵CD＝CB，∴∠CBD＝＝36°，∴∠ABD＝∠ABC﹣∠CBD＝72°，故答案为：72°．14．解：（1）如图2．∵△BPC绕点B逆时针旋转90°，得到了△BP′A，∴∠P′BP＝90°，BP′＝BP＝，P′A＝PC＝1，∠BP′A＝∠BPC，∴△BPP′为等腰直角三角形，∴PP′＝PB＝2，∠BP′P＝45°，在△APP′中，AP＝，PP′＝2，AP′＝1，∵（）2＝22+12，∴AP2＝PP′2+AP′2，∴△APP′为直角三角形，且∠AP′P＝90°∴∠BP′A＝45°+90°＝135°，∴∠BPC＝∠BP′A＝135°；（2）如图3．∵六边形ABCDEF为正六边形，∴∠ABC＝120°，把△BPC绕点B逆时针旋转120°，得到了△BP′A，∴∠P′BP＝120°，BP′＝BP＝4，P′A＝PC＝2，∠BP′A＝∠BPC，∴∠BP′P＝∠BPP′＝30°，过B作BH⊥PP′于H，∵BP′＝BP，∴P′H＝PH，在Rt△BP′H中，∠BP′H＝30°，BP′＝4，∴BH＝BP′＝2，P′H＝BH＝2，∴P′P＝2P′H＝4，在△APP′中，AP＝2，PP′＝4，AP′＝2，∵（2）2＝（4）2+22，∴AP2＝PP′2+AP′2，∴△APP′为直角三角形，且∠AP′P＝90°，∴∠BP′A＝30°+90°＝120°，∴∠BPC＝120°，过A作AG⊥BP′于G点，∴∠AP′G＝60°，在Rt△AGP′中，AP′＝2，∠GAP′＝30°，∴GP′＝AP′＝1，AG＝GP′＝，在Rt△AGB中，GB＝GP′+P′B＝1+4＝5，AB＝＝＝2，即正六边形ABCDEF的边长为2．故答案为135°；120°，2．15．解：∵⊙O经过正五边形OABCD的顶点A，D，∴∠AOD＝108°，∴∠E＝AOD＝54°，故答案为：54．16．解：∵AF是⊙O的直径，∴＝，∵五边形ABCDE是⊙O的内接正五边形，∴＝，∠BAE＝108°，∴＝，∴∠BAF＝∠BAE＝54°，∴∠BDF＝∠BAF＝54°，故答案为：54．17．解：连接OA、OB、OC，∠AOB＝＝72°，∵∠AOB＝∠BOC，OA＝OB，OB＝OC，∴∠OAB＝∠OBC，在△AOM和△BON中，∴△AOM≌△BON，∴∠BON＝∠AOM，∴∠MON＝∠AOB＝72°，故答案为：72．18．解：连接OA，∵五边形ABCDE是正五边形，∴∠AOB＝＝72°，∵△AMN是正三角形，∴∠AOM＝＝120°，∴∠BOM＝∠AOM﹣∠AOB＝48°，故答案为：48°．19．解：①∵∠BCD＝180°﹣72°＝108°，∠E＝108°，∴∠ADE＝×（180°﹣108°）＝36°，∴∠ADC＝108°﹣36°＝72°，∴∠BCD+∠ADC＝108°+72°＝180°，∴BC∥AD，故本选项正确；②∵∠BAE＝108°，∠CAD＝×＝36°，∴∠BAE＝3∠CAD，故本选项正确；③在△BAC和△EAD中，，∴△BAC≌△EAD（SSS），故本选项正确；④∵AB+BC＞AC，∴2CD＞AC，故本选项错误．故答案为：①②③．20．解；连接AO，∵正三角形AMN与正五边形ABCDE内接于⊙O，∴∠AOM＝×360°＝120°，∴∠AOB＝×360°＝72°，∵∠BOM＝∠AOM﹣∠AOB，∴∠BOM＝120°﹣72°＝48°故答案为：48°三．解答题（共4小题，满分40分）21．解：（1）①a；（1分）②a；（2分）（2）①a；（3分）②正方形ABCD的边被扇形纸板覆盖部分的总长度为a．（4分）理由：证明：连接OA、OD∵四边形ABCD是正方形，点O为中心∴OA＝OD，∠OAM＝∠ODN＝45°又∵∠AOD＝∠POQ＝90°∴∠AOM+∠AOQ＝90°∠DON+∠AOQ＝90°∴∠AOM＝∠DON∴△AOM≌△DON∴AM＝DN∴AM+AN＝DN+AN＝AD＝a（8分）（3）∵正五边形的内角为（5﹣2）×180°÷5＝108°∴当扇形纸板的圆心角α为72°时，正五边形的边被扇形纸板覆盖部分的总长度仍为定值a．（10分）（4）∵正多边形的中心角为，∴当扇形纸板的圆心角为时，正n边形的边被扇形纸板覆盖部分的总长度为定值a．（12分）22．（1）证明：∵五边形ABCDE是正五边形，∴AB＝BC＝CD，∠ABC＝∠BCD，（2分）∵F、G分别是BC、CD的中点，∴BF＝CG，（4分）在△ABF和BCG中，AB＝BC，∠ABC＝∠BCD，BF＝CG，（5分）∴△ABF≌△BCG；（6分）（2）解：由（1）知∠GBC＝∠F AB，∵∠AHG＝∠F AB+∠ABH＝∠GBC+∠ABH＝∠ABC（，7分）∵正五边形的内角为108°，∴∠AHG＝108°．（9分）（注：本小题直接正确写出∠AHG＝108°不扣分）23．解：相同点不同点①都有相等的边．①边数不同；②都有相等的内角．②内角的度数不同；③都有外接圆和内切圆．③内角和不同；④都是轴对称图形．④对角线条数不同；⑤对称轴都交于一点．⑤对称轴条数不同．24．解：（1）解：由正方形ABCD，可得：AC⊥BD，∴α4＝90°；由正五边形ABCDE，可得：AB＝BC＝CD，∠ABC＝∠BCD＝108°，∴∠DBC＝∠ACB＝＝36°，∴α5＝180°﹣∠DBC﹣∠ACB＝108°；同理：α6＝120°；（2）．。

北师版九年级数学下册《圆内接正多边形(2)》同步练习3

《圆内接正多边形（2）》同步练习3基础检测1.八边形的内角和等于________度．2.半径为R 的圆内接正三角形的面积是（） A ．232R B ．2πR C ．2332R D ．2334R3.如图，菱形花坛ABCD 的边长为6m ，∠B ＝60°，其中由两个正六边形组成的部分种花，则种花部分的图形周长为____________.4.（1）如图1，把等边三角形的各边三等分，分别以居中那条线段为一边向外作等边三角形，并去掉居中的那条线段，得到一个六角星，则这个六角星的边数是__________. （2）如图2，在5×5的网格中有一个正方形，把正方形的各边三等分，分别以居中那条线段为一边向外作正方形，并去掉居中的那条线段．请你把得到的图形画在图3中，并写出这个图形的边数．（3）现有一个正五边形，把正五边形的各边三等分，分别以居中那条线段为一边向外作正五边形，并去掉居中的那条线段，得到的图形的边数是多少？拓展提高1．如图，在平面直角坐标系中，四边形OABC 为正方形，顶点A 、C 在坐标轴上，以边AB 为弦的⊙M 与x 轴相切，已知点A 的坐标为(0，8)，则圆心M 的坐标为_________．（图1）（图2）（图3）ADB2.如图，已知在Rt ABC △中，Rt ACB ∠=∠，4AB =，分别以AC ，BC 为直径作半圆，面积分别记为1S ，2S ，则1S +2S 的值等于__________.3.如图，△PQR 是⊙O 的内接正三角形，四边形ABCD 是⊙O 的内接正方形，BC//QR ，则∠AOQ 的度数是_________.4.各边相等的圆内接多边形一定是正多边形吗？各角相等的圆内接多边形呢？如果是，说明为什么，如果不是，举出反例.5、图(1)、图(2)、图(3)是分别由两个公共顶点A 的正三角形、正四边形和正五边形组成的图形，且其中一个正多边形的顶点B ′在另一个正多边形的边BC 上． ⑴图(1)中，∠B′CC′=__________.(直接写出答案)⑵图(2)中，求∠B′CC′；（写出解答过程）⑶图(3)中，∠B′CC′=_________.(直接写出答案)P QR C BAODC ABS 1S 2⑷当满足条件的图形为正n 边形时(如图(4))，猜想：∠B ′CC ′=________(直接写出答案)．(1) (2) (3) (4) 体验中考1.（2009年,肇庆）若正六边形的边长为2，则此正六边形的边心距为__________. 2．（2009年,黄石市）如图，ABC △为O ⊙的内接三角形，130AB C =∠=，°，则O ⊙的内接正方形的面积为（）A ．2B ．4C ．8D ．16【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

九年级数学下册《圆内接正多边形》专项练习(含答案)

8 圆内接正多边形A 卷1．边长为a 的正六边形的边心距是__________，周长是____________，面积是___________.2．如图1，正方形的边长为a ，以顶点B 、D 为圆心，以边长a 为半径分别画弧，在正方形内两弧所围成图形的面积是___________.(1) (2) (3)3．圆内接正方形ABCD 的边长为2，弦AE 平分BC 边，与BC 交于F ，则弦AE 的长为__________.4．正六边形的面积是18，则它的外接圆与内切圆所围成的圆环面积为_________.5．圆内接正方形的一边截成的小弓形面积是2π-4，则正方形的边长等于__________.6．正三角形的内切圆半径、外接圆半径和高的比为___________.7．在半径为R 的圆中，内接正方形与内接正六边形的边长之比为___________.8．同圆的内接正n 边形与外切正n 边形边长之比是______________.9．正三角形与它的内切圆及外接圆的三者面积之比为_____________.10．正三角形的外接圆半径为4cm ，以正三角形的一边为边作正方形，则此正方形的外接圆半径长为___________.3B 卷1．正方形的内切圆半径为r ，这个正方形将它的外接圆分割出四个弓形，其中一个弓形的面积为_________.2．如果正三角形的边长为a ，那么它的外接圆的周长是内切圆周长的_______倍.3．如图2，正方形边长为a ，那么图中阴影部分的面积是__________.4．正多边形的一个内角等于它的一个外角的8倍，那么这个正多边形的边数是________.5．半径为R 的圆的内接正n 边形的面积等于__________.6．如果圆的半径为a ，它的内接正方形边长为b ，该正方形的内切圆的内接正方形的边长为c ，则a,b,c 间满足的关系式为___________.7．如图3，正△ABC 内接于半径为1cm 的圆，则阴影部分的面积为___________.8．如果圆内接正六边形的边长为10cm ，则它的边心距为_______cm ，正六边形的一边在圆上截得的弓形面积是____________.9．已知正方形的边长为a ，以各边为直径在正方形内画半圆，则所围成的阴影部分(如图)的面积为__________.10．周长相等的正方形和正六边形的面积分别为和，则和的大小关系为__________.24S 6S 4S 6S参考答案A 卷1．2．3．点B 到弦AE 的垂线段长为，由勾股定理或射影定理，求得弦AE 的长为. 4．由正六边形的面积为18，得正六边形的边长为2，边心距为3，从而正六边形的外接圆半径为2，内切圆半径为3，故所围成的圆环面积为3π. 5．设所求正方形的边长为x ，则外接圆的半径为，正方形的一边截成的小弓形面积为，即 = 2π- 4，于是，得正方形的边长等于4.6．设正三角形的边长为a ，则内切圆半径为，外接圆半径为，高为，故内切圆半径、外接圆半径和高的比为1：2：3.7．内接正方形的边长为R ，内接正六边形的边长为R ，其比为：1.8．设圆的半径为R ，则同圆的内接正π边形和外切正n 边形的边分别为2Rsin和2Rtg ，其比为cos . 9．设正三角形的边长为a ，则内切圆半径为，外接圆半径为，其面积分别为、和，三者之比为3：π：4π . 10．求得正三角形的边长即所作正方形的边长为4，从而外接圆的半径长为2.2233;6;23a a 222a a -π552558333x 22224181x x ππ-224181x x ππ-a 63a 33a 2322n ︒180n ︒180n︒180a 63a 33243a 2121a π231a π336B 卷1．由已知得正方形的边长为2r ，从而正方形的外接圆半径为r ，所求弓形的面积为. 2．边长为a 的正三角形的外接圆半径和内切圆半径分别为、，其周长分别为的πa 和，故它的外接圆周长是内切圆周长的2倍. 3．阴影部分面积为 4．设所求正多边形的边数为n ，则它的一个内角等于，相应的外角等于180°- ，则由已知，得=8×(180°-)，解之，得n = 18. 5．半径为R 的圆的内接正n 边形的边长为2Rsin ，边长距为Rcos ，则正n 边形的面积为= 6．半径为a 的圆的内接正方形的边长为a ，即 b =a ；边长为b 的正方形的内切圆的内接正方形的边长为b ，即 C = b ，从而得知 a =c ，故a,b,c 三者之间的关系为：7．设正△ABC 的边长为a ，则=1，a=，于是阴影部分的面积为π· 8．边心距×10=5()；正六边的一边在圆上截得的弓形的面积减去三角形的面积，即 22)221(r -πa 33a 63332a π3322241)22(21)2(41a a a πππ=-︒⋅-180)2(n n ︒⋅-180)2(nn ︒⋅-180)2(n n ︒⋅-180)2(nn n ︒180n︒180n n nR n R n R n ︒⋅︒=︒⋅︒⋅⋅180cos 180sin 180cos 180sin 2212222222222c a b +=a 333))(433()3(431222cm -=⋅-π2332cm )(325350104310321222cm -=⋅-⋅⋅ππ9．图中四个半圆都通过正方形的中心，用正方形的面积减去四隙的面积，剩下的就是阴影部分的面积，而正方形的面积减去两个半圆的面积就得两个空隙的面积，故所求阴影部分的面积为 10．设周长为a ，则正方形的正六边形的边长分别为，其面积分别为，故.22])2([22222a a a a a -=⨯⋅--ππa a 6141和222243)61(436161a a a =⋅⋅和64S S <。

北师大版九年级数学下《3.8圆内接正多边形》同步习题含答案

北师大版九年级数学下册第三章圆 3.8 圆内接正多边形同步习题一、选择题(9分×3＝27分)1．同圆的内接正三角形与内接正方形的边长的比是( )A.62 B.34 C.63 D.432．周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6之间的大小关系是( )A．S3＞S4＞S6B．S6＞S4＞S3C．S6＞S3＞S4D．S4＞S6＞S33．如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠AOQ的度数为( )A．60°B．65°C．72°D．75°二、填空题(9分×2＝18分)4．点M、N分别是正八边形相邻的边AB、BC上的点，且AM＝BN，点O是正八边形中心，则∠MON＝____________．,第4题图),第5题图)5．如图，在正八边形ABCDEFGH中，四边形BCFG的面积为20cm2，则正八边形的面积为_______cm2.三、解答题(17分＋18分＋20分＝55分)6．学习完正多边形和圆后，在师生共同小结与归纳时，下面有几位同学谈了自己的想法．针对以上三位同学的意见，谈谈自己的想法．7．如图，已知l是⊙O的切线，切点为A，点B在⊙O上，BC交⊙O于E，交直线l于C，OC交⊙O于F，且AB＝AO＝AC.一同学通过测量猜测，EF为⊙O的内接正二十四边形的一边，你认为他的猜测正确，请你证明；若你认为他的猜测不正确，请说明理由．8．如图1，2，3，…，n，M、N分别是⊙O的内接正三角形ABC，正方形ABCD，正五边形ABCDE，…，正n边形ABCDE…的边AB、BC上的点，且BM＝CN，连接OM、ON.(1)求图1中∠MON的度数；(2)图2中∠MON的度数是_______；图3中∠MON的度数是________；(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案)．答案：1. A2. B3. D4. 45°5. 406. 解：矩形不一定是正多边形，因为其各边不一定都相等，菱形不一定是正多边形，因为其各角不一定相等，正方形是正多边形；圆内接菱形是正方形，因为菱形各边相等，且各边所对的弧也相等，可推出其各内角也都相等；正多边形是轴对称图形，但不一定是中心对称图形．7. 解：猜测正确．证明：连接OE.∵AB＝AO＝AC，又OB＝OA，∴△OAB为等边三角形，∴∠OAB＝60°，由l切⊙O于A得OA⊥l，∴∠ABC ＝∠ACB ＝15°，∴∠AOE ＝30°，由OA ＝CA ，OA ⊥AC 得∠AOC ＝45°，∴∠EOF ＝15°，而360°15°＝24，故EF 为⊙O 的内接正二十四边形的一边．8. 解：(1)连接OB 、OC.∵正△ABC 内接于⊙O ，∴∠OBM ＝∠OCN ＝30°，∠BOC ＝120°，又∵BM ＝CN ，OB ＝OC ，∴△OBM ≌△OCN ，∴∠BOM ＝∠CON ，∴∠MON ＝∠BOC ＝120°(2)90°72°(3)∠MON ＝360°n。

《圆内接正多边形》同步练习 (精品)2022年附答案

3.8 圆内接正多边形1．以下边长为a的正多边形与边长为a的正方形组合起来，不能镶嵌成平面的是( )(1)正三角形(2)正五边形(3)正六边形(4)正八边形A．(1)(2) B．(2)(3) C．(1)(3) D．(1)(4)2．以下说法正确的选项是A．每个内角都是120°的六边形一定是正六边形．B．正n边形的对称轴不一定有n条．C．正n边形的每一个外角度数等于它的中心角度数．D．正多边形一定既是轴对称图形，又是中心对称图形．3.假设同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3，r4，r6，那么r3：r4：r6等于( )A．B．C．D．4.如图，假设正方形A1B1C1D1内接于正方形ABCD的内接圆，那么的值为〔〕A．B．C．D．5．正六边形ABCDEF内接于⊙O，图中阴影局部的面积为，那么⊙O的半径为______________________．第5题图第6题图6．如图，正方形ABCD内接于⊙O，点E在上，那么∠BEC= ．7．将一块正六边形硬纸片〔图1〕，做成一个底面仍为正六边形且高相等的无盖纸盒〔侧面均垂直于底面，见图2〕，需在每一个顶点处剪去一个四边形，例如图中的四边形AGA/H，那么∠GA/H 的大小是度．8．从一个半径为10㎝的圆形纸片上裁出一个最大的正方形，那么此正方形的边长为．9．如图五边形ABCDE 内接于⊙O,∠A=∠B=∠C=∠D=∠E ．求证：五边形ABCDE 是正五边形10．如图，10－1、10－2、10－3、…、10－n 分别是⊙O 的内接正三角形ABC ，正四边形ABCD 、正五边形ABCDE 、…、正n 边形ABCD …，点M 、N 分别从点B 、C 开始以相同的速度在⊙O 上逆时针运动。

(1)求图10－1中∠APN 的度数；(2)图10－2中，∠APN 的度数是_______，图10－3中∠APN 的度数是________。

(3)试探索∠APN 的度数与正多边形边数n 的关系〔直接写答案〕第17章一元二次方程17.1 一元二次方程◆随堂检测1、判断以下方程，是一元二次方程的有____________.〔1〕；〔2〕；〔3〕；〔4〕；〔5〕；〔6〕.〔提示：判断一个方程是不是一元二次方程，首先要对其整理成一般形式，然后根据定义判断.〕2、以下方程中不含一次项的是〔〕A ．B ．C ．D ．3、方程的二次项系数___________；一次项系数__________；常数项_________.4、1、以下各数是方程解的是〔〕N 图10－1N 图10－2 A M 图10－3M 图10－4A、6B、2C、4D、05、根据以下问题，列出关于的方程，并将其化成一元二次方程的一般形式.〔1〕4个完全相同的正方形的面积之和是25，求正方形的边长.〔2〕一个矩形的长比宽多2，面积是100，求矩形的长.〔3〕一个直角三角形的斜边长为10，两条直角边相差2，求较长的直角边长.分析：此题是含有字母系数的方程问题．根据一元一次方程和一元二次方程的定义，分别进行讨论求解.解：〔1〕由题意得，时，即时，方程是一元一次方程.〔2〕由题意得，时，即时，方程、一次项系数是、常数项是.◆课下作业●拓展提高1、以下方程一定是一元二次方程的是〔〕A、 B、C、 D、2、是关于的一元二次方程，那么的值应为〔〕A、＝2B、C、D、无法确定3.是一元二次方程的一个解，那么的值是〔〕A．-3 B．3 C．0 D．0或34.假设是关于的方程的根，那么的值为〔〕A．1 B．2 C．-1 D．-25.根据以下表格对应值：A、 B、3.24＜C、5＜D、＜6.假设一元二次方程有一个根为1，那么_________；假设有一个根是-1，那么b与、c之间的关系为________；假设有一个根为0，那么c=_________.7.下面哪些数是方程的根？-3、-2、-1、0、1、2、3、0，求的值是多少？9.关于的方程．〔1〕为何值时，此方程是一元一次方程？〔2〕为何值时，此方程是一元二次方程？并写出一元二次方程的二次项系数、一次项系数及常数项。

3.8 圆内接正多边形课后练习2020-2021学年北师大版九年级下册数学

第三章圆8.圆内接正多边形课后练习2020-2021学年下学期九年级下册初中数学北师大版一、单选题（共12题）⌢上，则∠P的度数为（）1.如图，正方形ABCD内接于⊙O，点P在ABA. 30°B. 45°C. 60°D. 90°2.⊙O是一个正n边形的外接圆，若⊙O的半径与这个正n多边形的边长相等，则n的值为（）A. 3B. 4C. 5D. 63.已知圆内接正六边形的半径为2，则该内接正六边形的边心距为（）A. 2B. 1C. √3D. √324.如图，五边形ABCDE是⊙O的内接正五边形，AF是⊙O的直径，则∠BDF的度数是（）A. 18°B. 36°C. 54°D. 72°5.如图，四边形ABCD为⊙O的内接正四边形，△AEF为⊙O的内接正三角形，若DF恰好是同圆的一个内接正n边形的一边，则n的值为（）A. 8B. 10C. 12D. 156.正多边形的内切圆与外接圆的半径之比为√2，则这个正多边形为（）2A. 正十二边形B. 正六边形C. 正四边形D. 正三角形7.一个圆的内接正六边形与内接正方形的边长之比为（）A. 3：2B. 1:√3C. 1:√2D. √2:√38.正方形外接圆的半径为4，则其内切圆的半径为（）A. 2 √2B. √2C. 1D. √229.已知正六边形ABCDEF内接于⊙O，若⊙O的直径为2，则该正六边形的周长是（）A. 12B. 6√3C. 6D. 3√310.半径为a的圆的内接正六边形的边心距是（）A. a2B. √2a2C. √3a2D. a11.半径为R的圆内接正三角形的面积是（）A. √32R2 B. πR2 C. 3√32R2 D. 3√34R212.如图，在圆内接正六边形ABCDEF中，BF，BD分别交AC于点G，H.若该圆的半径为15cm，则线段GH 的长为（）A. √5cmB. 5 √3cmC. 3 √5cmD. 10 √3cm二、填空题（共6题）13.如图，正五边形ABCDE内接于⊙O，点F在弧CD上，则∠BFE的度数为________14.如图，正方形ABCD和正六边形AEFCGH均内接于⊙O，连接HD；若线段HD恰好是⊙O 的一个内接正n边形的一条边，则n=________．15.若圆内接正方形的边心距为3，则这个圆内接正三角形的边长为________.16.数学家刘徽首创割圆术，用圆内接正多边形的面积去无限逼近圆面积并以此求出圆周率.如图，正六边形ABCDEF的边长为2，现随机向该图形内掷一枚小针，则针尖落在阴影区域的概率为________.17.如图，正六边形ABCDEF内接于⊙O，若AB=3cm，则⊙O的半径为________.18.我国古代数学家刘徽创造的“割圆术”，利用了圆内接正多边形和外切正多边形的面积或周长，无限逼近圆来近似估计圆的面积或周长，从而估算出π的范围.如图1，用圆内接正方形和外切正方形周长可得2 √2<r<4，那么利用图2中的圆内接正六边形和外切正六边形周长可进一步将π的范围缩小到________(结果保留根号)三、综合题（共4题）19.如图，已知圆O内接正六边形ABCDEF的边长为6cm，求这个正六边形的边心距n，面积S ．20.如图，ABCDE是⊙O的内接正五边形．求证：AE∥BD.21.试比较图中两个几何图形的异同，请分别写出它们的两个相同点和两个不同点。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

圆内接多边形练习题一、选择
1.圆内接四边形ABCD 中，//AD BC ，AC 与BD 交于点E ，在下图中全等三角形的对数为 A.2对 B.3对 C.4对 D.5对
2.如图，四边形ABCD 为圆内接四边形，AC 为BD 的垂直平分线，60,ACB AB a ∠== ，则CD =
A.
3a B.2
a C.12a D.13a
3．（2006年威海市）如图，若正方形A 1B 1C 1D 1内接于正方形ABCD 的内接圆，则AB
B A 1
1的值为（）
A ．
21 B ．22 C ．
41 D ．4
2 二、填空
1、已知正六边形ABCDEF 内接于⊙O ，图中阴影部分的面积为312，则⊙O 的半径为
______________________．
2．如图，正方形ABCD 内接于⊙O ，点E 在 AD 上，则∠BEC= ．
3．将一块正六边形硬纸片（图1），做成一个底面仍为正六边形且高相等的无盖纸盒（侧面均垂直于底面，见图2），需在每一个顶点处剪去一个四边形，例如图中的四边形AGA /
H ，那么∠GA /
H 的大小是度．
D
A
4如图，在正六边形ABCDEF 的内部，以AB 为边作正方形ABMN ，连接MC ，则∠BCM 的度数为（）
5.三角形三边长为5,12,13,则它的外接圆圆心到顶点的距离为 .
6.圆内接四边形ABCD 中，::1:2:3A B C ∠∠∠=，则D ∠= .
7.如图，AB 为半圆O 的直径，C 、D 为半圆上的两点，20BAC ∠=
，则ADC ∠= .
三、解答题
1.如图，锐角三角形ABC 中，60A ∠=
，BC 为圆O 的直径，⊙O 交AB 、AC 于D 、E ，求证：
2BC DE =.
B
2.如图，⊙O 的内接四边形ABCD 中，M 为CD 中点，N 为AB 中点，AC BD ⊥于点E ，连接ON 、ME ，并延长ME 交AB 于点F.求证：MF AB ⊥.
A
B
C
3.已知：如图所示，10,8,AB cm BC cm ==CD 平分ACB ∠. (1)求AC 和DB 的长； (2)求四边形ACBD 的面积.
4、(10分)某超市经销一种销售成本为每件40元的商品．据市场调查分析，如果按每件50
元销售，一周能售出500件；若销售单价每涨1元，每周销量就减少10件．设销售单价为x 元(x ≥50)，一周的销售量为y 件．
(1)写出y 与x 的函数关系式(标明x 的取值范围)；
(2)设一周的销售利润为S ，写出S 与x 的函数关系式，并确定当单价在什么范围内变化时，利润随着单价的增大而增大？
(3)在超市对该种商品投入不超过10000元的情况下，使得一周销售例如达到8000元，销售单价应定为多少？
（2012•临沂）如图，点A 在x 轴上，OA=4，将线段OA 绕点O 顺时针旋转120°至OB 的位置．
（1）求点B 的坐标；
（2）求经过点A 、O 、B 的抛物线的解析式；
（3）在此抛物线的对称轴上，是否存在点P ，使得以点P 、O 、B 为顶点的三角形是等腰三角形？若存在，求点P 的坐标；若不存在，说明理由．。