上海数学中考压轴题几何背景探究
有几何背景的综合题的复习探究
几何背景综合题的复习----------基本图形分析举例光明初级中学 刘颖颋 教学目标：1. 通过对一类基本图形进行研究，引导学生在复习中建立各自理解的几何背景，提高学生在解决有几何背景的综合题方面的能力。
2. 通过对基本图形的探究，感悟解几何背景综合题的一般思考方法。
3. 体会多种数学思想方法的综合运用以及透过现象看本质的辨证思维方法。
教学重点及难点：基本图形的分析中规律的探索和合理的运用。
教学过程：B例：已知：60MAN = ∠，点B 在射线AM 上， P 为射线AN 上一动点（点P 与点A 不重合），以BP 为边作等边三角形BPQ （点B P Q ，，按顺时针排列），O 是BPQ △的外心．求证：点O 在MAN ∠的平分线上；例：在Rt △ABC 中，∠C ＝ 90，AB ＝5,AC ＝4，BC ＝3，点M 是AB 边的中点，用一个直角三角板的直角顶点放在点M 处旋转，使两直角边与原Rt △ABC 的两边AC 、BC 分别交与E 、F 点，求MF ME的值。
课堂训练：如图，在Rt △ABC 中，∠C ＝ 90，AB ＝5,AC ＝4，BC ＝3，点P 、Q 、R 分别是AC 、BA 、BC 上的动点，且CR ＝AP ＝BQ ＝x ，在运动过程中求使得∠PQR ＝ 90的x 的值。
MCBARPCBA参考资料：背景1：一个直角三角板的直角顶点放在等腰直角三角形ABC 的斜边的中点M 处旋转，让两直角边与等腰直角三角形的两直角边交于E 、F 两点。
观察图形，会得到哪些结论？(i) △CFM ≌△AEM ；△CEM ≌△BFM ； (ii) ME ＝MF ；△MEF 是等腰直角三角形； (iii) ABC CEMF S S △四边形21=(iv) △CFM ∽△AEM ∽△FDM ∽△CDE ；△CEM ∽△BFM ∽△EDM ∽△CDF ； (v) MC MD MF ME ∙==22；FD ED CD MD ∙=∙；CM CD CF EC ∙=∙·· (vi) AB AC CF CE 或＝定值+(vii)以后我们遇上“直角对直角，并且直角与直角的顶点的连线平分一个直角”。
上海中考数学压轴题
上海中考数学压轴题近年来，上海中考数学压轴题备受关注。
这些题目难度较大，出题精细，考察学生对数学知识的理解和应用能力。
下面我们来分析一下近年来的上海中考数学压轴题的特点和解题技巧。
首先，上海中考数学压轴题在难度上相对较高。
这是因为上海地区的中考要求学生掌握更高层次的数学知识和技能。
压轴题往往涉及多个知识点的综合运用，需要学生具备较强的分析和解决问题的能力。
例如，一道常见的压轴题可能涉及到几何、代数、概率等多个领域的知识，考察学生对数学的综合应用能力。
其次，上海中考数学压轴题注重思维的拓展。
在解题过程中，学生需要进行逻辑推理、问题转化和数学模型的建立等思维活动。
这些题目往往需要学生灵活运用数学知识解决实际问题，培养学生的数学思维和创新能力。
因此，学生在备考中需要注重培养解决问题的思维方式，通过多做一些综合性的题目来提高解题能力。
另外，上海中考数学压轴题注重实践能力的考察。
在解题过程中，学生需要将数学知识运用到实际生活中的问题中去。
这样的题目能够培养学生的实际运用能力和解决实际问题的能力。
例如，一道压轴题可能涉及到购物打折、旅行路线规划等实际问题，学生需要将数学知识应用到这些问题中去解决。
因此，学生在备考中需要注重实际问题的练习，多思考数学知识与实际问题的联系。
最后，上海中考数学压轴题注重数学思想的培养。
这些题目旨在培养学生的数学思维方式和解决问题的能力，而不仅仅是对知识的简单记忆和运用。
学生在解题过程中需要思考问题的本质，从中抽象出数学模型，并运用数学知识解决问题。
因此，学生在备考中需要注重培养数学思维的培养，通过多做一些思维拓展的题目来提高数学思维的能力。
综上所述，上海中考数学压轴题在难度、思维拓展、实践能力和数学思想的培养等方面具有一定的特点。
学生在备考中需要注重综合能力的培养，多做一些综合性的题目，培养解决问题的思维方式，提高数学的应用能力和创新能力。
只有这样，才能在上海中考数学压轴题中取得较好的成绩。
上海市中考数学压轴题几何背景探寻和思考
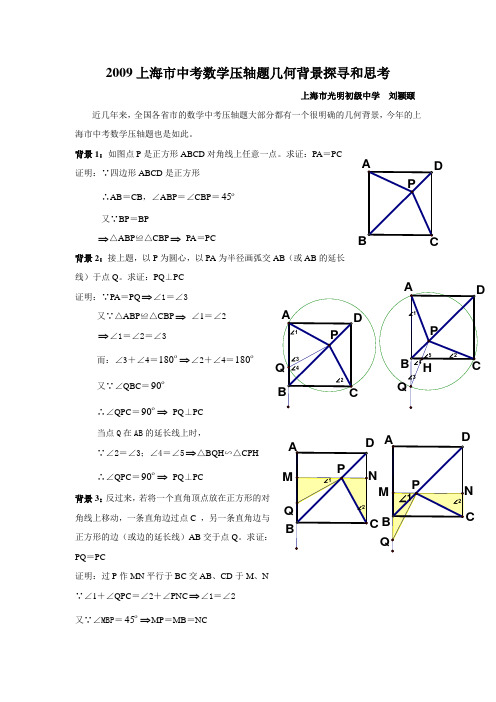
2009上海市中考数学压轴题几何背景探寻和思考上海市光明初级中学 刘颖颋 近几年来，全国各省市的数学中考压轴题大部分都有一个很明确的几何背景，今年的上海市中考数学压轴题也是如此。
背景1：如图点P 是正方形ABCD 对角线上任意一点。
求证：PA ＝PC 证明：∵四边形ABCD 是正方形∴AB ＝CB ，∠ABP ＝∠CBP ＝ο45 又∵BP ＝BP⇒△ABP ≌△CBP ⇒ PA ＝PC背景2：接上题，以P 为圆心，以PA 为半径画弧交AB （或AB 的延长 线）于点Q 。
求证：PQ ⊥PC 证明：∵PA ＝PQ ⇒∠1＝∠3又∵△ABP ≌△CBP ⇒ ∠1＝∠2⇒∠1＝∠2＝∠3而：∠3＋∠4＝ο180⇒∠2＋∠4＝ο180 又∵∠QBC ＝ο90∴∠QPC ＝ο90⇒ PQ ⊥PC 当点Q 在AB 的延长线上时，∵∠2＝∠3；∠4＝∠5⇒△BQH ∽△CPH ∴∠QPC ＝ο90⇒ PQ ⊥PC背景3：反过来，若将一个直角顶点放在正方形的对角线上移动，一条直角边过点C ，另一条直角边与正方形的边（或边的延长线）AB 交于点Q 。
求证：PQ ＝PC证明：过P 作MN 平行于BC 交AB 、CD 于M 、N ∵∠1＋∠QPC ＝∠2＋∠PNC ⇒∠1＝∠2 又∵∠MBP ＝ο45⇒MP ＝MB ＝NCM CMC而∠QMP ＝∠PNC ＝ο90⇒△QMP ≌△PNC ⇒ PQ ＝PC 从上述的几个背景看出，当∠QPC ＝ο90时，一定有PQ ＝PC ，即ABADPC PQ =；但反过来当ABAD PC PQ =，即PQ ＝PC 时，因为有PA ＝PC 时∠APC ＝ο90不一定成立，所以∠QPC ＝ο90不一定能够成立。
下面我们将背景弱化：背景4：若将一个直角顶点放在长方形的对角线上移动，一条直角边过点C ，另一条直角边与长方形的边（或边的延长线）AB 交于点Q 。
求证：ABADPC PQ =证明：易证：△QMP ∽△PNC⇒ABADMB MP NC MP PC PQ ===背景5：如图，矩形ABCD 的AB ＝a ，AD ＝b ，点P 在对角线BD 上运动，点Q 在射线AB 上运动，若ABADPC PQ =，试探索a ，b 满足什么条件时，会有PQ ⊥PC探索：正常情况下，NCMPMB MP AB AD PC PQ === ⇒△QMP ∽△PNC ⇒∠QPC ＝ο90⇒ PQ ⊥PC但若点Q 关于MN 的对称点1Q 也在射线AB 上时，如同上述背景一样，连P 1Q ，∠1Q PC ＝ο90就不一定成立了。
08-12年上海市中学考试数学压轴题分析报告
市08—12年中考数学压轴题解析1、（2012年第24题）如图，在平面直角坐标系中，二次函数26y ax x c =++过点(4A ，0) 和(1B -，0)，并与y 轴交于点C ，点D 在线段OC 上，设DO t =，点E 在第二象限，且90ADE ∠=︒，12tan DAE ∠=，EF OD ⊥于F 。
①求二次函数的解析式；②用含t 的代数式表示EF 和OF 的长；③当ECA CAO ∠=∠时，求t 的值.分析：①可直接运用待定系数法确定a 和c 的值，从而得出二次函数的解析式。
②很容易证 △DEF ∽△ADO ，只要知道它们的相似比问题就很容易解决了，而12tan DAE ∠=正是它们的相似比12DE AD =。
③这里只要列出一个关于t 的一元方程，解出t 即可，但要建立关于t 的一元方程是本题的难点。
根据已知条件可以作出一个与△AOC 相似的△CGA 且G 点在EC 上，这样可知EC=EG+GC ，GC 易求，接下来就是求EG ，Rt △AEG 中AG 易求、AE 可用含有t 的代数式表示，根据勾股定理就能确定EG 。
解：①把A(4,0)和B(-1,0)代入y=ax 2+6x+c 得： 16a+24+c=0 解得: a=-2 ∴ 二次函数的解析式为y=-2x 2+6x=8.②∵∠ADE=∠DFE=∠AOD=90∴∠ADO+∠FDE=90∠DEF+∠FDE=90∴∠DEF=∠ADO∴△DEF ∽△ADO∴ 1tan 2EF FD DE DAE DO OA AD ===∠=又∵DO=t , OA=4∴EF=12t , FD=2 ∴OF=DO-FD=t-2.③连结CA 、CE ，过A 点作CE 的垂线交CE 与G 点。
则在△CAG 和△ACO 中，∵∠ECA=∠CAO, ∠CGA=∠AOC=90o, CA=AC ∴△CAG ≌△ACO ∴GC=OA=4 AG=CO=8由①、②可知:点C 的坐标为（0,8）点E 的坐标为（-12t,t-2）∴EC 2=(-12t-0)2+( t-2-8)2=(12t)2+( t-10)2又∵EG =而 ∴ (12t)2+( t-10)22 解得： t 1=6t2=10(不合题意，舍去)∴ t=6.AOB，点C是弧AB上2、（2012年第25题）如图，在半径为2的扇形AOB中，∠=90的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．BC时，求线段OD的长；（1）当=1（2）在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；BD x，△DOE的面积为y，求y关于x的函数关系式，并写出它的定义域．（3）设=分析：解答本题关键要熟悉垂径定理。
2009年上海市中考数学压轴题几何背景探寻和思考
量 缓
中学数学 杂 志
２０ ０９年第 ８期
２０ ０９年 上 海市 中考数学 压轴题 几何 背景探 寻和 思考
上 海 市黄 浦 区光 明初 级 中学 近几 年来 ， 国各省 市 的数 学 中考 压 轴 题大 部 全 ２ ０ １ ０ ００
而
刘颖颞
／Ｑ ＭＰ ＝ ＬＰ Ｃ ＝ ９ 。 ＡＱ Ｎ ０ ＭＰ
方形 的边 （ 边 的延 长线 ） Ｂ交 于 点 Ｑ， 图 ６ ７ 或 Ａ 如 ，．
． 、 — ．
让
ＰＯ
：
Ａ Ｄ
‘
图２
图３
Ｄ
Ａ
Ｄ
证 明 因为 Ｐ ＝Ｐ 所 以 １＝ ／３ Ａ Ｑ， ，
又 因为 ａＡ Ｐ Ｂ ＡＣ Ｐ ／１ ＝ ２＝ １＝ Ｂ ＝ ＞
证明
ＭＰ ＡＤ
易证 ： ＭＰ￣ ＡＱ ＂ＡＰ Ｃ Ｐ ＝Ｍ ＝ Ｎ ￣ Ｑ Ｐ
ｐ
背 景 ３ 反 过 来 ， 将 一 个 直 角顶 点 放 在 正 方 若 形 的对 角线 上 移 动 ， 条 直角 边 过 点 Ｃ ， 一 另一 条直
角边 与 正 方 形 的边 （ 边 的延 长 线 ） Ｂ 交 于 点 Ｑ 或 Ａ ．
分都有一个很明确 的几何背景 ， 今年的上海市中考
数学 压 轴题也 是 如此． 背 景 １ 如 图 １点 Ｐ是正 方形 ，
ＡＰ ￣ＰＱ ＝Ｐ ． ＮＣ Ｃ
ＡＣ Ｂ Ｄ对角线 上任意一 点．求证 ：
ＰＡ ＝ 尸Ｃ．
证 明 因为 四边形 Ａ Ｃ Ｂ Ｄ是 正方 形 ， 以 Ａ ＝ Ｃ ＬＡ Ｐ ＝ 所 Ｂ Ｂ， Ｂ Ｃ Ｐ ＝４ 。 又 因为 Ｂ ＝Ｂ Ｂ ５， Ｐ Ｐ，
ＭＢ
上海中考数学压轴题带来的启示
条 条 大 路 通 罗 马-----2009年上海中考数学压轴题带来的启示今年上海中考数学试卷设计的思路是“注重双基、体现新意、适度区分”，尤其最后一题在体现新意方面做了一些有益的尝试。
（题目：已知∠ABC =90°，AB =2，BC =3，AD ∥BC ．P 为线段BD 上的动点，点Q 在射线AB 上，且满足ABADPC PQ =（如图1所示）． （1）当AD =2，且点Q 与点B 重合时（如图2所示），求线段PC 的长； （2）在图1中，联结AP ，当AD =23，且点Q 在线段AB 上时，设B 、Q 之间的距离为x ， y S S PBCAPQ =∆∆，其中APQ S ∆表示△APQ 的面积，PBC S ∆表示△PBC 的面积，求y 关于x 的函数解析式，并写出函数定义域；（3）当AD < AB,且点Q 在线段AB 的延长线上时（如图3所示），求∠QPC 的大小）一、稳中求变，变中求新，促进探究型教与学虽然，今年中考数学的压轴题仍然是“动态几何+函数”，但与往年的压轴题也有着几处明显的区别。
首先，体现在函数的定义域上。
往年也有求函数定义域的问题，但大都是以最初的动点（主动点）与某定点的线段长度为自变量，主要考查考生对动态图形的观察能力，特别是对特殊位置的观察；今年的函数自变量选择了从动点Q 与定点B 之间的距离为自变量x ，使得求函数定义域的主要手段不再是直观的观察，而是理性的推导和计算，体现了数学的理性思维要求，这一变化击中了我们几何复习教学的“软肋”：用直观观察代替理性思考。
其次，在判定三角形相似的方法上。
我们知道，一般情况下是不能用“SSA ”（边边角）来判定两个三角形相似的，但是在特殊情况下它是可以用来判定两个三角形相似的，例如，在两个直角三角形中、在两个钝角三角形中、在两个等腰三角形中。
平时教学中，老师们非常重视和强调一般情况下的“不能”，却缺乏引导学生进行反思和研究特殊情况下的“能”。
2021年上海市中考数学压轴题解析
2021年上海市中考数学压轴题解析这道题是2021年上海市中考数学的压轴题，上海的题目和江苏这边出题风格不一样，同样是几何类的压轴题，江苏喜欢考各种模型，上海就比较朴素了，就是纯几何考法，没有涉及到复杂模型。
几何题如果考模型，那么对于训练过的同学来说，是个好消息，如果没有考模型，那就是靠大家的眼力和基本功了。
第一问证明两个三角形相似这道题很简单，题目告诉我们AD∥BC，AD=DC，点O是直角△ABC的中点，因此OA=OB=OC,所以图中绿色的角全部都相等，这样两个三角形就相似了，说到这边，同学们应该都能推出来了，具体证明过程我就省略了。
第二问让我们求边之比，但是题目中没告诉我们边的具体长度，那么考虑特殊角由于BE⊥DC，又根据外角关系，得到红色角等于两个绿色角之和，所以在△OEC中，红色角和绿色角之和为90°，那么一个绿色角就是30°第三问告诉我们DE和OE的长，让我求CD的长，这就是最普通的问法，直接求一个长度就行了，相比于以前做的压轴题，不是问范围就是问最大最小值，这道题就问法来说还是比较容易看明白的。
这道题的难点就在于，告诉我们的条件不是很容易用上，而且并没有发现明显的模型，这个切入点就比较难找了。
在观察一下题目，发现BO是中线，而E又是在它延长线上，所以先尝试一下倍长中线，毕竟这是比较常见的中线辅助线作法我们倍长BO到G点，然后连接DG，乍一看，ADG应该在一条直线上，得想办法证明，AO=OC,BO=OG,加上对顶角，易证△AOD≌△COB，这样图中绿色角都相等了，所以DG∥BC，又因为AD∥BC，所以ADG在同一条直线上。
其实我们不用这么麻烦，换个说法就行了，我们可以延长BO,AD，交于点G，这样就不用上面那一步证明了。
那这么做用处是啥呢？仔细观察发现红蓝三角形相似，有同学会说，这里面这么多相似三角形，为啥要注意到这两个相似呢？因为这样我们才能用到题目所给的条件DE=2，OE=3，所以三角形相似比为2:3，假设DG=2x，OC=3x，那么AO=OG=OB=OC=3x，假设AD=DC=t，这样两个未知数，我们找出两个方程来就能解了还没结束，这道题还有第二种情况，因为题目说点E有可能在AD 上同样把BO延长交AD于点E，易证△AOE≌△COB，所以AE=BC，又因为AE∥BC，所以四边形ABCE是平行四边形，又因为∠ABC=90°，所以又变成了矩形，这样CE⊥AD，上述就是我们根据条件发掘出的结论1.几何类题目首先要把所有的条件都标注在图上，不然有时候你发现不了2.没告诉我们长度却让我们求长度比值，那么一定是特殊角度3.求定值，可以大胆假设，之后有几个未知数就构建几个方程就行了，这个和在坐标系中的差不多4.最重要的是眼力和敏感度，能看出模型就用模型，看不出就用相似全等，这就需要平时多练多总结。
解读上海中考数学压轴题(上海新教材)
二期课改最显著的两个特点:
从“一维”走向“三维”： 知识与技能 过程与方法 情感、态度与价值观 从“接受”走向“接受+探究”: 培养提问、质疑、思考、探究的 习惯，发掘思维探究的因素。
改变学习方式： 改变单一的接受性学习方式，倡导接 受与体验、探究、发现相结合的学习方式。 改变单一的个体学习方式，倡导独立 自主与合作交流相结合的学习方式。
A D
A P
D
A
D
Q
B
图4
C
B
图5
C
B
图6
C
分析：本题的第（3）小题就是探究符合要求的对象存在与否 以及使结论成立的条件是什么的问题。 这里的关键有两个方面：一是要用x表示出△PCQ三边的长，即
PC 2 x
QC 1 2 x
PQ
x 2 2x 1
另一方面是对哪两边作为等腰三角形的腰进行分类讨论。 通过解方程得到 x 0或x 1 所以使△PCQ成为等腰三角形的条件是
2、二期课改对中考数学压轴题的影响
突出新课改理念，加强对探究能力、数学思想方法、数学 思维能力，特别是数学思维的灵活性和数学发散思维能力等方 面进一步得到体现，应引起足够重视。
压轴题越来越“动”起来了，从过去静态的封闭的经 典
试题走向了现在为例说明
1、二期课改对中考数学命题的影响
1)、试题总量由原来27题改为25题(从2005年)，总分由原来 120分改为150分（从2006年），由多项选择改为单项选 择。 2)、试题的易、中、难的比由过去的7：2：1到现在的8：1：1
坚持“以能力立意”的命题原则。
3)、立足课本，注重考查“双基”。 4)、加强了获取信息和处理信息能力、图形操作能力、运用数 学知识解决问题能力的考查力度.
上海十年中考数学压轴题和答案解析
上海十年中考数学压轴题解析20XX 年上海市数学中考27．已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AD ＝5，AB ＝DC ＝2． （1）如图8，P 为AD 上的一点，满足∠BPC ＝∠A ．图8①求证；△ABP ∽△DPC ②求AP 的长．（2）如果点P 在AD 边上移动（点P 与点A 、D 不重合），且满足∠BPE ＝∠A ，PE 交直线BC 于点E ，同时交直线DC 于点Q ，那么①当点Q 在线段DC 的延长线上时，设AP ＝x ，CQ ＝y ，求y 关于x 的函数解析式，并写出函数的定义域；②当CE ＝1时，写出AP 的长（不必写出解题过程）．27．（1）①证明：∵∠ABP ＝180°－∠A －∠APB ，∠DPC ＝180°－∠BPC －∠APB ，∠BPC ＝∠A ，∴∠ABP ＝∠DPC ．∵在梯形ABCD 中，AD ∥BC ，AB ＝CD ，∴∠A ＝∠D ．∴△ABP ∽△DPC ．②解：设AP ＝x ，则DP ＝5－x ，由△ABP ∽△DPC ，得DCPD AP AB =，即252xx -=，解得x 1＝1，x 2＝4，则AP 的长为1或4．（2）①解：类似（1）①，易得△ABP ∽△DPQ ，∴DQ AP PD AB =．即yxx +=-252，得225212-+-=x x y ，1＜x ＜4．②AP＝2或AP＝3－5．（题27是一道涉及动量与变量的考题，其中（1）可看作（2）的特例，故（2）的推断与证明均可借鉴（1）的思路．这是一种从模仿到创造的过程，模仿即借鉴、套用，创造即灵活变化，这是中学生学数学应具备的一种基本素质，世上的万事万物总有着千丝万缕的联系，也有着质的区别，模仿的关键是发现联系，创造的关键是发现区别，并找到应付新问题的途径．）上海市20XX年中等学校高中阶段招生文化考试27．操作：将一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q．图567 探究：设A、P两点间的距离为x．（1）当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察得到结论；（2）当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数解析式，并写出函数的定义域；（3）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由．（图5、图6、图7的形状大小相同，图5供操作、实验用，图6和图7备用）五、（本大题只有1题，满分12分，（1）、（2）、（3）题均为4分）27．图1 图2 图3（1）解：PQ ＝PB ……………………（1分） 证明如下：过点P 作MN ∥BC ，分别交AB 于点M ，交CD 于点N ，那么四边形AMND 和四边形BCNM 都是矩形，△AMP 和△CNP 都是等腰直角三角形（如图1）．∴ NP ＝NC ＝MB ． ……………………（1分） ∵ ∠BPQ ＝90°，∴ ∠QPN ＋∠BPM ＝90°．而∠BPM ＋∠PBM ＝90°，∴ ∠QPN ＝∠PBM ． ……………………（1分） 又∵ ∠QNP ＝∠PMB ＝90°，∴ △QNP ≌△PMB ． ……………………（1分） ∴ PQ ＝PB ． （2）解法一由（1）△QNP ≌△PMB ．得NQ ＝MP ． ∵ AP ＝x ，∴ AM ＝MP ＝NQ ＝DN ＝x 22，BM ＝PN ＝CN ＝1－x 22， ∴ CQ ＝CD －DQ ＝1－2·x 22＝1－x 2． 得S △PBC ＝21BC ·BM ＝21×1×（1－x 22）＝21－42x ． ………………（1分） S △PCQ ＝21CQ ·PN ＝21×（1－x 2）（1－x 22）＝21－x 423＋21x 2 （1分） S 四边形PBCQ ＝S △PBC ＋S △PCQ ＝21x 2－x 2＋1． 即 y ＝21x 2－x 2＋1（0≤x ＜22）． ……………………（1分，1分）解法二作PT ⊥BC ，T 为垂足（如图2），那么四边形PTCN 为正方形．∴ PT ＝CB ＝PN ．又∠PNQ ＝∠PTB ＝90°，PB ＝PQ ，∴△PBT ≌△PQN ．S 四边形PBCQ ＝S △四边形PBT ＋S 四边形PTCQ ＝S 四边形PTCQ ＋S △PQN ＝S 正方形PTCN （2分）＝CN 2＝（1－x 22）2＝21x 2－x 2＋1 ∴ y ＝21x 2－x 2＋1（0≤x ＜22）． ……………………（1分）（3）△PCQ 可能成为等腰三角形①当点P 与点A 重合，点Q 与点D 重合，这时PQ ＝QC ，△PCQ 是等腰三角形， 此时x ＝0 ……………………（1分） ②当点Q 在边DC 的延长线上，且CP ＝CQ 时，△PCQ 是等腰三角形（如图3） ……………………（1分） 解法一 此时，QN ＝PM ＝x 22，CP ＝2－x ，CN ＝22CP ＝1－x 22． ∴CQ ＝QN －CN ＝x 22－（1－x 22）＝x 2－1． 当2－x ＝x 2－1时，得x ＝1． ……………………（1分） 解法二 此时∠CPQ ＝21∠PCN ＝22.5°，∠APB ＝90°－22.5°＝67.5°， ∠ABP ＝180°－（45°＋67.5°）＝67.5°，得∠APB ＝∠ABP ，∴ AP ＝AB ＝1，∴ x ＝1． ……………………（1分）上海市20XX年初中毕业高中招生统一考试27.如图，在正方形ABCD中，AB＝1，弧AC是点B为圆心，AB长为半径的圆的一段弧。
上海第四中学中考数学期末几何综合压轴题模拟汇编
上海第四中学中考数学期末几何综合压轴题模拟汇编一、中考几何压轴题1．已知：60AOC BOC ∠=∠=︒，过平面内一点P 分别向OA 、OB 、OC 画垂线，垂足分别为D 、E 、F ． （问题引入）如图①，当点P 在射线OC 上时，求证：OD OE =．（类比探究）（1）如图②，当点P 在AOC ∠内部，点E 在射线OB 上时，求证：OD OE OF +=．（2）当点P 在AOC ∠内部，点E 在射线OB 的反向延长线上时，在图③中画出示意图，并直接写出线段OD 、OE 、OF 之间的数量关系． （知识拓展）如图④，AB 、CD 、EF 是O 的三条弦，都经过圆内一点P ，且60FPD BPD ∠=∠=︒．判断PA PD PE ++与PB PC PF ++的数量关系，并证明你的结论．2．（问题发现）（1）如图1，在Rt △ABC 中，AB ＝AC ，D 为BC 边上一点（不与点B 、C 重合）将线段AD 绕点A 顺时针旋转90°得到AE ，连结EC ，则线段BD 与CE 的数量关系是 ，位置关系是 ；（探究证明）（2）如图2，在Rt △ABC 和Rt △ADE 中，AB ＝AC ，AD ＝AE ，将△ADE 绕点A 旋转，当点C ，D ，E 在同一直线时，BD 与CE 具有怎样的位置关系，并说明理由； （拓展延伸）（3）如图3，在Rt △BCD 中，∠BCD ＝90°，BC ＝2CD ＝4，将△ACD 绕顺时针旋转，点C 对应点E ，设旋转角∠CAE 为α（0°＜α＜360°），当点C ，D ，E 在同一直线时，画出图形，并求出线段BE 的长度．3．在ABC 中，AB AC =，点D ､E 分别是BC AC ､的中点，将CDE △绕点C 按顺时针方向旋转一定的角度，连接BD AE ､． 观察猜想（1）如图①，当60BAC ∠=︒时，填空： ①AEBD=______________； ②直线BD AE ､所夹锐角为____________； 类比探究（2）如图②，当90BAC ∠=︒时，试判断AEBD的值及直线BD AE ､所夹锐角的度数，并说明理由；拓展应用（3）在（2）的条件下，若2DE =，将CDE △绕着点C 在平面内旋转，当点D 落在射线AC 上时，请直接写出2AE 的值．4．点E 是矩形ABCD 边AB 延长线上的一动点，在矩形ABCD 外作Rt △ECF ，其中∠ECF ＝90°，过点F 作FG ⊥BC ，交BC 的延长线于点G ，连接DF ，交CG 于点H ．（1）发现：如图1，若AB ＝AD ，CE ＝CF ，猜想线段DH 与HF 的数量关系是 ； （2）探究：如图2，若AB ＝nAD ，CF ＝nCE ，则（1）中的猜想是否仍然成立？若成立，请给予证明；若不成立，请说明理由．（3）拓展：在（2）的基础上，若射线FC 过AD 的三等分点，AD ＝3，AB ＝4，则直接写出线段EF 的长．5．（问题发现）（1）如图1所示，在Rt ABC △中，90BAC ∠=︒，4AB AC ==，点D 在BC 边上，且3BD CD =，将线段AD 绕点A 顺时针旋转90°得到线段AE ，连接DE 、BE ，BE BD +的值为______；（类比探究）（2）如图2所示，在（1）的条件下，点P 为AB 的中点，3BD CD =，将线段PD 绕点P 顺时针旋转90°得到PE ，连接BE ，则BE BD +的值会发生改变吗？说明你的理由； （拓展延伸）（3）如图3所示，在钝角ABC 中，AB AC =，BAC α∠=，点P 在边BA 的延长线上，BP k =，连接PD ．将线段PD 绕着点P 顺时针旋转，旋转角EPD α∠=，连接DE ，则BD BE +=______（请用含有k ，α的式子表示）．6．（1）（操作）如图，请用尺规作图确定圆的圆心P ，保留作图痕迹，不要求写作法；（2）（探究）如图，若（1）中的圆P 的半径为2，放入平面直角坐标系中，使它与x 轴，y 轴分别切于点B 和C ，点A 的坐标为()8,0，过点A 的直线与圆P 有唯一公共点D （与B 不重合）时，求点D 的坐标；（3）（拓展）如图3，点M 从点()8,0A 出发，以每秒1个单位的速度沿x 轴向点O 运动，同时，点N 从原点O 出发，以每秒1个单位的速度沿y 轴向上运动，设运动时间为t （08s t <<），过点M ，N ，O 三点的圆，交第一象限角平分线OG 于点E ，当t 为何值时，MN 有最小值，求出此时OMEN S 四边形，并探索在变化过程中OMEN S 四边形的值有变化吗？为什么？7．（教材呈现）下面是华师版八年级下册教材第89页的部分内容．如图，G，H是平行四边形ABCD对角线AC上的两点，且AG=CH，E，F分别是边AB和CD 的中点求证：四边形EHFG是平行四边形证明：连接EF交AC于点O∵四边形ABCD是平行四边形∴AB=CD，AB∥CD又∵E，F分别是AB，CD的中点∴AE=CF又∵AB∥CD∴∠EAO=∠FCO又∵∠AOE=∠COF∴△AOE≌△COF请补全上述问题的证明过程．（探究）如图①，在△ABC中，E，O分别是边AB、AC的中点，D、F分别是线段AO、CO 的中点，连结DE、EF，将△DEF绕点O旋转180°得到△DGF，若四边形DEFG的面积为8，则△ABC的面积为．（拓展）如图②，GH是正方形ABCD对角线AC上的两点，且AG＝CH，GH＝AB，E、F分别是AB和CD的中点．若正方形ABCD的面积为16，则四边形EHFG的面积为．8．将抛物线y＝ax2的图像（如图1）绕原点顺时针旋转90度后可得新的抛物线图像（如图2），记为C：y2＝1ax．（概念与理解）将抛物线y1=4x2和y2=x2按上述方法操作后可得新的抛物线图像，记为：C1：_____________；C2：____________．（猜想与证明）在平面直角坐标系中，点M（x，0）在x轴正半轴上，过点M作平行于y轴的直线，分别交抛物线C1于点A、B，交抛物线C2于点C、D，如图3所示．（1）填空：当x=1时，ABCD=______；当x=2时，ABCD=_______；（2）猜想：对任意x（x＞0）上述结论是否仍然成立？若成立，请证明你的猜想；若不成立，请说明理由．（探究与应用）①利用上面的结论，可得△AOB与△COD面积比为；②若△AOB和△COD中有一个是直角三角形时，求△COD与△AOB面积之差；（联想与拓展）若抛物线C3：y2＝mx、C4：y2＝nx（0<m<n），M（k，0）在x轴正半轴上，如图所示，过点M作平行于y轴的直线，分别交抛物线C3于点A、B，交抛物线C4于点C、D．过点A 作x轴的平行线交抛物线C4于点E，过点D作x轴的平行线交抛物线C3于点F．对于x轴上任取一点P，均有△PAE与△PDF面积的比值1:3，请直接写出m和n之间满足的等量关系是______．9．（1）（问题发现）如图①，正方形AEFG的两边分别在正方形ABCD的边AB和AD上，连接CF．填空：①线段CF 与DG 的数量关系为______； ②直线CF 与DG 所夹锐角的度数为_______． （2）（拓展探究）如图②，将正方形AEFG 绕点A 逆时针旋转，在旋转的过程中，（1）中的结论是否仍然成立，请利用图②进行说明． （3）（解决问题）如图③，在正方形ADBC 中，AD AC =，点M 为直线BC 上异于B ，C 的一点，以AM 为边作正方形AMEF ，点N 为正方形AMEF 的中心，连接CN ，若4,2AC CM ==，直接写出CN 的长．10．综合与实践．特例感知．两块三角板△ADB 与△EFC 全等，∠ADB ＝∠EFC ＝90°，∠B ＝45°，AB ＝6．将直角边AD 和EF 重合摆放．点P 、Q 分别为BE 、AF 的中点，连接PQ ，如图1．则△APQ 的形状为 ．操作探究（1）若将△EFC 绕点C 顺时针旋转45°，点P 恰好落在AD 上，BE 与AC 交于点G ，连接PF ，如图2． ①FG ：GA ＝ ；②PF 与DC 的位置关系为 ； ③求PQ 的长； 开放拓展（2）若△EFC 绕点C 旋转一周，当AC ⊥CF 时，∠AEC 为 ．11．如图1，已知直角三角形ABC ，90ACB ∠=︒，30BAC ∠=︒，点D 是AC 边上一点，过D 作DE AB ⊥于点E ，连接BD ，点F 是BD 中点，连接EF ，CF ． （1）发现问题：线段EF ，CF 之间的数量关系为______；EFC ∠的度数为______； （2）拓展与探究：若将AED 绕点A 按顺时针方向旋转α角()030α︒<<︒，如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点BC=，连接EG，请直接写出EG的长度．==，3G，AD DG GB12．（问题情境）在△ABC中，BA＝BC，∠ABC＝α（0°＜α＜180°），点P为直线BC上一动点（不与点B、C重合），连接AP，将线段PA绕点P顺时针旋转得到线段PQ旋转角为α，连接CQ．（特例分析）（1）当α＝90°，点P在线段BC上时，过P作PF∥AC交直线AB于点F，如图①，易得图中与△APF全等的一个三角形是，∠ACQ＝°．（拓展探究）（2）当点P在BC延长线上，AB：AC＝m：n时，如图②，试求线段BP与CQ的比值；（问题解决）（3）当点P在直线BC上，α＝60°，∠APB＝30°，CP＝4时，请直接写出线段CQ的长．13．问题提出（1）如图（1），在等边三角形ABC中，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等边三角形AMN，连接CN，则∠ACN＝ °．类比探究（2）如图（2），在等边三角形ABC中，点M是BC延长线上的任意一点（不含端点C），其他条件不变，（1）中的结论还成立吗？请说明理由．拓展延伸（3）如图（3），在等腰三角形ABC中，BA＝BC，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等腰三角形AMN，使AM＝MN，连接CN．添加一个条件，使得∠ABC＝∠ACN仍成立，写出你所添加的条件，并说明理由．14．综合与实践问题情境：△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，点E是射线AD上的一个动点(不与点A重合)将线段AE绕点A顺时针旋转90°得到线段AF，连接CF交线段AB于点G，交AD于点H、连接EG．特例分析:(1)如图1，当点E与点D重合时，“智敏”小组提出如下问题，请你解答：①求证：AF=CD；②用等式表示线段CG与EG之间的数量关系为：_______；拓展探究:(2)如图2，当点E在线段AD的延长线上，且DE=AD时，“博睿”小组发现CF=2EG．请你证明；(3)如图3，当点E在线段AD的延长线上，且AE=AB时，EGCF的值为_______；推广应用:(4)当点E在射线AD上运动时，AE mAD n，则EGCF的值为______用含m.n的式子表示)．15．如图，四边形ABCD是正方形，点O为对角线AC的中点．（1）问题解决：如图①，连接BO ，分别取CB ，BO 的中点P ，Q ，连接PQ ，则PQ 与BO 的数量关系是_____，位置关系是____；（2）问题探究：如图②，AO E ∆'是将图①中的AOB ∆绕点A 按顺时针方向旋转45︒得到的三角形，连接CE ，点P ，Q 分别为CE ，BO '的中点，连接PQ ，PB ．判断PQB ∆的形状，并证明你的结论；（3）拓展延伸：如图③，AO E ∆'是将图①中的AOB ∆绕点A 按逆时针方向旋转45︒得到的三角形，连接BO '，点P ，Q 分别为CE ，BO '的中点，连接PQ ，PB ．若正方形ABCD 的边长为1，求PQB ∆的面积．16．（1）问题情境：如图1，已知等腰直角ABC ∆中，90ABC ∠=︒，6AB =，E 是AC 上的一点，且2CE =，过E 作ED BC ⊥于D ，取AE 中点F ，连接BF ，则BF 的长为_______（请直接写出答案） 小明采用如下的做法：延长AB 到H ，使AB BH =，连接EH ，B 为AH 中点，F 为AE 的中点，BF ∴是AEH ∆的中位线……请你根据小明的思路完成上面填空；（2）迁移应用：将图1中的CDE ∆绕点C 作顺时针旋转，当CE AC ⊥时，试探究BF 、AC 、CE 的数量关系，并证明你的结论．（3）拓展延伸：在旋转的过程中，当A 、C 、D 三点共线时，直接写出线段BF 的长． 17．综合与实践：问题情境：在数学课上，以“等腰直角三角形为主体，以点的对称为基础，探究线段间的变化关系”．如图1，在ABC 中，90ACB ∠=︒，AC BC =，点E 为ACB ∠的角平分线CD 上一动点但不与点C 重合，作点E 关于直线BC 的对称点为F ，连接AE 并延长交CB 延长线于点H ，连接FB 并延长交直线AH 于点G ．探究实践：（1）勤奋小组的同学发现AE BF =，请写出证明；探究发现：（2）智慧小组在勤奋小组的基础上继续探究，发现线段FG ，EG 与CE 存在数量关系，请写出他们的发现并证明；探究拓展：（3）如图2，奇异小组的同学在前两个小组探究的基础上，连接GC ，得到三条线段GE ，GC 与GF 存在一定的数量关系，请直接写出．18．问题情境：两张直角三角形纸片中，90BAC DAE ∠=∠=︒．连接BD ，CE ，过点A 作BD 的垂线，分别交线段BD ，CE 于点M ，N （ABC ∆与ADE ∆在直线MN 异侧）．特例分析：（1）如图1，当AB AC AD AE ===时，求证：2BD AN =；拓展探究：（2）当12AB AD AC AE ==，探究下列问题： ①如图2，当AB AD =时，直接写出线段BD 与AN 之间的数量关系： ； ②如图3，当AB AD ≠时，猜想BD 与AN 之间的数量关系，并说明理由；推广应用：（3）若图3中，AB AD k AC AE==，设ABD ∆的面积为S ，则ACE ∆的面积为 ．（用含k ，s 的式子表示）19．（1）尝试探究：如图①，在ABC ∆中，90ACB ∠=︒，30A ∠=︒，点E 、F 分别是边BC 、AC 上的点，且EF ∥AB ．①AFBE 的值为_________；②直线AF 与直线BE 的位置关系为__________；（2）类比延伸：如图②，若将图①中的CEF ∆绕点C 顺时针旋转，连接AF ，BE ，则在旋转的过程中，请判断AFBE 的值及直线AF 与直线BE 的位置关系，并说明理由；（3）拓展运用：若3BC =，2CE =，在旋转过程中，当,,B E F 三点在同一直线上时，请直接写出此时线段AF 的长．20．随着教育教学改革的不断深入，数学教学如何改革和发展，如何从“重教轻学”向自主学习探索为主的方向发展，是一个值得思考的问题．从数学的产生和发展历程来看分析，不外乎就是三个环节：（观察猜想）-（探究证明）-（拓展延伸）．下面同学们从这三个方面试看解决下列问题：已知：如图1所示将一块等腰三角板BMN 放置与正方形ABCD 的B 重含，连接 AN 、CM ，E 是AN 的中点，连接BE ．（观察猜想）（1）CM 与 BE 的数量关系是________，CM 与BE 的位置关系是___________；（探究证明）（2）如图2所示，把三角板 BMN 绕点B 逆时针旋转(090)αα<<，其他条件不变，线段CM 与BE 的关系是否仍然成立，并说明理由；（拓展延伸）（3）若旋转角45α=︒，且2NBE ABE ∠=∠，求BC BN的值．【参考答案】***试卷处理标记，请不要删除一、中考几何压轴题1．【问题引入】见解析；【类比探究】（1）见解析；（2）图见解析，；【知识拓展】 ，证明见解析【分析】[问题引入]利用AAS 证明△POE ≌△POD ，即可得出结论；[类比探究]（1）过点F 作FN解析：【问题引入】见解析；【类比探究】（1）见解析；（2）图见解析，OD OE OF -=；【知识拓展】PA PD PE PB PC PF ++=++，证明见解析【分析】[问题引入]利用AAS 证明△POE ≌△POD ，即可得出结论；[类比探究]（1）过点F 作FN ⊥OB ，FM ⊥OA ，垂足分别为N 、M ，FM 与PE 交于点Q ，先证明△PFQ 为等边三角形，得出FG =PH ，再运用矩形性质得出OM =12OF ，ON =12OF ，即可证得结论； （2）作FN ⊥OB 于点N ，FM ⊥OA 于点M ，射线FM 交PE 于点Q ，作PH ⊥FQ 于点H ，FG ⊥PQ 于点G ，同（1）可证：NE =FG =PH =MD ，ON =OM =12OF ，即可得出结论；[知识拓展]过点O 作OM ⊥AB ，ON ⊥EF ，OQ ⊥CD ，垂足分别为M 、N 、Q ，利用垂径定理可得出PB -PA =2PM ，PF -PE =2PN ，PD -PC =2PQ ，再运用[类比探究]得：PM +PN =PQ ，从而证得结论．【详解】[问题引入]证明：∵AOC BOC ∠=∠，PE OB ⊥，PD OA ⊥，∴90OEP ODP ∠=∠=︒．∵OC OC =，∴OEP ODP ≅△△．∴OD OE =．[类比探究]（1）过点F 作FN OB ⊥，FM OA ⊥，垂足分别为N 、M ，FM 与PE 交于点Q ．∵60AOC BOC ∠=∠=︒，PE OB ⊥，PD OA ⊥，则PFQ △为等边三角形，FQ 、PQ 边上的高相等，即FG PH =．在矩形EGFN 、矩形DPHM 中，有NE FG =，MD PH =，∴EN MD =．∴OD OE OM ON +=+．∵90FMO ∠=︒，60FOM ∠=︒， ∴1cos 2OM OF FOM OF =⋅∠=， 同理，12ON OF =， ∴OM ON OF +=，∴OD OE OF +=．（2）结论：OD OE OF -=．作FN OB ⊥于点N ，FM OA ⊥于点M ，射线FM 与PE 的交点为Q ，作PH FQ ⊥于点H ，FG PQ ⊥于点G ，同（1）可证NE FG PH MD ===，12ON OM OF ==， ∴OF OM ON OD MD NE OE OD OE =+=-+-=-．[知识拓展]数量关系：PA PD PE PB PC PF ++=++．理由如下：过点O 作OM AB ⊥，ON EF ⊥，OQ CD ⊥，垂足分别为M 、N 、Q ．由垂径定理可得AM BM =．∴()()2PB PA PM MB MA PM PM -=+--=．同理2PF PE PN -=，2PD PC PQ -=，由[类比探究]得PM PN PQ +=，∴222PM PN PQ +=，∴PB PA PF PE PD PC -+-=-．∴PA PD PE PB PC PF ++=++．【点睛】本题是圆的综合题，考查了全等三角形判定和性质，等边三角形判定和性质，角平分线性质，矩形性质，垂径定理等，熟练掌握全等三角形判定和性质及垂径定理等相关知识是解题关键．2．（1）BD ＝CE ，BD ⊥CE ；（2）BD ⊥CE ，理由见解析；（3）画出图形见解析，线段BE 的长度为．【分析】（1）由题意易得AD=AE，∠CAE=∠BAD，从而可证△ABD≌△ACE，然后根据三解析：（1）BD＝CE，BD⊥CE；（2）BD⊥CE，理由见解析；（3）画出图形见解析，线段BE 的长度为125．【分析】（1）由题意易得AD=AE，∠CAE=∠BAD，从而可证△ABD≌△ACE，然后根据三角形全等的性质可求解；（2）连接BD，由题意易得∠BAD=∠CAE，进而可证△BAD≌△CAE，最后根据三角形全等的性质及角的等量关系可求证；（3）如图，过A作AF⊥EC，由题意可知Rt△ABC∽Rt△AED，∠BAC＝∠EAD＝90°，然后根据相似三角形的性质及题意易证△BAE∽△CAD，最后根据勾股定理及等积法进行求解即可．【详解】解：（1）在Rt△ABC中，AB＝AC，∴∠B＝∠ACB＝45°，∵∠BAC＝∠DAE＝90°，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△BAD和△CAE中，AB ACBAD CAEAD AE=⎧⎪∠=∠⎨⎪=⎩，∴△BAD≌△CAE（SAS），∴BD＝CE，∠B＝∠ACE＝45°，∵∠ACB＝45°，∴∠BCE＝45°+45°＝90°，故答案为：BD＝CE，BD⊥CE；（2）BD⊥CE，理由：如图2，连接BD，∵在Rt△ABC和Rt△ADE中，AB＝AC，AD＝AE，∠AEC＝45°，∵∠CAB＝∠DAE＝90°，∴∠BAD＝∠CAE，∵AC＝AB，AE＝AD，∴△CEA≌△BDA（SAS），∴∠BDA ＝∠AEC ＝45°，∴∠BDE ＝∠ADB +∠ADE ＝90°，∴BD ⊥CE ；（3）如图3，过A 作AF ⊥EC ，由题意可知Rt △ABC ∽Rt △AED ，∠BAC ＝∠EAD ＝90°， ∴AB AC AE AD =，即AB AE AC AD=， ∵∠BAC ＝∠EAD ＝90°，∴∠BAE ＝∠CAD ，∴△BAE ∽△CAD ，∴∠ABE ＝∠ACD ，∵∠BEC ＝180°﹣（∠CBE +∠BCE ）＝180°﹣（∠CBA +∠ABE +∠BCE ）＝180°﹣（∠CBA +∠ACD +∠BCE ）＝90°，∴BE ⊥CE ，在Rt △BCD 中，BC ＝2CD ＝4，∴BD 22224225BC CD ++∵AC ⊥BD ，∴S △BCD ＝12AC •BD ＝12BC •AC ，∴AC ＝AE 455AD 255， ∴AF =45，CE ＝2CF ＝22165AC AF -=， ∴BE 22221612455BC CE ⎛⎫-=- ⎪⎝⎭． 【点睛】本题主要考查全等三角形的性质与判定及相似三角形的性质与判定，关键是根据题意得到三角形的全等，然后利用全等三角形的性质得到相似三角形，进而求解．3．（1）①1，②；（2）直线所夹锐角为，见解析；（3）满足条件的的值为【分析】（1）①②延长BD 交AE 的延长线于T ，BT 交AC 于O ．证明即可解决问题． （2）如图②中，设AC 交BD 于O ，AE 交BD解析：（1）①1，②60︒；（2）直线BD AE ､所夹锐角为45︒，见解析；（3）满足条件的2AE 的值为1042± 【分析】 （1）①②延长BD 交AE 的延长线于T ，BT 交AC 于O ．证明()BCD ACE SAS ≌即可解决问题．（2）如图②中，设AC 交BD 于O ，AE 交BD 于T ．证明BCD ACE ∽△△，推出22AE AC BE BC ==，CBD CAE ∠=∠可得结论． （3）分两种情形：①如图③-1中，当点D 落在线段AC 上时，作EH AC ⊥于H ．②如图③-2中，当点D 在AC 的延长线上时，分别利用勾股定理求解即可．【详解】解：（1）如图①中，延长BD 交AE 的延长线于T ，BT 交AC 于O ．,60AB AC BAC =∠=︒，ACB ∴是等边三角形，,60CA CB ACB ∴=∠=︒，11,,60?22CD BC CE AC ECD ACB -=∠=∠=， ,CD CE BCD ACE ∴=∠=∠，()BCD ACE SAS ∴≌，,BD AE CBD CAE ∴=∠=∠，1AE BD∴=， BOC AOT ∠=∠，60ATB ACB ∴∠=∠=︒，∴直线BD AE ､所夹锐角为60︒，故答案为1，60︒．（2）如图②中，设AC 交BD 于O ，AE 交BD 于T ．,90AB AC BAC ∠==︒，ACB ∴是等腰直角三角形， 245CB AC ACB ︒∴=∠=，， 11,,4522CD BC CE AC ECD ACB ︒==∠=∠=， 2CD CE BCD ACE ∴=∠=∠，，2BC CD AC CE∴==， BCD ACE ∴∽， 22AE AC CBD CAE BE BC ∴==∠=∠，， BOC AOT ∠=∠，45ATB ACB ∴∠=∠=︒，∴直线BD AE ､所夹锐角为45︒．（3）①如图③-1中，当点D 落在线段AC 上时，作EH AC ⊥于H ．由题意，222DE EC CD DE ====，，,90EH CD CED ⊥∠=︒，112222EH DH HC CD AC EC ∴======，， 221AH AC CH ∴=-=-，在Rt AEH 中，22222(221)11042AE AH EH =+=-+=-②如图③-2中，当点D 在AC 的延长线上时，同法可得222(221)11042AE =++=+，综上所述，满足条件的2AE 的值为1042±【点睛】本题考查几何变换综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形等知识，解题的关键是正确寻找全等三角形或相似三角形解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．4．(1)DH=HF ；(2)DH=HF 仍然成立，理由见解析；(3)或 ．【分析】(1)证明，得，则，则证，得出即可；(2)证，则，由矩形的性质得出，证，即可得出；(3)根据矩形的性质和已知得，则解析：(1)DH =HF ；(2)DH =HF 仍然成立，理由见解析；． 【分析】(1)证明()GCF BEC AAS ∆∆≌，得BC GF =，则CD GF =，则证()HCD HGF ASA ∆∆≌，得出DH HF =即可；(2)证FCG CEB ∆∆∽，则GF FC n BC CE ==，由矩形的性质得出CD n BC=，证()HCD HGF ASA ∆∆≌，即可得出DH HF =； (3)根据矩形的性质和已知得43AB n AD ==，则43CE CF =，分两种情况，根据勾股定理和平行线的性质进行解答即可．【详解】解：(1)DH HF =，理由如下：∵四边形ABCD 是矩形，AB AD =，∴四边形ABCD 是正方形，∴BC CD =，90ABC EBC BCD ∠=∠=∠=︒，∵FG BC ⊥，90ECF ∠=︒，∴//CD GF ，90CGF ECF EBC ∠=∠=∠=︒，∴+90GCF BCE ∠∠=︒，∵+90BCE BEC ∠∠=︒，∴=GCF BEC ∠∠，在GCF ∆和BEC ∆中，==GCF BEC CGF EBC CF CE ∠∠⎧⎪∠∠⎨⎪=⎩， ∴()GCF BEC AAS ∆∆≌，∴BC GF =，∴CD GF =，//CD GF∴=HDC HFG ∠∠，=HCD HGF ∠∠，在HCD ∆和HGF ∆中，==HDC HFG CD GFHCD HGF ∠∠⎧⎪=⎨⎪∠∠⎩， ∴()HCD HGF ASA ∆∆≌，∴DH HF =，故答案为DH HF =，(2) DH HF =仍然成立，理由如下：∵四边形ABCD 是矩形，FG BC ⊥，90ECF ∠=︒，∴90CGF ECF EBC ∠=∠=∠=︒∴+90FCG BCE ∠∠=︒，∵+90BCE CEB ∠∠=︒，∴=FCG CEB ∠∠，∴FCG CEB ∆∆， ∴GF FC n BC CE==， ∴四边形ABCD 是矩形，AB nAD =， ∴CD n BC=， ∴GF CD BC BC =， ∴GF CD =，∵四边形ABCD 是矩形，∴CD BC ⊥，∵FG BC ⊥，∴//CD FG ，∴HDC HFG ∠=∠，HCD HGF ∠=∠，在HCD ∆和HGF ∆中，==HDC HFG CD GFHCD HGF ∠∠⎧⎪=⎨⎪∠∠⎩， ∴()HCD HGF ASA ∆∆≌，∴DH HF =，(3)如图所示，延长FC 交AD 于R ，∵四边形ABCD 是矩形，∴4AB CD ==，3AD BC ==，90RDC ∠=︒，//RD CH ，∵AB nAD =，CF nCE =， ∴43AB n AD ==， ∴43CF CE =， 分两种情况：①当13AR AD =时， ∵3AD =，∴1AR =，2DR =，在Rt CDR ∆中，由勾股定理得：CR =∵//RD CH ，DH HF =， ∴RC CF ==∴34CE =⨯由勾股定理得：EF =②当13DR AD =时，同理可得：1DR =，4DC =，CF RC ==∴ CE = 由勾股定理得：∴ EF == 综上所说，若射线FC 过AD 的三等分点，3AD =，4AB =，则线段EF ． 【点睛】本题主要考查了正方形的判定与性质、矩形的性质、平行线的性质、全等三角形的判定与性质、勾股定理、相似三角形的判定与性质等知识，熟练掌握平行线的性质和相似三角形的判定与性质是解题的关键． 5．（1）；（2）BE+BD 的值不会发生改变，理由见解答；（3）2k•sin【分析】（1）只要证明，即可解决问题；（2）如图2中，作交于，过点作交于．利用（1）中结论即可解决问题；（3）如图③中解析：（1）42；（2）BE +BD 的值不会发生改变，理由见解答；（3）2k •sin2α 【分析】（1）只要证明BAE CAD ∆≅∆，即可解决问题；（2）如图2中，作//DM AC 交AB 于M ，过点P 作//PN BC 交MD 于N ．利用（1）中结论即可解决问题；（3）如图③中，作//PH AC 交BC 的延长线于H ，作PM BC ⊥于M ．只要证明EPB DPH ∆≅∆，可证BD BE BH +=，即可解决问题．【详解】解：（1）如图1中，90EAD BAC ∠=∠=︒，BAE CAD ∴∠=∠，AD AE =，AB AC =，()BAE CAD SAS ∴∆≅∆，BE DC ∴=，BE BD BD DC BC ∴+=+=，4AB AC ==，90BAC ∠=︒，42BC ∴=，42BE BD ∴+=，故答案为：42．（2）BE BD +的值不会发生改变，理由如下：作//DM AC 交AB 于M ，过点P 作//PN BC 交MD 于N ，AB AC =，90BAC ∠=︒，45ABC C ∴∠=∠=︒，//MD AC ，90BMD BAC ∴∠=∠=︒，BMD ∴∆是等腰直角三角形，DM BM ∴=，//PN BC ，45MPN ABC ∴∠=∠=︒，PMN ∴∆是等腰直角三角形，PM NM ∴=，BM PM DM NM ∴-=-，PB DN ∴=，由（1），知42BC =，3BD CD =，32BD ∴=，cos453BM BD ∴=⋅︒=，P 为AB 边上的中点，122AP BP AB ∴===， 321MN PM BM BP ∴==-=-=，222PN MN PM ∴=+=，90BPE DPM ∠+∠=︒，90PDM DPM ∠+∠=︒，BPE PDM ∴∠=∠，PD PE =，()PBE DNP SAS ∴∆≅∆，2BE PN ∴==，23242BE BD ∴+=+=；（3）如图3中，作//PH AC 交BC 的延长线于H ，作PM BC ⊥于M ．//AC PH ，ACB H ∴∠=∠，BPH BAC α∠=∠=，AB AC =，ABC ACB ∴∠=∠，PBH H ∴∠=∠，PB PH ∴=，EPD BPH α∠=∠=，BPE HPD ∴∠=∠，PE PD =，PB PH =，()EPB DPH SAS ∴∆≅∆，BE DH ∴=，BE BD BD DH BH ∴+=+=， =PB PH ，PM BH ⊥，BM MH ∴=，BPM HPM ∠=∠，sin 2BM MH BP α∴==⋅．2sin 2BD BE BH k α∴+==⋅． 故答案为：2sin2k α⋅．【点睛】 本题考查几何变换综合题、等腰三角形的性质、全等三角形的判定和性质、锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．6．（1）见解析；（2）；（3）当时，有最小值，此时；的值不变，见解析【分析】（1）在圆上任意取两条弦AC 、BC ，作AC 、BC 的垂直平分线，则它们的交点为P 点；（2）由题意得与相切于点，根据切线长解析：（1）见解析；（2）1618,55D ⎛⎫ ⎪⎝⎭；（3）当4t =时，MN 有最小值，此时16OMEN S =四边形；OMEN S 四边形的值不变，见解析【分析】（1）在圆上任意取两条弦AC 、BC ，作AC 、BC 的垂直平分线，则它们的交点为P 点； （2）由题意得AE 与P 相切于点D ，根据切线长定理和勾股定理求得10AE =，再证明ADF AEO ∽△△，利用相似三角形的性质即可求解；（3）根据勾股定理得()2228MN t t =-+22216642(4)32t t t =-+=-+，得到当4t =时，2MN 有最小值，即MN 有最小值．四边形OMEN 是正方形，即可求得此时OMEN S 四边形，根据MON MEN OMEN S S S =+四边形△△利用三角形面积公式，即可求解．【详解】（1）如图，点P 即为所作；（2）如图，过点D 作DF x ⊥轴于点F ，连接PC ，PB ，由题意得：P 与坐标轴相切，∴90OBP OCP COB ∠=∠=∠=︒，∴四边形OBPC 是矩形，∵2PC PB ==，∴四边形OBPC 是正方形，∴2OC OB ==，则6AB =，由题意得AE 与P 相切于点D ，∴6AB AD ==，设EC ED x ==，在Rt OAE △中，90AOE ∠=︒，8AO =，2EO x =+，6AE x =+，由勾股定理得：222OE OA AE +=，即：()()222286x x ++=+，解得4x =，∴10AE =， 由题意可得ADF AEO ∽△△， ∴AD DF AF AE EO AO ==， 即：61068DF AF ==， ∴185DF =，245AF =， 则2416855OF =-= ∴161855D ⎛⎫ ⎪⎝⎭，； （3）如图，在Rt OMN △中，90MON ∠=︒，8OM t =-，ON t =，则()2228MN t t =-+22216642(4)32t t t =-+=-+，当4t =时，2MN 有最小值，即MN 有最小值．此时，4OM ON ==，∵OG 平分第一象限，∴∠EON =∠EOM =45︒，∴△EON ≅△EOM ，∴∠ENO =∠EMO ，∵四边形OMEN 是圆内接四边形，∴∠ENO +∠EMO =180︒，∴∠ENO =∠EMO =90︒，又OM =ON ，∴四边形OMEN 是正方形，∴4416OMEN S =⨯=四边形；在这个变化过程中，16OMEN S =四边形没有变化，理由如下：∵OG 平分第一象限，∴EMN 是等腰直角三角形，∴NE ME = 则()()2222221118222NE MN OM ON t t ⎡⎤==+=-+⎣⎦， ∴MON MEN OMEN S S S =+四边形△△21122ON OM NE =⋅+ ()()2211188222t t t t ⎡⎤=-+⨯-+⎣⎦ 16=．【点睛】本题考查了坐标与图形，圆的切线的性质，相似三角形的判定和性质，二次函数最值的求解，解答本题的关键是明确题意，找出所求问题需要的条件，学会利用参数构建方程解决问题．7．教材呈现：见解析；探究：16；拓展：4【分析】教材呈现：先根据三角形全等的性质可得，再根据线段的和差可得，然后根据平行四边形的判定即可得证；探究：先由旋转的性质可得，再根据等底同高可得，从而可解析：教材呈现：见解析；探究：16；拓展：【分析】教材呈现：先根据三角形全等的性质可得,OE OF OA OC ==，再根据线段的和差可得OG OH =，然后根据平行四边形的判定即可得证；探究：先由旋转的性质可得4DGF S =，再根据等底同高可得2ADE DOE EOF S S S ===，从而可得4AOE S =，然后根据三角形中位线定理即可得；拓展：先根据正方形的性质和面积可得4,90AB BC B ==∠=︒，从而可得4,2AC GH AE ===，再根据等腰直角三角形和勾股定理可得OE =角形的面积公式可得EGH S =【详解】解：教材呈现：补充完整证明过程如下：∴OE ＝OF ，OA ＝OC ，又∵AG ＝CH ，∴OA －AG ＝OC －CH ，即OG ＝OH ，∴四边形EHFG 是平行四边形；探究：如图，连接OE ，BO ， 由旋转的性质得：118422DGF DEF DEFG S S S ===⨯=四边形， 点O 是AC 的中点，点D 是AO 的中点，点F 是CO 的中点，AD OD OF CF ∴===，由等底同高得：114222ADE DOE EOF DEF SS S S ====⨯=， 224AOE ADE DOE S S S ∴=+=+=， 又点E 是AB 的中点，点O 是AC 的中点，∴S △BEO =S △AEO =4，∴S △ABO = S △BEO +S △AEO =8，22816ABC AOB S S ∴==⨯=，故答案为：16；拓展：如图，过点E 作EO GH ⊥于点O ，四边形ABCD 是面积为16的正方形，4,90AB BC B ∴==∠=︒，在Rt △ABC 中，由勾股定理得22224424A C B B A C ++=∵AC 为正方形的对角线，∴∠EAO =45°，点E 是AB 的中点，122AE AB ∴==， ∵EO GH ⊥，∴45AEO EAO ∠=∠=︒，∴AO =EO ，在Rt △AEO 中由勾股定理的AO 2+EO 2=AE 2，即2OE 2=4解得2OE =GH AB =，4GH ∴=，11422222EGH S GH OE ∴=⋅=⨯⨯=， 由教材呈现可知，四边形EHFG 是平行四边形，则四边形EHFG 的面积为222242EGH S=⨯=， 故答案为：42．【点睛】本题考查了旋转的性质、三角形中线性质、平行四边形的判定与性质、正方形的性质，等腰直角三角形性质，勾股定理等知识点，较难的是拓展，通过作辅助线，构造等腰直角三角形是解题关键．8．【概念与理解】，；【猜想与证明】（1），；（2）成立，证明见解析；【探究与应用】①；②△COD 与△AOB 面积之差为或；【联想与拓展】n3=9m3．【分析】【概念与理解】：根据题意信息即可得出答案解析：【概念与理解】214y x =，2y x =；【猜想与证明】（1）12，12；（2）成立，证明见解析；【探究与应用】①12；②△COD 与△AOB 面积之差为116或12；【联想与拓展】n 3=9m 3．【分析】【概念与理解】：根据题意信息即可得出答案； 【猜想与证明】：（1）当x =1时，求出A ，B ，C ，D 的坐标进而得出AB ,CD 即可得出答案；当x =2时，求出A ，B ，C ，D 的坐标进而得出AB ,CD 即可得出答案；（2）任意x （x ＞0），求出A ，B ，C ，D 的坐标进而得出AB ,CD 即可得出答案；【探究与应用】：①根据已知条件表示出△AOB 与△COD 面积即可得出答案； ②设M （x ，0）（x ＞0），根据已知条件可得出2COD AOB x x S S -=△AOB 是直角三角形时解得14x =，当△COD 是直角三角形时，解得1x =，把x 代入即可； 【联想与拓展】：根据题意求出AEDF 的坐标然后表示出面积再利用△PAE 与△PDF 面积的比值1:3，即可得出关系式；【详解】【概念与理解】∵y 1=4x 2∴由题意可得C 1：214y x = ∵y 2=x 2∴由题意可得C 2：2y x =故答案为：C 1：214y x =，C 2：2y x =； 【猜想与证明】（1）当x =1时，∵点A 、B 在抛物线C 1上∴令x =1，则112y =± ∴A 1(1,)2，B 1(1,)2- ∴AB =1∵点C 、D 在抛物线C 2上∴令x =1，则21y ==±∴C (1,1)，D (1,1)-∴CD =2 ∴AB CD =12当x =2时，∵点A 、B 在抛物线C 1上∴令x =2，则1y ==∴A ，B (2, ∴AB∵点C 、D 在抛物线C 2上∴令x =2，则2y =∴C ，D (2,∴CD =∴ABCD 12= （2）对任意x （x ＞0）上述结论仍然成立理由如下：对任意x （x ＞0），1y =∴A (,)2x x ，B (,)2x x - ∴AB =x对任意x （x ＞0），2y x =± ∴C (,)x x ，D (,)x x -∴CD =2x∴AB CD =122x x = 【探究与应用】①连接OA ，OB ，OC ，OD12AOB SAB OM = 12COD S CD OM = ∴12AOBCODSAB S CD ==故答案为：12②设M （x ，0）（x ＞0），∵M （x ，0）∴1y = ∴AB∵M （x ，0）， ∴2y =∴CD =∵122AOB x SAB OM == 1222COD x S CD OM ==∴2COD AOB x S S -=当△AOB 是直角三角形时，由题意可知OA =OB∴△△AOB 为等腰直角三角形∴OM =AM∴x =解得：14x =∴1216COD AOB x S S -== 当△COD 是直角三角形时，由题意可知OD =OC∴△△COD 为等腰直角三角形∴OM=CM∴x =解得：1x =∴122COD AOB x S S -== 综上所述：△COD 与△AOB 面积之差为116或12 【联想与拓展】∵M （k ，0）且点A 、B 在抛物线C 3上∴令x =k ，则1y ==∴A (k∵AE ∥x 轴，且交C 4于点E∴E (km n ()km AE k n -∴= ∵M （k ，0）且点C 、D 在抛物线C 4上∴令x =k，则2y ==∴D (k∵DF ∥x 轴，且交C 3于点F∴F (kn m ()kn DF k m =∴- ∵AE ∥x 轴，且交C 4于点E∴△PEA 的高∵DF ∥x 轴，且交C 3于点F∴△PDF 的高∴11(22PEA km SAE km k n ==- 11(22PDF kn S FD kn k m ==-∵△PAE 与△PDF面积的比值1:3 ∴ 1(1213(2PEAPDF km k Sn kn S k m-==- ∴13= ∴339n m =故答案为：339n m =【点睛】本题考出了抛物线性质的综合运用以及旋转等知识，由特殊到一般的数学思想的运用，等腰直角三角形的性质的运用，三角形的面积公式的运用，轴对称的性质的运用，在解答本题时运用两个抛物线上的点的特征不变建立方程求解是关键．9．（1）①；②；（2）仍然成立，证明见解析；（3）或【分析】（1）【问题发现】连接．易证，，三点共线．易知．，推出，从而得出与所夹锐角的度数；（2）【拓展探究】连接，，延长交的延长线于点，交于点解析：（1）①CF =；②45︒；（2）仍然成立，证明见解析；（3【分析】。
上海华东师范大学第二附属中学中考数学期末几何综合压轴题易错汇编
上海华东师范大学第二附属中学中考数学期末几何综合压轴题易错汇编一、中考数学几何综合压轴题1．（1）探究发现：下面是一道例题及解答过程，请补充完整：如图①在等边△ABC内部，有一点P，若∠APB=150°，求证：AP2+BP2=CP2证明：将△APC绕A点逆时针旋转60°，得到△AP’B，连接PP’，则△APP’为等边三角形∴∠APP’=60° ，PA=PP’ ，PC=∵∠APB=150°，∴∠BPP’=90°∴P’P2+BP2= ，即PA2+PB2=PC2（2）类比延伸：如图②在等腰△ABC中，∠BAC=90°，内部有一点P，若∠APB=135°，试判断线段PA，PB，PC之间的数量关系，并证明．（3）联想拓展：如图③在△ABC中，∠BAC=120°，AB=AC，点P在直线AB上方，且∠APB=60°，满足（kPA）2+PB2=PC2（其中k＞0），请直接写出k的值．解析：（1）P’B，P’B2；（2）2PA2+PB2=PC2，见解析；（3）k=3【分析】（1）根据旋转的性质和勾股定理直接写出即可．（2）将△APC绕A点逆时针旋转90°，得到△AP′B，连接PP′，论证PP′=2PA，再根据勾股定理代换即可．（3）将△APC 绕A点顺时针旋转120°得到△AP′B，连接PP′，过点A作AH⊥PP′，论证PP′=3PA，再根据勾股定理代换即可．【详解】（1）PC=P’B，P’P2+BP2=P’B2（2）关系式为：2PA2+PB2=PC2证明：将△APC绕A点逆时针旋转90°，得到△AP’B，连接PP’，则△APP’为等腰直角三角形，∴∠A PP’=45°，PP’=2PA ，PC=P’B ，∵∠APB=135°，∴∠BPP’=90°，∴P’P 2+BP 2=P’B 2，∴2PA 2+PB 2=PC 2．（3）k=3将△APC 绕点A 顺时针旋转120°得到△AP’B ，连接PP’，过点A 作AH ⊥PP’，可得303,APP PP PA PC P B '︒''∠===60APB ︒∠=90BPP '︒∴∠=222P P BP P B ''∴+=222(3)PA PB PC ∴+=222()kPA PB PC +=3k ∴=【点睛】本题考查了旋转三角形的问题，掌握旋转的性质、勾股定理是解题的关键．2．[问题解决]（1）如图1．在平行四边形纸片ABCD （AD ＞AB ）中，将纸片沿过点A 的直线折叠，使点B 落在AD 上的点B '处，折线AE 交BC 于点E ，连接B 'E ．求证：四边形ABEB '是菱形．[规律探索]（2）如图2，在平行四边形纸片ABCD （AD ＞AB ）中，将纸片沿过点P 的直线折叠，点B 恰好落在AD 上的点Q 处，点A 落在点A ′处，得到折痕FP ，那么△PFQ 是等腰三角形吗？请说明理由．[拓展应用]（3）如图3，在矩形纸片ABCD （AD ＞AB ）中，将纸片沿过点P 的直线折叠，得到折痕FP ，点B 落在纸片ABCD 内部点B '处，点A 落在纸片ABCD 外部点A '处，A B ''与AD 交于点M ，且A 'M ＝B 'M ．已知：AB ＝4，AF ＝2，求BP 的长．解析：（1）证明见解析；（2）是，理由见解析；（3）422．【分析】（1）由平行线的性质和翻折可推出CEB ABE '∠=∠，即//AB B E '．故四边形ABEB '是平行四边形，再由翻折可知AB AB '=，即证明平行四边形ABEB '是菱形．（2）由翻折和平行线的性质可知BPF QPF ∠=∠，BPF QFP ∠=∠，即得出QPF QFP ∠=∠，即PFQ △是等腰三角形．（3）延长PB '交AD 于点G ，根据题意易证()FA M GB M ASA ''≅，得出结论2A F B G AF ''===，FM GM =．根据（2）同理可知PFG △为等腰三角形，即FG =PG ．再在Rt A FM '中，2222FM A M A F ''=+242PG FG FM ===422PB PB PG B G ''==-=．【详解】（1）由平行四边形的性质可知//AD BC ，∴AB E CEB ''∠=∠，由翻折可知AB E ABE '∠=∠，∴CEB ABE '∠=∠，∴//AB B E '．∴四边形ABEB '是平行四边形．再由翻折可知AB AB '=，∴四边形ABEB '是菱形．（2）由翻折可知BPF QPF ∠=∠，∵//AD BC ，∴BPF QFP ∠=∠，∴QPF QFP ∠=∠，∴QF =QP ，∴PFQ △是等腰三角形．（3）如图，延长PB '交AD 于点G ，根据题意可知90FA M GB M ''∠=∠=︒，在FA M '和GB M '中，90FA M GB M A M B M FMA GMB ''''∠=∠''=︒⎧⎪=⎨⎪∠=∠⎩， ∴()FA M GB M ASA ''≅，∴2A F B G AF ''===，FM GM =．根据（2）同理可知PFG △为等腰三角形．∴FG =PG ．∵2A F AM '==，∴在Rt A FM '中，2222FM A M A F ''=+=，∴242FG FM ==，∴42PG =，∴422PB PB PG B G ''==-=-．【点睛】本题为矩形的折叠问题．考查矩形的性质，折叠的性质，平行线的性质，菱形的判定，等腰三角形的判定和性质，全等三角形的判定和性质以及勾股定理，综合性强．掌握折叠的性质和正确的连接辅助线是解答本题的关键．3．（基础巩固）（1）如图1，在ABC ∆中，90ACB ∠=︒，直线l 过点C ，分别过AB 、两点作,AE l BD l ⊥⊥，垂足分别为E D 、．求证：BDCCEA ∆∆．（尝试应用）（2）如图2，在ABC ∆中，90ACB ∠=︒，D 是BC 上一点，过D 作AD 的垂线交AB 于点E ．若4,tan ,205BE DE BAD AC =∠==，求BD 的长． （拓展提高）（3）如图3，在ABCD 中，在BC 上取点E ，使得90AED ∠=︒，若4,,143BE AE AB CD EC ===，求ABCD 的面积．解析：（1）见解析；（2）32BD =；（3）710【分析】（1）由直角三角形的性质证得∠BDC =∠AEC ，由相似三角形的判定定理可得出结论； （2）过点E 作EF ⊥BC 于点F ，由相似三角形的性质得出DE DF DA AC=，由锐角三角函数的定义求出DF =16，则可求出答案；（3）过点A 作AM ⊥BC 于点M ，过点D 作DN ⊥BC ，交BC 的延长线于点N ，证明△ABM ≌△DCN （AAS ），由全等三角形的性质得出BM =CN ，AM =DN ，设BE =4a ，EC =3a ，由（1）得△AEM ∽△EDN ，得出比例线段AM EN ME DN =，求出a =1，b =10，由平行四边形的面积公式可得出答案．【详解】解：（1）∵90ACB ∠=︒，∴90BCD ACE ∠+∠=︒，∵AE CE ⊥，∴90AEC ∠=︒，∴90ACE CAE ∠+∠=︒，∴BCD CAE ∠=∠．∵BD DE ⊥，∴90BDC ∠=︒，∴BDC AEC ∠=∠，∴BDC CEA ∆∆（2）过点E 作EF BC ⊥于点F ，由（1）得EDFDAC ∆∆， ∴DE DF DA AC= ∵AD DE ⊥，4tan ,205BAD AC ∠==， ∴4520DF =， ∴16DF =∵BE DE =，∴BF DF =∴32BD =（3）过点A 作AM BC ⊥于点M ，过点D 作DN BC ⊥的延长线于点N ，∴090AMB DNC ∠=∠=∵四边形ABCD 是平行四边形，∴//,AB CD AB CD =，∴B DCN ∠=∠，∴ABM DCN ∆≅∆，∴,BM CN AM DN ==，∵,AB AE AM BC =⊥，∴BM ME = ∵43BE EC =，设4,3BE a EC a == ∴2,5BM ME CN a EN a ====∵90AED ∠=︒，由（1）得AEMEDN ∆∆， ∴AM EN ME DN =， ∴25b a a b= ∴b =∵CD =∴()22214a b += ∴1,a b ==∴ABCD 的面积172BC DN a b =⨯⨯=⨯=【点睛】本题是相似形综合题，考查了相似三角形的判定与性质，全等三角形的判定与性质，平行四边形的性质，锐角三角函数的定义，熟练掌握相似三角形的判定与性质是解题的关键． 4．如图，在菱形ABCD 中，120BAD ∠=，将边AB 绕点A 逆时针旋转至'AB ，记旋转角为α．过点D 作DF BC ⊥于点F ，过点B 作BE ⊥直线'B D 于点E ，连接EF ． （探索发现）(1)填空：当60α=时，'EBB ∠ = ．'EF DB 的值是 （验证猜想）(2)当0360α<<时，(1)中的结论是否仍然成立?若成立，请仅就图2的情形进行证明；若不成立，请说明理由；（拓展应用）(3)在(2)的条件下，若AB =BDE ∆是等腰直角三角形时，请直接写出线段EF 的长．解析：（1）3032）当0360α<<时，（1）中的结论仍然成立，理由见解析；（3）线段EF 的长为3333【分析】(1)当60α=时，点B ′与点C 重合，BE ⊥ CD ，由四边形ABCD 为菱形，可求∠ABE =90°，由120BAD ∠=，可求∠ABC =60°，'EBB ∠=30°，由DF ⊥BC ，DC ∥AB ，∠FDC =∠EBC =30°，由sin ∠FDC =sin ∠EBC =CF CE DC BC=，可得CF =CE ，可求∠CEF =∠FDC =30°即可； (2)当0360α<<时， (1)中的结论仍然成立．先求'60EB B ∠=︒，再证'EBB CBD ∠=∠．最后证'DBB FBE ∆∆∽即可；(3) 连接AC ，BD 交于点O ．先求6OB =23DE ='2EB =．分两种情况：①如图先求'232B D =，再证△B′BD ∽△EBF ，可得3EF B D ′②如图先求'32B D =．再证△B′BD ∽△EBF ，3EF B D ′ 【详解】(1)当60α=时，点B ′与点C 重合，∵BE ⊥ CD ，四边形ABCD 为菱形，CD ∥AB ，∴BE ⊥AB ，∴∠ABE =90°，∵120BAD ∠=，AD ∥BC ，∴∠ABC =180°-∠BAD =180°-120°=60°，∴'EBB ∠=∠ABE -∠ABC =90°-60°=30°，∵DF ⊥BC ，DC ∥AB ，∴DF ⊥AD ，∠CDA =180°-∠BAD =60°，∴∠FDC =90°-∠CDA =30°，∠FCD =90°-∠FDC =60°，∴∠FDC =∠EBC =30°，∴sin ∠FDC =sin ∠EBC =CF CE DC BC=， ∵DC =BC ，∴CF =CE ，∴∠CFE =∠CEF =12∠FCD =30°，∴∠CEF =∠FDC =30°，∴DF =FE ，∵cos ∠FDC =32DF DC =， ∴'EF DB =32DF DC =， 故答案为30，32． (2)当0360α<<时， (1)中的结论仍然成立．证明：如图1，连接BD ．'AB AD AB ==，1'(180)9022AB B αα∴∠=︒-=︒-，1'[180(120)]3022AB D αα∠=︒-︒-=︒+． '180''180(90)(30)6022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒， '30EBB ∴∠=︒． 11(180)3022CBD ABC BAD ∠=∠=︒-∠=︒． 'EBB CBD ∴∠=∠．'''EBB FBB CBD FBB ∴∠+∠=∠+∠，即'DBB EBF ∠=∠．3cos BF DBF BD ∠==3cos ''BE EBB BB ∠== 'BF BE BD BB ∴=． 'DBB FBE ∆∆∽．3''EF BE DB BB ∴==，(3)线段EF 的长为3333连接AC ，BD 交于点O ．AC DB ⊥，1602BAO BAD ∠=∠=︒，sin 6OB AB BAO ∴=⋅∠=226BD OB ∴== ∵DE =BE ，∠DEB =90°，∴∠EDB =∠EBD =45°，2sin 63DE BE BD DBE ∴==⋅∠== 'AB AD AB ==，∠B′EB =90°，1'(180)9022AB B αα∴∠=︒-=︒-，1'[180(120)]3022AB D αα∠=︒-︒-=︒+． '180''180(90)(30)6022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒， '30EBB ∴∠=︒． 3'tan '232EB BE EBB ∴=⋅∠==． 分两种情况：①如图，''232B D DE B E =+=，∵∠B′BE =∠DBF =30°，∴cos ∠B ′BE =cos ∠DBF =3EB FB B B DB =' 又∵∠B′BE +∠EBD =∠EBD +∠DBF ，∴∠B′BD =∠EBF ，∴△B′BD ∽△EBF ， ∴3=EB FB EF B B DB B D =''， 33(232)33EF B D '∴===．②如图，''232B D DE B E =-=-．∵∠B′BE =∠DBF =30°，∴cos ∠B′BE =cos ∠DBF =3=2EB FB B B DB ='， 又∵∠B′BE -∠FBB′=∠DBF-∠FBB ′，∴∠B′BD =∠EBF ，∴△B′BD ∽△EBF ，∴3==2EB FB EF B B DB B D =''， 33(232)3322EF B D '∴=⨯=⨯-=-．综上所述，线段EF 的长为33+33【点睛】本题考查图形旋转变换，菱形性质，锐角三角函数值，等腰直角三角形性质，三角形相似判定与性质，掌握图形旋转变换，菱形性质，锐角三角函数值，等腰直角三角形性质，三角形相似判定与性质是解题关键．5．（了解概念）定义：在平面直角坐标系xOy 中，组成图形的各点中，与点Р所连线段最短的点叫做点Р关于这个图形的短距点，这条最短线段的长度叫做点Р到这个图形的短距．（理解运用）（1）已知点()3,0P -，以原点为圆心，l 为半径作O ，则点Р关于O 的短距点的坐标是 ；（2）如图，点(3P ，等边三角形OAB 的顶点A 的坐标为()6,0，顶点B 在第一象限，判断点Р关于OAB 的短距点的个数，并说明理由； （拓展提升）（3）已知(),6P p p -+，()6,0A ，()0,6B ，点C 在第一象限内，且75CBO ∠=︒，90ACB ∠=︒，若点Р到四边形OACB 的短距大于2，请直接写出p 的取值范围．解析：（1）(-1，0)；（2）点Р关于OAB 的短距点的个数有3个；（3）当p ＜22p ＜4或p ＞2Р到四边形OACB 的短距大于2． 【分析】（1）连接PO ，交O 于点M ，点M 即是点Р关于O 的短距点，进而即可求解； （2）根据题意得点P 是三角形OAB 的中心，进而即可求解；（3）由题意得点P ，A ，B 在直线y =-x +6上，以点P 为圆心，半径长为2画圆，分3种情况：①当点P 在AB 的延长线上，圆P 过点B 时，②当点P 在线段AB 上，圆P 与BC 相切于点N ，过点P 作PM ⊥y 轴，③当点P 在BA 的延长线上，圆P 过点A 时，过点P 作PM ⊥y 轴，分别求解，即可得到答案． 【详解】解：（1）连接PO ，交O 于点M ，点M 即是点Р关于O 的短距点， ∵()3,0P -，、O 的半径为1， ∴M (-1，0)， 故答案是：(-1，0)；（2）∵点()3,3P ，等边三角形OAB 的顶点A 的坐标为()6,0， ∴点P 是三角形OAB 的中心，∴点P 到OA ，OB ，OC 的三条垂线段最短，三条垂线段都等于3， ∴点Р关于OAB 的短距点的个数有3个； （3）∵(),6P p p -+，()6,0A ，()0,6B ， ∴点P ，A ，B 在直线y =-x +6上， ∴∠ABO =∠BAO =45°，∵点C 在第一象限内，且75CBO ∠=︒，90ACB ∠=︒， ∴∠ABC =75°-45°=30°，以点P 为圆心，半径长为2画圆，如图所示：当点P 在AB 的延长线上，圆P 过点B 时，过点P 作PM ⊥y 轴，∵PB =2，∠PBM =45°， ∴PM 22 ∴p ＜2Р到四边形OACB 的短距大于2；①当点P 在线段AB 上，圆P 与BC 相切于点N ，过点P 作PM ⊥y 轴，则BP =2PN =2×2=4，PM =BP ×222②当点P在线段AB上，圆P与OA相切于点N，过点P作PM⊥y轴，则AP=2PN=22，BP=AB-AP=62-22=42，PM= BP×22=42×22=4，∴22＜p＜4时，点Р到四边形OACB的短距大于2；③当点P在BA的延长线上，圆P过点A时，过点P作PM⊥y轴，则PM=（62+2）×22=6+2，∴p＞6+2时，点Р到四边形OACB的短距大于2；综上所述：当p＜-2或22＜p＜4或p＞6+2时，点Р到四边形OACB的短距大于2．【点睛】本题主要考查图形与坐标以及圆的综合题，根据题意画出图形，掌握圆与直线相切的性质是解题的关键．6．已知△ABC是等腰三角形，AB=AC．（1）特殊情形：如图1，当DE∥BC时，有DB EC．（填“＞”，“＜”或“=”）（2）发现探究：若将图1中的△ADE绕点A顺时针旋转α（0°＜α＜180°）到图2位置，则（1）中的结论还成立吗？若成立，请给予证明；若不成立，请说明理由．（3）拓展运用：如图3，P是等腰直角三角形ABC内一点，∠ACB=90°，且PB=1，PC=2，PA=3，求∠BPC的度数．解析：（1）=；（2）成立，证明见解析；（3）135°.【分析】试题（1）由DE∥BC，得到DB ECAB AC=，结合AB=AC，得到DB=EC；（2）由旋转得到的结论判断出△DAB≌△EAC，得到DB=CE；（3）由旋转构造出△CPB≌△CEA，再用勾股定理计算出PE，然后用勾股定理逆定理判断出△PEA是直角三角形，再简单计算即可．【详解】（1）∵DE∥BC，∴DB ECAB AC=，∵AB=AC，∴DB=EC，故答案为=，（2）成立．证明：由①易知AD=AE，∴由旋转性质可知∠DAB=∠EAC，又∵AD=AE，AB=AC∴△DAB≌△EAC，∴DB=CE，（3）如图，将△CPB绕点C旋转90°得△CEA，连接PE，∴△CPB≌△CEA，∴CE=CP=2，AE=BP=1，∠PCE=90°，∴∠CEP=∠CPE=45°，在Rt△PCE中，由勾股定理可得，PE=22，在△PEA中，PE2=（22）2=8，AE2=12=1，PA2=32=9，∵PE2+AE2=AP2，∴△PEA是直角三角形∴∠PEA=90°，∴∠CEA=135°，又∵△CPB≌△CEA∴∠BPC=∠CEA=135°．【点睛】考点：几何变换综合题；平行线平行线分线段成比例.7．（问题情境）如图1，点E是平行四边形ABCD的边AD上一点，连接BE、CE．求证：BCE 1S2=S平行四边形ABCD．（说明：S表示面积）请以“问题情境”为基础，继续下面的探究（探究应用1）如图2，以平行四边形ABCD的边AD为直径作⊙O，⊙O与BC边相切于点H，与BD相交于点M．若AD＝6，BD＝y，AM＝x，试求y与x之间的函数关系式．（探究应用2）如图3，在图1的基础上，点F在CD上，连接AF、BF，AF与CE相交于点G，若AF＝CE，求证：BG平分∠AGC．（迁移拓展）如图4，平行四边形ABCD中，AB：BC＝4：3，∠ABC＝120°，E是AB的中点，F在BC上，且BF：FC＝2：1，过D分别作DG⊥AF于G，DH⊥CE于H，请直接写出DG：DH的值．解析：【问题情境】见解析；【探究应用1】18yx=；【探究应用2】见解析；【迁移拓1927【分析】（1）作EF⊥BC于F，则S△BCE＝12BC×EF，S平行四边形ABCD＝BC×EF，即可得出结论；（2）连接OH，由切线的性质得出OH⊥BC，OH＝12AD＝3，求出平行四边形ABCD的面积＝AD×OH＝18，由圆周角定理得出AM⊥BD，得出△ABD的面积＝12BD×AM＝12平行四边形的面积＝9，即可得出结果；（3）作BM⊥AF于M，BN⊥CE于N，同图1得：△ABF的面积＝△BCE的面积＝12平行四边形ABCD 的面积，得出12AF×BM ＝12CE×BN ，证出BM ＝BN ，即可得出BG 平分∠AGC ．（4）作AP ⊥BC 于P ，EQ ⊥BC 于Q ，由平行四边形的性质得出∠ABP ＝60°，得出∠BAP ＝30°，设AB ＝4x ，则BC ＝3x ，由直角三角形的性质得出BP ＝12AB ＝2x ，BQ ＝12BE ，AP ＝＝，由已知得出BE ＝2x ，BF ＝2x ，得出BQ ＝x ，EQ ，PF ＝4x ，QF ＝3x ，QC ＝4x ，由勾股定理求出AF ＝，CE ，连接DF 、DE ，由三角形的面积关系得出AF×DG ＝CE×DH ，即可得出结果． 【详解】（1）证明：作EF ⊥BC 于F ，如图1所示： 则S △BCE ＝12BC×EF ，S 平行四边形ABCD ＝BC×EF ， ∴12BCEABCDSS =．（2）解：连接OH ，如图2所示： ∵⊙O 与BC 边相切于点H ， ∴OH ⊥BC ，OH ＝12AD ＝3，∴平行四边形ABCD 的面积＝AD×OH ＝6×3＝18， ∵AD 是⊙O 的直径， ∴∠AMD ＝90°， ∴AM ⊥BD ，∴△ABD 的面积＝12BD×AM ＝12平行四边形的面积＝9， 即12xy ＝9，∴y 与x 之间的函数关系式y ＝18x； （3）证明：作BM ⊥AF 于M ，BN ⊥CE 于N ，如图3所示：同图1得：△ABF 的面积＝△BCE 的面积＝12平行四边形ABCD 的面积， ∴12AF×BM ＝12CE×BN ，∵AF ＝CE ， ∴BM ＝BN ， ∴BG 平分∠AGC ．（4）解：作AP ⊥BC 于P ，EQ ⊥BC 于Q ，如图4所示： ∵平行四边形ABCD 中，AB ：BC ＝4：3，∠ABC ＝120°， ∴∠ABP ＝60°，∴∠BAP ＝30°，设AB ＝4x ，则BC ＝3x ，∴BP ＝12AB ＝2x ，BQ ＝12BE ，AP ＝3BP ＝23x ， ∵E 是AB 的中点，F 在BC 上，且BF ：FC ＝2：1， ∴BE ＝2x ，BF ＝2x ， ∴BQ ＝x ，∴EQ ＝3x ，PF ＝4x ，QF ＝3x ，QC ＝4x ，由勾股定理得：AF ＝22AP PF +＝27x ，CE ＝22EQ QC +＝19x ， 连接DF 、DE ，则△CDE 的面积＝△ADF 的面积＝12平行四边形ABCD 的面积， ∴AF×DG ＝CE×DH ，∴DG ：DH ＝CE ：AF ＝19x :27x 19:27=．【点睛】本题是圆的综合题目，考查了圆周角定理、平行四边形的性质、三角形面积公式、含30°角的直角三角形的性质、勾股定理、角平分线的判定等知识；本题综合性强，需要添加辅助线，熟练掌握平行四边形的性质和勾股定理是解题的关键．8．如图所示，在△ABC 中，AB BC =，D 、E 分别是边AB 、BC 上的动点，且BD BE =，连结AD 、AE ，点M 、N 、P 分别是CD 、AE 、AC 的中点，设B α∠=．（1）观察猜想 ①在求MNCE的值时，小明运用从特殊到一般的方法，先令60α=︒，解题思路如下：如图1，先由,AB BC BD BE ==，得到CE AD =，再由中位线的性质得到PM PN =，60NPM ∠=︒，进而得出△PMN 为等边三角形，∴12MN NP CE CE ==． ②如图2，当90α=︒，仿照小明的思路求MNCE的值； （2）探究证明 如图3，试猜想MNCE的值是否与()0180αα︒<<︒的度数有关，若有关，请用含α的式子表示出MNCE，若无关，请说明理由； （3）拓展应用如图4，2,36AC B =∠=︒，点D 、E 分别是射线AB 、CB 上的动点，且AD CE =，点M 、N 、P 分别是线段CD 、AE 、AC 的中点，当1BD =时，请直接写出MN 的长． 解析：（1）②22MN CE =；（2）MN CE 的值与α的度数有关，sin 2MN CE α=；（3）MN 的长55-35+ 【分析】（1）②先根据线段的和差求出AD CE =，再根据中位线定理、平行线的性质得出,45PM PN APN CPM =∠=∠=︒，从而可得出90NPM ∠=︒，然后根据等腰直角三角形的性质即可得；（2）参照题（1）的方法，得出PMN 为等腰三角形和NPM ∠的度数，再利用等腰三角形的性质即可求出答案；（3）分两种情况：当点D 、E 分别是边AB 、CB 上的动点时和当点D 、E 分别是边AB 、CB 的延长线上的动点时，如图（见解析），先利用等腰三角形的性质与判定得出,ABC BCE CAB AFC ∠=∠∠=∠，再根据相似三角形的判定与性质得出BC 、CE 的长，由根据等腰三角形的三线合一性得出1,182BP AC CBP ABC ⊥∠=∠=︒，从而可得sin18︒的值，最后分别利用（2）的结论即可得MN 的长． 【详解】 （1）②,AB BC BD BE ==∴AD CE = ,90AB BC B =∠=︒∴ABC 为等腰直角三角形，45ACB CAB ∠=∠=︒∵点M 、N 、P 分别是CD 、AE 、AC 的中点 11//,,//,22PN CE PN CE PM AD PM AD ∴==,45,45PM PN APN ACB CPM CAB ∴=∠=∠=︒∠=∠=︒∴18090NPM APN CPM ∠=︒-∠-∠=︒∴PMN 为等腰直角三角形，∴222MN PN CE == 即22MN CE =； （2）MNCE的值与α的度数有关，求解过程如下： 由（1）可知，PM PN =，即PMN 为等腰三角形180180NPM APN CPM ACB CAB B α∠=︒-∠-∠=︒-∠-∠=∠=如图5，作PH MN ⊥ 则11,222NH MN NPH NPM α=∠=∠= 在Rt NPH 中，sin NHNPH PN∠=，即12sin 122MN CE α=则sin 2MN CE α=；（3）依题意，分以下两种情况： ①当点D 、E 分别是边AB 、CB 上的动点时如图6，作ACB ∠的角平分线交AB 边于点F ，并连结BP2,36,AC ABC AB AC =∠=︒=72ACB CAB ∴∠=∠=︒136,722ACE BCE ACB AFC ABC BCE ∴∠=∠=∠=︒∠=∠+∠=︒,ABC BCE CAB AFC ∴∠=∠∠=∠2BF CF AC ∴===，ACF ABC ~AF ACAC AB∴=，即2AC AF AB =⋅ 设==AB BC x ，则2AF AB BF x =-=- 22(2)x x ∴=-解得15x 或15x =-即15BC =1515CE BC BE BC BD ∴=-=-=由（2）可知，36sin sin182MN CE ︒==︒ sin185sin18MN CE ∴=⋅︒=︒点P 是AC 上的中点1,182BP AC CBP ABC ∴⊥∠=∠=︒，112CP AC ==（等腰三角形的三线合一）在Rt CBP 中，sin CP CBP BC ∠=，即151sin18415-︒==+51555sin18544MN --∴=︒=⨯=②如图7，当点D 、E 分别是边AB 、CB 的延长线上的动点时 同理可得：15BC =+15125CE BC BE BC BD ∴=+=+=++=+5135sin18(25)44MN CE -+∴=⋅︒=+⨯=综上，MN 的长为554-或354+．【点睛】本题考查了中位线定理、平行线的性质、相似三角形的判定与性质、等腰三角形的性质、解直角三角形等知识点，较难的是题（3），依据题意，正确分两种情况，并结合题（2）的结论是解题关键．9．数学课上，李老师出示了如下框中的题目．在等边三角形ABC 中，点E 在AB 上，点D 在CB 的延长线上，且ED EC =，如图，试确定线段AE 与DB 的大小关系，并说明理由．（1）特殊情况，探索结论当点E为AB的中点时，如图1，确定线段AE与的DB大小关系．请你直接写出结论：AE_____DB（填“>”，“<”或“=”）．（2）特例启发，解答题目解：如图2，题目中，AE与DB的大小关系是：AE____DB（填“>”“<”或“=”）．理由如下：（请你完成以下解答过程）（3）拓展结论，设计新题=．若ABC的在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED EC边长为1，2AE=，求CD的长（请你直接写出结果）．解析：（1）=；（2）=；（3）3或1【分析】（1）根据等边三角形性质和等腰三角形的性质求出∠D=∠ECB=30°，求出∠DEB=30°，求出BD=BE即可；（2）过E作EF∥BC交AC于F，求出等边三角形AEF，证△DEB和△ECF全等，求出BD=EF即可；（3）当D在CB的延长线上，E在AB的延长线式时，由（2）求出CD=3，当E在BA的延长线上，D在BC的延长线上时，求出CD=1．【详解】EF BC，交AC于点F，解：（1）如图 1 ，过点E作//ABC ∆为等边三角形，60AFE ACB ABC ∴∠=∠=∠=︒，∠A=60°，∴AEF ∆为等边三角形，120EFC EBD ∴∠=∠=︒，EF AE =，ED EC =，EDB ECB ∴∠=∠，ECB FEC ∠=∠，EDB FEC ∴∠=∠，在BDE ∆和FEC ∆中，EBD EFC EDB FEC ED EC ∠=∠⎧⎪∠=∠⎨⎪=⎩()BDE FEC AAS ∴∆≅∆，BD EF ∴=，AE BD ∴=，故答案为：=；（2）如图1，过E 作EF ∥BC 交AC 于F ，∵等边三角形ABC ，∴∠ABC=∠ACB=∠A=60°，AB=AC=BC ，∴∠AEF=∠ABC=60°，∠AFE=∠ACB=60°，即∠AEF=∠AFE=∠A=60°，∴△AEF 是等边三角形，∴AE=EF=AF ，∵∠ABC=∠ACB=∠AFE=60°，∴∠DBE=∠EFC=120°，∠D+∠BED=∠FCE+∠ECD=60°，∵DE=EC ，∴∠D=∠ECD ，∴∠BED=∠ECF ，在△DEB 和△ECF 中，DEB ECF DBE EFC DE CE ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△DEB ≌△ECF （AAS ），∴BD=EF=AE ，即AE=BD ，故答案为：=．（3）CD=1或3，理由是：分为两种情况：①如图2过A 作AM ⊥BC 于M ，过E 作EN ⊥BC 于N ，则AM ∥EN ，∵△ABC 是等边三角形，∴AB=BC=AC=1，∵AM ⊥BC ，∴BM=CM=12BC=12，∵DE=CE ，EN ⊥BC ，∴CD=2CN ，∵AB=1，AE=2，∴AB=BE=1，∵EN ⊥DC ，AM ⊥BC ，∴∠AMB=∠ENB=90°，在△ABM 和△EBN 中， ABM EBN AMB ENB AB BE ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△AMB ≌△ENB （AAS ），∴BN=BM=12，∴CN=1+12=32， CD=2CN=3；②如图3，作AM ⊥BC 于M ，过E 作EN ⊥BC 于N ，则AM ∥EN ，∵△ABC 是等边三角形，∴AB=BC=AC=1，∵AM ⊥BC ，∴BM=CM=12BC=12，∵DE=CE ，EN ⊥BC ，∴CD=2CN ，∵AM ∥EN ， ∴AB BM AE MN =， ∴1122MN=，∴MN=1，∴CN=1-12=12，∴CD=2CN=1，即CD=3或1．【点睛】本题综合考查了等边三角形的性质和判定，等腰三角形的性质，全等三角形的性质和判定，三角形的外角性质等知识点的应用，解（2）小题的关键是构造全等的三角形后求出BD=EF ，解（3）小题的关键是确定出有几种情况，求出每种情况的CD 值，注意，不要漏解啊．10．综合与实践（1）（探索发现）在ABC ∆中. AC BC =，ACB α∠=，点D 为直线BC 上一动点（点D 不与点B ，C 重合），过点D 作//DF AC 交直线AB 于点F ，将AD 绕点D 顺时针旋转α得到ED ，连接BE ．如图（1），当点D 在线段BC 上，且90α=︒时，试猜想：①AF 与BE 之间的数量关系：______；②ABE ∠=______．（2）（拓展探究）如图（2），当点D 在线段BC 上，且090α︒<<︒时，判断AF 与BE 之间的数量关系及ABE ∠的度数，请说明理由．（3）（解决问题）如图（3），在ABC ∆中，AC BC =，4AB =，ACB α∠=，点D 在射线BC 上，将AD 绕点D 顺时针旋转α得到ED ，连接BE ．当3BD CD =时，直接写出BE 的长．解析：（1）①AF BE =；②90︒；（2）AF BE =，ABE α∠=．理由见解析；（3）BE 的长为1或2．【分析】（1）由“SAS”△ADF ≌△EDB ，可得AF=BE ，再利用“8字型”字母∠OBE=∠ADO=90°即可解决问题；（2）结论：AF=BF ，∠ABE=a ．由“SAS”△ADF ≌△EDB ，即可解决问题；（3）分当点D 在线段BC 上和当点D 在BC 的延长线上两种情形讨论，利用平行线分线段成比例可求解．【详解】解：（1）如图1中，设AB 交DE 于O ．∵∠ACB=90°，AC=BC ，∴∠ABC=45°，∵DF ∥AC ，∴∠FDB=∠C=90°，∴∠DFB=∠DBF=45°，∴DF=DB ，∵∠ADE=∠FDB=90°，∴∠ADF=∠EDB ，且DA=DE ，DF=DB∴△ADF ≌△EDB （SAS ），∴AF=BE ，∠DAF=∠E ，∵∠AOD=∠EOB ，∴∠ABE=∠ADO=90°故答案为AF=BE ，90°．（2）AF BE =，ABE α∠=.理由：∵//DF AC ，∴FDB ACB α∠=∠=，CAB DFB ∠=∠.∵AC BC =，∴ABC CAB ∠=∠.∴ABC DFB ∠=∠.∴DB DF =∵ADE FDB α∠==∠，ADF ADE FDE ∠=∠-∠，EDB FDB FDE ∠=∠-∠，∴ADF EDB ∠=∠.又∵AD DE =，∴ADF EDB ∆≅∆.∴AF BE =，AFD EBD ∠=∠.∴AFD ABC FDB ∠=∠+∠，DBE ABD ABE ∠=∠+∠，∴ABE FDB α∠=∠=.（3）1或2.解：当点D 在线段BC 上时，过点D 作//DF AC 交直线AB 于点F ，如图（1）.∵//DF AC ，∴3BF BD AF CD==. ∵4AB BF AF =+=，∴1AF =.∵//DF AC ，∴BDF C ADE α∠=∠=∠=，DFB CAB ∠=∠.∵ADF ADE FDE ∠=∠-∠，EDB FDB FDE ∠=∠-∠，∴ADF EDB ∠=∠.∵AC BC =，∴CAB CBA ∠=∠.∴DFB DBF ∠=∠.∴DF DB =.又AD DE =，∴ADF EDB ∆≅∆，1BE AF ==.当点D 在线段BC 的延长线上时，过点D 作//DF AC '交BA 的延长线于点F '，如图（2）. ∵//DF AC '， ∴2AB BC AF CD=='. ∴24AB AF '==.∴2AF '=.同理可得2BE AF '==.综上可得，BE 的长为1或2.【点睛】本题考查几何变换综合题、等腰三角形的性质、全等三角形的判定和性质、平行线分线段成比例定理等知识，解题的关键是正确寻找全等三角形解决问题，属于中考压轴题． 11．数学课外活动小组的同学在学习了完全平方公式之后，针对两个正数之和与这两个正数之积的算术平方根的两倍之间的关系进行了探究，请阅读以下探究过程并解决问题． 猜想发现：由5525510+=⨯；11112233333+=⨯=；0.40.420.40.40.8+=⨯=；1155255+>⨯=；0.2 3.220.2 3.2 1.6+>⨯；1111128282+>⨯ 猜想：如果0a >，0b >，那么存在2a b ab +≥（当且仅当a b =时等号成立）． 猜想证明：∵20a b ≥∴①0a b ，即a b =时，0a ab b -=，∴2a b ab +=；②0a b ≠，即a b 时，20a ab b ->，∴a b ab +>综合上述可得：若0a >，0b >，则2a b ab +≥成立（当日仅当a b =时等号成立）． 猜想运用：（1）对于函数()10y x x x=+>，当x 取何值时，函数y 的值最小？最小值是多少？变式探究：（2）对于函数()133y x x x =+>-，当x 取何值时，函数y 的值最小？最小值是多少？拓展应用：（3）疫情期间、为了解决疑似人员的临隔离问题．高速公路榆测站入口处，检测人员利用检测站的一面墙（墙的长度不限），用63米长的钢丝网围成了9间相同的长方形隔离房，如图．设每间离房的面积为S （米2）．问：每间隔离房的长、宽各为多少时，可使每间隔离房的面积S 最大？最大面积是多少？解析：（1）1x =，函数y 的最小值为2；（2）4x =，函数y 的最小值为5；（3）每间隔离房长为72米，宽为218米时，S 的最大值为214716米 【分析】猜想运用：根据材料以及所学完全平方公式证明求解即可； 变式探究：将原式转换为1333y x x =+-+-，再根据材料中方法计算即可； 拓展应用：设每间隔离房与墙平行的边为x 米，与墙垂直的边为y 米，依题意列出方程，然后根据两个正数之和与这两个正数之积的算术平方根的两倍之间的关系探究最大值即可．【详解】猜想运用：∵0x >， ∴10x>， ∴1122y x x x x =+≥⋅， ∴当1x x=时，min 2y =， 此时21x =，只取1x =，即1x =时，函数y 的最小值为2．变式探究：∵3x >，∴30x ->，103x ， ∴()1133233533y x x x x =+-+≥⋅-=--， ∴当133x x =--时，min 5y =， 此时()231x -=，∴14x =，22x =（舍去）， 即4x =时，函数y 的最小值为5.拓展应用： 设每间隔离房与墙平行的边为x 米，与墙垂直的边为y 米，依题意得：91263x y +=，即3421x y +=，∵30x >，40y >， ∴34234x y x y +≥⋅，即21234x y ⋅≥，整理得：14716xy ≤， 即14716S ≤， ∴当34x y =时max 14716S =， 此时72x =，218y =， 即每间隔离房长为72米，宽为218米时，S 的最大值为214716米． 【点睛】本题主要考查根据完全平方公式探究两个正数之和与这两个正数之积的算术平方根的两倍之间的关系，熟练运用完全平方公式并参照材料中步骤进行计算是解题关键，属于创新探究题．12．定义：如果一个三角形一条边上的高与这条边的比值是3：5，那么称这个三角形为“准黄金”三角形，这条边就叫做这个三角形的“金底”．（概念感知）（1）如图1，在ABC 中，12AC =，10BC =，30ACB ∠=︒，试判断ABC 是否是“准黄金”三角形，请说明理由．（问题探究）（2）如图2，ABC 是“准黄金”三角形，BC 是“金底”，把ABC 沿BC 翻折得到DBC △，连AB 接AD 交BC 的延长线于点E ，若点C 恰好是ABD △的重心，求AB BC的值． （拓展提升）（3）如图3，12l l //，且直线1l 与2l 之间的距离为3，“准黄金”ABC 的“金底”BC 在直线2l上，点A 在直线1l 上．105AB BC =，若ABC ∠是钝角，将ABC ∠绕点C 按顺时针方向旋转()090αα︒<<︒得到A B C ''，线段A C '交1l 于点D ．①当30α=︒时，则CD =_________；②如图4，当点B 落在直线1l 上时，求AD CD的值．解析：（1）ABC 是“准黄金”三角形，理由见解析；（2）329AB BC =3）①12515②35AD CD =． 【分析】 （1）过点A 作AD BC ⊥于点D ，先求出AD 的长度，然后得到61035AD BC ==，即可得到结论； （2）根据题意，由“金底”的定义得:3:5AE BC =，设3AE k =，5BC k =，由勾股定理求出AB 的长度，根据比值即可求出AB BC的值； （3）①作AE ⊥BC 于E ，DF ⊥AC 于F ，先求出AC 的长度，由相似三角形的性质，得到AF=2DF ，由解直角三角形，得到3CF DF =，则(23)35AC x ==DF 的长度，然后得到CD 的长度；②由①可知，得到CE 和AC 的长度，分别过点B '，D 作B G BC '⊥，DF AC ⊥，垂足分别为点G ，F ，然后根据相似三角形的判定和性质，得到DF AF AE EC =，然后求出CD 和AD 的长度，即可得到答案．【详解】解：（1）ABC 是“准黄金”三角形．理由：如图，过点A 作AD BC ⊥于点D ，∵12AC =，30ACB ∠=︒，∴162AD AC ==． ∴:6:103:5AD BC ==．∴ABC 是“准黄金”三角形．（2）∵点A ，D 关于BC 对称， ∴BE AD ⊥，AE ED =． ∵ABC 是“准黄金”三角形，BC 是“金底”，∴:3:5AE BC =． 不防设3AE k =，5BC k =， ∵点C 为ABD △的重心， ∴:2:1BC CE =． ∴52k CE =，152k BE =． ∴2215329(3)22k AB k k ⎛⎫=+= ⎪⎝⎭． ∴329329:5210AB k k BC ==． （3）①作AE ⊥BC 于E ，DF ⊥AC 于F ，如图：由题意得AE=3， ∵35AE BC =， ∴BC=5， ∵10AB BC =， ∴10AB，在Rt △ABE 中，由勾股定理得：22(10)31BE =-=， ∴156EC =+=， ∴223635AC +=∵∠AEC=∠DFA=90°，∠ACE=∠DAF ， ∴△ACE ∽△DAF ，∴3126AE E D C F AF ===， 设DF x =，则2AF x =， ∵∠ACD=30°， ∴3CF x =，∴(23)35AC x =+=， 解得：65315DF x ==- ∴2125615CD DF ==-．②如图，过点A 作AE BC ⊥于点E ，则3AE =． ∵ABC 是“准黄金”三角形，BC 是“金底”，∴:3:5AE BC =． ∴5BC =． ∵105AB BC =， ∴10AB．∴221BE AB AE =-=．∴6CE BE BC =+=，2236935AC CE AE =+=+=． 分别过点B '，D 作B G BC '⊥，DF AC ⊥，垂足分别为点G ，F ，∴90B GC DFC '∠=∠=︒，3B G '=，5C B B C '==，则CG 4=． ∵GCB FCD α'∠=∠=，∴AEC DFA ∽△△．∴::::3:4:5DF FC CD B G GC CB ''==． ∴设3DF k =，4FC k =，5CD k =． ∵12l l //，∴ACE CAD ∠=∠，且90AEC AFD ∠=∠=︒． ∴AEC DFA ∽△△． ∴DF AFAE EC=． ∴33543k k-=35k =∴3552CD k ==，2222959595102AF DF AD ⎛⎫⎛⎫+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=． ∴9335253552AD CD ===． 【点睛】本题属于相似形综合题，主要考查了重心的性质，等腰直角三角形的性质，勾股定理，解直角三角形，旋转的性质以及勾股定理的综合运用，解决问题的关键是依据题意画出图形，根据数形结合的思想进行解答． 13．如图1，在中，，，点，分别在边，上，，连接，点，，分别为，，的中点.（1）观察猜想 图1中，线段与的数量关系是 ，位置关系是 ；（2）探究证明 把绕点逆时针方向旋转到图2的位置，连接，，，判断的形状，并说明理由； （3）拓展延伸 把绕点在平面内自由旋转，若，，请直接写出面积的最大值.解析：（1）PM=PN ，；（2）等腰直角三角形，理由详见解析；（3）.【详解】试题分析：(1)已知 点，，分别为，，的中点，根据三角形的中位线定理可得,,,根据平行线的性质可得∠DPM=∠DCE ，∠NPD=∠ADC ，在中，，，，可得BD=EC ，∠DCE+∠ADC=90°，即可得PM=PN ，∠DPM+∠NPD=90°，即；（2）是等腰直角三角形，根据旋转的性质易证△BAD ≌△CAE ，即可得BD=CE ，∠ABD=∠ACE ，根据三角形的中位线定理及平行线的性质（方法可类比（1）的方法）可得PM="PN," ∠MPD=∠ECD ，∠PNC=∠DBC ，所以∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD ，∠DPN=∠PNC+∠PCN =∠DBC+∠PCN ，即可得∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°，即△PMN 为等腰直角三角形；（3）把绕点旋转到如图的位置，此时PN=(AD+AB)="7," PM=(AE+AC)=7,且PN、PM的值最长，由（2）可知PM=PN，，所以面积的最大值为 .试题解析：（1）PM=PN，；（2）等腰直角三角形，理由如下：由旋转可得∠BAD=∠CAE，又AB=AC,AD=AE∴△BAD≌△CAE∴BD=CE，∠ABD=∠ACE，∵点，分别为，的中点∴PM是△DCE的中位线∴PM=CE，且,同理可证PN=BD，且∴PM="PN," ∠MPD=∠ECD，∠PNC=∠DBC，∴∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD，∠DPN=∠PNC+∠PCN =∠DBC+∠PCN，∴∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°，即△PMN为等腰直角三角形.(3).考点：旋转和三角形的综合题.14．（探究函数y=x+的图象与性质）（1）函数y=x+的自变量x的取值范围是；（2）下列四个函数图象中函数y=x+的图象大致是；（3）对于函数y=x+，求当x＞0时，y的取值范围．请将下列的求解过程补充完整．解：∵x＞0∴y=x+=（）2+（）2=（﹣）2+∵（﹣）2≥0∴y≥．[拓展运用]（4）若函数y=，则y的取值范围．解析：（1）x≠0；（2）C（3）4；4；（4）y≥13【解析】试题分析：根据反比例函数的性质，一次函数的性质；二次函数的性质解答即可.试题解析：（1）函数y=x+的自变量x的取值范围是x≠0；（2）函数y=x+的图象大致是C；（3）解：∵x＞0∴y=x+=（）2+（）2=（﹣）2+4∵（﹣）2≥0∴y≥4．（4）y==x+﹣5═（）2+（）2﹣5=（+）2+13。
初一数学沪科版代数式的实际意义与几何背景压轴题
初一数学沪科版代数式的实际意义与几何背景压轴题
1、函数ｙ１＝ｋｘ＋ｋ，ｙ２＝在同一坐标中的图像大致是（）答案C 解析
2、如图，点分别是各边的中点，下列说法中，错误的是 A．平分B．C．与互相平分D．△DEF是△ABC的位似图形答案A 解析
3、在下列图形中，既是轴对称图形又是中心对称图形的是答案D 解析
4、下列图形中，是中心对称的图形是( 答案B 解析
5、计算-a-a的结果是A．0B．2aC．-2aD．答案C 解析
6、（2014?襄阳）用一条长40cm的绳子围成一个面积为64cm2的长方形．设长方形的长为xcm，则可列方程为（答案B 解析试题分析：本题可根据长方形的周长可以用x表示宽的值，然后根据面积公式即可列出方程．解：设长为xcm，∵长方形的周长为40cm，∴宽为=（20﹣x）（cm），得x（20﹣x）=64．故选：B．点评：本题考查了一元二次方程的运用，要掌握运用长方形的面积计算公式S=ab来解题的方法．
7、下面各角能成为某多边形的内角和是（）A．4300°B．4343°C．43 答案C 解析
8、如图，点分别是各边的中点，下列说法中，错误的是（;）答案A 解析
9、下列各式中，可以在有理数范围内进行因式分解的是（;）答案D 解析
10、单项式的系数是答案C 解析
11、若一次函数的图象不经过第二象限，则k 的取值范围是（答案C 解析
初二数学冀教版基本作图
12。
【小题1】解方程：3x2+7x+2=0【小题2】解不等式组答案解析13，观察图a－图d,对应每个图形下面都有一个推理或判断.4个推理或判断中，你认为正确的个数有（）.
答案B 解析14、。
上海第二初级中学中考数学几何综合压轴题易错专题
上海第二初级中学中考数学几何综合压轴题易错专题一、中考数学几何综合压轴题1．观察猜想：（1）如图1，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，点D与点C重合，点E在斜边AB上，连接DE，且DE＝AE，将线段DE绕点D顺时针旋转90°得到线段DF，连接EF，则EFAD＝______，sin∠ADE＝________，探究证明：（2）在（1）中，如果将点D沿CA方向移动，使CD＝13AC，其余条件不变，如图2，上述结论是否保持不变？若改变，请求出具体数值：若不变，请说明理由．拓展延伸（3）如图3，在△ABC中，∠ACB＝90°，∠CAB＝a，点D在边AC的延长线上，E是AB上任意一点，连接DE．ED＝nAE，将线段DE绕着点D顺时针旋转90°至点F，连接EF．求EFAD和sin∠ADE的值分别是多少？（请用含有n，a的式子表示）解析：（1612；（2）不变；（3）EFAD222cos sinnnαα+-sin∠ADE＝sinnα．【分析】（1）由等腰三角形的性质和等边三角形的判定得到∠A＝∠ACE＝30°，△BEC是等边三角形，据此求得CE的长度，根据等腰直角三角形的性质来求EF的长度，易得答案；（2）不变．理由：如图2，过点D作DG∥BC交AB于点G，构造直角三角形：△ADG，结合含30度角的直角三角形的性质和锐角三角函数的定义，结合方程求得答案；（3）如图3，过点E作EG⊥AD于点G，构造直角三角形，根据锐角三角函数的定义列出方程并解答．【详解】（1）如图1，∵在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，∴∠B＝60°．又CE＝AE，∴∠ACE＝∠A＝30°，∴∠BCE＝60°，∴△BEC是等边三角形，∴BE＝CE．∴AE＝CE＝BE．∴AD．又由旋转的性质知：FC＝EC，∠FCE＝90°，∴EFCE，∴EFAD．∵∠ADE＝30°，∴sin∠ADE＝12．12；（2）不变，理由：如图2，过点D作DG∥BC交AB于点G，则△ADG是直角三角形．∵∠DAG＝30°，DE＝AE，设DG＝x，∴∠AED＝30°，AD，∠DEG＝∠DGE＝60°．∴DE＝DF＝x，sin∠ADE＝12．∵∠EDF＝90°，∴EFx．∴EFAD∵∠ADE＝30°，∴sin∠ADE＝12．（3）过点E作EG⊥AD于点G，设AE＝x，则DE＝nx．∵∠CAB＝a，∴AG＝cosα•x，EG＝sinα•x．∴DG．∴AD＝•x．∵∠EDF＝90°，DE＝DF，∴EFDE nx．∴EFAD，sin∠ADE＝GEDE＝sin xnxα⋅＝sinnα．【点睛】本题考查了等腰三角形的性质和等边三角形的判定，作辅助线构造直角三角形，根据锐角三角函数的定义求解．2．（1）（问题背景）如图1，在Rt ABC 中，90BAC ∠=︒，AB AC =，D 是直线BC 上的一点，将线段AD 绕点A 逆时针旋转90°至AE ，连接CE ，求证：ABD ACE △≌△； （2）（尝试应用）如图2，在（1）的条件下，延长DE ，AC 交于点G ，BF AB ⊥交DE 于点F ．求证：2FG AE =；（3）（拓展创新）如图3，A 是BDC 内一点，45ABC ADB ∠=∠=︒，90BAC ∠=︒，3BD =，直接写出BDC 的面积为_____________．解析：（1）见解析；（2）见解析；（3）32 【分析】（1）【问题背景】如图1，根据SAS 证明三角形全等即可．（2）【尝试应用】如图2，过点D 作DK ⊥DC 交FB 的延长线于K ．证明△ECG ≌△DKF （AAS ），推出DF ＝EG ，再证明FG ＝DE 2即可．（3）【拓展创新】如图3中，过点A 作AE ⊥AD 交BD 于E ，连接CE ．利用全等三角形的性质证明CE ＝BD ，CE ⊥BD ，再根据三角形面积公式即可求解．【详解】（1）【问题背景】证明：如图1，∵90BAC DAE ∠=∠=︒，∴DAB EAC ∠=∠，在ABD △和ACE 中，AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩， ∴()ABD ACE SAS △≌△．（2）【尝试应用】证明：如图2，过点D 作DK DC ⊥交FB 的延长线于K ．∵DK CD ⊥，BF AB ⊥，∴90BDK ABK ∠=∠=︒，∵AB AC =，90BAC ∠=︒，∴45ABC ACB ∠=∠=︒，∴45DBK K ∠=∠=︒，∴DK DB =，∵ABD ACE △≌△，∴135ABD ACE ∠=∠=︒，DB EC DK ==，∴45ECG ∠=︒，∵BF AB ⊥，CA AB ⊥，∴AG BF ∥，∴G DFK ∠=∠，在ECG 和DKF △中，ECG K G DFK CE KD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()ECG DKF AAS ≌△△，∴DF EG =， ∵2DE AE =，∴2DF EF AE +=， ∴2EG EF AE +=，即2FG AE =．（3）【拓展创新】如图3中，过点A 作AE AD ⊥交BD 于E ，连接CE ．∵45ADB ∠=︒，90DAE ∠=︒， ∴ADE 与ABC 都是等腰直角三角形，同法可证ABD ACE △≌△，∴3CE BD ==∵45AEC ADB ∠=∠=︒，∴90CED CEB ∠=∠=︒，∴11333222BDC S BD CE =⋅⋅==△． 故答案为：32． 【点睛】本题属于几何变换综合题，考查了等腰直角三角形的判定和性质，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考压轴题．3．如图，在菱形ABCD 中，120BAD ∠=，将边AB 绕点A 逆时针旋转至'AB ，记旋转角为α．过点D 作DF BC ⊥于点F ，过点B 作BE ⊥直线'B D 于点E ，连接EF ． （探索发现）(1)填空：当60α=时，'EBB ∠ = ．'EF DB 的值是 （验证猜想）(2)当0360α<<时，(1)中的结论是否仍然成立?若成立，请仅就图2的情形进行证明；若不成立，请说明理由；（拓展应用）(3)在(2)的条件下，若22AB =BDE ∆是等腰直角三角形时，请直接写出线段EF 的长．解析：（1）3032）当0360α<<时，（1）中的结论仍然成立，理由见解析；（3）线段EF 的长为3333【分析】(1)当60α=时，点B ′与点C 重合，BE ⊥ CD ，由四边形ABCD 为菱形，可求∠ABE =90°，由120BAD ∠=，可求∠ABC =60°，'EBB ∠=30°，由DF ⊥BC ，DC ∥AB ，∠FDC =∠EBC =30°，由sin ∠FDC =sin ∠EBC =CF CE DC BC=，可得CF =CE ，可求∠CEF =∠FDC =30°即可； (2)当0360α<<时， (1)中的结论仍然成立．先求'60EB B ∠=︒，再证'EBB CBD ∠=∠．最后证'DBB FBE ∆∆∽即可；(3) 连接AC ，BD 交于点O ．先求6OB =23DE ='2EB =．分两种情况：①如图先求'232B D =，再证△B′BD ∽△EBF ，可得3EF B D ′②如图先求'32B D =．再证△B′BD ∽△EBF ，3EF B D ′ 【详解】(1)当60α=时，点B ′与点C 重合，∵BE ⊥ CD ，四边形ABCD 为菱形，CD ∥AB ，∴BE ⊥AB ，∴∠ABE =90°，∵120BAD ∠=，AD ∥BC ，∴∠ABC =180°-∠BAD =180°-120°=60°，∴'EBB ∠=∠ABE -∠ABC =90°-60°=30°，∵DF ⊥BC ，DC ∥AB ，∴DF ⊥AD ，∠CDA =180°-∠BAD =60°，∴∠FDC =90°-∠CDA =30°，∠FCD =90°-∠FDC =60°，∴∠FDC =∠EBC =30°，∴sin ∠FDC =sin ∠EBC =CF CE DC BC=， ∵DC =BC ，∴CF =CE ，∴∠CFE =∠CEF =12∠FCD =30°，∴∠CEF =∠FDC =30°，∴DF =FE ，∵cos ∠FDC =32DF DC =， ∴'EF DB =32DF DC =， 故答案为30，32． (2)当0360α<<时， (1)中的结论仍然成立．证明：如图1，连接BD ．'AB AD AB ==，1'(180)9022AB B αα∴∠=︒-=︒-，1'[180(120)]3022AB D αα∠=︒-︒-=︒+． '180''180(90)(30)6022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒， '30EBB ∴∠=︒． 11(180)3022CBD ABC BAD ∠=∠=︒-∠=︒． 'EBB CBD ∴∠=∠．'''EBB FBB CBD FBB ∴∠+∠=∠+∠，即'DBB EBF ∠=∠．3cos BF DBF BD ∠==3cos ''BE EBB BB ∠== 'BF BE BD BB ∴=． 'DBB FBE ∆∆∽．3''EF BE DB BB ∴==，(3)线段EF 的长为3333连接AC ，BD 交于点O ．AC DB ⊥，1602BAO BAD ∠=∠=︒，sin 6OB AB BAO ∴=⋅∠=226BD OB ∴== ∵DE =BE ，∠DEB =90°，∴∠EDB =∠EBD =45°，2sin 63DE BE BD DBE ∴==⋅∠== 'AB AD AB ==，∠B′EB =90°，1'(180)9022AB B αα∴∠=︒-=︒-，1'[180(120)]3022AB D αα∠=︒-︒-=︒+． '180''180(90)(30)6022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒， '30EBB ∴∠=︒． 3'tan '232EB BE EBB ∴=⋅∠==． 分两种情况：①如图，''232B D DE B E =+=，∵∠B′BE =∠DBF =30°，∴cos ∠B ′BE =cos ∠DBF =3EB FB B B DB =' 又∵∠B′BE +∠EBD =∠EBD +∠DBF ，∴∠B′BD =∠EBF ，∴△B′BD ∽△EBF ， ∴3=EB FB EF B B DB B D =''， 33(232)33EF B D '∴===．②如图，''232B D DE B E =-=-．∵∠B′BE =∠DBF =30°，∴cos ∠B′BE =cos ∠DBF =3=2EB FB B B DB ='， 又∵∠B′BE -∠FBB′=∠DBF-∠FBB ′，∴∠B′BD =∠EBF ，∴△B′BD ∽△EBF ，∴3==2EB FB EF B B DB B D =''， 33(232)3322EF B D '∴=⨯=⨯-=-．综上所述，线段EF 的长为33+33【点睛】本题考查图形旋转变换，菱形性质，锐角三角函数值，等腰直角三角形性质，三角形相似判定与性质，掌握图形旋转变换，菱形性质，锐角三角函数值，等腰直角三角形性质，三角形相似判定与性质是解题关键．4．定义：如图（1），点P 沿着直线l 翻折到P '，P 到P '的距离PP '叫做点P 关于l 的“折距”．已知，如图（2），矩形ABCD 中，,AB x BC y ==，等腰直角AEG △中，6AE AG ==，点G 在AD 上，E 、B 在AD 的两侧，点F 为EG 的中点，点P 是射线AD 上的动点，把AEG △沿着直线BP 翻折到A E G '''，点F 的对应点为F '，理解：（1）当4,9x y ==时，①若点A '在边BC 上，则点A 关于BP 的“折距”为______；②若点E 关于BP 的“折距”为12，则AP =______．应用：（2）若9y =，当点E '、G '、C 、D 能构成平行四边形时，求出此时x 的值 拓展：（3）当7,13x y ==时，设点E 关于BP 的“折距”为t ，直接写出当射线A F ''与边BC 有公共点时t 的范围．解析：（1）①42②3；（2）62x =3）2724t ＜＜【分析】（1）①根据垂直平分线的性质和正方形的性质计算即可；②设EE '和BP 相交于M ，证明ABP MBE △△，即可得解；（2）根据平行四边形的性质求解即可；（3）当A '在BC 上时为最小值，当F '在BC 上时为最大值，通过相似三角形的判定与性质求解即可；【详解】（1）当4,9x y ==时，①若A '在BC 上时，则AB BA '=，此时四边形ABA P '为正方形，在Rt ABA '中，2242AA AB BA ''=+∵点A 关于BP 的“折距”为AA '，∴点A 关于BP 的“折距”为42②由题意可知12EE '=，设EE '和BP 相较于M ，则EM BP ⊥，且162EM EE '==， 在ABP △与MBE △中，ABP MBE BAP BME ∠=∠⎧⎨∠=∠⎩， ∴ABP MBE △△， ∴AB MB AP ME=， 又()224668MB =+-=，即486AP =， 解得3AP =；（2）当点E '、G '、C 、D 能构成平行四边形时，则G E '与DC 平行且相等， 在Rt AEG 中，226662EG =+又EG E G ''=，∴62DC AB E G EG ''====， 即62x =；（3）当7,13x y ==时，点E 关于BP 的“折距”为t ，且射线A F ''与边BG 的公共点范围如图所示，当A '在BC 上时为最小值，当F '在BC 上时为最大值，∴6713EB =+=，∴EB BC =，∴BCE 为等腰直角三角形，E 到BP 的距离为2t，当A '在BC 上时，72AA '=，设AA '与BP 交于点Q ，EE '与BP 交于点N ，∴722AQ =， 又ABQ EBN △△，∴BA EQ BE BN=， ∴1322BE AQ EN BA ==， ∴132t =，当F '在BC 上时，∵F 为EG 中点，如图FM BC ⊥于M ，∴333913444MF BE ==⨯=，33944MC BE ==， ∴3924FF '=， ∴t 的取值范围为392724t ＜＜；【点睛】本题主要考查了四边形综合应用，结合勾股定理和相似三角形的判定与性质计算是解题的关键．5．综合与实践数学问题：（1）如图1，ABC是等腰直角三角形，过斜边的中点D作正方形DECF，分别交BC，AC于点E，F，则AB，BE，AF之间的数量关系为______．问题解决：（2）如图2，在任意Rt ABC内，找一点D，过点D作正方形DECF，分别交BC，AC 于点E，F，若AB BE AF∠的度数；=+，求ADB图2拓展提升：（3）如图3，在（2）的条件下，分别延长ED ，FD ，交AB 于点M ，N ，则MN ，AM ，BN 的数量关系为______．图3（4）在（3）的条件下，若3AC =，4BC =，则MN =______．解析：（1）)2AB AF BE +；（2）135°；（3）222MN AM BN =+；（4）2512【分析】（1）根据等腰直角三角形的斜边与直角边的关系及正方形的性质即可得出数量关系； （2） 延长AC 至点P ，使FP BE =，连接DP ，根据正方形的性质易证DFP DEB △△≌，从而可得DP =DB ，进而可证ADP ADB △△≌，从而可得12DAC DAB CAB ∠=∠=∠，12ABD CBD ABC ∠=∠=∠，由三角形内角和定理即可求得∠ADB 的度数； （3）由正方形的对边平行的性质易得AM =DM ，BN =DN ，从而在Rt △MDN 中，由勾股定理即可得MN 、AM 、BN 的数量关系；（4）由（2）知FP =BE ，即可求得DE =DF =1，根据相似三角形的性质可分别求得EM 、FN 的长，从而可得DM 、DN 的长，在Rt △MDN 中，由勾股定理即可求得MN 的长．【详解】（1）∵ABC 是等腰直角三角形，且AB =AC ， ∴2AB =，∠A =∠B =45°，∵四边形DECF 是正方形，且D 是AB 的中点，∴DF =FC =CE =DE ，∠DFA =∠DEB =90°，DF ∥BC ，DE ∥AC ，∴∠ADF =∠B =45°，∠BDE =∠A =45°，∴AF =DF ，BE =DE ，∴F 、E 分别是AC 、BC 的中点，∴CF =BE ，∴AC =AF +CF =AF +BE ， ∴()2AB AF BE =+；（2）延长AC 至点P ，使FP BE =，连接DP ．∵四边形DECF 是正方形，∴DF DE =，90DFC DEC ∠=∠=︒．∵FP BE =，90DFC DEB ∠=∠=︒，DF DE =，∴()SAS DFP DEB ≌△△．∴DP DB =．∵AB AF BE =+，AP AF FP =+，FP BE =，∴AP AB =．又∵DP DB =，AD AD =，∴()SSS ADP ADB ≌△△．∴12DAC DAB CAB ∠=∠=∠． 同理可得：12ABD CBD ABC ∠=∠=∠． ∵90ACB ∠=︒，∴90CAB CBA ∠+∠=︒．∴()1452DAB ABD CAB CBA ∠+∠=∠+∠=︒． ∴()180135ADB DAB ABD ∠=︒-∠+∠=︒．（3）∵DF ∥BC ，DE ∥AC ，∴∠CBD =∠NDB ， ∠DAC =∠ADM ，∵ABD CBD ∠=∠，DAC DAB ∠=∠，∴∠ABD =∠NDB ，∠ADM =∠DAB ，∴BN =DN ，AM =DM ．在Rt △MDN 中，由勾股定理得：22222MD DN MN AM BN ==++故答案为：222MN AM BN =+，（4）∵△ABC 是直角三角形，AC =3，BC =4，∴由勾股定理得：AB =5，设正方形DECF 的边长为x ，由（2）知，AP =AB =5，BE =FP ，CP =AP -AC =2，∵FP =CP +CF ，BE =BC -CE ，即4-x =2+x ，解得x =1，∴BE =BC -CE =3，AF =AC -CF =2，∵EM ∥AC ，FN ∥BC ，∴△BME ∽△BAC ，△AFN ∽△ACB ∴34ME BE AC BC ==，23FN AF BC AC ==， ∴94ME =，83FN =． ∵DM =ME -DE =54，DN =FN -DF =53， 222255254312MN DM DN ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭． 故答案为：2512MN =． 【点睛】 本题考查了正方形的性质，等腰三角形的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理等知识，截长补短法作辅助线是本题的关键．6．（概念学习）在平面直角坐标系xOy 中，O 的半径为1，若O 平移d 个单位后，使某图形上所有点在O 内或O 上，则称d 的最小值为O 对该图形的“最近覆盖距离”．例如，如图①，()(),3,04,0A B ，则O 对线段AB 的“最近覆盖距离”为3．（概念理解）（1）O 对点()3,4的“最近覆盖距离”为_ ．（2）如图②，点Р是函数24y x =+图像上一点，且O 对点Р的“最近覆盖距离”为3，则点Р的坐标为_ ．（拓展应用）（3）如图③，若一次函数4y kx =+的图像上存在点C ，使O 对点C 的“最近覆盖距离”为1，求k 的取值范围．（4）()()3,4,1D m E m +、，且42m -<<，将О对线段DE 的“最近覆盖距离”记为d ，则d 的取值范围是 ．解析：（1）4；（2）()0,4或1612,55⎛⎫-- ⎪⎝⎭；（3）k ≥k ≤4）3d ≤<【分析】（1）求出点(3,4)与原点的距离，这个距离与1的差即是所求结果；（2）设点P 的坐标为(),24x x +，根据P 到圆心的距离为4及勾股定理，可得关于x 的方程，解方程即可求得点P 的坐标；（3）考虑临界状态，当OC =2时，函数图象上存在点C ，使O 对点C 的“最近覆盖距离”为1，利用三角形相似求出k =同理，另一个临界状态为k =（4）由题意可得DE 是一条倾斜角度为45°,且等长的弦AB 、FG ，如果D 落在弧AF 上，或者落在弧BG 上，进而求解．【详解】（1）点(3,4)5=，而5－1=4，则O 对点()3,4的“最近覆盖距离”为4；故答案为：4（2）由题意可知，Р到圆的最小距离为3，即Р到圆心的距离为4由点P 在直线24y x =+上，故设,2()4P x x +，则()2222416OP x x =++= 解得12160,5x x ==- 故点P 的坐标为：()0,4或1612,55⎛⎫-- ⎪⎝⎭ 故答案为：()0,4或1612,55⎛⎫-- ⎪⎝⎭ （3）如图，考虑临界状态，过O 作OC ⊥DE 于C 点，当2OC =时，函数图像上存在点C ，使O 对点C 的“最近覆盖距离”为1,OCD EOD ODC EDO ∠=∠∠=∠OCD EOD ∴∆∆ OC OD OE DE ∴= 则12OE OC DE OD == 设,OE x =则2DE x = 由勾股定理可得：()22162x x +=解得12443,333x x ==-（舍） 43,03E ⎛⎫∴- ⎪⎝⎭此时3k =．同理，另一个临界状态为3k =-经分析可知，函数相比临界状态更靠近y 轴，则存在点C3k ∴≥或3k ≤-()4332d ≤<由题意可知，DE 是一条倾斜角度为45，长度为2的线段可在圆上找到两条与之平行且等长的弦,AB FG如果D 落在弧AF 上，或者E 落在弧BG 上，则成立当12m -≤<时，E 到弧BG 的最小距离为1EO -此时34,d ≤<当41m -<<-时，E 到弧BG 的最小距离为EB 此时332d <<综上332d ≤<【点睛】本题是圆的综合题，主要考查了一次函数的性质、圆的基本知识、三角形相似的判定与性质、新定义等，数形结合是本题解题的关键．7．在ABC 中，点D ，E 分别是AB AC ，边上的点，//DE BC ．基础理解：（1）如图1，若43AD BD ==，，求AE AC 的值； 证明与拓展：（2）如图2，将ADE 绕点A 逆时针旋转a 度，得到11AD E △，连接11,BD CE ； ①求证：11BD AD CE AE=； ②如图3，若90,6,BAC AB AC AD ADE ∠=︒<=，在旋转的过程中，点1D 恰好落在DE 上时，连接1113,4BD EE CE =，则11E D E 的面积为________． 解析：（1）47；（2）①见详解；②13.44 【分析】（1）利用平行线分线段定理，直接求解即可；、（2）①先推出11AD AB AE AC=，从而得11ABD ACE ∽，进而即可得到结论；②先推出AE =AE 1 =8，DE =D 1E 1=10，过点A 作AM ⊥DE 于点M ，则DM = 3.6，D 1E =2.8，再证明∠D 1EE 1=90°，进而即可求解．【详解】解：（1）∵//DE BC ，43AD BD ==，，∴AE AC =44437AD AB ==+； （2）①∵将ADE 绕点A 逆时针旋转a 度，得到11AD E △，∴1AD =AD ，1AE =AE ，∠BAD 1=∠CAE 1，∵//DE BC ， ∴AD AE AB AC =，即AD AB AE AC =， ∴11AD AB AE AC =， ∴11ABD ACE ∽， ∴1111BD AD AD CE AE AE==； ②由①可知11ABD ACE ∽， ∴111134BD AD CE AE ==， ∵将ADE 绕点A 逆时针旋转，得到11AD E △，点1D 恰好落在DE 上，∴AD 1=AD =6，∠D 1AE 1=∠DAE =90°，∴AE =AE 1=43AD 1=8，DE =D 1E 1=226810+=， 过点A 作AM ⊥DE 于点M ，则DM =D 1M =AD ×cos ∠ADE = AD ×AD DE =6×610=3.6，∴D 1E =10-3.6 ×2=2.8，∵∠D 1AE 1=∠DAE =90°，∴∠DAD 1=∠EAE 1，又∵AD 1=AD ，AE =AE 1，∴∠ADE =11118018022DAD EAE AEE ︒-∠︒-∠==∠， ∴∠AED +1AEE ∠=∠AED +∠ADE =90°，即：∠D 1EE 1=90°，∴22110 2.89.6EE -，∴11E D E 的面积=12D 1E ∙EE 1=12×2.8×9.6=13.44． 故答案是：13.44．【点睛】本题主要考查相似三角形的判定和性质，解直角三角形，勾股定理，平行线分线段成比例定理，旋转的性质，熟练掌握相似三角形的判定和性质，是解题的关键．8．定义：有一组对角互补的四边形叫做“对补四边形”，例如，四边形ABCD 中，若180A C ∠+∠=︒或180B D ∠+∠=︒，则四边形ABCD 是“对补四边形”．（概念理解）（1）如图1，四边形ABCD 是“对补四边形”． ①若::3:2:1A B C ∠∠∠=，则D ∠=________；②若90B ∠=︒．且3,2AB AD ==时．则22CD CB -=_______； （拓展提升）（2）如图，四边形ABCD 是“对补四边形”，当AB CB =，且12EBF ABC ∠=∠时，图中,,AB CF EF 之间的数量关系是 ，并证明这种关系；（类比应用）（3）如图3，在四边形ABCD 中，,AB CB BD =平分ADC ∠； ①求证：四边形ABCD 是“对补四边形”； ②如图4，连接AC ，当90ABC ∠=︒，且12ACD ABCS S=时，求tan ACD ∠的值． 解析：（1）①90︒，②5；（2）AE CF EF +=，理由见解析；（3）①见解析，②23 【分析】（1）①根据“对补四边形”的定义，结合::3:2:1A B C ∠∠∠=，即可求得答案； ②根据“对补四边形”的定义，由90B ∠=︒，得D ∠90=︒，再利用勾股定理即可求得答案；（2）延长EA 至点K ，使得AK CF =，连接BK ，根据“对补四边形”的定义，可证明ABK CBF △≌△，继而证明BEK BEF △≌△，从而可得结论；（3）①过点B 作BM AD ⊥于点M ，BN AC ⊥于点N ，则90BMA BNC ∠=∠=︒,可证Rt ABM Rt CBN △≌△，进而可证四边形ABCD 是“对补四边形”；②设,AD a DC b ==，则tan aACD b∠=根据222AC a b =+，再运用12ACD ABCS S=建立方程，解方程即可求得tan ACD ∠． 【详解】 （1）::3:2:1A B C ∠∠∠=，设3,2,A x B x C x ∠=∠=∠=， 根据“对补四边形”的定义， 180A C ∠+∠=︒，即3180x x +=︒，x=︒，解得45∴∠==︒，290B xB D∠+∠=︒，180D∴∠=︒．90故答案为：90︒．②如图1，连接AC，∠+∠=︒，B D90∠=︒，180B∴∠=︒，90D在Rt ABC中22=-，BC AC AB在Rt ADC中222=-，CD AC AD22222222∴-=---=-，CD CB AC AD AC AB AB AD()AB AD==，3,22222∴-=-=，325CD CB故答案为：5．+=，理由如下：（2）AE CF EF=，连接BK，如图2，延长EA至点K,使得AK CF四边形ABCD是“对补四边形”，∴180∠+∠=︒，BAD CBAK BAD∠+∠=︒，180∴BAK C∠=∠，,AK CF AB CB ==，∴()ABK CBF SAS △≌△， ∴,ABK CBF BK BF ∠=∠=， ∴ABK ABF CBF ABF ∠+∠=∠+∠，即KBF ABC ∠=∠，12EBF ABC ∠=∠，∴12EBF KBF ∠=∠， ∴EBK EBF ∠=∠，,BK BF BE BE ==，∴()BEK BEF SAS △≌△,∴EK EF =，∴AE CF AE AK EK EF +=+==，即AE CF EF +=， 故答案为：AE CF EF +=．（3）①证明：如图3，过点B 作BM AD ⊥于点M ，BN AC ⊥于点N ，则90BMA BNC ∠=∠=︒，BD 平分ADC ∠，BM BN ∴=，AB CB =，()Rt ABM Rt CBN HL ∴△≌△，BAM C ∴∠=∠， 180BAM BAD ∠+∠=︒，180C BAD ∴∠+∠=︒，BAD ∴∠与C ∠互补，∴四边形ABCD 是“对补四边形”；②由①可知四边形ABCD 是“对补四边形”， 180ABC ADC ∴∠+∠=︒，90ABC ∠=︒，90ADC ∴∠=︒，设AD a DC b ==，，则22222AC AD CD a b =+=+，AB BC =，2222211()22AB BC AC a b ∴===+， 1122ACD S AD CD ab ∴=⋅=△， 222111()224ABC S AB BC AB a b =⋅==+△， 12ACD ABCS S=， 22112=12()4ab a b ∴+，整理得：2()410a ab b-⨯+=，解得：23ab=±． 在Rt ABC 中，tan a ACD b∠=，∴tan ACD ∠=23±．【点睛】本题考查了勾股定理，四边形内角和定理，全等三角形的性质与判定，解一元二次方程，三角函数的定义等知识，熟练掌握勾股定理和全等三角形的判定和性质，准确理解新定义是解题的关键．9．ABC 和DCE 都是等边三角形，DCE 绕点C 旋转，连接,AE BD ．猜测发现 ：（1）如图1，AE 与BD 是否相等？若相等，加以证明；若不相等，请说明理由．问题解决 ：（2）若B C E 、、三点不在一条直线上，且30,4,3ADC AD CD ∠=︒==，求BD 的长．拓展运用 ：（3）若B C E 、、三点在一条直线上（如图2），且ABC 和DCE 的边长分别为1和2，ACD △的面积及tan ADC ∠的值．解析：（1）AE =BD ，理由见解析；（2）5；（33tan ADC ∠3【分析】（1）根据等边三角形的性质，容易证明△BCD ≌△ACE ，从而问题即可解决；（2）根据∠ADC=30゜及△DCE 是等边三角形，可得∠ADE=∠ADC+∠CDE=90゜，从而可计算出AE ，再由（1）即可得BD 的长；（3）过A 点作AF ⊥CD 于F ，根据ABC 和DCE 都是等边三角形，可得∠ACD=60゜，于是在直角△ACF 中利用三角函数知识可求得AF 的长，从而可求得△ACD 的面积；在△ACF 中还可求得CF 的长 ，从而可得DF 的长，这样在直角△ADF 中即可求得结论． 【详解】 （1）AE =BD ． 理由如下： ∵ABC 和DCE 都是等边三角形，∴,,60AC BC DC EC ACB DCE ==∠=∠=︒， ∴ACB ACD DCE ACD ∠+∠=∠+∠， 即BCD ACE ∠=∠， 在BCD △和ACE 中，CD CE BCD ACE BC AC =⎧⎪∠=∠⎨⎪=⎩， ∴() ACE BCD SAS ≅△△， ∴AE BD =；（2）如图3，由（1）得：BD AE =， ∵DCE 是等边三角形，∴60,3CDE CD DE ∠=︒==， ∵30ADC ∠=︒，∴306090ADE ADC CDE ∠=∠+∠=︒+︒=︒， 在Rt ADE △中，4,3AD DE ==， ∴2222435AE AD DE =+=+=， ∴5BD =；（3）如图2，过A 作AF CD ⊥于F ， ∵B C E 、、三点在一条直线上， ∴180BCA ACD DCE ∠+∠+∠=︒， ∵ABC 和DCE 都是等边三角形，∴60BCA DCE ∠=∠=︒， ∴60ACD ∠=︒，在Rt ACF 中，sin AFACF AC∠=， ∴33sin 122AF AC ACF =⨯∠=⨯=，11cos 122CF AC ACF =⨯∠=⨯=， ∴113322222ACDSCD AF =⨯⨯=⨯⨯=，13222FD CD CF =-=-=， 在Rt AFD 中，3tan 3AF ADC DF ∠==． 【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质、三角函数等知识，带有一定的综合性．10．如图，E F ，分别为ABC 中AC AB ，上的动点（点、、A B C 除外），连接EB FC ，交于点P ，6BC =.我们约定：线段BC 所对的CPB ∠，称为线段BC 的张角. 情景发现（1）已知三角形ABC 是等边三角形，AE BF =， ①求线段BC 的张角CPB ∠的度数； ②求点P 到BC 的最大距离；③若点P 的运动路线的长度称为点P 的路径长，求点P 的路径长. 拓展探究（2）在（1）中，已知A BC '是圆P 的外切三角形，若点A '的运动路线的长度称为点A '的路径长，试探究点A '的路径长与点P 的路径长之间有何关系？请通过计算说明.解析：（1）①BPC ∠＝120°，②点P 到BC 的最大距离3PN =433π；（2）点A '的路径长与点P 的路径长的比值是2：1（或点A '的路径长是点P 的路径长的2倍）. 【分析】（1）①利用等边三角形的性质证△AEB 与△BCF 全等，得到∠EBA ＝∠BCF ，利用三角形的内角和定理即可求出∠CPB 的度数；②由题意可知当PO ⊥BC 于点N 时，点P 到BC 的距离最大，根据垂径定理及三角函数即可求出点P 到BC 的最大距离；③由题意知点P 的路径长为弧BC 的长，在②的基础上直接利用公式即可求出结果； （2）由题意可知张角∠CPB 的度数始终为120°，可得∠CBP ＋∠BCP ＝60°，因为圆P 是△A'BC 的内切圆，由此可推出A'是等边三角形ABC 外接圆上优弧BAC 上的一动点，其半径为23，圆心角240°，根据弧长公式可直接求出其长度，并计算出点A'的路径长是点P 的路径长的2倍． 【详解】 解：（1）①∵ABC 是等边三角形，∴60CBA A AB BC ∠∠︒=＝＝，，∵AE BF =， ∴AEB BCF △≌△， ∴EBABCF ∠∠＝. ∵60180EBA EBC EBC BCF BPC ∠+∠︒∠+∠+∠︒＝，＝， ∴180180BPC EBC BCF EBC EBA ∠︒-∠-∠=︒-∠-∠＝， 180********ABC ︒-∠=︒-︒︒＝＝.②（2）如图所示，由于BPC ∠始终为120︒，故过点B C P 、、作圆O, ∴120BOC ∠︒＝. 当PO BC ⊥于点N 时，点P 到BC 的距离最大. ∵OB OC =，∴1160,322BOP BOC NB BC ∠∠=︒==＝，∴3,23ON OB ==，∴点P 到BC 的最大距离2333PN =-=.③由②可知点P 的路径为BC 的长度，即x（2）点A '的路径长与点P 的路径长的比值是2:1（或点A '的路径长是点P 的路径长的2倍），理由：由（1）中题意可知张角CPB ∠的度数始终为120︒，可得60CBP BCP ∠+∠=︒， 又因为圆P 是A BC '△的内切圆， 所以120CBA BCA ''∠+∠=︒， 所以 60CA B ∠'=︒，所以A '是等边三角形ABC 外接圆上优弧BAC 上的一动点，由题意可得等边三角形ABC 外接圆的半径为23，点A '的路径是优弧BAC 的长度，即以240︒的圆心角，半径为23的弧长，如图，所以点A '的路径长=24023831801803n r πππ⋅==， 点A '的路径长与点P 的路径长的比值是：843:32:133ππ=， 所以点A '的路径长与点P 的路径长的比值是2：1（或点A '的路径长是点P 的路径长的2倍）.【点睛】本题考查了等边三角形的性质，圆的有关性质，弧长公式等，解题的关键是能够根据题意画出图形.11．某数学兴趣小组在数学课外活动中，对多边形内两要互相垂直的线段做了如下探究： （观察与猜想）（1）如图1，在正方形ABCD 中，点E ，F 分别是AB ，AD 上的两点，连接DE ，CF ，DE CF ⊥，则DECF的值为__________；（2）如图2，在矩形ABCD 中，7AD =，4CD =，点E 是AD 上的一点，连接CE ，BD ，且CE BD ⊥，则CEBD的值为__________；（类比探究）（3）如图3，在四边形ABCD 中，90A B ∠=∠=︒，点E 为AB 上一点，连接DE ，过点C 作DE 的垂线交ED 的延长线于点G ，交AD 的延长线于点F ，求证：DE AB CF AD ⋅=⋅；（拓展延伸）（4）如图4，在Rt ABD ∆中，90BAD ∠=︒，9AD =，1tan 3ADB ∠=，将ABD ∆沿BD 翻折，点A 落在点C 处得CBD ∆，点E ，F 分别在边AB ，AD 上，连接DE ，CF ，且DE CF ⊥．①求DECF的值； ②连接BF ，若1AE =，直接写出BF 的长度．解析：（1）1；（2）47；（3）证明见解析；（4）①53；②3295BF =【分析】（1）先根据正方形的性质可得,90AD DC A CDF =∠=∠=︒，再根据直角三角形的性质可得ADE DCF ∠=∠，然后根据三角形全等的判定定理与性质可得DE CF =，由此即可得出答案；（2）先根据矩形的性质可得90A CDE ∠=∠=︒，再根据直角三角形的性质可得ADB DCE ∠=∠，然后根据相似三角形的判定与性质即可得；（3）如图（见解析），先根据矩形的判定与性质可得,90A B CH G H A ∠=∠===∠︒，再根据直角三角形的性质、对顶角相等可得FCH EDA ∠=∠，然后根据相似三角形的判定可得DEA CFH ~，由此即可得证；（4）①如图（见解析），先证出DEA CFG ~，从而可得9DE AD CF CG CG==，再分别在Rt ABD △和Rt ADH中，解直角三角形可得AH =DH的性质可得,2DH AC AC AH ⊥=ADC 的面积公式求出CG 的长，由此即可得出答案；②先根据（4）①中，相似三角形的性质可得53DE A FG CF E ==，可求出35FG =，再根据翻折的性质可得9CD AD ==，然后在Rt CDG 中，利用勾股定理可得365DG =，从而可得65AF =，最后在Rt ABF 中，利用勾股定理即可得． 【详解】解：（1）四边形ABCD 是正方形， ,90AD DC A CDF ∴=∠=∠=︒，90ADE CDE ∴∠+∠=︒，DE CF ⊥，90DCF CDE ∴∠+∠=︒，ADE DCF ∴∠=∠，在ADE 和DCF 中，90A CDF AD DC ADE DCF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩，()ADE DCF ASA ∴≅，DE CF ∴=，1DECF∴=； （2）四边形ABCD 是矩形，90A CDE ∴∠=∠=︒， 90ADB CDB ∴∠+∠=︒，CE BD ⊥，90DCE CDB ∴∠+∠=︒， ADB DCE ∴∠=∠，在ADB △和DCE 中，90A CDE ADB DCE∠=∠=︒⎧⎨∠=∠⎩， ADB DCE ∴~， 47CE CD BD AD =∴=； （3）如图，过点C 作CH AF ⊥交AF 的延长线于点H ，∵CG EG ⊥，90A B ∠=∠=︒，∴90G H A B ∠=∠=∠=∠=︒，∴四边形ABCH 为矩形，∴AB CH =，90FCH CFH DFG FDG ∠+∠=∠+∠=︒，CFH DFG ∠=∠，FCH FDG ∴∠=∠，EDA FDG ∠=∠，FCH EDA ∴∠=∠，在DEA △和CFH △中，90EDA FCH A H ∠=∠⎧⎨∠=∠=︒⎩， ∴DEA CFH ~，∴DE AD CF CH =， ∴DE AD CF AB=， ∴DE AB CF AD ⋅=⋅；（4）①过C 作CG AD ⊥于点G ，连接AC 交BD 于点H ，∵CF DE ⊥，90BAD ∠=︒，∴90FCG CFG CFG EDA ∠+∠=∠+∠=︒，∴FCG EDA ∠=∠，在DEA △和CFG △中，90EDA FCG EAD FGC ∠=∠⎧⎨∠=∠=︒⎩， ∴DEA CFG ~， ∴DE AD CF CG=， 在Rt ABD △中，1tan 3AB ADB AD ∠==，9AD =， ∴3AB =， 在Rt ADH 中，1tan 3AH ADH DH ∠==， 设AH a =，则3DH a =， ∴222AH DH AD +=，即()22239a a +=，∴aa =∴AH =DH =由翻折的性质得：,2DH AC AC AH ⊥==1122ADC S AC DH AD CG =⋅=⋅，∴11922CG =⨯， 解得275CG =， ∴952735DE AD CF CG ===；②由（4）①已证：DEA CFG ~，53DE CF =， 53DE C AE FG F ∴==， 1AE =，513FG ∴=，解得35FG =， 由翻折的性质得：9CD AD ==， 在Rt CDG中，365DG =， 33669555AF AD FG DG ∴=--==--， 在Rt ABF中，BF === 【点睛】本题考查了正方形的性质、相似三角形的判定与性质、翻折的性质、解直角三角形等知识点，较难的是题（4）①，通过作辅助线，构造直角三角形和相似三角形是解题关键． 12．小明研究了这样一道几何题：如图1，在ABC 中，把AB 绕点A 顺时针旋转()0180a a ︒<<︒得到AB '，把AC 绕点A 逆时针旋转β得到AC '，连接B C ''．当180a β+=︒时，请问AB C ''△边B C ''上的中线AD 与BC 的数量关系是什么？以下是他的研究过程：特例验证：（1）①如图2，当ABC 为等边三角形时，猜想AD 与BC 的数量关系为AD =_______BC ；②如图3，当90BAC ∠=︒，8BC =时，则AD 长为________． 猜想论证：（2）在图1中，当ABC 为任意三角形时，猜想AD 与BC 的数量关系，并给予证明．拓展应用：（3）如图4，在四边形ABCD ，90C ∠=︒，120A B ∠+∠=︒，123BC =6CD =，63DA =P ，使PDC △与PAB △之间满足小明探究的问题中的边角关系？若存在，请画出点P 的位置（保留作图痕迹，不需要说明）并直接写出PDC △的边DC 上的中线PQ 的长度；若不存在，说明理由．解析：（1）①12；②4，（2）12AD BC =；理由见解析，（3）存在；313【分析】（1）①首先证明ADB '∆是含有30的直角三角形，可得1122AD AB BC '==，即可解决问题；②首先证明BAC B AC ''∆∆≌，根据直角三角形斜边中线定理即可解决问题． （2）AD 与BC 的数量关系为12AD BC =，如图5，延长AD 到M ，使AD DM =，连接B M '、C M '，先证四边形AC MB ''是平行四边形，再证明BAC AB M '∆∆≌，即可解决问题．（3）存在，如图6，延长AD 交BC 的延长线于M ，作BE AD ⊥于E ，做直线BC 的垂直平分线交BE 于P ，交BC 于F ，连接PA 、PD 、PC ，作PDC ∆的中线PQ ，连接DF 交PC 于O ，先证明PA PD =，PB PC =，再证明+180APD BPC ∠∠=︒，即可得出结论，再在Rt PDQ ∆中，根据勾股定理，即可求出PQ 的长．【详解】（1）①如图2，∵ABC ∆是等边三角形，把AB 绕点A 顺时针旋转α得到AB '，把AC 绕点A 逆时针旋转β得到AC '，∴===AB AC BC AB AC ''=，又∵AD 是AB C ''△边B C ''上的中线，∴=DB DC ''，∴AD B C ''⊥，即90ADB '∠=︒，∵60BAC ∠=︒，180BAC B AC ''∠+∠=︒，∴120B AC ''∠=︒，∴=30B C ''∠∠=︒，∴在ADB '∆中，90ADB '∠=︒，30B '∠=︒， ∴1122AD AB BC '==． 故答案为：12． ②如图3，∵90BAC ∠=︒，+=180BAC B AC ''∠∠︒，∴==90BAC B AC ''∠∠︒，即ABC ∆和AB C ''∆为直角三角形，∵把AB 绕点A 顺时针旋转α得到AB '，把AC 绕点A 逆时针旋转β得到AC '， ∴=AB AB '，=AC AC '，∴在ABC ∆和AB C ''∆中，===AB AB BAC B AC AC AC '''∠'⎧⎪∠⎨⎪⎩∴BAC B AC ''∆∆≌，∴=BC B C ''，∵AD 是AB C ''△边B C ''上的中线，AB C ''∆为直角三角形，∴1122AD B B C C ''==， 又∵8BC =， ∴11=8=422AD BC =⨯． 故答案为：4． （2）12AD BC =， 如图5，延长AD 到M ，使AD DM =，连接B M '、C M '，图5∵=B D DC ''，AD DM =，∴四边形AC MB ''是平行四边形，∴AC B M AC ''==，∵+=180BAC B AC ''∠∠︒，+=180B AC AB M '''∠∠︒，∴=BAC AB M '∠∠，∵=AB AB '，∴在BAC ∆和AB M '∆中，==AC B M BAC AB M AB AB ''=⎧'⎪∠∠⎨⎪⎩∴BAC AB M '∆∆≌，∴BC AM =， ∴12AD BC =． （3）存在，如图6，延长AD 交BC 的延长线于M ，作BE AD ⊥于E ，作直线BC 的垂直平分线交BE 于P ，交BC 于F ，连接PA 、PD 、PC ，作PDC ∆的中线PQ ，连接DF 交PC 于O ，图6∵+=120A B ∠∠︒，∴=180=60M A B ∠︒-∠-∠︒， ∵=90C ∠︒，∴=180=30MDC M MCD ∠︒-∠-∠︒，在Rt DCM ∆中，∵=6CD ，=90DCM ∠︒，=30MDC ∠︒， ∴3CM =43DM =60M ∠︒， 在Rt BEM ∆中，∵=90BEM ∠︒，143BM BC CM =+==30MDC ∠︒，∴1732EM BM ==， ∴33DE EM DM =-= ∵=63AD ∴=AE DE ，∵BE AD ⊥，∴PA PD =，PB PC =，在Rt CDF ∆中，∵=6CD ，=63CF∴tan 3CDF ∠=∴60CDF CPF =︒=∠∠，∴FCP CFD ∆∆≌，∴CD PF =，∵//CD PF ，∴四边形CDPF 是矩形，∴=90CDP ∠︒，∴=60ADP ADC CDP ∠∠-∠=︒，∴ADP ∆是等边三角形， ∴==63PA PD AD =，∵=60BPF CPF ∠∠=︒，∴120BPC ∠=︒，∴+180APD BPC ∠∠=︒，∴PDC ∆与PAB ∆之间满足小明探究的问题中的边角关系，在Rt PDQ ∆中，∵=90PDQ ∠︒，63PD PA AD ===，132DQ CD ==， ∴()2222=363313PQ DQ DP +=+=．【点睛】 本题考查了三角形的综合问题．掌握全等三角形的性质以及判定定理、直角三角形斜边中线定理、解直角三角形、勾股定理、中线的性质是解题的关键．在处理三角形的边旋转问题时，旋转前后边长不变，根据已知角度变化，求得线段之间关系．在证明某点是否存在问题时，先假设这点存在，能求出相关线段或坐标，即证实存在性．13．定义：如果一个三角形一条边上的高与这条边的比值是3：5，那么称这个三角形为“准黄金”三角形，这条边就叫做这个三角形的“金底”．（概念感知）（1）如图1，在ABC 中，12AC =，10BC =，30ACB ∠=︒，试判断ABC 是否是“准黄金”三角形，请说明理由．（问题探究）（2）如图2，ABC 是“准黄金”三角形，BC 是“金底”，把ABC 沿BC 翻折得到DBC △，连AB 接AD 交BC 的延长线于点E ，若点C 恰好是ABD △的重心，求AB BC的值． （拓展提升）（3）如图3，12l l //，且直线1l 与2l 之间的距离为3，“准黄金”ABC 的“金底”BC 在直线2l 上，点A 在直线1l 上．10AB BC =ABC ∠是钝角，将ABC ∠绕点C 按顺时针方向旋转()090αα︒<<︒得到A B C ''，线段A C '交1l 于点D ．①当30α=︒时，则CD =_________；②如图4，当点B 落在直线1l 上时，求AD CD 的值． 解析：（1）ABC 是“准黄金”三角形，理由见解析；（2）32910AB BC =；（3）①125615-；②355AD CD =． 【分析】 （1）过点A 作AD BC ⊥于点D ，先求出AD 的长度，然后得到61035AD BC ==，即可得到结论； （2）根据题意，由“金底”的定义得:3:5AE BC =，设3AE k =，5BC k =，由勾股定理求出AB 的长度，根据比值即可求出AB BC的值； （3）①作AE ⊥BC 于E ，DF ⊥AC 于F ，先求出AC 的长度，由相似三角形的性质，得到AF=2DF ，由解直角三角形，得到3CF DF =，则(23)35AC x =+=，即可求出DF 的长度，然后得到CD 的长度；②由①可知，得到CE 和AC 的长度，分别过点B '，D 作B G BC '⊥，DF AC ⊥，垂足分别为点G ，F ，然后根据相似三角形的判定和性质，得到DF AF AE EC =，然后求出CD 和AD 的长度，即可得到答案．【详解】解：（1）ABC 是“准黄金”三角形．理由：如图，过点A 作AD BC ⊥于点D ，∵12AC =，30ACB ∠=︒，∴162AD AC ==． ∴:6:103:5AD BC ==．∴ABC 是“准黄金”三角形．（2）∵点A ，D 关于BC 对称，∴BE AD ⊥，AE ED =．∵ABC 是“准黄金”三角形，BC 是“金底”，∴:3:5AE BC =．不防设3AE k =，5BC k =，∵点C 为ABD △的重心，∴:2:1BC CE =． ∴52k CE =，152k BE =． ∴2215329(3)22k AB k k ⎛⎫=+= ⎪⎝⎭． ∴329329:5210AB k k BC ==． （3）①作AE ⊥BC 于E ，DF ⊥AC 于F ，如图：由题意得AE=3，∵35AE BC =， ∴BC=5， ∵10AB BC =， ∴10AB ，在Rt △ABE 中，由勾股定理得：22(10)31BE =-=，∴156EC =+=，∴223635AC +=∵∠AEC=∠DFA=90°，∠ACE=∠DAF ，∴△ACE ∽△DAF ，∴3126AE E D C F AF ===， 设DF x =，则2AF x =，∵∠ACD=30°，∴3CF x =，。
上海民办茸一中学中考数学几何综合压轴题易错专题
上海民办茸一中学中考数学几何综合压轴题易错专题一、中考数学几何综合压轴题1．在△ABC中，AD为BC边上的中线，E为AD上一动点，设DE＝nEA，连接CE并延长，交AB于点F．（1）尝试探究：如图1，当∠BAC＝90°，∠B＝30°，DE＝EA时，BF，BA之间的数量关系是；（2）类比延伸：如图2，当△ABC为锐角三角形，DE＝EA时，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（3）拓展迁移：如图3，当△ABC为锐角三角形，DE＝nEA时，请直接写出BF，BA之间的数量关系．解析：（1）23BFAB=；（2）仍然成立，见解析；（3）221BF nAB n=+【分析】（1）尝试探究：过点D作DM CF，交AB于M，可证BDM BCF∽,，AFE AMD∽，可得11,22BD BM AE AFBC BF AD AM====，可证BM MF AF＝＝，可得BF，BA之间的数量关系；（2）类比延伸：过点D作DM CF，交AB于M，可证BDM BCF∽，AFE AMD∽，可得11,22BD BM AE AFBC BF AD AM====，可证BM MF AF＝＝，可得BF BA，之间的数量关系；（3）拓展迁移：过点D作DM CF，交AB于M，由平行线分线段成比例可得BM MF FM nAF＝，＝，可得22AB nAF AF BF nAF+＝，＝，即可求BF BA，之间的数量关系．【详解】解：（1）尝试探究如图，过点D作DM CF，交AB于M∵AD 是中线，AE DE ＝∴1122BD CD BC AE AD ＝＝，＝∵DM CF ，∴BDM BCF ∽，AFE AMD ∽∴11,22BD BM AE AF BC BF AD AM ==== ∴22BF BM AM AF ＝，＝ ∴BM MF AF FM ＝，＝ ∴BM MF AF ＝＝ ∴23BF AB = （2）类比延伸： 结论仍然成立， 理由如下： 如图，过点D 作DMCF ，交AB 于M∵AD 是中线,AE DE ＝∴1122BD CD BC AE AD ＝＝，＝∵DM CF ，∴BDM BCF ∽，AFE AMD ∽∴11,22BD BM AE AF BC BF AD AM ==== ∴22BF BM AM AF ＝，＝ ∴BM MF AF FM ＝，＝ ∴BM MF AF ＝＝ ∴23BF AB = （3）拓展迁移 如图，过点D 作DMCF ，交AB 于M∵DM FC ，且BD CD ＝ ∴1BD BMDC FM== ∴BM MF ＝∵DM CF DE nEA ，＝ ∴1AE AF DE FM n== ∴FM nAF ＝ ∴BM MF nAF ＝＝∴2AB nAF AF +＝ 2BF nAF ＝ ∴221BF nAB n =+ 【点睛】本题主要考查了相似三角形的判定和性质综合，根据题干条件作出辅助线并得到对应的相似三角形是解决本题的关键.2．定义：如图（1），点P 沿着直线l 翻折到P '，P 到P '的距离PP '叫做点P 关于l 的“折距”．已知，如图（2），矩形ABCD 中，,AB x BC y ==，等腰直角AEG △中，6AE AG ==，点G 在AD 上，E 、B 在AD 的两侧，点F 为EG 的中点，点P 是射线AD 上的动点，把AEG △沿着直线BP 翻折到A E G '''，点F 的对应点为F '，理解：（1）当4,9x y ==时，①若点A '在边BC 上，则点A 关于BP 的“折距”为______； ②若点E 关于BP 的“折距”为12，则AP =______．应用：（2）若9y =，当点E '、G '、C 、D 能构成平行四边形时，求出此时x 的值 拓展：（3）当7,13x y ==时，设点E 关于BP 的“折距”为t ，直接写出当射线A F ''与边BC有公共点时t 的范围．解析：（1）①42；②3；（2）62x =；（3）392724t ＜＜ 【分析】（1）①根据垂直平分线的性质和正方形的性质计算即可；②设EE '和BP 相交于M ，证明ABP MBE △△，即可得解； （2）根据平行四边形的性质求解即可；（3）当A '在BC 上时为最小值，当F '在BC 上时为最大值，通过相似三角形的判定与性质求解即可； 【详解】（1）当4,9x y ==时，①若A '在BC 上时，则AB BA '=， 此时四边形ABA P '为正方形，在Rt ABA '中，2242AA AB BA ''=+=， ∵点A 关于BP 的“折距”为AA '， ∴点A 关于BP 的“折距”为42；②由题意可知12EE '=， 设EE '和BP 相较于M ， 则EM BP ⊥，且162EM EE '==， 在ABP △与MBE △中，ABP MBEBAP BME ∠=∠⎧⎨∠=∠⎩， ∴ABP MBE △△， ∴AB MBAP ME=， 又()224668MB =+-=，即486AP =， 解得3AP =；（2）当点E '、G '、C 、D 能构成平行四边形时，则G E '与DC 平行且相等， 在Rt AEG 中，226662EG =+ 又EG E G ''=，∴62DC AB E G EG ''==== 即62x =；（3）当7,13x y ==时，点E 关于BP 的“折距”为t ，且射线A F ''与边BG 的公共点范围如图所示， 当A '在BC 上时为最小值，当F '在BC 上时为最大值， ∴6713EB =+=， ∴EB BC =， ∴BCE 为等腰直角三角形，E 到BP 的距离为2t ，当A '在BC 上时，72AA '=设AA '与BP 交于点Q ，EE '与BP 交于点N ， ∴722AQ =又ABQ EBN △△， ∴BA EQBE BN=， ∴1322BE AQ EN BA == ∴132t = 当F '在BC 上时， ∵F 为EG 中点， 如图FM BC ⊥于M ，∴333913444MF BE ==⨯=，33944MC BE ==， ∴3924FF '=， ∴t 的取值范围为392724t ＜＜；【点睛】本题主要考查了四边形综合应用，结合勾股定理和相似三角形的判定与性质计算是解题的关键． 3．（了解概念）定义：在平面直角坐标系xOy 中，组成图形的各点中，与点Р所连线段最短的点叫做点Р关于这个图形的短距点，这条最短线段的长度叫做点Р到这个图形的短距．（理解运用）（1）已知点()3,0P -，以原点为圆心，l 为半径作O ，则点Р关于O 的短距点的坐标是 ；（2）如图，点(3P ，等边三角形OAB 的顶点A 的坐标为()6,0，顶点B 在第一象限，判断点Р关于OAB 的短距点的个数，并说明理由； （拓展提升）（3）已知(),6P p p -+，()6,0A ，()0,6B ，点C 在第一象限内，且75CBO ∠=︒，90ACB ∠=︒，若点Р到四边形OACB 的短距大于2，请直接写出p 的取值范围．解析：（1）(-1，0)；（2）点Р关于OAB 的短距点的个数有3个；（3）当p ＜22p ＜4或p ＞2Р到四边形OACB 的短距大于2． 【分析】（1）连接PO ，交O 于点M ，点M 即是点Р关于O 的短距点，进而即可求解； （2）根据题意得点P 是三角形OAB 的中心，进而即可求解；（3）由题意得点P ，A ，B 在直线y =-x +6上，以点P 为圆心，半径长为2画圆，分3种情况：①当点P 在AB 的延长线上，圆P 过点B 时，②当点P 在线段AB 上，圆P 与BC 相切于点N ，过点P 作PM ⊥y 轴，③当点P 在BA 的延长线上，圆P 过点A 时，过点P 作PM ⊥y 轴，分别求解，即可得到答案． 【详解】解：（1）连接PO ，交O 于点M ，点M 即是点Р关于O 的短距点， ∵()3,0P -，、O 的半径为1， ∴M (-1，0)， 故答案是：(-1，0)；（2）∵点()3,3P ，等边三角形OAB 的顶点A 的坐标为()6,0， ∴点P 是三角形OAB 的中心，∴点P 到OA ，OB ，OC 的三条垂线段最短，三条垂线段都等于3， ∴点Р关于OAB 的短距点的个数有3个； （3）∵(),6P p p -+，()6,0A ，()0,6B ， ∴点P ，A ，B 在直线y =-x +6上， ∴∠ABO =∠BAO =45°，∵点C 在第一象限内，且75CBO ∠=︒，90ACB ∠=︒， ∴∠ABC =75°-45°=30°，以点P 为圆心，半径长为2画圆，如图所示：当点P 在AB 的延长线上，圆P 过点B 时，过点P 作PM ⊥y 轴，∵PB =2，∠PBM =45°， ∴PM 22 ∴p ＜2Р到四边形OACB 的短距大于2；①当点P 在线段AB 上，圆P 与BC 相切于点N ，过点P 作PM ⊥y 轴，则BP =2PN =2×2=4，PM =BP ×222②当点P在线段AB上，圆P与OA相切于点N，过点P作PM⊥y轴，则AP=2PN=22，BP=AB-AP=62-22=42，PM= BP×22=42×22=4，∴22＜p＜4时，点Р到四边形OACB的短距大于2；③当点P在BA的延长线上，圆P过点A时，过点P作PM⊥y轴，则PM=（62+2）×22=6+2，∴p＞6+2时，点Р到四边形OACB的短距大于2；综上所述：当p＜-2或22＜p＜4或p＞6+2时，点Р到四边形OACB的短距大于2．【点睛】本题主要考查图形与坐标以及圆的综合题，根据题意画出图形，掌握圆与直线相切的性质是解题的关键．4．平面上，矩形ABCD与直径为QP的半圆K如图摆放，分别延长DA和QP交于点O，且∠BOQ＝60°，OQ＝OD＝3，OP＝2，OA＝AB＝1．让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向形如旋转，设旋转角为α（0°≤α≤60°）．发现（1）当α＝0°，即初始位置时，点P____直线AB上．（填“在”或“不在”）求当α是多少时，OQ经过点B？（2）在OQ旋转过程中．简要说明α是多少时，点P，A间的距离最小？并指出这个最小值：（3）如图，当点P恰好落在BC边上时．求α及S阴影．拓展如图．当线段OQ与CB边交于点M，与BA边交于点N时，设BM＝x（x＞0），用含x的代数式表示BN的长，并求x的取值范围．探究当半圆K与矩形ABCD的边相切时，求sin α的值．解析：发现：（1）在，15°；（2）当α=60°时，最小距离为1；（3）30°，3=+1624S π阴影．拓展：x 的范围是0221x <≤-； 探究：sinα的值为43310-或62110-或32． 【详解】 解：发现（1）在；当OQ 过点B 时，在Rt △OAB 中，AO ＝AB ， 得∠DOQ ＝∠ABO ＝45°， ∴α＝60°－45°＝15°． （2）如图3．连AP ，有OA ＋AP≥OP ，当OP 过点A ，即α＝60°时等号成立． ∴AP≥OP －OA ＝2－1＝1．∴当α＝60°时．P ，A 间的距离最小． ∴PA 的最小值为1． （3）如图3，设半圆K 与PC 交点为R ，连接RK ，过点P 作PH ⊥AD 于点H ，过点R 作RE ⊥KQ 于点E ． 在Rt △OPH 中，PH ＝AB ＝1，OP ＝2，∴∠POH ＝30°， ∴α＝60°－30°＝30°．由AD//BC 知，∠RPQ ＝∠POH ＝30°． ∴∠RKQ ＝2×30°＝60°．2160236024KRQS ππ⎛⎫⋅ ⎪⎝⎭∴==扇形， 在Rt △RKE 中，3sin 604RE RK =⋅︒=， 13·216PRK S PK RE ∆∴==， 32416S π∴=+阴影； 拓展如图5，∠OAN ＝∠MBN ＝90°，∠ANO ＝∠BNM ，所以△AON ∽△BMN ． ∴AN AO BN BM =，即11BN BN x-=， ∴1xBN x =+． 如图4，当点Q 落在BC 上时，x 取最大值，作QF ⊥AD 于点F ． 2222311221BQ AF OQ QF AO ==--=--=-．∴x 的范围是0221x <≤-．【注：如果考生答“221x ≤-或221x <-”均不扣分】探究半圆与矩形相切，分三种情况：①如图5，半圆K 与BC 切于点T ，设直线KT 与AD 和OQ 的初始位置所在直线分别交于S ，O′，则∠KSO ＝∠KTB ＝90°，作KG ⊥OO′于点G ． Rt △OSK 中，222253222OS OK SK ⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭．Rt △OSO′中，tan 6023SO OO ︒''==，3232KO '=-． Rt △KGO′中，∠O′=30°，KG=13=3-.24KO 'Rt △OGK 中，334334sin 5102KGOKα--===②半圆K 与AD 切于点T ，如图6，同理可得 11()22sin 5522O K O T KT KG OKα''-=== 225113222621510⎛⎫⎛⎫-⨯-⎪ ⎪-⎝⎭⎝⎭==．③当半圆K 与CD 相切时，成Q 与点D 重合，且为切点． ∴α＝60°，∴3sin sin 60α=︒= 综上述，sinα433-621-3考点：圆，直线与圆的位置关系，锐角三角函数，相似，三角形法则求最值5．已知△ABC是等腰三角形，AB=AC．（1）特殊情形：如图1，当DE∥BC时，有DB EC．（填“＞”，“＜”或“=”）（2）发现探究：若将图1中的△ADE绕点A顺时针旋转α（0°＜α＜180°）到图2位置，则（1）中的结论还成立吗？若成立，请给予证明；若不成立，请说明理由．（3）拓展运用：如图3，P是等腰直角三角形ABC内一点，∠ACB=90°，且PB=1，PC=2，PA=3，求∠BPC的度数．解析：（1）=；（2）成立，证明见解析；（3）135°.【分析】试题（1）由DE∥BC，得到DB ECAB AC=，结合AB=AC，得到DB=EC；（2）由旋转得到的结论判断出△DAB≌△EAC，得到DB=CE；（3）由旋转构造出△CPB≌△CEA，再用勾股定理计算出PE，然后用勾股定理逆定理判断出△PEA是直角三角形，再简单计算即可．【详解】（1）∵DE∥BC，∴DB ECAB AC=，∵AB=AC，∴DB=EC，故答案为=，（2）成立．证明：由①易知AD=AE，∴由旋转性质可知∠DAB=∠EAC，又∵AD=AE，AB=AC∴△DAB≌△EAC，∴DB=CE，（3）如图，将△CPB绕点C旋转90°得△CEA，连接PE，∴△CPB≌△CEA，∴CE=CP=2，AE=BP=1，∠PCE=90°，∴∠CEP=∠CPE=45°，在Rt△PCE中，由勾股定理可得，PE=22，在△PEA中，PE2=（22）2=8，AE2=12=1，PA2=32=9，∵PE2+AE2=AP2，∴△PEA是直角三角形∴∠PEA=90°，∴∠CEA=135°，又∵△CPB≌△CEA∴∠BPC=∠CEA=135°．【点睛】考点：几何变换综合题；平行线平行线分线段成比例.6．（问题情境）如图1，点E是平行四边形ABCD的边AD上一点，连接BE、CE．求证：BCE 1S2=S平行四边形ABCD．（说明：S表示面积）请以“问题情境”为基础，继续下面的探究（探究应用1）如图2，以平行四边形ABCD的边AD为直径作⊙O，⊙O与BC边相切于点H，与BD相交于点M．若AD＝6，BD＝y，AM＝x，试求y与x之间的函数关系式．（探究应用2）如图3，在图1的基础上，点F在CD上，连接AF、BF，AF与CE相交于点G，若AF＝CE，求证：BG平分∠AGC．（迁移拓展）如图4，平行四边形ABCD中，AB：BC＝4：3，∠ABC＝120°，E是AB的中点，F在BC上，且BF：FC＝2：1，过D分别作DG⊥AF于G，DH⊥CE于H，请直接写出DG：DH的值．解析：【问题情境】见解析；【探究应用1】18yx=；【探究应用2】见解析；【迁移拓1927【分析】（1）作EF⊥BC于F，则S△BCE＝12BC×EF，S平行四边形ABCD＝BC×EF，即可得出结论；（2）连接OH，由切线的性质得出OH⊥BC，OH＝12AD＝3，求出平行四边形ABCD的面积＝AD×OH＝18，由圆周角定理得出AM⊥BD，得出△ABD的面积＝12BD×AM＝12平行四边形的面积＝9，即可得出结果；（3）作BM ⊥AF 于M ，BN ⊥CE 于N ，同图1得：△ABF 的面积＝△BCE 的面积＝12平行四边形ABCD 的面积，得出12AF×BM ＝12CE×BN ，证出BM ＝BN ，即可得出BG 平分∠AGC ．（4）作AP ⊥BC 于P ，EQ ⊥BC 于Q ，由平行四边形的性质得出∠ABP ＝60°，得出∠BAP ＝30°，设AB ＝4x ，则BC ＝3x ，由直角三角形的性质得出BP ＝12AB ＝2x ，BQ ＝12BE ，AP ＝＝，由已知得出BE ＝2x ，BF ＝2x ，得出BQ ＝x ，EQ ，PF ＝4x ，QF ＝3x ，QC ＝4x ，由勾股定理求出AF ＝，CE ，连接DF 、DE ，由三角形的面积关系得出AF×DG ＝CE×DH ，即可得出结果． 【详解】（1）证明：作EF ⊥BC 于F ，如图1所示： 则S △BCE ＝12BC×EF ，S 平行四边形ABCD ＝BC×EF ， ∴12BCEABCDSS =．（2）解：连接OH ，如图2所示： ∵⊙O 与BC 边相切于点H ， ∴OH ⊥BC ，OH ＝12AD ＝3，∴平行四边形ABCD 的面积＝AD×OH ＝6×3＝18， ∵AD 是⊙O 的直径， ∴∠AMD ＝90°， ∴AM ⊥BD ，∴△ABD 的面积＝12BD×AM ＝12平行四边形的面积＝9， 即12xy ＝9，∴y 与x 之间的函数关系式y ＝18x； （3）证明：作BM ⊥AF 于M ，BN ⊥CE 于N ，如图3所示：同图1得：△ABF 的面积＝△BCE 的面积＝12平行四边形ABCD 的面积， ∴12AF×BM ＝12CE×BN ，∵AF ＝CE ， ∴BM ＝BN ， ∴BG 平分∠AGC ．（4）解：作AP ⊥BC 于P ，EQ ⊥BC 于Q ，如图4所示： ∵平行四边形ABCD 中，AB ：BC ＝4：3，∠ABC ＝120°，∴∠ABP ＝60°，∴∠BAP ＝30°，设AB ＝4x ，则BC ＝3x ，∴BP ＝12AB ＝2x ，BQ ＝12BE ，AP ＝3BP ＝23x ， ∵E 是AB 的中点，F 在BC 上，且BF ：FC ＝2：1， ∴BE ＝2x ，BF ＝2x ， ∴BQ ＝x ，∴EQ ＝3x ，PF ＝4x ，QF ＝3x ，QC ＝4x ，由勾股定理得：AF ＝22AP PF +＝27x ，CE ＝22EQ QC +＝19x ， 连接DF 、DE ，则△CDE 的面积＝△ADF 的面积＝12平行四边形ABCD 的面积， ∴AF×DG ＝CE×DH ，∴DG ：DH ＝CE ：AF ＝19x :27x 19:27=．【点睛】本题是圆的综合题目，考查了圆周角定理、平行四边形的性质、三角形面积公式、含30°角的直角三角形的性质、勾股定理、角平分线的判定等知识；本题综合性强，需要添加辅助线，熟练掌握平行四边形的性质和勾股定理是解题的关键．7．如图所示，在△ABC 中，AB BC =，D 、E 分别是边AB 、BC 上的动点，且BD BE =，连结AD 、AE ，点M 、N 、P 分别是CD 、AE 、AC 的中点，设B α∠=．（1）观察猜想①在求MNCE的值时，小明运用从特殊到一般的方法，先令60α=︒，解题思路如下： 如图1，先由,AB BC BD BE ==，得到CE AD =，再由中位线的性质得到PM PN =，60NPM ∠=︒，进而得出△PMN 为等边三角形，∴12MN NP CE CE ==． ②如图2，当90α=︒，仿照小明的思路求MNCE的值； （2）探究证明 如图3，试猜想MNCE的值是否与()0180αα︒<<︒的度数有关，若有关，请用含α的式子表示出MNCE，若无关，请说明理由； （3）拓展应用如图4，2,36AC B =∠=︒，点D 、E 分别是射线AB 、CB 上的动点，且AD CE =，点M 、N 、P 分别是线段CD 、AE 、AC 的中点，当1BD =时，请直接写出MN 的长． 解析：（1）②2MN CE =2）MN CE 的值与α的度数有关，sin 2MN CE α=；（3）MN 的长55-35+ 【分析】（1）②先根据线段的和差求出AD CE =，再根据中位线定理、平行线的性质得出,45PM PN APN CPM =∠=∠=︒，从而可得出90NPM ∠=︒，然后根据等腰直角三角形的性质即可得；（2）参照题（1）的方法，得出PMN 为等腰三角形和NPM ∠的度数，再利用等腰三角形的性质即可求出答案；（3）分两种情况：当点D 、E 分别是边AB 、CB 上的动点时和当点D 、E 分别是边AB 、CB 的延长线上的动点时，如图（见解析），先利用等腰三角形的性质与判定得出,ABC BCE CAB AFC ∠=∠∠=∠，再根据相似三角形的判定与性质得出BC 、CE 的长，由根据等腰三角形的三线合一性得出1,182BP AC CBP ABC ⊥∠=∠=︒，从而可得sin18︒的值，最后分别利用（2）的结论即可得MN 的长． 【详解】 （1）②,AB BC BD BE ==∴AD CE = ,90AB BC B =∠=︒∴ABC 为等腰直角三角形，45ACB CAB ∠=∠=︒∵点M 、N 、P 分别是CD 、AE 、AC 的中点 11//,,//,22PN CE PN CE PM AD PM AD ∴==,45,45PM PN APN ACB CPM CAB ∴=∠=∠=︒∠=∠=︒∴18090NPM APN CPM ∠=︒-∠-∠=︒ ∴PMN 为等腰直角三角形，∴222MN PN CE == 即22MN CE =； （2）MNCE的值与α的度数有关，求解过程如下： 由（1）可知，PM PN =，即PMN 为等腰三角形180180NPM APN CPM ACB CAB B α∠=︒-∠-∠=︒-∠-∠=∠=如图5，作PH MN ⊥ 则11,222NH MN NPH NPM α=∠=∠= 在Rt NPH 中，sin NHNPH PN∠=，即12sin 122MN CE α=则sin 2MN CE α=；（3）依题意，分以下两种情况： ①当点D 、E 分别是边AB 、CB 上的动点时如图6，作ACB ∠的角平分线交AB 边于点F ，并连结BP2,36,AC ABC AB AC =∠=︒=72ACB CAB ∴∠=∠=︒136,722ACE BCE ACB AFC ABC BCE ∴∠=∠=∠=︒∠=∠+∠=︒,ABC BCE CAB AFC ∴∠=∠∠=∠2BF CF AC ∴===，ACF ABC ~AF ACAC AB∴=，即2AC AF AB =⋅ 设==AB BC x ，则2AF AB BF x =-=- 22(2)x x ∴=-解得15x 或15x =-即15BC =+1515CE BC BE BC BD ∴=-=-=+-=由（2）可知，36sin sin182MN CE ︒==︒ sin185sin18MN CE ∴=⋅︒=︒点P 是AC 上的中点1,182BP AC CBP ABC ∴⊥∠=∠=︒，112CP AC ==（等腰三角形的三线合一）在Rt CBP 中，sin CP CBP BC ∠=，即151sin18415-︒==+51555sin18544MN --∴=︒=⨯=②如图7，当点D 、E 分别是边AB 、CB 的延长线上的动点时 同理可得：15BC =+15125CE BC BE BC BD ∴=+=+=++=+5135sin18(25)44MN CE -+∴=⋅︒=+⨯=综上，MN 的长为554-或354+．【点睛】本题考查了中位线定理、平行线的性质、相似三角形的判定与性质、等腰三角形的性质、解直角三角形等知识点，较难的是题（3），依据题意，正确分两种情况，并结合题（2）的结论是解题关键．8．（感知）如图1，在平面直角坐标系中，点C 的坐标为(0,0.5)，点A 的坐标为(1,0)，将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ，过点B 作BM y ⊥轴，垂足为点M ，易知AOC CMB ∆∆≌，得到点B 的坐标为(0.5,1.5)．（探究）如图2，在平面直角坐标系中，点A 的坐标为(1,0)，点C 的坐标为(0,)(0)m m >，将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ．（1）求点B 的坐标．（用含m 的代数式表示）（2）求出BC 所在直线的函数表达式．（拓展）如图3，在平面直角坐标系中，点A 的坐标为(1,0)，点C 在y 轴上，将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ，连结BO 、BA ，则BO BA +的最小值为_______．解析：【探究】（1）点B 坐标为(,1)m m +；（2）1y x m m=+；【拓展】5． 【分析】探究:（1）证明△AOC ≌△CMB （AAS ），即可求解；（2）根据点B 的坐标为（m ，m+1），点C 坐标()0,m ，即可求解；拓展：BO+BA=2222(1)(1)(1)m m m m +++-++，BO+BA 的值，相当于求点P （m ，m ）到点M （1，-1）和点N （0，-1）的最小值，即可求解．【详解】解：探究：（1）过点B 作BM y ⊥轴，垂足为点M ．BMC 90∠∴=︒，MCB B 90∠∠∴+=︒．线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ，BCA 90CB CA ∠∴=︒=，．MCB ACO 90∠∠∴+=︒．B ACO ∠∠∴=．ACO 90∠=︒，ΔAOC ΔCMB ∴≌，MC OA,MB OC ∴==．点C 坐标()0,m ，点A 坐标()1,0，∴点B 坐标为()m,m 1+（2）∵点B 的坐标为（m ，m+1），点C 为（0，m ），设直线BC 为：y=kx+b ，1b m km b m =⎧⎨+=+⎩，解得：1k m b m ⎧=⎪⎨⎪=⎩， ∴1y x m m=+； 则BC 所在的直线为：1y x m m=+； 拓展：如图作BH ⊥OH 于H ．设点C 的坐标为（0，m ），由（1）知：OC=HB=m ，OA=HC=1，则点B （m ，1+m ），则：BO+BA=2222(1)(1)(1)m m m m +++-++，BO+BA 的值，相当于求点P （m ，m ）到点M （1，-1）和点N （0，-1）的最小值，相当于在直线y=x 上寻找一点P （m ，m ），使得点P 到M （0，-1），到N （1，-1）的距离和最小，作M 关于直线y=x 的对称点M′（-1，0），易知PM+PN=PM′+PN≥NM′， M′N=22(11)(01)5--++=，故：BO+BA 的最小值为5，故答案为：5．【点睛】本题为一次函数综合题，主要考查的是三角形全等的思维拓展，其中拓展，将BO+BA 的值转化点P （m ，m ）到点M （1，-1）和点N （0，-1）的最小值，是本题的新颖点 9．（基础巩固）（1）如图1，在ABC 中，M 是AB 的中点，过B 作//BD AC ，交CM 的延长线于点D ．求证：AC BD =；（尝试应用）（2）在（1）的情况下载线段CM 上取点E （如图2），已知34BE AC ==，2CE =，4EM =，求tan D ；（拓展提高）（3）如图3，菱形ABCD 中 ，点P 在对角线AC 上，且2CP AP =，点E 为线段DP 上一点，BE BC =．若2PE =，3PD =，求菱形ABCD 的边长．解析：（1）证明见解析；（2）35；（321 【分析】(1)证明()ACM BDM AAS △≌△，即可求解；(2)过点B 作BH CD ⊥于点H ，得到()22234253BH BD DH --=，进而求解；(3) 延长DP 交AB 于G ，交CB 延长线于F ，连结CE ，可得BE BF BC ==，所以90CEF ∠=︒，设菱形边长为x ，进而可得出结论．【详解】解：（1）证明：//AC BD ，A MBD ∴∠=∠，ACM D ∠=∠，M 是AB 的中点，AM MB ∴=，ACM BDM ∴△≌△，AC BD ∴=．（2）由（1）得6CM MD CE EM ==+=，34BE AC BD ===，作BH CD ⊥，垂足为H ，如图所示：5EH HD ∴==，在Rt BDH △中， ()22234253BH BD DH =-=-=，3tan 5BH D HD ∴==． （3）延长DP 交AB 于G ，交CB 延长线于F ，连结CE ，如图所示：//,AB CD,APG CPD ∴∽1,2AG PG AP CD PD CP ∴=== 1113,,2222AG CD AB PG PD ∴==== 393,8,22FG DG FE ∴==+== 过B 作BH CD ⊥于,H 由//,AB CD∴ BE BF BC ==，90CEF ∴∠=︒，设菱形边长为x ，在Rt CDE △和Rt CFE ∆中22222CD DE CE CF EF -==-，即221464x x -=-，解得21x =∴菱形ABCD 21【点睛】本题考查四边形综合题，主要考查了菱形的性质、相似三角形的判定与性质，解直角三角形、勾股定理的运用，正确作出辅助线是解题的关键．10．如图，在ABC ∆中，90ACB ∠=︒，2AC BC ==，点D 是射线BC 上一动点，过点B 作BE AD ⊥，垂足为点E ，交直线AC 于点P ．（问题发现）（1）如图1，若点D 在BC 的延长线上，试猜想AP ，CD ，BC 之间的数量关系为_______；（类比探究）（2）如图2，若点D 在线段BC 上，试猜想AP ，CD ，BC 之间的数量关系，并说明理由；（拓展应用）（3）当点E 为BP 的中点时，直接写出线段CD 的长度．解析：（1）BC AP CD =+；（2）AP BC CD =+，理由见解析；（3）CD 的长为22或222【分析】（1）通过证明BPC ADC ≅，可得CP CD =，再根据,AP CP AC BC AC +==，即可得证AP CD BC +=；（2）通过证明()ACD BCP ASA ∆∆≌，可得CD CP =，再根据AP AC CP =+，即可得证AP BC CD =+；（3）分两种情况：①当点D 在线段BC 上时；②当点D 在线段BC 的延长线上时，求解即可．【详解】解：（1）如图1，若点D 在BC 的延长线上，且点E 在线段AD 上，AP ，CD ，BC 之间的数量关系为BC AP CD =+，理由如下90ACB ︒∠=9018090PBC BPC ACD ACB ︒︒︒∴∠+∠=∠=-∠=，BE AD ⊥，垂足为点E90BED ︒∴∠=90PBC ADC ︒∴∠+∠=BPC ADC ∴∠=∠在△BPC 和△ADC 中90BPC ADC BCP ACD BC AC ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩BPC ADC ∴≅CP CD ∴=,AP CP AC BC AC +==AP CD BC ∴+=（2）AP BC CD =+．理由如下，如图∵90ACB ∠=︒，BE AD ⊥∴90P PAE ∠+∠=︒，90P PBC ∠+∠=︒，∴PAE PBC ∠=∠∵90ACB BCP ∠=∠=︒，AC BC =∴()ACD BCP ASA ∆∆≌∴CD CP =∵AP AC CP =+∴AP BC CD =+ （3）CD 的长为222-或222+①当点D 在线段BC 上时∵()APE ABE SAS ∆∆≌，∴22AP AB ==∴222CP AP AC =-=-∴222CD CP ==-②当点D 在线段BC 的延长线上时222CD CP AP AC ==+=+【点睛】本题考查了全等三角形的综合问题，掌握全等三角形的性质以及判定定理是解题的关键． 11．德国著名的天文学家开普勒说过：“几何学里有两件宝，一个是勾股定理，另一个是黄金分割．如果把勾股定理比作黄金矿的话，那么可以把黄金分割比作钻石矿”．如图①，点C 把线段AB 分成两部分，如果510.6182CB AC -=≈，那么称点C 为线段AB 的黄金分割点．（1）特例感知：在图①中，若100AB =，求AC 的长；（2）知识探究：如图②，作⊙O 的内接正五边形：①作两条相互垂直的直径MN 、AI ；②作ON 的中点P ，以P 为圆心，PA 为半径画弧交OM 于点Q ；③以点A 为圆心，AQ 为半径，在⊙O 上连续截取等弧，使弦AB BC CD DE AQ ====，连接AE ；则五边形ABCDE 为正五边形．在该正五边形作法中，点Q 是否为线段OM 的黄金分割点？请说明理由．（3）拓展应用：国旗和国徽上的五角星是革命和光明的象征，是一个非常优美的几何图形，与黄金分割有着密切的联系．延长题（2）中的正五边形ABCDE 的每条边，相交可得到五角星，摆正后如图③，点E 是线段PD 的黄金分割点，请利用题中的条件，求cos72︒的值．解析：（1）61.8；（2）是，理由见解析；（351- 【分析】（1）根据黄金分割的定义求解即可；（2）设⊙O 的半径为a ，则OA =ON =OM =a ，利用勾股定理求出PA ，继而求出OQ ，MQ ，即可作出判断；（3）先求出正五边形的每个内角，即可得到∠PEA =∠PAE =18010872︒-︒=︒，根据已知条件可知cos 72°=12AE PE，再根据点E 是线段PD 的黄金分割点，即可求解．【详解】解：（1）∵510.618CB AC -=≈， ∴510.618A C AC B A --=≈，即510.6181020AC AC --=≈， 解得：AC ≈61.8；（2）Q 是线段OM 的黄金分割点，理由如下：设⊙O 的半径为a ，则OA =ON =OM =a ，∴OP =1122ON a =， ∴225PA OP OA PQ =+==， ∴OQ =PQ -OP 51-， ∴MQ =OM -OQ 35-， 355151MQ OQ --==- ∴Q 是线段OM 的黄金分割点；（3）正五边形的每个内角为：()521801085-⨯︒=︒，∴∠PEA =∠PAE =18010872︒-︒=︒，∴cos 72°=12AE PE，∵点E 是线段PD 的黄金分割点，∴51DE PE -= 又∵AE =ED ，∴512AE PE -=， ∴cos 72°=15124AE PE -=． 【点睛】本题考查黄金分割、勾股定理、锐角三角函数，解题的关键是读懂题意正确解题． 12．如图1，边长为4的正方形与边长为()14a a <<的正方形CFEG 的顶点C 重合，点E 在对角线AC 上．问题发现（1）如图1，AE 与BF 的数量关系为______．类比探究（2）如图2，将正方形CFEG 绕点C 旋转m 度（030m ︒<<︒）．请问（1）中的结论还成立吗？若不成立，请说明理由．拓展延伸（3）若F 为BC 的中点，在正方形CFEG 的旋转过程中，当点A ，F ，G 在一条直线上时，线段AG 的长度为______．解析：（1）2AE BF ；（2）成立，见解析；（3302302【分析】 问题发现：证出AB ∥EF ，由平行线分线段成比例定理得出2AE CE BF CF =论；类比探究：证明△ACE ∽△BCF ，得出2AE AC BF CB== 拓展延伸：分两种情况，连接CE 交GF 于H ，由正方形的性质得出AB=BC=4，242AC ==2GF CE CF =，GH=HF=HE=HC ，得出122CF BC ==，22GF CE ==2HF HE HC ===2230AH AC HC -得出答案．【详解】[问题发现]解：2AE BF =，理由如下：∵四边形ABCD 和四边形CFEG 是正方形，∴∠B=∠CFE=90°，∠FCE=∠BCA=45°，CE=2CF ，CE ⊥GF ， ∴AB ∥EF ， ∴2AE CE BF CF∴==， 2AE BF ∴=； 故答案为：2AE BF ∴=；[类比探究]解：上述结论还成立，理由如下： 连接CE ，如图2所示：∵∠FCE=∠BCA=45°，∴∠BCF=∠ACE=45°-∠ACF ， 在Rt △CEG 和Rt △CBA 中，2,2CE CF CA CB ==，2CE CA CF CB∴==， ∴△ACE ∽△BCF ， 2AE AC BF CB ∴==， 2AE BF ∴=；[拓展延伸]解：分两种情况：①如图3所示：连接CE 交GF 于H ，∵四边形ABCD 和四边形CFEG 是正方形， ∴AB=BC=4，22，2，HF=HE=HC ， ∵点F 为BC 的中点，∴CF=12BC=2，22∴2222AH AC HC=-=-=，(42)(2)30∴302=+=+；AG AH HG②如图4所示：连接CE交GF于H，同①得：GH=HF=HE=HC=2，∴2222AH AC HC=-=-=，(42)(2)30∴302=-=-；AG AH HG故答案为：302-．+或302【点睛】本题是四边形综合题目，考查了正方形的性质、旋转的性质、平行线分线段成比例定理、相似三角形的判定与性质、勾股定理等知识；熟练掌握正方形的性质，证明三角形相似是解题的关键．13．问题背景：已知的顶点在的边所在直线上（不与，重合）．交所在直线于点，交所在直线于点．记的面积为，的面积为．（1）初步尝试：如图①，当是等边三角形，，，且，时，则；（2）类比探究：在（1）的条件下，先将点沿平移，使，再将绕点旋转至如图②所示位置，求的值；（3）延伸拓展：当是等腰三角形时，设．（I）如图③，当点在线段上运动时，设，，求的表达式（结果用，和的三角函数表示）．（II）如图④，当点在的延长线上运动时，设，，直接写出的表达式，不必写出解答过程．解析：(1)12;(2)12；（3）（ab）2sin2α．（ab）2sin2α．【解析】试题分析：（1）首先证明△ADM，△BDN都是等边三角形，可得S1=•22=，S2=•（4）2=4，由此即可解决问题；（2）如图2中，设AM=x，BN=y．首先证明△AMD∽△BDN，可得，推出，推出xy=8，由S1=•AD•AM•sin60°=x，S2=DB•sin60°=y，可得S1•S2=x•y=xy=12；（3）Ⅰ如图3中，设AM=x，BN=y，同法可证△AMD∽△BDN，可得xy=ab，由S1=•AD•AM•sinα=axsinα，S2=DB•BN•sinα=bysinα，可得S1•S2=（ab）2sin2α．（Ⅱ）结论不变，证明方法类似；试题解析：（1）如图1中，∵△ABC是等边三角形，∴AB=CB=AC=6，∠A=∠B=60°，∵DE∥BC，∠EDF=60°，∴∠BND=∠EDF=60°，∴∠BDN=∠ADM=60°，∴△ADM，△BDN都是等边三角形，∴S1=•22=，S2=•（4）2=4，∴S1•S2=12，（2）如图2中，设AM=x，BN=y．∵∠MDB=∠MDN+∠NDB=∠A+∠AMD，∠MDN=∠A，∴∠AMD=∠NDB，∵∠A=∠B，∴△AMD∽△BDN，∴，∴，∴xy=8，∵S1=•AD•AM•sin60°=x，S2=DB•sin60°=y，∴S1•S2=x•y=xy=12．（3）Ⅰ如图3中，设AM=x，BN=y，同法可证△AMD∽△BDN，可得xy=ab，∵S1=•AD•AM•sinα=axsinα，S2=DB•BN•sinα=bysinα，∴S1•S2=（ab）2sin2α．Ⅱ如图4中，设AM=x，BN=y，同法可证△AMD∽△BDN，可得xy=ab，∵S1=•AD•AM•sinα=axsinα，S2=DB•BN•sinα=bysinα，∴S1•S2=（ab）2sin2α．考点：几何变换综合题．14．如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．（1）证明与推断：①求证：四边形CEGF 是正方形； ②推断：AGBE的值为 ： （2）探究与证明：将正方形CEGF 绕点C 顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG 与BE 之间的数量关系，并说明理由： （3）拓展与运用：正方形CEGF 在旋转过程中，当B ，E ，F 三点在一条直线上时，如图（3）所示，延长CG 交AD 于点H ．若AG=6，GH=22，则BC= ．解析：（1）①四边形CEGF 是正方形；22）线段AG 与BE 之间的数量关系为2；（3）5【分析】（1）①由GE BC ⊥、GF CD ⊥结合BCD 90∠=可得四边形CEGF 是矩形，再由ECG 45∠=即可得证；②由正方形性质知CEG B 90∠∠==、ECG 45∠=，据此可得CG2CE=、GE //AB ，利用平行线分线段成比例定理可得；（2）连接CG ，只需证ACG ∽BCE 即可得； （3）证AHG ∽CHA 得AG GH AHAC AH CH==，设BC CD AD a ===，知AC 2a =，由AG GH AC AH =得2AH a 3=、1DH a 3=、10CH =，由AG AH AC CH =可得a 的值． 【详解】（1）①∵四边形ABCD 是正方形， ∴∠BCD=90°，∠BCA=45°， ∵GE ⊥BC 、GF ⊥CD ， ∴∠CEG=∠CFG=∠ECF=90°，∴四边形CEGF 是矩形，∠CGE=∠ECG=45°， ∴EG=EC ，∴四边形CEGF 是正方形； ②由①知四边形CEGF 是正方形， ∴∠CEG=∠B=90°，∠ECG=45°，∴2CGCE=，GE ∥AB ， ∴2AG CGBE CE==， 故答案为2； （2）连接CG ，由旋转性质知∠BCE=∠ACG=α， 在Rt △CEG 和Rt △CBA 中， CE CG 2CB CA 2， ∴CG CE =2CACB= ∴△ACG ∽△BCE ， ∴2AG CABE CB== ∴线段AG 与BE 之间的数量关系为2； （3）∵∠CEF=45°，点B 、E 、F 三点共线， ∴∠BEC=135°， ∵△ACG ∽△BCE ， ∴∠AGC=∠BEC=135°， ∴∠AGH=∠CAH=45°， ∵∠CHA=∠AHG ， ∴△AHG ∽△CHA ， ∴AG GH AHAC AH CH==， 设BC=CD=AD=a ，则2a ， 则由AG GH AC AH =222a = ∴AH=23a ，则DH=AD ﹣AH=13a ，22CD DH +10，∴由AG AH AC CH=得2632103aa a =， 解得：a=35，即BC=35， 故答案为35． 【点睛】本题考查了正方形的性质与判定，相似三角形的判定与性质等，综合性较强，有一定的难度，正确添加辅助线，熟练掌握正方形的判定与性质、相似三角形的判定与性质是解题的关键.15．（1）问题发现如图1，在△OAB 和△OCD 中，OA=OB ，OC=OD ，∠AOB=∠COD=40°，连接AC ，BD 交于点M ．填空： ①ACBD的值为 ； ②∠AMB 的度数为 ． （2）类比探究如图2，在△OAB 和△OCD 中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC 交BD 的延长线于点M ．请判断ACBD的值及∠AMB 的度数，并说明理由； （3）拓展延伸在（2）的条件下，将△OCD 绕点O 在平面内旋转，AC ，BD 所在直线交于点M ，若OD=1，OB=7，请直接写出当点C 与点M 重合时AC 的长．解析：（1）①1；②40°；（2390°；（3）AC 的长为33 【分析】（1）①证明△COA ≌△DOB （SAS ），得AC=BD ，比值为1；②由△COA ≌△DOB ，得∠CAO=∠DBO ，根据三角形的内角和定理得：∠AMB=180°-（∠DBO+∠OAB+∠ABD ）=180°-140°=40°；（2）根据两边的比相等且夹角相等可得△AOC ∽△BOD ，则3AC OC BD OD＝形的性质得∠AMB 的度数；（3）正确画图形，当点C 与点M 重合时，有两种情况：如图3和4，同理可得：△AOC ∽△BOD ，则∠AMB=90°，3ACBD＝，可得AC 的长． 【详解】 （1）问题发现： ①如图1，∵∠AOB=∠COD=40°， ∴∠COA=∠DOB ， ∵OC=OD ，OA=OB ， ∴△COA ≌△DOB （SAS ）， ∴AC=BD ， ∴1ACBD，= ②∵△COA ≌△DOB ， ∴∠CAO=∠DBO ， ∵∠AOB=40°， ∴∠OAB+∠ABO=140°，在△AMB 中，∠AMB=180°-（∠CAO+∠OAB+∠ABD ）=180°-（∠DBO+∠OAB+∠ABD ）=180°-140°=40°， （2）类比探究： 如图2，3ACBD=∠AMB=90°，理由是：Rt △COD 中，∠DCO=30°，∠DOC=90°， ∴303OD tan OC ︒＝ 同理得：303OB tan OA ︒＝ ∴OD OB OC OA＝， ∵∠AOB=∠COD=90°， ∴∠AOC=∠BOD ， ∴△AOC ∽△BOD ，∴3AC OC BD OD＝ ，∠CAO=∠DBO ， 在△AMB 中，∠AMB=180°-（∠MAB+∠ABM ）=180°-（∠OAB+∠ABM+∠DBO ）=90°； （3）拓展延伸：①点C 与点M 重合时，如图3，同理得：△AOC ∽△BOD ， ∴∠AMB=90°，3ACBD＝， 设BD=x ，则AC=3x ，Rt △COD 中，∠OCD=30°，OD=1， ∴CD=2，BC=x-2，Rt △AOB 中，∠OAB=30°，OB=7， ∴AB=2OB=27，在Rt △AMB 中，由勾股定理得：AC 2+BC 2=AB 2， (3x )2+(x −2)2＝(27)2， x 2-x-6=0， （x-3）（x+2）=0， x 1=3，x 2=-2， ∴AC=33；②点C 与点M 重合时，如图4，同理得：∠AMB=90°，3ACBD＝ 设BD=x ，则3，在Rt △AMB 中，由勾股定理得：AC 2+BC 2=AB 2， 3)2+（x+2）27)2. x 2+x-6=0，（x+3）（x-2）=0，x1=-3，x2=2，∴AC=23；.综上所述，AC的长为33或23．【点睛】本题是三角形的综合题，主要考查了三角形全等和相似的性质和判定，几何变换问题，解题的关键是能得出：△AOC∽△BOD，根据相似三角形的性质，并运用类比的思想解决问题，本题是一道比较好的题目．16．(1)方法选择如图①，四边形ABCD是O的内接四边形，连接AC，BD，AB BC AC==．求证：BD AD CD=+.小颖认为可用截长法证明：在DB上截取DM AD=，连接AM…小军认为可用补短法证明：延长CD至点N，使得DN AD=…请你选择一种方法证明．(2)类比探究（探究1）如图②，四边形ABCD是O的内接四边形，连接AC，BD，BC是O的直径，AB AC=．试用等式表示线段AD，BD，CD之间的数量关系，并证明你的结论．（探究2）如图③，四边形ABCD是O的内接四边形，连接AC，BD．若BC是O的直径，30ABC∠=︒，则线段AD，BD，CD之间的等量关系式是______．(3)拓展猜想如图④，四边形ABCD是O的内接四边形，连接AC，BD．若BC是O的直径，::::BC AC AB a b c=，则线段AD，BD，CD之间的等量关系式是______．解析：(1)方法选择：证明见解析；(2)【探究1】：2BD CD=；【探究2】32BD CD AD=+；(3)拓展猜想：c aBD CD ADb b=+.【分析】（1）方法选择：根据等边三角形的性质得到∠ACB=∠ABC=60°，如图①，在BD上截取DM=AD，连接AM，由圆周角定理得到∠ADB=∠ACB=60°，得到AM=AD，根据全等三角形的性质得到BM=CD，于是得到结论；（2）类比探究：如图②，由BC是⊙O的直径，得到∠BAC=90°，根据等腰直角三角形的性质得到∠ABC=∠ACB=45°，过A作AM⊥AD交BD于M，推出△ADM是等腰直角三角形，求得2根据全等三角形的性质得到结论；。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
上海市中考数学压轴题几何背景探寻近几年来，全国各省市的数学中考压轴题大部分都有一个很明确的几何背景，今年的上海市中考数学压轴题也是如此。
背景1：如图点P是正方形ABCD对角线上任意一点。
求证：PA＝PC
证明：∵四边形ABCD是正方形
∴AB＝CB，∠ABP＝∠CBP＝
45
又∵BP＝BP
⇒△ABP≌△CBP⇒PA＝PC
背景2：接上题，以P为圆心，以PA为半径画弧交AB（或AB的延长线）于点Q。
求证：PQ⊥PC
证明：∵PA＝PQ⇒∠1＝∠3
又∵△ABP≌△CBP⇒∠1＝∠2
⇒∠1＝∠2＝∠3
而：∠3＋∠4＝
180⇒∠2＋∠4＝
180
又∵∠QBC＝
90
∴∠QPC＝
90⇒PQ⊥PC
当点Q在AB的延长线上时，
∵∠2＝∠3；∠4＝∠5⇒△BQH∽△CPH
∴∠QPC＝
90⇒PQ⊥PC
背景3：反过来，若将一个直角顶点放在正方形的对
角线上移动，一条直角边过点C ，另一条直角边与
正方形的边（或边的延长线）AB交于点Q。
求证：
PQ＝PC
证明：过P作MN平行于BC交AB、CD于M、N
∵∠1＋∠QPC＝∠2＋∠PNC⇒∠1＝∠2
又∵∠MBP＝
45⇒MP＝MB＝NC
而∠QMP＝∠PNC＝
90⇒△QMP≌△PNC⇒PQ＝PC
M
C
M
C
从上述的几个背景看出，当∠QPC ＝
90时，一定有PQ ＝PC ，即AB
AD PC
PQ =
；但反过来
当
AB
AD PC
PQ =
，即PQ ＝PC 时，因为有PA ＝PC 时∠APC ＝
90不一定成立，所以∠QPC
＝
90不一定能够成立。
下面我们将背景弱化：
背景4：若将一个直角顶点放在长方形的对角线上移动，一条直角边过点C ，另一条直角边与长方形的边（或边的延长线）AB 交于点Q 。
求证：
AB
AD PC
PQ =
证明：易证：△QMP ∽△PNC
⇒
AB
AD MB
MP NC
MP PC
PQ ===
背景5：如图，矩形ABCD 的AB ＝a ，AD ＝b ，点P 在对角线BD 上运动，点Q 在射线AB 上运动，若AB
AD PC
PQ =
，试探索a ，b 满足什么条件时，会
有PQ ⊥PC 探索：正常情况下，
NC
MP MB
MP AB
AD PC
PQ =
==
⇒△QMP ∽△PNC ⇒∠QPC ＝
90⇒ PQ ⊥PC
但若点Q 关于MN 的对称点1Q 也在射线AB 上时，如同上述背景一样，连P 1Q ，∠1Q PC ＝
90就不一定成立了。
这里：
a
b PC PQ PN
MQ ==；
a
b CD
BC AM
PN DN
PN =
=
=
两式相乘：
12
2≤=
a
b AM
MQ
b a b a b a
b
≤⇒≤-+⇒≤-⇒0))((02
2
从这两个背景看出，当∠QPC ＝
90时，一定有
AB
AD PC
PQ
=；AB
AD PC
PQ =时，∠QPC ＝
90若遇到b ＞a 时就一定能成立。
背景6：如图四边形ABCD 是梯形，AD ∥BC ，∠ABC ＝
90，若将一个直角顶点放在对角线BD 上移动，一条直角边过点C ，另
M
一条直角边与腰AB （或AB 的延长线）交于点Q 。
求证：AB
AD PC
PQ =
证明：易证：△QMP ∽△PNC
⇒
AB
AD MB
MP NC
MP PC
PQ ===
背景7：如图，四边形ABCD 是梯形，AD ∥BC ，∠ABC ＝
90， AB ＝a ，BC ＝b ，AD=x,点P 在对角线BD 上运动，点Q 在射线AB 上运动，若AB
AD PC
PQ =
，试探索x 与a 、b 之间
应该满足什么条件时，一定会有PQ ⊥PC 探索：正常情况下，
NC
MP MB
MP AB
AD PC
PQ =
==
⇒△QMP ∽△PNC ⇒∠QPC ＝
90⇒ PQ ⊥PC
但若点Q 关于MN 的对称点1Q 也在射线AB 上时，如同上述背景一样，连P 1Q ，∠1Q PC ＝
90就不一定成立了。
所以这里我们应该关注当点1Q “最低”时点P 的位置，其实无论AD 边的长度如何要使得点1Q 的位置“最低”，那么点P 的位置只能与点B 重合。
这时△Q 'DP ∽△PQC ，且P Q '＝PQ b
a
x b a a
x 2
=
⇒=⇒
又∵
AB
AD PC
PQ =
，而当AD ＞
b
a
2
时，在AB 、BC 都是定值的情况下，PQ 也就变大了，
C
即Q '点就不在射线AB 上了（而是在射线BA 上了），那样∠Q 'PC ＝
90就一定成立了
所以结论就是当AD ＞b
a
2
时，∠Q 'PC ＝
90一定成立
09上海市中考数学压轴题：
25．（本题满分14分，第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）
已知9023A B C A B B C A D B C P ∠===°，，，∥，为线段B D 上的动点，点Q 在射线A B 上，且满足
P Q A D P C
A B
=
（如图8所示）．
（1）当2A D =，且点Q 与点B 重合时（如图9所示），求线段P C 的长； （2）在图8中，联结A P ．当32
A D =
，且点Q 在线段A B 上时，设点B Q 、之间的距离
为x ，
A P Q P
B C
S y S =△△，其中A P Q S △表示A P Q △的面积，P B C S △表示P B C △的面积，求y 关
于x 的函数解析式，并写出函数定义域；
（3）当AD AB <，且点Q 在线段A B 的延长线上时（如图10所示），求Q P C ∠的大小．
第一步：对所给的主条件进行分析，做“先期准备”，我们发现当“点P 为线段B D 上的动点，点Q 在射线A B 上，且满足
P Q A D P C
A B
=（如图8所示）”时，一定有∠QPC ＝
90
A
D P
C
B
Q 图8
D
A
P
C
B
（Q ） 图9
图10
C
A
D
P B Q
第二步：做第一小题时，我们知道AD ＝AB 时一定有PB ＝PC ，又因为有∠BAD ＝
90
9045
45
459045
＝＝－＝＝BPC PCB PBC ABD ∠⇒=∠⇒∠⇒∠⇒
又∵BC ＝32
232
3=
=
⇒PC 。
出题者的本意是想给同学一个∠QPC
＝
90的提示的。
但是这个提示不明显，直接影响了后面的作图和解决问题，第一小题“铺垫”的目的没有很好地达到。
第三步：第二小题的条件在主条件上加了一个
3
2A D =
，所以我们还要对
这个图形单独地做个分析：这是的△ADB 和△PQC 都是3︰4︰5的直角三角形，因为BC ＝2AD ，也容易证明△DBC 为等腰三角形，DC ＝DB 等等。
第四步：画出所有运动状态，在“极限图形”中求出x 等于多少？y 存在还是不存在？ 要注意这里的“点P 为线段B D 上的动点，点Q 在线段A B 上”，所以有三个图：
在图1中x ＝0，y 是存在的，在图3中8
154
32
543=⇒=
⇒
==PQ PQ AB
AD PC
PQ
而878
98
122
3=
⇒=
⇒=
=
x AQ AD ，这时y 也是存在的。
所以x 的取值范围应该是：8
70≤
≤x 。
在图2中我们容易知道：4
24
33
23
23
232
1
)2(2
1
2
12
1
x x AB
AD x h h x h h x y -=
⨯
-=
∙
-=
∙
-=
⨯⨯-=
第五步：在做第三小题时，由于题中已经明确有“点Q 在线段A B 的延长线上时、如图10所示”两个明确条件，所以我们在背景中考虑的另类情况在这里就没有必要讨论了。
C
Q C
H C
C
最后看来，除了第一小题有点值得商榷外，今年上海市的压轴题紧扣教材（所有的背景都在初二几何证明部分中出现过），注重双基，不偏不怪，也有一定的分析问题、解决问题的能力要求和数学计算要求。
确实是一道好题。
以上的几何背景分析也许能反映作者平时理解问题的不简捷，简单问题往往复杂化，再加上写得匆忙没来得及仔细斟酌合适的表达语句，错误之处还望各位同行或专家批评指正。