初中数学竞赛:平面几何中的最值问题
平面几何的最值问题及求法

数 学教 学
21 年第 5 00 期
平 面几何 的最值 问题 及 求法
55 21 3 0广东 省东莞市常 学( 部 平中 高中 )陈 洪波
一
、
利用三角形的性质
利用三 角形 “ 两边之和大 于第三边, 两边之
设正 △AB 的边长为 2 M 是 J 边上的中点, , E ; j是边B [ ) 上的任意一点, +P 的最大值 P M 和最小值分别记为s , 和t 则求 s 一t的值. 解: 如图 2 . P ≤ ,’ ,F ≤ M, ’ J ) PA+ PM ≤ CA+ CM = 2+ 、3 /. /
所 以P P = xOp 2 / ' +O " P
例2 ( 0 年全国初中数学联合竞赛试题) 2 0 0
21 年第 5 00 期
=  ̄ OP2+ OP2= 1 v - / 0 / 2
.
数 学教 学
52 —5
解: 以点 为旋转 中心, ABC 将 E按顺时针 方向旋转 6 。 ABG 连结 EF, AB 0到 F, 则 EF为
A1
、
‘ \ ,
‘
、 \\ M 、1 ^
=
3 。 0 .
j、 、 ‘ , N
图4
设 正方 形 边 长 为 , BG = , 则 GH = - , 4 x
B 日 : 日 :
( ) + .
由G H 十 日 =AG , 得
1 2 +
分析: 因河宽一定的, 以桥 M Ⅳ 的长度一 所 定, 只须使 M +BⅣ 最短即可. 可平移 M ( 或
于 B. ’Rc . △DD G中, DG. 。DD . DD > . .
>
M 连结 CM 则 . , M = 9 。 所以 0, M xA +C = / C2 = 、7 . = 、 . /,’ / .£ / / 7 从而 8 一t =( 十 ) 一7 4 . 。 。 2 。 =4 5 二、 利用对称变换 例3 (00 20 年黄 冈初 中数学竞赛试题) 如图 3 , (B = 4 。 二 ) 5 角内有一 点P, PO = 1, 0 在 角的两条 边上有两点 Q 均不 同于点 D, 、 求 AP R的周长的最小值. Q
几何中的最值问题

几何中的最值问题作为一门重要的数学学科,几何中有许多重要的概念和方法,其中最值问题是一个广泛研究的内容。
在几何中,最值问题是指在某些条件下,某个几何量(如长度、面积、体积等)的最大值或最小值问题。
本文将从不同角度介绍几何中的最值问题及其应用。
一、最值问题的基础概念在几何问题中,最值问题最常见的便是一些面积、长度和体积的最值问题。
最常见的方法是使用微积分的极值定理,通过计算导数为0的点来找到函数的最大值和最小值。
此外,还有最大和最小的边界问题。
这些问题需要考虑的是给定条件下的最大可行解或最小可行解。
例如,给定一个面积固定的矩形,我们需要求出其长度和宽度的最大或最小值。
这些问题与微积分密切相关,但在解决这些问题时需要更多的几何知识和直觉。
二、平面几何中的最值问题在平面几何中,最值问题通常涉及三角形、四边形和圆形等形状。
这些形状的特性可以用来求解最值问题,通常需要使用各种几何知识和技巧。
例如,对于一个给定面积的三角形,在其周长恒定的情况下,需要求出该三角形的最大或最小长度。
为解决这类问题,我们可以利用三角形的海涅定理或余弦定理,通过微积分的极值定理得到最优解。
对于圆形,最值问题可能涉及到面积和周长问题,这些需要用到圆相关的特点和公式,如半径、直径、周长和面积等,通常需要通过微积分的方法求解。
另一方面,对于四边形最值问题,我们需要利用它们的对角线和相邻边的关系来解决,这通常需要将四边形划分为三角形或矩形来计算。
三、空间几何中的最值问题在空间几何中,最值问题通常涉及立体体积,包括长方体、正方体、棱锥和棱柱等。
这些问题需要利用空间几何的特点和公式来求解,常用的方法包括微积分的极值定理和立体几何的体积计算公式。
例如,对于一个矩形长方体,在其表面积固定的情况下,需要求出其有最大或最小的体积。
如果我们设该矩形长方体的长、宽和高分别为x、y和z,那么该矩形长方体的体积可以表示为V(x,y,z)=xyz。
通过微积分的方法,可以证明只有当x=y=z时,该方体的体积最大。
初中几何最值问题类型

初中几何最值问题类型
初中几何中的最值问题类型有以下几种:
1.最大值最小值问题:
求某个几何图形的最大面积或最小周长,如矩形、三角形等。
求抛物线的最高点或最低点,即顶点的坐标。
2.极值问题:
求函数图像与坐标轴的交点。
求函数在某个区间内的最大值或最小值,如求二次函数的最
值等。
3.最优化问题:
求物体从一个点到另一个点的路径问题,如两点之间的最短
路径、最快速度等。
4.最长边最短边问题:
求三角形的最长边或最短边,如用三根木棍构成三角形,求
最长边的长度。
5.相等问题:
求两个几何形状中的某个参数,使得它们的某个关系成立,
如求两个相似三角形的边长比、两个等腰三角形的底角角度等。
这些问题类型都需要通过合理的分析和运用相关的几何定理
来解决。
对于初中学生来说,熟练掌握基本的几何概念和定理,灵活运用数学思维和方法,可以较好地解决这些最值问题。
通
过多做练习和思考,培养几何思维和解决问题的能力。
数学竞赛中平面几何最值问题的解法

(98 武 汉 市 中学 数 学 竞 赛 ) 15 ,
解 : 图 3 如 ,
O
设 O B为扇形 , A 有 A B=10 , O 2 ̄
OA = 1. C DEF
.
为 其 内 接矩 形 .
设 C = , D
图 3
O =Y 过 0 作 D ,
即 A+O 的最小值为 O C
.
4 二 次 函数 法
3 判 别 式 法
利 用 二 次 函数 的性 质 求 得 结 果 .
例 4 已知 △ A C 是 边 长 为 1的 正 三 角 B
根据 问 题 的 条 件 , 欲 求 最 值 的 几 何 对 将
象 变 为 某 实 二 次 方 程 的 系 数 , 方 程 的 根 为 由
1 综 合 法
又 O :1 故 0 ≥√ M , , 2—1 .
即 D ,的最 小 值 为 √ 2—1 .
2 猜 测 法
根 据 已 知 条 件 , 接 利 用 平 面 几 何 中 的 直
有关知识求得结 果 . 例 1 在 R △ A t BC 中 , 边 A :2 0 斜 C , 为A C的 中点 , 是 △ A , BC的 内心 . D 求 ,的最 小值 . 解 : 图 1 以 0 为 如 , 圆心、 A为半径 作 圆, O 连 延 长 交 o 于 M . c 0
AC : 2. MA : . MI: MA : .
平 面几 何 问 题 是 数 学 竞 赛 的 重 要 内 容 ,
而其 中的最 值 问题 更 是 数学 竞 赛 中的难 点 , 且 题 目均 具 有 较 大 难 度 . 文 将 结 合 具 体 实 本 例 , 其解法作一介 绍 . 对
初中数学几何最值存在性问题(word版+详解答案)

几何最值的存在性问题【考题研究】在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。
从历年的中考数学压轴题型分析来看,经常会考查到距离或者两条线段和差最值得问题,并且这部分题目在中考中失分率很高,应该引起我们的重视。
几何最值问题再教材中虽然没有进行专题讲解,到却给了我们很多解题模型,因此在专题复习时进行压轴训练是必要的。
【解题攻略】最值问题是一类综合性较强的问题,而线段和(差)问题,要归归于几何模型:(1)归于“两点之间的连线中,线段最短”凡属于求“变动的两线段之和的最小值”时,大都应用这一模型.(2)归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时,大都应用这一模型.两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,PA与PB的差的最大值就是AB,此时点P在AB的延长线上,即P′.解决线段和差的最值问题,有时候求函数的最值更方便,建立一次函数或者二次函数求解最值问题.【解题类型及其思路】解决平面几何最值问题的常用的方法有:(1)应用两点间线段最短的公理(含应用三角形的三边关系)求最值;(2)应用垂线段最短的性质求最值;(3)应用轴对称的性质求最值;(4)应用二次函数求最值;(5)应用其它知识求最值。
【典例指引】类型一【确定线段(或线段的和,差)的最值或确定点的坐标】【典例指引1】(2018·天津中考模拟)如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x 轴、y轴的正半轴上.点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC 交于点E.(I)证明:EO=EB;(Ⅱ)点P是直线OB上的任意一点,且△OPC是等腰三角形,求满足条件的点P的坐标;(Ⅲ)点M是OB上任意一点,点N是OA上任意一点,若存在这样的点M、N,使得AM+MN最小,请直接写出这个最小值.【举一反三】(2020·云南初三)如图,抛物线y=ax2+bx+3经过点B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.(1)求抛物线的表达式;(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.类型二【确定三角形、四边形的周长的最值或符合条件的点的坐标】【典例指引2】(2020·重庆初三期末)如图,抛物线2y ax bx =+(0a >)与双曲线k y x =相交于点A 、B ,已知点A 坐标()1,4,点B 在第三象限内,且AOB ∆的面积为3(O 为坐标原点).(1)求实数a 、b 、k 的值;(2)在该抛物线的对称轴上是否存在点P 使得POB ∆为等腰三角形?若存在请求出所有的P 点的坐标,若不存在请说明理由.(3)在坐标系内有一个点M ,恰使得MA MB MO ==,现要求在y 轴上找出点Q 使得BQM ∆的周长最小,请求出M 的坐标和BQM ∆周长的最小值.【举一反三】(2019·重庆实验外国语学校初三)如图1,已知抛物线y =﹣23384x +x +3与x 轴交于A 和B 两点,(点A 在点B 的左侧),与y 轴交于点C .(1)求出直线BC 的解析式.(2)M 为线段BC 上方抛物线上一动点,过M 作x 轴的垂线交BC 于H ,过M 作MQ ⊥BC 于Q ,求出△MHQ 周长最大值并求出此时M 的坐标;当△MHQ 的周长最大时在对称轴上找一点R ,使|AR ﹣MR |最大,求出此时R 的坐标.(3)T 为线段BC 上一动点,将△OCT 沿边OT 翻折得到△OC ′T ,是否存在点T 使△OC ′T 与△OBC 的重叠部分为直角三角形,若存在请求出BT 的长,若不存在,请说明理由.类型三 【确定三角形、四边形的面积最值或符合条件的点的坐标】【典例指引3】(2019·甘肃中考真题)如图,已知二次函数y =x 2+bx+c 的图象与x 轴交于点A (1,0)、B (3,0),与y 轴交于点C .(1)求二次函数的解析式;(2)若点P 为抛物线上的一点,点F 为对称轴上的一点,且以点A 、B 、P 、F 为顶点的四边形为平行四边形,求点P 的坐标;(3)点E 是二次函数第四象限图象上一点,过点E 作x 轴的垂线,交直线BC 于点D ,求四边形AEBD 面积的最大值及此时点E 的坐标.【举一反三】(2019·内蒙古中考真题)如图,在平面直角坐标系中,已知抛物线22(0)y ax bx a =++≠与x 轴交于()1,0A -),()3,0B 两点,与y 轴交于点C ,连接BC .(1)求该抛物线的解析式,并写出它的对称轴;(2)点D 为抛物线对称轴上一点,连接CD BD 、,若DCB CBD ∠=∠,求点D 的坐标;(3)已知()1,1F ,若(),E x y 是抛物线上一个动点(其中12x <<),连接CE CF EF 、、,求CEF ∆面积的最大值及此时点E 的坐标.(4)若点N 为抛物线对称轴上一点,抛物线上是否存在点M ,使得以,,,B C M N 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M 的坐标;若不存在,请说明理由.【新题训练】1.如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.(1)求二次函数的表达式;(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴,y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F、E的坐标.2.(2019·江苏中考真题)如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.(1)如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为_____;(2)如图2,当PB=5时,若直线l//AC,则BB’的长度为;(3)如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;(4)当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.3.(2019·湖南中考真题)如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y 轴的正半轴上随之上下移动.(1)当∠OAD=30°时,求点C的坐标;(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为212时,求OA的长;(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.4.(2018·江苏中考真题)如图,在平面直角坐标系中,一次函数y=﹣23x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.(1)当t=13秒时,点Q的坐标是;(2)在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;(3)若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.5.(2020·江苏初三期末)已知二次函数223y x x =--+的图象和x 轴交于点A 、B ,与y 轴交于点C ,点P 是直线AC 上方的抛物线上的动点.(1)求直线AC 的解析式.(2)当P 是抛物线顶点时,求APC ∆面积.(3)在P 点运动过程中,求APC ∆面积的最大值.6.(2020·江苏初三期末)如图,抛物线265y ax x =+-交x 轴于A 、B 两点,交y 轴于点C ,点B 的坐标为()5,0,直线5y x =-经过点B 、C .(1)求抛物线的函数表达式;(2)点P 是直线BC 上方抛物线上的一动点,求BCP ∆面积S 的最大值并求出此时点P 的坐标;(3)过点A 的直线交直线BC 于点M ,连接AC ,当直线AM 与直线BC 的一个夹角等于ACB ∠的3倍时,请直接写出点M 的坐标.7.(2019·石家庄市第四十一中学初三)如图,在平面直角坐标系中,抛物线y =x (x ﹣b )﹣与y 轴相交于A 点,与x 轴相交于B 、C 两点,且点C 在点B 的右侧,设抛物线的顶点为P .(1)若点B 与点C 关于直线x =1对称,求b 的值;(2)若OB =OA ,求△BCP 的面积;(3)当﹣1≤x≤1时,该抛物线上最高点与最低点纵坐标的差为h ,求出h 与b 的关系;若h 有最大值或最小值,直接写出这个最大值或最小值.8.(2020·江西初三期中)如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.(1)求抛物线的解析式;(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.9.(2020·山东初三期末)如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.(1)求直线CD 的解析式;(2)求抛物线的解析式;(3)将直线CD 绕点C 逆时针方向旋转45°所得直线与抛物线相交于另一点E ,求证:△CEQ ∽△CDO ; (4)在(3)的条件下,若点P 是线段QE 上的动点,点F 是线段OD 上的动点,问:在P 点和F 点移动过程中,△PCF 的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由. 10.(2020·盘锦市双台子区第一中学初三月考)如图①,已知抛物线y=ax 2+bx+c 的图像经过点A (0,3)、B (1,0),其对称轴为直线l :x=2,过点A 作AC ∥x 轴交抛物线于点C ,∠AOB 的平分线交线段AC 于点E ,点P 是抛物线上的一个动点,设其横坐标为m.(1)求抛物线的解析式;(2)若动点P 在直线OE 下方的抛物线上,连结PE 、PO ,当m 为何值时,四边形AOPE 面积最大,并求出其最大值;(3)如图②,F 是抛物线的对称轴l 上的一点,在抛物线上是否存在点P 使△POF 成为以点P 为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.11.(2020·四川初三)如图,一次函数122y x =-+的图像与坐标轴交于A 、B 两点,点C 的坐标为(1,0)-,二次函数2y ax bx c =++的图像经过A 、B 、C 三点.(1)求二次函数的解析式(2)如图1,已知点(1,)D n 在抛物线上,作射线BD ,点Q 为线段AB 上一点,过点Q 作QM y ⊥轴于点M ,作QN BD ⊥于点N ,过Q 作//QP y 轴交抛物线于点P ,当QM 与QN 的积最大时,求点P 的坐标;(3)在(2)的条件下,连接AP ,若点E 为抛物线上一点,且满足APE ABO ∠=∠,求点E 的坐标.12.(2019·广东初三)如图,已知抛物线y =﹣3x 2+bx +c 与x 轴交于原点O 和点A (6,0),抛物线的顶点为B .(1)求该抛物线的解析式和顶点B 的坐标;(2)若动点P 从原点O 出发,以每秒1个长度单位的速度沿线段OB 运动,设点P 运动的时间为t (s ).问当t 为何值时,△OPA 是直角三角形?(3)若同时有一动点M 从点A 出发,以2个长度单位的速度沿线段AO 运动,当P 、M 其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t (s ),连接MP ,当t 为何值时,四边形ABPM 的面积最小?并求此最小值.13.(2019·山东初三期中)如图,已知抛物线经过两点A (﹣3,0),B (0,3),且其对称轴为直线x =﹣1.(1)求此抛物线的解析式.(2)若点Q 是对称轴上一动点,当OQ +BQ 最小时,求点Q 的坐标.(3)若点P 是抛物线上点A 与点B 之间的动点(不包括点A ,点B ),求△PAB 面积的最大值,并求出此时点P 的坐标.14.(2019·四川中考真题)如图,抛物线212y x bx c =-++过点(3,2)A ,且与直线72y x =-+交于B 、C两点,点B 的坐标为(4,)m .(1)求抛物线的解析式;(2)点D 为抛物线上位于直线BC 上方的一点,过点D 作DE x ⊥轴交直线BC 于点E ,点P 为对称轴上一动点,当线段DE 的长度最大时,求PD PA +的最小值;(3)设点M 为抛物线的顶点,在y 轴上是否存在点Q ,使45AQM ︒∠=?若存在,求点Q 的坐标;若不存在,请说明理由.15.(2019·天津中考真题)已知抛物线2y x bx c =-+(b c ,为常数,0b >)经过点(1,0)A -,点(,0)M m 是x 轴正半轴上的动点.(Ⅰ)当2b =时,求抛物线的顶点坐标;(Ⅱ)点(,)D D b y 在抛物线上,当AM AD =,5m =时,求b 的值;(Ⅲ)点1(,)2QQ b y+在抛物线上,当22AM QM+的最小值为3324时,求b的值.16.(2019·湖南中考真题)如图,抛物线y=ax2+bx(a>0)过点E(8,0),矩形ABCD的边AB在线段OE上(点A在点B的左侧),点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA:AD=1:3.(1)求抛物线的解析式;(2)F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值;(3)在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为610?若存在,求出点P的坐标;若不存在,请说明理由;(4)矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL 平分矩形的面积时,求抛物线平移的距离.17.(2019·辽宁中考真题)如图,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线经过点D(﹣2,﹣3)和点E(3,2),点P是第一象限抛物线上的一个动点.(1)求直线DE和抛物线的表达式;(2)在y 轴上取点F (0,1),连接PF ,PB ,当四边形OBPF 的面积是7时,求点P 的坐标;(3)在(2)的条件下,当点P 在抛物线对称轴的右侧时,直线DE 上存在两点M ,N (点M 在点N 的上方),且MN =22,动点Q 从点P 出发,沿P→M→N→A 的路线运动到终点A ,当点Q 的运动路程最短时,请直接写出此时点N 的坐标.18.(2019·湖南中考真题)已知抛物线2(0)y ax bx c a =++≠过点(1,0)A ,(3,0)B 两点,与y 轴交于点C ,=3OC .(1)求抛物线的解析式及顶点D 的坐标;(2)过点A 作AM BC ⊥,垂足为M ,求证:四边形ADBM 为正方形;(3)点P 为抛物线在直线BC 下方图形上的一动点,当PBC ∆面积最大时,求点P 的坐标; (4)若点Q 为线段OC 上的一动点,问:12AQ QC +是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.几何最值的存在性问题【考题研究】在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。
(完整)八年级平面几何最值问题
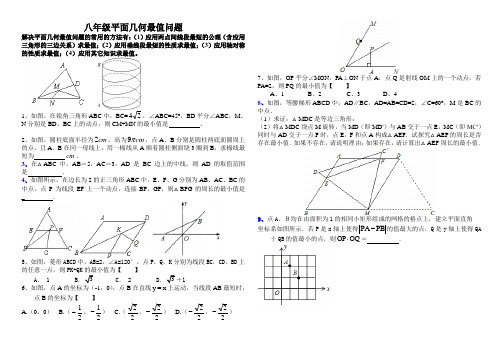
八年级平面几何最值问题解决平面几何最值问题的常用的方法有:(1)应用两点间线段最短的公理(含应用三角形的三边关系)求最值;(2)应用垂线段最短的性质求最值;(3)应用轴对称的性质求最值;(4)应用其它知识求最值。
1、如图,在锐角三角形ABC 中,BC=24,∠ABC=45°,BD 平分∠ABC ,M 、N 分别是BD 、BC 上的动点,则CM+MN 的最小值是 。
2、如图,圆柱底面半径为2cm ,高为9cm π,点A 、B 分别是圆柱两底面圆周上的点,且A 、B 在同一母线上,用一棉线从A 顺着圆柱侧面绕3圈到B ,求棉线最短为 cm 。
3、在△ABC 中,AB =5,AC =3,AD 是BC 边上的中线,则AD 的取值范围是 .4、如图所示,在边长为2的正三角形ABC 中,E 、F 、G 分别为AB 、AC 、BC 的中点,点P 为线段EF 上一个动点,连接BP 、GP ,则△BPG 的周长的最小值是 _ .5、如图,菱形ABCD 中,AB=2,∠A=120°,点P ,Q ,K 分别为线段BC ,CD ,BD 上的任意一点,则PK+QK 的最小值为【 】A . 1B .3C . 2D .3+1 6、如图,点A 的坐标为(-1,0),点B 在直线y x =上运动,当线段AB 最短时,点B 的坐标为【 】A.(0,0)B.(21-,21-) C.(22,22-) D.(22-,22-)7、如图,OP 平分∠MON ,PA ⊥ON 于点A ,点Q 是射线OM 上的一个动点,若PA=2,则PQ 的最小值为【 】 A 、1 B 、2 C 、3 D 、48、如图,等腰梯形ABCD 中,AD ∥BC ,AD=AB=CD=2,∠C=60°,M 是BC 的中点.(1)求证:△MDC 是等边三角形;(2)将△MDC 绕点M 旋转,当MD (即MD ′)与AB 交于一点E ,MC (即MC′)同时与AD 交于一点F 时,点E ,F 和点A 构成△AEF .试探究△AEF 的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△AEF 周长的最小值.9、点A 、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角 坐标系如图所示.若P 是x 轴上使得PA PB -的值最大的点,Q 是y 轴上使得QA十QB 的值最小的点,则OP OQ ⋅= .答案:1.4 2.15 3.1<AD<4 4.3 5.B 6.B 7.B 8.2+9.5。
中考数学专题复习 平面几何的最值问题_答案

7. C 提示:当点 P 与点 D 重合时,四边形 ACBP 的周长最大.
8. (1)连结 ME,过 N 作 NF⊥AB 于 F,可证明 Rt△EB A≌Rt△MNF,得 MF=AE=x.∵
ME2=AE2+AM2,故 MB2=x2+AM2,即(2-AM)2=x2+AM2,AM=1- 1 x2,∴S= 4
y
的取值范围内,所以
y=
5 2
不是极值点,当
y=3
时,S(3)
=12,当
y=4
时,S(4)=8,故
Smax=12.此时,钢板的最大利用率
42
12 1
2
1
=80%.
例
2
6 设 PD=x(x>1),则 PC= x2 1 ,由 Rt△PCD∽△PAB,得 AB= CD PA x 1 ,令 y
PC
x2 1
l22 ,当
r>
4h 2
4
时, l12
l22
,当
r<
4h 2
4
时, l12
l22
.
例5
设 DN=x,PN=y,则 S=xy,由△APQ∽△
ABF,得
2
4
4
y
x
1 2
即
x=10-2y,代入
S=xy 得 S=xy=y(10-2y),即 S=-2
y
5 2
2
25 2
,
因
3≤y≤4,而
y=
5 2
不在自变量
11. (1)点 P 恰好在 BC 上时,由对称性知 MN 是△ABC 的中位线,∴当 MN= 1 BC=3 时, 2
点 P 在 BC 上.(
2)由已知得△ABC 底边上的高 h= 52 -32 =4. ①当 0<x≤3 时,如图 1,连结 AP 并延长交
九年级数学竞赛专题5 平面几何的最值问题_答案

专题25 平面几何的最值问题例1125 提示:当CM ⊥AB 时,CM 值最小,CM =125AC BC AB ⋅= 例2 如图,B ′M +MN 的最小值为点B ′到AB 的距离B ′F ,BE =AB BCAC⋅=,BB ′=,AE =.在△ABB ′中,由12BB ′•AE =12AB •B ′F ,得B ′F =16cm .故BM +MN 的最小值为16cm . 例3 由△APD ∽△BPQ ,得AP AD BP BQ =,即BQ =()b a x AD BP AP x -⋅=,∴AP +BQ =x +ab b x -.∵x +abx ≥=x =abx即x APAP +BQ 最小,其最小值为b .例4 ⑴22125l π=+,22l =49,l 1<l 2,故要选择路线l 较短. ⑵()2221l h r π=+,()2222l h r =+,()2221244l l r r h π⎡⎤-=--⎣⎦.当r =244h π-时,2212l l =,当r >244h π-时,2212l l >,当r <244h π-时,2212l l <. 例5 设DN =x ,PN =y ,则S =xy ,由△APQ ∽△ABF ,得()41242y x -=--即x =10-2y ,代入S =xy 得S =xy =y (10-2y ),即S =-2252522y ⎛⎫-+ ⎪⎝⎭,因3≤y ≤4,而y =52不在自变量y 的取值范围内,所以y =52不是极值点,当y =3时,S (3)=12,当y =4时,S (4)=8,故S max =12.此时,钢板的最大利用率21214212-⨯⨯=80%. 例6 设PD =x (x >1),则PC 由R t △PCD ∽△PAB ,得AB =CD PA PC ⋅=,令y =AB •S △PAB ,则y =12AB ×PA ×AB =()()2121x x +-,求y 的最小值,有下列不同思路:①配方:y =2122421x x -++=+-,=即当x =3时,y 有最小值4.②运用基本不等式:y =122221x x -++≥- 322=4,∴当12x -=21x -,即当x =3时,y 有最小值4. ③借用判别式,去分母,得x 2+2(1-y )x +1+2y =0,由△=4(1-y )2-4(1+2y )=4y (y -4)≥0,得y ≥4,∴y 的最小值为4. A 级1. 17 提示:当两张纸条的对角重合时,菱形周长最大.2. 83.4.D5. D6. B7. C 提示:当点P 与点D 重合时,四边形ACBP 的周长最大.8. (1)连结ME ,过N 作NF ⊥AB 于F ,可证明Rt △EB A ≌Rt △MNF ,得MF =AE =x.∵ME 2=AE 2+AM 2,故MB 2=x 2+AM 2,即(2-AM )2=x 2+AM 2,AM =1-14x 2,∴S =2AM DN +×AD =2AM AF +×2=AM +AM +MF =2 AM +AE =2(1-14x 2)+x =-12x 2+x +2.(2)S =-12(x 2-2 x +1)+52=-12(x -1)2+52.故当AE =x =1时,四边形ADNM 的面积最大,此时最大值为52.9. (1)BC 长为23rπ.(2)提示:连结BD . (3)过点B 作BM ⊥AD 于M ,由(2)知四边形ABCD 为等腰梯形,从而BC =AD -2 AM =2r -2 AM .由△BAM ∽△DAB ,得AM =2AB AD =22x r ,∴BC =2r -2x r .同理,EF =2 r -2x r .l =4 x +2(2 r -2x r)=-x r (x -r )2+6 r(0<x r )..当x =r 时,l 取得最大值6 r .10. (1)∵∠APE =∠ADQ ,∠AEP =∠AQD ,∴△APE ∽△ADQ .(2)由△APE ∽△ADQ ,△PDF ∽△ADQ ,S △PEF =12S □PEQF ,得S △PEF =-13x 2+x =-13(x -32)2+34.故当x =32时,即P 是AD 的中点时,S △PEF 取得最大值,(3)作A 关于直线BC 的对称点A′,连结DA′交BC 于Q ,则这个Q 点就是使△ADQ 周长最小的点,此时Q 是BC 的中点. 11. (1)点P 恰好在BC 上时,由对称性知MN 是△ABC 的中位线,∴当MN =12BC =3时,点P 在BC 上.(2)由已知得△ABC 底边上的高h=4. ①当0<x ≤3时,如图1,连结AP 并延长交BC 于点D ,AD 与MN 交于点O .由△AMN ∽△ABC ,得AO =23x ,y =S △PMN =S △AMN =12·x ·23x =13x 2即y =13x 2.当=3时,y 的值最大,最大值是3.②当3<x <6时,如图2,设△PMN 与BC 相交于点E ,F ,AP 与BC 相交于D .由①中知AO =23x ,∴AP =43x ,∴PD =AP -AD =43x -4,∵△PEF ∽△ABC .,∴PEFABCS S ∆∆=(PD AD )2=(4434x -)2,即PEF ABC S S ∆∆=2-3)9x (.∵S △ABC =12,∴S △PEF =43(x -3)2.∴y =S △AMN -S △PEF =13x 2-43(x -3)2=-x 2+8x -12=-(x -4)2+4.故当x =4时,y 的最大值为4.综上,当x =4时,y 的值最大,最大值为4. B 级1.832 提示:当∠CAB =∠ACD =90°时,四边形ABCD 的面积达到最大值. 2. 0<r ≤1 提示:设BC =a ,CA =b ,AB =c ,b +c =r +1),又12bc sin60°=S △ABC =12(a +b +c )r ,即12bc ·2=12[r +1)]r ,. bc =4r (r +2). b ,c 为方程x 2-r +1)x +4r (r +2)=0的两个根,由△≥0,得(r +1)≤22.因r >0,r +1>0,故r +1≤2,即0<r ≤1. 3.249π提示:过P 作垂直于OP 的弦AB ,此时弓形面积最小. 4.13 提示:设AD AB =x ,则BD BA =1-x =CG CA ,ADG ABC S S ∆∆=x 2,BDE ABC S S ∆∆=(1-x )2=CFG ABCS S ∆∆,S 梯形DEFG =1―x 2―2(1-x )2=-3(x -23)2+13.5.12a 提示:当OA =OB 时,OC 的长最大. 6. C 7. (1)由Rt △ABP ∽Rt △PCQ ,得BP CQ =AB CP ,即x y =44x-,y =-14(x -2)2+1(0<x <4).当x =2时, y 最大值=1cm.(2)由14=-14(x -2)2+1,得x =(2cm 或(2cm.8. 当过A ,B 两点的圆与x 轴正半轴相切时,切点C 为所求.作O′D ⊥A B 于D .,O′D 2= O′B2-B D 2=2()2a b +-2()2a b -=ab ,O′DC0).9. (1)如图,延长CB 到L ,使BL =DN ,则Rt △ABL ≌Rt △ADN ,得AL =AN ,∠1=∠2,又∵N =2―CN ―CM =DN +BM =BL +BM =ML ,且AM =AM ,∠NAL =∠DAB =90°.∴△AMN ≌△AML ,故∠MAN =∠MAL =902=45°. (2)设CM =x ,CN =y ,MN =z ,则2222222,2,x y z x y z x y z x y z ++==--⎧⎧⇔⎨⎨+=+=⎩⎩,于是,(2―y ―z )2+y 2=z 2.整理得2y 2+(2z -4)y +(4-4z )=0.∵y >0,故△=4(z -2)2-32(1-z )≥0,即(z +2+(z +2-≥0.又∵z >0,故z2,当且仅当x =y =2.由于S △AMN =S △AML=12·ML ·AB =12 MN ×1=2z ,因此,△AMN 1.10. (1)提示:证明△ADF ∽△BAC .(2)①AB =15,BC =9,∠ACB =90°,∴AC12=,∴CF =AF =6,∴()()19632702y x x x =+⨯=+>. ②∵BC =9(定值),∴△PBC 的周长最小,就是PB +PC 最小,由(1)知,点C 关于直线DE 的对称点是点A ,所以PB +PC =PB +PA ,故只要求PB +PA 最小.显然当P 、A 、B 三点共线时PB +PA 最小,此时DP =DE ,PB +PA =AB . 由(1),角∠ADF =∠FAE ,∠DFA =∠ACB =90°,得△DAF ∽△ABC .EF ∥BC ,得AE =BE =12AB =152,EF =92.∴ AF ∶BC =AD ∶AB ,即6∶9=AD ∶15,∴AD =10.Rt △ADF 中,AD =10,AF =6,∴DF =8.∴DE =DF +FE =8+92=252.∴当x =252时,△PBC 的周长最小,此时y =1292.11.(1)令k =1,得y =x +2;令k =2,得y =2x +6,联立解得x =4,y =2,故定点(4,2). (2)取x =0,得OB =2-4k (k <0),取y =0,得OA =()420k k k-<.于是△ABO 的面积()()114224022k S OA OB k k k-==-<,化简得()28820k S k +-+=.由()28640S ∆=--≥得2160S S -≥,故S ≥16.将S =16代入上述方程,得k =12-.故当k =12-,S 值最小.12.(1)如图,延长EF 交AC 于点D ,DF ∥BC ,Rt △ADF ∽Rt △ACB ,AE =AC =x ,DE ==,x y x -=,2x -2y -xy =,两边平方整理得(x 2+2x +2)y 2-(x 3+2x 2+4x )y +2x 2=0.解得2222xy x x =++(y =x 舍去) .(2)由(1)212yxx==++.当且仅当2xx=,即x=等号成立.故当x=y1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学竞赛:平面几何中的最值问题
在平面几何中,我们常常遇到各种求最大值和最小值的问题,有时它和不等式联系在一起,统称最值问题.如果把最值问题和生活中的经济问题联系起来,可以达到最经济、最节约和最高效率.下面介绍几个简例.
例1 已知AB是半圆的直径,如果这个半圆是一块铁皮,ABDC是内接半圆的梯形,试问怎样剪这个梯形,才能使梯形ABDC的周长最大(图3-91)?
分析本例是求半圆AB的内接梯形的最大周长,可设半圆半径为R.由于AB ∥CD,必有AC=BD.若设CD=2y,AC=x,那么只须求梯形ABDC的半周长u=x+y+R 的最大值即可.
解作DE⊥AB于E,则
x2=BD2=AB·BE
=2R·(R-y)=2R2-2Ry,
所以
所以求u的最大值,只须求-x2+2Rx+2R2最大值即可.
-x2+2Rx+2R2=3R2-(x-R)2≤3R2,
上式只有当x=R时取等号,这时有
所以2y=R=x.
所以把半圆三等分,便可得到梯形两个顶点C,D,这时,梯形的底角恰为60°和120°.
例2 如图3-92是半圆与矩形结合而成的窗户,如果窗户的周长为8米(m),怎样才能得出最大面积,使得窗户透光最好?
分析与解设x表示半圆半径,y表示矩形边长AD,则必有
2x+2y+πx=8,
若窗户的最大面积为S,则
把①代入②有
即当窗户周长一定时,窗户下部矩形宽恰为半径时,窗户面积最大.
例3 已知P点是半圆上一个动点,试问P在什么位置时,PA+PB最大(图3-93)?
分析与解因为P点是半圆上的动点,当P近于A或B时,显然PA+PB渐小,在极限状况(P与A重合时)等于AB.因此,猜想P在半圆弧中点时,PA+PB取最大值.
设P为半圆弧中点,连PB,PA,延长AP到C,使PC=PA,连CB,则CB是切线.为了证PA+PB最大,我们在半圆弧上另取一点P′,连P′A,P′B,延长AP′到C′,使P′C′=BP′,连C′B,CC′,则
∠P′C′B=∠P′BC=∠PCB=45°,
所以A,B,C′,C四点共圆,所以
∠CC′A=∠CBA=90°,
所以在△ACC′中,AC>AC′,即
PA+PB>P′A+P′B.
例4 如图3-94,在直角△ABC中,AD是斜边上的高,M,N分别是△ABD,△ACD的内心,直线MN交AB,AC于K,L.求证:S△ABC≥2S△AKL.
证连结AM,BM,DM,AN,DN,CN.因为在△ABC中,∠A=90°,AD⊥BC于D,所以
∠ABD=∠DAC,∠ADB=∠ADC=90°.因为M,N分别是△ABD和△ACD的内心,所以
∠1=∠2=45°,∠3=∠4,
所以△ADN∽△BDM,
又因为∠MDN=90°=∠ADB,所以
△MDN∽△BDA,
所以∠BAD=∠MND.
由于∠BAD=∠LCD,所以
∠MND=∠LCD,
所以D,C,L,N四点共圆,所以
∠ALK=∠NDC=45°.
同理,∠AKL=∠1=45°,所以AK=AL.因为
△AKM≌△ADM,
所以AK=AD=AL.
而
而
从而
所以 S△ABC≥S△AKL.
例5 如图3-95.已知在正三角形ABC内(包括边上)有两点P,Q.求证:PQ≤AB.
证设过P,Q的直线与AB,AC分别交于P1,Q1,连结P1C,显然,PQ≤P1Q1.因为∠AQ1P1+∠P1Q1C=180°,所以∠AQ1P1和∠P1Q1C中至少有一个直角或钝角.若∠AQ1P1≥90°,则
PQ≤P1Q1≤AP1≤AB;
若∠P1Q1C≥90°,则
PQ≤P1Q1≤P1C.
同理,∠AP1C和∠BP1C中也至少有一个直角或钝角,不妨设∠BP1C≥90°,则
P1C≤BC=AB.
对于P,Q两点的其他位置也可作类似的讨论,因此,PQ≤AB.
例6 设△ABC是边长为6的正三角形,过顶点A引直线l,顶点B,C到l 的距离设为d1,d2,求d1+d2的最大值(1992年上海初中赛题).
解如图3-96,延长BA到B′,使AB′=AB,连B′C,则过顶点A的直线l或者与BC相交,或者与B′C相交.以下分两种情况讨论.
(1)若l与BC相交于D,则
所以
只有当l⊥BC时,取等号.
(2)若l′与B′C相交于D′,则
所以
上式只有l′⊥B′C时,等号成立.
例7 如图3-97.已知直角△AOB中,直角顶点O在单位圆心上,斜边与单位圆相切,延长AO,BO分别与单位圆交于C,D.试求四边形ABCD面积的最小值.
解设⊙O与AB相切于E,有OE=1,从而
即AB≥2.
当AO=BO时,AB有最小值2.从而
所以,当AO=OB时,四边形ABCD面积的最小值为
练习十八
1.设M为圆O外一定点,P为圆O上一动点.试求MP的最大值和最小值.
2.设AB是圆O的动切线,直线OA,OB保持互相垂直.如果圆O的半径为r,试求OA+OB的最小值.
3.一直角三角形的周长为10厘米(cm),则其面积的最大值是多少厘米?
4.已知l1∥l2,A,B是直线l1上的两个定点,且AB=10,l1,l2的距离为8,P为直线l2上的一个动点,试求△ABP周长的最小值.
5.如果矩形ABCD的周长为40厘米,那么这个矩形面积的最大值是多少平方厘米?。
