复数的概念(1)精选练习及答案
复数的概念及运算练习卷(含答案详解)

复数的概念及运算[基础巩固]1.已知复数z 1=a +2i ,z 2=3+(a 2-7)i ,a ∈R ,若z 1=z 2,则a =( )A .2B .3C .-3D .9 解析 因为z 1=a +2i ,z 2=3+(a 2-7)i ,且z 1=z 2,所以有⎩⎪⎨⎪⎧ a =3,a 2-7=2,解得a =3.故选B.答案 B2.若a ,b ∈R ,i 是虚数单位,a +2022i =2-b i ,则a 2+b i =( )A .2022+2iB .2022+4iC .2+2022iD .4-2022i 解析 因为a +2022i =2-b i ,所以a =2,-b =2022,即a =2,b =-2022,所以a 2+b i =4-2022i.答案 D3.(多选题)下列命题错误的是( )A .若x ,y ∈C ,则x +y i =1+i 的充要条件是x =y =1B .纯虚数集相对于复数集的补集是虚数集C .若(z 1-z 2)2+(z 2-z 3)2=0,则z 1=z 2=z 3D .若实数a 与a i 对应,则实数集与复数集一一对应解析 A 取x =i ,y =-i ,则x +y i =1+i ,但不满足x =y =1,故A 错误;B ,C 错误;对于D ,a =0时,a i =0,D 错误.答案 ABCD4.若复数z =a 2-3+2a i 的实部与虚部互为相反数,则实数a =________. 解析 由条件知a 2-3+2a =0,解得a =1或a =-3.答案 1或-35.如果(m 2-1)+(m 2-2m )i >1,则实数m =____________.解析 由题意得⎩⎪⎨⎪⎧m 2-2m =0,m 2-1>1,解得m =2. 答案 26.分别求满足下列条件的实数x ,y 的值.(1)2x -1+(y +1)i =x -y +(-x -y )i ;(2)x 2-x -6x +1+(x 2-2x -3)i =0. 解析 (1)∵x ,y ∈R ,∴由复数相等的定义得⎩⎪⎨⎪⎧ 2x -1=x -y ,y +1=-x -y ,解得⎩⎪⎨⎪⎧x =3,y =-2. (2)∵x ∈R ,∴由复数相等的定义得⎩⎪⎨⎪⎧ x 2-x -6x +1=0,x 2-2x -3=0,即⎩⎪⎨⎪⎧x =3或x =-2,且x ≠-1,x =3或x =-1,∴x =3. [能力提升]7.i 2021的虚部为( )A .1B .-1C .iD .-i解析 直接利用i 4=1,化简i 2021,再得到其虚部.因为i 2021=(i 4)505·i =i ,∴i 2021的虚部为1.故选A .答案 A8.已知z 1=(-4a +1)+(2a 2+3a )i ,z 2=2a +(a 2+a )i ,其中a ∈R .若z 1>z 2,则a 的取值集合为________.解析 ∵z 1>z 2,∴⎩⎪⎨⎪⎧ 2a 2+3a =0,a 2+a =0,-4a +1>2a ,∴a =0,故所求a 的取值集合为{0}.答案 {0}9.若复数z 1=m 2+1+(m 3+3m 2+2m )i ,z 2=4m -2+(m 2-5m )i ,m 为实数,且z 1>z 2,则实数m 的取值集合为________.解析 ∵z 1>z 2,∴⎩⎪⎨⎪⎧ m 3+3m 2+2m =0,m 2-5m =0,m 2+1>4m -2,解得m =0,∴实数m 的取值集合为{0}. 答案 {0}10.已知复数z 1=4-m 2+(m -2)i ,z 2=λ+2sin θ+(cos θ-2)i(其中i 是虚数单位,m ,λ,θ∈R ).(1)若z 1为纯虚数,求实数m 的值;(2)若z 1=z 2,求实数λ的取值范围. 解析 (1)∵z 1为纯虚数, 则⎩⎪⎨⎪⎧ 4-m 2=0,m -2≠0,解得m =-2. (2)由z 1=z 2,得⎩⎪⎨⎪⎧4-m 2=λ+2sin θ,m -2=cos θ-2, ∴λ=4-cos 2θ-2sin θ=sin 2θ-2sin θ+3 =(sin θ-1)2+2.∵-1≤sin θ≤1,∴当sin θ=1时,λmin =2, 当sin θ=-1时,λmax =6, ∴实数λ的取值范围是[2,6].[探索创新]11.定义运算⎪⎪⎪⎪⎪⎪ab c d =ad -bc ,如果(x +y )+(x +3)i =⎪⎪⎪⎪⎪⎪3x +2y i -y 1,求实数x ,y 的值. 解析 由定义运算⎪⎪⎪⎪⎪⎪a b c d =ad -bc ,得⎪⎪⎪⎪⎪⎪3x +2y i -y 1=3x +2y +y i , 故有(x +y )+(x +3)i =3x +2y +y i.因为x ,y 为实数,所以有⎩⎪⎨⎪⎧ x +y =3x +2y ,x +3=y , 得⎩⎪⎨⎪⎧2x +y =0,x +3=y ,得x =-1,y =2.。
《复数的概念》考点讲解复习与同步训练
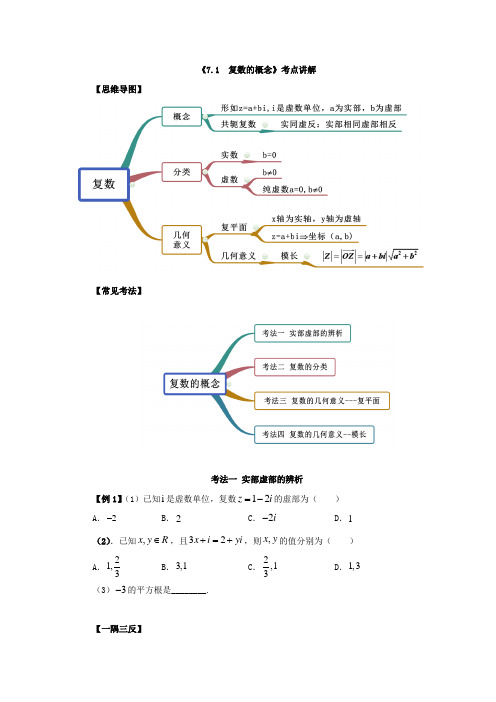
《7.1 复数的概念》考点讲解【思维导图】【常见考法】考法一 实部虚部的辨析【例1】(1)已知i 是虚数单位,复数12z i =-的虚部为( )A .2-B .2C .2i -D .1(2).已知,x y R ∈,且32x i yi +=+,则,x y 的值分别为( )A .21,3B .3,1C .2,13D .1,3(3)3-的平方根是________.【一隅三反】1. 1-的平方根为______.2.复数2(i 是虚数单位)的实部为( )A .2B .C .22-D .03.若复数1(1)2z i =-+,则z 的共轭复数的虚部是( ) A .12i - B .12i C .12- D .124.以2i -2+的实部为虚部的复数是( )A .2i +B .22i + CD .45i -考法二 复数的分类 【例2】已知复数()2262153m m z m m i m --=+--+(i 是虚数单位) (1)复数z 是实数,求实数m 的值;(2)复数z 是虚数,求实数m 的取值范围;(3)复数z 是纯虚数,求实数m 的值.【一隅三反】1.已知复数()()223183,z m m m m i m R =+-+-∈,其中i 为虚数单位.(1)若复数z 是实数,求实数m 的值;(2)若复数z 是纯虚数,求实数m 的值.2.复数()()()2152615z i m i m i =++-+-. (1)实数m 取什么数时,z 是实数;(2)实数m 取什么数时,z 是纯虚数;(3)实数m 取什么数时,z 对应的点在直线70x y ++=上.考法三 复数的几何意义--复平面【例3】(1)已知复数34z i =-+(i 虚单位),则复数z 在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限 (2)在复平面内,若复数()()2246z m m m m i =-+--所对应的点在第二象限,则实数m 的取值范围是( )A .()0,3B .(),2-∞-C .()2,0-D .()3,4 【一隅三反】1.在复平面内,复数1i +的共轭复数所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 2.设复数2z i =+,则z 的共轭复数z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.若()()11z m m i =++-(i 是虚数单位)在复平面内对应的点位于第四象限,则实数m 的取值范围为( )A .(),1-∞-B .(),1-∞C .()1,1-D .()1,-+∞考法四 复数的几何意义--模长【例4】(1)设i 虚数单位,复数12z i =+,则||z =( )A B .5 C .1 D .2(2)已知(26)12i x yi +=+,其中x 、y 是实数,则||x yi +=( )A .12B .32C .2D .2(3)设复数z 满足2z i -=,z 在复平面内对应的点为(),x y ,则( )A .()2214x y ++=B .()2212x y ++= C .()2214x y -+=D .()2214x y +-=【一隅三反】1.已知i 为虚数单位,实数x ,y 满足()3x i i y i +=-,则x yi +=( )A .10 BC .3D .12.复数12z i =-(其中i 为虚数单位),则3z i +=( )A .5 BC .2 D3.已知复数z 满足|2|1-+=z i ,则||z 的最小值为( )A1 B1 C1 D14.已知复数z 满足条件1z =,那么z i ++的最大值为______.《7.1 复数的概念(精讲)》考点讲解答案解析考法一 实部虚部的辨析【例1】(1)已知i 是虚数单位,复数12z i =-的虚部为( )B .2- B .2C .2i -D .1(2).已知,x y R ∈,且32x i yi +=+,则,x y 的值分别为( )A .21,3B .3,1C .2,13D .1,3(3)3-的平方根是________.【答案】(1)A (2)C (3)【解析】(1)复数12z i =-的虚部为2-.故选:A.(2)由题意知,321x y =⎧⎨=⎩,解得231x y ⎧=⎪⎨⎪=⎩,故选: C. (3)由()23=-得解.【一隅三反】1.1-的平方根为______.【答案】i ±【解析】()21i ±=-,因此,1-的平方根为i ±.故答案为i ±.2.复数2(i 是虚数单位)的实部为( )A .2B .C .2-D .0【答案】A【解析】根据复数的基本概念,可得复数22-的实部为2.故选:A . 3.若复数1(1)2z i =-+,则z 的共轭复数的虚部是( ) A .12i -B .12iC .12-D .12 【答案】D 【解析】因为复数111(1)222z i i =-+=--,所以z 的共轭复数1122z i =-+,虚部是12,故选:D .4.以2i -2+的实部为虚部的复数是( )A .2i +B .22i +CD .45i - 【答案】B【解析】22i i =的虚部为222+=+的实部为2,则复数为22z i =+故选:B.考法二 复数的分类【例2】已知复数()2262153m m z m m i m --=+--+(i 是虚数单位) (1)复数z 是实数,求实数m 的值;(2)复数z 是虚数,求实数m 的取值范围;(3)复数z 是纯虚数,求实数m 的值.【答案】(1)5m =;(2)5m ≠且3m ≠-;(3)3m =或2.【解析】(1)复数z 是实数,则2215030m m m ⎧--=⎨+≠⎩,解得5m =; (2)复数z 是虚数,则221503m m m ⎧--≠⎨≠-⎩,解得5m ≠且3m ≠-;(3)复数是纯虚数,则226032150m m m m m ⎧--=⎪≠-⎨⎪--≠⎩,解得3m =或2.【一隅三反】1.已知复数()()223183,z m m m m i m R =+-+-∈,其中i 为虚数单位.(1)若复数z 是实数,求实数m 的值;(2)若复数z 是纯虚数,求实数m 的值.【答案】(1)0或3;(2)6-.【解析】(1)若复数z 是实数,则230m m -=所以0m =或3m =. (2)若复数z 是纯虚数,则22303180m m m m ⎧-≠⎨+-=⎩所以6m =-. 2.复数()()()2152615z i m i m i =++-+-. (1)实数m 取什么数时,z 是实数;(2)实数m 取什么数时,z 是纯虚数;(3)实数m 取什么数时,z 对应的点在直线70x y ++=上.【答案】(1)5m =或3-;(2)2m =-;(3)12m =或2- 【解析】复数222(1)(52)(615)(56)(215)z i m i m i m m m m i =++-+-=+++--.(1)由22150m m --=,解得5m =或3-.5m ∴=或3-时,复数z 为实数.(2)由225602150m m m m ⎧++=⎨--≠⎩,解得2m =-.2m ∴=-时,复数z 为纯虚数.(3)由22(56)(215)70m m m m +++--+=.化为:22320m m +-=, 解得12m =或2-.12m ∴=或2-,z 对应点在直线70x y ++=上.考法三 复数的几何意义--复平面【例3】(1)已知复数34z i =-+(i 虚单位),则复数z 在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限 (2)在复平面内,若复数()()2246z m m m m i =-+--所对应的点在第二象限,则实数m 的取值范围是( )A .()0,3B .(),2-∞-C .()2,0-D .()3,4【答案】(1)B (2)D【解析】(1)由复数的几何意义知,复数34z i =-+在复平面内对应的点为()3,4-,即在第二象限,故选:B(2)∵在复平面内,若复数()()2246z m m m m i =-+--所对应的点在第二象限, ∴224060m m m m ⎧-<⎨-->⎩解得34x <<∴实数m 的取值范围是()3,4故选:D. 【一隅三反】1.在复平面内,复数1i +的共轭复数所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】D 【解析】复数1i +的共轭复数为1i -,∴其对应的点()1,1-位于第四象限.故选:D.2.设复数2z i =+,则z 的共轭复数z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】D【解析】复数2z i =+的共轭复数2z i =-,则对应点的坐标为()2,1-,该点位于第四象限,故选:D.3.若()()11z m m i =++-(i 是虚数单位)在复平面内对应的点位于第四象限,则实数m 的取值范围为( )A .(),1-∞-B .(),1-∞C .()1,1-D .()1,-+∞【答案】C 【解析】()()11z m m i =++-对应的点为()1,1m m +-,因为对应的点位于第四象限,得1010m m +>⎧⎨-<⎩,解得11m -<<.故选:C.考法四 复数的几何意义--模长【例4】(1)(设i 虚数单位,复数12z i =+,则||z =( )A B .5 C .1 D .2(2)已知(26)12i x yi +=+,其中x 、y 是实数,则||x yi +=( )A .12B .32C .2D .2(3)设复数z 满足2z i -=,z 在复平面内对应的点为(),x y ,则( )A .()2214x y ++=B .()2212x y ++=C .()2214x y -+=D .()2214x y +-= 【答案】(1)A (2)C (3)D【解析】(1)||z == A(2)因为2612x xi yi +=+,所以21x =,62x y =,解得12x =,332y x ==,所以x yi +==,故选:C. (3)z 在复平面内对应的点为(),x y ,则复数()=,z x yi x y R +∈, 则()=12z i x y i -=+-,由复数的模长公式可得()22+1=4x y -,故选:D 【一隅三反】1.已知i 为虚数单位,实数x ,y 满足()3x i i y i +=-,则x yi +=( )A .10BC .3D .1【答案】B【解析】由(3)x i i y i +=-,得3xi y i -+=-,1x ∴=-,3y =-.则||x yi +故选:B .2.复数12z i =-(其中i 为虚数单位),则3z i +=( )A .5B C .2 D 【答案】B【解析】因为12z i =-,所以31231z i i i i +=-+=+所以3z i +==故选:B .3.已知复数z 满足|2|1-+=z i ,则||z 的最小值为( )A 1B 1C 1D 1 【答案】A【解析】设z a bi =+,则()2211a bi i a b i +-+=-++==, 由()()22211x y -++=,表示为以()2,1-为圆心,1为半径的圆,1,因为z =1,故选:A.4.已知复数z 满足条件1z =,那么z i ++的最大值为______.【答案】4【解析】因为1z =,所以复数z 对应的点在单位圆上,z i +表示复数z 对应的点与复数i -对应的点()1M --之间的距离,而3OM ==.所以z i +的最大值为14OM r OM +=+=.故答案为:4《7.1 复数的概念(精练)》同步练习【题组一 实部虚部辨析】1.若(2)x i i y i +=+,其中,x y R ∈,i 为虚数单位,则复数z x yi =+的虚部为( )A .1B .iC .2-D .2i -2.设i 为虚数单位,则复数55z i =-的实部为( )A .5-B .5i -C .5D .5i3.复数3z i =-的虚部是( )A .1B .iC .-1D .i -4.数24i z =--的虚部是( )A .2-B .2C .4-D .45.已知复数1z i =-,其中i 是虚数单位,则复数z 的虚部为( )A .iB .i -C .1-D .1【题组二 复数的分类】1.已知复数()()1i 1i z m =--+是纯虚数,则实数m =( )A .-2B .-1C .0D .1 2. i 为虚数单位,已知复数21(1)a a i -+-是纯虚数,则a 等于( )A .±1B .1C .1-D .03.设复数i z a b =+(其中a b R ∈、,i 为虚数单位),则“0a =”是“z 为纯虚数”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件4.已知a 为实数,若复数()24(2)z a a i =-++为纯虚数,则复数z 的虚部为( )A .2B .4iC .2±D .4 5.已知i 为虚数单位,a R ∈,复数()242a a i -+-是纯虚数,则a =( )A .2B .-2C .4D .-2或26.若复数(1)(2)z m m i =++-(m ∈R )是纯虚数,则m =______ 7.已知复数223(3)z m m m i =--+-为纯虚数,则实数m =_____________8.实数m 取怎样的值时,复数()22153m m z i m --=-+是: (1)实数? (2)虚数? (3)纯虚数?9.已知复数()()11z m m i m R =++-∈. (1)m 取什么值时,z 为实数; (2)m 取什么值时,z 为纯虚数.10.已知m 为实数,i 为虚数单位,设复数()()2256253z m m m m i =++++-. (1)当复数z 为纯虚数时,求m 的值;(2)当复数z 对应的复点在直线70x y -+=的右下方,求m 的取值范围.【题组三 复数的几何意义--复平面】1.在复平面内,复数1i -+所对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限2.若,a b ∈R ,则复数()()224526a a b b i -++-+-表示的点在( ) A .在第一象限 B .在第二象限 C .在第三象限D .在第四象限3.复数()()2lg 2221()x xz x i x R -=-+-+-∈在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限4.设复数1z ,2z 在复平面内对应的点关于虚轴对称,且12z i =+,则2z =( ) A .2i +B .2i -+C .2i -D .2i --5.已知()()214Z m m i =++-在复平面内对应的点在第二象限,则实数m 的取值范围是____.6.已知复数()()22lg 223z m m m m i =-++-若复数z 是实数,则实数m =_____;若复数z 对应的点位于复平面的第二象限,则实数的取值范围为________.7.在复平面内,复数()()222z m m m i =++--对应的点在第一象限,求实数m 的取值范围是________.【题组四 复数的几何意义--模长】1.已知a R ∈,若有a i -=i 为虚数单位),则a =( ) A .1B .2-C .2±D .±12.设复数z 满足1z i -=,z 在复平面内对应的点为(),x y 则x ,y 满足的关系式为______.3.已知a ,b R ∈,()123ai b a i +=++,则a =______,3a bi +=______. 4.知i 是虚数单位,若1z i =+,则22z z -=________. 5.若z C ∈且342z i ++≤,则z 的取值范围为__________. 【题组五 复数综合应用】1.(多选)已知复数1z i =+(其中i 为虚数单位),则以下说法正确的有( )A .复数z 的虚部为iB .z =C .复数z 的共轭复数1z i =-D .复数z 在复平面内对应的点在第一象限2.若复数12z i =+(i 为虚数单位),则下列命题正确的是( )A .z 是纯虚数B .z 的实部为2C .z 的共轭复数为12i -+D .z 3.已知复数z 在复平面上对应的点为()1,1-,则( ) A .z i +是实数(i 为虚数单位) B .z i +是纯虚数(i 为虚数单位) C .1z +是实数 D .1z +是纯虚数4.关于复数3-4i 的说法正确的是( )①实部和虚部分别为3和-4;②复数模为5③在复平面内对应的点在第四象限;④共轭复数为3+4i A .①③ B .①②④C .①②③④D .①③④《7.1 复数的概念(精练)》同步练习答案解析【题组一 实部虚部辨析】1.若(2)x i i y i +=+,其中,x y R ∈,i 为虚数单位,则复数z x yi =+的虚部为( ) A .1 B .iC .2-D .2i -【答案】C【解析】由于(2)x i i y i +=+,则1x=且2y =-,所以12z x yi i =+=-,所以复数z 的虚部为2-.故选:C.2.设i 为虚数单位,则复数55z i =-的实部为( ) A .5- B .5i -C .5D .5i【答案】C【解析】复数55z i =-的实部为5.故选:C. 3.复数3z i =-的虚部是( ) A .1 B .iC .-1D .i -【答案】C【解析】由复数虚部的定义得复数3z i =-的虚部是1-.故选:C 4.复数24i z =--的虚部是( ) A .2- B .2C .4-D .4【答案】C【解析】因为24i z =--,所以由复数定义可知虚部是4-,故选:C. 5.已知复数1z i =-,其中i 是虚数单位,则复数z 的虚部为( ) A .i B .i -C .1-D .1【答案】C【解析】因为1z i =-,则虚部为1-.故选:C.【题组二 复数的分类】1.已知复数()()1i 1i z m =--+是纯虚数,则实数m =( ) A .-2 B .-1C .0D .1【答案】D【解析】()()()1i 1i 11i z m m m =--+=--+,因为z 为纯虚数且m 为实数,故1010m m -=⎧⎨+≠⎩,故1m =, 故选:D2. i 为虚数单位,已知复数21(1)a a i -+-是纯虚数,则a 等于( ) A .±1 B .1C .1-D .0【答案】C【解析】复数21(1)a a i -+-是纯虚数,所以21010a a ⎧-=⎨-≠⎩,得1a =-.故选:C.3.设复数i z a b =+(其中a b R ∈、,i 为虚数单位),则“0a =”是“z 为纯虚数”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件【答案】B【解析】若复数i z a b =+是纯虚数,则0a =,0b ≠, 则0a =不能证得z 为纯虚数,z 为纯虚数可以证得0a =, 故“0a =”是“z 为纯虚数”的必要非充分条件, 故选:B.4.已知a 为实数,若复数()24(2)z a a i =-++为纯虚数,则复数z 的虚部为( ) A .2 B .4iC .2±D .4【答案】D【解析】2(4)(2)z a a i =-++为纯虚数,∴24020a a ⎧-=⎨+≠⎩,即2a =.∴复数z 的虚部为4.故选:D .5.已知i 为虚数单位,a R ∈,复数()242a a i -+-是纯虚数,则a =( )A .2B .-2C .4D .-2或2【答案】B【解析】因为复数()242a a i -+-是纯虚数,所以240,202a a a -=-≠∴=-故选:B6.若复数(1)(2)z m m i =++-(m ∈R )是纯虚数,则m =______ 【答案】-1【解析】复数(1)(2)z m m i =++-(m ∈R )是纯虚数,则1020m m +=⎧⎨-≠⎩,所以1m =-. 故答案为:-17.已知复数223(3)z m m m i =--+-为纯虚数,则实数m =_____________【答案】1-【解析】由题意,复数223(3)z m m m i =--+-为纯虚数,则满足223030m m m ⎧--=⎨-≠⎩,解得1m =-,即实数m 的值为1-.故答案为:1-.8.实数m 取怎样的值时,复数()22153m m z i m --=-+是: (1)实数? (2)虚数? (3)纯虚数?【答案】(1)5m =或3m =-;(2)5m ≠且3m ≠-;(3)3m =. 【解析】(1)若22150m m --=,则z 为实数,此时3m =-或者5m =. (2)若22150m m --≠,则z 为虚数,此时3m ≠-且5m ≠.(3)若2302150m m m -=⎧⎨--≠⎩ ,则z 为纯虚数,此时3m =.9.已知复数()()11z m m i m R =++-∈.(1)m 取什么值时,z 为实数; (2)m 取什么值时,z 为纯虚数. 【答案】(1)1m =(2)1m =-【解析】(1)复数()()11z m m i m R =++-∈,若z 为实数,则10m -=,即1m =(2)若z 为纯虚数,则1010m m +=⎧⎨-≠⎩,解得1m =-10.已知m 为实数,i 为虚数单位,设复数()()2256253z m m m m i =++++-. (1)当复数z 为纯虚数时,求m 的值;(2)当复数z 对应的复点在直线70x y -+=的右下方,求m 的取值范围. 【答案】(1)2-;(2)(4,4)-.【解析】(1)由题意得:225602530m m m m ⎧++=⎨+-≠⎩,解得2m =-;(2)复数z 对应的点的坐标为22(56,253)m m m m +++-, 直线70x y -+=的右下方的点的坐标(),x y 应满足70x y -+>, 所以22(56)(253)70m m m m ++-+-+>, 解得44m -<<,所以m 的取值范围为(4,4)-. 【题组三 复数的几何意义--复平面】1.在复平面内,复数1i -+所对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】B【解析】由题,1i -+在复平面内对应的点为()1,1-,在第二象限,故选:B 2.若,a b ∈R ,则复数()()224526a a b b i -++-+-表示的点在( ) A .在第一象限 B .在第二象限 C .在第三象限 D .在第四象限【答案】D【解析】因为()2245210a a a -+=-+>,()2226150b b b -+-=---<, 所以由复数的几何意义知该复数表示的点在第四象限.故选:D3.复数()()2lg 2221()x xz x i x R -=-+-+-∈在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】C【解析】复数()()2lg 2221()x xz x i x R -=-+-+-∈的实部()2lg 2a x -=+、虚部()221x x b -=-+-.因为()22221lg 20x x +≥>⇒+>,所以0a <. 因为21122202x x x x --≥-+⇒≥>+,所以0b <. 所以复数z 在复平面内对应的点位于第三象限.故选:C4.设复数1z ,2z 在复平面内对应的点关于虚轴对称,且12z i =+,则2z =( ) A .2i + B .2i -+C .2i -D .2i --【答案】B 【解析】12z i =+,1z ∴在复平面内对应点的坐标为(2,1),由复数1z ,2z 在复平面内对应的点关于虚轴对称,可知2z 在复平面内对应的点的坐标为(2,1)-,22z i ∴=-+,故选:B .5.已知()()214Z m m i =++-在复平面内对应的点在第二象限,则实数m 的取值范围是____.【答案】(),2-∞-【解析】()()214Z m m i =++-在复平面内对应的点()21,4m m +-在第二象限,所以21040m m +<⎧⎨->⎩,解得2m <-,即实数m 的取值范围是(),2-∞-.故答案为:(),2-∞-6.已知复数()()22lg 223z m m m m i =-++-若复数z 是实数,则实数m =________;若复数z 对应的点位于复平面的第二象限,则实数的取值范围为________.【答案】3- 21m <<【解析】z 为实数,则2230m m +-=,解得1m =或3-,又220m m ->,所以3m =-.z对应点在第二象限,则22lg(2)0230m m m m ⎧-<⎨+->⎩,解得21m <<+.故答案为:3-;21m <<.7.在复平面内,复数()()222z m m m i =++--对应的点在第一象限,求实数m 的取值范围是________.【答案】()()2,12,--+∞【解析】根据题意得出22020m m m +>⎧⎨-->⎩,解得21m -<<-或>2m ,所以实数m 的取值范围是()()2,12,--+∞.故答案为:()()2,12,--+∞.【题组四 复数的几何意义--模长】1.已知a R ∈,若有a i -=i 为虚数单位),则a =( ) A .1 B .2-C .2±D .±1【答案】C【解析】因为a R ∈所以a i -==,即215a +=,解得2a =±,故选:C2.设复数z 满足1z i -=,z 在复平面内对应的点为(),x y 则x ,y 满足的关系式为______.【答案】22(1)1y x +-=【解析】由题意,设复数(,)z x yi x y R =+∈,因为1z i -=1=,整理得22(1)1y x +-=,即复数z 在复平面内对应的点为(),x y 则,x y 满足的关系式为22(1)1y x +-=.故答案为:22(1)1y x +-=.3.已知a ,b R ∈,()123ai b a i +=++,则a =______,3a bi +=______.【答案】3-【解析】∵()123ai b a i +=++∴123ba a =⎧⎨=+⎩,解得31a b =-⎧⎨=⎩,则333a bi i +=-+===故答案为:(1)3-;(2)4.已知i 是虚数单位,若1z i =+,则22z z -=________. 【答案】2【解析】根据复数模的计算公式得:22212+222z z i i i -=+--=.故答案为:2 5.若z C ∈且342z i ++≤,则z 的取值范围为__________. 【答案】[]3,7【解析】342z i ++≤的几何意义为复平面内动点Z 到定点()3,4A --的距离小于等于2的点的集合,z 表示复平面内动点Z 到原点的距离,∵||5OA ==,5252z ∴-≤≤+.∴z 的取值范围为[]3,7. 故答案为:[]3,7. 【题组五 复数综合应用】1.(多选)已知复数1z i =+(其中i 为虚数单位),则以下说法正确的有( )A .复数z 的虚部为iB .z =C .复数z 的共轭复数1z i =- D .复数z 在复平面内对应的点在第一象限【答案】BCD【解析】因为复数1z i =+, 所以其虚部为1,即A 错误;z ==B 正确;复数z 的共轭复数1z i =-,故C 正确;复数z 在复平面内对应的点为()1,1,显然位于第一象限,故D 正确. 故选:BCD.2.若复数12z i =+(i 为虚数单位),则下列命题正确的是( )A .z 是纯虚数B .z 的实部为2C .z 的共轭复数为12i -+D .z 【答案】D【解析】复数12z i =+(i 为虚数单位)显然不是纯虚数,12z i =+的实部是1,z 的共轭复数为12i -,z =D 正确,故选:D.3.已知复数z 在复平面上对应的点为()1,1-,则( ) A .z i +是实数(i 为虚数单位) B .z i +是纯虚数(i 为虚数单位) C .1z +是实数 D .1z +是纯虚数 【答案】D【解析】由题意可得,1z i =-+,则1z i +=为纯虚数,12z i i +=-+是虚数,但不是纯虚数,故选:D .4.关于复数3-4i 的说法正确的是( ) ①实部和虚部分别为3和-4;②复数模为5③在复平面内对应的点在第四象限;④共轭复数为3+4i A .①③ B .①②④C .①②③④D .①③④【答案】C【解析】复数3-4i 的实部和虚部分别为3和-4,①正确;复数模为5,②正确; 在复平面内对应的点为(3,4)-在第四象限,③正确;复数3-4i 的共轭复数为3+4i ,④正确.故选:C.。
复数练习题附答案

复数练习题附答案复数是数学中的一个基本概念,它拓展了实数的概念,允许我们处理像-1的平方根这样的数。
复数可以表示为a + bi的形式,其中a和b是实数,i是虚数单位,满足i^2 = -1。
下面是一些复数的练习题,以及它们的答案。
练习题1:计算以下复数的加法:\[ (3 + 4i) + (1 - 2i) \]答案1:首先分别将实部和虚部相加:\[ 3 + 1 = 4 \]\[ 4i - 2i = 2i \]所以,结果是 \( 4 + 2i \)。
练习题2:计算以下复数的乘法:\[ (2 + 3i) \times (1 - 4i) \]答案2:使用分配律:\[ 2 \times 1 + 2 \times (-4i) + 3i \times 1 + 3i \times (-4i) \]\[ = 2 - 8i + 3i - 12i^2 \]由于 \( i^2 = -1 \),所以:\[ = 2 - 5i + 12 \]结果是 \( 14 - 5i \)。
练习题3:求复数 \( z = 3 - 2i \) 的共轭复数。
答案3:共轭复数是将虚部的符号改变得到的数,所以:\[ \bar{z} = 3 + 2i \]练习题4:求复数 \( z = 2 + i \) 的模(magnitude)。
答案4:复数的模定义为:\[ |z| = \sqrt{a^2 + b^2} \]其中 \( a \) 和 \( b \) 分别是复数的实部和虚部。
所以:\[ |2 + i| = \sqrt{2^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5} \] 练习题5:求复数 \( z = 1 + i \) 的逆。
答案5:复数的逆通过公式 \( \frac{1}{z} =\frac{\bar{z}}{|z|^2} \) 计算。
首先求模:\[ |1 + i| = \sqrt{1^2 + 1^2} = \sqrt{2} \]然后求共轭复数:\[ \bar{z} = 1 - i \]最后求逆:\[ \frac{1}{1 + i} = \frac{1 - i}{2} \]因为 \( |1 + i|^2 = 2 \)。
(完整版)复数经典例题

经典例题透析类型一:复数的有关概念例1.已知复数22276(56)()1a az a a i a Ra-+=+--∈-,试求实数a分别取什么值时,z分别为:(1)实数;(2)虚数;(3)纯虚数.思路点拨:根据复数z为实数、虚数及纯虚数的概念,判断实部与虚部取值情况.利用它们的充要条件可分别求出相应的a值.解析:(1)当z为实数时,有2256010a aa⎧--=⎪⎨-≠⎪⎩1661a aaa=-=⎧⇒⇒=⎨≠±⎩或,∴当6a=时,z为实数. (2)当z为虚数时,有2256010a aa⎧--≠⎪⎨-≠⎪⎩16161a aa aa≠-≠⎧⇒⇒≠±≠⎨≠±⎩且且,∴当a∈(-∞,-1)∪(-1,1)∪(1,6)∪(6,+∞)时,z为虚数. (3)当z为纯虚数时,有222560761a aa aa⎧--≠⎪⎨-+=⎪-⎩166a aaa≠-≠⎧⇒⇒∈∅⎨=⎩且∴不存在实数a使z为纯虚数.总结升华:由于a∈R,所以复数z的实部与虚部分为22761a aa-+-与256a a--.①求解第(1)小题时,仅注重虚部等于零是不够的,还需考虑它的实部是否有意义,否则本小题将出现增解;②求解第(2)小题时,同样要注意实部有意义的问题;③求解第(3)小题时,既要考虑实数为0(当然也要考虑分母不为0),还需虚部不为0,两者缺一不可.举一反三:【变式1】设复数z=a+bi (a 、b ∈R ),则z 为纯虚数的必要不充分条件是( )A .a=0B .a=0且b ≠0C .a ≠0且b=0D .a ≠0且b ≠0【答案】A ;由纯虚数概念可知:a=0且b ≠0是复数z=a+bi (a 、b ∈R )为纯虚数的充要条件.而题中要选择的是必要不充分条件,对照各选择支的情况,应选择A.【变式2】若复数2(32)(1)a a a i -++-是纯虚数,则实数a 的值为( )A.1B.2C.1或2D.-1【答案】B ;∵2(32)(1)a a a i -++-是纯虚数,∴2320a a -+=且10a -≠,即2a =.【变式3】如果复数2()(1)m i mi ++是实数,则实数m=( )A .1B .-1 CD.【答案】B ;【变式4】求当实数m 取何值时,复数22(2)(32)z m m m m i =--+-+分别是:(1)实数; (2)虚数; (3)纯虚数.【答案】(1)当2320m m -+=即1m =或2m =时,复数z 为实数;(2)当2320m m -+≠即1m ≠且2m ≠时,复数z 为虚数;(3)当⎪⎩⎪⎨⎧≠+-=--0230222m m m m 即1m =-时,复数z 为纯虚数. 类型二:复数的代数形式的四则运算例2. 计算:(1)()n i n N +∈; (2)8(1)i +(3)(12)(12)i i +÷-; (4)ii i i 4342)1)(41(++++- 解析:(1)∵21i =-,∴32i i i i =⋅=-,4221i i i =⋅=,同理可得:当41()n k k N +=+∈时,4144()k k k i i i i i i +=⋅=⋅=当42()n k k N +=+∈时,42421k k i i i +=⋅=-,当43()n k k N +=+∈时,4343k k ii i i +=⋅=- 当44()n k k N +=+∈时,4444()1k k k i i i i =⋅==,∴4114243144n i n k k N n k k N i i n k k N n k k N =+∈⎧⎪-=+∈⎪=⎨-=+∈⎪⎪=+∈⎩(,)(,)(,)(,)()n N +∈ (2)8(1)i +24444[(1)](2)216i i i =+=== (3)(12)(12)i i +÷-1212i i+=-2222(12)(12)1(2)43434(12)(12)1(2)555i i i i i i i i i ++++-+====-+-+- (4)i i i i 4342)1)(41(++++-1432434i i i +-++=+227(7)(34)3434i i i i ++-==++ 21432825251.2525i i i i ++--===- 总结升华:熟练运用常见结论: 1)ni 的“周期性”(n N +∈)2)2(1)2i i ±=±3)22()()a bi a bi a b +-=+ 举一反三:【变式1】计算:(1)(5―6i)+(―2―i)―(3+4i)(2)(12)(34)(2)i i i +--(3)23100i i i i ⋅⋅⋅⋅L(4)3322(1)(1)(1)(1)i i i i +--+-- ; 【答案】(1)(5―6i)+(―2―i)―(3+4i)=[(5―2)+(―6―1)i]―(3+4i)=(3―7i)―(3+4i)=(3―3)+(―7―4)i=―11i.(2)(12)(34)(2)(112)(2)247i i i i i i +--=+-=-(3)231001210050504126222()1i i i i i i i i i +++⋅⋅⋅⋅===⋅==-L L(4)332222(1)(1)(1)(1)(1)(1)2(1)2(1)(1)(1)2(2)4i i i i i i i i i i i i i i i +--+⋅+---++-==+----2214i i⋅== 【变式2】复数()221i i +=( )A.4-B.4C.4i -D.4i【答案】A ;()()222121212244i i i i i i i +=+-=⨯==-【变式3等于( )i +i 【答案】A1-i i ===,故选A 【变式4】复数31()i i -等于( )A.8B.-8C.8iD.-8i【答案】D ;333311()()(2)88i i i i i i i--=+===-. 类型三:复数相等的充要条件例3、已知x 是实数,y 是纯虚数,且满足(2x ―1)+(3―y)i=y ―i ,求x 、y.思路点拨:因x ∈R ,y 是纯虚数,所以可设y=bi (b ∈R 且b ≠0),代入原式,由复数相等的充要条件可得方程组,解之即得所求结果.解析:∵y 是纯虚数,可设y=bi (b ∈R ,且b ≠0),则(2x ―1)+(3―y)i =(2x ―1)+(3―bi )i =(2x -1+b )+3i ,y ―i =bi -i=(b -1)i由(2x ―1)+(3―y)i=y ―i 得(2x ―1+b )+3i=(b ―1)i , 由复数相等的充要条件得42103132b x b b x =⎧-+=⎧⎪⇒⎨⎨-==-⎩⎪⎩, ∴32x =-,4y i =. 总结升华:1. 复数定义:“形如z a bi =+(,a b R ∈)的数叫复数”就意味凡是复数都能写成这一形式,求一个复数,使用一个复数都可通过这一形式将问题化虚为实,把复数问题转化为实数问题来研究.这是解决复数问题的常用方法.2.复数相等是复数问题实数化的有效途径之一,由两复数a+bi 与c+di (a ,b ,c ,d ∈R )相等的充要条件是a=c 且b=d ,可得到两个实数等式.3.注意左式中的3―y 并非是(2x ―1)+(3―y)i 的虚部,同样,在右边的y ―i 中y 也并非是实部.举一反三:【变式1】设x 、y 为实数,且5______1-1-21-3x y x y i i i+=+=,则 【答案】由51-1-21-3x y i i i +=得5(1)(12)(13)2510x y i i i +++=+ 即5x(1+i)+2y(1+2i)=5(1+3i),即(5x+2y-5)+(5x+4y-15)i=0,故52-50-154-1505x y x x y y +==⎧⎧⎨⎨+==⎩⎩,解得 ∴4x y +=【变式2】若z ∈C 且(3+z)i=1(i 为虚数单位),则z=____.【答案】设z=a+bi(a,b ∈R),则(3+z)i=-b+(3+a)i=1由复数相等的充要条件得 b=-1且a=-3,即z=-3-i.【变式3】设复数z 满足12i i z+=,则z =( ) A .2i -+ B .2i -- C .2i - D .2i + 【答案】12(12)2211i i i i z i i ++-====---,故选C. 类型四:共轭复数例4:求证:复数z 为实数的充要条件是z z =思路点拨:需要明确两个复数相等的条件以及共轭复数的概念解析:设z a bi =+(a ,b ∈R ),则z a bi =- 充分性:--0;z z a bi a bi b b b z R =⇒+=⇒=⇒=⇒∈Q 必要性:,0-z R b a bi a bi z z ∈=⇒+=⇒=Q综上,复数z 为实数的充要条件为z z =举一反三:【变式1】,x y R ∈,复数(32)5x y xi ++与复数(2)18y i -+的共轭复数相等,求x ,y. 【答案】(2)1818(2)y i y i -+=+-3218-218-(-2)(32)52-512x y x y i x y xi y x y +==⎧⎧∴=++⇒⇒⎨⎨==⎩⎩ 【变式2】若复数z 同时满足2z z i -=,z iz =(i 为虚数单位),则z=________.【答案】―1+i【变式3】已知复数z=1+i ,求实数a 、b 使22(2)az bz a z +=+.【答案】∵z=1+i ,∴2(2)(2)az bz a b a b i +=++-,22(2)(2)44(2)a z a a i +=+-++2(4)4(2)a a a i =+++∵a 、b 都是实数,∴由22(2)az bz a z +=+得224,24(2).a b a a a b a ⎧+=+⎨-=+⎩ 两式相加,整理得a 2+6a+8=0解得a 1=―2,a 2=―4,对应得b 1=-1,b 2=2.∴所求实数为a=―2,b=―1或a=-4,b=2.类型五:复数的模的概念例5、已知数z 满足z+|z|=2+8i ,求复数z.法一:设z=a+bi (a ,b ∈R),则||z =代入方程得28a bi i +=+.∴28a b ⎧⎪=⎨=⎪⎩,解得158a b =-⎧⎨=⎩∴z=-15+8i法二:原式可化为:z=2-|z|+8i ,∵|z|∈R ,∴2-|z|是z 的实部.于是||z =|z|2=68-4|z|+|z|2,∴|z|=17,代入z=2-|z|+8i得z=-15+8i.举一反三:【变式】已知z=1+i ,a ,b 为实数.(1)若234z z ω=+-,求||ω; (2)若2211z az b i z z ++=--+,求a ,b 的值. 【答案】(1)2(1)3(1)4i i ω=++--2341i i i =+--=-∴||ω=(2)∵2222(1)(1)1(1)(1)1z az b i i a b z z i i ++++++=-++-++(2)(2)()a i b a a b a i i+++==+-+ ∴(2)()1a a b i i +-+=-∴21112a a ab b +==-⎧⎧⇒⎨⎨+==⎩⎩ 类型六:复数的几何意义例6、已知复数22(23)(43)z m m m m i =--+-+(m ∈R )在复平面上对应的点为Z ,求实数m 取什么值时,点Z (1)在实轴上;(2)在虚轴上;(3)在第一象限.思路点拨:根据点Z 的位置确定复数z 实部与虚部取值情况.解析:(1)点Z 在实轴上,即复数z 为实数,由2-43031m m m m +=⇒==或∴当31m m ==或时,点Z 在实轴上.(2)点Z 在虚轴上,即复数z 为纯虚数或0,故2230m m --=-13m m ⇒==或∴当-13m m ==或时,点Z 在虚轴上.3)点Z 在第一象限,即复数z 的实部虚部均大于0由22230430m m m m ⎧-->⎪⎨-+>⎪⎩ ,解得m <―1或m >3∴当m <―1或m >3时,点Z 在第一象限.终结升华:复平面上的点与复数是一一对应的,点的坐标的特点即为复数实部、虚部的特征.举一反三:【变式1】在复平面内,复数sin 2cos2z i =+对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】∵22ππ<<,∴sin 20>,cos20<,故相应的点在第四象限,选D.【变式2】已知复数2(352)(1)z m m m i =-++-(m R ∈),若z 所对应的点在第四象限,求m 的取值范围.【答案】∵2(352)(1)z m m m i =-+-- ∴⎩⎨⎧<-->+-0)1(02532m m m ,解得1m >.∴m 的取值范围为(1,)m ∈+∞.【变式3】已知z 是复数,2z i +和i-z z 均为实数,且复数2()z ai +对应的点在第一象限,求实数a 的取值范围.【答案】设z x yi =+(,x y R ∈),∴2(2)z i z x y i +==++,由题意得2y =-, 2111(2)(2)(22)(4)22555z x i x i i x x i i i -==--=++---, 由题意得4x =,∴42z i =-∵22()(124)8(2)z ai a a a i +=+-+-, 根据已知条件有212408(2)0a a a ⎧+->⎨->⎩,解得26a <<, ∴实数a 的取值范围是(2,6)a ∈.【变式4】已知复数z 对应的点在第一象限的角平分线上,求复数1z zω=+在复平面上对应的点的轨迹方程.【答案】设z=a+ai(a>0)则1111()()22 z a ai a a i z a ai a a ω=+=++=++-+令1212x aay aa⎧=+⎪⎪⎨⎪=-⎪⎩,消a得x2-y2=2(x≥.。
复数知识点总结和例题

复数知识点总结和例题一、名词的复数形式1. 一般情况下,名词构成复数的规则是在单数形式后面加上-s,如book-books,cat-cats,dog-dogs等。
2. 以-s, -ss, -sh, -ch, -x结尾的名词,复数形式应在词尾加-es,如bus-buses,class-classes,box-boxes等。
3. 以辅音字母+y结尾的名词,复数形式应将y变为i再加上-es,如baby-babies,city-cities等。
4. 以-f或-fe结尾的名词,复数形式应将f变为v再加上-es,如leaf-leaves,knife-knives 等。
5. 一些名词的复数形式是不规则变化的,需要独立记忆,如child-children,man-men,woman-women等。
二、不可数名词不可数名词是指不能用于单复数变化的名词,它们通常表示一种概念、物质或抽象事物,如water, milk, money, information等。
不可数名词没有复数形式,不能与不定冠词a/an连用,通常用于表示数量的量词或用作可数名词的量词修饰。
例题一:1. The teacher gave us some useful _______ for the exam. (information)A. informationsB. informC. informationD. informs答案:C. information2. There are too many ______ in the river. (fish)A. fishsB. fishC. fishesD. fishies答案:B. fish3. He bought two new ______ at the bookstore yesterday. (novel)A. novellsB. novlesC. novelD. novels答案:D. novels4. There is some ______ on the table, could you please pass me the ______? (butter)A. buttersB. butterC. buttersD. butteries答案:B. butter5. Please give me some more ______ for my cup of ______. (milk)A. milksB. milkC. milkieD. milkies答案:B. milk三、名词的数量表达1. 在表示数量的名词或代词前,应使用相应的量词来修饰,如a few, a little, some, many, much, a lot of, plenty of等。
复数的概念及其运算-2018精品之高中数学(理)黄金100题系列(Word版含答案)

第94题 复数的概念及其运算I .题源探究·黄金母题【例1】使复数为实数的充分而不必要条件是 ( ) A .z z -= B .z z = C .2z 为实数 D .z z -+为实数【答案】B【解析】即要找出由选项能推出“复数z 为实数”,但“复数z 为实数”不能推出选项成立,故选B .【例2】若复数sin 2(1cos 2)z a i a =--是纯虚数,则a = . 【答案】1,2k k α=π+π∈Z 【解析】依题意得sin 201cos 20αα=⎧⎨-≠⎩,即21,,222k k k k ααα=π⎧∴=π+π∈⎨≠π⎩Z .【例3】如果35a <<,复数()()22815514i z a a a a =-++--在复平面上的对应点Z 在 象限. 【答案】三【例4】设,C z ∈满足条件.12141log 21->--+-z z 的复数z 所对应的点Z 的集合表示什么图形?【答案】表示以()10,为圆心以8为半径的圆的外部. 【解析】由1214log 112z z -+>---,得140212Z Z -+<<--,化简得18Z ->,∴复数z 所对应的点Z 的集合表示以()10,为圆心以8为半径的圆的外部.【例5】20181i 22⎛⎫+ ⎪ ⎪⎝⎭的共轭复数为 ( )精彩解读【试题来源】例1、例2:人教A 版选修2-2P 103例1改编;例3:人教A 版选修2-2习题3.1A 组P 106T 5改编;例5:人教A 版选修2-2复习参考题P 116B 组T 2改编.【母题评析】考查复数的基本概念、复数代数形式的四则运算、复数加减法的几何意义等,突出考查基本运算能力与数形结合思想. 【思路方法】复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可.复数(,)z a bi a b =+∈R ,当0b ≠时,z 为虚数,当0b =时,z 为实数,当0,0a b =≠时,z 为纯虚数.复数的几何意义:复数z =a +b i 复平面内的点Z (a ,b )(a ,b ∈R).复数z =a +b i(a ,b ∈R)平面向量 OZ .A.122-+ B.122-- C.122+ D.1i 22- 【答案】B【解析】3211111122222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫==-=- ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,67220183211112222⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥∴=+=-+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,201812⎛⎫∴ ⎪ ⎪⎝⎭的共轭复数为12-,故选B . II .考场精彩·真题回放【例1】【2017高考新课标1理3】设有下面四个命题1p :若复数z 满足1z∈R ,则z ∈R ;2p :若复数z 满足2z ∈R ,则z ∈R ;3p :若复数12,z z 满足12z z ∈R ,则12z z =;4p :若复数z ∈R ,则z ∈R . 其中的真命题为 A .13,p pB .14,p pC .23,p pD .24,p p【答案】B也属于实数,故4p 正确,故选B . 【例2】【2017高考新课标2理1】31ii+=+( ) A .12i + B .12i - C .2i + D .2i - 【答案】D【解析】由复数除法的运算法则有:()()3+13212i i i i i -+==-+,故选D . 【命题意图】这类题主要考查复数的基本概念、复数代数形式的四则运算、复数加减法的几何意义等. 【考试方向】这类试题在考查题型上,通常以选择题或填空题的形式出现,难度中等偏易. 【难点中心】1.要熟悉复数相关基本概念、复数的分类等,如复数(,)+∈a bi a b R 的实部为a 、虚部为b应点为(,)a b 、共轭为.-a bi2.复数i(,)a b a b +∈R 的共轭复数是i(,)a b a b -∈R ,据此结合已知条件,求得a 的方程即可.共轭与模是复数的重要性质,注意运算性质有: (1)1212z z z z ±=±;【例3】【2017高考山东,理2】已知a R ∈,i是虚数单位,若,4z a z z =⋅=,则a= ( )A .1或-1 BC .D【答案】A【解析】由,4z a z z =⋅=得234a +=,所以1a =±,故选A . 【例4】【2017高考新课标3理2】设复数z 满足(1+i )z =2i ,则∣z ∣= A .12BCD .2【答案】C【解析】由题意可得:21iz i =+,由复数求模的法则:1121z z z z =可得:21i z i===+C . 【例5】【2017高考北京理2】若复数()()1i a i -+在复平面内对应的点在第二象限,则实数a 的取值范围是 ( ) A .(–∞,1) B .(–∞,–1) C .(1,+∞) D .(–1,+∞) 【答案】B【解析】()()()()111z i a i a a i =-+=++-,因为对应的点在第二象限,所以1010a a +<⎧⎨->⎩,解得:1a <-,故选B .【例6】【2017高考江苏2】 已知复数(1i)(12i),z =++其中i 是虚数单位,则z 的模是 .【解析】(1)(12)112z i i i i =++=++==.【例7】【2017高考浙江12】已知a ,b ∈R ,2i 34i a b +=+()(i 是虚数单位)则22a b += ,ab = . 【答案】5,2(2) 1212z z z z ⨯=⨯; (3)22z z z z ⋅==; (4)121212z z z z z z -≤±≤+. (5)1212z z z z =⨯; (6)1121z z z z =. 3.对于复数的四则运算,要切实掌握其运算技巧和常规思路.复数代数形式的加减乘除运算的法则是进行复数运算的理论依据,加减运算类似于多项式的合并同类项,乘法法则类似于多项式乘法法则,除法运算则先将除式写成分式的形式,再将分母实数化.注意下面结论的灵活运用:(1)()21i 2i ±=±;(2)1i 1ii i 1i 1i+-==--+,.【解析】由题意可得22234a b abi i -+=+,则2232a b ab ⎧-=⎨=⎩,解得2241a b ⎧=⎨=⎩,则225,2a b ab +==.【例8】【2017高考天津理9】已知a ∈R ,i 为虚数单位,若i2ia -+为实数,则a 的值为 . 【答案】2- 【解析】()(2)(21)(2)2122(2)(2)555a i a i i a a i a a i i i i -----+-+===-++-为实数,则20,25a a +==-. III .理论基础·解题原理1.复数的概念(1)虚数单位i ;(2)复数的代数形式()i ,z a b a b =+∈R ;(3)复数的实部、虚部,虚数与纯虚数.2.复数的分类:复数()i ,z a b a b =+∈R (0)(0,0)(0)(0,0)b a b b a b =⎧⎪=≠⎧⎨≠⎨⎪≠≠⎩⎩实数纯虚数虚数非纯虚数3.相关公式:(1)i i ,a b c d a b c d +=+⇔==;(2)i 00a b a b +=⇔==;(3)i z a b =+=(4)z a bi =-.z z ,指两复数实部相同,虚部互为相反数(互为共轭复数). 4.复数运算(1)复数加减法:()()()()i i i a b c d a c b d +±+=±+±; (2)复数的乘法:()()()()i i i a b c d ac bd bc ad ++=-++;(3)复数的除法:()()()()i i i i i i a b c d a b c d c d c d +-+=++-()()222222i i ac bd bc ad ac bd bc adc d c d c d ++-+-==++++ (类似于无理数除法的分母有理化→虚数除法的分母实数化)(4)复数加法、乘法的运算定律:复数的加法满足交换律和结合律,即对任意复数123,,z z z ,有()()1221123123,z z z z z z z z z z +=+++=++;复数的乘法满足交换律、结合律和乘法对加法的分配律,即对任意复数123,,z z z ,有()()()12211231231231213,,z z z z z z z z z z z z z z z z z ⋅=⋅⋅⋅=⋅⋅⋅+=⋅+⋅.5.常见的运算规律①z z =;②2,2z z a z z bi +=-=;③2222z z z za b ⋅===+;④z z =;⑤z z z =⇔∈R ;⑥41424344i i ,i 1,i i ,i1n n n n ++++==-=-=;⑦()21i i ±=±;⑧21i 1i i ,i ,i 1i 1i +-==-=±-+;⑨设12ω-+=是1的立方虚根,则231323310,,,1n n n ωωωωωωω+++++====. 6.复数的几何意义(1)复平面:用来表示复数的直角坐标系,其中x 轴叫做复平面的实轴,y 轴叫做复平面的虚轴.复数的模:i z OZ a b ==+= .()i ,z a b Z a b OZ=+←−−−→一一对应复数复平面内的点平面向量(2)复数加法、减法的几何意义:若复数12,z z 对应的向量12,OZ OZ 不共线,则复数12z z +是以12,OZ OZ为邻边的平行四边形对角线OZ 所对应的复数;复数12z z -是连接向量12,OZ OZ 终点,并指向被减数向量1OZ,即向量21Z Z所对应的复数. IV .题型攻略·深度挖掘【考试方向】这类试题主要考查复数的基本概念、复数代数形式的四则运算、复数加减法的几何意义等,突出考查基本运算能力与数形结合思想.在考查题型上,通常以选择题或填空题的形式出现,为容易题.【技能方法】1.处理有关复数概念的问题,首先要找准复数的实部与虚部(若复数为非标准的代数形式,则应通过代数运算化为代数形式),然后根据定义解题.2.在进行复数的加减法运算时,可类比合并同类项,运用法则(实部与实部相加减,虚部与虚部相加减)计算即可.3.在进行复数的乘法运算时:(1)复数的乘法类似于两个多项式相乘,即把虚数单位i 作字母,然后按多项式的乘法法则进行运算,最后只要在所得的结果中把2i 换成1-,并且把实部和虚部分别结合即可,但要注意把i 的幂写成简单的形式;(2)实数范围内的运算法则在复数范围内仍然适用,如交换律、结合律以及乘法对加法的分配律、正整数指数幂的运算律,这些对复数仍然成立.4.在进行复数的除法运算时,关键是分母“实数化”,其一般步骤如下:(1)分子、分母同时乘分母的共轭复数;(2)对分子、分母分别进行乘法运算;(3)整理、化简成实部、虚部分开的标准形式.【易错指导】在进行复数的运算时,不能把实数集的某些法则和性质照搬到复数集中来,如下面的结论,当z ∈C 时不一定成立:(1)()nm mn zz =(,m n 为分数时不成立);(2)m nz z m n =⇒=(i z =时等式不成立);(3)22121200z z z z +=⇔==(121i ,1i z z =+=-时不成立). V .举一反三·触类旁通考向1 复数的有关概念对于复数()i ,z a b a b =+∈R ,,a b 取不同值其类别也不一样:①0a ≠且0b ≠,则z 为虚数;②0a =且0b ≠,则z 为纯虚数;③0b =,则z 为实数. 【例1】【2018衡水金卷信息卷(五)】已知i 为虚数单位,复数()11i ai z i+=+的虚部为2,则实数a =A .1B .2C .3D .4 ( ) 【答案】C【例2】【2018天津高三9校联考】若复数z 满足121ii z-=-,则其共轭复数z 在复平面内对应的点位于 ( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】A 【解析】∵12i z -=1﹣i ,∴z= ()()()()121123111122i i i i i i i -+-==---+,∴3122z i =+,则z 在复平面内对应的点的坐标为(3122,),位于第一象限.故选A .【例3】已知a ∈R ,i 为虚数单位,若i2ia -+为实数,则a 的值为 . 【答案】2- 【解析】()(2)(21)(2)2122(2)(2)555a i a i i a a i a a i i i i -----+-+===-++-为实数,则20,25a a +==-. 【名师点睛】1.复数()i ,a b a b +∈R 的实部为a 、虚部为b (),a b 、共轭复数为i a b -. 2.复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可. 【跟踪练习】1.【2018山西联考】i 是虚数单位,若()2ii ,1ia b a b +=+∈+R ,则()lg a b +的值是( ) A .2- B .1- C .0 D .12【答案】C 【解析】()()()()()2i 1i 3i 3131i i ,,,lg 01i 1i 22222a b a b a b +--+===-∴==-∴+=+- ,故选C .2.【2018河南六市联考】已知i 为虚数单位,a ∈R ,若2ii-+a 为纯虚数,则复数2z a =的模等于( )A B C D 【答案】C3.【2018重庆高三二模】已知i 是虚数单位,则复数()211i z i-=+的虚部是 ( )A .1-B .1C .i -D .i 【答案】A【解析】由题得()211i z i -=+=()()()2211+22221.11112i i i i i ii i i i i -----====-+++-所以()211i z i -=+的虚部是-1.故选A .4.【2018上海浦东新区高三一模】已知i 是虚数单位,复数z 满足()11z ⋅+=,则z =________ 【答案】12【名师点睛】复数的乘法.复数的乘法类似于多项式的四则运算,可将含有虚数单位i 的看作一类同类项,不含i 的看作另一类同类项,分别合并即可.复数的除法.除法的关键是分子分母同乘以分母的共轭复数,解题中要注意把i 的幂写成最简形式. 考向2 复数的运算复数的加、减、乘运算可以类比多项式的运算,除法关键是分子分母同乘以分母的共轭复数,注意把i 的幂写成最简形式.记住几个常用结论,在解题时很有用:(1)()21i 2i ±=±;1i i 1i +=-;1ii 1i-=-+. (2)44142434414243i 1,i i ,i 1,i i ,i i i i 0,n n n n n n n n n ++++++*===-=-+++=∈N .【例4】31ii+=+ ( ) A .12i + B .12i - C .2i + D .2i -【答案】D【解析】由复数除法的运算法则有:()()3+13212i i i i i -+==-+,故选D . 【例5】已知复数()()()1i i 24i ,a b a b ++=+∈R ,则函数()2sin 6f x ax b π⎛⎫=++ ⎪⎝⎭图象的一个对称中心是( )A .,16π⎛⎫-⎪⎝⎭ B .,018π⎛⎫- ⎪⎝⎭ C .,36π⎛⎫- ⎪⎝⎭ D .,1185π⎛⎫⎪⎝⎭【答案】D【解析】()()()()()()24i 1i 24i 1i i 24i ,i 3i ,311i 1i 1i a b a b a b +-+++=+∴+===+∴==++- ,.()2sin 316f x x π⎛⎫∴=++ ⎪⎝⎭,令36183k x k x k πππ+=π,∴=-+,∈Z .令1k =,得18x 5π=,()2sin 316f x x π⎛⎫∴=++ ⎪⎝⎭图象的一个对称中心是,1185π⎛⎫⎪⎝⎭,故选D .【例6】【2018陕西联考改编】如图,在复平面内,复数12,z z 对应的向量分别是,OA OB,则复数1212,z z z z +-对应点的坐标分别为 .【答案】()2,0- ()2,2--【跟踪练习】1.已知,i a ∈R 是虚数单位,若,4z a z z =⋅=,则a =( )A .1或1-BC .D 【答案】A【解析】由,4z a z z =⋅=得234a +=,所以1a =±,故选A . 2.【2018四川资阳高三4月模拟考试(三诊)】复数z 满足()11i 1iz -=+,则z = ( )A .22- B .22+ C .1i - D .1i + 【答案】B【解析】()()()()21111,1111z i z i i i i i-=+∴-+=++ ,())2111z i i i =-+=+,z ∴=,故选B . 3.【2018湖南永州高三下三模】已知i 为虚数单位,复数z 满足()25i z -=,则z 的虚部为( ) A .1- B .0 C .1 D .2 【答案】C 【解析】()()()5252222i z i i i i +===+--+,所以虚部为1,故选C .4.【2018衡水金卷调研五】已知复数123z i =+,2z a i =+(a R ∈,i 为虚数单位),若1218z z i =+,则a 的值为A .12B .1C .2D .4 【答案】C【解析】()()()12232323z z i a i a a i =++=-++,由已知有1218z z i =+,所以231{ 238a a -=+=,解出2a =,选C .5.已知,a b ∈R ,2i 34i a b +=+()(i 是虚数单位)则22a b += ,ab = . 【答案】5,2【解析】由题意可得222i 34i a b ab -+=+,则2232a b ab ⎧-=⎨=⎩,解得2241a b ⎧=⎨=⎩,225a b ∴+=.6.32i -+是方程220x px q ++=的一个根,且,p q ∈R ,则p q +=________. 【答案】38【解析】由题意得()()2232i 32i 0p q -++-++=,即()2512i 32i 0p p q --++=,即()()103242i 0p q p -++-+=,1030,2420,p q p -+=⎧∴⎨-+=⎩解得12,3826,p p q q =⎧∴+=⎨=⎩. 考向3 复数的几何意义复数的加法、减法的几何意义在解决点的坐标、轨迹,及一些简单几何问题的证明中要注意使用,并且要有意识地与向量知识联系,体现数形结合的思想.共轭与模是复数的重要性质,主要有:(1)1212z z z z ±=±;(2)1212z z z z ⨯=⨯;(3)22z z z z ⋅==; (4)121212z z z z z z -≤±≤+;(5)1212z z z z =⨯;(6)1121z z z z =. 【例7】【2018贵州省高三适应性考试】在复平面内,复数1iz i=+对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 【答案】A【解析】()()()111112i i i iz i i i -+===++-,∴z 在复平面内对应的点为1122⎛⎫ ⎪⎝⎭,,在第一象限,故选A .【例8】(1)设复数z 满足()1i 2i z +=,则z = ( )A .12B .2C D .2 (2)若复数()()1i a i -+在复平面内对应的点在第二象限,则实数a 的取值范围是( ) A .(),1-∞ B .(),1-∞- C .()1,+∞ D .()1,-+∞【答案】(1)C ;(2)B .【名师点睛】复数的几何意义及应用(1)复数z 、复平面上的点Z 及向量OZ 相互联系,即()()i ,,z a b a b Z a b OZ =+∈⇔⇔R .(2)由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.【例9】【2018河北衡水金卷调研五】设i 为虚数单位,现有下列四个命题:1p :若复数z 满足()()5z i i --=,则6z i =;2p :复数22z i=-+的共轭复数为1+i 3p :已知复数1z i =+,设()1,i a bi a b R z-+=∈,那么2a b +=-; 4p :若z 表示复数z 的共轭复数,z 表示复数z 的模,则2zz z =.其中的真命题为( )A .13,p pB .14,p pC .23,p pD .24,p p【答案】B【解析】1p :若复数z 满足()()5z i i --=,56z i i i ∴=+=-,故1p 正确;2p :22z i=-+所以4p 正确,故选B .【跟踪练习】1.【2018贵州凯里一中高三下学期黄金卷(三)】已知复数()1z i i =-,其中i 是虚数单位,则在复平面内,z 的共轭复数z 对应的点所在象限是( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】D【解析】()211z i i i i i =-=-=+,1z i =-,所以z 所对应的点在第四象限,故选D .2.【2018衡水金卷调研(三)】复数()2i z x x =++(其中i 为虚数单位,R x ∈)满足2i z+是纯虚数,则z =( )A B . C D 【答案】D 【解析】根据题意可设()2i 0bi b R b z+=∈≠且,∴()()2i 2i 2x x bi b x xbi ⎡⎤+=++⨯=-++⎣⎦,∴()22{ 1b x xb=-+=,解得:2x 3=-,∴2433z i =-+,∴3z =,故选D . 3.【2018齐鲁名校教科研协作体山东、湖北部分重点中学高考冲刺模拟】已知复数12z z 、在复平面内对应的点关于实轴对称,若()23201812i z i i i i -⋅=++++ (其中i 是虚数单位),则复数2z 的虚部等于A .15-B .15C .35-D .15i - 【答案】A【解析】因为n i (*n N ∈)的取值呈现周期性,周期为4,234110i i i i i i +++=--+=,所以()2320182121i z i i i i i i i -⋅=++++=+=-+ ,所以11325i i z i -+-+==-,所以 235i z --=,所以2z 的虚部等于15-.故选A . 4.已知复数()()1i 12i ,z =++其中i 是虚数单位,则z 的模是 .【解析】()()1i 12i 1i 12i z =++=++==5.【2018上海杨浦区高三下学期质量调研(二模)】若复数z 满足1z =,则z i -的最大值是________【答案】2 【解析】设()i ,z a b a b =+∈R .1z = ,221a b ∴+=,1b =6.【2018上海长宁、嘉定区高三第一次质量调研(一模)】已知复数z 满足z =,2z 的虚部为2.(1)求复数z ;(2)设22,,z z z z -在复平面上的对应点分别为A ,B ,C ,求△ABC 的面积.【答案】(1)1i z =+或1i z =--(2) 1ABC S ∆=.【解析】试题分析:(1)设i z x y =+,根据条件列出方程即可求解;(2)根据复数对应点的含义,求出三角形顶点坐标,即可求出三角形面积.(2)由(1)知,1i z =+时,22i z =,21i z z -=-,所以,()1,1A ,()0,2B ,()1,1C -, 1ABC S ∆=.当1i z =--时,22i z =,213i z z -=--,所以()1,1A --,()0,2B ,()1,3C --,1ABC S ∆=.【名师点睛】复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数,共轭复数这些重要概念,复数的运算主要考查除法运算,通过分母实数化,转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分.。
(精选试题附答案)高中数学第七章复数典型例题
(名师选题)(精选试题附答案)高中数学第七章复数典型例题单选题1、已知i 为虚数单位,则i +i 2+i 3+⋅⋅⋅+i 2021=( )A .iB .−iC .1D .-1答案:A分析:根据虚数的运算性质,得到i 4n +i 4n+1+i 4n+2+i 4n+3=0,得到i +i 2+i 3+⋅⋅⋅+i 2021=i 2021,即可求解. 根据虚数的性质知i 4n +i 4n+1+i 4n+2+i 4n+3=1+i −1−i =0,所以i +i 2+i 3+⋅⋅⋅+i 2021=505×0+i 2021=i .故选:A.2、已知a,b ∈R ,a1+i +b1−i =1,则a +2b =( )A .3B .√3C .√2D .1答案:A分析:等式两边同乘(1+i )(1−i ),整理化简后利用复数相等的条件可求得a +2b 的值因为a 1+i +b1−i =1 ,所以a(1−i )+b(1+i )=(1+i )(1−i )=1−i 2=2即(a +b)+(b −a)i=2所以{a +b =2b −a =0解得{a =1b =1 ,所以a +2b =3 故选:A3、在复平面内,复数z =(a 2−2a )+(a 2−a −2)i (a ∈R )是纯虚数,则( )A .a =0或a =2B .a =0C .a ≠1且a ≠2D .a ≠1或a ≠2答案:B分析:利用复数是纯虚数的条件,即:实部为零且虚部不为零求解参数的值.复数z =(a 2−2a )+(a 2−a −2)i (a ∈R )是纯虚数,所以{a 2−2a =0a 2−a −2≠0,解得:a =0, 故选:B.4、已知i 是虚数单位,则复数z =2−i 20202+i 2021对应的点所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限答案:D分析:先化简i 2020,i 2021,再利用复数的除法化简得解.z =2−i 20202+i 2021=12+i =2−i (2+i)(2−i)=2−i 5. 所以复数对应的点(25,−15)在第四象限,故选:D小提示:名师点评复数z =x +yi(x,y ∈R)对应的点为(x,y),点(x,y)在第几象限,复数对应的点就在第几象限.5、已知z =(m +3)+(m −1)i (m ∈R )在复平面内对应的点在第四象限,则复数z 的模的取值范围是( )A .[2√2,4)B .[2,4]C .(2√2,4)D .(2,4)答案:A分析:根据z =(m +3)+(m −1)i (m ∈R )在复平面内对应的点在第四象限,求出m 的范围,再根据复数的模结合二次函数的性质即可得出答案.解:因为z =(m +3)+(m −1)i (m ∈R )在复平面内对应的点在第四象限,所以{m +3>0m −1<0,解得−3<m <1, |z |=√(m +3)2+(m −1)2=√2m 2+4m +10=√2(m +1)2+8,因为−3<m <1,所以(m +1)2∈[0,2),则2(m +1)2+8∈[2√2,4),所以复数z 的模的取值范围是[2√2,4).故选:A.6、z 1、z 2是复数,则下列结论中正确的是( )A .若z 12+z 22>0,则z 12>−z 22B .|z 1−z 2|=√(z 1+z 2)2−4z 1⋅z 2C .z 12+z 22=0⇔z 1=z 2=0D .|z 12|=|z 1|2答案:D解析:举反例z 1=2+i ,z 2=2−i 可判断选项A 、B ,举反例z 1=1,z 2=i 可判断选项C ,设z 1=a +bi ,(a,b ∈R ),分别计算|z 12|、|z 1|2即可判断选项D ,进而可得正确选项.对于选项A :取z 1=2+i ,z 2=2−i ,z 12=(2+i )2=3+2i ,z 22=(2−i )2=3−2i , 满足z 12+z 22=6>0,但z 12与z 22是两个复数,不能比较大小,故选项A 不正确;对于选项B :取z 1=2+i ,z 2=2−i ,|z 1−z 2|=|2i |=2,而√(z 1+z 2)2−4z 1⋅z 2=√42−4(2+i )(2−i )=√16−20无意义,故选项B 不正确;对于选项C :取z 1=1,z 2=i ,则z 12+z 22=0,但是z 1≠0,z 2≠0,故选项C 不正确;对于选项D :设z 1=a +bi ,(a,b ∈R ),则z 12=(a +bi )2=a 2−b 2+2abi |z 12|=√(a 2−b 2)2+4a 2b 2=√(a 2+b 2)2=a 2+b 2,z 1=a −bi ,|z 1|=√a 2+b 2,所以|z 1|2=a 2+b 2,所以|z 12|=|z 1|2,故选项D 正确.故选:D.7、若复数z 满足z ⋅(2+i)=z ⋅(1−i)+1,则复数z 的实部为( )A .−32B .−1C .−12D .1答案:D分析:利用复数的四则运算以及共轭复数的概念,根据对应相等即可求解.设z =a +bi (a 、b ∈R ),则(a +bi)⋅(2+i)=(a −bi)⋅(1−i)+1,化简得(2a −b)+(a +2b)i =(a −b +1)−(a +b)i ,根据对应相等得:{2a −b =a −b +1a +2b =−(a +b ) ,解得a =1,b =−23,故选:D.8、已知z =a −2+(1+2a)i 的实部与虚部相等,则实数a =( )A .2B .−2C .3D .−3答案:D分析:由题可得a −2=1+2a ,即得.由题可知a −2=1+2a ,解得a =−3.故选:D .9、设复数z 满足z ⋅i =−1+i ,则|z |=( )A .1B .√2C .√5D .√10答案:B分析:利用复数的四则运算以及复数模的运算即可求解.解析因为z =−1+i i =(−1+i )⋅i i ⋅i =−i −1−1=1+i ,所以z =1−i ,|z |=√2.故选:B10、在复平面内,点A(cosθ,sinθ),B(sin(−θ),cos(−θ))分别对应复数z 1,z 2,则z 2z 1=()A .−1B .1C .−iD .i答案:D分析:根据复数几何意义,求得z 1,z 2,再结合复数的除法的运算法则,即可求解.由点A(cosθ,sinθ)和B(sin(−θ),cos(−θ))分别对应复数z1,z2,可得z1=cosθ+i sinθ,z2=sin(−θ)+i cos(−θ)=−sinθ+i cosθ,所以z2z1=−sinθ+i cosθcosθ+i sinθ=(−sinθ+i cosθ)(cosθ−i sinθ)(cosθ+i sinθ)(cosθ−i sinθ)=(sin2θ+cos2θ)icos2θ+sin2θ=i.故选:D.填空题11、设复数z1,z2在复平面内的对应点关于虚轴对称,且z1=1−i(i为虚数单位),则|z12+z2|=______.答案:√10分析:首先根据复数的几何意义得到z2=−1−i,再求|z12+z2|即可.因为复数z1,z2在复平面内的对应点关于虚轴对称,且z1=1−i,所以z2=−1−i.所以|z12+z2|=|(1−i)2+(−1−i)|=|−1−3i|=√10.所以答案是:√1012、若|z1|=|z2|=400,且|z1+z2|=400√3,则|z1−z2|=___________.答案:400分析:根据|z|2=zz̅转化|z1+z2|=400√3,可求得z1z2̅+z2z1̅=4002,同理转化|z1−z2|即可求值.|z1+z2|2=(z1+z2)(z1̅+z2̅)=|z1|2+|z2|2+z1z2̅+z2z1̅=3×4002,又|z1|=|z2|=400,∴z1z2̅+z2z1̅=4002,而|z1−z2|2=(z1−z2)(z1̅−z2̅)=|z1|2+|z2|2−z1z2̅−z2z1̅,∴|z1−z2|2=4002,则|z1−z2|=400.所以答案是:40013、若复数z=a(1+i)+i2013为实数,则实数a=________.答案:−1分析:根据复数代数形式的乘方及加法运算化简,再根据复数的类型求出参数的值.解:因为z=a+a i+i4×503+1=a+(a+1)i为实数,所以a+1=0,即a=−1.所以答案是:−114、设z1=x+2i,z2=3-yi(x,y∈R),且z1+z2=5-6i,则z1-z2=__________答案:-1+10i分析:先利用复数加法运算计算z1+z2,根据题意利用复数相等的定义列方程即得参数x,y,再写出z1,z2,计算z1-z2即可.∵z1+z2=5-6i,∴(x+2i)+(3-yi)=5-6i,即(x+3)+(2−y)i=5−6i,∴{x+3=52−y=−6即{x=2y=8,∴z1=2+2i,z2=3-8i,∴z1-z2=(2+2i)-(3-8i)=-1+10i. 所以答案是:-1+10i.15、计算z=12(−1+√3i)9√3+i)100(1+2√3i)100=_______.答案:-511解析:利用复数的运算公式,化简求值.原式=1212×(−12+√32i)√3)100[−i×(i−2√3)]100=36(−12+√32i)+1(−i)100=−29+1=−511.所以答案是:−511小提示:思路点睛:本题考查复数的n次幂的运算,注意(−12+√32i)3=1,(1+i)2=2i,以及(1+i)12=[(1+i)2]6,等公式化简求值.解答题16、已知复数z=(m−1)+(2m+1)i(m∈R)(1)若z为纯虚数,求实数m的值;(2)若z在复平面内的对应点位于第二象限,求实数m的取值范围及|z|的最小值答案:(1)1;(2)m ∈(−12,1),|z|min =3√55. 解析:(1)利用纯虚数的定义,实部为零,虚部不等于零即可得出.(2)利用复数模的计算公式、几何意义即可得出.解:(1)∵z =(m −1)+(2m +1)i(m ∈R)为纯虚数,∴m −1=0且2m +1≠0∴m =1(2)z 在复平面内的对应点为(m −1,2m +1))由题意:{m −1<02m +1>0,∴ −12<m <1. 即实数m 的取值范围是(−12,1).而|z|=√(m −1)2+(2m +1)2=√5m 2+2m +2=√5(m +15)2+95,当m =−15∈(−12,1)时,|z|min =√95=3√55.17、已知z =1+i ,i 为虚数单位.(1)若ω=z 2+3z̅−4,求|ω|;(2)若z 2+az+bz 2−z+1=1−i ,求实数a ,b 的值.答案:(1)|ω|=√2;(2){a =−1b =2 解析:(1)求出z =1+i 的共轭复数,代入ω=z 2+3z̅−4化简,再求|ω|;(2)根据z 2+az+bz 2−z+1=1−i ,得到(a +b)+(a +2)i =1+i ,列方程组即可求解.(1)已知z =1+i ,∴z̅=1−i ,∴ω=(1+i)2+3(1−i)−4=−1−i ,∴|ω|=√2.(2)∵z 2+az+bz 2−z+1=(a+b)+(a+2)i i =1−i ,∴(a +b)+(a +2)i =1+i ,∴{a +b =1a +2=1,解得{a =−1b =2. 小提示:此题考查复数的基本运算,涉及共轭复数,复数的模长,根据两个复数相等列方程组求解.18、已知复数z =(1+ai )(1+i )+2+4i (a ∈R ).(1)若z 在复平面中所对应的点在直线x −y =0上,求a 的值;(2)求|z −1|的取值范围.答案:(1)a =−1;(2)[7√22,+∞).解析:(1)化简z ,得z 在复平面中所对应的点的坐标,代入直线x −y =0计算;(2)代入模长公式表示出|z −1|,再利用二次函数的性质求解最值即可.(1)化简得z =(1+ai )(1+i )+2+4i =(3−a )+(a +5)i ,所以z 在复平面中所对应的点的坐标为(3−a,a +5),在直线x −y =0上,所以3−a −(a +5)=0,得a =−1.(2)|z −1|=|(2−a)+(a +5)i |=√(2−a)2+(a +5)2=√2a 2+6a +29,因为a ∈R ,且2a 2+6a +29≥492,所以|z −1|=√2a 2+6a +29≥7√22,所以|z −1|的取值范围为[7√22,+∞). 19、复数z =(1+i )m 2+(5−2i )m +(6−15i ).(1)实数m 取什么数时,z 是实数;(2)实数m 取什么数时,z 是纯虚数;(3)实数m 取什么数时,z 对应的点在直线x +y +7=0上.答案:(1)m =5或−3;(2)m =−2;(3)m =12或−2分析:复数z =(1+i)m 2+(5−2i)m +(6−15i)=(m 2+5m +6)+(m 2−2m −15)i .(1)由m 2−2m −15=0,解得m 即可得出.(2)由{m 2+5m +6=0m 2−2m −15≠0 ,解得m 即可得出. (3)由(m 2+5m +6)+(m 2−2m −15)+7=0.解出即可得出.解:复数z=(1+i)m2+(5−2i)m+(6−15i)=(m2+5m+6)+(m2−2m−15)i.(1)由m2−2m−15=0,解得m=5或−3.∴m=5或−3时,复数z为实数.(2)由{m2+5m+6=0m2−2m−15≠0,解得m=−2.∴m=−2时,复数z为纯虚数.(3)由(m2+5m+6)+(m2−2m−15)+7=0.化为:2m2+3m−2=0,解得m=12或−2.∴m=12或−2,z对应点在直线x+y+7=0上.小提示:本题考查了复数的运算法则及其有关概念,考查了推理能力与计算能力,属于中档题.。
复数练习题及答案
复数练习题及答案复数是英语语法中的一个重要概念,它用来表示多个个体或物体。
掌握复数形式对于学习英语来说至关重要。
在这篇文章中,我们将提供一些复数练习题及答案,帮助读者加深对复数的理解和应用。
第一部分:基础练习1. 将下列名词变为复数形式:a) bookb) catc) appled) boxe) child答案:a) booksb) catsc) applesd) boxese) children2. 将下列名词变为复数形式,并注意特殊变化:a) manb) womanc) childd) tooth答案:a) menb) womenc) childrend) teethe) feet第二部分:规则变化3. 根据名词的词尾变化,将下列名词变为复数形式:a) dogb) penc) bookd) hate) cup答案:a) dogsb) pensc) booksd) hatse) cups4. 将下列名词变为复数形式,并注意词尾变化规则:a) tomatoc) brushd) watche) box答案:a) tomatoesb) potatoesc) brushesd) watchese) boxes第三部分:不规则变化5. 将下列名词变为复数形式,并注意不规则变化规则:a) childb) mousec) toothd) foote) woman答案:a) childrenb) micec) teethd) feet6. 将下列名词变为复数形式,并注意不规则变化规则:a) oxb) deerc) sheepd) fishe) aircraft答案:a) oxenb) deerc) sheepd) fishe) aircraft第四部分:应用练习7. 用适当的复数形式填空:a) There are three _______ on the table.b) My sister has two _______.c) The _______ in the zoo are very cute.d) I need two _______ for this recipe.e) The _______ in the pond swim gracefully.答案:a) booksb) catsc) monkeysd) cupse) fish8. 用适当的复数形式填空,并注意不规则变化:a) The _______ are playing in the garden.b) I saw two _______ in the field.c) The dentist pulled out three _______.d) She bought a pair of _______.e) The _______ are grazing in the meadow.答案:a) childrenb) deerc) teethd) jeanse) sheep复数练习题及答案到此结束。
2024-2025年北师大版数学必修第二册5.1.1-2复数的概念及其几何意义(带答案)
第五章 复数§1 复数的概念及其几何意义1.1 复数的概念1.2 复数的几何意义必备知识基础练知识点一 复数的概念与分类1.1-i 的虚部为( )A .iB .-iC .1D .-12.当实数m 取什么值时,复数(m 2-3m +2)+(m 2-4)i :①是实数?②是虚数?③是纯虚数?④在复平面内对应点位于第四象限?知识点二 复数相等3.若复数4-3a -a 2i 与复数a 2+4a i 相等,则实数a =( )A .1B .1或-4C .-4D .0或-44.如果(x +y )i =x -1,则实数x ,y 的值分别为( )A .x =1,y =-1B .x =0,y =-1C .x =1,y =0D .x =0,y =0知识点三 复数的模与几何意义的应用5.已知复数z =1+i ,其中i 为虚数单位,则|z |=( )A .12B .22C .2D .2 6.(多选题)已知复数z =(cos α+sin α)+(cos α-sin α)i ,则下列说法正确的是( )A .当α∈(0,π4)时,复数z 在复平面内对应的点在第一象限内 B .当α∈(π4 ,π2)时,复数z 在复平面内对应的点在第一象限内 C .复数z 的模的最大值为2D .复数z 的模长为定值7.在复平面内,复数6+5i ,-2+3i 对应的点分别为A ,B .若C 为线段AB 的中点,则点C 对应的复数是( )A .4+8iB .8+2iC .2+4iD .4+i关键能力综合练一、选择题1.当m <1时,复数1+(m -1)i 在复平面内对应的点位于( )A .第四象限B .第三象限C .第二象限D .第一象限2.已知i 为虚数单位,m ∈R ,复数z =(-m 2+2m +8)+(m 2-8m )i ,若z 为负实数,则m 的取值集合为( )A .{0}B .{8}C .{x |-2<x <4}D .{x |-4<x <2}3.若复数(m 2-m )+3i 是纯虚数,则实数m =( )A .1B .0或1C .1或2D .1或34.设a ,b 为实数,若复数1+2i =(a -b )+(a +b )i ,则( )A .a =32 ,b =12B .a =3,b =1C .a =12 ,b =32D .a =1,b =3 5.(易错题)设复数z =(2t 2-5t +3)+(t 2-2t +3)i ,t ∈R ,则以下结论中正确的是( )A .复数z 对应的点在第二象限B .复数z 一定不是纯虚数C .复数z 对应的点在实轴上方D .复数z 一定是实数二、填空题6.若复数z 在复平面内对应的点位于第二象限,且|z |=2,则z =________.(写出一个即可)7.若z 1=-3-4i ,z 2=(n 2-3m -1)+(n 2-m -6)i ,且z 1=z 2,则实数m =________,n =________.8.若复数z 1=m 2+1+(m 3+3m 2+2m )i ,z 2=4m -2+(m 2-5m )i ,m 为实数,且z 1>z 2,则实数m 的取值集合为________.三、解答题9.(探究题)(1)若复数z =2a -1a +2+(a 2-a -6)i(a ∈R )是实数,求z 1=(a -1)+(1-2a )i 的模;(2)已知复数z =3+a i(a ∈R ),且|z |<4,求实数a 的取值范围.学科素养升级练1.关于复数,下列说法错误的是( )A .若|z |=1,则z =±1或±iB .复数6+5i 与-3+4i 分别对应向量OA → 与OB → ,则向量AB → 对应的复数为9+iC .若z 是复数,则z 2+1>0D .若复数z 满足1≤|z |<2 ,则复数z 对应的点所构成的图形面积为π2.(学科素养——数学抽象)已知复数z 在复平面内对应的点位于第四象限.(1)若z 的实部与虚部之和为7,且|z |=13,求z ;(2)若|z |=6 ,且z 2+z 的实部不为0,讨论z 2+z 在复平面内对应的点位于第几象限.§1 复数的概念及其几何意义1.1 复数的概念1.2 复数的几何意义必备知识基础练1.答案:D解析:由复数虚部定义可知,1-i 的虚部为-1.故选D.2.解析:设z =(m 2-3m +2)+(m 2-4)i.①要使z 为实数,必须有m 2-4=0,得m =-2或m =2,即m =-2或m =2时,z 为实数.②要使z 为虚数,必有m 2-4≠0,即m ≠-2且m ≠2.故m ≠-2且m ≠2时,z 为虚数.③要使z 为纯虚数,必有⎩⎪⎨⎪⎧m 2-4≠0,m 2-3m +2=0, 所以⎩⎪⎨⎪⎧m ≠-2且m ≠2,m =1或m =2. 所以m =1,故m =1时,z 为纯虚数.④由已知得⎩⎪⎨⎪⎧m 2-3m +2>0,m 2-4<0, 解得-2<m <1. 3.答案:C解析:由复数相等的充要条件得⎩⎪⎨⎪⎧4-3a =a 2,-a 2=4a ,∴a =-4.故选C. 4.答案:A解析:∵(x +y )i =x -1,∴⎩⎪⎨⎪⎧x +y =0,x -1=0, ∴x =1,y =-1.故选A. 5.答案:C解析:因为复数z =1+i ,所以根据复数模的运算公式可得,|z |=12+12 =2 .故选C.6.答案:AD解析:因为cos α+sin α=2 sin (α+π4),cos α-sin α=2 cos (α+π4 ), 所以z =2 [sin (α+π4 )+icos (α+π4)]. 当α∈(0,π4 )时,α+π4 ∈(π4 ,π2), 所以sin (α+π4 )>0,cos (α+π4)>0,所以z 在复平面内对应的点在第一象限,故A 正确;当α∈(π4 ,π2 )时,α+π4 ∈(π2 ,3π4), 所以sin (α+π4 )>0,cos (α+π4)<0,所以z 在复平面内对应的点在第四象限,故B 错误;复数z 的模为2 × sin 2(α+π4)+cos 2(α+π4) =2 ,故C 错误,D 正确.故选AD.7.答案:C解析:由题意知A (6,5),B (-2,3),则AB 中点C (2,4)对应的复数为2+4i.关键能力综合练1.答案:A解析:∵m <1,∴m -1<0,∴复数1+(m -1)i 在复平面内对应的点位于第四象限.故选A.2.答案:B 解析:由题意得-m 2+2m +8<0,m 2-8m =0,解得m =8.即m 的取值集合为{8}.故选B.3.答案:B解析:因为复数(m 2-m )+3i 是纯虚数,所以m 2-m =0,解得:m =0或m =1.故选B.4.答案:A解析:由1+2i =(a -b )+(a +b )i ,得⎩⎪⎨⎪⎧a -b =1,a +b =2, 解得⎩⎪⎨⎪⎧a =32,b =12. 故选A. 5.答案:C解析:∵z 的虚部t 2-2t +3=(t -1)2+2恒为正,∴z 对应的点在实轴上方,且z 一定是虚数,排除D.又z 的实部2t 2-5t +3=(t -1)(2t -3)可为正、为零、为负,∴选项A 、B 不正确.故答案为C.6.答案:-1+3 i(答案不唯一)解析:设z =a +b i ,a ,b ∈R ,因为复数z 在复平面内对应的点在第二象限,所以a <0,b >0,又因为|z |=2,所以a 2+b 2=4,显然当a =-1,b =3 时,符合题意,故答案为-1+3 i(答案不唯一).7.答案:2 ±2解析:两个复数相等,则实部和虚部分别相等,所以⎩⎪⎨⎪⎧n 2-3m -1=-3,n 2-m -6=-4, 解得m =2,n =±2.8.答案:{0}解析:∵z 1>z 2,∴⎩⎪⎨⎪⎧m 3+3m 2+2m =0,m 2-5m =0,m 2+1>4m -2,解得m =0,∴实数m 的取值集合为{0}.9.解析:(1)∵z 为实数,∴a 2-a -6=0,∴a =-2或3.∵a =-2时,z 无意义,∴a =3,∴z 1=2-5i ,∴|z 1|=29 .(2)方法一 ∵z =3+a i(a ∈R ),∴|z |=32+a 2 ,由已知得32+a 2<42,∴a 2<7,∴a ∈(-7 ,7 ).方法二 利用复数的几何意义,由|z |<4知,z 在复平面内对应的点在以原点为圆心,以4为半径的圆内(不包括边界),由z =3+a i 知z 对应的点在直线x =3上,所以线段AB (除去端点)为动点Z 的集合.由图可知:-7 <a <7 .学科素养升级练1.答案:ABC解析:取z =12 +32 i ,则|z |=1,故A 错误;AB → =OB → -OA → =-3+4i -(6+5i)=-9-i ,故B 错误;取z =i ,但i 2=-1,z 2+1=0,知C 错误;设复数z =x +y i(x ,y ∈R ),则由1≤|z |<2 可知1≤x 2+y 2<2,故复数z 对应的点所构成的图形面积为π×2-π×1=π,故D 正确.故选ABC.2.解析:(1)依题意可设z =a +b i(a ,b ∈R ,a >0,b <0),因为z 的实部与虚部之和为7,且|z |=13,所以⎩⎨⎧a >0,b <0,a +b =7,a 2+b 2=13, 解得a =12,b =-5,故z =12-5i.(2)依题意可设z =a +b i(a ,b ∈R ),因为z 2+z =a 2-b 2+a +(2ab +b )i(a >0,b <0),所以a 2-b 2+a ≠0,且2ab +b =b (2a +1)<0.因为|z |=6 ,所以a 2+b 2=6,所以a 2-b 2+a =a 2-(6-a 2)+a =2a 2+a -6.当0<a <32时,2a 2+a -6<0,z 2+z 在复平面内对应的点位于第三象限; 当a >32时,2a 2+a -6>0,z 2+z 在复平面内对应的点位于第四象限.。
复数的概念及四则运算(含答案详解)
复数的概念及四则运算[基础巩固]1.复数(1+i)2(2+3i)=( )A .6-4iB .-6-4iC .6+4iD .-6+4i解析 (1+i)2(2+3i)=2i(2+3i)=-6+4i.答案 D2.复数(1+2i )23-4i=( ) A .-1B .1C .-iD .i解析 (1+2i )23-4i =-3+4i 3-4i=-1. 答案 A3.(多选题)(2021·东莞高一期末)已知复数z (z ≠0),z -是z 的共轭复数,则下列结论正确的是( )A .若z =z -,则z ∈RB .若|z |=1,则z ·z -=1C .若z z -∈R ,则z ∈RD .若z 2+z 2=0,则z =0 解析 设z =a +b i(a ,b ∈R ),代入计算,根据复数的定义判断,也可举反例说明. 设z =a +b i(a ,b ∈R ),若z =z -,即a +b i =a -b i ,所以b =-b =0,z =a ∈R ,A 正确;若|z |=1,则a 2+b 2=1,所以z ·z -=(a +b i)(a -b i)=a 2+b 2=1,B 正确;若z =2i ,则z z -=2i -2i =-1∈R ,C 错误; 若z =1+i ,则z 2+z 2=(1+i)2+(1-i)2=2i -2i =0,D 错误.故选A ,B. 答案 AB4.设复数z =1+2i ,则z 2-2z =________.解析 ∵z =1+2i ,∴z 2-2z =z (z -2)=(1+2i)(1+2i -2)=(1+2i)(-1+2i)=-3.答案 -35.已知2-3i z=-i ,则复数z =________. 解析 因为2-3i z=-i , 所以z =2-3i -i=(2-3i)i =3+2i. 答案 3+2i6.计算(1)(-1+i )(2+i )i 3;(2)(1+2i )2+3(1-i )2+i; (3)⎝ ⎛⎭⎪⎫1+i 1-i 6+2+3i 3-2i. 解析 (1)(-1+i )(2+i )i 3=-3+i -i=-1-3i. (2)(1+2i )2+3(1-i )2+i =-3+4i +3-3i 2+i =i 2+i =i (2-i )5=15+25i. (3)⎝ ⎛⎭⎪⎫1+i 1-i 6+2+3i 3-2i =⎣⎡⎦⎤(1+i )226+i (3-2i )3-2i=i 6+i =-1+i.[能力提升]7.(2022·全国乙卷)已知z =1-2i ,且z +a z +b =0,其中a ,b 为实数,则( )A .a =1,b =-2B .a =-1,b =2C .a =1,b =2D .a =-1,b =-2解析 由题设,z =1-2i ,z =1+2i ,所以a +b +1+(2a -2)i =0,故a =1,b =-2,选择A .答案 A8.(多选题)已知z =a +b i(a ,b ∈R )为复数,z -是z 的共轭复数,则下列命题一定正确的是( )A .z ·z -=|z |2B .若1z∈R ,则z ∈R C .若z 2为纯虚数,则a =b ≠0D .若|z -i|=1,则|z |的最大值为2解析 根据共轭复数的定义、复数的运算、复数的定义和复数模的三角不等式计算求解后判断各选项.对于A ,z ·z -=(a +b i)(a -b i)=a 2+b 2=|z |2,所以A 正确;对于B ,1z =1a +b i =a -b i (a +b i )(a -b i )=a a 2+b 2-b a 2+b 2i , 因为1z∈R ,所以b =0,从而z ∈R ,所以B 正确; 对于C ,z 2=(a +b i)2=()a 2-b 2+2ab i 为纯虚数,所以⎩⎪⎨⎪⎧a 2-b 2=0,2ab ≠0,即a =±b ≠0,所以C 错误;对于D ,由复数模的三角不等式可得|z |=|(z -i)+i|≤|z -i|+|i|=2,所以D 正确.故选A ,B ,D.答案 ABD9.写出一个虚数z ,使z 2的实部为0,则z =________.解析 设复数z =a +b i ,()b ≠0,则z 2=a 2-b 2+2ab i ,使z 2的实部为0,得a =±b ,即可得解.设复数z =a +b i ,()b ≠0,则z 2=a 2-b 2+2ab i ,因为z 2的实部为0,所以a 2-b 2=0,即a =±b ,所以答案可为1-i 或1+i.答案 1-i 或1+i(答案不唯一,凡符合a +a i 或a -a i(a ∈R 且a ≠0)形式的均正确)10.已知复数z =1+i ,求实数a ,b ,使az +2b z -=(a +2z )2.解析 因为z =1+i ,所以az +2b z =(a +2b )+(a -2b )i ,(a +2z )2=(a +2)2-4+4(a +2)i =(a 2+4a )+4(a +2)i.因为a ,b 都是实数,所以由az +2b z =(a +2z )2,得⎩⎪⎨⎪⎧a +2b =a 2+4a ,a -2b =4(a +2),解得a =-2或a =-4,对应得b =-1或b =2,所以所求实数为a =-2,b =-1或a =-4,b =2.[探索创新]11.复数z =(1+i )3(a +b i )1-i且|z |=4,z 对应的点在第一象限,若复数0,z ,z -对应的点是正三角形的三个顶点,求实数a ,b 的值.解析 z =(1+i )2·(1+i )1-i(a +b i) =2i·i(a +b i)=-2a -2b i.由|z |=4,得a 2+b 2=4,①∵复数0,z ,z 对应的点构成正三角形, ∴|z -z |=|z |.把z =-2a -2b i 代入化简得|b |=1.②又∵z 对应的点在第一象限,∴a <0,b <0.由①②得⎩⎨⎧ a =-3,b =-1.故所求值为a =-3,b =-1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复数的概念(1)一、选择题1、若z1与z2互为共轭虚数,则满足条件|z-z1|2-|z-z2|2=|z1-z2|2的复数z在平面上表示的图形是(A)双曲线 (B)平行于x轴的直线 (C)平面于y轴的直线 (D)一个点翰林汇2、设z是纯虚数,则 ( )(A)|z|2=z2 (B)|z|2=-z2 (C)=-z2 (D)z2=-z2翰林汇3、已知全集C={复数},Q={有理数},S={无理数},R={实数},P={虚数},那么∪为( )(A)S (B)C (C)R (D)Q翰林汇4、已知M={1,2,m2-3m-1+(m2-5m-6)i},N={-1,3},M∩N={3},则实数m为(A)-1或6 (B)-1或4 (C)-1 (D)4翰林5、若(m2-3m-4)+(m2-5m-6)i是纯虚数,则实数m的值为 ( )(A)-1 (B)4 (C)-1或4 (D)不存在翰林汇6、设集合C={复数},R={实数},M={纯虚数},其中C为全集,则 ( )(A)M∪R=C(B)R∪=C(C)M∩R={0}(D)C∩=M翰林汇7、在复平面内,与复数z=-1-i的共轭复数对应的点位于 ( )(A)第一象限 (B)第二角限(C)第三象限 (D)第四象限翰林汇8、如果用C、R和I分别表示复数集、实数集和纯虚数集,其中C为全集,则(A)=C∩I(B)R∩I={0}(C)R∩I=Æ(D)C=R∪I翰林汇9、复数(i-)3的虚部是(A) -8 (B)-8i (C)8 (D) 0翰林汇10、设z为复数,且(z-1)2=|z-1|2那么z是 ( )(A)纯虚数(B)实数(C)虚数 (D)1翰林汇11、在复平面内,复数z满足1<|z|<2,则z所对应的点P的集合构成的图形是(A)圆 (B)直线 (C)线段 (D)圆环翰林汇12、下列命题中正确的是 ( )(A)每个复数都有唯一的模和唯一的辐角主值(B)复数与复平面内的点是一一对应的(C)共轭虚数的n次方仍是共轭复数(D)任何两个复数都不能比较大小翰林汇13、设复数z=sin500-icos500则arg 等于(A)100 (B)800 (C)2600 (D)3500翰林汇14、已知π<θ<,复数z=|cosθ|+ i |sinθ|的辐角主值是 ( ) (A)π-θ (B)π+θ(C)θ-π (D)θ翰林汇15、已知π<θ<,复数z=|cosθ|+ i |sinθ|的辐角主值是 ( )(A)π-θ (B)π+θ (C)θ-π (D)θ翰林汇16、设z为虚数,则z2一定是 ( )(A)非负实数或虚数 (B)负数或虚数(C)虚数(D)有可能是正数翰林汇17、下列命题正确的是 ( )(A)|z|<1-1<z<1 (B)共轭复数的差一定是纯虚数(C)|z|=1 (D)共轭复数的辐角之和为零翰林汇18、复数z1=(a+bi)n,z2=(a-bi)n(a,b R且b≠0,n N),则z1与z2的关系是 ( )(A)共轭复数 (B)共轭复数或相等实数(C)相等的实数 (D)以上都不对翰林汇19、设复数z1、z2,则z1=的一个必要不充分条件是(A)|z1-|=0 (B)=z2 (C)z1=z2 (D)|z1|=|z2|翰林汇20、复数z=2i-3的共轭复数是 ( )(A)-3+2i (B)2i+3 (C)-2i+3 (D)-2i-3翰林汇二、填空题1、已知x,y是纯虚数,且满足(2x-1)+i=y-(3-y)i,则x=___,y=___。
翰林汇2、复数z=(a2-2a)+(a2-a-2)i的对应点在虚轴上,则实数a的值是______。
翰林汇3、若aÎR,z=1+ai,则z+ÎR的充要条件是_________。
翰林汇4、z为复数,由复数z,所组成的集合,最多含__个元素。
翰林汇5、设x是实数,y是纯虚数且满足(2x-1)+i=y-(3-i)i则x=_____,y=________.翰林汇6、|z1|=10,z2=6+8i,且z1·为纯虚数,则z1=________.翰林汇7、已知(2x-1)+i=y-(3-y)i, x , y 则x=________,y=________.翰林汇8、设m R复数z=(m2-m-2)+(m2-1)i对应的点在第二象限,则m____; 而当m=________时, z为实数;当m=______时, z为纯虚数。
翰林汇9、如果x-1+yi, 与i-3x 是共轭复数则实数x与y分别是______。
翰林汇10、已知复数z的模为2,虚部为-1,它在复平面上的对应点位于第三象限,则z的共轭复数是_____。
翰林汇三、判断题1、判断下列命题是否正确:(1) 若z1 , z2∈C , 且| z1 | = | z2 | , 则z1= ±z2 ( )(2) 若a, b ∈R,且a >b ,则ai>bi ( )(3) 与自身共轭的复数一定是实数 ( )翰林汇2、判断下列各命题是否正确:(1) 若z12 + z22 = 0 , 则z1 = 0 且z2 = 0 ( )(2) 若z1-z2>0 , 则z1>z2( )翰林汇3、判断下列各命题是否正确:(1) 若z∈C, 则z2≥0 ( )(2) 若z1·z2 = 0 , 则 z1 = 0 或z2 = 0 ( )翰林汇4、判断命题的真假:任意两个复数都不能比较大小。
( )翰林汇5、判断命题的真假:若x,y∈R,且x=y,则(x-y)+(x+y)是纯虚数 ( )翰林汇6、判断命题的真假:的充要条件是x1=x2,且y1=y2. ( )翰林汇7、若z是复数,判断下面命题的真假:(1)|z2|=|z|2( );(2)|z|≤1-1≤z≤1 ( )翰林汇8、若z是复数,判断下面命题的真假:(1)|z|2=z2 ( ); (2)|z|2z2( )翰林汇9、若z,z1,z2都是复数,判断下面命题的真假:(1) ( ); (2)若|z1|=|z2|,则z1=z2( )翰林汇10、若z是复数,判断下面命题的真假:(1)是实数();(2)是纯虚数()翰林汇11、若z是复数,判断下面命题的真假:(1)z2≥0 ( ); (2)若|z|=1,则 ( )翰林汇12、若z,z1,z2都是复数,判断下面命题的真假:(1) ( ); (2)若,则z1=z2=0 ( )翰林汇四、解答题1、设复数z满足|z|=2,且(z-a)2=a,求实数a的值.翰林汇2、z1,z2是复数,z1·z2≠0,A=z1+z2,B=z1+z2,问A,B可不可比较大小?若不可以比说明原因,若可以比说明大小关系并证明之.翰林汇3、已知复数z1、z2满足10z12+5z22=2z1z2,且z1+2z2为纯虚数,求证3z1-z2为实数.翰林汇4、满足z+是实数,且z+3的辐角主值是的虚数z是否存在?若存在,求出虚数z;若不存在,说明理由。
翰林汇5、已知复数当实数k和分别为何值时,是纯虚数?翰林汇复数的概念(1)〈答案〉一、选择题1、 B 翰林汇2、 B 翰林汇3、 B 翰林汇4、 C 翰林汇5、 B 翰林汇6、 B 翰林汇7、 B 翰林汇8、 C 翰林汇9、 A 翰林汇10、 B 翰林汇11、 D 翰林汇12、 B 翰林汇13、 D 翰林汇14、 C 翰林汇15、 C 翰林汇16、 B 翰林汇17、 C 翰林汇18、 B 翰林汇19、 D 翰林汇20、 D 翰林汇二、填空题1、-翰林汇2、翰林汇3、a=±1或a=0 翰林汇4、4翰林汇5、0,4i翰林汇翰林汇7、翰林汇8、(1,2),翰林汇9、翰林汇10、-翰林汇三、判断题1、(1) ╳ (2) ╳ (3) √ .翰林汇2、(1) ╳ (2) ╳.翰林汇3、(1) ╳(2) √ .翰林汇4、╳翰林汇5、翰林汇6、╳翰林汇7、(1)√;(2)╳翰林汇8、(1)╳;(2)╳.翰林汇9、(1)√;(2)╳翰林汇10、(1)√;(2)╳.翰林汇11、(1)╳;(2)√.翰林汇12、(1)√;(2)╳.翰林汇四、解答题1、解: (1)若实数a≥0,则z必为实数,此时z=2或z=-2, 当z=2时,a2-5a+4=0 解得 a1=1, a2=4.当z=-2时,a2+3a+4=0 此方程无实数解.(2)若实数a<0,则z必为虚数,且, ∵|z|=2, ∴a2-a-4=0, 解得.注意到a<0,故有,∴所求实数a的值为1, 4,翰林汇2、A≤B。
翰林汇3、由10z12+5z22=2z1z2,得10z12+5z22-2z1z2=0.∴(3z1-z2)2+(z1+2z2)2=0. 又∵z1+2z2为纯虚数,∴假设z1+2z2=bi(b∈R,b≠0),则(3z1-z2)2=-(bi)2=b2.∴3z1-z2=±|b|∈R.故3z1-z2为实数.翰林汇4、不存在翰林汇5、当k=-1且或当且时,为纯虚数.翰。
