几种常见的统计图表
讲解Excel的16种图表类型的“含义”，知道该怎么画图了！
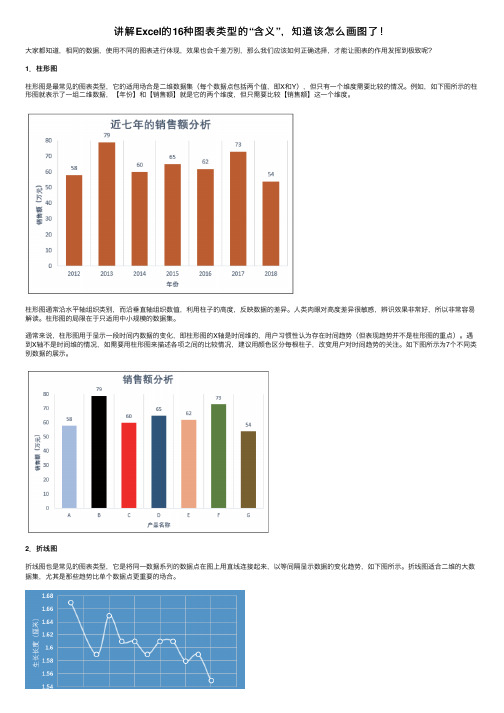
讲解Excel的16种图表类型的“含义”，知道该怎么画图了！⼤家都知道，相同的数据，使⽤不同的图表进⾏体现，效果也会千差万别，那么我们应该如何正确选择，才能让图表的作⽤发挥到极致呢？1．柱形图柱形图是最常见的图表类型，它的适⽤场合是⼆维数据集（每个数据点包括两个值，即X和Y），但只有⼀个维度需要⽐较的情况。
例如，如下图所⽰的柱形图就表⽰了⼀组⼆维数据，【年份】和【销售额】就是它的两个维度，但只需要⽐较【销售额】这⼀个维度。
柱形图通常沿⽔平轴组织类别，⽽沿垂直轴组织数值，利⽤柱⼦的⾼度，反映数据的差异。
⼈类⾁眼对⾼度差异很敏感，辨识效果⾮常好，所以⾮常容易解读。
柱形图的局限在于只适⽤中⼩规模的数据集。
通常来说，柱形图⽤于显⽰⼀段时间内数据的变化，即柱形图的X轴是时间维的，⽤户习惯性认为存在时间趋势（但表现趋势并不是柱形图的重点）。
遇到X轴不是时间维的情况，如需要⽤柱形图来描述各项之间的⽐较情况，建议⽤颜⾊区分每根柱⼦，改变⽤户对时间趋势的关注。
如下图所⽰为7个不同类别数据的展⽰。
2．折线图折线图也是常见的图表类型，它是将同⼀数据系列的数据点在图上⽤直线连接起来，以等间隔显⽰数据的变化趋势，如下图所⽰。
折线图适合⼆维的⼤数据集，尤其是那些趋势⽐单个数据点更重要的场合。
折线图可以显⽰随时间⽽变化的连续数据（根据常⽤⽐例设置），它强调的是数据的时间性和变动率，因此⾮常适⽤于显⽰在相等时间间隔下数据的变化趋势。
在折线图中，类别数据沿⽔平轴均匀分布，所有的值数据沿垂直轴均匀分布。
折线图也适合多个⼆维数据集的⽐较，如下图所⽰为两个产品在同⼀时间内的销售情况⽐较。
不管是⽤于表现⼀组或多组数据的⼤⼩变化趋势，在折线图中数据的顺序都⾮常重要，通常数据之间有时间变化关系才会使⽤折线图。
3．饼图饼图虽然也是常⽤的图表类型，但在实际应⽤中应尽量避免使⽤饼图，因为⾁眼对⾯积的⼤⼩不敏感。
例如，对同⼀组数据使⽤饼图和柱形图来显⽰，效果如下图所⽰。
常见的六种图表类型
常见的六种图表类型1、柱形图，又称长条图、柱状统计图，是一种以长方形的长度为变量的统计图表。
作为我们最常用的图表之一，通常是为了表现数据大小的对比。
柱形图经久不衰，正是因为它的可读性与简洁性。
2、饼图，或称饼状图，是一个划分为几个扇形的圆形统计图表，用于描述数量、频率或百分比之间的相对关系。
在饼图中，每个扇区的弧长（以及圆心角和面积）大小为其所表示的数量的比例。
这些扇区合在一起刚好是一个完全的圆形。
3、环形图是由两个及两个以上大小不一的饼图叠在一起，挖去中间的部分所构成的图形，主要是为了区分或表明某种关系。
环形图与饼图类似，但又有区别。
环形图中间有一个“空洞”，每个样本用一个环来表示，样本中的每一部分数据用环中的一段表示。
因此环形图可显示多个样本各部分所占的相应比例，从而有利于构成的比较研究。
4、气泡图，即以气泡形状为主，绘制展示信息的图。
它可以直接做散状气泡，可以与坐标系结合，也可以在它们之间用各种连接线表达关系。
气泡图因为它外观简洁直观、可视化数据信息；种类多，应用领域广；帮助整理思维，启发思维和想象等优点，越来越受到职场人的追捧和学习。
5、对比图就是将两个或两个以上的主体，通过一张图来进行多维度同步分析的一种分析方法。
这种图形我们日常在分析不同产品型号、竞品分析、产品功能分析中常见。
6、甘特图又称为横道图、条状图，其通过条状图来显示项目，进度，和其他时间相关的系统进展。
该图表以提出者亨利·劳伦斯·甘特（Henry Laurence Gantt）先生的名字命名。
甘特图横轴是时间线，纵轴是项目名称。
可以看出每个项目需要多少时间，在所有项目中某个特定项目开始和结束的时间点，发现有多少项目正在同时进行、哪些项目快到期，明确项目紧急性，从而及时做出调整。
几种常见的统计图表
R
W
扇形图(sector diagram)
概念：以一个圆面积为100%，用圆内 各扇形面积所占的百分比来表示各 部分所占的构成比例 适用资料：构成比资料 绘制要点： ①每3.6o为1%，用3.6乘以百分数即为 请问：如何表示 所占扇形的度数。用量角器画出. 扇形内各部分所 ②从相当于时钟12点或9点的位置开始 顺时针方向绘图. ③每部分用不同线条或颜色表示，并在 图上标出百分比，下附图例说明. ④当比较不同资料的百分构成时，可以 画两个相等大小的圆，在每个圆的 下面写明标题，并用相同的图例表 示同一个构成部分. 应用：描述各部分的百分构成.
展变化或一种现象随另一种现象变迁的情况 2、适用资料：连续性资料。 3、绘制要点： ①坐标轴：横轴表示时间或组段，纵轴表示频数或频率。 纵轴坐标可以不从0开始，因此在看图时要注意纵轴的 起点坐标。 ②数据点画在组段中间位置。相邻的点用直线连接，不要 用平滑的曲线连接。无数据的组段用虚线连接。直线 不能任意外延。 ③同一张折线图上不要画太多条曲线，否则不易分清。当 有两条或两条以上曲线在同一张折线图上时，须用不 同颜色或不同的图形形式加以区分，并附图例加以说 明。 4、应用：反映事物的连续的动态变化规律。
190 180 170 160 150 40 45 50 ©Û ¤ 55 Ç ª± (cm)
ì ß É µ (cm)
Í 10.Ä ³ 20Ë Ä Ç Ä É µ · Ç Û ± Ä ¶ Ï ¼ ± Ø ê Ð ê ì ß Í ©ª¤³ Ø ³
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 5 10 15 20 25 30
9% 18% 43%
ô · « ² È Ï ä Æ
ü ³ ° ¡ Î Ï ¼ ° ¾ ¡ È ° ë Ô ° ¡ Ì Ð ¼ ° ü Ë
统计技术(新老七种工具)
直方图（频数直方图）
• ⑹画直方图: 在横轴上以每组对应的组距为底，以该组的频数 为高，作直方图。计算样本平均值（X），样本标准偏差值 （S），在图上标出公差范围（T），样本量（n），样本平均值 （X），样本标准偏差（S）和X的位置。
• 计算公式: （以替换数法）
∑ fi ui • X= Xo+ h× n
控制图
•
2.计数值控制图
• ⑴不合格品率控制图（P）
• ⑵不合格品数控制图（nP）
• ⑶单位不合格品数控制图（u）
• ⑷不合格数控制图（C）
控制图
•
四、常规控制图的判断准则
• 1.在点子随机排列的情况下，出现下列情况之
一，就判断过程处于稳态，即没有异常波动的 状态。
• ⑴连续25个点，落在控制界外的点数为0；
• 产品质量的波动分为正常波动和异常波动两 类。
• 控制图就是用来及时反映和区分正常波动 与异常波动的一种工具, 控制图上的控制界限是 区分正常波动与异常波动的科学界限。
控制图
• 三、常规控制图的分类 • 一般按数据的性质分为计量值控制图和计数
值控制图两大类。 • 1.计量值控制图 • ⑴均值——极差控制图（X-R） • ⑵均值——标准差控制图（X-S） • ⑶中位数——极差控制图（X～-R） • ⑷单值——移动极差控制图（X-Rs）
•
S= h ×∑ fi u2i
-（ ∑ fi ui
）2
n
n
•
其中: Xo——频数最大的组中值。
•
fi——各组频数
•
ui——各组替换数，设定频数最大的一组u=0，以此往上分
别为-1,-2,-3……，往下分别为1，2，3…..
华师大版-数学-八年级上册-华师 几种常见的统计图表 教案
【同步教育信息】一. 本周教学内容：华师七上第五章几种常见的统计图表教案二. 教学目标1、理解数据的频数、频率及频率分布的意义，会就一组数据列出频数分布表和画出频数分布直方图，频数折线图。
2、了解不同统计图的特征，能根据具体问题选择合适的统计图来清晰地描述数据。
三. 教学重点和难点重点：理解条形、折线、扇形、直方统计图的特点，并会制作统计图。
难点：能根据不同的问题，选择不同的统计图。
［教学过程］知识点归纳：知识点1 频数和频率的概念在调查中每个对象所出现的次数称为频数。
一般我们称落在不同小组中的数据个数为该组的频数。
频数与数据总数的比为频率。
频率反映了各组频数的大小在总数中所占的分量，频率 100%就是百分比。
知识点2 数据的表示方法（1）条形图用一个单位长度表示一定的数量，根据数量的多少画成长短不同的直条，再把这些直条按照一定的顺序排列起来，这样的统计图叫做条形统计图。
条形统计图能清楚地表示出每个项目的具体数字，即根据条形统计图可以直接看被统计对象的准确数据。
例如：某校八年级学生共300人，到学校上学的方式有骑自行车的，有步行的，有坐车的，还有其它方式的，这四种方式的人数可用条形统计图表示出来。
知识点3 数据的表示方法（2）扇形图利用圆和扇形来表示总体和部分的关系，圆代表总体，圆中的各个扇形分别代表总体中的不同部分，扇形统计图能清楚地表示出每个部分在总体中所占的百分比，即根据统计图可看出被统计对象所占比例。
例如：上面用条形图表示的某校八年级学生到校上学方式的情况，可用扇形统计图形表示。
知识点4 数据的表示方法（3）折线图用一个单位长度表示一定的数量，根据数量的多少描出各点，然后把各点用线段顺次连接起来，所得的统计图叫做折线统计图。
折线统计图能清楚地反映事物的变化情况。
即根据折线统计图能清楚地看出事物变化的趋势。
年龄（岁） 5 10 15 20 25身高（cm）92 140 178 183 185该同学的生长情况，可用折线统计图表示出来，如图所示。
12.1 几种常见的统计图表(3)(含答案)-
12.1 几种常见的统计图表（3）1．常见的统计图表有_______、________、_______、________四种，其中能够显示每组中的具体数据且易于比较数据之间的差别的是_________；能表示部分在总体中所占的百分比且易于显示每组数据相对于总数的大小的是_______；易于显示数据的变化趋势的是________；•能够显示各组频数分布的情况且易于显示各组之间频数的差别的是_________．2．某班组织25名团员为灾区捐款，其中捐款数额前三名的是10元5人，5元10•人，2元5人，其余每人捐1元，那么捐10元的学生出现的频率是________．3．一个样本含有下面10个数据：52，51，49，50，47，48，50，51，48，53，•则最大的值是_______，最小的值是______，最大值与最小值的差是_______，如果组距为1．5，•则应分为_______组．4．频数分布直方图（如图所示）显示了学生半分钟心跳数情况，•总共统计了____学生的心跳数情况，______次人数段的学生数最多，约占_______，如果半分钟心跳数30～39属于正常范围，心跳次数属于正常范围的学生约占_______．5．频数分布直方图中长方形的高是该组数据的（）A．频率 B．个数 C．所占总体的百分比 D．与该组数据无关6．在2000个数据中，用适当的方法抽取50个作为样本进行统计，在频数分布直方图中，54.5～57.5这一组的频数为6，那么估计总体数据在54.5～57.5之间的约有（ •）A．240 B．120 C．24 D．127．一个容量为50的样本，在整理频率分布时，将所有频率相加，其和是（）A．50 B．0.02 C．0.1 D．18．对某班学生一次数学测试成绩进行统计分析，各分数段的人数如图所示（分数取正整数），请观察图并回答下列问题：（1）该班有多少名学生？（2）89.5～99.5这一组的频数，频率分别为多少？（3）估算该班这次测验的平均成绩．9．甲、乙两人连续7年调查某县养鸡业的情况，提供了两方面的信息图，•甲调查表明：养鸡场的平均产鸡数从第1年的1万只上升到第7年的2．8万只；乙调查表明，•养鸡场的个数由第1年的46个减少到第7年的22个.现给出四个判断：①该县第二年养鸡场产鸡的数量为1．3万只；②该县第二年养鸡场产鸡的数量低于第一年养鸡场产鸡的数量；③该县这7年养鸡场产鸡的数量逐年增大；④这7年中，•第5年该县养鸡场出产鸡的数量最多根据甲、乙两人提供的信息，可知其中正确的判断有（）A．2个 B．1个 C．0个 D．3个10．为了掌握学生的身体发育情况，对某年级同龄的40名男生的身高进行调查，•结果如下．（单位：cm）161 163 163 160 165 162 164 161 156 173166 160 158 168 166 155 159 178 160 156155 160 159 178 152 158 166 154 163 170169 161 173 159 166 155 160 169 171 158请对数据适当分组，列出频数分布表，画出频数分布直方图，并分析这个年龄的男生的身高在哪个范围表示发育正常．11．某校课外活动小组为了了解本校九年级学生的睡眠时间情况，对学校若干名九年级学生的睡眠时间进行了抽查，•将所得数据整理后画出了频数分布直方图的一部分，如图所示，已知图中从左到右前5个小组的频率分别是0.04，0.08，0.24，0.28，0.24，第二小组的频数为4，请回答：（1）这次被抽查的学生人数是多少人？并补全频率分布直方图；（2）被调查的学生中，睡眠时间在哪个范围内的人数最多？•这一范围的人数是多少？（3）如果该学校有900名九年级学生，若合理的睡眠时间为7≤t<9，那么请你估计一下这个学校九年级学生中睡眠时间在此范围的人数是多少．12．现从我市区近期卖出的不同面积的商品房中随机抽取1000套进行统计，并根据结果绘出如图所示的统计图，请结合图中的信息，解答下列问题：（1）卖出面积为110～130m2的商品房有_______套，并在下图中补全统计图；（2）从图中可知，卖出最多的商品房约占全部卖出商品房的______%；（3）假如你是房地产开发商，根据以上提供的信息，•你会多建住房面积在什么范围内的住房？为什么？答案:1．条形图，扇形图，折线图，直方图；条形图，扇形图，折线图，直方图2．0.2 3．53，47，6，4 4．27名，30～33，26%，56% 5．B 6．A 7．D 8．（1）该班共有4+•8+•10+12+16=50人，（2）89.5～99.5这一组的频数共12人，频率为0.24，（3）略 9．D10．图略，身高在156～164之间都表示发育正常11．（1）50（人），根据第六组的人数为6•个来补全直方图，图略，（2）睡眠时间在6≤t<7的人数最多，14人，（3）324人 •12．（1）150，图略（2）45（3）由上可知，一般会建住房面积在90～110m2范围的住房较多人需求，易卖出去．。
常见的统计图
第33讲常见的统计图知识梳理一、几种常见的统计图1.条形统计图用长方形的高来表示数据的图形.（2）易于比较各组数据之间的差别. 它的特点：（1）能够显示每组中的具体数据；2.折线统计图用几条线段连成的折线来表示数据的图形. 它的特点：易于显示数据的变化趋势.3.扇形统计图（1）用一个圆代表总体，圆中的各个扇形分别代表总体中的不同部分，扇形的大小反映部分在总体中所占百分比的大小，这样的统计图叫做扇形统计图;⑵百分比的意义：在扇形统计图中，每部分占总体的百分比等于该部分所对扇形的圆心角的度数与360°的比;⑶扇形的圆心角=360°＜该部分占总体的百分比二、频数分布直方图1.数据中每个对象出现的次数叫做频数，每个对象出现的次频数 数与总次数的 比（或百分比）叫做频率，即频率=数频数数.2. 与频数、频率相关的公式 （1） 频数=频率X 总数； （2） 各组频数之和等于总数； （3） 各组频率之和等于1._ pt 畔溼M 如考点一统计图表的简单应用例1 （2016泰安）某学校将为初一学生开设 ABCDEF 共6门选 修课，现选取若干学生进行了 我最喜欢的一门选修课”调查，将调 查结果绘制成如图统计图表（不完整）.根据图表提供的信息，下列结论错误的是 A .这次被调查的学生人数为400人 B .扇形统计图中E 部分扇形的圆心角为C .被调查的学生中喜欢选修课 E , F 的人数分别为80, 70D .喜欢选修课C 的人数最少【点拨】本题考查了条形统计图、扇形统计图的内容.考点~二n 八、、—"例2 （2016泰州）某校为更好地开展 传统文化进校园”活动，随 机抽查了部分学生，了解他们最喜爱的传统文化项目类型（分为书法、 围棋、戏剧、国画共4类），并将统计结果绘制成如图不完整的频数 分布表及频数分布直方图.选修课 A BC DEF人数4060100频数分布直方图的应用o72 最喜欢的传统文北顼目类型最喜爱的传统文化项目类型频数分布表项目类型频数频率书法类18 a围棋类14 0.28戏剧类8 0.16国画类 b 0.20根据以上信息完成下列问题：(1)直接写出频数分布表中a的值；(2)补全频数分布直方图；(3 )若全校共有学生1 500名，估计该校最喜爱围棋的学生大约有多少人？【点拨】本题考查了频数分布表、频数分布直方图、用样本估计总体和概率计算的有关知识考点三统计的综合应用例3 (2016济南)随着教育信息化的发展，学生的学习方式日益增多，教师为了指导学生有效利用网络进行学习，对学生进行了随机问卷调查(问卷调查表如图所示)，并用调查结果绘制了图1、图2两幅统计图(均不完整)，请根据统计图解答以下问题：(1)本次接受问卷调查的学生共有人，在扇形统计图中“D选项所占的百分比为；(2)扇形统计图中，“ B”选项所对应扇形圆心角为度；(3)请补全条形统计图；(4)若该校共有1 200名学生，的时间在“A选项的有多少人？【点拨】本题考查了条形统计图、扇形统计图以及用样本估计总体的思想.-、选择题1. （2016安徽）自来水公司调查了若干用户的月用水量 x （单位:吨），按月用水量将用户分成 A 、B 、C 、D 、E 五组进行统计，并制 作了如图所示的扇形统计图.已知除B 组以外，参与调查的用户共64户，则所有参与调查的用户中用水量在 6吨以下的共有（ ）户数的百分比为 1- 10% - 35% - 30% - 5% = 20% ,则所有 参与调查的用户中月用水量在6吨以下的共有80 *10% +20%） = 24（户）.故选 D .【答案】D2. （2016滨州）某校男子足球队的年龄分布如图所示， 则根据图中信 息可知这些队员年龄的平均数、中位数分别是 （ ）A . 18 户B . 20 户C . 22 户24户组别月用水量x （单位：吨）A 0$<3B 3$<6C 6$<9D 9§<12 EX 羽2【解析】根据题意，参与调查的户数为64 10% + 35% + 30% + 5%二80（户）'其中B 组用户数占被调查3(iS DC0 1 2 3 4 5 6 7 8刃角份C . 15, 15.5【解析】根据图中信息可知这些队员年龄的平均数为13^+ 14"+ 15"+ 16灯+ 17怎+18*=15（岁）,该足球队共有队员2+6+8+3+2+ 1 = 22（人）,则第11名和第12名 的平均年龄即为年龄的中位数 ，故中位数为15岁.故选D . 【答案】Dh y/TL3. （2016北京）在1〜7月份，某 种水果的每斤进价与出售价的信息 如图所示，则出售该种水果每斤利润 最大的月份是（） A . 3月份B . 4月份2+6+8+3+2+1D . 15, 15C. 5月份D. 6月份11109576 5 4 3 2\ '\每斤售价\ \每斤进价\50【答案】B4. 某学校教研组对八年级360名学 生就 分组合作学习”方式的支持程度进行了调查，随机抽取了若干名学 生进行调查，并制作统计图，据此统 计图估计该校八年级支持分组合作 学习”方式的学生为（含非常喜欢和 喜欢两种情况）（B ）A . 216 人B . 252 人C . 288 人D . 324 人出了频数分布表:通话时间x/min0<x < 55< x< 1010<x < 1515< x < 20频数（通话次数）2016 9 5则通话时间不超过15 min 的频率为（ ）A . 0.1B . 0.4C . 0.5D . 0.9【解析】样本容量为20+16+9+ 5= 50,而通话时间不超过15 min 的频数和为45,所以通话时间不超过 15 min 的【解析】各 人数月每斤利润为3月：7.5 -4.5= 3（兀）,4 月：6-2.5= 3.5（元）,5月：4.5 - 2 = 12 "FT非常喜欢不喜无所 祁款 •眾 谓=1.5（元）,所以2.5（元）,6 月：3 -1.55.小明统计了他家今年5月份打电话的次数及通话时间,并列频率为0.9.故选D .【答案】D11，10，9，6, 4，共有50人，故A 正确；年龄在 42小组的教职工人数为 10人，占总人数的百分比为=20% ,故B 正确；总人数为 50人，则第25和第26个数据的平均数为中位数,观察直方图可知应落在 40< X V 42这组，故C 正确;【解析】由直方图可知，各个小组的人数分别是4, 6, 40 < X V100%6 .如图是某学校全体教职工年龄的频数分布直方图 （统计中采 用 上限不在内”的原则，如年龄为36岁统计在36< XV 38小组，而B .年龄在40< X V42小组的教职工人数占该学校总人数的 20%C .教职工年龄的中位数一定落在 40WXV42这一组D .教职工年龄的众数一定在 38< X V 40这一组虽然38< X V 40这一组人数最多,但具体岁数不知道, 故众数不一定在这一组，故D 错误．故选D ．答案】D50。
几种常见统计图的比较与选择
几种常见统计图的比较与选择我们已经学习了几种常见的统计图，这些统计图各有其优点和缺点，所以在平时的具体应用时，应根据统计图的各自特点灵活选择运用.一、条形统计图表示各种数量的多少用条形统计图.条形统计图的优点是能清楚地表示出每个项目的具体数目；缺点是不能准确地描述各部分量之间的关系.例1北京奥组委从4月15日起分三个阶段向境内公众销售门票，开幕式门票分为五个档次，票价分别为人民币5000元、3000元、1500元、800元和200元.某网点第一周内开幕式门票的销售情况见如图1所示的统计图，那么第一周售出的门票票价．．的众数是（ ） A.1500元B.11张C.5张D.200元简析 从条形图中我们清楚地看到票价分别为人民币5000元、3000元、1500元、800元和200元的门票分别销售2张、5张、11张、5张和6张，由此可知这第一周售出的门票票价的众数是1500元，故应选A .二、扇形统计图表示各部分数量同总数之间的关系用扇形统计图. 扇形统计图的优点是能清楚地表示出各部分在总体中所占的百分比；缺点是不能从统计图上看出具体的数量.扇形统计图的制作步骤是：（1）数据的采集，即各部分的数据的收集；（2）数据的整理，即计算出各部分的总和，再计算各部分所占的百分比；（3）作图，即根据百分比计算出各部分对应圆心角的大小（将百分比乘以360°），再用量角器画出各个扇形；（4）标上各部分的名称和它所占的百分比.例2 已知小明家五月份总支出共计1200元，各项支出如图2所示，那么其中用于教育5000 3000 1500 800 200 档（元）第一周开幕式门票销售情况统计图数量（张）图1图2上的支出是元.简析从扇形统计图中可知小明家五月份用于教育上的支出的百分数是18％，而五月份总支出共计1200元，所以小明家五月份用于教育上的支出是1200×18％＝216（元）.三、折线图表示数量的多少及数量增减变化的情况用折线图. 折线图的优点是能清楚地反映事物的变化情况；缺点是不能反映每一个数据在总体中的具体情况.例3（2007·义乌市）“义乌·中国小商品城指数” 简称“义乌指数”.如图3是2007年3月19日至2007年4月23日的“义乌指数”走势图，下面关于该指数图的说法正确的是（）DA.4月2日的指数位图中的最高指数B.4月23日的指数位图中的最低指数C.3月19至4月23日指数节节攀升D.4月9日的指数比3月26日的指数高简析由折线统计图可知4月16日的指数位图中的最高指数，3月19日的指数位图中的最低指数，3月19至4月2日指数节节攀升，即A、B、C的选择支都是错误的，而4月9日的指数比3月26日的指数高的说法是正确的，故应选D.图3四、直方图落在不同小组中的数据个数为该组的频数，频数与数据总数的比为频率，频率能反映各组频数的大小在总数中所占的份量.直方图能直观清楚地反映数据在各个范围内的分布情况，从而更全面、准确、细致地反映事物的属性.绘制频数分布直方图的一般步骤是：（1）计算最大值与最小值的差，目的是知道数据波动的大小，把它作为分组的依据；（2）决定组距与组数；（3）决定分点；（4）列频数分布表；（5）绘制频数分布直方图.例4 抽取某校学生一个容量为150的样本，测得学生身高后，得到身高频数分布直方图如图4，已知该校有学生1500人，则可以估计出该校身高位于160cm至165cm之间的学生大约有人.简析 从频数分布直方图中可知150人中身高位于160cm 至165cm 之间的学生有30人，所以该校有学生1500人中可以估计出身高位于160cm 至165cm 之间的学生大约有1500150×30＝300（人）. 下面几道题目供同学们自己练习：1、某射击小组有20人，教练根据他们某次射击的数据绘制成如图5所示的统计图，则这组数据的众数和中位数分别是（ ）A.7、7B.8、7.5C.7、7.5D.8、6.52、某校七年级（1）班36位同学的身高的频数分布直方图如图6所示.问： （1）身高在哪一组的同学最多？ （2）身高在160cm 以上的同学有多少人？（3）该班同学的平均身高约为多少（精确到0.1cm ）？3、在2004年雅典奥运会上，中国队取得了令人瞩目的成绩，获得金牌32枚、银牌17枚、铜牌14枚，在金牌榜上位居第二.请用扇形统计图表示中国队所获奖牌中，金、银、铜牌的分布情况.(cm)图4图5cm ）图6参考答案： 1、C .2、（1）通过观察频数分布直方图知，身高在160.5cm ～165.5cm 这一组人数最多.（2）由频数分布直方图知，身高在160cm 以上的同学有：12+8+3＝23（人）.（3）该班同学的平均身高为41539158121638168317336⨯+⨯+⨯+⨯+⨯＝162（cm ）.3、中国队所获的奖牌是由金牌、银牌、铜牌组成，它们是总量和分量的关系．先求出金、银、铜牌分别占奖牌总数的百分比，在根据百分比算出扇形的圆心角，进而画出扇形统计图.即①中国队共获奖牌63枚，其中金牌32枚，占奖牌总数的百分比为：32÷63≈50.79％.银牌17枚，占奖牌总数的百分比为：17÷63≈26.99％.铜牌14枚，占奖牌总数的百分比为：14÷63≈22.22％.②反映在扇形统计图上，扇形的圆心角为：金牌应为：360°×50.79％≈182.8°，银牌应为：360°×26.99％≈97.2°，铜牌应为：360°×22.22％≈80°.③绘制扇形统计图，如图所示.4、（1）5月6日新增确诊病例138人.（2）5月9日至5月11日三天共新增确诊病例为118+85+69＝272（人）.（3）从折线统计图中可清楚看到5月上半月新增确诊病例总体的趋势是下降的.两类复合条形图特征对比条形图是一种重要的统计图，其特点是：（1）能够显示每组中的具体数据；（2）易于比较数据之间的差别。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第十二章数据的描述
12.1 几种常见的统计图表
[教学目标]
1．知识与能力：
认识条形图、扇形图、折线图、直方图，能够从统计图中获取相关信息．
2．过程与方法：
从问题的解决过程中体会各个统计图的优点和缺点，感受统计图的作用．
3．情感、态度与价值观：
培养学生运用统计图的能力以及用数据说话的习惯．
[重点难点]
1．教学重点：能够利用条形图、扇形图、折线图、直方图描述数据，能够从统计图中获取相关信息．
2．教学难点：读图、识图、获取信息.
[教学方法]
创设情境——主体探究——合作交流——应用提高．
[教学过程]
一、创设情境，激发学生兴趣，认识条形图和扇形图
问题 1：展示空气质量图（课本 54 页），2002 年 1 月 1 日，这 31 个城市中，空气质量为一级，二级，…，五级的城市各有多少个？各占百分之几？
学生活动设计：
学生分组合作、共同解决问题．按空气质量级别对这 31 个数据分组，数出每一组的城市个数，再计算它们所占的百分比，列出下表：
级别划记
频数
（城市个数）
频率
（频数/31）
百分比
一级一 1 0.032 3.2% 二级正8 0.258 25.8% 三级正正正19 0.613 61.3%
四级 2 0.065 6.5%
五级一 1 0.032 3.2%
合计31 31 1 100% 从表中可以看出空气质量为各级的城市个数及其所占百分比.如空气质量为二级的有8 个城市，占 25.8%．
教师活动设计：
教师在学生解决问题的基础上作以下归纳：
落在不同小组中的数据个数为该组的频数，频数与数据总数的比为频率．
在此过程中，注重学生参与活动的程度．
问题 2：对于上述数据我们可以怎样描述呢？
学生活动设计：
学生根据所学知识，想到可以利用条形图和扇形图来描述数据．为了清楚地描述空气质量为各个级别的城市的个数，可以用条形图[如图（1）]来描述；为了清楚地看出各个空气质量级别的城市个数占总城市数（31 个）的百分比，可以用扇形图[如图（2）]来描述.
图（1）
图（2）
学生独立完成上述统计图的制作，在制作过程中，让学生体会上述两种图形的制作方法，最后引导学生对两种图形的优缺点进行分析．
条形图：
（1）能够显示每组中的具体数据；
（2）易于比较数据之间的差别．
扇形图：
（1）用扇形的面积表示部分在总体中所占的百分比；
（2）易于清楚地看出各个项目占总数的百分比，但不能看出各个项目的频数以及数据总数．
二、小组合作，认识折线图
问题 3：出示图片（课本第 58 页：两会漫笔）分析上面报纸中的数据（文中提到 1993 年，当年的国内生产总值为 34 561 亿元），用什么样的统计图可以很好地描述我国 GDP （国内生产总值）的变化趋势？你能制作相应的统计图吗？
学生活动设计：
学生独立思考，发现可以用折线图来描述数据的变化趋势，然后小组合作，制作折线图，如图（3）．
年份1986 1991 1993 1997 1999 2001 GDP/万亿元 1.02 2.17 3.46 7.31 8.04 9.59
图（3）
在学生解决问题后，引导学生归纳折线图的特点：
易于显示数据的变化趋势．
三、主体探究，认识直方图
问题 4：为了研究 800 米赛跑后学生心率的分布情况，体育老师统计了全班同学一分时间脉搏的次数，并整理成下面的表格. 根据下列表格，你能用统计图描述表中的数据吗？
脉搏次数x（次/分）频数（学生人数）
130≤x＜135 1
135≤x＜140 2
140≤x＜145 4
145≤x＜150 6
150≤x＜155 9
155≤x＜160 14
160≤x＜165 11
165≤x＜170 2
学生活动设计：
学生小组讨论，发现可以用类似条形图的方法进行描述，如图（4）．
图（4）
通过上述统计图可以发现：
（1）脉搏次数x在 155≤x＜160 范围的学生最多，有 14 个；
（2）脉搏次数x在 135≤x＜140 范围的学生有 2 个；
（3）脉搏次数x在 150≤x＜155 范围的学生比在 160≤x＜165 范围的学生少 2 个；
（4）全班一共有 49 个学生.
教师活动设计：
引导学生作以下归纳：
体育老师把全班学生的脉搏次数按范围分成成 8 组，每一组的两个端点的差都是 5. 我们把分成的组的个数称为组数，每一组两个端点的差称为组距，上述这样的表格称为频数分布表，利用频数分布表画出的统计图叫做直方图．
归纳直方图的特点：
（1）能够显示各组频数分布的情况；
（2）易于显示各组之间频数的差别．
四、应用提高、拓展创新
问题 5：随着我国对外开放程度的不断扩大，我国对外贸易迅速发展．下表是我国近几年的进出口额数据．你能用统计图来描述这两组数据，从而对它们进行比较吗？
年份1985 1990 1995 1998 2000 2002 出口额（亿美元）274 621 1 488 1 837 2 492 3 256
进口额（亿美元）423 534 1 321 1 402 2 251 2 952 师生活动设计：
教师引导学生利用折线图和复合条形图来描述这两组数据，如图（5）（6）．
图（5）
图（6）五、归纳小结、布置作业
小结：
描述数据的方法——几种常见的统计图．
作业：
习题 12.1．。