【校级联考】浙江省义乌市稠州中学教育集团2018-2019学年上学期期中考试八年级语文试卷
浙江省义乌市稠州中学教育集团2018-2019学年上学期期中考试七年级语文试卷

浙江省义乌市稠州中学教育集团2018-2019学年上学期期中考试七年级语文试卷1.下列字形和加点字注音全部正确的一项是( )A. 愠.怒(yùn) 棱.镜(léng)伫.蓄(zhù)疲倦不堪B. 盔.甲(hūi) 莅.临(lì)倘.若(tǎng) 美不胜收C. 屋檐.(yán) 急躁.(zào)发髻.(jì) 人声鼎沸D. 搓捻.(niǎn) 澄.清(chéng) 分岐.(qí)各得其所2.下列句子中重音、停连标识有误的一项是()(注:“.”是重音标记,“∨”是停顿标记,“^”是连接标记。
)A. 风里带来些∨新翻的泥土的气息.....,混着∨青草味儿....,还有各种花的香.。
B. 牛背上∨牧童的短笛..地响。
..,这时候也成天在嘹亮C. 真.的,济南的人们∨在冬天是面上含笑....的。
D. 明天∨也许就是春天...了吧?..了吧?这样的温暖..,今天∨夜里山草也许就绿起来3.下列关于文学文化常识的表述有误的一项是( )A. 老舍,原名舒庆春,字舍予,满族人。
代表作有长篇小说《骆驼祥子》《四世同堂》,戏剧《茶馆》《龙须沟》。
被称为“人民艺术家”。
B. 古人称谓有谦称和尊称的区别,如谦称自己的意见为“高论”。
C. 《秋天的怀念》中的母亲,是一位活得最苦,却又无比慈爱、包容、细心、无私、坚忍、睿智的母亲。
D. 《世说新语》,南朝宋的临川王刘义庆组织编写的一部志人小说集,主要记载汉末至东晋士大夫的言谈、轶事。
4.对下列各句修辞方法判断有误的一项是()A. 每一棵树仿佛都睁开特别明亮的眼睛。
(比喻)B. 山坡上卧着些小村庄,小村庄的房顶上卧着点儿雪。
(拟人)C. 那点儿薄雪好像忽然害了羞,微微露出点儿粉色。
(拟人)D. 像牛毛,像花针,像细丝。
(比喻,排比)5.古诗文默写填空。
(1)乡书何处达?_____________。
浙江省金华市义乌市稠州教育集团2018-2019学年九年级上学期科学期中试卷及参考答案
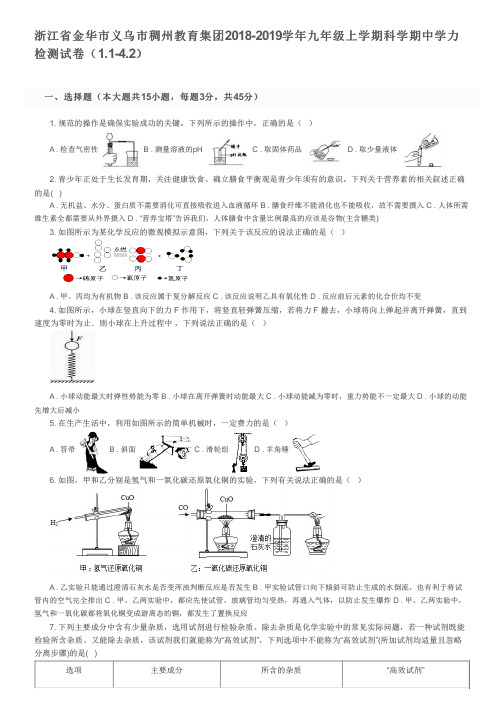
一 、 选 择 题 ( 本 大 题 共 15小 题 , 每 题 3分 , 共 45分 )
1. 规范的操作是确保实验成功的关键。下列所示的操作中,正确的是( )
A . 检查气密性
B . 测量溶液的pH
13. 往FeCl3和CuCl2的混合溶液中加入铁粉。已知反应的先后顺序、化学方程式分别为:2FeCl3+Fe=3FeCl2 , CuCl2 +Fe=FeCl2+Cu,下图为反应后混合液质量与加入铁粉质量的关系曲线,N、M、P、Q是曲线上的点,则下列说法错误的
是( )
A . 若b=2a,则反应过程中溶液质量的增加量与减小量之比为8:7 B . 若b=2a,则原混合液中FeCl3和CuCl2的质量分数之比为65 :27 C . 与M、P、Q对应的溶液中的溶质种类分别是3、2、1种 D . N→P发生的反应为化合反应,P→Q发生的反应为置换反应
3. 如图所示为某化学反应的微观模拟示意图,下列关于该反应的说法正确的是( )
A . 甲、丙均为有机物 B . 该反应属于复分解反应 C . 该反应说明乙具有氧化性 D . 反应前后元素的化合价均不变 4. 如图所示,小球在竖直向下的力 F 作用下,将竖直轻弹簧压缩,若将力 F 撤去,小球将向上弹起并离开弹簧,直到 速度为零时为止.则小球在上升过程中 ,下列说法正确的是( )
A . 绳子自由端F1、F2移动的速度大小相同 B . F1做功比F2做功少 C . 两种方法中所做的有用功一样多 D . 两种方法中机械效率
相同
9. 向一定量的稀盐酸中加入过量 NaOH 溶液,下列图象能正确反映其对应变化关系的是( )
浙江省义乌市稠州中学教育集团2018-2019学年八年级上学期数学期中考试试卷

浙江省义乌市稠州中学教育集团2018-2019学年八年级上学期数学期中考试试卷一、单选题(共10题;共10分)1.下列图形中,不是轴对称图形的是()A. B. C. D.【答案】C【解析】【解答】解:根据轴对称图形的概念,可知:选项C中的图形不是轴对称图形.故答案为:C.【分析】将一个平面图形沿着某条直线折叠,直线两旁的部分能完全重合的图形就是轴对称图形,根据定义即可一一判断出得出答案。
2.在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是()A. 4cmB. 5cmC. 9cmD. 13cm【答案】C【解析】【解答】根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,即9-4=5,9+4=13.∴第三边取值范围应该为:5<第三边长度<13,故只有C选项符合条件.故答案为:C.【分析】根据三角形的三边关系两边之和大于第三边,两边之差小于第三边,得到第三边取值范围.3.若x<y成立,则下列不等式一定成立的是()A. 4x<3yB. ﹣2x<﹣2yC. x2<y2D. x-2018<y-2018【答案】 D【解析】【解答】解:∵x<y成立,∴A、4x与3y无法比较大小,不符合题意;B、-x>-y,不符合题意;C、x2<y2不一定成立,不符合题意;D、x-2018<y-2018,不等式的两边减2018,不等号方向不变,符合题意.故答案为:D.【分析】不等式的性质:在不等式的两边都加上或减去同一个数或整式,不等号方向不变;再不等式的两边都乘以或除以同一个正数不等号方向不变;在不等式的两边都乘以或除以同一个负数,不等号方向改变;根据法则即可一一判断得出答案。
4.如图,△ABC中,∠C=80°,若沿图中虚线截去∠C,则∠1+∠2=()A. 360°B. 260°C. 180°D. 140°【答案】B【解析】【解答】解:∵∠1、∠2是△CDE的外角,∴∠1=∠4+∠C,∠2=∠3+∠C,即∠1+∠2=∠C+(∠C+∠3+∠4)=80°+180°=260°.故答案为:B.【分析】利用三角形的外角和定理得∠1=∠4+∠C,∠2=∠3+∠C,再根据角的和差得出结论。
浙江省金华市义乌市稠州中学九年级(上)期中物理试卷
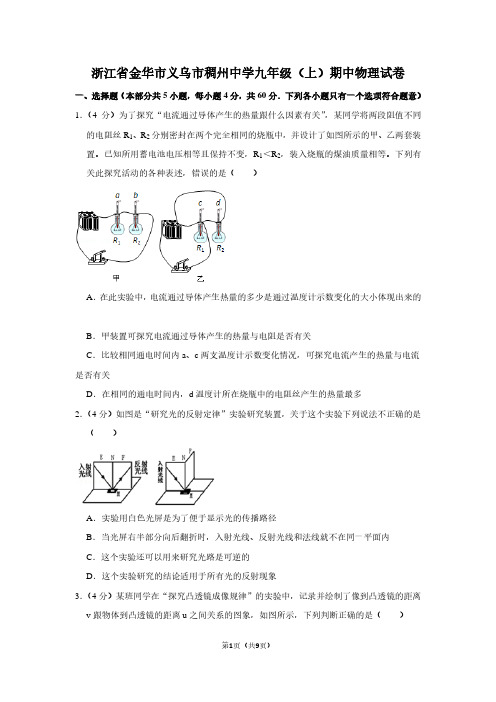
浙江省金华市义乌市稠州中学九年级(上)期中物理试卷一、选择题(本部分共5小题,每小题4分,共60分.下列各小题只有一个选项符合题意)1.(4分)为了探究“电流通过导体产生的热量跟什么因素有关”,某同学将两段阻值不同的电阻丝R1、R2分别密封在两个完全相同的烧瓶中,并设计了如图所示的甲、乙两套装置。
已知所用蓄电池电压相等且保持不变,R1<R2,装入烧瓶的煤油质量相等。
下列有关此探究活动的各种表述,错误的是()A.在此实验中,电流通过导体产生热量的多少是通过温度计示数变化的大小体现出来的B.甲装置可探究电流通过导体产生的热量与电阻是否有关C.比较相同通电时间内a、c两支温度计示数变化情况,可探究电流产生的热量与电流是否有关D.在相同的通电时间内,d温度计所在烧瓶中的电阻丝产生的热量最多2.(4分)如图是“研究光的反射定律”实验研究装置,关于这个实验下列说法不正确的是()A.实验用白色光屏是为了便于显示光的传播路径B.当光屏右半部分向后翻折时,入射光线、反射光线和法线就不在同一平面内C.这个实验还可以用来研究光路是可逆的D.这个实验研究的结论适用于所有光的反射现象3.(4分)某班同学在“探究凸透镜成像规律”的实验中,记录并绘制了像到凸透镜的距离v跟物体到凸透镜的距离u之间关系的图象,如图所示,下列判断正确的是()A.该凸透镜的焦距是16cmB.当u=12cm时,在光屏上能得到一个缩小的像C.把物体从距凸透镜12cm处移动到24cm处的过程中,像逐渐变小D.当u=20cm时成放大的像,投影仪就是根据这一原理制成的4.(4分)2015年春节期间大量中国游客涌入日本疯狂席卷各大商场,图为最受欢迎的为自动电热马桶盖,一度造成断货,后发现部分标签上竟然标注着:“Made in china”,产地为杭州下沙。
国人这种巨大的消费潜力扭曲的爆发,既是一种警醒,又是一种鞭策。
下表为小明家安装的某品牌自动电热马桶盖的详细参数(在小明家的电能表上标着3600r/kW •h,)。
浙江省义乌市绣湖中学教育集团2018-2019学年九年级上学期数学期中考试试卷

第1页,总25页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………姓名:____________班级:____________学号:___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………浙江省义乌市绣湖中学教育集团2018-2019学年九年级上学期数学期中考试试卷考试时间:**分钟 满分:**分姓名:____________班级:____________学号:___________题号 一 二 三 四 总分 核分人 得分注意事项:1、填写答题卡的内容用2B铅笔填写2、提前 15 分钟收取答题卡第Ⅰ卷 客观题第Ⅰ卷的注释评卷人 得分一、单选题(共10题)1. 如图,△ABC 内接于△O ,AB 是△O 的直径,△B=30°,CE 平分△ACB 交△O 于E ,交AB 于点D ,连接AE ,则S △ADE :S △CDB 的值等于( )A . 1:B . 1:C . 1:2D . 2:32. 如图,小明为检验四边形MNPQ 四个顶点是否在同一圆上,用尺规分别作了MN,MQ 的垂直平分线交于点O ,则M,N,P ,Q 四点中,不一定在以O 为圆心,OM 为半径的圆上的点是( )A . 点MB . 点NC . 点PD . 点Q 3. 抛物线的对称轴是( )答案第2页,总25页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………A . 直线B . 直线C . 直线D . 直线4. 下列各组图形一定相似的是( ) A . 两个矩形 B . 两个等边三角形 C.有一内角是80°的两个等腰三角形D . 两个菱形5. 一个不透明的布袋里装有7个只有颜色不同的球,其中3个红球,4个白球,从布袋中随机摸出一个球,摸出的球是红球的概率是( )A .B .C .D .6. 如图是小刘做的一个风筝支架示意图,已知 BC//PQ ,AB :AP=2:5,AQ=20 cm ,则 CQ 的长是( )A . 8 cmB . 10 cmC . 12 cmD . 15 cm7. 如图,点P 为△O 外一点,点A 、B 在圆上,PA ,PB 交优弧AB 于点C, D ,若△AOB= ,则判断△APB大小正确的是( )A . △APB=B . △APB >C . △APB <D . 不能确定8. 如图,抛物线(a >0)与直线y=1的交点坐标为(1,1),(3,1),则不等式的解集为( )。
稠中九年级数学期中试题卷

义乌市稠州中学教育集团九年级数学综合检测试题卷温馨提示:请仔细审题,细心答题,相信你一定会有出色的表现!全卷共4页,有3大题,24小题. 满分为120分.请将班级、姓名、学号写在试卷左上角.一、选择题(每小题3分,共30分)1. 抛物线()31-2+=x y 的顶点坐标是 ( )A.(1,3)B.(1,-3)C.(-1,3)D.(-1,-3) 2. 把ad bc =写成比例式,不正确...的是 ( ) A.a cb d = B .a d bc = C .b ad c = D .b da c= 3.如图,C 是⊙O 上一点,O 是圆心.若∠AOB =70°,则∠ACB 的度数为( ) A.70B.30C.35D.4504. 两个相似三角形的面积比是9:16,则这两个三角形的相似比是 ( ) A. 9:16 B. 3:4 C.9:4 D.3:165.如图⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,则弦AB 的长是( )A.4B.6C.7D.86. 已知),1(1y -,),2(2y -,),4(3y -是抛物线m x x y +--=822上的点,则( ) )A .123y y y <<B .213y y y <<C .312y y y <<D .132y y y << 7. 一个点到圆的最小距离为4,最大距离为9,则该圆的半径..是 ( ) A. 5 或13 B. 2.5 C. 6.5 D. 2.5 或6.58. 一个袋中有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,都是蓝色珠子的概率是 ( )A.12 B. 13 C. 14 D. 169. 给出下列一些命题:①直径相等的圆是等圆;②弦是直径;③圆上的任意两点都能将圆分成一条劣弧和一条优弧;④一个圆有且只有一条直径;⑤平分弦的直径垂直于弦,并且平分弦所对的弧。
【校级联考】浙江省义乌市稠州中学教育集团2018-2019学年八年级上学期期中考试数学试卷

【校级联考】浙江省义乌市稠州中学教育集团2018-2019学年八年级上学期期中考试数学试卷学校_________ 班级__________ 姓名__________ 学号__________一、单选题1. 下列图形中,不是轴对称图形的是()C.D.A.B.2. 在下列长度的四根木棒中,能与、长的两根木棒钉成一个三角形的是()A.B.C.D.3. 若x<y成立,则下列不等式一定成立的是()A.4x<3y B.﹣2x<﹣2y C.x2<y2D.x-2018<y-2018 4. 如图,在△ABC中,∠C=70º,沿图中虚线截去∠C,则∠1+∠2=()A.360ºB.250ºC.180ºD.140º5. 在下列条件:①∠A+∠B=∠C,②∠A∶∠B∶∠C=3∶4∶5,③∠C=∠A-∠B,④a∶b∶c=3∶4∶5 中,能确定△ABC是直角三角形的条件有( ) A.1个B.2个C.3个D.4个6. 等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角为()A.50°B.130°C.40°或130°D.50°或130°7. 把不等式组的解集表示在数轴上,下列选项正确的是()A.B.C.D.8. 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A =50°,则∠CDE的度数为( )A.50°B.51°C.51.5°D.52.5°9. 如图,将直角边AC=6cm,BC=8cm的直角△ABC纸片折叠,使点B与点A 重合,折痕为DE,则CD等于()A.B.C.D.10. 有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了右图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2018次后形成的图形中所有的正方形的面积和是()A.2017 B.2018 C.2019 D.1二、填空题11. 命题:“三角形内角和为180°”是_________命题(填“真”或“假”).12. 如果一个直角三角形的两条直角边的长分别为5、12,则斜边上的高的长度为______.13. 如图,在中,与的平分线交于点.若,则______.14. 不等式组的解集是x>2,则m的取值范围是_____.15. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E在同一直线上,∠1=20°,∠2=35°,则∠ACB=__________度.16. 已知如图:直线AB⊥BC,四边形ABCD是正方形,且AB=6,点P是BD上一点,且PD=2,一块三角板的直角顶点放在点P上,另两条边与BC、AB所在直线相交于点E、F,在三角板绕点P旋转的过程中,使得△PBF是等腰三角形,(1)线段BD=________,(2)请写出所有满足条件的BF的长__________.三、解答题17. 解不等式(组)并把不等式组的解集在数轴上表示出来:(1)7x-2≥5x+2 ;(2)18. 已知:如图,∠ABC,射线BC上一点D,求作:等腰△PB D,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P 到∠ABC两边的距离相等.(不写作法,保留作图痕迹)19. 如图,AC⊥BC,AD⊥BD,AD=BC,那么请你判断阴影部分图形的形状,并说明理由.20. 问题背景:在△ABC中,AB、BC、AC三边的长分别为、、,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.(1)请你将△ABC的面积直接填写在横线上:.思维拓展:(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别a、a、a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.21. 今年义乌市准备争创全国卫生城市,某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.(1)求温馨提示牌和垃圾箱的单价各是多少元?(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?22. 如图,在△ABC中,AB=AC,D,E分别是边BC,AC上的点,且BD=EC,∠ADE=∠B.(1)求证:AD=DE;(2)若∠ADE=,求∠ADB的度数(用含x的代数式表示).23. 连接四边形不相邻两个顶点的线段叫做四边形的对角线,如图1,四边形ABCD中线段AC、线段BD就是四边形ABCD 的对角线.把对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD的平方和与BC,AD 的平方和之间的数量关系.猜想结论:(要求用文字语言叙述)______写出证明过程(先画出图形,写出已知、求证).(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.24. 已知:如图,∠A=90°,BC∥AD,AB=6cm,点P从A出发沿射线AD运动,速度是每秒1cm,点R从点B出发沿射线BC运动,速度是每秒2cm,点Q在点P的右侧,且PQ=10cm,时间为t秒;求:(1)△PQR的面积;(2)当t=1秒时,求PR的长;(3)当t为何值时,△PQR是等腰三角形?。
2018-2019学年浙江省金华市义乌市部分学校九年级(上)期中数学试卷(附答案详解)

2018-2019学年浙江省金华市义乌市部分学校九年级(上)期中数学试卷一、选择题(本大题共10小题,共30.0分)1.二次函数y=(x+1)2−2的顶点坐标是()A. (−1,−2)B. (−1,2)C. (1,−2)D. (1,2)2.三张扑克牌背面都写着一个数字,其中两张写着1,π,另一张被弄脏了,已知从这2,则弄脏的那一张背面的数字可能是三张牌中抽一张背面数字是无理数的概率是23()D. 0.4A. −6B. −√2C. 273.如图⊙O中,∠BAC=35°,则∠BCO=()A. 35°B. 55°C. 70°D. 50°4.将抛物线y=2x2向左平移2个单位,得到的抛物线是()A. y=2(x+2)2B. y=2(x−2)2C. y=2x2+2D. y=2x2−25.已知线段a=4,b=8,则线段a,b的比例中项为()A. ±32B. 32C. ±4√2D. 4√26.如图,要使△ACD∽△ABC,需要补充的一个条件是()A. AC⋅BC=BA⋅CDB. AC⋅DC=BC⋅ADC. CD2=AD⋅DBD. AC2=AD⋅AB7.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是()A. a=√2bB. a=2bC. a=2√2bD. a=4b8.下列说法正确的是()A. 垂直于弦的直线必经过圆心B. 平分弦的直径垂直于弦C. 平分弧的直径平分弧所对的弦D. 同一平面内,三点确定一个圆9.已知抛物线y=−x2+mx的对称轴为直线x=2,若关于x的一元二次方程−x2+mx−t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是()A. t>−5B. −5<t<3C. 3<t≤4D. −5<t≤410.把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…现有等式A m=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2017=()A. (31,47)B. (31,48)C. (32,47)D. (32,48)二、填空题(本大题共6小题,共24.0分)11.已知:ab =12,则a+bb=______.12.从长度分别为2,4,6,7的四条线段中随机取三条,能构成三角形的概率是______.13.已知点P是线段AB的黄金分割点,PA>PB,AB=2cm,那么PA=______ cm.14.在半径为1的⊙O中,两条弦AB、AC的长分别为√2,√3,则由两条弦AB与AC所夹的锐角的度数为______.15.如图圆O直径AB上一点P,AB=2,∠BAC=20°,D是弧BC中点,则PD+PC的最小值为______.16.抛物线y=x2−2x−3与x轴交于点A、B(点A在点B的左边),点P在抛物线上.(1)点C是x轴上一个动点,四边形ACPQ是正方形,则满足条件的点Q的坐标是______;(2)连接AP,以AP为一条对角线作平行四边形AMPN,使点M在以点(1,0),(0,1)为端点的线段上,则当点N的纵坐标取最小值时,N的坐标为______.三、解答题(本大题共8小题,共66.0分)17.在平面直角坐标系中,抛物线y=ax2+bx经过点A(2,4)和点B(6,0).(1)求这条抛物线所对应的二次函数的表达式;(2)求抛物线顶点坐标.18.某篮球运动员带了2件上衣和3条短裤(上衣和短裤分别装在两个包里),上衣的颜色是红色和白色,短裤的颜色是红色、白色、黄色.(1)他随意拿出一件上衣和一条短裤配成一套,用画树状图或列表的方法列出所有可能出现的结果.(2)他随意拿出一件上衣和一条短裤,颜色正好相同的概率是多少?19.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).(1)求证:AC=BD;(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.20.如图,在△ABC中,D,E分别是AB,AC上的点,∠AED=∠ABC,∠BAC的平分线AF交DE于点G,交BC于点F.(1)试写出图中所有的相似三角形,并说明理由;(2)若AGGF =32,求DEBC的值.21.如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.(1)当CQ=10时,求S△APQS△PQB的值;(2)当x为何值时,PQ//BC;(3)是否存在某一时刻,使△APQ与△CQB相似?若存在,求出此时AP的长;若不存在,请说明理由.22.为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的11,且A产品采购9单价不低于1200元,求该商家共有几种进货方案;(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.23.将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;(2)在图②中,若AP1=2,则CQ等于多少?(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.24.小明合作学习小组在探究旋转、平移变换.如图△ABC,DEF均为等腰直角三角形,各顶点坐标分别为A(1,1),B(2,2),C(2,1),D(√2,0),E(2√2,0),F(3√22,−√22).(1)他们将△ABC绕C点按顺时针方向旋转45°得到△A1B1C1.请你写出点A1,B1的坐标,并判断A1C和DF的位置关系;(2)他们将△ABC绕原点按顺时针方向旋转45°,发现旋转后的三角形恰好有两个顶点落在抛物线y=2√2x2+bx+c上,请你求出符合条件的抛物线解析式;(3)他们继续探究,发现将△ABC绕某个点旋转45°,若旋转后的三角形恰好有两个顶点落在抛物线y=x2上,则可求出旋转后三角形的直角顶点P的坐标,请你直接写出点P的所有坐标.答案和解析1.【答案】A【解析】解:二次函数y=(x+1)2−2的图象的顶点坐标为(−1,−2).故选:A.直接根据二次函数的顶点式即可求得顶点坐标.本题考查了二次函数的性质,根据二次函数的顶点式,找出函数图象的顶点坐标是解题的关键.2.【答案】B【解析】解:由题意可知,弄脏的那一张背面的数字是无理数,,0.4是有理数,−√2是无理数,而−6,27故选:B.根据概率的意义可得弄脏的那一张背面的数字是无理数,只要从选项中找出无理数即可.本题考查概率的意义,无理数和有理数,理解无理数、有理数以及概率的意义是正确判断的前提.3.【答案】B【解析】解:∵∠BAC=35°∴∠BOC=2∠A=70°∵OB=OC∴∠OBC=∠OCB∴∠BCO=(180°−∠BOC)÷2=55°.故选:B.由圆周角定理求得BOC的度数了,再根据等边对等角及三角形内角和公式即可求得∠BCO的度数.本题利用了三角形内角和定理和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半求解.4.【答案】A【解析】解:由“左加右减”的原则可知,抛物线y=2x2向左平移2个单位后,得到的抛物线的解析式是y=2(x+2)2.故选:A.直接根据“左加右减”的原则进行解答即可.本题考查的是二次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.5.【答案】D【解析】【分析】设线段x是线段a,b的比例中项,根据比例中项的定义列出等式,利用两内项之积等于两外项之积即可得出答案.本题主要考查比例线段,掌握比例中项的性质是解题的关键.【解答】解:设线段a、b的比例中项为x,则x2=ab,即x2=4×8,解得x=4√2或x=−4√2<0(舍去),故选:D.6.【答案】D【解析】解:∵∠CAD=∠BAC,∴当∠ACD=∠B时,△ACD∽△ABC;当ACAB =ADAC,即AC2=AD⋅AB时,△ACD∽△ABC.故选:D.由于两三角形有公共角,若根据有两组角对应相等的两个三角形相似添加条件,则∠ACD=∠B;若根据两组对应边的比相等且夹角对应相等的两个三角形相似添加条件,则ACAB =ADAC,然后对各选项进行判断.本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.7.【答案】B【解析】解:对折两次后的小长方形的长为b,宽为14a,∵小长方形与原长方形相似,∴ab =b14a,∴a=2b.故选:B.根据对折表示出小长方形的长和宽,再根据相似多边形的对应边成比例列式计算即可得解.本题考查了相似多边形对应边成比例的性质,准确表示出小长方形的长和宽是解题的关键.8.【答案】C【解析】解:A、根据垂直于弦的直径必经过圆心,故此选项错误;B、平分弦(不是直径)的直径垂直于弦,故此选项错误;C、平分弧的直径平分弧所对的弦,故此选项正确;D、不在同一直线上的三点确定一个圆,故此选项错误;故选C.根据垂径定理及推论、确定圆的条件分别对每一项进行分析即可.此题主要考查了命题与定理,了解垂径定理及推论、确定圆的条件是解题的关键,难度不大.9.【答案】D【解析】解:如图,关于x的一元二次方程−x2+mx−t=0的解就是抛物线y=−x2+ mx与直线y=t的交点的横坐标,由题意可知:m=4,当x=1时,y=3,当x=5时,y=−5,由图象可知关于x的一元二次方程−x2+mx−t=0(t为实数)在1<x<5的范围内有解,直线y=t在直线y=−5和直线y=4之间包括直线y=4,∴−5<t≤4.故选:D.如图,关于x的一元二次方程−x2+mx−t=0的解就是抛物线y=−x2+mx与直线y=t的交点的横坐标,利用图象法即可解决问题.本题考查了二次函数的应用,抛物线与x轴的交点、一元二次方程等知识,解题的关键是学会利用图象法解决问题,画出图象是解决问题的关键,属于中考选择题中的压轴题.10.【答案】D=1009个数,【解析】解:2017是第2017+12设2017在第n组,则1+3+5+7+⋯+(2n−1)≥1009,≥1009,即(1+2n−1)⋅n2解得:n≥√1009,当n=31时,1+3+5+7+⋯+61=961;当n=32时,1+3+5+7+⋯+63=1024;故第1009个数在第32组,第1024个数为:2×1024−1=2047,第32组的第一个数为:2×962−1=1923,+1)=48个数.则2017是(2017−19232故A 2017=(32,48),故选:D.先计算出2017是第1009个数,然后判断第1009个数在第几组,再判断是这一组的第几个数即可.此题考查数字的变化规律,找出数字之间排列的规律,得出数字的运算规律,利用规律解决问题.11.【答案】32【解析】解:∵ab =12,∴a+bb =32.根据比例式的合比性质可直接求出a+bb的值.注意观察要求的式子和已知式子的关系,能够根据比例合比性质求解.12.【答案】12【解析】解:∵从长度分别为2,4,6,7的四条线段中随机取三条,可能的结果为:2,4,6;2,4,7;2,6,7;4,6,7共4种,能构成三角形的是2,6,7;4,6,7;∴能构成三角形的概率是:24=12.故答案为:12.由从长度分别为2,4,6,7的四条线段中随机取三条,可能的结果为:2,4,6;2,4,7;2,6,7;4,6,7共4种,能构成三角形的是2,6,7;4,6,7;直接利用概率公式求解即可求得答案.此题考查了列举法求概率的知识.用到的知识点为:概率=所求情况数与总情况数之比.13.【答案】√5−1【解析】解:由于P为线段AB=2的黄金分割点,且AP是较长线段;则AP=2×√5−12=(√5−1)cm.故答案为:(√5−1)cm.根据黄金分割点的定义,知AP 是较长线段;则AP =√5−12AB ,代入运算即可.此题考查了黄金分割的定义,应该识记黄金分割的公式:较短的线段=原线段的√5−12,难度一般.14.【答案】75°或15°【解析】解:作OM ⊥AB ,ON ⊥AC ;由垂径定理,可得AM =12,AN =12,∵弦AB 、AC 分别是√2、√3,∴AM =√22,AN =√32;∵半径为1∴OA =1; ∵AM OA=√22∴∠OAM =45°;同理,∵AN OA=√32,∴∠OAN =30°;当OA 在AB 和AC 之间时,如图1,∴∠BAC =∠OAM +∠OAN =45°+30°=75°; 当B 、C 在OA 的同一侧时,如图2, ∠BAC =∠OAM −∠OAN =45°−30°=15°. ∴∠BAC =75°或15°. 故答案是:75°或15°.径为1,弦AB 、AC 分别是√2、√3,作OM ⊥AB ,ON ⊥AC ;利用余弦函数,可求出∠OAM =45°,∠OAN =30°;AC 的位置情况有两种,如图所示;故∠BAC 的度数为45°+30°或45°−30°.问题可求.本题综合性强,关键是画出图形,作好辅助线,利用垂径定理和直角三角形的特殊余弦值求得角的度数.15.【答案】1【解析】解:作D 点关于AB 的对称点E ,连CE 交AB 于P 点,连OE ,如图, ∴CD⏜=BD ⏜=BE ⏜, ∴∠COD =∠BOD =∠BOE =20°,∴∠COE=60°,∴CE的长度是PD+PC的最小值.又∵OC=OE,∴△COE为等边三角形.∴CE=OC=OD=1,∴PD+PC的最小值为1.故答案为:1.作D点关于AB的对称点E,连CE交AB于P点,连OE,则DC⏜=BD⏜,PD=PE,根据两点之间线段最短得到CE的长是PD+PC的最小值.本题考查了轴对称−最短路线问题,圆周角定理,垂径定理,等边三角形的判定和性质,熟记在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.16.【答案】(−1,−3)或(−1,5)或(2,3)或(4,−5)(0,−5)【解析】解:(1)令y=0,则0=x2−2x−3,∴x1=3,x2=−1,∴点A(−1,0),点B(3,0),如图1,若AC为边,设点C(x,0),∴CA=|x+1|∵四边形ACPQ是正方形,∴CA=CP=AQ=QP,∠QAC=90°,∴|x+1|=|x2−2x−3|,∴x+1=x2−2x−3或−x−1=x2−2x−3∴x1=−1(不合题意舍去),x2=2,x3=4,∴点C(2,0)或(4,0)∴AC=AQ=3或5,∴点Q(−1,−3)或(−1,5);若AC为对角线,则AC的中点坐标为(x+12,0)∴CA=|x+1|∵正方形的对角线互相垂直平分且相等,∴|x+1|2=|(x+12)2−2×x+12−3|,∴x+12=(x+12)2−2×x+12−3或−x+12=(x+12)2−2×x+12−3∴x1=−1(不合题意舍去),x2=5,x3=9,∴AC的中点坐标为(2,0),(4,0),∴点Q坐标为(2,3)或(4,−5)故答案为(−1,−3)或(−1,5)或(2,3)或(4,−5);(2)∵四边形ANPM是平行四边形,∴对角线互相平分,∴y A+y P=y M+y N,∴y N=0+x2−2x−3−y M,∴当x2−2x−3取最小值,y M取最大值时,y N有最小值,∵x2−2x−3=(x−1)2−4,∴当x=1时,x2−2x−3最小值=−4,点P(1,−4)∵0≤y M≤1,∴y M最大值=1∴y N最小值=−4−1=−5.∴故答案为:(0,−5).(1)先求出点A,点B坐标,设点C(x,0),由正方形的性质CA=CP=AQ=QP,可得|x+1|=x2−2x−3,可求点C坐标,即可求点Q坐标;(2)设点M(m,−m+1),由平行四边形的性质可得AN=PM,AN//MP,当AN⊥AB时,且在x轴下方上,点N的纵坐标有最小值,由二次函数的性质可求解.本题是二次函数综合题,考查了二次函数的性质,正方形的性质,平行四边形的性质,灵活运用这些性质进行推理是本题的关键.17.【答案】解:(1)∵抛物线y=ax2+bx经过点A(2,4)和点B(6,0),∴{4a+2b=436a+6b=0,解得{a=−12b=3,∴这条抛物线所对应的二次函数的表达式为y=−12x2+3x;(2)∵y=−12x2+3x=−12(x−3)2+92,∴该抛物线开口向下.顶点坐标为(3,92).【解析】(1)把A点和B点坐标代入y=ax2+bx中得到关于a、b的方程组,然后解方程组求出a、b即可;(2)把(1)中的解析式配成顶点式,然后根据二次函数的性质求解.本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.18.【答案】解:(1)树状图如下:(2)由树状图可知,共有6种等可能的结果,其中上衣和短裤颜色正好相同的有2种情况,所以P(颜色相同)=26=13.【解析】(1)根据题意画出树状图即可;(2)由树状图求得所有等可能的结果与某篮球运动员穿的上衣和裤子恰好是相同颜色的情况,再利用概率公式即可求得答案.此题考查了用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.19.【答案】(1)证明:过O作OE⊥AB于点E,则CE=DE,AE=BE,∴BE−DE=AE−CE,即AC=BD;(2)解:由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,∴OE=6,∴CE=√OC2−OE2=√82−62=2√7,AE=√OA2−OE2=√102−62=8,∴AC=AE−CE=8−2√7.【解析】(1)过O作OE⊥AB,根据垂径定理得到AE=BE,CE=DE,从而得到AC=BD;(2)由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,再根据勾股定理求出CE及AE的长,根据AC=AE−CE即可得出结论.本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.20.【答案】解:(1)∵∠AED=∠ABC,∠EAD=∠BAC,∴△ABC∽△AED.∵∠AED=∠ABC,∠EAG=∠BAF,∴△AEG∽△ABF.∵∠EDG=∠ACF,∠DAG=∠CAF,∴△ADG∽△ACF.(2)∵AGGF =32,∴AGAF =35,∵△ADG∽△ACF,∴DEBC =AGGF=35.【解析】(1)根据两组对应角相等可判断△ABC∽△AED,△ADG∽△ACF,△AEG∽△ABF.(2)根据相似三角形的对应高相等可以进行计算.(1)本题考查了相似三角形的判定,解答本题,要找到两组对应角相等. (2)本题考查了相似三角形的对应高的比等于相似比,灵活运用是关键.21.【答案】解:(1)当CQ =10时,3x =10,∴x =103,∴AP =4x =403,∴BP =20−403=203∴S △APQ S △PQB=AP PB=2.(2)由题可得AP =4x ,CQ =3x . ∵BA =BC =20,AC =30, ∴BP =20−4x ,AQ =30−3x . 若PQ//BC , 则有△APQ∽△ABC , ∴AP AB =AQ AC, ∴4x20=30−3x 30, 解得:x =103.∴当x =103时,PQ//BC ;(3)存在. ∵BA =BC , ∴∠A =∠C , 要使△APQ∽△CQB , 只需APCQ =AQCB . 此时4x3x =30−3x 20,解得:x =109,∴AP =4x =409.【解析】此题是相似形综合题,主要考查了相似三角形的判定与性质、等腰三角形的性质、解方程、两个三角形的面积比等于两个底的比(这两底上的高相等)等知识,利用相似三角形的性质是解决本题的关键.(1)当CQ =10时,可求出x ,从而求出AP ,即可求出BP ,然后根据两个三角形两底上的高相等时,这两个三角形的面积比等于这两个底的比,就可解决问题; (2)由题可得AP =4x ,CQ =3x ,BP =20−4x ,AQ =30−3x.若PQ//BC ,则有△APQ∽△ABC ,然后运用相似三角形的性质即可解决问题;(3)由BA =BC 得∠A =∠C.要使△APQ∽△CQB ,只需APCQ =AQCB ,此时4x3x =30−3x 20,解这个方程就可解决问题.22.【答案】解:(1)设y 1与x 的关系式y 1=kx +b ,由表知{1480=k +b1460=2k +b ,解得k =−20,b =1500,即y 1=−20x +1500(0<x ≤20,x 为整数),(2)根据题意可得 {x ≥119(20−x)−20x +1500≥1200,解得11≤x ≤15, ∵x 为整数,∴x 可取的值为:11,12,13,14,15, ∴该商家共有5种进货方案;(3)解法一:y 2=−10(20−x)+1300=10x +1100, 令总利润为W ,则W =(1760−y 1)x +(20−x)×[1700−(10x +1100)]=30x 2−540x +12000, =30(x −9)2+9570, ∵a =30>0,∴当x ≥9时,W 随x 的增大而增大, ∵11≤x ≤15,∴当x =15时,W 最大=10650;解法二:根据题意可得B 产品的采购单价可表示为: y 2=−10(20−x)+1300=10x +1100, 则A 、B 两种产品的每件利润可分别表示为:1760−y1=20x+260,1700−y2=−10x+600,则当20x+260>−10x+600时,A产品的利润高于B产品的利润,即x>343=1113时,A产品越多,总利润越高,∵11≤x≤15,∴当x=15时,总利润最高,此时的总利润为(20×15+260)×15+(−10×15+600)×5=10650.答:采购A种产品15件时总利润最大,最大利润为10650元.【解析】(1)设y1与x的关系式y1=kx+b,由表列出k和b的二元一次方程,求出k和b的值,函数关系式即可求出;(2)首先根据题意求出x的取值范围,结合x为整数,即可判断出商家的几种进货方案;(3)令总利润为W,根据利润=售价−成本列出W与x的函数关系式W=30x2−540x+ 12000,把一般式写成顶点坐标式,求出二次函数的最值即可.本题主要考查二次函数的应用的知识点,解答本题的关键是明确销售单价与销售件数之间的函数关系式,会表达单件的利润及总利润,此题难度一般.23.【答案】(1)证明:∵∠B1CB=45°,∠B1CA1=90°,∴∠B1CQ=∠BCP1=45°,∵在△B1CQ和△BCP1中,{∠B1CQ=∠BCP1 B1C=BC∠B1=∠B,∴△B1CQ≌△BCP1(ASA),∴CQ=CP1;(2)作P1D⊥CA于D,∵∠A=30°,∴P1D=12AP1=1,∵∠P1CD=45°,∴P1DCP1=sin45°=√22,∴CP1=√2P1D=√2,又∵CP1=CQ,∴CQ=√2;(3)∵∠P1BE=90°,∠ABC=60°,∴∠A=∠CBE=30°,∴AC=√3BC,由旋转的性质可得:∠ACP1=∠BCE,∴△AP1C∽△BEC,∴AP1:BE=AC:BC=√3:1,设AP1=x,则BE=√33x,在Rt△ABC中,∠A=30°,∴AB=2BC=2,∴S△P1BE=12×√33x(2−x)=−√36x2+√33x=−√36(x−1)2+√36,故当x=1时,S△P1BE(max)=√36.【解析】(1)先判断∠B1CQ=∠BCP1=45°,利用ASA即可证明△B1CQ≌△BCP1,从而得出结论.(2)作P1D⊥CA于D,在RtADP1中,求出P1D,在Rt△CDP1中求出CP1,继而可得出CQ 的长度.(3)证明△AP1C∽△BEC,则有AP1:BE=AC:BC=√3:1,设AP1=x,则BE=√33x,得出S△P1BE关于x的表达式,利用配方法求最值即可.本题考查了相似三角形的判定与性质,解答本题需要我们熟练掌握含30°角的直角三角形的性质、勾股定理及配方法求二次函数的最值,有一定难度.24.【答案】解:(1)A 1(2−√22,1+√22),B 1(2+√22,1+√22). A 1C 和DF 的位置关系是平行.(2)∵△ABC 绕原点按顺时针方向旋转45°后的三角形即为△DEF ,∴①当抛物线经过点D 、E 时,根据题意可得:{2√2×(√2)2+√2b +c =02√2×(2√2)2+2√2b +c =0,解得{b =−12c =8√2∴y =2√2x 2−12x +8√2;②当抛物线经过点D 、F 时,根据题意可得:{2√2×(√2)2+√2b +c =02√2×(3√22)2+3√22b +c =−√22,解得{b =−11c =7√2∴y =2√2x 2−11x +7√2;③当抛物线经过点E 、F 时,根据题意可得:{2√2×(2√2)2+2√2b +c =02√2×(3√22)2+3√22b +c =−√22,解得{b =−13c =10√2∴y =2√2x 2−13x +10√2.(3)在旋转过程中,可能有以下情形:①顺时针旋转45°,点A 、B 落在抛物线上,如答图1所示:易求得点P 坐标为(0,1−√22);②顺时针旋转45°,点B 、C 落在抛物线上,如答图2所示:设点B′,C′的横坐标分别为x 1,x 2.易知此时B′C′与一、三象限角平分线平行,∴设直线B′C′的解析式为y =x +b , 联立y =x 2与y =x +b 得:x 2=x +b ,即x 2−x −b =0,∴x 1+x 2=1,x 1x 2=−b .∵B′C′=1,∴根据题意易得:|x 1−x 2|=√22, ∴(x 1−x 2)2=12,即(x 1+x 2)2−4x 1x 2=12∴1+4b =12,解得b =−18.∴x 2−x +18=0,解得x =2+√24或x =2−√24. ∵点C′的横坐标较小,∴x =2−√24. 当x =2−√24时,y =x 2=3−2√28, ∴P(2−√24,3−2√28); ③顺时针旋转45°,点C 、A 落在抛物线上,如答图3所示:设点C′,A′的横坐标分别为x 1,x 2.易知此时C′A′与二、四象限角平分线平行,∴设直线C′A′的解析式为y =−x +b , 联立y =x 2与y =−x +b 得:x 2=−x +b ,即x 2+x −b =0,∴x 1+x 2=−1,x 1x 2=−b .∵C′A′=1,∴根据题意易得:|x 1−x 2|=√22, ∴(x 1−x 2)2=12,即(x 1+x 2)2−4x 1x 2=12∴1+4b =12,解得b =−18.∴x 2+x +18=0,解得x =√2−24或x =−√2−24. ∵点C′的横坐标较大,∴x =√2−24. 当x =√2−24时,y =x 2=3−2√28, ∴P(√2−24,3−2√28);④逆时针旋转45°,点A 、B 落在抛物线上.因为逆时针旋转45°后,直线A′B′与y 轴平行,因此,与抛物线最多只能有一个交点,故此种情形不存在;⑤逆时针旋转45°,点B 、C 落在抛物线上,如答图4所示:与③同理,可求得:P(√2−24,3−2√28); ⑥逆时针旋转45°,点C 、A 落在抛物线上,如答图5所示:与②同理,可求得:P(2+√24,3+2√28). 综上所述,点P 的坐标为:(0,1−√22),(2−√24,3−2√28),(√2−24,3−2√28),(2+√24,3+2√28).【解析】(1)由旋转性质及等腰直角三角形边角关系求解;(2)首先明确△ABC 绕原点按顺时针方向旋转45°后的三角形即为△DEF ,然后分三种情况进行讨论,分别计算求解;(3)旋转方向有顺时针、逆时针两种可能,落在抛物线上的点有点A 和点B 、点B 和点C 、点C 和点D 三种可能,因此共有六种可能的情形,需要分类讨论,避免漏解.本题考查了旋转变换与二次函数的综合题型,难度较大.第(3)问是本题难点所在,解题关键是:第一,旋转方向有两种可能,落在抛物线上的点有三种可能,因此共有六种可能的情形,需要分类讨论;第二,针对每一种可能的情形,按照旋转方向与旋转角度,确定图形形状并进行计算.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【校级联考】浙江省义乌市稠州中学教育集团2018-2019学年上学期期中考试八年级语文试卷一、综合性学习1 . 阅读下面文字,根据语境完成后面的题目。
①他们有的坐火车旅行漫长的路程,有的从图拉驾车而来,在客厅里正(jīn)危坐地等待这位大师的接见。
②那个炉子即使把它烧到(chì)热的程度,也令人完全失望。
③外祖母大人因年老关系,今年不比往年健康,但仍不劳作,尤喜纺棉。
④于是点上一支烟,再继续写些为“正人君子”之流所深恶痛疾的文字。
(1)根据拼音写出①②句中相应的汉字。
正(jīn)____危坐(chì)_____热(2)填入③句中_____的文字正确的一项是_____ A.缀 B.辍(3)④句中加点字“恶”在文中读音正确的一项是_____ A.è B.wù非文学类作品阅读职业生涯规划,你准备好了吗随着中小学课程改革的持续推进,“职业生涯规划”如今不再是新名词,中学生职业生涯规划教育已在高中大面积推开,并逐步向初中生普及。
职业生涯规划是指针对个人职业选择的主观和客观因素进行分析和测定,确定个人的奋斗目标并努力实现这一目标的过程。
换句话说,职业生涯规划要来根据自身的兴趣、特长,将自已定位在一个最能发挥自已长处的位置,选择最适合自己能力的职业。
(调查研究)“中学生职业生涯规划实践研究”课题组对某校高一新生,做了关于“职业生涯规划现状”的问卷调查,调查结果如下:(学子心声)爽爽是大四学生,学的是会计专业,但是找了大半年工作,始终没有找到合适的。
问她到底喜欢什么,想做什么,她都说不清。
“我觉得我适合当护士,可我学的是会计。
当初填志愿的时候,我明明填的是浙江某大学的英语专业,可是,等我和同学出去玩了,我爸爸偷改了我的志愿,学校和专业全改了。
”由于不喜欢所学专业,她学得不开心,几度厌学,现在找工作又特别迷茫。
听说有职业生涯规划辅导后,她不禁感慨:“要是我那时候能有这样的辅导多好,怎会走这些弯路?真是郁闷!” (规划辅导)中学生在接受职业生涯规划辅导时,指导师往往会对他们进行这样的“心理测试”:今天,你准备去一个很远的地方旅行。
刚走出家门,一个白胡子的神仙突然在你面前出现。
他告诉你,他可以送给你一个礼物,作为你旅途的坐骑,你会选择哪一个?A. 一头强壮的大象B. 一头被视为神物的单峰白骆驼C. 一匹《射雕英雄传》里提到的汗血宝马一般人的逻辑是不是这样的?我喜欢宝马,因为很威风,很漂亮,而且跑得很快,我喜欢这种奔驰的感觉。
我不喜欢骆驼和大象,因为太慢了!但如果是去沙漠,骑大象走不出二十公里就得渴死。
如果是去草原,要一头骆驼又有何用?不管你的答案是什么,都要明白:关键是看你要去哪里旅行。
(专家说法)中国青少年研究中心少儿研究所所长孙宏艳:美国早在1989年就颁布了《国家职业发展指导方针》,明确规定职业生涯教育要从6岁开始。
日本也要求从小学开始就必须进行职业生涯方面的教育教学活动。
与发达国家相比,我国开展高中生的职业生涯教育太迟了!在填报志愿时,许多学生不但对大学的专业学什么、将来能做什么一无所知,就连对自己的兴趣与适合的东西也不够了解。
在大学阶段,许多学生由于选择了不感兴趣的专业而表现得很懈怠,甚至荒废了学业。
深圳市光明新区教科研中心刘会金:绝大多数高中生职业生涯规划意识淡薄。
大学生毕业时有将近40%的同学认为自己学错了专业,近65%的同学将跨专业选择职业,就业过程相当痛苦。
每年填报高考志愿时,很多家长、教师习惯于“分数优先”原则,很少考虑孩子的兴趣、志向。
温州市教育研究院副院长马玉斌:职业生涯规划课主要是帮学生更好地认识自己,以及自己和职业的匹配度。
高中阶段的生涯规划教育,并不是让学生通过学习,就定下具体明确的职业方向,而是要让学生在认识自己和社会的过程中,逐渐认识到自己的兴趣和能力所在,学会把兴趣转变成学科优势、职业兴趣和事业追求,在选课和选专业方面能够有的放矢,激发个人的内在价值和潜力,去实现自己的职业目标。
(摘自互联网,有删改)2 . 下列表述与“职业生涯规划现状”查结果相符的一项是( )3 . 阅读“规划辅导”部分,分析指导师给中学生做心理测试的意图。
4 . 阅读“学子心声”部分,结合文本相关材料写出爽爽的案例给你的职业生涯规划带来的启示。
A.少数家长对孩子“职业生涯规划”的帮助不大。
B.多数学生赞同在高中阶段进行“职业生涯规划”。
C.多数学生对各个职业了解较多并希望进行体验。
D.初中学校没有开设“职业生涯规划”的指导课。
二、句子默写5 . 古诗文名句默写。
(1)何夜无月?何处无竹柏?①_________________。
(苏轼《记承天寺夜游》)(2)岂不罹凝寒,②_____________________。
(刘祯《赠从弟》其二)(3)春秋两季,物候变换明显,容易引发诗人的情思。
在春天,晏殊感叹“③____________________,似曾相识燕归来”;李煜长吟“别时容易见时难,流水落花春去也,④_________________”;白居易则用“⑤___________,⑥____________”抒发了自己对西湖春日美景的喜爱之情;与绘春相对应的是写秋。
王绩在《野望》中描绘了这样一幅浓郁的秋色图:“⑦_________,山山唯落晖”;范仲淹《渔家傲·秋思》用“塞下秋来风景异,⑧________”写出了塞外秋天的凄清、肃杀。
三、文言文阅读6 . 解释下列加点的文言词语(1)自三峡七百里中(2)未复有能与其奇者(3)念无与为乐者(4)任意东西(5)仍怜故乡水(6)千里殊风雨阅读下面的文言文,完成后面的题目。
(王羲之)性好鹅,会稽有孤居姥①养一鹅,善鸣,求市未能得,遂携新友命驾就观。
姥闻羲之将至,烹以待之,羲之叹惜弥日。
又山阴有一道士,养好鹅,羲之往观焉,意甚悦,固求市之。
道士云为写《道德经》当举群相送耳。
羲之欣然写毕,笼鹅而归,甚以为乐。
尝至门生家,见篚②几滑净,因书之,真草相半。
后为其父误刮去之,门生惊懊者累日。
羲之书为世所重,皆此类也。
每自称:“我书比钟繇(yáo),当抗④行;比张芝草,犹当雁行也。
”曾与人书云:“张芝临池学书,池水尽黑,使人耽⑤之若是,未必后人也。
”(选自《晋书·王羲之列传》)(注释)①姥(mǔ):老妇。
②篚(fěi):圆形竹筐。
③真草:楷书,草一书。
④抗:抗衡,相当。
⑤耽dān:沉溺,沉迷。
7 . 下列各组句子中,加点词语的释义相同的一组是() 8 . 用“/”给文中画线句子断句。
(限断两处)道士云为写《道德经》当举群相送耳9 . 翻译句子。
羲之书为世所重,皆此类也。
10 . 王羲之爱鹅、写鹅是他的人生寄寓。
古今中外,有人生寄寓的名人还很多,请仿照下列示例,另举一例。
示例:梅是林和靖的人生寄托。
名句:疏影横斜水清浅,暗香浮动月黄昏。
A.(王羲之)性好鹅/好鸟相鸣B.张芝临池学书/与朱元思书C.甚以为乐/急湍甚箭D.羲之欣然写毕/ /欣然起行四、选择题11 . 下列有关律诗的说法,不正确的一项是。
A.律诗句子字数整齐划一,每句或五言,或七言,分别称五言律诗、七言律诗。
B.律诗通常每首八句,每二句成一联,计四联,习惯上称第一联为首联,第二联为颔联,第三联为颈联,第四联为尾联。
C.每首律诗的二、三两联(即颔联、颈联)的上下句必须是对偶句。
D.律诗要求全首通押一韵,限平声韵,第一、三、五、七句必须押韵,其它句子可押可不押。
五、名著阅读12 . 选择题(1)下列关于《红星照耀中国》的叙述不正确的是____A、“在某种意义上讲,这次大迁移是历史上最大的一次流动的武装宣传。
”这里的“大迁移”指的是红军长征。
B、这是一部具有新闻报道性的作品,及时是他畅销不衰的首要和基本因素。
C、该书以作者陕北之行的经历为线索,切实报道共产党人的生活和精神。
D、此书充满激情的政论,忠于客观事实,具有“事实胜于雄辩”的威力。
(2)王树增在《长征》解读了长征精神的基本内涵,其中不是他解读的一项是_______A、对共产主义坚定信仰和革命乐观主义精神。
B、热爱祖国,为国献身的爱国主义精神。
C、是顾全大局、团结友爱的集体主义精神。
D、是不畏艰险、勇往直前,一不怕苦、二不怕死的无私奉献精神。
13 . 填空《飞向太空港》的作者是_______。
记录了中国西昌卫星发射中心以“________”运载火箭成功发射外国卫星——美国“_______”的故事,其中既有中美专家在大凉山深处的合作与友情,也有东西方文明在现代卫星发射场上交汇时的碰撞与冲突。
六、现代文阅读文学类作品阅读一个人的麦田①我读高三的时候,在我们那个地方,盛行陪读。
我所在的那个班,一半以上的家长都在陪读。
而我,似乎是一个孤独的“另类”,因为,整整三年,我的父亲从未到学校来看过我,我虽然并不奢望父亲陪读,可见到那些陪读的父母,心里还是隐隐发酸,直到那年高考,我才明白:父亲对我有着别样的期待,我并不是孤军作战。
②高考前两天,学校让我们自己调整,我调转方向,打道回家。
半年的闭关苦读,我和世界完全脱钩,回到家才惊地发现,满地金黄,漫天麦香,已到收麦季节。
时间过得真快。
更让我措手不及的是,巍峨多年的父亲已经开始佝偻,满头白发了。
③对于我的火线回归,父亲很欣慰,“上阵父子兵”,麦收是父亲最重要的战役。
多年来,我们一直并肩作战,把时光打得颗粒归仓,父亲拿起一把镰刀,试试锋刃,递给我,今年麦倒伏,要用手割了,我心生忐忑——过去割麦。
是跟在收割机后,零打碎敲,对抗性为零,现在回到冷兵器时代,和麦子打“阵地战”,我还真有些力不从心。
我接过镰刀,掂了掂,我明白,我再怎么做也做不到像父亲那样游刃有余。
④六月,阳光如炽,我不时直起腰,沿着脊梁沟,汗水一泻而下,酸痛逆流而上。
我低估了弱不禁风的小麦,要把镰刀临阵倒戈,把我的掌心磨满水泡,我暴露在麦芒般刺眼的阳光里,孤立无援,父亲却像个无坚不摧的坦克,所向披靡。
在这里,父亲总是火力十足。
我不得不承认,这片麦田是父亲的主场,我则是他一个人的啦啦队。
⑤田间休息,我给父亲端上了茶水,父亲看看我的手:“使不惯?别攥太紧,和拿笔一样。
”我点点头,父亲可以在他的麦田纵横驰骋,只是他没能教会我,或者说,他压根儿就没有想过要教会我。
⑥喝罢水,父亲问我:“快高考了吧?”我说,“后天。
”父亲怔住,满身的汗珠也如麦粒般静止,父亲拿毛巾擦拭着我的额头,似乎要把我湿漉漉的疲惫赶走。
很快,他督促道:“快回家歇着吧,别累着,高考才是你该干的事。
养足精神去收你的麦子,那个我帮不上。
”⑦父亲又开始埋首割麦,把对我的歉意,肆虐在麦子身上。
在这里,镰刀是笔,麦子是墨,麦田是纸,父亲在麦田挥毫泼墨。
麦收是父亲的高考,更是为我而设的特殊陪考!⑧阳光烘烤着麦田,我拖着沉沉的步子。
