第5章部分习题解答
第5章 相平衡习题解答

⑵ 图中,组成为 xB=0.800 的液相的泡点: t 110.2 C ; ⑶ 图中,组成为 yB =0.800 的气相的露点: t 112.8 C ; ⑷ 求 105℃时气-液平衡两相的组成: xB 0.417 , yB 0.544 ;
xB
1
xA
0.541
p pA pB 54.22 0.459 136.12 0.541 98.53kPa
yA
pA pA pB
54.22 0.541
0.2526
54.22 0.459 136.12 0.541
yB
pB pA pB
136.12 0.459
0.7474
54.22 0.459 136.12 0.541
答: ⑴ p=98.54kPa,yB=0.7476;⑵ p=80.40kPa,xB=0.3197; ⑶ yB=0.6825,xB=0.4613,nB(l)=1.709mol,nB(g)=3.022mol 5-7 在 101.325kPa 下,水(A) -醋酸(B)系统的气-液平衡数据如下:
t/℃
100
100 92 0.45
2.415
mB (2.415 100 / 92) 18 23.91kg
第五章 相平衡习题解答
5-1 指出下列平衡系统中的物种数 S、组分数 C、相数 P 和自由度数 f。 ⑴ C2H5OH 与水的溶液; ⑵ I2(s)与 I2(g)成平衡; ⑶ NH4HS(s)与任意量的 H2S(g)及 NH3(g)达到平衡; ⑷ NH4HS(s)放入抽空的容器中分解达平衡; ⑸ CaCO3(s)与其分解产物 CaO(s)和 CO2(g)成平衡; ⑹ CHCl3 溶于水中、水溶于 CHCl3 中的部分互溶系统及其蒸气达到相平衡。 解:(1)物种数 S=2,组分数 C=2、相数 P=1,自由度数 f=C-P+2=3;
第5章感应电机习题与解答

C ;D 。
答A
6.★三相异步电动机气隙增大,其他条件不变,则空载电流( )。
A 增大 ; B 减小 ;
C 不变 ; D 不能确定。
答A
7.三相感应电动机等效电路中的附加电阻 上所消耗的电功率应等于():
A输出功率 ;B输入功率 ;
C电磁功率 ;D总机械功率 。
答D
8.与普通三相感应电动机相比,深槽、双笼型三相感应电动机正常工作时,性能差一些,主要是()。
答A
12.★设计在 电源上运行的三相感应电动机现改为在电压相同频率为 的电网上,其电动机的()。
A 减小, 减小, 增大;B 减小, 增大, 减小;
C 减小, 减小, 减小;D 增大, 增大, 增大。
答C
13.一台绕线式感应电动机,在恒定负载下,以转差率 运行,当转子边串入电阻 ,测得转差率将为()( 已折算到定子边)。
。
答1,
4.★感应电动机起动时,转差率 ,此时转子电流 的值, ,主磁通比,正常运行时要 ,因此起动转矩 。
答 1,很大,很小,小一些,不大
5.★一台三相八极感应电动机的电网频率 ,空载运行时转速为735转/分,此时转差率为,转子电势的频率为。当转差率为0.04时,转子的转速为,转子的电势频率为。
答0.02, , ,
6.三相感应电动机空载时运行时,电机内损耗包括,,,和,电动机空载输入功率 与这些损耗相平衡。
答定子铜耗,定子铁耗,机械损耗,附加损耗
7.三相感应电机转速为 ,定子旋转磁场的转速为 ,当 时为运行状态;当 时为运行状态;当 与 反向时为运行状态。
答电动机,发电机,电磁制动
8.增加绕线式异步电动机起动转矩方法有 ,。
A4极, ; B6极, ;
第5章思考题和习题解答

第五章 电气设备的选择5-1 电气设备选择的一般原则是什么?答:电气设备的选择应遵循以下3项原则:(1) 按工作环境及正常工作条件选择电气设备a 根据电气装置所处的位置,使用环境和工作条件,选择电气设备型号;b 按工作电压选择电气设备的额定电压;c 按最大负荷电流选择电气设备和额定电流。
(2) 按短路条件校验电气设备的动稳定和热稳定 (3) 开关电器断流能力校验5-2 高压断路器如何选择? 答:(1)根据使用环境和安装条件来选择设备的型号。
(2)在正常条件下,按电气设备的额定电压应不低于其所在线路的额定电压选择额定电压,电气设备的额定电流应不小于实际通过它的最大负荷电流选择额定电流。
(3)动稳定校验(3)max shi i ≥ 式中,(3)sh i 为冲击电流有效值,max i 为电气设备的额定峰值电流。
(4)热稳定校验2(3)2th th ima I t I t ∞≥式中,th I 为电气设备在th t 内允许通过的短时耐热电流有效值;th t 为电气设备的短时耐热时间。
(5)开关电器流能力校验对具有分断能力的高压开关设备需校验其分断能力。
设备的额定短路分断电流不小于安装地点最大三相短路电流,即(3).max cs K I I ≥5-3跌落式熔断器如何校验其断流能力?答:跌落式熔断器需校验分断能力上下限值,应使被保护线路的三相短路的冲击电流小于其上限值,而两相短路电流大于其下限值。
5-4电压互感器为什么不校验动稳定,而电流互感器却要校验?答:电压互感器的一、二次侧均有熔断器保护,所以不需要校验短路动稳定和热稳定。
而电流互感器没有。
5-5 电流互感器按哪些条件选择?变比又如何选择?二次绕组的负荷怎样计算? 答:(1)电流互感器按型号、额定电压、变比、准确度选择。
( 2)电流互感器一次侧额定电流有20,30,40,50,75,100,150,200,400,600,800,1000,1200,1500,2000(A )等多种规格,二次侧额定电流均为5A ,一般情况下,计量用的电流互感器变比的选择应使其一次额定电流不小于线路中的计算电流。
第5章习题解答

第五章可编程序控制器及其工作原理5-1 可编程序控制器具有哪些特点?答:可编程序控制器特点:1)抗干扰能力强,可靠性高;2)控制系统结构简单、通用性强、应用灵活;3)编程方便,易于使用;4)功能完善,扩展能力强;5)PLC控制系统设计、安装、调试方便;6) 维修方便,维修工作量小;7) 体积小、重量轻,易于实现机电一体化。
5-2 整体式PLC、组合式PLC由哪几部分组成?各有何特点?答:整体式结构的PLC是将中央处理单元(CPU)、存储器、输入单元、输出单元、电源、通信端口、I∕O扩展端口等组装在一个箱体内构成主机。
另外还有独立的I/O扩展单元等通过扩展电缆与主机上的扩展端口相连,以构成PLC不同配置与主机配合使用。
整体式结构的PLC结构紧凑、体积小、成本低、安装方便。
小型机常采用这种结构。
组合式结构的PLC是将CPU、输入单元、输出单元、电源单元、智能I∕O单元、通信单元等分别做成相应的电路板或模块,各模块可以插在带有总线的底板上。
装有CPU的模块称为CPU模块,其他称为扩展模块。
组合式的特点是配置灵活,输入接点、输出接点的数量可以自由选择,各种功能模块可以依需要灵活配置。
5-3 PLC控制与继电器控制比较,有何相同之处?有何不同之处?答:PLC控制与继电器控制的比较见下表:5-4 PLC的硬件指的是哪些部件?它们的作用是什么?答:PLC的基本结构由中央处理器(CPU),存储器,输入、输出接口,电源,扩展接口,通信接口,编程工具,智能I/O接口,智能单元等组成。
1)中央处理器(CPU)中央处理器(CPU)其主要作用有①接收并存储从编程器输入的用户程序和数据。
②诊断PLC内部电路的工作故障和编程中的语法错误。
③用扫描的方式通过I∕O部件接收现场的状态或数据,并存入输入映像存储器或数据存储器中。
④PLC进入运行状态后,从存储器逐条读取用户指令,解释并按指令规定的任务进行数据传送、逻辑或算术运算等;根据运算结果,更新有关标志位的状态和输出映像存储器的内容,再经输出部件实现输出控制、制表打印或数据通信等功能。
应用多元统计分析课后习题答案高惠璇第五章部分习题解答

u (2) a (2)
1 89765
(32,33)
2205
1465 4.8897 89765
u (1) u (2)
当X (1)
20 20
时,
u(
X
(1)
)
1 89765
(32,33)
20 20
4.3390
因u( X (1) ) 4.3390 u* , 判X (1) G2.
当X (1)
15 20
解 : (a) (ad )2 (ad )(ad )
aSa
aSa
a( X
(1)
X
(2) )( X aSa
(1)
X
(2) )a
def
aBa aSa
1
其中1为S 1B的最大特征值,且仅当a 1对应的
特征向量时等号成立.
又S 1B ( X (1) X (2) )( X (1) X (2) )S 1与
判X G2 , 当W ( X ) 0, 试求错判概率P(2 |1)和P(1| 2).
解 : 记a 1 ( (1) (2) ),W ( X ) ( X )a是X的
线性函数,当X
G1时,W
(X
)
~
N1
(
1
,
2 1
),
且
21
第五章 判别分析
1
E(W ( X
))
( (1)
)a
1 2
( (1)
2
PU a PU b
(1) 2
(2) 1
(1) 1
(2) 2
.
.
(b) (a)
4
第五章 判别分析
5-2 设三个总体的分布分别为: G1为N(2,0.52), G2为
第5章作业解答
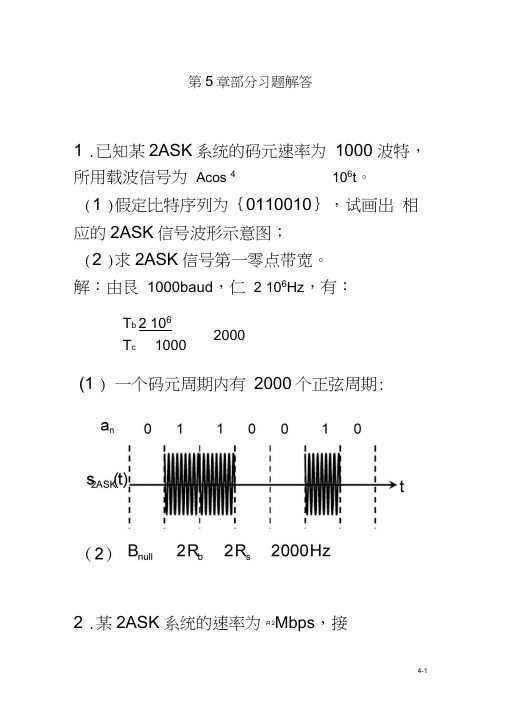
4-1第5章部分习题解答1 .已知某2ASK 系统的码元速率为 1000 波特,所用载波信号为 Acos 4106t 。
(1 )假定比特序列为{0110010},试画出 相应的2ASK 信号波形示意图; (2 )求2ASK 信号第一零点带宽。
解:由艮 1000baud ,仁 2 106Hz ,有:2 .某2ASK 系统的速率为R 2Mbps ,接T b 2 106T c 10002000(1 ) 一个码元周期内有 2000个正弦周期:4-2收机输入信号的振幅 A 40 N , AWGN 信 道的单边功率谱密度为 N o 5 1018W/H Z ,试 求传输信号的带宽与系统的接收误码率。
解:传输信号的(第一零点)带宽为:B T 2% 4MHz平均码元能量: 匚 A 2T bEb 4系统的接收误码率:(1 )若是包络检波,其误码率为(最窄带宽接收):(2)若是相干解调:其误码率为(MF 接收):E b A 2T b A N o4N o 4R b N o40 10 4 2 1065 10 1840E b /N °2401.03 104-33.某2FSK 发送码1时,信号为 Si tAsin wt 1 ,0 t T s ;发送码 o 时信号为 S o t Asin W o t o ,0 t T s 。
式中1及0为均匀分布随机变量,2 1 8 /Ts ,码1与0等概率出现。
(1 )画出包络检波形式的接收机框图; (2)设码元序列为11010,画出接收机中 的主要波形(不考虑噪声);(3 )若接收机输入高斯噪声功率谱密度为N °/2,试给出系统的误码率公式。
解:(1 )由P195图5.2.5可得1.27 1010Q \ 404-4(2)o2 i 8 /T s , f o2f i4/T s , f i2R s 2R由f o f i f i 2R b ,此2FSK 系统的频差足够大,可保证信号正确解调D FSK tr i tww —w -- 「0 t---- WMW y i t / \ J \y o t r\ r\a niii(3)由非相干解调(包络检波)的误码率公式 P199 (5.2.12 ),2A 2/4x---------2, A 2/41 2 P e -e 1I O B BPFe22A2/4A2T ST N g R b14N。
第5章 相平衡习题解答
5-5 根据下面给出的 I2 的数据,绘制相图。(已知: s l )
三相点
临界点
熔点
t/℃
113
512
114
p/kPa
12.159
11754
101.325
解:碘的相图如下:
答:t=84℃
沸点 184 101.325
解:(1)由表中的数据,绘制水(A) -醋酸(B)系统的温度-组成图如下:
⑵ 图中,组成为 xB=0.800 的液相的泡点: t 110.2 C ; ⑶ 图中,组成为 yB =0.800 的气相的露点: t 112.8 C ; ⑷ 求 105℃时气-液平衡两相的组成: xB 0.417 , yB 0.544 ;
答:⑴ S=2,C=2,P=1,f=2; ⑵ S=1,C=1,P=2,f=1; ⑶ S=3,C=3,P=2,f=2; ⑷ S=3,C=1,P=2,f=1; ⑸ S=3,C=2,P=2,f=2; ⑹ S=2,C=2,P=3,f=1
5-2 试求下列平衡系统的组分数 C 和自由度数 f 各是多少? ⑴ 过量的 MgCO3(s)在密闭抽空容器中,温度一定时,分解为 MgO(s)和 CO2(g); ⑵ H2O(g)分解为 H2(g) 和 O2(g); ⑶ 将 SO3(g)加热到部分分解; ⑷ 将 SO3(g)和 O2(g)的混合气体加热到部分 SO3(g)分解。 解:(1)物种数 S=3,组分数 C=2、相数 P=3,自由度数 f*=C-P+1=0;
所以,压力降到 98.53kPa 时,开始产生气相,此气相的组成 yB=0.7474;
(2)当气相组成: yB 0.541时,
yB
自动控制原理第五章习题及答案
第五章习题与解答5-1试求题5-1图(a)、(b)网络的频率特性。
u r R1u cR2CR2R1u r u c(a) (b)题5-1图R-C网络解(a)依图:⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(RRCRRTCRRRRKsTsKsCRsCRRRsUsUrcττωωτωωωωω11121212121)1()()()(jTjKCRRjRRCRRjRjUjUjGrca++=+++==(b)依图:⎩⎨⎧+==++=+++=CRRTCRsTssCRRsCRsUsUrc)(1111)()(2122222212ττωωτωωωωω2221211)(11)()()(jTjCRRjCRjjUjUjGrcb++=+++=="5-2某系统结构图如题5-2图所示,试根据频率特性的物理意义,求下列输入信号作用时,系统的稳态输出)(tcs和稳态误差)(tes(1)tt r2sin)(=(2))452cos(2)30sin()(︒--︒+=ttt r题5-2图反馈控制系统结构图解 系统闭环传递函数为: 21)(+=Φs s 频率特性:2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=-系统误差传递函数: ,21)(11)(++=+=Φs s s G s e则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e(1)当t t r 2sin )(=时,2=ω,r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ (2) 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ>)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m ss ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m ss ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0--+=t t5-3 若系统单位阶跃响应 h t e e t tt()..=-+≥--11808049试求系统频率特性。
概率论第五章习题解答(全)
X
i 1
i
0.5 5000
5000 0.1
10 } 50
1 (
10 ) 1 (1.414) =1-0.9207=0.0793。 7.07
5、有一批建筑房屋用的木柱,其中 80%的长度不小于 3m,现从这批木柱中随机地取 100 根,求其中至少有 30 要短于 3m 的概率。 解 把从这批木柱中随机地取一根看作一次试验,并假定各次试验相互独立,在 100 次试验中长度不小于 3m 的根数记作 X ,则 X 是随机变量 X ,且 X b(100, 0.8) , 其分布律为
2\(1)一保险公司有 10000 个汽车保险投保人,每个投保人索赔金额的数学期望为 280 美 元,标准差为 800 美元,求索赔总金额不超过 2700000 美元的概率; (2)一公司有 50 张签约保险单,每张保险单的索赔金额为 X i , i 1, 2, ,50 (以千美元 计)服从韦布尔分布,均值 E ( X i ) 5 ,方差 D ( X i ) 6 求 50 张保险单索赔的合计总金额 大于 300 的概率。 解 (1)设每个投保人索赔金额为 X i , i 1, 2, ,10000 ,则索赔总金额为 X 又 E ( X i ) 280 , D ( X i ) 800 ,所以,
以 X 表示总收入,即 X
300 i 1
X
i 1
300 i 1
300
i
,由独立同分布中心极限定理,得
X i 300 1.29
300 0.0489
X
i
387 N (387,14.67)
14.67
则收入超过 400 元的概率为
P{ X i 400} 1 P{ X i 400}
第5章 习题及答案
第五章 汇编语言程序设计1、画图说明下列语句所分配的存储器空间及初始化的数据值。
难度:2(1) BYTE_VAR DB ‘BYTE’,12,-12H ,3 DUP(0,2 DUP(1,2),7) (2) WORD_VAR DW 3 DUP(0,1,2),7,-5,’BY’,’TE’,256H 答:(1) (2)07H BYTE_V AR 42H WORD_V AR 00H 00H 59H 00H FBH 54H 01H FFH 45H 00H 59H 0CH 02H 42H EEH 00H 45H 00H 00H 54H 01H 00H 56H 02H 01H 02H 01H 00H 02H 02H 07H 00H 00H 00H 01H 00H 02H 01H 01H 00H 02H 02H 07H 00H 00H 00H 01H 00H 02H 01H 01H 00H 02H 02H07H00H2、假设程序中的数据定义如下: PARTNO DW ?PNAME DB 16 DUP(?) COUNT DD ? PLENTH EQU $- PARTNO 问:PLENTH 的值为多少?他表示什么意义? 答:PLENTH 的值为22,它表示当前已分配单元空间。
《微型计算机原理》第5章习题与解答3、有符号定义语句如下:难度:2BUF DB 1,2,3,’123’EBUF DB 0L EQU EBUF-BUF问:L的值是多少?答:L的值为6;4、假设成序中的数据定义如下:难度:2LNAME DB 30 DUP(?)ADDRESS DB 30 DUP(?)CITY DB 15 DUP(?)CODE_LIST DB 1,7,8,3,2(1)用一条MOV指令将LNAME的偏移地址存入BX。
(2)用一条指令将CODE_LIST的头两个字节的内容放入SI。
(3)写一条伪指令定义符使CODE_LENGTH的值等于 CODE_LIST域的实际长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章部分习题解答
解: (1)
2 0 2a 4b 8c(rad)
2 0 2a 4b 8c(rad)
d 2 1 a 2bt 3ct (rad .s ) dt d 2b 6ct (rad .s 2 ) dt
(2)
解:
S圆 R
2
1 2 S 挖 R 4
R
O'
2
3 S 剩 S圆 4
R
O
第5章部分习题解答
1 m挖 m 3
4 m圆 m 3
由平行轴定理可得
R 2 J圆 J 剩 J 挖 m挖 ( ) 2
即
2 2 1 4 1 1 R 1 R m R2 J 剩 m m 2 3 2 3 4 3 4
第5章部分习题解答
如图所示,一质量M,半径为R,并以角速度 绕定轴转动着的匀质飞轮,在某一瞬时突然有一 质量为m的小碎片从飞轮的边缘飞出.设碎片脱 离飞轮时的速度方向正好竖直向上.试求: (1) 以飞出点为起点,碎片能上升的最大高度;
P153题5.3.19
(2) 剩余部分的角速度、角动量和转动动能.
13 J剩 mR 2 24
2010.4.13
第5章部分习题解答
P153:5.3.11 某飞轮摩擦力矩作用做减速转动,如果 角加速度与角速度成正比,即 k ,式 中k为比例常量.设初始时刻角速度为0 , 试求: (1)飞轮角速度随时间变化的关系; (2)角速度由 0 减为 0 2 所需的时间及 在此时间内飞轮转过的转数.
'
1 L剩 J 剩 ' ( MR 2 mR 2 ) 2
1 1 1 2 Ek J 剩 ' ( MR 2 mR 2 ) 2 2 2 2 2010.4.14
第5章部分习题解答
P153题5.3.20 如图所示,将一质量为m=0.05kg的小球系 于不能伸长的轻绳一端, 绳穿过一竖直的光滑 细管,手拉绳的另一端,先使小球以角速度大小 为3rad.s-1,在半径r1=0.2m的水平圆周上运动, 然后将绳向下拉,小球看作质点,当r2=0.1m时, (1) 小球的角速度是多大? (2) 该小球的转动动能变化了多少?
P153题5.3.16 如图所示,质量为m,长为l的质量均匀分布的 细杆,可绕其一端的垂直于纸面的水平轴O转动. 如果把棒拉到水平位置后放手,棒落到竖直位置 时,与放置在水平面上A处的质量为M静止的物 体做完全弹性碰撞,物体在水平面上向右滑行了 一段距离S后停止.设物体与水平面间的摩擦系 6m 2 l 数 处处相同.求证: 2
第 5章 部分习题解答
第5章部分习题解答
P151:5.3.3 某发动机飞轮转动的角坐标与时间的关 2 3 系为 0 at bt ct (rad),如果 0 、a、b、 c均为常数, 求: (1) t=2s时的角坐标,t=2s内的角位移; (2) 飞轮角速度和角加速度的表达式; (3) t=2s时刻的角速度和角加速度大小.
第5章部分习题解答
解:
(1)碎片飞出时的速度 为 v R ,上升过程,机械 能守恒,设上升高度为h,碎 片飞出位置为势能零点, 则
1 1 2 mgh mv m( R ) 2 2 2
m
O
R
M
O'
R 2 2 h 2g
第5章部分习题解答
(2) 设剩下部分的转动惯量为 J 剩 ,则有
2n0 n0 0 60 30
2n 60
n
30
0 t
0
t
4 (rad .s )
2
第5章部分习题解答
1 2 0t t 2
N 58.3(r ) 2
(2) 设从开始转动到停下来所需时间为 t全 则
1 0 t全
1 0
t全 8.3(s)
t ' t剩 8.3 5 3.3(s)
第5章部分习题解答
也可以
1 t ' 1 0
t ' 3.3(s)
2010.4.13
第5章部分习题解答
P152:5.3.7
一块质量为M的均匀的长方形薄 板 ,边长分别为a、b,中心O取为坐标原 点,直角坐标系OXYZ如图所示. (1)证明对OX轴和OY轴的转动惯量分 2 2 J Ma 12, ; 别为: J ox Mb 12, oy (2)证明薄板对OZ轴的转动惯量为:
第5章部分习题解答
解: 碰撞过程中,棒的角动量守恒 参考正方向如图,则
L/2
n
O
2L
L 1 L 2 2 mv0 [ m(2 L) m( ) ] 2 12 2
L/2
v0
L
6 v0 7L
第5章部分习题解答
P153题5.3.18
如图所示,轮对中心轴O的转动惯量为J,半径 为r,如果在轮边缘上绕一轻绳,下端一质量为m的 重物,设轮转动时所受的阻力矩为M 0 .求重物自 静止开始下落距离h时轮的角速度.设绳与轮间无 相对滑动. 解: 受力情况及坐标系如图,由转动定 律和牛顿第二定律可得
第5章部分习题解答
解: (1)根据题意
d k dt
d
0
k dt
0
t
0ekt
(2)由题意
1 ln kt 21源自 kt 0 0 e 2ln 2 t k
第5章部分习题解答
d 0 e kt dt
d 0ekt dt
a 2 a 2
b 2 b 2
a 2 a 2
b 2 b 2
1 2 2 y dy M (a b ) 12
2
第5章部分习题解答
也可以用正交轴定理求解
1 2 2 J oz J ox J oy M (a b ) 12
第5章部分习题解答
P152题5.3.9 在一半径为R的均匀薄圆盘中,挖出一个直 径为R的圆形面积,所剩余部分的质量为m,圆形 空盘面积的中心 O 距圆盘中心 O'为R/2,求所剩 部分对通过盘心且与盘垂直的轴的转动惯量.
第5章部分习题解答
解: (1) 在题述过程中,小球的角动量守恒(规定 角动量的正向为小球实际转动方向),则
2 2 mr mr 2 2 1 1
mr 2 1 12rad.s 1 mr
1 1 2 (2) Ek J 22 J112 2.7 10 2 J 2 2
J oz M (a 2 b2 ) 12,
第5章部分习题解答
解: (1)如图在坐标y处取一面 元ady,设质量面密度为 ,则 M ab
bdx Y
b O
M
a Z
ady
X
J ox y ady ...
2
b 2 b 2
dxdy
1 2 Mb 12
第5章部分习题解答
在坐标x处取一面元bdx,则
0 0
t
转数
0
k
(1 e ) ...
kt
0
2k
0 N ... 2 4k
第5章部分习题解答
P153题5.3.15 如图所示,质量为M、半径为R的质量均匀 分布的实心球体,以角速度 0 绕通过球心且垂 直于纸平面的水平轴转动.质量为m,初速度为 v0 的一小质点与球相碰撞,并粘在球的边缘上. 求碰撞后该系统的角速度大小表达式.
1 J oy a x bdx ... Ma 2 12 2 (2)在坐标(x、y)处取一面元dxdy,则
2 2
a
J oz ( x y )dxdy x dxdy y dxdy
2 2 2 2 s s s
x dx dy dx
2
(m 3M ) .S
第5章部分习题解答
解: 杆从水平位置到竖直位置的过程中, 机械能守恒(势能零点如图)
1 l 2 mgl J0 mg ......( 1) 2 2
O
杆与物体碰撞时,系统的 角动量,动能都守恒
lm
M
S
J0 J Mvl......(2)
A 重力势能零点
M
1 1 1 2 2 J0 J Mv 2 .....(3) 2 2 2
2 1 2 2
m
r
O
2010.4.14
第5章部分习题解答
(3)
2 a 4b 12c(rad.s 1 )
2 2b 12c(rad.s 2 ) 2010.4.13
第5章部分习题解答
P151题5.3.4 一飞轮在5s内转速由1000r.min-1均匀地减 小到400r.min-1.求角速度大小和5s内的总转数; 还需要经过多长时间,飞轮才停止转动? 解: (1)
第5章部分习题解答
解: 在两物体碰撞的过程中,m与球组成的 系统的角动量守恒.参考正方向如图所示. 设系统的末角速度为
mv0 R J0 ( J mR )
2
mv0
n
O M R
0
2 mv0 R MR 20 5 2 MR 2 m R2 5
2010.4.13
第5章部分习题解答
第5章部分习题解答
M向右滑动过程中,由动能定理得:
1 MgS 0 Mv 2 ......(4) 2
由(1)到(4)式可得
6m 2 l 2 (m 3M ) .S
2010.6.19
第5章部分习题解答
P153题5.3.17 如图所示,一均质棒长2L,质量为m,以与棒 长方向相垂直的速度v0 在水平面内运动时与固 定的O点发生完全非弹性碰撞,发生相碰处距棒 中心为L/2.求棒在碰撞后的瞬时绕O点转动的 角速度大小 .
