弦切角定理及其推论
圆的弦切角定理
圆的弦切角定理
弦切角定理又叫做斜接角定理，它是由现代先驱理论家、著名数学家笛卡尔所提出的
几何定理，它讲述了弦和圆在一起时所形成的夹角大小。
这个定理本质上是一个几何定理，在经典几何学中被广泛使用。
定理的具体内容如下：设弦切线在圆上的作用点分别是A、B，AB是弦切点，AB垂直
线与圆的圆心O相交得到点C，AB点分别延长到P和Q使OP与OQ延长，则OC、OP、OQ
三角形内角的大小依次为：π的一半（90°）OCA弧与APO角，AOC弧与POC角，BOC弧
与QOC角。
证明：AOC为OCB的补角，POC和QOC绕O旋转就变为AOC，而AOC与AB垂直线合成
了直角，故总之，证明弦切角定理的关键是正确建立AOC和AB垂直线，即点C是A、B垂
直线的交点。
由于圆的拉格朗日定义及圆的定义，可得知BOC的中点的P的投影到OA上必是OA的
中点O，故点P必等于点C，从而证明了AB垂直线的交点为点C.
于是，AOC是一个直角，而AOC弧与APO角、AOC弧与POC角、BOC弧与QOC角就是其对应角，因此就可以看出弦切角定理了。
以上就是弦切角定理的证明，弦切角定理一般应用于圆面内不存在直线或点的情况，
这时，计算机就可以采用其求得弦和圆之间的夹角大小。
弦切角定理的证明与推导
弦切角定理的证明与推导弦切角定理的证明与推导弦切角定理是数学的一种定理，这种定理的证明是怎么一回事呢？下面就是啦店铺给大家整理的弦切角定理的证明内容，希望大家喜欢。
弦切角定理示范弦切角定理：定义弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半. (弦切角就是切线与弦所夹的角)弦切角定理证明证明：设圆心为O，连接OC，OB，OA。
过点A作TP的平行线交BC于D则∠TCB=∠CDA∵∠TCB=90-∠OCD∵∠BOC=180-2∠OCD∴,∠BOC=2∠TCB证明：分三种情况(1)圆心O在∠BAC的一边AC上∵AC为直径，AB切⊙O于A∴弧CmA=弧CA∵为半圆(2)圆心O在∠BAC的内部.过A作直径AD交⊙O于D弦切角定理介绍弦切角定理：弦切角的度数等于它所夹的弧所对的圆心角度数的一半，等于它所夹的弧所对的圆周角度数。
(与圆相切的直线，同圆内与圆相交的弦相交所形成的.夹角叫做弦切角。
)顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
如图所示线段PT所在的直线切圆O于点C，BC、AC为圆O的弦，∠TCB、∠TCA、∠PCA、∠PCB都为弦切角。
弦切角定理衍生问题及其证明已知：AC是⊙O的弦，AB是⊙O的切线，A为切点，弧CmA是弦切角∠BAC所夹的弧.求证：弦切角∠BAC的度数等于它所夹的弧的度数的一半证明：分三种情况(1)圆心O在∠BAC的一边AC上∵AC为直径∴弧CmA=弧CA∵弧CA为半圆,∴弧CmA的度数为180°∵AB为圆的切线∴∠CAB=90°∴弦切角∠BAC的度数等于它所夹的弧的度数的一半(2)圆心O在∠BAC的内部.过A作直径AD交⊙O于D,在优弧m所对的劣弧上取一点E，连接EC、ED、EA。
则∵弧CD=弧CD∴∠CED=∠CAD∵AD是圆O的直径∴∠DEA=90°∵AB为圆的切线∴∠BAD=90°∴∠DEA=∠BAD∴ ∠CEA=∠CED+∠DEA=∠CAD+∠BAD=∠BAC又∠CEA的度数等于弧CmA的度数的一半∴弦切角∠BAC的度数等于它所夹的弧的度数的一半(3)圆心O在∠BAC的外部过A作直径AD交⊙O于D，连接CD【弦切角定理的证明与推导】。
弦切角定理圆幂定理之割线相交弦切割线定理
弦切角定理及其应用极点在圆上，一边和圆订交，另一边和圆相切的角叫做弦切角。
(弦切角就是切线与弦所夹的角）弦切角定义图1如右图所示，直线 PT 切圆 O 于点 C，BC 、AC 为圆 O 的弦，∠TCB 、∠ TCA 、∠PCA 、∠PCB 都为弦切角。
弦切角定理弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半.如上图，∠ PCA=1/2 ∠ COA= ∠ CBA弦切角定理证明：证明一：设圆心为O，连结 OC， OB, 。
∵∠ TCB=90 ° -∠ OCB∵∠ BOC=180 ° -2 ∠ OCB∴,∠ BOC=2 ∠ TCB（定理：弦切角的度数等于它所夹的弧所对的圆心角的度数的一半）∵∠ BOC=2 ∠CAB （同一弧所对的圆心角等于圆周角的两倍）∴∠ TCB= ∠ CAB （定理：弦切角的度数等于它所夹的弧的圆周角）证明已知： AC 是⊙ O 的弦， AB 是⊙ O 的切线， A 为切点，弧是弦切角∠BAC 所夹的弧.求证：（弦切角定理）证明：分三种状况：（1）圆心 O 在∠ BAC 的一边 AC 上∵ AC 为直径， AB 切⊙ O 于 A ，∴弧 CmA= 弧 CA∵为半圆 ,∴∠ CAB=90= 弦 CA 所对的圆周角（ 2）圆心 O 在∠ BAC 的内部 . (B点应在A点左边)过 A 作直径 AD 交⊙ O 于 D,若在优弧 m 所对的劣弧上有一点 E那么，连结 EC 、ED 、 EA则有：∠ CED= ∠CAD 、∠ DEA= ∠DAB∴ ∠ CEA= ∠CAB∴ （弦切角定理）（ 3）圆心 O 在∠ BAC 的外面 ,过 A 作直径 AD 交⊙ O 于 D那么∠ CDA+ ∠CAD= ∠ CAB+ ∠ CAD=90 °∴∠ CDA= ∠ CAB∴（弦切角定理）3弦切角推论推论内容若两弦切角所夹的弧相等，则这两个弦切角也相等应用举例例1：如图，在⊙ O 中，⊙ O 的切线 AC 、 BC 交与点C ，求证：∠ CAB= ∠ CBA 。
弦切角定理 证明-概念解析以及定义
弦切角定理证明-概述说明以及解释1.引言1.1 概述弦切角定理是几何学中一个重要的定理，被广泛应用于圆的相关问题中。
根据该定理，如果一个弦切割了一个圆，并且与该圆的切线相交于切点，那么与这个弦相对的角与这个切线相交的角是相等的。
这个定理基于圆的几何性质而推导得出，它不仅具有理论的重要性，还被大量应用于解决实际问题。
无论是在数理推导中，还是在物理、工程等实际应用中，弦切角定理都被广泛运用。
本文将会系统地介绍弦切角定理的定义、证明要点和应用。
在正文部分，我们将详细阐述定理的定义，解释证明该定理所需的关键要点，并通过推理和几何演绎来证明这一定理的正确性。
同时，我们也将结合实际问题，展示弦切角定理在实际中的应用。
结论部分将对弦切角定理的意义进行总结，并回顾全文的主要内容。
通过阅读本文，读者将能够深入了解弦切角定理的定义、证明过程，并能够灵活运用该定理解决与圆相关的问题。
同时，本文也为读者展示了弦切角定理在实际中的重要性和应用价值。
在接下来的章节中，我们将逐步介绍弦切角定理的定义、证明要点以及其在实际问题中的应用。
希望读者通过对本文的阅读和理解，能够对弦切角定理有一个全面而深入的认识，从而在解决相关问题时能够能够灵活运用并取得理想的结果。
1.2 文章结构文章结构部分的内容可以按照以下方式编写：在本文中，我将探讨弦切角定理的证明。
本文分为引言、正文和结论三部分。
引言部分将对弦切角定理进行概述，介绍其定义、重要性和应用领域。
然后我会详细说明本文的结构以及每个部分的内容。
正文部分将详细介绍弦切角定理的证明。
首先，我将给出弦切角定理的定义，并解释其背后的数学原理。
然后，我会重点讨论证明该定理所需的关键要点。
第一要点将涉及到几何图形的构建和性质推导，第二要点将涉及到角度关系的推理和推导。
通过详细的推导和证明过程，读者将能够全面理解弦切角定理的证明方法。
结论部分将归纳总结弦切角定理的应用和意义。
我将讨论该定理在几何学中的实际应用，以及它对其他几何定理的推导和应用的重要性。
弦切角定理推理过程-概述说明以及解释
弦切角定理推理过程-概述说明以及解释1.引言1.1 概述概述部分：弦切角定理是数学中的一条基本几何定理，它描述了一个圆内切线与弦之间的关系。
通过研究弦切角定理，我们可以深入理解圆与其内切线的几何性质。
本文将详细介绍弦切角定理的定义、推导过程以及应用场景，并展望了其进一步的研究方向。
在几何学中，圆是最基本的几何图形之一，而弦则是圆上的一条线段。
弦切角定理是指当一个线段在圆上截取弦时，与该弦相交的切线与该弦之间的角度相等。
这个定理的重要性在于它提供了切线和弦之间的几何关系，使我们在解决实际问题时能够更加便利和高效。
本文将首先介绍弦切角定理的定义，明确其几何意义和表述方式。
其次，我们将详细推导弦切角定理，从最基本的几何性质出发，逐步推导得出定理的数学表达式。
通过推导过程，我们可以深入理解弦切角定理的本质和原理。
接着，我们将探讨弦切角定理的应用场景。
弦切角定理广泛应用于数学和物理等领域，例如在测量和计算过程中，我们可以利用弦切角定理来求解未知量或优化问题。
此外，弦切角定理还与圆的切线、割线等几何性质密切相关，对于深入理解圆的性质具有重要意义。
最后，我们将总结弦切角定理的重要性，指出它在几何学中的地位和作用。
同时，我们还将探讨弦切角定理的实际应用场景，例如在建筑、地理勘测、机械工程等领域的应用。
同时，对于弦切角定理的进一步研究也是不可忽视的，我们将展望弦切角定理在更广泛领域的应用和深化研究的可能性。
通过本文的阐述，读者将能全面了解弦切角定理的概念、推导过程和应用场景，进一步认识到弦切角定理在数学和实际问题求解中的重要性和实用性。
同时也将对弦切角定理的未来研究方向产生更多的兴趣和思考。
1.2 文章结构文章结构部分的内容可以按照以下方式编写:文章结构:本文将按照以下结构进行论述：引言、正文和结论。
引言部分将概述本文的研究对象——弦切角定理，并介绍文章的结构和目的。
正文部分将包含弦切角定理的定义、推导过程和应用。
弦切角定理及推论
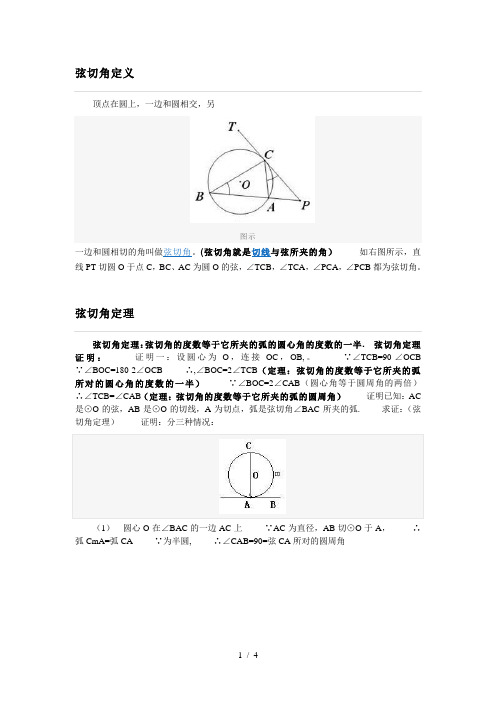
弦切角定义顶点在圆上，一边和圆相交，另图示一边和圆相切的角叫做弦切角。
(弦切角就是切线与弦所夹的角）如右图所示，直线PT切圆O于点C，BC、AC为圆O的弦，∠TCB，∠TCA，∠PCA，∠PCB都为弦切角。
弦切角定理弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半.弦切角定理证明：证明一：设圆心为O，连接OC，OB,。
∵∠TCB=90-∠OCB ∵∠BOC=180-2∠OCB ∴,∠BOC=2∠TCB（定理：弦切角的度数等于它所夹的弧所对的圆心角的度数的一半）∵∠BOC=2∠CAB（圆心角等于圆周角的两倍）∴∠TCB=∠CAB（定理：弦切角的度数等于它所夹的弧的圆周角）证明已知：AC 是⊙O的弦，AB是⊙O的切线，A为切点，弧是弦切角∠BAC所夹的弧. 求证：（弦切角定理）证明：分三种情况：（1）圆心O在∠BAC的一边AC上∵AC为直径，AB切⊙O于A，∴弧CmA=弧CA ∵为半圆, ∴∠CAB=90=弦CA所对的圆周角B点应在A点左侧（2）圆心O在∠BAC的内部. 过A作直径AD交⊙O于D, 若在优弧m所对的劣弧上有一点E 那么，连接EC、ED、EA 则有：∠CED=∠CAD、∠DEA=∠DAB ∴∠CEA=∠CAB ∴（弦切角定理）（3）圆心O在∠BAC的外部, 过A作直径AD交⊙O于 D 那么∠CDA+∠CAD=∠CAB+∠CAD=90 ∴∠CDA=∠CAB ∴（弦切角定理）弦切角推论推论内容若两弦切角所夹的弧相等，则这两个弦切角也相等应用举例例1：如图，在Rt△ABC中，∠C=90，以AB为弦的⊙O与AC相切于点A，∠CBA=60° , AB=a 求BC长. 解：连结OA，OB. ∵在Rt△ABC中, ∠C=90 ∴∠BAC=30°∴BC=1/2a(RT△中30°角所对边等于斜边的一半）例2：如图，AD是ΔABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB，AC分别相交于E，F. 求证：EF∥BC. 证明：连DF. AD是∠BAC的平分线∠BAD=∠DAC ∠EFD=∠BAD ∠EFD=∠DAC ⊙O切BC于 D ∠FDC=∠DAC ∠EFD=∠FDC EF∥BC例3：如图，ΔABC内接于⊙O，AB是⊙O直径，CD⊥AB于D，MN切⊙O于C，求证：AC平分∠MCD，BC平分∠NCD. 证明：∵AB是⊙O直径∴∠ACB=90 ∵CD⊥AB ∴∠ACD=∠B，∵MN切⊙O于 C ∴∠MCA=∠B，∴∠MCA=∠ACD，即AC平分∠MCD，同理：BC平分∠NCD.。
九年级数学弦切角定理、相交弦定理浙江版知识精讲
九年级数学弦切角定理、相交弦定理某某版【本讲教育信息】一. 教学内容：弦切角定理、相交弦定理二. 教学重、难点：重点：正确理解弦切角定理与相交弦定理难点：弦切角定理以及相交弦定理的应用三. 补充：弦切角定理与相交弦定理的知识要点：1. 学习和识别弦切角需注意两个方面（1）顶点在圆上（2）一边与圆相交成弦，另一边与圆相切于顶点．2. 弦切角定理：弦切角的度数等于它所夹弧的度数的一半．推论：弦切角等于它所夹弧所对的圆周角．3. 相交弦定理：圆内的两条弦相交，则被交点分成的两条线段长的积相等．如图，弦AB、CD相交于P，则PA·PB=PC·PD．【典型例题】例1. 如图，AB是圆O的弦，P在AB上，AB=10cm，PA=4cm，OP=5cm，求圆O的半径．解析：由P为AB上一点且已知PA、PB，可联想到相交弦定理，不妨向两方延长OP，分别交圆O于C、D．由相交弦定理：BP·AP=CP·DP又CP=CO+OP ，DP=OD －OP 且CO=DO ．∴BP ·AP=（CO+OP ）（CO －OP ）=CO 2－PO 2 ∴当AB=10，PA=4时，BP=6 又OP=5∴解得CO=7即圆O 的半径为7cm ．例2. 如图，圆内接四边形ABCD 的对角线AC 平分∠C ，BD 交AC 于点F ，过A 作圆O 的切线AE 交CB 的延长线于点E 。
求证：①AE//DB ②AE DF AD 2⋅=E解析：AE 切圆O ，ACB EAB ∠=∠∴（弦切角定理） 又ABD DCA ∠=∠A ∠∴是DCB ∠的平分线。
DB //AE ,ABD EAB ∴∠=∠∴ AEDF AD AD AB BCA DCA AD AEDF AB ,DFA ~ABE )(ADB BAE DACDBC E 2⋅=∴=∠=∠=∴∆∆∴∠=∠∠=∠=∠∴ 又弦切角定理例3. 如图，已知圆O 中，AB//CD ，BG 切圆O 于B ，P 为⋂CD 上一点，PA 、PB 交CD 于E 、F 。
【初中数学】圆中弦切角及弦切角定理
【初中数学】圆中弦切角及弦切角定理一、弦切角1、定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
如图：2、弦切角的三种情况（1）圆心在弦切角外；（2）圆心在弦切角的一条边上；（3）圆心在弦切角内；二、弦切角定理及证明定理：弦切角的度数等于它所夹的弧的圆周角；弦切角的度数等于它所夹的弧的圆心角度数的一半。
已知：如图，PQ是圆O的切线，切点为P。
求证：∠APQ=∠ABP，2∠APQ=∠AOP.（1）当圆心在弦切角外部时证明：连接OA，OP，在非弦切角所夹弧优弧PA上任取一点B，连接BP和BA。
∵ OA=OP∴ ∠OPA=∠OAP∵ ∠OPA+∠OAP+∠POA=180°∴2∠OPA+∠POA=180°∵ PO为圆的切线，OP为半径∴ ∠OPA+∠APQ=90°∴ ∠OPA=90°-∠APQ∴ 2（90°-∠APQ）+∠POA=180°∴∠POA=2∠APQ∵ ∠POA=2∠ABP（同弧所对的圆心角是圆周角的2倍）∴ ∠APQ=∠ABP（2）当圆心在弦切角的一边上时证明：在非弦切角所夹弧AP上任取一点B，连接AB、PB ∵ AP为直径∴ ∠ABP=90°∵ PQ为圆的切线，OP为半径∴ ∠APQ=90°∴∠APQ=∠ABP∴2∠APQ=∠AOP（同弧所对的圆心角是圆周角的2倍）. （3）当圆心在弦切角的内部时证明：连接OA，OP，在非弦切角所夹弧劣弧PA上任取一点B，连接BP和BA。
∵ OA=OP∴ ∠OPA=∠OAP∵ ∠OPA+∠OAP+∠1=180°∴2∠OPA+∠1=180°∵ PO为圆的切线，OP为半径∴ ∠OPA=∠APQ-90°∴ 2（∠APQ-90°）+∠1=180°∴ ∠1+2∠APQ=360°∵ ∠1+∠2=360°∴∠2=2∠APQ∴ ∠POA=2∠APQ（这里的∠POA是大于180°的角，是优弧AP所对的圆心角）∵ ∠POA=2∠ABP（同弧所对的圆心角是圆周角的2倍）∴ ∠APQ=∠ABP三、例题例1、已知：如图，直线BC切⊙O于B点，AB=AC，AD=BD，求∠A．解：由弦切角定理可得，∠DBC=∠A∵ AD=BD∴ ∠A=∠ABD∵ AB=AC∴ ∠ABC=∠ACB=2∠A∵ ∠A+∠ABC+∠ACB=180°∴5∠A=180°∴ ∠A=36°例2、已知：如图，直线DC与⊙O相切于点C，AB为⊙O直径，AD⊥DC于D，∠DAC=28°，求∠CAB的值。
弦切角定理证明及例题
弦切角定理证明及例题弦切角定理弦切角定义顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角??PCA=?PBC(?PCA为弦切角)弦切角定理弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半. (弦切角就是切线与弦所夹的角)弦切角定理证明证明:设圆心为O，连接OC，OB，OA。
过点A作TP的平行线交BC于D，则?TCB=?CDA??TCB=90-?OCD??BOC=180-2?OCD更清楚的?,?BOC=2?TCB(弦切角的度数等于它所夹的弧的圆心角的度数的一半)??BOC=2?CAB??TCB=?CAB(弦切角的度数等于它所夹的弧的圆周角)证明已知:AC是?O的弦，AB是?O的切线，A为切点，弧是弦切角?BAC所夹的弧.求证:.(弦切角定理)证明:分三种情况:(1) 圆心O在?BAC的一边AC上?AC为直径，AB切?O于A，?弧CmA=弧CA?为半圆,??CAB=90=弦CA所对的圆周角B点应在A点左侧 (2) 圆心O在?BAC的内部.过A作直径AD交?O于D,若在优弧m所对的劣弧上有一点E那么，连接EC、ED、EA则有:?CED=?CAD、?DEA=?DAB? ?CEA=?CAB? (弦切角定理)(3) 圆心O在?BAC的外部,过A作直径AD交?O于D那么 ?CDA+?CAD=?CAB+?CAD=90??CDA=?CAB?(弦切角定理)弦切角推论推论内容若两弦切角所夹的弧相等，则这两个弦切角也相等应用举例例1:如图，在中，?C=90，以AB为弦的?O与AC相切于点A，?CBA=60? , AB=a 求BC长.解:连结OA，OB.?在中, ?C=90??BAC=30??BC=1/2a(,,?中30?角所对边等于斜边的一半)例2:如图，AD是ΔABC中?BAC的平分线，经过点A的?O与BC切于点D，与AB，AC分别相交于E，F.求证:EF?BC.证明:连DF.AD是?BAC的平分线 ?BAD=?DAC?EFD=?BAD?EFD=?DAC?O切BC于D ?FDC=?DAC?EFD=?FDCEF?BC例3:如图，ΔABC内接于?O，AB是?O直径，CD?AB于D，MN切?O于C，求证:AC平分?MCD，BC平分?NCD.证明:?AB是?O直径??ACB=90?CD?AB??ACD=?B，?MN切?O于C??MCA=?B，??MCA=?ACD，即AC平分?MCD，同理:BC平分?NCD.。
弦切角定理及其应用
弦切角定理及其应用顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
(弦切角就是切线与弦所夹的角）弦切角定义图1如右图所示，直线PT切圆O于点C，BC、AC为圆O的弦，∠TCB、∠TCA、∠PCA、∠PCB都为弦切角。
弦切角定理弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半.如上图，∠PCA=1/2∠COA=∠CBA弦切角定理证明：证明一：设圆心为O，连接OC，OB,。
∵∠TCB=90°-∠OCB∵∠BOC=180°-2∠OCB∴,∠BOC=2∠TCB（定理：弦切角的度数等于它所夹的弧所对的圆心角的度数的一半）∵∠BOC=2∠CAB（同一弧所对的圆心角等于圆周角的两倍）∴∠TCB=∠CAB（定理：弦切角的度数等于它所夹的弧的圆周角）证明已知：AC是⊙O的弦，AB是⊙O的切线，A为切点，弧是弦切角∠BAC所夹的弧.求证：（弦切角定理）证明：分三种情况：（1）圆心O在∠BAC的一边AC上∵AC为直径，AB切⊙O于A，∴弧CmA=弧CA∵为半圆,∴∠CAB=90=弦CA所对的圆周角（2）圆心O在∠BAC的内部. (B点应在A点左侧)过A作直径AD交⊙O于D,E若在优弧m所对的劣弧上有一点那么，连接EC、ED、EA则有：∠CED=∠CAD、∠DEA=∠DAB∴∠CEA=∠CAB∴（弦切角定理）（3）圆心O在∠BAC的外部,过A作直径AD交⊙O于D那么∠CDA+∠CAD=∠CAB+∠CAD=90°∴∠CDA=∠CAB∴（弦切角定理）3弦切角推论推论内容若两弦切角所夹的弧相等，则这两个弦切角也相等应用举例例1：如图，在⊙O中，⊙O的切线AC、BC交与点C，求证：∠CAB=∠CBA。
解：⊙O的切线AC、BC交与点C，∴AC=BC（切线长定理）。
∴∠CAB=∠CBA。
（等腰三角形“等边对等角”）。
例2：如图，AD是ΔABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB，AC分别相交于E，F. 求证：EF//BC.证明：连接DFAD是∠BAC的平分线∠BAD=∠DAC ∠EFD=∠BAD ∠EFD=∠DAC⊙O切BC于D ,∠FDC=∠DAC ∠EFD=∠FDCEF∥BC例3：如图，ΔABC内接于⊙O，AB是⊙O直径，CD⊥AB于D，MN切⊙O于C，求证：AC平分∠MCD，BC平分∠NCD.证明：∵AB是⊙O直径∴∠ACB=90∵CD⊥AB ∴∠ACD=∠B，∵MN切⊙O于C ∴∠MCA=∠B，∴∠MCA=∠ACD，即AC平分∠MCD，同理：BC平分∠NCD。
第3课时弦切角定理
第3课时弦切角定理弦切角定理【知识要点:】1.弦顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
(弦切角就是切线与弦所夹的角)如下图所示，直线PT切圆O于点C，BC、AC为圆O的弦，?TCB，?TCA，?PCA，?PCB都为弦切角。
2(弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半. 3(定理:弦切角的度数等于它所夹的弧的圆周角4(推论:若两弦切角所夹的弧相等，则这两个弦切角也相等5(圆幂定理:过任意不在圆上的一点P引两条直线L1、L2，L1与圆交于A、B(可重合，即切线)，L2与圆交于C、D(可重合)，则有PA?PB=PC?PD【经典例题:】1例1.如图1，正方形ABCD的边长为1，以BC为直径。
在正方形内作半圆O，过A作半圆切线，切点为F，交CD于E，求DE:AE的值。
图1例2.?O中的两条弦AB与CD相交于E，若AE,6cm，BE,2cm，CD,7cm，那么CE,_________cm。
图2例3.已知PA是圆的切线，PCB是圆的割线，则________。
2例4.如图3，P是?O外一点，PC切?O于点C，PAB是?O的割线，交?O于A、B 两点，如果PA:PB,1:4，PC,12cm，?O的半径为10cm，则圆心O到AB的距离是___________cm。
图3【课堂练习题:】一、选择题1.已知:PA、PB切?O于点A、B，连结AB，若AB,8，弦AB的弦心距3，则PA,( )A. B. C. 5 D. 82.下列图形一定有内切圆的是( )A.平行四边形B.矩形C.菱形D.梯形3.已知:如图1直线MN与?O相切于C，AB为直径，?CAB,40?，则?MCA的度数( )图1A. 50?B. 40?C. 60?D. 55?4.圆内两弦相交，一弦长8cm且被交点平分，另一弦被交点分为1:4，则另一弦长为( )A. 8cmB. 10cmC. 12cmD. 16cm5.若PA为?O的切线，A为切点，PBC割线交?O于B、C，若BC,20，，则PC的长为_____________。
24弦切角的性质
(1)
(2)
(3)
(4)
图(1)中，缺少“顶点在圆上”的条件； 图(2)中，缺少“一边和圆相交”的条件； 图(3)中，缺少“一边和圆相切”的条件； 图(4)中，缺少“顶点在圆上”和“另一边和圆相切”的条件。
练习：
如图所示，AB是e O的一条弦，D 是 e O 上的任一点（不与A, B重合）， 则下列为弦切角的是（ C ）
RtVCAE : RtVCBD, RtVCBF : RtVCAD CA CE , CB CF
C2 CE • CF
CD CF
总结：
1.利用弦切角定理证明线段相等的技巧：
利用弦切角定理证明线段相等时，常常通过弦切角定理获得 角相等，然后再转化为线段相等的关系，从而解决问题。
例7：如图，PA, PB是e O的切线，点C在 »AB上， CD AB,CE PA,CF PB，垂足分别为D, E, F。求证：CD2 CE • CF 证明：连接 CA, CB Q PA, PB是e O的切线 CAP CBA,CBP CAB 又Q CD AB,CE PA,CF PB
(2)弦切角的一边是过切点的一条弦所在的射线，角的另一边是以 切点为端点且与切线重合的一条射线； (3)弦切角的度数等于它所夹的弧的度数的一半。
2.利用弦切角解决与角有关的问题的步骤： (1)根据图形及弦切角的定义找出与题目有关的弦切角；
(2)利用弦切角定理找出与其相等的角；
(3)综合运用相关的知识，进行角的求解。
而PAB PCB BCE BAC
综上所述，猜想成立。
1.弦切角：
(1)定义：
顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切 角。 (2)分类： ★圆心在角的外部：
★圆心在角的一边上：
《弦切角定理》《圆幂定理》练习题及答案
《弦切角定理》定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
弦切角定理：弦切角的度数等于它所夹的弧的圆心角度数的一半，等于它所夹的弧的圆周角度数。
那怎么证明呢？《圆幂定理》（1）相交弦定理：圆内两弦相交，交点分得的两条线段的乘积相等。
即：在⊙O 中，∵弦AB 、CD 相交于点P ，∴PA PB PC PD ⋅=⋅（2）推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项。
即：在⊙O 中，∵直径AB CD ⊥， ∴2CE AE BE =⋅（3）切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。
即：在⊙O 中，∵PA 是切线，PB 是割线∴ 2PA PC PB =⋅（4）割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等（如上图）。
即：在⊙O 中，∵PB 、PE 是割线 ∴PC PB PD PE ⋅=⋅【精典例题】1、如图，PA 、PB 是⊙O 的切线，AC 是⊙O 的直径，∠P=50°，则∠BOC 的度数为（ ） A ．50°B ．25°C ．40°D ．60°2、如图，BD 为圆O 的直径，直线ED 为圆O 的切线，A ．C 两点在圆上，AC 平分∠BAD 且交BD 于F 点．若∠ADE ＝19°，则∠AFB 的度数为何？（ ） A ．97°B ．104°C ．116°D ．142°解答：解：∵PA 、PB 是⊙O 的切线， ∴∠OAP =∠OBP =90°， 而∠P =50°，∴∠AOB =360°﹣90°﹣90°﹣50°= 130°， 又∵AC 是⊙O 的直径，∴∠BOC =180°﹣130°=50°． 故选A ．BADB3、如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ，且CO=CD ，则∠PCA=（ ）A 、30°B 、45°C 、60°D 、67.5°4、已知⊙O 的半径为1，圆心O 到直线l 的距离为2，过l 上任一点A 作⊙O 的切线，切点为B ，则 线段AB 长度的最小值为（ ）A 、1B 、2C 、3D 、2解答：如右图所示，OA ⊥l ，AB 是切线，连接OB ， ∵OA ⊥l ，∴OA=2， 又∵AB 是切线， ∴OB ⊥AB ，在Rt △AOB 中，AB =22OB OA -=2212-=3．故选C ．5、如图是油路管道的一部分，延伸外围的支路恰好构成一个直角三角形， 两直角边分别为6m 和8m.按照输油中心O 到三条支路的距离相等来连接管 道，则O 到三条支路的管道总长（计算时视管道为线，中心O 为点） 是（ ）A.2mB.3mC.6mD.9m解答：在Rt △ABC 中，BC =8m,AC =6m,AB =22BC AC +=2286+=10． ∵中心O 到三条支路的距离相等，设距离是r ．△ABC 的面积=△AOB 的面积+△BOC 的面积+△AOC 的面积 即：12AC •BC =12AB •r+12BC •r+12AC •r 即：6×8=10r+8r+6r ∴r=4824=2． 故O 到三条支路的管道总长是2×3=6m ．故选C ．解答：解：∵BD 是圆O 的直径， ∴∠BAD ＝90°， 又∵AC 平分∠BAD ，∴∠BAF ＝∠DAF ＝45°， ∵直线ED 为圆O 的切线， ∴∠ADE ＝∠ABD ＝19°，∴∠AFB ＝180°－∠BAF －∠ABD ＝180°－45°－19°＝116°． 故选C ．解答：解：如图：∵PD 切⊙O 于点C ， ∴OC ⊥PD ， 又∵OC=CD ， ∴∠COD=45°， 连接AC ，∵AO=CO ， ∴∠ACO=22.5°，∴∠PCA=90°-22.5°=67.5°． 故选D ．O（第5题图）6、如图，AB 是⊙O 的直径，BC 交⊙O 于点D ，DE ⊥AC 于点E ，要使DE 是⊙O 的切线，还需补充一个条件，则补充的条件不正确．．．的是（ ） A. DE ＝DO B. AB ＝AC C. CD ＝DB D. AC ∥OD7、已知AB 是⊙O 的直径，点P 是AB 延长线上的一个动点，过P 作⊙O 的切线，切点为C ，∠APC 的平分线交AC 于点D ，则∠CDP 等于（ ）A 、30°B 、60°C 、45°D 、50°解答：连接OC ，∵OC=OA ，，PD 平分∠APC ，∴∠CPD=∠DPA ，∠A=∠ACO ， ∵PC 为⊙O 的切线，∴OC ⊥PC ，∵∠CPD+∠DPA+∠A+∠ACO=90°，∴∠DPA+∠A=45°，即∠CDP=45°． 故选C ．8、如图，CB 切⊙O 于点B ，CA 交⊙O 于点D 且AB 为⊙O 的直径，点E 是ABD 上异于点A 、D 的一点．若∠C =40°，则∠E 的度数为 ．9、已知：如图，三个半圆以此相外切，它们的圆心都在x 轴的正半轴上并与直线y ＝x 相切，设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1、r 2、r 3，则当r 1＝1时，r 3＝解答：由三个半圆依次与直线y ＝x 相切并且圆心都在x 轴上，∴y ＝x 倾斜角是30°，∴得，OO 1=2r 1，OO 1=2r 2，001=2r 3，r 1＝1，∴r3=9．故答案为9．333333解答：当AB=AC 时，连接AD ，∵AB 是⊙O 的直径，∴AD ⊥BC ，∴CD=BD ， ∵AO=BO ，∴OD 是△ABC 的中位线，∴OD ∥AC ，∵DE ⊥AC ，∴DE ⊥OD ，∴DE 是⊙O 的切线．所以B 正确． 当CD=BD 时，AO=BO ，∴OD 是△ABC 的中位线，∴OD ∥AC ∵DE ⊥AC ∴DE ⊥OD ∴DE 是⊙O 的切线．所以C 正确．当AC ∥OD 时，∵DE ⊥AC ，∴DE ⊥OD ．∴DE 是⊙O 的切线．所以D 正确． 故选A ．ABCD P· OE解答：如图：连接BD ，∵AB 是直径，∴∠ADB =90°，∵BC 切⊙O 于点B ，∴∠ABC =90°， ∵∠C =40°，∴∠BAC =50°，∴∠ABD =40°，∴∠E =∠ABD =40°． 故答案为：40°．10、如图，在Rt △ABC 中，∠ABC 是直角，AB=3，BC=4，P 是BC 边上的动点，设BP=x ，若能在AC 边上找到一点Q ，使∠BQP=90°，则x 的取值范围是 ．解答：解：过BP 中点以BP 为直径作圆，连接QO ，当QO ⊥AC 时，QO 最短，即BP 最短， ∵∠OQC=∠ABC=90°，∠C=∠C ，∴△ABC ∽△OQC ，∴=，∵AB=3，BC=4，∴AC=5， ∵BP=x ，∴QO=x ，CO=4﹣x ，∴=，解得：x=3，当P 与C 重合时，BP=4，∴BP=x 的取值范围是：3≤x ≤4， 故答案为：3≤x ≤4．11、如图，AD 是⊙O 的弦，AB 经过圆心O ，交⊙O 于点C ，∠DAB=∠B=30°. (1)直线BD 是否与⊙O 相切？为什么？ (2)连接CD ，若CD=5，求AB 的长.解答：（1）直线BD 与⊙O 相切．如图连接OD ，CD ， ∵∠DAB=∠B=30°，∴∠ADB=120°， ∵OA=OD ，∴∠ODA=∠OAD=30°，∴∠ODB=∠ADB ﹣∠ODA=120°﹣30°=90°． 所以直线BD 与⊙O 相切．（2）连接CD ，∠COD=∠OAD+∠ODA=30°+30°=60°， 又OC=OD ，∴△OCD 是等边三角形，即：OC=OD=CD=5=OA ，∵∠ODB=90°，∠B=30°，∴OB=10，∴AB=AO+OB=5+10=15．12、已知：如图，AB 为⊙O 的直径，⊙O 过AC 的中点D ，DE ⊥BC 于点E ． （1）求证：DE 为⊙O 的切线；（2）若DE =2，tan C =12，求⊙O 的直径．【解析】（1）证明：联结OD ． ∵ D 为AC 中点， O 为AB 中点，∴ OD 为△ABC 的中位线． ∴OD ∥BC ． ∵ DE ⊥BC ， ∴∠DEC=90°.∴∠ODE=∠DEC=90°. ∴OD ⊥DE 于点D. ∴ DE 为⊙O 的切线．（2）解：联结DB ． ∵AB 为⊙O 的直径， ∴∠ADB=90°． ∴DB ⊥AC ． ∴∠CDB=90°. ∵ D 为AC 中点， ∴AB=AC ．在Rt △DEC 中，∵DE=2 ，tanC=12， ∴EC=4tan DEC=. 由勾股定理得：DC=在Rt △DCB 中， BD=tan DC C ⋅ BC=5. ∴AB=BC=5. ∴⊙O 的直径为5.【巩固练习】1．已知⊙O 的半径为10cm ，如果一条直线和圆心O 的距离为10cm ，那么这条直线和这个圆的位置关系为（ ）A. 相离B. 相切C. 相交D. 相交或相离2．如右图，A 、B 是⊙O 上的两点，AC 是⊙O 的切线，∠B=70°，则∠BAC 等于（ ）A. 70°B. 35°C. 20°D. 10°（第2题） （第3题） （第4题） （第5题）3．如图，PA 切⊙O 于A ，PB 切⊙O 于B ，OP 交⊙O 于C ，下列结论中，错误的是（ ）A. ∠1=∠2B. PA=PBC. AB ⊥OPD. 2PA PC ·PO4．如图，已知⊙O 的直径AB 与弦AC 的夹角为30°，过C 点的切线PC 与AB 的延长线交于P ，PC=5，则⊙O 的半径为（ ）A.335 B. 635 C. 10 D. 55．如图已知AB 是⊙O 的直径，弦AD 、BC 相交于点P ，那么AB ︰CD 等于∠BPD 的（ ）A. 正弦B. 余弦C. 正切D. 余切6．如图A 、B 、C 是⊙O 上三点，AB ⌒的度数是50°，∠OBC=40°，则∠OAC 等于（ ）A. 15°B. 25°C. 30°D. 40°（第6题） （第7题） （第8题） （第9题）7．如图AB 为⊙O 的一条固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C ，作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当C 点在半圆（不包括A 、B 两点）上移动时，点P （ ）A. 到CD 的距离不变B. 位置不变C. 等分DB ⌒D. 随C 点的移动而移动8．如图AD 、AE 和BC 分别切⊙O 于D 、E 、F ，如果AD=20，则△ABC 的周长为（ ） A. 20 B. 30 C. 40 D. 21359．如图在⊙O 中，直径AB 、CD 互相垂直，BE 切⊙O 于B ，且BE=BC ，CE 交AB 于F ，交⊙O 于M ，连结MO 并延长，交⊙O 于N ，则下列结论中，正确的是（ ）A. CF=FMB. OF=FBC. BM⌒的度数是22.5° D. BC ∥MN 10．如图⊙O 的两条弦AB 、CD 相交于点P ，已知AP=2cm ，BP=6cm ，CP ︰PD =1︰3，则DP=_________．（第10题） （第11题） （第12题） （第13题）11．如图AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，P 是BA 的延长线上的点，连结PC ，交⊙O 于F ，如果PF=7，FC=13，且PA ︰AE ︰EB = 2︰4︰1，则CD =_________．12．从圆外一点P 引圆的切线PA ，点A 为切点，割线PDB 交⊙O 于点D 、B ，已知PA=12，PD=8，则=∆∆DAP ABP S S :__________．13．⊙O 的直径AB=10cm ，C 是⊙O 上的一点，点D 平分BC ⌒，DE=2cm ，则AC=_____． 14．如图，AB 是⊙O 的直径，∠E=25°，∠DBC=50°，则∠CBE=________．（第14题） （第15题） （第17题） （第18题）15．点A 、B 、C 、D 在同一圆上，AD 、BC 延长线相交于点Q ，AB 、DC 延长线相交于点P ，若∠A=50°，∠P=35°，则∠Q=________．16.在Rt △ABC 中,∠C=90°，AC=12cm ，BC=5cm ，以点C 为圆心，6cm 的长为半径的圆与直线AB 的位置关系是________.17.如图,在△ABC 中,AB=AC,∠BAC=120°,⊙A 与BC 相切于点D,与AB 相交于点E,则∠ADE 等于___度. 18.如图,PA 、PB 是⊙O 的两条切线,A 、B 为切点,直线OP 交⊙A 于点D 、E,交AB 于C.图中互相垂直的线段有_________(只要写出一对线段即可).19.已知⊙O 的半径为4cm,直线L 与⊙O 相交,则圆心O 到直线L 的距离d 的取值范围是____.E A PO EC D BA20.如图,PA 、PB 是⊙O 的切线,切点分别为A 、B,且∠APB=50°,点C 是优弧AB 上的一点,则∠ACB 的度数为________.（第20题） （第21题） （第22题） （第23题）21.如图,⊙O 为△ABC 的内切圆,D 、E 、F 为切点,∠DOB=73°,∠DOE=120°, 则∠DOF=_______度,∠C=______度,∠A=_______度.22.如图,AB 、AC 为⊙O 的切线,B 、C 是切点,延长OB 到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ ADO 等于_______23.如图AB 是⊙O 的直径，AC 是⊙O 的切线，，A 为切点，连结BC 交圆0于点D,连结AD,若∠ABC ＝45°,则下列结论正确的是（ ）A.AD ＝BCB.AD ＝ACC.AC ＞ABD.AD ＞DC24.如图，在平面直角坐标系中，⊙P 与x 轴相切于原点O ，平行于y 轴的直线交⊙P 于M,N 两点．若点M 的坐标是(2,-1)，则点N 的坐标是（ ）A ．(2,-4) B. (2,-4.5) C.(2,-5) D.(2,-5.5)（第24题） （第25题） （第26题） （第27题）25、如图，AB 是⊙O 的直径，AD 是⊙O 的切线，点C 在⊙O 上，BC ∥OD ，AB ＝2,OD ＝3,则BC 的长为（ ）A ．B ． CD26、已知圆O 的半径为R ，AB是圆O 的直径，D 是AB 延长线上一点，DC是圆O 的切线，C 是切点，连结AC ，若∠CAB ＝30°，则BD 的长为（ ）A ．BC ．D 27、如图，在平面直角坐标系中，⊙A 与y 轴相切于原点O ，平行于x 轴的直线交⊙A 于M 、M 两点，若点M 的坐标是（-4,-2），则点N 的坐标为（ ）A ．（-1,-2）B ．（1,2）C ．（-1.5,-2）D ．（1.5,-2）PO C BA212123322R R R28、如图，AB 是圆O 的直径，AC 是圆O 的切线，A 为切点，连结BC 交圆于点D ，连结AD ，若∠ABC ＝45°，则下列结论正确的是（ ）A ．B ．C ．D ．（第28题） （第29题） （第30题） （第31题）29、如图，AB 是⊙O 的直径，⊙O 交BC 的中点于D,DE ⊥AC 于E,连接AD,则下列结论正确的个数是( ）①AD ⊥BC ②∠EDA ＝∠B ③OA ＝AC ④DE 是⊙O 的切线A ．1 个B ．2个C ．3 个D ．4个30、一个钢管放在V 形架内，右图是其截面图，O 为钢管的圆心．如果钢管的半径为25 cm ，∠MPN ＝60︒，则OP ＝( )A ．50 cmB ．25cm C ．cm D ．50cm 31、如图，DB 为半圆的直径，A 为BD 延长线上一点，AC 切半圆于点E ，BC ⊥AC 于点C ，交半圆于点 F ．已知BD ＝2，设AD ＝x ，CF ＝y ，则y 关于x 的函数解析式是 ．32、如图， AB 与⊙O 相切于点B ，线段OA 与弦BC 垂直于点D ，∠AOB ＝60°，BC ＝4cm ，则切线AB ＝ cm.（第32题） （第33题） （第34题） （第35题）33、如图，直线AB 切⊙O 于C 点，D 是⊙O 上一点，∠EDC ＝30º，弦EF ∥AB ，连结OC 交EF 于H 点，连结CF ，且CF ＝2，则HE 的长为_________．34、如图，点A 、B 、C 在⊙O 上，切线CD 与OB 的延长线交于点D ，若∠A ＝30°，CD ＝，则⊙O 的半径长为 ．35、如图，在中，，与相切于点，且交于两点，则图中阴影部分的面积是 （保留）．O 12AD BC =12AD AC =AC AB >AD DC >12333503第19题图ABC DO32ABC △120AB AC A BC =∠==，°，A ⊙BC D AB AC 、M N 、π36、如图，⊙O 内切于△ABC ，切点分别为D ，E ，F .∠B ＝50°，∠C ＝60°，连结OE ，OF ，DE ，DF ，则∠EDF 等于( )A ．40°B ．55°C ．65°D ．70°（第36题） （第73题） （第38题）37、如图，一个边长为4 cm 的等边三角形ABC 的高与⊙O 的直径相等．⊙O 与BC 相切于点C ，与AC 相交于点E ，则CE 的长为________cm.38、如图，直线l 与半径为4的⊙O 相切于点A ，P 是⊙O 上的一个动点(不与点A 重合)，过点P 作PB ⊥l ，垂足为B ，连结PA .设PA ＝x ，PB ＝y ，则x －y 的最大值是________．39、如图，AB 是半圆O 的直径，C 为半圆上一点，过C 作半圆的切线，连接AC, 作直线AD ，使∠DAC=∠CAB ，AD 交半圆于E,交过C 点的切线于点D. (1)试判断AD 与CD 有何位置关系,并说明理由; (2)若AB=10,AD=8,求AC 的长.40、如图，点A ，B ，C 在半径为8的⊙O 上，过点B 作BD ∥AC ，交OA 延长线于点D ，连结BC ，且∠BCA ＝∠OAC ＝30°.(1)求证：BD 是⊙O 的切线； (2)求图中阴影部分的面积．答案：8、据切线长定理有AD=AE，BE=BF，CD=CF；则△ABC的周长=AB+BC+AC=AB+BF+CF+AC=AB+BE+AC+CD=AD+AE=2AD=40．故选C．9、解：A错，F显然不是弦的平分点；B错，F不是半径的中点；C错，M点平分应为45°；D对，∵BE为圆O的切线，∴BE⊥AB，∵CD⊥AB，∴BE∥CD，∴∠BEF=∠DCF，∵BC=BE，∴∠BCE=∠BEF，∴∠BCE=∠DCF，∵OC=OM，∴∠DCF=∠CMN，∴∠BCE=∠CMN，∴BC∥MN．故选D．10、解：如图利用相交弦定理可知：11、根据割线定理，PF*PC=PA*PB，设EB=X则PA=2X，AE=4X，PB=7X7*（7+13）=2X*7X，X2=10在三角形PCE中，CE2=PC2-PE2=400-360=40，CD=2CE=10412、由切割线定理可得PA2=PD×PB，∵PA=12，PD=8 ∴PB=18．由弦切角和公共角易知△PAD∽△PBA．∴S△PAD：S△PBA=PA2：PB2=4：9．⌒，∴OD平分BC，∴OE为△ABC的中位线，13、∵点D平分BC又∵⊙O的直径AB=10cm，∴OD=5cm，DE=2cm，∴0E=3cm，则弦AC=6cm．故答案为6cm．14、连接AC，∵∠DBA和∠DCA都为AD所对的圆周角，∴∠DBA=∠DCA，∵AB为⊙O的直径，∴∠BCA=90°，∴∠CBA+∠CAB=90°，∵∠CAB=∠E+∠DCA，∴∠CBD+∠DBA+∠E+∠DBA=90°，∵∠E=25°，∠DBC=50°，∴∠DBA=7.5°，∴∠CBE=∠DBA+∠DBC=57.5°15、∠A=50°,故∠BCD=130°（因为是圆,同弧的角互补)，由P=35°计得∠CDQ=85°,故可以计出∠Q=45°.16.相交 17.60 18.如OA⊥PA,OB⊥PB,AB⊥OP等. 19.0≤d<4. 20.65°21. 146°,60°,86° 22.64°23、【答案】Ａ 24、【答案】A 25、【答案】A 26、【答案】C27、【答案】C 28、【答案】A 29、【答案】D 30、【答案】A31、 32、【答案】433、【答案】34、【答案】2．3536、B 由∠B ＝50°，∠C ＝60°可求出∠A ＝70°，则易求得∠EOF ＝110°，∴∠EDF ＝12∠EOF ＝55°.37、过O 作OF ⊥AC 于F ，连结OC ，如图．则CE ＝2CF .根据△ABC 为等边三角形，且边长为4 cm ，易求得它的高为2 3 cm ，即OC ＝ 3 cm.∵BC 与⊙O 相切，∴∠OCB ＝90°.又∠ACB ＝60°，∴∠OCF ＝30°.3π3在Rt△OFC中，可得CF＝OC·cos 30°＝3×32＝32(cm)，故CE＝2CF＝3 cm.38、如图，连结OA，过点O作OC⊥AP于点C，所以∠ACO＝90°，AC＝12AP.易证△OAC∽△APB，所以OA AP ＝ACPB，即4x＝x2y，所以y＝x28.所以x－y＝x－x28＝－18(x－4)2＋2，所以x－y的最大值是2.39.(1)AD⊥CD.理由:连接OC,则OC⊥CD.∵OA=OC,∴∠OAC=∠OCA,又∠OAC= ∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∴AD⊥CD.(2)连接BC,则∠ACB=90°由(1)得∠ADC=∠ACB,又∠DAC=∠CAB.∴△ACD∽△ABC,∴AC ADAB AC=,即AC2=AD·AB=80,故40、22．(1)证明：如图，连结OB，交CA于点E.∵∠C＝30°，∠C＝12∠BOA，∴∠BOA＝60°.∵∠OAC＝30°，∴∠AEO＝90°.∵BD∥AC，∴∠DBE＝∠AEO＝90°.∴OB⊥BD.∴BD是⊙O的切线．(2)解：∵AC∥BD，∴∠D＝∠OAC＝30°.∵∠OBD＝90°，OB＝8，∴BD＝3OB＝8 3.∴S阴影＝S△BDO－S扇形AOB＝12×8×83－60·π×82360＝323－32π3.。
弦切角定理怎么证明
弦切角定理怎么证明弦切角定理是几何学中一个基本的定理，它描述了一个弦与其所对的角的关系。
根据弦切角定理，一个弦所对的角等于其对应弧所对的角等于该弦所夹的两个弧的角和的一半。
为了证明弦切角定理，我们可以利用以下步骤：步骤1: 假设在一个圆上有一个弦AB，它所对的角为∠ACB。
我们需要证明∠ACB = 1/2(∠AOB + ∠APB)。
步骤2: 通过圆心O作弦AB的垂线，交弦AB于点P，并延长OP使其与圆相交于点C。
步骤3: 由于AO = OB（弦AB的中垂线），所以∠AOP = ∠BOP = α。
同时，由于∠OCP是弧APB所对的角，根据圆心角定理，我们知道∠OCP = 1/2∠APB = β。
步骤4: 观察三角形ACP和BCP。
根据直角三角形的定义，我们知道∠ACP = 90° - α，∠BCP = 90° - α。
步骤5: 由于三角形ACP和BCP的两个角分别等于∠ACB的两个角，根据三角形角和定理，我们可以得到∠ACB = ∠ACP + ∠BCP = (90° - α) + (90° - α) = 180° - 2α。
步骤6: 同时，我们可以通过两个角β和∠OCP的和来计算∠AOB。
根据直角三角形定义，我们知道∠OCP = 90° - β。
因此，∠AOB = ∠AOP + ∠BOP + ∠OCP = α + α + (90° - β) = 180° - 2β。
步骤7: 根据步骤5和步骤6的结果，我们可以得到∠ACB = 1/2 (∠AOB + ∠APB)。
这就证明了弦切角定理。
弦切角定理在几何学中具有广泛的应用，特别是在证明和解决与圆相关的问题时非常有用。
它不仅可以帮助我们计算弦所对的角，还可以用于证明弦所夹的两个弧的角和等于360°。
九年级数学弦切角、相交弦定理、割线定理、切割线定理首师大版知识精讲
初三数学弦切角、相交弦定理、割线定理、切割线定理首师大版【同步教育信息】一. 本周教学内容：弦切角、相交弦定理、割线定理、切割线定理（一）弦切角：1. 定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
满足三个条件：（1）顶点在圆上；（2）一边和圆相交；（3）一边和圆相切。
判断下列图形中的∠BAC是不是弦切角：图A中，缺少“顶点在圆上”的条件；图B中，缺少“一边和圆相交”的条件；圆C中，缺少“一边和圆相切”的条件；圆D中，缺少“顶点在圆上”和“一边和圆相切”两个条件。
所以，图中的∠BAC都不是弦切角。
2. 分类（以圆心的位置分）：（1）圆心在角的外部；（2）圆心在角的一边上；（3）圆心在角的内部。
3. 弦切角的度理定理：弦切角的度数等于它所夹的弧的度数的一半。
推论1：弦切角定理：弦切角等于它所夹的弧对的圆周角。
推论2：在同圆或等圆中，如果两个弦切角所夹的弧相等，那么这两个弦切角也相等。
（二）相交弦定理圆的两条弦相交，被交点分成的两条线段长的积相等。
如图1（1），在⊙O中，AB、CD相交于点P，则PA·PB＝PC·PD。
（三）割线定理从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。
如图1（3），有PA·PB＝PC·PD。
（四）切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。
如图1（4），有PA2＝PC·PD。
当点P从圆内运动到圆上、圆外时（从图1（1）到图1（3）），总有PA·PB＝PC·PD，图1（2）中，点B、D与点P重合，PB＝PD＝0，PA·PB＝PC·PD同样成立。
当割线PBA绕着点P旋转到切线PA的位置时，点B与A重合，结论不变，仍有PA·PB ＝PC·PD，此时PA＝PB，所以PA2＝PC·PD。
弦切角定理
弦切角定理弦切角定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
(弦切角就是切线与弦所夹的角）如图所示，直线PT切圆O于点C，BC、AC为圆O的弦，∠TCB，∠TCA，∠PCA，∠PCB都为弦切角。
弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半.已知：AC是⊙O的弦，AB是⊙O的切线，A为切点，弧是弦切角∠BAC所夹的弧.求证：（弦切角定理）证明：分三种情况：（1）圆心O在∠BAC的一边AC上∵AC为直径，AB切⊙O于A，∴弧CmA=弧CA∵为半圆,∴∠CAB=90=弦CA所对的圆周角B点应在A点左侧（2）圆心O在∠BAC的内部.过A作直径AD交⊙O于D,若在优弧m所对的劣弧上有一点E那么，连接EC、ED、EA则有：∠CED=∠CAD、∠DEA=∠DAB∴∠CEA=∠CAB∴（弦切角定理）（3）圆心O在∠BAC的外部,过A作直径AD交⊙O于D那么∠CDA+∠CAD=∠CAB+∠CAD=90∴∠CDA=∠CAB∴（弦切角定理）切线长定理切线长的概念．如图，P是⊙O外一点，PA，PB是⊙O的两条切线，我们把线段PA，PB叫做点P到⊙O的切线长．切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．切线长定理推论：圆的外切四边形的两组对边的和相等相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等。
（经过圆内一点引两条弦，各弦被这点所分成的两段的积相等）相交弦定理说明：若弦AB、CD交于点P则PA·PB=PC·PD（相交弦定理）推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项若AB是直径，CD垂直AB于点P，则PC2=PA·PB（相交弦定理推论）割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等。
如图直线ABP和CDP是自点P引的⊙O的两条割线，则PA·PB=PC·PD证明:连接AD、BC∵∠A和∠C都对弧BD∴由圆周角定理，得∠A=∠C又∵∠APD=∠CPB∴△ADP∽△CBP∴AP:CP=DP:BP, 也就是AP·BP=CP·DP切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。
弦切角定理
又∵⊙O切BC于D, ∴∠FDC= ∠DAC. ∴∠FDC= ∠EFD
∴ EF∥BC
E B
A
O F
D
C
课堂练习：
1.如图，AC是⊙O的弦，BD切⊙O于C， 则图中弦切角有 4 个.
证明：连接BC． ∵AB是⊙O的直径,
B O
∴ ∠ACB＝900. ∴ ∠B +∠CAB＝900.
∵AD⊥CE, ∴ ∠ADC＝900.
A
E
C
D
∴ ∠ACD +∠DAC＝900.
又∵AC是弦,且直线CE和⊙O切于点 C, ∴ ∠ACD =∠B.
∴ ∠DAC=∠CAB,即AC平分∠BAD.
Байду номын сангаас
例2: 如图,AD是△ABC中 ∠BAC的平分线,经过点A 的⊙O与BC切于点D,与AB、 AC分别相交于E、F. 求证： EF∥BC.
若∠AOC=1200,则∠ ACD = 600 .
A O
∠ACD, ∠ACB, ∠OCD, ∠OCB.
BC D
2.如图，直线MN切⊙O于C，AB是⊙O的直
径,若∠ BCM=400,则∠ ABC等于（ B ）
O
A
A.400 B. 500 C. 450 D.600
3.已知⊙O是△ABC的内切圆,D,E,F 为切点,若∠ A: ∠ B: ∠ C=4:3:2,
5.EF切⊙O于点C,过弦AB的两端点A、B E 分别作AE⊥AB,BF⊥AB,OC交AB于点D. 求证:(1)CE·CF=AD·DB;(2)CD2=AE·BF.
C F
弦切角定理及其推论
弦切角定理及其推论定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半.证明：设圆心为O，连接OC，OB,。
∵∠TCB=90°-∠OCB∵∠BOC=180°-2∠OCB∴∠BOC=2∠TCB （定理：弦切角的度数等于它所夹的弧所对的圆心角的度数的一半）∵∠BOC=2∠CAB（同一弧所对的圆心角等于圆周角的两倍）∴∠TCB=∠CAB （定理：弦切角的度数等于它所夹的弧的圆周角）弦切角定理推论：两弦切角所夹的弧相等，则这两个弦切角也相等。
应用举例：第一个算出地球周长的人──埃拉托色尼2000多年前，有人用简单的测量工具计算出地球的周长。
这个人就是古希腊的埃拉托色尼。
埃拉托色尼博学多才，他不仅通晓天文，而且熟知地理；又是诗人、历史学家、语言学家、哲学家，曾担任过亚历山大博物馆的馆长。
细心的埃拉托色尼发现：离亚历山大城约800公里的塞恩城(今埃及阿斯旺附近)，夏日正午的阳光可以一直照到井底，因而这时候所有地面上的直立物都应该没有影子。
但是，亚历山大城地面上的直立物却有一段很短的影子。
他认为：直立物的影子是由亚历山大城的阳光与直立物形成的夹角所造成。
从地球是圆球和阳光直线传播这两个前提出发，从假想的地心向塞恩城和亚历山大城引两条直线，其中的夹角应等于亚历山大城的阳光与直立物形成的夹角。
按照相似三角形的比例关系，已知两地之间的距离，便能测出地球的圆周长。
埃拉托色尼测出夹角约为7度，是地球圆周角(360度)的五十分之一，由此推算地球的周长大约为4万公里，这与实际地球周长(40076公里)相差无几。
他还算出太阳与地球间距离为1.47亿公里，和实际距离1.49亿公里也惊人地相近。
这充分反映了埃拉托色尼的学说和智慧。
埃拉托色尼是首先使用“地理学”名称的人，从此代替传统的“地方志”，写成了三卷专著。
书中描述了地球的形状、大小和海陆分布。
教学内容：弦切角
教学内容：弦切角【学习目标】1．理解弦切角的概念，掌握弦切角定理及其推论，并会运用它们解决有关问题．2．通过弦切角定理的证明，进一步了解分情况证明数学命题的思想和方法．【主体知识归纳】1．顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角．2．弦切角等于它所夹弧所对的圆周角．3．如果两个弦切角所夹的弧相等，那么这两个弦切角也相等．【基础知识讲解】1．弦切角的定义要注意以下两点：(1)角的顶点在圆上，实际上就是角的顶点是圆的一条切线的切点；(2)角的一边是过切点的一条弦(所在的射线)，角的另一边是切线上以切点为端点的一条射线．2．弦切角定理的证明与圆周角定理的证明相仿，也分三种情况．第一种情况是特殊情况，其他两种是一般情况，通过作辅助线可转化为第一种情况．3．弦切角是与圆有关的又一种角，要能在图形中准确地识别，并能正确应用弦切角定理及其推论．它给我们提供了证明角相等的又一个重要依据，它常常与圆周角、圆心角性质联合应用来进行证明、求解．【例题精讲】例1：如图7—170，△ABC中，AD为∠A的平分线，⊙O过A点切BC于D点，且与AB、AC分别交于E、F点．求证：EF∥BC．剖析：欲证EF∥BC，可证同位角相等或内错角相等．由于同位角的关系不易找，所以设想构造内错角，连结DF，因为∠4是弦切角，所以∠4＝∠2,又∠3＝∠1,∠1＝∠2,易得∠3＝∠4．证明：连结DF．BC是切线⇒∠=∠⇒⎪⎪⎭⎪⎪⎬⎫∠=∠∠=∠∠=∠⇒43211324EF∥BC．说明：(1)本例通过作辅助线DF，利用弦切角定理、圆周角定理的推论，证明两个角相等，从而证得两直线平行．体现观察、分析、构造、联想、综合解决问题的几个环节．观察、分析、联想、构造、综合应用是解决几何问题的重要手段．(2)本例中，设AD与EF交于G．有结论：DF2＝DG·DA．例2：如图7—171，已知⊙O的弦AB∥CD，过A点作⊙O的切线交CD的延长线于E．求证：AD2＝DE·AB．剖析：欲证AD2＝DE·AB，需证AD：DE＝AB：AD．因为AB∥CD ，所以＝，知BC＝AD，需证AD：DE＝AB：BC．连结AC，只需证△ABC∽△ADE即可．证明：连结AC，说明：(1)本例是利用弦切角定理和圆内接四边形的性质定理，找出相等的角，然后在证明三角形相似的基础上再证明等积式．这种方法在以后证题时还要用到，要注意掌握．(2)本题还可直接连结BD，证△ABD∽△ADE．例3：如图7—172，AB为⊙O的直径，过B点作⊙O的切线BC，OC交⊙O于点E，AE的延长线交BC于点D．(1)求证：CE2＝CD·CB；(2)若AB＝BC＝2 cm，求：CE、CD的长．剖析：要证CE2＝CD·CB，连结BE，证△CED∽△CBE即可．(1)证明：连结BE．由(1)知CE2＝CD·CB，而CB＝2，∴(5－1)2＝2·CD，∴CD ＝(3－5) cm ．说明：有切线，并需要寻找角的关系时常添辅助线，为利用弦切角定理创造条件．例4：如图7—173，AB 是半圆O 的直径，AC ⊥AB ，BD ⊥AB ，CD 切⊙O 于E ．求证：OE 2＝AC ·BD ．证法一：连结AE 、OE 、BE ．∵AB 是⊙O 的直径，BD ⊥AB ，CA ⊥AB ∴CA 、DB 是⊙O 的切线．∵CD 切⊙O 于E ，∴CE ＝CA ，∴∠CAE ＝∠CEA ．∵OB ＝OE ，∴∠OEB ＝∠OBE ．∵∠CAE ＝∠OBE ，∴∠CAE ＝∠CEA ＝∠OBE ＝∠OEB ．∴△ACE ∽△BOE ． ∴AC OE AEBE =． 同理可证 △AOE ∽△BDE ． ∴OE BD AEBE =． ∴OE BD ACOE =． 则OE 2＝AC ·BD ．证法二：如图7—174，分别延长DC 、BA 交于点P ，连结OE 、AE 、BE ．∵CD 是⊙O 的切线，∴OE ⊥CD 即∠PEO ＝90°又 CA ⊥AB ，DB ⊥AB∴∠CAP ＝∠DBP ＝90°∴Rt △PAC ∽Rt △PEO ∽Rt △PBD ． 则PE PB OE BD PA PE AC OE ==,． ∵PD 是⊙O 的切线，∴∠PEA ＝∠EBP ．∴△PEA ∽△PBE ． ∴PE PB PAPE =． ∴OE BD AC OE =．即OE 2＝AC·BD ．证法三：如图7—175，连结OC 、OD∵CD 、AC 、BD 分别是⊙O 的切线，∴AC ＝CE ，BD ＝DE ，∠1＝∠3，∠2＝∠4，AC ∥BD ．∴∠1＋∠2＝21(∠ACD ＋∠BDC)＝ 21×180°＝90°．∴OE ⊥CD ．∴△OCE ∽△ODE ．∴OE 2＝CE ·BE ．∴OE 2＝AC ·BD ．说明：(1)此例是以切线的判定、切线的性质、弦切角、切线长定理、相似三角形等知识构成的．证法一、证法三中要用到切线长定理及切线的性质，所以要先证明CA 、BD 是圆的切线．(2)本例题的结论是证明线段成比例，前两种证法用“等比代换”，第三种证法是“等线段代换”．思路是这样分析的：结论中的三条线段OE 、AC 、BD 不在一个三角形中，则不能直接用三角形相似来解决．由于图中有和OE 、AC 、BD 相等的线段，所以可以想到用“等线段代换”．例5：如图7—176，设点P 是等边三角形ABC 外接圆上的一点，AP 交BC 于D ．求证：(1)PA ＝PB ＋PC ；(2)PA 2＝BC 2＋PB ·PC ； (3)PC PB PD 111+=．剖析：证明PA ＝PB ＋PC ，可在AP 上截取AE ＝BP ，然后再证明PE ＝PC 即可．由结论(1)可知，要证明PA 2＝BC 2＋PB·PC ，只要证明△PBD ∽△PAC 和△PAB ∽△BAD,得PA·PD ＝PC·PB ，AB 2＝PA·AD ．再结合(1)的结论，即可得证．第(3)问，可先把结论整理变形为PC PB PB PC PD⋅+=1，又由(1)知，PC ＋PB ＝PA ，所以结论可变为PD·PA ＝PB·PC ，由△PBD ∽△PAC 即可证得．证明：(1)在PA 上截取AE ＝PB ，连结EC ．∵△ABC 是等边三角形，∴BC ＝AC ．∵∠CAE ＝∠PBC ，∴△AEC ≌△BPC ．∴CE ＝CP,∴∠CPA ＝∠CBA ＝60°．∴△PCE 是等边三角形．即PC ＝PE ，∴PA ＝PB ＋PC ．(2)∵∠BPD ＝∠APC ＝60°,∠CAP ＝∠CBP,∴△PBD ∽△PAC ． ∴PD PC PB PA =,即PA·PD ＝PB·PC ①又∵∠ABC ＝∠BPA ＝60°,∠BAD ＝∠BAP,∴△PAB ∽△BAD ． ∴AD AB AB PA =,即PA·AD ＝AB 2②①＋②,得PA(PD ＋AD)＝AB 2＋PB·PC又∵PA ＝PD ＋AD ，AB ＝BC ，∴PA 2＝BC 2＋PB ·PC ．(3)由(2)中得，PA ·PD ＝PB ·PC ， ∴PC PB PA PD⋅=1， 由PA ＝PB ＋PC ，代入上式，得PC PB PC PB PD⋅+=1， ∴PC PB PD 111+=．【同步达纲练习】1．选择题(1)AB 是⊙O 的弦，CD 是经过⊙O 上点M 的切线，若CD ∥AB ，则AM 和BM 的关系是A ．AM ＞BMB ．AM ＝BMC ．AM ＜BMD ．无法确定(2)如图7—177，PC 与⊙O 相切于C 点，割线PAB 过圆心O ，∠P ＝40°，则∠ACP 等于A．20°B．25°C．30°D．40°(3)如图7—178，四边形ABCD内接于⊙O，AB是直径，过C点作⊙O的切线MN，若∠BCM＝38°，则∠B等于A．32°B．42°C．52°D．48°(4)如图7—179，△ABC内接于⊙O，PC切⊙O于C点，∠PCD＝20°，则∠A等于A．20°B．30°C．40°D．50°(5)如图7—180，AP平分∠BAC，过P点的切线交AC的延长线于D，若AB＝3，AD＝6，则AP等于A．18B．9C．32D．23(6)如图7—181，PC与⊙O相切于C点，割线PAB过圆心O，若的度数为70°，则∠P等于A．25°B．20°C．35°D．55°(7)如图7—182，PA 、PB 切⊙O 于A 、B ，∠P ＝50°，则∠D 的度数为A ．65°B ．75°C ．40°D ．130°(8)如图7—183，AD 是⊙O 的切线，A 是切点，则∠ACB 、∠BAD 与∠AOB 之间的关系是A ．∠ACB ＝2∠BAD ＝∠AOBB ．∠ACB ＝∠BAD ＝∠AOBC ．∠ACB ＝∠BAD ＝21∠AOBD ．∠AOB ＝21∠ACB ＝21∠BAD(9)如图7—184，△ABC 内接于⊙O ，BC ＝AC ，过B ，C 分别作⊙O 的切线，两条切线相交于P ，∠P ＝80°，则∠ABC 等于A．50°B．65°C．75°D．100°(10)如图7—185，已知PA、PB分别切⊙O于A、B，∠APB＝60°，若PA＝10 cm，则⊙O半径的长为A．3310cmB．5 cmC．103cmD．53cm2．填空题(1)△ABC内接于⊙O，∠B＝25°，∠C＝75°，过A作⊙O的切线交BC延长线于P，则∠P＝________；(2)如图7—186，在⊙O中，AC是弦，AD是切线，CB⊥AD，垂足为B，又CB与⊙O交于E，若AE平分∠BAC，则∠ACB＝________；(3)如图7—187，CD、BC切⊙O于D、B，直径DA的延长线交CB的延长线于E的度数为60°，则∠BDC＝________，∠C＝________，∠E＝________；(4)如图7—188，⊙O是△ABC的内切圆，D、E、F为切点，∠A：∠B：∠C＝4：3：2，则∠DEF ＝________，∠FEC＝________；(5)已知：⊙O的弦AB＝2，BC切⊙O于B，且∠ABC＝30°，则⊙O的直径为________；(6)已知：如图7—189，CD是⊙O的直径，AE切⊙O于点B，DC的延长线交AB于点A，∠A＝20°，则∠DBE＝________；(7)如图7—190，BC 为⊙O 的直径，DE 切⊙O 于A 点，BD ⊥DE ．若∠ABD ＝50°，则的度数为________；(8)如图7—191，已知△ABC 内接于⊙O ，DE ∥BC ，且与⊙O 切于点F ，则图中与∠BFD 相等的角的个数是_________________．(9)如图7—192，已知四边形ABCD 内接于⊙O ，AB 是⊙O 的直径，D 是AC 的中点，ＭC 切⊙O 于点C ，∠BC Ｍ＝30°，则c ｏｓACD ＝_________．3．如图7—193，△ABC 的一边BC 切⊙O 于点F ，点A 在⊙O 上，AB 、AC 与⊙O 分别交于D 、E ，且＝．求证：BF BD AC FC ． 4．如图7—194，⊙O 是△ABC 的外接圆，PD 是⊙O 的切线，与AC 的延长线交于点P ，D 是切点，且BC∥DP．求证：DE·DP＝BD·CP．5．已知：如图7—195，PA、PB分别切⊙O于A、B，∠P＝60°，C为劣弧上任一点，CD∥PA，CE∥PB，D、E在AB上，求证：DE是AD、BE的比例中项．6．如图7—196，已知⊙O中，OB⊥OA，P为OA的延长线上任一点，BP与⊙O相交于点Q，过点Q作⊙O的切线QR，与PO相交于点R．求证：ＲP＝ＲQ．7．如图7—197，已知M是以AB为直径的圆上一动点，过M点的切线与分别过点A、B的AB的垂线AD、BC相交于D、C两点．求证：OA 2＝AD ·BC ．8．如图7—198，AB 是⊙O 的弦，⊙O 的割线交⊙O 于点Ｍ、P ，过点A 、B 分别作AB 的垂线交直线MP 于两点D 和C ，过点M 、P 分别作MP 的垂线交AB 于N 、Q 两点．求证：ＭN ·PQ ＝AD ·BC ．9．如图7—199，延长⊙O 半径OA 至B ，使OA ＝AB ，D Ｔ为⊙O 的切线，T 为切点，BC ⊥D Ｔ于C ，D 、O 、A 共线．求证：∠ACB ＝31∠CAD ．参考答案【同步达纲练习】1．7)A (8)C (9)A2．2 (6)55°(7)100° (8)5个 (9)233．过点B 作AC 的平行线，交AF 的延长线于G ．得AB ＝BG ，FC BF AC BG =． ∴AB BF ACFC =． 由切割线定理，得BF 2＝BD ·BA ． ∴BF BD AC FC =． 4．连结CD ，证△PCD ∽△DEB ．5．连结AC 、BC ．证明△ADC ∽△CEB,得CE AD BECD =． 再证△CDE 是等腰三角形，得CD ＝CE ＝DE ．∴DE 2＝AD ·BE ．6．延长BO 交⊙O 于C ，连结CQ ．利用同角的余角相等，得∠C ＝∠P ．再证∠P ＝∠PQR ．7．连结OD 、OC 、OM ．证OM 2＝DM ·CM ，OM ＝OA ，DM ＝AD ，CM ＝BC ．∴OA 2＝AD ·BC ．8．延长CD 、BA 交于点E ，利用同角的余角相等及平行线性质证角相等．从而证明 △ADM ∽△PQB 及△AMN ∽△PBC ．9．连结OT 、AT ．作AM ⊥DC ，垂足为M ．得OT ∥AM ∥BC ，A 为OB 的中点．∴M 为TC 的中点．∴∠ACB ＝∠MAC ＝∠TAM ＝∠OTA ＝∠OAT ．∴∠ACB ＝31∠CAD ．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
弦切角定理及其推论
定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半.
证明：设圆心为O，连接OC，OB,。
∵∠TCB=90°-∠OCB
∵∠BOC=180°-2∠OCB
∴∠BOC=2∠TCB （定理：弦切角的度数等于它所夹的弧所对的圆心角的度数的一半）∵∠BOC=2∠CAB（同一弧所对的圆心角等于圆周角的两倍）
∴∠TCB=∠CAB （定理：弦切角的度数等于它所夹的弧的圆周角）
弦切角定理推论：两弦切角所夹的弧相等，则这两个弦切角也相等。
应用举例：
第一个算出地球周长的人
──埃拉托色尼
2000多年前，有人用简单的测量工具计算出地球的周长。
这个人就是古希腊的埃拉托色尼。
埃拉托色尼博学多才，他不仅通晓天文，而且熟知地理；又是诗人、历史学家、语言学家、哲学家，曾担任过亚历山大博物馆的馆长。
细心的埃拉托色尼发现：离亚历山大城约800公里的塞恩城(今埃及阿斯旺附近)，夏日正午的阳光可以一直照到井底，因而这时候所有地面上的直立物都应该没有影子。
但是，亚历山大城地面上的直立物却有一段很短的影子。
他认为：直立物的影子是由亚历山大城的阳光与直立物形成的夹角所造成。
从地球是圆球和阳光直线传播这两个前提出发，从假想的地心向塞恩城和亚历山大城引两条直线，其中的夹角应等于亚历山大城的阳光与直立物形成的夹角。
按照相似三角形的比例关系，已知两地之间的距离，便能测出地球的圆周长。
埃拉托色尼测出夹角约为7度，是地球圆周角(360度)的五十分之一，由此推算地球的周长大约为4万公里，这与实际地球周长(40076公里)相差无几。
他还算出太阳与地球间距离为1.47亿公里，和实际距离1.49亿公里也惊人地相近。
这充分反映了埃拉托色尼的学说和智慧。
埃拉托色尼是首先使用“地理学”名称的人，从此代替传统的“地方志”，写成了三卷专著。
书中描述了地球的形状、大小和海陆分布。
埃拉托色尼还用经纬网绘制地图，最早把物理学的原理与数学方法相结合，创立了数理地理学。