新编人教版八年级数学上册1312线段的垂直平分线的性质PPT课件
合集下载
13.1.2线段的垂直平分线的性质课件ppt17197
y
B (-4, 2)
·
5 4 3 2
1 1 2
· C’(-3, -4)
-4 -3 -2 -1 0 -1 -2 -3 -4
思考: 关于y轴 B’ (4, 2) 对称的 点的坐 标具有 x 3 4 5 怎样的 关系?
·
· C(3, -4)
归纳:关于y轴对称的点的坐标的特 点是:
练习:
横坐标互为相反数,纵坐标相等. (简称:纵轴纵相等)
过这个点分别做x轴和y轴的垂线段,垂足分别ห้องสมุดไป่ตู้ 是这个点的横坐标和纵坐标,记做(x,y)。 4、怎样做一个点关于一条直线的对称点?
探究1: 请同学们在直角坐标系中标出下列各点 并画出下列各点关于x轴对称的对称点. A (2,3) B (-4, 2) C(3, - 4)
思考:关于x轴对称的点的坐标具有 怎样的关系?
A
2 3 4 5
B
-4
-3
-2
-1
x
轴对称关系(关于y轴对称)
活动二:
2、已知右边圆脸中眼睛A的坐标 (4,3)嘴角 ) 为( C的 (2,3)B的坐标为( 坐标为( ( 4,1)D的坐标为( (2,1)。 )
5
y
你能根据 轴对称的 性质写出 左边圆脸 的眼睛和 嘴角的坐 标吗?
· · C D · ·
13.1.2线段的垂直平分线的性质
P1 P2 P3 A B
l
线段垂直平分线:
经过线段的中点并且垂直于这条 线段的直线,叫做这条线段的垂 直平分线。
∵直线l是线段AB的垂直平分线
A
o
B
∴AO=BO l⊥AB
l
探索并证明线段垂直平分线的性质
如图,直线l 垂直平分线段AB,P1,P2,P3,…是 l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距 离之间的数量关系. P3 相等. P2 性质1:线段垂直平分线上的点与这条 P1 线段两个端点的距离相等. A B l
B (-4, 2)
·
5 4 3 2
1 1 2
· C’(-3, -4)
-4 -3 -2 -1 0 -1 -2 -3 -4
思考: 关于y轴 B’ (4, 2) 对称的 点的坐 标具有 x 3 4 5 怎样的 关系?
·
· C(3, -4)
归纳:关于y轴对称的点的坐标的特 点是:
练习:
横坐标互为相反数,纵坐标相等. (简称:纵轴纵相等)
过这个点分别做x轴和y轴的垂线段,垂足分别ห้องสมุดไป่ตู้ 是这个点的横坐标和纵坐标,记做(x,y)。 4、怎样做一个点关于一条直线的对称点?
探究1: 请同学们在直角坐标系中标出下列各点 并画出下列各点关于x轴对称的对称点. A (2,3) B (-4, 2) C(3, - 4)
思考:关于x轴对称的点的坐标具有 怎样的关系?
A
2 3 4 5
B
-4
-3
-2
-1
x
轴对称关系(关于y轴对称)
活动二:
2、已知右边圆脸中眼睛A的坐标 (4,3)嘴角 ) 为( C的 (2,3)B的坐标为( 坐标为( ( 4,1)D的坐标为( (2,1)。 )
5
y
你能根据 轴对称的 性质写出 左边圆脸 的眼睛和 嘴角的坐 标吗?
· · C D · ·
13.1.2线段的垂直平分线的性质
P1 P2 P3 A B
l
线段垂直平分线:
经过线段的中点并且垂直于这条 线段的直线,叫做这条线段的垂 直平分线。
∵直线l是线段AB的垂直平分线
A
o
B
∴AO=BO l⊥AB
l
探索并证明线段垂直平分线的性质
如图,直线l 垂直平分线段AB,P1,P2,P3,…是 l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距 离之间的数量关系. P3 相等. P2 性质1:线段垂直平分线上的点与这条 P1 线段两个端点的距离相等. A B l
13.1.2《线段的垂直平分线的性质》PPT课件人教版数学八年级上册

B
∵E是AC上的一点, ∴BE=DE.
在△ABE和△ADE中,∵AB=AD, BE=DE, AE=AE,
∴ △ABE≌△ADE. ∴∠ABE=∠ADE.
课堂小结
线
性质
段
的
垂
判定
直
平
分
尺规
线
作图
线段垂直平分线上的点与这条 线段两个端点的距离相等
与线段两个端点距离相等的点 在这条线段的垂直平分线上
画一个轴对称图形或成轴对称 图形的对称轴
我把线段AB沿着直线l对折,发
现线段P1A与P1B,线段P2A与 A P2B,线段P3A与P3B……都是重
P1 P2 P3
B
合的,因此它们也分别相等.
l
新知探究 知识点1 线段的垂直平分线的性质
线段的垂直平分线的性质:线段垂直平分线上的点与这
条线段两个端点的距离相等.
P
符号表示:如图, 直线l⊥AB,垂足
例1 尺规作图:经过已知直线外一点作这条直线的垂线. 分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴,为此作出到点A,B距离相等的两点,即线段
AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
和点C在AB的两旁; =8 cm.
符号表示:如图,已知线段AB,∵PA=PB,
l
新知探究 知识点3 尺规作图
例1 尺规作图:经过已知直线外一点作这条直线的垂线. 已知:直线AB和AB外一点C(如图). 求作:AB的垂线,使它经过点C.
.C
A
B
例1 尺规作图:经过已知直线外一点作这条直线的垂线.
符号表示:如图,已知线段AB,∵PA=PB,
作法:(1)任意取一点K,使点K C =8 cm.
人教版八级数学上册1312 尺规作图(共13张PPT)

∵ CD=CE
通过折叠,如果这(两)个图形能够互相重合,则这(两)个图形是轴对称的.
常 见 方 法 【想一想】下图中的五角星有几条对称轴?如何作出这些对称轴呢?
(3)用刻度尺先取一对对称点连线的中 为此作出到点A、B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
点,然后作垂线
属于基本作图之一,必须熟练掌握
(1)将图形对折; (2)作出线段AB的垂直平分线l.
特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.
属于基本作图之一,必须熟练掌握
作 对 称 轴 的 用尺规作图; (2) 分析:我们只要连结点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴.
新课讲解
作法:(1)分别以点A和B为圆心,
以大于1 AB的长为半径作弧,
2
两弧交于C、D两点.
A
(2)作直线CD.
CD就是所求作的直线.
C B
D
特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们
也可以用这种方法确定线段的中点.
新课讲解
2 作轴对称图形的对称轴
【想一想】下图中的五角星有几条对称轴?如何作出这些对
对称点A和B,连结AB. 第2课时 线段垂直平分线的有关作图 ∵ CD=CE 思考:为什么直线CF就是所求作直线的垂线? 作法:(1)找出五角星的一对 分析:我们只要连结点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴. 思考:为什么直线CF就是所求作直线的垂线? 特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点. 1.能用尺规作已知线段的垂直平分线.(重点) 【想一想】下图中的五角星有几条对称轴?如何作出这些对称轴呢? 则l就是这个五角星的一条对称轴.
通过折叠,如果这(两)个图形能够互相重合,则这(两)个图形是轴对称的.
常 见 方 法 【想一想】下图中的五角星有几条对称轴?如何作出这些对称轴呢?
(3)用刻度尺先取一对对称点连线的中 为此作出到点A、B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
点,然后作垂线
属于基本作图之一,必须熟练掌握
(1)将图形对折; (2)作出线段AB的垂直平分线l.
特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.
属于基本作图之一,必须熟练掌握
作 对 称 轴 的 用尺规作图; (2) 分析:我们只要连结点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴.
新课讲解
作法:(1)分别以点A和B为圆心,
以大于1 AB的长为半径作弧,
2
两弧交于C、D两点.
A
(2)作直线CD.
CD就是所求作的直线.
C B
D
特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们
也可以用这种方法确定线段的中点.
新课讲解
2 作轴对称图形的对称轴
【想一想】下图中的五角星有几条对称轴?如何作出这些对
对称点A和B,连结AB. 第2课时 线段垂直平分线的有关作图 ∵ CD=CE 思考:为什么直线CF就是所求作直线的垂线? 作法:(1)找出五角星的一对 分析:我们只要连结点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴. 思考:为什么直线CF就是所求作直线的垂线? 特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点. 1.能用尺规作已知线段的垂直平分线.(重点) 【想一想】下图中的五角星有几条对称轴?如何作出这些对称轴呢? 则l就是这个五角星的一条对称轴.
13.1.2.1 线段的垂直平分线的性质 课件(共22张PPT)人教版数学八年级上册

例5:如图,在Rt△ABC中,∠ACB=90°,D是AB上一点, BD=BC,过点D作AB的垂线交AC于点E,连接BE.求证: BE垂直平分CD.
证明:∵∠ACB=90°,DE⊥AB, ∴∠EDB=∠ACB=90°.∵BD=BC,BE=BE, ∴Rt△BED≌Rt△BEC,点B在CD的垂直平分线上, ∴DE=CE,∴点E在CD的垂直平分线上, ∴BE垂直平分CD.
13.1 轴对称
13.1.2线段的垂直平分线的性质
13.1.2.1 线段的垂直平分线的性质
学习目标
1.通过学生自主探究,理解并掌握线段垂直平分线的性质和判定,会用 线段的垂直平分线的性质和判定解决简单的数学问题,培养学生解决问 题的能力.
2.学生经历动手实践、合作交流、演绎推理的过程,培养学生的动手操 作能力和逻辑推理能力.
4.如果将已知、求证换一下位置,还能成立吗?试着探究一下.
如图,已知 PA=PB,
求证:点 P 在 AB 的垂直平分线上.
证明:如图,过点 P 作 AB 的垂线 l 交 AB 于点 C,
在
R
t△PAC
和
Rt△PB
C
中,
PA=PB, CP=CP,
∴R t △PAC≌R t △PB C(H L ).
∴AC=BC.∴直线 l 垂直平分 AB,
∴点 P 在 AB 的垂直平分线上.
小组讨论
1.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平 分线ON交于点O,分别交BC于点D,E,△ADE的周长为5 cm. (1)求BC的长;(2)求证:点O在线段BC的垂直平分线上.
(1)解:∵OM,ON分别是线段AB,AC的垂直平分线, ∴AD=BD,AE=CE.∵△ADE的周长=AD+AE+DE=5 cm, ∴BC=BD+DE+EC=5 cm.
13.1.2线段垂直平分线性质课件(共34张PPT)
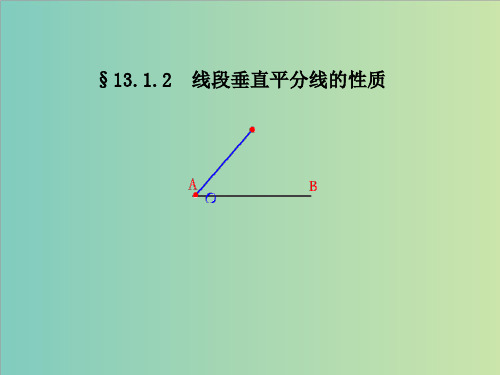
B的距离.你有什么发现?再取几个点试试.你能说明理由吗?
发现: P到A的距离与P到B的距离相等.
P
已知:如图.AC=BC. PC⊥AB,P是MN上任意一点.
求证:PA=PB.
证明:∵MN⊥AB, ∴ ∠PCA=∠PCB=90° 在△APC与△BPC中:
PC=PC(公共边) ∠PCA=∠PCB(已证) AC=BC(已知) ∴△PCA≌△PCB(SAS) ∴PA=PB(全等三角形的对应边相等)
五角星的对称轴有什么特点? 相交于一点.
练习
1.作出下列图形的一条对称轴.和同学比较一下.你们 作出的对称轴一样吗?
练习
2.如图,角是轴对称图形吗?如果是,它的对称轴是什 么?
练习
3.如图,与图形A 成轴对称的是哪个图形?画出它的 对称轴.
A
B
C
D
做一做
1.正方形ABCD边长为a,点E,F分别是对角线BD上的两点, 过点E,F分别作AD,AB的平行线,如图所示,则图中阴影 部分的面积之和等于 1 a 2 .
B A
5.求作一点P,使它和已△ABC的三个顶点 距离相等.
A
·P
B
C
试一试
N
已 知 : P为 M ON内 一 点 。 P与 A关 于 ON对 称 , A
P与 B关 于 OM 对 称 。 若 AB长 为 15cm
求 : PCD的 周 长 .
D P
解: P与A关于ON对称
ON为PA的中垂线(
? …)
F
∴PA=PB 同理:PB=PC
P E
∴PA=PB=PC
A
N
B
结论:三角形三边的垂直平分线交于一 点,并且这点到三个顶点的距离相等.
1312线段的垂直平分线的性质课件

添加 标题
边的垂直平分线性质:垂直平分线上的点 到线段两端点的距离相等,利用这一性质 可以证明等腰三角形的性质。
添加 标题
垂直平分线的性质在三角形中的应用:利用垂直 平分线的性质,可以证明三角形中的中垂线定理, 即三角形中垂线上的点到三角形三个顶点的距离 相等。
添加 标题
垂直平分线的性质在四边形中的应用:利用垂直 平分线的性质,可以证明四边形中的对角线性质, 即四边形中对角线被垂直平分线所截得的线段相 等。
通过线段中点作垂直平分线
连接线段两端点 分别以线段两端点为圆心,以线段长度为半径画圆 画出两个圆的交点 连接交点和线段中点
利用直角三角形的性质作垂直平分线
准备一张直角三角形纸片,并标记直角顶点为A,斜边中点为B。 将纸片沿中线对折,使斜边重合,得到一条折痕。 将纸片展开,再次沿中线对折,使斜边重合,得到另一条折痕。 连接两条折痕的交点,即为垂直平分线的中点。
分别过线段两端作中垂线的垂线
连接垂足,得到垂直平分线
汇报人:
应用:垂直平分线在几何学中有着广泛的应用,例如在三角形、四边形等几何图形中。
垂直平分线的性质
定义:垂直平分线是一条线,它经过某一点并与该点相对的线段垂直。 性质:垂直平分线上的任意一点到线段两端点的距离相等。 定理:垂直平分线上的任意一点到线段两端点的距离是垂直平分线最短的。
应用:在几何学中,垂直平分线是重要的概念,它在解决几何问题时有着广泛的应用。
判定定理的应用
三角形中的垂直平分线:判定三角形中的垂直平分线,并确定垂直平分线上的点到三角形顶 点的距离相等。
圆的垂直平分线:判定圆中的垂直平分线,并确定垂直平分线上的点到圆心的距离相等。
角的平分线:判定角的平分线,并确定角平分线上的点到角的两边距离相等。
线段的垂直平分线的性质(第1课时)人教数学八年级PPT课件

的距离都相等;反过来,与A,B 的距离相
等的点都在直线l上,所以直线l 可以看成与
两点A,B 的距离相等的所有点的集合.
A C
B
探究新知
素养考点 线段垂直平分线的判定定理的应用
例 如图,已知:在△ABC中,AB=AC,O是△ABC内一点, 且OB=OC,求证:AO⊥BC.
证明:∵OB=OC, ∴点O在BC的垂直平分线上. 又AB=AC, ∴点A在BC的垂直平分线上, 即A,O均在BC的垂直平分线上, ∴AO⊥BC.
课堂检测
拓广探索题
如图,已知AB比AC长2 cm,BC的垂直平分线交AB于点D,
交BC于点E,△ACD的周长是14 cm,求AB和AC的长.
解:∵DE垂直平分BC, ∴DB=DC. ∵AC+AD+DC=14 cm, ∴AC+AD+BD=14 cm. 即AC+AB=14 cm. 设AB=x cm,AC=y cm.
求证:PA =PB.
l
P
A
C
B
探究新知
证明:∵ l⊥AB,
l
∴ ∠PCA =∠PCB.
P
又 AC =CB,PC =PC,
A
∴ △PCA ≌△PCB(SAS).
C
B
∴ PA =PB.
用符号语言表示为:∵ CA =CB,l⊥AB,∴ PA =PB.
探究新知
归纳总结
线段垂直平分线的性质: 线段垂直平分线上的点到这条线段两个端
B.10 cm
C.15 cm
D.17.5 cm
课堂检测
2. 如图,在△ABC中,D为BC上一点,且BC=BD+AD,则 点D在线段 _____A_C____ 的垂直平分线上. 解析:∵BC=BD+AD, 又∵BC=BD+DC, ∴AD=DC. ∴点D在线段AC的垂直平分线上.
人教版八年级上册13.1.2线段的垂直平分线的性质(第一课时)课件

A
D E
B
C
例 已知,如图,AM是△ABC的角平分线,MF是线段 BC的垂直平分线,MD⊥AB于D,ME⊥AE于E, 求证:BD=CE.
A
分析:由AM是△ABC的角平分线
MD⊥AB于D,ME⊥AE于E可知,
D F
B
M
MD=ME. C 由MF是线段BC的垂直平分线可知, E 要连MB,MC,有MB=MC.
A
分析:由题意可知AB=AC=CE.
而DE=CE+DC
=AB+BD
B
DC
E
例 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上. (1)AB,AC,CE的长度有什么关系?AB+BD与DE有什么 关系?
A
解: AD BC, BD DC,
AB AC.
B
DC
E
∵点C在AE的垂直平分线上,
AC CE.
进而可证Rt△BDM≌Rt△CEM(HL). 因此,BD=CE.
证明:连接MB,MC,
A
∵AM是△ABC的角平分线,
MD⊥AB,ME⊥AE,
D
∴MD=ME.
F
C
B
∵MF是线段BC的垂直平分线,
E
∴MB=MC. ∵MD⊥AB,ME⊥AE, ∴∠BDM=∠CEM=90°. ∵在Rt△BDM和Rt△CEM中
用刻度尺和三角板画出线段AB的垂直平分线,在直线l上任取一些点P1,P2,P3,…分别量一量P1,P2,P3 ,…到点A与点B的距离,你有什么发现?
∵在Rt△BDM和Rt△CEM中
线段垂直平分线上的点与这条线段两个端
如图,已知l⊥AB,垂足为C,AC=CB,点P在直线l上,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线段垂直平分线上的点与这条 线段两个端点的距离相等.
A
P3 P2
P1 B
l
探索并证明线段垂直平分线的性质
命题:“线段垂直平分线上的点到线段两端点的距
离相等.”
已知:如图,直线l⊥AB,垂足为C,AC =CB,点
P 在l 上.
求证:PA =PB.
l
P
A
C
B
探索并证明线段垂直平分线的性质
证明:∵ l⊥AB,
垂直平分线上,AB,AC,CE 的长度有什么关系?
AB+BD与DE 有什么关系?
解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平 分线上,
A
∴ AC =CE.
∴ AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.B D C
A
D
E
P C
B
证明:连结PB。
A D
∵ PD是AB的垂直平分线(已知)
∴ PA=PB(线段的垂直平分线 上的点和这条线段的两个端点的 B 距离相等)
∵ PA=PC(已知)
等的点,在这条线段的垂直平分
线上.
A C
B
探索并证明线段垂直平分线的判定
你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点?
这些点能组成什么几何图形?
P
在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、 A
E
即 AB +BD =DE .
例1、如图,在△ABC中,ED垂直平分AB, 1) 若BD=10,则AD= 10 。 2) 若∠A=50°,则∠ABD= 50°。 3) 若AC=14,△BCD的周长为24,则BC= 10 。
生活中的数学
A
在某高速公路L的同侧,有两个工厂A、B,为了便
于两厂的工人看病,市政府计划在公路边上修建一所医 院,使得两个工厂的工人都没意见,问医院的院址应选 在何处?你的方案是什么?
• 线段垂直平分线的判定定理的已知条件是一个点与一线 段两端点的距离相等,结论是这个点在线段的垂直平分 线上.
• 线段垂直平分线的性质是解决线段相等问题的一种重要 方法;线段垂直平分线的判定可用来证明两线的位置关 系(垂直平分).
A
1、∵ AD为BC的中垂,线
B
∴AB=AC( 线__段_垂__直__平_分__线__上_的__点__与_这__条__线_段)
如图,直线l 垂直平分线段AB,P1,P2,P3,…是 l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距 离之间的数量关系.
P3
相等.
P2
你能用不同的方法验证
这一结论吗?
A
P1 B
l
探索并证明线段垂直平分线的性质
请在图中的直线l 上任取一点,那么这一点与线段 AB 两个端点的距离相等吗?
P
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
A C
B
∴ 点P 在线段AB 的垂直平分线上.
探索并证明线段垂直平分线的判定
用数学符号表示为:
∵ PA =PB,
P
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相
人教版八年级数学 上册
13.1 轴对称 (第2课时)
课件说明
• 学习目标: 1.理解线段垂直平分线的性质和判定. 2.能运用线段垂直平分线的性质和判定解决实际问 题. 3.会用尺规经过已知直线外一点作这条直线的垂线, 了解作图的道理.
• 学习重点: 线段垂直平分线的性质.ຫໍສະໝຸດ 索并证明线段垂直平分线的性质B
L
高速公路
探索并证明线段垂直平分线的判定
反过来,如果PA =PB,那么点P 是否在线段AB 的 垂直平分线上呢?
P 点P 在线段AB 的垂直平分线上.
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.
A C
B
探索并证明线段垂直平分线的判定
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
M
A
D
B
N
课堂练习
练习3 如图,AB =AC,MB =MC.直线AM 是线段
BC 的垂直平分线吗? A
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC, ∵ 点M 在BC 的垂直平分线上,
M
∴ 直线AM 是线段BC 的垂直
平分线.
B
D
C
知识应用
在⊿ABC中,PD,PE分别是AB,AC的垂 直平分线,并相交于点P,求证:点P也在 BC的垂直平分线上。
C
B
B 的距离相等的所有点的集合.
辨析:
性质:在线段垂直平分线上的点到线段两个端 点距离都相等。 判定:与线段两个端点距离相等的点都在线段 的垂直平分线上。
线段垂直平分线的集合定义:
线段垂直平分线可以看作是与 线段两个端点距离相等的所有点的 集合。
线段垂直平分线的性质与判定定理的区别
• 二者是互逆定理,线段垂直平分线的性质定理的已知条 件是线段垂直平分线,结论是垂直平分线上的点与这条 线段两端点的距离相等.
线段垂直平分线的性质: 线段垂直平分线上的点与这条线段两个端点的距离
相等.
提示:这个结论是经常用来证明 两条线段相等的根据之一.
课堂练习
练习1 如图,在△ABC 中,BC =8,AB 的中垂线 交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等 于___8___.
A
B
DE
C
课堂练习
练习2 如图,AD⊥BC,BD =DC,点C 在AE 的
∴ ∠PCA =∠PCB= 90° .
在△APC与△BPC中
PC=PC(公共边) ∠PCA=∠PCB(已证)
AC=BC(已知)
∴ △PCA ≌△PCB(SAS).
l
∴ PA =PB(全等三角形的对应边相等). P
用符号语言表示为:
∵ CA =CB,l⊥AB,
A
∴ PA =PB.
C
B
探索并证明线段垂直平分线的性质
两个端点的距离相等.
D
C
2、∵ _______A_B__=__A_C__________ ,
∴ A在线段BC的中垂线上(与_一__条__线__段__两__个__端__点__距__离__相等的
_______ )
点,在这条线段的垂直平分线上。
3、如图, NM是线段AB的中垂线, 下列说法正确的有:①②③。 ①AB⊥MN,②AD=DB, ③ MN⊥AB, ④MD=DN,⑤AB是
