实验1 一元函数的图形
实验库1:一元函数微分学2

实验一 一元函数微积分学实验2 极限与连续(基础实验)实验目的 通过计算与作图, 从直观上揭示极限的本质,加深对极限概念的理解. 掌握用Mathematica 画散点图, 以及计算极限的方法. 深入理解函数连续的概念,熟悉几种间断点的图形 特征,理解闭区间上连续函数的几个重要性质.1、作散点图例2.1 (教材 例2.1) 分别画出坐标为)10,,2,1(),4,(),,(3222 =+i i i i i i 的散点图, 并画出折线图. 分别输入命令t1=Table[i^2,{i,10}]; g1=ListPlot[t1,PlotStyle->PointSize[0.02]]; g2=ListPlot[t1,PlotJoined->True];Show[g1,g2]; t2=Table[{i^2,4i^2+i^3},{i,10}];g1=ListPlot[t2,PlotStyle->PointSize[0.02]]; g2=ListPlot[t2,PlotJoined->True];Show[g1,g2]; 则分别输出所求图形.例2.2 画出前25个素数的散点图. 输入命令Table[Prime[n],{n,25}];ListPlot[Table[Prime[n],{n,25}],PlotStyle->PointSize[0.015]];则分别输出所求图形.2、数列极限的概念例2.3 观察数列}{n n 的前100项变化趋势. 输入命令t=N[Table[n^(1/n),{n,1,100}]]; ListPlot[t,PlotStyle->PointSize[0.015]];则分别输出所求图形. 从图中可看出, 这个数列似乎收敛于1.下面我们以数值的方式来说明这一变化趋势. 输入以下语句, 并观察其数值结果.m=2;xn=0;For[i=1,i<=1000,i+=50,If[Abs[xn-1]>10^(-m),xn=N[n^(1/n),20]]]; Print[i, " ",xn];设该数列收敛于),0(1≥+=u u A 不妨取,102-=u 下面考察n n 与A 的接近程度. 输入以下Mathematica 语句.u = 10^9(-2); A = 1 + u; m = 5; n = 3; an = Sqrt[3]; While[Abs[A-an] >= 10^(-m), n++; an = N[n^(1/n)]]; Print[" n=", n, " an=", an, "|A-an|=", Abs[A - an]]; 结果表明: 当01.1,651==n a n 时, n a 与2101-+的距离小于.105-例2.4 观察Fibonacci 数列的变化趋势.Fibonacci 数列具有递推关系,,1,12110--+===n n n F F F F F 令1+=n nn F F R . 输入命令fn1=1;fn2=1;rn=1; For[i=3,i<=14,i++,Fn=fn2+fn1;fn2=fn1;fn1=fn;rn=N[fn2/fn1,20];dn=rn-rn1; rn1=rn;Print[i, " ", fn1, " ", rn, " ",dn]];其中第二列给出了Fibonacci 数列的前14项, 第3列给出了n R 的值, 由第4列可以看出, .01→--n n R R 我们也可以用散点图来观察Fibonacci 数列的变化趋势如图所示, 输入命令Clear[f]; f[n_]:= f[n-1]+f[n-2];f[0]=1;f[1]=1;fab20=Table[f[i],{i,0,20}];ListPlot[fab20,PlotStyle ->PointSize[0.02]]; Infab20=Log[fab20];ListPlot[Infab20,PlotStyle-> PointSize[0.02]];则输出所求散点图.为了更好地观察数列的变化趋势, 我们可以利用Mathematica 的动画功能来进一步观察数列随着n 的增大的变化趋势.例2.5 通过动画观察当∞→n 时数列21n a n =的变化趋势.输入Clear[tt];tt={1,1/2^2,1/3^2}; Do[tt=Append[tt,N[1/i^2]];ListPlot[tt,PlotRange->{0,1},PlotStyle->PointSize[0.02]],{i,4,20}]则输出所求图形动画. 从图中可以看出所画出的点逐渐接近于x 轴.例2.6 研究极限.1512lim 33++∞→n n n输入Print[n, " ", Ai, " ",0.4-Ai];For[i=1, i<=15, i++,Aii=N[(2 i^3+1)/(5 i^3+1),10]; Bii=0.4-Aii; Print[i, " ", Aii, " ", Bii]]则输出n Ai 0.4-Ai 1 0.5–0.1 2 0.414634 –0.0146341 3 0.404412 –0.00441176 4 0.401869 –0.00186916 5 0.400958 –0.000958466 6 0.400555 –0.000555042 7 0.40035 –0.00034965 8 0.400234 –0.000234283 9 0.400165 –0.000164564100.40012–0.00011997611 0.40009 –0.000090144212 0.400069 –0.0000694364 13 0.400055 –0.000054615 14 0.400044 –0.0000437286 150.400036–0.0000355534观察所得数表. 第一列是下标n . 第二列是数列的第n 项,151233++n n 它与0.4越来越接近. 第三列是 数列的极限0.4与数列的项的差, 逐渐接近0.再输入fn=Table[(2 n^3+1)/(5 n^3+1),{n,15}]; ListPlot[fn,PlotStyle->{PointSize[0.02]}]则输出散点图. 观察所得散点图, 可见表示数列的点逐渐接近于直线.4.0=y注:命令For 的格式见项目二中实验1的基本命令.3、函数的极限例2.7 在区间]4,4[-上作出函数xx xx x f --=339)(的图形, 并研究)(lim x f x ∞→ 和 ).(lim 1x f x →输入命令Clear[f];f[x_]=(x^3-9x)/(x^3-x); Plot[f[x],{x,-4,4}];则输出)(x f的图形. 从图可猜测 )(lim ,9)(lim 1x f x f x x →→=不存在.例2.8 观察函数x x x f sin 1)(2=当+∞→x 时的变化趋势. 取一个较小的区间[1, 10], 输入命令f[x_]=Sin[x]/x^2;Plot[f[x],{x,1,20}];则输出)(x f 在这一区间上的图形. 从图中可以看出图形逐渐趋于0. 事实上, 逐次取更 大的区间, 可以更有力地说明当+∞→x 时, .0)(→x f作动画: 分别取区间]100,10[,],20,10[],15,10[ 画出函数的图形, 输入以下命令:i=3;While[i<=20,Plot[f[x],{x,10,5*i},PlotRange->{{10,100},{-0.008,0.004}}];i++]则输出17幅图, 点黑右边的线框, 并选择从前向后的播放方式播放这些图形, 可得函数x x x f sin 1)(2=当∞→x 时变化趋势的动画, 从而可以更好地理解此时函数的变化趋势. 例2.9 考虑函数.arctan x y = 输入Plot[ArcTan[x],{x,-50,50}]则输出该函数的图形. 观察当∞→x 时, 函数值的变化趋势.分别输入Limit[ArcTan[x],x->Infinity,Direction->+1] Limit[ArcTan[x],x->Infinity,Direction->-1]输出分别为2π与.2π- 考虑函数.sgn x y =分别输入Limit[Sign[x],x->0,Direction->+1] Limit[Sign[x],x->0,Direction->-1]输出分别为-1与1.4、两个重要极限例2.10 考虑第一个重要极限.sin lim0xxx →输入Plot[Sin[x]/x,{x,-Pi,Pi}]则输出函数xxsin 的图形. 观察图中当0→x 时, 函数值的变化趋势. 输入 Limit[Sin[x]/x,x->0]输出为1, 结论与图形一致.例2.11 研究第二个重要极限.11lim xx x ⎪⎭⎫ ⎝⎛+∞→输入Limit[(1+1/n)^n,n->Infinity]输出为e. 再输入Plot[(1+1/x)^x,{x,1,100}]则输出函数xx ⎪⎭⎫ ⎝⎛+11的图形. 观察图中函数的单调性. 理解第二个重要极限.11lim e x xx =⎪⎭⎫ ⎝⎛++∞→4、无穷大例2.12 考虑无穷大. 分别输入Plot[(1+2 x)/(1-x),{x,-3,4}] Plot[x^3-x,{x,-20,20}]则分别输出两个给定函数的图形. 在第一个函数的图形中,1→x 时函数的绝对值无限增大,在第 二个函数的图形中,∞→x 时函数的绝对值在无限增大. 输入Limit[(1+2x)/(1-x),x->1]Mathematica 输出的是-∞. 这个结果应该是右极限.例2.13 考虑单侧无穷大. 分别输入Plot[E^(1/x),{x,-20,20},PlotRange->{-1,4}] Limit[E^(1/x),x->0,Direction->+1] Limit[E^(1/x),x->0,Direction->-1]则输出所给函数的图形、左极限0和右极限值∞. 再输入Limit[E^(1/x),x->0]Mathematica 的输出仍然为∞.这又是右极限(同上例). 因此在没有指明是左右极限时, 命令Limit 给出的是右极限.例2.14 输入Plot[x+4*Sin[x],{x,0,20 Pi}]则输出所给函数的图形. 观察函数值的变化趋势. 当∞→x 时, 这个函数是无穷大. 但是, 它并不是单调增加. 于是, 无穷大并不要求函数单调.例2.15输入Plot[x*Sin[x],{x,0,20 Pi}]则输出所给函数的图形.观察图中函数的变化趋势. 这个函数无界, 但是, 当∞→x 时, 这个函数不是无穷大. 即 趋向于无穷大的函数当然无界, 而无界函数并不一定是无穷大.5、连续与间断例2.16 考察函数x x f sin )(=在5=x 处的连续性.选取几个},{n x 考察当5→n x 时, n x sin 的变化趋势, 依次取,11ln ,1)1(5,155nn n n n n x n x n x ⎪⎭⎫ ⎝⎛+=-+=+=当∞→n 时, 他们的极限均为5.输入命令g1 = ListPlot[Table[Sin[5 + 1/n], {n, 1, 1000, 5}],PlotStyle -> RGBColor[1, 0, 0]]; g2 = ListPlot[Table[Sin[5 + (-1)^n/Sqrt[n]], {n, 1, 1000, 5}],PlotStyle -> RGBColor[0, 1, 0]];g3 = ListPlot[Table[Sin[5*n*Log[(1 + 1/n)]], {n, 1, 1000, 5}],PlotStyle -> RGBColor[0, 0, 1]];g = Show[g1, g2, g3];则输出相应的)sin ,(n n x x 的散点图. 由图可看出它们趋于同一极限值.例2.17 观察可去间断. 分别输入Plot[Tan[x]/x,{x,-1,1}] Plot[(Sin[x]-x)/x^2,{x,-Pi,Pi}]则输出所给函数的图形. 从图可见,0=x 是所给函数的可去间断点.11例2.18 观察跳跃间断. 分别输入Plot[Sign[x],{x,-2,2}]Plot[(E^(1/x)-1)/(E^(1/x)+1),{x,-2,2}]则分别输出所给函数的图形. 从图可见,0 x 是所给函数的跳跃间断点.12例2.19 观察无穷间断. 分别输入Plot[1/(1-x^2),{x,-3,3}]则输出所给函数的图形. 从图可见,0=x 是所给函数的跳跃间断点.例2.20 观察振荡间断. 分别输入Plot[Cos[1/x],{x,-Pi,Pi}]则输出所给函数的图形. 从图可见,0=x 是所给函数的跳跃间断点. 再输入Limit[Sin[1/x],x->0]Mathematica4.0输出为Interval[{-1,1}]. 读者可猜测这是什么意思.例2.21 有界量乘以无穷小. 分别输入Plot[x*Sin[1/x],{x,-Pi,Pi}] Limit[x*Sin[1/x],x->0]则分别输出所给函数的的图形和所求极限0. 因为无穷小乘以有界函数得无穷小.13例2.22观察无穷间断. 输入Plot[Tan[x],{x,-2Pi,2Pi}]则输出函数x y tan =的图形. 从图可见,0=x 是所给函数的跳跃间断点.例2.23 观察振荡间断. 输入Plot[Sin[1/x],{x,-Pi,Pi}]则输出函数x1sin 的图形. 从图可见,0=x 是所给函数的跳跃间断点.再输入Limit[Sin[1/x],x->0]则输出为Interval[{-1,1}]. 表示函数极限不存在,且在-1与1之间振荡.。
一元、二元函数图像绘制

⼀元、⼆元函数图像绘制⽬录概述本篇博客主要是在上⼀篇的基础上,进⼀步说明“函数”在函数式编程中的重要作⽤。
强调了函数和普通类型⼀样,可以赋值、存储、传参以及作为另外函数的返回值。
本⽂附带了⼀个Demo,该Demo可以将任意字符串函数表达式解析之后⽣成对应的函数(⼀元、⼆元以及三元),如果你输⼊的是⼀元或者⼆元函数表达式,则可以绘制出相应的函数图像。
⼀元函数图像为平⾯曲线,⼆元函数图像为⽴体曲⾯。
看下图:函数表达式中只识别X、Y、Z三个⾃变量。
字符串表达式解析字符串解析是重点。
怎样去识别⼀串字符串函数表达式呢?如x^2+sin(x)*cos(y)。
之后怎样去计算函数值呢?其实原理很简单,由于每个函数表达式中包含的有效符号是有限的,如X、Y、Z、+、-、*、/以及⼀些函数诸如log、sin、cos等等,只要我们将这些有效符号均识别筛选出来之后,再根据这些符号的优先级别⽣成⼀个函数语法树即可。
如上图所⽰,使⽤⼀个“树结构”去存储最终的语法树。
最后带⼊X、Y(⼆元)求得函数值。
表达式解析这块难点是语法树的构建和最终求值。
语法树的构建有点复杂,⼤家可以参见源码;最终求值的原理是,判断当前符号(节点)是单⽬运算符号(如cos、sin、负号等)还是双⽬运算符号(如+ - * /等),如果是单⽬运算⽐如cos函数,则先计算⼦节点(只有⼀个⼦节点)的值,然后将得到的值进⾏cos运算(Math.Cos(⼦节点的值));相反,如果是双⽬运算符⽐如+符号,那么先计算左⼦节点和右⼦节点的值,最后将两个值进⾏+操作(左⼦节点的值+右⼦节点的值),依次递归计算得到最终的函数值。
图像绘制图像绘制这块就⽐较简单了。
根据前⼀步得到的语法树,我们可以创建出对应的⼀元函数、⼆元函数以及三元函数(委托的形式)。
事先定义的委托结构如下:/// <summary>/// ⼀元函数/// </summary>/// <param name="x"></param>/// <returns></returns>public delegate double UnaryFunction(double x);/// <summary>/// ⼆元函数/// </summary>/// <param name="x"></param>/// <param name="y"></param>/// <returns></returns>public delegate double BinaryFunction(double x,double y);/// <summary>/// 三元函数/// </summary>/// <param name="x"></param>/// <param name="y"></param>/// <param name="z"></param>/// <returns></returns>public delegate double MultiFunction(double x,double y,double z);很简单就可以看出,⼀元函数接收⼀个参数,返回⼀个值;⼆元函数接收两个参数,返回⼀个值;三元函数接收三个参数,返回⼀个值。
2013年下学期数学实验作业

数学实验与数学建模实验报告学院:专业班级:姓名:学号:完成时间:2014 年1 月6日实验一 图形的画法1. 做出下列函数的图像:(1))2sin()(22--=x x x x y ,22≤≤-x (分别用plot 、fplot ) (2)22/9/251x y +=(用参数方程)(3) 在同一图形窗口中,画出四幅不同图形(用subplot 命令):1cos()y x =,2sin(/2)y x pi =-,23cos()y x x pi =-,sin()4x y e =(]2,0[π∈x )2 作出极坐标方程为)cos 1(2t r -=的曲线的图形.3 作出极坐标方程为10/t e r =的对数螺线的图形.4 绘制螺旋线⎪⎩⎪⎨⎧===t z t y t x ,sin 4,cos 4在区间[0,π4]上的图形.在上实验中,显示坐标轴名称。
5 作出函数22y x xye z ---=的图形.6 作出椭球面1194222=++z y x 的图形.(该曲面的参数方程为,cos ,sin sin 3,cos sin 2u z v u y v u x === (ππ20,0≤≤≤≤v u ).)7 作双叶双曲面13.14.15.1222222-=-+z y x 的图形.(曲面的参数方程是,csc 3.1,sin cot 4.1,cos cot 5.1u z v u y v u x ===其中参数πππ<<-≤<v u ,20时对应双叶双曲面的一叶, 参数πππ<<-<≤-v u ,02时对应双叶双曲面的另一叶.)8 作出圆环v z u v y u v x sin 7,sin )cos 38(,cos )cos 38(=+=+=,(πππ22/,2/30≤≤≤≤v u )的图形.9 作出球面22222=++z y x 和柱面1)1(22=+-y x 相交的图形.10 作出锥面222z y x =+和柱面1)1(22=+-y x 相交的图形.11用动画演示由曲线],0[,sin π∈=z z y 绕z 轴旋转产生旋转曲面的过程. (该曲线绕z 轴旋转所得旋转曲面的方程为,sin 222z y x =+ 其参数方程为])2,0[],,0[(,,sin sin ,cos sin ππ∈∈===u z z z u z y u z x ) 12. 画出变上限函数⎰xdt t t 02sin 及其导函数的图形.13.迪卡尔曲线)03(13,1333222=-++=+=axy y x tat y t at x 14.蔓叶线)(1,1322322x a x y tat y t at x -=+=+= 15.摆线)cos 1(),sin (t b y t t a x -=-=16.内摆线(星形线))(sin ,cos 32323233a y x t a y t a x =+==17.圆的渐伸线(渐开线))cos (sin ),sin (cos t t t a y t t t a x -=+=18.空间螺线ct z t b y t a x ===,sin ,cos 19.阿基米德线0,≥=r a r ϕ。
数学实验1-3章习题答案
ans =
18.3287
函数的单调区间为:
(1)单调递增区间:-2<x<-1.5326 -0.7315<x<0以及1.5951<x<2;
(2)单调递减区间:-1.5326<x<-0.7315以及0<x<1.5951.
(2)
函数的图形为:
clear
>> fplot('3*x^5-20*x^3+10',[-3,3])
ans =
-3
最值2:
x=1:0.1:3;
>> y=3.*x.^5-20.*x.^3+10;
>> [m k]=max(y)
m =
199
k =
21
>> x(k)
ans =
3
驻点1及相应的二阶导数值:
clear
>> syms x y
>> y=3*x^5-20*x^3+10;
>> yxx=diff(y,x,2);
>> grid on
f=inline('100*acos(1-1/200*(r^2))+r^2*acos(1/20*r)-10*sqrt(r^2-1/400*r^4)-50*pi','r');
>> y=fzero(f,12)
y =
11.5873
3.求解下列非线性方程组在远点附近的根:
clear
>> syms x y z
>> [x y z]=solve('9*x^2+36*y^2+4*z^2-36','x^2-2*y^2-20*z','16*x-x^3-2*y^2-16*z^2',x,y,z)
02-一次函数的图像及性质-教师版
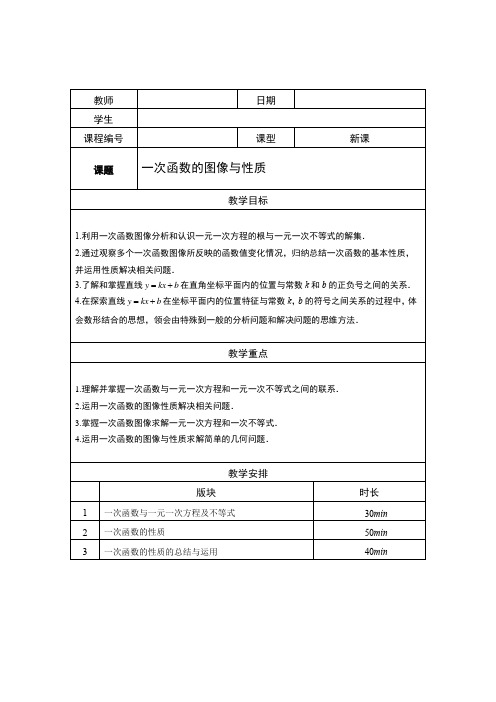
1、 一元一次方程与一次函数(1) 对于一次函数m ,由它的函数值0y =就得到关于x 的一元一次方程0kx b +=,解这个方程得bx k=-,于是可以知道一次函数m 的图像与x 轴的交点坐标为(0)b k -,; (2) 若已知一次函数m 的图像与x 轴的交点坐标,也可以知道这个交点的横坐标bx k =-,其就是一元一次方程0kx b +=的根.2、 一元一次不等式与一次函数(1) 由一次函数y kx b =+的函数值y 大于0(或小于0),就得到关于x 的一元一次不等式0kx b +>(或0kx b +<)的解集.(2) 在一次函数m 的图像上且位于x 轴上方(或下方)的所有点,它们的横坐标的取值范围就是不等式0kx b +>(或0kx b +<)的解集.一次函数知识结构知识精讲模块一:一次函数与不等式yx6Oyx-2O 没【例1】 已知一次函数经过(20)A ,和(13)B -,,在直角坐标系中画出函数图像且求在这个一次函数图像上且位于x 轴上方所有点的横坐标的取值范围. 【难度】★【答案】图像如图,2x >. 【解析】图像如图,2x >.【总结】本题考察了一次函数与一元一次不等式的关系.【例2】 已知(0)y kx b k =+≠的函数图像如图所示:(1)求在这个函数图像上且位于x 轴上方所有点的横坐标的取值范围;(2)求不等式0kx b +≤的解集. 【难度】★【答案】(1)6x <; (2)6x ≥. 【解析】(1)由图像可得:6x <; (2)由图像可得:6x ≥.【总结】本题考察了一次函数与一元一次不等式的关系.【例3】 已知(0)y kx b k =+≠的函数图像如图所示:(1)求在这个函数图像上且位于y 轴左侧所有点的横坐标的取值范围; (2)求在这个函数图像上且位于y 轴右侧所有点的纵坐标的取值范围; (3)求2016y x b =-+在y 轴上的截距. 【难度】★【答案】(1)0x <;(2)2y >-;(3)2-. 【解析】(1)由图像可得:0x <; (2)由图像可得:0x >; (3)由图像可得:2b =-∴2016y x b =-+在y 轴上的截距是2-.【总结】本题考察了一次函数与不等式的关系,注意分析清楚题目中所要求的结果.例题解析【例4】已知一次函数解析式是132y x=-.(1)当x取何值时,2y=?(2)当x取何值时,2y>?(3)当x取何值时,2y<?(4)当x取何值时,02y<<?【难度】★★【答案】(1)10x=;(2)10x>;(3)10x<;(4)610x<<.【解析】(1)令1322x-=,解得:10x=;(2)令1322x->,解得:10x>;(3)令1322x-<,解得:10x<;(4)令10322x<-<,解得:610x<<.【总结】本题考察了一次函数与不等式的关系,本题也可以通过函数图像求解.【例5】已知函数()31f x x=-+.(1)当x取何值时,()2f x=-?(2)当x取何值时,4()2f x>>-?(3)在平面直角坐标系中,在直线()31f x x=-+上且位于x轴下方所有点,它们的横坐标的取值范围是什么?【难度】★★【答案】(1)1x=;(2)11x-<<;(3)13 x>.【解析】(1)令312x-+=-,解得:1x=;(2)令4312x>-+>-,解得:11x-<<;(3)令310x-+<,解得:13 x>.【总结】本题考察了一次函数与不等式的关系,本题也可以通过函数图像求解.【例6】已知方程20(0)ax a-=>的解为4x=,(1)求出函数2y ax=-与x轴的交点坐标;(2)解不等式20ax-≥.【难度】★★【答案】(1)(4,0);(2)4x≥.【解析】由一次函数与方程不等式的关系得:(1)2y ax =- 与x 轴的交点坐标为:(4,0); (2)20ax -≥的解集为:4x ≥.【总结】本题考察了一次函数与方程不等式的关系,本题也可由一次函数的图像或者是函数的性质求得最终结果.【例7】 已知一次函数y ax b =+与y mx n =+交于点(34),,根据其图像回答下列问题:(1)求解不等式组:44ax b mx n +>⎧⎨+≤⎩;(2)求解方程组:y b axmx y n -=⎧⎨=-⎩;(3)求解不等式:ax b mx n +≤+.【难度】★★★【答案】(1)3x >;(2)34x y =⎧⎨=⎩; (3)3x ≤.【解析】由一次函数与方程不等式的关系得:(1)由4ax b +>可得:3x >;由4mx n +≤可得:3x ≥; ∴3x >;(2)y b axmx y n -=⎧⎨=-⎩的解即为两条直线交点坐标,即:34x y =⎧⎨=⎩;(3)ax b mx n +≤+解集为y ax b =+在y mx n =+上方时x 的范围,即3x ≤. 【总结】本题考察了一次函数与方程及不等式的关系,主要是根据图像进行求解.【例8】 当-1≤x ≤2时,函数6y ax =+满足10y <,求出常数a 的取值范围. 【难度】★★★ 【答案】42a -<<.【解析】当0a >时,max 2610y a =+<,解得:2a <; 当0a <时,min 610y a =-+<,解得:4a >-; 当0a =时,66y ax =+=,满足10y <; ∴42a -<<.【总结】本题考察了一次函数的性质,注意解题时要分类讨论.1、 一次函数的增减性:一般地,一次函数y kx b =+(,k b 为常数,0k ≠)具有以下性质: 当0k >时,函数值y 随自变量x 的值增大而增大,图像为上升; 当0k <时,函数值y 随自变量x 的值增大而减小,图像为下降.2、 一次函数图像的位置情况:直线y kx b =+(0k ≠,0b ≠)过(0,)b 且与直线y kx =平行,由直线y kx =在平面直角坐标系内的位置情况可知:(要用图像的平移推导可得) 当0k >,且0b >时,直线y kx b =+经过一、二、三象限; 当0k >,且0b <时,直线y kx b =+经过一、三、四象限; 当0k <,且0b >时,直线y kx b =+经过一、二、四象限; 当0k <,且0b <时,直线y kx b =+经过二、三、四象限. 把上述条件反过来叙述,也是正确的.(这部分知识概念也可以按照下面表格进行讲解和整理)0b >0b <0b =0k >经过第一、二、三象限经过第一、三、四象限经过第一、三象限图象从左到右上升,y 随x 的增大而增大0k <经过第一、二、四象限经过第二、三、四象限经过第二、四象限图象从左到右下降,y 随x 的增大而减小知识精讲模块二:一次函数的性质【例9】 已知函数:①2y x =-+;② 132y x =+;③ 53y x =;④ 32xy -=;⑤11(1)45y x x =--.在这些函数中,函数值y 随自变量x 的值增大而减小的函数有_______________. 【难度】★ 【答案】①④.【解析】由一次函数的性质,当0k <时,y 随x 的增大而减小,故选①④. 【总结】本题考察了一次函数的性质.【例10】 已知一次函数(32)1y m x m =-++,函数值y 随自变量x 的值增大,而减小.(1)求m 的取值范围; (2)其函数图像经过那些象限?【难度】★ 【答案】(1)32m >; (2)经过一、二、四象限. 【解析】(1)由已知得:320m -<,解得:32m >; (2)此时10m +>,一次函数经过一、二、四象限. 【总结】本题考察了一次函数的性质及图像所过的象限.【例11】 已知点(1)A a -,和(4)B b ,在函数13y x m =-+的图像上,试比较a 与b 的大小. 【难度】★ 【答案】a b >.【解析】由已知得:103k =-<,所以y 随x 的增大而减小,∴a b >.【总结】本题考察了一次函数的性质,也可用特殊值法比较大小.【例12】 完成下列填空:(1) 直线25y x =--是________(填“上升”或“下降”)的,并且与y 轴的______半轴相交,因此这条直线经过第________象限,截距为_______;(2) 直线7(2)y x =-是________(填“上升”或“下降”)的,并且与y 轴的______半轴相交,因此这条直线经过第________象限,截距为_______.例题解析【难度】★【答案】(1)下降,负,二、三、四,-5; (2)上升,负,一、三、四,-14. 【解析】略.【总结】本题考察了一次函数的性质,要熟记不同的情况.【例13】 直线2(1)1y m x m =+++与y 轴的交点坐标是(03),,且直线经过第一、二、四象限,则该直线与x 轴的交点为__________. 【难度】★★【答案】30),.【解析】由已知得:21310m m ⎧+=⎨+<⎩, 解得:m = ∴(1)3y x =+.令0y =,解得:3x =,∴与x 轴的交点坐标是:30),. 【总结】本题考察了一次函数的性质及交点坐标;【例14】 直线2(1)3y m x =--上有两点11()A x y ,和点22()B x y ,,且12x x >,12y y <,则常数m 的取值范围是_______________. 【难度】★★ 【答案】11m -<<.【解析】由已知得:y 随x 的增大而减小, 则210m -<, 解得:11m -<<.【总结】本题考察了一次函数的性质,注意对于一元二次不等式的求解方法.【例15】 已知一次函数y kx b =+的图像是与直线23y x =-平行的直线.(1) 随着自变量x 的值的增大,函数值y 增大还是减小? (2) 直线4y kx =-经过哪几个象限? (3) 直线y kx b =+经过哪几个象限? 【难度】★★【答案】(1)y 随着x 的增大而减小; (2)二、三、四象限; (3)①当0b <时,经过二、三、四象限; ②当0b =时,经过二、四象限; ③当0b >时,经过一、二、四象限.【解析】(1)由已知得:203k =-<,故y 随着x 的增大而减小;(2)∵00k b <<,,经过二、三、四象限; (3)①当0b <时,经过二、三、四象限; ②当0b =时,经过二、四象限; ③当0b >时,经过一、二、四象限. 【总结】本题考察了一次函数的图像及性质的运用.【例16】 已知直线(21)3y m x m =-+,分别根据下列条件求m 的值或m 的取值范围:(1) 这条直线经过原点; (2) 这条直线经过一二四象限; (3) 这条直线不经过第三象限; (4) 这条直线与2 1.5y x =-+平行. 【难度】★★【答案】(1)0m =; (2)102m <<; (3)102m ≤≤; (4)12m =-. 【解析】(1)由已知得:30m =,解得:0m =; (2)由已知得:21030m m -<⎧⎨>⎩,解得:102m <<;(3)由已知得:21030m m -≤⎧⎨≤⎩,解得:102m ≤≤;(4)由已知得:212m -=-,解得:12m =-.【总结】主要考察了一次函数的性质的运用,本题中要特别注意题干中说的是直线,因此包含了常值函数在里面,从而第(3)小问中k 可以为零.【例17】 函数y ax b =+与y bx a =+的图象在同一坐标系内的大致位置正确的是( ).AB CD【难度】★★ 【答案】B【解析】本题型可以将每个选项中两条直线的k 、b 范围写出来,不矛盾即为正确选项, 故选B .【总结】本题考察了一次函数的图像与函数解析式中k 、b 的关系.【例18】 点(1,m ),(2,n )在函数2(963)3(3)y a a x a a =-+-+-≠的图象上,则m 、n 的大小关系是____________. 【难度】★★★ 【答案】m n >.【解析】转化得:2[(31)2]3y a x a =---+-, ∵2(31)20a ---<, ∴y 随x 的增大而减小, ∴m n >.【总结】本题考察了一次函数的性质,注意对比例系数进行配方,从而判定正负性.【例19】 无论p 为何值,除0以外,直线2y px p =+一定经过__________象限. 【难度】★★★ 【答案】二、三.【解析】(1)当0p >时,直线经过一、二、四象限; (2)当0p <时,直线经过二、三、四象限; 故直线一定经过二、三、象限; 【总结】本题考察了一次函数的象限特点.【例20】 不论k 为何值,解析式(21)(3)(11)0k x k y k --+--=表示的函数的图象必过定点,求此定点的坐标. 【难度】★★★ 【答案】(23),.【解析】转化得:(21)3110x y k x y ----+= ∵不论k 为何值,图象必过定点, ∴2103110x y x y --=⎧⎨--+=⎩, 解得:23x y =⎧⎨=⎩,∴定点坐标为:(23),.【总结】本题考察了函数恒过定点的问题,此题型只要令可取任意值的字母系数为零 即可解决.1、一次函数y kx b =+(,k b 为常数,0k ≠)中k 、b 的意义: k (称为斜率)表示直线y kx b =+(0k ≠)的倾斜程度;b (称为截距)表示直线y kx b =+(0k ≠)与y 轴交点是(0,)b ,也表示直线在y 轴上的截距.2、同一平面内,不重合的两直线1(0)a ≠与2(0)a ≠的位置关系: 当1212a a b b =≠,时,两直线平行.当12a a ≠时,两直线相交,交点为方程组1122y a x b y a x b =+⎧⎨=+⎩的解.当12b b =时,两直线交于y 轴上同一点.【例21】 已知一次函数y =kx +b ,y 随x 的增大而增大,且kb <0,指出一次函数的图像经过的象限. 【难度】★★ 【答案】一、三、四;【解析】由已知得:0k >,又kb <0, ∴b <0. ∴一次函数图像经过一、三、四象限.【总结】本题考察了一次函数图像经过的象限的特点.【例22】 若直线1l :23y x =-与直线2l :3y x =-+相交于点P ,(1)求P 点坐标;(2)求1l ,2l 与x 轴所围成的三角形的面积; (3)求1l ,2l 与y 轴所围成的三角形的面积; (4)求1l ,2l 与坐标轴所围成的四边形的面积. 【难度】★★【答案】(1)P (2,1);(2)34; (3)6; (4)274. 【解析】(1)联立:233y x y x =-⎧⎨=-+⎩, 解得:21x y =⎧⎨=⎩, ∴交点坐标为P (2,1);11b x a y +=22b x a y +=例题解析知识精讲模块三:一次函数的性质的总结与运用(2)易得233y x y x =-=-+与分别与x 轴交于(302,)、(3,0), ∴1331224S =⨯⨯=;(3)易得233y x y x =-=-+与分别与y 轴交于(03-,)、(0,3), ∴16262S =⨯⨯=;(4)由题意可知,所求的四边形为图中红色边的四边形,∴1313276322224S =⨯⨯+⨯⨯=.【总结】本题考察了一次函数围成图形的面积,规则图形用公式法,不规则图形用割补法;【例23】 已知:如图,直线PA 是一次函数(0)y x n n =+>的图象,直线PB 是一次函数2(0)y x m m =-+>的图象,其中点Q 是直线PA 与y 轴的交点.(1)用m ,n 来分别表示点P ,A ,B ,Q 的坐标;(2)四边形PQOB 的面积是56,AB =2,试求P 点的坐标,并写出直线PA 与PB 的解析式. 【难度】★★【答案】(1)(0)Q n ,,(0)A n -,,(0)2m B ,,2()33m n m nP -+,; (2)14()33P ,, :1PA y x =+, :22PB y x =-+.【解析】(1)易得:(0)Q n ,,(0)A n -,,(0)2mB ,; 联立:2y x n y x m =+⎧⎨=-+⎩, 解得:323m n x m n y -⎧=⎪⎪⎨+⎪=⎪⎩, ∴2()33m n m n P -+,;(2)由已知得:212152232622m n n m n +⎧⨯⨯-=⎪⎪⎨⎪+=⎪⎩, 解得:21m n =⎧⎨=⎩,∴14()33P ,, :1PA y x =+, :22PB y x =-+.【总结】本题考察了一次函数与几何的综合,综合性较强,解题时注意认真分析. 【例24】 已知一次函数f (x )=ax +2a +1,当11x -≤≤时,f (x )的值有正有负,求a 的取值范围. 【难度】★★★【答案】113a -<<-.【解析】由已知得:(1)(1)0f f -⋅<,∴(1)(31)0a a ++<,解得:113a -<<-.【总结】本题考察了一次函数的性质及根据取值范围得到两个函数值的正负,从而求出不等式的解集.【例25】 已知m 为正整数,直线5214x m y -++=和233my x =-+的交点在第四象限,求这两条直线与x 轴围成的三角形的面积. 【难度】★★★【答案】1140S =.【解析】联立5214233x m y m y x -++⎧=⎪⎪⎨⎪=-+⎪⎩, 解得:2307207m x m y +⎧=>⎪⎪⎨-⎪=<⎪⎩,∵交点在第四象限, ∴可解得:322m -<<, 又∵m 为正整数, ∴1m =.∴534x y -+=和213x y -+=两直线交点坐标为:(5177-,) 两直线与x 轴交点坐标为:(305,),(102,), ∴13111()2527140S =⨯-⨯=.【总结】本题考察了一次函数交点坐标及围成三角形面积的求法.【习题1】已知,直线2(1)2y k x k =-++在y 轴上的截距为4,且y 随x 的增大而增大,则k =_____________.【难度】★ 【答案】2.【解析】∵224k +=,∴22k =, ∴2k =±, ∵10k ->, ∴2k =. 【习题2】若点P (,)a b -在第二象限内,则直线y ax b =-不经过________. 【难度】★随堂检测【答案】第二象限.【解析】由题意可得:00a b>>,,则直线经过一、三、四象限,故不经过第二象限.【总结】本题考察了一次函数图像性质.【习题3】若0bc<,0ab>,则一次函数a cy xb b=--的图像经过第_________象限.【难度】★★【答案】第一、二、四象限.【解析】由题意可得一次函数图像经过一、二、四象限.【总结】本题考察了一次函数的图像的性质.【习题4】已知点A(2)a-,、B(3)b-,在直线(5)2y k x=++上,且a b≥,则k的取值范围是__________.【难度】★★【答案】5k≥-.【解析】∵a b≥,∴y随x的增大而增大,∴50k+≥,∴5k≥-.【总结】本题考察了一次函数的图像的性质及增减性的综合运用.【习题5】根据图中所画的直线1y kx k=--,则一次函数213ky kx k-=+在y轴上的截距为__________,与坐标轴围成的三角形面积为__________.【难度】★★【答案】.【解析】∵211k-=,∴k=由图可知,0k<,∴k=∴213ky kx k-=+=--∴此一次函数在y轴上的截距为【总结】本题考察了一次函数的概念和图像,注意认真分析题目中的条件.【习题6】(1)一次函数(63)24y m x n=-+-不经过第三象限,则m、n的范围是________;(2)直线(63)24y m x n=-+-不经过第三象限,则m、n的范围是_________.【难度】★★【答案】(1)2m >,2n ≥; (2)2m ≥,2n ≥.【解析】(1)∵一次函数图像不经过第三象限,∴630m -<,240n -≥, ∴2m >,2n ≥;(2)∵直线不经过第三象限, ∴630m -≤,240n -≥, ∴2m ≥,2n ≥.【总结】本题考察了函数图像的性质与函数解析式的系数的关系.【习题7】已知直线(0)y kx b k =+≠与x 轴的交点在x 轴的正半轴,下列结论:(1)00k b >>,;(2)00k b ><,;(3)00k b <>,;(4)00k b <<,.其中正确的是_________. 【难度】★★ 【答案】(2)、(3).【解析】画图可知(2)、(3)正确.【总结】本题考察了一次函数的图像与函数解析式系数的关系.【习题8】直线111:l y k x a =+,222:l y k x b =+的交点坐标是(1,2),则使1y <2y 的x 取值范围是__________【难度】★★ 【答案】1x <.【解析】由图易得1y <2y 的x 取值范围是1x <. 【总结】本题考察了学生观察、识图的能力.【习题9】若一次函数(0)y kx b k =+≠的自变量x 的取值范围是26x -≤≤,相应的函数值的范围是119x -≤≤,求此函数的解析式,以及其经过哪些象限?【难度】★★★【答案】562y x =-,函数图像经过一、三、四象限;或542y x =-+,函数图像经过一、二、四象限;【解析】由题意易得函数经过点(-2,-11)和(6,9)或者过(-2,9)和(6,-11),∴11296k b k b -=-+⎧⎨=+⎩或 92116k b k b =-+⎧⎨-=+⎩, 解得: 526k b ⎧=⎪⎨⎪=-⎩ 或 524k b ⎧=-⎪⎨⎪=⎩,∴函数的解析式为:562y x =-,函数图像经过一、三、四象限;或542y x =-+,函数 图像经过一、二、四象限.【习题10】已知方程1(0)ax b a -=<的解为x =(1)求出函数1y ax b =--与x 轴的交点坐标; (2)解不等式10ax b --≥;(3)试求函数1y ax b=--与一次函数2(y x =-的交点坐标.【难度】★★★【答案】(10); (2)x ≤; (30). 【解析】观察图像可知.【总结】本题考察了学生对函数的识图能力和与方程的联系.【习题11】如图,直线L :122y x =-+与x 轴、y 轴分别交于A 、B 两点,在y 轴上有一点C (04),,动点M 从A 点以每秒1个单位的速度沿x 轴向左移动. (1)求A 、B 两点的坐标;(2)求△COM 的面积S 与点M 的移动时间t 之间的函数关系式; (3)当t 何值时△COM ≌△AOB ,并求此时M 点的坐标. 【难度】★★★【答案】(1)A (4,0), B (0,2);(2)S =8-2t (04t ≤<),S =2t -8 (4t >); (3)t =2时,M (2,0); t =6时,M (-2,0). 【解析】(1)易得A (4,0), B (0,2);(2)114422S OM OC t =⋅=-⋅;当04t ≤≤时,82S t =-, 当4t >时,28S t =-;(3)当04t ≤<时,t =2时,M (2,0); 当4t >时, t =6时,M (-2,0). 【总结】本题考察了函数的综合应用.【习题12】一个一次函数图象与直线514y x =-平行,与x 轴、y 轴的交点分别为A 、B , 并且过点(125)--,,则在线段AB 上(包括端点A 、B ),横、纵坐标都是整数的点有哪些?【难度】★★★【答案】(3,-20),(7,-15),(11,-10),(15,-5),(19,0);【解析】设54y x b=+,代入点(125)--,得:5254b-+=-,解得:954b=-,∴该一次函数的解析式为:5954xy-=,转化,得:49541955yx y+==+,∴当y 为5的倍数时,x为整数,∴满足条件的点有:(3,-20),(7,-15),(11,-10),(15,-5),(19,0).【总结】本题考察了一次函数的图像和性质以及对整数点坐标的理解.【习题13】已知:不论k取什么实数,关于x的函数236kx a x bky+-=-(a、b是常数)始终经过点(11),,试求a、b的值.【难度】★★★【答案】724ab⎧=⎪⎨⎪=-⎩.【解析】把(1,1)代入,得:211 36k a bk+--=,化简得:(4)(27)0b k a++-=,∵函数236kx a x bky+-=-(a、b是常数)始终经过点(11),,∴40270ba+=⎧⎨-=⎩,解得:724ab⎧=⎪⎨⎪=-⎩.【总结】本题考察了一次函数恒过点的问题,主要是将问题转化为方程的解为任意实数的问题.课后作业【作业1】已知一次函数y kx b =+的图像交y 轴于正半轴,且y 随x 的增大而减小,请写出符合上述条件的一个解析式___________. 【难度】★【答案】1y x =-+等,不唯一. 【解析】只需要00k b <>,即可. 【总结】本题考察了一次函数的性质.【作业2】(1)已知m 是整数,且一次函数(4)2y m x m =+++的图像不经过第二象限,则m 为__________;(2)一次函数(2)43y a x a =-+-的图像与y 轴的交点在x 轴的下方,则a 的取值范围是__________. 【难度】★【答案】(1)3-; (2)34a <. 【解析】(1)由已知,得:4020m m +>⎧⎨+≤⎩, 解得:42m -<<-,∵m 是整数, ∴3m =-;(2)由已知,得:43020a a -<⎧⎨-≠⎩, 解得:34a <.【总结】本题考察了一次函数的性质,注意对图像不经过第几象限的准确理解.【作业3】已知直线2(0)y mx m m =+<.(1)当x 取何值时,0y =?(2)当x 取何值时,0y >? (3)当x 取何值时,0y <?(4)在m 的取值范围内,直线在平面直角坐标系始终经过哪些象限? 【难度】★★【答案】(1)2x =-; (2)2x <-; (3)2x >-; (4)二、三、四象限. 【解析】(1)令0y =,解得:2x =-; (2)令0y >,解得:2x <-; (3)令0y <,解得:2x >-; (4)易得:图像经过二、三、四象限. 【总结】本题考察了一次函数的图像及性质. 【作业4】已知(0)y kx b k =+≠的函数图像如图所示:(1)求在这个函数图像上且位于x (2)求解不等式0kx b +≥.【难度】★★【答案】(1)5x >-; (2)5x ≤-.【解析】(1)由图像可得:5x >-; (2)由图像可得:5x ≤-. 【总结】本题考察了一次函数与方程、不等式的关系.【作业5】函数y kx k =+与ky x=(0)k ≠在同一坐标系内的图象可能是( ).ABCD【难度】★★ 【答案】C .【解析】本题型可以将每个选项中两条直线的k,b 范围写出来,不矛盾即为正确选项,故选C .【总结】本题考察了一次函数与反比例函数的图像.【作业6】已知一次函数2(3)2y m x m =--+,函数值y 随自变量x 的值增大而减小.(1)求m 的取值范围; (2)其函数图像经过那些象限?【难度】★★【答案】(1)3m >; (2)二、三、四象限. 【解析】(1)由已知得:30m -<,解得:3m >;(2)由已知得:00k b <<,,图像经过二、三、四象限.【总结】本题考察了一次函数的图像及性质.【作业7】已知点(3)a A y ,和(3)b B y -,在函数2(3)y m x m =--+的图像上,试比较a y 与b y 的大小.【难度】★★ 【答案】a b y y <.【解析】由已知得:230k m =--<, ∴y 随x 的增大而减小, ∵33>-, ∴a b y y <. 【总结】本题考察了一次函数的性质的运用.【作业8】k 在为何值时,直线2154k x y +=+与直线23k x y =+的交点在第四象限? 【难度】★★【答案】322k -<<.【解析】联立:215423k x y k x y +=+⎧⎨=+⎩, 解得:23727k x k y +⎧=⎪⎪⎨-⎪=⎪⎩∵交点在第四象限, ∴2307207k k +⎧>⎪⎪⎨-⎪<⎪⎩, ∴322k -<<.【总结】本题考察了一次函数的交点坐标问题.【作业9】画出函数32y x =--的图像,利用图像求:(1)方程320x --=的根; (2)不等式320x --≥的解集; (3)当7y ≤时,求x 的取值范围;(4)当11x -≤≤时,求y 的取值范围; (5)求图像与坐标轴围成的三角形的面积; 【难度】★★【答案】(1)23x =-;(2)23x ≤-;(3)3x ≥-; (4)51y -≤≤;(5)23;【解析】(1)23x =-;(2)23x ≤-;(3)当7y =时,3x =-, ∴7y ≤时,3x ≥-;(4)当1x =-时,1y =; 当1x =时,5y =-; ∴当11x -≤≤时,51y -≤≤;(5)1222233S =⨯⨯=. 【总结】本题考察了一次函数与方程不等式的关系,主要是对函数图像的正确理解.【作业10】已知直线23y mx m m =-++分别根据下列条件求m 的值或m 的取值范围:(1)直线经过(13),;(2)直线经过原点;(3)直线与1y x =-平行; (4)直线在y 轴上的截距4;(5)直线经过一三四象限.【难度】★★【答案】(1)31m =-或;(2)30m =-或;(3)m =(4)41m =-或;(5)30m -<<. 【解析】(1)代入(1,3)得:233m m m -++=,解得:31m =-或;(2)代入(0,0)得:230m m +=,解得:30m =-或;(3)由已知得:m -=,解得:m = (4)由已知得:234m m +=,解得:41m =-或;(5)由已知得:2030m m m ->⎧⎨+<⎩解得:30m -<<. 【总结】本题考察了一次函数的性质,注意对直线过原点的正确理解.【作业11】若一次函数(0)y kx b k =+≠,当31x -≤≤时,对应的函数y 值为19y ≤≤,则一次函数的解析式为_____________.【难度】★★★【答案】27y x =+或23y x =-+.【解析】(1)当0k >时,函数经过(-3,1)和(1,9)时,代入两点得:319k b k b -+=⎧⎨+=⎩ 解得:27k b =⎧⎨=⎩, ∴一次函数的解析式为:27y x =+;(2)当0k <时,函数经过(1,1)和(-3,9)时,代入两点得:139k b k b +=⎧⎨-+=⎩解得:23k b =-⎧⎨=⎩图1图2图3∴一次函数的解析式为:23y x =-+,综上,一次函数的解析式为:27y x =+或23y x =-+.【总结】本题考察了一次函数的图像及性质,注意分类讨论.【作业12】已知2y x =-+与x 轴、y 轴分别交于点A 和点B ,另一直线(0)y kx b k =+≠经 过点(10)C ,,且把△AOB 分成两部分.(1)若把△AOB 被分成的两部分面积相等,求k 、b 的值; (2)若△AOB 被分成的两部分面积之比为1:5,求k 、b 的值.【难度】★★★【答案】(1)22k b =-=,; (2)1133k b =-=,或1122k b ==,. 【解析】(1)如图1,易得:点C 为OA 中点∴BC 分△AOB 被分成的两部分面积相等∴22y x =-+即22k b =-=,;(2)由已知,得:1163AOB S S ∆∆==, ∴13h =. 1º:如图2,直线经过(0,13) ∴1133y x =-+,11,33k b =-=; 2º:如图3,直线经过(5133,) ∴1122y x =-,11,22k b ==; 综上:1133k b =-=,或1122k b ==,. 【总结】本题考察了一次函数的综合运用,注意当涉及到 面积比时,由于没说清楚哪部分大哪部分小,因此要分类 讨论.。
一次函数的图象和性质(提高)知识讲解

= 300 −900
所以 s2 =300 t -900(6<t≤10).
(2)李明返回时所用的时间为 (2100-900)÷(900÷6)+900÷[(2100-900)÷(10-6)]=8+3=11(分钟). 因此,李明返回时所用的时间为 11 分钟.
【总结升华】从图象中获得点的坐标,再用待定系数法求出函数解析式是解题的关键.注意放学途中上 坡路程和下坡路程分别是上学时下坡路程和上坡路程.
在直线 l2 上,点 P2 (x2 , y2 ) 为直线 l1 、 l2 的交点.其中 x2 < x1 , x2 < x3 则( )
A. y1 < y2 < y3 B. y3 < y1 < y2 C. y3 < y2 < y1 D. y2 < y1 < y3
【答案】A; 提示:由于题设没有具体给出两个一次函数的解析式,因此解答本题只能借助于图象.观察直
全体实数
过(0, b )和( − b ,0)点的一条直线 k
k >0
k <0
b>0
b<0
b>0
b<0
经过一、二、三 经过一、三、四 经过一、二、四 经过二、三、四
位置
象限
象限
象限
象限
趋势
从左向右上升
从左向右下降
函数 变化规律
y 随 x 的增大而增大
y 随 x 的增大而减小
3. k 、 b 对一次函数 =y kx + b 的图象和性质的影响:
∴k + b =1.
∴当 k = 1 时, b = 2 , A(−2, 0) ;
3
3
当 k = − 1 时, b = 4 , A(4, 0) .
一元一次函数图像及性质

第三单元 函数及其图像第13课时 反比例函数教学目标【考试目标】1.了解反比例函数的意义,根据已知条件确定反比例函数的表达式;会用待定系数法求函数的表达式;2.会画反比例函数的图象,根据反比例函数的图象性质和解析表达式理解其性质;【教学重点】了解反比例函数的概念,以及反比例函数解析式的变形.掌握反比例函数的图象与性质.掌握用待定系数法求反比例函数的解析式.熟悉反比例函数与其他几何图形结合.教学过程体系图引入,引发思考引入真题,深化理解【例1】(2016年锦州)在同一直角坐标系中,一次函数y=ax-a 与反比例函数 a y x(a≠0)的图象可能是 (C )【解析】此题中a 的符号不确定,所以要进行分类讨论才能解决此题.当a >0时,一次函数y=ax-a 图象必过一、三象限,反比例函数 在一、三象限内,故可以排除A 选项.∵a >0,∴-a <0,∴一次函数y=ax-a 图象与y 轴交点在原点下方,所以B 不符合题意,C 符合题意.当a <0时,一次函数y=ax-a 图象必过二、四象限,反比例函数 图象也在二、四象限,并且-a >0,所以一次函数y=ax-a 图象与y 轴交点在原点上方,所以D 选项不符合题意,故选择C 选项. 【考点】考查了一次函数、反比例函数的图象与性质,利用分类讨论的思想便于解题.【例2】(2016年龙东地区)已知反比例函数 ,当1<x <3时,y 的最小整数值是(A )A.3B.4C.5D.6【解析】∵6>0,∴该反比例函数在1<x <3单调递减,此时y 的范围为2<y <6.∴y 的最小整数值是3.故选择A.【考点】考查了反比例函数的增减性.掌握了反比例函数的增减性,此题不难解出.【例3】(2016年通辽)如图,点A 和点B 都在反比例函数 的图象上,且线段AB 过原点,过点A 作x 轴的垂线段,垂足为C ,P 是线段OB 上的动点,连接CP.设△ACP 的面积为S ,则下列说法正确的是(D )A.S >2B.S >4C.2<S <4D.2≤S≤4【解析】根据题目可知,S=S △AOC+S △COP ,2S △AOC=k=4,∴S △AOC=2.当点P 在原点O 时,Smin=2.当点P 运动到点B 时,S 最大,此时求出S △COP 的面积即可求出Smax.因为点A 、B 均在反比例函数的图像 上,且线段AB 过原点,根据反比例函数图象的对称 性,可以得到A 、B 两点关于原点对称,所以A 、B 两点纵坐标的绝对值相等,△AOC 与△BOC 可以看作是以OC 为底,不难看出这两个三角形同底等高,,面积相等,∴Smax=2+2=4.∴选择D 选项.【考点】考查了反比例函数系数的几何意义,反比例函数的对称性,三角形的面积公式.【例4】【例4】(2016年安徽)如图,一次函数y=kx+b 的图象分别与反比例函数 的图象在第一象限a y x =a y x =a y x =6y x =4y x =a y x =内交于点A (4,3),与y 轴负半轴交于点B ,且OA=OB.(1)求函数y=kx+b 和 的表达式; (2)已知点C (0,5),试在该一次函数图象上确定一点M ,使得MB=MC ,求此时点M 的坐标. 【解析】把点A (4,3)代入函数 得:a=12,∴ . ∵OA=OB ,∴OB=5,∴点B 的坐标为(0,-5).把B (0,-5),A (4,3)代入y=kx+b 得: 解得 .∴y=2x-5.(2)∵点M 在一次函数y=2x-5上,设点M 坐标为(x ,2x-5),∵MB=MC ,∴ 解得:x=2.5,∴点M 的坐标为(2.5,0).【考点】本题考查了反比例函数与一次函数的综合应用,考查了利用待定系数法求反比例函数以及一次函数的解析式,考查了点到点的距离等.【例5】(2016年重庆)在平面直角坐标系中,一次函数y=ax+b (a ≠0)的图形与反比例函数 (k ≠0)的图象交于第二、四象限内的A 、B 两点,与y 轴交于C 点,过点A 作AH ⊥y 轴,垂足为H ,OH=3, 点B 的坐标为(m ,-2). 求△AOH 的周长; 求反比例函数和一次函数的解析式. 【解析】(1)由OH=3, ,得AH=4. 即A (-4,3).根据勾股定理得:△AOH 的周长=AO+AH+OH=3+4+5=12.(2)将A 点坐标代入 (k ≠0),得k=-4×3=-12,反比例函数的解析式为 ;当y=-2时, ,解得x=6,即B (6,-2).将A 、B 点坐标代入y=ax+b ,得5OA ==25k b =⎧⎨=-⎩543b k b =-⎧⎨+=⎩=4tan 3AOH ∠=5,AO ==1,21a b ⎧=-⎪⎨⎪=⎩462a a b -+⎧⎨+=-⎩1 1.2y x =-+a y x =12y x =k y x =4tan 3AOH ∠=k y x=12y x =-122x -=-一次函数的解析式为【考点】此题考查了一次函数与反比例函数的交点问题,利用待定系数法是解决此题的关键.三、师生互动,总结知识先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.课后作业布置作业:同步导练教学反思同学们对本节内容理解很好,但是对于那些反比例函数与其他知识结合的综合性问题略有欠缺,希望大家下课后能多加练习,巩固知识,提升自己.。
matlab--函数图形绘制实验报告1

实验报告课程名称: 数学实验学院名称: 数学与统计学院班级:姓名:学号:2012-2013 学年第学期数学与统计学院制(二)参数方程作图例2: 画出星形线{ 及旋轮线{ 的图形解: 输入以下命令:%星形线作图t=linspace(0,2*pi,5000);x=2*(cos(t)).^3;y=2*(sin(t)).^3;plot(x,y),grid;结果:%旋轮线作图t=linspace(0,4*pi,5000); x=2*(t-sin(t));y=2*(1-cos(t));plot(x,y),axis equal; axis(0,8*pi,0,5);grid;结果:(三)极坐标方程图形例3:画出四叶玫瑰线的图形。
知其极坐标方程: ρ=acos(2 )。
解: 取a=5做图。
在命令窗口输入下命令theta=linspace(0,2*pi);r=2*cos(2*theta);polar(theta,r)结果:(四)空间曲面(线)的绘制例4: 绘制双曲抛物面z= 。
解:将其化为参数方程:{ , 编写m文件运行以下命令r=linspace(-4,4,30);s=r;[u,v]=meshgrid(r,s);x=u;y=v;z=(u.^2-v.^2)./4;surf(x,y,z);bix on;结果:(五)空间曲线在坐标平面上的投影曲面和投影柱面例5: 画出螺旋线{ , 在xOz面上的正投影曲线的图形。
解:化为参数方程{ , 运行下列程序t=linspace(-2*pi,2*pi);x=10*cos(t);z=2*t;h=plot(x,z);grid;xlabel('x');ylabel('z');set(h,'linewidth',2);结果:(一)实验分析:(二)在本次实验中我们初步了解了matlab。
(三)学会了一些简单绘图。
(四)在编制中我们要很明确“点乘的重要性”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验1 一元函数的图形
实验目的
1. 学习matlab一元函数绘图命令.进一步理解函数概念.
实验内容
1. 学习matlab命令.
matlab绘图命令比较多,我们选编一些常用命令,并简单说明其作用,这些命令的调用格式,可参阅例题及使用帮助help查找.
表1.1 二维绘图函数
表1.2 基本线型和颜色
表1.3 二维绘图工具
表1.4 axis命令
linspace 创建数组命令,调用格式为:
x=linspace(x1,x2,n),创建了x1到x2之间有n个数据的数组.
funtool函数工具,在matlab指令窗键入funtool可打开“函数计算器”图形用户界面。
2.绘制函数图形举例.
例1.1.画出y=sinx的图形
解:首先建立点的坐标,然后用plot命令将这些点绘出并用直线连接起来,采用中学五点作图法,选取五点(0,0)、(π/2,1)、(π,0)、(3π/2,-1)、(2π,0). 输入命令:
x=[0,pi/2,pi,3*pi/2,2*pi];y=sin(x);plot(x,y)
这里分号表示该命令执行结果不显示.
可以想象,随点数增加,图形越来越接近y=sinx的图象.例如,在0到2π之间取30个数据点,绘出的图形与y=sinx的图象已经非常接近了。
x=linspace(0,2*pi,30);y=sin(x);plot(x,y)
也可以如下建立该图形.
x=0:0.1:2*pi;y=sin(x);plot(x,y)
还可以给图形加标记、格栅线.
x=0:0.1:2*pi;
y=sin(x);
plot(x,y,’r—‘)
title(‘正弦曲线’)
xlabel(‘自变量x’)
ylabel(‘函数y=sinx’)
text(5.5,0,‘y=sinx’)
grid
上述命令第三行选择了红色虚线,第四行给图加标题“正弦曲线”,第五行给x轴加标题“自变量x”,第六行给y轴加标题“函数y=sinx”,第七行在点(5.5,0)处放置文本“y=sinx”,第八行给图形加格栅线.
例1.2.画出y=2x和y=(1/2)x的图象.
解:输入命令:
x=-4:0.1:4;y1=2.^x;y2=(1/2).x;plot(x,y1,x,y2);
axis([-4,4,0,8])
matlab允许在一个图形中画多条曲线.plot(x1,y1,x2,y2,x3,y3)指令绘制y1=f(x1)、y2=f(x2)等多条曲线.matlab自动给这些曲线以不同颜色.
例1.3.画出y=arctanx的图象.
解:输入命令:
x=-20:0.1:20;y=arctan(x);
plot(x,y,[-20,20],[pi/2,pi/2],[-20,20],[-pi/2,-pi/2])
grid
从图上看,y=arctanx是有界函数,y=±π/2是其水平渐近线.
例1.4.在同一坐标系中画出y=sinx,y=x,y=tanx的图象.
解:输入命令:
x=-pi/2:0.1:pi/2;y1=sin(x);y2=tan(x);
plot(x,x,x,y1,x,y2)
axis equal
axis([-pi/2,pi/2,-3,3])
grid
从图上看,当x>0时,sinx<x<tanx,当x<0时,sinx>x>tanx,y=x是y=sinx 和y=tanx在原点的切线,因此,当|x|很小时,sinx≈x,tanx≈x.
例1.5.画出y=10x-1及y=lg(x+1)的图形.
解:输入命令:
x1=-1:0.1:2;y1=10.x1-1;x2=-0.99:0.1:2;y2=log10(x2+1);
plot(x1,y1,x2,y2)
从图上看,这两条曲线与我们所知的图象相差很远,这是因为坐标轴长度单位不一样的缘故.y=10^x-1与y=lg(x+1)互为反函数,图象关于y=x对称,为更清楚看出这一点,我们再画出y=x的图象
hold on
x=-1:0.01:2;y=x;plot(x,y,’r’)
axis([-1,2,-1,2])
axis square;hold off
plot语句清除当前图形并绘出新图形,hold on语句保持当前图形.
例1.6.画出心形线r=3(1+cosa)的图象.
解:输入命令:
x=-2*pi:0.1:2*pi;r=3*(1+cos(x));polar(x,r)
例1.7.画出星形线x=3(cost)3,y=3(sinx)3的图象.
解:这是参数方程,可化为极坐标方程.
r =
3
((c o s a)
(2/3)
+(s i n a)
(2/3)
)(3/2)
输入命令:
x=0:0.01:2*pi;
r=3./(((cos(x)).2).(1/3)+((sin(x)).2).(1/3)).(3/2);
polar(x,r)
注意,如果建立r与t的关系,此时t只是参数,不是极坐标系下的极角.
练习
1.画出y=arcsin x的图象
2.画出y=sec x在[0,pi]之间的图象
3.在同一坐标系中画出y=x,y= x2,y=3x,y=x3,y=x 的图象
4.画出f(x)=(1-x) +(1+x) 的图象,并根据图象特点指出函数f(x)的奇偶性。
5.画出y=1+ln(x+2)及其反函数的图象。
6.画出y=321
x及其反函数的图象。
