第 7 章 弯曲强度
合集下载
建筑力学第7章平面弯曲杆件
成品质量控制
对已完成的平面弯曲杆件进行成品质量控制，包括尺寸、 平整度、垂直度等方面的检测和控制，确保其符合设计要 求和相关规范。
工艺质量控制
对平面弯曲杆件的施工工艺进行质量控制，包括施工过程 的规范性、工艺参数的控制等方面的检测和控制，确保其 符合设计要求和相关规范。
不合格品处理
对不合格的平面弯曲杆件进行处理和控制，包括返工、返 修、报废等方面的处理和控制，确保产品的质量和安全。
弹性变形与塑性变形
分析杆件在受力后的弹性变形 和塑性变形，了解其力学性能 。
平面弯曲杆件的稳定性分析
01
02
03
稳定性分析概述
对平面弯曲杆件的稳定性 进行分析，以确定其在受 到外力作用时是否会发生 失稳。
临界荷载
研究不同外力作用下杆件 的临界荷载，了解失稳的 临界条件。
稳定性措施
根据分析结果，采取相应 的稳定性措施，提高杆件 的稳定性。
建筑结构
建筑的梁、板、柱等结构形式也属于平面弯曲杆件 ，用于承受垂直和水平荷载。
机械零件
某些机械零件如连杆、曲轴等也采用平面弯曲杆件 的设计，以满足特定的功能需求。
02
平面弯曲杆件的力学分析
平面弯曲杆件的受力分析
80%
受力分析概述
对平面弯曲杆件进行受力分析， 需要明确杆件所受的力，包括外 力、内力和约束反力。
平面弯曲杆件的材料选择Βιβλιοθήκη 钢材混凝土木材
其他复合材料
强度高、塑性好，适用 于承受较大载荷和变形
的结构。
抗压强度高、耐久性好， 适用于承受静载的结构。
轻质、易加工，适用于 临时结构或低层建筑。
如玻璃纤维、碳纤维等， 具有高强度、轻质等特 点，适用于特定场合。
对已完成的平面弯曲杆件进行成品质量控制，包括尺寸、 平整度、垂直度等方面的检测和控制，确保其符合设计要 求和相关规范。
工艺质量控制
对平面弯曲杆件的施工工艺进行质量控制，包括施工过程 的规范性、工艺参数的控制等方面的检测和控制，确保其 符合设计要求和相关规范。
不合格品处理
对不合格的平面弯曲杆件进行处理和控制，包括返工、返 修、报废等方面的处理和控制，确保产品的质量和安全。
弹性变形与塑性变形
分析杆件在受力后的弹性变形 和塑性变形，了解其力学性能 。
平面弯曲杆件的稳定性分析
01
02
03
稳定性分析概述
对平面弯曲杆件的稳定性 进行分析，以确定其在受 到外力作用时是否会发生 失稳。
临界荷载
研究不同外力作用下杆件 的临界荷载，了解失稳的 临界条件。
稳定性措施
根据分析结果，采取相应 的稳定性措施，提高杆件 的稳定性。
建筑结构
建筑的梁、板、柱等结构形式也属于平面弯曲杆件 ，用于承受垂直和水平荷载。
机械零件
某些机械零件如连杆、曲轴等也采用平面弯曲杆件 的设计，以满足特定的功能需求。
02
平面弯曲杆件的力学分析
平面弯曲杆件的受力分析
80%
受力分析概述
对平面弯曲杆件进行受力分析， 需要明确杆件所受的力，包括外 力、内力和约束反力。
平面弯曲杆件的材料选择Βιβλιοθήκη 钢材混凝土木材
其他复合材料
强度高、塑性好，适用 于承受较大载荷和变形
的结构。
抗压强度高、耐久性好， 适用于承受静载的结构。
轻质、易加工，适用于 临时结构或低层建筑。
如玻璃纤维、碳纤维等， 具有高强度、轻质等特 点，适用于特定场合。
弯曲应力计算 (1)
第7章弯曲应力引言前一章讨论了梁在弯曲时的内力——剪力和弯矩。
但是，要解决梁的弯曲强度问题，只了解梁的内力是不够的，还必须研究梁的弯曲应力，应该知道梁在弯曲时，横截面上有什么应力，如何计算各点的应力。
在一般情况下，横截面上有两种内力——剪力和弯矩。
由于剪力是横截面上切向内力系的合力，所以它必然与切应力有关；而弯矩是横截面上法向内力系的合力偶矩，F时，就必然有切应力τ；所以它必然与正应力有关。
由此可见，梁横截面上有剪力Q有弯矩M时，就必然有正应力 。
为了解决梁的强度问题，本章将分别研究正应力与切应力的计算。
弯曲正应力纯弯曲梁的正应力由前节知道，正应力只与横截面上的弯矩有关，而与剪力无关。
因此，以横截面上只有弯矩，而无剪力作用的弯曲情况来讨论弯曲正应力问题。
在梁的各横截面上只有弯矩，而剪力为零的弯曲，称为纯弯曲。
如果在梁的各横截面上，同时存在着剪力和弯矩两种内力，这种弯曲称为横力弯曲或剪切弯曲。
例如在图7-1所示的简支梁中，BC段为纯弯曲，AB段和CD段为横力弯曲。
分析纯弯曲梁横截面上正应力的方法、步骤与分析圆轴扭转时横截面上切应力一样，需要综合考虑问题的变形方面、物理方面和静力学方面。
图7-1变形方面为了研究与横截面上正应力相应的纵向线应变，首先观察梁在纯弯曲时的变形现象。
为此，取一根具有纵向对称面的等直梁，例如图7-2(a)所示的矩形截面梁，并在梁的侧面上画出垂直于轴线的横向线m-m、n-n和平行于轴线的纵向线d-d、b -b 。
然后在梁的两端加一对大小相等、方向相反的力偶e M ，使梁产生纯弯曲。
此时可以观察到如下的变形现象。
纵向线弯曲后变成了弧线''a a 、''b b , 靠顶面的aa 线缩短了，靠底面的bb 线伸长了。
横向线m -m 、n -n 在梁变形后仍为直线，但相对转过了一定的角度，且仍与弯曲了的纵向线保持正交，如图7-2(b)所示。
梁内部的变形情况无法直接观察，但根据梁表面的变形现象对梁内部的变形进行如下假设：(1) 平面假设 梁所有的横截面变形后仍为平面．且仍垂直于变形后的梁的轴线。
工程力学课件-第7章 梁的强度问题
h
3
2
b
三、抗弯截面系数 矩形截面 实心圆截面
bh 12 bh W h 2 h 2 6 W d 2
W
z y d z y
Iz
d
64 d d 2 32
4
4
3
空心圆截面 型钢
D 3
32
(1 )
d D
D d
z y
可查型钢表或用组合法求
纯弯曲时的正应力：例题
[例1]如图所示的悬臂梁，其横截面为直径等于200mm 的实心圆，试计算轴内横截面上最大正应力。
横向弯曲(Transverse Bending) —既有弯矩，又有剪力
P
C F FQ S
C
a
A B
a
P
D
（如图中AC 段和BD 段 ）
P
P
D x
A
B
P
Pa
B D x
C M
A
三、弯曲构件横截面上的应力
m
M
内力
剪力FQ 弯矩M
切应力
正应力
m FQ
• 弯曲切应力
m
——横截面上切向分布内力的集度 • 弯曲正应力
b
h
Iz
y 2 dA
A
y 2 bdy
z y
bh 3 12
h 2
（1）矩形截面
b
Iz
（2）实心圆截面
bh 12
3
h z y
Iz Iy
Ip 2
d 4
64
d z y
4
（3）空心圆截面（形心重合）
3
2
b
三、抗弯截面系数 矩形截面 实心圆截面
bh 12 bh W h 2 h 2 6 W d 2
W
z y d z y
Iz
d
64 d d 2 32
4
4
3
空心圆截面 型钢
D 3
32
(1 )
d D
D d
z y
可查型钢表或用组合法求
纯弯曲时的正应力：例题
[例1]如图所示的悬臂梁，其横截面为直径等于200mm 的实心圆，试计算轴内横截面上最大正应力。
横向弯曲(Transverse Bending) —既有弯矩，又有剪力
P
C F FQ S
C
a
A B
a
P
D
（如图中AC 段和BD 段 ）
P
P
D x
A
B
P
Pa
B D x
C M
A
三、弯曲构件横截面上的应力
m
M
内力
剪力FQ 弯矩M
切应力
正应力
m FQ
• 弯曲切应力
m
——横截面上切向分布内力的集度 • 弯曲正应力
b
h
Iz
y 2 dA
A
y 2 bdy
z y
bh 3 12
h 2
（1）矩形截面
b
Iz
（2）实心圆截面
bh 12
3
h z y
Iz Iy
Ip 2
d 4
64
d z y
4
（3）空心圆截面（形心重合）
工程力学c材料力学部分第七章 应力状态和强度理论
无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0
理论力学第七章梁的应力
WZ
IZ y max
圆截面
IZ
d 4 64
d 3 W Z 32
空心圆截面
IZ
D4
64
(14)
WZ
D3
32
(14)
矩形截面
IZ
bh 3 12
WZ
bh 2 6
空心矩形截面
IZ
b0h03 12
bh3 12
WZ(b1 0h023b13h2)/(h0/2)
q=40kN/m
横力弯曲时，梁的横截面上既有正应力又有切应力.切应力 使横截面发生翘曲， 横向力引起与中性层平行的纵截面的挤压 应力，纯弯曲时所作的平面假设和单向受力假设都不成立.
虽然横力弯曲与纯弯曲存在这些差异，但进一步的分析表 明，工程中常用的梁，纯弯曲时的正应力计算公式，可以精确的 计算横力弯曲时横截面上的正应力.
k
d
o
k'
o'
y
最大切应力发生在中性轴上
maxFISzSb*z
4FS 3A
式中 A πd 2 为圆截面的面积. 4
4.圆环形截面梁
z
k
图示为一段薄壁环形截面梁.环壁厚度为
，环的平均半径为r0，由于 «r0 故可假设
z （a）横截面上切应力的大小沿壁厚无变化；
d
o
k'
o'
y
（b）切应力的方向与圆周相切.
A
C
FAY
1.5m l = 3m
解：
B
x
FBY
FS 90kN
x
90kN 1. 绘制内力图
x
M
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 .
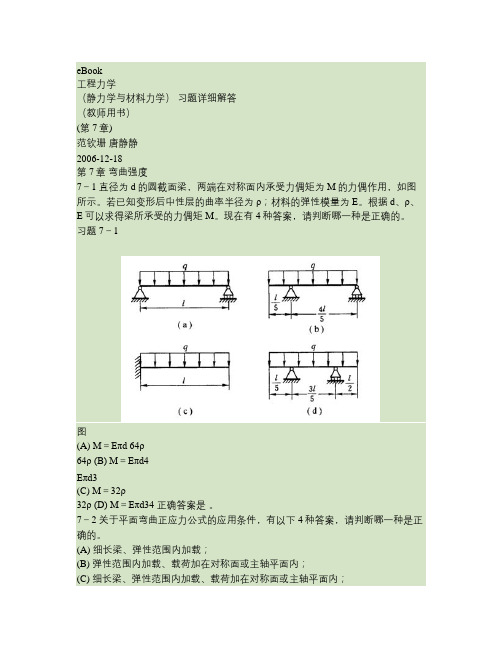
eBook工程力学（静力学与材料力学）习题详细解答（教师用书）(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7－1 直径为d的圆截面梁，两端在对称面内承受力偶矩为M的力偶作用，如图所示。
若已知变形后中性层的曲率半径为ρ；材料的弹性模量为E。
根据d、ρ、E可以求得梁所承受的力偶矩M。
现在有4种答案，请判断哪一种是正确的。
习题7－1图(A) M＝Eπd 64ρ64ρ (B) M＝Eπd4Eπd3(C) M＝32ρ32ρ (D) M＝Eπd34 正确答案是。
7－2 关于平面弯曲正应力公式的应用条件，有以下4种答案，请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载；(B) 弹性范围内加载、载荷加在对称面或主轴平面内；(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内；(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7－3 长度相同、承受同样的均布载荷q作用的梁，有图中所示的4种支承方式，如果从梁的强度考虑，请判断哪一种支承方式最合理。
l 5习题7－3图正确答案是7－4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm。
求：梁的1－1截面上A、 2B两点的正应力。
习题7－4图解：1. 计算梁的1－1截面上的弯矩：M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1－1截面上A、B两点的正应力：A点：⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点：⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127－5 简支梁如图所示。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第7章 弯曲强度
[ ]
[]
0.5 x 0.4125
M(kN.m)
7
习题 7－10 图
解：画弯矩图如图所示： 对于梁：
M max = 0.5q M 0.5q σ max = max ≤ [σ ] , ≤ [σ ] W W [σ ]W = 160 ×106 × 49 ×10−6 = 15.68 ×103 N/m=15.68kN/m q≤ 0.5 0.5
A
B
W
a + Δa
W + ΔW
B
A
a图
b图
整理后得
Δa =
ΔW (l − a ) (W + ΔW )
此即为相邻跳水者跳水时，可动点 B的调节距离 Δa 与他们体重间的关系。 7－ 14 利用弯曲内力的知识，说明为何将标准双杠的尺寸设计成 a=l/4。
9
习题 7－14 图
解：双杠使用时，可视为外伸梁。 其使用时受力点应考虑两种引起最大弯矩的情况。如图a、b所示。
[ ]＋
[σ ]－ ＝120 MPa。试校核梁的强度是否安全。
6
30 x 10 M(kN.m) C 截面
+ = σ max － σ max
40
习题 7－9 图
30 ×103 N ⋅ m × 96.4 ×10−3 m = 28.35 × 106 Pa=28.35 MPa 1.02 ×108 ×10−12 m 4 30 ×103 N ⋅ m ×153.6 ×10−3 m = = 45.17 ×106 Pa=45.17 MPa 1.02 ×108 × 10−12 m 4 40 ×103 N ⋅ m ×153.6 ×10−3 m = 60.24 ×106 Pa=60.24 MPa> [σ ] 8 −12 4 1.02 ×10 × 10 m 40 ×103 N ⋅ m × 96.4 × 10−3 m = = 37.8 × 106 Pa=37.8 MPa 8 −12 4 1.02 × 10 × 10 m
《建筑力学》课件 第七章
【例 7-3】 图（a）中 20 号工字钢悬臂梁承受均布荷载 q 和 集 中 力 F qa / 2 ， 已 知 钢 的 许 用弯 曲 正 应力 [ ] 160 MPa ， a 1 m 。试求梁的许可荷载集度 [q] 。
【解】 ① 将集中力沿两主轴分解。
Fy F cos 40 0.383qa
引起的正应力叠加，得最大应力 max 为
max
m ax
max
M z max ymax Iz
M y max zmax Iy
M z max Wz
M y max Wy
（a） （d） （g）
（b） （e）
（c）
图7-4
（f）
（h）
（i）
若材料的抗拉和抗压强度相等，则斜弯曲梁的强度条件可表示为
max
3．应力分析
根据危险截面上的内力值，分析危险截面上的应力分布，确 定危险点所在位置，并求出危险截面上危险点处的应力值。
4．强度分析 根据危险点的应力状态和杆件的材料强度理论进行强度计
算。
第二节 拉伸（压缩）与弯曲的组合变形
等直杆在横向力和轴向力共同作用下，杆件将发生弯曲与拉伸（压 缩）组合变形。图中的烟囱在横向力水平风力和轴向力自重作用下产生 的就是压缩与弯曲的组合变形。对于弯曲刚度EI较大的杆件，由于横向 力引起的挠度与横截面尺寸相比很小，因此，由轴向力引起的附加弯矩 可以忽略不计。于是，可分别计算由横向力和轴向力引起的杆件截面上 的弯曲正应力和拉压正应力，然后按叠加原理求其代数和，即得到杆件 在拉伸（压缩）和弯曲组合变形下横截面上的正应力。
一、双向偏心压缩（拉伸）的强度计算
在偏心压缩（或拉伸）中，当外力F的作用线与柱轴线平 行，但只通过横截面其中一根形心主轴时，称为单向偏心压缩 （拉伸）；当外力F的作用线与柱轴线平行，但不通过横截面 任何一根形心主轴时，称为双向偏心压缩（拉伸）。下面以双 向偏心压缩（拉伸）为例进行强度计算。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3、作剪力图和弯矩图
a
F C
b
A FQ
Fb l
l
Fb FQ1 x l Fa B FQ2 x l Fb M1 x x l Fa l x M 2 ( x) l x
* 集中力作用处剪力 图有突变，突变值的 大小等于集中力的大 小。弯矩图有折角。
Fa l
需求内力的截面处，假想地将梁切开，并选切 开后的任一段为研究对象；
画出所选梁段的受力图，图中，剪力FQ与弯矩M 可假设为正；
由平衡方程∑Fy =0 计算剪力 FQ; 由平衡方程∑Mc=0 计算弯矩 M ，式中，C为所切 横截面的形心。
例 题 7-1 已知q=9kN/m，F=45kN，M0=48kN· m，
q A
B FB
F y 0 FQ x FA qx 0
M(x)
x ql qx FQ
2
qlx qx 2 M x 2 2
(0 x l )
FA
x
FQ(x)
x M C 0 M x FA x qx 0 2
(0 x l )
例 题 7-7
q A
FA
qa
qa D
q B a
外伸梁受力的大小和方 向如图示。 试画出剪力和弯矩图 解：1．确定约束力
FA qa ， FD 2qa
a
FQ
0
a
FD
qa
2．确定控制面并求 x 出对应的剪力和弯矩
0 qa
qa
M
0
qa2/2 0 qa2/2
3．建立坐标系 建立 FQ－x 和 M－x 坐 标系并标出对应的控制 面上的剪力和弯矩
qa2
2 2 A FA
q B 2a
1
FB
解：1. 求支反力 2.求指定截面剪力和弯矩 FA=2qa （↑） FB = qa（↑） FQ1 = －qa FQ2 = FA－qa= qa M1 = －qa2 M2 =－qa2＋qa2= 0
四、
剪力方程与弯矩方程
q
q
x
1 2 M ( x ) qx , 2
a x l
3.作剪力图和弯矩图
a
Me C
b
Me B FQ x l Me M1 x x 0 x a l x M e l x M2 l a x l
A FQ
l
Me l
x
M
M ea l M eb l
x
b>a时
M max
q
A
M0
B
F
1 x
求梁的1-1截面内力。 解：1）求约束反力：
Fy=FAy+FE-F-4q=0
FAy FAy
A
4m 7m
C E 1D 2m 2m 4m
FE
q
MA(F )=12FE+M0-8F-4q×2=0 FAy=49kN；FE=32kN
M0
B C
M1
FQ1
2) 截面法求内力
F
y
F Ay 4q FQ1 0
§7-3 剪力图与弯矩图
1.剪力图：表示剪力随截面位置的变化规律的图形称 为剪力图。 2.弯矩图：表示弯矩随截面位置的变化规律的图形称 为弯矩图。 3.用剪力方程和弯矩方程作剪力图与弯矩图的步骤 先求出约束反力； 确定分段点； 分段列出剪力方程和弯矩方程； 根据剪力方程和弯矩方程画出剪力图 和弯矩图；
一、 静矩、形心及其相互关系
y
z
1.
dA
静矩（面积矩）
S y zdA
A
z
O
y
图形对于 y 轴的静矩
S z yd A
A
图形对于 z 轴的静矩 代数量 单位：m3
2.形心
y
z
y
zC
dA
y
C
yC
O
AC 段
Fb FQ1 x l
Fb M1 x x l
0 x a
0 x a
a
F
b
A
FA
CB段
x
C
M2(x)
B
FB
B FB
FQ2(x)
Fa FQ2 x FB l
a x l
a x l
Fa l x M 2 x FB ( l x ) l
第 7 章 弯曲强度
§7-1 工程中的弯曲构件 §7-2 剪力方程与弯矩 §7-3 剪力图与弯矩图 §7-4 平面弯曲时梁横截面上的正应力 与应力分析相关的截面图形几何量 §7-5
§7-6 平面弯曲正应力公式应用举例
§7-7 梁的强度计算 §7-8 结论与讨论
§7-1 工程中的弯曲构件 一、工程实例
FAy
C E 1D 2m 2m 4m
FQ 1 F FE） 13KN （
M1
FQ1
F FE
M
1c
M 1 F 1m FE 5m 0
M 1 F 1m FE 5m 115KN m
三、重要结论：
(1) 横截面上的剪力在数值上等于截面左侧或右侧梁段上 外力的代数和。 左侧梁段：向上的外力为正，向下的外力为负。 右侧梁段：向下的外力为正，向上的外力为负
x const.
FN
A
A x
x
dA FN
FN x A
z
y
x Cy
x
Mz
Mz y dA y M x Iz
I z A y dA
2
这些几何量不仅与截面的大小有关，而且与截面的几 何形状有关。
研究杆件的应力与变形，研究失效问题 以及强度、刚度、稳定问题，都要涉及到 与截面图形的几何形状和尺寸有关的量。 这些量统称为几何量，包括：形心、静矩、 惯性矩、惯性半径、极惯性矩、惯性积、主 轴等。
(0 x l )
1.剪力方程
反映梁的横截面上的剪力随截面位置 变化的函数式
FQ FQ ( x )
2.弯矩方程
反映梁的横截面上的弯矩随截面位置 变化的函数式
M M (x)
x
FQ ( x ) qx ,
(0 x l )
A
B
M
L
FQ
注意
不能用一个函数表达的要分段列出剪力和弯矩方程
F ＝0， M ＝0
y A
求得A、F 二处的约束力
9 3 FAy＝ qa , FBy＝ qa 4 4
q
D
2．确定控制面
B
A
E 4a FAy
9qa/4
a FBy
xE
qa
3．建立坐标系，求出控 制面的剪力和弯矩标在 相应的坐标系中 4．根据平衡微分关系 画出剪力和弯矩图
e
FQ
FQE
x
O
FS
一、弯曲时梁横截面上的剪力与弯矩 F2 1. 剪力： FQ F1 M
x
FA
梁受弯时，横截面上存在
平行于截面的内力（剪力）。
FB
y
FA
F1
M M
FQ
F2
M
2. 弯矩：M
梁受弯时，横截面上存 FB 在垂直于截面的内力偶矩 （弯矩）。
x FQ
内力总是成对的，大小相等，方向相反， 正负号如何规定？
二、剪力与弯矩的正负号规则
工厂厂房的吊车大梁：
火车的轮轴：
F
F
F
F
楼房的横梁
阳台的挑梁
二、弯曲的概念
弯曲——如果作用于杆件上的外力都垂直于杆的轴线， 那么杆的轴线由直线变为一条曲线。 这种变形称为弯曲变形 受力特点——作用于杆件上的外力都垂直于杆的轴线。 变形特点——杆轴线由直线变为一条曲线。
P q
FA
M
主要产生弯曲变形的杆--- 梁。
ql 2
ql 2
ql 2 8
ql2 8
M
x
例 题 7-4 图示简支梁受集中荷载F作用。 试作梁的剪力图和弯矩图。
a
F C
b
A FA 解：1、求支反力
Fb FA l
B
l
Fa FB l
FB
2、列剪力方程和弯矩方程 ——需分两段列出
a
F
b
A
x
C
M1(x)
B
FA
A FA
x
FB
FQ1(x)
左上右下， 剪力为正
(2) 横截面上的弯矩在数值上等于截面左侧或右侧梁段 上外力对该截面形心的力矩之代数和。 左侧梁段：顺时针的力矩为正，逆时针的力矩为负。 右侧梁段：逆时针的力矩为正，顺时针力矩为负。
左顺右逆,
弯矩为正
左上右下， 剪力为正；左顺右逆，弯矩为正。
例 题 7-2
qa 1 C a
求指定截面内力
1. 剪力的正负号
FQ
FQ
FQ
FQ
FQ
FQ
FQ
FQ
左上右下，剪力为正
左下右上，剪力为负
顺时针为正
逆时针为负
2. 弯矩的正负号
上凹下凸
M M
M M
表示方法
引起的变形
使梁上压下拉的弯矩为正。
左顺右逆,弯矩为正
上凸下凹
M M M
表示方法
引起的变形
使梁上拉下压的弯矩为负。 左逆右顺, 弯矩为负
三、截面法确定指定截面上的剪力和弯矩
x
4.根据平衡微分关系 画出剪力和弯矩图
例 题 7-8
qa2 q
A
2a
FA