高二下学期数学第一次月考试卷
重庆市九龙坡区2023-2024学年高二下学期第一次月考数学试题含答案
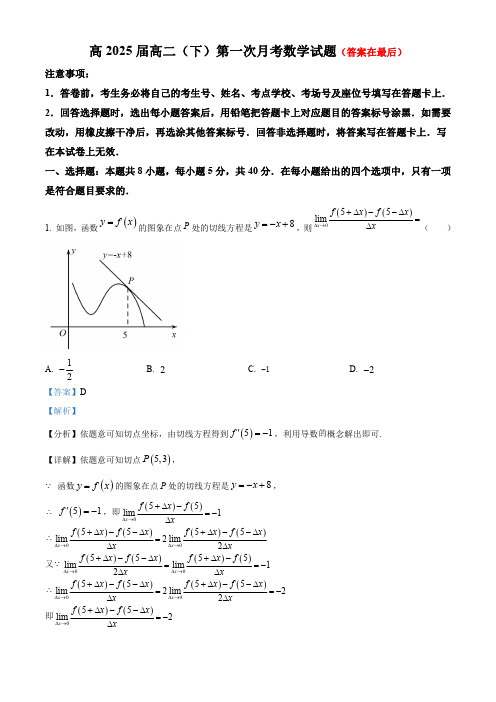
高2025届高二(下)第一次月考数学试题(答案在最后)注意事项:1.答卷前,考生务必将自己的考生号、姓名、考点学校、考场号及座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需要改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,函数()y f x=的图象在点P处的切线方程是8y x=-+,则()()55limxf x f xx∆→+∆--∆=∆()A.12- B.2 C.1- D.2-【答案】D【解析】【分析】依题意可知切点坐标,由切线方程得到()51f'=-,利用导数的概念解出即可.【详解】依题意可知切点()5,3P,函数()y f x=的图象在点P处的切线方程是8y x=-+,∴()51f'=-,即()()55lim1xf x fx∆→+∆-=-∆∴()()()()005555lim2lim2x xf x f x f x f xx x∆→∆→+∆--∆+∆--∆=∆∆又()()()()005555lim lim12x xf x f x f x fx x∆→∆→+∆--∆+∆-==-∆∆∴()()()()005555lim2lim22x xf x f x f x f xx x∆→∆→+∆--∆+∆--∆==-∆∆即()()55lim2xf x f xx∆→+∆--∆=-∆2.丹麦数学家琴生(Jensen )是19世纪对数学分析做出卓越贡献的巨人,特别是在函数的凸凹性与不等式方面留下了很多宝贵的成果.设函数()f x 在(),a b 上的导函数为()f x ',()f x '在(),a b 上的导函数为()f x '',在(),a b 上()0f x ''>恒成立,则称函数()f x 在(),a b 上为“凹函数”.则下列函数在()0,2π上是“凹函数”的是()A.()sin f x x x =-B.2()sin f x x x=+ C.()ln f x x x=+ D.()ln x f x e x x=-【答案】B 【解析】【分析】根据“凹函数”的定义逐项验证即可解出.【详解】对A ,()()1cos ,sin f x x f x x '''=-=,当(),2x ∈ππ时,()0f x ''<,所以A 错误;对B ,()2cos f x x x '=+,()2sin 0f x x ''=->在()0,2π上恒成立,所以B 正确;对C ,()11fx x '=+,()210f x x''=-<,所以C 错误;对D ,()ln 1xf x e x '=--,()1xf x e x ''=-,因为110e f e e e ⎛⎫''=-< ⎪⎝⎭,所以D 错误.故选:B .3.已知()()21220222022ln 2f x x xf x '=+-,则()2022f '=()A.2021B.2021- C.2022D.2022-【答案】B 【解析】【分析】根据导数的运算法则求出函数的导函数,再代入求值即可.【详解】解:因为()()21220222022ln 2f x x xf x '=+-,所以()()202222022f x x f x ''=+-,所以()()202220222022220222022f f ''=+-,解得()20222021f '=-;故选:B4.若函数()()2ln f x x x ax x =+-的极值点是1,则()2=f '()A.4ln 21+B.2ln 21+C.2ln2D.1【答案】B【分析】求导,利用(1)=0f '求得=2a ,进而求出(2)f '.【详解】因为2()()ln f x x x ax x =+-,所以21()=1+(2)ln +()f x x a x x ax x--⋅'1(2)ln x a x a x =+-+-,由题意,得(1)=0f ',即20a -=,解得=2a ,即()=1+2(1)ln f x x x x --',则(2)=1+2ln2f '.故选:B.5.已知定义在R 上的函数()f x 满足()11f =,且()f x 的导函数()f x '在R 上恒有()12f x '<,则不等式()122x f x <+的解集为()A.()1,+∞ B.(),1-∞ C.()1,1- D.()(),11,-∞+∞ 【答案】A 【解析】【分析】令()()122x g x f x =--,根据题意可得()g x 在R 为单调递减函数,进而即得.【详解】因为()122x f x <+可化为()1022x f x --<,令()()122x g x f x =--,则()()12g x f x ''=-,因为()12f x '<,所以()0g x '<,所以()g x 在R 上单调递减,因为()11f =,所以()()1111022=--=g f ,所以()()1g x g <,所以1x >,即不等式()122x f x <+的解集为()1,+∞.故选:A .6.函数()()e ln xf x x m =-+在[]0,1上单调递增,则实数m 的取值范围为()A.[)1,+∞ B.11,e ⎡⎫-+∞⎪⎢⎣⎭C.(]0,1 D.1,1e ⎛⎤-∞- ⎥⎝⎦【答案】A 【解析】【分析】根据函数()()e ln xf x x m =-+在[]0,1上单调递增,可得()0f x ¢³在[]0,1上恒成立,然后利用分离参数法即可求解.【详解】因为()()e ln xf x x m =-+,所以()1e xf x x m'=-+.因为函数()()e ln xf x x m =-+在[]0,1上单调递增,所以()1e 0xf x x m'=-≥+在[]0,1上恒成立,所以1e x m x ≥-在[]0,1上恒成立,即max 1e x m x ⎛⎫≥- ⎪⎝⎭,[]0,1x ∈即可令()1ex g x x =-,[]0,1x ∈则由函数单调性的性质知,()g x 在[]0,1上减函数,()()0max 1001e g x g ==-=,即m 1≥.所以实数m 的取值范围为[)1,+∞。
江苏省南通市海安高级中学2022-2023学年高二下学期第一次月考数学试题

2022-2023学年第二学期高二年级阶段检测(一)数学一、单顶选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设2i1i3i z +=-+,则||z =( )A. 1B.32C. 2D.522. 已知()πcos 2cos π2αα⎛⎫+=- ⎪⎝⎭,则πtan 4α⎛⎫-= ⎪⎝⎭( )A -3B. 3C. 13-D.133. 已知圆锥内切球(与圆锥侧面、底面均相切的球)的半径为2,当该圆锥的表面积最小时,其外接球的表面积为( )A. 81πB. 96πC. 108πD. 126π4. 设2012(12)n nn x a a x a x a x +=++++ ,若78a a =,则n =( )A. 8B. 9C. 10D. 115. 春节期间,某地政府在该地的一个广场布置了一个如图所示的圆形花坛,花坛分为5个区域.现有5种不同的花卉可供选择,要求相邻区域不能布置相同的花卉,且每个区域只布置一种花卉,则不同的布置方案有( )A 120种B. 240种C. 420种D. 720种6. 从集合{1,2,3}U =的非空子集中随机选择两个不同的集合A ,B ,则{1}A B ⋂=的概率为( )A.421B.542C.17D.5567. 某公园有如图所示A 至H 共8个座位,现有2个男孩2个女孩要坐下休息,要求相同性别的孩子不坐在同一行也不坐在同一列,则不同的坐法总数为( )..ABC DE F GHA. 168B. 336C. 338D. 848. 已知两点A ,M 在双曲2222:1(0,0)x y C a b a b -=>>右支上,点A 与点B 关于原点对称,BM 交y 轴于点N ,若AB AM ⊥ ,且280ON OA ON+⋅=,则双曲线C 的离心率为( )A.B.C.D. 二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的选项中,至少有两项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分.9. 已知m ,n 为异面直线,直线l 与m ,n 都垂直,则下列说法正确的是( )A. 若l⊥平面α,则m α∥,n α∥B. 存在平面α,使得l α⊥,m α⊂,n α∥C. 有且只有一对互相平行平面α和β,其中m α⊂,n β⊂D. 至多有一对互相垂直的平面α和β,其中m α⊂,n β⊂10. 已知甲袋中有5个大小、质地相同的球,其中有4个红球,1个黑球;乙袋中有6个大小、质地相同的球,其中有4个红球,2个黑球.下列说法中正确的是( )A. 从甲袋中随机摸出1个球是红球的概率为45B. 从乙袋中随机摸出1个球是黑球的概率为23C. 从甲袋中随机摸出2个球,则2个球都是红球的概率为35D. 从甲、乙袋中各随机摸出1个球,则这2个球是1红1黑的概率为2511. 关于712x x ⎛⎫- ⎪⎝⎭的二项展开式,下列说法正确的是( )A. 二项式系数和为128 B. 各项系数和为7-C. 1x -项的系数为280- D. 第三项和第四项的系数相等12. 已知函数()2tan f x x x =-,则( )A. 函数()f x 不是周期函数的的B. 函数()f x 的图象只有一个中心对称点C. 函数()f x 的单调减区间为ππ2π,2π,44k k k ⎛⎫-+∈ ⎪⎝⎭Z D. 曲线()ππ22y f x x ⎛⎫=-<< ⎪⎝⎭只有一条过点()1,0的切线三、填空题:本题共4小题,每小题5分,共20分.13. 431x x ⎛⎫- ⎪⎝⎭的展开式中常数项是______.(用数字作答)14. 数列{}n a 的各项均为正数,其前n 项和为11()2n n na S a +=,则100S =__________.15. 在一次晚会上,9位明星共上演n 个“三人舞”节目,若在这些节目中,任两个人都曾合作过一次,且仅合作一次,则n =___________.16. 三棱锥-P ABC 中,,,PA PB PC两两垂直,PA PB PC ===M 为平面ABC 内的动点,且满足PM =,记直线PM 与直线AB 的所成角的余弦值的取值范围为_____________.四、解答题:本题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17. 设2012()(1)(1)(1)(1)nknk n a x a a x a x a x a x +=++++++++++ ,其中,a n *∈∈R N .(1)当0,2023a n ==时,求1352023a a a a ++++ 的值;(2)当2a =时,化简:31202341n a a a a a n ++++++ .18. 已知数列{}n a 中,11a =,()11232n n n a a n -*+=+⨯∈N .(1)判断数列2n n a ⎧⎫⎨⎬⎩⎭否为等差数列,并说明理由;(2)求数列{}n a 的前n 项和nS 19. 在ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,满足()()a b c a b c ab +++-=(1)求角C ;(2)若角C 的平分线交AB 于点D ,且2CD =,求2a b +的最小值.20. 如图所示,四棱锥S ABCD -中,底面ABCD 为矩形,AC 与BD 交于点O ,点E 在线段SD 上,且//OE 平面SAB ,二面角S AB C --,二面角S AD C --均为直二面角.是(1)求证:SE DE =;(2)若2SA AD ==,且钝二面角A BE C --的余弦值为,求AB 的值.21. 已知椭圆:C 22184x y +=,直线l :(0)y kx n k =+>与椭圆C 交于,M N 两点,且点M 位于第一象限.(1)若点A 是椭圆C 的右顶点,当0n =时,证明:直线AM 和AN 的斜率之积为定值;(2)当直线l 过椭圆C 的右焦点F 时,x 轴上是否存在定点P ,使点F 到直线NP 的距离与点F 到直线MP 的距离相等?若存在,求出点P 的坐标;若不存在,说明理由.22. 设函数()e 2x f x ax =--(1)求()f x 的单调区间(2)若1a =,k 为整数,且当0x >时()()10x k f x x '-++>,求k 的最大值2022-2023学年第二学期高二年级阶段检测(一)数学一、单顶选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.【1题答案】【答案】D【2题答案】【答案】C【3题答案】【答案】A【4题答案】【答案】D【5题答案】【答案】C【6题答案】【答案】A【7题答案】【答案】B【8题答案】【答案】D二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的选项中,至少有两项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分.【9题答案】【答案】BC【10题答案】【答案】ACD【11题答案】【答案】AC【12题答案】【答案】AD三、填空题:本题共4小题,每小题5分,共20分.【13题答案】【答案】4-【14题答案】【答案】10【15题答案】【答案】12【16题答案】【答案】⎡⎢⎣四、解答题:本题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.【17题答案】【答案】(1)20222 (2)()11211+-+n n 【18题答案】【答案】(1)是等差数列,理由见解析 (2)()12342n n S n -=+-⋅【19题答案】【答案】(1)23π(2)6+【20题答案】【答案】(1)证明见解析. (2)3AB =.【21题答案】【答案】(1)见解析; (2)存在,(4,0)P .【22题答案】【答案】(1)答案见解析 (2)2。
山西省忻州市高二下学期第一次月考数学试题(解析版)

高二下学期第一次月考数学试题一、单选题1.为了方便广大市民接种新冠疫苗,提高新冠疫苗接种率,某区卫健委在城区设立了12个接种点,在乡镇设立了29个接种点.某市民为了在同一接种点顺利完成新冠疫苗接种,则不同接种点的选法共有( ) A .31种 B .358种C .41种D .348种【答案】C【分析】根据题意该市民可选择的接种点为两类,一类为乡镇接种点,另一类为城区接种点,由加法原理计算可得答案.【详解】该市民可选择的接种点为两类,一类为乡镇接种点,另一类为城区接种点,所以共有种不同接种点的选法. 29+12=41故选:C . 2.( ) 9969A A =A .6B .24C .360D .720【答案】A【分析】由排列数公式计算可得答案.【详解】. 9969A 9876543216A 987654⨯⨯⨯⨯⨯⨯⨯⨯==⨯⨯⨯⨯⨯故选:A.3.从由1,2,3,4,5组成的没有重复数字的两位数中任取一个,则这个两位数大于40的个数是( ) A .6 B .8 C .10 D .12【答案】B【分析】数字排列问题,根据符合题意的要求选取十位数为4或5,个位数不重复则在剩余的4个数字里选择1个,即可计算结果.【详解】这个两位数大于40的个数为. 2×48=故选:B .4.的展开式中,的系数与常数项之差为( )()()22122x x x --+2xA .-3B .-1C .5D .7【答案】C【分析】取即可得常数项,将多项式化为,根据二项式定理,分别求出0x =()()4211x x +--,中的项数,再求和,即可求得的系数,即可得出结果.()41x -()21x -2x 2x 【详解】解:因为, ()()()()()()22222412211111x x x x x x x ⎡⎤++⎣--+=--=--⎦取可得常数项为:,0x =()()24121--+=在中,含的项为,()41x -2x ()2222341C 6T x x -==在中,含的项为,()21x -2x ()0202121C T x x -==所以的展开式中,的系数为,()()22122x x x --+2x 617+=所以的系数与常数项之差为. 2x 72=5-故选:C5.如图,一圆形信号灯分成四块灯带区域,现有3种不同的颜色供灯带使用,要求在每,,,A B C D 块灯带里选择1种颜色,且相邻的2块灯带选择不同的颜色,则不同的信号总数为( )A .18B .24C .30D .42【答案】A【分析】根据涂色问题,按照使用颜色种数进行分类,再结合分步计数原理,即可得总的方法数. 【详解】若用3种不同的颜色灯带都使用,故有两块区域涂色相同,要么,要么相同,有,A C ,B D 2种方案,则不同的信号数为;332A 12=若只用2种不同的颜色灯带,则颜色相同,颜色相同,只有1种方案,则不同的信号数为,A C ,B D ;2232C A 6=则不同的信号总数为. 12618+=故选:A .6.已知,则()()()()()7292012921111x x a a x a x a x --=+-+-++-…( )()()1357924682a a a a a a a a a ++++++++=A .8 B .5C .2D .4【答案】D【分析】取代入等式可得,分别取,代入等式,组成方程组,联立即可得1x =0a 2x =0x =,代入即可求得结果.135792468,a a a a a a a a a +++++++【详解】解:因为,()()()()()7292012921111x x a a x a x a x --=+-+-++-…取代入可得:,1x =00a =取代入可得:①, 2x =23456780192a a a a a a a a a a ++++++++=+取代入可得:②, 0x =23456780192a a a a a a a a a a -+-++-+-=-①+②再除以2可得:,所以, 246802a a a a a +++=+24682a a a a ++=+①-②再除以2可得:, 135790a a a a a ++++=所以. ()()1357924682224a a a a a a a a a ++++++++=⨯=故选:D7.的个位数字为( ) 20232023A .6 B .7 C .8 D .9【答案】B【分析】先将写为,用二项式定理展开可知,的个位数字与相20232023()202332020+2023202320233同,将写为,再将用二项式定理展开可知的个位数字与20233()10113101⨯-()1011101-20233相同,计算结果选出选项即可. ()()101010111010110110101110113C 1013C 101⨯⨯-+⨯⨯-【详解】解:因为()20232023202332020+=, 0202301202212202122023020232023202320232023C 32020C 32020C 32020C 32020=⨯+⨯+⨯++⨯ 而个位数均为0, 1220232020,2020,,2020 所以的个位数字与相同,2023202302023020232023C 320203⨯=而()1011202320221011333393101=⨯=⨯=⨯-因为()()()()1101010110101111010101011011010111011101110113C 1013C 1013C 1013C 101=⨯⨯-+⨯⨯-++⨯⨯-+⨯⨯-个位数均为0,22101110,10,,10 所以的个位数字与相同,20233()()101010111010110110101110113C 1013C 1013101110330327⨯⨯-+⨯⨯-=⨯⨯-=故的个位数字为7. 20232023故选:B8.已知,,,则a ,b ,c 的大小关系为( ) 0.9ln 0.9a =- 1.1ln1.1b =- 1.001 1.001ln1.001c =-⨯A . B . b<c<a c b a <<C . D .c a b <<b a c <<【答案】B【分析】设,,利用导函数可得的单调性,()()ln 0f x x x x =->()()ln 0g x x x x x =->()(),f x g x 可得,,令,利用导函数可得在单a c >a c >()()()()ln 1ln 1211h x x x x x =+----<<()h x ()1,1-调递增,从而有,即可得出答案.a b >【详解】设,,则有, ()ln f x x x =-0x >()111x f x x x-'=-=所以当时,,单调递减; 01x <<()0f x '<()f x 当时,,单调递增.1x >()0f x ¢>()f x 所以,,即有,. ()()0.911f f >=()()1.111f f >=0.9ln 0.91a =-> 1.1ln1.11b =->令,则, ()()ln 0g x x x x x =->()()1ln 1ln g x x x =-+=-所以当时,,单调递增; 01x <<()0g x '>()g x 当时,,单调递减.1x >()0g x '<()g x 所以,即,故,, ()()1.00111g g <= 1.001 1.001ln1.0011c =-⨯<a c >b c >令,有, ()()()()ln 1ln 1211h x x x x x =+----<<()2211220111x h x x x x =+-=>+--'可得函数单调递增,故有,可得, ()h x ()()0.100h h >=ln1.1ln 0.90.20-->可得,故,综上所述,. 0.9ln 0.9 1.1ln1.1->-a b >c b a <<故选:B .【点睛】方法点睛: 对于比较实数大小方法:(1)利用基本函数的单调性,根据函数的单调性判断,(2)利用中间值“1”或“0”进行比较,(3)构造函数利用函数导数及函数单调性进行判断.二、多选题9.若,则m 的值可以是( )1231313C C m m +-=A .3 B .4 C .5 D .6【答案】BC【分析】利用组合数的计算即可求解【详解】因为,1231313C C m m +-=所以或,解得或5. 123m m +=-12313m m ++-=4m =故选:BC .10.下列说法正确的是( )A .可表示为10111220⨯⨯⨯⨯ (10)20A B .6个朋友聚会,见面后每两人握手一次,一共握手15次 C .若把英文“”的字母顺序写错,则可能出现的错误共有59种sorry D .将4名医护人员安排到呼吸、感染两个科室,要求每个科室至少有1人,则共有18种不同的安排方法 【答案】BC【分析】根据排列数的计算公式可判断A ;两两握手,即随便选出两人握手的所有可能结果数,通过计算即可判断B ;先对进行排列,再将放入位置中即可,列出式子计算即可判断C ;分3,,s o y r 人,1人一组,和2人,2人一组两种情况,分别求出对应的安排方法,相加即可.【详解】因为,故A 错误;102011121320A =⨯⨯⨯⨯…因为6人两两握手,共握(次),故B 正确;2615C =先在5个位置中选出3个位置,对进行全排列,剩下两个位置将放入即可,,,s o y r 故有:(种),而正确的共有1种,35A 54360=⨯⨯=所以可能出现的错误共有(种),故C 正确; 60159-=因为,41322=+=+当按3,1分组时,先选1人单独一组,剩下3人为一组,再将两组分配到两个不同科室中:共(种)分法,2142C A 8=当按2,2分组,在4人中选出2人到呼吸科,剩下2人自动去感染科,故有:(种)分法,故共有(种)安排方法,故D 错误.24C 6=8614+=故选:BC11.已知关于x 的方程的四个根是公差为2的等差数列的前四项,()()22880x x m x x t -+-+={}n a 为数列的前n 项和,则( )n S {}n a A .B . 12a =22m t +=C .D .253S a =10100S =【答案】BCD【分析】根据韦达定理可得,进而求得首项,即可得,即可判断选项A ,14238a a a a +=+=,n n a S C ,D ;由韦达定理可知代入即可判断D. 1423m t a a a a +=+【详解】解:因为为等差数列,所以, {}n a 14238a a a a +=+=因为,可得,,,, 2d =11a =23a =35a =47a =所以数列的通项公式为, {}n a ()12121n a n n =+-=-故,代入可得,,,()2122n n n S n n -=+⨯=35a =525S =10100S =故选项A 不正确,选项C ,D 正确;根据韦达定理可得,,故选项B 正确. 142371522m t a a a a +=+=+=故选:BCD .12.已知函数,下列说法正确的是( )()()21ln 08f x ax x x a =+-≠A .存在a 使得是函数的极值点 1x =()f x B .当时,存在两个极值点 10a -<<()f x C .“”是“为减函数”的充要条件 1a ≤-()f x D .存在a 使得函数有且仅有两个零点 ()f x 【答案】BC【分析】求出,由是函数的一个极值点可得值可判断A ;当()2444+'-=ax x f x x 1x =()f x a 0a >时记方程的两个根分别为,,由韦达定理可得函数的单调区间,2440ax x +-=1x ()212x x x <()f x 再利用函数值可判断函数的零点;当时可得函数单调递减,由可()f x 1a ≤-0∆≤()f x ()0f x '≤得可判断C 及此时函数零点个数;当时,由韦达定理可得函数211412⎛⎫≤-- ⎪⎝⎭a x ()f x 10a -<<的单调区间及极值点个数可判断B ;令,令可得求出函数()f x ()()11ln 122g x x x x =-+>()0g x '>的单调性可判断D.()g x 【详解】由题可知函数的定义域为,,()f x ()0,∞+()21144144+-=+-='ax x ax x f x x 对于A 选项,若是函数的一个极值点,有,可得,与矛盾,故1x =()f x ()104'==af 0a =0a ≠A 选项错误;当时,,记一元二次方程的两个根分别为,,有0a >16160a ∆=+>2440ax x +-=1x ()212x x x <,,可得, 1240x x a +=-<1240x x a=-<1201x x <<<可得函数的减区间为,增区间为,()f x ()20,x ()2,x +∞有,此时函数没有零点;()()2222221ln ln 08f x f x ax x x x =+->->≥()f x 当时,,可得,此时函数单调递减,1a ≤-16160a ∆=+≤2440ax x +-≤()f x 由可得,所以,故C 正确;可得此时()()244004'+-=≤>ax x f x x x 224411412-⎛⎫≤=-- ⎪⎝⎭x a x x 1a ≤-函数最多只有一个零点;()f x 当时,,有,,可得,可得函数10a -<<16160a ∆=+>124>0x x a+=-1240x x a=->120x x <<的减区间为,,增区间为, ()f x ()10,x ()2,x +∞()12,x x 故存在两个极值点,故B 正确;()f x 且有,,21144ax x =-()()21111111ln 488f x ax x x x =+-=-111111ln ln 22x x x x +-=-+令,有,令可得,()()11ln 122g x x x x =-+>()11222x g x x x -'=-=()0g x '>2x >故函数的减区间为,增区间为,有.故有()g x ()0,2()2,+∞()()3312ln 2ln e 0222=->-=>≥g g x,可得此时函数最多只有一个零点,由上知D 错误. ()10f x >()f x 故选:BC .【点睛】方法点睛:函数由零点求参数的取值范围的常用方法与策略:1、分类参数法:一般命题情境为给出区间,求满足函数零点个数的参数范围,通常解法为从()f x 中分离参数,然后利用求导的方法求出由参数构造的新函数的最值,根据题设条件构建关于参数的不等式,再通过解不等式确定参数的取值范围;2、分类讨论法:一般命题情境为没有固定的区间,求满足函数零点个数的参数范围,通常解法为结合函数的单调性,先确定参数分类标准,在每个小范围内研究零点的个数是否符合题意,将满足题意的参数的各个小范围并在一起,即可为所求参数的范围.三、填空题13.从甲地去乙地有4班火车,从乙地去丙地有3班轮船,若从甲地去丙地必须经过乙地中转,则从甲地去丙地可选择的出行方式有______________种. 【答案】12【分析】由分步乘法计数原理可得答案.【详解】由分步乘法计数原理知从甲地去丙地可选择的出行方式有(种). 3412⨯=故答案为:12.14.用数字0,1,2,3,4,5组成没有重复数字的4位数,其中奇数的个数为______. 【答案】144【分析】根据题意,分3步进行分析:①从1、3、5三个数中取一个排个位,②0不能在千位,则千位的安排方法有4种,③在剩下的4个数中任选2个,安排在百位、十位,由分步计数原理计算可得答案.【详解】解:根据题意,分3步进行分析:①从1、3、5三个数中取一个排个位,有3种安排方法, ②0不能在千位,则千位的安排方法有4种,③在剩下的4个数中任选2个数字,排在百位与十位,有种情况,2412A =则符合题意的奇数的个数是为个; 3412144⨯⨯=故答案为:.14415.已知是正项等比数列的前n 项和,,则的最小值为n S {}n a 22S =64254S S S -+______________. 【答案】8-【分析】设的公比为q ,则通过等比数列的性质可得,利用二次函{}n a ()426422544S S S q q S -+-=数的性质即可求解【详解】设的公比为,因为,{}n a ()0q q >22S =则64254S S S -+()()()24264242254S S S S S S S S S ⎡⎤⎡⎤=+-+⎣⎦⎣-⎦+-+-, ()()()()2242422222215144228q q S q S S q q S q =++-++=-=--8-≥当且仅当的最小值为 q =64254S S S -+8-故答案为:8-16.已知函数,若恒成立,则k 的取值范围是______________.()2e x f x x -=()()ln 1f x k x x --≥【答案】(],1-∞【分析】将表示为,原不等式恒成立,即恒成立,对()f x ln 2e x x --()ln 2eln 1x x k x x --≥--ln 1x x --进行换元,构造函数求出新元的范围,则原不等式即可化为,,分两种情1e t kt -≥()0t ≥0,0t t =>况讨论,当时,代入可知恒成立,当时,对不等式进行全分离,构造新函数,求导求单调0=t 0t >性求出最值即可得k 的取值范围.【详解】解:因为恒成立,所以,()()ln 1f x k x x --≥0x >因为,由恒成立, ()22ln 2ln e e =ee x x x x xf x x ----==()()ln 1f x k x x --≥即①恒成立,令,()ln 2eln 1x x k x x --≥--()ln 1h x x x =--所以,即在上,,单调递减, ()111x h x x x-'=-=()0,1()0h x '<()h x 在上,,单调递增,故, ()1,+∞()0h x '>()h x ()()10h x h ≥=令,①式可化为②,()ln 10t x x t =--≥1e t kt -≥当时,②式可化为:,此时不等式恒成立,故;0=t 10e≥R k ∈当时,②式可化为:恒成立,故只需即可,0t >1e t k t -≤1min e t k t -⎛⎫≤ ⎪⎝⎭令,有, ()()1e 0t g t t t -=>()()121e t t g t t--'=在上,,单调递减, ()0,1()0g x '<()g x 在上,,单调递增, ()1,+∞()0g x '>()g x 所以,故, ()()min 11g t g ==1k ≤综上:k 的取值范围为. (],1-∞故答案为:(],1-∞【点睛】方法点睛:该题考查函数与导数的综合应用,属于难题,关于恒成立问题的方法有: (1)若,恒成立,则只需; x D ∀∈()f x a ≥()min f x a ≥(2)若,恒成立,则只需; x D ∃∈()f x a ≥()max f x a ≥(3)若,恒成立,则只需; x D ∀∈()f x a ≤()max f x a ≤(4)若,恒成立,则只需;x D ∃∈()f x a ≤()min f x a ≤(5)若,恒成立,则只需; 12,x A x B ∀∈∀∈()()12f x g x ≤()()max min f x g x ≤(6)若,恒成立,则只需; 12,x A x B ∀∈∃∈()()12f x g x ≤()()max max f x g x ≤(7)若,恒成立,则只需; 12,x A x B ∃∈∀∈()()12f x g x ≤()()min min f x g x ≤(8)若,恒成立,则只需.12,x A x B ∃∈∃∈()()12f x g x ≤()()min max f x g x ≤四、解答题17.已知二项式的展开式中共有10项.(2n(1)求展开式的第5项的二项式系数; (2)求展开式中含的项. 4x 【答案】(1)126 (2) 418x【分析】(1)根据项数可求得,根据二项式系数与项数之间关系列出等式,解出即可; 9n =(2)由(1)中的,求出通项,使的幂次为4,求出含的项即可. 9n =x 4x 【详解】(1)解:因为二项式的展开式中共有10项,所以,9n =所以第5项的二项式系数为;49C 126=(2)由(1)知,记含的项为第项,9n =4x 1r +所以, (()992199C 2C 21rr r rr rr r T x --+==-取,解得,所以, 42r =8r =()88814299C 2118T x x =-=故展开式中含的项为.4x 418x 18.已知函数的图象在点处的切线l 过坐标原点.()2ln f x x a x =-()()1,1P f (1)求实数a 的值;(2)若直线l 与抛物线相切,求抛物线的对称轴方程.2y x mx m =-++【答案】(1)1(2). 12x =-【分析】(1)求出,再由、可得曲线在点P 处的切线方程,代()f x '()12f a '=-()11f =()y f x =入原点可得答案;()0,0(2)求出直线l 的方程与抛物线方程联立,利用解得,可得抛物线的方程为及对称轴方Δ0=m 程.【详解】(1)由,再由,, ()2a f x x x='-()12f a '=-()11f =可得曲线在点P 处的切线方程为,()y f x =()()121y a x -=--整理为,()21y a x a =-+-代入原点,有,可得,()0,001a =-1a =故实a 值为1;(2)由(1)可知直线l 的方程为,y x =联立方程,消去y 后整理为, 2y x mx m y x⎧=-++⎨=⎩()210x m x m +--=有,解得, ()2140m m ∆=-+=1m =-可得抛物线的方程为,故抛物线的对称轴方程为. 21y x x =---12x =-19.现有4名男生、3名女生站成一排照相.(用数字作答)(1)两端是男生,有多少种不同的站法?(2)任意两名男生不相邻,有多少种不同的站法?(3)男生甲要在女生乙的右边(可以不相邻),有多少种不同的站法?【答案】(1)1440(2)144(3)2520【分析】(1)特殊位置特殊考虑,先取两位男生放置在两端,另5位全排列,列出等式,计算即可;(2)不相邻问题插空,先将另3名女生全排列,空出4个位置,让男生插空站入, 列出等式,计算即可;(3)排序问题,先在7个位置中找到5个位置,让除甲乙外的另5人排列,后将甲乙站入, 列出等式,计算即可.【详解】(1)解:先选2名男生排两端有种方法,再排其余学生有种方法,24A 55A 所以两端是男生的不同站法有(种); 2545A A 1440=(2)先排3名女生有种方法,再将4名男生插入4个空隙中有种方法,33A 44A 所以任意两名男生不相邻的不同站法有(种); 4343A A 144=(3)先在7个位置中找到5个位置,让除甲乙外的另5人排列共有:种方法,57A 再将甲乙按照甲在乙右边的顺序,放置另两个位置中共1种,所以男生甲要在女生乙的右边的不同站法有(种). 57A 2520=20.已知等差数列的前n 项和是,,.{}n a n S 13416a a +=528S a =(1)求数列的通项公式;{}n a (2)若成立,求正整数m ,k 的值.119m k m S S +-=【答案】(1)31n a n =-(2),.2m =7k =【分析】(1)设出公差建立方程组,解出即可得通项公式;(2)由(1)的通项公式化简可得,根据,所以m k m S S +-()6312717k m k ++=⨯⨯*,N m k ∈,所以或,对分类讨论,即可得出结果.3631k m k <++2k =7k =k【详解】(1)解:设等差数列的公差为d ,由题意有, {}n a ()()111142165108a a d a d a d ⎧++=⎪⎨+=+⎪⎩解得,,所以,12a =3d =()23131n a n n =+-=-故数列的通项公式为;{}n a 31n a n =-(2)由 ()1122m m k m k m m m m k k a a S S a a a +++++++-=+++= , ()()311312k m m k ⎡⎤+-++-⎣⎦=()6312k m k ++=有,可得, ()6311192k m k ++=()6312717k m k ++=⨯⨯因为,所以,*,N m k ∈*631N m k ++∈因为,所以或,6313m k k ++>2k =7k =①当时,可得,由m 为正整数,不合题意,舍; 2631717k m k =⎧⎨++=⨯⎩2563k m =⎧⎪⎨=⎪⎩②当时,可得,满足题意, 7631217k m k =⎧⎨++=⨯⎩72k m =⎧⎨=⎩综上:,.2m =7k =21.已知(n 为正整数)的二项展开式. 21nx ⎛⎫ ⎪⎝⎭(1)若,求展开式中所有项的系数之和; 012C C C C 64n n n n n +++⋯+=(2)若,求展开式中的无理项的个数;12C C 465n n n -+=(3)若,求展开式中系数最大的项.20n =【答案】(1)729(2)15(3)展开式中系数最大的项为和57635043840-=T x 1528635043840-=T x【分析】(1)由求出,再令可得答案; 012C C C C 2+++⋯+=n n n n n n n 1x =(2)由求出,求出展开式的通项公式,再由的指数不为整数可得答案;12C C 465n n n -+=n x (3)求出展开式的通项公式由解不等式可得答案. 201212020201192020C 2C 2C 2C 2r r rr r r rr ----+-⎧≥⎨≥⎩【详解】(1)由可得,0122=C C C C 64+++⋯+=n n n n n n =6n 令可得, 1x =661237291⎛⎫+== ⎪⎝⎭所以展开式中所有项的系数之和为729;(2)若,则,解得,或舍去, 12C C 465n n n-+=()14652-+=n n n 30n =31n =-设的通项为, 3021⎛⎫ ⎪⎝⎭x (030520130303321C C 2-+--⎛⎫== ⎪⎝⎭r r r r rr r T x x 且,{}0,1,2,,30∈ r 所以当时可得展开式中的无理项,所以共有15个无理项;1,3,5,,29r =(3)设的通项为, 2021⎛⎫ ⎪⎝⎭x (020520120202221C C 2-+--⎛⎫== ⎪⎝⎭r r r r rr r T x x 且,{}0,1,2,,20∈ r 则,解得, 201212020201192020C 2C 2C 2C 2r r rr r r r r ----+-⎧≥⎨≥⎩67r ≤≤,,2030652720206C 2635043840---==T x x 1515722220870C 2635043840---==T x x 所以展开式中系数最大的项为和. 57635043840-=T x 1528635043840-=T x 22.已知函数. ()()3211132f x x a x ax =+--(1)若,求函数的极值;2a =()f x (2)当时,若对,恒成立,求的最小值.1a >0x ∀≥()e 0x f x x b ++≥4b a -【答案】(1)极小值为,极大值为 103-76(2) 2142e 3--【分析】(1)求导,再根据极值的定义即可得出答案;(2)令,求导得,由函数单调()()()e 0x g x x x x f b =++≥()()()1e x g x x a x '=++-()e x h x x a =+-递增及,,可知存在,使得,即,从而可()010h a =-<()e 0a h a =>()0,m a ∈()0h m =e m a m =+求出函数的最小值,,恒成立,则,从而可将表示出()g x 0x ∀≥()e 0x f x x b ++≥()min 0g x ≥b来,【详解】(1)若,可得, 2a =()3211232f x x x x =--有,()()()2212f x x x x x =--=+-'令,可得,令,则或,()0f x '<12x -<<()0f x ¢>1x <-2x >故函数的增区间为,,减区间为,()f x (),1-∞-()2,+∞()1,2-函数的极小值为,极大值为; ()f x ()1023f =-()716f -=(2)令,()()()e 0x g x x x x f b =++≥有,()()()()()()()()211e 11e 1e x x x g x a x a x x x a x x x a x '=+--++=+-++=++-由函数单调递增及,,()e x h x x a =+-()010h a =-<()e 0a h a =>可知存在,使得,即,()0,m a ∈()0h m =e m a m =+当时,,当时,,x >m ()0g x '>0x m <<()0g x '<所以函数的减区间为,增区间为,()g x [)0,m (),m +∞可得 ()()()32min 111e 32m g m m a m am m b g x ==+--++, ()()32322111111e e e e 32622m m m m m m m m m m b m m m b =+---+++=---+由,恒成立,0x ∀≥()e 0x f x x b ++≥有,可得, ()0g m ≥322111e 622m b m m m ≥++有, ()3221114e 4e 622m m b a m m m m -≥++-+可得, 3221114e 44e 622m m b a m m m m -≥++--令, ()()322111e 44e 0622x x x x x x x x ϕ=++-->有 ()()()2221112e 44e 4e 1222x x x x x x x x x x ϕ⎛⎫'=+++--=+-+ ⎪⎝⎭, ()()()124e 12x x x =-++令,则,令,则,()0x ϕ'>2x >()0x ϕ'<02x <<所以函数的减区间为,增区间为,()x ϕ()0,2()2,+∞所以, ()()222414222e 84e 2e 33x ϕϕ≥=++--=--故的最小值为. 4b a -2142e 3--【点睛】方法点睛:对于利用导数研究不等式的恒成立与有解问题的求解策略:1、通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;2、利用可分离变量,构造新函数,直接把问题转化为函数的最值问题.3、根据恒成立或有解求解参数的取值时,一般涉及分离参数法,但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况,进行求解,若参变分离不易求解问题,就要考虑利用分类讨论法和放缩法,注意恒成立与存在性问题的区别.。
重庆市第一中学校2023-2024学年高二下学期第一次月考数学试题

重庆市第一中学校2023-2024学年高二下学期第一次月考数学试题学校:___________姓名:___________班级:___________考号:___________二、多选题9.在某次学科期末检测后,从全部考生中选取100名考生的成绩(百分制,均为整数)分成[50,60),[)[)60,70,70,80,[80,90),[90,100)五组后,得到频率分布直方图(如右图),则下列说法正确的是()据学校共有的人数,得到关于高一人数的方程,解方程得到高一人数,用人数乘以抽取的比例,得到结果.本题考查分层抽样,在分层抽样之前有一个小型的运算,是一个基础题,运算量不大,可以作为选择和填空出现.分层抽样主要用于个体数量较多,且个体间具有明显差异的,这时采用分层抽样合适.4.D【分析】分甲得2个和甲得1个磁力片两种情况分类求解,再由分类加法计数原理得解.【详解】若甲分得两个磁力片,共有1232C A 6=种分法,若甲只分得一个磁力片,共有2232C A 6=种分法,由分类加法计数原理,可得共有6612+=种分法.故选:D 5.A【分析】根据递推关系式可知数列{}n a 是以6为周期的周期数列,根据周期性和对数运算法则可求得结果.【详解】由题意知:0n a >,31n n a a +=Q ,361n n a a ++\=,6n n a a +\=,即数列{}n a 是以6为周期的周期数列;()()()1234561425361a a a a a a a a a a a a ==Q ,()()()33712202412202412345612ln ln ln ln ln ln a a a a a a a a a a a a a a \++×××+=×××××=+ln1ln 2ln 2=+=.故选:A.6.C【分析】根据题意找出相应的规律,第37个数为第21行第3个数,从而可求解.【详解】由题意可得每行有2个数且从第3行开始计数,所以第37项为“杨辉三角”中第21行第3个数,所以20n =,3r =,所以3122020C C 190-==.故C 正确.故选:C.=。
安徽省高二下学期第一次月考数学试题(解析版)

高二下学期第一次月考数学试题一、单选题1.已知数列的前4项为:l ,,,,则数列的通项公式可能为{}n a 12-1314-{}n a A . B .1n a n=1n a n=-C .D .(1)nn a n -=1(1)n n a n--=【答案】D【分析】分母与项数一样,分子都是1,正负号相间出现,依此可得通项公式【详解】正负相间用表示,∴.1(1)n --1(1)n n a n--=故选D .【点睛】本题考查数列的通项公式,属于基础题,关键是寻找规律,寻找与项数有关的规律. 2.若为数列的前项和,且,则( )n S {}n a n 1n nS n =+51a =A .B .C .D .305665130【答案】D【分析】根据公式直接求出,进一步求出答案. 1n n n a S S -=-5a 【详解】∵ 5545454151416530=-=-=-=++a S S ∴. 5130a =故选:D.【点睛】本题考查数列前项和与通项公式的关系,属于基础题. n 3.已知数列满足,,则( ){}n a 13a =()111n n a a n n +=++n a =A .B .C .D .14n +14n -12n +12n-【答案】B【分析】由,利用累加法得出. 1111n n a a n n +-=-+n a 【详解】由题意可得,()111111n n a a n n n n +-==-++所以,,…,, 21112a a -=-321123a a -=-1111n n a a n n--=--上式累加可得()()()121321--=-+-++- n n n a a a a a a a a,111111112231=-+-++-=-- n n n 又,所以.13a =14=-n a n故选:B .4.中国古代数学著作《算法统宗》中有这样一个“九儿问甲歌”问题:一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百又零七,借问长儿多少岁,各儿岁数要详推.在这个问题中,记这位公公的第个儿子的年龄为,则 n n a 3456719a a a a a a a ++++--=A . B . C . D .466992138【答案】B【详解】由题意得数列成等差数列,公差为-3,所以9111998(3)20735;2S a a =+⨯⨯⨯-=∴= 选B.3456719a a a a a a a ++++--=131269.a d +=5.已知在数列中,且,设为的前项和,若,则{}n a *11(n n a a n N -=+∈2)n ≥n S {}n a n 972S =9a =( ) A . B . C . D .8121636【答案】B【分析】由题意得到数列是以公差为的等差数列,根据,求得的值,{}n a 1()9195992S a a a =+=5a 然后利用,即可求解.954a a d =+【详解】因为在数列中,且,{}n a *11(n n a a n N -=+∈2)n ≥可得且,所以数列是以为公差的等差数列,*11(n n a a n N --=∈2)n ≥{}n a 1d =又因为为的前项和,且, n S {}n a n 972S =所以,解得, ()919599722S a a a =+==58a =又由,所以. 9544a a d -==95412a a =+=故选:B .6.已知数列的前项和为,,且,,则当取得最大值时,{}n a n n S 212n n n a a a +++=113a =211a =n Sn =A .5 B .6C .7D .8【答案】C【分析】由题意,可得数列为等差数列,求得数列的通项公式为,进而得到当{}n a {}n a 152n a n =-时,,当时,,即可得到答案. 17,n n N +≤≤∈0n a >8,n n N +≥∈0n a <【详解】由题意,数列满足,即, {}n a 212n n n a a a +++=211n n n n a a a a +++-=-所以数列为等差数列,{}n a 设等差数列的公差为,则,{}n a d 222d a a =-=-所以数列的通项公式为, {}n a 2(1)13(1)(2)152n a a n d n n =+-=+-⨯-=-令,即,解得, 0n a ≥1520n -≥152n ≤所以当时,,当时,, 17,n n N +≤≤∈0n a >8,n n N +≥∈0n a <所以数列中前项的和最大,故选C.{}n a 77S 【点睛】本题主要考查了等差数列的中项公式的应用,以及前n 项和的最值问题,其中解答中根据等差数列的中项公式,得出数列为等差数列,得出等差数列的通项公式是解答的关键,着重考查了推理与计算能力,属于基础题.7.根据全球摩天大楼的统计,至2019年,安徽省合肥市的摩天大楼已经有95座在中国城市中排名第10位,全球排名第15位,目前合肥恒大中心建设中的最高楼,外形设计成了“竹节”的形态,既体现了力量超凡,又象征着向上生长的强烈意志,更预示了未来的繁荣和兴旺.它与传承千年的“微文化”相得益彰,建成后将跻身世界十大摩天大楼之列,若大楼由9节“竹节”组成,最上部分的4节高228米,最下部分3节高204米,且每一节高度变化均匀(即每节高度自上而下成等差数列),则该摩天大楼的总高度为( ) A .518米 B .558米C .588米D .668米【答案】B【分析】根据题意,构造等差数列,求出数列的基本量,即可用公式求得其前项和. 9【详解】设大楼自上而下每一节高度构成等差数列, {}n a 设数列的首项为,公差为, 1a d 由题可知,496228,204S S S =-=,; 146228a d +=1321204a d +=联立方程组解得.154,2a d ==故可得. 91936549362558S a d =+=⨯+⨯=故选:B.【点睛】本题考查等差数列通项公式的基本量的计算,属基础题;本题的难点是要根据题意提取信息.8.设是等比数列,且,,则( ) {}n a 1231a a a ++=234+2a a a +=678a a a ++=A .12 B .24 C .30 D .32【答案】D【分析】根据已知条件求得的值,再由可求得结果.q ()5678123a a a q a a a ++=++【详解】设等比数列的公比为,则, {}n a q ()2123111a a a a q q ++=++=,()232234111112a a a a q a q a q a q q q q ++=++=++==因此,.()5675256781111132a a a a q a q a q a q q q q ++=++=++==故选:D.【点睛】本题主要考查等比数列基本量的计算,属于基础题.二、多选题9.数列的前项和为,且满足,,则下列说法正确的有( ){}n a n n S 11a =121n n n a n a n a +⎧⎪=⎨⎪⎩,是奇数,是偶数A . B .是周期数列 C .D .42a ={}n a 20222a =1820S =【答案】BC【分析】根据题意,分别求得,得到数列构成以为周期的周期数列,12345,,,,,a a a a a {}n a 11,2,,12逐项判定,即可求解.【详解】由题意,数列满足 {}n a 11211n n n a n a a n a +⎧⎪==⎨⎪⎩,为奇数,,,为偶数当时,; 1n =2122a a ==当时,; 2n =32112a a ==当时,;3n =4321a a ==当时,; 4n =5411a a ==当时,; 5n =6522a a ==当时,;, 6n =76112a a == 归纳可得数列构成以为周期的周期数列,所以A 不正确,B 正确;{}n a 11,2,,12又由,所以C 正确; 20225054222a a a ⨯+===因为,所以,所以D 错误.12341912122a a a a +++=+++=189412212S =⨯++=故选:BC .10.已知数列的前项和为,若,,则下列说法正确的是( ) {}n a n n S 110a =-13n n a a +=+A .是递增数列B .是数列中的项{}n a 10{}n a C .数列中的最小项为 D .数列是等差数列{}n S 4S n S n ⎧⎫⎨⎬⎩⎭【答案】ACD【分析】利用数列的单调性可判断A 选项;求出数列的通项公式,解方程,可判断B{}n a 10n a =选项;解不等式,可判断C 选项;求出数列的通项公式,利用等差数列的定义可判断0n a ≤n S n ⎧⎫⎨⎬⎩⎭D 选项.【详解】由已知,,所以,数列是首项为,公差为的等差数列, 110a =-13n n a a +-={}n a 10-3所以,.()1031313n a n n =-+-=-对于A 选项,因为,所以,是递增数列,A 对; 13n n a a +-={}n a 对于B 选项,令,可得,B 错; 31310n a n =-=233n *=∉N 对于C 选项,令可得,所以,数列中的最小项为,C 对; 3130n a n =-≤133n ≤{}n S 4S 对于D 选项,,则, ()()2110313323222n n n a a n n n nS +-+--===3232n S n n -=所以,,()1312332331222n n n S Sn n n ++---=-=+故数列为等差数列,D 对.n S n ⎧⎫⎨⎬⎩⎭故选:ACD.11.已知数列是等比数列,则下列结论中正确的是( ){}n aA .数列是等比数列 2{}n a B .若则4123,27,a a ==89a =±C .若则数列是递增数列 123,a a a <<{}n a D .若数列的前n 和则r =-1 {}n a 13,n n S r -=+【答案】AC【解析】根据等比数列定义判断A;根据等比数列通项公式判断B,C;根据等比数列求和公式求项判断D.【详解】设等比数列公比为{}n a ,(0)q q ≠则,即数列是等比数列;即A 正确; 222112(n n n na a q a a ++==2{}n a 因为等比数列中同号,而 所以,即B 错误;{}n a 4812,,a a a 40,a >80a >若则或,即数列是递增数列,C 正确; 123,a a a <<1211101a a a q a q q >⎧<<∴⎨>⎩1001a q <⎧⎨<<⎩{}n a 若数列的前n 和则{}n a 13,n n S r -=+111221313231,2,6a S r r a S S a S S -==+=+=-==-=所以,即D 错误32211323(1),3a a q r r a a ===∴=+=-故选:AC【点睛】等比数列的判定方法 (1)定义法:若为非零常数),则是等比数列; 1(n na q q a +={}n a (2)等比中项法:在数列中,且,则数列是等比数列;{}n a 0n a ≠212n n a a a a ++={}n a (3)通项公式法:若数列通项公式可写成均是不为0的常数),则是等比数列;(,nn a cq c q ={}n a (4)前项和公式法:若数列的前项和为非零常数),则是等比数n {}n a n (0,1,nn S kq k q q k =-≠≠{}n a 列.12.已知有一段路共有米,有一人从第二天起每天走的路程减半,天恰好走完了这段路则下1865.列说法正确的是( )A .第一天走的路程比后四天走的路程多米B .第二天走了米648C .第三天走了全程的D .后三天共走了米18144【答案】AB【分析】设此人第天走米,根据已知条件,结合等比数列的前项和公式,推出,即可依次n n a n n a 求解判断各项正误.【详解】设此人第天走米, n n a 则数列是首项为,公比为的等比数列, {}n a 1a 12q =因为,5186S =所以,解得,155112186112a S ⎛⎫- ⎪⎝⎭==-196a = ,11962n n a -⎛⎫∴=⋅ ⎪⎝⎭对于A ,因为第一天走的路程为米, 96所以后四天走的路程为, 1869690-=因为,96906-=所以此人第一天走的路程比后四天走的路程多米,所以 A 正确; 6对于B ,由于,所以B 正确; 2196482a =⨯=对于C ,由于,,所以C 不正确; 3196244a =⨯=2411868>对于D ,由于,, 12144a a +=18614442-=所以后三天一共走了米,所以D 不正确. 42故选:AB .三、填空题13.数列的前项和为,,则通项公式______.{}n a n n S 21nn S =+n a =【答案】 13122n n n -=⎧⎨≥⎩,,【分析】利用公式进行求解.1112n nn S n a S S n -=⎧=⎨-≥⎩,,【详解】由题知,当时,,1n =111213a S ==+=当时, ①2n ≥1121n n S --=+又 ②21nn S =+由②减去①有:,12n n a -=当不满足上式,所以. 1n =13122n n n a n -=⎧=⎨≥⎩,,故答案为:. 13122n n n -=⎧⎨≥⎩,,14.《九章算术》卷七“盈不足”有这样一段话:“今有良马与弩马发长安至齐.齐去长安三千里,良马初日行一百九十三里.日增十三里,驽马初日行九十七里,日减半里.”意思是:今有良马与弩马从长安出发到齐国,齐国与长安相距3000里,良马第一日走193里,以后逐日增加13里,弩马第一日走97里,以后逐日减少0.5里.则8天后两马之间的距离为___________里. 【答案】1146【分析】由题意,良马与驽马日行里数分别构成等差数列,由等差数列通项公式可得.【详解】良马日行里数构成以193为首项,13为公差的等差数列;驽马日行里数则构成以97为首项,-0.5为公差的等差数列,则两马同时出发后第8日,良马日行里数里), 871938131908 (2⨯⨯+⨯=而驽马日行里数(里), ()879780.57622⨯⨯+⨯-=所以良马较驽马日行里数多1908-762=1146里. 故答案为:1146.【点睛】本题考查等差数列的应用,涉及等差数列的通项公式,属于基础题,理解题意是解题的关键.15.设等比数列的公比为,其前项和为,若,,则{}n a q n n S 2232S a =+4432S a =+q =__________. 【答案】或1-32【分析】根据已知条件,由首项和公比列方程组求解.【详解】等比数列的公比为,若,,则, {}n a q 2232S a =+4432S a =+1q ≠则有,①,()11132a q a q +=+② 4311(1)32,1a q a q q-=+-②-①,化简可得:,解得或 2230q q --=1q =-32q =故答案为: 或1-3216.已知数列的前项积为,,,,,则___. {}n a n n T 0n a ≠212n n n a a a ++=213a =59a =5T =【答案】1【分析】由已知得数列为等比数列,利用通项即可求得首项和公比,从而求得. {}n a 5T 【详解】由已知可得数列为等比数列,设等比数列公比为q,212n n n a a a ++={}n a 即9=,解得q=3,则,352,a a q =313q 119a =前项积 5123451010511111151319T a a q a q a q a q a q =⨯⨯⨯⨯==⨯=故答案为1【点睛】本题考查等比数列通项的应用,考查学生计算能力,属于基础题.四、解答题17.给出一个三角数阵: 第一行 1第二行 23第三行4567第四行 89101112131415若等差数列的前项和为,,比数阵第八行所有数的个数多.{}()*N n a n ∈n n S 23a =12S 16(1)求数列的通项公式;{}n a (2)求数列的前项和.11n n a a +⎧⎫⎨⎬⎩⎭n n T 【答案】(1); 21n a n =-(2). 21n n T n =+【分析】(1)由等比数列通项公式求数阵第八行的数的的个数,设的的公差为,由条件列方{}n a d程求,由此可得数列的通项公式;d {}n a (2)利用裂项相消法求数列的前项和.11n n a a +⎧⎫⎨⎬⎩⎭n n T 【详解】(1)由数阵可知各行数的个数构成一个首项为,公比为的等比数列, 12所以数阵第行所有数的个数为. 872128=因为比数阵第行所有数的个数多, 12S 816所以,即. 1212816S -=12144S =设的的公差为, {}n a d 则,1211266144S a d =+=,解得,, 213a a d =+=2d =11a =所以 ()1121n a a n d n =+-=-;(2)因为,()()()111111221212121n n a a n n n n +==--+-+所以. 11111111112335212122121n nT n n n n ⎛⎫⎛⎫=-+-++-=-=⎪ ⎪-+++⎝⎭⎝⎭L 18.已知等差数列{an }的所有项和为150,且该数列前10项和为10,最后10项的和为50. (1)求数列{an }的项数; (2)求a 21+a 22+…+a 30的值. 【答案】(1)50 (2)30【分析】(1)推导出(a 1+an )+(a 2+an ﹣1)+(a 3+an ﹣2)+…+(a 10+an ﹣9)=60,由等差数列性质知,a 1+an =a 2+an ﹣1=a 3+an ﹣2=…=a 10+an ﹣9,从而10(a 1+an )=60,由此能求出数列{an }的项数.(2)推导出,由此能求出,从而能求出结果.112496292a d a d +=⎧⎨+=⎩()212223302130102a a a a a a ++++=+ 【详解】(1)据题意,得a 1+a 2+a 3+…+a 10=10,an +an ﹣1+an ﹣2+…+an ﹣9=50, ∴(a 1+an )+(a 2+an ﹣1)+(a 3+an ﹣2)+…+(a 10+an ﹣9)=60, 又据等差数列性质知,a 1+an =a 2+an ﹣1=a 3+an ﹣2=…=a 10+an ﹣9, ∴10(a 1+an )=60,∴a 1+an =6, 又,()11502n n a a +=∴n =50,即数列{an }的项数为50.(2)据(1)求解知,, 1501610910102a a a d +=⎧⎪⎨⨯+=⎪⎩即, 112496292a d a d +=⎧⎨+=⎩∴, 11120110a d ⎧=⎪⎪⎨⎪=⎪⎩∴5(2a 1+49d )30. ()212223302130102a a a a a a ++++=+= 11152492010⎛⎫=⨯+⨯= ⎪⎝⎭19.已知等比数列{an }中,an > 0,公比q ∈(0,1),且a 1a 5+2a 3a 5+a 2a 8=25, a 3与a 5的等比中项为2.(1)求数列{an }的通项公式;(2)设bn =log 2an ,求数列{bn }的前n 项和Sn .【答案】(1)an =.(2)Sn =.52n -()92n n -【分析】(1)利用等比数列通项公式、等比中项得到a 3a 5=4,a 3+a 5=5,从而a 3,a 5是方程x 2﹣5x +4=0的两个根,且a 3>a 5,由此能求出数列{an }的通项公式.(2)推导出bn =log 2an 5﹣n ,由此能求出数列{bn }的前n 项和.52log 2n -==【详解】解:(1)∵在等比数列{an }中,,公比q ∈(0,1), ()*0n a n N∈>且a 1a 5+2a 3a 5+a 2a 8=25,a 3与a 5的等比中项为2,∴(a 3+a 5)2=25,, 2233552a a a a ++=23544a a a ==∴a 3a 5=4,a 3+a 5=5,即a 3,a 5是方程x 2﹣5x +4=0的两个根,且a 3>a 5,解方程x 2﹣5x +4=0,得a 3=4,a 5=1,,,, 25314a q a ==12q =31216a a q ==∴数列{an }的通项公式an =16×=. 11()2n -52n -(2)∵bn =log 2an 5﹣n ,52log 2n -==∴数列{bn }的前n 项和:Sn =5n ﹣(1+2+3+…+n )=5n . ()()1922n n n n +--=20.年月日,小刘从各个渠道融资万元,在某大学投资一个咖啡店,年月日正20199125202011式开业,已知开业第一年运营成本为万元,由于工人工资不断增加及设备维修等,以后每年成本6增加万元,若每年的销售额为万元,用数列表示前年的纯收入注:前年的纯收入231{}n a n .(n =前年的总收入前年的总支出投资额n -n -)(1)试求年平均利润最大时的年份年份取正整数,并求出最大值;()(2)若前年的收入达到最大值时,小刘计划用前年纯收入的对咖啡店进行重新装修,请问:小n n 13刘最早从哪一年对咖啡店进行重新装修?并求小刘计划装修的费用.【答案】(1)年,万元;202516(2)年,万元.203348【分析】(1)每年的运营成本构成一个等差数列,每年的销售额是一个常数列,根据题意,列出等式年平均利润为,之后应用基本不等式,结合求得结果; 2256n a n n n ⎛⎫=-+ ⎪⎝⎭*N n ∈(2)由(1)知,利用二次函数的性质以及的条件,得到当时,22625n a n n =-+-*N n ∈13n =na 取得最大值,进而得到结果.144【详解】(1)由条件可知,每年的运营成本构成首项为,公差为的等差数列,62, ()2131622526252n n n a n n n n ⎡⎤-∴=-+⨯-=-+-⎢⎥⎣⎦()*N n ∈则年平均利润为, 2256n a n n n ⎛⎫=-+ ⎪⎝⎭由,当且仅当,即时取等号. 2510n n +≥25n n=5n =此时,取最大值. n a n 16到年,年平均利润最大,最大值为万元;∴202516(2)由Ⅰ可得, ()()()22*262513144N n a n n n n =-+-=--+∈当时,取得最大值.13n =n a 144万元144348(÷=).故小刘最早从年对咖啡店进行重新装修,计划装修费用为万元.20334821.Sn 为等比数列{an }的前n 项和,已知a 4=9a 2,S 3=13,且公比q >0.(1)求an 及Sn ;(2)是否存在常数λ,使得数列{Sn +λ}是等比数列?若存在,求λ的值;若不存在,请说明现由.【答案】(1)an =3n -1,Sn =;(2)存在,. 312n -12【分析】(1)根据等比数列的通项公式前n 项和公式,通过解方程组求出等比数列的首项和公比,进而求出通项公式和前n 项和;(2)运用假设法,结合等比数列的通项公式和等比数列的性质和定义进行求解即可.【详解】(1)由题意可得,解得a 1=1,q =3, ()31131911310a q a q a q q q ⎧=⎪-⎪=⎨-⎪⎪>⎩所以an =3n -1,Sn ==. 1313n--312n -(2)假设存在常数λ,使得数列{Sn +λ}是等比数列,因为S 1+λ=λ+1,S 2+λ=λ+4,S 3+λ=λ+13,所以(λ+4)2=(λ+1)(λ+13),解得λ=,此时Sn +=×3n ,则=3, 12121211212n n S S +++故存在常数λ=,使得数列是等比数列. 1212n S ⎧⎫+⎨⎬⎩⎭【点睛】本题考查了等比数列通项公式和前n 项和公式的应用,考查了等比数列的定义和性质的应用,考查了数学运算能力.22.已知无穷数列的前项中的最大项为,最小项为,设.{}n a n n A n B n n n b A B =+(1)若,求数列的通项公式;21n a n =-{}n b (2)若,求数列的前项和; 212n n n a -={}n b n n S (3)若数列是等差数列,求证:数列是等差数列.{}n b {}n a 【答案】(1);(2),当时,;2n n n b A B n =+=11,s =29,4s =372s =4n ≥19323842n n n n S +=+-(3)证明见解析【分析】(1)利用数列的通项公式判断其增减性,从而确定,的表达式,进而求出数列{}n a n A n B 的通项公式;{}n b(2)由计算,时,数列单调递减,所以当时,212n nn a -=11322n n n n a a ++--=2n ≥4n ≥32142n n n b -=+,利用分组求和和错位相减法求和计算即可得到答案;(3)设数列的公差为,则,讨论,三种情{}n b d 111n n n n n n b b A A B B d +++-=-+-=0,d >0d <0d =况,分别证明数列为等差数列即可.{}n a 【详解】(1)由得是递增数列,21n a n =-{}n a 所以,21,n n A a n ==-11n B a ==所以.2n n n b A B n =+=(2)由得, 212n n n a -=111212132222n n n n n n n n a a ++++---=-=当,,即;1n =10n n a a +->12a a <当,,即.2n ≥10n n a a +-<2341a a a a >>>又, 11,2a =23,4a =315,8a a =>41716a a =<所以,当时,, 11,b =25,4b =354b =4n ≥32142n n n b -=+所以, 11,=S 29,4=S 372S =当时,令, 4n ≥13213(1)42422n n n n n k n b kn b b ---++=+=+-则,即. 2,k =3b =13213212342422n n n n n n n b --++=+=+-所以 344517391111132123(3)24222222-++⎛⎫⎛⎫⎛⎫=+-+-+-+⋯+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭n n n n S n n . 373923(3)2422n n n +=+-+-19323842n n n +=+-综上所述,,当时,. 11,=S 29,4=S 372S =4n ≥19323842n n n n S +=+-(3)设数列的公差为,{}n b d 则,111n n n n n n b b A A B B d +++-=-+-=由题意,11,n n n n A A B B ++≥≤①,对任意都成立,0,d >1n n A A +>*n ∈N 即,所以是递增数列.11++=>=n n n n A a A a {}n a所以,,n n A a =1n B a =所以,111n n n n n n d A A B B a a +++=-+-=-所以数列是公差为的等差数列;{}n a d ②当时,对任意都成立,0d <1n n B B +<*n ∈N 进面,11n n n n B a B a ++=<=所以是递减数列.,{}n a 1,n A a =n n B a =所以111n n n n n n d A A B B a a +++=-+-=-所以数列是公差为的等差数列;{}n a d ③当时,,0d =110n n n n A A B B ++-+-=因为与中至少有一个为0,1n n A A +-1n n B B +-所以二者都为0,进而可得数列为常数列,{}n a 综上所述,数列为等差数列.{}n a 【点睛】本题考查数列的通项公式、前n 项和公式、利用等差数列的定义证明等差数列、利用分组求和和错位相减进行数列求和;考查运算求解能力和逻辑推理能力;熟练掌握等差数列的定义和数列求和的方法是求解本题的关键;属于综合型、难度大型试题.。
人教版高二数学下学期第一次月考试题解析版

一、单选题
1.设 是可导函数,当 时, 则 =( )
A.2B. C.-2D.
【答案】C
【解析】
分析:根据导数的定义即可求出.
详解:当h→0时, ,
可得
则 ﹣2,
故选C.
点睛:本题考查了导数的定义属于基础题.
2.已知函数 在 处的切线与直线 垂直,则 ( )
A.2B.0C.1D.-1
A. B. C. D.
【答案】C
【解析】
【分析】
直线OA,OB,OC的斜率即为 , , ,令函数 ,利用导数讨论函数单调性,即得斜率大小关系。
【详解】由题得,令 ,则有 ,令 ,解得 ,当 时, , 单调递增,当 时, , 单调递减,则 是函数在定义域上的最大值,直线OA,OB,OC的斜率 ,则 最大,又 ,则有 .
一周时间内进行网络搜题的频数区间
男生频数
女生频数
18
4
10
8
12
13
6
15
4
10
将学生在一周时间内进行网络搜题频数超过 次的行为视为“经常使用网络搜题”,不超过20次的视为“偶尔或不用网络搜题”.
(1)根据已有数据,完成下列 列联表(单位:人)中数据的填写,并判断是否在犯错误的概率不超过 %的前提下有把握认为使用网络搜题与性别有关?
经常使用网络搜题
偶尔或不用网络搜题
合计
男生
22
28
50
女生
38
12
50
合计
60
40
100
计算观测值
,
所以在犯错误的概率不超过 %的前提下有把握认为使用网络搜题与性别有关.
(2)将上述调查所得到的频率视为概率,从该校所有参与调查的学生中,采用随机抽样的方法抽取一人,抽到经常使用网络搜题的学生的概率为 .
福建省莆田市第二十五中学2024_2025学年高二数学下学期第一次月考试题理

莆田其次十五中学2024-2025学年下学期月考一试卷高二理科数学考试时间:120分钟;留意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(选择题)一、单选题1.已知命题,. 则为()A., B., C., D.,2.椭圆的离心率为()A. B. C. D.3.若函数,则()A. B. C.1 D.04.一质点沿直线运动,假如由始点起经过秒后的位移与时间的关系是,那么速度为零的时刻是A.0秒 B.1秒末 C.4秒末 D.1秒末和4秒末5.椭圆的两个焦点分别为、,且椭圆上一点到两个焦点的距离之和是20,则椭圆的方程为A. B.C. D.6.已知函数,则()A.0 B.-1 C.1 D.-27.我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点,且法向量为的直线(点法式)方程为:,化简得.类比以上方法,在空间直角坐标系中,经过点,且法向量为的平面的方程为()A. B.C. D.8.若方程表示焦点在轴上的椭圆,则实数的取值范围是A .B .C .D .9.以下有关命题的说法错误的是( )A .命题“若2320x x -+=,则1x =”的逆否命题为“若1x ≠,则2320x x -+≠”B .“1x =”是“2320x x -+=”的充分不必要条件C .命题“在△ABC 中,若,sin sin A B A B >>则”的逆命题为假命题;D .对于命题:p x R ∃∈,使得210x x ++<,则:p x R ⌝∀∈,则210x x ++≥10.直线是曲线的一条切线,则实数的值为( )A .2B .C .D .11.如图,已知正方体中,异面直线与所成的角的大小是A .B .C .D .12.已知点,,则,两点的距离的最小值为A .B .C .D .第II 卷(非选择题)二、填空题13.命题“若,则”的逆否命题是______.14.焦点为()0,2的抛物线标准方程是__________.15.已知长轴长为2a ,短轴长为2b 椭圆的面积为ab π,则dx x ⎰--332912=___________。
天津高二下学期第一次月考数学试题(解析版)

一、单选题1.下列各式正确的是( ) A .B . ()cos sin x x '=()ln x x a a a '=C . D .ππsin cos 1212'⎛⎫= ⎪⎝⎭()5615xx --'=-【答案】B【分析】根据基本初等函数的求导公式判断.【详解】;;,,只有B 正确.(cos )sin x x '=-πsin 012'⎛⎫= ⎪⎝⎭56()5x x --'=-()ln x xa a a '=故选:B .2.函数的单调递减区间是( ) (e 3)()x f x x =-A . B . C . D .(),2-∞()0,3()1,4()2,+∞【答案】A【分析】求出导函数,由得减区间. ()f x '()0f x '<【详解】由已知, ()(3)(2)x x x f x e x e x e '=+-=-时,,时,,2x <()0f x '<2x >()0f x '>所以的减区间是,增区间是; ()f x (,2)-∞(2,)+∞故选:A .3.曲线在处的切线l 与坐标轴围成的三角形的面积为( )()2ln f x x x =x e =A .B .C .D .24e 2e 22e 22e 【答案】D【解析】先利用导数的几何意义求出切线方程,再分别求出直线与两坐标轴的交点坐标,即可得l 到切线l 与坐标轴围成的三角形的面积.【详解】由,得,则,,所以曲线在()2ln f x x x =()22ln f x x '=+()2f e e =()224f e '=+=()f x 处的切线的方程为,即.令得;令得.所以直x e =l ()24y e x e -=-42y x e =-0x =2y e =-0y =2ex =线与两坐标轴的交点坐标分别为,,所以切线与坐标轴围成的三角形的面积为l ()0,2e -,02e ⎛⎫⎪⎝⎭l . 212222e e e ⨯⨯=故选D.4.若对任意的实数恒成立,则实数的取值范围是( ) 0,ln 0x x x x a >--≥a A . B .C .D .(,1]-∞-(,1]-∞[1,)-+∞[1,)+∞【答案】A【解析】构造函数,利用导数研究函数在单调性,并计算()ln f x x x x a =--()f x ()0,∞+,可得结果.()min 0f x ≥【详解】令,()ln f x x x x a =--()0,x ∈+∞则,令()'ln f x x =()'01f x x =⇒=若时,01x <<()'0f x <若时,1x >()'0f x >所以可知函数在递减,在递增 ()f x ()0,1()1,+∞所以()()min 11f x f a ==--由对任意的实数恒成立 0,ln 0x x x x a >--≥所以 ()min 101f x a a =--≥⇒≤-故选:A【点睛】本题考查利用导数解决恒成立问题,关键在于构建函数,通过导数研究函数性质,属基础题.5.已知R 上的可导函数的图象如图所示,则不等式的解集为( )()f x ()()20x f x '->A .B . ()(),21,-∞-+∞ ()()212-∞-,,UC .D .()(),12,-∞+∞ ()()1,12,-+∞ 【答案】D【分析】由函数图象得出和的解,然后用分类讨论思想求得结论. ()0f x '>()0f x '<【详解】由图象知的解集为,的解集为,()0f x '>(,1)-∞-(1,)⋃+∞()0f x '<(1,1)-或,(2)()0x f x '->20()0x f x -⇔'>⎧⎨>⎩20()0x f x -<<'⎧⎨⎩所以或,解集即为. 2x >11x -<<()()1,12,-+∞ 故选:D .6.若函数在区间内存在单调递增区间,则实数的取值范围是( )2()ln 2f x x ax =+-1,22⎛⎫⎪⎝⎭a A . B . C . D .(,2]-∞-1,8⎛⎫-+∞ ⎪⎝⎭12,8⎛⎫-- ⎪⎝⎭(2,)-+∞【答案】D【分析】求出函数的导数,问题转化为在有解,进而求函数的最值,即212a x >-1(,2)221()2g x x =可求出的范围.a 【详解】∵, 2()ln 2f x x ax =+-∴,1()2f x ax x'=+若在区间内存在单调递增区间,则有解,()f x 1(,2)21()0,(,2)2f x x '>∈故, 212a x >-令,则在单调递增, 21()2g x x =-21()2g x x =-1(,2)2,1()()22∴>=-g x g 故. 2 a >-故选:D.7.已知函数在处有极值10,则的值为( ) 322()f x x ax bx a =--+1x =a b 、A ., B .,或, 4a =-11b =3a =3b =-4a =-11b =C ., D .以上都不正确1a =-5b =【答案】A【解析】根据条件函数在处有极值10,则有且,解出的值,然后()f x 1x =1(1)0f =()01f '=a b 、再代入检验是否满足条件,得出答案【详解】解:函数的导数为, 2()32f x x ax b '=--因为函数在处有极值10, 322()f x x ax bx a =--+1x =所以且.1(1)0f =()01f '=即,解得或. 2320110a b a b a --=⎧⎨--+=⎩33a b =⎧⎨=-⎩411a b =-⎧⎨=⎩当,,,3a =3b =-22()3633(1)0f x x x x '=-+=-…此时函数单调递增,所以此时函数没有极值,所以不满足条件. 所以经检验值当,时,满足条件. 4a =-11b =故选:A .【点睛】本题考查函数取极值的情况,求参数的值,注意要检验,属于中档题. 8.定义在R 上的偶函数,其导函数,当x ≥0时,恒有,若()f x ()f x '()()02xf x f x '+-<,则不等式的解集为( ) 2()()g x x f x =()(12)g x g x <-A .(,1)B .(∞,)∪(1,+∞)13-13C .(,+∞)D .(∞,)13-13【答案】A【分析】由已知可得,即在上单调递减,再利用函数的奇偶()[2()()]0g x x f x xf x ''=+<()g x [0,)+∞性、单调性,求解题设不等式即可.【详解】当时,,又, 0x ≥2()2()()[2()()]g x xf x x f x x f x xf x '=+''=+()()()()022x xf x f x f x f x ''+-=+<∴,即在上单调递减. ()0g x '<()g x [0,)+∞∵是定义在R 上的偶函数, ()f x ∴是定义在R 上的偶函数,()g x 由不等式,则有, ()(12)g x g x <-(||)(|12|)g x g x <-∴,解得:. |||12|x x >-113x <<∴不等式的解集为. ()(12)g x g x <-1(,1)3故选:A9.设函数与是定义在同一区间上的两个函敉,若对任意的,都有()f x ()g x [],a b [],x a b ∈,则称与在上是“k 度和谐函数”,称为“k 度密切区()()()0f x g x k k -≤>()f x ()g x [],a b [],a b 间”.设函数与在上是“e 度和谐函数”,则m 的取值范围是( ) ()ln f x x =()1mx g x x -=1,e e ⎡⎤⎢⎥⎣⎦A .B .[]e 1,1--[]1,e 1-+C .D .1e,1e e ⎡⎤-+⎢⎥⎣⎦11e,1e e ⎡⎤+-+⎢⎥⎣⎦【答案】B【分析】由新定义转化为不等式恒成立,再转化为求函数的最值,从而得出结论. 【详解】由题意在时恒成立,即在时恒成1ln e mx x x --≤1[e]e x ∈,1e ln e m x m x-≤+≤+1[e]e x ∈,立, 设,则,1()ln h x x x=+22111()x h x x x x -'=-=时,,单调递减,时,,单调递增, 11ex ≤<()0h x '<()h x 1e x <≤()0h x '>()h x 所以,又,,所以,min ()(1)1h x h ==1(e 1e h =-1(e)1e 1e h =+<-max ()e 1h x =-因此由在时恒成立得:1e ln e m x m x-≤+≤+1[e]e x ∈,且,所以.e 1m -≤e e 1m +≥-1e 1m -≤≤+故选:B .【点睛】方法点睛:不等式恒成立问题的处理方法,解决函数不等式恒成立的常用方法是分离参数法,即不等式变形把参数与自变量分离,然后构造新函数,利用导数求得函数的最值,然后解相x 应不等式得参数范围.二、填空题10.已知函数的导函数为,且满足,则________. ()f x ()f x '()()121f x xf x'=+()1f '=【答案】1【分析】根据题意,求导可得,然后令,即可得到结果. ()f x '1x =【详解】因为,则, ()()121f x xf x '=+()()2121f x f x''=-令,可得,解得. 1x =()()1211f f ''=-()11f '=故答案为: 111.函数的单调减区间为_______ . ()219ln 2f x x x =-【答案】.()0,3【解析】利用导数研究函数单调性即可得到结论. 【详解】解:∵,, ()219ln 2f x x x =-0x >则,299()x f x x x x'-=-=由,即,解得 ,()0f x '<290x -<33x -<<,即函数的单调减区间为, 0,03x x >∴<< ()0,3故答案为:.()0,3【点睛】本题主要考查函数单调区间的求解,根据函数的导数和单调性之间的关系是解决本题的关键.12.函数的图象在点处的切线的倾斜角为__________ ()cos x f x e x =(0,(0))f 【答案】4π【详解】因为, ()cos sin x x f x e x e x -'=00(0)cos 0sin 01f e e -'==所以函数的图象在点处的切线的倾斜角为()cos x f x e x =(0,(0))f 4π13.已知函数对区间上任意的都有,则实数m 的最小3()3f x x x =-[3,2]-1,x 2x ()()12f x f x m -≤值是________. 【答案】20【分析】求出在上的最大值和最小值后由两者差可得的范围,即得的最小值、 ()f x [3,2]-m m 【详解】,则=0,,当或时,,3()3f x x x =-2()33f x x '=-1x =±31x -≤<-12x <≤()0f x '>递增,当时,,递减.()f x 11x -<<()0f x '<()f x 所以,,又,, ()(1)2f x f =-=极大值()2f x =-极小值(3)18f -=-(2)2f =所以在上,,[3,2]-()2,()18f x f x ==-最大值最小值所以的最大值为,即,所以的最小值为20. 12()()f x f x -2(18)20--=20m ≥m 故答案为:20.【点睛】本题考查用导数研究函数的最值,解题关键是命题对区间上任意的都有[3,2]-1,x 2x ,转化继.()()12f x f x m -≤12()()()()f x f x f x f x -≤-最大值最小值14.当时,函数有两个极值点,则实数m 的取值范围___________.0x >()22x f x e mx =-+【答案】 2e m >【分析】函数有两个极值点转化为方程有两个不同的实数根,等价于与有两个2xe m x =y m =2x e y x=不同的交点,构造函数,即可求出结果.()(0)2xe h x x x =>【详解】有两个极值点, 2()2xf x e mx =-+所以有两个不同的实数根,'()20x f x e mx =-+=即有两个不同的实数根,2xe m x=等价于与有两个不同的交点,y m =2xe y x =设, ()(0)2x e h x x x =>2(1)'()(0)2x e x h x x x -=>当单调递减, (0,1),'()0,()x h x h x ∈<当单调递增, (1+),'()0,()x h x h x ∈∞>,所以 min ()(1)2eh x h ==当;0()x h x →→+∞,+()x h x →∞→+∞,所以与要有两个不同的交点,只需y m =2xe y x=2e m >故答案为:2em >【点睛】方法点睛:含参方程有根的问题转化为函数图像的交点问题,数形结合,是常用的方法.本题考查了运算求解能力和数形结合思想,属于一般题目.三、双空题15.(1)设函数,其中,若存在唯一的整数,使得,则()()e 21xf x x ax a =--+1a <0x ()00f x <a 的取值范围是________.(2)已知,,若,,使得成立,则实数a 的()e xf x x =()()21g x x a =-++1x ∃2x ∈R ()()21f x g x ≤取值范围________. 【答案】3,12e ⎡⎫⎪⎢⎣⎭1,e ⎡-+∞⎫⎪⎢⎣⎭【分析】(1)根据题意转化为存在唯一的整数,使得在直线的下方,求导得0x ()0g x y ax a =-,然后结合图像即可得到结果;()g x '(2)根据题意,将问题转化为,然后求导得极值,即可得到结果.()()min max f x g x ≤【详解】(1)函数,其中,()()e 21xf x x ax a =--+1a <设,()()e 21,xg x x y ax a =-=-因为存在唯一的整数,使得,0x ()00f x <所以存在唯一的整数,使得在直线的下方, 0x ()0g x y ax a =-因为,所以当时,,()()e 21xg x x '=+12x <-()0g x '<当时,,12x =-()12min 12e 2g x g -⎛⎫=-=- ⎪⎝⎭当时,, 0x =()()01,1e>0g g =-=直线恒过点,斜率为,y ax a =-()1,0a 故,且,解得 ()01a g ->=-()113e g a a --=-≥--32ea >所以的取值范围是a 3,12e ⎡⎫⎪⎢⎣⎭(2),,使得成立,等价于,1x ∃2x ∈R ()()21f x g x ≤()()min max f x g x ≤因为,所以,()e x f x x =()()1e xf x x '=+当时,,则函数递减; 1x <-()0f x '<()f x 当时,,则函数递增; 1x >-()0f x ¢>()f x 所以时,,=1x -()min 1ef x =-因为,所以,()()21g x x a =-++()max g x a =所以,则实数的取值范围是.1e a -≤m 1,e ⎡-+∞⎫⎪⎢⎣⎭故答案为: (1);(2)3,12e ⎡⎫⎪⎢⎣⎭1,e ⎡-+∞⎫⎪⎢⎣⎭四、解答题16.已知函数(a ,),其图象在点处的切线方程为()()322113f x x ax a x b =-+-+b ∈R ()()1,1f .30x y +-=(1)求a ,b 的值;(2)求函数的单调区间和极值; ()f x (3)求函数在区间上的最大值. ()f x []2,5-【答案】(1),;1a =83b =(2)的增区间是和,减区间是,极大值是,极小值是;()f x (,0)-∞(2,)+∞(0,2)8(0)3f =()423f =(3)最大值是,最小值是. 5834-【分析】(1)由出导函数,计算和,由切线方程列方程组解得; ()f x '(1)f '(1)f ,a b (2)由得增区间,由得减区间,从而可得极值;()0f x '>()0f x '<(3)结合(2)可得函数在上的单调性,再计算出区间端点处的函数值,,与[2,5]-(2)f -(5)f (2)中极值比较可得最值.【详解】(1),,22()21f x x ax a '=-+-22(1)1212f a a a a '=-+-=-,2212(1)133f a a b a a b =-+-+=-+-又图象在点处的切线方程为,()()1,1f 30x y +-=所以,解得; 222121(303a a a a b ⎧-=-⎪⎨+-+--=⎪⎩183a b =⎧⎪⎨=⎪⎩(2)由(1)得,,3218()33f x x x =-+2()2(2f x x x x x '=-=-)或时,,时,,0x <2x >()0f x '>02x <<()0f x '<所以的增区间是和,减区间是, ()f x (,0)-∞(2,)+∞(0,2)极大值是,极小值是;8(0)3f =()423f =(3)由(2)知在和上递增,在上单调递减, ()f x [2,0]-[2,5](0,2)又,, (2)4f -=-58(5)3f =所以在上的最大值是,最小值是. ()f x [2,5]-5834-17.已知函数,其中是自然对数的底数,.()()21e xf x ax x =+-e a R ∈(1)若,求的单调区间;a<0()f x (2)若,函数的图象与函数的图象有个不同的交点,求实数的1a =-()f x ()321132g x x x m =++3m 取值范围.【答案】(1)答案见解析(2) 31,1e 6⎛⎫--- ⎪⎝⎭【分析】(1)求得,对实数的取值进行分类讨论,分析导数的符号变()()221e xf x ax a x '⎡⎤=++⎣⎦a 化,由此可得出函数的增区间和减区间;()f x (2)由可得出,构造函数()()f x g x =()232111e 32xm x x x x -=-+++,可知直线与函数的图象有三个交点,利用导数分析函()()232111e 32x h x x x x x =-+++y m =-()h x 数的单调性与极值,数形结合可得出实数的取值范围.()h x m 【详解】(1)解:当时,因为,该函数的定义域为, 0a <()()21e xf x ax x =+-R ,()()()()2221e 1e 21e x x xf x ax ax x ax a x '⎡⎤=+++-=++⎣⎦由可得或. ()0f x '=0x =21a x a+=-①当时,即当时,210a a+-<12a <-由可得或,由可得, ()0f x '<21a x a +<-0x >()0f x ¢>210a x a+-<<此时函数的单调递减区间为、,单调递增区间为; ()f x 21,a a +⎛⎫-∞- ⎪⎝⎭()0,∞+21,0a a +⎛⎫-⎪⎝⎭②当时,即当时,对任意的,且不恒为零, 210a a+-=12a =-x R ∈()0f x '≤()f x '此时函数的减区间为,无增区间; ()f x (),-∞+∞③当时,即当时,210a a+->102a -<<由可得或,由可得, ()0f x '<0x <21a x a +>-()0f x ¢>210a x a+<<-此时函数的单调递减区间为、,单调递增区间为.()f x (),0∞-21,a a ∞+⎛⎫-+ ⎪⎝⎭210,a a +⎛⎫- ⎪⎝⎭综上所述,当时,函数的单调递减区间为、,单调递增区间为12a <-()f x 21,a a +⎛⎫-∞- ⎪⎝⎭()0,∞+; 21,0a a +⎛⎫- ⎪⎝⎭当时,函数的减区间为,无增区间; 12a =-()f x (),-∞+∞当时,函数的单调递减区间为、,单调递增区间为102a -<<()f x (),0∞-21,a a ∞+⎛⎫-+ ⎪⎝⎭. 210,a a +⎛⎫- ⎪⎝⎭(2)解:当时,,1a =-()()21e x f x x x =-+-由可得,可得, ()()f x g x =()232111e 32x x x x x m -+-=++()232111e 32x m x x x x -=-+++令,则, ()()232111e 32x h x x x x x =-+++()()()2e 1x h x x x '=++由可得或,由可得.()0h x '>1x <-0x >()0h x '<10x -<<所以,函数的增区间为、,减区间为,()h x (),1-∞-()0,∞+()1,0-函数的极大值为,极小值为, ()h x ()311e 6h -=+()01h =因为函数、的图象有三个交点,()f x ()g x 所以,直线与函数的图象有三个交点,如下图所示:y m =-()h x由图可知,当时,即当时, 311e 6m <-<+311e 6m --<<-直线与函数的图象有三个交点,y m =-()h x 因此,实数的取值范围是. m 31,1e 6⎛⎫--- ⎪⎝⎭【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与轴的交点问题,突出导数的工具作用,体现了转化与化x 归思想、数形结合思想和分类讨论思想的应用;(2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由分离变量得出,将问题等价转化为直线与函数()0f x =()a g x =y a =的图象的交点问题.()y g x =18.已知函数()ln 1x f x me x =--(1)设是的极值点,求m ,并求的单调区间;2x =()f x ()f x (2)当时,求证:1m >()1f x >(3)当时,求证: 1m e>()0f x >【答案】(1),在上单调递减,在上单调递增; 21=2m e ()y f x =()0,2()2,∞+(2)证明见解析;(3)证明见解析.【分析】(1)先由是的极值点求出m ,再直接求单调区间;2x =()f x (2)用分析法,只需证明即可,构造函数,利用导数证明ln 20x e x -->()()ln 20x g x e x x =-->,即证;()min 0g x >(3)先判断时,,构造函数,利用导数证明当1m e >()ln 1xe f x x e >--()()ln 10x e p x x x e=-->时,,即证.0x >()()10p x p =≥【详解】解:定义域为 ()ln 1x f x me x =--()01()x f x me x=∞'+-,,(1)∵是的极值点,2x =()f x ∴,解得:. 21(2)=02f me '=-21=2m e 此时, 22111()ln 1()22x x f x e x f x e e e x'=--=-,当时;当时;02x <<()0f x '<2x >()0f x '>所以在上单调递减,在上单调递增.()y f x =()0,2()2,∞+(2)当时,,只需证即可.1m >()1ln 2ln 2x x f x me x e x -=-->--ln 20x e x -->令,则 ()()ln 20x g x e x x =-->()()111x x g x e =xe x x=--'令,则,()()10x h x xe x =->()0x x h x e xe '=>+∵∴存在,使得即,也可化为()121110,110,22h e h e ⎛⎫=-<=-> ⎪⎝⎭01,12x ⎛⎫∈ ⎪⎝⎭()00h x =0010x x e =-00ln 0x x +=∴在上,,则单调递减;在上,,则单调递增.()00x ,()0g x '<()g x ()0x +∞,()0g x '>()g x 所以 ()()000000000min 1ln 221221012x x g x g x =e x =e x x x x x ⎛⎫=--+->++-=-><< ⎪⎝⎭∵即证.(3)当时,, 1m e >()ln 1xe f x x e>--令,则 ()()ln 10x e p x x x e=-->()1x e p x e x '=-令,解得x =1, ()10x e p x =e x'=-∴在上,,则单调递减;在上,,则单调递增. ()01,()0p x '<()p x ()1+∞,()0p x '>()p x ∴,故当时,.()()min 10p x =p =0x >()()10p x p =≥∴时,都有. 1m e>()0f x >【点睛】导数的应用主要有:(1)利用导数研究原函数的单调性,求极值(最值);(2)利用导数求参数的取值范围.(3)构造新函数,利用导数判断单调性,证明不等式成立19.已知函数,.()ln f x x x =()()1g x a x a =+-(1)求函数的极值;()()()h x f x g x =-(2)若存在时,使成立,求的取值范围.[]1,e x ∈()223f x x ax ≥-+-a (3)若不等式对任意恒成立,求实数的取值范围.()()()12e x h x x a a -≤--+[)1,x ∈+∞a 【答案】(1)函数有极小值,无极大值;()h x ()ee a a h a =-(2); 32e e a ≤++(3).(],0-∞【分析】(1)由题可得,然后根据导数与函数极值的关系即得;()()ln 1x x x h x a a =-++(2)由题可得存在,成立,构造函数,利用导[]1,e x ∈32ln a x x x ≤++()[]32ln ,1,e F x x x x x=++∈数求函数的最值即得;(3)设,由题可得对任意恒成立,利用导数可得()()1e xg x x a =--()()ln 1g x g x ≤-[)1,x ∈+∞,进而可得只需在上单调递增,即在0ln 1x x ≤≤-()()1e x g x x a =--[)0,+∞()()e 0x g x x a '=-≥上恒成立,即得.[)0,+∞【详解】(1)因为,()()()()ln 1h x x x x a x a f x g =-=++-∴,()()ln 1n 1l h x x a x a -+='+-=由,可得,由,可得,()0h x '<0e a x <<()0h x '>e a x >∴在上单调递减,在上单调递增, ()h x ()0,e a ()e ,a+∞所以,当时,函数有极小值,无极大值;e a x =()h x ()e e a a h a =-(2)由,可得, ()222ln 3f x x x x ax =≥-+-32ln a x x x≤++即存在,成立, []1,e x ∈32ln a x x x≤++设,则, ()[]32ln ,1,e F x x x x x =++∈()()()22132310x x F x x x x -+'=+-=≥所以函数在上单调递增,, ()F x []1,e ()()max 3e 2e eF x F ==++所以; 32e ea ≤++(3)由题可知对任意恒成立, ()()()1ln 12ex x x a x x a --+≤--[)1,x ∈+∞即对任意恒成立, ()()()1ln ln 1e 11ex x x a x a ---≤---⎡⎤⎣⎦[)1,x ∈+∞设,则对任意恒成立,()()1e x g x x a =--()()ln 1g x g x ≤-[)1,x ∈+∞下面证明对任意恒成立,0ln 1x x ≤≤-[)1,x ∈+∞设,,()ln 1t x x x =-+[)1,x ∈+∞则在上恒成立,且仅在时取等号, ()1110x t x x x-'=-=≤[)1,+∞=1x 所以在上单调递减,()ln 1t x x x =-+[)1,+∞∴,即,()()10t x t ≤=0ln 1x x ≤≤-所以对任意恒成立,只需在上单调递增, ()()ln 1g x g x ≤-[)1,x ∈+∞()()1e xg x x a =--[)0,+∞即在上恒成立,()()e 0x g x x a '=-≥[)0,+∞所以在上恒成立,a x ≤[)0,+∞所以,即实数的取值范围为.0a ≤a (],0-∞【点睛】方法点睛:恒(能)成立问题的解法:若在区间上有最值,则()f x D (1)恒成立:;; ()()min ,00x D f x f x ∀∈>⇔>()()max ,00x D f x f x ∀∈<⇔<(2)能成立:;. ()()max ,00x D f x f x ∃∈>⇔>()()min ,00x D f x f x ∃∈<⇔<若能分离常数,即将问题转化为:(或),则 ()a f x >()a f x <(1)恒成立:;; ()()max a f x a f x >⇔>()()min a f x a f x <⇔<(2)能成立:;. ()()min a f x a f x >⇔>()()max a f x a f x <⇔<。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二下学期数学第一次月考试卷
姓名:________ 班级:________ 成绩:________
一、单选题 (共17题;共34分)
1. (2分)(2017·长沙模拟) 复数(2+i)i的共轭复数的虚部是()
A . 2
B . ﹣2
C . 2i
D . ﹣2i
2. (2分)四名同学争夺跑步、跳高、跳远三项冠军,则可能的结果数是()
A .
B .
C .
D .
3. (2分)下列函数求导数,正确的个数是()
①;②;③;④
A . 0
B . 1
C . 2
D . 3
4. (2分) (2017高三上·烟台期中) 设函数f(x)= ,已知曲线y=f(x)在点(1,f(1))处的切线斜率为﹣2,则实数a的值为()
A . ﹣1或﹣
B . ﹣
C . ﹣
D . 1或﹣
5. (2分) (2018高二下·陆川期末) 已知复数,则()
A . 2
B . -2
C . 2i
D . -2i
6. (2分)甲、乙、丙、丁、戊五人并排站成一排,如果甲必须站在乙的右边(甲、乙可以不相邻)那么不同的排法共有()
A . 24种
B . 60种
C . 90种
D . 120种
7. (2分)设函数则的单调减区间()
A .
B .
C .
D .
8. (2分)已知等比数列{an}中,各项都是正数,且a1 ,a3 , 2a2成等差数列,则=()
A . 1+
B . 1﹣
C . 3+2
D . 3﹣2
9. (2分)(2020·攀枝花模拟) 在这组数据中,随机取出五个不同的数,则数字是取出的五个不同数的中位数的所有取法为()
A . 24种
B . 18种
C . 12种
D . 6种
10. (2分) (2013·福建理) 已知复数z的共轭复数(i为虚数单位),则z在复平面内对应的点位于()
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
11. (2分)已知是定义域为R的奇函数,,的导函数的图象如图所示,若两正数a,b满足,则的取值范围是()
A .
B .
C .
D .
12. (2分)用8个数字1,1,2,2,3,3,4,4可以组成不同的四位数个数是()
A . 168
B . 180
C . 204
D . 456
13. (2分) (2016高二下·日喀则期末) 若(1+2x)2015=a0+a1x+a2x2+a3x3+…+a2015x2015(x∈R),则﹣
的值为()
A . ﹣2
B . ﹣1
C . 1
D . 2
14. (2分) (2015高二下·河南期中) 9件产品中,有4件一等品,3件二等品,2件三等品,现在要从中抽出4件产品来检查,至少有两件一等品的抽取方法是()
A . C •C
B .
C +C +C
C . C +C
D . C •C +C •C +C •C
15. (2分) (2016高二下·新余期末) 设复数z满足 =()
A . 0
B . 1
C .
D . 2
16. (2分)已知实数成等比数列,且对函数,当时取到极大值,则等于()
A .
B . 0
C . 1
D . 2
17. (2分)“a≥0”是“函数在区间(-∞,0)内单调递减”的()
A . 充要条件
B . 必要不充分条件
C . 充分不必要条件
D . 即不充分也不必要条件
二、多选题 (共3题;共9分)
18. (3分)下列关系中,能成立的是()
A .
B .
C .
D .
19. (3分)已知复数满足,,则实数的值可能是()
A . 1
B .
C . 0
D . 5
20. (3分)(2019高三上·济南期中) 定义在上的函数的导函数为 ,且
对恒成立.下列结论正确的是()
A .
B . 若 ,则
C .
D . 若 ,则
参考答案一、单选题 (共17题;共34分)
1-1、
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
11-1、
12-1、
13-1、
14-1、
15-1、
16-1、
17-1、
二、多选题 (共3题;共9分) 18-1、
19-1、
20-1、。
