丰泽区初三数学质量检测检测试3
中考数学初中学业质量检查数学试卷.doc

2016年丰泽区初中学业质量检查数 学 试 题(满分:150分;考试时间:120分钟)友情提示:所有答案必须填写到答题卡相应的位置上.毕业学校 姓名 考生号一、选择题(每小题3分,共21分):每小题有四个答案,其中有且只有一个答案是正确的.请在答题卡上相应题目的答题区域内作答,答对的得3分,答错或不答一律得0分. 1、-2016的倒数是 ( ) A .2016B .-2016C .20161D .20161-2、下列运算正确的是( )A. a a a =÷33B. 32a a a =⋅ C. 532)(a a = D. ba b a 22)(=3、一组数据:-2、1、1、0、2、1,则这组数据的众数是( ) A .2B .1C .0D .-24、不等式组36012x x ->⎧⎨-≥-⎩的解集在数轴上表示为( ).5、如图几何体的俯视图是( )A .B . C. D.6、如图,△ABC 内接于⊙O ,OD ⊥BC 于D ,∠COD =50°,则∠A 的度数是( )A .40°B .45°C .50°D .60°7、如图,△ABC 的周长为12,G 、H 分别为AB 、AC 的中点,分别以AB 、AC 为斜边向外作Rt △ADB 和Rt △AEC ,连接DG 、GH 、EH ,则DG+GH+EH 的值为( ) A .6 B .7 C .8 D .9二、填空题(每小题4分,共40分):在答题卡上相应题目的答题区域内作答.A.B .C .D . (第5题图)(第6题图)8、分解因式:a a 42-=____________________.9、某校学生在“爱心传递”活动中,共筹得捐款37400元, 请你将数字37400用科学计数法表示为 .10、如图,已知直线AB ∥CD ,∠ E = 90 °,∠A = 30°,则∠C = 度. 11、n 边形的内角和等于720°,则n = ________. 12、计算:._______222=-+-ax xx a a13、已知等腰三角形的一个底角为70,则它的顶角为 度. 14、已知扇形的圆心角为45o,半径为2cm ,则该扇形的面积为 cm 2.. 15、如果2(1a =+b a ,为有理数),那么b a +等于 .16、如图,点A 、B 、C 、D 在⊙O 上,点O 在D ∠的内部,四边形OABC 为平行四边形, 则∠OAD + ∠OCD = °.17、在平面直角坐标系中,四边形OABC 是正方形,B 点的坐标为(-3,3),E 是线段BC 上一点,且60AEB ∠= ; (1)BE= ;(2)沿AE 折叠后B 点落在点F 处,那么点F 的坐标是 . 三、解答题(共89分):在答题卡上相应题目的答题区域内作答. 18、(9分)计算:1)21()2016(|2|28---+--÷π19、(9分)先化简,再求值: 22)1(3)1(a a a --++,其中2016=a .20、(9分)如图,已知FE AC //,FE AC =,BF AD =,点F B D A 、、、FDE ABC ∆∆≌.21、(9分)在一个不透明的布袋中,放入分别标注3、4-、5三个不同数字的小球,小球除了数字不同外,其余都相同. 某同学闭上眼睛先把小球搅均,再从该布袋中摸出第一个小球,记小球上的数字为x ,把球重新放回..布袋中搅均,摸出第二个小球,记小球上的数字为y . (1)求第一次摸出的小球上的数字为“正数”的概率;(2)若第一次摸出的数字x 为点A 的横坐标,第二次摸出的数字y 为点A 的纵坐标,求点A 落在第一象限的概率.22、(9分)某市教育局为了了解初一学生第一学期参加社会实践活动的情况,随机抽查了本市部分初一学生第一学期参加社会实践活动的天数,并将得到的数据绘制成了下面两幅不完整的统计图.请根据图中提供的信息,回答下列问题:(1)扇形统计图中a 的值为 ,该扇形中活动时间为3天的圆心角度数为 度; (2)补全条形统计图;(3)如果该市共有初一学生20000人,请你估计“活动时间不少于6天及6天以上”的大约有多少人?23、(9分)如图,一次函数5+=kx y (k 为常数,且0≠k )的图像与反比例函数xy 8-=的图像交于()b A ,2-,B 两点.(1)求一次函数的表达式;(2)若将直线AB 向下平移)0(>m m 个单位长度后与反比例函数的图像有且只有一个公共点,求m 的值.24、(9分)泉州市丰泽区某公司专销产品A,第一批产品A 上市40天恰好全部售完.该公司对第一批产品A 上市后的市场销售情况进行了跟踪调查,调查结果如图1和图2所示,其中图1中的折线表示是市场日销售量y (万件)与上市时间t (天)的关系,图2中的折线表示的是每件产品A 的日销售利润w (元)与上市时间t (天)的关系.(1)试写出第一批产品A 的市场日销售量y (万件)与上市时间t (天)的关系式; (2)第一批产品A 上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元天和7天以上53天学生参加实践活动天数 的人数分布扇形统计图7天和7天以上学生参加实践活动天数)25、(12分)如图,已知AM ∥BN ,∠B=90°,AB=4,点D 是射线AM 上的一个动点(点D 与点A 不重合),点E 是线段AB 上的一个动点(点E 与点A 、B 不重合),连接DE ,过点E 作CE ⊥DE ,交射线BN 于点C ,连接DC .(1)当AD = AE = 2时,四边形ABCD 为 形; (2)设AE=x ,BC=y ,AD = m ,AD + DE = a .①当m = 1时,求y 关于x 的函数关系式;②在动点D 、E 的运动过程中,始终满足△BCE 的周长为定值8,请求出a 的值.26、(14分)如图,已知抛物线的图像过点A (0,﹣1),且顶点坐标为P (2,1),过点A 作A B ∥x 轴交抛物线于点B ,过B 作BC ∥y 轴交AP 延长线于点C .(1)填空:点B 坐标( , ),点C 坐标( , );(2)平移抛物线,使点P 在直线AC 上滑动,且与AC 交于另一点Q ,与BC 交于点M ,当△PQM 的面积等于32时,求点P 的坐标. (3)在(2)的条件下,取BC 的中点N ,连接NP ,BQ .PN+BQ 的最小值.。
2010-2023历年福建省丰泽区九年级上学期期末质量监测数学试卷(带解析)

2010-2023历年福建省丰泽区九年级上学期期末质量监测数学试卷(带解析)第1卷一.参考题库(共10题)1.在一个不透明的袋子里装有黄色、白色乒乓球共40个,除颜色外其他完全相同.从这个袋子中随机摸出一球,放回.通过多次摸球实验后发现,摸到黄色球的概率稳定在15%附近,则袋中黄色球可能有个.2.抛物线的顶点坐标是.3.抛物线的对称轴是()A.B.C.D.4.如图,已知△ABC∽△DEF,∠A=70°,∠C=50°,则∠E=°.5.二次函数的图象与轴交点的横坐标是()A.和B.和C.和D.和6.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.(1)在图上标出位似中心D的位置,并写出该位似中心D的坐标是;(2)求△ABC与△A′B′C′的面积比.7.求值: .8.以直线为对称轴的抛物线与轴交于A、B两点,其中点A的坐标为.(1)求点B的坐标;(2)设点M、N在抛物线线上,且,试比较、的大小.9.某旅游商店8月份营业额为15万元,9月份下降了20%.受“十一”黄金周以及经济利好因素的影响,10月份、11月份营业额均比上一个月有所增长,10月份增长率是11月份增长率的1.5倍,已知该旅游商店11月份营业额为24万元.(1)问:9月份的营业额是多少万元?(2)求10月份营业额的增长率.10.解方程:第1卷参考答案一.参考题库1.参考答案:6.试题分析:设袋中黄色球可能有x个.根据题意,任意摸出1个,摸到黄色乒乓球的概率是:,解得:x=6.故答案是6.考点:利用频率估计概率.2.参考答案:(0,-6).试题分析:由抛物线可知,顶点坐标是(0,-6). 故答案是(0,-6).考点:二次函数的性质.3.参考答案:A.试题分析:已知解析式为顶点式,可直接根据顶点式的坐标特点,所以顶点坐标(2,-1),从而得出对称轴.故选A.考点:二次函数的性质.4.参考答案:60.试题分析:根据相似三角形的性质可得∠A=∠D=70°,∠C=∠F=50°,然后利用三角形内角和定理可得∠E=180°﹣70°﹣50°=60°.故答案是60.考点:相似三角形的性质.5.参考答案:B.试题分析:令y=0,把函数转化为方程,根据十字相乘法求出方程的根 ,从而求出二次函数的图象与x轴交点的横坐标和.故选B.考点:抛物线与x轴的交点.6.参考答案:(1)图形见解析,;(2).试题解析:⑴如图:;⑵∵∽∴.考点:位似.7.参考答案:.试题分析:将各特殊角的三角函数值代入,然后合并运算.故答案是.考点:特殊角的三角函数值.8.参考答案:(1);(2).试题分析:(1)根据抛物线的对称轴直接解答即可;(2)先判断函数的增减性,再比较大小.试题解析:(1)由已知,可得:,所以;⑵∵∴抛物线开口向下,∴在对称轴左侧,随的增大而增大;∵,∴.考点:二次函数图像.9.参考答案:(1)9月份的营业额是12万元;(2)10月份的增长率为50%.试题分析:(1)9月份的营业额=8月份的营业额;(2)设11月份的增长率为,找出9月份的营业额与11月份营业额之间的关系即可.试题解析:⑴9月份的营业额=(万元);⑵设11月份的增长率为,则10月份的增长率为 ,依题意,得:解之,得:(不合题意,舍去)∴10月份的增长率为.答:10月份的增长率为50%.考点:二元一次方程的应用.10.参考答案:.试题分析:先化成一般式,再用公式法解题. 试题解析:原方程可化为:∴考点:解二元一次方程.。
丰泽区初中学业质量检测及答案.doc

丰泽区初中学业质量检测及答案姓名:_____________ 年级:____________ 学号:______________一、选择题(共2题)1.阅读下面一段话,按要求作答。
(7分)“如果你是一滴水,你是否滋润了一寸土地?如果你是一线阳光,你是否照亮了一分黑暗?如果你是一粒粮食,你是否哺育了有用的生命?如果你是一颗最小的螺丝钉,你是否永远坚守着你生活的岗位……”雷锋,一位普通的士兵,在平凡的岗位上做出了不平凡的业绩,他铸就了生命的辉煌,诠释了人生的真谛。
⑴下列加点字读音____________,江春入旧年。
③人生自古谁无死,____________,____________肉食者谋之,又何____________便扶向路,处处____________14.文章叙述了两个关于矿泉水的故事,请简要概括。
(6分)①____________②____________15.比较文中两位父亲有何异同之处。
(5分)相同点:____________不同点:__________________16.文中两个划线句都属景物描写,请分析它们在表达感情方面的作用。
(4分)第①句的作用:__________________第②句的作用:__________________17.“那种味道,应该是儿子一生的记忆吧。
”这句话有何深刻含义?请结合生活实际谈谈你的理解。
(6分)____________________________________【答案】13.(4分)矿泉水的味道(2分)父亲的汗水和体温(父爱的味道)(2分)14.(6分)(1)小时候,在外打工的父亲给儿子带来两瓶矿泉水并骗儿子说自己喝过,临终前儿子才发现这是父亲善意的谎言。
(2)南方雪灾时,父亲把冰冷的矿泉水焐在胸口,自己却没舍得喝一口,全都留给了儿子。
15.(5分)相同点:都有无私的爱子之情(2分)不同点:表达爱意的方式不同,一个用善意的方言,一个用自己的肩膀和胸怀给儿子留下“味道”。
丰泽区2013-2014学年初三(上)数学试卷参考答案及评分...

丰泽区2013—2014学年初三(上)数学试卷参考答案及评分标准一、选择题(每小题3分,共21分)1.D ,2.D ,3.C ,4.C ,5.A ,6.B ,7.B.二、填空题(每小题4分,共40分)8.3,9.23,10.3±=x ,11.()6,0-,12.60,13.6,14.15+,15.5,16.①③, 17.⑴()0,1、⑵⎪⎪⎭⎫ ⎝⎛23,5.1006. 三、解答题(共89分) 18.(9分)解:原式=23323-+-----------------------------------(7分) =22--------------------------------------------------------(9分)19.(9分)解:原方程可化为:0132=+-x x ------------------------------(2分) ∴2532,1±=x ----------------------------------------------(9分) 20.(9分)解:⑴ 正确标出点D ------------------------------------------(2分) ()0,7D ------------------------------------------------------(4分) ⑵∵ABC ∆∽C B A '''∆-----------------------------------------(5分) ∴41212=⎪⎭⎫ ⎝⎛='''∆∆C B A ABC S S -----------------------------------------(9分) 21.(9分)解:在ADC Rt ∆中,∵CAD AC CD ∠=sin -------------------------(2分) ∴77.523560sin 5sin ≈=︒=∠=CAD CD AC (米)----------------(5分) ∵CAD ADCD ∠=tan -------------------------------------------(6分) ∴89.23560tan 5tan ≈=︒=∠=CAD CD AD (米)----------------(9分) 22.(9分)解:⑴32------------------------------------------------------(3分) ⑵正确列表或画出树状图----------------------------------------(6分)∴P (两次摸出白球)=3162=-----------------------------------(9分) 23.(9分)解:由已知,可得:1)1(2=-⨯-b --------------------------------(2分) ∴2=b --------------------------------------------------------(4分) ⑵ ∵01<-=a ∴抛物线开口向下∴在对称轴1=x 左侧,y 随x 的增大而增大-----------------------(7分) ∵121<<x x∴21y y <-----------------------------------------------------(9分)24.(9分)⑴ 证明:∵CD AB //∴BAC ACD ∠=∠ ︒=∠=∠90DAB D -----------------------(2分) ∵BC AC ⊥∴D BAC ∠=︒=∠90------------------------------------------(4分) ∴ADC ∆∽BCA ∆----------------------------------------------(5分) ⑵ 解:∵ADC ∆∽BCA ∆∴BAAC AC CD =--------------------------------------------------(8分) ∴4966=⨯=⨯=BA AC AC CD (cm )----------------------------(9分) 25.(12分)解:⑴ 9月份的营业额=12%)201(15=-⨯(万元)--------------(4分) ⑵ 设11月份的增长率为x ,则10月份的增长率为x 5.1------------(5分) 依题意,得:()()2415.1112=++x x ----------------------------(8分)解之,得:2,3121-==x x (不合题意,舍去)------------------(11分) ∴10月份的增长率为5.0315.1=⨯ 答:10月份的增长率为50%.-----------------------------------(12分)26.(14分)解:⑴ 由题意,得:⎩⎨⎧=+=+2240416b a b a -----------------------------(2分) 解得:2,21=-=b a -------------------------------------------(4分) ⑵ 过点B 作x BC ⊥轴于点C ,则2===AC BC OC ------------(6分)∴︒=∠=∠=∠=∠45ABC BAC OBC BOC∴AB OB OBA =︒=∠,90∴OAB ∆是等腰直角三角形-------------------------------------(9分) ⑶ ∵OAB ∆是等腰直角三角形,4=OA∴22==AB OB由题意,得:点A '坐标为()22,22--------------------------(11分) ∴B A ''的中点P 的坐标为()22,2--------------------------(12分)当2-=x 时,()()22222212-≠-⨯+-⨯-=y ∴点P 不在抛物线上.-----------------------------------------(14分)A 'B 'C。
【2009年】丰泽区初中学业质量检查
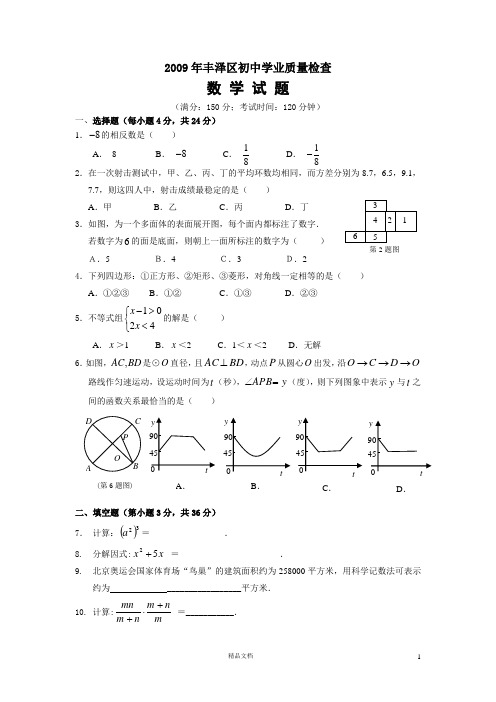
2009年丰泽区初中学业质量检查数 学 试 题(满分:150分;考试时间:120分钟)一、选择题(每小题4分,共24分) 1.8-的相反数是( )A . 8B . 8-C .18 D . 18- 2.在一次射击测试中,甲、乙、丙、丁的平均环数均相同,而方差分别为8.7,6.5,9.1,7.7,则这四人中,射击成绩最稳定的是( ) A .甲B .乙C .丙D .丁3.如图,为一个多面体的表面展开图,每个面内都标注了数字. 若数字为6的面是底面,则朝上一面所标注的数字为( ) A.5B.4C.3D.24.下列四边形:①正方形、②矩形、③菱形,对角线一定相等的是( ) A .①②③ B .①②C .①③D .②③5.不等式组1024x x ->⎧⎨<⎩的解是( )A .x >1B .x <2C .1<x <2D .无解6.如图,BD AC ,是⊙O 直径,且BD AC ⊥,动点P 从圆心O 出发,沿O D C O →→→ 路线作匀速运动,设运动时间为t (秒),y APB =∠(度),则下列图象中表示y 与t 之间的函数关系最恰当的是( )二、填空题(第小题3分,共36分) 7. 计算:()32a =_________________.8. 分解因式:x x 52+ =_______________________.9. 北京奥运会国家体育场“鸟巢”的建筑面积约为258000平方米,用科学记数法可表示约为 _________________平方米. 10. 计算:mnm n m mn +⋅+ =___________. 第2题图(第6题图)ABC DOP B .D .A .C .11. 六边形的内角和等于________________度. 12. 反比例函数xy 3-=的图象在第二象限和第___________象限. 13.在右图方格纸中,把ABC ∆绕A 逆时针旋转_________度后 可得C B A ''∆.14.在一个不透明的摇奖箱内装有20个形状、大小、质地等完全相同的小球,其中只有5个球标有中奖标志,则随机抽取一个小球中奖的概率是___________. 15.某个圆锥的侧面展开图形是一个半径为6cm ,圆心角为︒120的扇形,则这个圆锥的底面半径为______________cm . 16.如图,不添加辅助线,请写出一个能判定AC EB //的条件: .17.某工地实施爆破,操作人员点燃导火线后,必须在炸药爆炸前跑到m 400外安全区域,若导火线燃烧的速度为cm 1.1/秒,人跑步的速度为m 5/秒,则导火线的长x 应满足的不等式是: . 18.下面是一个三角形数阵: 1------------------------第1行2 3 ------------------第2行 4 5 6------------------第3行 7 8 9 10------------第4行……根据该数阵的规律,第8行第2个数是 . 三、解答题(共90分)在答题卡上相应题目的答题区域内作答.19.(8分)计算:421200910--⎪⎭⎫⎝⎛+-20.(8分)先化简下面代数式,再求值:)3()2)(2(x x x x -+-+,其中12+=x .A(第16题图)BCDE21.(8分)如图,E是正方形ABCD的边DC上的一点,过A作A F⊥AE,交CB延长线于点F,求证:△ADE≌△ABF.22.(8分)右边下面两图是根据某校初三(1)班同学的上学方式情况调查所制作的条形和扇形统计图,请你根据图中提供的信息,解答以下问题:(1)求该班学生人数,并将条形统计图补充完整;(2)若该校初三年有600名学生,试估计该年级乘车上学的人数.骑自行车20%乘车步行50%_ F_ E_ D_ C_ B_ A23.(8分)如图,小岛A 位于港口P 的西偏南︒39方向,小岛B 位于P 的正西方向,且位于A 的正北方向,已知小岛A 与港口P 相距81海里. (1)求小岛B 与港口P 的距离(精确到1海里);(2)甲船从P 出发驶向A ,乙船从B 出发驶向P ,甲、乙两船的行驶速度分别为12海里/小时和9海里/小时.两船同时出发,问:几小时后,它们与P 的距离相等?24.(8分)有3张背面相同的纸牌A ,B ,C ,其正面分别画有三个不同的几何图形(如图).将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.(1)求出两次摸牌的所有等可能结果(用树状图或列表法求解,纸牌可用A ,B ,C 表示); (2)求摸出两张牌面图形都是中心对称图形的纸牌的概率. 25.(8分)如图,已知ABC ∆的面积为8,16=BC .现将ABC △沿直线BC 向右平移a 个单位到DEF △的位置.(1)当4=a 时,求ABC △所扫过的面积; (2)连结AE 、AD ,设5=AB ,当ADE ∆是以DE 为一腰的等腰三角形时,求a 的值.DEC B A26.(8分) 如图,O 为坐标原点,点A )5,1(和点B )1,(m 均在反比例函数xky =图象上. (1)求m 、k 的值;(2)设直线AB 与x 轴交于点C ,求AOC ∆的面积.27.(13分)某公司经销某品牌运动鞋,年销售量为10万双,每双鞋按250元销售,可获利25﹪,设每双鞋的成本价为a 元. (1)试求a 的值;(2)为了扩大销售量,公司决定拿出一定量的资金做广告,根据市场调查,若每年投入广告费为x (万元)时,产品的年销售量将是原销售量的y 倍,且y 与x 之间的关系如图所示,可近似看作是抛物线的一部分.①根据图象提供的信息,求y 与x 之间的函数关系式;②求年利润S (万元)与广告费x (万元)之间的函数关系式,并请回答广告费x (万元)在什么范围内,公司获得的年利润S (万元)随广告费的增大而增多? (注:年利润S =年销售总额-成本费-广告费)28.(13分)如图,在平面直角坐标系中,B A ,两点的坐标分别为)8,0(),2,0(-,以AB 为11.36 1.64一边作正方形ABCD ,再以CD 为直径的半圆P .设x 轴交半圆P 于点E ,交边CD 于点F .(1)求线段EF 的长;(2)连接BE ,试判断直线BE 与⊙P 的位置关系,并说明你的理由;(3)直线BE 上是否存在着点Q ,使得以Q 为圆心、r 为半径的圆,既与y 轴相切又与⊙P 外切?若存在,试求r 的值;若不存在,请说明理由.四、附加题(共10分)在答题卡上相应题目的答题区域内作答.友情提示:①全卷得分低于90分,则本题得分计入总分,否则本题得分不计入总分;②计入后总分不得超过90分.1.(5分)计算:)5()3(-⨯-=______________________. 2. (5分)如图,ABC ∆中,,50,60︒=∠︒=∠B A点D 在的延长线上,则ACD ∠=__________度.2009年丰泽区初中学业质量检查ABD数学试题参考答案及评分标准一、选择题(每小题4分,共24分) 1、A ,2、B ,3、D ,4、B ,5、C ,6、C 二、填空题(第小题3分,共36分)7、6a ,8、)5(+x x ,9、51058.2⨯,10、n ,11、720,12、四,13、︒90,14、41,15、4,16、略,17、54001.1>x ,18、30 三、解答题(共90分)19.(8分)解:原式=421-+--------(6分)=1----------------(8分)20.(8分)解:原式=2234x x x -+-------------------(4分) =43-x --------------------------(6分) 当12+=x 时,原式=123-------------(8分)21.(8分)证明:∵ABCD 是正方形∴AB AD = ︒=∠=∠=∠90DAB ABF D -------------(2分) ∵A F ⊥AE ∴DAE EAB BAF ∠=∠-︒=∠90-------(4分) 在ADE ∆和ABF ∆中,∵AE AD BAF DAE ABF D =∠=∠∠=∠,,∴△ADE ≌△ABF------------------------------------------------(8分)22.(8分)解:(1)该班学生人数为40%5020=(人) 图画对(略)-------------------------------------(4分)(2)该年级乘车上学的人数约为1806004012=⨯(人)-------(8分) 23.(8分)解:(1)在PBA Rt ∆中,∵PAPBAPB =∠cos -----------------------------------(3分) ∴6339cos 81cos ≈︒⨯=∠=APB PA PB (海里)-----------(5分) (2)设出发x 小时,依题意得: x x 96312-= 解得:3=x答:3小时后,它们与P 的距离相等;----------------(8分)24.(8分)解:(1)9种(解略)----------(5分) (2)94-----------------------(8分) 25.(8分) 解:(1)(解法一)ABC ∆所扫过面积即梯形ABFD 的面积 作BC AH ⊥于H 483232162116===⇒=⋅⇒=∆BC AH AH BC S ABC)3(324)124(21)(21'-----=⨯+=⨯+⨯=AH BF AD S ABFD(解法二)设AC 与DE 交于点G ,则∵DE AB // E 为BC 中点⇒G 为AC 中点 又 ∵EC AD // ∴CGE AGD S S ∆∆=∴ABC ∆所扫过面积=)3(322'-----==+∆∆ABC ACFD ABC S S S (2)① 当DE AD =时,)4(5'------------------=a ② 当DE AE =时,取BE 中点M ,则)5('-----⊥BC AM416821162116=⇒=⨯⨯⇒=⨯⨯⇒=∆AM AM AM BC S ABC在AMB Rt ∆中,3452222=-=-=AM AB BM 此时,62==BM a综上,)8(6,5'----------------=a26.(8分) 解:(1)5,5==k m --------------------------------------(3分) (2)(解法一)作x AE ⊥轴于E ,x BF ⊥轴于F , 则BF AE //,从而AEC ∆∽BFC ∆---------------(5分)1514=⇒=+⇒=CF CF CF AF BF CE CF6=+=CF OF OC ------------------------(7分)15562121=⨯⨯=⨯=∆AE OC S AOC ----------(8分)(解法二)设直线AB 所对应的一次函数关系式为:b ax y +=-------(4分) 6,1155=-=⇒⎩⎨⎧=+=+b a b a b a ∴6+-=x y -------------------(6分) 令0=y ,得6=x ,即6=OC ----------------------------------------------(7分)27.(13分) 解:(1)200250%)251(=⇒=+a a (元)------------------------(3分) (2)依题意,设y 与x 之间的函数关系式为:12++=bx ax y ------(4分)⎩⎨⎧=-=⇒=++=++2.0,01.064.1141636.1124b a b a b a ∴12.001.02++-=x x y --------------------------------------(9分) (3)x x x S -⨯-⨯⨯++-=2001025010)12.001.0(2 500499252++-=x x S01.2990)98.9(252+--=x S ----------------------------(12分) ∴当98.90<<x 时,公司获得的年利润随广告费的增大而增多.(13分) 注:98.90,98.90≤≤≤<x x 均可D E B A G H D FE BAM28.(13分) (1)连接PE ,)3(435222'---=-=-=PF PE EF(2)(解法一)∵23410,248=-===PF EO EF BO∴BOE Rt ∆∽EFP Rt ∆ ∴FEP OBE ∠=∠)6(909090'---------︒=∠⇒︒=∠+∠⇒︒=∠+∠∴BEP OEB FEP OEB OBE∴相切)7('--------------- (解法二)连接PB ,在PCB Rt ∆中,12510522222=+=+=BC PC PB在BOE Rt ∆中,1006822222=+=+=OE BO BE在PEB ∆中,22225100PB PE BE =+=+ ∴)6(90'------------︒=∠PEB(3)连接PQ ,∵⊙Q 与⊙P 外切 ∴)8(5'--+=r PQ 过Q 作y QM ⊥轴于M ,交CD 于N∵⊙Q 与y 轴相切∴r QM = ∴)9(10'----=-=r QM MN QN ∵⇒OE MQ //BMQ ∆∽BOE ∆ 3468rr BM OE MQ BO BM =⨯=⇒=⇒∴)11(345'----=--=-=-=rPF BM BO PF MO PF NF NP (另解:直线DE 所对应的函数关系式为834+-=x y ,设),(h r Q ,代入得834+-=r h ,即834+-=r NF ,从而345rNP -=) 在QNP Rt ∆中,222PQ NP QN=+()()222534510r r r +=⎪⎭⎫ ⎝⎛-+-⇒)21(0900390162'---=+-⇒r r解得,)31(1623625195'----------------------±=r四、附加题(共10分) 1.(5分)15-,2. (5分)110.。
2019-2020上期末质量监测九年级数学参考答案及评分标准

九年级数学试卷参考答案及评分标准(2020.01)一、选择题题号123456789101112答案CBBDAABCBDAC二、填空题三、解答题17.(6分)(1)2450x x +-=解:1)(5x x -+()=0………………………1分121,5x x ==-………………………3分(备注:其他方法亦可)(2)()()2323x x -=-解:()()23230x x ---=………………………4分()()3230x x --+=………………………5分123,1x x ==………………………6分18.(6分)(1)小智被分配到A 项目“全程马拉松”项目组的概率为……2分(2)记这三个项目分别为A 、B 、C ,画树状图为:共有9种等可能的结果数,其中小智和小慧被分配到同一个项目组的结果数为3,所以小智和小慧被分到同一个项目组进行志愿服务的概率=.………………6分19.(6分)(1)证明:∵四边形ABCD 是矩形,∴∠D =∠1=∠2+∠3=90°,…………………1分∵CF ⊥CE∴∠4+∠3=90°∴∠2=∠4,…………………2分∴△CDE ∽△CBF ;…………………3分(2)∵四边形ABCD 是矩形,∴CD =AB ,∵B 为AF 的中点∴BF =AB ,…………………4分设CD =BF =x∵△CDE ∽△CBF ,∴BF DECB CD =…………………5分∴x x 13=∵x >0,∴x =3…………………6分即CD 的长为320.(8分)(1)如图,过点作轴的垂线,垂足为.∵点的坐标为,∴,.∴.…………………1分∴.………………………2分∴点的坐标为.………………………3分∴.………………………4分(2)如图,将菱形沿轴正方向平移,使得点落在函数32(0)y xx=>的图象上的处,过点作轴的垂线,垂足为.∵,∴.……………………5分∴点的纵坐标为.∴点在32yx=的图象上,∴323x=,解得323x=,即32'3OF=.………………………7分∴3220'433 FF=-=.∴菱形沿轴正方向平移的距离为20 3.………………………8分21.(8分)(1)可设年平均增长率为x,依题意有220128.8x+()=…………………2分解得1x=0.2=20%,2x=﹣2.2(舍去).…………………3分答:年平均增长率为20%;…………………4分(2)设每杯售价定为y元时,依题意有(y﹣6)[300+30(25﹣y)]=6300,………………6分解得1y=20,2y=21,………………7分∵要让顾客能获得最大优惠,∴y=20.………………8分答:当每杯售价定为20元时,既能让顾客获得最大优惠,又可让店家在此款奶茶实现每天6300元利润额.22.(8分)(1)如图1中,在△ABC 中,∵∠ACB =90°,AB =20,BC =12,∴AC 222012 16,…………………1分设HQ =x ,∵HQ ∥BC ,∴=,∴AQ =x ,…………………2分∵S △ABC =9S △DHQ ,∴×16×12=9××x ×x ,∴x =4或﹣4(舍弃),∴HQ =4,…………………3分(2)如图2中,由翻折不变性可知:AE =EM ,AF =FM ,∠AFE =∠MFE ,∵FM ∥AC ,∴∠AEF =∠MFE ,∴∠AEF =∠AFE ,∴AE =AF ,…………………4分∴AE =AF =MF =ME ,∴四边形AEMF 是菱形.…………………5分(3)如图3中,设AE =EM =FM =AF =4m ,则BM =3m ,FB =5m ,∴4m +5m =20,∴m =209,∴AE =EM =809,∴EC =16﹣809=649,∴CM ==163,∵QH =4,AQ =163,…………………6分∴QC =323,设PQ =x ,当=时,△HQP ∽△MCP ,∴4163233x x=-,解得:x =327,…………………7分当=时,△HQP ∽△PCM ,∴4321633xx =-解得:x =8或83,经检验:x =8或83是分式方程的解,且符合题意,综上所,满足条件长QP 的值为327或8或83.…………………8分23.(9分)解:(1)a =-1,b =-2;…………………2分∵+23+b +a )(=0,且≥0,23+b +a )(≥0,∴,解得:,(2)∵a =-1,b =-2∴A (-1,0),B (0,-2),∵E 为AD 中点,∴D x =1,设D(1,t),又∵DC∥AB,∴C(2,t-2),∴t=2t-4,∴t=4,∴D(1,4);…………………4分(3)∵由(1)知k=4,∴反比例函数的解析式为y =,∵点P 在双曲线上,点Q在y轴上,∴设Q(0,y),P(x ,),当AB为边时:如图1所示:若ABPQ为平行四边形,则=0,解得x=1,此时P1(1,4),Q1(0,6);…………………5分如图2所示;若ABQP为平行四边形,则AP∥BQ,所以PA⊥x轴,故x=-1,此时P2(-1,-4),Q2(0,-6);…………………6分当AB为对角线时,如图3所示:AP=BQ,且AP∥BQ;∴PA⊥x轴,故得x=-1,∴P3(-1,-4),Q3(0,2);…………………7分故Q1(0,6);Q2(0,-6);Q3(0,2);(3)连NH、NT、NF,∵MN是线段HT的垂直平分线,∴NT=NH,∵四边形AFBH是正方形,∴∠ABF=∠ABH,在△BFN与△BHN 中,图3图2图1∵,∴△BFN≌△BHN,…………………8分∴NF=NH=NT,∴∠NTF=∠NFT=∠AHN,∴∠TNH=∠TAH=90°,∴MN=HT,∴=.…………………9分。
2012年泉州市丰泽区中考质量检查数学试卷(含答案)

2012年泉州市丰泽区初中质量检查 数学试题参考答案及评分标准一、选择题(每小题3分,共21分)1.A ; 2.D ; 3.B ; 4.D ; 5.A ; 6.C ;7.B . 二、填空题(每小题4分,共40分)8.4; 9.()22-a a ; 10.9103.1⨯; 11.30; 12.1; 13.︒135;14.︒105; 15.32; 16.8; 17. ︒60; 35π . 三、解答题(共89分) 18.(本题9分)解:原式33321++-+=…………………………………………(8分)6=. ……………………………………………………………(9分)19. (本题9分)解:原式41222+-++=x x x ………………………………………(4分)52+=x ……………………………………………(6分)当21=x 时,原式5212+⨯=………………………………………(7分)6= ………………………………………………(9分)20.(本题9分)证明:21,2,1∠=∠∠+∠=∠∠+∠=∠CAD CAE CAD BADCAE BAD ∠=∠∴……………(4分)∵AB=AC ,AD=AE∴BAD ∆≌CAE ∆……………(7分) ∴BD=CE ………………………(9分)21. (本题9分)解: (1)41…… (4分) (2)解法一(画树状图):开始A B C DB C DA C DA B DA B C开关1 开关 2……………………………………………………………………………………………(8分) 解法二(列表):开关1开关2A B C D A (A ,B )(A ,C ) (A ,D ) B (B ,A ) (B ,C )(B ,D ) C (C ,A ) (C ,B ) (C ,D )D(D ,A )(D ,B )(D ,C )……………………………………………………………………………………………(8分)P (正好一盏灯亮和一个扇转)32128= ……………………………………………(9分)22. (本题9分) 解:(1) 抽测的男生人数50%2010=÷=,抽测成绩的众数为5, ……………………(4分)……………………………………(6分)(2)2523505061416=⨯++,答:该校九年级男生中估计有252人体能达标. …(9分)23.(本题9分) 解:(1)依题意,得:⎩⎨⎧=+=+8.84124.648b a b a ……………………………………………………(4分)解得:4.0,6.0==b a …………………………………………………………(6分) (2) 设用电量为x ,依题意,得:()6.10204.06.0≤-+x x解得:13≤x ……………………………………………………………………(8分)答:用电量至多为13万度.…………………………………………………………(9分) 24.(本题9分)(1) 证明:∵四边形ABCD 是平行四边形 ∴AD ∥BC AB ∥CD∴∠ADF=∠DEC ∠B+∠C=180°(2分) ∵∠AFE+∠AFD=180 ∠AFE=∠B∴∠AFD=∠C …………………………(4分) ∴△ADF ∽△DEC …………………(5分)人数/人20 16 12 8 4 4 10146抽测成绩/次16(2)解:∵△ADF ∽△DEC ∴DC AF DE AD = ∴5.38.24=DE ∴5=DE ………………………(8分) 在Rt △ADE 中,3452222=-=-=AD DE AE∴平行四边形ABCD 的面积1234=⨯=⨯=AE BC …………………(9分) 25.(本题13分)解:(1)∵抛物线4412++-=bx x y 经过点(-0,2) ∴()()0422412=+-⨯+-⨯-b ∴23=b ……………………………………(3分)(2)令0423412=++-x x 解得:8,221=-=x x∴()()0,8,0,2C B - ∴()0,3,10D BC = ……………………………(6分)令0=x 得:4=y ∴4=OA ∴BC OD OA AD 215342222==+=+=……………………………(7分) ∴点A D 在⊙D 上…………………………………………………………………(8分) (3)连接OP ,设()y x P ,,则四边形PAOC 的面积为:⎪⎭⎫ ⎝⎛++-+=+=⋅+⋅=+=∆∆42341424221212x x x y x y OC x OA S S S POC PAO ()32416822++-=++-=x x x ………………………………………(12分)∴当4=x ,即P 的坐标为()6,4时,S 最大.…………………………(13分)26.(本题13分) 解: (1)过点B 作BC ⊥y 轴于点C , ∵A(0,2),△AOB 为等边三角形, ∴AB=OB=2,∠BAO=60°,∴OC=AC=1,即B 1). ………………(3分) (2)当点P 在x 轴上运动(P 不与Q 重合)时,不失一般性, ∵∠PAQ=∠OAB=60°,∴∠PAO=∠QAB , 在△APO 和△AQB 中, ∵AP=AQ ,∠PAO=∠QAB ,AO=AB ∴△APO ≌△AQB 总成立, ∴∠ABQ=∠AOP=90°总成立,∴当点P 在x 轴上运动(P 不与Q 重合)时,∠ABQ 为定值90°.………………(7分) (3)由(2)可知,点Q 总在过点B 且与AB 垂直的直线上, 可见AO 与BQ 不平行。
2011年泉州市丰泽区初中质量检查

2011年丰泽区初中学业质量检查(含答案)数 学 试 题(满分:150分;考试时间:120分钟)学校 姓名一、 选择题(每小题3分,共21分)每小题有四个答案,其中有且只有一个答案是正确的.请在答题卡上相应题目的答题区域内作答,答对的得3分,答错、不答或答案超过一个的一律得0分. 1.5-的倒数是 ( ) A .5 B .15 C .5- D .15- 2.下列运算正确的是 ( )A .235a a a =· B.222()ab a b +=+ C.235()a a = D.235a a a +=3.如图,直线AB ∥CD ,直线EF 与AB 、CD 相交,若︒=∠502, 则=∠1( ) A .︒40B .︒50C .︒130D .︒1404.如图是由四个相同的小正方体组成的立体图形,它的俯视图...是( )5.把不等式组11x x +⎧⎨≤⎩>0, 的解集表示在数轴上,则下图正确的是( )6.甲、乙、丙、丁四位选手各10次射击成绩的平均数都是9.2环,方差如下表:则这四人中成绩发挥最稳定的是( )A.甲B.乙C.丙D.丁 7.一辆汽车和一辆摩托车分别从A ,B 两地去同一城市,它们离A 地的路程随时间变化的图象如图所示.则下列结论错误..的是( )A.摩托车比汽车晚到1 hB.汽车的速度为60 km/hC. 摩托车的速度为45km/hD. A ,B 两地的路程为20 km选 手甲乙丙 丁方差(环2)0.0350.0150.0250.027A.B .C .D .第4题图主视方向 -1 0 1 -10 1 -10 1 -10 1 A .B .C .D .第7题图第3题图FA BCDOO A BCD二.填空题:(每小题4分,共40分)在答题卡上相应题目的答题区域内作答. 8.写出一个比0小的实数_______.9.若正多边形的一个外角是45°,则该正多边形的边数是_______.10. 太阳半径约为696000千米,数字696000用科学记数法表示为 . 11.已知一组数据2, 1,-1,2, 3,则这组数据的众数是______. 12.计算111x x x ---结果是_____________. 13.分解因式:222m m -= .14.如图,在△ABC 中,AB =AC =8,AD 是底边上的高,E 为AC 中点,则DE = . 15.已知圆锥的底面半径为4cm ,高为3cm ,则这个圆锥的侧面积为__________cm 2. 16. 如图,在平行四边形ABCD 中,请再添加一个..条件,使它成为菱形,则该条件可以是 . 17.如图,在平面直角坐标系xoy 中,分别平行x 、y 轴的两直线a 、b 相交于点A (3,4).连接OA ,(1)线段OA 的长 ;(2)若在直线a 上存在点P ,使△AOP 是等腰三角形.那么所有满足条件的点P 的坐标是 .三.解答题:(9个小题,共89分)在答题卡上相应题目的答题区域内作答.18.(9分)计算:1019(2)20113-⎛⎫--+- ⎪⎝⎭19.(9分)先化简,再求值: (2)(2)(2)a a a a +-+-,其中22a =+.20.(9分)如图, △ABD 、△BCD 都是等边三角形,E 、F 分别是AD 、CD 上的两个动点,且满足DE =CF .(1)求证:△BDE ≌△BCF ;(2)指出△BCF 是由△BDE 经过如何变换得到的?20第题图AB D EC14第题图第16题图bayxAO第17题图跳绳 第21题图2 4 6 8 1012 14 16 18踢毽子 乒乓球 羽毛球 其他项目学生人数(人)9 97 15 第一个班级“学生最喜欢的运动”人数的条形统计图第二个班级“学生最喜欢的运动”人数的扇形统计图其他 16%羽毛球 20%跳绳 28%踢毽子 18% 乒乓球21.(9分)某校在九年级中随机抽取两个班级进行了一次“你最喜欢的运动”的问卷调查,每名学生都选了一项.已知被调查的两个班级的学生人数均为50人,根据收集到的数据,绘制成如下统计图(不完整):根据统计图表中的信息,解答下列问题:(1)在本次随机调查中,第一个班级中喜欢“踢毽子”项目的学生有_________ 人,并将条形统计图补充完整;(温馨提示:请画在答题卷相对应的上)(2)第二个班级中喜欢“乒乓球”项目的学生人数所对应的圆心角度数是_________; (3)若该校九年级共有400名学生,请你估计该校喜欢“羽毛球”项目的学生总人数. 22.(9分)有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张. (1) 分别用a 、b 表示小敏、小颖袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出(a ,b ) 的所有取值;(2)求点(a ,b )在落在反比例函数y=6x的图象的概率. 23. (9分)如图,AB 是⊙O 的直径,BC 是弦,OD ⊥BC 于E ,交 BC于D . (1)请写出两个不同类型的正确结论; (2)若BC =8,ED =2,求sinA 的值.23第题图24. (9分 )某工艺品销售公司今年5月份调整了职工的月工资分配方案,调整后月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售的件数).右表是甲、乙两位职工今年5月份的工资情况信息:(1)试求月工资y 元与月销售件数x 件之间的函数关系式;(2)若职工丙今年6月份的工资不低于3000元,那么丙该月至少应销售多少件产品?职工甲乙 月销售件数(x 件) 200 300 月工资(y 元)2000250025.(12分)如图,直线MN 分别与x 轴、y 轴交于点M ,N ,与反比例函数y =x k(x>0)的图象相交于点A ,B .过点A 分别作AC ⊥x 轴,AE ⊥y 轴,垂足分别为C ,E ;过点B 分别作BF ⊥x 轴,BD ⊥y 轴,垂足分别为F ,D ,AC 与BD 交于点K ,连接CD . (1)比较大小:S 四边形AEOCS 四边形ODBF ;(填“>,=,<”)(2)求证:BK AK =DKCK; (3)试判断AN 与BM 有怎样的数量关系,并说明理由.26.(14分)如图,已知直线y =43x -1与y 轴交于点C ,将抛物线y =-41(x-2)2向上平移n 个单位(n >0)后与x 轴交于A ,B 两点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年丰泽区初中学业质量检查数 学 试 卷(满分:150分;考试时间:120分钟)一、选择题(每小题4分,共24分)1.计算(2)3-⨯所得结果正确的是( )A .5B .6C .5-D .6-2.投掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,则掷得向上一面的点数为奇数的概率是( ) A .12B .13C .14D .153.下图所示的几何体的左视图是( )4.两个圆的半径分别是3cm 和4cm ,圆心距为5cm ,则这两个圆的位置关系是( )A.内切B.相交C.外切D.外离5.不等式组21x x <⎧⎨>-⎩,的解集为( )A.1x >- B.2x < C.12x -<< D.无解 6.如图,点O 是等边ABC △内一点,︒=∠110AOB︒=∠145BOC .将BOC △绕点C 按顺时针方向旋转60得ADC △,连接OD .则=∠AOD ( )A.︒40B.︒45C.︒50D.︒55二、填空题(每小题3分,共36分) 7.3-的相反数是________________.8.分解因式:42-x =________________.9. 北京2008年第29届奥运会火炬接力传递总里程约137000千米,用科学记数法表示约为________________千米.10.将一件进价为100元的商品先提价50%,再打8折(即标价的80%)卖出,则卖出这件商品所获利润是 元.11.甲、乙两人进行射击比赛,在相同条件下各射击10次,他们的平均成绩A BCDO 110145°均为8环,10次射击成绩的方差分别是:22S =甲,21.2S =乙,那么,射击成绩较为稳定的是 .(填“甲”或“乙”) 12.计算:111---x x x = ________________. 13.六边形的内角和等于________________度. 14.如图,已知点A B C ,,在⊙O 上,若40ACB ∠=°,则AOB ∠= 度. 15.反比例函数xy 3-=的图象在第二象限与第_____象限. 16.已知圆锥的母线长为30,侧面展开后所得扇形的圆心角为120°,则该圆锥的底面半径为 .17.如图,请你填写一个适当的条件: ______________,使BE ∥AC . 18.如图:是用火柴棍摆出的一系列三角形图案, 按这种方式摆下去,当每边上摆6(即n =6) 根时,需要的火柴棍总数为 ___根.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1=n 2=n 3=n 第20题图三、解答题19.(8分)计算:42131--⎪⎭⎫⎝⎛+-20.(8分)先化简下面的代数式,再求值: )4()2(2-++x x x , 其中2=x .21.(8分)如图,已知点E 、F 分别是菱形ABCD的边AB 、AD 上,BE=DF , 求证:AE=AF .22.(8分)有关部门准备对某居民小区的自来水管网系统进行改造,为此,需了解该小区的自来水用水的情况.该部门通过随机抽样,调查了其中的20(第14题图) B ABE DFA (第17题图)BCD E(1(2)若该居民小区共有400户家庭,试估计该小区的月用水量?23.(8分)如图,一枚运载火箭从地面O 处发射,几秒后到达A 点.当火箭到达A 点时,从地面B 处的雷达站测得AB 的距离是6千米,仰角是43°. 求火箭到达A 点时距离地面的高度AO (精确到0.01千米/秒).24.(8分)在一个布口袋中有装着只有颜色不同,其它都相同的白、红、黑三种颜色的小球各一只,甲、乙两人进行摸球游戏:甲先从袋中摸出一个球看清颜色后放回,再由乙从袋中摸出一个球.如果规定:乙摸到与甲相同颜色的球为乙胜,否则乙负,试求乙在游戏中能获胜的概率. (要求用画树状图或列表的方法求解)25.(8分) 如图,在12×6的网格图中(每个小正方形的边长均为1个单位长), 有一个R t △ABC 和一个半圆O (A 、B 、C 、O 均为格点),∠C=90°, 半圆O 的半径为2. (1)将R t △ABC 沿AC 方向向右平移2个单位,请画出平移后的R t △DEF,其中A 、B 、C 的对应点分别是D 、E 、F (不必写画法);(2)将R t △ABC 沿AC 方向向右平移m 个单位时,其斜边恰好与半圆O 相切,求m 的值.26.(8分) 已知动点P 以每秒v 厘米的速度沿图甲的边框按从A F E D CB →→→→→的路径移动,相应的PAB ∆的面积S 关于时间t 的函数图象如图乙.若cm AB 6=.(1)求v 的值;(2)求图乙中的a 和b 的值.43º╭AB ┐ A BCD EF 24 )(2cm S a A B C O27.(13分)某班级组织有奖知识竞赛,派小明和小亮去超市购买钢笔和笔记本作为奖品. 该超市某品牌的钢笔每支a 元,笔记本每本b 元,若购买钢笔2支,笔记本5本,需要19元;若购买钢笔1支,笔记本10本,需要23元.(1)求a 、b 的值;(2)根据竞赛活动的设奖情况,他们决定购买该品牌的钢笔和笔记本共40件.①问:130元最多能买钢笔多少支? ②如果所购买钢笔的数量不少于笔记本的数量的41,那么他们应如何购买,才能使所花的钱最少?此时花了多少钱?28.(13分) 已知:抛物线12)1(2++++-=k x k x y 经过点)3,0(A . (1)求k 的值;(2)设抛物线交x 轴于B 、C 两点(B 在C 右边),点),(n m P 是抛物线上的一个动点,且位于直线AB 上方,设PAB ∆的面积为s ,试写出s 关于x 的函数关系式,并求出s 的最大值;(3)平行于x 轴的一条直线交抛物线于E 、F 两点,若以EF 为直径的圆恰好与x 轴相切,求此圆的半径.四、附加题(共10分)友情提示:若你全卷得分低于90分,则本题得分计入总分,但计入后总分最多不超过90分;若你全卷已经达到或超过90分,则本题得分不计入总分.1.比较大小:3______2-(填“>”“=”“<”)2. 如图,AB ∥CD ,若∠1=45°,则∠2=__________度.A BC D 1 22008年丰泽区初中学业质量检查 数学试卷•参考答案及评分标准(满分:150分;考试时间:120分钟)一、选择题(每小题4分,共24分)1.D .2.A . 3.A .4.B . 5.C.6.B . 二、填空题(每小题3分,共36分)7.3.8.)2)(2(-+x x .9. 51037.1⨯.10.20.11.乙.12.1. 13.720.14.︒80.15.四.16.10.17.略.18.63. 三、解答题(共90分)19.(8分)计算:421310--⎪⎭⎫⎝⎛+-解:原式=421-+----------------(6分) =1-------------------------(8分)20.(8分)先化简下面的代数式,再求值: )4()2(2-++x x x , 其中2=x .解:原式=x x x x 44422-+++----------(4分) =422+x -----------------------(6分) 当2=x 时,原式=84)2(22=+----------(8分)21.(8分)如图,已知点E 、F 分别是菱形ABCD的边AB 、AD 上,BE=DF , 求证:△ABE ≌△ADF .证明:∵ABCD 是菱形∴AB=AD, ∠B=∠D---------(4分)∵AB=AD, ∠B=∠D, BE=DF∴△ABE ≌△ADF -------------(8分)22.(8分)有关部门准备对某居民小区的自来水管网系统进行改造,为此,需了解该小区的自来水用水的情况.该部门通过随机抽样,调查了其中的(1(2)若该居民小区共有400户家庭,试估计该小区的月用水量? 解:(1)6.16)(3m --------------(4分)(2) 该小区的月用水量为:)(66406.164003m =⨯--------(8分)ABE DF C23.(8分)如图,一枚运载火箭从地面O 处发射,几秒后到达A 点.当火箭到达A 点时,从地面B 处的雷达站测得AB 的距离是6千米,仰角是43°. 求火箭到达A 点时距离地面的高度AO (精确到0.01千米/秒).解:在AOB Rt ∆中, ∵BOAOB =sin ∴︒⨯=⋅=43sin 6sin 0BB AO答: 火箭到达A 点时距离地面的高度AO 是---------(8分)24.(8分)在一个布口袋中有装着只有颜色不同,其它都相同的白、红、黑三种颜色的小球各一只,甲、乙两人进行摸球游戏:甲先从袋中摸出一个球看清颜色后放回,再由乙从袋中摸出一个球.如果规定:乙摸到与甲相同颜色的球为乙胜,否则乙负,试求乙在游戏中能获胜的概率. (要求用画树状图或列表的方法求解) 解:43º╭AB ┐ 白 红黑 白 红 黑白 红 黑 白红 黑25.(8分) 如图,在12×6的网格图中(每个小正方形的边长均为1个单位长),有一个R t △ABC 和一个半圆O (A 、B 、C 、O 均为格点),∠C=90°, 半圆O 的半径为2. (1)将R t △ABC 沿AC 方向向右平移2个单位,请画出平移后的R t △DEF,其中A 、B 、C 的对应点分别是D 、E 、F (不必写画法);(2)将R t △ABC 沿AC 方向向右平移m 个单位时,其斜边恰好与半圆O 相切,求m 的值. 解:(1)(略)画对给4分;(2)如图,当R t △ABC 移到R t △GMN 时, 其斜边GM 恰好与半圆O 相切,切点为P. ∵∠OPG=∠MNG=90° ∠OGP=∠MGN∴R t △OPG ∽R t △MNG ∴MNOPMG OG =---------(6分) ∵5432822=+==-=-=MG OP mAG OA OG∴2114258=⇒=-m m --------(8分)26.(8分) 已知动点P 以每秒v 厘米的速度沿图甲的边框按从A F E D CB →→→→→的路径移动,相应的PAB ∆的面积S 关于时间t 的函数图象如图乙.若cm AB 6=.(1)求v 的值;(2)求图乙中的a 和b 的值.解: (1)由图知,)/(2244621s cm v v =⇒=⋅--------(3分)(2))(632),(422),(842cm DE cm CD cm BC =⨯==⨯==⨯=A B C D EF (图甲)24 4 )(2cm S )(s tb a o 9 6 (图乙)GM NOP∴4214621)(21=⨯⨯=+⨯⨯=DE BC AB a ------(6分) )(17234s v FA EF DE CD BC b ==++++=-------(8分)27.(13分)某班级组织有奖知识竞赛,派小明和小亮去超市购买钢笔和笔记本作为奖品. 该超市某品牌的钢笔每支a 元,笔记本每本b 元,若购买钢笔2支,笔记本5本,需要19元;若购买钢笔1支,笔记本10本,需要23元.(1)求a 、b 的值;(2)根据竞赛活动的设奖情况,他们决定购买该品牌的钢笔和笔记本共40件.①问:130元最多能买钢笔多少支? ②如果所购买钢笔的数量不少于笔记本的数量的41,那么他们应如何购买,才能使所花的钱最少?此时花了多少钱? 解: (1)由题意得:⎩⎨⎧⎩⎨⎧==⇒=+=+8.1523101952b a b a b a -------------------(4分) (2)设买钢笔x 支,由题意得:130)40(8.15≤-+x x ---------------(6分) 125.18≤⇒x∵x 是正整数,∴18=x答: 最多能买钢笔18支.------------------(8分) (3)设买钢笔x 支,由题意得:8)40(41≥⇒-≥x x x ---------------(10分) 设买钢笔x 支,笔记本x -40本,共需y 元,则722.3)40(8.15+=-+=x x x y ∵02.3>=k ∴y 随x 增大而增大 ∴当8=x 时,6.97min =y答:购买8支钢笔和32本笔记本, 所花的钱最少,此时花了6.97元.--(13分)28.(13分) 已知:抛物线12)1(2++++-=k x k x y 经过点)3,0(A . (1)求k 的值;(2)设抛物线交x 轴于B 、C 两点(B 在C 右边),点),(n m P 是抛物线上的一个动点,且位于直线AB 上方,设PAB ∆的面积为s ,试写出s 关于x 的函数关系式,并求出s 的最大值;(3)平行于x 轴的一条直线交抛物线于E 、F 两点,若以EF 为直径的圆恰好与x 轴相切,求此圆的半径. 解:(1) ∵抛物线经过点)3,0(A∴312=+k∴1=k ---------——————(3分)(2)作x PD ⊥轴于点D ,由题意得:2923233321)3(2123-+=⨯⨯--⋅-⋅+=m n n m n m s ------(5分)∵点),(n m P 在抛物线上 ∴322++-=m m nmm m m m s 29232923296322+-=-+++-=∴-----------(6分) ∴82723232+⎪⎭⎫ ⎝⎛--=m s∴当23=m 时,s 取最大值为827------------(7分) (3)设圆的半径为r .①当EF 在x 轴上方时,由抛物线及直线与圆相切等性质可得: 点F 的坐标为),1(r r +代入322++-=x x y 得:r r r =++++-3)1(2)1(2042=-+⇒r r解得:2171±-=r (r 取正数)-----------(10分) ②当EF 在x 轴下方时,由抛物线及直线与圆相切等性质可得: 点F 的坐标为),1(r r -+ 代入322++-=x x y 得:r r r -=++++-3)1(2)1(2 042=--⇒r r 解得:2171±=r (r 取正数) 由①②知:2171+-=r 或2171+=r ------(13分)四、附加题(共10分) 1.<.--------------(5分) 2.45----------(5分)。
