正弦波逆变器脉宽调制技术的调制模型分析
正弦脉宽调制SPWM逆变器原理图以及特点
正弦脉宽调制SPWM逆变器原理图以及特点
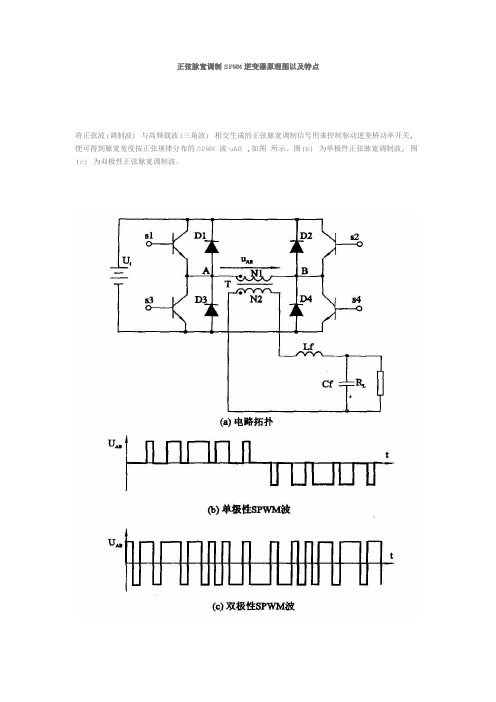
将正弦波(调制波) 与高频载波(三角波) 相交生成的正弦脉宽调制信号用来控制驱动逆变桥功率开关, 便可得到脉宽宽度按正弦规律分布的SPWM 波uAB ,如图所示。
图(b) 为单极性正弦脉宽调制波, 图(c) 为双极性正弦脉宽调制波。
正弦脉宽调制SPWM 逆变器电路的特点为:
1) 变压器仍工作在工频, 体积大且笨重, 体积与重量仅和输出电压频率有关, 与逆变器开关频率无关, 提高逆变器开关频率并不能减小变压器体积和重量;
2) 输出滤波器体积、重量小;
3) 对于输入电压和负载的波动, 系统的动态响应特性好;
4) 变压器和输出滤波电感产生的音频噪音得到改善;
5) 功率器件开关频率高, 开关损耗增加, 降低了系统变换效率。
在低频环节DCöA C 逆变技术中, 由于工频变压器的体积和逆变器的开关频率无关, 只和输出电压的频率有关。
为克服此缺点, 必须采用高频环节逆变技术。
正弦波脉冲宽度调制(SPWM)逆变电路

5.3.1 SPWM波形控制基本原理 5.3.2 单相SPWM控制原理 5.3.3 三相桥式SPWM逆变电路 5.3.4 SPWM逆变电路的同步调制和异步调制
第4章 电工测量与工厂输配电和安全用电
5.3.1 SPWM波形控制基本原理
5.3.1 SPWM波形控制基本原理 面积相等而形状不同的窄脉冲加在具有惯性的环节上,
一定频率范围内,采用同步调制可以保持波形对称 的优点;低频段又采纳了 异步调制的长处。
11 目录 返回
上页 下页 退出
53正弦波脉冲宽度调制spwm逆变电路531531spwmspwm波形控制基本原理波形控制基本原理532532单相spwm控制原理533533三相桥式三相桥式spwmspwm逆变电路逆变电路534534spwmspwm逆变电路的同步调制和异步调制逆变电路的同步调制和异步调制目录退出返回上页下页531spwm531spwm波形控制基本原理波形控制基本原理面积相等而形状不同的窄脉冲加在具有惯性的环节上其效果基本相同
1. 载波比N为常数,变频时三角载波频率和正弦 调制频率同步变化的调制方式称为同步调制方式
2异步调制 载波比N不为常数,变频范围内三角载波频率和正弦 调制频率不保持同步变化关系的调制方式称为异步
调制方式。 一般来说,同步调制适用于输出的高频段,
异步调制适用于输出的低频段。
10 目录 返回
上页 下页 退出
如把上述脉冲列用同数量等幅不等宽的矩形脉冲列来 代替,使矩形脉冲的中点和相应正弦等分的中点重合,
且使矩形脉冲和相应正弦部分面积(冲量)相等, 就得到图6-10(b)所示的脉冲序列PWM波形。如 PWM波形的脉冲宽度按正弦规律变化称为SPWM波。
正弦脉宽调制波的研究分析

正弦脉宽调制波的研究分析[摘要] 本文全面阐述了SPWM波的基本特征与个性,以电子变流技术为研究对象,通过确立比较规范的参考基准,便于控制策略的实施及逐步深入的探讨或研究。
[关键词] 正弦波逆变技术脉宽调制1.引言正弦脉宽调制(Sinusoidal PWM 简称SPWM)应用以来,经过不断的研究发展,正弦逆变技术也渐趋成熟而服务于广泛的交流应用场合,为应用的持续发展奠定了坚实的基础,并且越来越多的与其他科学领域相互关联、相互交叉和相互渗透,继而应用系统逐渐朝高性能、高效率、大功率、高频化和智能化的方向发展,同时随着工程发展的日益需求,对逆变系统提出了更高的要求。
2.正弦脉宽调制波产生的原理由于正弦交流量是典型的模拟量,传统发电机难以完成高频交流电流输出,而功率半导体器件于模拟状态工作时产生的动态损耗剧增,于是,用开关量取代模拟量成为必由之路,并归结为脉冲电路的运行过程,从而构成了运动控制系统中的功率变换器或电源引擎。
在交流应用场合,多数负载要求输入的是正弦波电流。
电工学认为,周期性的非正弦交流量是直流、正弦波和余弦波等分量的集合,或者是非正弦波也可以分解为相位差和频率不同的正弦波以及直流分量。
不良波形或失真严重的正弦交流量必然产生大量的低次、高次及分数谐波,丰富的谐波分量与基波叠加的情景使得正负峰值几乎同时发生,换向突变时急剧的运动状态将对负载造成冲击并导致负载特性的不稳定或漂移,又加重了滤波器件的负担,损耗也随之增大,非但降低了电网的功率因数,还对周边设备造成不良影响。
在高频化和大功率电力变换场合,装置内部急剧的电流变化,不但使器件承受很大电磁应力,并向装置周围空间辐射有害电磁波污染环境,这种电磁干扰(Electro Magnetic Interference 简称EMI)还会引发周围设备的误动作及造成电能计量紊乱。
抑制谐波和EMI的防御仍为重要课题或技术指标。
图1 正弦化交流量的样本波形可见,简单的方波在功率应用场合下显示出了不尽如人意的一面。
11.8正弦波脉宽调制(SPWM)逆变电路

图11.8.8 通过比较器产生的波形
11.8.3 SPWM逆变电路 SPWM逆变电路如图11.8.9(a)(b)所 示。图中函数发生器XFG1产生1kHz的三角波信 号作为载波信号uc,函数发生器XFG1产生50Hz 的正弦波信号作为调制信号ur ,XFG1和XFG2 对话框设置如图11.8.6所示。
11.8正弦脉宽调制( SPWM)逆变电路 11.8正弦脉宽调制( SPWM) 正弦脉宽调制
11.8.1正弦脉宽调制(SPWM) 11.8.1正弦脉宽调制(SPWM)逆变电路工作原理 正弦脉宽调制 1. SPWM控制的基本原理 图11.8.1(a)示出正弦彼的正半周波形, 并将其划分为N等份,这样就可把正弦半波看成 由N个彼此相连的脉冲所组成的波形。这些脉冲 的宽度相等,都等于π/ N,但幅值不等,且 脉冲顶部是曲线,各脉冲的幅值按正弦规律变 化。
如果将每一等份的正弦曲线与横轴所包围的面 积用一个与此面积相等的等高矩形脉冲代替, 就得到图11.8.1(b)所示的脉冲序列。这样, 由N个等幅而不等宽的矩形脉冲所组成的波形 与正弦波的正半周等效,正弦波的负半周也可 用相同的方法来等效。
SPWM(Sine Pulse Width Modulation正弦波 脉宽调制)的控制思想,就是利用逆变器的 开关元件,由控制线路按一定的规律控制开 关元件的通断,从而在逆变器的输出端获得 一组等幅、等距而不等宽的脉冲序列。其脉 宽基本上按正弦分布,以此脉冲列来等效正 弦电压波。
控制VT4或VT3通断的方法如图11.8.3所示。载 波uc在调制信号波ur的正半周为正极性的三角 波,在负半周为负极性的三角波。调制信号ur 为正弦波。在ur和uc的交点时刻控制晶体管VT4 或VT3的通断。在ur的正半周,VT1保持导通, 当ur> uc时使VT4导通,负载电压uo= UD,
multisim仿真教程正弦波脉宽调制SPWM逆变电路业界精制

技术教育
1
如果将每一等份的正弦曲线与横轴所包围的面 积用一个与此面积相等的等高矩形脉冲代替, 就得到图11.8.1(b)所示的脉冲序列。这样, 由N个等幅而不等宽的矩形脉冲所组成的波形 与正弦波的正半周等效,正弦波的负半周也可 用相同的方法来等效。
技术教育
2
SPWM(Sine Pulse Width Modulation正弦波 脉宽调制)的控制思想,就是利用逆变器的 开关元件,由控制线路按一定的规律控制开 关元件的通断,从而在逆变器的输出端获得 一组等幅、等距而不等宽的脉冲序列。其脉 宽基本上按正弦分布,以此脉冲列来等效正 弦电压波。
方向变化,所得到输出电压的PWM波形也只在 一个方向变化的控制方式称为单极性PWM控制 方式。
3. 双极性PWM控制方式
技术教育
15
图11.8.2的单相桥式逆变电路采用双极性PWM 控制方式的波形如图11.8.4所示。在双极性方
式中ur的半个周期内,三角波载波是在正、负
两个方向变化的,所得到的PWM波形也是在两
11.8.1正弦脉宽调制(SPWM)逆变电路工作原理
1. SPWM控制的基本原理 图11.8.1(a)示出正弦彼的正半周波形,
并将其划分为N等份,这样就可把正弦半波看成 由N个彼此相连的脉冲所组成的波形。这些脉冲 的宽度相等,都等于π/ N,但幅值不等,且 脉冲顶部是曲线,各脉冲的幅值按正弦规律变 化。
技术教育
8
如负载电流较大,那么直到使VT4再一次导通之 前,VD3一直持续导通。如负载电流较快地衰减 到零,在VT4再一次导通之前,负载电压也一直
为零。这样,负载上的输出电压uo就可得到零
和UD交替的两种电平。
技术教育
9
正弦脉宽调制(SPWM)控制
正弦脉宽调制(SPWM)控制2010-09-18 ylw527+关注献花(4)为了使变压变频器输出交流电压的波形近似为正弦波,使电动机的输出转矩平稳,从而获得优秀的工作性能,现代通用变压变频器中的逆变器都是由全控型电力电子开关器件构成,采用脉宽调制(pulse width modulation, 简称pwm ) 控制的,只有在全控器件尚未能及的特大容量时才采用晶闸管变频器。
应用最早而且作为pwm控制基础的是正弦脉宽调制(sinusoidal pulse width modulation, 简称spwm)。
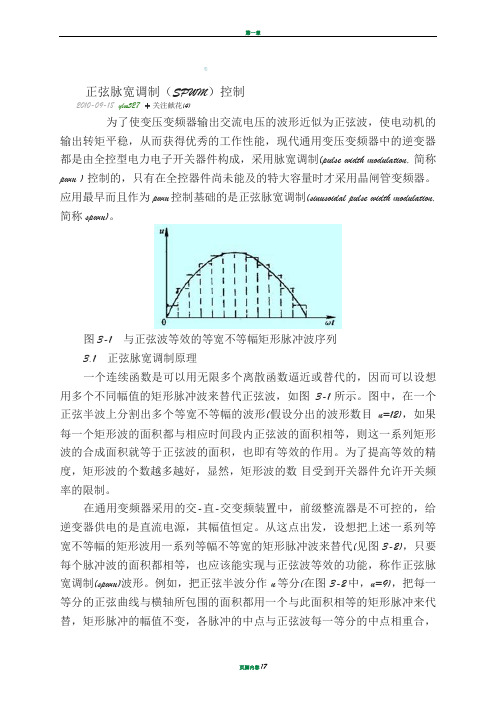
图3-1与正弦波等效的等宽不等幅矩形脉冲波序列3.1正弦脉宽调制原理一个连续函数是可以用无限多个离散函数逼近或替代的,因而可以设想用多个不同幅值的矩形脉冲波来替代正弦波,如图3-1所示。
图中,在一个正弦半波上分割出多个等宽不等幅的波形(假设分出的波形数目n=12),如果每一个矩形波的面积都与相应时间段内正弦波的面积相等,则这一系列矩形波的合成面积就等于正弦波的面积,也即有等效的作用。
为了提高等效的精度,矩形波的个数越多越好,显然,矩形波的数目受到开关器件允许开关频率的限制。
在通用变频器采用的交-直-交变频装置中,前级整流器是不可控的,给逆变器供电的是直流电源,其幅值恒定。
从这点出发,设想把上述一系列等宽不等幅的矩形波用一系列等幅不等宽的矩形脉冲波来替代(见图3-2),只要每个脉冲波的面积都相等,也应该能实现与正弦波等效的功能,称作正弦脉宽调制(spwm)波形。
例如,把正弦半波分作n等分(在图3-2中,n=9),把每一等分的正弦曲线与横轴所包围的面积都用一个与此面积相等的矩形脉冲来代替,矩形脉冲的幅值不变,各脉冲的中点与正弦波每一等分的中点相重合,这样就形成spwm波形。
同样,正弦波的负半周也可用相同的方法与一系列负脉冲波等效。
这种正弦波正、负半周分别用正、负脉冲等效的spwm波形称作单极式spwm。
脉冲宽度调制(PWM)技术原理

一、PWM技术原理由于全控型电力半导体器件的出现,不仅使得逆变电路的结构大为简化,而且在控制策略上与晶闸管类的半控型器件相比,也有着根本的不同,由原来的相位控制技术改变为脉冲宽度控制技术,简称PwM技术。
PwM技术可以极其有效地进行谐波抑制,在频率、效率各方面有着明显的优点使逆变电路的技术性能与可靠性得到了明显的提高。
采用PwM方式构成的逆变器,其输人为固定不变的直流电压,可以通过PwM技术在同一逆变器中既实现调压又实现调频。
由于这种逆变器只有一个可控的功率级,简化了主回路和控制回路的结构,因而体积小、质量轻、可靠性高。
又因为集凋压、调频于一身,所以调节速度快、系统的动态响应好。
此外,采用PwM技术不仅能提供较好的逆变器输出电压和电流波形,而且提高了逆变器对交流电网的功率因数。
把每半个周期内,输出电压的波形分割成若干个脉冲,每个脉冲的宽度为每两个脉冲间的间隔宽度为t2,则脉冲的占空比γ为此时,电压的平均值和占空比成正比,所以在调节频率时,不改变直流电压的幅值,而是改变输出电压脉冲的占空比,也同样可以实现变频也变压的效果。
二、正弦波脉宽调制(sPwM)1.sPwM的概念工程实际中应用最多的是正弦PwM法(简称sPwM),它是在每半个周期内输出若干个宽窄不同的矩形脉冲波,每一矩形波的面积近似对应正弦波各相应每一等份的正弦波形下的面积可用一个与该面积相等的矩形来代替,于是正弦波形所包围的面积可用这N个等幅(Vd)不等宽的矩形脉冲面积之和来等效。
各矩形脉冲的宽度自可由理论计算得出,但在实际应用中常由正弦调制波和三角形载波相比较的方式来确定脉宽:因为等腰三角形波的宽度自上向下是线性变化的,所以当它与某一光滑曲线相交时,可得到一组幅值不变而宽。
度正比于该曲线函数值的矩形脉冲。
若使脉冲宽度与正弦函数值成比例,则也可生成sPwM波形。
在工程应用中感兴趣的是基波,假定矩形脉冲的幅值Vd恒定,半周期内的脉冲数N也不变,通过理论分析可知,其基波的幅值V1m脉宽δi有线性关系在进行脉宽调制时,使脉冲系列的占空比按正弦规律来安排。
第二节正弦波脉宽调制SPWM控制法

第二节正弦波脉宽调制SPWM控制法1(2(1 正弦波脉宽调制SPWM逆变器结构典型的交流-直流,交流逆变器的结构如图2-1-3所示。
图2-1-3: 变压变频器主电路结构图图2-1-3中,单相交流或三相交流供电经非控全波整流,变成单极性直流电压;该直流电压经有源或无源功率因素校正电路PFC(Power Factor Correct)得到直流母线电压 Udc,某些情况下功率因素校正电路可以省略。
逆变器的核心电路是由六个功率开关器件Q1-Q6构成的三相逆变桥,每个桥有上下两个桥臂;上桥臂上端接直流母线电压正端(DC+),下桥臂下端接直流母线参考端(DC-);对于交流异步电机的驱动,为防止直通,上、下桥臂通常设置为互补工作方式:上桥臂导通时,下桥臂截止;下桥臂导通时,上桥臂截止。
三桥臂中间输出接至负载:三相感应电机的UVW输入端。
功率开关器件Q1-Q6可以是晶闸管GTO,双极性功率晶体管BJT,金属氧化膜功率场效应管MOSFET,绝缘栅型双极性功率晶体管IGBT。
IGBT具有开关速度快、承载电流大、耐压高、管耗小等特点,在电源逆变器中得到最为广泛的应用。
对于感性负载(电机),为了保护IGBT,常需加续流二极管D1-D6,用以在开关管关断时形成电流回路。
IGBT通常已与续流二极管封装在一起。
电容C用于能量缓冲,可保持直流母线电压Udc相对稳定。
为了在电机的UVW端线上输入三相平衡的交流电,通常做法是依一定规则用PWM信号PWM1L-PWM3H去控制逆变器的六个开关管的开关状态。
所谓的正弦波SPWM(Sinusoidally PWM)技术,就是用正弦波去调制PWM信号的脉宽,即:功率管的输出为一系列等幅不等宽的矩形脉冲波形,其宽度依正弦波规律变化;对交流输出波形的幅度对称性及相位要求不是非常苛刻的应用来说,PWM 信号的频率通常保持不变。
这种控制策略也叫异步控制法,即载波信号的频率独立于调制波频率。
见图2-1-4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦波逆变器脉宽调制技术的调制模型分析王立乔(燕山大学电气工程学院,河北省秦皇岛市066004)摘要:高频脉宽调制(PWM )正弦波逆变器的应用越来越广泛,对其调制模型的定量分析对系统参数设计和方案优化有重要帮助。
通过双重傅里叶变换得到了正弦波逆变器3种主要PWM 方法的调制模型,提出了一种新型单极性正弦波PMW (SPWM )方法,并给出了其调制模型。
通过对各种调制方法的分析和比较,确定了在不同场合下的最佳调制策略:对于单相全桥逆变器,倍频式SPWM 和单极性SPWM 为最佳;对于组合型三相逆变器,新型单极性SPWM 为最佳。
仿真和实验验证表明了理论分析的正确性。
关键词:脉宽调制(PWM );正弦波逆变器;双重傅里叶变换;调制模型;调制策略中图分类号:TM461收稿日期:2008205228;修回日期:2008207202。
国家自然科学基金资助项目(50707028);燕山大学博士科学基金资助项目(B155)。
0 引言高频脉宽调制(PWM )正弦波逆变器已经得到广泛应用,是目前最为重要和常用的电力电子变流设备,不但在不间断电源(U PS )、变频器等传统领域,而且在有源电力滤波器[124]、可再生能源发电[526]等各个方面都有广泛应用。
对于单相全桥逆变器而言,正弦波PWM (SPWM )技术有3种基本的调制方式:双极性SPWM 、单极性SPWM 和倍频式SPWM 。
这3种调制方式经常使用,在很多文献中也有记述[7],但只有少数文献对双极性SPWM 的调制模型和谐波特性进行了详细的定量分析[8],而对于单极性SPWM 和倍频式SPWM ,对其调制模型和谐波特性的详细定量分析鲜见。
通过双重傅里叶变换可以建立SPWM 技术的精确调制模型,并能对其谐波特性进行定量分析。
鉴于双极性SPWM 的调制模型和谐波特性已有定量分析[9],本文将进一步给出单极性SPWM 和倍频式SPWM 的调制模型和谐波特性分析。
在深入分析常规单极性SPWM 调制模型的基础上,本文提出一种新的单极性SPWM 方法,对其调制模型和谐波特性也进行了定量分析。
在此基础上,本文对3种基本的SPWM 方式的技术特点进行了详细分析比较,得到了一些对于正弦波逆变器开关调制策略的优化选择有一定实用意义的结论。
1 单相全桥逆变器输出电压波形与触发脉冲的关系电压型单相全桥逆变器电路拓扑结构见图1。
图1 电压型单相全桥逆变器电路结构Fig.1 Structure of voltage source single phasefull 2bridge inverter图1中,所有触发脉冲均为二逻辑函数,假定: u g y =1 触发脉冲为高电平-1 触发脉冲为低电平(1)式中:y =1,2,3,4。
根据单相全桥逆变器电路的工作原理可得:u 0=12(u g1+u g3)U dc(2)2 SPWM 的调制模型2.1 双极性SPWM 的调制模型对于自然采样双极性SPWM (调制原理参见附录A 图A1),载波与正弦调制波相比较,交点作为开关点,同时控制V T 1和V T 3,于是式(2)就可简化为u 0=u g1U dc 。
假设调制波的数学表达为:M (t )=a co s (ωm t +<m )(3)式中:a 为幅度调制比;ωm 为调制波频率;<m 为调制波相位。
—54—第32卷 第17期2008年9月10日Vol.32 No.17Sep.10,2008文献[9]对自然采样双极性SPWM 的调制模型进行了深入研究,通过双重傅里叶变换得到u g1的调制模型为: u g1(t )=a co s (ωm t +<m )+∑∞k =14J 0k πa 2k πsin kπ2cos k (ωc t +<c )+∑∞k =1∑±∞n =±14J nk πa 2πsin k +n 2π・co s (k (ωc t +<c )+n (ωm t +<m ))(4)式中:ωc 为调制波频率;<c 为调制波相位;J n (・)为n 阶贝塞尔函数,并且有:J n (x )=∑∞l =1(-1)lxn+2l2n+2l l !(n +l )!(5) 由式(4)可以看出,双极性SPWM 有以下特点:①基波成分与调制波完全相同;②不含偶数次载波谐波;③不含k +n 为偶数次的边带谐波;④谐波出现在载波频率整数倍频率附近。
图2给出了载波比N =ωc /ωm =24、幅度调制比a =1时,双极性SPWM 的波形及其频谱。
图2 双极性SPWM 的波形和频谱Fig.2 Bipolar SPWM w aveform with its spectrum2.2 倍频式SPWM 的调制模型倍频式SPWM 技术含有2个频率和幅值大小相同、相位相反的双极性三角载波,如图3所示。
图3 倍频式SPWM 原理Fig.3 Principle of double 2frequency SPWM倍频式SPWM 技术的2个三角载波与正弦波相比较生成2路驱动信号,其中一路作为V T 1的驱动信号,另一路作为V T 3的驱动信号。
从式(2)可知,输出电压u 0的形状与(u g1+u g3)/2完全相同,只是在幅值上相差U dc 倍,因此,只要分析出(u g1+u g3)/2的调制模型,就可以知道u 0的谐波特性,而u g1和u g3的调制模型与式(4)一致,只是相角有区别。
将式(4)代入式(2),并考虑相关的相角,可以推导得到u 0的调制模型为: u 0(t )=aU dc sin ωm t +∑∞k =1∑±∞n =±12U dc J n (kπa )kπsin 2n π2・sin (2kωc t +n ωm t )(6) 从式(6)可以看出,倍频式SPWM 的输出电压有以下特点:①基波成分与调制波完全相同;②不含载波谐波;③不含偶数次谐波;④谐波出现在载波频率偶数倍频率附近。
图4给出了载波比N =12,幅度调制比a =1时,倍频式SPWM 的波形及其频谱。
图4 倍频式SPWM 的波形和频谱Fig.4 Double 2frequency SPWM w aveform withits spectrum2.3 单极性SPWM 的调制模型2.3.1 常规单极性SPWM 的调制模型单极性SPWM 的调制原理如图5所示。
正弦调制波与2个三角载波进行调制,2个三角载波以零线为界;零线以上的三角载波与正弦调制波相比较生成驱动信号u g1供给V T 1,零线以下的三角载波与正弦调制波相比较生成驱动信号u g3供给V T 3。
常规单极性SPWM 的2个三角载波的频率和峰—峰值相同,相位相反。
利用双重傅里叶变换推导得到单极性SPWM 的调制模型为:—64—2008,32(17) 图5 单极性SPWM 原理Fig.5 Principle of unipolar SPWM u 0(t )=aU dc sin ωm t +∑∞k =1∑±∞n =±12U dc J nk πa 2kπsin 2n π2・cos kπsin (k ωc t +n ωm t )(7) 从式(7)可以看出,常规单极性SPWM 有以下特点:①基波成分与调制波完全相同;②不含载波谐波;③不含n 为偶数次的谐波;④谐波出现在载波频率附近。
图6给出了载波比N =24、幅度调制比a =1时,常规单极性SPWM 的波形及其频谱。
图6 常规单极性SPWM 的波形和频谱Fig.6 U nipolar SPWM w aveform with its spectrum对比式(6)和式(7)可以发现,在输出电压波形脉动频率相同时,常规单极性SPWM 与倍频式SPWM 的调制模型完全相同,谐波特性也完全一致。
上述结论也可以从图4和图6中清楚看出来。
2.3.2 新型单极性SPWM 的调制模型在常规单极性SPWM 方式的基础上,本文提出一种新型单极性SPWM 方式,其调制原理如图7所示。
新型单极性SPWM 的调制方法与常规单极性SPWM 基本相同,只是新型单极性SPWM 的2个三角载波的频率、峰—峰值和相位完全相同。
经推导可以得到新型单极性SPWM 的调制模型为:图7 新型单极性SPWM原理Fig.7 Principle of new unipolar SPWMu 0(t )=aU dc sin ωm t +U dc∑∞k =14sin2k π2∑∞l =1J 2l-1(k πa )2l -1kπ2cos kωc t +∑∞k =1∑±∞n =±12U dc sin 2(k +n )π2kπ2∑∞l =1J2l-1(k πa )・D cos (kωc t +n ωm t )n ≠2l-1+πsin (k ωc t +n ωm t )n =2l-1(8)式中:D =4(2l -1)cos 2lπ2(2l -1)2-n 2(9) 从式(8)和式(9)可以看出,新型单极性SPWM 有以下特点:①基波成分与调制波完全相同;②不含偶数次载波谐波;③不含n +k 为偶数次的谐波;④谐波出现在载波频率附近。
图8给出了载波比N =24、幅度调制比a =1时,新型单极性SPWM 的波形及其频谱。
图8 新型单极性SPWM 的波形和频谱Fig.8 N ew unipolar SPWM w aveform with its spectrum从前面分析可以看出,新型单极性SPWM 波形与双极性SPWM 波形的频谱分布具有类似性质,亦—74—・学术研究・ 王立乔 正弦波逆变器脉宽调制技术的调制模型分析即两者在输出电压脉动频率和幅度调制比相同时,所含谐波的次数完全相同。
比较式(4)和式(8)及图2(b )和图8(b )可以发现,双极性SPWM 的载波谐波和距离载波频率最近的边带谐波比新型单极性SPWM 的对应次数谐波的含量高很多,新型单极性SPWM 距离载波频率较远的边带谐波比双极性SPWM 对应次数谐波的含量高一些。
3 各种SPWM 技术的分析与比较3.1 谐波品质分析表1列出了在相同载波频率ωc 下,上述各种SPWM 方法应用于单相全桥电路时各自的总开关频率ωT (即所有器件开关频率的总和)、输出电压脉动频率ωo 以及最低次谐波群中心频率ωh 。
此外,表1还给出了总开关频率与输出电压脉动频率的比值k =ωT /ωo 。
表1 各种SPWM 方法的相关参数比较T able 1 R elative p arameter comparison of some SPWMmethods调制方式ωTωoωh k双极性SPWM 4ωc ωc ωc4倍频式SPWM 4ωc2ωc 2ωc 2常规单极性SPWM 2ωc +2ωm ωc ωc 2+ωm /ωc 新型单极性SPWM2ωc +2ωmωcωc2+ωm /ωc从表1可以看出,当载波频率相同时,双极性SPWM 的总开关频率比单极性SPWM 高几乎1倍;而从图2、图6和图8的波形频谱中也可以看出,在相同幅度调制比的情况下,双极性SPWM 的谐波特性比单极性SPWM 差一些。
