江苏省2014届高三高考模拟专家卷数学(2) Word版含答案

合集下载

江苏省2014届高三高考模拟专家卷(1)地理(纯Word版含答案)

试卷第1页，总15页绝密★启用前江苏省2014届高三高考模拟专家卷（1）文综地理试题考试范围：高中；考试时间：150分钟；命题人：黄文华注意事项：注意事项：1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上．用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上． 2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上．3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答．漏涂、错涂、多涂的，答案无效．5．考生必须保持答题卡的整洁．考试结束后，将试卷和答题卡一并交回．一、选择题：本题共35小题，每小题4分，共140分。

每小题给出的四个选项中，只有一个选项符合题目要求。

读“某日晨昏线图”，图中甲、乙表示一段完整的晨线或昏线，此时地球公转速度较慢，完成1—2题。

1．甲地经度为A ．20°WB ．20°EC ． 160°WD ．160°E 2．此日，丙地正午太阳高度为 A ．70° B ．60° C ．30° D ．20°读图，回答3～4题。

试卷第2页，总15页3．若该洋流是一支寒流，则其可能位于 A ．北半球中低纬度的大陆西岸 B ．北半球中高纬度的大洋东岸 C ．南半球中低纬度的大陆西岸 D ．南半球中低纬度的大洋西岸 4．若该洋流位于南半球，则该洋流 A ．流经地区渔业资源丰富 B ．流经地区沿岸气候干燥C ．是形成沿岸温带海洋性气候的因素之一D ．促进了高低纬之间的热量平衡下图为四个不同地点的气候资料。

2014高考数学二轮专题复习(苏教版文科)Word版训练专题提升训练阶段检测卷2

阶段检测卷(二)一、填空题(每小题5分，共70分)1．已知α∈⎝ ⎛⎭⎪⎫π，3π2，cos α＝－55，tan 2α等于________．解析由于α∈⎝ ⎛⎭⎪⎫π，3π2，cos α＝－55，则sin α＝－1－cos 2α＝－255，那么tan α＝sin αcos α＝2，则tan 2α＝2tan α1－tan 2 α＝－43. 答案－432．已知向量a ＝(2,1)，a ·b ＝10，|a ＋b |＝52，则|b |等于________．解析由于|a |＝5，而|a ＋b |2＝(a ＋b )2＝a 2＋2a ·b ＋b 2＝5＋2×10＋b 2＝(52)2，则有b 2＝25，解得|b |＝5. 答案 53．(2013·苏锡常镇调研)已知钝角α满足cos α＝－35，则tan ⎝ ⎛⎭⎪⎫α2＋π4的值为________．解析因为α是钝角，所以α2是锐角， cos α＝2cos 2α2－1＝－35，所以cos α2＝55，sin α2＝255，tan α2＝2，所以tan ⎝ ⎛⎭⎪⎫α2＋π4＝2＋11－2＝－3.答案－34．已知向量a ，b 满足|a |＝2，|b |＝1，且(a ＋b )⊥⎝ ⎛⎭⎪⎫a －52b ，则a 与b 的夹角为________．解析因为(a ＋b )⊥⎝ ⎛⎭⎪⎫a －52b ，所以(a ＋b )·⎝ ⎛⎭⎪⎫a －52b ＝a 2－52b 2－32a·b ＝0.又因为|a |＝2，|b |＝1，所以4－52－32a·b ＝0.所以a·b ＝1.又a·b ＝|a ||b |cos 〈a ，b 〉＝1，所以cos 〈a ，b 〉＝12.又a 与b 的夹角的取值范围是[0，π]，所以a 与b 的夹角为π3. 答案 π35．(2013·南京模拟)函数y ＝A sin(ωx ＋φ)⎝ ⎛⎭⎪⎫A ＞0，ω＞0，|φ|＜π2的图象如图所示，则f (0)＝________.解析由图知，A ＝2.函数的周期(用区间长度表示)为8π3－⎝ ⎛⎭⎪⎫－4π3＝4π，∴2πω＝4π，ω＝12.又∵⎝ ⎛⎭⎪⎫－4π3，0在函数的图象上，∴2sin ⎣⎢⎡⎦⎥⎤12×⎝ ⎛⎭⎪⎫－4π3＋φ＝0，得12×⎝ ⎛⎭⎪⎫－4π3＋φ＝0，即φ＝2π3. ∴函数的解析式为f (x )＝2sin ⎝ ⎛⎭⎪⎫x 2＋2π3，∴f (0)＝ 3. 答案36．若M 为△ABC 所在平面内一点，且满足(MB →－MC →)·(MB →＋MC →－2MA →)＝0，则△ABC 为________三角形．解析由(MB →－MC →)·(MB →＋MC →－2MA →)＝0，可知CB →·(AB →＋AC →)＝0，设BC 的中点为D ，则AB →＋AC →＝2A D →，故CB →·AD →＝0，所以CB →⊥AD →.又D 为BC 中点，故△ABC 为等腰三角形．答案等腰7．在△ABC 中，AB ＝2，AC ＝3，BC ＝4，则角A ，B ，C 中最大角的余弦值为________．解析根据三角形的性质：大边对大角，由此可知角A 最大，由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝32＋22－422×3×2＝－14.答案－148．(2012·南京、盐城模拟)已知正△ABC 的边长为1，CP →＝7CA →＋3CB →，则CP →·AB →＝________.解析 CP →·AB →＝(7CA →＋3CB →)·AB →＝7CA →·AB →＋3CB →·AB→＝－72＋32＝－2. 答案－29．(2013·盐城调研)△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，向量m ＝ (2sin B,2－cos 2B )，n ＝⎝ ⎛⎭⎪⎫2sin 2⎝ ⎛⎭⎪⎫π4＋B 2，－1，m ⊥n ，∠B ＝________.解析由m ⊥n ，得m ·n ＝0，所以4sin B ·sin 2⎝ ⎛⎭⎪⎫π4＋B 2＋cos 2B －2＝0，所以2sin B ⎣⎢⎡⎦⎥⎤1－cos ⎝ ⎛⎭⎪⎫π2＋B ＋cos 2B －2＝0，即2sin B ＋2sin 2B ＋1－2sin 2B －2＝0，也即sin B ＝12，又因为0<B <π，所以B ＝π6或56π. 答案 π6或56π10．如图，在△ABC 中，D 是边AC 上的点，且AB ＝AD,2AB ＝3BD ，BC ＝2BD ，则sin C 的值为________．解析设AB ＝c ，则AD ＝c ，BD ＝2c 3，BC ＝4c3，在△ABD 中，由余弦定理得cos A ＝c 2＋c 2－43c 22c2＝13，sin A ＝223，在△ABC 中，由正弦定理得csin C ＝4c 3223，解得sin C ＝66. 答案 6611．在△ABC 所在的平面上有一点P 满足P A→＋PB→＋PC →＝AB →，则△PBC 与△ABC的面积之比是________．解析因为P A →＋PB →＋PC →＝AB →，所以P A →＋PB →＋PC →＋BA →＝0，即PC →＝2AP →，所以点P 是CA 边上的靠近A 点的一个三等分点，故S △PBC S △ABC ＝PC AC ＝23. 答案 2312．在△ABC 中，若AB ＝1，AC ＝3|A B →＋A C →|＝|B C →|，则BA →·BC →|BC →|＝______.解析如图， AB →＋AC →＝AD →，依题意，得|AD →|＝|BC →|，所以四边形ABDC 是矩形，∠BAC ＝90°. 因为AB ＝1，AC ＝3，所以BC ＝2.cos ∠ABC ＝AB BC ＝12，BA →·BC→|BC →|＝|BA →|| BC →|cos ∠ABC| BC →|＝|BA→|cos ∠ABC ＝12.答案 1213．已知f (x )＝sin x ，x ∈R ，g (x )的图象与f (x )的图象关于点⎝ ⎛⎭⎪⎫π4，0对称，则在区间[0,2π]上满足f (x )≤g (x )的x 的范围是________．解析设(x ，y )为g (x )的图象上任意一点，则其关于点⎝ ⎛⎭⎪⎫π4，0对称的点为⎝ ⎛⎭⎪⎫π2－x ，－y ，由题意知该点在f (x )的图象上，所以－y ＝sin ⎝ ⎛⎭⎪⎫π2－x ，即g (x )＝－sin ⎝ ⎛⎭⎪⎫π2－x ＝－cos x ，由sin x ≤－cos x ，得sin x ＋cos x ＝2sin ⎝ ⎛⎭⎪⎫x ＋π4≤0，又因为x ∈[0,2π]，从而解得3π4≤x ≤7π4. 答案 ⎣⎢⎡⎦⎥⎤3π4，7π414．(2013·泰州模拟)如图，在直角三角形ABC 中，AC ＝3，BC ＝1，点M ，N 分别是AB ，BC 的中点，点P 是△ABC (包括边界)内任一点，则AN →·MP →的取值范围为________．解析以点C 为原点，CB 所在直线为x 轴，CA 所在直线为y 轴，建立如图所示直角坐标系，设P (x ，y )，则由题可知B (1,0)，A (0，3)，N ⎝ ⎛⎭⎪⎫12，0，M ⎝ ⎛⎭⎪⎫12，32，所以AN →＝⎝ ⎛⎭⎪⎫12，－3，MP →＝⎝ ⎛⎭⎪⎫x －12，y －32，所以AN →·MP →＝x 2－14－3y ＋32＝x 2－3y ＋54，直线AB 的方程为3x ＋y －3＝0.由题可知⎩⎨⎧x ≥0，y ≥0，3x ＋y －3≤0，由线性规划知识可知，当直线x 2－3y ＋54－z ＝0过点A 时有最小值－74，过点B 时有最大值74. 答案 ⎣⎢⎡⎦⎥⎤－74，74二、解答题(共90分)15．(本小题满分14分)已知a ＝(sin α，1), b ＝(cos α，2)，α∈⎝ ⎛⎭⎪⎫0，π4.(1)若a ∥b ，求tan α的值； (2)若a ·b ＝125，求sin ⎝ ⎛⎭⎪⎫2α＋π4的值．解 (1)因为a ∥b ，所以2sin α＝cos α，所以tan α＝12. (2)因为a ·b ＝125，所以sin αcos α＋2＝125即sin 2α＝45. 因为α∈⎝ ⎛⎭⎪⎫0，π4，所以2α∈⎝ ⎛⎭⎪⎫0，π2，所以cos 2α＝1－sin 22α＝35.所以sin ⎝ ⎛⎭⎪⎫2α＋π4＝sin 2αcos π4＋cos 2αsin π4＝45×22＋35×22＝7210. 16．(本小题满分14分)已知函数f (x )＝3sin 2x ＋sin x cos x ，x ∈⎣⎢⎡⎦⎥⎤π2，π.(1)求f (x ) 的零点；(2)求f (x )的最大值和最小值．解 (1)令f (x )＝0得sin x ·(3sin x ＋cos x )＝0，所以sin x ＝0，或tan x ＝－33. 由sin x ＝0，x ∈⎣⎢⎡⎦⎥⎤π2，π，得x ＝π；由tan x ＝－33，x ∈⎣⎢⎡⎦⎥⎤π2，π，得x ＝5π6.综上，函数f (x )在⎣⎢⎡⎦⎥⎤π2，π上的零点为5π6或π.(2)f (x )＝32(1－cos 2x )＋12sin 2x ＝sin ⎝ ⎛⎭⎪⎫2x －π3＋32.因为x ∈⎣⎢⎡⎦⎥⎤π2，π，所以2x －π3∈⎣⎢⎡⎦⎥⎤2π3，5π3.当2x －π3＝2π3，即x ＝π2时，f (x )的最大值为3；当2x －π3＝3π2，即x ＝11π12时，f (x )的最小值为－1＋32.17．(本小题满分14分)已知函数f (x )＝M sin(ωx ＋φ)(M >0，ω>0，|φ|<π2)的部分图象如图所示．(1)求函数f (x )的解析式；(2)在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，若(2a －c )cos B ＝b cos C ，求f ⎝ ⎛⎭⎪⎫A 2的取值范围．解 (1)由图象知M ＝1，f (x )的最小正周期T ＝4×⎝ ⎛⎭⎪⎫5π12－π6＝π，故ω＝2πT ＝2.将点⎝ ⎛⎭⎪⎫π6，1代入f (x )的解析式得sin ⎝ ⎛⎭⎪⎫π3＋φ＝1，即π3＋φ＝2k π＋π2，φ＝2k π＋π6，k ∈Z ，又|φ|<π2∴φ＝π6.故函数f (x )的解析式为f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6.(2)由(2a －c )cos B ＝b cos C ，得 (2sin A －sin C )cos B ＝sin B cos C ， ∴2sin A cos B ＝sin(B ＋C )＝sin A . ∵sin A ≠0，∴cos B ＝12， ∴B ＝π3，∴A ＋C ＝2π3. ∵f ⎝ ⎛⎭⎪⎫A 2＝sin ⎝ ⎛⎭⎪⎫A ＋π6，又∵0<A <2π3，∴A ＋π6∈⎝ ⎛⎭⎪⎫π6，56π.∴sin ⎝ ⎛⎭⎪⎫A ＋π6∈⎝ ⎛⎦⎥⎤12，1，∴f ⎝ ⎛⎭⎪⎫A 2∈⎝ ⎛⎦⎥⎤12，1. 18．(本小题满分16分)(2013·湖北卷)在△ABC 中，角A ，B ，C 对应的边分别是a ，b ，c .已知cos 2A －3cos(B ＋C )＝1. (1)求角A 的大小；(2)若△ABC 的面积S ＝53，b ＝5，求sin B sin C 的值．解 (1)由cos 2A －3cos(B ＋C )＝1，得2cos 2A ＋3cos A －2＝0，即(2cos A －1)(cos A ＋2)＝0，解得cos A ＝12或cos A ＝－2(舍去)．因为0<A <π，所以A ＝π3，(2)由S ＝12bc sin A ＝12bc ·32＝34bc ＝53，得bc ＝20.又b ＝5，知c ＝4. 由余弦定理，得a 2＝b 2＋c 2－2bc cos A ＝25＋16－20＝21，故a ＝21. 又由正弦定理得sin B sin C ＝b a sin A ·ca sin A ＝ bc a 2sin 2A ＝2021×34＝57.19．(本小题满分16分)(2013·江西卷)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知cos C ＋(cos A －3sin A )cos B ＝0. (1)求角B 的大小；(2)若a ＋c ＝1，求b 的取值范围．解 (1)由已知得－cos(A ＋B )＋cos A cos B －3sin A cos B ＝0，即有sin A sin B －3sin A cos B ＝0，因为sin A ≠0，所以sin B －3cos B ＝0，即3cos B ＝sin B . 所以tan B ＝3，又因为0<B <π，所以B ＝π3.(2)由余弦定理得b 2＝a 2＋c 2－2ac cos B ，因为a ＋c ＝1，cos B ＝12，所以b 2＝(a ＋c )2－3ac ≥(a ＋c )2－3⎝⎛⎭⎪⎫a ＋c 22＝14(a ＋c )2＝14，∴b ≥12. 又a ＋c >b ，∴b <1，∴12≤b <1.20．(本小题满分16分)(2013·江苏卷)如图，游客从某旅游景区的景点A 处下山至C 处有两种路径．一种是从A 沿直线步行到C ，另一种是先从A 沿索道乘缆车到B ，然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山，甲沿AC 匀速步行，速度为50 m/min.在甲出发2 min 后，乙从A 乘缆车到B ，在B 处停留1 min 后，再从B 匀速步行到C .假设缆车匀速直线运动的速度为130 m/min ，山路AC 长为1 260 m ，经测量cos A ＝1213，cos C ＝35. (1)求索道AB 的长；(2)问乙出发多少分钟后，乙在缆车上与甲的距离最短？(3)为使两位游客在C 处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？解 (1)在△ABC 中，因为cos A ＝1213，cos C ＝35，所以sin A ＝513， sin C ＝45.从而sin B ＝sin[π－(A ＋C )]＝sin(A ＋C )＝sin A cos C ＋cos A sin C ＝513×35＋1213×45＝6365.由正弦定理AB sin C ＝AC sin B ，得AB ＝ACsin B ×sin C ＝ 1 2606365×45＝1 040(m)．所以索道AB 的长为1 040 m.(2)假设乙出发t 分钟后，甲、乙两游客距离为d ，此时，甲行走了(100＋50t )m ，乙距离A 处130t m ，所以由余弦定理得d 2＝(100＋50t )2＋(130t )2－2×130t ×(100＋50t )×1213＝200(37t 2－70t ＋50)，因0≤t ≤1 040130，即0≤t ≤8，故当t ＝3537(min)时，甲、乙两游客距离最短．(3)由正弦定理BC sin A ＝AC sin B ，得BC ＝AC sin B ×sin A ＝1 2606365×513＝500(m)．乙从B 出发时，甲已走了50×(2＋8＋1)＝550(m)，还需走710 m 才能到达C.设乙步行的速度为v m/min ，由题意得－3≤500v －71050≤3，解得1 25043≤v ≤62514，所以为使两位游客在C 处互相等待的时间不超过3分钟，乙步行的速度应控制在⎣⎢⎡⎦⎥⎤1 25043，62514(单位：m/min)范围内．备课札记：。

江苏省南京市2014届高三考前冲刺训练(南京市教研室) 数学 Word版含答案

0＜k＜1)．曲线C1上的点A在第一象限，过A分别作x轴、y轴的平行线交曲线C2分别于点B、D，过点B作y轴的平行线交曲线C3于点C．若四边形ABCD为矩形，则k的值是___________．
【答案】．
【提示】设A(t，2 log2t)(t＞1)，则B(t2，2 log2t)，D(t，log2t)，C(t2，2klog2t)，则有log2t＝2klog2t，
【答案】x＋y－2＝0．
【说明】本题考查直线与圆相切问题和最值问题．
6．已知双曲线－＝1(a＞0，b＞0)的离心率等于2，它的右准线过抛物线y2=4x的焦点，则双曲线的方程为．
【答案】－＝1．
【解析】本题主要考查了双曲线、抛物线中一些基本量的意义及求法．
7．在平面直角坐标系xOy中，已知曲线C1、C2、C3依次为y＝2log2x、y＝log2x、y＝klog2x(k为常数，
【答案】π．
【提示】设圆锥的底面半径为r，母线长为l，由题意知＝ π，且 ·2πr·l＝2 π，解得l＝2，r＝，所以圆锥高h＝1，则体积V＝ πr2h＝π．
【说明】本题考查圆锥的侧面展开图及体积的计算．
5．设圆x2＋y2＝2的切线l与x轴正半轴，y轴正半轴分别交于点A，B．当线段AB的长度最小值时，切线l的方程为____________．
当直线过点A时，t最大．由解得A( ， )，
所以tmax＝－＝．
因此的取值范围是[－， ]．
【说明】本题含三个变量，解题时要注意通过换元减少变量的个数．利用消元、换元等方法进行减元的思想是近年高考填空题中难点和热点，对于层次很好的学校值得关注．
9．已知四数a1，a2，a3，a4依次成等比数列，且公比q不为1．将此数列删去一个数后得到的数列(按原来的顺序)是等差数列，则正数q的取值集合是．

江苏省南通市2014届高三数学学科基地密卷(3) Word版含答案

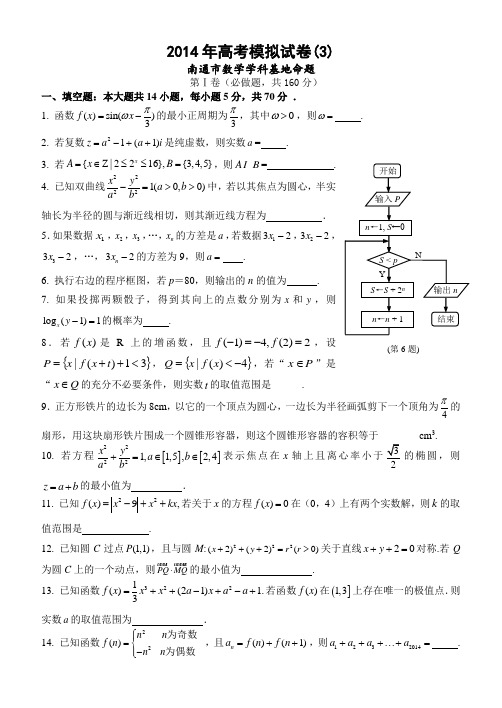
2014年高考模拟试卷(3)南通市数学学科基地命题第Ⅰ卷（必做题，共160分）一、填空题：本大题共14小题，每小题5分，共70分．1. 函数()sin()3f x x πω=-的最小正周期为3π，其中0ω>，则ω= .2. 若复数21(1)z a a i =-++是纯虚数，则实数a = .3. 若{Z |2216},{3,4,5}x A x B =∈≤≤=，则AB = .4. 已知双曲线22221(0,0)x ya b a b-=>>中，若以其焦点为圆心，半实轴长为半径的圆与渐近线相切，则其渐近线方程为． 5．如果数据1x ，2x ，3x ，…，n x 的方差是a ，若数据132x -，232x -，332x -，…，32n x -的方差为9，则a = .6. 执行右边的程序框图，若p ＝80，则输出的n 的值为 .7. 如果投掷两颗骰子，得到其向上的点数分别为x 和y ，则log (1)1x y -=的概率为 . 8．若)(x f 是R 上的增函数，且2)2(,4)1(=-=-f f ，设{}31)(|<++=t x f x P ，{}4)(|-<=x f x Q ，若“P x ∈”是“Q x ∈的充分不必要条件，则实数t 的取值范围是______.9．正方形铁片的边长为8cm ，以它的一个顶点为圆心，一边长为半径画弧剪下一个顶角为4π的扇形，用这块扇形铁片围成一个圆锥形容器，则这个圆锥形容器的容积等于________cm 3.10. 若方程[][]22221,1,5,2,4x y a b a b+=∈∈表示焦点在x 轴上且离心率小于的椭圆，则z a b =+的最小值为．11. 已知22()9,f x x x kx =-++若关于x 的方程()0f x =在（0，4）上有两个实数解，则k 的取值范围是 .12. 已知圆C 过点(1,1)P ，且与圆M :222(2)(2)(0)x y r r +++=>关于直线20x y ++=对称.若Q 为圆C 上的一个动点，则PQ MQ ⋅的最小值为 .13. 已知函数3221()(21) 1.3=++-+-+f x x x a x a a 若函数()f x 在(]1,3上存在唯一的极值点．则实数a 的取值范围为．14. 已知函数22 () n n f n n n ⎧⎪=⎨-⎪⎩为奇数为偶数，且()(1)n a f n f n =++，则1232014a a a a +++⋯+=.(第6题)二、解答题：本大题共6小题，共90分.15.（本小题满分14分）已知ABC ∆的三个内角,,A B C 所对的边分别为,,a b c ,向量(1,2)m =，2(cos2,cos )2An A =，且1m n ⋅=.(1)求角A 的大小；(2)若2b c a +==,求证：ABC ∆为等边三角形.16.（本小题满分14分）在直三棱柱111ABC A B C -中，AC=4,CB=2,AA 1=2，60ACB ∠=，E 、F 分别是11,AC BC 的中点．（1）证明：平面AEB ⊥平面1B CF ；（2）设P 为线段BE 上一点，且2EP PB =，求三棱锥11P B C F -的体积．P F EC 1B 1A 1CBA17.（本小题满分14分）设椭圆方程22221x y a b+=(0)a b >>，椭圆上一点到两焦点的距离和为4，过焦点且垂直于x 轴的直线交椭圆于A ，B 两点，AB =2．（1）求椭圆方程；（2）若M ，N 是椭圆C 上的点，且直线OM 与ON 的斜率之积为12-，是否存在动点00(,)P x y ，若2OP OM ON =+，有22002x y +为定值．18. (本小题满分16分) 某固定在墙上的广告金属支架如图所示，根据要求，AB 至少长3米，C 为AB 的中点，B 到D 的距离比CD 的长小0.5米，∠BCD=600（1）若,CD x =,BC y =将支架的总长度表示为y 的函数，并写出函数的定义域.（注：支架的总长度为图中线段AB 、BD 和CD 长度之和）（2）如何设计,AB CD 的长，可使支架总长度最短．19.（本小题满分16分）若数列{}n a 的前n 项和为n S ，且满足等式23n n a S +=.（1）能否在数列中找到按原来顺序成等差数列的任意三项，说明理由；（2）能否从数列中依次抽取一个无穷多项的等比数列，且使它的所有项和S 满足9116013S <<，如果这样的数列存在，这样的等比数列有多少个？（注：设等比数列的首项为1,a ，公比为(||1)q q <，则它的所有项的和定义为11a q-）20.（本小题满分16分）已知函数32()(63)x f x x x x t e =-++，t R ∈. （1）若函数()y f x =有三个极值点，求t 的取值范围；（2）若()f x 依次在,,()x a x b x c a b c ===<<处取到极值，且22a c b +=，求()f x 的零点；（3）若存在实数[0,2]t ∈，使对任意的[1,]x m ∈，不等式()f x x ≤恒成立，试求正整数m 的最大值.第Ⅱ卷（附加题，共40分）21．[选做题]本题包括A 、B 、C 、D 四小题，每小题10分；请选定其中两题，并在相应的答题区域．．．．．．．．．．．．．．．．．内作答．．．． A ．（选修４－１：几何证明选讲）在ABC ∆中，,=AB AC 过点A 的直线与其外接圆交于点P,交BC 延长线于点D. 求证：⋅=⋅AP AD AB ACB ．（选修４－２：矩阵与变换）ABC ∆的顶点A （1，2），B （3，3），C （2，1），求在矩阵2002⎡⎤⎢⎥-⎣⎦对应的变换下所得图形的面积．C ．（选修４－４：坐标系与参数方程）已知直线11:()5x tl t y =+⎧⎪⎨=-+⎪⎩为参数和直线2:0l x y --=的交于点P . （1）求P 点的坐标；（2）求点P 与(1,5)Q -的距离.D ．（选修４－５：不等式选讲）设,a b 是正数，证明：3322222a b a b a b+++≥⋅.【必做题】第22题、第23题，每题10分，共计20分.22．在如图所示的几何体中，四边形ABCD 为矩形，平面ABEF ⊥平面ABCD ， EF // AB ，PDC BA∠BAF =90º， AD = 2，AB =AF =2EF =1，点P 在棱DF 上．（1）若P 是DF 的中点，求异面直线BE 与CP 所成角的余弦值；（2）若二面角D -AP -CPF 的长度．23．数列{}n a 满足2121n n a a +=-，1N a =且11N a -≠，其中{}2,3,4,N ∈（1）求证：1||a ≤1；（2）求证：()12cos 2N k a k Z π-=∈．PFEDCAB2014年高考模拟试卷(3)参考答案南通市数学学科基地命题第Ⅰ卷（必做题，共160分）一、填空题 1. 6．263T ππωω==⇒= ;2. 1.将复数表示为(,)z a bi a b R =+∈的形式，然后由0,0a b =≠即可求；3.{}3,4.142216,222,14x x x ≤≤∴≤≤∴≤≤，即{}1,2,3,4A =. {}3,4,5B = ，{}3,4A B ∴⋂=；4. y x =±.设焦点为(,0)c ，渐近线方程为by xa=±，即0,bx ay ±=所以a =所以,a b =即渐近线方程为y x =±;5. 3.原数据的方差为a ，则新方差为2a ，而已知新方差为9，所以3a =;6. 7 .依次产生的S 和n 值分别为2,2;6,3;14,4;30,5;62,6;126,7;所以，输出的n 值为7;7.19.因为抛掷两枚均匀的正方体骰子的基本事件数为36种，又由l o g (1)1x y -=知1(1)y x x =+>，所以，满足条件的事件有: (2，3)，(3，4)，(4，5)，(5，6)共4种，则log (1)1x y -=的概率为19;8.3>t .{}|()13{()2}{()(2)}P x f x t x f x t x f x t f =++<=+<=+<，{}|()4{()(1)}Q x f x x f x f =<-=<-，因为函数)(x f 是R 上的增函数，所以{}|2{2}P x x t x x t =+<=<-，{}|1Q x x =<-，要使“P x ∈”是“Q x ∈的充分不必要条件，则有21t -<-，即3t >；9..由题意知，弧长为4π×8＝2π，即围成圆锥形容器底面周长为2π，所以圆锥底面半径为r ＝1，可得圆锥高h ＝，所以容积V ＝13πr 2×h ＝13π×1.⨯;10. 4 .方程22221x y a b+=表示焦点在x 的椭圆时，有22a b c e a ⎧>⎪⎨==⎪⎩，即22224a b a b ⎧>⎨<⎩，化简得2a b a b >⎧⎨<⎩，又[1,5]a ∈，[2,4]b ∈，画出满足不等式组的平面区域，如右图阴影部分所示，令z y x =+，平移直线,y x z =-+当过(2,2)时，min 4Z =; 11. 23(,3).4--()0f x =可以转化为22|9|x x kx -+=-，记22()|9|g x x x =-+，则()0f x =在（0，4）上有两个实数解，可以转化为函数2229,03()929,34x g x x x x x <≤⎧=-+=⎨-<<⎩与()h x kx =-的图象，结合图像和特殊点(3,9),(4,23)A B 可知23(,3)4k ∈--; 12.－4.设圆心C (,)a b ，则222022212a b b a --⎧++=⎪⎪⎨+⎪=⎪+⎩，解得00a b =⎧⎨=⎩，则圆C 的方程为222x y r +=，将点P 的坐标代入得22r =，故圆C 的方程为222x y +=，设(,)Q x y ，则222x y +=，且(1,1)(2,2)PQ MQ x y x y ⋅=--⋅++=224x y x y +++-=2x y +-，法一：令x α，y α=，则2sin()4x y πα+=+≥-2法二：令x y t +=，则y x t =-+，所以2PQ MQ x y ⋅=+-≥-4，PQ MQ ⋅的最小值为4- ; 13. [)7,1--.2()221'=++-f x x x a ，若函数()f x 在(]1,3上存在唯一的极值点，则方程2221++-x x a =0在区间(]1,3上有唯一解.因为抛物线21122=--+a x x 的对称轴为1=-x ，函数21122=--+a x x 在区间(]1,3单调递减，所以[)7,1∈--a ；14. 2014. n 为奇数时 1+n 为偶数，22(1)21=-+=--n a n n n ， n 为偶数时，1+n 为奇数，22(1)21=-++=+n a n n n ∴ 13=-a ，25=a ，37=-a ，49=a ，511=-a ，713=a ，…… ，∴ 122+=a a ，342+=a a ，即1220142014a a a ++=.二、解答题15. (1)由(1,2)m =，2(cos2,cos )2A n A =，得222cos22cos 2cos 1cos 12cos cos 2Am n A A A A A ⋅=+=-++=+ …………4分又因为1m n ⋅=，所以，22cos cos 1A A +=解得1cos 2A =或cos 1A =- …………6分0,3A A ππ<<∴=……7分(2)在ABC ∆中，2222cos a b c bc A =+-且a =所以，22222122b c bc b c bc=+-⋅=+-① …………9分又b c +=b c =，代入①整理得230c -+=，解得c =b于是a b c ===， .…………13分即ABC △为等边三角形. .…………14分 16．（1）在ABC ∆中，∵AC =2，BC =4,060ACB ∠=，∴AB =222AB BC AC +=， ∴AB BC ⊥.………………………………3分由已知1AB BB ⊥，1BB BC B =，∴11AB BB C C ⊥面. …………………5分又∵AB ABE ⊂面，11ABE BB C C ⊥故平面平面，即平面AEB ⊥平面1B CF ……7分（2）取11B C 的中点H ，连结EH ，则//EH AB且12EH AB ==由（1）11AB BB C C ⊥面，∴11EH BB C C ⊥面， ……10分C 1A 1A∵2EP PB =，∴111111111333P B C F E B C F B C F V V S EH --∆==⨯⋅=. ……14分17. （1）因为24a =，所以，2a = ---------------------------------2分∵过焦点且垂直于x 轴的直线交椭圆于A ，B 两点，AB =2．∴由椭圆的对称性知，椭圆过点(,1)c ，即22114c b+= --------------------4分224c b =-，解得22b =椭圆方程为22142x y += ------------------------------------------------------------7分（2）存在这样的点00(,)P x y .设11(,)M x y ，22(,)N x y ，则121212OM ON y y k k x x ==-，化简为 121220x x y y += ---------------------9分 ∵M ，N 是椭圆C 上的点，∴2211142x y +=，2222142x y += 由2OP OM ON =+得0121222x x x y y y =+⎧⎨=+⎩- ----------------------------------------11分所以22220012122(2)(2)x y x x y y +=+++ 222211221212(2)4(2)4(2)x y x y x x y y =+++++444020=+⨯+=即存在这样的点00(,)P x y -----------------------------------------------------14分 18. （1）由,CD x =则(0.5)BD x m =-，设CB y =，则支架的总长度为AC BC BD CD +++，在BCD ∆中，由余弦定理2222cos60(0.5)x y xy x +-=-化简得 20.25y xy x -=-+ 即20.250y xy x -+-= ① ……4分记0.5220.5l y y x x y x =++-+=+- 由20.250y xy x -+-=，则20.251y x y -=-222220.2520.52220.5420.5220.520.50.50.51111y y y y y y y l y y y y y y ---+---=+⨯-=+-=-=--------------6分（2）由题中条件得23y ≥，即 1.5y ≥设1(0.5)y t t -=≥则原式224(1)2(1)0.5484220.50.50.5t t t t t l t t+-+-++---=-=-=246 1.5 1.5 1.50.5460.54 5.5t t t t t t t++-=++-=++ ……10分0.5t ≥由基本不等式 1.54t t∴+≥有且仅当24 1.5t = ，即t =时成立，又由t = 满足0.5t ≥1y ∴=，x ∴= ∴当2,AB CD =+=金属支架总长度最短． (16)分19. （1）当1n =时，1123a a +=，则11a =.又23n n a S +=，所以1123n n a S +++=，两式相减得113n n a a +=，即 {}n a 是首项为1，公比为13的等比数列，所以113n n a -=------------------------------------------------------4分假设存在三项按原来顺序成等差数列，记为,,,()p q r a a a p q r << 则111211333q p r ---=+，即211333q p r=+，所以2331r q r p --⋅=+，即2331r q r p --⋅-=，即3(23)1r q q p ---=又p q r <<，*,r q r p N ∴--∈，所以33,230r q q p -->-<所以3(23)0r q q p ---<∴假设不成立，所以不存在三项按原来顺序成等差数列 --------8分（2）设抽取的等比数列首项为13m ，公比为13n，项数为k ，且,,m n k N +∈则111[1()]333()111133k m nmn nS k -=<--， -------------------------------------------10分因为9116013S <<，所以191311601313<<-， ------------------12分所以1311(1)3391609(2)33m nn m ⎧<-⎪⎪⎨⎪<+⎪⎩由（1）得到113133nm +<，所以3,1m n ≥≥， ------------13分由（2）得到1609933m n +>， --------------------------------14分当3,1m n ==时，适合条件，这时等比数列首项为311327=，公比为11133= 当3,1m n =>时，均不适合. 当3,1m n >≥时，均不适合.综上可得满足题意的等比数列有只有一个. ------------------16分20. （1）①23232()(3123)(63)(393)x x f x x x e x x x t x x x t e '=-++-++=--++∵()f x 有3个极值点，∴323930x x x t --++=有3个不同的根， --------2分令32()393g x x x x t =--++，则2()3693(1)(3)g x x x x x '=--=+-，从而函数()g x 在(,1)-∞-，(3,)+∞上递增，在(1,3)-上递减.∵()g x 有3个零点，∴(1)0(3)0g g ->⎧⎨<⎩，∴824t -<<. -----------------4分（2）,,a b c 是()f x 的三个极值点∴3232393()()()()()x x x t x a x b x c x a b c x ab bc ac x abc --++=---=-+++++-----6分∴23932a b c ab ac bc t abca c b++=⎧⎪++=-⎪⎨+=-⎪⎪+=⎩，∴1b =或32-（舍∵(1,3)b ∈-）∴111a b c ⎧=-⎪=⎨⎪=+⎩，所以，()f x的零点分别为1-1，1+ -------------------10分（3）不等式()f x x ≤，等价于32(63)x x x x t e x -++≤，即3263x t xe x x x -≤-+-. 转化为存在实数[0,2]t ∈，使对任意的[1,]x m ∈，不等式3263x t xe x x x -≤-+-恒成立. 即不等式32063x xe x x x -≤-+-在[1,]x m ∈上恒成立.即不等式2063x e x x -≤-+-在[1,]x m ∈上恒成立. ----------------12分设2()63x x e x x ϕ-=-+-，则()26x x e x ϕ-'=--+. 设()()26x r x x e x ϕ-'==--+，则()2x r x e -'=-.因为1x m ≤≤，有()0r x '<. 所以()r x 在区间[1,]m 上是减函数. 又1(1)40r e -=->，2(2)20r e -=->，()3330r -=-<，故存在()02,3x ∈，使得00()()0r x x ϕ'==.当01x x ≤<时，有()0x ϕ'>，当0x x >时，有()0x ϕ'<. 从而()y x ϕ=在区间0[1,]x 上递增，在区间0[,)x +∞上递减. 又1(1)40e ϕ-=+>，2(2)50e ϕ-=+>，3(3)60e ϕ-=+>，4(4)50e ϕ-=+>，5(5)20e ϕ-=+>，6(6)30e ϕ-=-<.所以，当15x ≤≤时，恒有()0x ϕ>；当6x ≥时，恒有()0x ϕ<. 故使命题成立的正整数m 的最大值为5. -----------------16分第Ⅱ卷（附加题，共40分）21. A. 由AB AC =，所以ABC ACB ∠=∠，所以,,∠=∠∠=∠ACD APC CAP CAP 所以,APCACD ∆∆所以,=AP ACAC AD所以2,=⋅AC AP AD 由AB AC =，所以⋅=⋅AP AD AB AC .………10分B ．由20120224⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦，所以，A ，B ，C 在矩阵变换下变为(2,4),(6,6),(4,2)A B C '''---，从而可得A B B C A C ''''''===，可得S=6． ………10分C. （1）将15x t y =+⎧⎪⎨=-+⎪⎩代入0x y --=得t =得(1P +， ………5分（2）由(1,5)Q -，得PQ =. ………10分D. 332233222()()()222a b a b a ba b a b a b +++≥⋅⇔+≥++ ……3分3322332222()()()a b a b ab a b a b ab a a b b a b ⇔+≥+⇔+-+=--- ……6分 2()()0a b a b ⇔+-≥.当且仅当a b =时等号成立. ……10分22. （1）因为∠BAF=90º，所以AF ⊥AB ，因为平面ABEF ⊥平面ABCD ，且平面ABEF ∩平面ABCD= AB ，所以AF ⊥平面ABCD ，因为四边形ABCD 为矩形，所以以A 为坐标原点，AB ，AD ，AF 分别为x ，y ，z 轴，建立如图所示空间直角坐标系O xyz -．所以 (1,0,0)B ，1(,0,1)2E ，1(0,1,)2P ，(1,2,0)C ．所以 1(,0,1)2BE =-，1(1,1,)2CP =--，所以4cos ,||||BE CP BE CPBE CP ⋅<>==⋅即异面直线BE 与CP ． -----------------------------5分（2）因为AB ⊥平面ADF ，所以平面APF 的法向量为1(1,0,0)n =．设P 点坐标为(0,22,)t t -，在平面APC 中，(0,22,)AP t t =-，(1,2,0)AC =，所以平面APC 的法向量为222(2,1,)t nt-=-，所以，121212||cos ,||||n n n n n n ⋅<>==⋅解得23t =，或2t =（舍）．所以PF = ---------------10分 23. （1）猜想：N K a -≤1，1≤k <N －1，k ∈N *，接下来用数学归纳法对k 进行证明：当k =1时，由2121n n a a +=-，1N a = 得 21N a -=12N a +=1 但11N a -≠ ∴1-N a =－1，∴11N a -≤成立 --------------------------------------------2分假设k =m (1≤m <N －1，m ∈*N )时，1N m a -≤ 则21N m a --=12N m a -+∈[0，1] 所以11N m a --≤ 所以k =m+1时结论也成立.综上，有1N K a -≤，1≤k <N －1，k ∈*N 故有11a ≤ ----------------5分（2）当N=2时，由12=a 且11≠a 得11cos a π=-=成立假设N=m (m ≥2)时，存在Z k ∈，使得12cos2m k a π-= ------------------7分则当N=m ＋1时，由归纳假设，存在k ，使得23cos 2m k a π-=，则21a =212a +=3cos 122m k π-+=22cos 2m k π- 所以12cos 2m k a π-==(1)22cos 2m k π+-或12cos 2m k a π-=-=(1)2(1)2(22)cos 2m m k π+-+-- 所以无论N 取任何大于1的正整数，都存在k 使得()12cos2N k a k Z π-=∈ --10。

江苏省2014届高三高考模拟专家卷语文(2) Word版含答案

2014江苏高考语文模拟卷之二注意事项：1．本试卷共6页。

满分160分。

考试时间为150分钟。

2．答题前，考生务必将学校、姓名、班级、学号写在答卷纸的密封线内。

答案写在答卷纸上的指定位置。

考试结束后，交回答卷纸。

1．下列词语中加点的字，每对读音都相同的一组是（3分）A. 戏谑．/ 头皮屑．揶揄．/ 向隅．而泣参．拜 / 功过参．半B. 傲．慢／拗．口令辗．转／龙车凤辇．通缉． / 开门揖．盗C. 勘．测／看．家戏讥诮．/ 峭．拔刚劲裨．益 / 奴颜婢．膝D. 媲．美／庇．护所昙．花／弹．冠相庆绝．唱 / 角．逐激烈C (A.xuâ/xiâ、yú cān ；B.ào,zhǎn/niǎn, jī/yī；C.kān, qiào、bì；D.pì/bì,tán,juã)2．下列各句中，加线的成语使用恰当的一句是（3分）（）A．我们考虑问题时，他习惯从大的方面着眼，我总是从具体方法入手，虽然南辕北辙，但总能殊途同归。

B．珠宝专卖店的柜台里各种各样的名贵宝石俯拾即是，吸引了许多的顾客。

C．在伊拉克战争期间，一些女记者直接到前线去采访，其冒险程度无异于火中取栗。

D．在签名售书活动开始前，作者诚恳地说，书中不少看法都是一孔之见，欢迎大家批评指正。

D．（A．南辕北辙：心里想往南去，却驾车往北走。

比喻行动和目的相反。

不合语境。

B.俯拾即是：只要低下头来捡取，到处都是。

形容要找的某一类例证，多而易得。

用错对象。

C.火中取栗：冒危险给别人出力，自己却上了大当，一无所得。

也指冒险行事，使自己蒙受损失。

不合语境。

（3分）3．请用简明平实的语言表述下面材料中雕匠一段话的深刻含意。

（4分）有两段树根，一段被雕匠雕成了神，一段被雕匠雕成了猴。

于是两段树根有了不同的命运：一段被人供奉膜拜，一段成了人的玩物。

被雕成猴的树根埋怨雕匠说：“我们同是树根，命运却如此截然不同，都是因为你，我们的命运都是你一手雕刻而成的啊！”“我哪有这等本事，去雕刻别人的命运！”雕匠缓缓说道：“其实，从土里出来的时候，你们一个长得像神，一个长得像猴，我只是按你们的形状略加雕刻而已。

专题12 概率和统计-2014届高三名校数学(理)试题解析分项汇编(第02期) Word版含解析[ 高考]

一．基础题组1. 【广东省广州市执信、广雅、六中2014届高三10月三校联考(理）】已知2~(3,)N ξσ，若(2)0.2P ξ≤=，则ξ≤P(4)等于( )A ．2.0B ．3.0C ．7.0D ．8.02. 【河北省邯郸市2014届高三9月摸底考试数学理科】已知随机变量ξ服从正态分布2(4,)N σ，若(8)0.4P ξ>=，则(0)P ξ<=( )A ．0.3B ．0.4C ．0.6D ．0.73. 【湖北省武汉市2014届高三10月调研测试数学（理）】某学校随机抽取20个班，调查各班中有网上购物经历的人数，所得数据的茎叶图如图所示．以组距为5将数据分组成[0，5)，[5，10)，…，[30，35)，[35，40]时，所作的频率分布直方图是 ( )4.【广东省广州市执信、广雅、六中2014届高三10月三校联考(理）】某小学对学生的身高进行抽样调查，如图，是将他们的身高（单位：厘米）数据绘制的频率分布直方图．若要从身高在［120，130），［130，140），［140，150］三组内的学生中，用分层抽样的方法选取18人，则从身高在［140，150］内的学生中选取的人数应为________.5.【江苏省阜宁中学2014届高三年级第一次调研考试】下图茎叶图是甲、乙两人在5次综合测评中成绩，其中一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率为.二．能力题组1.【中原名校联盟2013-2014学年高三上期第一次摸底考试理】在圆22＋＝--(2)(2)4x y内任取一点，则该点恰好在区域50303x x y x ⎧⎪⎨⎪⎩＋2y －≥－2＋≥≤内的概率为（）A ．18π B ．14π C ．12π D ．1π考点：二元一次不等式组表示的平面区域和几何概型等知识, 考查学生的基本运算能力．2. .【山西省山大附中2014届高三9月月考数学理】抛一枚均匀硬币，正反每面出现的概率都是12，反复这样投掷，数列{}a n 定义如下：a n n n =-⎧⎨⎪⎩⎪11，第次投掷出现正面，第次投掷出现反面，若S a a a n N n n =+++∈12 ()*，则事件“280,2S S ≠=”的概率是（）A ．1256 B.13128 C.12 D.732三．拔高题组1. 【湖北省武汉市2014届高三10月调研测试数学（理）】现有A ，B 两球队进行友谊比赛，设A 队在每局比赛中获胜的概率都是23．（Ⅰ）若比赛6局，求A 队至多获胜4局的概率；（Ⅱ）若采用“五局三胜”制，求比赛局数ξ的分布列和数学期望．（Ⅱ）由题意可知，ξ的可能取值为3，4，5．考点：排列组合，分布列，期望.2.【浙江省温州八校2014届高三10月期初联考数学(理)】一个袋子里装有7个球, 其中有红球4个, 编号分别为1，2，3，4；白球3个, 编号分别为2，3，4. 从袋子中任取4个球(假设取到任何一个球的可能性相同).(Ⅰ) 求取出的4个球中, 含有编号为3的球的概率；(Ⅱ) 在取出的4个球中, 红球编号的最大值设为X，求随机变量X的分布列和数学期望.(Ⅱ)随机变量X的所有可能取值为1，2，3，4. ……6分考点：概率，分布列，期望.3. 【浙江省嘉兴一中2014届高三上学期入学摸底数学(理)】一个口袋中有红球3个，白球4个．（Ⅰ）从中不放回地摸球，每次摸2个，摸到的2个球中至少有1个红球则中奖，求摸2次恰好第2次中奖的概率；（Ⅱ）每次同时摸2个，并放回，摸到的2个球中至少有1个红球则中奖，连续摸4次，求中奖次数X 的数学期望E(X)．(Ⅱ) 设“每次同时摸2个,恰好中奖”为事件B ，则75C C )(27141323=+=C C B P随机变量X 的所有可能取值为1，2，3，4. ……6分4314716075175)1(=⎪⎭⎫ ⎝⎛-⋅⋅==C X P ， 42224760075175)2(=⎪⎭⎫ ⎝⎛-⋅⎪⎭⎫ ⎝⎛==C X P ， 43347100075175)3(=⎪⎭⎫ ⎝⎛-⋅⎪⎭⎫ ⎝⎛==C X P ， 4444762575)4(=⎪⎭⎫ ⎝⎛==C X P ，……10分所以随机变量X 的分布列是随机变量X 的数学期望240168607625471000376002716014444=⨯+⨯+⨯+⨯=EX . ……14分考点：组合公式、概率，分布列，期望4. 【广东省广州市执信、广雅、六中2014届高三10月三校联考(理）】(本题满分12分)在某校教师趣味投篮比赛中,比赛规则是:每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖.已知教师甲投进每个球的概率都是23. (Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X 的分布列及数学期望；(Ⅱ)求教师甲在一场比赛中获奖的概率.【答案】(Ⅰ)X 的分布列数学期望4EX =；(Ⅱ)81. 【解析】试题分析：(Ⅰ)先定出X 的所有可能取值，易知本题是6个独立重复试验中成功的次数的离散概率分布，即为二项分布.由二项分布公式可得到其分布列以及期望.(Ⅱ)根据比赛获胜的规定，教师甲前四次投球中至少有两次投中，后两次必须投中，即可能的情况有1.前四次投中2次（六投四中）；考点：1.二项分布；2.离散型随机变量的分布列与期望；3.随机事件的概率.5.【2014届广东高三六校第一次联考理】甲乙丙三人商量周末去玩，甲提议去市中心逛街，乙提议去城郊觅秋，丙表示随意。

【2014南京盐城一模】江苏省南京市、盐城市2014届高三第一次模拟考试数学试题 Word版含答案

南京市、盐城市2014届高三第一次模拟考试数学一、填空题1.已知集合{3,1,1,2}A =--，集合[0,)B =+∞，则AB = .2.若复数(1)(3)z i ai =+-（i 为虚数单位）为纯虚数，则实数a = .3.现从甲、乙、丙3人中随机选派2人参加某项活动，则甲被选中的概率为 .4.根据如图所示的伪代码，最后输出的S 的值为 .110Print S For I From To S S I End For S←←+ 5.若一组样本数据2，3，7，8，a 的平均数为5，则该组数据的方差2s = . 6.在平面直角坐标系xOy 中，若中心在坐标原点上的双曲线的一条准线方程为12x =，且它的一个顶点与抛物线24y x =-的焦点重合，则该双曲线的渐进线方程为 .7.在平面直角坐标系xOy 中，若点(,1)P m 到直线4310x y --=的距离为4，且点P 在不等式23x y +≥表示的平面区域内，则m = .8.在四棱锥P ABCD -中，底面ABCD 是边长为2的菱形，60BAD ∠=，侧棱PA ⊥底面ABCD ，2PA =，E 为AB 的中点，则四面体PBCE 的体积为 .9.设函数()cos(2)f x x ϕ=+，则“()f x 为奇函数”是“2πϕ=”的条件.（选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”）10.在平面直角坐标系xOy 中，若圆22(1)4x y +-=上存在A ，B 两点关于点(1,2)P 成中心对称，则直线AB 的方程为 .11.在ABC ∆中，2BC =，23A π=，则AB AC ⋅的最小值为 . 12.若函数()f x 是定义在R 上的偶函数，且在区间[0.)+∞上是单调增函数.如果实数t 满足1(l n )(l n )2(1)f t f f t+<时，那么t 的取值范围是 .13.若关于x 的不等式2(20)lg 0aax x-≤对任意的正实数x 恒成立，则实数a 的取值范围是 .14.已知等比数列{}n a 的首项为43，公比为13-，其前n 项和为n S ，若1n n A S B S ≤-≤对*n N ∈恒成立，则B A -的最小值为 .二、解答题15.在ABC ∆中，角A ，B ，C 所对的边分别是a ，b ，c ，已知2c =，3C π=.（2）若sin sin()2sin 2C B A A +-=，求ABC ∆的面积.16.如图，在正三棱锥111ABC A B C -中，E ，F 分别为1BB ，AC 的中点.（1）求证：//BF 平面1A EC ；（2）求证：平面1A EC ⊥平面11ACC A .17.如图，现要在边长为100m 的正方形ABCD 内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为xm （x 不小于9）的扇形花坛，以正方形的中心为圆心建一个半径为215x m 的圆形草地.为了保证道路畅通，岛口宽不小于60m ，绕岛行驶的路宽均不小于10m .（1）求x 的取值范围；取1.4）（2）若中间草地的造价为a 元2/m ，四个花坛的造价为433ax 元2/m ，其余区域的造价为1211a元2/m ，当x 取何值时，可使“环岛”的整体造价最低？18.在平面直角坐标系xOy 中，已知过点3(1,)2的椭圆C ：22221(0)x y a b a b +=>>的右焦点为(1,0)F ，过焦点F 且与x 轴不重合的直线与椭圆C 交于A ，B 两点，点B 关于坐标原点的对称点为P ，直线PA ，PB 分别交椭圆C 的右准线l 于M ，N 两点. （1）求椭圆C 的标准方程；（2）若点B 的坐标为8(,55，试求直线PA 的方程；（3）记M ，N 两点的纵坐标分别为M y ，N y ，试问M N y y ⋅是否为定值？若是，请求出该定值；若不是，请说明理由.19.已知函数()x f x e =，2()1(,)g x ax bx a b R =++∈.（1）若0a ≠，则a ，b 满足什么条件时，曲线()y f x =与()y g x =在0x =处总有相同的切线？（2）当1a =时，求函数()()()g x h x f x =的单调减区间；（3）当0a =时，若()()f x g x ≥对任意的x R ∈恒成立，求b 的取值的集合.20.设等差数列{}n a 的前n 项和为n S ，已知12a =，622S =. （1）求n S ；（2）若从{}n a 中抽取一个公比为q 的等比数列{}n k a ，其中11k =，且12n k k k <<<，*n k N ∈.①当q 取最小值时，求{}n k 的通项公式；②若关于*()n n N ∈的不等式16n n S k +>有解，试求q 的值.数学附加题21.（选做题）（在A 、B 、C 、D 四小题中只能选做2题）A ．如图，AB ，CD 是半径为1的圆O 的两条弦，它们相交于AB 的中点P ，若98PC =，12OP =，求PD的长.B ．已知曲线C ：1xy =，若矩阵22M -⎢⎥=⎥⎥⎦对应的变换将曲线C 变为曲线C '，求曲线C '的方程.C ．在极坐标系中，圆C 的方程为2cos a ρθ=，以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，直线l 的参数方程为3242x t y t =+⎧⎨=+⎩（t 为参数），若直线l 与圆C 相切，求实数a 的值.D ．已知1x ，2x ，3x 为正实数，若1231x x x ++=，求证：2223211231x x x x x x ++≥.（必做题）22.已知点(1,2)A 在抛物线Γ：22y px =上.（1）若ABC ∆的三个顶点都在抛物线Γ上，记三边AB ，BC ，CA 所在直线的斜率分别为1k ，2k ，3k ，求123111k k k -+的值；（2）若四边形ABCD 的四个顶点都在抛物线Γ上，记四边AB ，BC ，CD ，DA 所在直线的斜率分别为1k ，2k ，3k ，4k ，求12341111k k k k -+-的值.23.设m 是给定的正整数，有序数组（1232,,,m a a a a ）中2i a =或2-(12)i m ≤≤.（1）求满足“对任意的1k m ≤≤，*k N ∈，都有2121k ka a -=-”的有序数组（1232,,,m a a a a ）的个数A ；（2）若对任意的1k l m ≤≤≤，k ，*l N ∈，都有221||4li i k a =-≤∑成立，求满足“存在1k m ≤≤，使得2121k ka a -≠-”的有序数组（1232,,,m a a a a ）的个数B南京市、盐城市2014届高三年级第一次模拟考试数学参考答案一、填空题：本大题共14小题，每小题5分，计70分.1. {1,2}2. －33.23 4. 55 5. 2656. y =、必要不充分 10. 30x y +-= 11. 23-12. 1[,]e e13.14.5972二、解答题：15．解：（1）由余弦定理及已知条件得，224a b ab +-=， …………2分又因为ABC △，所以1sin 2ab C =4ab =． …………4分联立方程组2244a b ab ab ⎧+-=⎨=⎩，，解得2a =，2b =． …………7分（2）由题意得sin()sin()4sin cos B A B A A A ++-=，即sin cos 2sin cos B A A A =，当cos 0A =时，2A π=，6B π=，a =b = …………10分当cos 0A ≠时，得sin 2sin B A =，由正弦定理得2b a =，联立方程组2242a b ab b a ⎧+-=⎨=⎩，，解得a =b =． …………13分所以ABC △的面积1sin 2S ab C ==． …………14分 16．证：（1）连1AC 交1A C 于点O ，F 为AC 中点， ∴111//=2OF CC OF CC 且，E 为1BB 中点，∴111//=2BE CC BE CC 且，∴//=BE OF BE OF 且，∴四边形BEOF 是平行四边形， ………4分 ∴//BF OE ，又BF ⊄平面1A EC ，OE ⊂平面1A EC ，∴//BF 平面1A EC .……7分（2）由（1）知//BF OE ，AB CB =，F 为AC 中点，所以BF AC ⊥，所以OE AC ⊥，………9分又因为1AA ⊥底面ABC ，而BF ⊂底面ABC ，所以1AA BC ⊥，则由//BF OE ，得1OE AA ⊥，而1,AA AC ⊂平面11ACC A ，且1AA AC A =，所以OE ⊥面11ACC A ， …………12分又OE ⊂平面1A EC ，所以平面1A EC ⊥平面11ACC A . …………14分17．解：（1）由题意得，29,100260,122210,5x x x x ≥⎧⎪-≥⎪⎨⎪-⨯≥⨯⎪⎩…………4分解得9,20,2015,x x x ≥⎧⎪≤⎨⎪-≤≤⎩即915x ≤≤. …………7分（2）记“环岛”的整体造价为y 元，则由题意得222422214121()(10())533115a y a x ax x x x ππππ=⨯⨯+⨯+⨯-⨯-432414[(12)1210]11253a x x x π=-+-+⨯， …………10分令43214()12253f x x x x =-+-，则32241()4244(6)2525f x x x x x x x '=-+-=--+，由()0f x '=，解得10x =或15x =， …………12分答：当10x =m 时，可使“环岛”的整体造价最低. …………14分18．解：（1）由题意，得24a ==，即2a =， …2分又1c =，∴23b =，∴椭圆C 的标准方程为22143x y +=. ………5分（2）8(,)55B ，∴8(,55P--，又(1,0)F， ∴AB k = ∴直线AB ：1)y x =-， …………7分联立方程组221431)x y y x ⎧+=⎪⎨⎪=-⎩，解得(0,A ， …………9分 ∴直线PA ：4y x =-40y ++=. …………10分（3）当AB k 不存在时，易得9m n y y =-, 当AB k 存在时，设11(,)A x y ，22(,)B x y ，则22(,)P x y --，∴2211143x y +=，2222143x y +=，两式相减，得21212121()()()()43x x x x y y y y +-+-=-， ∴21212121()()3()()4PA AB y y y y k k x x x x +-=-=⋅+-，令221AB y k k x ==-，则34PA k k=-，…12分∴ 直线PA 方程：223()4y y x x k +=-+，∴223(4)4M y x y k=-+-，∴22223(4)(1)4M x x y y y +-=--， ∴ 直线PB 方程：22y y x x =⋅，∴224N yy x =， 14分 ∴222222(4)(1)43M N x x y y y x x +-=-⨯-，又2222143x y +=，∴22224123y x =-， ∴2222(4)(1)4339M N x x x y y +-+-=-⨯=-，所以M N y y 为定值9-. ……16分19．解：（1）()x f x e '=，∴(0)1f '=，又(0)1f =，∴()y f x =在0x =处的切线方程为1y x =+， ……………2分又()2g x ax b '=+，∴(0)g b '=，又(0)1g =，∴()y g x =在0x =处的切线方程为1y bx =+，所以当0,a a R ≠∈且1b =时，曲线()y f x =与()y g x =在0x =处总有相同的切线 ………4分（2）由1a =，21()x x bx h x e ++=，∴2(2)1()x x b x b h x e -+-+-'=，∴2(2)1(1)((1))()x xx b x b x x b h x e e-+-+----'==-， ………7分由()0h x '=，得11x =，21x b =-，∴当0b >时，函数()y h x =的减区间为(,1)b -∞-，(1,)+∞；当0b =时，函数()y h x =的减区间为(,)-∞+∞；当0b <时，函数()y h x =的减区间为(,1)-∞，(1,)b -+∞. ………10分（3）由1a =，则()()()1xx f x g x e bx ϕ=-=--，∴()xx e b ϕ'=-，①当0b ≤时，()0x ϕ'≥，函数()x ϕ在R 单调递增，又(0)0ϕ=，∴ (,0)x ∈-∞时， ()0x ϕ<，与函数()()f x g x ≥矛盾，………12分 ②当0b >时，∴()0x ϕ'>，ln x b >；∴()0x ϕ'<，ln x b <∴函数()x ϕ在(,ln )b -∞单调递减；(ln ,)b +∞单调递增，（Ⅰ）当01b <<时，∴ln 0b <，又(0)0ϕ=，∴(ln )0b ϕ<，与函数()()f x g x ≥矛盾，（Ⅱ）当1b >时，同理(ln )0b ϕ<，与函数()()f x g x ≥矛盾，（Ⅲ）当1b =时， ln 0b =，∴函数()x ϕ在(,0)-∞单调递减；(0,)+∞单调递增，∴()(0)0x ϕϕ≥=，故1b =满足题意.综上所述，b 的取值的集合为{}1. ……………16分20．解：（1）设等差数列的公差为d ，则611665222S a d =+⋅⋅=，解得23d =，……2分所以(5)3n n n S +=. ………4分若22=k ，则由382=a ，得3412==a a q ，此时932)34(223=⋅=k a ，由)2(32932+=n ，解得*310N n ∉=，所以22>k ，同理32>k ； ……6分若42=k ，则由44=a ，得2=q ，此时122-⋅=n k n a ，另一方面，2(2)3n k n a k =+，所以2(2)23n n k +=，即1322n n k -=⨯-， ………8分所以对任何正整数n ，n k a 是数列}{n a 的第2231-⋅-n 项．所以最小的公比2=q ．所以2231-⋅=-n n k ． ………10分（3）因为12423n n n k k a q -+==，得132n n k q -=-，而1q >，所以当1q >且q N ∈时，所有的132n n k q -=-均为正整数，适合题意；当2q >且q N ∉时，132n n k q N -=-∈不全是正整数，不合题意.而16n n S k +>有解，所以2(5)213nn n q ++>有解，经检验，当2q =，3q =，4q =时，1n =都是2(5)213nn n q++>的解，适合题意； ………12分下证当5q ≥时，2(5)213n n n q ++>无解, 设2(5)23nnn n b q ++=，则212[(1)(75)7]3n n nq n q n q b b q +-+-+--=，因为57022q q-<-，所以2()2[(1)(75)7]f n q n q n q =-+-+-在*n N ∈上递减，又因为(1)0f <，所以()0f n <恒成立，所以10n n b b +-<，所以1n b b ≤恒成立，又因为当5q ≥时，11b <，所以当5q ≥时，16n n S k +>无解. ………15分综上所述，q 的取值为2,3,4. ……………16分附加题答案21. A 、解：P 为AB 中点，∴OP AB ⊥，∴PB ==………5分又234PC PD PA PB PB ⋅=⋅==，由98PC =，得23PD =. ………10分B 、解：设曲线C 一点(,)x y ''对应于曲线C '上一点(,)x y ，∴22x x '⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎥⎢⎥⎥=⎢⎥⎢⎥⎥，∴22x y x ''-=，22x y y ''+=，……5分∴x '=y '=，∴1x y ''==，∴曲线C '的方程为222y x -=. …10分 C 、解：易求直线l ：4320x y --=，圆C ：222()x a y a -+=，a =，解得229a =-或. ……10分D 、证：2223211231231232()2x x x x x x x x x x x x +++++≥=++=， ∴ 2223211231x x x x x x ++≥. …10分22．解：（1）由点(1,2)A 在抛物线F ，得2p =，∴抛物线F ：24y x =， …3分设211(,)4y B y ，222(,)4y C y ， ∴222212121212123121211221114444122444y y y y y y y y k k k y y y y ---+++-+=-+=-+=---. ……7分 (2)另设233(,)4y D y ，则323121123422111104444y y y y y y k k k k ++++-+-=-+-=.…10分 23．解：（1）因为对任意的1k m ≤≤，都有2121k ka a -=-，则212(,)(2,2)k k a a -=-或212(,)(2,2)k k a a -=-，共有2种，所以1232(,,,,)m a a a a ⋅⋅⋅共有2m 种不同的选择，所以2m A =. ……5分（2）当存在一个k 时，那么这一组有12m c 种，其余的由（1）知有12m -，所有共有1122m m c -；当存在二个k 时，因为条件对任意的1k l m ≤≤≤,都有221||4li i k a =-≤∑成立得这两组共有22m c ，其余的由（1）知有22m -，所有共有2222m m c -；依次类推得：1122222222(32)m m mm m m m m B c c c --=++⋅⋅⋅+=-. ………10分。

江苏省扬州中学2014届高三上学期期中考试模拟数学试题_Word版含答案

江苏省扬州中学2013—2014期中考试模拟试题数学 2013.11一、填空题（本大题共14小题，每小题5分，共70分，）1．已知全集{}4,3,2,1=U ，集合{}{}1,2,2,3P Q ==，则()U P Q = ð . 2．复数ii215+的实部是 3．“6πα=”是“1sin 2α=”的条件． (填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”) 4．若以连续掷两次骰子分别得到的点数n m ,作为点P 的横、纵坐标，则点P 在直线5=+y x 上的概率为 . 5．如图是某学校学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率之比为1:2:3，第2小组的频数为10，则抽取的学生人数是 .6．若样本321,,a a a 的方差是2，则样本32,32,32321+++a a a 的方差是 7．执行右边的程序框图,若15p =，则输出的n = . 8．已知函数2log (0)(),3(0)xx x f x x >⎧=⎨≤⎩则1[()]4f f 的值是 . 9．等差数列{}n a 中，若124a a +=, 91036a a +=，则10S = .10．已知实数x 、y 满足20350x y x y x y -≤⎧⎪-+≥⎪⎨>⎪⎪>⎩，则y x z )21()41(⋅=的最小值为 .11．设向量(c os ,s i n a αα= ，(cos ,sin )b ββ=，其中πβα<<<0，若|2||2a b a b +=-，则βα-= . 12．若函数()f x =(],2-∞上有意义，则实数k 的取值范围是_ ___．13．若函数22()243f x x a x a =++-的零点有且只有一个，则实数a =.14．对于在区间[a ，b ]上有意义的两个函数)()(x n x m 与，如果对于区间[a ，b ]中的任意x均有1|)()(|≤-x n x m ，则称)()(x n x m 与在[a ，b ]上是“密切函数”， [a ，b ]称为“密切区间”，若函数43)(2+-=x x x m 与32)(-=x x n 在区间[a ，b ]上是“密切函数”，则b a -的最大值为 .二、解答题：（本大题共6道题，计90分．解答应写出必要的文字说明、证明过程或演算步骤）15．（本题满分14分）已知函数2()2sin cos 1f x x x x =-++ ⑴求()f x 的最小正周期及对称中心； ⑵若[,]63x ππ∈-，求()f x 的最大值和最小值.16．（本题满分14分）如图，在△OAB 中，已知P 为线段AB 上的一点，.OP x OA y OB =⋅+⋅（1）若BP PA =，求x ，y 的值；（2）若3BP PA = ，||4OA = ，||2OB =，且OA 与OB 的夹角为60°时，求OP AB ⋅的值。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（第 3 题图） 0.012 0.008 0.004 0.002 O 20 40 60 80 100 分数/分 0.024 频率组距
． ▲
．
Y
(第 4 题图）
4．上图是一次考试结果的频率分布直方图，若规定 60 分以上(含 60)为考试合格，则这次考试的合格率为 ▲ ． 5．在一个袋子中装有分别标注数字 1，2，3，4 的四个小球，这些小球除标注的数字外完全相同．现从中随机取出 2 个小球，则取出的小球标注的数字之和为 5 的概率是 ▲ ． →→ 6、在边长为 3 的正方形 ABCD 中，E 为 DC 的中点，AE 与 BD 相交于点 F，则 FD · DE 的值为 ▲ ． ▲ ． ▲ ．
二、解答题：本大题共 6 小题，共计 90 分．解答应写出文字说明、证明过程或演算步骤．请把答案写在答卷纸相应位置上．．．． 15．（本题满分 14 分）已知 a，b，c 分别为△ABC 的内角 A，B，C 的对边，且 acosC＋ccosA＝2bcosB．（1）求角 B 的大小；（2）求 sinA＋sinC 的取值范围．
16．（本题满分 14 分）如图，在矩形 ABCD 中，AD＝2，AB＝4，E，F 分别为边 AB，AD 的中点．现将△ADE 沿 DE 折起，得四棱锥 A－BCDE．（1）求证：EF∥平面 ABC；（2）若平面 ADE⊥平面 BCDE，求四面体 FDCE 的体积．
D
A
A A F D C （第 16 题图） E B F E B
2014 年江苏高考数学模拟试题（二）
一、填空题：本大题共 14 小题，每小题 5 分，共 70 分．请把答案填写在答题卡相应位置上．．．．．．．． 1．已知集合 M＝{x｜y＝lgx}，N＝{ x｜y＝ 1－x}，则 M∩N＝ ▲ 2．已知复数 z 满足(z－2)i＝1＋i（i 是虚数单位），则复数 z 的实部为 3．根据如图所示的算法流程图，输出的结果 T 为 ▲ ．开始 I←2 T←1 I←I＋2 T←T× I T≤30 N 输出 I 结束
D
C
17.（本小题满分 14 分）如图，现有一个以∠AOB 为圆心角、湖岸 OA 与 OB 为半径的扇形湖面 AOB．现欲在弧 AB 上取不同于 A、B 的点 C，用渔网沿着弧 AC(弧 AC 在扇形 AOB 的弧 AB 上)、半径 OC 和线段 CD( 其中 CD∥OA)，在该扇形湖面内隔出两个养殖区域 —— 养殖区域Ⅰ和养殖区域 π Ⅱ．若 OA＝1km， ∠AOB＝．求所需渔网长度(即图中弧 AC、半径 OC 和线段 CD 长度之和) 3 的取值范围． B B
＋c2＋„＋cn，求Sn．数学附加题21．【选做题】在 A、B、C、D 四小题中只能选做 2 题，每小题 10 分，共 20 分．请在答题．．卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．．．．．．． A．选修 4—1：几何证明选讲如图， AB 是⊙O 的直径，点 P 在 AB 的延长线上， PC 与⊙O 相切于点 C， PC＝AC＝1．求 ⊙O 的半径．
若以 MN 为直径的圆恰好过点 F1，求 m 的值．
19．（本题满分 16 分）已知函数 f(x)＝x3＋x2－ax(a∈R)．（1）当 a＝0 时，求与直线 x－y－10＝0 平行，且与曲线 y＝f (x)相切的直线的方程； f(x) （2）求函数 g(x)＝－alnx (x＞1)的单调递增区间； x （3）如果存在 a∈[3，9]，使函数 h(x)＝f(x)＋f(x)(x∈[－3，b])在 x＝－3 处取得最大值，试求 b 的最大值．
D
养殖区域Ⅱ
C
O
A O
养殖区域Ⅰ
A
18．（本题满分 16 分）已知椭圆 C： x2 y2 ＋＝1（a＞b＞0）的左焦点为 F1（－3，0），过点 F1 作一条直线 l 交 a2 b2
16 椭圆于 A， B 两点，点 A 关于坐标原点 O 的对称点为 A1，两直线 AB， A1B 的斜率之积为－． 25 （1）求椭圆 C 的方程；高考资源网（2）已知 D（m，0）为 F1 右侧的一点，连 AD，BD 分别交椭圆左准线于 M，N 两点，
7．若直线 y＝kx－3 与曲线 y＝2lnx 相切，则实数 k＝
－
3x 1，x≤0， 8．定义在 R 上的函数 f(x)满足 f(x)＝则 f(2013)＝ f(x－1)－f(x－2)，x＞0，
9．定义在 R 上的奇函数 f(x)，当 x∈(－∞，0)时，f(x)＝x2＋2x－1，则不等式 f(x)＜－1 的解
13．在平面区域 ( x, y ) | x | 1,| y | 1 上恒有 ax 2by 2 ，则动点 P(a, b) 所形成平面区域的面积为 ▲ ． 14．如图，已知正方形 ABCD 的边长为 1，过正方形中心 O 的直线 MN 分别交正方形的边 MN AB，CD 于点 M，N，则当取最小值时，CN＝ ▲ BN ．
集是
▲
． ▲ ． ▲ （填
10. 已知锐角 A, B 满足 tan( A B) 2 tan A ，则 tan B 的最大值是
11．已知 f ( x) x2 2 x 3 ，则“|k|≤2”是“f(x)≥g(x)在 R 上恒成立”的 g ( x) kx 1 ，
“充分但不必要条件” 、 “必要但不充分条件” 、 “充要条件” 、 “既不充分也不必要条件” 中的一个．） 12．已知数列{an}满足 3an＋1+an＝4(n∈N*)，且 a1＝9，其前 n 项之和为 Sn，则满足不等式|Sn 1 －n－6|< 的最小整数 n 是 125 ▲ ．
20．（本题满分 16 分）已知数列 an 满足
an 1 an 1 n （n∈N*），且a2=6． an 1 an 1
（1）求数列{an}的通项公式；（2）设 bn bn an （n∈N*，c为非零常数），若数列{bn}是等差数列，记cn＝ n，Sn＝c1 2 nc