2013届高考数学一轮复习精讲精练(新人教A版)第12章 导数及其应用
高考数学第一轮复习 第二篇 第12讲 导数的综合应用课件 理 新人教A版
(1)第(2)问证明抓住两点: 一是转化为证明当m=2时,f(x)>0; 二是依据f′(x0)=0,准确求f(x)=ex-ln(x+2)的 最小值. (2)对于该类问题,可从不等式的结构特点出发, 构造函数,借助导数(dǎo shù)确定函数的性质, 借助单调性或最值实现转化.
第十二页,共20页。
②当 a<0 时,若 0<x< -21a,则 f′(x)>0,
故 f(x)在0, -21a上是增函数; 若 x> -21a,则 f′(x)<0,故 f(x)在 -21a,+∞上是减函数.
综上,当 a≥0 时,f(x)在(0,+∞)上是增函数;
第十三页,共20页。
导数(dǎo shù)在不等式 中的应用
第三页,共20页。
两个转化
两点注意
一是利用导数研究含参函 数的单调性,常化为不等 式恒成立问题.注意分类 讨论与数形结合思想的应 用;
二是函数的零点、不等式 证明常转化为函数的单调 性、极(最)值问题处理, 如(2).
一是注意实际问题中函数定义域, 由实际问题的意义和解析式共同 确定,如(3).
二是在实际问题中,如果函数在 区间内只有一个极值点,那么可 直接根据实际意义判定是最大值 还是最小值,如(4).若在开区间 内有极值,则一定有最优解.
解 由 f(x)=x2+xsinx+cosx,
得 f′(x)=2x+sinx+x(sinx)′-sinx=x(2+cosx).
审题路线
(1)因为曲线 y=f(x)在点(a,f(a))处与直线 y=b 相切,
所以 f′(a)=a(2+cosa)=0,b=f(a).
解得 a=0,b=f(0)=1.
(2)设 g(x)=f(x)-b=x2+xsinx+cosx-b.
高考数学总复习 专题一 导数应用问题专题精讲课件 理 新人教A版共64页

25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
பைடு நூலகம்
高考数学总复习 专题一 导数应用问 题专题精讲课件 理 新人教A版
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
(江西专用)高考数学一轮复习 2.12 导数的综合应用课件 文 新人教A版

1 x
变式训练2 已知函数f(x)=ax +cx+d(a≠0)是R上的奇函数, 当x=1时,f(x)取得极值-2. (1)求f(x)的单调区间; (2)证明:对任意x1、x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立. 【解析】(1)∵f(x)为R上的奇函数, ∴f(-x)=-f(x)⇒d=0. ∴f(x)=ax +cx,f'(x)=3ax +c.
a 1, 3 6a 9a 0, 即 则有 4 12 12 a 9 a 0, a , 7
2
∴a≥1,
∴a的取值范围是[1,+∞). 【点评】在处理函数在某个区间上恒为增函数或减函数的 问题时,注意检验端点值是否合适.
变式训练1 已知定义在R上的函数f(x)=x (ax-3),其中a为常数. (1)若x=1是f(x)的一个极值点,求a的值及f(x)的单调区间; (2)若函数f(x)在区间(-1,0)上是增函数,求a的取值范围. 【解析】(1)f(x)=ax -3x ,f'(x)=3ax -6x=3x(ax-2),∵x=1是f(x)的 一个极值点,∴f'(1)=3(a-2)=0,得a=2,经检验a=2为所求. 由a=2,得f'(x)=6x(x-1),又f(x)的定义域为R,
间(-1,0)内恒成立,
∴a≥-2,故实数a的取值范围为[-2,+∞).
题型2 利用导数证明不等式问题
ax b 例2 已知函数f(x)= 在点(-1,f(-1))的切线方程为x+y+3=0. x2 1
(1)求函数f(x)的解析式; (2)设g(x)=ln x,求证:g(x)≥f(x)在x∈[1,+∞)上恒成立. 【分析】要证明 g(x)≥f(x),通过等价转化后构造新的函数, 在x∈[1,+∞)上恒大于或等于0.
高三数学一轮复习 第十二章导数导数的综合应用课件 文

数的最值恒大于0或者小于0的问题.
3.利用导数研究方程的根的个数,其具体步骤为:①将方程移项、整 理,转化为方程F(x)=0;②利用导数研究函数y=F(x)图象的变化情况; ③利用数形结合思想研究F(x)与x轴交点的个数,从而得到方程根的 个数.
1.已知函数f(x)的导函数f‘(x)的图象如图所示, 那么函数f(x)的图象最有可能的是 ( )
常规函数(由基本初等函数构成)等,这些函数尤其适合利用导数解 决.在复习过程中,要注意等价转化、分类讨论、数形结合等数学思 想方法的训练.在解决导数的综合应用题中,这些思想始终贯穿于其 中,是解决问题的关键,在研究函数的有关性质时,一定要注意优先考 虑定义域.
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月4日星期五2022/3/42022/3/42022/3/4 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/42022/3/42022/3/43/4/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/42022/3/4March 4, 2022 •4、享受阅读快乐,提高生活质量。2022/3/42022/3/42022/3/42022/3/4
(A)1.
(B) 1 . (C) 5 .
(D) 2 .
2
2
2
【解析】由题可知|MN|=x2-ln x(x>0),不妨令h(x)=x2-ln x,则h'(x)=2x- 1 ,
令h'(x)=0解得x= ,因x∈(0, )时,h'(x)<0,当x∈( ,+∞)时,h'(x)>0x,
高考数学一轮复习 2.12导数的应用(一)讲解与练习 理 新人教A版

第十二节导数的应用Ⅰ[备考方向要明了]考什么怎么考1.了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数一般不超过三次).2.了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(其中多项式函数一般不超过三次). 利用导数研究函数的单调区间、极值或最值,其考查题型有:(1)利用导数求单调区间,如2012年北京T18等.(2)利用单调性求参数范围,如2011年江苏T19等,(3)利用导数求函数的极值,或最值,如2012年陕西T7,安徽T19等.(4)已知函数的极值或最值求参数,如2012年江苏T18等.[归纳·知识整合]1.函数的单调性与导数[探究] 1.若函数f(x)在(a,b)内单调递增,那么一定有f′(x)>0吗?f′(x)>0是否是f(x)在(a,b)内单调递增的充要条件?提示:函数f(x)在(a,b)内单调递增,则f′(x)≥0,f′(x)>0是f(x)在(a,b)内单调递增的充分不必要条件.2.函数的极值与导数(1)函数的极小值:若函数y=f(x)在点x=a处的函数值f(a)比它在点x=a附近其他点的函数值都小,且f′(a)=0,而且在点x=a附近的左侧f′(x)<0,右侧f′(x)>0,则a点叫做函数的极小值点,f(a)叫做函数的极小值.(2)函数的极大值:若函数y=f(x)在点x=b处的函数值f(b)比它在点x=b附近其他点的函数值都大,且f′(b)=0,而且在点x=b附近的左侧f′(x)>0,右侧f′(x)<0,则b点叫做函数的极大值点,f(b)叫做函数的极大值,极大值和极小值统称为极值.[探究] 2.导数值为0的点一定是函数的极值点吗?“导数为0”是函数在该点取得极值的什么条件?提示:不一定.可导函数的极值点导数为零,但导数为零的点未必是极值点;如函数f(x)=x3,在x=0处,有f′(0)=0,但x=0不是函数f(x)=x3的极值点;其为函数在该点取得极值的必要而不充分条件.3.函数的最值与导数(1)函数f(x)在[a,b]上有最值的条件:一般地,如果在区间[a,b]上,函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.(2)求函数y=f(x)在[a,b]上的最大值与最小值的步骤为①求函数y =f (x )在(a ,b )内的极值;②将函数y =f (x )的各极值与端点处的函数值f (a ),f (b )比较,其中最大的一个是最大值,最小的一个是最小值.[探究] 3.函数的极值和函数的最值有什么联系和区别?提示:极值是局部概念,指某一点附近函数值的比较,因此,函数在极大(小)值,可以比极小(大)值小(大);最值是整体概念,最大、最小值是指闭区间[a ,b ]上所有函数值的比较.因而在一般情况下,两者是有区别的,极大(小)值不一定是最大(小)值,最大(小)值也不一定是极大(小)值,但如果连续函数在区间(a ,b )内只有一个极值,那么极大值就是最大值,极小值就是最小值.[自测·牛刀小试]1.(教材习题改编)函数f (x )=e x-x 的单调递增区间是( ) A .(-∞,1] B .[1,+∞) C .(-∞,0]D .(0,+∞)解析:选D ∵f (x )=e x-x ,∴f ′(x )=e x-1, 由f ′(x )>0,得e x-1>0,即x >0.2.(教材习题改编)函数f (x )=13x 3-4x +4有( )A .极大值283,极小值43B .极大值-43,极小值283C .极大值43,极小值-283D .极大值283,极小值-43解析:选D ∵f (x )=13x 3-4x +4,∴f ′(x )=x 2-4,令f ′(x )=0,则x =±2. 当x ∈(-∞,-2)时,f ′(x )>0; 当x ∈(-2,2)时,f ′(x )<0; 当x ∈(2,+∞)时,f ′(x ) >0.∴f (x )极大值=f (-2)=283,f (x )极小值=f (2)=-43.3.已知函数f (x )的导函数f ′(x )=ax 2+bx +c 的图象如图所示,则f (x )的图象可能是( )解析:选D 当x<0时,由导函数f′(x)=ax2+bx+c<0,知相应的函数f(x)在该区间上单调递减;当x>0时,由导函数f′(x)=ax2+bx+c的图象可知,导数在区间(0,x1)内的值是大于0的,则在此区间内函数f(x)单调递增.4.(教材习题改编)函数f(x)=x3-3x2+2在区间[-1,1]上的最大值是________.解析:由题意,得f′(x)=3x2-6x,令f′(x)=0,得x=0或x=2(舍去).由于f(-1)=-2,f(1)=0,f(0)=2,故f(x)在[-1,1]上的最大值为2.答案:25.若函数f(x)=x3+x2+mx+1是R上的单调增函数,则m的取值范围是________.解析:∵f(x)=x3+x2+mx+1,∴f′(x)=3x2+2x+m.又∵f(x)在R上是单调函数,∴Δ=4-12 m ≤0,即m ≥13答案:⎣⎢⎡⎭⎪⎫13,+∞运用导数解决函数的单调性问题[例1] (2013·郑州模拟)已知函数f (x )=ax +x ln x ,且图象在点⎝ ⎛⎭⎪⎫1e ,f ⎝ ⎛⎭⎪⎫1e 处的切线斜率为1(e 为自然对数的底数).(1)求实数a 的值; (2)设g (x )=f x -xx -1,求g (x )的单调区间;(3)当m >n >1(m ,n ∈Z )时,证明:m n n m>n m . [自主解答] (1)f (x )=ax +x ln x ,f ′(x )=a +1+ln x ,依题意f ′⎝ ⎛⎭⎪⎫1e =a =1,所以a =1.(2)因为g (x )=f x -x x -1=x ln xx -1,所以g ′(x )=x -1-ln xx -12.设φ(x )=x -1-ln x ,则φ′(x )=1-1x. 当x >1时,φ′(x )=1-1x>0,φ(x )是增函数,对∀x >1,φ(x )>φ(1)=0,即当x >1时,g ′(x )>0, 故g (x )在(1,+∞)上为增函数;当0<x <1时,φ′(x )=1-1x<0,φ(x )是减函数,对∀x ∈(0,1),φ(x )>φ(1)=0,即当0<x <1时,g ′(x )>0,故g (x )在(0,1)上为增函数.所以g (x )的单调递增区间为(0,1),(1,+∞).(3)要证mn n m>n m ,即证ln n m -ln m n >ln n -ln m , 即n -1n ln m >m -1m ln n ,m ln m m -1>n ln nn -1.(*) 因为m >n >1,由(2)知,g (m )>g (n ),故(*)式成立,所以m n n m>nm . ———————————————————1.导数法求函数单调区间的一般步骤(1)确定函数f (x )的定义域; (2)求导数f ′(x );(3)在函数f (x )的定义域内解不等式f ′(x )>0和f ′(x )<0; (4)根据(3)的结果确定函数f (x )的单调区间. 2.导数法证明函数f (x )在(a ,b )内的单调性的步骤 (1)求f ′(x );(2)确认f ′(x )在(a ,b )内的符号;(3)作出结论:f ′(x )>0时为增函数;f ′(x )<0时为减函数. 3.导数法求参数的取值范围已知函数的单调性,求参数的取值范围,应用条件f ′(x )≥0(或f ′(x )≤0),x ∈(a ,b ),转化为不等式恒成立求解.1.已知函数f (x )=3x a-2x 2+ln x ,其中a 为常数.(1)若a =1,求函数f (x )的单调区间;(2)若函数f (x )在区间[1,2]上为单调函数,求a 的取值范围. 解:(1)若a =1时,f (x )=3x -2x 2+ln x , 定义域为(0,+∞),f ′(x )=1x -4x +3=-4x 2+3x +1x =-4x +1x -1x(x >0).当f ′(x )>0,x ∈(0,1)时,函数f (x )=3x -2x 2+ln x 单调递增. 当f ′(x )<0,x ∈(1,+∞)时,函数f (x )=3x -2x 2+ln x 单调递减. 故函数f (x )的单调递增区间为(0,1), 单调递减区间为(1,+∞).(2)f ′(x )=3a -4x +1x,若函数f (x )在区间[1,2]上为单调函数,即在[1,2]上,f ′(x )=3a -4x +1x≥0或f ′(x )=3a -4x +1x≤0,即3a -4x +1x ≥0或3a -4x +1x≤0在[1,2]上恒成立.即3a≥4x -1x 或3a ≤4x -1x.令h (x )=4x -1x,因为函数h (x )在[1,2]上单调递增,所以3a ≥h (2)或3a≤h (1),即3a ≥152或3a≤3, 解得a <0或0<a ≤25或a ≥1.利用导数解决函数的极值问题[例2] (2012·重庆高考)设f (x )=a ln x +12x +32x +1,其中a ∈R ,曲线y =f (x )在点(1,f (1))处的切线垂直于y 轴.(1)求a 的值;(2)求函数f (x )的极值.[自主解答] (1)因f (x )=a ln x +12x +32x +1,故f ′(x )=a x -12x 2+32.由于曲线y =f (x )在点(1,f (1))处的切线垂直于y 轴,故该切线斜率为0,即f ′(1)=0,从而a -12+32=0,解得a =-1.(2)由(1)知f (x )=-ln x +12x +32x +1(x >0),f ′(x )=-1x -12x 2+32=3x 2-2x -12x 2=3x +1x -12x2.令f ′(x )=0,解得x 1=1,x 2=-13(因x 2=-13不在定义域内,舍去).当x ∈(0,1)时,f ′(x )<0,故f (x )在(0,1)上为减函数; 当x ∈(1,+∞)时,f ′(x )>0,故f (x )在(1,+∞)上为增函数. 故f (x )在x =1处取得极小值f (1)=3.———————————————————求可导函数f (x )的极值的步骤(1)求导数f ′(x ); (2)求方程f ′(x )=0的根;(3)检验f ′(x )在方程f ′(x )=0的根的附近两侧的符号:具体如下表:x x <x 0 x 0 x >x 0 f ′(x ) f ′(x )>0f ′(x )=0f ′(x )<0f (x ) 增极大值f (x 0)减x x <x 0 x 0 x >x 0 f ′(x ) f ′(x )<0f ′(x )=0f ′(x )>0f (x )减极小值f (x 0)增2.已知函数f (x )=e-kx·⎝ ⎛⎭⎪⎫x 2+x -1k (k <0).(1)求f (x )的单调区间;(2)是否存在实数k ,使得函数f (x )的极大值等于3e -2?若存在,求出k 的值;若不存在,请说明理由.解:(1)f (x )的定义域为R .f ′(x )=-k e -kx ⎝⎛⎭⎪⎫x 2+x -1k +e -kx (2x +1)=e-kx[-kx 2+(2-k )x +2],即f ′(x )=-e -kx(kx -2)(x +1)(k <0).令f ′(x )=0,解得x =-1或x =2k.当k =-2时,f ′(x )=2e 2x(x +1)2≥0, 故f (x )的单调递增区间是(-∞,+∞). 当-2<k <0时,f (x ),f ′(x )随x 的变化情况如下: x ⎝ ⎛⎭⎪⎫-∞,2k2k⎝ ⎛⎭⎪⎫2k ,-1 -1 (-1,+∞)f ′(x ) +0 -0 + f (x )极大值极小值所以函数f (x )的单调递增区间是⎝ ⎛⎭⎪⎫-∞,2k 和(-1,+∞),单调递减区间是⎝ ⎛⎭⎪⎫2k ,-1.当k <-2时,f (x ),f ′(x )随x 的变化情况如下: x (-∞,-1)-1 ⎝ ⎛⎭⎪⎫-1,2k2k⎝ ⎛⎭⎪⎫2k ,+∞f ′(x ) +0 -0 + f (x )极大值极小值所以函数f (x )的单调递增区间是(-∞,-1)和⎝ ⎛⎭⎪⎫2k ,+∞,单调递减区间是⎝ ⎛⎭⎪⎫-1,2k .(2)当k =-1时,f (x )的极大值等于3e -2. 理由如下:当k =-2时,f (x )无极大值.当-2<k <0时,f (x )的极大值为f ⎝ ⎛⎭⎪⎫2k =e -2⎝⎛⎭⎪⎫4k 2+1k,令e -2⎝ ⎛⎭⎪⎫4k 2+1k =3e -2,即4k 2+1k =3,解得k =-1或k =43(舍去).当k <-2时,f (x )的极大值为f (-1)=-ekk.因为e k <e-2,0<-1k <12,所以-e kk <12e -2.因为12e -2<3e -2,所以f (x )的极大值不可能等于3e -2.综上所述,当k =-1时,f (x )的极大值等于3e -2.利用导数解决函数的最值问题[例3] 已知函数f (x )=(x -k )e x. (1)求f (x )的单调区间;(2)求f(x)在区间[0,1]上的最小值.[自主解答] (1)f′(x)=(x-k+1)e x.令f′(x)=0,得x=k-1.f(x)与f′(x)的情况如下:x (-∞,k-1)(k-1)(k-1,+∞)f′(x)-0+f(x)-e k-1所以,f(x)的单调递减区间是(-∞,k-1);单调递增区间是(k-1,+∞).(2)当k-1≤0,即k≤1时,函数f(x)在[0,1]上单调递增,所以f(x)在区间[0,1]上的最小值为f(0)=-k;当0<k-1<1,即1<k<2时,由(1)知f(x)在[0,k-1)上单调递减,在(k-1,1]上单调递增,所以f(x)在区间[0,1]上的最小值为f(k-1)=-e k-1;当k-1≥1,即k≥2时,函数f(x)在[0,1]上单调递减,所以f(x)在区间[0,1]上的最小值为f(1)=(1-k)e.保持本例条件不变,求f(x)在[0,1]上的最大值.解:由本例(2)可知.①当k≤1时,函数f(x)在[0,1]上单调递增.所以f(x)在区间[0,1]上的最大值为f(1)=(1-k)e.②当1<k<2时,由于f(0)=-k,f(1)=(1-k)e.令f(1)-f(0)=(1-k)e+k=0,得k=ee-1.∴当1<k<ee-1时,f(1)>f(0).此时f(x)在[0,1]上的最大值为f(1)=(1-k)e.当ee-1<k<2时,f(1)<f(0).此时f(x)在[0,1]上的最大值是f(0)=-k.③当k≥2时,函数f(x)在[0,1]上单调递减,所以f(x)在区间[0,1]上的最大值为f(0)=-k.综上所述,当k<ee-1时,f(x)在[0,1]上的最大值为(1-k)e;当k>ee-1时,f(x)在[0,1]上的最大值为-k.———————————————————利用导数求函数最值的方法求解函数的最值时,要先求函数y=f(x)在[a,b]内所有使f′(x)=0的点,再计算函数y=f(x)在区间内所有使f′(x)=0的点和区间端点处的函数值,最后比较即得,也可利用函数的单调性求得.3.(2012·江西高考)已知函数f (x )=(ax 2+bx +c )e x在[0,1]上单调递减且满足f (0)=1,f (1)=0.(1)求a 的取值范围;(2)设g (x )=f (x )-f ′(x ),求g (x )在[0,1]上的最大值和最小值. 解:(1)由f (0)=1,f (1)=0得c =1,a +b =-1, 则f (x )=[ax 2-(a +1)x +1]e x,f ′(x )=[ax 2+(a -1)x -a ]e x .依题意须对于任意x ∈(0,1),有f ′(x )<0.当a >0时,因为二次函数y =ax 2+(a -1)x -a 的图象开口向上,而f ′(0)=-a <0,所以须f ′(1)=(a -1)e<0,即0<a <1;当a =1时,对任意x ∈(0,1)有f ′(x )=(x 2-1)e x<0,f (x )符合条件; 当a =0时,对于任意x ∈(0,1),f ′(x )=-x e x<0,f (x )符合条件; 当a <0时,因f ′(0)=-a >0,f (x )不符合条件. 故a 的取值范围为0≤a ≤1.(2)因g (x )=(-2ax +1+a )e x,所以g ′(x )=(-2ax +1-a )e x.(ⅰ)当a =0时,g ′(x )=e x>0,g (x )在x =0处取得最小值g (0)=1,在x =1处取得最大值g (1)=e.(ⅱ)当a =1时,对于任意x ∈(0,1)有g ′(x )=-2x e x<0,g (x )在x =0处取得最大值g (0)=2,在x =1处取得最小值g (1)=0.(ⅲ)当0<a <1时,由g ′(x )=0得x =1-a2a>0.①若1-a 2a ≥1,即0<a ≤13时,g (x )在[0,1]上单调递增,g (x )在x =0处取得最小值g (0)=1+a ,在x =1处取得最大值g (1)=(1-a )e.②若1-a 2a <1,即13<a <1时,g (x )在x =1-a 2a 处取得最大值g ⎝ ⎛⎭⎪⎫1-a 2a =2a e 12aa-,在x =0或x =1处取得最小值,而g (0)=1+a ,g (1)=(1-a )e ,则当13<a ≤e -1e +1时,g (x )在x =0处取得最小值g (0)=1+a ;当e -1e +1<a <1时,g (x )在x =1处取得最小值 g (1)=(1-a )e.1个流程——解决函数极值问题的一般流程2个防范——解决函数的极值或最值应注意的问题(1)根据极值的定义,导数为0的点只是一个可疑点,不一定是极值点,只有在该点两侧导数的符号相反,即函数在该点两侧的单调性相反时,该点才是函数的极值点,另一方面,极值点处的导数也不一定为0,还要考察函数在该点处的导数是否存在.(2)求函数最值时,不可想当然地认为极值点就是最值点,要通过认真比较才能下结论.答题模板——函数的单调性、极值、最值问题[典例] (2012·北京高考)(本小题满分13分)已知函数f (x )=ax 2+1(a >0),g (x )=x 3+bx .(1)若曲线y =f (x )与曲线y =g (x )在它们的交点(1,c )处具有公共切线,求a ,b 的值; (2)当a 2=4b 时,求函数f (x )+g (x )的单调区间,并求其在区间(-∞,-1]上的最大值.[快速规范审题]第(1)问1.审条件,挖解题信息观察条件:曲线y =f (x )与曲线y =g (x )在它们的交点(1,c )处有公共切线――――――――――――――――→两曲线在x =1处的纵坐标及导数相同⎩⎪⎨⎪⎧f 1=g 1,f ′1=g ′1.2.审结论,明确解题方向 观察所求结论:求a ,b 的值―――――――――――――→需要建立关于a ,b 的方程组将⎩⎪⎨⎪⎧f 1=g 1f ′1=g ′1用a ,b 表示即可.3.建联系,找解题突破口问题转化为解方程组⎩⎪⎨⎪⎧f 1=g 1f ′1=g ′1――――――――――→须求f ′x 和g ′xf ′(x )=2ax ,g ′(x )=3x 2+b ―――――――→将x =1代入 ⎩⎪⎨⎪⎧a +1=b +12a =3+b⇒a =b =3. 第(2)问1.审条件,挖解题信息 观察条件:a 2=4b―――――――――――――――――――――→可消掉一个参数,使f x 与g x 含有同一个参数f (x )=ax 2+1(a >0),g (x )=x 3+14a 2x .2.审结论,明确解题方向观察所求结论:求函数f (x )+g (x )的单调区间及其在区间(-∞,-1]上的最大值―――――――――――――→f x +g x 含x 3及参数a应利用导数解决. 3.建联系,找解题突破口问题转化为求函数h (x )=f (x )+g (x )=x 3+ax 2+14a 2x +1的导数―――――――――――――――→由h ′x >0和h ′x <0确定单调区间 单调递增区间为⎝ ⎛⎭⎪⎫-∞,-a 2和⎝ ⎛⎭⎪⎫-a 6,+∞,单调递减区间为⎝ ⎛⎭⎪⎫-a2,-a 6(]126aa-∞-−−−−−−−−−−−−→讨论-及-与区间,的关系,求最值 ⎩⎪⎨⎪⎧当-1≤-a2,即0<a ≤2时,h xmax=h -1=a -a 24,当-a 2<1<-a6,即2<a <6时,h xmax=h ⎝ ⎛⎭⎪⎫-a 2=1,当-1≥-a 6,即6≤a 时,h x max =h ⎝ ⎛⎭⎪⎫-a 2=1.[准确规范答题](1)f ′(x )=2ax ,g ′(x )=3x 2+b ,⇨(2分)因为曲线y =f (x )与曲线y =g (x )在它们的交点(1,c )处具有公切线,所以⎩⎪⎨⎪⎧f 1=g 1,f ′1=g ′1,⇨(3分)即⎩⎪⎨⎪⎧a +1=b +1,2a =3+b ,解得a =b =3.⇨(4分)(2)设h (x )=f (x )+g (x ), ∵a 2=4b ,∴h (x )=f (x )+g (x )=x 3+ax 2+14a 2x +1,则h ′(x )=3x 2+2ax +14a 2,令h ′(x )=0,解得,x 1=-a 2,x 2=-a 6.a >0时,h (x )与h ′(x )的变化情况如下:x ⎝ ⎛⎭⎪⎫-∞,-a 2-a2⎝ ⎛⎭⎪⎫-a 2,-a 6 -a6⎝ ⎛⎭⎪⎫-a 6,+∞ h ′(x ) +-+ h (x )∴函数h (x )的单调递增区间为⎝⎛⎭⎪⎫-∞,-a 2和⎝ ⎛⎭⎪⎫-a 6,+∞,单调递减区间为⎝ ⎛⎭⎪⎫-a2,-a 6.⇨(6分)①当-1≤-a2,即0<a ≤2时,函数h (x )在区间(-∞,-1]上单调递增,h (x )在区间(-∞,-1]上的最大值为h (-1)=a -a 24;⇨(8分)②当-a 2<-1≤-a6,即2<a ≤6时,函数h (x )在区间⎝⎛⎭⎪⎫-∞,-a 2上单调递增,h (x )在区间⎝ ⎛⎦⎥⎤-a 2,-1上单调递减,在区间(-∞,-1]上的最大值为h ⎝ ⎛⎭⎪⎫-a2=1;⇨(10分)③当-1>-a6,即a >6时,函数h (x )在区间⎝⎛⎭⎪⎫-∞,-a 2上单调递增,在区间⎝ ⎛⎭⎪⎫-a 2,-a 6上单调递减,在区间⎝ ⎛⎦⎥⎤-a6,-1上单调递易忽视条件“在它们的交点1,c 处具有公切线”的双重性而造成条件缺失,不能列出关于a ,b 的方程组,从而使题目无法求解.易将单调递增区间写成并集“⎝ ⎛⎭⎪⎫-∞,-a 2∪⎝ ⎛⎭⎪⎫-a 6,+∞”或“⎝ ⎛⎭⎪⎫-∞,-a 2或⎝ ⎛⎭⎪⎫-a6,+∞”而导致错误.易忽视对a 的分类讨论或分类不准确造成解题错误.增,又因为h ⎝ ⎛⎭⎪⎫-a 2-h (-1)=1-a +14a 2=14(a -2)2>0,所以h (x )在区间(-∞,-1]上的最大值为h ⎝ ⎛⎭⎪⎫-a 2=1.⇨(12分)综上所述:当a ∈(0,2]时,最大值为h (-1)=a -a 24;当a ∈(2,+∞)时,最大值为h ⎝ ⎛⎭⎪⎫-a 2=1.⇨(13分)[答题模板速成]用导数求给定区间上的函数的最值问题一般可用以下几步解答:第一步 求导 求函数f (x )的导数f ′(x )⇒ 第二步 判断单调性求函数f (x )在给定区间上的单调性⇒第三步 求极点求函数f (x )在给定区间上的极值⇒第四步 求端点值求函数f (x )在给定区间上的端点值⇒第五步 确定最值 比较函数f (x )的各极值与端点值的大小,确定函数f (x )的最大值和最小值⇒第六步 反思回顾查看关键点,易错点和解题规范.如本题的关键点是确定函数单调区间;易错点是对参数的讨论一、选择题(本大题共6小题,每小题5分,共30分)1.已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是( )A.f(b)>f(c)>f(d)B.f(b)>f(a)>f(e)C.f(c)>f(b)>f(a)D.f(c)>f(e)>f(d)解析:选C 依题意得,当x∈(-∞,c)时,f′(x)>0;当x∈(c,e)时,f′(x)<0;当x∈(e,+∞)时,f′(x)>0.因此,函数f(x)在(-∞,c)上是增函数,在(c,e)上是减函数,在(e,+∞)上是增函数,又a<b<c,所以f(c)>f(b)>f(a).2.函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′x>2,则f(x)>2x+4的解集为( )A.(-1,1) B.(-1,+∞)C.(-∞,-1) D.(-∞,+∞)解析:选B 令函数g(x)=f(x)-2x-4,则g′(x)=f′(x)-2>0,因此,g(x)在R 上是增函数,又g(-1)=f(-1)+2-4=2+2-4=0.所以,原不等式可化为g(x)>g(-1),由g(x)的单调性,可得x>-1.3.(2012·陕西高考)设函数f(x)=x e x,则( )A.x=1为f(x)的极大值点B.x=1为f(x)的极小值点C.x=-1为f(x)的极大值点D.x=-1为f(x)的极小值点解析:选D 求导得f′(x)=e x+x e x=e x(x+1),令f′(x)=e x(x+1)=0,解得x=-1,易知x =-1是函数f (x )的极小值点.4.函数f (x )=x 33+x 2-3x -4在[0,2]上的最小值是( )A .-173B .-103C .-4D .-643解析:选A f ′(x )=x 2+2x -3, 令f ′(x )=0得x =1(x =-3舍去), 又f (0)=-4,f (1)=-173,f (2)=-103,故f (x )在[0,2]上的最小值是f (1)=-173.5.(2013·咸宁模拟)已知函数y =x 3-3x +c 的图象与x 轴恰有两个公共点,则c =( )A .-2或2B .-9或3C .-1或1D .-3或1解析:选A ∵y ′=3x 2-3,∴当y ′=0时,x =±1. 则x ,y ′,y 的变化情况如下表:x (-∞,-1)-1 (-1,1) 1 (1,+∞)y ′ +-+yc +2 c -2因此,当函数图象与x 轴恰有两个公共点时,必有c +2=0或c -2=0,∴c =-2或c =2.6.(2012·福建高考)已知f (x )=x 3-6x 2+9x -abc ,a <b <c ,且f (a )=f (b )=f (c )=0.现给出如下结论:①f (0)f (1)>0;②f (0)f (1)<0; ③f (0)f (3)>0;④f (0)f (3)<0. 其中正确结论的序号是( ) A .①③ B .①④ C .②③D .②④解析:选C ∵f ′(x )=3x 2-12x +9=3(x -1)(x -3), 由f ′(x )<0,得1<x <3,由f ′(x )>0,得x <1或x >3, ∴f (x )在区间(1,3)上是减函数,在区间(-∞,1),(3,+∞)上是增函数.又a<b<c,f(a)=f(b)=f(c)=0,∴y极大值=f(1)=4-abc>0,y极小值=f(3)=-abc<0.∴0<abc<4.∴a,b,c均大于零,或者a<0,b<0,c>0.又x=1,x=3为函数f(x)的极值点,后一种情况不可能成立,如图.∴f(0)<0.∴f(0)f(1)<0,f(0)f(3)>0.∴正确结论的序号是②③.二、填空题(本大题共3小题,每小题5分,共15分)7.函数f(x)=x3-15x2-33x+6的单调减区间为________.解析:由f(x)=x3-15x2-33x+6得f′(x)=3x2-30x-33,令f′(x)<0,即3(x-11)(x +1)<0,解得-1<x<11,所以函数f(x)的单调减区间为(-1,11).答案:(-1,11)8.已知函数f(x)=e x-2x+a有零点,则a的取值范围是______________.解析:由原函数有零点,可转化为方程e x-2x+a=0有解,即方程a=2x-e x有解.令函数g(x)=2x-e x,则g′(x)=2-e x,令g′(x)>0,得x<ln 2,所以g(x)在(-∞,ln 2)上是增函数,在(ln 2,+∞)上是减函数,所以g(x)的最大值为g(ln 2)=2ln 2-2.因此,a的取值范围就是函数g(x)的值域,所以a的取值范围为(-∞,2ln 2-2].答案:(-∞,2ln 2-2]9.已知函数f(x)=-x3+ax2-4在x=2处取得极值,若m,n∈[-1,1],则f(m)+f′(n)的最小值是________.解析:由题求导得f′(x)=-3x2+2ax,由函数f(x)在x=2处取得极值知f′(2)=0,即-3×4+2a×2=0,∴a=3.由此可得f(x)=-x3+3x2-4,f′(x)=-3x2+6x,易知f(x)在(-1,0)上单调递减,在(0,1)上单调递增,∴当m∈[-1,1]时,f(m)min=f(0)=-4.又∵f′(x)=-3x2+6x的图象开口向下,且对称轴为x=1,∴当n∈[-1,1]时,f′(n)min=f′(-1)=-9.故f(m)+f′(n)的最小值为-13.答案:-13三、解答题(本大题共3小题,每小题12分,共36分)10.已知函数f(x)=x3+ax2+bx+c在点x0处取得极小值-5,其导函数y=f′(x)的图象经过点(0,0),(2,0).(1)求a,b的值;(2)求x0及函数f(x)的表达式.解:(1)由题设可得f′(x)=3x2+2ax+b.∵f ′(x )的图象过点(0,0),(2,0),∴⎩⎪⎨⎪⎧b =0,12+4a +b =0,解得a =-3,b =0.(2)由f ′(x )=3x 2-6x >0,得x >2或x <0,∴在(-∞,0)上f ′(x )>0,在(0,2)上f ′(x )<0,在(2,+∞)上f ′(x )>0.∴f (x )在(-∞,0),(2,+∞)上递增,在(0,2)上递减,因此f (x )在x =2处取得极小值.所以x 0=2.由f (2)=-5,得c =-1.∴f (x )=x 3-3x 2-1.11.已知函数f (x )=x ln x ,g (x )=-x 2+ax -2. (1)求函数f (x )在[t ,t +2](t >0)上的最小值;(2)若函数y =f (x )与y =g (x )的图象恰有一个公共点,求实数a 的值;(3)若函数y =f (x )+g (x )有两个不同的极值点x 1,x 2(x 1<x 2),且x 2-x 1>ln 2,求实数a 的取值范围.解:(1)令f ′(x )=ln x +1=0得x =1e,①当0<t <1e 时,函数f (x )在⎝ ⎛⎭⎪⎫t ,1e 上单调递减,在⎝ ⎛⎭⎪⎫1e ,t +2上单调递增, 此时函数f (x )在区间[t ,t +2]上的最小值为f ⎝ ⎛⎭⎪⎫1e =-1e ;②当t ≥1e 时,函数f (x )在[t ,t +2]上单调递增,此时函数f (x )在区间[t ,t +2]上的最小值为f (t )=t ln t .(2)由题意得,f (x )-g (x )=x ln x +x 2-ax +2=0在(0,+∞)上有且仅有一个根, 即a =ln x +x +2x在(0,+∞)上有且仅有一个根,令h (x )=ln x +x +2x ,则h ′(x )=1x +1-2x 2=x 2+x -2x 2=1x2(x +2)(x -1), 易知h (x )在(0,1)上单调递减,在(1,+∞)上单调递增,所以a =h (x )min =h (1)=3. (3)由题意得,y =f (x )+g (x )=x ln x -x 2+ax -2,则其导函数为y ′=ln x -2x +1+a ,由题意知y ′=ln x -2x +1+a =0有两个不同的实根x 1,x 2, 等价于a =-ln x +2x -1有两个不同的实根x 1,x 2,且x 1<x 2,等价于直线y =a 与函数G (x )=-ln x +2x -1的图象有两个不同的交点. 由G ′(x )=-1x +2,得G (x )在⎝ ⎛⎭⎪⎫0,12上单调递减,在⎝ ⎛⎭⎪⎫12,+∞上单调递增,画出函数G (x )图象的大致形状(如图).由图象易知,当a >G (x )min =G ⎝ ⎛⎭⎪⎫12=ln 2时,x 1,x 2存在, 且x 2-x 1的值随着a 的增大而增大. 而当x 2-x 1=ln 2时,则有⎩⎪⎨⎪⎧ln x 1-2x 1+1+a =0,ln x 2-2x 2+1+a =0,两式相减可得ln x 2x 1=2(x 2-x 1)=2ln 2, 得x 2=4x 1,代入上述方程组解得x 1=ln 23,x 2=43ln 2,此时实数a =23ln 2-ln ⎝ ⎛⎭⎪⎫ln 23-1,所以实数a 的取值范围为a >23ln 2-ln ⎝ ⎛⎭⎪⎫ln 23-1. 12.已知函数f (x )=x -12ax 2-ln(1+x ),其中a ∈R .(1)若x =2是f (x )的极值点,求a 的值; (2)求f (x )的单调区间;(3)若f (x )在[0,+∞)上的最大值是0,求a 的取值范围. 解:(1)f ′(x )=x 1-a -axx +1,x ∈(-1,+∞).依题意,得f ′(2)=0,解得a =13.经检验,a =13时,符合题意.故a =13.(2)①当a =0时,f ′(x )=xx +1,由f ′(x )>0和f ′(x )<0,易得f (x )的单调递增区间是(0,+∞),单调递减区间是(-1,0). ②当a >0时,令f ′(x )=0,得x 1=0或x 2=1a-1.当0<a <1时,f (x )与f ′(x )的变化情况如下表:x (-1,x 1) x 1 (x 1,x 2) x 2 (x 2,+∞)f ′(x ) - 0 + 0 - f (x )f (x 1) f (x 2)所以,f (x )的单调递增区间是⎝⎛⎭⎪⎫0,1a-1,单调递减区间是(-1,0)和⎝ ⎛⎭⎪⎫1a -1,+∞.当a =1时,f (x )的单调递减区间是(-1,+∞). 当a >1时,-1<x 2<0,f (x )与f ′(x )的变化情况如下表:x (-1,x 2)x 2(x 2,x 1) x 1(x 1,+∞)f ′(x ) -+- f (x )f (x 2) f (x 1)所以,f (x )的单调递增区间是⎝ ⎛⎭⎪⎫1a -1,0,单调递减区间是⎝⎛⎭⎪⎫-1,1a-1和(0,+∞).③当a <0时,f (x )的单调递增区间是(0,+∞),单调递减区间是(-1,0). 综上,当a ≤0时,f (x )的单调递增区间是(0,+∞),单调递减区间是(-1,0);当0<a <1时,f (x )的单调递增区间是⎝⎛⎭⎪⎫0,1a-1,单调递减区间是(-1,0)和⎝ ⎛⎭⎪⎫1a -1,+∞;当a =1时,f (x )的单调递减区间是(-1,+∞);当a >1时,f (x )的单调递增区间是⎝ ⎛⎭⎪⎫1a-1,0,单调递减区间是⎝⎛⎭⎪⎫-1,1a-1和(0,+∞). (3)由(2)知a ≤0时,f (x )在(0,+∞)上单调递增,由f (0)=0,知a ≤0时不合题意.当0<a <1时,f (x )在(0,+∞)上的最大值是f ⎝ ⎛⎭⎪⎫1a-1,由f ⎝ ⎛⎭⎪⎫1a-1>f (0)=0,知0<a <1时不合题意.当a ≥1时,f (x )在(0,+∞)上单调递减,可得f (x )在[0,+∞)上的最大值是f (0)=0,符合题意.所以f (x )在[0,+∞)上的最大值是0时,a 的取值范围是[1,+∞).1.已知函数f (x )=ln x -ax +1-ax-1(a ∈R ).(1)当a =-1时,求曲线y =f (x )在点(2,f (2))处的切线方程; (2)当a ≤12时,讨论f (x )的单调性.解:(1)当a =-1时,f (x )=ln x +x +2x-1,x ∈(0,+∞).所以f ′(x )=x 2+x -2x 2,x ∈(0,+∞).因此f ′(2)=1,即曲线y =f (x )在点(2,f (2))处的切线斜率为1. 又f (2)=ln 2+2,所以曲线y =f (x )在点(2,f (2))处的切线方程为y -(ln 2+2)=x -2,即x -y +ln 2=0.(2)因为f (x )=ln x -ax +1-ax-1,所以f ′(x )=1x -a +a -1x 2=-ax 2-x +1-ax2,x ∈(0,+∞). 令g (x )=ax 2-x +1-a ,x ∈(0,+∞). ①当a =0时,g (x )=-x +1,x ∈(0,+∞), 所以当x ∈(0,1)时,g (x )>0, 此时f ′(x )<0,函数f (x )单调递减;当x ∈(1,+∞)时,g (x )<0,此时f ′(x )>0,函数f (x )单调递增; ②当a ≠0时,由f ′(x )=0,即ax 2-x +1-a =0,解得x 1=1,x 2=1a-1.a .当a =12时,x 1=x 2,g (x )≥0恒成立,此时f ′(x )≤0,函数f (x )在(0,+∞)上单调递减;b .当0<a <12时,1a-1>1>0.x ∈(0,1)时,g (x )>0,此时f ′(x )<0,函数f (x )单调递减;x ∈⎝ ⎛⎭⎪⎫1,1a -1时,g (x )<0,此时f ′(x )>0,函数f (x )单调递增;x ∈⎝ ⎛⎭⎪⎫1a -1,+∞时,g (x )>0,此时f ′(x )<0,函数f (x )单调递减;c .当a <0时,由于1a-1<0,x ∈(0,1)时,g (x )>0,此时f ′(x )<0,函数f (x )单调递减;x ∈(1,+∞)时,g (x )<0,此时f ′(x )>0,函数f (x )单调递增.综上所述:当a ≤0时,函数f (x )在(0,1)上单调递减, 函数f (x )在(1,+∞)上单调递增;当a =12时,函数f (x )在(0,+∞)上单调递减;当0<a <12时,函数f (x )在(0,1)上单调递减,函数f (x )在⎝⎛⎭⎪⎫1,1a-1上单调递增,函数f (x )在⎝ ⎛⎭⎪⎫1a-1,+∞上单调递减.2.设f (x )=-13x 3+12x 2+2ax .(1)若f (x )在⎝ ⎛⎭⎪⎫23,+∞上存在单调递增区间,求a 的取值范围; (2)当0<a <2时,f (x )在[1,4]上的最小值为-163,求f (x )在该区间上的最大值.解:(1)由f ′(x )=-x 2+x +2a =-⎝ ⎛⎭⎪⎫x -122+14+2a ,当x ∈⎣⎢⎡⎭⎪⎫23,+∞时,f ′(x )的最大值为f ′⎝ ⎛⎭⎪⎫23=29+2a ;令29+2a >0,得a >-19.所以,当a >-19时,f (x )在⎝ ⎛⎭⎪⎫23,+∞上存在单调递增区间.(2)令f ′(x )=0,得两根x 1=1-1+8a2,x 2=1+1+8a2. 所以f (x )在(-∞,x 1),(x 2,+∞)上单调递减,在(x 1,x 2)上单调递增. 当0<a <2时,有x 1<1<x 2<4,所以f (x )在[1,4]上的最大值为f (x 2). 又f (4)-f (1)=-272+6a <0,即f (4)<f (1).所以f (x )在[1,4]上的最小值为f (4)=8a -403=-163,得a =1,x 2=2,从而f (x )在[1,4]上的最大值为f (2)=103.3.设x =1与x =2是函数f (x )=a ln x +bx 2+x 的两个极值点. (1)试确定常数a 和b 的值;(2)试判断x =1,x =2是函数f (x )的极大值点还是极小值点,并说明理由. 解:(1)f ′(x )=a x+2bx +1,由题意得f ′(1)=0,f ′(2)=0,∴⎩⎪⎨⎪⎧a +2b +1=0,a2+4b +1=0,解得⎩⎪⎨⎪⎧a =-23,b =-16.(2)由(1)知f (x )=-23ln x -16x 2+x ,所以f ′(x )=-23x -x 3+1=-x 2-3x +23x=-13·x -1x -2x.又∵x >0,∴0<x <1时,f ′(x )<0,1<x <2时,f ′(x )>0,x >2时,f ′(x )<0.∴函数f (x )在(0,1)和(2,+∞)上是减函数,在(1,2)上是增函数.∴x =1是函数f (x )的极小值点,x =2是函数f (x )的极大值点.。
2013届高考数学第1轮总复习12.5导数的应用(第3课时)课件理(广西专版)

把实际问题转化为数学问题,然后利用求 函数最值的方法求得最值.注意求得的解要 符合实际意义.
统计表明,某种型号的汽车在匀速行驶中每小时的耗 油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表 示为:y=1281000x3-830x+8(0<x≤120).
• 解:因为f ′(x)=x2+ax+b,
• 所以f ′(1)=1+a+b.又
f 1 1 a b,
32
• 所以直线l的方程为
y ( 1 a b) (1 a b) ( x 1), 32
即y 1 a b x 2 a .
32
令g x f x [1 a b x 2 a]
• 1.利用导数确定函数的单调区间,求函数的极 值和最值,是导数应用中的三类基本问题.对 变通后的变式问题或综合性问题,都要化归 为上述基本问题来解决.导数的应用与方程、 不等式等方面的知识联系密切,对运算、变 形能力有较高的要求.
• 2. 利用导数处理不等式问题,关键是构造函 数,然后将问题转化为研究函数的单调性或 最值,这是导数应用中的一个难点.
(2)当速度为 x 千米/小时时,汽车从甲地到乙地行驶了 10x0小时,设耗油量为 h(x)升,
依题意得:
h(x)=(1281000x3-830x+8)·10x 0 =12180x2+80x0-145(0<x≤120), 则 h′(x)=64x0-8x020=x63-408x023(0<x≤120). 令 h′(x)=0,得 x=80.
• x∈[9,11].
• (2)L′(x)=(12-x)2-2(x-3-a)(12-x)
高考数学一轮复习课件2.12导数的综合应用
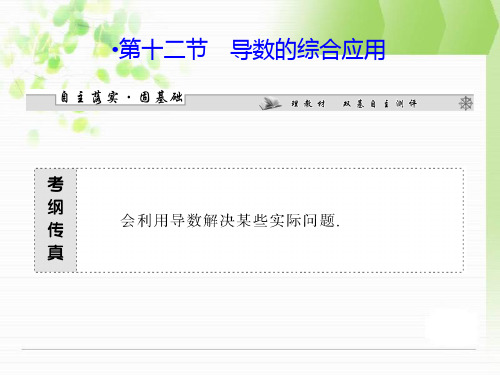
由已知得a= 2x,h=60-22x= 2(30-x),0<x<30. (1)S=4ah=8x(30-x)=-8(x-15)2+1 800, 所以当x=15时,S取得最大值. (2)V=a2h=2 2(-x3+30x2),
V′=6 2x(20-x).
•【解析】 函数f(x)=ex-2x+a有零点,即 方程ex-2x+a=0有实根,即函数g(x)=2x -ex,y=a有交点,而g′(x)=2-ex,易知函 数g(x)=2x-ex在(-∞,ln 2)上递增,在(ln 2,+∞)上递减,因而g(x)=2x-ex的值域为 (-∞,2ln 2-2],所以要使函数g(x)=2x- ex,y=a有交点,只需a≤2ln 2-2即可.
•(2013·梅州模拟)设函数f(x)=a2ln x-x2+ax, a>0.
•(1)求f(x)的单调区间;
•(2)求所有的实数a,使e-1≤f(x)≤e2对x∈[1, e]恒成立.(其中,e为自然对数的底数).
【解】 (1)因为f(x)=a2ln x-x2+ax,其中x>0, 所以f′(x)=ax2-2x+a=-(x-a)x(2x+a). 由于a>0,所以f(x)的增区间为(0,a),减区间为(a, +∞).
•(2)求函数y=f(x)的导数f′(x),解方程f′(x)=0 得出定义域内的实根,确定极值点;
•(3)比较函数在区间端点和极值点处的函数值 大小,获得所求的最大(小)值;
•(4)还原到实际问题中作答.
某地建一座桥,两端的桥墩已建好,这两墩相距m 米.余下工程只需建两端桥墩之间的桥面和桥墩.经测 算,一个桥墩的工程费用为256万元;距离为x米的相邻两
=256(mx -1)+mx (2+ x)x=25x6m+m x+2m-256. (2)由(1)知,f′(x)=-25x62m+12mx-12 =2mx2(x32-512).
最新高考数学1轮复习精讲精练(新人教A版)第12章 导数及其应用

最|新高中数学精讲精练第十二章导数及其应用【知识图解】【方法点拨】导数的应用极其广泛 ,是研究函数性质、证明不等式、研究曲线的切线和解决一些实际问题的有力工具 ,也是提出问题、分析问题和进行理性思维训练的良好素材 .同时 ,导数是初等数学与高等数学紧密衔接的重要内容 ,表达了高等数学思想及方法 .1.重视导数的实际背景 .导数概念本身有着丰富的实际意义 ,对导数概念的深刻理解应该从这些实际背景出发 ,如平均变化率、瞬时变化率和瞬时速度、加速度等 .这为我们解决实际问题提供了新的工具 ,应深刻理解并灵活运用 .2.深刻理解导数概念 .概念是根本 ,是所有性质的根底 ,有些问题可以直接用定义解决 .在理解定义时 ,要注意 "函数()f x 在点0x 处的导数0()f x '〞与 "函数()f x 在开区间(,)a b 内的导数()f x '〞之间的区别与联系 .3.强化导数在函数问题中的应用意识 .导数为我们研究函数的性质 ,如函数的单调性、极值与最|值等 ,提供了一般性的方法 .4.重视 "数形结合〞的渗透 ,强调 "几何直观〞 .在对导数和定积分的认识和理解中 ,在研究函数的导数与单调性、极值、最|值的关系等问题时 ,应从数值、图象等多个方面 ,尤其是几何直观加以理解 ,增强数形结合的思维意识 .5.加强 "导数〞的实践应用 .导数作为一个有力的工具 ,在解决科技、经济、生产和生活中的问题 ,尤其是最|优化问题中得到广泛的应用 .6. (理科用 )理解和体会 "定积分〞的实践应用 .定积分也是解决实际问题 (主要是几何和物理问题 )的有力工具 ,如可以用定积分求一些平面图形的面积、旋转体的体积、变速直线运动的路程和变力作的功等 ,逐步体验微积分根本定理 .第1课 导数的概念及运算【考点导读】1.了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等);2.掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念;3.熟记根本导数公式;4.掌握两个函数和、差、积、商的求导法那么;5.了解复合函数的求导法那么.会求某些简单函数的导数. (理科 ) 【根底练习】1.设函数f (x )在x =x 0处可导,那么0lim→h hx f h x f )()(00-+与x 0,h 的关系是仅与x 0有关而与h 无关 .2.)1()('23f x x x f +=, 那么=)2('f 0 . 3.),(,cos 1sin ππ-∈+=x x x y ,那么当2'=y 时,=x 32π± .4.a x x a x f =)(,那么=)1('f 2ln a a a + .5.两曲线ax x y +=3和c bx x y ++=2都经过点P (1,2 ) ,且在点P 处有公切线 ,试求a,b,c 值 . 解:因为点P (1,2 )在曲线ax x y +=3上 ,1=∴a函数ax x y +=3和c bx x y ++=2的导数分别为a x y +='23和b x y +='2 ,且在点P 处有公切数b a +⨯=+⨯∴12132 ,得b =2又由c +⨯+=12122,得1-=c【范例导析】例1.以下函数的导数:①2(1)(231)y x x x =++-②y =()(cos sin )xf x e x x =⋅+分析:利用导数的四那么运算求导数 .解:①法一:13232223-++-+=x x x x x y 125223-++=x x x ∴26102y x x '=++法二:)132)(1()132()1(22'-+++-+'+='x x x x x x y =1322-+x x +)1(+x )34(+x ②231212332----+-=x x xx y∴252232123233---+-+='x x x x y③()f x '=e -x(cos x +sin x ) +e -x(-sin x +cos x )=2e -xcos x ,点评:利用根本函数的导数、导数的运算法那么及复合函数的求导法那么进行导数运算 ,是(高|考)对导数考查的根本要求 .例2. 如果曲线103-+=x x y 的某一切线与直线34+=x y 平行 ,求切点坐标与切线方程.分析:此题重在理解导数的几何意义:曲线()y f x =在给定点00(,())P x f x 处的切线的斜率0()k f x '= ,用导数的几何意义求曲线的斜率就很简单了 .解: 切线与直线34+=x y 平行 , 斜率为4又切线在点0x 的斜率为0320(10)31x x x x y x x x ==''=+-=+∵41320=+x ∴10±=x∴⎩⎨⎧-==8100y x 或⎩⎨⎧-=-=12100y x∴切点为 (1 , -8 )或 ( -1 , -12 )切线方程为)1(48-=+x y 或)1(412+=+x y 即124-=x y 或84-=x y点评:函数导数的几何意义揭示了导数知识与平面解析几何知识的密切联系 ,利用导数能解决许多曲线的切线问题 ,其中寻找切点是很关键的地方 .变题:求曲线32y x x =-的过点(1,1)A 的切线方程 . 答案:20,5410x y x y +-=--=点评:此题中 "过点(1,1)A 的切线〞与 "在点(1,1)A 的切线〞的含义是不同的 ,后者是以A 为切点 ,只有一条切线 ,而前者不一定以A 为切点 ,切线也不一定只有一条 ,所以要先设切点 ,然后求出切点坐标 ,再解决问题 . 【反应演练】1.一物体做直线运动的方程为21s t t =-+ ,s 的单位是,m t 的单位是s ,该物体在3秒末的瞬时速度是5/m s .2.设生产x 个单位产品的总本钱函数是2()88x C x =+ ,那么生产8个单位产品时 ,边际本钱是 2 .3.函数f (x )在x =1处的导数为3,那么f (x )的解析式可能为 (1 ) .(1 )f (x ) = (x -1 )2+3 (x -1 ) (2 )f (x ) =2 (x -1 )(3 )f (x ) =2 (x -1 )2(4 )f (x ) =x -1 4.假设曲线4y x =的一条切线l 与直线480x y +-=垂直 ,那么l 的方程为430x y --= . 5.在函数x x y 83-=的图象上 ,其切线的倾斜角小于4π的点中 ,坐标为整数的点的个数是 3 . 6.过点 (0 ,-4 )与曲线y =x 3+x -2相切的直线方程是y =4x -4 . 7. 求以下函数的导数:(1)y =(2x 2-1)(3x +1) (2)x x y sin 2=(3))1ln(2x x y ++=(4)11-+=x x e e y (5)x x x x y sin cos ++= (6)x x x y cos sin 2cos -=解: (1 )34182-+='x x y , (2)x x x x y cos sin 22+=';(3)211xy +=', (4)2)1(2--='x xe e y ;(5)2)sin (1cos sin sin cos x x x x x x x x y +--+--=', (6)x x y cos sin -='. 直线1l 为曲线22-+=x x y 在点(0,2)-处的切线 ,2l 为该曲线的另一条切线 ,且21l l ⊥(Ⅰ )求直线2l 的方程;(Ⅱ )求由直线1l ,2l 和x 轴所围成的三角形的面积解:设直线1l 的斜率为1k ,直线2l 的斜率为2k ,'21y x =+ ,由题意得10'|1x k y ===,得直线1l 的方程为2y x =-211,1x x +=-=-令得,212,2x y x x y =-=+-=-将代入得2l ∴与该曲线的切点坐标为(1,2),A --由直线方程的点斜式得直线2l 的方程为:y x =--(Ⅱ )由直线1l 的方程为2y x =-,令0=2y x =得: 由直线2l 的方程为3y x =-- ,令0=3y x =-得:由23y x y x =-⎧⎨=--⎩得:52y =-设由直线1l ,2l 和x 轴所围成的三角形的面积为S ,那么:1525[2(3)]224s =⋅-⋅--=第2课 导数的应用A【考点导读】1. 通过数形结合的方法直观了解函数的单调性与导数的关系 ,能熟练利用导数研究函数的单调性;会求某些简单函数的单调区间 .2. 结合函数的图象 ,了解函数的极大 (小 )值、最|大 (小 )值与导数的关系;会求简单多项式函数的极大 (小 )值 ,以及在指定区间上的最|大 (小 )值 . 【根底练习】1.假设函数()f x mx n =+是R 上的单调函数 ,那么,m n 应满足的条件是0,m n R ≠∈ .2.函数5123223+--=x x x y 在[0 ,3]上的最|大值、最|小值分别是5 ,-15 . 3.用导数确定函数()sin ([0,2])f x x x π=∈的单调减区间是3[,]22ππ.4.函数1()sin ,([0,2])2f x x x x π=+∈的最|大值是π ,最|小值是0 . 5.函数2()xf x x e =⋅的单调递增区间是 ( -∞, -2)与(0, + ∞) .【范例导析】例1.32()32f x x x =-+在区间[]1,1-上的最|大值是2 . 解:当-1≤x <0时 ,()f x '>0 ,当0<x ≤1时 ,()f x '<0 ,所以当x =0时 ,f (x )取得最|大值为2 . 点评:用导数求极值或最|值时要掌握一般方法 ,导数为0的点是否是极值点还取决与该点两侧的单调性 ,导数为0的点未必都是极值点 ,如:函数3()f x x = . 例2. 求以下函数单调区间:(1 )5221)(23+--==x x x x f y (2 )xx y 12-=(3 )x xk y +=2)0(>k (4 )x x y ln 22-= 解: (1 )∵232--='x x y )1)(23(-+=x x ∴)32,(--∞∈x ),1(∞+ 时0>'y )1,32(-∈x 0<'y ∴)32,(--∞ ,),1(∞+↑)1,32(-↓ (2 )221xx y +='∴)0,(-∞ ,),0(∞+↑ (3 )221xk y -=∴),(k x --∞∈),(∞+k 0>'y , ),0()0,(k k x -∈0<'y∴),(k --∞ ,↑∞+),(k )0,(k - ,),0(k ↓(4 )xx x x y 14142-=-='定义域为),0(∞+)21,0(∈x 0<'y ↓),21(∞+∈x 0>'y ↑点评:熟练掌握单调性的求法 ,函数的单调性是解决函数的极值、最|值问题的根底 .例3.设函数f(x) = 3223(1)1, 1.x a x a --+≥其中 (Ⅰ )求f(x)的单调区间; (Ⅱ )讨论f(x)的极值 . 解:由得[]'()6(1)f x x x a =-- ,令'()0f x = ,解得120,1x x a ==- .(Ⅰ )当1a =时 ,'2()6f x x = ,()f x 在(,)-∞+∞上单调递增;当1a >时 ,()'()61f x x x a =--⎡⎤⎣⎦ ,'(),()f x f x 随x 的变化情况如下表:从上表可知 ,函数()f x 在(,0)-∞上单调递增;在(0,1)a -上单调递减;在(1,)a -+∞上单调递增 . (Ⅱ )由 (Ⅰ )知 ,当1a =时 ,函数()f x 没有极值;当1a >时 ,函数()f x 在0x =处取得极大值 ,在1x a =-处取得极小值31(1)a -- .点评:本小题主要考查利用导数研究函数的最|大值和最|小值的根底知识 ,以及运用数学知识解决实际问题的能力 . 【反应演练】1.关于函数762)(23+-=x x x f ,以下说法不正确的选项是 (4 ) .(1 )在区间 (∞- ,0 )内 ,)(x f 为增函数 (2 )在区间 (0 ,2 )内 ,)(x f 为减函数(3 )在区间 (2 ,∞+ )内 ,)(x f 为增函数 (4 )在区间 (∞- ,0 )),2(+∞⋃内 ,)(x f 为增函数 2.对任意x ,有34)('x x f = ,(1)1f =- ,那么此函数为 2)(4-=x x f . 3.函数y =2x 3-3x 2-12x +5在[0,3]上的最|大值与最|小值分别是5 , -15 . 4.以下函数中 ,0x =是极值点的函数是 (2 ) . (1 )3y x =- (2 )2cos y x = (3 )tan y x x =- (4 )1y x=5.以下说法正确的选项是 (4 ) . (1 )函数的极大值就是函数的最|大值 (2 )函数的极小值就是函数的最|小值 (3 )函数的最|值一定是极值 (4 )在闭区间上的连续函数一定存在最|值 6.函数32()35f x x x =-+的单调减区间是 [0 ,2] . 7.求满足条件的a 的范围: (1 )使ax x y +=sin 为R 上增函数;(2 )使a ax x y ++=3为R 上的增函数; (3 )使5)(23-+-=x x ax x f 为R 上的增函数 . 解: (1 )∵a x y +='cos 由题意可知:0y '>对x R ∀∈都成立 ∴1>a 又当1=a 时 x x y +=sin 也符合条件 ∴),1[∞+∈a (2 )同上 ),0[∞+∈a (3 )同上 ),31[∞+∈a8.函数c bx x ax x f -+=44ln )((x>0)在x = 1处取得极值c --3 ,其中,,a b c 为常数 . (1 )试确定,a b 的值; (2 )讨论函数f(x)的单调区间 .解: (I )由题意知(1)3f c =-- ,因此3b c c -=-- ,从而3b =-. 又对()f x 求导得()34341ln 4'bx xax x ax x f +⋅+=3(4ln 4)x a x a b =++. 由题意(1)0f '= ,因此40a b += ,解得12a =.(II )由 (I )知3()48ln f x x x '= (0x > ) ,令()0f x '= ,解得1x =.当01x <<时 ,()0f x '< ,此时()f x 为减函数;当1x >时 ,()0f x '> ,此时()f x 为增函数. 因此()f x 的单调递减区间为(01), ,而()f x 的单调递增区间为(1)+,∞.第3课 导数的应用B【考点导读】1. 深化导数在函数、不等式、解析几何等问题中的综合应用 ,加强导数的应用意识 .2. 利用导数解决实际生活中的一些问题 ,进一步加深对导数本质的理解 ,逐步提高分析问题、探索问题以及解决实际应用问题等各种综合能力 . 【根底练习】1.假设)(x f 是在()l l ,-内的可导的偶函数 ,且)(x f '不恒为零 ,那么关于)(x f '以下说法正确的选项是 (4 ) .(1 )必定是()l l ,-内的偶函数 (2 )必定是()l l ,-内的奇函数 (3 )必定是()l l ,-内的非奇非偶函数 (4 )可能是奇函数 ,也可能是偶函数 2.()f x '是()f x 的导函数 ,()f x '的图象如右图所示 ,那么()f x 的图象只可能是 (4 ) . (1 ) (2 ) (3 ) (4 )3.假设t R ∈ ,曲线3y x =与直线3y x t =-在[0,1]x ∈上的不同交点的个数有 至|多1个 . 4.把长为60cm 的铁丝围成矩形 ,要使矩形的面积最|大 ,那么长为 15cm ,宽为 15cm . 【范例导析】例1.函数c bx ax x x f +++=23)( ,过曲线)(x f y =上的点))1(,1(f P 的切线方程为13+=x y (1 )假设)(x f y =在2-=x 时有极值 ,求f (x )的表达式; (2 )在 (1 )的条件下 ,求)(x f y =在]1,3[-上最|大值;(3 )假设函数)(x f y =在区间]1,2[-上单调递增 ,求b 的取值范围 解: (1 )(2 ))2)(23(44323)(22'4514121)1(=+⨯-⨯+=f ]1,3[)(-∴在x f 上最|大值为13(3 )]1,2[)(-=在区间x f y 上单调递增又02)1(,23)(2=+++='b a b ax x x f 知由b bx x x f +-='∴23)(依题意]1,2[03,0)(]1,2[)(2-≥+-≥'-'在即上恒有在b bx x x f x f 上恒成立.①在603)1()(,16≥∴>+-='='≥=b b b f x f bx 小时②在0212)2()(,26≥++=-'='-≤=b b f x f bx 小时∅∈∴b ③在.6001212)(,1622≤≤≥-='≤≤-b b b x f b 则时小 综合上述讨论可知 ,所求参数b 取值范围是:b ≥0 .点评:此题把导数的几何意义与单调性、极值和最|值结合起来 ,属于函数的综合应用题 . 例2.请您设计一个帐篷 .它下部的形状是高为1m 的正六棱柱 ,上部的形状是侧棱长为3m 的正六棱锥 (如右图所示 ) .试问当帐篷的顶点O 到底面中|心1O 的距离为多少时 ,帐篷的体积最|大 ?分析:此题应该先建立模型 ,再求体积的最|大值 .选择适当的变量很关键 ,设1OO 的长度会比拟简便 . 解:设1()OO x m =,那么由题设可得正六棱锥底面边长为2223(1)82x x x --=+- (单位:m ) .于是底面正六边形的面积为 (单位:m 2):222223333(1)6(82)(82)42x x x x x --=+-=+- . 帐篷的体积为 (单位:m 3): 求导数 ,得23()(123)2V x x '=-; 令()0V x '=解得x = -2(不合题意 ,舍去),x =2 .当1<x<2时 ,()0V x '>,V(x)为增函数;当2<x<4时 ,()0V x '<,V(x)为减函数 .所以当x =2时,V(x)最|大 .答:当OO 1为2m 时 ,帐篷的体积最|大 .点评:此题是结合空间几何体的体积求最|值 ,加深理解导数的工具作用 ,主要考查利用导数研究函数的最|大值和最|小值的根底知识 ,以及运用数学知识解决实际问题的能力 . 【反应演练】1.设()f x '是函数()f x 的导函数 ,将()y f x =和()y f x '=的图象画在同一个直角坐标系中 ,不可能正确的选项是图4 . 2.二次函数2()f x ax bx c =++的导数为'()f x ,'(0)0f > ,对于任意实数x 都有()0f x ≥ ,那么(1)'(0)f f 的最|小值为 32 .3.假设π02x << ,那么以下命题正确的选项是 (3 ). (1 )2sin πx x < (2 )2sin πx x > (3 )3sin πx x <(4)3sin πx x >yx O y x O y x O yxO 图1 图2 图3 图44.函数()ln (0)f x x x x =>的单调递增区间是1,e ⎡⎫+∞⎪⎢⎣⎭.5.函数32()f x x bx cx d =+++的图象过点P (0 ,2 ) ,且在点M (-1 ,f (-1 ) )处的切线方程为076=+-y x .(Ⅰ )求函数y =f(x)的解析式; (Ⅱ )求函数y =f(x)的单调区间.解: (Ⅰ )由f(x)的图象经过P (0 ,2 ) ,知d =2 ,所以,2)(23+++=cx bx x x f .23)(2c bx x x f ++='由在M( -1,f( -1))处的切线方程是076=+-y x , 知.6)1(,1)1(,07)1(6=-'=-=+---f f f 即 故所求的解析式是 .233)(23+--=x x x x f (Ⅱ )22()36 3.3630,f x x x x x '=----=令2210.x x --=即 解得 .21,2121+=-=x x当;0)(,21,21>'+>-<x f x x 时或 当.0)(,2121<'+<<-x f x 时故)21,()(--∞在x f 内是增函数 ,在)21,21(+-内是减函数 ,在),21(+∞+内是增函数.点评:此题考查函数的单调性、导数的应用等知识 ,考查运用数学知识分析问题和解决问题的能力. 6.如图 ,有一块半椭圆形钢板 ,其半轴长为2r ,短半轴长为r ,方案将此钢板切割成等腰梯形的形状 ,下底AB 是半椭圆的短轴 ,上底CD 的端点在椭圆上 ,记2CD x = ,梯形面积为S .(I )求面积S 以x 为自变量的函数式 ,并写出其定义域; (II )求面积S 的最|大值.解: (I )依题意 ,以AB 的中点O 为原点建立直角坐标系O xy - (如图 ) , 那么点C 的横坐标为x .点C 的纵坐标y 满足方程22221(0)4x y y r r+=≥ ,解得)y x r =<< 所以221(22)22S x r r x =+-222()x r r x =+- ,其定义域为{}0x x r <<.(II )记222()4()()0f x x r r x x r =+-<<, , 那么2()8()(2)f x x r r x '=+-.令()0f x '= ,得12x r =.因为当02r x <<时 ,()0f x '>;当2rx r <<时 ,()0f x '< , 所以()f x 在(0,)2r 上是单调递增函数 ,在(,)2rr 上是单调递减函数 ,所以12f r ⎛⎫⎪⎝⎭是()f x 的最|大值. A因此 ,当12x r =时 ,S 也取得最|大值 ,最|22r =.即梯形面积S 的最|2. 7.设函数22()21(0)f x tx t x t x t =++-∈>R ,. (Ⅰ )求()f x 的最|小值()h t ;(Ⅱ )假设()2h t t m <-+对(02)t ∈,恒成立 ,求实数m 的取值范围. 解: (Ⅰ )23()()1(0)f x t x t t t x t =+-+-∈>R , ,∴当x t =-时 ,()f x 取最|小值3()1f t t t -=-+- ,即3()1h t t t =-+-.(Ⅱ )令3()()(2)31g t h t t m t t m =--+=-+-- , 由2()330g t t '=-+=得1t = ,1t =- (不合题意 ,舍去 ). 当t 变化时()g t ' ,()g t 的变化情况如下表:()g t ∴在(02),内有最|大值(1)1g m =-.()2h t t m <-+在(02),内恒成立等价于()0g t <在(02),内恒成立 ,即等价于10m -< ,所以m 的取值范围为1m >.点评:此题主要考查函数的单调性、极值以及函数导数的应用 ,考查运用数学知识分析问题解决问题的能力.8.设函数2()ln()f x x a x =++,假设当1x =-时 ,()f x 取得极值 ,求a 的值 ,并讨论()f x 的单调性.解:1()2f x x x a '=++ ,依题意有(1)0f '-= ,故32a =. 从而2231(21)(1)()3322x x x x f x x x ++++'==++.()f x 的定义域为32⎛⎫-+ ⎪⎝⎭,∞ , 当312x -<<-时 ,()0f x '>;当112x -<<-时 ,()0f x '<;当12x >-时 ,()0f x '>.公众号:惟微小筑从而 ,()f x 分别在区间31122⎛⎫⎛⎫---+ ⎪ ⎪⎝⎭⎝⎭,,,∞单调增加 ,在区间112⎛⎫-- ⎪⎝⎭,单调减少.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013高中数学精讲精练 第十二章 导数及其应用【知识图解】【方法点拨】导数的应用极其广泛,是研究函数性质、证明不等式、研究曲线的切线和解决一些实际问题的有力工具,也是提出问题、分析问题和进行理性思维训练的良好素材。
同时,导数是初等数学与高等数学紧密衔接的重要内容,体现了高等数学思想及方法。
1.重视导数的实际背景。
导数概念本身有着丰富的实际意义,对导数概念的深刻理解应该从这些实际背景出发,如平均变化率、瞬时变化率和瞬时速度、加速度等。
这为我们解决实际问题提供了新的工具,应深刻理解并灵活运用。
2.深刻理解导数概念。
概念是根本,是所有性质的基础,有些问题可以直接用定义解决。
在理解定义时,要注意“函数()f x 在点0x 处的导数0()f x '”与“函数()f x 在开区间(,)a b 内的导数()f x '”之间的区别与联系。
3.强化导数在函数问题中的应用意识。
导数为我们研究函数的性质,如函数的单调性、极值与最值等,提供了一般性的方法。
4.重视“数形结合”的渗透,强调“几何直观”。
在对导数和定积分的认识和理解中,在研究函数的导数与单调性、极值、最值的关系等问题时,应从数值、图象等多个方面,尤其是几何直观加以理解,增强数形结合的思维意识。
5.加强“导数”的实践应用。
导数作为一个有力的工具,在解决科技、经济、生产和生活中的问题,尤其是最优化问题中得到广泛的应用。
6.(理科用)理解和体会“定积分”的实践应用。
定积分也是解决实际问题(主要是几何和物理问题)的有力工具,如可以用定积分求一些平面图形的面积、旋转体的体积、变速直线运动的路程和变力作的功等,逐步体验微积分基本定理。
第1课 导数的概念及运算【考点导读】1.了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等);2.掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念;3.熟记基本导数公式;4.掌握两个函数和、差、积、商的求导法则;5.了解复合函数的求导法则.会求某些简单函数的导数.(理科) 【基础练习】1.设函数f (x )在x =x 0处可导,则0lim→h hx f h x f )()(00-+与x 0,h 的关系是 仅与x 0有关而与h 无关 。
2.已知)1()('23f x x x f +=, 则=)2('f 0 。
3.已知),(,cos 1sin ππ-∈+=x xx y ,则当2'=y 时,=x 32π±。
4.已知a x x a x f =)(,则=)1('f 2ln a a a +。
5.已知两曲线ax x y +=3和c bx x y ++=2都经过点P (1,2),且在点P 处有公切线,试求a,b,c 值。
解:因为点P (1,2)在曲线ax x y +=3上,1=∴a函数ax x y +=3和c bx x y ++=2的导数分别为a x y +='23和b x y +='2,且在点P 处有公切数b a +⨯=+⨯∴12132,得b=2又由c +⨯+=12122,得1-=c【范例导析】例1.下列函数的导数:①2(1)(231)y x x x =++- ②y=③()(cos sin )xf x e x x =⋅+分析:利用导数的四则运算求导数。
解:①法一:13232223-++-+=x x x x x y 125223-++=x x x ∴ 26102y x x '=++法二:)132)(1()132()1(22'-+++-+'+='x x x x x x y =1322-+x x +)1(+x )34(+x26102x x =++② 231212332----+-=xxxx y∴ 252232123233---+-+='xxxx y③()f x '=e -x(cos x +sin x )+e -x(-sin x +cos x )=2e -xcos x ,点评:利用基本函数的导数、导数的运算法则及复合函数的求导法则进行导数运算,是高考对导数考查的基本要求。
例2. 如果曲线103-+=x x y 的某一切线与直线34+=x y 平行,求切点坐标与切线方程. 分析:本题重在理解导数的几何意义:曲线()y f x =在给定点00(,())P x f x 处的切线的斜率0()k f x '=,用导数的几何意义求曲线的斜率就很简单了。
解: 切线与直线34+=x y 平行, 斜率为4又切线在点0x 的斜率为0320(10)31x x x x y x x x ==''=+-=+∵ 41320=+x ∴10±=x ∴⎩⎨⎧-==8100y x 或⎩⎨⎧-=-=12100y x∴切点为(1,-8)或(-1,-12)切线方程为)1(48-=+x y 或)1(412+=+x y 即124-=x y 或84-=x y点评:函数导数的几何意义揭示了导数知识与平面解析几何知识的密切联系,利用导数能解决许多曲线的切线问题,其中寻找切点是很关键的地方。
变题:求曲线32y x x =-的过点(1,1)A 的切线方程。
答案:20,5410x y x y +-=--=点评:本题中“过点(1,1)A 的切线”与“在点(1,1)A 的切线”的含义是不同的,后者是以A 为切点,只有一条切线,而前者不一定以A 为切点,切线也不一定只有一条,所以要先设切点,然后求出切点坐标,再解决问题。
【反馈演练】1.一物体做直线运动的方程为21s t t =-+,s 的单位是,m t 的单位是s ,该物体在3秒末的瞬时速度是5/m s 。
2.设生产x 个单位产品的总成本函数是2()88xC x =+,则生产8个单位产品时,边际成本是 2 。
3.已知函数f (x )在x =1处的导数为3,则f (x )的解析式可能为 (1) 。
(1)f (x )=(x -1)2+3(x -1) (2)f (x )=2(x -1) (3)f (x )=2(x -1)2 (4)f (x )=x -14.若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为430x y --=。
5.在函数x x y 83-=的图象上,其切线的倾斜角小于4π的点中,坐标为整数的点的个数是 3 。
6.过点(0,-4)与曲线y =x 3+x -2相切的直线方程是 y =4x -4 . 7. 求下列函数的导数:(1)y=(2x 2-1)(3x+1) (2)x x y sin 2= (3))1ln(2x x y ++=(4)11-+=xxe e y (5)xx x x y sin cos ++=(6)xx x y cos sin 2cos -=解:(1)34182-+='x x y , (2)x x x x y cos sin 22+='; (3)211xy +=', (4)2)1(2--='xx e ey ;(5)2)sin (1cos sin sin cos x x x x x x x x y +--+--=', (6)x x y cos sin -='.8 已知直线1l 为曲线22-+=x x y 在点(0,2)-处的切线,2l 为该曲线的另一条切线,且21l l ⊥(Ⅰ)求直线2l 的方程;(Ⅱ)求由直线1l ,2l 和x 轴所围成的三角形的面积解: 设直线1l 的斜率为1k ,直线2l 的斜率为2k ,'21y x =+,由题意得10'|1x k y ===,得直线1l 的方程为2y x =-122111l l k k ⊥∴=-=-211,1x x +=-=-令得,212,2x y x x y =-=+-=-将代入得2l ∴与该曲线的切点坐标为(1,2),A --由直线方程的点斜式得直线2l 的方程为:3y x =--(Ⅱ)由直线1l 的方程为2y x =-,令0=2y x =得: 由直线2l 的方程为3y x =--,令0=3y x =-得:由23y x y x =-⎧⎨=--⎩得:52y =-设由直线1l ,2l 和x 轴所围成的三角形的面积为S ,则:1525[2(3)]224s =⋅-⋅--=第2课 导数的应用A【考点导读】1. 通过数形结合的方法直观了解函数的单调性与导数的关系,能熟练利用导数研究函数的单调性;会求某些简单函数的单调区间。
2. 结合函数的图象,了解函数的极大(小)值、最大(小)值与导数的关系;会求简单多项式函数的极大(小)值,以及在指定区间上的最大(小)值。
【基础练习】1.若函数()f x mx n =+是R 上的单调函数,则,m n 应满足的条件是 0,m n R ≠∈ 。
2.函数5123223+--=x x x y 在[0,3]上的最大值、最小值分别是 5,-15 。
3.用导数确定函数()sin ([0,2])f x x x π=∈的单调减区间是3[,]22ππ。
4.函数1()sin ,([0,2])2f x x x x π=+∈的最大值是π,最小值是0。
5.函数2()xf x x e =⋅的单调递增区间是 (-∞,-2)与(0,+ ∞) 。
【范例导析】例1.32()32f x x x =-+在区间[]1,1-上的最大值是 2 。
解:当-1≤x <0时,()f x '>0,当0<x ≤1时,()f x '<0, 所以当x =0时,f (x )取得最大值为2。
点评:用导数求极值或最值时要掌握一般方法,导数为0的点是否是极值点还取决与该点两侧的单调性,导数为0的点未必都是极值点,如:函数3()f x x =。
例2. 求下列函数单调区间:(1)5221)(23+--==x x x x f y (2)xx y 12-=(3)x xky +=2)0(>k (4)x x y ln 22-=解:(1)∵232--='x x y )1)(23(-+=x x ∴)32,(--∞∈x ),1(∞+ 时0>'y )1,32(-∈x 0<'y ∴ )32,(--∞,),1(∞+↑ )1,32(-↓(2)221xx y +=' ∴ )0,(-∞,),0(∞+↑(3)221xk y -= ∴ ),(k x --∞∈),(∞+k 0>'y , ),0()0,(k k x -∈0<'y∴ ),(k --∞,↑∞+),(k )0,(k -,),0(k ↓(4)xx xx y 14142-=-='定义域为),0(∞+ )21,0(∈x 0<'y ↓ ),21(∞+∈x0>'y ↑点评:熟练掌握单调性的求法,函数的单调性是解决函数的极值、最值问题的基础。
