6、有理数的乘方专项练习题
有理数的乘除乘方运算(含答案)

有理数的运算(乘、除、乘方)教学目的:1、理解有理数的乘法法则;掌握异号两数的乘除运算的规律;2、会进行有理数的乘法、除法、乘方的运算,能灵活运用运算律进行简化运算。
教学重点:1、有理数的乘法、除法法则;2、熟练的进行有理数乘法、除法、乘方运算。
教学难点:若干个有理数相乘,积的符号的确定,乘方的符号确定。
有理数的乘法有理数的乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。
例1:计算(1) )3()5(-⨯-(2) 4)7(⨯-(3))109()35(-⨯-例题目的:掌握有理数的乘法法则。
有理数乘法法则的推广:(1)几个不等于0的数相乘,积的符号由负因数的个数决定。
当负数的个数为奇数时,积为负,当负因数为偶数个时,积为正。
(2)几个数相乘,有一个因数为0,积为0。
例2:(1))4()37(21-⨯-⨯ (2) )253()5.2()94(321-⨯-⨯-⨯例题目的:会算两个以上有理数的乘法,并能判定积的符号。
有理数乘法的运算律:在有理数运算中,乘法的交换律,结合律以及乘法对加法的分配律仍然成立。
乘法交换律:两个数相乘,交换因数的位置,积不变,用式子表示为a·b =b·a 乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变.用式子表示成(a·b)·c =a·(b·c)乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘. 用字母表示成:a(b +c)=a·b +a·c例3:计算:(1) 25.18)5.4(⨯⨯- (2) )]23()3[()2(-+-⨯-(3) )8(161571-⨯例题目的:掌握有理数乘法的运算律。
有理数的除法法则1:两个有理数相除,同号得正,异号向负,并把绝对值相除。
0除以任何非0的数都得0。
倒数与负倒数的概念:乘积为1的两个有理数互为倒数,即若a , b 互为倒数,则1=ab ;乘积为1-的两个有理数互为负倒数,即若b a ,互为负倒数,则1-=⋅b a法则2:除以一个数等于乘以这个数的倒数,即a ÷b )0(1≠⋅=b ba 例4:1. 求下列各数的倒数,负倒数。
有理数的乘方

n a
指数
n是相同 n是相同 因数的个数
幂
读作: 次方” 读作 “a的n次方”或“a的n次 的 次方 的 次 n a 叫做底数 n a 中, 叫做底数, 叫做 底数, 在 幂”
指数。 指数。
注意: 注意:
• 负数的乘方,在书写时一定要把 负数的乘方, 整个负数(连同符号), ),用小括号 整个负数(连同符号),用小括号 括起来.分数的乘方, 括起来.分数的乘方,在书写的时 一定要把整个分数 整个分数用小括号括起 一定要把整个分数用小括号括起 来.
• 区分:教案
口答练习一 1)在
12
10 中,12是
底 数,10是 ;
指 数,读作 12的10次方
7
2 2) 2 的底数是 3 ,指数是 7 , 3 2 的7次方 ; 读作 3
退出
返回 上一张下一张
3)在 (− 3) 中,-3是 底 数,16是 指 数,
16
读作
-3的16次方
作业
•习题1.5 习题1.5 习题 •1、3、7、8、(写在书上) 、(写在书上 写在书上) 1 •三级训练:做完 三级训练: 三级训练 •习题1.4做完(写在书上) 习题1.4做完( 习题1.4做完 写在书上)
有理数的乘方
练习一(课前测评) 1、边长为 a 的正方形的面积为 a ; 2、棱长为 a 的正方体的体积为 a ; 3、(-2)×(-2)×(-2)= -8 ; 4、(-1)×(-2)×(-3)×(-4)×5= 120 ; 5、(-1)×(-1)×(-1)×(-1)×(-1)= -1 。
3
2
a a
3、 (− 2) 的结果是 负 数(填“正”或 “负”);
15
4、计算: (− 2) =
有理数的加减乘除乘方混合运算专题训练(带答案)
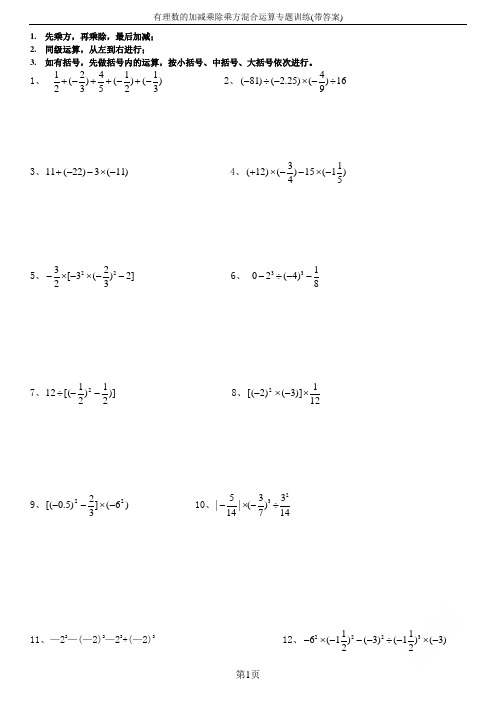
1. 先乘方,再乘除,最后加减;2. 同级运算,从左到右进行;3. 如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
1、12411 ()()()23523+-++-+-2、4(81)( 2.25)()169-÷-⨯-÷3、11(22)3(11)+--⨯-4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、 33102(4)8-÷--7、)]21)21[(122--÷ 8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯-- 10、23533||()14714-⨯-÷223 3 222113、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、-10 + 8÷(-2 )2 -(-4 )×(-3 ) 16、-49 + 2×(-3 )2 + (-6 )÷(-91)17、-14 + ( 1-0.5 )×31×[2×(-3)2] 18、(-2)2-2×[(-21)2-3×43]÷51.19、)8()4()6(52-÷---⨯ 20、0)132()43(2⨯+-+-35722523、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6-(-12)÷2)2(- 26、(-48)÷ 8 -(-5)÷2)21(-27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯- 30、(-5)×6+(-125) ÷(-5)331、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+-1、【基础题】计算:(1)618-÷)(-)(-312⨯; (2))(-+51232⨯;(3))(-)(-49⨯+)(-60÷12; (4)23)(-×[ )+(--9532 ].(1))(-)+(-2382⨯; (2)100÷22)(--)(-2÷)(-32;(3))(-4÷)(-)(-343⨯; (4))(-31÷231)(--3214)(-⨯.(1)36×23121)-(; (2)12.7÷)(-1980⨯;(3)6342+)(-⨯; (4))(-43×)-+(-31328;(5)1323-)(-÷)(-21; (6)320-÷34)(-81-;(7)236.15.02)-(-)(-⨯÷22)(-; (8))(-23×[ 2322-)(- ];(9)[ 2253)-(-)(- ]÷)(-2; (10)16÷)(-)-(-)(-48123⨯.(1)11+(-22)-3×(-11); (2)0313243⨯⨯)-(-)(-;(3)2332-)(-; (4)23÷[ )-(-)(-423];(5))-(8743÷)(-87; (6))+()(-654360⨯;(7)-27+2×()23-+(-6)÷()231-; (8))(-)-+-(-4151275420361⨯⨯.(1))-(-258÷)(-5; (2)-33121)(--⨯;(3)223232)-(-)(-⨯⨯; (4)0132432⨯⨯)+(-)(-;(5))(-+51262⨯; (6)-10+8÷()22--4×3;(7)-51-()()[]55.24.0-⨯-; (8)()251--(1-0.5)×31;(1)(-8)×5-40; (2)(-1.2)÷(-13)-(-2);(3)-20÷5×14+5×(-3)÷15; (4)-3[-5+(1-0.2÷35)÷(-2)];(5)-23÷153×(-131)2÷(132)2; (6)-52+(1276185+-)×(-2.4)参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-20 16、23 17、2 18、24 19、-28 20、9/16 21、1 22、10 23、-1/12 24、104/3 25、9 26、14 27、-31 28、-81又1/81 29、-9 30、-29 31、-1/5 32、91、【答案】 (1)17; (2)511; (3)31; (4)-112、【答案】 (1)-10; (2)22; (3)-16; (4)-253、【答案】 (1)1; (2)0; (3)42; (4)423; (5)18; (6)0; (7)-4.64;(8)37; (9)8; (10)-25.4、【答案】 (1)22; (2)0; (3)-17; (4)-423; (5)71; (6)-95; (7)-85;(8)6 .5、【答案】 (1)3; (2)1; (3)-54; (4)0; (5)526; (6)-20; (7)-2; (8)-67. 6、【答案】(1)-80; (2)5.6; (3)-2; (4)16; (5)-516; (6)-2.9复习 有理数的乘除、乘方运算测试题一、填空题(每小题3分,共30分) 1.3×(-2)=________,(-6)×(-31)=________. 2.(-3)2的底数是________,结果是________;-32的底数是________,结果是________.3.(-61)÷(+23)=________;-493÷(-176)=________;(+8)÷(-41)=________.4.23×(-41)3=________;(-91)÷(+34)2=________.5.(-32)×________=1;(-32)×________=-16.-65×(-2.4)×(-53)=________.7.-32×(-5)2÷(-21)3=________.8.我国台湾省的面积约为3600平方公里,用科学记数法表示为________. 9.+121的倒数是________;________的倒数是-54. 10.用“>”“<”填空: ①23________22②(21)2________(21)3③32________22④(-2)3________(-2)2二、判断题(每小题1分,共5分) 11.零除以任何数都得零( )12.互为相反数的两个数的积为负数( ) 13.如果ab >0,则a >0且b >0( )14.1除以一个非零数的商叫做这个数的倒数( )15.(-3)5表示5个-3相乘( )三、选择题(每小题3分,共21分) 16.下列说法,其中错误的有①一个数与1相乘得原数;②一个数乘以-1得原数的相反数;③0乘以任何数得0;④同号两数相乘,符号不变.A .1个B .2个C .3个D .4个17.下列各对数:①1与1;②-1与1;③a -b 与b -a ;④-1与-1;⑤-5与|6|,其中互为倒数的是A .①②③B .①③⑤C .①③④D .①④ 18.下列各题中两个式子的值相等的是A .-23与(-2)3B .32与23C .(-2)2与 -22D .|-2|与-|-2| 19.下列结论中,其中正确的个数为①0的倒数是0;②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等;③其倒数等于自身的数是±1;④若a ,b 互为倒数,则-ab=-1.A .4B .3C .2D .1 20.下列各式中结果大于0的是A .1-910×3B .(1-910)×3C .1-(9×3)10D .(1-9)10×3 21.下列说法中正确的是 A .一个数的平方必为正数B .一个数的平方必小于这个数的绝对值C .一个数的平方必大于这个数D .一个数的平方不可能为负数22.用科学记数法表示的数2.89×104,原来是A .2890B .2890000C .28900D .289000四、计算题(共35分)23.(3分)(-3)×(-5)×(+12)×(-21) 24.(3分)-6÷(+3)÷(-4)×(+2) 25.(3分)-5-6÷(-3)26.(3分)(-81)÷241×91÷(-16)27.(3分)-22×(-3)÷5428.(3分)(-1)2000×(-1)2001×(-1)2002÷(-1)200329.(3分)(-2)×(-2001)×[-21-(-21)]×1-200230.(3分)-)45()45(5222-÷-⨯⨯31.(3分)(-5)2÷5×632.(3分)(-2.5)÷(-310)×(-3)33.(5分)30×(21-31+53-109)五、解答题(9分)34.已知A=a+a 2+a 3+……+a 2000(1)若a =1,求A 的值.(2)若a =-1,求A 的值.参考答案一、1.-6 2 2.-3 9 3 -9 3.-91 913 -32 4.-81 -161 5.-23 23 6.-1.2 7.1800 8.3.6×103平方公里 9.32 -141 10.> > > < 二、11.× 12.× 13.× 14.√ 15.√三、16.A 17.D 18.A 19.B 20.D 21.D 22.C四、23.-90 24.1 25.-3 26.41 27.15 28.1 29.-2002 30.1 31.30 32.-49 33.-4 五、34.(1)2000 (2)0。
有理数的乘方专项小练习(附详细答案)

《有理数的乘方》练习题一、 填空题1、6(2)-中指数为 ,底数为 ,结果为 ;62-中指数为 ,底数为 ,结果为 。
2、平方得641的数是 ,立方得641的数是 。
3、一个数的15次幂是负数,那么这个数的1999次幂是 数。
4、(-9)²表示的意义是 ;-9²表示的意义是 。
5、平方等于本身的数是 ;立方等于本身的数是 ;相反数等于本身的数是 ;倒数等于本身的数是 ;绝对值等于本身的数是 。
6、我国研制的“曙光3000超级服务器”,它的峰值计算速度达到403,200,000,000次/秒,用科学记数法可表示为 次/秒.二、 选择题7. 任何一个有理数的2次幂是( )A. 正数B. 负数C. 非正数D. 非负数8. 20012002(1)(1)-+-的结果是( )A. -1B. 0C. 1D. 29. 一个数的平方等于它的倒数,这个数一定是( )A. 0B. 1C. –1D. ±110、如果一个数的平方等于它的绝对值,那么这个数是( )A. 0B. 1C. -1D. 0、1、-111、人类的遗传物质就是DNA ,人类的DNA 是很长的链,最短的22号染色体也长达30000000个核苷酸,30000000用科学记数法表示为( )A.7103⨯B.8103⨯C.6103⨯D.8103.0⨯12、下列各组数中,不相等的一组是( )A. (—2)3和—23B. (—2)2和—22C. (—2)4和—24D.│—2│3和│2│3三、解答题13、 计算(1)4(2)-- (2)2005(1)- (3)3( 1.5)--(4)6200.53-÷ (5)560.25(4)-⨯- (6)()1-2003+()20041-《有理数的乘方》练习题三、 填空题2、6(2)-中指数为 6 ,底数为 -2 ,结果为 64 ;62-中指数为 6 ,底数为 2 ,结果为 -64 。
2、平方得641的数是 81± ,立方得641的数是 41 。
有理数的乘方练习题(含参考答案)

有理数的乘方练习题(含参考答案)一.选择题 1、118表示( )A 、11个8连乘B 、11乘以8C 、8个11连乘D 、8个别1相加2、-32的值是( )A 、-9B 、9C 、-6D 、63、下列各对数中,数值相等的是( )A 、 -32与 -23B 、-23与 (-2)3C 、-32与(-3)2D 、(-3×2)2与-3×224、下列说法中正确的是( )A 、23表示2×3的积 B 、任何一个有理数的偶次幂是正数 C 、-32与 (-3)2互为相反数 D 、一个数的平方是94,这个数一定是325、下列各式运算结果为正数的是( )A 、-24×5 B 、(1-2)×5 C 、(1-24)×5D 、1-(3×5)66、如果一个有理数的平方等于(-2)2,那么这个有理数等于( ) A 、-2 B 、2 C 、4D 、2或-27、一个数的立方是它本身,那么这个数是( ) A 、 0 B 、0或1 C 、-1或1D 、0或1或-1 8、如果一个有理数的正偶次幂是非负数,那么这个数是( )A 、正数B 、负数C 、 非负数D 、任何有理数9、-24×(-22)×(-2) 3=( )A 、 29B 、-29C 、-224D 、22410、两个有理数互为相反数,那么它们的n 次幂的值( ) A 、相等 B 、不相等 C 、绝对值相等D 、没有任何关系11、一个有理数的平方是正数,则这个数的立方是( ) A 、正数 B 、负数 C 、正数或负数 D 、奇数 12、(-1)2001+(-1)2002÷1-+(-1)2003的值等于( )A 、0B 、 1C 、-1D 、2二、填空题1、(-2)6中指数为 ,底数为 ;4的底数是 ,指数是 ;523⎪⎭⎫⎝⎛-的底数是 ,指数是 ,结果是 ;2、根据幂的意义,(-3)4表示 ,-43表示 ; 3、平方等于641的数是 ,立方等于641的数是 ; 4、一个数的15次幂是负数,那么这个数的2003次幂是 ; 5、平方等于它本身的数是 ,立方等于它本身的数是 ;6、=⎪⎭⎫ ⎝⎛-343 ,=⎪⎭⎫⎝⎛-343 ,=-433 ; 7、()372⋅-,()472⋅-,()572⋅-的大小关系用“<”号连接可表示为 ;8、如果44a a-=,那么a 是 ;9、()()()()=----20022001433221 ;10、如果一个数的平方是它的相反数,那么这个数是 ;如果一个数的平方是它的倒数,那么这个数是 ;11、若032>b a -,则b 0计算题1、()42-- 2、3211⎪⎭⎫⎝⎛3、()20031- 4、()33131-⨯--5、()2332-+- 6、()2233-÷-7、()()3322222+-+-- 8、()34255414-÷-⎪⎭⎫ ⎝⎛-÷9、()⎪⎭⎫ ⎝⎛-÷----721322246 10、()()()33220132-⨯+-÷---三、解答题1、有一张厚度是0.2毫米的纸,如果将它连续对折10次,那么它会有多厚?2、某种细菌在培养过程中,每半小时分裂一次(由一个分裂成两个),若这种细菌由1个分裂为16个,则这个过程要经过多长时间?3、你吃过“手拉面”吗?如果把一个面团拉开,然后对折,再拉开,再对折,……如此往复下去,对折10次,会拉出多少根面条?探究创新乐园 1、你能求出1021018125.0⨯的结果吗?2、若a 是最大的负整数,求2003200220012000a a a a +++的值。
有理数的乘方典型练习题

有理数的乘方典例解析及练习【知识梳理】1.乘方的有关概念.(1)求n 个相同因数a 的积的运算叫乘方,乘方的结果叫幂.a 叫底数,n 叫指数,a n读作:a 的n 次幂(a 的n 次方). (2)乘方的意义:a n表示n 个a 相乘.n an a a a a a =⨯⨯⨯⨯个(3)写法的注意:当底数是负数或分数时,底数必然要打括号,不然意义就全变了.如:(32-)2=(32-)×(32-),表示两个32-相乘.而322-=322⨯-,表示2个2相乘的积除以3的相反数. 2.a n 与-a n的区别.(1)a n表示n 个a 相乘,底数是a ,指数是n ,读作:a 的n 次方.(2)-a n表示n 个a 乘积的相反数,底数是a ,指数是n ,读作:a 的n 次方的相反数. 如:(-2)3底数是-2,指数是3,读作(-2)的3次方,表示3个(-2)相乘. (-2)3=(-2)×(-2)×(-2)=-8.-23底数是2,指数是3,读作2的3次方的相反数.-23=-(2×2×2)=-8. 注:(-2)3与-23的结果尽管都是-8,但表示的含义并非同. 3.乘方运算的符号规律.(1)正数的任何次幂都是正数. (2)负数的奇次幂是负数. (3)负数的偶次幂是正数.(4)0的奇数次幂,偶次幂都是0.因此,任何数的偶次幂都是正数或0.4.乘方如何运算?乘方运算确实是依照乘方的意义把它转化为乘法进行计算.如:33=333=27.5. 把一个大于 10 的数记成 a10n的形式,其中 a 是整数数位只有一名的数,这种记数法叫做科学记数法。
注意:一个数的科学记数法中,10 的指数比原数的整数位数少 1,如原数有 8 位整数,指数确实是7。
【重点难点】有理数乘方的意义及乘方的运算。
【典例解析】例1、计算:(1)35;(2)(—2)4;(3)—24;(4)—(—4)2(5)3×52.解:(1)35=3×3×3×3×3=243;(2)(—2)4=(—2)×(—2)×(—2)×(—2)=16;(3)—24=—2×2×2×2=—16;(4)—(—4)2=—(—4)×(—4)×(—4)×(—4)=—256;(5)3×52=3×5×5=75.说明:计算乘方,必然要分清底数和指数,专门注意(2)、(3)两小题的区别.例2、计算:(1)3×23(2)(2×3)3 (3)(-32)3解:(1)3×23=3×2×2×2=24(2)(2×3)3=63=6×6×6=216(3)(-32)3=(-6)3=(-6)(-6)(-6)=-216注意:运算顺序是:先算乘方,再算乘除,最后算加减,若是有括号的,要先算括号里面的。
有理数的乘方练习题精选及答案

有理数的乘方一.选择题 1、118表示( )A 、11个8连乘B 、11乘以8C 、8个11连乘D 、8个别1相加 2、-32的值是( )A 、-9B 、9C 、-6D 、6 3、下列各对数中,数值相等的是( ) A 、 -32与 -23B 、-23与 (-2)3C 、-32与(-3)2D 、(-3×2)2与-3×224、下列说法中正确的是( )A 、23表示2×3的积 B 、任何一个有理数的偶次幂是正数 C 、-32与 (-3)2互为相反数 D 、一个数的平方是94,这个数一定是32 5、下列各式运算结果为正数的是( )A 、-24×5 B 、(1-2)×5 C 、(1-24)×5D 、1-(3×5)66、如果一个有理数的平方等于(-2)2,那么这个有理数等于( ) A 、-2 B 、2 C 、4D 、2或-2 7、一个数的立方是它本身,那么这个数是( ) A 、 0 B 、0或1 C 、-1或1D 、0或1或-1 8、如果一个有理数的正偶次幂是非负数,那么这个数是( ) A 、正数 B 、负数 C 、 非负数 D 、任何有理数 9、-24×(-22)×(-2) 3=( )A 、 29B 、-29C 、-224D 、22410、两个有理数互为相反数,那么它们的n 次幂的值( ) A 、相等 B 、不相等 C 、绝对值相等D 、没有任何关系 11、一个有理数的平方是正数,则这个数的立方是( ) A 、正数 B 、负数 C 、正数或负数 D 、奇数 12、(-1)2001+(-1)2002÷1-+(-1)2003的值等于( )A 、0B 、 1C 、-1D 、2 二、填空题1、(-2)6中指数为 ,底数为 ;4的底数是 ,指数是 ;523⎪⎭⎫⎝⎛-的底数是 ,指数是 ,结果是 ;2、根据幂的意义,(-3)4表示 ,-43表示 ; 3、平方等于641的数是 ,立方等于641的数是 ;4、一个数的15次幂是负数,那么这个数的2003次幂是 ;5、平方等于它本身的数是 ,立方等于它本身的数是 ;6、=⎪⎭⎫ ⎝⎛-343 ,=⎪⎭⎫⎝⎛-343 ,=-433 ; 7、()372⋅-,()472⋅-,()572⋅-的大小关系用“<”号连接可表示为 ;8、如果44a a -=,那么a 是 ;9、()()()()=----20022001433221 ;10、如果一个数的平方是它的相反数,那么这个数是 ;如果一个数的平方是它的倒数,那么这个数是 ;11、若032>b a -,则b 0 计算题1、()42-- 2、3211⎪⎭⎫⎝⎛3、()20031- 4、()33131-⨯--5、()2332-+- 6、()2233-÷-7、()()3322222+-+-- 8、()34255414-÷-⎪⎭⎫ ⎝⎛-÷9、()⎪⎭⎫ ⎝⎛-÷----721322246 10、()()()33220132-⨯+-÷---解答题1、按提示填写:2、有一张厚度是0.2毫米的纸,如果将它连续对折10次,那么它会有多厚?3、某种细菌在培养过程中,每半小时分裂一次(由一个分裂成两个),若这种细菌由1个分裂为16个,则这个过程要经过多长时间?4、你吃过“手拉面”吗?如果把一个面团拉开,然后对折,再拉开,再对折,……如此往复下去,对折10次,会拉出多少根面条?探究创新乐园 1、你能求出1021018125.0⨯的结果吗?2、若a 是最大的负整数,求2003200220012000a a a a +++的值。
1.6有理数的乘方(6大题型提分练)2024-2025学年七年级数学上册同步精品课堂「含答案」

1.6 有理数的乘方题型一 有理数幂的概念1.底数是35,指数是2的幂写成 .2.代数式6n 的意义可以是( )A .6个n 相加B .6个n 相乘C .n 个6相加D .n 个6相乘3.对于式子()32-,下列说法不正确的是( )A .指数是3B .底数是2-C .结果为8-D .表示3与2-相乘4.42-的底数、指数、结果分别是( )A .2416--,,B .2416-,,C .2,4,16D .2416-,,5.35-表示( )A .3个5-相乘B .3个5相乘的相反数C .5个3-相乘D .5个3相乘的相反数6.下列说法正确的是( )A .82-的底数是2-B .52表示5个2相加C .3(3)-与33-意义相同D .323-的底数是2题型二 有理数的乘方运算7.()23-=.8.计算:20241-= .9.下列各组的两个数中,运算后结果相等的是( )A .23-与()23-B .35与53C .37-与()37-D .334æö-ç÷èø与33410.计算:(1)2023(1)-= ;(2)2(0.2)-= ;(3)212æö-=ç÷èø;(4)4112æö-=ç÷èø .11.计算:(1)3(3)--(2)234æö-ç÷èø;(3)323æö-ç÷èø(4)()20151-.题型三 有理数乘方的符号规律12.在()20211-,32-,()117-,0中,非负数有( )A .1个B .2个C .3个D .4个13.下列各数()33-,(3)--,()43-,3--,33-中,负数有( )A .2个B .3个C .4个D .5个14.数学课上,李老师在黑板上写了一道题目:当n 为正整数时,计算()()111nn +-+-的结果.琪琪说:因为n 的值不确定,所以()()111nn +-+-的结果也不能确定;聪聪说:()()111nn +-+-的结果是不变的,可以求出.你同意谁的说法?请给出你的答案并说明理由.题型四 有理数乘方错解复原15.老师出了一道计算题,计算:3123æö-ç÷èø.嘉嘉的计算过程如下:解:原式331(2)3æö=-´ç÷èø(第一步)()1827=-´(第二步)827=-.(第三步)(1)请问嘉嘉的计算过程是从第几步开始出错的?(2)请把正确的计算过程写出来.题型五 有理数乘方在生活中的应用有理数乘法有关的新定义问题16.如果10b n =,那么b 为n 的“劳格数”,记为()b d n =.由定义可知:10b n =与()b d n =表示b 、n 两个量之间的同一关系.(1)根据“劳格数”的定义,填空:(10)d = ,2(10)d -=______;(2)“劳格数”有如下运算性质:若m 、n 为正数,则()()()d mn d m d n =+,()()()md d m d n n =-;根据运算性质,填空:3()()d a d a =________.(a 为正数)(3)若2d ()0.3010=,分别计算4d ();5d ().题型六 科学记数法的相关问题17.设n 是一个正整数,则10n 是( )A .10个n 相乘所得的积B .一个()1n -位整数C .一个n 位整数D .一个1后面有n 个0的数18.今年我国春节档电影票房达80.16亿元,其中数据80.16亿用科学记数法表示为( )A .880.1610´B .88.01610´C .100.801610´D .98.01610´19.近十年来,我国扎实开展国土绿化行动,持续推进科学绿化,累计完成国土绿化面积1680000000亩,将数据“1680000000”用科学记数法表示为( )A .81.6810´B .91.6810´C .816.810´D .100.16810´20.将12000000-用科学记数法可表示为( )A .71.210-´B .81.210-´C .61210-´D .80.1210-´21.一个数用科学记数法表示为62.34510´,则这个数有 个整数位.22.将下列用科学记数法表示的数还原成原数.(1)51.210´;(2)72.310´;(3)83.610´;(4)64.210-´.23.已知22,9x y ==,且x y >,求x y +的值.24.已知()23a -与4b +互为相反数,求()202323b a a b -++的值.25.阅读下面的材料,然后按照材料中提供的方法计算.计算:1220171222++++L .解:设1220171222=++++L S ,则123201822222=++++L S ,所以()()1232018122017222221222-=++++-++++L L S S 123201812201722221222=++++-----L L 201821=-,即1220182018122221++++=-L .按照上面的方法,计算:220191333++++L .26.你能比较20232022和20222023的大小吗?为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比较1n n +和(1)n n +的大小(n 为正整数),我们从1,2,3n n n ===…这些简单的情况入手,从中发现规律,经过归纳,猜出结论(1)通过计算,比较下列各组数字大小:①21__________12; ②32__________23; ③43__________34;④54__________45; ⑤65__________56; ⑥76__________67…(2)将第(1)题的结果进行归纳,你能得出什么结论?(3)根据上面的归纳猜想得到的结论,试比较两个数的大小:20232022__________20222023(填><“”“”或“”=).1.235æöç÷èø【分析】本题考查了幂的概念,根据幂的书写规则即可求解.注意分数为底时,需要把底数加括号.【详解】解:底数为35,指数为2,写成235æöç÷èø,故答案为:235æöç÷èø.2.D【分析】根据幂的定义,乘法的定义,依次判断,即可求解,本题考查了,幂的概念理解,解题的关键是:理解幂的概念.【详解】解:A 、6个n 相加,表示为:6n ,不符合题意,B 、6个n 相乘,表示为:6n ,不符合题意,C 、n 个6相加,表示为:6n ,不符合题意,D 、n 个6相乘,表示为:6n ,符合题意,故选:D .3.D【分析】本题考查有理数的乘方,根据有理数的乘方的定义解答.【详解】解:式子()32-中:指数是3,故A 选项正确;底数是2-,故B 选项正确;结果为8-,故C 选项正确;表示3个2-相乘,故D 选项错误;故选D .4.D【分析】本题主要考查了有理数幂的概念,有理数的乘方计算,对于式子()0ma a ¹,其中a叫做底数,m 叫做指数,据此结合有理数乘方计算法则求解即可.【详解】解:42-的底数是2,指数是4,其结果为16-,故选:D .5.B【分析】本题考查有理数幂的概念理解,掌握()0na a ¹表示n 个a 相乘,进行判断即可.【详解】解:35-表示3个5相乘的相反数;故选B .6.D【分析】本题主要考查了有理数的乘方.根据乘方的意义,进行判断即可.【详解】解:A 、82-Q 的底数是2,∴此选项的说法错误,故不符合题意;B 、52Q 表示5个2相乘,∴此选项的说法错误,故不符合题意;C 、3(3)-Q 表示3个(3)-相乘,33-表示3个3相乘的相反数,∴它们表示的意义不同,故不符合题意;D 、Q 323-的底数是2,∴此选项的说法正确,故此选项符合题意,故选:D .7.9【分析】本题考查了乘方的运算法则,解题的关键是掌握运算法则,正确的进行解题.根据乘方的运算法则,分别进行计算,即可得到答案.【详解】解:()239-=,故答案为:9.8.1-【分析】本题考查了有理数的乘方,熟练掌握并灵活应用是解题的关键.根据有理数的乘方法则计算即可.【详解】解:202411-=-,故答案为:1-.9.C【分析】根据有理数的乘方的定义对各选项分析判断利用排除法求解.【详解】A 、239-=-,()239-=,不相等,故A 选项错误;B 、35125=,53243=,不相等,故B 选项错误;C 、37353-=-,()37353-=-,相等,故C 选项正确;D 、3327464æö-=-ç÷èø,332744=,不相等,故D 选项错误.故选:C .【点睛】此题考查有理数的乘方,解题的关键在于掌握运算法则.10.(1)1-(2)0.04(3)14(4)8116【分析】根据有理数的乘方运算计算即可.【详解】(1)解:2023(1)1-=-;故答案为:1-;(2)解:224=0(0.2).20.0-=;故答案为:0.04;(3)解:2241112=2-æèöç÷èøæö=ç÷ø;故答案为:14;(4)解:444381==216111122æöæö-æöç÷èø=ç÷ç÷èøèø.故答案为:8116.【点睛】本题考查了有理数的乘方运算,熟练掌握有理数的乘方运算法则是解题关键.11.(1)27(2)916(3)827-(4)1-【分析】可根据乘方的意义,先把乘方转化为乘法,再根据乘法的运算法则来计算;或者先用符号法则来确定幂的符号,再用乘法求幂的绝对值.【详解】(1)3(3)(3)(3)(3)(27)27---´-´--=-=-=(2)2333944416æöæöæö-=-´-=ç÷ç÷ç÷èøèøèø(3)322228333327æöæöæöæö-=-´-´-=-ç÷ç÷ç÷ç÷èøèøèøèø(4)()201511-=-【点睛】本题主要考查有理数乘方的运算,乘方的运算可以利用乘法的运算来进行.负数的奇数次幂是负数,负数的偶数次幂是正数;1-的奇数次幂是1-,1-的偶数次幂是1.12.A【分析】本题考查有理数乘方中的符号问题,判断每个数的正负号即可求解.【详解】解:∵()2021110-=-<,302-<,()1111770-=-<,∴()20211-,32-,()117-,0中,只有0是非负数.故选:A .13.B【分析】根据有理数乘方符号法则:负数的奇次幂是负数,负数的偶次幂是正数,以及相反数和绝对值去判断负数的个数.【详解】()3327-=-,(3)3--=,()4381-=,33--=-,3327-=-,所以负数有3个.故选:B【点睛】本题主要考查了有理数的乘方,以及绝对值和相反数,牢记乘方的符号法则是解题的关键.14.同意聪聪的说法,()()1110nn +-+-=,理由见解析【分析】分类讨论,分别把当n 为偶数时和当n 为奇数时的两种情况列出来,代入式子求解即可.【详解】解:同意聪聪的说法,()()1110nn +-+-=,理由如下:∵n 为正整数,∴n 可能为偶数,也可能为奇数,当n 为偶数时,1n +为奇数,此时()()()111110n n +-+-=+-=,当n 为奇数时,1n +为偶数,此时()()()111110nn +-+-=-+=,∴()()111nn +-+-的结果是不变的,可以求出,∴聪聪的说法是正确的.【点睛】本题考查了有理数的乘方,对n 进行分类讨论是解题的关键.15.(1)第一步开始出错(2)过程见解析【分析】(1)根据题意可直接进行求解;(2)根据有理数的乘方运算可进行求解【详解】(1)嘉嘉的计算过程是从第一步开始出错的.(2)解:3333773433327123æö=-=-=-çæö-÷øèçè÷ø【点睛】本题主要考查有理数的乘方运算,熟练掌握有理数的乘方运算是解题的关键.16.(1)1,2-(2)3(3)0.6020,0.699.【分析】本题考查新定义,有理数的运算;理解题意,将新定义转化为同底数幂的乘除法、幂的乘方与积的乘方运算是解题的关键.(1)1010b =,1b =,则有(10)1d =;21010b -=,2b =-,则有2(10)2d -=-;(2)根据()()()d mn d m d n =+,()()()md d m d n n=-进行求解即可;(3)由题意得:4d()22d =()0.6020=,5d ()10()(10)22d d d ==-()10.30100.699=-=.【详解】(1)由题意得:1010b =,1b \=,(10)1d \=;由题意得:21010b -=,2b \=-,2(10)2d -\=-;故答案为:1,2-;(2)∵d mn d m d n =+()()(),m d d m d n n =-()()(),∴()()()()333d a d a d a d a ==故答案为3;(3)2dQ ()0.3010=,4d \()()22d =0.6020=,5d ()10()(10)22d d d==-()10.30100.699=-=.17.D【分析】本题考查了有理数乘方的定义,根据乘方的定义逐项判断即可得出答案,解决本题的关键是一定要完全理解n a 表示n 个a 相乘.【详解】解:n 是一个正整数,则10n 表示的是n 个10相乘所得的结果,它是一个()1n +位的整数,故A 、B 、C 错误,D 正确,故选:D .18.D【分析】此题考查科学记数法的表示方法.科学记数法的表示形式为10n a ´的形式,其中1||10a £<,n 为整数,表示时关键要正确确定a 的值以及n 的值.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值10³时,n 是正整数;当原数的绝对值1<时,n 是负整数.【详解】解:80.16亿980160000008.01610==´,故选:D 19.B【分析】本题主要考查了用科学记数法表示较大的数,一般形式为10n a ´,其中110a £<,确定a 与n 的值是解题的关键.用科学记数法表示较大的数时,一般形式为10n a ´,其中110a £<,n 为整数,且n 比原来的整数位数少1,据此判断即可.【详解】91680000000 1.6810=´,故选:B .20.A【分析】本题主要考查了用科学记数法表示较大的数,一般形式为10n a ´,其中110a £<,确定a 与n 的值是解题的关键.用科学记数法表示较大的数时,一般形式为10n a ´,其中110a £<,n 为整数,且n 比原来的整数位数少1,据此判断即可.【详解】解:712000000 1.210-=-´故选:A .21.7##七【分析】本题考查了科学记数法,用科学记数法表示的数还原成原数时,0n >时,n 是几,小数点就向后移几位.【详解】解:62.345102345000´=,用科学记数法表示为62.34510´,则这个数有7个整数位.故答案为:7.22.(1)120000(2)23000000(3)360000000(4)4200000-【分析】本题考查写出用科学记数法表示的原数.将科学记数法10n a ´表示的数,“还原”成通常表示的数,就是把a 的小数点向右移动n 位所得到的数.(1)根据将科学记数法还原成原数的方法即可得出答案;(2)根据将科学记数法还原成原数的方法即可得出答案;(3)根据将科学记数法还原成原数的方法即可得出答案;(4)根据将科学记数法还原成原数的方法即可得出答案.【详解】(1)解:51.210120000´=;(2)解:72.31023000000´=;(3)解:83.610360000000´=;(4)解:64.2104200000=--´.23.1-或5-【分析】本题考查了有理数的乘方,绝对值,有理数的加法,熟练掌握其运算规则,利用分类讨论思想是解题的关键.先根据22,9x y ==,求出,x y 的值,再根据x y >分情况讨论计算即可.【详解】解:22,9x y ==Q ,2x \=±,3=±y ,x y >Q ,\ 当2,3x y ==-时,1x y +=-;当2,3x y =-=-时,5x y +=-;故x y +的值为:1-或5-.24.232023()12b a a b -++=-【分析】此题考查了相反数和绝对值得定义的应用能力,关键是能准确理解几个非负数的和为0时,这几个非负数都为0;根据几个非负数的和为0时,这几个非负数都为0列出算式,求出a 、b 的值,代入计算即可.【详解】Q ()23a -与4b +互为相反数,\()2340a b -++=,∴30a -=,40b +=即:3a =,4b =-∴232023()b a a b -++,232023(4)334=--+-() ,202316271=-+-(),12=-25.2020312-【分析】本题主要考查有理数的乘方运算,解题的关键是理解题中所给运算方法.设220191333=++++L S ,然后两边同乘以3,进而按照题中所给方法进行求解即可.【详解】解:设220191333=++++L S 则220203333=+++L S 所以())22019201920203333(13331S S -=+++-+++=-L L ,2020312-\=S 即2020220193113332-++++=L .26.(1)①<;②<;③>;④>;⑤>;⑥>(2)当12n ££时,1(1)n n n n +<+;当2n >时,1(1)n nn n +>+(3)>【分析】(1)分别计算后比大小,然后作答即可;(2)根据(1)的结果,归纳后作答即可;(3)根据(2)的结论作答即可.【详解】(1)解:①211122=<=;②322893=<=;③34381644=>=;④45410246255=>=;⑤6551562577766=>=;⑥6762799361176497=>=;故答案为:①<;②<;③>;④>;⑤>;⑥>;(2)解:把第(1)题的结果经过归纳得出:当12n ££时,1(1)n n n n +<+;当2n >时,1(1)n n n n +>+.(3)解:∵20222>,∴2023202220222023>,故答案为:>.【点睛】本题考查了有理数的乘方,有理数比较大小.解题的关键在于正确的运算,并归纳出正确的结论.。
