第一章 坐标系
新人教版物理必修一第一章第一节《质点 参考系 坐标系》课件 (共24张PPT)

三、物体和质点
1、质点的定义:用来代替物体的 有质量的点。
2、物体可以看作质点的条件:
物体的形状、大小、体积对所 研究的问题的影响可以忽略不计。
3、理解:
①质点是一种科学抽象的理想模型;
②物体本身大小不是能否看成质点 的标准;
③物体能否看成质点取决于所研究 问题的性质,同一物体有时可看成 质点,有时不可看作质点。
第一பைடு நூலகம் 运动的描述
物理学家海森堡说:“为 了理解现象,首要条件是引入 适当的概念,我们才能真正知 道观察到了什么。”
第一节 质点 参考系和坐标系
毛主席著名诗词《送瘟神》 中:“坐地日行八万里, 巡天 遥看一天河”
从这句话中描述的:人 到底是运动还是静止的呢?
大家一起来讨论下边这幅图车 中的人是静止还是运动的?
5. 关于质点的下列说法中,正确 的是 ( ) A.质量很小的物体都可看作质点 B.体积很小的物体都可看作质点 C.在任何情况下,地球都不可以 看作质点 D.凡是做平动的物体都可看作质 点
如果一个可以看做
质点的物体沿直线运动, 怎样定量的描述物体的 位置变化呢?
四、坐标系 1、坐标系:
一维
x/m
运动,结果往往是不同;
③参考系的选取可以是任意的, 实际解题应以观测方便和使物体 的运动尽可能简单为原则;
④通常选取地面为参考系;
⑤比较两个物体的运动应选同一 参考系。
例.太阳从东边升起,西边落下,是地球上 的自然现象。但是在某些条件下,在纬度较 高地区上空飞行的飞机上,旅客可以看到太 阳从西边升起的奇妙现象,这些条件是(C ) A. 时间必须是在清晨,飞机正在由东向西飞 行,飞机的速率必须较大 B. 时间必须是在清晨,飞机正在由西向东飞 行,飞机的速率必须较大 C. 时间必须是在傍晚,飞机正在由东向西飞 行,飞机的速率必须较大 D. 时间必须是在傍晚,飞机正在由西向东飞 行,飞机的速率不能太大
高一物理必修一第一章第一节:质点、参考系和坐标系(48张PPT)

(3)质点的条件
①物体的形状、大小可忽略时,一般可以看作质点 例如:研究地球的公转 抛出去的手榴弹在空中的运动
②平动的物体一般可以看作质点 例如:平直公路上行驶的汽车, 分析:车身上各部分的运动情况相同,当我们把汽车作为 一个整体来研究它的运动的时候,就可以把汽车当作质点。
③物体只做转动时,不能看做质点 例如:乒乓球在空中只做旋转运 动时
注意
坐标系是在参考系的基础上抽象出来的概念,是 抽象化的参考系。
(2)坐标系的构成要素
原点 单位长度 正方向
数字 物理量的符号 单位
直线坐标系
(3)坐标系的种类
①一维坐标(直线坐标系) 描述物体在一条直线上运动,即物体做一维运动时,可以以 这条直线为 x 轴,在直线上规定原点、正方向和单位长度,建立 直线坐标系。如图所示,若某一物体运动到A点,此时它的位置坐 标 xA=3m,若它运动到B点,则此时它的坐标 xB=-2m(“-” 表示沿 x 轴负方向)。
练习1
问题思考:
送瘟神
绿水青山枉自多 千村薜荔人遗矢 坐地日行八万里 牛郎欲问瘟神事
毛泽东
华佗无奈小虫何 万户萧疏鬼唱歌 巡天遥看一千河 一样悲欢逐逝波
我看见某位同学坐在位子上,一动不动,毛主席却说他 “坐地日行八万里”,这是怎么回事?
运动是绝对的 静止是相对的
练一练
一般来说,可以把撑杆跳高运动分为如下几个阶段:助跑、 撑杆起跳、越过横杆。在下列几种情况下运动员能否看作质点, 从中体会质点模型的建立过程。
(1)质点的定义
我们在处理这些问题时,常常不考虑物体各部分的差 异,把物体简化成没有大小、形状的点,或者说用一个有 质量的点来代替物体。
名词解释
用来代替 物体的有质量的点叫做质点。 实际物体运动的描述 质点运动的描述
第一章向量与坐标

y1 y2 y3 y4
z1 1 z2 1 z3 1 z4 1 0
x3 x1 y3 y1 z3 z1 0 或 x4 x1 y4 y1 z4 z1
2
x3 x4
例2. 求解以向量为未知元的线性方程组
① 5x 3y a ② 3x 2 y b 其中 a ( 2, 1, 2 ) ,b ( 1, 1, 2 ) .
2 1 , ) 2 2
(3 , 3 2 , 3)
故点 A 的坐标为 (3 , 3 2 , 3) .
1. 设 m 3 i 5 j 8 k , n 2 i 4 j 7 k , p 5 i j 4 k , 求向量 a 4 m 3 n p 在 x 轴上的投影及在 y
2×① -3×② , 得
解:
x 2 a 3 b (7 , 1,10)
代入②得 1 y (3 x b ) (11, 2 ,16) 2
例3. 已知两点
及实数 1, 如图所示
在AB直线上求一点 M , 使
解: 设 M 的坐标为
A M B
AM MB AM OM OA MB OB OM
a b (a x bx , a y by , a z bz )
定理1.5.3 数乘向量的坐标等于这个数与向量的对应坐标的 积。 a ( a , a , a ),
为实数 , ( a , a , a ) a x y z
x y z
二、利用坐标作向量的线性运算
9
(1) 如何求在 xoy 面上与A , B 等距离之点的轨迹方程?
(2) 如何求在空间与A , B 等距离之点的轨迹方程 ?
第一章 §1.3 1.3.1 空间直角坐标系

§1.3 空间向量及其运算的坐标表示1.3.1 空间直角坐标系学习目标 1.了解空间直角坐标系.2.能在空间直角坐标系中写出所给定点、向量的坐标. 导语我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法….”吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算. 一、空间直角坐标系 知识梳理1.空间直角坐标系:在空间选定一点O 和一个单位正交基底{i ,j ,k },以O 为原点,分别以i ,j ,k 的方向为正方向,以它们的长为单位长度建立三条数轴:x 轴、y 轴、z 轴,它们都叫做坐标轴,这时我们就建立了一个空间直角坐标系Oxyz .2.相关概念:O 叫做原点,i ,j ,k 都叫做坐标向量,通过每两条坐标轴的平面叫做坐标平面,分别称为Oxy 平面、Oyz 平面、Ozx 平面,它们把空间分成八个部分. 注意点:(1)基向量:|i |=|j |=|k |=1,i ·j =i ·k =j ·k =0.(2)画空间直角坐标系Oxyz 时,一般使∠xOy =135°(或45°),∠yOz =90°. (3)建立的坐标系均为右手直角坐标系. 二、求空间点的坐标 知识梳理在空间直角坐标系Oxyz 中,i ,j ,k 为坐标向量,对空间任意一点A ,对应一个向量OA →,且点A 的位置由向量OA →唯一确定,由空间向量基本定理,存在唯一的有序实数组(x ,y ,z ),使OA →=x i +y j +z k .在单位正交基底{i ,j ,k }下与向量OA →对应的有序实数组(x ,y ,z ),叫做点A 在空间直角坐标系中的坐标,记作A (x ,y ,z ),其中x 叫做点A 的横坐标,y 叫做点A 的纵坐标,z 叫做点A 的竖坐标.问题 空间直角坐标系中坐标轴、坐标平面上的点的坐标有什么特点? 提示点的位置 x 轴上 y 轴上 z 轴上 坐标的形式 (x ,0,0) (0,y ,0) (0,0,z ) 点的位置 Oxy 平面内 Oyz 平面内 Ozx 平面内 坐标的形式(x ,y ,0)(0,y ,z )(x ,0,z )例1 (1)画一个正方体ABCD -A 1B 1C 1D 1,若以A 为坐标原点,以棱AB ,AD ,AA 1所在的直线分别为x 轴、y 轴、z 轴,取正方体的棱长为单位长度,建立空间直角坐标系,则 ①顶点A ,D 1的坐标分别为________________; ②棱C 1C 中点的坐标为________;③正方形AA 1B 1B 对角线的交点的坐标为________. 答案 ①(0,0,0),(0,1,1) ②⎝⎛⎭⎫1,1,12 ③⎝⎛⎭⎫12,0,12 (2)已知正四棱锥P -ABCD 的底面边长为4,侧棱长为10,试建立适当的空间直角坐标系,写出各顶点的坐标.解 ∵正四棱锥P -ABCD 的底面边长为4,侧棱长为10,∴正四棱锥的高为223.以正四棱锥的底面中心为原点,平行于BC ,AB 所在的直线分别为x 轴、y 轴,垂直于平面ABCD 的直线为z 轴,建立如图所示的空间直角坐标系,则正四棱锥各顶点的坐标分别为A (2,-2,0),B (2,2,0),C (-2,2,0),D (-2,-2,0),P (0,0,223). 答案不唯一.反思感悟(1)建立空间直角坐标系的原则①让尽可能多的点落在坐标轴上或坐标平面内.②充分利用几何图形的对称性.(2)求某点M的坐标的方法作MM′垂直于平面Oxy,垂足为M′,求M′的横坐标x,纵坐标y,即点M的横坐标x,纵坐标y,再求M点在z轴上射影的竖坐标z,即为M点的竖坐标z,于是得到M点的坐标(x,y,z).跟踪训练1设正四棱锥S-P1P2P3P4的所有棱长均为2,建立适当的空间直角坐标系,求各个顶点的坐标.解如图所示,建立空间直角坐标系,其中O为底面正方形的中心,P1P2⊥Oy轴,P1P4⊥Ox 轴,SO在Oz轴上.∵P1P2=2,且P1,P2,P3,P4均在Oxy平面上,∴P1(1,1,0),P2(-1,1,0).在Oxy平面内,P3与P1关于原点O对称,P4与P2关于原点O对称,∴P3(-1,-1,0),P4(1,-1,0).又SP1=2,OP1=2,∴在Rt△SOP1中,SO=2,∴S(0,0,2).(答案不唯一,也可选择其他的点建系)三、空间点的对称问题例2在空间直角坐标系中,已知点P(-2,1,4).(1)求点P关于x轴对称的点的坐标;(2)求点P关于Oxy平面对称的点的坐标;(3)求点P关于点M(2,-1,-4)对称的点的坐标.解 (1)由于点P 关于x 轴对称后,它在x 轴的分量不变,在y 轴、z 轴的分量变为原来的相反数,所以对称点坐标为P 1(-2,-1,-4).(2)由点P 关于Oxy 平面对称后,它在x 轴、y 轴的分量不变,在z 轴的分量变为原来的相反数,所以对称点坐标为P 2(-2,1,-4).(3)设对称点为P 3(x ,y ,z ),则点M 为线段PP 3的中点, 由中点坐标公式,可得x =2×2-(-2)=6, y =2×(-1)-1=-3,z =2×(-4)-4=-12, 所以P 3的坐标为(6,-3,-12). 反思感悟 空间点对称问题的解题策略(1)空间点的对称问题可类比平面直角坐标系中点的对称问题,要掌握对称点的变化规律,才能准确求解.(2)对称点的问题常常采用“关于谁对称,谁保持不变,其余坐标相反”这个结论. 跟踪训练2 已知点P (2,3,-1)关于坐标平面Oxy 的对称点为P 1,点P 1关于坐标平面Oyz 的对称点为P 2,点P 2关于z 轴的对称点为P 3,则点P 3的坐标为__________. 答案 (2,-3,1)解析 点P (2,3,-1)关于坐标平面Oxy 的对称点P 1的坐标为(2,3,1),点P 1关于坐标平面Oyz 的对称点P 2的坐标为(-2,3,1),点P 2关于z 轴的对称点P 3的坐标是(2,-3,1).四、空间向量的坐标 知识梳理向量的坐标:在空间直角坐标系Oxyz 中,给定向量a ,作OA →=a ,由空间向量基本定理,存在唯一的有序实数组(x ,y ,z ),使a =x i +y j +z k .有序实数组(x ,y ,z )叫做a 在空间直角坐标系Oxyz 中的坐标,可简记作a =(x ,y ,z ).例3 已知在直三棱柱ABC -A 1B 1C 1中,∠BAC =90°,AB =AC =AA 1=4,M 为BC 1的中点,N 为A 1B 1的中点,建立适当的空间直角坐标系,求向量AB →,AC 1→,BC 1→的坐标. 解 建立如图所示的空间直角坐标系,设14AB →=i ,14AC →=j ,14AA 1→=k ,AB →=4i +0j +0k =(4,0,0), AC 1→=AA 1→+AC → =0i +4j +4k =(0,4,4), ∴BC 1→=BC →+CC 1→ =BA →+AC →+CC 1→ =-4i +4j +4k =(-4,4,4).反思感悟 向量坐标的求法(1)点A 的坐标和向量OA →的坐标形式完全相同;(2)起点不是原点的向量的坐标可以通过向量的运算求得.跟踪训练3 如图所示,以长方体ABCD -A 1B 1C 1D 的顶点D 为坐标原点,过D 的三条棱所在的直线为坐标轴,建立空间直角坐标系,若DB 1→的坐标为(4,3,2),则C 1的坐标是( )A .(0,3,2)B .(0,4,2)C .(4,0,2)D .(2,3,4)答案 A解析 ∵DB 1→的坐标为(4,3,2),D 为坐标原点, ∴B 1的坐标为(4,3,2), ∴BC =4,DC =3,CC 1=2, ∴C 1的坐标为(0,3,2).1.知识清单:(1)空间直角坐标系的概念. (2)空间点的坐标. (3)空间向量的坐标.2.方法归纳:数形结合、类比联想.3.常见误区:混淆空间点的坐标和向量坐标的概念,只有起点在原点的向量的坐标才和终点的坐标相同.1.在空间直角坐标系中,点P (1,3,-5)关于平面Oxy 对称的点的坐标是( ) A .(-1,3,-5) B .(1,3,5) C .(1,-3,5) D .(-1,-3,5)答案 B2.在空间直角坐标系中,点P (-1,-2,-3)到平面Oyz 的距离是( ) A .1 B .2 C .3 D.14 答案 A解析 点到平面Oyz 的距离就是点的横坐标的绝对值.3.点P (1,1,1)关于Oxy 平面的对称点P 1的坐标为______,点P 关于z 轴的对称点P 2的坐标为________.答案 (1,1,-1) (-1,-1,1)解析 点P (1,1,1)关于Oxy 平面的对称点P 1的坐标为(1,1,-1),点P 关于z 轴的对称点P 2的坐标为(-1,-1,1).4.在长方体ABCD -A 1B 1C 1D 1中,若D (0,0,0),A (4,0,0),B (4,2,0),A 1(4,0,3),则向量AC 1→的坐标为________. 答案 (-4,2,3)解析 AC 1→=AD →+DC 1→=AD →+DC →+CC 1→=-4i +2j +3k =(-4,2,3).课时对点练1.(多选)下列命题中正确的是 ( )A .在空间直角坐标系中,在x 轴上的点的坐标一定是(0,b ,c )B .在空间直角坐标系中,在Oyz 平面上的点的坐标一定是(0,b ,c )C .在空间直角坐标系中,在z 轴上的点的坐标可记作(0,0,c )D .在空间直角坐标系中,在Ozx 平面上的点的坐标是(a,0,c ) 答案 BCD解析 空间直角坐标系中,在x 轴上的点的坐标是(a ,0,0).故A 错误,B ,C ,D 正确. 2.在空间直角坐标系Oxyz 中,点(1,-2,4)关于y 轴对称的点为( ) A .(-1,-2,-4) B .(-1,-2,4) C .(1,2,-4) D .(1,2,4)答案 A解析 关于y 轴对称,则y 值不变,x 和z 的值变为原来的相反数,故所求的点的坐标为(-1,-2,-4).3.如图,在长方体OABC -O 1A 1B 1C 1中,OA =3,OC =5,OO 1=4,点P 是B 1C 1的中点,则点P 的坐标为( )A .(3,5,4) B.⎝⎛⎭⎫32,3,4 C.⎝⎛⎭⎫32,5,4 D.⎝⎛⎭⎫5,32,2 答案 C解析 由题图知,点P 在x 轴、y 轴、z 轴上的射影分别为P 1,P 2,P 3,它们在坐标轴上的坐标分别是32,5,4,故点P 的坐标是⎝⎛⎭⎫32,5,4. 4.在空间直角坐标系中,点(1,2,3)与点(-1,2,3)( ) A .关于Oxy 平面对称 B .关于Ozx 平面对称 C .关于Oyz 平面对称D .关于x 轴对称答案 C解析 空间中的两个点(1,2,3)和(-1,2,3),y ,z 轴上的两个坐标相同,x 轴上的坐标相反,故此两点关于Oyz 平面对称.5.在空间直角坐标系中,已知点P (1,2,3),过点P 作平面Oyz 的垂线PQ ,则垂足Q 的坐标为( ) A .(0,2,0) B .(0,2,3) C .(1,0,3) D .(1,2,0)答案 B解析 由于垂足在平面Oyz 上,所以纵坐标,竖坐标不变,横坐标为0.6.如图,在空间直角坐标系中,正方体ABCD -A 1B 1C 1D 1的棱长为1,B 1E =14A 1B 1,则BE →等于( )A.⎝⎛⎭⎫0,14,-1 B.⎝⎛⎭⎫-14,0,1 C.⎝⎛⎭⎫0,-14,1 D.⎝⎛⎭⎫14,0,-1 答案 C解析 BE →=BB 1→+B 1E —→=k -14j =⎝⎛⎭⎫0,-14,1. 7.设{i ,j ,k }是空间向量的一个单位正交基底,a =2i -4j +5k ,b =i +2j -3k ,则向量a ,b 的坐标分别为________. 答案 (2,-4,5),(1,2,-3)解析 由空间向量坐标概念知a =(2,-4,5),b =(1,2,-3).8.如图是一个正方体截下的一角P -ABC ,其中P A =a ,PB =b ,PC =c .建立如图所示的空间直角坐标系,则△ABC 的重心G 的坐标是________.答案 ⎝⎛⎭⎫a 3,b 3,c 3解析 由题意知A (a ,0,0),B (0,b ,0),C (0,0,c ). 由重心坐标公式得点G 的坐标为⎝⎛⎭⎫a 3,b 3,c 3.9.建立空间直角坐标系如图所示,正方体DABC -D ′A ′B ′C ′的棱长为a ,E ,F ,G ,H ,I ,J 分别是棱C ′D ′,D ′A ′,A ′A ,AB ,BC ,CC ′的中点,写出正六边形EFGHIJ 各顶点的坐标.解 正方体DABC -D ′A ′B ′C ′的棱长为a ,且E ,F ,G ,H ,I ,J 分别是棱C ′D ′,D ′A ′,A ′A ,AB ,BC ,CC ′的中点,∴正六边形EFGHIJ 各顶点的坐标为E ⎝⎛⎭⎫0,a2,a ,F ⎝⎛⎭⎫a 2,0,a ,G ⎝⎛⎭⎫a ,0,a 2,H ⎝⎛⎭⎫a ,a 2,0,I ⎝⎛⎭⎫a 2,a ,0,J ⎝⎛⎭⎫0,a ,a2. 10.如图所示,过正方形ABCD 的中心O 作OP ⊥平面ABCD ,已知正方形的边长为2,OP =2,连接AP ,BP ,CP ,DP ,M ,N 分别是AB ,BC 的中点,以O 为原点,⎩⎨⎧⎭⎬⎫OM →,ON →,12OP →为单位正交基底建立空间直角坐标系.若E ,F 分别为P A ,PB 的中点,求点A ,B ,C ,D ,E ,F 的坐标.解 由题意知,点B 的坐标为(1,1,0). 由点A 与点B 关于x 轴对称,得A (1,-1,0), 由点C 与点B 关于y 轴对称,得C (-1,1,0), 由点D 与点C 关于x 轴对称,得D (-1,-1,0). 又P (0,0,2),E 为AP 的中点,F 为PB 的中点, 所以由中点坐标公式可得E ⎝⎛⎭⎫12,-12,1,F ⎝⎛⎭⎫12,12,1.11.在空间直角坐标系中,点M (1,2,3)到z 轴的距离为( ) A. 5 B .3 C.10 D.13 答案 A解析 空间直角坐标系中,点M (1,2,3)到z 轴的距离为12+22= 5.12.(多选)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =5,AD =4,AA 1=3,以直线DA ,DC ,DD 1分别为x 轴、y 轴、z 轴,建立空间直角坐标系,则下列说法正确的是( )A .点B 1的坐标为(4,5,3)B .点C 1关于点B 对称的点为(5,8,-3) C .点A 关于直线BD 1对称的点为(0,5,3) D .点C 关于平面ABB 1A 1对称的点为(8,5,0) 答案 ACD解析 根据题意知,点B 1的坐标为(4,5,3),选项A 正确; B 的坐标为(4,5,0),C 1的坐标为(0,5,3),故点C 1关于点B 对称的点为(8,5,-3),选项B 错误; 在长方体中AD 1=BC 1=AD 2+AA 21=5=AB , 所以四边形ABC 1D 1为正方形,AC 1与BD 1垂直且平分, 即点A 关于直线BD 1对称的点为C 1(0,5,3),选项C 正确; 点C 关于平面ABB 1A 1对称的点为(8,5,0),选项D 正确.13.已知在长方体ABCD -A 1B 1C 1D 1中,向量a 在基底{AB →,AD →,AA 1→}下的坐标为(2,1,-3),则向量a 在基底{DA →,DC →,DD 1→}下的坐标为( ) A .(2,1,-3) B .(-1,2,-3) C .(1,-8,9) D .(-1,8,-9)答案 B解析 ∵a =2AB →+AD →-3AA 1→=2DC →-DA →-3DD 1→=-DA →+2DC →-3DD 1→,∴向量a 在基底{DA →,DC →,DD 1→}下的坐标为(-1,2,-3).14.在三棱锥P -ABC 中,∠ABC =90°,PB ⊥平面ABC ,AB =BC =PB =1,M ,N 分别是PC ,AC 的中点,建立如图所示的坐标系Bxyz ,则向量MN →的坐标为________.答案 ⎝⎛⎭⎫12,0,-12 解析 MN →=MB →+BN →=-12(BP →+BC →)+12(BA →+BC →)=12BA →-12BP →=12i -12k =⎝⎛⎭⎫12,0,-12.15.已知向量p 在基底{a ,b ,c }下的坐标为(2,1,-1),则p 在基底{2a ,b ,-c }下的坐标为________,在基底{a +b ,a -b ,c }下的坐标为________.答案 (1,1,1) ⎝⎛⎭⎫32,12,-1 解析 由题意知p =2a +b -c ,则向量p 在基底{2a ,b ,-c }下的坐标为(1,1,1).设向量p 在基底{a +b ,a -b ,c }下的坐标为(x ,y ,z ),则p =x (a +b )+y (a -b )+z c =(x +y )a +(x -y )b +z c ,又∵p =2a +b -c ,∴⎩⎪⎨⎪⎧ x +y =2,x -y =1,z =-1,解得x =32,y =12,z =-1, ∴p 在基底{a +b ,a -b ,c }下的坐标为⎝⎛⎭⎫32,12,-1.16.如图所示,正四面体ABCD 的棱长为1,G 是△BCD 的中心,建立如图所示的空间直角坐标系,则AG →的坐标为________,AB →的坐标为________.答案 ⎝⎛⎭⎫0,0,-63 ⎝⎛⎭⎫0,-33,-63 解析 由题意可知,BG =23BE =23×32=33, 所以AG =AB 2-BG 2=63, 所以AG →=-63k =⎝⎛⎭⎫0,0,-63, AB →=GB →-GA →=-33j -63k =⎝⎛⎭⎫0,-33,-63.。
第1章 1.3 1.3.1 空间直角坐标系课件(共50张PPT)

·
情 景
【例3】 如图,在直三棱柱ABC-A1B1C1的底面△ABC中,CA
课 堂
导
小
学 =CB=1,∠BCA=90°,棱AA1=2,M,N分别为A1B1,A1A的中 结
·
探
提
新 知
点,试建立恰当的坐标系求向量B→N,B→A1,A→1B的坐标.
素 养
合
作
课
探
时
究
分
层
释
作
疑
业
难
返 首 页
·
33
·
情
课
·
情
课
景
堂
导
小
学
结
·
探
提
新 知
2.在空间直角坐标系中,若A(x1,y1,z1),B(x2,y2,z2),则线
素 养
合 作 探
段AB的中点坐标为x1+2 x2,y1+2 y2,z1+2 z2.
课 时
究
分
层
释
作
疑
业
难
返 首 页
·
27
·
情
[跟进训练]
课
景
堂
导 学
2.点P(-3,2,-1)关于平面xOz的对称点是________,关于z轴
学
结
·
探 新
标为(1,-1,1),
提 素
知
养
合
而B→A1=C→A1-C→B=C→A-C→B+C→C1,
分 层
释
作
疑 难
坐标中只有竖坐标不同,|BB1|=|AA1|=5,则B1(3,4,5).
业
返 首 页
·
18
·
情
大学物理 第一章(1)
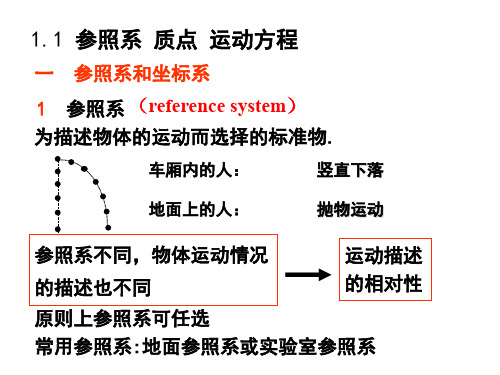
a
v2 R
n0
dv dt
t0
R―曲率半径
思考 求抛体运动过程中的曲率半径?
如B 点 at 0 , an g ,v B v 0cosθ
RB
v2
B an
(v 0cosθ)2
g
y v
B
思考
· a4 v
· a1
a·2
O
a3
O
x C
上图中分别是什么情形? a4情形是否存在?
(2)物体各点运动情况相同
本课程力学部分,除刚体外,一般都可视为质点.
2 位置矢量(position vector of a particle)
表征某时刻质点位置的矢量, 简称位矢或矢径
r xi yj zk
r 位矢 的大小:
y
r r x2 y2 z2 r 位矢 的方向余弦:
a
ddtv
20
2
sin2ti
16
2
t 1s
cos 2tj
dt
t 1s
16 2 j (m / s2 )
x 5 sin2t
x2 y2
{
y 4 cos 2t
52 42 1
解题思路:
位移(求矢量差)
1 运动方程 轨道 方程(消去t)
:
an
v2 R
n0
(改变速度方向)
切向加速度(tangential acceleration)
:at
dv dt t0
v
aτ
(改变速度大小)
v2 dv a R n0 dt t0
1平面直角坐标系

证法二(向量法)
在 ▱ABCD 中 ,������������ = ������������ + ������������ , 两边平方得������������ 2 =|������������ |2=|������������ |2+|������������ |2+2������������ ·������������ , 同理得������������ 2 =|������������ |2=| ������������|2+|������������ |2+2������������ ·������������ , 以上两式相加,得 |������������ |2+|������������ |2=2(| ������������ |2+| ������������ |2)+2������������ · (������������ + ������������)=2(|������������|2+| ������������ |2), 即 |AC|2+|BD|2=2(|AB|2+|AD|2).
思考辨析 判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打 “×”. (1)若曲线C上的点都是方程f(x,y)=0的解,则曲线C是方程f(x,y)=0的 曲线. ( × ) (2)以方程x2+y2=4的解为坐标的点都是曲线“在y轴右侧到原点的 距离等于2的点的集合”上的点. ( × ) (3)已知等腰三角形ABC的底边为AB,且A(-1,1),B(3,7),则顶点C的轨 迹方程为2x+y-5=0. ( × ) (4)方程(x-a)2+(y-b)2=r2的曲线经过点(1,2)的充要条件是(1-a)2+(2b)2=r2. ( ) √
质点运动学

例1-1 已知质点在xy平面内运动,其运动方程是 x R cost ,y R sin t 。 式中R、 均为正常数。求(1)质点的轨迹方程;(2)质点在任意时刻的位矢、 速度和加速度;(3)质点在 t1 0 到 t2 3 2 时间内的位移。
解:(1) 由运动方程消去时间参量,可得质点轨迹方程
O
y
x
s
p2
p1
r
r1 r2
| r | p1p2 | r2 r1 |
s : 路程即弧线 p1p 2
路程s是标量
| r |
|r| || r2| |r1| |
图中 s | r | |r|
平均速度
平均速率
r v t
v2
2 ac tan
vy vx
(3)求加速度 a
3 y
2 1 a a
dv d a (2 i 2t j ) 2 j dt dt
a
2
-1
-2 -3
a
4
x
沿y轴负方向 矢量有两个重要特征: 大小 方向
a a
例1-2 汽车在半径 R 300.0m 的轨道上加速运动,其路程与时间的关系是 s 5.0t 2 0.1t 3 m ,求时 t 1.0s ,汽车的加速度大小。
(
v x i v y j vz k
dt
dt
( xi yj zk )
dt
i
dt
j
dt
k
r (t )
O
v
v | v |
2 2 2 vx v y vz
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一 平面直角坐标系
题型一:坐标法证明
题型二:求轨迹方程
1.求以()()2,0,2,0M N -为斜边的直角三角形顶点P 的轨迹方程
2.等腰三角形的顶点是A (4,2),底边一个端点是B (3,5),求另一个端点C 的轨迹方程,并说它明的轨迹是什么.
3.过点P (2,4)作两条互相垂直的直线l 1,l 2,若l 1交x 轴于A 点,l 2交y 轴于B 点,求线段AB 的中点M 的轨迹方程.
4.(1)已知圆O 的方程为x 2+y 2
=9,求过点A (1,2)的弦的中点P 的轨迹方程.
(2)已知圆O 的方程为x 2+y 2=9,求过点A (4,0)的直线交圆于,B C ,求弦BC 的中点P 的轨迹方程.
5.已知线段AB 的端点()4,3B ,端点A 在圆()2
214x y ++=上运动,求线段AB 的中点M 的轨迹方程
6.已知圆C :x 2+(y -3)2=9,过原点作圆C 的弦OP ,求OP 中点Q 的轨迹方程.
7.已知△ABC ,A(-2,0),B(0,-2),第三个顶点C 在曲线y =3x 2-1上移动,求△ABC 的重心的轨迹方程.
8.已知一条直线l 和它上方的一个点A ,点A 到l 的距离是2,一条曲线也在l 的上方,它上面的每一点到A 的距离减去到l 的距离的差都是2,建立适当的坐标系,求这条曲线的方程. 题型三:伸缩变换(由对应图形寻找变换)
1.(1)怎样由sin y x =得到曲线3sin y x =
(2)图形的变化本质都是点的变化,从点的角度,上述变换的实质是什么?
2. (1)怎样由sin y x =得到曲线sin 2y x =,写出上述坐标变换
(2)怎样由sin y x =得到曲线3sin 2y x =,写出上述坐标变换
3.在同一坐标系下,求满足下列图形变换的伸缩变换
(1)将22
1x y +=变为22
149x y ''+= (2)将2244x y -=变为22
1x y ''-=
4.在同一坐标系下,求满足下列图形变换的伸缩变换
(1)将直线22=-y x 变成直线42='-'y x ,
(2)曲线0222=--x y x 变成曲线0416/22=-'-'x y x
题型三:伸缩变换(由变换寻找对应平行)
1.在同一坐标系中,求下列图形经过伸缩变换1312
x x y y ⎧'=⎪⎪⎨⎪'=⎪⎩后得到的图形
(1)22194x y += (2)22
11812
x y -= (3)22y x = (4);025=+y x 2.在同一直角坐标系中,经过伸缩变换⎩⎨
⎧='='y y x x 35后,曲线C 变为曲线18222='+'y x 则曲线C 的方程为( )
A .1725022=+y x B.1100922=+y x C .12410=+y x D.19825222=+y x。
