高中数学必修四第一章 (三)正弦型函数y=Asin(ωx+φ)的图象
高中 函数y=Asin(ωx+φ)的图象及性质 知识点+例题 全面
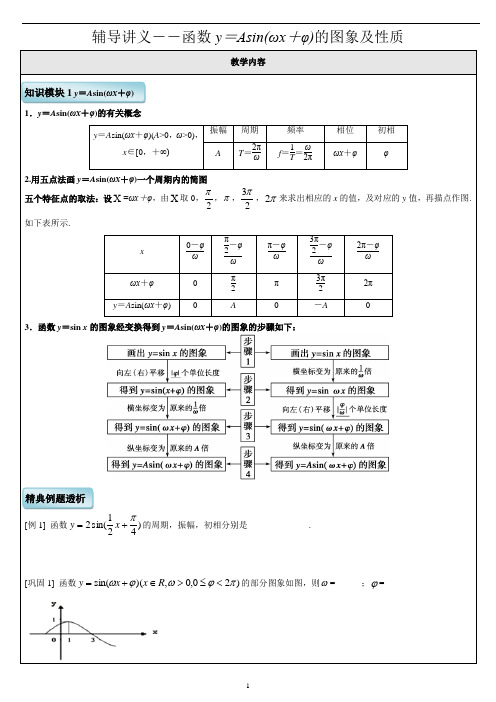
辅导讲义――函数y =Asin(ωx +φ)的图象及性质教学内容1.y =A sin(ωx +φ)的有关概念y =A sin(ωx +φ)(A >0,ω>0),x ∈[0,+∞)振幅 周期 频率 相位 初相 AT =2πωf =1T =ω2πωx +φφ2.用五点法画y =A sin(ωx +φ)一个周期内的简图 五个特征点的取法:设X =ωx +φ,由X 取0,2π,π,23π,π2来求出相应的x 的值,及对应的y 值,再描点作图.如下表所示.x0-φω π2-φω π-φω 3π2-φω 2π-φω ωx +φ 0 π2 π 3π2 2π y =A sin(ωx +φ)A-A3.函数y =sin x 的图象经变换得到y =A sin(ωx +φ)的图象的步骤如下:[例1] 函数)421sin(2π+=x y 的周期,振幅,初相分别是______________.[巩固1] 函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图,则ω=______;ϕ=______知识模块1 y =A sin(ωx +φ)精典例题透析[巩固] 若关于x 的方程01sin sin 2=+-+m x x 有解,则实数m 的取值范围为_____________.[例5] 要得到)21sin(x y -=的图象,只需将)621sin(π--=x y 的图象_______________.[巩固1] 为得到函数)3cos(π+=x y 的图象,只需将函数x y sin =的图象_____________________.[巩固2] 为得到函数)62sin(π-=x y 的图象,只需将函数x y 2cos =的图象_____________________.[例6] 已知函数x x f πsin )(=的图象的一部分如左图,则右图的函数图象所对的函数解析式为_____________.[巩固1] 函数)0,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的部分图象如图所示,则)(x f 的解析式为____________.[巩固2] 已知函数),0,)(sin()(πϕπωϕω<<->∈+=R x x A x f 的部分图象如图所示,则函数)(x f 的解析式 是_______________.[例7] 设函数f (x )=3sin(ωx +φ)(ω>0,-π2<φ<π2)的图象关于直线x =2π3对称,它的周期是π,则下列说法正确的是________.(填序号)[例](1)已知函数f (x )=2sin(ωx +φ)(其中ω>0,|φ|<π2)的最小正周期是π,且f (0)=3,则ω=_____,φ=_______.(2)已知函数f (x )=A sin(ωx +φ) (A >0,|φ|<π2,ω>0)的图象的一部分如图所示,则该函数的解析式为____________.[巩固] 如图为y =A sin(ωx +φ)的图象的一段.(1)求其解析式;(2)若将y =A sin(ωx +φ)的图象向左平移π6个单位长度后得y =f (x ),求f (x )的对称轴方程.题型三:函数y =A sin(ωx +φ)的性质[例] (2014·重庆改编)已知函数f (x )=3sin(ωx +φ)(ω>0,-π2≤φ<π2)的图象关于直线x =π3对称,且图象上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)当x ∈[0,π2]时,求函数y =f (x )的最大值和最小值.[巩固] 已知函数f (x )=A sin(ωx +φ)(x ∈R ,ω,A >0,0<φ<π2)的最大值为2,最小正周期为π,直线x =π6是其图象的一条对称轴.(1)求函数f (x )的解析式;(2)求函数g (x )=f (x -π12)-f (x +π12)的单调递增区间.1.(2013·山东)将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( )A .3π4B .π4C .0D .-π42.(2013·浙江)函数f (x )=sin x cos x +32cos 2x 的最小正周期和振幅分别是__________.3.已知函数f (x )=2sin(ωx +φ)(ω>0,且|φ|<π2)的部分图象如图所示,则函数f (x )的一个单调递增区间是______________.4.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图象如右图所示,则当t =1100秒时,电流强度是_____________.5.已知函数f (x )=2sin ωx 在区间[-π3,π4]上的最小值为-2,则ω的取值范围是_________________.6.设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图象如图所示,△KLM 为等腰直角三角形,∠KML =90°, KL =1,则f (16)的值为________.,7.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎡⎦⎤π6(x -6) (x =1,2,3,…,12,A >0)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值 为________℃.夯实基础训练。
经典:高中数学必修4-第一章三角函数课件函数y=Asin(ωx+φ)的图象

(2) (3)
连描y线点((用定光出滑五的个曲关线键顺点次) 连结五个点)
-
1-
ycosx
图象的最高点
(0,1) (2,1)
与x轴的交点
-1
o
6
-
2
3
2 3
5
7
6
6
4 3
3 5
2
3
11 6
2
x
(
2
,0)
(
3 2
,0)
图象的最低点 (,1)
-1 -
复习回顾
ysixn ,x [0,2]的图象
关键点: (0,0), ( ,1), (,0), ( 3 ,-1), (2,0) .
作是把 y=sinx 的图象上所有点的横坐标缩短
(当>1时)或伸长(当0<<1时) 倍(纵坐标不变) 而得到的。
到原来的
1
3.y=Asinx与y=sinx图象的关系
例3、作函数
y2sinx 及
y 1 sin x 2
的简图.
解:列表
描点作图
x
0
2
π
3 2
2π
y
2
sinx 0 1 0 -1 0 1
y=sinx
1
1
y= sinx
o
2
-1
2
2 x
3
2
-2
三、函数y=Asinx(A>0)图象
函数y=Asinx(A>0且A≠1)的图象可以看作 是把y=sinx的图象上所有点的纵坐标伸长(当A>1 时 )或缩短(当0<A<1时 )到原来的A倍(横坐 标不变)而得到的。y=Asinx, x∈R的值域是[-A, A],最大值是A,最小值是-A。
函数y=Asin(ωx+φ)的图象课件

1 2
参数ω对周期的影响 随着ω的增大,函数y=asin(ωx+φ)的周期会减 小;反之,随着ω的减小,函数的周期会增大。
参数φ对相位的影响 当φ增加时,函数图像会沿x轴向右移动;反之, 当φ减小时,图像会向左移动。
3
参数a对振幅的影响
a的大小决定了函数图像的振幅。当a增大时,图 像的振幅增大;反之,当a减小时,振幅减小。
使用数学软件绘制图像
MATLAB
MATLAB是一款强大的数学软件,可以用来绘制各种复杂的函数图像,包括函数 y=asin(ωx+φ)。使用MATLAB,用户可以自定义ω和φ的值,观察图像的变化。
Python (Matplotlib)
Matplotlib是Python的一个绘图库,也可以用来绘制函数y=asin(ωx+φ)。通过 Matplotlib,用户可以轻松地定制图像的样式和颜色。
在通信系统中,信号的传输通常会受到噪声和其他干扰的影响。利用函数 y=asin(ωx+φ)进行信号调制可以提高信号的抗干扰能力和传输质量。例如,在调 频(FM)通信中,调制信号的频率会随着声音信号的变化而变化,解调后可以得到 还原的声音信号。
04 函数y=asin(ωx+φ)的变 种形式
多参数变化的影响
函数图像的基本特征
周期性
极值点
由于正弦函数的周期性,函数 y=asin(ωx+φ)的图像也具有周期性, 周期取决于ω的取值。
函数图像在每个周期内有两个极值点, 极值点的位置和高度取决于参数ω、 φ的取值。
对称性
函数图像具有对称性,包括轴对称和 中心对称,具体对称轴和对称中心取 决于参数φ的取值。
02 函数y=asin(ωx+φ)的图 像绘制
最新-2018高中数学 第一章133函数y=Asin(ωxφ)的图象课件 必修4 精品

互动探究 将本例中原函数改为y=3sin(x +),x∈R,回答同样的问题.
解:列表:
描点画图,如图.
求三角函数的解析式
解决这类问题的关键在于确定参数 A,ω,φ 的 值.其方法是在观察图象的基础上,利用待定系 数法求解,具体地:①A:一般可由图象的最大与 最小值来确定;②ω:一般由 T=2ωπ来确定;③φ: 取特殊点代入所求式子求 φ 值.
2 . 函 数 y = 2sinx+1 的 定 义 域 为 __[_-__π6_+__2_k_π_,__7_6π_+__2_k_π_]_(_k_∈__Z_)_______,值域为
_[_0_,___3_]___.
知新益能
2.A、ω、φ 对函数 y=Asin(ωx+φ)图象的影响 (1)A 对函数 y=Asin(ωx+φ)图象的影响
例2 右图是函数y=Asin(ωx+ φ),其中A>0,ω>0的图象, 试确定A、ω、φ的值,并写出其 一个函数解析式.
【思路点拨】 由最高点确定 A,由周期确定 ω,
由(π3,0)确定 φ.
【解】 法一:(逐一定参法)由图象知振幅 A= 3, 又 T=56π-(-π6)=π,∴ω=2Tπ=2.由点(-π6, 0),令-π6·2+φ=0,得 φ=π3,∴y=3sin(2x+π3).
方法感悟
1.三角函数图象的变换,重点在于平移:沿x 轴平移,按“左加右减”法则;沿y轴平移,按 “上加下减”法则. 无论是哪种变形,切记每一个变换总是对字母x 而言的,即图象变换要看“变量”起多大变化, 而不是角变化多少.
2.对于 φ 的求法,A,ω,φ 三个量中初相 φ 的确 定是一个难点,除使用初始点(-ωφ ,0)外,还可利 用五点法中其他点确定初相 φ,即在五点中找两个
新课标人教必修4第一章三角函数第5节y=Asin(ωx+φ)的图象

x-
4
3 4
5 4
4
0
0
2
0
7 4 3 2
9 4
2
0
sin( x - ) 4
1
-1
描点作图:
2
y 1
4 2
3 4
7 4
9 4
2
O
-1
5 4
x
y sin( x - ) 4
y
2
y sin x
7 6
1
3
3 2
5 4
7 4
9 4
§1.5 函数 y A sin( x ) 的图象
一. 情境设置
弹簧挂着的小球作上下运动,它在t时刻与 相对于平衡位置的高度h之间的关系.
y 5 x
O
0.01 0.02
0.03
-5
其函数解析式形如
y A sin( x )
二. 合作探究
(一)探索对y sin (x ), x R的图象的影响.
(2)如果从O点算起,到曲线上的哪一点,表示完成了一 次往复运动?如果从A点算起呢?
(3)写出这个简谐运动的函数表达式.
y/cm
A 0.4 B 0.8 D F 2 E 1.2
O
x/s
C
解:(1)从图像上可知,这个简谐振动的振幅为 2cm;周期为8s;频率为1.25
(2)如果从O点算起,到曲线上的D点,表示完 成了一次往复运动;如果从A点算起,则到曲线 上的E点,表示完成了一次往复运动
作函数y=3sin(2x+
3
)的图象,
并观察与函数y = sin (2x+ ) 的图 3 象之间的关系.
高中 函数y=Asin(ωx+φ)的图象及性质 知识点+例题 全面

辅导讲义――函数y =Asin(ωx +φ)的图象及性质教学内容1.y =A sin(ωx +φ)的有关概念y =A sin(ωx +φ)(A >0,ω>0),x ∈[0,+∞)振幅 周期 频率 相位 初相 AT =2πωf =1T =ω2πωx +φφ2.用五点法画y =A sin(ωx +φ)一个周期内的简图 五个特征点的取法:设X =ωx +φ,由X 取0,2π,π,23π,π2来求出相应的x 的值,及对应的y 值,再描点作图.如下表所示.x0-φω π2-φω π-φω 3π2-φω 2π-φω ωx +φ 0 π2 π 3π2 2π y =A sin(ωx +φ)A-A3.函数y =sin x 的图象经变换得到y =A sin(ωx +φ)的图象的步骤如下:[例1] 函数)421sin(2π+=x y 的周期,振幅,初相分别是______________.[巩固1] 函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图,则ω=______;ϕ=______知识模块1 y =A sin(ωx +φ)精典例题透析[巩固] 若关于x 的方程01sin sin 2=+-+m x x 有解,则实数m 的取值范围为_____________.[例5] 要得到)21sin(x y -=的图象,只需将)621sin(π--=x y 的图象_______________.[巩固1] 为得到函数)3cos(π+=x y 的图象,只需将函数x y sin =的图象_____________________.[巩固2] 为得到函数)62sin(π-=x y 的图象,只需将函数x y 2cos =的图象_____________________.[例6] 已知函数x x f πsin )(=的图象的一部分如左图,则右图的函数图象所对的函数解析式为_____________.[巩固1] 函数)0,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的部分图象如图所示,则)(x f 的解析式为____________.[巩固2] 已知函数),0,)(sin()(πϕπωϕω<<->∈+=R x x A x f 的部分图象如图所示,则函数)(x f 的解析式 是_______________.[例7] 设函数f (x )=3sin(ωx +φ)(ω>0,-π2<φ<π2)的图象关于直线x =2π3对称,它的周期是π,则下列说法正确的是________.(填序号)[例](1)已知函数f (x )=2sin(ωx +φ)(其中ω>0,|φ|<π2)的最小正周期是π,且f (0)=3,则ω=_____,φ=_______.(2)已知函数f (x )=A sin(ωx +φ) (A >0,|φ|<π2,ω>0)的图象的一部分如图所示,则该函数的解析式为____________.[巩固] 如图为y =A sin(ωx +φ)的图象的一段.(1)求其解析式;(2)若将y =A sin(ωx +φ)的图象向左平移π6个单位长度后得y =f (x ),求f (x )的对称轴方程.题型三:函数y =A sin(ωx +φ)的性质[例] (2014·重庆改编)已知函数f (x )=3sin(ωx +φ)(ω>0,-π2≤φ<π2)的图象关于直线x =π3对称,且图象上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)当x ∈[0,π2]时,求函数y =f (x )的最大值和最小值.[巩固] 已知函数f (x )=A sin(ωx +φ)(x ∈R ,ω,A >0,0<φ<π2)的最大值为2,最小正周期为π,直线x =π6是其图象的一条对称轴.(1)求函数f (x )的解析式;(2)求函数g (x )=f (x -π12)-f (x +π12)的单调递增区间.1.(2013·山东)将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( )A .3π4B .π4C .0D .-π42.(2013·浙江)函数f (x )=sin x cos x +32cos 2x 的最小正周期和振幅分别是__________.3.已知函数f (x )=2sin(ωx +φ)(ω>0,且|φ|<π2)的部分图象如图所示,则函数f (x )的一个单调递增区间是______________.4.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图象如右图所示,则当t =1100秒时,电流强度是_____________.5.已知函数f (x )=2sin ωx 在区间[-π3,π4]上的最小值为-2,则ω的取值范围是_________________.6.设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图象如图所示,△KLM 为等腰直角三角形,∠KML =90°, KL =1,则f (16)的值为________.,7.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎡⎦⎤π6(x -6) (x =1,2,3,…,12,A >0)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值 为________℃.夯实基础训练。
高中数学(人教A版必修4)课件1.5函数y=Asin(ωx+φ)的图像

变式训练 1
1 用“五点法”作出函数 y= cos2x 的简图. 2
解
列表 2x x 1 2cos2x 0 0 1 2 π 2 π 4 0 π π 2 1 -2 3 π 2 3 π 4 0 2π π 1 2
描点连线,如下图所示.
将这个函数在一个周期内的图像向左、右扩展,即得 y 1 =2cos2x 的图像.
π y=sinx-3的图像, 再把 π y=sinx-3的图像上各点的横坐标 1 π y=sin2x-3的图像,
伸长到原来的 2 倍(纵坐标不变),得到 最后把
1 π y=sin2x-3的图像上各点纵坐标伸长到原来的 1 π y=2sin2x-3的图像.
解 列表 1 π 2x+6 x
1 π 2sin2x+6
0 π - 3 0
π 2 2 π 3 2
π 5 π 3 0
3 2π 8 π 3 -2
2π 11 π 3 0
描点连线,如下图所示.
将这个函数在一个周期内的图像向左、右两边平移即得
1 π y=2sin2x+6的图像.
特别提醒:①注意先平移后伸缩与先伸缩后平移的区别; ②在作图像时,提倡先相位变换再周期变换.不论哪一 种变换,都是对字母 x 而言的,即看“变量”起多大变化, 而不是“角变化”多少.
典例剖析
类型一 例1
作函数y=Asin(ωx+φ)的图像
1 π 用“五点法”画出y=2sin2x+6的图像.
第一章
三角函数
§1.5 函数 y=Asin(ω x+φ )的图像
课前热身
名师讲解
典例剖析
考题精选
技能提升
课前热身
1.函数 y=Asin(ωx+φ)的图像的两种画法 π 3π (1)五点法:①列表(ωx+φ 通常取 0, ,π, ,2π 这五 2 2 个值);②描点;③________.
最新人教版高中数学必修4第一章函数y=asin(ωx+φ)的图象

π 6
的图象;
π 6 1 2
的图象上各点的横坐标缩短到原来的 ,而纵坐 的图象;
π + 6
标不变,可以得到函数 y=sin 2������ +
1 (3)将函数 y=sin 2������ 的图象上的各点的纵坐标缩短到原来的 , 2 1 π 而横坐标不变,可以得到函数 y= sin 2������ + 的图象; 2 6 1 π 5 (4)再把得到的 y= sin 2������ + 的图象向上平移 个单位长度,就能 2 6 4 1 π 5 得到 y= sin 2������ + + 的图象. 2 6 4
章末整合提升
问题导学 当堂检测
知识网络构建 课前预习导学
KEQIAN YUXI DAOXUE
专题归纳整合 课堂合作探究
KETANG HEZUO TANJIU
的 ,而纵坐标不变,得到函数 y=sin2x 的图象; (2)将 y=sin2x 的图象向左平移 个单位长度,可以得到函数 y=sin 2������ +
1.5
函数 y=Asin(ωx+φ)的图象
章末整合提升
目标导航 预习引导
知识网络构建 课前预习导学
KEQIAN YUXI DAOXUE
专题归纳整合 课堂合作探究
KETANG HEZUO TANJIU
学目标
1.会用五点法画出 y=Asin(ωx+φ)的简图; 2.能够利用图象变换画出 y=Asin(ωx+φ)的简图; 3.知道 y=Asin(ωx+φ)的实际意义,并会用其性质解题. 重点:用五点法画出 y=Asin(ωx+φ)的简图; 难点:用图象变换画出 y=Asin(ωx+φ)的简图.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人大附中分校高一数学导学学案
题目 1.3.1正弦型函数y =A sin (ωx +φ)的图象
课型 新授课 教材 数学B 版必修4§1.3.1
学 习 要 求 1.理解振幅、周期、频率、初相的定义;
2.理解振幅变换、相位变换和周期变换的规律;
3.会用“五点法”画出y =A sin(ωx +φ)的简图,明确A 、ω和φ对函数图象的影响作用;
重 点 难 点
重点:熟练地对y =sin x 进行振幅、周期和相位变换。
难点:理解振幅变换、周期变换和相位变换的规律。
导 学 学 案
一.自学课本P44~45,通过观察、考虑观缆车,得出振幅、周期、频率、初相的概念。
在函数)sin(φω+=t R y 中,点P 旋转一周所需要的时间ω
π
2=T ,叫做点P 的转动周期。
在1秒内,点P 转动的周数π
ω
21=
=
T f ,叫做转动的频率。
0OP 与x 轴正方向的夹角φ叫做初相。
二.归纳总结:
函数y =A sin(ωx +φ),其中0,0>>ωA 表示一个振动量时,
A 就表示这个量振动时离开平衡位置的最大距离,通常称为这个振动的振幅; 往复一次所需的时间ω
π
2=
T ,称为这个振动的周期;
单位时间内往复振动的次数π
ω
21=
=
T f ,称为振动的频率; φω+x 称为相位; 0=x 时的相位φ称为初相。
三.例题:
例1.在同一坐标系中,画出函数y =2sin x x ∈R ;y =2
1
sin x x ∈R 的图象(简图) (比较它们的振幅的大小与A 的关系)
y =sin x -1
12π
π
y
x
O
结论:一般地,函数x A y sin =的值域是[]
,,A A -最大值是A ,最小值是A -,由此可知,A 的大
小,反映曲线x A y sin =波动幅度的大小。
因此A 也称为振幅。
