第5讲 数字谜(一)
小学奥数基础教程五年级

小学奥数基础教程(五年级)第1讲数字迷(一)第2讲数字谜(二)第3讲定义新运算(一)第4讲定义新运算(二)第5讲数的整除性(一)第6讲数的整除性(二)第7讲奇偶性(一)第8讲奇偶性(二)第9讲奇偶性(三)第10讲质数与合数第11讲分解质因数第12讲最大公约数与最小公倍数(一)第13讲最大公约数与最小公倍数(二)第14讲余数问题第15讲孙子问题与逐步约束法第16讲巧算24第17讲位置原则第18讲最大最小第19讲图形的分割与拼接第20讲多边形的面积第21讲用等量代换求面积第22 用割补法求面积第23讲列方程解应用题第24讲行程问题(一)第25讲行程问题(二)第26讲行程问题(三)第27讲逻辑问题(一)第28讲逻辑问题(二)第29讲抽屉原理(一)第30讲抽屉原理(二)?第1讲数字谜(一)数字谜的内容在三年级和四年级都讲过,同学们已经掌握了不少方法。
例如用猜想、拼凑、排除、枚举等方法解题。
数字谜涉及的知识多,思考性强,所以很能锻炼我们的思维。
这两讲除了复习巩固学过的知识外,还要讲述数字谜的代数解法及小数的除法竖式问题。
例1 把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式成立(每个运算符号只准使用一次):(5○13○7)○(17○9)=12。
分析与解:因为运算结果是整数,在四则运算中只有除法运算可能出现分数,所以应首先确定“÷”的位置。
当“÷”在第一个○内时,因为除数是13,要想得到整数,只有第二个括号内是13的倍数,此时只有下面一种填法,不合题意。
(5÷13-7)×(17+9)。
当“÷”在第二或第四个○内时,运算结果不可能是整数。
当“÷”在第三个○内时,可得下面的填法:(5+13×7)÷(17-9)=12。
例2 将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×□□=□□×□□=5568。
小学数学四年级奥数基础教程目录

小学奥数基础教程(四年级)第1讲速算与巧算(一)第2讲速算与巧算(二)第3讲高斯求和第4讲 4,8,9整除的数的特征第5讲弃九法第6讲数的整除性(二)第7讲找规律(一)第8讲找规律(二)第9讲数字谜(一)第10讲数字谜(二)第11讲归一问题与归总问题第12讲年龄问题第13讲鸡兔同笼问题与假设法第14讲盈亏问题与比较法(一)第15讲盈亏问题与比较法(二)第16讲数阵图(一)第17讲数阵图(二)第18讲数阵图(三)第19将乘法原理第20讲加法原理(一)第21讲加法原理(二)第22讲还原问题(一)第23讲还原问题(二)第24讲页码问题第25讲智取火柴第26讲逻辑问题(一)第27讲逻辑问题(二)第28讲最不利原则第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲速算与巧算(一)计算是数学的基础,小学生要学好数学,必须具有过硬的计算本领。
准确、快速的计算能力既是一种技巧,也是一种思维训练,既能提高计算效率、节省计算时间,更可以锻炼记忆力,提高分析、判断能力,促进思维和智力的发展。
我们在三年级已经讲过一些四则运算的速算与巧算的方法,本讲和下一讲主要介绍加法的基准数法和乘法的补同与同补速算法。
例1 四年级一班第一小组有10名同学,某次数学测验的成绩(分数)如下:86,78,77,83,91,74,92,69,84,75。
求这10名同学的总分。
分析与解:通常的做法是将这10个数直接相加,但这些数杂乱无章,直接相加既繁且易错。
观察这些数不难发现,这些数虽然大小不等,但相差不大。
我们可以选择一个适当的数作“基准”,比如以“80”作基准,这10个数与80的差如下:6,-2,-3,3,11,-6,12,-11,4,-5,其中“-”号表示这个数比80小。
于是得到总和=80×10+(6-2-3+3+11-=800+9=809。
实际计算时只需口算,将这些数与80的差逐一累加。
为了清楚起见,将这一过程表示如下:通过口算,得到差数累加为9,再加上80×10,就可口算出结果为809。
乘除法数字谜(一)(含详细解析)

【关键词】走美杯,四年级,初赛,第12题,五年级,初赛,第11题
【解析】由 知,“美”不为1,且“美”ד妙”<10,如果“美”为2,根据“美”ד学”的个位数为“妙”,那么“妙”为偶数,即为4,推出“学”为7,又由“Байду номын сангаас”+“学”=“数”,可知“数”为9,所以 2497。
【解析】因为竖式中五位数乘4仍是五位数,所以“客”是人于0小于3的偶数,只能是2,并推知“居” 8。因为“上”乘4不向上进位,且是奇数,所以“上” 1,并推知“然” 7。则所表示的三位数是978。
【答案】
【例 4】下面算式(1)是一个残缺的乘法竖式,其中□≠2,那么乘积是多少?
【考点】乘法数字谜【难度】2星【题型】填空
【答案】
【例 16】如图所示的除法算式中,每个 各代表一个数字,则被除数是。
【考点】除法数字谜【难度】3星【题型】填空
【关键词】希望杯,4年级,初赛,8题
【解析】先确定商首位是8,再估量出除数首位是5,确定商的末位1,得到被除数为4620.
【答案】
【例 17】右边的除法算式中,商数是。
【考点】除法数字谜【难度】3星【题型】填空
【考点】乘法数字谜【难度】3星【题型】填空
1【解析】首先从式子中可以看出“思” ,另外第三个部分积的首位只能为9,所以“学”只能为3.由于3个部分积都是四位数,而且第三个部分积的首位为9,所以它比其它两个部分积要大,从而“学”比“而”和“杯”都大,所以“而”和“杯”只能分别为1和2,这样“学而思杯”就可能为3102或3201.分别进行检验,发现 ,与算式不相符,而 符合,所以“学而思杯”代表的数字分别为3、2、0、1.
小学思维数学讲义:最值中的数字谜(一)-带详解

小学思维数学讲义:最值中的数字谜(一)-带详解最值中的数字谜(一)1. 掌握最值中的数字谜的技巧2. 能够综合运用数论相关知识解决数字谜问题数字谜中的最值问题常用分析方法1. 数字谜一般分为横式数字谜和竖式数字谜.横式数字谜经常和数论里面的知识结合考察,有些时候也可以转化为竖式数字谜;2. 竖式数字谜通常有如下突破口:末位和首位、进位和借位、个位数字、位数的差别等.3. 数字谜的常用分析方法有:个位数字分析法、高位数字分析法、数字大小估算分析法、进位错位分析法、分解质因数法、奇偶分析法等.4. 除了数字谜问题常用的分析方法外,还会经常采用比较法,通过比较算式计算过程的各步骤,得到所求的最值的可能值,再验证能否取到这个最值.5. 数字谜问题往往综合了数字的整除特征、质数与合数、分解质因数、个位数字、余数、分数与小数互化、方程、估算、找规律等题型。
【例1】有四个不同的数字,用它们组成最大的四位数和最小的四位数,这两个四位数之和是11469,那么其中最小的四位数是多少?【考点】加减法的进位与借位【难度】3星【题型】填空【解析】设这四个数字是a b c d >>>,如果0d ≠,用它们组成的最大数与最小数的和式是11469a b c dd c b a +,由个位知9a d +=,由于百位最多向千位进1,所以此时千位的和最多为10,与题意不符.所以0d =,最大数与最小数的和式为0011469a b c c b a +,由此可得9a =,百位没有向千位进位,所以11a c +=,2c =;64b c =-=.所以最小的四位数cdba 是2049.【答案】2049【例2】将一个四位数的数字顺序颠倒过来,得到一个新的四位数,如果新数比原数大7902,那么所有符合这样条件的四位数中原数最大的是.7902D C B AA B C D -例题精讲知识点拨教学目标【考点】加减法的进位与借位【难度】4星【题型】填空【解析】用A 、B 、C 、D 分别表示原数的千位、百位、十位、个位数字,按题意列减法算式如上式.从首位来看A 只能是1或2,D 是8或9;从末位来看,102A D +-=,得8D A =+,所以只能是1A =,9D =.被减数的十位数B ,要被个位借去1,就有1B C -=.B 最大能取9,此时C 为8,因此,符合条件的原数中,最大的是1989.【答案】1989【例 3】在下面的算式中,A 、B 、C 、D 、E 、F 、G 分别代表1~9中的数字,不同的字母代表不同的数字,恰使得加法算式成立.则三位数EFG 的最大可能值是.2006A B C DE F G +【考点】加减法的进位与借位【难度】4星【题型】填空【解析】可以看出,1A =,6D G +=或16.若6D G +=,则D 、G 分别为2和4,此时10C F +=,只能是C 、F 分别为3或7,此时9B E +=,B 、E 只能分别取()1,8、()2,7、()3,6、()4,5,但此时1、2、3、4均已取过,不能再取,所以D G +不能为6,16D G +=.这时D 、G 分别为9和7;且9C F +=,9B E +=,所以它们可以取()3,6、()4,5两组.要使EFG 最大,百位、十位、个位都要尽可能大,因此EFG 的最大可能值为659.事实上134********+=,所以EFG 最大为659.【答案】659【巩固】如图,相同的汉字代表相同的数字,不同的汉字代表不同的数字,那么四位数“奥林匹克”最大是奥林匹克+奥数网2008【考点】加减法的进位与借位【难度】4星【题型】填空【关键词】学而思杯,6年级,1试,第2题【解析】显然“2≤奥”,所以“1=奥或2”,如果“2=奥”,则四位数与三位数的和超过2200,显然不符合条件,所以“1=奥”,所以“9≤林”,如果“9=林”那么“200819001008+=--=匹克数网”,“0=匹=数”,不符合条件,所以“林”最大只能是8,所以“20081800100108+=--=匹克数网”,为了保证不同的汉字代表不同的数字,“匹克”最大是76,所以“奥林匹克”最大是1876。
五年级下册数学讲义-竞赛专题:第5讲-数阵图、数字谜(含答案解析)人教版

知识概述1.数阵图的一般解题思路:由于数阵图中没有填充之前各个数的位置无法确定,从每一个单个数上无法进行判断,所以我们采用的是整体与个体相结合考虑的方法,即利用所有相关数和全部相加进行分析。
2.数字谜:①数字谜介绍:数字谜从形式上可以分成为横式数字谜与竖式数字谜,从内容上可以分为加减乘除4种数字谜,横式数字谜一般可以转化为竖式数字谜。
②数字谜常用的分析法介绍解决数字谜问题最重要的就是找到突破口,突破口你的寻找是需要一定得技巧性,一般来说,首先是观察题目中给出数字的位置,同时找出涉及这些已知数字的所有相关计算,然后根据各种分析法进行突破,突破的顺序一般是三位分析法(个位分析,高位分析和进位借位分析)另外加入三大技巧(估算技巧——结合数位,奇偶分析技巧和分解素因数技巧)等、而且一般应该先从涉及乘法的地方入手,然后在考虑加法后减法的分析(并不完全都是这样)。
数阵图、数字谜数阵图与数字谜这类问题在历届杯赛中经常出现,属于各大杯赛的高频考点,因为这类题是正确率很高的题目,所以要想取得好成绩,必须掌握这类题型的解题方法。
名师点题将1~11填入图中的○内,使得每条线段上的三个圆圈内数字之和等于22。
【解析】首先求出数阵图中关键位置的数,在数阵图的中间位置,是:(22×5-66)÷4=11,剩下的数从下到大排列,首尾配对即可:1配10,2配9,,3配8,4配7,5配6。
在下图中填9个数,使每行、每列、对角线上的三个数的和都相等。
那么b处应该填入的数是()。
【解析】这是一个三阶幻方,每行、每列、每条对角线上三个数的和相等,我们称这个相等的和是幻和,幻和是中央的数的3倍,幻和=3b=1.9+b+0.9= 2.8+b,进而得到2b=2.8,b=1.4。
在右边的算式中,相同的符号代表相同的数字,不同的符号代表不同的数字,根据这个算式,可以推算出:例3例2例1△□□〇+〇□□△□□☆☆那么:口+○+△+☆=_________。
数字迷(一)
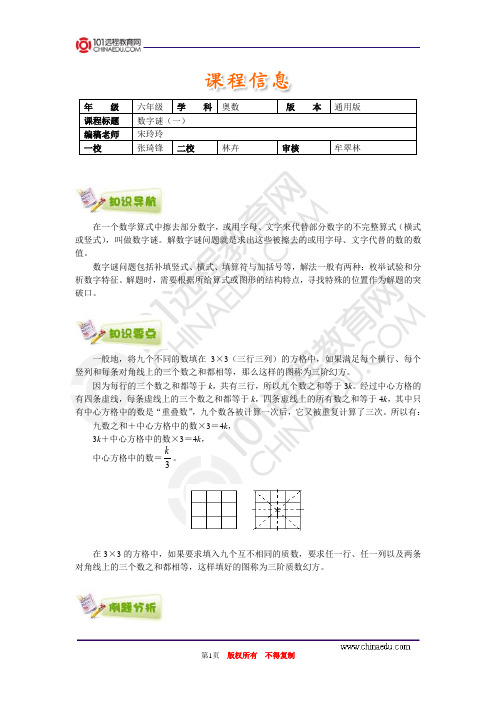
年 级 六年级 学 科 奥数版 本通用版课程标题 数字谜(一)编稿老师 宋玲玲 一校张琦锋二校林卉审核牟翠林在一个数学算式中擦去部分数字,或用字母、文字来代替部分数字的不完整算式(横式或竖式),叫做数字谜。
解数字谜问题就是求出这些被擦去的或用字母、文字代替的数的数值。
数字谜问题包括补填竖式、横式、填算符与加括号等,解法一般有两种:枚举试验和分析数字特征。
解题时,需要根据所给算式或图形的结构特点,寻找特殊的位置作为解题的突破口。
一般地,将九个不同的数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列和每条对角线上的三个数之和都相等,那么这样的图称为三阶幻方。
因为每行的三个数之和都等于k ,共有三行,所以九个数之和等于3k 。
经过中心方格的有四条虚线,每条虚线上的三个数之和都等于k ,四条虚线上的所有数之和等于4k ,其中只有中心方格中的数是“重叠数”,九个数各被计算一次后,它又被重复计算了三次。
所以有: 九数之和+中心方格中的数×3=4k , 3k +中心方格中的数×3=4k , 中心方格中的数=3k。
在3×3的方格中,如果要求填入九个互不相同的质数,要求任一行、任一列以及两条对角线上的三个数之和都相等,这样填好的图称为三阶质数幻方。
例1. 有一个四位整数,在它的某位数字前面加上一个小数点,再与这个四位数相加,得数是2001.82。
这个四位数是多少?【分析与解】设在四位整数A的某位数字前加上一个小数点得到一个新的数B,A与B 的和为2001.82。
因为小数只能由B得到,且0.82为B的小数部分,所以小数点只能加在A的百位与十位之间,即将A缩小了100倍。
由以上分析,可列出算式A+0.01A=2001.82,解得A=1982。
例2. 4个相连的小三角形的顶点处有6个圆圈(如下图)。
在这些圆圈中分别填上6个质数(每个小三角形3个顶点上的数字不能相同),它们的和是30,每个小三角形3个顶点上的数之和相等。
小学数学奥数基础教程(三年级)目30讲全

小学奥数基础教程(三年级)- 1 -小学奥数基础教程(三年级)第1讲加减法的巧算第2讲横式数字谜(一)第3讲竖式数字谜(一)第4讲竖式数字谜(二)第5讲找规律(一)第6讲找规律(二)第7讲加减法应用题第8讲乘除法应用题第9讲平均数第10讲植树问题第11讲巧数图形第12讲巧求周长第13讲火柴棍游戏(一)第14讲火柴棍游戏(二)第15讲趣题巧解第16讲数阵图(一)第17讲数阵图(二)第18讲能被2,5整除的数的特征第19讲能被3整除的数的特征第20讲乘、除法的运算律和性质第21讲乘法中的巧算第22讲横式数字谜(二)第23讲竖式数字谜(三)第24讲和倍应用题第25讲差倍应用题第26讲和差应用题第27讲巧用矩形面积公式第28讲一笔画(一)第29讲一笔画(二)第30讲包含与排除一、两、三位数乘一位数(一)二、两、三位数乘一位数(二)三、乘法分配律数学智慧园(一)四、等量替换五、两、三位数除以一位数(一)六、两、三位数除以一位数(二)七、和差问题数学智慧园(二)八、图形空格填数九、归一问题十、和倍问题十一、差倍问题数学智慧园(三)十二、两积之和第2讲横式数字谜(一)在一个数学式子(横式或竖式)中擦去部分数字,或用字母、文字来代替部分数字的不完整的算式或竖式,叫做数字谜题目。
解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。
例如,求算式324+□=528中□所代表的数。
根据“加数=和-另一个加数”知,□=582-324=258。
又如,求右竖式中字母A,B所代表的数字。
显然个位数相减时必须借位,所以,由12-B=5知,B=12-5=7;由A-1=3知,A=3+1=4。
解数字谜问题既能增强数字运用能力,又能加深对运算的理解,还是培养和提高分析问题能力的有效方法。
这一讲介绍简单的算式(横式)数字谜的解法。
解横式数字谜,首先要熟知下面的运算规则:(1)一个加数+另一个加数=和;(2)被减数-减数=差;(3)被乘数×乘数=积;(4)被除数÷除数=商。
小学数学竞赛:乘除法数字谜(一).教师版解题技巧 培优 易错 难

1【解析】首先从式子中可以看出“思” ,另外第三个部分积的首位只能为9,所以“学”只能为3.由于3个部分积都是四位数,而且第三个部分积的首位为9,所以它比其它两个部分积要大,从而“学”比“而”和“杯”都大,所以“而”和“杯”只能分别为1和2,这样“学而思杯”就可能为3102或3201.分别进行检验,发现 ,与算式不相符,而 符合,所以“学而思杯”代表的数字分别为3、2、0、1.
⑴数字谜中的文字,字母或其它符号,只取 中的某个数字;
⑵要认真分析算式中所包含的数量关系,找出尽可能多的隐蔽条件;
⑶必要时应采用枚举和筛选相结合的方法(试验法),逐步淘汰掉那些不符合题意的数字;
⑷数字谜解出之后,最好验算一遍.
模块一、乘法数字谜
【例 1】下面是一个乘法算式:问:当乘积最大时,所填的四个数字的和是多少?
【关键词】希望杯,五年级,初赛,第11题,4分
【解析】除数的百位是6,积是一个三位数,所以商的十位一定是1,除数的个位是7,被除数个位是1,所以商的个位是3,所以商是3
【答案】
【例 18】右面算式中的每个“奇”字代表1、3、5、7、9中的一个,每个“偶”字代表0、2、4、6、8中的一个,为使算式成立,求出它们所代表的值。
【解析】因为竖式中五位数乘4仍是五位数,所以“客”是人于0小于3的偶数,只能是2,并推知“居” 8。因为“上”乘4不向上进位,且是奇数,所以“上” 1,并推知“然” 7。则所表示的三位数是978。
【答案】
【例 4】下面算式(1)是一个残缺的乘法竖式,其中□≠2,那么乘积是多少?
【考点】乘法数字谜【难度】2星【题型】填空
【答案】
【例 16】如图所示的除法算式中,每个 各代表一个数字,则被除数是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5讲数字谜(一)
在一个数学算式(横式或竖式)中,擦去部分数字或全部数字,用字母、文字或□等来代替部分数字的不完整的横式或竖式,叫做数字谜题目。
解数字谜题就是把算式中擦去的数或字母、文字或□等表示的数填出来。
横式数字谜
点燃你思维
【例1】下列算式中,□、○、△、▲、☆各代表什么数字?
(1)□+8=24-3 (2)47-○=14+8
(3)6×△=30 (4)▲÷4=5
(5)36÷☆=6
【思路导航】
(1)观察这个算式,我们发现,首先能算出等号右边的结果:24—3=21,于是□+8=21,根据“加数=和一另一个加数”可知,□=21—8=13。
(2)此算式类似于第(1)个算式,首先能算出等号右边的结果:14+8=22,于是47-○=22,根据“减数=被减数-差”可知,○=47—22=25。
(3)此算式是乘法算式,已知被乘数与积,根据“乘数=积÷被乘数”
=30÷6=5。
(4)此算式是除法算式,已知除数与商,根据“被除数=除数×商”可知,▲=4×5=20。
(5)此算式也是除法算式,已知被除数与商,根据“除数=被除数÷商”可知,☆=36÷6=6。
【例2】下列算式中,□、○、△、☆各代表什么数字?
(1)□+□+□+□=24
(2)7+○+○+○=27-○
(3)3×△-2×3=12
(4)6×6-16÷☆=32
【思路导航】
(1)由于口表示的是同一个数,根据乘法的意义可
知,□+□+□+□=□×4,所以□=24÷4=6。
(2)把等号左边(7+○+○+○)看做一个数,由加法运算规则知,7+○+○+○+○=27,7+○×4=27,把○×4看做一人数,就有○×4=27-7
○×4=30
○=20÷4=5
(3)把3×△看做一个数,就有
3×△=12+2×3,
3×△=18,
△=18÷3=6。
(4)把16÷☆看做一个数,就有
16÷☆=6×6-32,
16÷☆=4,
☆=16÷4=4。
【例3】要使下面的4个算式同时成立,□、○、△、☆各代表什么数字?
(1)□+△=10 (3)△÷☆=4
(2)□-○=3 (4)△×△=16
观察上面的四个算式,看一看哪个算式最容易填出呢?
【思路导航】
观察上面的4个算式,首先应明确,□在各个算式中所代表的是同一个数,△在各个等式中所代表的也是相同的数。
填一些复杂的数字谜一般要分3步,下面我们结合本题来说明。
第一步:审题就是通过对题目的分析,找出算式中数量之间的关系或特征,它们是确定各空格内应该填什么数字的主要依据。
4个算式中,(1)式是两个不同的数相加,(2)式是两个不同的数相减,(3)式是两个不同的数相除,(4)式是两个相同的数相乘。
第二步:选择突破口在认真审题的基础上认真分析思考,找出算式中容易填出或关键性的空格,作为解题的突破口。
由于△×△=16,而16=4×4,所以△=4,这是解题的突破口。
第三步:确定各空格填什么数字从突破口开始,依据算式的已知条件,逐个填出空格中的数字。
把△=4代入(3)式,有4÷☆=4;易知☆=1。
把△=4代入(1)式,有□+4=10,易知□=6。
再把□=6代入(2)式,有6一○=3,易知○=3。
所以,□=6,△=4,○=3,☆=1。
【例4】把1-9这9个数字填在下面的9个□里,组成3个等式(每个数字只能用一次)
□+□=□
□-□=□
□×□=□
【思路导航】
上面的3个算式,哪个算式的填法最少呢?
如果从加法与减法算式人手,那么会出现多种情形。
如果从乘法算式入手,由于每个数字只能填一次,那么只有下面两种情况:
2×3=6 或 2×4=8,
所以应当从乘法算式入手。
若乘法算式是2×4=8,则剩下的6个数是:1,3,5,6,7,9,用这6个数中的3个只能组成3个算式:1+5=6,1+6=7,3+6=9,显然,用这6个数不能同时组成两个加法算式,因此,当乘法算式是2×4=8时,不能用其他数同时填出加法与减法两个算式(减法算式可变形为加法算式)。
若乘法算式是2×3=6,则剩下的6个数是:1,4,5,7,8,9,用这6个数中的3个只能组成4个算式:1+4=5,1+7=8,1+8=9,4+5=9。
观察这4个算式,容易看出,用剩下的6个数能同时组成两个加法算式:1+7=8,4+5=9,将其中的一个加法算式改为减法算式,即可得到本题的答案:(答案不惟一)
1+7=8
9-4=5
2×3=6
1、下列各式中,□、○、△、☆各代表什么数字?
17+□=24+8 ○×3=18
△÷=4 20÷☆=5
2、下列各式中,□、○、△、☆各代表什么数字?
(1)□+□+□=18
(2)5+○+○+○=17+○
(3)4×△+5×3=31
(4)4×6-☆÷2=26
3、要使下面的4个算式同时成立,□、○、△、☆各代表什么数字?
(1)□+○=28 (3)☆÷△=3
(2)○-☆=2 (4)△×△=36
4、将0,1,2,3,4,5这六个数字分别填入下式中的□中,使得等式成立:
□+□=□=□□÷□
5、把1-13这13个数中选出12个不同的数,分别填入下面的□中,组成4个等式(每个数字只能用一次)。
□+□=□
□-□=□
□×□=□
□÷□=□
6、下面的算式是由1~9这9个数字组成的,其中“9”、“4”已填好,请你将余下的各数填入□中,使得等式成立:
□+□=□×□=9-4=□+□-□。
