点的运动学
工程力学之点的运动学

简谐振动
点在平衡位置附近作周期性往 复运动,加速度与位移成正比 、方向相反。
抛体运动
点在重力作用下沿抛物线轨迹 的运动,如平抛、斜抛等。
一般平面曲线运动
点在平面内沿任意曲线轨迹的 运动,加速度和速度方向可任
意变化。
05
工程应用实例分析
机械手臂的运动控制
运动学建模
01
通过D-H参数法或旋量理论建立机械手臂的运动学模型,描述
在航空航天工程中,点的运动学可用于分 析飞行器的飞行轨迹和姿态控制,为航空 航天技术的发展提供理论支持。
土木工程
生物医学工程
在土木工程中,点的运动学可用于研究结 构的动力响应和稳定性问题,为工程结构 的设计和施工提供科学依据。
在生物医学工程中,点的运动学可用于分 析人体运动系统的生物力学特性,为医疗 器械的设计和康复治疗提供理论指导。
曲线运动的合成与分解
运动的合成
将点的运动分解为沿不同坐标轴的分运动,通过矢量合成得到点 的实际运动。
运动的分解
根据实际需要,将点的曲线运动分解为多个简单的直线或圆周运动, 便于分析和计算。
运动的叠加原理
多个独立的分运动可以线性叠加,形成复杂的曲线运动。
曲线运动的特殊形式
匀速圆周运动
点绕固定中心以恒定速率作圆 周运动,加速度始终指向圆心
速直线运动。
特点
速度大小随时间均匀变化,加速度 大小和方向保持不变。
公式
s = v0t + 1/2at^2,其中s为位移, v0为初速度,a为加
已知分运动求合运动,其位移、速度、加速度遵 循平行四边形定则。
分解
已知合运动求分运动,可将合运动分解为两个简 单的分运动进行处理。
第6章例题-纯滚动圆盘
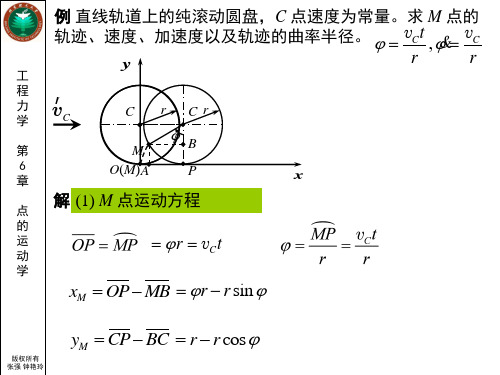
例 直线轨道上的纯滚动圆盘,C 点速度为常量。求 M 点的 轨迹、速度、加速度以及轨迹的曲率半径。 ϕ = vC t , ϕ = vC & r r y
r vC
C M O(M) A
r
Cr
ϕ
B P
x
解 (1) M 点运动方程
= ϕ r = vC t
ቤተ መጻሕፍቲ ባይዱ
xM = OP − MB = ϕ r − r sin ϕ yM = CP − BC = r − r cos ϕ
消去 ϕ 得轨迹方程:
版权所有 张强 钟艳玲
yM 2 ⇒ xM = r arccos 1 − − 2ryM − yM r
旋轮线 (摆线)
工 程 力 学 第 6 章 点 的 运 动 学
例 直线轨道上的纯滚动圆盘,C 点速度为常量。求 M 点的 轨迹、速度、加速度以及轨迹的曲率半径。 ϕ = vC t , ϕ = vC & r r y xM = ϕ r − r sin ϕ r yM = r − r cos ϕ v Cr
例 直线轨道上的纯滚动圆盘,C 点速度为常量。求 M 点的 轨迹、速度、加速度以及轨迹的曲率半径。
工 程 力 学 第 6 章 点 的 运 动 学
版权所有 张强 钟艳玲
C
ϕ
M O A
B P
x
解 (2) M 点速度-大小
vMx = vC (1 − cos ϕ ) = 2vC sin
2
ϕ
2 cos
vMy = vC sin ϕ
⇒ vM = v
2 Mx
= 2vC sin
2 My
ϕ
2
ϕ
理论力学教案-运动学

论力学--运动学运动学研究点和刚体运动的几何规律,即运动方程、轨迹、速度、加速度或角速度、角加速度等运动特征量。
第六章 点的运动学点的运动学是研究一般物体运动的基础,又具体独立的应用意义。
描述点的运动有矢径法、直角坐标法、自然法三种方法。
§6.1 矢量法一.矢量法表示点的运动方程设动点M 在空间作曲线运动,在参考坐标系上任取 某确定的点O 为坐标原点,则动点的位置可用原点至动 点的矢径r 表示。
当动点M 运动时,矢径r 的大小和方 向一般也随时间而改变,并且是时间的单值连续函数, 即)(t r r =上式称为用矢量表示的点的运动方程。
动点M 在运动过程中,其矢径r 的末端在空间 描绘出的曲线,称为动点M 的运动轨迹。
也称为矢径r 的矢端曲线。
二.矢量法表示点的速度)()(t t t r r r -+=∆∆平均速度tt t t t ∆∆∆∆)()(r r r υ-+== 瞬时速度dtd t t t rr υυ===→→∆∆∆∆00limlim 三.矢量法表示点的加速度 )()(t t t υυυ-+=∆∆ 平均加速度tt t t t ∆∆∆∆)()(υυυa -+==瞬时加速度2200lim lim dt d dt d t t t rυυa a ====→→∆∆∆∆结论:动点的速度等于它的矢径r 对时间的一阶导数,其加速度等于动点的速度对时间的一阶导数,也等于动点的矢径r 对时间的二阶导数。
§6.2 直角坐标法一.直角坐标表示动点的运动方程由于k j i r z y x ++=,当动点在轨迹上运动时,r 随时间而变化,则动点M 的坐标值x ,y 和z 随时间 而变化。
即⎪⎩⎪⎨⎧===)()()(321t f z t f y t f x消去方程中的参数t ,则得到动点运动的轨迹。
二.直角坐标表示动点的运动速度由于动点M 的矢径可表示为 k j i r z y x ++=,所以动点M 的速度可表示为 k j i r υdtdzdt dy dt dx dt d ++==将动点M 的速度写成投影形式,即k j i υz y x υυυ++=比较以上两式,可得dt dx x =υ,dt dy y =υ,dtdz z =υ 三.直角坐标表示动点运动的加速度动点M 的速度可表示为k j i r υdtdz dt dy dt dx dt d ++==,其加速度可表示为 k j i υa 222222dtzd dt y d dt x d dt d ++==将动点M 的加速度写成投影形式,即k j i a z y x a a a ++=比较以上两式,可得 22dt x d a x =,22dt y d a y =,22dt z d a z =结论:动点的速度在各坐标轴上的投影等于各对应的坐标对时间的一阶导数,动点的加速度在各坐标轴上的投影等于各对应的坐标对时间的二阶导数。
第6章例题-点的运动例题-all

dx vx = dt = 4 − 4t v = dy = 2 − 2t y dt
加速度的大小:| a |= ax 2 + a y 2 = 20(m/s 2 )
版权所有 张强 钟艳玲
2
例 dy-2 直杆 AB 两端分别沿铅锤和水平直线运动。已知
MA = l1 , MB = l2 , ϕ = ωt (ω = const.)
例 dy-1 已知动点在 xOy 平面内的运动方程为
工 程 力 学 第 6 章 点 的 运 动 学
x = 4t − 2t 2 y = 2t − t 2
单位:m, s
求动点的轨迹方程,速度和加速度的大小。 解 (1) 消去参数 t,得到轨迹方程
x − 2y = 0
(2) 求速度
t≥0
⇒ x ≤ 2, y ≤ 1
2 vC vC t = sin r r 2 vC vC t = cos r r
指向圆盘中心
tan β =
版权所有 张强 钟艳玲
aMy aMx
vC t π vC t π = cot = tan − = tan − ϕ r 2 r 2
13
工 程 力 学 第 6 章 点 的 运 动 学
旋轮线
8
工 程 力 学 第 6 章 点 的 运 动 学
例 dy-5 直线轨道上的纯滚动圆盘,C 点速度为常量。求 M 点的轨迹、速度、加速度以及轨迹的曲率半径。 vC t y D xM = vC t − r sin r r y = r − r cos vC t vC Cr M r ϕ
dx vx = dt = 4 − 4t v = dy = 2 − 2t y dt
点的运动自然法

法面:通过P点与切线T垂直的平面
(副法线)
法线 —— 法面内的
法
面 (主法线)
s+
直线
(无数条)
P-空间曲线上的动点
从
切
面
s-
b
n
t
密切面 P
(切线)
主法线N —— 法面 与密切面的交线
副法线B —— 法面内 与主法线垂直的法线
自然轴系 坐标原点为P点的直角坐标系
t n b —— 构成了自然坐标系的单位矢量
rr(1(1yy'2'2))22
dd22yy
ddddx2x2y2y2 8L8Lh2h2
an L=32m
h x
ddxx22
at 特dd别vtdd;a提yx醒1a4L:0anh22L(a82L1vr=02f2a;L2n28x法)0h.向78加0m.dd7速yx8/ x度sm2L。会//2s2产。0r生a“r81Lr离1r0f2r2心(L1828L8力d8dLLf22hyx2f2ft”2'y22),(230从曲;.7而线8 减m平dd2少/坦t2ys轮2)。子8L2f ;
运动方程的建立:
杆AB绕A轴以 = 5t( 以rad计、t以s计)的规律转动,其
上一小环M将杆AB和半径为R(以m计)的固定大圆环套在一 起。若以直角坐标Oxy为参考系,则小环M的运动方程为
___x_=__R_c_o_s_(_1_0_t )____y_=__R_s_i_n_(1_0_t_)_____。
的方法
称为 自然法
自然轴系
密切面
当P´点无限接近于 P 点时,过这两点的切 线所组成的平面,称为 P 点的密切面。
lim α α
PP
理论力学 第一章 点的运动学

已知速度的投影求速度
大小
v v v v
2 x 2 y
2 z
方向由方向余弦确定
cosv , i v x v cosv , j v y v cosv , k v z v
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
§ 1.1点的运动矢量分析方法
加
速
度
t 瞬时: 速度 v(t) t+ t 瞬时:速度 v(t + t ) 或v
t 时间间隔内速度的改变量
v ( t ) = v ( t + t ) - v( t )
点在 t 瞬时的加速度
§ 1.2 点的运动的直角坐标法
加速度
a ax i a y j az k
dv x d 2 x ax 2 dt dt dv y d 2 y ay 2 dt dt dv z d 2 z az 2 dt dt
dv y dv x dv z d2 y d2x d2z a i j k 2 i 2 j 2 k dt dt dt dt dt dt
方 cosa, i a x a, 向 cosa, j a y a, 余 弦 cosa, k a z a
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
§1.3 点的运动的自然坐标法
在点的运动轨迹已知的情况下,可建立弧
坐标和自然轴系来描述该点的运动,这种方
点的切线所组成的 平面,称为P点的密 切面。
P P
lim a1 a
清华大学理论力学课件--点的运动学

瞬时速度和平均速度可以提供关于物体运动状态的详细信息。
匀加速直线运动
定义
匀加速直线运动是指速度在运动过程中以相同的速 率增加或减少的运动。
加速度公式
加速度 = (末速度 - 初始速度)/ 时间,表征物体 加速或减速的程度。
运动方程
匀加速直线运动中速度和位移之间存在一些重要的 关系。
自由落体运动
曲线运动
曲线运动在三维空间中体现了物体的复杂轨迹和多 维运动。
均匀速直线运动
特点
均匀速直线运动是指速度在 运动过程中保持速度乘以时间。
示例
一个车以20 m/s的速度匀速 直线行驶10秒,位移等于200 米。
变速直线运动
定义
变速直线运动是速度在运动过程中发生变化的运动。
自由落体运动是一种特殊的匀加速直线运动,对象 只受重力作用。
清华大学理论力学课件-点的运动学
本课件将详细介绍点的运动学,包括位移、速度和加速度的定义,以及一维 直线运动、二维平面运动和三维空间运动等内容。
点的运动学概述
基本概念
点的运动学研究物体的位置、速度和加速度等运动状态。
重要性
点的运动学是理论力学的基础,对各种物体的运动进行描述和分析。
应用领域
点的运动学在工程、物理学和运动控制等领域具有广泛的应用。
速度-时间曲线
变速直线运动可以用速度-时间曲线来描述和分析。
加速度-时间曲线
加速度-时间曲线可以表征速度变化的幅度和方向。
运动方程
运用运动方程可以计算变速直线运动中的各个参量。
瞬时速度和平均速度
定义
瞬时速度是指物体在某一时刻的瞬时速度,而平均速度是指物体在整个运动过程中的平均速 度。
理论力学第5章(点的运动)

(2) 运动学: 研究点与刚体运动的几何性质。
包括位移、轨迹、速度、加速度。 (与力无关、也是变形体运动基础)
A B
F
C
B
刚体运动
C
变形(包含刚体位移和相对位移)
(3) 动力学: 研究物体所受力与运动间的关系。
包括质点系、刚体,变形体的动力效应。
第五章 点的运动学
§5-1 运动学的基本概念
速度
已知: OC AC BC l , MC a , t。 求:运动方程、轨迹、速度和加速度。
x l a cost ax v x 2 a y vy y l a sin t
2
加速度
a a a
F ( x, y) 0
二、点的速度v
又
r = xi + yj + zk
式中 v x 所以得
dr dx dy dz v i j k dt dt dt dt v = vx i + vy j + vz k
、v y
、v z
vx
dx dt
v
表明:“动点的速度在坐标轴上的投影,等于动点对应的位置 坐标对时间 t 的一阶导数”。 则速度的大小和方向余弦为
弧坐标的运动方程sf切向加速度表示速度大小的变化三点的加速度法向加速度表示速度方向的变化匀速运动v常数常数常数匀变速直线运动匀速圆周运动匀速直线运动或静止直线运动匀速运动圆周运动匀速运动直线运动匀速曲线运动匀变速曲线运动点作曲线运动画出下列情况下点的加速度方向
(1) 静力学: 研究物体所受力系的简化、平衡规律及其应用。
△r称为在△t时间内动点M的位移。
间间隔△t内的平均速度。以 v*表示。则: Δr v Δt 平均速度表示动点在△t内平均运动的快慢和运动方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题3 已知:R,= t ( 为常数),求:(1)小环M的运动方程、 s B 速度、加速度;(2)小环M相对于 AB 杆的速度、加速度
解(1)建立图示弧坐标
运动方程 速度 加速度
C
s R(2 ) 2 R t
2
O
a
M
ds v 2 R dt
dv v2 at 0, an 4 R 2 dt R
v
t 时间间隔内矢径的改变量
r r (t t ) r (t ) —点M的位移
r v 动点M在时间间隔△t 内的平均速度 t r dr r (2)点的瞬时速度 v lim t 0 t dt
速度 — 描述点在 t 瞬时运动快慢和运动方向的力学量。速度的 方向沿着运动轨迹的切线;指向与点的运动方向一致;速度大 小等于速度矢量的模。
τ
?
1
v
曲率定义:曲线切线的转角 对弧长的一阶导数的绝对值。 曲率的倒数称为曲率半径。 曲率半径用ρ表示。
dτ dτ d ds dt d ds dt
s
M′
?
sin
1
v
2
τ
M
τ
τ
dτ τ lim lim 0 0 d
T(切线)
密切面
b= × n
自然轴系P-nb
自然轴系的特点:跟随动点在轨迹上作空间曲线运动。
自然轴系的单位矢量、n、b 是方向在不断变化的单位矢量。 固定的直角坐标系的单位矢量i、j、k则是常矢量。
3、点的速度
经过△t 时间间隔,点沿轨迹由M 到 M′
M
r
r (t )
s
τ
M′
v
r dr v lim t 0 t dt
dτ n d
dv v2 τ n dt
dv v2 a τ n dt
加速度表示为自然轴系投影形式
a at τ an n ab b
dv d 2 s at 2 dt d t
切向加速度
an
v
2
a a t an
法向加速度
ab 0
几 点 讨 论
切向加速度
解:取M点与地接触,开始时该点
与直角坐标轴原点重合,建立图示直 角坐标系。
y
E
v
M
由纯滚动条件 OC MC r rt
直角坐标表示的M点运动方程:
O1 x C
O
x OC O1M sin r t sin t y O1C O1M cos r 1 cos t
消去上式中的角 ,即得M点的
轨迹方程:
轨迹演示 y B
A
x y 2 1 2 ( a b) b
O
22C源自xy Mx
思考题:M点的轨迹是什么曲线 ?
例题2 半径为 r 的轮子沿直线纯滚(不滑动),轮转角 = t ( 为 常量),求轮上任一点M的运动方程、速度和加速度。
轨 迹 演 示
dx dy dz , vy , vz z vx x y dt dt dt
点的速度矢量在直角坐标轴上的投影等于点的相应坐标对时间 的一阶导数。
速度的大小:
dx 2 dy 2 dz 2 v ( ) ( ) ( ) dt dt dt (v x ) 2 (v y ) 2 (v z ) 2
2、点的加速度矢量
(1)点的平均加速度
v1
速度端图
v2
O
v1 v2
v3
M
v (t )
O
v2
t v (t )
t t v (t t )
t 时间间隔内速度的改变量
v3
a
a
M
v v (t t ) v (t )
v 动点M在时间间隔△t 内的平均加速度a t
v
v
x′ B
A C
2
(2) 建立图示直角坐标系 运动方程 速度 加速度
x M 2 R cos 2 R cos t
dx M v 2 R sin t M dt
y′ O A
M
dv 2 M a 2 R cos t M dt
例题4 销钉B可沿半径等于R的固定圆弧滑道DE和摆杆的直槽中滑 π 动,OA=R=0.1 m。已知摆杆的转角 sin 2πt(时间以s计, φ 8 以rad计),试求销钉在t1=1/4 s和t2=1 s时的加速度。
第六章 点的运动学
§6–1 描述点运动的矢量法 §6–2 描述点运动的直角坐标法
§6–3 自然法
结论与讨论
§6-1 矢量法
1、点的运动方程—变矢量形式
运动方程用点在任意瞬时t的位置 矢量r(t)表示。 r(t)简称为矢径。 运动方程
z
M M
r (t ) r (t ) r (t )
O
r r (t )
dv at s dt
表示速度矢量大小的变化率; 法向加速度
an
v2
表示速度矢量方向的变化率;
ab 0 表明加速度 a 在副法线方向没有分量;
还表明速度矢量v和加速度矢量a都位于密切面内。 点的加速度的大小和方向
2 dv v 2 2 a a t an dt 2 2
2 2 a ax ay r 2
2
§6-3 自然法
1、弧坐标要素与运动方程
思路:如果点沿着已知的轨迹 运动,则点的运动方程,可用 点在已知轨迹上所走过的弧长 随时间变化的规律描述。 弧坐标具有以下要素: (1)有坐标原点(一般在轨迹上任选一参考点作为坐标原点); (2)有正、负方向(一般以点的运动方向作为正向); (3)有相应的坐标系(自然轴系)。 弧坐标形式的运动方程: s = f (t)
2
z
M
ay
ax
r
i k O
j
az z
a
y
x
y
x
d2 x 2 d2 y 2 d2 z 2 加速度的大小: a ( 2 ) ( 2 ) ( 2 ) dt dt dt
点的加速度矢量在直角坐标轴上的投影等于点的相应坐 标对时间的二阶导数。
az ay ax cos ( a , k ) cos(a, j ) 加速度的方向余弦: cos(a, i ) a a a
(+)
O (-) s
M
2、自然轴系
(1)密切面
当P´点无限接近于P 点时,过这两点的切线所 组成的平面,称为P点的 密切面。
① 空间曲线上的任意点都存在密切面,而且是惟一的。 结 论 ② 空间曲线上的任意点无穷小邻域内的一段弧长,可以看作是 : 位于密切面内的平面曲线。 ③ 对于平面曲线而言,密切面就是该曲线所在的平面。
速度的方向余弦:
i
z
vz
M
v
vx
vy
r
k O
j
z
a
y
vx cos(v , i ) v vy cos(v , j ) v vz cos(v , k ) v
x
y
x
3、点的加速度
设: a a x i a y j a z k
dvx d x 2 x dt dt dv y d 2 y ay 2 y dt dt dvz d 2 z az 2 z dt dt ax
(2)自然轴系 P-空间曲线上的动点; B(副法线) N(主法线)
T —过动点P的密切面内的切
线,其正向指向弧坐标正向; N —密切面内垂直于切线 的直线,其正向指向曲率中心; sB —过动点P垂直于切线和主法 线的直线,其正向由B=T × N确定。 自然轴系的基矢量:、n、b
法平面
s+
b n P
不受约束的点在空间有3个自由度, 在直角坐标系中,点在空间的位置 由3个方程确定: (1)点的运动方程
z z
M
v
z
r
i k O
j
a
y
x f1 (t ) x(t ) y f 2 (t ) y (t ) z f 3 (t ) z (t )
(2)点的轨迹方程 平面曲线 x
y
x
f ( x, y, z ) 0(与时间t无关) f ( x, y ) 0
lim
0
2 τ sin
τ
0 (τ , τ ) (τ , τ ) 2 2 2 2 v dτ v an n a n dt
2
2 1
和´以及 同处于M点的密切面内, 的极限方向垂直于 ,亦即n方向。
tan
at an
几 点 讨 论
若 at = 恒量,则动点的运动称为曲线匀变速运动 由 dv = at d t 积分得 v = v 0 + at t 1 2 a t 同理,得 s = s 0 + v0 t + t 2
上两式虽与点的直线运动的公式完全相似,但式at不是 a,
at反映点作曲线运动的运动速度大小变化。 曲线匀速运动: at = 0 注意:曲线运动中,除 v = 0的瞬时外,点的法向加速度总不 为零。直线或曲线的拐点处ρ→∞,法向加速度等于零。
(1)反映速度大小变化的加速度
2
at
dv d s at τ 2 τ dt dt
v
at
at
dv 0 dt
at 方向沿轨迹切线。称为切向加速度。
v dv 0 dt
(2)反映速度方向变化的加速度
an
s
