(完整版)第五章-点的运动学
理论力学习题答案

第三章 空间力系
一、是非题判断题
3.1.1对一空间任意力系,若其力多边形自行封闭,则该力系的主矢为零。 (∨)
平面力系中,若其力多边形自行闭合,则力系平衡。(×)
3.1.2只要是空间力系就可以列出6 个独立的平衡方程。 (×)
2.3.4悬臂式吊车的结构简图如图所示,由DE、AC二杆组成,A、B、C为铰链连接。已知P1=5kN,P2=1kN,不计杆重,试求杆AC杆所受的力和B点的支反力。
(答案:FBx=3.33kN,FBy=0.25kN,FAC=6.65kN)
2.3.5由AC和CD构成的组合粱通过铰链C连接,它的支承和受力如图所示,已知均布载荷强度q=10kN/m,力偶矩M=40kN.m,不计梁重,求支座A、B、D的约束反力和铰链C处所受的力。
3.1.3若由三个力偶组成的空间力偶系平衡,则三个力偶矩矢首尾相连必构成自行封闭的三角形。(∨)
3.1.4空间汇交力系平衡的充分和必要条件是力系的合力为零;空间力偶系平衡的充分和必要条件是力偶系的合力偶矩为零。(∨)
二、填空题
3.2.1若一空间力系中各力的作用线平行于某一固定平面,则此力系有5个独立的平衡方程。
3.3.3如图所示,三圆盘A、B、C的半径分别为15cm、10cm、5cm,三根轴OA、OB、OC在同一平面内,∠AOB为直角,三个圆盘上分别受三个力偶作用,求使物体平衡所需的力F和α角。
3.3.4某传动轴由A、B两轴承支承。圆柱直齿轮的节圆直径d=17.3cm,压力角 =20º,在法兰盘上作用一力偶矩为M=1030N.m的力偶,如轮轴的自重和摩擦不计,求传动轴匀速转动时A、B两轴承的约束反力。(答案:FAx=4.2kN,FAz=1.54kN,FBz=7.7kN,FBz.=2.79kN)
(完整版)点的运动学

dz dt
z
★点的速度矢量在直角坐标轴上的投影等于点的相应坐标对时间
的一阶导数。
点的运动学
速度的大小:
v (dx )2 (dy )2 (dz )2 dt dt dt
(vx )2 (v y )2 (vz )2
速度的方向余弦: cos(v, i )vx源自cos(v ,j)
v vy
v
cos(v ,
k)
vz
v
直角坐标法
z
vz
M
vy
rz
v
vx
a
k
O j
y
i
x
xy
点的运动学
3、点的加速度
设: a axi a y j azk
ax
dv x dt
d2 x dt 2
x
ay
dv y dt
d2 y dt 2
y
az
dvz dt
d2z dt 2
z
直角坐 标法
z
vz
M
vy
rz
v
vx
a
k
d2r dt 2
r
v(t )
v2 a
M a
r
M
v(t t)
a
加速度 — 描述点在 t 瞬时速度大小和方向变化O率的力学量。加速度
的方向为v的极限方向(指向与轨迹曲线的凹向一致) 加速度大小等
于矢量 a 的模。
点的运动学
§6-2 直角坐标法
直角坐标法
1、点的运动方程和轨迹方程
不受约束的点在空间有3个自由度,
r (t )
M
r (t )
末端将描绘出一条连续曲线,称为
矢径端图,它就是动点运动的轨迹。 O
理论力学运动学基础

第五章运动学基础一、是非题1.已知直角坐标描述的点的运动方程为X=f1(t),y=f2(t),z=f3(t),则任一瞬时点的速度、加速度即可确定。
()2.一动点如果在某瞬时的法向加速度等于零,而其切向加速度不等于零,尚不能决定该点是作直线运动还是作曲线运动。
()3.切向加速度只表示速度方向的变化率,而与速度的大小无关。
()4.由于加速度a永远位于轨迹上动点处的密切面内,故a在副法线上的投影恒等于零。
()5.在自然坐标系中,如果速度υ=常数,则加速度α=0。
()6.在刚体运动过程中,若其上有一条直线始终平行于它的初始位置,这种刚体的运动就是平动。
()7.刚体平动时,若刚体上任一点的运动已知,则其它各点的运动随之确定。
()8.若刚体内各点均作圆周运动,则此刚体的运动必是定轴转动。
()9.定轴转动刚体上点的速度可以用矢积表示为v=w×r,其中w是刚体的角速度矢量,r是从定轴上任一点引出的矢径。
()10、在任意初始条件下,刚体不受力的作用、则应保持静止或作等速直线平动。
()二、选择题1、已知某点的运动方程为S=a+bt2(S以米计,t以秒计,a、b为常数),则点的轨迹。
①是直线;②是曲线;③不能确定。
2、一动点作平面曲线运动,若其速率不变,则其速度矢量与加速度矢量。
①平行;②垂直;③夹角随时间变化。
3、刚体作定轴转动时,切向加速度为,法向加速度为。
①r×ε②ε×r③ω×v④v×ω4、杆OA绕固定轴O转动,某瞬时杆端A点的加速度α分别如图(a)、(b)、(c)所示。
则该瞬时的角速度为零,的角加速度为零。
①图(a)系统;②图(b)系统;③图(c)系统。
三、填空题1、点在运动过程中,在下列条件下,各作何种运动?①aτ=0,a n=0(答):;②aτ≠0,a n=0(答):;③aτ=0,a n≠0(答):;④aτ≠0,a n≠0(答):;2、杆O1B以匀角速ω绕O1轴转动,通过套筒A带动杆O2A绕O2轴转动,若O1O2=O2A=L,α=ωt,则用自然坐标表示(以O1为原点,顺时针转向为正向)的套筒A 的运动方程为s=。
理论力学运动学知识点总结

理论力学运动学知识点总结第一篇:理论力学运动学知识点总结运动学重要知识点一、刚体的简单运动知识点总结1.刚体运动的最简单形式为平行移动和绕定轴转动。
2.刚体平行移动。
·刚体内任一直线段在运动过程中,始终与它的最初位置平行,此种运动称为刚体平行移动,或平移。
·刚体作平移时,刚体内各点的轨迹形状完全相同,各点的轨迹可能是直线,也可能是曲线。
·刚体作平移时,在同一瞬时刚体内各点的速度和加速度大小、方向都相同。
3.刚体绕定轴转动。
• 刚体运动时,其中有两点保持不动,此运动称为刚体绕定轴转动,或转动。
• 刚体的转动方程φ=f(t)表示刚体的位置随时间的变化规律。
• 角速度ω表示刚体转动快慢程度和转向,是代数量,以用矢量表示。
,当α与ω。
角速度也可• 角加速度表示角速度对时间的变化率,是代数量,同号时,刚体作匀加速转动;当α 与ω异号时,刚体作匀减速转动。
角加速度也可以用矢量表示。
• 绕定轴转动刚体上点的速度、加速度与角速度、角加速度的关系:。
速度、加速度的代数值为。
• 传动比。
一、点的运动合成知识点总结1.点的绝对运动为点的牵连运动和相对运动的合成结果。
• 绝对运动:动点相对于定参考系的运动;• 相对运动:动点相对于动参考系的运动;• 牵连运动:动参考系相对于定参考系的运动。
2.点的速度合成定理。
• 绝对速度:动点相对于定参考系运动的速度;• 相对速度:动点相对于动参考系运动的速度;• 牵连速度:动参考系上与动点相重合的那一点相对于定参考系运动的速度。
3.点的加速度合成定理。
• 绝对加速度:动点相对于定参考系运动的加速度;• 相对加速度:动点相对于动参考系运动的加速度;• 牵连加速度:动参考系上与动点相重合的那一点相对于定参考系运动的加速度;• 科氏加速度:牵连运动为转动时,牵连运动和相对运动相互影响而出现的一项附加的加速度。
• 当动参考系作平移或 = 0,或与平行时,= 0。
第五章 第一节 三种方法表示点的运动的比较
x
第一节 三种方法表示点的运动的比较
a r
O z a r O y M z x v y M v 直角坐标法 自然法 x=f1(t) 运 y=f2(t) 动 s = f(t) r = r(t) z=f3(t) 方 r=xi+yj+zk 程 g1(x,y)=0 轨 已知 矢端曲线 g2(x,z)=0 迹 vx = x vy= y 速 v=dr/dt r v =s vz = z = 度 沿轨迹切线 v = vt v= vxi+vy j+vzk a=at+an ax= v x 加 ay= v x =att+ann r 速 a= v = az= v z at= v an=v2/r 度 a=axi+ay j+azk an指向曲率中心 矢量法
第五章 点的运动学
本章将研究点的运动 包括点的运动方程、运动轨迹、速度、加速度等。 三种方法: (1)矢量法(主要用于理论分析) (2)直角坐标法(主要用于实际应用) (3) 自然法(主要用于实际应用) 还有柱坐标法和球坐标法(略)
第一节 三种方法表示点的运动的比较
a r
O z a r O y M z x v y M v 直角坐标法 x=f1(t) 运 y=f2(t) 动 z=f3(t) 方 r = r(t) r=xi+yj+zk 程 g1(x,y)=0 轨 矢端曲线 g2(x,z)=0 迹 vx = x vy= y 速 v=dr/dt r vz = z = 度 沿轨迹切线 v= vxi+vy j+vzk ax= v x 加 ay= v x r 速 a= v = az= v z 度 a=axi+ay j+azk 矢量法 自然法
理论力学-运动学

绝对运动 = 相对运动 + 牵连运动
三、 点的合成运动
3、速度合成定理
G GG va = vr + ve
绝对速度
相对速度
牵连速度
牵连速度 —— 动系上与动点重合之点 (牵连点)的绝对速度,称为牵连速度。
三、 点的合成运动
4、加速度合G成定理G G G aa = ae + ar + aC
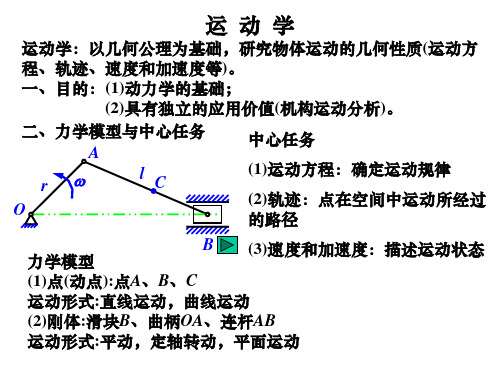
运动学的主要内容 研究物体运动的几何性质
运动学所涉及的研究内容包括: 1、 建立物体的运动方程 2、 分析运动的速度、加速度、
角速度、角加速度等 3、 研究运动的分解与合成规律
一、 点的运动学
采用以下三种方法研究点的运动方程、 运动的速度和加速度:
U 描述点运动的矢量法 U 描述点运动的直角坐标法 U 描述点运动的自然法
(2)投影法 vB= vA+ vBA
vBcosϕ= vAcosθ
y y´ vBA vB
S
Bϕ
ω
vA
Aθ
x´
O
vA x
速度投影定理:平面图形上任意两点的速度 在这两点连线上的投影相等。
2、平面图形内各点的速度
(3)瞬心法
vC = 0
vA= vAC
vA= vC+ vAC
vA = ω ⋅ AC vB = ω ⋅ CB
y
G j+
G z k =
vx
G i + vy
G j + vz
G k
vx = x , vy = y , vz = z
(aG3=)vG加 =速x度iG+
y
G j+
G zk =
理论力学-点的运动学

求该瞬时动点A的 x ,y , x , y ,
y v
30 0
A
0 v 10 cos 30 ( m/s 解: x x
0 y v 10 sin 30 ( m/s) y
o
v v v
x y z
a
x y z
x
x y z
18
2.速度:
v M v r
ds v dt
_
r
0
S M* +
`
r*
19
3
点的切向加速度和法向加速度
dv a a a n dt
n
M
+
dv a dt
v an n
2
20
自然轴系
21
例:已知图示瞬时动点A的速度和加速度,其中
2 :v ,设动点的坐标为x , y 10 m/s, a 10 m/s
z
r o
x
M
y
一、矢量法
1、运动方程
r r(t)
2、速度
3、加速度
dr v r dt 2 d v dr a 2 v r d t d t
8
二、直角坐标法
x x (t) 1、运动方程 y y (t) r x i y j z k z z(t)
0??za??yrx15三自然坐标法1运动方程tss?xyzoms0r2曲线的几何性质?曲率curvaturesks??????0limmtt??smm??mtk1???曲率半径radiuscurvaturemtt极限位置的平面称为密切面osculatingplane已知点的运动轨迹16mtt极限位置的平面称为密切面面osculatingplane17bn??????法面ms?密切面切线b副法线主法线nbn??自然轴系trihedralaxesonacurve1
点的运动教案

a 成正比 方向指向轴心
M
36
§6–3转动刚体内各点的速度和加速度
一 转动刚体内各点的速度和加速度的计算
2 加速度计算逆运算
at
dv dt
d dt
(R)
R
d
dt
R
an
v2
( R ) 2
R
R 2
A
加速转动的刚体,已知其上
一点A的切向加速度
O
判断 角加速度的转向 计算角加速度的大小
❖ 2 在车轮上观察得到的点的运动轨迹? P147例5-6
❖
运动的相对性
24
习题 P 153-154 5-4 注意:1 坐标原点选在固定的点
2 动点选在一般位置
25
§ 5-3 自然法
应用的场合以及如何应用? 1 运动方程 ?速度如何计算? 2 加速度如何计算? 一 弧坐标
O (+)
s
M (-)
s f (t)
dt dt
d
dt
vA 各点速度的大小与该点
vD D
A 到轴心的距离成正比
vB 速度的方向垂直于该点到
O
轴心的连线,指向图形
B 转动的一方。
34
§7–3转动刚体内各点的速度和加速度
一 转动刚体内各点的速度和加速度的计算 速度计算的逆运算
v ds R d R
dt dt
vB OB
vB
8 刚体绕定轴转动时,其上各点的加速度大小 与点到轴心的距离成正比例关系。
A
B
O
66
判断题 9 平面直角折杆绕定轴转动,其中OA=L AB=a 则B点的速度与AB垂直 大小等于角速度与AB长 度的乘积
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: 炸弹的运动方程
x vt cos45
y vt sin 45 gt2 / 2
炸弹的初速度
求炸弹落到地面的时间,由 1800 277.8t sin 45 gt2 / 2
得 t 7.688s
可求出炸弹与目标的水平距离,
40
45 40 5
得: 又: 比较两式得:
速度在各坐标轴上的投影等于动点的各对应坐标对时间的一阶导数。
Part two 运动学
运动学是研究 物体运动的几何性质的学科。
研究一个物体的机械运动,必须选取另一个物体作为 参考,这个参考的物体称为参考体。
运动学研究 点和刚体的运动。
点的运动学 是研究一般物体运动的基础,又 具有独立的应用意义.
研究点的简单运动,研究点相对某一个参考系的 几何位置随时间变动的规律。
(4)求点M速度矢、加速度矢的大小、方向。
x=asin=asinωt 轨迹方程: y=bcos=bcosωt
大小、方向均可求
例:如图,物体M自O点以速度v0 与水平成 角抛出,求M 点的运动规律及轨迹。
解:依题意,建坐标,有:
当t=0时: 得:
所以,有: V0 cos0t C3
V0 sin0t gt2 2 C4
连接各矢量端点构成矢量端点的连续曲线,称为速度
矢端曲线。
见flash
动点的加速度矢a 的方向与速度矢端曲线在相应点的切线相平行。
r1 r2 r3
v1 a
v2 v3
v1
v2
v v3
a
§5-2 直角坐标法
动点M的位置可以用r表示,也可 用坐标x、y、z来表示,如图所示。
矢径原点与坐标原点重合时,有:
当t=0时,有: x 0, y 0 得 C3 C4 0
有: x V0 cos0t y V0 sin0t gt2 2
消去t得:
y
tan0
1 2
g
V02
x2 cos2
0
两类问题: (1)已知运动求速度、加速度,微分; (2)已知速度、加速度求运动,积分。 由已知条件求积分常数
例:牵引车A自O点匀速沿水平方向开 出,速度VA=0.4m/s,用绳索拉动B车, B车高于A车1.5m。求当A车驶出距离 OA=2m时,B车的速度和加速度。
解:需建立运动方程,以B0为原点,建立坐标,由几何关系有:
B0C CO BC CA
于是
B0C BC CA CO
即
x h2 (OA)2 h
而: OA vAt s
x h2 (vAt)2 h
求导
代入数据, vB 0.32m s
再求导
aB
dvB dt
v
2 A
h2 (vAt)2
a
dv dt
d2s dt 2
、n、b分别为切线、主法线、 副法线上的单位矢量。 切线、主法线、副法线这三轴称为自然轴, 这三个正交轴组成的正交坐标系称为自然坐标系。
在研究曲线运动中,轨迹的曲率或曲率半径是一个 重要的参数,表示曲线的弯曲程度。
曲率:曲线切线的转角对弧长一阶导数的绝对 值,曲率的倒数称为曲率半径。
3、速度与加速度
r是时间的单值连续函数,x、y、z
也是时间的单值连续函数。 是以直角坐标表示的点的运动方程。
工程中,常遇到点在平面内运动的情形, 此时点的轨迹为一平面曲线。
取轨迹所在的平面为坐标平面Oxy,则点 的运动方程为:
消去t,得轨迹方程: f(x,y)=0
例:飞机以角度=45俯冲投弹,其俯冲速 度v=1000km/h,高度h=1800m,问飞机俯冲 时应超前 多少度 投弹方能击中目标。
矢径r 的 “矢端曲线” 就是动点M的运动轨迹。
点的速度是矢量。动点的速度矢等于它的 矢径r 对时间 的一阶导数,即:
动点速度矢:沿 r 的矢端曲线的切线,即沿动点运动轨 迹的切线,并与此点运动的方向一致。
速度的大小,即速度矢v的模,表明点运动的快慢,其 量纲为: dim v LT 1
在国际单位制中速度v的单位:
t0
速度大小为动点弧坐标对时间导数的绝对值。
v ds 是代数量,s>0,s随t增大而增大,
dt
向正向运动
加速度
反映速度大小变化,切向加速度;
反映速度方向变化, 法向加速度a永n 为正, 方向沿主法线指
向曲率中心。
flash
均在密切面内,
全加速度也在密切面内。
(vA2t)2
3
h2 (vAt)2 2
0.023 m s2
§5-3 自然法
1、弧坐标
如图,动点M的坐标由弧长决定,即:
s=f(t) 称为点沿轨迹的运动方程,或弧坐标表示的运动方程。
2、自然轴系
两平面交线为主法线,单位矢量为n, 指向内侧。
过M与切线及主法线垂直的直线为副法 线,单位矢量为b。
加速度在副法线方向的分量为零(无投影)。
tg a
an
:与法线夹角
速度和切向加速度方位相同,投影同号,加速运动。
a为常数时,匀变速运动。
dv dt
a
v v0 a t
V0、S0为t=0时的速度和弧坐标。 除直线运动或v=0的瞬时外,法向加速度总不为0。
小结 s=f(t)
flash
v ds dt
点的速度矢对时间的变化率称为加速度。 点的加速度也是矢量,表征速度大小和方向的变化。 动点加速度矢等于该点的 速度矢对时间的一阶导数: 加速度的量纲为: dim a LT 2
国际单位制中加速度a的单位:
在空间任意取一点o,把动点M在连 续不同瞬时的速度矢 v、 v’、v” …等 都平行地移到点o。
包括以下内容: •点的运动方程 •点的运动轨迹
•速度和加速度
§5-1 矢量法
选取参考系上某确定点O为坐标原点: 自点O向动点M作矢量 r,
称 “r” 为点M相对 原点O 的位置矢量,简称矢径。
当动点M运动时,矢径r随时间而变化,并且是时间 的单值连续函数,即:
上式称为以矢量表示的点的运动方程。
动点M在运动过程中,其矢径r的末端描绘出一条连续 曲线,称为矢端曲线。
同理: 可得出:
加速度在直角坐标轴上的投影等于动点的各对应坐标对 时间的二阶导数。
例:如图,直杆AB两端分别沿ox、oy运动,确定杆上一点M 的运动方程和轨迹方程、速度以及加速度。
得运动方程:
解: (1)建立坐标系,由几何关系求出动点M的坐 标,即得到点M的运动方程;
(2)消去t,得到轨迹方程;
(3)对点M的运动方程求一阶、二阶导数(v,a的 投影);
