最新高三数学专题复习资料直线平面平行的判定及其性质
2023年新高考数学一轮复习8-4 直线、平面平行的判定及性质(知识点讲解)含详解

专题8.4 直线、平面平行的判定及性质(知识点讲解)【知识框架】【核心素养】以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理,运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题,凸显逻辑推理、直观想象、数学运算的核心素养.【知识点展示】(一)空间平行关系1.直线与平面平行的判定与性质a∥α,a⊂β,2.利用线面平行的定义,一般用反证法;利用线面平行的判定定理(a ⊄α,b ⊂α,a ∥b ⇒a ∥α),其关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言的叙述;)利用面面平行的性质定理(α∥β,a ⊂α⇒a ∥β); 利用面面平行的性质(α∥β,a ⊄β,a ∥α⇒a ∥β). (二)平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行,即若a ⊥α,a ⊥β,则α∥β. (2)垂直于同一个平面的两条直线平行,即若a ⊥α,b ⊥α,则a ∥b. (3)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.【常考题型剖析】题型一:与线、面平行相关命题的判定例1. (2023·全国·高三专题练习)已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列结论中正确的是( ) A .若m //α,m //n ,则n //α B .若m //α,n //α,则m //n C .若m //α,n ⊂α,则m //nD .若m //α,m ⊂β,αβ=n ,则m //n例2.(2022·上海静安·二模)在下列判断两个平面α与β平行的4个命题中,真命题的个数是( ). (1)α、β都垂直于平面r ,那么α∥β. (2)α、β都平行于平面r ,那么α∥β. (3)α、β都垂直于直线l ,那么α∥β.(4)如果l 、m 是两条异面直线,且l ∥α,m ∥α,l ∥β,m ∥β,那么α∥β A .0B .1C .2D .3例3.(四川·高考真题(文))下列命题正确的是( ) A .若两条直线和同一个平面所成的角相等,则这两条直线平行 B .若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D .若两个平面都垂直于第三个平面,则这两个平面平行例4. (2022·云南师大附中模拟预测(理))若α,β是两个不同平面,m ,n 是两条不同直线,则下列4个推断中正确的是( )A .m α∥,m β∥,n ⊂α,n m n β⊂⇒∥B .m α⊂,n β⊂,m n αβ⇒∥∥C .m α∥,n α∥,m β⊂,n βαβ⊂⇒∥D .m α⊂,n β⊂,m n αβ⇒∥∥ 【方法技巧】直线、平面间平行的判定方法(1)关注是否符合判定定理与性质定理,并注意定理中易忽视的条件. (2)结合题意构造或绘制图形,结合图形作出判断. (3)利用实物进行空间想象,比较判断.(4)熟记一些常见结论,如垂直于同一条直线的两个平面平行等. 题型二:直线与平面平行的判定例5.(2023·全国·高三专题练习)在直三棱柱111ABC A B C -中,D 、E 、F 、M 、N 分别是BC 、11B C 、1AA 、1CC 、1A C 的中点,给出下列四个判断:①//EF 平面1ADB ;②//EM 平面1ADB ; ③//EN 平面1ADB ; ④1//A M 平面1ADB , 错误的序号为___________.例6.【多选题】(2017·全国·高考真题(文))如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 平行的是( )A.B.C.D.例7.(2023·全国·高三专题练习)如图,AB是圆O的直径,点C是圆O上异于,A B的点,直线PC 平面ABC,,E F分别是PA,PC的中点.记平面BEF与平面ABC的交线为l,求证:直线l//平面PAC【总结提升】证明直线与平面平行的方法(1)线面平行的定义:一条直线与一个平面无公共点(不相交).(2)线面平行的判定定理:关键是找到平面内与已知直线平行的直线.常利用三角形的中位线、平行四边形的对边、成比例线段出现平行线或过已知直线作一平面找其交线.注意内外平行三条件,缺一不可.题型三:线面平行性质定理的应用例8.(福建·高考真题(文))如图,在正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD 上.若EF∥平面AB1C,则线段EF的长度等于________.例9.(2019·全国卷Ⅰ改编)如图,直四棱柱ABCD A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.证明:MN ∥平面C 1DE .例10.如图,在直四棱柱ABCD A 1B 1C 1D 1中,E 为线段AD 上的任意一点(不包括A ,D 两点),平面CEC 1∩平面BB 1D =FG .证明:FG ∥平面AA 1B 1B .【总结提升】 1.思路方法:(1)通过线面平行可得到线线平行,其中一条线应是两平面的交线,要树立这种应用意识. (2)利用线面平行性质必须先找出交线. 2.易错提醒(1)在推证线面平行时,一定要强调直线不在平面内,否则,会出现错误.(2)线面平行关系证明的难点在于辅助面和辅助线的添加,在添加辅助线、辅助面时一定要以某一性质定理为依据,绝不能主观臆断.(3)解题中注意符号语言的规范应用. 题型四:平面与平面平行的判定与性质例11.(2023·全国·高三专题练习)已知长方体1111ABCD A B C D -中,4AB AD ==,12AA =,E ,F 分别为棱11A B 和11A D 的中点,M 为长方体表面上任意一点.若BM ∥平面AEF ,则BM 的最大值为( )A.B .C .D .6例12.(2020·全国·高三专题练习(文))如图,平面//α平面β,PAB △所在的平面与α,β分别交于CD 和AB ,若2PC =,3CA =,1CD =,则AB =______.例13.(2023·全国·高三专题练习)如图,在正方体1111ABCD A B C D -中,E ,F分别为棱11,DD CC 的中点.求证:平面1//AEC 平面BDF例14.(陕西·高考真题(文))如图,四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O∥平面ABCD, 12AB AA ==.(1)证明: 平面A 1BD // 平面CD 1B 1;(2)求三棱柱ABD -A 1B 1D 1的体积.【规律方法】 1.证明面面平行的常用方法 (1)利用面面平行的定义.(2)利用面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. (3)利用“垂直于同一条直线的两个平面平行”.(4)利用“如果两个平面同时平行于第三个平面,那么这两个平面平行”. (5)利用“线线平行”“线面平行”“面面平行”的相互转化.2.面面平行的应用(1)两平面平行,构造与之相交的第三个平面,可得交线平行.(2)两平面平行,其中一个平面内的任意一条直线与另一个平面平行,可用于证明线面平行.3.三种平行关系之间的转化其中线面平行是核心,线线平行是基础,要注意它们之间的灵活转化.专题8.4 直线、平面平行的判定及性质(知识点讲解)【知识框架】【核心素养】以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理,运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题,凸显逻辑推理、直观想象、数学运算的核心素养.【知识点展示】(一)空间平行关系1.直线与平面平行的判定与性质a∥α,a⊂β,2.利用线面平行的定义,一般用反证法;利用线面平行的判定定理(a ⊄α,b ⊂α,a ∥b ⇒a ∥α),其关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言的叙述;)利用面面平行的性质定理(α∥β,a ⊂α⇒a ∥β); 利用面面平行的性质(α∥β,a ⊄β,a ∥α⇒a ∥β). (二)平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行,即若a ⊥α,a ⊥β,则α∥β. (2)垂直于同一个平面的两条直线平行,即若a ⊥α,b ⊥α,则a ∥b. (3)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.【常考题型剖析】题型一:与线、面平行相关命题的判定例1. (2023·全国·高三专题练习)已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列结论中正确的是( ) A .若m //α,m //n ,则n //α B .若m //α,n //α,则m //n C .若m //α,n ⊂α,则m //n D .若m //α,m ⊂β,αβ=n ,则m //n【答案】D 【解析】 【分析】举例说明判断A ,B ,C ;利用线面平行的性质判断D 作答. 【详解】如图,长方体1111ABCD A B C D -中,平面1111D C B A 视为平面α,对于A ,直线AB 视为m ,直线11A B 视为n ,满足m //α,m //n ,而n ⊂α,A 不正确;对于B,直线AB视为m,直线BC视为n,满足m//α,n//α,而m与n相交,B不正确;A D视为n,满足m//α,n⊂α,显然m与n是异面直线,C不正确;对于C,直线AB视为m,直线11对于D,由直线与平面平行的性质定理知,D正确.故选:D例2.(2022·上海静安·二模)在下列判断两个平面α与β平行的4个命题中,真命题的个数是().(1)α、β都垂直于平面r,那么α∥β.(2)α、β都平行于平面r,那么α∥β.(3)α、β都垂直于直线l,那么α∥β.(4)如果l、m是两条异面直线,且l∥α,m∥α,l∥β,m∥β,那么α∥βA.0B.1C.2D.3【答案】D【解析】【分析】由面面平行的判定定理及其相关结论分析可得结果.【详解】由面面平行的判定定理分析可知(1)错,(2),(3),(4)正确.故选:D例3.(四川·高考真题(文))下列命题正确的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行【答案】C【解析】【详解】若两条直线和同一平面所成角相等,这两条直线可能平行,也可能为异面直线,也可能相交,所以A错;一个平面不在同一条直线的三点到另一个平面的距离相等,则这两个平面平行,故B错;若两个平面垂直同一个平面两平面可以平行,也可以垂直;故D错;故选项C正确.例4. (2022·云南师大附中模拟预测(理))若α,β是两个不同平面,m ,n 是两条不同直线,则下列4个推断中正确的是( )A .m α∥,m β∥,n ⊂α,n m n β⊂⇒∥B .m α⊂,n β⊂,m n αβ⇒∥∥C .m α∥,n α∥,m β⊂,n βαβ⊂⇒∥D .m α⊂,n β⊂,m n αβ⇒∥∥【答案】A【解析】【分析】利用线面,面面位置关系逐项分析即得.【详解】对于A ,如图,n ⊂α,n n βαβ⊂⇒⋂=,结合m α,m β,可知m n ∥,故A 正确;对于B ,如图,m ,n 可能异面,故B 错误;对于C ,如图,α,β可能相交,故C 错误;对于D ,如图,αβ,可能相交,故D 错误.故选:A .【方法技巧】直线、平面间平行的判定方法(1)关注是否符合判定定理与性质定理,并注意定理中易忽视的条件.(2)结合题意构造或绘制图形,结合图形作出判断.(3)利用实物进行空间想象,比较判断.(4)熟记一些常见结论,如垂直于同一条直线的两个平面平行等.题型二:直线与平面平行的判定例5.(2023·全国·高三专题练习)在直三棱柱111ABC A B C -中,D 、E 、F 、M 、N 分别是BC 、11B C 、1AA 、1CC 、1A C 的中点,给出下列四个判断:①//EF 平面1ADB ;②//EM 平面1ADB ;③//EN 平面1ADB ;④1//A M 平面1ADB ,错误的序号为___________.【答案】①②④【解析】【分析】连接DE 、1A E 、CE 、EF 、EM 、EN 、1A M 、FM ,证明出平面1//A CE 平面1AD B ,利用面面平行的性质结合假设法可判断①②③④的正误.【详解】连接DE 、1A E 、CE 、EF 、EM 、EN 、1A M 、FM ,在三棱柱111ABC A B C -中,因为11//BB CC 且11BB CC =,所以,四边形11BB C C 为平行四边形,则11//BC B C 且11BC B C =,D 、E 分别为BC 、11B C 的中点,则1//CD B E 且1CD B E =,故四边形1CDB E 为平行四边形,则1//CE B D ,CE ⊄平面1ADB ,1B D ⊂平面1ADB ,故//CE 平面1ADB ,同理可证四边形1BB ED 为平行四边形,则11////DE BB AA ,11DE BB AA ==,则四边形1AA ED 为平行四边形,所以,1//A E AD ,1A E ⊄平面1ADB ,AD ⊂平面1ADB ,则1//A E 平面1ADB ,1CE A E E =,故平面1//A CE 平面1AD B ,EN ⊂平面1A CE ,则//EN 平面1ADB ,③对;对于①,若//EF 平面1ADB ,EF EN E =,则平面//EFN 平面1ADB ,因为过点E 且与平面1ADB 平行的平面只有一个,矛盾,故①错,同理可知,②④均错.故答案为:①②④.例6.【多选题】(2017·全国·高考真题(文))如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 平行的是( )A .B .C .D .【答案】BCD【解析】【分析】利用线面平行判定定理逐项判断可得答案.【详解】对于选项A,OQ∥AB,OQ与平面MNQ是相交的位置关系,故AB和平面MNQ不平行,故A错误;对于选项B,由于AB∥CD∥MQ,结合线面平行判定定理可知AB∥平面MNQ,故B正确;对于选项C,由于AB∥CD∥MQ,结合线面平行判定定理可知AB∥平面MNQ:故C正确;对于选项D,由于AB∥CD∥NQ,结合线面平行判定定理可知AB∥平面MNQ:故D正确;故选:BCD例7.(2023·全国·高三专题练习)如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,直线PC ⊥平面ABC ,,E F 分别是PA ,PC 的中点.记平面BEF 与平面ABC 的交线为l ,求证:直线l //平面PAC【答案】证明见解析【解析】【分析】先通过//EF AC 可得出//EF 平面ABC ,再利用线面平行的性质即可证明.【详解】因为,E F 分别是,PA PC 的中点,所以//EF AC ,又因为AC ⊂平面ABC ,EF ⊄平面ABC ,所以//EF 平面ABC ,又EF ⊂平面BEF ,平面BEF 与平面ABC 的交线为l ,所以//EF l ,而l ⊄平面PAC ,EF ⊂平面PAC ,所以//l 平面P AC .【总结提升】证明直线与平面平行的方法(1)线面平行的定义:一条直线与一个平面无公共点(不相交).(2)线面平行的判定定理:关键是找到平面内与已知直线平行的直线.常利用三角形的中位线、平行四边形的对边、成比例线段出现平行线或过已知直线作一平面找其交线.注意内外平行三条件,缺一不可. 题型三:线面平行性质定理的应用例8.(福建·高考真题(文))如图,在正方体ABCD -A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上.若EF ∥平面AB 1C ,则线段EF 的长度等于________.【解析】【分析】根据直线与平面平行的性质定理可得//EF AC ,再根据E 为AD 的中点可得F 为CD 的中点,从而根据三角形的中位线可得.【详解】如图:因为//EF 平面1AB C ,EF ⊂平面DABC ,且平面1A C B 平面ABCD AC =,所以//EF AC ,又因为E 为AD 的中点,所以F 为CD 的中点, 所以12EF AC =,因为正方体的棱长为2.所以AC =所以EF =故答案为.例9.(2019·全国卷Ⅰ改编)如图,直四棱柱ABCD A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M,N分别是BC,BB1,A1D的中点.证明:MN∥平面C1DE.【答案】见解析【解析】证明:连接B1C,ME.因为M,E分别为BB1,BC的中点,所以ME∥B1C,且ME=12B1C.又因为N为A1D的中点,所以ND=12A1D.由题设知A1B1//=DC,可得B1C//=A1D,故ME//=ND,因此四边形MNDE为平行四边形,所以MN∥ED.又MN⊄平面C1DE,ED⊂平面C1DE,所以MN∥平面C1DE.例10.如图,在直四棱柱ABCDA1B1C1D1中,E为线段AD上的任意一点(不包括A,D两点),平面CEC1∩平面BB1D=FG.证明:FG∥平面AA1B1B.【答案】见解析【解析】证明:在直四棱柱ABCDA1B1C1D1中,BB1∥CC1,BB1⊂平面BB1D,CC1⊄平面BB1D,所以CC1∥平面BB1D.又CC1⊂平面CEC1,平面CEC1∩平面BB1D=FG,所以CC1∥FG.因为BB1∥CC1,所以BB1∥FG.而BB1⊂平面AA1B1B,FG⊄平面AA1B1B,所以FG∥平面AA1B1B.【总结提升】1.思路方法:(1)通过线面平行可得到线线平行,其中一条线应是两平面的交线,要树立这种应用意识.(2)利用线面平行性质必须先找出交线.(1)在推证线面平行时,一定要强调直线不在平面内,否则,会出现错误.(2)线面平行关系证明的难点在于辅助面和辅助线的添加,在添加辅助线、辅助面时一定要以某一性质定理为依据,绝不能主观臆断.(3)解题中注意符号语言的规范应用.题型四:平面与平面平行的判定与性质例11.(2023·全国·高三专题练习)已知长方体1111ABCD A B C D -中,4AB AD ==,12AA =,E ,F 分别为棱11A B 和11A D 的中点,M 为长方体表面上任意一点.若BM ∥平面AEF ,则BM 的最大值为( )A.B .C .D .6【答案】C【解析】【分析】由面面平行的性质结合题意可确定点M 所在的平面,再由平面几何的性质即可确定BM 的值为最大值时的位置,即可求解【详解】如图所示,取G ,H 分别为棱11B C 和11D C 的中点,连接11,,,BG DH BD B D ,由题意易知1111,BF B D GH B D ∥∥,所以BF GH ∥;又易知AF BG ∥,故可以证明平面BGHD ∥平面AEF ;又BM ∥平面AEF ,由面面平行的性质可知M ∈平面BGHD ,所以由题意可知M 在等腰梯形BGHD 四条边上运动,过点H 作HQ BD ⊥,交BD 于点Q ,由题意可知BD GH DH BG DQ ====所以HQ BQ BD DQ =-=所以BH又BD BH ==,所以故当M 与D 点重合时,BM 的值为最大值,此时BM BD ==例12.(2020·全国·高三专题练习(文))如图,平面//α平面β,PAB △所在的平面与α,β分别交于CD 和AB ,若2PC =,3CA =,1CD =,则AB =______. 【答案】52【解析】【分析】根据面面平行的性质,证得//CD AB ,结合CD PC AB PA =,即可求解. 【详解】由题意,平面//α平面β,PAB △所在的平面与α,β分别交于CD 和AB , 根据面面平行的性质,可得//CD AB ,所以CD PC AB PA =, 因为2PC =,3CA =,1CD =,所以15522CD PA AB PC ⋅⨯===.故答案为:52. 例13.(2023·全国·高三专题练习)如图,在正方体1111ABCD A B C D -中,E ,F 分别为棱11,DD CC 的中点.求证:平面1//AEC 平面BDF【答案】证明见解析【解析】【分析】根据1//DF EC ,可证明1//EC 平面BDF ;又//BF AE ,可得//AE 平面BDF .进而根据线面平行证明面面平行.【详解】证明:在正方体1111ABCD A B C D -中,E ,F 分别为棱11,DD CC 的中点, 所以11111,22DE DD C F CC ==. 因为11CC DD =,且11//CC DD ,所以1DE C F =,且1//DE C F ,所以四边形1DEC F 是平行四边形,所以1//DF EC 又DF ⊂平面BDF ,1EC ⊄平面BDF ,所以1//EC 平面BDF .同理,//BF AE ,又BF ⊂平面BDF ,AE ⊄平面BDF , 所以//AE 平面BDF .又1AE EC E ⋂=,1,AE EC ⊂平面1AEC ,所以平面1//AEC 平面BDF 例14.(陕西·高考真题(文))如图,四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O∥平面ABCD, 1AB AA =(1)证明: 平面A 1BD // 平面CD 1B 1;(2)求三棱柱ABD -A 1B 1D 1的体积.【答案】(1)证明见解析;(2)1.【解析】【详解】试题分析:(1)要证明1A C ⊥平面11BB D D ,只要证明1A C 垂直于平面11BB D D 内的两条相交直线即可,由已知可证出1A C ⊥BD ,取11B D 的中点为1E ,通过证明四边形11A OCE 为正方形可证1A C ⊥1E O .由线面垂直的判定定理问题得证;(2)由已知1A O 是三棱柱ABD ﹣A 1B 1D 1的高,由此能求出三棱柱ABD ﹣A 1B 1D 1的体积 试题解析:(Ⅰ)∵四棱柱ABCD ﹣A 1B 1C 1D 1的底面ABCD 是正方形,O 为底面中心,A 1O ⊥平面ABCD ,AB=AA 1=,由棱柱的性质可得BB 1和DD 1平行且相等,故四边形BB 1D 1D 为平行四边形,故有BD 和B 1D 1平行且相等.而BD 不在平面CB 1D 1内,而B 1D 1在平面CB 1D 1内,∴BD ∥平面CB 1D 1.同理可证,A 1BCD 1为平行四边形,A 1B ∥平面CB 1D 1.而BD 和A 1B 是平面A 1BD 内的两条相交直线,故有平面A 1BD ∥平面CD 1B 1 .(Ⅱ)由题意可得A 1O 为三棱柱ABD ﹣A 1B 1D 1的高.三角形A 1AO 中,由勾股定理可得A 1O===1,∴三棱柱ABD ﹣A 1B 1D 1的体积V=S △ABD •A 1O=•A 1O=×1=1.【规律方法】1.证明面面平行的常用方法 (1)利用面面平行的定义.(2)利用面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(3)利用“垂直于同一条直线的两个平面平行”.(4)利用“如果两个平面同时平行于第三个平面,那么这两个平面平行”.(5)利用“线线平行”“线面平行”“面面平行”的相互转化.2.面面平行的应用(1)两平面平行,构造与之相交的第三个平面,可得交线平行.(2)两平面平行,其中一个平面内的任意一条直线与另一个平面平行,可用于证明线面平行.3.三种平行关系之间的转化其中线面平行是核心,线线平行是基础,要注意它们之间的灵活转化.。
数学新高考第3节 直线、平面平行的判定及其性质

线平行”)
[提醒] 应用判定定理时,要注意“内”“外”“平行”三个条件必须都具 备,缺一不可.
6
直线、平面平行的判定及其性质
《高考特训营》 ·数学 返 回
2.平面与平面平行的判定定理和性质定理
文字语言 一个平面内的两条相交直 判定 线与另一个平面平行,则这 定理 两个平面平行(简记为“线 面平行⇒面面平行”)
13
直线、平面平行的判定及其性质
《高考特训营》 ·数学 返 回
1.[易错诊断]下列命题中正确的是( D ) A.若 a,b 是两条直线,且 a∥b,那么 a 平行于经过 b 的任何平面 B.若直线 a 和平面 α 满足 a∥α,那么 a 与 α 内的任何直线平行 C.平行于同一条直线的两个平面平行
【易错点拨】判断直线与平面的位置关系时,忽视“直线在平面内”致误.
15
直线、平面平行的判定及其性质
《高考特训营》 ·数学 返 回
2.[教材改编]如图是长方体被一平面所截得的几何体,四边形EFGH为截 面,则四边形EFGH的形状为________.
答案:平行四边形
解析:因为平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平 面EFGH∩平面DCGH=HG,所以EF∥HG.同理,EH∥FG,所以四边形 EFGH是平行四边形.
202直2届线、平面平行的判定及其性质
《高考特《训高营考》特·训数营学》 ·返数回学
第3节 直线、平面平行的判定及 其性质
1 1
直线、平面平行的判定及其性质
《高考特训营》 ·数学 返 回
课标要求
命题方向
数学素养
1.从基本事实出发,借助长方 1.线面平行的判定与性 逻辑推理、直观想象
体,通过直观感知,了解空间 质
最新高考数学总复习——第7章 第3节 直线、平面平行的判定及其性质

解答此类问题时,特别注意定理所要求的条件是否完 备,图形是否有特殊情况,可通过举反例否定结论或用反证法推断 命题是否正确.
考点2 直线与平面平行的判定与性质 直线与平面平行的判定
证明线面平行的常用方法 (1)利用线面平行的定义(无公共点). (2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α). (3)利用面面平行的性质定理(α∥β,a⊂α⇒a∥β). (4)利用面面平行的性质(α∥β,a⊄β,a∥α⇒a∥β).
∴O为AC的中点. 又∵F是PC的中点,∴FO∥AP. ∵FO⊂平面BEF,AP⊄平面BEF, ∴AP∥平面BEF.
(2)连接FH,OH, ∵F,H分别是PC,CD的中点, ∴FH∥PD. ∵PD⊂平面PAD,FH⊄平面PAD, ∴FH∥平面PAD. 又∵O是AC的中点,H是CD的中点,∴OH∥AD. 又∵AD⊂平面PAD,OH⊄平面PAD,
(2)在△ABC中,E,F分别为AB,AC的中点, ∴EF∥BC. ∵EF⊄平面BCHG,BC⊂平面BCHG, ∴EF∥平面BCHG. ∵A1G EB, ∴四边形A1EBG是平行四边形,则A1E∥GB.
∵A1E⊄平面BCHG,GB⊂平面BCHG, ∴A1E∥平面BCHG. ∵A1E∩EF=E,∴平面EFA1∥平面BCHG.
⊂平面PBC,
所以FM∥平面PBC.
直线与平面平行的性质 应用线面平行的性质定理的关键是如何确定交线的位 置,有时需要经过已知直线作辅助平面来确定交线.
如图所示,四边形ABCD是平行四边形,点P是平面 ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面 交平面BDM于GH.
求证:AP∥GH.
高考数学总复习
7.3 直线、平面平行 的判定及其性质
高中数学-直线平面平行的性质及判定

一、空间几何体的表面积1棱柱、棱锥的表面积:各个面面积之和2 圆柱的表面积3 圆锥的表面积2r rl S ππ+=4 圆台的表面积22R Rl r rl S ππππ+++=5 球的表面积24R S π=二、空间几何体的体积1柱体的体积 h S V ⨯=底2锥体的体积 h S V ⨯=底313台体的体积 hS S S S V ⨯++=)31下下上上( 4球体的体积 334R V π=三、直线、平面平行的判定与性质1、直线与平面平行的判定定理平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行, 用符号表示为a ⊄α,b ⊂α,且a ∥b ⇒a ∥α。
(1)运用直线与平面平行的判定定理时,必须具备三个条件: ①平面外一条直线;②平面内一条直线;③两条直线相互平行.(2)直线与平面平行的判定定理的关键是证明两直线平行,证两直线平行是平面几何的问题,所以该判定定理体现了空间问题平面化的思想.(3)判定直线与平面平行有以下方法:一是判定定理;二是线面平行定义;三是面面平行的性质定理.【例1】 如右图所示,已知P 、Q 是单位正方体ABCD —A 1B 1C 1D 1的面A 1B 1BA 和面ABCD 的中心.求证:PQ ∥平面BCC 1B 1.证:如右图,取B 1B 中点E ,BC 中点F ,连结PE 、QF 、EF , ∵△A 1B 1B 中,P 、E 分别是A 1B 和B 1B 的中点, ∴PE12A 1B 1.同理QF 12AB .又A 1B 1AB ,∴PE QF .∴四边形PEFQ 是平行四边形. ∴PQ ∥EF .又PQ ⊄平面BCC 1B 1,EF ⊂平面BCC 1B 1, ∴PQ ∥平面BCC 1B 1.222r rl S ππ+=2、平面与平面平行的判定定理一个平面内的两条相交直线与另一个平面相交直线,则这两个平面平行.用符号表示为:a ⊂β,b ⊂β,a∩b=P ,a ∥α,b ∥α⇒β∥α(1)运用判定定理证明平面与平面平行时,两直线是相交直线这一条件是关键,缺少这一条件则定理不一定成立.(2)证明面与面平行常转化为证明线面平行,而证线面平行又转化为证线线平行,逐步由空间转化到平面.(3)证明平面与平面平行的方法有:判定定理、线面垂直的性质定理、定义. (4)平面与平面的平行也具有传递性.【例2】 如右图所示,正三棱柱ABC —A 1B 1C 1各棱长为4,E 、F 、G 、H 分别是AB 、AC 、A 1C 1、A 1B 1的中点, 求证:平面A 1EF ∥平面BCGH .思晨分析:本题证面面平行,可证明平面A 1EF 内的两条相交直线分别与平面BCGH 平行,然后根据面面平行的判定定理即可证明. 证明:△ABC 中,E 、F 分别为AB 、AC 的中点, ∴EF ∥BC .又∵EF ⊄ 平面BCGH ,BC ⊂平面BCGH , ∴EF ∥平面BCGH .又∵G 、F 分别为A 1C 1,AC 的中点,∴A 1G FC .∴四边形A 1FCG 为平行四边形. ∴A 1F ∥GC .又∵A 1F ⊄平面BCGH ,CG ⊂平面BCGH , ∴A 1F ∥平面BCGH . 又∵A 1F ∩EF =F ,∴平面A 1EF ∥平面BCGH .3、直线与平面平行的性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线 与该直线平行。
最新高三数学专题复习资料直线、平面平行的判定及其性质
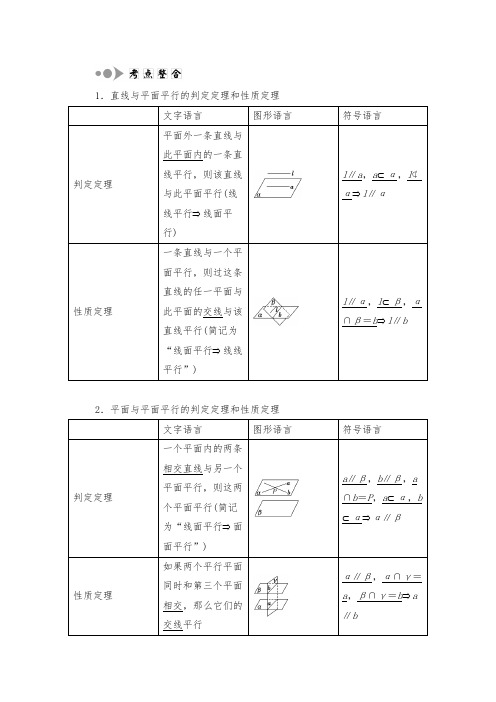
1.直线与平面平行的判定定理和性质定理2.平面与平面平行的判定定理和性质定理1.如果一条直线和平面内一条直线平行,那么这条直线和这个平面平行吗?提示:不一定.只有当此直线在平面外时才有线面平行.2.如果一条直线和一个平面平行,那么这条直线和这个平面内的任意一条直线都平行吗?提示:不都平行.对于任意一条直线而言,存在异面的情况.3.如果一个平面内有无数条直线与另一个平面平行,那么这两个平面平行吗?提示:不一定.可能平行,也可能相交.4.如果两个平面平行,则一个平面内的直线与另一个平面有什么位置关系?提示:平行.1.若两条直线都与一个平面平行,则这两条直线的位置关系是( )A.平行 B.相交C.异面 D.以上均有可能解析:选D 与一个平面平行的两条直线可以平行、相交,也可以异面.2.下列命题中,正确的是( )A.若a∥b,b⊂α,则a∥αB.若a∥α,b⊂α,则a∥bC.若a∥α,b∥α,则a∥bD.若a∥b,b∥α,a⊄α,则a∥α解析:选D 由直线与平面平行的判定定理知,三个条件缺一不可,只有选项D正确.3.设l为直线,α,β是两个不同的平面.下列命题中正确的是( ) A.若l∥α,l∥β,则α∥βB.若l⊥α,l⊥β,则α∥βC.若l⊥α,l∥β,则α∥βD.若α⊥β,l∥α,则l⊥β解析:选B l∥α,l∥β,则α与β可能平行,也可能相交,故A项错;由面面平行的判定定理可知B项正确;由l⊥α,l∥β可知α⊥β,故C项错;由α⊥β,l∥α可知l与β可能平行,也可能相交,故D项错.4.(教材习题改编)已知平面α∥β,直线a⊂α,有下列命题:①a与β内的所有直线平行;②a与β内无数条直线平行;③a与β内的任意一条直线都不垂直.其中真命题的序号是________.解析:由面面平行的性质可知,过a与β相交的平面与β的交线才与a平行,故①错误;②正确;平面β内的直线与直线a平行,异面均可,其中包括异面垂直,故③错误.答案:②5.已知正方体ABCDA1B1C1D1,下列结论中,正确的结论是________(只填序号).①AD1∥BC1;②平面AB1D1∥平面BDC1;③AD1∥DC1;④AD1∥平面BDC1.解析:连接AD1、BC1,所以四边形AD1C1B为平行四边形,故AD1∥BC1,从而①正确;易证BD∥B1D1,AB1∥DC1,又AB1∩B1D1=B1,BD∩DC1=D,故平面AB1D1∥平面BDC1,从而②正确;由图易知AD1与DC1异面,故③错误;因AD1∥BC1,AD1⊄平面BDC1,BC1⊂平面BDC1,故AD1∥平面BDC1,故④正确.答案:①②④1.线面平行的判定及性质是每年高考的必考内容,多出现在解答题中的第(1)、(2)问,难度适中,属中档题.2.高考对线面平行的判定及性质的考查常有以下两个命题角度:(1)以多面体为载体,证明线面平行问题;(2)以多面体为载体,考查与线面平行有关的探索性问题.[例1] (1)(A.金华模拟)如图,在四棱锥PABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC =3,AD=4,∠PAD=60°.①当正视方向与向量AD―→的方向相同时,画出四棱锥PABCD的正视图(要求标出尺寸,并写出演算过程);②若M为PA的中点,求证:DM∥平面PBC;③求三棱锥DPBC的体积.(2)(A.四川高考)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.①若AC⊥BC,证明:直线BC⊥平面ACC1A1;②设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.[自主解答] (1)法一:①在梯形ABCD中,过点C作CE⊥AB,垂足为E.由已知得,四边形ADCE为矩形,AE=DC=3,在Rt△BEC中,由BC=5,CE=4,依勾股定理得BE=3,从而AB=6.又由PD⊥平面ABCD,得PD⊥AD,所以在Rt△PDA中,由AD=4,∠PAD=60°,得PD=AD tan 60°=4 3.正视图如图(1)所示:图(1)图(2)②证明:如图(2)所示,取PB中点N,连接MN,CN. 在△PAB中,∵M是PA中点,∴MN∥AB且MN=12AB=3.∵又CD∥AB,CD=3,∴MN∥CD,MN=CD,∴四边形MNCD为平行四边形,∴DM∥CN.∵DM⊄平面PBC,CN⊂平面PBC,∴DM∥平面PBC.③V DPBC=V PDBC=13S△DBC·PD,又∵S△DBC=6,PD=43,∴V DPBC=8 3.法二:①同法一.②证明:取AB的中点E,连接ME,DE.在梯形ABCD中,BE∥CD,且BE=CD,∴四边形BCDE为平行四边形,∴DE∥BC.∵DE⊄平面PBC,BC⊂平面PBC,∴DE∥平面PBC.∵在△PAB中,ME∥PB,ME⊄平面PBC,PB⊂平面PBC,∴ME∥平面PBC.∵DE∩ME=E,∴平面DME∥平面PBC.∵DM⊂平面DME,∴DM∥平面PBC.③同法一.(2)①证明:因为四边形ABB1A1和ACC1A1都是矩形,所以AA1⊥AB,AA1⊥AC.因为AB,AC为平面ABC内两条相交直线,所以AA1⊥平面ABC.因为直线BC⊂平面ABC,所以AA1⊥BC.又由已知,AC⊥BC,AA1,AC为平面ACC1A1内两条相交直线,所以BC⊥平面ACC1A1.②取线段AB的中点M,连接A1M,MC,A1C,AC1,设O为A1C,AC1的交点.由已知,O为AC1的中点.连接MD,OE,则MD,OE分别为△ABC,△ACC1的中位线,连接OM,从而四边形MDEO为平形四边形,则DE∥MO.因为直线DE⊄平面A1MC,MO⊂平面A1MC,所以直线DE∥平面A1MC.即线段AB上存在一点M(线段AB的中点),使直线DE∥平面A1MC.线面平行问题的常见类型及解题策略(1)线面平行的证明问题.判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α);③利用面面平行的性质(α∥β,a⊂α⇒a∥β);④利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒a∥β).(2)线面平行的探索性问题.①对命题条件的探索常采用以下三种方法:a.先猜后证,即先观察与尝试给出条件再证明;b.先通过命题成立的必要条件探索出命题成立的条件,再证明其充分性;c.把几何问题转化为代数问题,探索命题成立的条件.②对命题结论的探索常采用以下方法:首先假设结论存在,然后在这个假设下进行推理论证,如果通过推理得到了合乎情理的结论就肯定假设,如果得到了矛盾的结果就否定假设.1.(B.新课标全国卷Ⅱ)如图,直三棱柱ABCA1B1C1中,D,E分别是AB,BB1的中点.(1)证明:BC1∥平面A1CD;(2)设AA1=AC=CB=2,AB=22,求三棱锥CA1DE的体积.解:(1)证明:连接AC1交A1C于点F,则F为AC1的中点.又D是AB中点,连接DF,则在△ABC1中,BC1∥DF.因为DF⊂平面A1CD,BC1⊄平面A1CD,所以BC1∥平面A1CD.(2)因为ABCA1B1C1是直三棱柱,所以AA1⊥平面ABC,则AA1⊥CD.由已知AC=CB,D为AB的中点,所以CD⊥AB.又AA1∩AB=A,AA1,AB⊂平面ABB1A1,所以CD⊥平面ABB1A1.由AA1=AC=CB=2,AB=22,得∠ACB=90°,CD=2,A1D=6,DE=3,A1E=3,故A1D2+DE2=A1E2,即DE⊥A1D.所以VCA1DE=13×12×6×3×2=1.2.(A.湖州模拟)如图所示,在直四棱柱ABCDA1B1C1D1中,已知DC=DD1=2AD =2AB,AD⊥DC,AB∥DC.(1)求证:D1C⊥AC1;(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.解:(1)证明:在直四棱柱ABCDA1B1C1D1中,连接C1D,∵DC=DD1,∴四边形DCC1D1是正方形,∴DC1⊥D1C.又AD⊥DC,AD⊥DD1,DC∩DD1=D,DC,DD1⊂平面DCC1D1,∴AD⊥平面DCC1D1,又D1C⊂平面DCC1D1,∴AD⊥D1C.∵AD⊂平面ADC1,DC1⊂平面ADC1,且AD∩DC1=D,∴D1C⊥平面ADC1,又AC1⊂平面ADC1,∴D1C⊥AC1.(2)连接AD1,AE,D1E,设AD1∩A1D=M,BD∩AE=N,连接MN,∵平面AD1E∩平面A1BD=MN,要使D1E∥平面A1BD,可使MN∥D1E,又M是AD1的中点,则N是AE的中点.又易知△ABN≌△EDN,∴AB=DE.即E是DC的中点.综上所述,当E是DC的中点时,可使D1E∥平面A1BD.[例2]如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EFA1∥平面BCHG.[自主解答] (1)∵G,H分别是A1B1,A1C1的中点,∴GH是△A1B1C1的中位线,∴GH∥B1C1.又∵B1C1∥BC,∴GH∥BC,∴B,C,H,G四点共面.(2)∵E,F分别是AB,AC的中点,∴EF∥BC.∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.∴四边形A1EBG是平行四边形,∴A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG.∵A1E∩EF=E,∴平面EFA1∥平面BCHG.互动探究在本例条件下,若D1,D分别为B1C1,BC的中点,求证:平面A1BD1∥平面D.AC1证明:如图所示,连接A1C交AC1于点H,∵四边形A1ACC1是平行四边形,∴H是A1C的中点,连接HD,∵D为BC的中点,方法规律判定面面平行的四种方法(1)利用定义:即证两个平面没有公共点(不常用).(2)利用面面平行的判定定理(主要方法).(3)利用垂直于同一条直线的两平面平行(客观题可用).(4)利用平面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行(客观题可用).如图,四棱柱ABCDA1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1= 2.(1)证明:平面A1BD∥平面CD1B1;(2)求三棱柱ABDA1B1D1的体积.[例3]如图所示,平面α∥平面β,点A∈α,点C∈α,点B∈β,点D∈β,点E,F分别在线段AB,CD上,且AE∶EB=CF∶FD.(1)求证:EF∥平面β;(2)若E,F分别是AB,CD的中点,AC=4,BD=6,且AC,BD所成的角为60°,求EF的长.[自主解答] (1)证明:①当AB,CD在同一平面内时,由平面α∥平面β,平面α∩平面ABDC=AC,平面β∩平面ABDC=BD,∴AC∥BD.∵AE∶EB=CF∶FD,∴EF∥BD.又EF⊄β,BD⊂β,∴EF∥平面β.②当AB与CD异面时,如图所示,设平面ACD∩平面β=DH,且DH=AC.∵平面α∥平面β,平面α∩平面ACDH=AC,∴AC∥DH,∴四边形ACDH是平行四边形,在AH上取一点G,使AG∶GH=CF∶FD,连接EG,FG,BH. 又∵AE∶EB=CF∶FD=AG∶GH,∴GF∥HD,EG∥BH.又EG∩GF=G,BH∩HD=H,∴平面EFG∥平面β.又EF⊂平面EFG,∴EF∥平面β.综合①②可知EF∥平面β.(2)如图所示,连接AD,取AD的中点M,连接ME,MF.∵E,F分别为AB,CD的中点,∴ME∥BD,MF∥AC,且ME=12BD=3,MF=12AC=2.∴∠EMF为AC与BD所成的角或其补角,∴∠EMF=60°或120°.∴在△EFM中,由余弦定理得EF=ME2+MF2-2ME·MF·cos∠EMF=32+22±2×3×2×12=13±6,即EF=7或EF=19.方法规律1.解决本题的关键是构造过EF且平行平面α和平面β的平面.2.通过线面、面面平行的判定和性质,可实现线线、线面、面面平行的转化.(A.安徽高考)如图,四棱锥PABCD的底面是边长为8的正方形,四条侧棱长均为217.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH ⊥平面ABCD,BC∥平面GEFH.(1)证明:GH∥EF;(2)若EB=2,求四边形GEFH的面积.解:(1)证明:因为BC∥平面GEFH,BC⊂平面PBC,且平面PBC∩平面GEFH =GH,所以GH∥BC.同理可证EF∥BC,因此GH∥EF.(2)连接AC,BD交于点O,BD交EF于点K,连接OP,GK.因为PA=PC,O是AC的中点,所以PO⊥AC,同理可得PO⊥BD.又BD∩AC=O,且AC,BD都在底面ABCD内,所以PO⊥底面ABCD.又因为平面GEFH⊥平面ABCD,且PO⊄平面GEFH,所以PO∥平面GEFH.因为平面PBD∩平面GEFH=GK,所以PO∥GK,且GK⊥底面ABCD,从而GK⊥EF.所以GK是梯形GEFH的高.由AB=8,EB=2得EB∶AB=KB∶DB=1∶4,从而KB=14DB=12OB,即K为OB的中点.再由PO∥GK得GK=12PO,即G是PB的中点,且GH=12BC=4.由已知可得OB=42,PO=PB2-OB2=68-32=6,所以GK=3.故四边形GEFH的面积S=GH+EF2·GK=4+82×3=18.——————————————[课堂归纳——通法领悟]———————————————1个转化——三种平行关系间的转化2个注意——证明平行问题应注意的两个问题(1)在推证线面平行时,必须满足三个条件:一是直线a在已知平面外;二是直线b在已知平面内;三是两直线平行.(2)把线面平行转化为线线平行时,必须说清经过已知直线的平面与已知平面相交,则该直线与交线平行.数学思想(九)转化与化归思想在证明平行关系中的应用线线平行、线面平行和面面平行是空间中三种基本平行关系,它们之间可以相互转化,其转化关系如下:证明平行的一般思路是:欲证面面平行,可转化为证明线面平行;欲证线面平行,可转化为证明线线平行.[典例] (B.辽宁高考)如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.(1)求证:BC⊥平面PAC;(2)设Q为PA的中点,G为△AOC的重心.求证:QG∥平面PBC.[解题指导] (1)利用线面垂直的判定定理证明;(2)可证明QG所在的平面与平面PBC平行.[解] (1)由AB是圆O的直径,得AC⊥BC.由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC.又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.(2)连接OG并延长交AC于M,连接QM,QO,由G为△AOC的重心,得M为AC 中点.由Q为PA中点,得QM∥PC.又O为AB的中点,得OM∥BC.因为QM∩MO=M,QM⊂平面QMO,MO⊂平面QMO,BC∩PC=C,BC⊂平面PBC,PC⊂平面PBC,所以平面QMO∥平面PBC.因为QG⊂平面QMO,所以QG∥平面PBC.[题后悟道] 1.本例(2)巧妙地将线面平行的证明转化为面面平行,进而由面面平行的性质得出结论的证明.2.利用相关的平行判定定理和性质定理实现线线、线面、面面平行关系的转化,也要注意平面几何中一些平行的判断和性质的灵活应用,如中位线、平行线分线段成比例等,这些是空间线面平行关系证明的基础.如图所示,几何体EABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.证明:(1)取BD的中点O,连接CO,EO.由于CB=CD,所以CO⊥BD,又EC⊥BD,EC∩CO=C,CO,EC⊂平面EOC,所以BD⊥平面EOC,所以BD⊥EO,又O为BD的中点,所以BE=DE.(2)法一:取AB的中点N,连接DM,DN,MN,因为M是AE的中点,所以MN∥BE.又MN⊄平面BEC,BE⊂平面BEC,所以MN∥平面BEC.又因为△ABD为正三角形,所以∠BDN=30°.又CB=CD,∠BCD=120°,因此∠CBD=30°,所以DN∥BC.又DN⊄平面BEC,BC⊂平面BEC,所以DN∥平面BEC.又MN∩DN=N,故平面DMN∥平面BEC.又DM⊂平面DMN,所以DM∥平面BEC.法二:延长AD,BC交于点F,连接EF.因为CB=CD,∠BCD=120°,所以∠CBD=30°.因为△ABD为正三角形,所以∠ABD=∠BAD=60°,∠ABC=90°,因此∠AFB=30°,所以AB=12 AF.又AB=AD,所以D为线段AF的中点.连接DM,由于点M是线段AE的中点,所以在△AFE中,DM∥EF.又DM⊄平面BEC,EF⊂平面BEC,所以DM∥平面BEC.[全盘巩固]1.平面α∥平面β,点A,C∈α,点B,D∈β,则直线AC∥直线BD的充要条件是( )A.AB∥CD B.AD∥CBC.AB与CD相交 D.A,B,C,D四点共面解析:选D 充分性:A,B,C,D四点共面,由平面与平面平行的性质知AC∥BD.必要性显然成立.2.(A.嘉兴模拟)设m,n是空间两条直线,α,β是空间两个平面,则下列选项中不正确的是( )A.当m⊂α时,“n∥α”是“m∥n”的必要不充分条件B.当m⊂α时,“m⊥β”是“α⊥β”的充分不必要条件C.当n⊥α时,“n⊥β”是“α∥β”成立的充要条件D.当m⊂α时,“n⊥α”是“m⊥n”的充分不必要条件解析:选A A错误,应为既不充分也不必要条件,B,C,D易知均正确,故选A.3.在空间中,下列命题正确的是( )A.若a∥α,b∥a,则b∥αB.若a∥α,b∥α,a⊂β,b⊂β,则α∥βC.若α∥β,b∥α,则b∥βD.若α∥β,a⊂α,则a∥β解析:选D 若a∥α,b∥a,则b∥α或b⊂α,故选项A错误;B中当a ∥b时,α、β可能相交,故选项B错误;若α∥β,b∥α,则b∥β或b⊂β,故选项C错误;选项D为两平面平行的性质,故选D.4.给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题:①若l与m为异面直线,l⊂α,m⊂β,则α∥β;②若α∥β,l⊂α,m⊂β,则l∥m;③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.其中真命题的个数为( )A.3 B.2 C.1 D.0解析:选C 当异面直线l、m满足l⊂α,m⊂β时,α、β也可以相交,故①错;若α∥β,l⊂α,m⊂β,则l、m平行或异面,故②错;如图所示,设几何体三个侧面分别为α、β、γ.交线为l、m、n,若l∥γ,则l∥m,l∥n,则m∥n,故③正确.5.(A.湖州模拟)如图所示,正方体ABCDA1B1C1D1中,E、F分别为棱AB、CC的中点,在平面ADD1A1内且与平面D1EF平行的直线1( )A.不存在 B.有1条C.有2条 D.有无数条解析:选D 平面ADD1A1与平面D1EF有公共点D1,由平面的基本性质中的公理知必有过该点的公共线l,在平面ADD1A1内与l平行的线有无数条,且它们都不在平面D1EF内,由线面平行的判定定理知它们都与平面D1EF平行,故选D.6.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )A.①③ B.①④ C.②③ D.②④解析:选B ①如图1,由平面ABC∥平面MNP,可得AB∥平面MNP.图1 图2④如图2,由AB∥CD,CD∥NP,得AB∥NP,又AB⊄平面MNP,NP⊂平面MNP,所以AB∥平面MNP.7.在四面体ABCD中,M、N分别是△ACD、△BCD的重心,则四面体的四个面中与MN平行的是________.解析:如图所示,取CD的中点E.则EM∶MA=1∶2,EN∶BN=1∶2,所以MN ∥AB .又MN ⊄平面ABD ,MN ⊄平面ABC ,AB ⊂平面ABD ,AB ⊂平面ABC , 所以MN ∥平面ABD ,MN ∥平面ABC . 答案:平面ABD 与平面ABC8.(A.台州模拟)考察下列三个命题,在“________”处都缺少同一个条件,补上这个条件使其构成真命题(其中l ,m 为不同直线,α、β为不重合平面),则此条件为________.①⎭⎬⎫m ⊂αl ∥m⇒l ∥α;②⎭⎬⎫l ∥mm ∥α ⇒l ∥α;③⎭⎬⎫l ⊥βα⊥β⇒l ∥α.解析:线面平行的判定中指的是平面外的一条直线和平面内的一条直线平行,故此条件为:l ⊄α.答案:l ⊄α9.已知l ,m 是两条不同的直线,α,β是两个不同的平面,下列命题: ①若l ⊂α,m ⊂α,l ∥β,m ∥β,则α∥β; ②若l ⊂α,l ∥β,α∩β=m ,则l ∥m ; ③若α∥β,l ∥α,则l ∥β; ④若l ⊥α,m ∥l ,α∥β,则m ⊥β.其中真命题是________(写出所有真命题的序号).解析:当l ∥m 时,平面α与平面β不一定平行,①错误;由直线与平面平行的性质定理,知②正确;若α∥β,l ∥α,则l ⊂β或l ∥β,③错误;∵l ⊥α,l ∥m ,∴m ⊥α,又α∥β,∴m ⊥β,④正确,故填②④.答案:②④10.在多面体ABCDEF 中,点O 是矩形ABCD 的对角线的交点,三角形CDE 是等边三角形,棱EF∥BC且EF=12BC.求证:FO∥平面CDE.证明:如图所示,取CD中点M,连接OM,EM,在矩形ABCD中,OM∥BC且OM=12 BC,又EF∥BC且EF=12 BC,则EF∥OM且EF=OM.所以四边形EFOM为平行四边形,所以FO∥EM.又因为FO⊄平面CDE,EM⊂平面CDE,所以FO∥平面CDE.11.如图所示,直棱柱ABCDA1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC =90°,AB=2AD=2CD=2.(1)证明:AC⊥平面BB1C1C;(2)在A1B1上是否存在一点P,使得DP与平面ACB1平行?证明你的结论.解:(1)证明:在直棱柱ABCDA1B1C1D1中,BB1⊥平面ABCD,∴BB1⊥AC.又∵∠BAD=∠ADC=90°,AB=2AD=2CD=2,∴AC=2,∠CAB=45°,在△ABC中,由余弦定理可得BC=AC2+AB2-2AC·AB·cos∠CAB= 2. ∴BC2+AC2=AB2,∴BC⊥AC.又BB1∩BC=B,BB1,BC⊂平面BB1C1C,∴AC⊥平面BB1C1C.(2)存在点P,P为A1B1的中点可满足要求.由P为A1B1的中点,有PB1∥AB,且PB1=12 AB,又∵CD∥AB且CD=12 AB,∴CD∥PB1且CD=PB1,∴CDPB1为平行四边形,∴DP∥CB1.又CB1⊂平面ACB1,DP⊄平面ACB1,∴DP∥平面ACB1.12.(A.金华模拟)如图所示,在正四棱锥PABCD中,底面是边长为2的正方形,侧棱PA=6,E为BC的中点,F为侧棱PD上的一动点.(1)求证:AC⊥BF;(2)当直线PE∥平面ACF时,求三棱锥FACD的体积.解:(1)证明:连接BD,设AC∩BD=O,连接PO,则PO⊥平面ABCD.∴AC ⊥PO .∵四边形ABCD 为正方形, ∴AC ⊥BD .又BD ∩PO =O ,BD ,PO ⊂平面PBD , ∴AC ⊥平面PBD . 又BF ⊂平面PBD , ∴AC ⊥BF .(2)连接DE ,交AC 于点G ,连接FG . ∵PE ∥平面ACF , ∴PE ∥FG ,∴DG DE =DF DP. 又CE =12BC =12AD ,BC ∥AD ,∴CE AD =GE DG =12, ∴DG DE =23, ∴DF DP =23.过F作FH⊥DB,垂足为H,则FH∥OP,∴FHOP=DFDP=23,∴FH=23 OP,∵正方形ABCD的边长为2,∴AO= 2. ∴OP=PA2-AO2=2.∴FH=4 3 .∴三棱锥FACD的体积VFACD =13S△ACD·FH=13×12×22×43=89.[冲击名校]如图所示,在棱长均为4的三棱柱ABCA1B1C1中,D,D1分别是BC和B1C1的中点.(1)求证:A1D1∥平面AB1D;(2)若平面ABC⊥平面BCC1B1,∠B1BC=60°,求三棱锥B1ABC的体积.解:(1)证明:如图所示,连接DD1,在三棱柱ABCA1B1C1中,因为D,D1分别是BC与B1C1的中点,所以B1D1∥BD且B1D1=BD.所以四边形B1BDD1为平行四边形,所以BB1∥DD1,且BB1=DD1. 又因为AA1∥BB1,且AA1=BB1,所以AA1∥DD1,且AA1=DD1,所以四边形AA1D1D为平行四边形,所以A1D1∥AD.又A1D1⊄平面AB1D,AD⊂平面AB1D,所以A1D1∥平面AB1D.(2)在△ABC中,因为AB=AC,D为BC的中点,所以AD⊥BC. 因为平面ABC⊥平面BCC1B1,且交线为BC,AD⊂平面ABC,所以AD⊥平面BCC1B1,即AD是三棱锥AB1BC的高.在△ABC中,由AB=AC=BC=4,得AD=2 3.在△B1BC中,B1B=BC=4,∠B1BC=60°,所以S△B1BC=34×42=43,所以三棱锥B1ABC的体积,即三棱锥AB1BC的体积V=13S△B1BC×AD=13×43×23=8.[高频滚动]1.α、β、γ是三个平面,a、b是两条直线,有下列三个条件:①a∥γ,b⊂β;②a∥γ,b∥β;③b∥β,a⊂γ.如果命题“α∩β=a,b⊂γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(填上你认为正确的所有序号).解析:①a∥γ,a⊂β,b⊂β,β∩γ=b⇒a∥b(线面平行的性质).②如图所示,在正方体中,α∩β=a,b⊂γ,a∥γ,b∥β,而a、b异面,故②错.③b∥β,b⊂γ,a⊂γ,a⊂β,β∩γ=a⇒a∥b(线面平行的性质).答案:①③2.过三棱柱ABCA1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有________条.解析:过三棱柱ABCA1B1C1的任意两条棱的中点作直线,记AC、BC、A1C1、B 1C1的中点分别为E、F、E1、F1,则直线EF、E1F1、EE1、FF1、E1F、EF1均与平面ABB1A1平行,故符合题意的直线共有6条.答案:6。
7.3直线平面平行的判定与性质课件高三数学一轮复习

易错点睛:(1)面面平行的判定中易忽视“面内两条相交直线”这一条件. (2)对面面平行性质定理理解不深致误.
课堂考点突破
——精析考题 提升能力
考点一 直线与平面平行的判定与性质 角度 1:直线与平面平行的判定 【例 1】 如图,直四棱柱 ABCD-A1B1C1D1 的底面是菱形,AA1=4,AB=2,∠BAD =60°,E,M,N 分别是 BC,BB1,A1D 的中点.
2.(角度 2)如图,在四棱锥 P-ABCD 中,PA⊥底面 ABCD,AD∥BC,∠DAB=90°, AB=BC=PA=12AD=2,E 为 PB 的中点,F 是 PC 上的点.
(1)若 EF∥平面 PAD,证明:F 为 PC 的中点; (2)求点 C 到平面 PBD 的距离.
【解】 (1)证明:因为 BC∥AD,BC⊄平面 PAD,AD⊂平面 PAD,所以 BC∥平面 PAD. 因为 P∈平面 PBC,P∈平面 PAD,所以可设平面 PBC∩平面 PAD=PM, 又因为 BC⊂平面 PBC,所以 BC∥PM, 因为 EF∥平面 PAD,EF⊂平面 PBC, 所以 EF∥PM,从而得 EF∥BC. 因为 E 为 PB 的中点,所以 F 为 PC 的中点.
【解析】 根据面面平行的判定定理可知 A 错误,D 正确;根据面面平行的定义可 知 B 错误,C 正确.故选 BC.
4.如图,在正方体 ABCD-A1B1C1D1 中,E 为 DD1 的中点,则 BD1 与平面 ACE 的位 置关系为__平__行____.
【解析】 连接 BD,则 AC∩BD=O,连接 OE(图略),则 OE∥BD1,OE⊂平面 ACE, BD1⊄平面 ACE,∴BD1∥平面 ACE.
3.(多选)下面命题中正确的是( BC ) A.若一个平面内有两条直线与另一个平面平行,则这两个平面平行 B.若一个平面内有无数条直线与另一个平面平行,则这两个平面平行 C.若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行 D.若一个平面内的两条相交直线分别与另一个平面平行,则这两个平面平行
高考数学总复习考点知识与题型专题讲解30---直线、平面平行的判定和性质

高考数学总复习考点知识与题型专题讲解直线、平面平行的判定和性质【考纲要求】1、掌握直线和平面平行的判定定理和性质定理;2、掌握两个平面平行的判定定理和性质定理.3、能运用公理、定理和已经获得的结论证明一些空间图形的平行关系的简单命题。
【知识网络】【考点梳理】考点一、直线与平面平行的判定 1、判定定理:(1)内容: 如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.(2)符号语言:直线、平面平行判定定理性质定理 线面平行面面平行判定定理性质定理2、判定直线与平面平行,主要有三种方法:(1)利用定义(常用反证法);(2)利用判定定理:关键是找平面内与已知直线平行的直线。
可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线。
(3)利用面面平行的性质定理:当两平面平行时,其中一个平面内的任一直线平行于另一平面。
要点诠释:线面平行关系没有传递性,即平行线中的一条平行于一平面,另一条不一定平行于该平面。
考点二、直线与平面平行的性质1、性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.2、符号语言:.考点三、平面与平面平行的判定1、面面平行的定义:如果两个平面没有公共点,那么这两个平面互相平行.2、图形表示:画两个平面平行时,通常把表示这两个平面的平行四边形的相邻两边分别画成平行的.3、 平行平面的判定定理: 如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面互相平行.4、 符号语言:5、判定平面与平面平行的常用方法: ①利用定义(常用反证法);②利用判定定理:转化为判定一个平面内的两条相交直线分别平行于另一个平面。
客观题中,也可直接利用一个平面内的两条相交线分别平行于另一个平面的两条相交线来证明两平面平行;③利用面面平行的传递性:////.//αβαγγβ⎫⇒⎬⎭④利用线面垂直的性质://l l ααββ⊥⎫⇒⎬⊥⎭。
高中数学复习:直线、平面平行的判定与性质

(
×
)
(3)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平
行.
(
×
)
教材研读
栏目索引
(4)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异
面.
(
√
)
(5)若直线a与平面α内无数条直线平行,则a∥α. (
(6)若α∥β,直线a∥α,则a∥β.( Nhomakorabea×
)
答案 (1)× (2)× (3)× (4)√ (5)× (6)×
答案 D 与一个平面平行的两条直线可以平行、相交,也可以异面.
教材研读
栏目索引
4.如果直线a∥平面α,那么直线a与平面α的位置关系可另等价表述,下列
表述正确的是 ( D )
A.直线a上有无数个点不在平面α内
B.直线a与平面α内的所有直线平行
C.直线a与平面α内无数条直线不相交
D.直线a与平面α内的任意一条直线都不相交
×
)
教材研读
2.对于直线m,n和平面α,若n⊂α,则“m∥n”是“m∥α”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案
D
栏目索引
( D )
教材研读
栏目索引
3.若两条直线都与一个平面平行,则这两条直线的位置关系是 ( D )
A.平行
B.相交
C.异面
D.以上均有可能
(5)如果一个平面内有两条相交直线分别平行于另一个平面内的两条直
线,那么这两个平面平行.
教材研读
栏目索引
1.判断正误(正确的打“√”,错误的打“✕”)
(1)若一条直线平行于一个平面内的一条直线,则这条直线平行于这个
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四节直线、平面平行的判定及其性质1.平面α∥平面β,点A,C∈α,点B,D∈β,则直线AC∥直线BD的充要条件是( )A.AB∥CD B.AD∥CBC.AB与CD相交 D.A,B,C,D四点共面2.(A.嘉兴模拟)设m,n是空间两条直线,α,β是空间两个平面,则下列选项中不正确的是( )A.当m⊂α时,“n∥α”是“m∥n”的必要不充分条件B.当m⊂α时,“m⊥β”是“α⊥β”的充分不必要条件C.当n⊥α时,“n⊥β”是“α∥β”成立的充要条件D.当m⊂α时,“n⊥α”是“m⊥n”的充分不必要条件3.在空间中,下列命题正确的是( )A.若a∥α,b∥a,则b∥αB.若a∥α,b∥α,a⊂β,b⊂β,则α∥βC.若α∥β,b∥α,则b∥βD.若α∥β,a⊂α,则a∥β4.给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题:①若l与m为异面直线,l⊂α,m⊂β,则α∥β;②若α∥β,l⊂α,m⊂β,则l∥m;③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.其中真命题的个数为( )A.3 B.2 C.1 D.05.(A.湖州模拟)如图所示,正方体ABCDA1B1C1D1中,E、F分别为棱AB、CC的中点,在平面ADD1A1内且与平面D1EF平行的直线1( )A.不存在 B.有1条C.有2条 D.有无数条6.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )A.①③ B.①④ C.②③ D.②④7.在四面体ABCD中,M、N分别是△ACD、△BCD的重心,则四面体的四个面中与MN平行的是________.8.(A.台州模拟)考察下列三个命题,在“________”处都缺少同一个条件,补上这个条件使其构成真命题(其中l,m为不同直线,α、β为不重合平面),则此条件为________.①⎭⎬⎫m ⊂αl ∥m⇒l ∥α;②⎭⎬⎫l ∥mm ∥α ⇒l ∥α;③⎭⎬⎫l ⊥βα⊥β⇒l ∥α.9.已知l ,m 是两条不同的直线,α,β是两个不同的平面,下列命题: ①若l ⊂α,m ⊂α,l ∥β,m ∥β,则α∥β; ②若l ⊂α,l ∥β,α∩β=m ,则l ∥m ; ③若α∥β,l ∥α,则l ∥β; ④若l ⊥α,m ∥l ,α∥β,则m ⊥β.其中真命题是________(写出所有真命题的序号).10.在多面体ABCDEF 中,点O 是矩形ABCD 的对角线的交点,三角形CDE 是等边三角形,棱EF ∥BC 且EF =12BC .求证:FO ∥平面CDE .11.如图所示,直棱柱ABCD A 1B 1C 1D 1中,底面ABCD 是直角梯形,∠BAD =∠ADC =90°,AB =2AD =2CD =2.(1)证明:AC ⊥平面BB 1C 1C ;(2)在A 1B 1上是否存在一点P ,使得DP 与平面ACB 1平行?证明你的结论.12.(A.金华模拟)如图所示,在正四棱锥PABCD中,底面是边长为2的正方形,侧棱PA=6,E为BC的中点,F为侧棱PD上的一动点.(1)求证:AC⊥BF;(2)当直线PE∥平面ACF时,求三棱锥FACD的体积.[冲击名校]如图所示,在棱长均为4的三棱柱ABCA1B1C1中,D,D1分别是BC和B1C1的中点.(1)求证:A1D1∥平面AB1D;(2)若平面ABC⊥平面BCC1B1,∠B1BC=60°,求三棱锥B1ABC的体积.[高频滚动]1.α、β、γ是三个平面,a、b是两条直线,有下列三个条件:①a∥γ,b⊂β;②a∥γ,b∥β;③b∥β,a⊂γ.如果命题“α∩β=a,b⊂γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(填上你认为正确的所有序号).2.过三棱柱ABCA1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有________条.答案[全盘巩固]1.解析:选D 充分性:A,B,C,D四点共面,由平面与平面平行的性质知AC∥BD.必要性显然成立.2.解析:选A A错误,应为既不充分也不必要条件,B,C,D易知均正确,故选A.3.解析:选D 若a∥α,b∥a,则b∥α或b⊂α,故选项A错误;B中当a ∥b时,α、β可能相交,故选项B错误;若α∥β,b∥α,则b∥β或b⊂β,故选项C错误;选项D为两平面平行的性质,故选D.4.解析:选C 当异面直线l、m满足l⊂α,m⊂β时,α、β也可以相交,故①错;若α∥β,l⊂α,m⊂β,则l、m平行或异面,故②错;如图所示,设几何体三个侧面分别为α、β、γ.交线为l、m、n,若l∥γ,则l∥m,l∥n,则m∥n,故③正确.5.解析:选D 平面ADD1A1与平面D1EF有公共点D1,由平面的基本性质中的公理知必有过该点的公共线l,在平面ADD1A1内与l平行的线有无数条,且它们都不在平面D1EF内,由线面平行的判定定理知它们都与平面D1EF平行,故选D.6.解析:选B ①如图1,由平面ABC∥平面MNP,可得AB∥平面MNP.图1 图2④如图2,由AB∥CD,CD∥NP,得AB∥NP,又AB⊄平面MNP,NP⊂平面MNP,所以AB∥平面MNP.7.解析:如图所示,取CD的中点E.则EM∶MA=1∶2,EN∶BN=1∶2,所以MN∥AB.又MN⊄平面ABD,MN⊄平面ABC,AB⊂平面ABD,AB⊂平面ABC,所以MN∥平面ABD,MN∥平面ABC.答案:平面ABD与平面ABC8.解析:线面平行的判定中指的是平面外的一条直线和平面内的一条直线平行,故此条件为:l⊄α.答案:l⊄α9.解析:当l∥m时,平面α与平面β不一定平行,①错误;由直线与平面平行的性质定理,知②正确;若α∥β,l∥α,则l⊂β或l∥β,③错误;∵l ⊥α,l∥m,∴m⊥α,又α∥β,∴m⊥β,④正确,故填②④.答案:②④10.证明:如图所示,取CD中点M,连接OM,EM,在矩形ABCD中,OM∥BC且OM=12 BC,又EF∥BC且EF=12 BC,则EF∥OM且EF=OM.所以四边形EFOM为平行四边形,所以FO∥EM.又因为FO⊄平面CDE,EM⊂平面CDE,所以FO∥平面CDE.11.解:(1)证明:在直棱柱ABCDA1B1C1D1中,BB1⊥平面ABCD,∴BB1⊥AC. 又∵∠BAD=∠ADC=90°,AB=2AD=2CD=2,∴AC=2,∠CAB=45°,在△ABC中,由余弦定理可得BC=AC2+AB2-2AC·AB·cos∠CAB= 2.∴BC2+AC2=AB2,∴BC⊥AC.又BB1∩BC=B,BB1,BC⊂平面BB1C1C,∴AC⊥平面BB1C1C.(2)存在点P,P为A1B1的中点可满足要求.由P为A1B1的中点,有PB1∥AB,且PB1=12 AB,又∵CD∥AB且CD=12 AB,∴CD∥PB1且CD=PB1,∴CDPB1为平行四边形,∴DP∥CB1.又CB1⊂平面ACB1,DP⊄平面ACB1,∴DP∥平面ACB1.12.解:(1)证明:连接BD ,设AC ∩BD =O ,连接PO ,则PO ⊥平面ABCD .∴AC ⊥PO .∵四边形ABCD 为正方形, ∴AC ⊥BD .又BD ∩PO =O ,BD ,PO ⊂平面PBD , ∴AC ⊥平面PBD . 又BF ⊂平面PBD , ∴AC ⊥BF .(2)连接DE ,交AC 于点G ,连接FG . ∵PE ∥平面ACF , ∴PE ∥FG , ∴DG DE =DF DP. 又CE =12BC =12AD ,BC ∥AD ,∴CE AD =GE DG =12, ∴DG DE =23,∴DFDP=23.过F作FH⊥DB,垂足为H,则FH∥OP,∴FHOP=DFDP=23,∴FH=23 OP,∵正方形ABCD的边长为2,∴AO= 2. ∴OP=PA2-AO2=2.∴FH=4 3 .∴三棱锥FACD的体积VFACD =13S△ACD·FH=13×12×22×43=89.[冲击名校]解:(1)证明:如图所示,连接DD1,在三棱柱ABCA1B1C1中,因为D,D1分别是BC与B1C1的中点,所以B1D1∥BD且B1D1=BD.所以四边形B1BDD1为平行四边形,所以BB1∥DD1,且BB1=DD1. 又因为AA1∥BB1,且AA1=BB1,所以AA1∥DD1,且AA1=DD1,所以四边形AA1D1D为平行四边形,所以A1D1∥AD.又A1D1⊄平面AB1D,AD⊂平面AB1D,所以A1D1∥平面AB1D.(2)在△ABC中,因为AB=AC,D为BC的中点,所以AD⊥BC. 因为平面ABC⊥平面BCC1B1,且交线为BC,AD⊂平面ABC,所以AD⊥平面BCC1B1,即AD是三棱锥AB1BC的高.在△ABC中,由AB=AC=BC=4,得AD=2 3.在△B1BC中,B1B=BC=4,∠B1BC=60°,所以S△B1BC=34×42=43,所以三棱锥B1ABC的体积,即三棱锥AB1BC的体积V=13S△B1BC×AD=13×43×23=8.[高频滚动]1.解析:①a∥γ,a⊂β,b⊂β,β∩γ=b⇒a∥b(线面平行的性质).②如图所示,在正方体中,α∩β=a,b⊂γ,a∥γ,b∥β,而a、b异面,故②错.③b∥β,b⊂γ,a⊂γ,a⊂β,β∩γ=a⇒a∥b(线面平行的性质).答案:①③2.解析:过三棱柱ABCA1B1C1的任意两条棱的中点作直线,记AC、BC、A1C1、B 1C1的中点分别为E、F、E1、F1,则直线EF、E1F1、EE1、FF1、E1F、EF1均与平面ABB1A1平行,故符合题意的直线共有6条.答案:6。
