广东省深圳市2021届高三下学期第二次调研(二模)文科数学试卷及答案(pdf版)

合集下载

2021届广东省深圳市高三下学期二模数学试题(解析版)

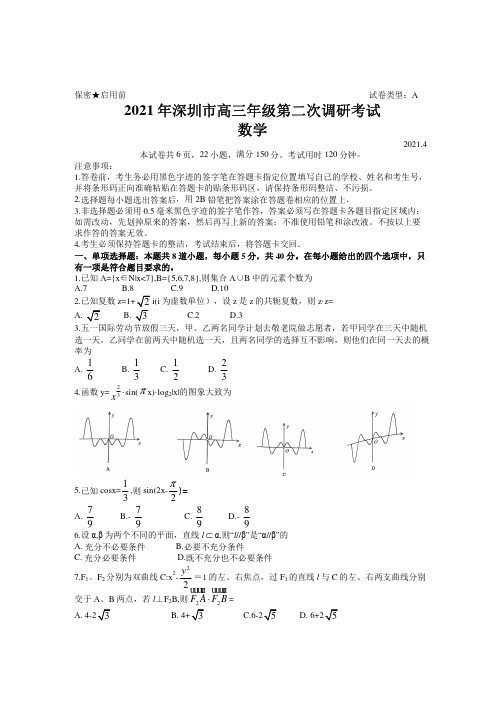
2021届广东省深圳市高三下学期二模数学试题一、单选题1．已知{|7}A x x =∈<N ，{5,6,7,8}B =，则集合A B 中的元素个数为（）A ．7B ．8C ．9D ．10【答案】C【分析】确定集合A 中元素，求得并集可得元素个数．【详解】{0,1,2,3,4,5,6}A =，{0,1,2,3,4,5,6,7,8}A B =，共9个元素．故选：C ．2．已知复数1z =（i 为虚数单位），设z 是z 的共轭复数，则z z ⋅=（）A ．BC ．2D ．3【答案】D【分析】写出共轭复数，然后由复数乘法计算．【详解】由已知1z =，所以22(1)(1)13z z ⋅==+=．故选：D ．3．五国际劳动节放假三天，甲、乙两名同学计划去敬老院做志愿者，若甲同学在三天中随机选一天，乙同学在前两天中随机选一天，且两名同学的选择互不影响，则他们在同一天去的概率为（） A ．16B ．13C ．12D ．23【答案】B【分析】利用乘法原理计算出他们在同一天去和总的方法，再利用古典概型概率计算公式可得答案.【详解】甲同学在三天中随机选一天共有3种方法，乙同学在前两天中随机选一天共有2种方法，所以一共有326⨯=种方法，他们在同一天去共有2种，所以他们在同一天去的概率为2163=. 故选：B.4．函数()232sin log x y x x π=⋅⋅的图象大致为（）A ．B ．C ．D ．【答案】B【分析】分析函数()232sin log x y x x π=⋅⋅的定义域、奇偶性及其在()0,1上的函数值符号，结合排除法可得出合适的选项. 【详解】设()()()232322sin log sin log f x x x x x x x ππ=⋅⋅⋅，该函数的定义域为{}0x x ≠，()()()()()232322sin log sin log f x x x x x x x f x ππ-=--⋅-=-⋅=-，函数()f x 为奇函数，排除AC 选项；当01x <<时，0x ππ<<，()sin 0x π>，则()0f x <，排除D 选项. 故选：B.【点睛】思路点睛：函数图象的辨识可从以下方面入手：（1）从函数的定义域，判断图象的左右位置；（2）从函数的值域，判断图象的上下位置．（3）从函数的单调性，判断图象的变化趋势；（4）从函数的奇偶性，判断图象的对称性；（5）函数的特征点，排除不合要求的图象. 5．已知1cos 3x =，则sin 22x π⎛⎫-= ⎪⎝⎭（）A ．79 B ．79-C ．89D ．89-【答案】A【分析】利用二倍角的余弦公式以及诱导公式可求得结果.【详解】2217sin 2cos 212cos 12239x x x π⎛⎫⎛⎫-=-=-=-⨯= ⎪ ⎪⎝⎭⎝⎭. 故选：A.6．设,αβ为两个不同的平面，直线l α⊂，则“//l β”是“//αβ”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】B【分析】根据充分性及必要性的概念对线面，线线关系进行判断即可.【详解】充分性：直线l α⊂，若1l αβ⋂=，使1//l l ，则//l β，但,αβ相交，故“//l β”是“//αβ”的不充分条件；必要性：直线l α⊂，且//αβ时，//l β，故“//l β”是“//αβ”的必要条件；故“//l β”是“//αβ”的必要不充分条件，故选：B7．1 F 、2F 分别为双曲线22:12y C x -=的左、右焦点，过1F 的直线l 与C 的左、右两支曲线分别交于A 、B 两点，若2l F B ⊥，则22F A F B ⋅=（）A ．4-B ．4+C ．6-D ．6+【答案】C【分析】利用勾股定理结合双曲线的定义可求得2BF ，结合平面向量数量积的运算性质可求得结果.【详解】在双曲线C 中，1a =，b =c =()1F 、)2F ，因为直线l 过点1F ，由图可知，直线l 的斜率存在且不为零，2l F B ⊥，则12F BF 为直角三角形，可得222121212BF BF F F +==，由双曲线的定义可得122BF BF -=，所以，()2221212121242122BF BF BF BF BF BF BF BF =-=+-⋅=-⋅，可得124BF BF ⋅=，联立121224BF BF BF BF ⎧-=⎪⎨⋅=⎪⎩，解得251BF =，因此，()()2222222251625F A F B F B BA F B F B BA F B ⋅=+⋅=+⋅==-.故选：C.【点睛】方法点睛：求两个向量的数量积有三种方法：（1）利用定义：（2）利用向量的坐标运算；（3）利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用． 8．在一个正三角形的三边上，分别取一个距顶点最近的十等分点，连接形成的三角形也为正三角形（如图1所示，图中共有2个正三角形）．然后在较小的正三角形中，以同样的方式形成一个更小的正三角形，如此重复多次，可得到如图2所示的优美图形（图中共有11个正三角形），这个过程称之为迭代．在边长为243的正三角形三边上，分别取一个三等分点，连接成一个较小的正三角形，然后迭代得到如图3所示的图形（图中共有10个正三角形），其中最小的正三角形面积为（）A ．334B ．1C ．32D ．34【答案】A【分析】记第n 个正三角形的边长为n a ，第1n +个正三角形的边长为1n a +，根据n a 与1n a +的关系判断出{}n a 为等比数列，由此求解出最小的正三角形的边长，从而面积可求.【详解】设第n 个正三角形的边长为n a ，则1n +个正三角形的边长为1n a +，由条件可知：1243a =，又由图形可知：222112122cos1203333n n n n n aa a a a +⎛⎫⎛⎫=+-⨯⨯⨯︒ ⎪ ⎪⎝⎭⎝⎭，所以2211,03n n n a a a +=>，所以13n n a a +=，所以{}n a 是首项为2433 所以12433n n a -=⨯，所以113n n a -=，所以103a =，所以最小的正三角形的面积为：1333332=⎝，故选：A.【点睛】关键点点睛：解答本题的关键是将已知问题转化为等比数列问题，通过每一次的迭代分析正三角形的边长之间的关系，从而分析得到正三角形的边长成等比数列，据此可进行相关计算.二、多选题9．设直线():1l y kx k =+∈R 与圆22:5C x y +=，则下列结论正确的为（）A ．l 与C 可能相离B ．l 不可能将C 的周长平分C ．当1k =时，l 被CD ．l 被C 截得的最短弦长为4 【答案】BD【分析】求出直线l 所过定点的坐标，可判断A 选项的正误；假设假设法可判断B 选项的正误；利用勾股定理可判断CD 选项的正误.【详解】对于A 选项，直线l 过定点()0,1，且点()0,1在圆C 内，则直线l 与圆C 必相交，A 选项错误；对于B 选项，若直线l 将圆C 平分，则直线l 过原点，此时直线l 的斜率不存在，B 选项正确；对于C 选项，当1k =时，直线l 的方程为10x y -+=，圆心C 到直线l 的距离为2d =，所以，直线l 被C 截得的弦长为=C 选项错误；对于D 选项，圆心C 到直线l 的距离为1d =≤，所以，直线l 被C 截得的弦长为4≥，D 选项正确. 故选：BD.【点睛】方法点睛：圆的弦长的常用求法（1）几何法：求圆的半径为r ，弦心距为d ，弦长为l ，则l =（2）代数方法：运用根与系数的关系及弦长公式12AB x =-.10．为方便顾客购物，某网上购鞋平台统计了鞋号y （单位：码）与脚长x （单位：毫米）的样本数据(),i i x y ，发现y 与x 具有线性相关关系，用最小二乘法求得回归方程为0.210y x =-，则下列结论中正确的为（） A ．回归直线过样本点的中心(),x y B ．y 与x 可能具有负的线性相关关系C ．若某顾客的鞋号是40码，则该顾客的脚长约为250毫米D ．若某顾客的脚长为262毫米，在“不挤脚”的前提下，应选择42码的鞋【答案】AC【分析】利用回归直线过样本中心点可判断A 选项的正误；利用回归直线的斜率可判断B 选项的正误；将40y =代入回归直线方程可判断C 选项的正误；将262x =代入回归直线方程，可判断D 选项的正误.【详解】对于A 选项，回归直线过样本点的中心(),x y ，A 选项正确；对于B 选项，y 与x 具备正相关性，B 选项错误；对于C 选项，在回归直线方程中，令40y =，可得0.21040x -=，可得250x =，C 选项正确；对于D 选项，在回归直线方程中，令262x =，则0.22621042.4y =⨯-=，若某顾客的脚长为262毫米，在“不挤脚”的前提下，应选择43码的鞋，D 选项错误. 故选：AC.11．摩天轮常被当作一个城市的地标性建筑，如深圳前海的“湾区之光”摩天轮，如图所示，某摩天轮最高点离地面高度128米，转盘直径为120米，设置若干个座舱，游客从离地面最近的位置进舱，开启后按逆时针匀速旋转t 分钟，当15t =时，游客随舱旋转至距离地面最远处．以下关于摩天轮的说法中，正确的为（）A ．摩天轮离地面最近的距离为4米B ．若旋转t 分钟后，游客距离地面的高度为h 米，则60cos 6815h t π⎛⎫=-+⎪⎝⎭C ．若在1t ，2t 时刻，游客距离地面的高度相等，则12t t +的最小值为30D ．1t ∃，[]20,20t ∈，使得游客在该时刻距离地面的高度均为90米【答案】BC【分析】易知摩天轮离地面最近的距离，从而可判断A ；求出t 分钟后，转过的角度，即可求出h 关于t 的表达式，即可判断B ；由余弦型函数的性质可求出12t t +的最小值即可判断C ；求出h 在[]0,20t ∈上的单调性，结合当20t =时，9890h =>即可判断D.【详解】解：由题意知，摩天轮离地面最近的距离为1281208-=米，故A 不正确；t 分钟后，转过的角度为15t π，则6060cos860cos681515h t t ππ=-+=-+，B 正确；60cos6815h t π=-+周期为23015ππ=，由余弦型函数的性质可知，若12t t +取最小值，则[]12,0,30t t ∈，又高度相等，则12,t t 关于15t =对称，则12152t t +=，则1230t t +=；令015t ππ≤≤，解得015t ≤≤，令215t πππ≤≤，解得1530t ≤≤，则h 在[]0,15t ∈上单调递增，在[]15,20t ∈上单调递减，当15t =时，max 128h =，当20t =时，60cos 2068989015h π=-⨯+=>，所以90h =在[]0,20t ∈只有一个解；故选:BC.【点睛】关键点睛:本题的关键是求出h 关于t 的表达式，结合三角函数的性质进行判断.12．设函数()xf x e ex =-和()()()21ln 122g x x kx k x k =-+-+∈R ，其中e 是自然对数的底数()2.71828e =，则下列结论正确的为（）A ．()f x 的图象与x 轴相切B ．存在实数0k <，使得()g x 的图象与x 轴相切 C ．若12k =，则方程()()f x g x =有唯一实数解 D ．若()g x 有两个零点，则k 的取值范围为10,2⎛⎫ ⎪⎝⎭【答案】ACD【分析】通过导数的几何意义分别判断函数()f x ，()g x 与x 轴的相切情况；12k =时，求得()g x 的单调区间及最值，判断方程()()f x g x =是否有唯一实数解；对k 分类讨论，求得()g x 有两个零点时应满足的条件，从而判断选项正误.【详解】()x f x e e '=-，若()f x 的图象与x 轴相切，则()01xf x e e x '=-=⇒=，又(1)0f =，则切点坐标为(1,0)，满足条件，故A 正确；()()212(12)1(1)(12)212kx k x x kx g x kx k x x x-+-++-'=-+-==，()0x >，当0k <时，易知()0g x '>恒成立，不存在为0的解，故不存在实数0k <，使得()g x 的图象与x 轴相切，B 错误；由上所述，()f x 在(0,1)x ∈上单减，(1,)x ∈+∞上单增，则()(1)0f x f ≥=；若12k =，()211ln 22g x x x =-+，()(1)(1)x x g x x+-'=，()g x 在(0,1)x ∈上单增，(1,)x ∈+∞上单减，()(1)0g x g ≤=，故方程()()f x g x =有唯一实数解1x =，故C正确；()(1)(12)x kx g x x+-'=，()0x >，当0k ≤时，()0g x '>恒成立，()g x 单增，不存在2个零点，故舍去；当0k >时，()g x 在1(0,)2k 上单增，在1(,)2k+∞上单减，且0x →时，()g x →-∞，x →+∞时，()g x →-∞，故若()g x 有两个零点，则应使最大值102g k ⎛⎫> ⎪⎝⎭，即()21111111ln ()12ln 202222242g k k k k k k k k ⎛⎫=-+-+=-->⎪⎝⎭，令11()ln 242h k k k =--，易知()h k 单调递减，且1()02h =，因此()0h k >的解集为1(0,)2k ∈，D 正确；故选：ACD【点睛】关键点点睛：利用导数来研究函数的单调性，最值问题，把方程的根的问题，零点问题转化为图像交点问题，利用导数求得最值，从而得证.三、填空题13．已知椭圆C 的焦点在x 轴上，且离心率为12，则C 的方程可以为______．【答案】22143x y +=【分析】设椭圆的方程为22221,0x y a b a b +=>>，由离心率可得2234b a =，从而可写出正确答案.【详解】解：因为焦点在x 轴上，所以设椭圆的方程为22221,0x y a b a b +=>>，因为离心率为12，所以12c a =，所以2222214c a b a a -==，则2234b a =，故答案为: 22143x y +=.14．设恒等式()2345501234512a a x a x a x a x a x x =+++-++，则03a a +=____________．【答案】79-【分析】利用()512x -的展开式进行求解即可；【详解】()512x -的展开式为：()152rr rr T C x +=-；()0001521T C x =-=，0a 的对应项为：01a =；()333345280T C x x =-=-，3a 的对应项为：380a =-；则有03a a +=79- 故答案为：79-【点睛】关键点睛：先得出()512x -的展开式为：()152rr r r T C x +=-，然后找出0a 和3a 所对应的项；主要考察二项式的定理15．若在母线长为5，高为4的圆锥中挖去一个小球，则剩余部分体积的最小值为______________．【答案】152π．【分析】球是圆锥的内切球时，剩余部分体积最小．求出球的半径即可得．【详解】如图是圆锥的轴截面，它的内切圆是圆锥的内切球的大圆．设半径为R ，易知母线长为5，高为4时，底面半径为r =3=，因此1164(556)22R ⨯⨯=++，32R =，所以剩余部分体积的最小值为3232141431534333322V r h R πππππ⎛⎫=-=⨯⨯-⨯= ⎪⎝⎭．故答案为：152π．16．著名的费马问题是法国数学家皮埃尔德费马（1601-1665）于1643年提出的平面几何极值问题：“已知一个三角形，求作一点，使其与此三角形的三个顶点的距离之和最小．”费马问题中的所求点称为费马点，已知对于每个给定的三角形，都存在唯一的费马点，当ABC 的三个内角均小于120︒时，则使得120APB BPC CPA ∠=∠=∠=︒的点P 即为费马点．已知点P 为ABC 的费马点，且AC BC ⊥，若||||||PA PB PC λ+=，则实数λ的最小值为_________．【答案】232【分析】根据题意120APB BPC CPA ∠=∠=∠=︒，不妨设PCB α∠=，故,,326CBP ACP CAP πππααα∠=-∠=-∠=-，进而得,63ππα⎛⎫∈⎪⎝⎭，所以在BCP 和ACP △中，由正弦定理得sin sin 3BP PCαπα=⎛⎫- ⎪⎝⎭，sin 2sin 6PA PC παπα⎛⎫- ⎪⎝⎭=⎛⎫- ⎪⎝⎭，故sin sin 2sin sin 36πααλππαα⎛⎫- ⎪⎝⎭=+⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，在结合三角恒等变换化简整理求函数最值即可.【详解】根据题意, 点P 为ABC 的费马点，ABC 的三个内角均小于120︒, 所以120APB BPC CPA ∠=∠=∠=︒，设PCB α∠=，所以在BCP 和ACP △中，,,3236CBP ACP CAP ACP ππππααα∠=-∠=-∠=-∠=-，且均为锐角，所以,63ππα⎛⎫∈⎪⎝⎭所以由正弦定理得：sin sin 3BPPC παα=⎛⎫- ⎪⎝⎭，sin sin 26PA PCππαα=⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，所以sin sin 3BP PC απα=⎛⎫- ⎪⎝⎭，sin 2sin 6PA PC παπα⎛⎫- ⎪⎝⎭=⎛⎫- ⎪⎝⎭，因为||||||PA PB PC λ+=所以333sin cos sin sin cos 44sin 2233sin sin sin cos sin cos 3644πααααααλππαααααα⎛⎫⎛⎫-- ⎪-- ⎪⎝⎭⎝⎭=+==⎛⎫⎛⎫---- ⎪ ⎪⎝⎭⎝⎭ 3341132sin 23sin cos 4ααα=-=---，因为,63ππα⎛⎫∈⎪⎝⎭，所以22,33ππα⎛⎫∈ ⎪⎝⎭，所以(2sin 230,23α⎤-∈-⎦，所以)31232,2sin 23α⎡-∈++∞⎣- 故实数λ的最小值为232+. 故答案为：232+【点睛】本题考查数学文化背景下的解三角形，三角恒等变换解决三角函数取值范围问题，考查运算求解能力，数学建模能力，化归转化思想，是难题.本题解题的关键在于根据题目背景，通过设PCB α∠=，进而建立解三角形的模型，再根据正弦定理及三角恒等变换化简求最值即可.四、解答题17．在①2122b a a =+，②28b a =，③35T a =这三个条件中选择一个，补充在下面问题中，并作出解答．问题：已知数列{}n a 的前n 项和221n S n n =-，等比数列{}n b 的前n 项和为n T ，13b a =，且，判断是否存在唯一的()*k k ∈N ，使得1k b >，且11k b +<．若存在，求出k 的值；若不存在，请说明理由．【答案】①；不存在，理由见解析；（②；存在，3k =，理由见解析；或③；不存在，理由见解析；均可）【分析】选择三个条件中的一个，由221n S n n =-求得222n a n =-，配合条件求得等比数列{}n b 的通项公式，根据单调性判断是否满足题设条件即可. 【详解】若选择条件①，由题知212[21(1)(1)]22221n n n S n n n a S n n ------==-=-，2n ≥，当1n =时，1121120a S ==-=，满足条件，则222n a n =-，2318,16a a ==，故1316b a ==，212238129a b b a =⇒==+，则数列{}n b 是以16为首项，1916为公比的等比数列，11916()16n n b -=⋅，易知n b 单增，1161n b b ≥=>，故不存在唯一的()*k k ∈N ，使得1k b >，且11k b +<．若选择条件②，由题知212[21(1)(1)]22221n n n S n n n a S n n ------==-=-，2n ≥，当1n =时，1121120a S ==-=，满足条件，则222n a n =-，132816,6b a b a ====，数列{}n b 是以16为首项，38为公比的等比数列，1316()8n n b -=⋅，易知n b 单减，233916()184b =⋅=>，3432716()1832b =⋅=<，故存在唯一的3k =，使得1k b >，且11k b +<．若选择条件③，由题知212[21(1)(1)]22221n n n S n n n a S n n ------==-=-，2n ≥，当1n =时，1121120a S ==-=，满足条件，则222n a n =-，1316b a ==，设等比数列{}n b 的公比为q ，则116n n b q-=，23516161612T q q a =++==，解得12q =-，1116()2n n b -=-，当6n ≥时，161116()122n n b b -=⋅≤=<，又123456116,8,4,2,1,2b b b b b b ==-==-==-，则存在1k =或3，使得1k b >，且11k b +<，即不存在唯一的()*k k ∈N ，使得1k b >，且11k b +<．【点睛】关键点点睛：求得数列{}n a 的通项，根据选择的条件求得数列{}n b 的通项，从而利用单调性判断数列是否满足题设条件.18．ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，设222sin sin sin sin A B C A B +-=⋅．（1）求C ；（2）若3cos 5B =，D 是边BC 上一点，且4CD BD =，ACD △的面积为75，求AC ．【答案】（1）4π；（2）2 【分析】（1）根据正弦定理将角化为边，在利用余弦定理求得cos C ，从而求得C .（2）由3cos 5B =求得4sin 5B =，sin sin()10A B C =+=，根据正弦定理求得sin sin 8A a b B =⋅=，又4510CD a ==，然后利用三角形面积公式，求得AC 的长.【详解】（1）由正弦定理知，222a b c +-=，则由余弦定理知，222cos 22a b c C ab +-==，在ABC 中，(0,)C π∈，故4C π（2）由3cos 5B =，知4sin 5B =，43sin sin()525210A B C =+=⨯+⨯=，由正弦定理知，sin sin 8A a bB =⋅=，又4CD BD =，则472510CD a b ==，21172277sin 22102205ACDSCD AC C b b b =⋅⋅⋅=⨯⨯⨯==，则2AC b ==【点睛】关键点点睛：在解三角形过程中，利用正弦定理及余弦定理进行边角互化，从而根据条件解得未知量.19．如图，在直四棱柱1111ABCD A BC D -中，//AB CD ，2DC =，13AA =，1AB BC AD ===，点E 和F 分别在侧棱1AA 、1CC 上，且11A E CF ==．（1）求证：//BC 平面1D EF ；（2）求直线AD 与平面1D EF 所成角的正弦值．【答案】（1）证明见解析；（221. 【分析】（1）分别取1D F 、CD 的中点N 、M ，证明四边形AENM 、ABCM 为平行四边形，可得出//EN AM ，//AM BC ，利用平行线的传递性结合线面平行的判定定理可证得结论成立；（2）以点A 为坐标原点，AB 为x 轴，平面ABCD 内垂直于AB 的直线为y 轴，1AA 为z 轴建立空间直角坐标系，利用空间向量法可求得直线AD 与平面1D EF 所成角的正弦值.【详解】（1）分别取1D F 、CD 的中点N 、M ，连接AM 、MN 、EN ，如图所示：M 、N 分别为CD 、1D F 的中点，则MN 为梯形1CFD D 的中位线，所以，11////MN CC DD ，且有()11122MN CC DD =+=， 11A E =，11//AA DD ，所以，2AE MN ==，且//AE MN ，所以，四边形AENM 为平行四边形，故//EN AM ，M 为CD 的中点，则12CM CD AB ==，因为//AB CD ，则//CM AB ，所以，四边形ABCM 为平行四边形，则//AM BC ，故//BC EN ，BC ⊄平面1D EF ，EN ⊂平面1D EF ，因此，//BC 平面1D EF ；（2）以点A 为坐标原点，AB 为x 轴，平面ABCD 内垂直于AB 的直线为y 轴，1AA 为z 轴建立如下图所示的空间直角坐标系，则()0,0,0A 、1322D ⎛⎫- ⎪ ⎪⎝⎭、113,22D ⎛⎫- ⎪ ⎪⎝⎭、()0,0,2E 、33,22F ⎛⎫ ⎪ ⎪⎝⎭，设平面1D EF 的法向量为(),,m x y z =，132AD ⎛⎫=- ⎪ ⎪⎝⎭，113,122D E ⎛⎫=-- ⎪ ⎪⎝⎭，()12,0,2D F =-，由1100m D E m D F ⎧⋅=⎪⎨⋅=⎪⎩，可得13022220x y z x z ⎧--=⎪⎨⎪-=⎩，令3x =(3,3m =-，321cos ,77AD m AD m AD m⋅-<>===-⋅因此，直线AD 与平面1D EF 所成角的正弦值为217.【点睛】方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin hlθ=（l 为斜线段长），进而可求得线面角；（3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.20．已知某高校共有10000名学生，其图书馆阅览室共有994个座位，假设学生是否去自习是相互独立的，且每个学生在每天的晚自习时间去阅览室自习的概率均为0.1．（1）将每天的晚自习时间去阅览室自习的学生人数记为X ，求X 的期望和方差；（2）18世纪30年代，数学家棣莫弗发现，如果随机变量X 服从二项分布(),B n p ，那么当n 比较大时，可视为X 服从正态分布()2,N u σ．任意正态分布都可变换为标准正态分布（0μ=且1σ=的正态分布），如果随机变量()2,YN u σ，那么令Y Z μσ-=，则可以证明()0,1ZN ．当()0,1Z N 时，对于任意实数a ，记()()a P Z a φ=<．已知下表为标准正态分布表（节选），该表用于查询标准正态分布对应的概率值．例如当0.16a =时，由于0.160.10.06=+，则先在表的最左列找到数字0.1（位于第三行），然后在表的最上行找到数字0.06（位于第八列），则表中位于第三行第八列的数字0.5636便是()0.16φ的值．（i ）求在晚自习时间阅览室座位不够用的概率；（ii ）若要使在晚自习时间阅览室座位够用的概率高于0.7，则至少需要添加多少个座位？【答案】（1）随机变量X 的期望是1000，方差是900；（2）（i ）0.5793；（ii ）阅览室至少还要增加22个座位.【分析】（1）根据随机变量X 服从二项分布，结合n =10000，p =0.1，代入公式求解；（2）（i ）由于（1）中的二项分布n 值较大，可以认为随机变量X 服从正态分布，由()10000,130X N -，先求得 ()()99410.2p X ϕ<=-，再由()()9941994p X p X ≥=-<求解；（ii ）由表可得：()0.530.7019ϕ=，易得()1015.90.7019p X <=求解. 【详解】（1）由题意得：随机变量X 服从二项分布，其中n =10000，p =0.1，则()()1000,(1)10000.10.9900E X NP D X np p ===-=⨯⨯=，所以随机变量X 的期望是1000，方差是900；（2）（i ）由于（1）中的二项分布n 值较大，所以可以认为随机变量X 服从正态分布，由（1）知()1000,30,1000,900XN μσ==，则()10000,130X N -，()()10009940.20.230X p X p ϕ-⎛⎫<=<-=-⎪⎝⎭，由标准正态分布的性质可知 ()()0.210.2φφ-=-，所以 ()()99410.2p X ϕ<=-，所以()()()99419940.20.5793p X p X ϕ≥=-<==，故在晚自习时间阅览室座位不够用的概率是0.5793；（ii ）查表可得：()0.530.7019ϕ=，则10000.530.701930X p -⎛⎫<=⎪⎝⎭，即()1015.90.7019p X <=，而()()100010150.50.50.69150.730X p X p ϕ-⎛⎫<=<==<⎪⎝⎭，故座位数至少要1016个，由于1016-994=22，则阅览室至少还要增加22个座位.【点睛】关键点点睛：本题第二问关键是理解正态分布于标准正态分布的转化：()()Y p Y M P a a μφσ-⎛⎫<=<= ⎪⎝⎭.21．在平面直角坐标系xOy 中，O 是坐标原点，P 是直线2x =-上的动点，过P 作两条相异直线1l 和2l ，其中1l 与抛物线2:4C y x =交于A 、B 两点，2l 与C 交于M 、N 两点，记1l 、2l 和直线OP 的斜率分别为1 k 、2k 和3k ．（1）当P 在x 轴上，且A 为PB 中点时，求1k ；（2）当AM 为PBN 的中位线时，请问是否存在常数μ，使得31211k k k μ+=？若存在，求出μ的值；若不存在，请说明理由．【答案】（1）123k =；（2）存在2μ=-满足条件，理由见解析. 【分析】（1）设出直线1l 的方程，然后联立直线1l 与抛物线的方程，得到关于,A B y y 的韦达定理形式，再根据A 为PB 的中点，得到,A B y y 的关系，结合韦达定理可得关于1k 的方程，由此求解出结果；（2）根据已知条件将12,k k 先表示为坐标形式，然后根据AM 为中位线得到,A B y y 以及,M N y y 的关系，结合抛物线方程得到,A M y y 所满足的方程，由此确定出,A M y y 的关系，即可计算出1211k k +关于P y 的表示，再结合P 点坐标可求解出3k ，则μ的值可确定.【详解】（1）由条件知()2,0P -且10k ≠，设()11:2l y k x =+，所以()1224y k x y x⎧=+⎨=⎩，消去x 可得21480y y k -+=，所以14,8A B A B y y y y k +==，又因为A 为PB 中点，所以2P B A y y y +=，所以2B A y y =，所以2143,28A A y y k ==，所以21443k ⎛⎫= ⎪⎝⎭，所以123k =；（2）设()2222,,,,,,,,2,4444NA B MA B M N y y y y A y B y M y N y P a ⎛⎫⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，所以122444A B A B A B A B A B y y y y k y y x x y y --===-+-，222444M N M N N M M N M N y y y y k y y x x y y --===-+-，所以121144M NA B y y y y k k +++=+，因为AM 为PBN 的中位线，所以A 为PB 的中点，M 是PN 的中点，所以2,22P B B A x x x x +-+==即22121442BA y y -+=，即2211224A B y y =-+，又22P B B A y y a y y ++==，所以2B A y y a =-，所以()22112224A A y y a =-+-，所以222480A A y ay a -+-=①；又因为2,22P N N Mx x x x +-+==即22121442N M y y -+=，即2211224M N y y =-+， 22P N NM y y a y y ++==，所以2N M y y a =-，所以()22112224M M y y a =-+-，所以222480M My ay a -+-=②；由①②可知：,A M y y 是满足方程222480y ay a -+-=的两个根，所以2A M y y a +=，所以()()1222114444A A M M M N AB y y a y y a y y y y k k +-+-+++=+=+，所以()1232116244A M y y a a aa k k +--+===，又3122P P y a k a x ===--，所以312112k k k +=-，所以2μ=-，所以存在常数2μ=-使得31211k k k μ+=成立. 【点睛】关键点点睛：解答本题第二问的关键在于点坐标设法以及对于中位线的分析，利用抛物线方程设出点的坐标，根据中位线得到点的坐标之间的关系，通过,A M 的纵坐标所满足方程的特点，确定出,A M 纵坐标的关系，故1211k k +与3k 的关系可分析出.22．已知定义在R 上的函数()()()2cos 2xf x x a x a ea -=++-∈R ．（其中常数e 是自然对数的底数， 2.71828e =）（1）当2a =时，求()f x 的极值；（2）（i ）若()f x 在[]0,π上单调递增，求实数a 的取值范围；（ii ）当*n ∈N 时，证明：()111142tan n k n n n k n k =>-+++∑．【答案】（1）极小值为()02f =，无极大值；（2）（i ）(],2-∞；（ii ）证明见解析.【分析】（1）利用导数分析函数()22cos f x x x =+的单调性，由此可求得函数()f x 的极大值和极小值；（2）（i ）利用参变量分离法可得出()2sin x x x e a x e --+≤+对任意的[]0,x π∈恒成立，求出函数sin xx x e y x e--+=+在区间[]0,π上的最小值，由此可得出实数a 的取值范围；（ii ）证明得出：当[)1,x ∈+∞时，111112121tan x x x x⎛⎫>-- ⎪-+⎝⎭，依次可得出()1111121231tan 1n n n n ⎛⎫>-- ⎪++⎝⎭++，()1111123252tan 2n n n n ⎛⎫>-- ⎪++⎝⎭++，，1111141412tan 2n n n n⎛⎫>-- ⎪-+⎝⎭，利用不等式的基本性质可证得所证不等式成立. 【详解】（1）当2a =时，()22cos f x x x =+，该函数的定义域为R ，则()22sin f x x x '=-，()22cos 0f x x ''=-≥，所以，函数()f x '在R 上为增函数，且()00f '=，当0x <时，()()00f x f ''<=，此时函数()f x 单调递减，当0x >时，()()00f x f ''>=，此时函数()f x 单调递增.所以，函数()f x 的极小值为()02f =，无极大值；（2）（i ）()()2cos 2x f x x a x a e -=++-，则()()2sin 2x f x x a x a e -'=---， ()f x 在[]0,π上单调递增，则()()2sin 20x f x x a x a e -'=---≥对任意的[]0,x π∈恒成立，可得()2sin x x x e a x e --+≤+，下面证明：1sin x x x e x e--+≥+，其中[]0,x π∈，即证sin x x x e x e --+≥+，即证sin 0x x -≥，其中[]0,x π∈，由（1）可知，对任意的[]0,x π∈，sin 0x x -≥，又当0x =时，1sin xx x e x e--+=+， 2a ∴≤，故实数a 的取值范围是(],2-∞；（ii ）由（1）可知，当2a =时，()22cos f x x x =+在[]0,π上单调递增，当(]0,1x ∈时，()()02f x f >=，即2cos 12x x >-，当[)1,x ∈+∞时，(]10,1x ∈，则110sin 1x x<<≤， 11sin11cos 111tan tan tan xx x x x x x ∴=>=，当[)1,x ∈+∞时，()()22112211cos 111124*********x x x x x x x ⎛⎫>->-=-=-- ⎪--+-+⎝⎭，所以，111112121tan x x x x ⎛⎫>-- ⎪-+⎝⎭，所以，()1111121231tan 1n n n n ⎛⎫>-- ⎪++⎝⎭++， ()1111123252tan 2n n n n ⎛⎫>-- ⎪++⎝⎭++，，1111141412tan 2n n n n ⎛⎫>-- ⎪-+⎝⎭，将上述不等式全部相加得()111111112141214242tan n k n n n n n n n n n k n k =>-+>-+=-+++++++∑.故原不等式得证.【点睛】方法点睛：利用导数证明不等式问题，方法如下：（1）直接构造函数法：证明不等式()()f x g x >（或()()f x g x <）转化为证明()()0f x g x ->（或()()0f x g x -<），进而构造辅助函数()()()h x f x g x =-；（2）适当放缩构造法：一是根据已知条件适当放缩；二是利用常见放缩结论；（3）构造“形似”函数，稍作变形再构造，对原不等式同解变形，根据相似结构构造辅助函数.。

2021届广东省深圳市高三下学期4月第二次调研考试(二模) 化学

保密★启用前试卷类型：A2021年深圳市高三年级第二次调研考试化学2021.4 本试卷共10页，21小题，满分100分。

考试用时75分钟。

注意事项：1.答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。

用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。

将条形码横贴在答题卡右上角“条形码粘贴处”。

2.作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答案信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试卷上。

3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按上述要求作答无效。

4.考生必须保证答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

可能用到的相对原子质量：H 1 O 16 Na 23 Mg 24 S 32 Cl 35.5 Co 59 Se 79 Bi 209一、选择题：本题共16小题，共44分。

第1～10小题，每小题2分；第11～16小题，每小题4分。

在每小题给出的四个选项中，只有一项是符合题意要求的。

1.化学与生产、生活密切相关。

下列关于物质用途的说法错误的是A.NH4Cl溶液用作除锈剂B.还原铁粉用作抗氧化剂C.NaHCO3用作糕点膨松剂D.干冰用作Na着火时的灭火剂2.NH4ClO4可用作火箭燃料，其分解反应为2NH4ClO4∆==N2↑＋Cl2↑＋2O2↑＋4H2O。

下列有关该反应中各微粒的描述错误的是A.NH4ClO4为含有共价键的离子化合物B.N2的电子式为N::NC.Cl原子的M电子层有7个电子D.16O2分子中的质子数与中子数之比为1：13.铅霜(醋酸铅)，又称为“铅糖”，其古代制法为“以铅杂水银十五分之一，合炼作片，置醋瓮中，密封，经久成霜。

”下列相关说法正确的是A.“铅糖”有甜味，可充当食品甜味剂B.“瓮”为铁质容器C.“经久成霜”是结晶的过程D.该制法以铅作正极，汞作负极，发生电化学腐蚀4.下列有关物质分类的说法错误的是A.SiO2、P2O5均为酸性氧化物B.碘酒、水玻璃均为混合物C.糖类、蛋白质均为高分子化合物D.NaCl晶体、HCl气体均为电解质5.下列与实验相关的操作或方案正确的是6.异烟肼是一种抗结核药物的主要成分，可通过以下路线合成。

2021届广东深圳市高考二模化学试题(及答案)

4－甲基阰唗
异烟酸
异烟阱
A. 4 — 甲基咄唗的所有原子不可能处千同一平面 B.异烟酸的分子式为c6压N02
c. CD和＠的反应类型均为取代反应
D.异烟阱可与压发生加成反应
7.设阿伏加德罗常数的值为NA。下列说法正确的是 A. 0.1 molCh溶千水制成饱和氯水，转移电子数目为 O.INA B. 12.0 gNaHS04与MgS04的固体混合物中含有离子总数为0.2 NA C.标准状况下，11.2 L CH2Ch所含氢原子数为NA D. 1 molCH冲含有电子数为IO NA
2A1+6H+ =2Al 3+ +3H2 个，小组成员认为应产生Cu(OH)2 , 但实际实验中并未观察
到蓝色沉淀。千是他们提出了以下两种猜测并进行相关验证。完成下列表格：
猜测
i. CD
ii. Cu(OH)2 与Al3十发生了反应
实验取少最 Cu(OH)2悬浊液，加入打磨过的铝片，振荡
2021 年深圳市高三年级笫二次调研考试化学试题笫 2 页共 10 页
9. 常温下，向100 mL 0.1 mol•L-1比S溶液中缓慢通入S02 气体，可发生反应2H2S+S02
=3SJ+2H心。下列关千该过程的说法错误的是 A. pH先增大后减小，最终保持不变
B. 恰好完全反应时，反应消耗112 mL SO辽标准状况）
C.
c2(HS-) c(H2S) • c(S2- )
的值减小
D. 0.1 mol•L-1H心溶液中：c(H+)=c(HS-)+2c(S2-)+c(OH-)
10. 以Fe203/Ab03为氧载体，化学链制氢联合甲炕干重整制备合成气(CO、H2 )的原理如下图所示。下列有关叙述错误的是

2021届广东省深圳市高三第二次调研考试文科数学试卷

时间
周一
周二
周三
周四
周五
车流量（万辆）
的浓度（微克/立方米）
（1）根据上表数据，请在下列坐标系中画出散点图；
（2）根据上表数据，用最小二乘法求出关于的线性回归方程；
（3）若周六同一时间段车流量是万辆，试根据（2）求出的线性回归方程预测，此时的浓度为多少（保留整数）？
18．（本小题满分14分）如图，是边长为的等边三角形，是等腰直角三角形，，平面平面，且平面， .
（1）求曲线的方程；
（2）恰好存在唯一一个同时满足以下条件的圆：
①以曲线的弦为直径；
②过点；
③直径．求的取值范围．
21．已知函数（，），且对任意，都有 .
（Ⅰ）用含的表达式表示；
（Ⅱ）若存在两个极值点，，且，求出的取值范围，并证明；
（Ⅲ）在（Ⅱ）的条件下，判断零点的个数，并说明理由.
【解析】
试题分析：根据特称命题的否定形式，可知应该为B.
考点：特称命题的否定形式.
5．D
【解析】
试题分析：对于A项，能够得出，所以A不对，对于B项，可以成任意角，所以B不对，对于C项，垂直于同一个平面的两个平面可以成任意角，所以C不对，只有D项，平面平行具有传递性，故选D.
考点：空间平行垂直关系.
A． B． C． D．
3．已知集合，，则
A． B． C． D．
4．命题，，则为（）
A．， B．，
C．， D．，
5．已知直线，平面，则下列能推出的条件是
A．， B．，
C．， D．，
6．已知某路口最高限速，电子监控测得连续辆汽车的速度如图的茎叶图（单位：）．若从中任取辆，则恰好有辆汽车超速的概率为（）

广东省深圳市2021届新高考数学二模试卷含解析

广东省深圳市2021届新高考数学二模试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下图中的图案是我国古代建筑中的一种装饰图案，形若铜钱，寓意富贵吉祥．在圆内随机取一点，则该点取自阴影区域内（阴影部分由四条四分之一圆弧围成）的概率是（）A ．12B ．13C ．41π- D ．42π-【答案】C 【解析】令圆的半径为1，则()22'41S P S ππππ--===-，故选C ． 2．已知函数()xf x a =（0a >，且1a ≠）在区间[],2m m 上的值域为[],2m m ，则a =（）A 2B ．14C ．1162 D ．14或4 【答案】C 【解析】【分析】对a 进行分类讨论，结合指数函数的单调性及值域求解. 【详解】分析知，0m >.讨论：当1a >时，22m m a ma m ⎧=⎨=⎩，所以2m a =，2m =，所以2a =01a <<时，22m ma m a m⎧=⎨=⎩，所以12ma =，14m =，所以116a =.综上，116a =或2a = C. 【点睛】本题主要考查指数函数的值域问题，指数函数的值域一般是利用单调性求解，侧重考查数学运算和数学抽象的核心素养.3．设函数()()21ln 11f x x x=+-+，则使得()()1f x f >成立的x 的取值范围是（）． A ．()1,+∞ B ．()(),11,-∞-+∞ C ．()1,1- D ．()()1,00,1-【答案】B【解析】【分析】由奇偶性定义可判断出()f x 为偶函数，由单调性的性质可知()f x 在[)0,+∞上单调递增，由此知()f x 在(],0-∞上单调递减，从而将所求不等式化为1x >，解绝对值不等式求得结果. 【详解】由题意知：()f x 定义域为R ，()()()()()2211ln 1ln 111f x x x f x x x -=+--=+-=++-，()f x ∴为偶函数，当0x ≥时，()()21ln 11f x x x=+-+， ()ln 1y x =+在[)0,+∞上单调递增，211y x =+在[)0,+∞上单调递减， ()f x ∴在[)0,+∞上单调递增，则()f x 在(],0-∞上单调递减，由()()1f x f >得：1x >，解得：1x <-或1x >，x 的取值范围为()(),11,-∞-+∞.故选：B . 【点睛】本题考查利用函数的单调性和奇偶性求解函数不等式的问题；奇偶性的作用是能够确定对称区间的单调性，单调性的作用是能够将函数值的大小关系转化为自变量的大小关系，进而化简不等式. 4．数列{}n a 满足：3111,25n n n n a a a a a ++=-=，则数列1{}n n a a +前10项的和为 A ．1021B ．2021C ．919D ．1819【答案】A 【解析】分析：通过对a n ﹣a n+1=2a n a n+1变形可知1112n n a a +-=，进而可知121n a n =-，利用裂项相消法求和即可．详解：∵112n n n n a a a a ++-=，∴1112n na a +-=，又∵31a =5，∴()3112n 32n 1n a a =+-=-，即121n a n =-，∴()111111222121n n n n a a a a n n ++⎛⎫=-=- ⎪-+⎝⎭，∴数列{}1n n a a +前10项的和为1111111110112335192122121⎛⎫⎛⎫-+-++-=-= ⎪ ⎪⎝⎭⎝⎭，故选A ．点睛：裂项相消法是最难把握的求和方法之一，其原因是有时很难找到裂项的方向，突破这一难点的方法是根据式子的结构特点，常见的裂项技巧：(1)()1111n n k k n n k ⎛⎫=- ⎪++⎝⎭；（2）1k=；（3）()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭；（4）()()11122n n n =++ ()()()11112n n n n ⎡⎤-⎢⎥+++⎢⎥⎣⎦；此外，需注意裂项之后相消的过程中容易出现丢项或多项的问题，导致计算结果错误. 5．在复平面内，31ii+-复数（i 为虚数单位）的共轭复数对应的点位于（） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【答案】D 【解析】【分析】将复数化简得=12z i +,12z i =-,即可得到对应的点为()1,2-,即可得出结果. 【详解】3(3)(1)12121(1)(1)i i i z i z i i i i +++===+⇒=---+，对应的点位于第四象限. 故选:D . 【点睛】本题考查复数的四则运算,考查共轭复数和复数与平面内点的对应,难度容易.6．据国家统计局发布的数据，2019年11月全国CPI （居民消费价格指数），同比上涨4.5%，CPI 上涨的主要因素是猪肉价格的上涨，猪肉加上其他畜肉影响CPI 上涨3.27个百分点．下图是2019年11月CPI 一篮子商品权重，根据该图，下列结论错误的是（）A ．CPI 一篮子商品中所占权重最大的是居住B ．CPI 一篮子商品中吃穿住所占权重超过50%C ．猪肉在CPI 一篮子商品中所占权重约为2.5%D ．猪肉与其他畜肉在CPI 一篮子商品中所占权重约为0.18% 【答案】D 【解析】【分析】A.从第一个图观察居住占23%，与其他比较即可.B. CPI 一篮子商品中吃穿住所占23%+8%+19.9%=50.9%，再判断.C.食品占19.9%，再看第二个图，分清2.5%是在CPI 一篮子商品中，还是在食品中即可.D. 易知猪肉与其他畜肉在CPI 一篮子商品中所占权重约为2.1%+2.5%=4.6%. 【详解】A. CPI 一篮子商品中居住占23%，所占权重最大的，故正确.B. CPI 一篮子商品中吃穿住所占23%+8%+19.9%=50.9%，权重超过50%，故正确.C.食品占中19.9%，分解后后可知猪肉是占在CPI 一篮子商品中所占权重约为2.5%，故正确.D. 猪肉与其他畜肉在CPI 一篮子商品中所占权重约为2.1%+2.5%=4.6%，故错误. 故选：D 【点睛】本题主要考查统计图的识别与应用，还考查了理解辨析的能力，属于基础题.7．如图，已知平面αβ⊥，l αβ⋂=，A 、B 是直线l 上的两点，C 、D 是平面β内的两点，且DA l ⊥，CB l ⊥，3AD =，6AB =，6CB =．P 是平面α上的一动点，且直线PD ，PC 与平面α所成角相等，则二面角P BC D --的余弦值的最小值是（）A ．55B ．32C ．12D ．1【答案】B 【解析】【分析】PBA ∠为所求的二面角的平面角，由DAP CPB ~得出PAPB，求出P 在α内的轨迹，根据轨迹的特点求出PBA ∠的最大值对应的余弦值【详解】DA l ⊥，αβ⊥，l αβ⋂=，AD β⊂ AD α∴⊥，同理BC α⊥DPA ∴∠为直线PD 与平面α所成的角，CPB ∠为直线PC 与平面α所成的角DPA CPB ∴∠=∠，又90DAP CBP ∠=∠=︒DAP CPB ∴~，12PA DA PB BC == 在平面α内，以AB 为x 轴，以AB 的中垂线为y 轴建立平面直角坐标系则()()3030A B -，，，，设()()0P x y y >， ()()2222233x y x y ∴++=-+()22516x y ++=P ∴在α内的轨迹为()50M -，为圆心，以4为半径的上半圆平面PBC ⋂平面BC β=，PB BC ⊥，AB BC ⊥PBA ∴∠为二面角P BC D --的平面角，∴当PB 与圆相切时，PBA ∠最大，cos PBA ∠取得最小值此时4843PM MB MP PB PB ==⊥=，，，433cos 82PB PBA MB ∠===故选B 【点睛】本题主要考查了二面角的平面角及其求法，方法有：定义法、三垂线定理及其逆定理、找公垂面法、射影公式、向量法等，依据题目选择方法求出结果．8．下图所示函数图象经过何种变换可以得到sin 2y x =的图象（）A ．向左平移3π个单位 B ．向右平移3π个单位 C ．向左平移6π个单位 D ．向右平移6π个单位【答案】D 【解析】【分析】根据函数图像得到函数的一个解析式为()sin 23f x x π⎛⎫=+ ⎪⎝⎭，再根据平移法则得到答案. 【详解】设函数解析式为()()sin f x A x b ωϕ=++，根据图像：1,0A b ==，43124T πππ=-=，故T π=，即2ω=， sin 1126f ππϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，2,3k k Z πϕπ=+∈，取0k =，得到()sin 23f x x π⎛⎫=+ ⎪⎝⎭，函数向右平移6π个单位得到sin 2y x =. 故选：D . 【点睛】本题考查了根据函数图像求函数解析式，三角函数平移，意在考查学生对于三角函数知识的综合应用. 9．已知命题p ：任意4x ≥，都有2log 2x ≥；命题q ：a b >，则有22a b >．则下列命题为真命题的是（） A ．p q ∧ B ．()p q ∧⌝C ．()()p q ⌝∧⌝D ．()p q ⌝∨【答案】B 【解析】【分析】先分别判断命题,p q 真假，再由复合命题的真假性，即可得出结论. 【详解】p 为真命题；命题q 是假命题，比如当0a b >>,或=12a b =-，时，则22a b > 不成立. 则p q ∧，()()p q ⌝∧⌝，()p q ⌝∨均为假. 故选:B 【点睛】本题考查复合命题的真假性，判断简单命题的真假是解题的关键，属于基础题.10．已知函数()()1xe a axf x e ⎛⎫=-+ ⎪⎝⎭，若()()0f x x R ≥∈恒成立，则满足条件的a 的个数为（）A ．0B ．1C ．2D ．3【答案】C 【解析】【分析】由不等式恒成立问题分类讨论：①当0a =，②当0a <，③当0a >，考查方程1lna ae=-的解的个数，综合①②③得解．【详解】①当0a =时，1()00x f x e -=>，满足题意， ②当0a <时，0x e a ->，01(x ae ∃∈-，)+∞，10ax e+<，故()0()f x x R ∈不恒成立， ③当0a >时，设()x g x e a =-，1()h x ax e=+，令()0xg x e a =-=，得x lna =，1()0h x ax e =+=，得1x ae=-，下面考查方程1lna ae=-的解的个数，设ϕ（a ）alna =，则ϕ'（a ）1lna =+ 由导数的应用可得：ϕ（a ）alna =在1(0,)e为减函数，在1(e，)+∞为增函数，则ϕ（a ）1min e=-，即1lna ae=-有一解，又()xg x e a =-，1()h x ax e=+均为增函数，所以存在1个a 使得()0()f x x R ∈成立，综合①②③得：满足条件的a 的个数是2个，故选：C ．【点睛】本题考查了不等式恒成立问题及利用导数研究函数的解得个数，重点考查了分类讨论的数学思想方法，属难度较大的题型.11．正项等比数列{}n a 中，153759216a a a a a a ++=，且5a 与9a 的等差中项为4，则{}n a 的公比是 ( ) A ．1 B ．2 C ．22D ．2【答案】D 【解析】【分析】设等比数列的公比为q ，q 0>，运用等比数列的性质和通项公式，以及等差数列的中项性质，解方程可得公比q ．【详解】由题意，正项等比数列{}n a 中，153759a a 2a a a a 16++=，可得222337737a 2a a a (a a )16++=+=，即37a a 4+=，5a 与9a 的等差中项为4，即59a a 8+=，设公比为q ，则()2237q a a 4q 8+==，则q 2(=负的舍去)，故选D ．【点睛】本题主要考查了等差数列的中项性质和等比数列的通项公式的应用，其中解答中熟记等比数列通项公式，合理利用等比数列的性质是解答的关键，着重考查了方程思想和运算能力，属于基础题．12．如图，在ABC 中，,(,),2AD AB BD xAB yAC x y R AD ⊥=+∈=，且12AC AD ⋅=，则2x y +=（）A ．1B ．23-C ．13-D ．34-【答案】C 【解析】【分析】由题可0,12AD AB AC AD ⋅=⋅=,所以将已知式子中的向量用AD AB AC ，，表示，可得到的,x y 关系，再由,,B D C 三点共线，又得到一个关于,x y 的关系，从而可求得答案【详解】由BD xAB yAC =+，则(1),[(](1)AD x AB y AC AD AD AD x AB y AC x AD AB y AD AC =++⋅=⋅++=+⋅+⋅，即412y =，所以13y =，又,,B D C 共线，则1111,,233x y x x y ++==-+=-. 故选：C 【点睛】此题考查的是平面向量基本定理的有关知识，结合图形寻找各向量间的关系，属于中档题. 二、填空题：本题共4小题，每小题5分，共20分。

广东省深圳市2021届高三数学第二次调研测试试题理（深圳二模）(1)

广东省深圳市2021届高三4月第二次调研考试数学（理科）一、选择题1.函数)1ln(+=x y 的概念域是A. )0,1(-B. ),0(+∞C. ),1(+∞-D. R2.方程014=-z 在复数范围内的根共有 A.1个 B. 2个 C. 3个 D. 4个3.两条异面直线在同一个平面上的正投影不．可能是 A.两条相交直线 B.两条平行直线 C.两个点 D.一条直线和直线外一点4.在以下直线中，与非零向量),(B A n = 垂直的直线是A. 0=+By AxB. 0=-By AxC. 0=+Ay BxD. 0=-Ay Bx5.已知函数)(x f y =的图像与函数11+=x y 的图像关于原点堆成，那么=)(x f A. 11+x B. 11-x C. 11+-x D. 11--x 6.已知△ABC 中，C B C B A sin sin sin sin sin 222++=，那么=AA.6π B. 3π C. 32π D. 65π 7.已知不等式x x a y y 224+≤-+对任意实数y x ,都成立，那么常数a 的最小值为 A.1 B. 2 C. 3 D. 48.如图1，咱们明白，圆环也可看做线段AB 绕圆心O 旋转一周所形成的平面图形，又圆环的面积22)()(22r R r R r R S +⨯⨯-=-=ππ.因此，圆环的面积等于是以线段r R AB -=为宽，以AB 中点绕圆心O 旋转一周所形成的圆的周长22r R +⨯π为长的矩形面积.请将上述方式拓展到空间，并解决以下问题：绕y 轴旋假设将平面区域d)r 0}()(|),{(222<<≤+-=其中r y d x y x M 转一周，那么所形成的旋转体的体积是A. d r 22πB. d r 222π C. 22rd π D. 222rd π二、填空题(一)必做题:9.如图2，在独立性查验中，依照二维条形图回答，抽烟与患肺病（填“有”或“没有”）. 10.在4)32(+x 的二项展开式中，含3x 项的系数是 .PB11.以抛物线x y 42=的核心为极点，极点为中心，离心率为2的双曲线方程是 .12.设变量y x ,知足⎩⎨⎧≤+≤≤110y y x ，那么y x +的取值范围是 .13.在程序中，RND x =表示将运算机产生的[0,1]区间上的均匀随机数赋给变量x .利用图3的程序框图进行随机模拟，咱们发觉：随着输入N 值的增加,输出的S 值稳固在某个常数上.那个常数是 .(要求给出具体数值) 注:框图中的“=”,即为“←”或为 “:=”.(二)选做题:14.(坐标系与参数方程选做题)极坐标系中,B A ,别离是直线05sin 4cos 3=+-θρθρ和圆θρcos 2=上的动点,那么B A ,两点之间距离的最小值是 .15.(几何证明选讲选做题)如图4,△OAB 是等腰三角形,P 是底边AB延长线上一点,且4,3=•=PB PA PO ,那么腰长OA= .三、解答题:16.(本小题总分值12分)已知函数)6cos(sin )(πωω++=x x x f ,其中R x ∈,ω为正常数. (1) 当2=ω时,求)3(πf 的值; (2) 记)(x f 的最小正周期为T ,假设1)3(=πf ,求T 的最大值. 17.( 本小题总分值12分)某班联欢晚会玩飞镖抛掷游戏,规那么如下:每人持续抛掷5支飞镖,积存3支飞镖掷中目标即可获奖;不然不获奖.同时要求在以下两种情形下中止抛掷:①积存3支飞镖掷中目标;②积存3支飞镖没有掷中目标.已知小明同窗每支飞镖掷中目标的概率是常数)5.0(>p p ,且掷完3支飞镖就中止抛掷的概率为31. (1) 求p 的值； (2) 记小明终止游戏时，抛掷的飞镖支数为X ，求X 的散布列和数学期望.18.( 本小题总分值14分)如图5,已知△ABC 为直角三角形,∠ACB 为直角.以AC 为直径作半圆O,使半圆O 所在平面⊥平面ABC,P 为半圆周异于A,C 的任意一点.(1) 证明:AP ⊥平面PBC(2) 假设PA=1,AC=BC=2,半圆O 的弦PQ ∥AC,求平面PAB 与平面QCB 所成锐二面角的余弦值.19.( 本小题总分值14分)设等差数列}{n a 的公差为d ,n S 是}{n a 中从第12-n 项开始的持续12-n 项的和,即(1) 若1S ,2S ,3S 成等比数列,问:数列}{n S 是不是成等比数列?请说明你的理由;(2) 若04151>=d a ,证明:*),14121(981111321N n d S S S S n n ∈+-≤++++ . 20.( 本小题总分值14分)已知a 为正常数,点A,B 的坐标别离是)0,(),0,(a a -,直线AM,BM 相交于点M,且它们的斜率之积是21a -. (1) 求懂点M 的轨迹方程,并指出方程所表示的曲线;(2) 当2=a 时,过点)0,1(F 作直线AM l ∥,记l 与(1)中轨迹相交于两点P,Q,动直线AM 与y 轴交与点N,证明AN AM PQ为定值.21.( 本小题总分值14分)设f （x ）是概念在［a ，b ］上的函数，假设存在c (,)a b ∈，使得f （x ）在［a ，c ］上单调递增，在［c ，b ］上单调递减，那么称f （x ）为［a ，b ］上单峰函数，c 为峰点。

广东省深圳市2021届高三数学第二次调研考试试题理

广东省深圳市2021届高三数学第二次调研考试试题理一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设21(1)iz i +=-则|z|=A．12B ．22C ．1D ．22．已知集合2{|2},{|320},xA y yB x x x ===-+则 A ．A∩B=B ．A ∪B=RC ．A BD ．B A3．设α为平面，m ，n 为两条直线,若m ⊥α,则“m ⊥n ”是”n ⊂α”的 A ．充分必要条件 B ．充分不必要条件 C ．必要不充分条件 D ．既不充分也不必要条件4．已知双曲线2222:10,0)(y x C a b a b-=>>的两条渐近线互相垂直，则C 的离心率为A ．2B ．2C ．3D ．35．已知定义在R 上的函数f(x)满足()()2,f x f x +=当01x ≤≤时，13()f x x =，则178f ⎛⎫⎪⎝⎭= A ．12B ．2 C.18 D ．86.若x 1，x 2，…，x n 的平均数为a ，方差为b ，则1223,23,23n x x x +++的平均数和方差分别为A ．2a ，2bB ．2a ，4bC ．2a+3，2bD ．2a+3，4b 7．记等差数列{a n }的前n 项和为S n ，若244,2,S S ==则6S = A ．-6 B ．-4 C ．-2 D ．08．函数()()14sin 2xxx f x -=的部分图象大致为9已知椭圆C ：22213x y a +=的右焦点为F ，O 为坐标原点，C 上有且只有一个点P 满足|OF|=|FP|,则C 的方程为A ．221123x y += B.22183x y += C ．22163x y += D.22143x y += 10．下面左图是某晶体的阴阳离子单层排列的平面示意图其阴离子排列如下面右图所示，右图中圆的半径均为1，且相邻的圆都相切，A ，B ，C ，D 是其中四个圆的圆心，则AB CD ⋅=A ．24B ．26C ．28D ．3211．意大利数学家斐波那契(1175年—1250年)以兔子繁殖数量为例，引入数列：1，1，2，3，5，8，…，该数列从第三项起，每一项都等于前两项之和，即()21,n n n a a a n +++=+∈N 故此数列称为斐波那契数列，又称“兔子数列”，其通项公式为1515()().5n n n a ⎡⎤+-=-⎥⎦(设n 是不等式2log 5)(15)211x x x ->+的正整数解，则n 的最小值为A ．10B ．9C ．8D ．712．已知直线y ω=与函数()()()sin 01x f x ϕωω=+<<的图象相交，将其中三个相邻交点从左到右依次记为A ，B ，C ，且满足()*.N AC nBC n =∈有下列结论： ①n 的值可能为2②当n=3，且|φ|<π时，f(x)的图象可能关于直线x=-φ对称 ③当φ=6π时，有且仅有一个实数ω，使得(),11f x ππωω⎡⎤-⎢⎥++⎣⎦在上单调递增; ④不等式n ω>1恒成立其中所有正确结论的编号为 A ．③ B ．①② C ．②④ D ．③④二、填空题：本大题共4小题，每小题5分，共20分.13．曲线y=xlnx 在点(1,0)处的切线方程为 ▲14.若x ，y 满足约束条件20,0,30,y x y x y -≤⎧⎪-≤⎨⎪+-≥⎩则y z x =的最大值为 ▲15．2021年初，湖北成为全国新冠疫情最严重的省份，面临医务人员不足和医疗物资紧缺等诸多困难，全国人民心系湖北，志愿者纷纷驰援若将4名医生志愿者分配到两家医院(每人去一家医院，每家医院至少去1人)，则共有 ▲ 种分配方案16．已知正方形ABCD 边长为3，点E ，F 分别在边AB ，AD 上运动(E 不与A ，B 重合，F 不与A ，D 重合)，将△AEF 以EF 为折痕折起，当A ，E ，F 位置变化时，所得五棱锥A-EBCDF 体积的最大值为 ▲ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答。

广东省深圳市2021届高三下学期4月第二次调研考试(二模)数学试题含答案

保密★启用前2021本试卷共注意事项：1.答卷前，考生务必用黑色字迹并将条形码正向准确粘贴在答2.选择题每小题选出答案后，3.非选择题必须用0.5毫米黑色如需改动，先划掉原来的答案求作答的答案无效。

4.考生必须保持答题卡的整洁一、单项选择题：本题共有一项是符合题目要求的。

1.已知A={x∈N|x<7},B={5,6,72.已知复数i(i为虚数A. B.3.五一国际劳动节放假三天，选一天，乙同学在前两天中随率为A.16B.13C.4.函数y=23x·sin(πx)·log25.已知cosx=13,则sin(2x-A.79B.-796.设α,β为两个不同的平面，A. 充分不必要条件B.C. 充分必要条件7.F1、F2分别为双曲线C:x2交于A、B两点，若l⊥F2年深圳市高三年级第二次调研考试数学6页，22小题，满分150分。

考试用时120分钟色字迹的签字笔在答题卡指定位置填写自己的学校贴在答题卡的贴条形码区，请保持条形码整洁、不污损，用2B铅笔把答案涂在答题卷相应的位置上．米黑色字迹的签字笔作答，答案必须写在答题卡各题的答案，然后再写上新的答案；不准使用铅笔和涂改液整洁，考试结束后，将答题卡交回．8道小题，每小题5分，共40分。

在每小题给出的四个选项中。

{5,6,7,8},则集合A∪B中的元素个数为C.9D.10为虚数单位），设z是z的共轭复数，则z·z=C.2D.3，甲、乙两名同学计划去敬老院做志愿者，若甲同天中随机选一天，且两名同学的选择互不影响，则他们12D.23|x|的图象大致为2π)=C.89D.-89，直线l⊂α,则“l//β”是“α//β”的B.必要不充分条件D.既不充分也不必要条件-22y＝1的左、右焦点，过F1的直线l与C的左B,则22F A F B⋅u uu u r u u u u r=试卷类型：A深圳市高三年级第二次调研考试2021.4分钟。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3 3 x绝密★启用前试卷类型：A深圳市 2019 年高三年级第二次调研考试数学（文科）2019．4本试卷共 6 页，23 小题，满分 150 分．考试用时 120 分钟．注意事项：1．答卷前，考生务必用黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号，并将条形码正向准确粘贴在答题卡的贴条形码区，请保持条形码整洁、不污损． 2．选择题每小题选出答案后，用 2B 铅笔把答案涂在答题卷相应的位置上． 3．非选择题必须用 0.5 毫米黑色字迹的签字笔作答，答案必须写在答题卡各题目指定区域内；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．作答选做题时，请先用 2B 铅笔填涂选做题的题号对应的信息点，再作答． 5．考生必须保持答题卡的整洁，考试结束后，将答题卡交回．第Ⅰ卷一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设集合 A = {x x 2- 2x < 0} ， B = {x 1 < x < 3}，则 A, 3)2．复数 2 1+ i的共轭复数是1-i23．已知双曲线C ： - y 2 a 2= 1(a > 0)的渐近线方程为 y =± x ，则该双曲线的焦距为B =（A ） (0,1) （B ）(0, 3) （C ）(1, 2) （D ） (2（A ）1+ i（B ）1- i（C ） -1+ i（D ） -第 6 题图0.06 0.04 a0.02 0.01O5 10 15 20 25 30第 4 题图（A ） 2（B ） 2 （C ） 2 2 （D ） 44．某学校随机抽取了部分学生，对他们每周使用手机的时间进行统计，得到如下的频率分布直方图．若从每周使用时间在[15, 20) ， [20, 25) ， [25,30]三组内的学生中，用分层抽样的方法选取8 人进行访谈，则应从使用时间在[20, 25) 内的学生中选取的人数为（A ）1（B ） 2 （C ） 3 （D ） 45．已知角α 为第三象限角，若 tan(α + π) = 3 ，则sin α =4 5 5 556．如图所示，网格纸上小正方形的边长为1，粗实（虚）线画出的是某几何体的三视图，则该几何体的体积为8π 10π（C ）37．若函数 f (x ) = sin(ωx - π) (ω > 0) 图象的两个相邻最高点的距离为 π ，则函数 f (x )6的一个单调递增区间为（A ）3（B ）314π （D ）10π（A ） - 2 5 （B ） - 5 （C ） 5（D ）2 5-, -, -,⎡π π⎤（A）⎡π π⎤（B）⎡π π⎤（C）⎡π 2π ⎤（D）,⎣⎢ 6 3 ⎥⎦ ⎣⎢ 2 2 ⎥⎦ ⎣⎢ 3 6 ⎥⎦ ⎢⎣6 3 ⎥⎦8．函数f (x) =的图象大致为（A）（B）（C）（D）9．十九世纪末，法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”，即：“在一个圆内任意选一条弦，这条弦的弦长大于这个圆的内接正三角形边长的概率是多少？” 贝特朗给出了“随机半径”、“随机端点”、“随机中点”三个合理求解的方法，但结果都不相同，这类悖论的矛头直击概率概念本身，强烈地刺激了概率论基础的严格化．其中“随机端点”的求法如下：设A 为圆O 上的一个定点，在圆周上随机取一点B ，连接AB ，求所得弦长大于圆O 的内接正三角形边长的概率．则由“随机端点”求法所求得的概率为5 4 3 210．已知正方体ABCD -A1B1C1D1 ，P 为棱CC1 上的动点，Q 为棱AA1 的中点，设直线m 为平面BDP 与平面B1D1P 的交线，以下关系中正确的是D1Q11．已知F1 、x2F2分别是椭圆：a2y2+b2BB1A1=（1 a >b > 0）的左、右焦点，点A是F1关于直线bx +ay =ab 的对称点，且AF2 ⊥x 轴，则椭圆的离心率为2 2 2 21-x2lg x第10 题图（A）1（B1 1）（C）（D）1（A）m// D1Q （B）m// 平面B1（C）m ⊥B1Q（D）m ⊥平面A（A）3 -11（B）（C）5 -1 （D）3x 6 D12．若函数 f (x ) = x - - a ln x 在区间(1, +∞) 上存在零点，则实数a 的取值范围为（A ） (0, 1)2（B ） (1, e)2（C ） (0，+∞) （D ） (1, +∞)2第Ⅱ卷本卷包括必考题和选考题两部分．第 13～21 题为必考题，每个试题考Th 都必须作答．第 22～23 题为选考题，考Th 根据要求作答．二、填空题：本大题共 4 小题，每小题 5 分．⎧x 2 + 3x , 13．设函数 f (x ) = ⎨ x ≥ 0, 则 f (-3) ＝．⎩ f (x + 2), x < 0,14．设∆ABC 的内角 A 、 B 、C 的对边分别为a 、b 、c ，且c = ，c os C =- 1， 4sin A = 2sin B ，则b ＝．15．已知等边∆ABC 的边长为2 ，若点 D 满足 AD =2DC ，则BD ⋅ AC = ．16．如图（1），在等腰直角∆ABC 中，斜边 AB = 4 ， D 为 AB 的中点，将△ ACD 沿CD 折叠得到如图（2）所示的三棱锥C - A 'BD ．若三棱锥C - A 'BD 的外接球的半径为 5 ，则∠A 'DB =．CB第 16 题图(1)A'B第 16 题图(2)三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分 12 分）已知数列{a }满足a = 2 , a= a + 2n + 2 (n ∈ N * ) ．n1 n +1n（1）判断数列{a n - 2n } 是否为等差数列，并说明理由；（2）记S n 为数列{a n }的前n 项和，求 S n ．D FA EB∑ ∑ b = 18．（本小题满分 12 分）某网店经销某商品，为了解该商品的月销量 y （单位：千件）与当月售价 x （单位：元/件）之间的关系，收集了5 组数据进行了初步处理，得到如下数表：x 5 6 789 y864.53.53（1 ）统计学中用相关系数来衡量两个变量之间线性相关关系的强弱，若r ∈[0.75,1] ，则认为相关性很强；若 r ∈[0.3, 0.75) ，则认为相关性一般；若 r ∈[0, 0.25] ，则认为相关性较弱. 请根据上表数据计算 y 与 x 之间的相关系数r （精确到0.01），并说明 y 与 x 之间的线性相关关系的强弱；（2）求 y 关于 x 的线性回归方程；（3）根据（2）中的线性回归方程，估计当售价 x 定为多少时，月销售金额最大？(月销售金额=月销售量⨯ 当月售价) 附注：≈ 12.85 ，n(xi- x )( y i - y )参考公式：相关系数r = i =1，nn∑(x - x )2∑( y - y )2iii =1i =1n(x i - x )( y i- y )线性回归方程 y = bx + a ， i =1，a = y - bx . n∑(x i- x )219．（本小题满分 12 分）i =1在边长为4 的正方形 ABCD 中，点 E 、F 分别为边 AB 、AD 的中点，以CE 和CF 为折痕把△ DFC 和△ BEC 折起，使点 B 、 D 重合于点 P 位置，连结 PA ，得到如图所示的四棱锥 P - AECF .（1）在线段 PC 上是否存在一点G ，使 PA 与平面EFG 平行？若存在，求 PG的值；若不存在，请说明理由.PGC（2）求点 A 到平面PEC 的距离． C第 19 题图深圳市 2019 年高三年级第二次调研考试数学（文科）试题第 5 页共 7页165⎩ 20．（本小题满分 12 分）设点 P 是直线 y = -2 上一点，过点 P 分别作抛物线C : x 2 = 4y 的两条切线 PA 、PB ，其中 A 、 B 为切点.（1）若点 A 的坐标为 (1, 1) 4 ，求点 P 的横坐标；（2）当△ ABP 的面积为 27时，求 AB .221．（本小题满分 12 分）已知函数 f (x ) = a e x+2x -1，其中常数e = 2.71828...... ，是自然对数的底数．（1）讨论函数 f (x ) 的单调性；（2）证明：对任意的a ≥ 1，当 x > 0 时， f (x ) ≥ (x + a e)x ．请考Th 在第 22、23 两题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做的第一题计分，作答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑． 22．（本小题满分 10 分）选修 4－4：坐标系与参数方程在平面直角坐标系 xOy 中，曲线C 的参数方程为⎧x = 2 c os α, （α 为参数），圆C1⎨ y = sin α,2的方程为(x - 2)2 + y 2 = 4 ，以原点O 为极点，x 轴正半轴为极轴建立极坐标系，射线l 的极坐标方程为θ = θ0 (ρ ≥ 0) ．（1）求曲线C 1 和圆C 2 的极坐标方程；（2）当0 < θ< π时，若射线l 与曲线C 和圆C 分别交于异于点O 的M 、N 两点， 021 2且| ON |= 2 | OM | ，求△ MC 2 N 的面积． 23.（本小题满分 10 分）选修 4－5：不等式选讲1已知函数 f (x ) =| x - m | + | x +| (m > 1) ．m（1）当m = 2 时，求不等式f (x) > 3 的解集；（2）证明：f (x) +1m(m -1)≥ 3 ．2 x 2x - x - 2a x x x 0 22019 年深圳市高三第二次调研考试文科数学试题答案及评分参考第Ⅰ卷一．选择题（1） C （2） A （3） D （4） C （5） B （6）C （7） A（8） B （9） C（10）B（11）C（12）D12.【解法 1】 f '(x ) = 1-1- a= ．x2x注意到函数 y = 2x - 在(1，+∞)上单调递增，且2x - > 1．若 a ≤ 1，则1- 2a ≥ 0 ，则 2不合题意，应舍去．f '(x ) > 0 ，函数 f (x ) 在(1，+∞)上单调递增，故 f (x ) > f (1) = 0 ，当 a > 1时，此时存在 x ∈ (1，+ ∞) ，使得当 x ∈ (1，x ) 时， f (x ) 单调递减，当x ∈ (x , +∞) 20 0 0时， f (x ) 单调递增．因为 f (1) = 0 ，所以a f (x >) <10 ．又因为 f a ((a >+1)2 )1> 0 ，故此时x f ∈((1，x + ∞))在 0 22(1，+∞)上必定存在零点．综上所述，答案为 D ．【解法 2】函数 f (x ) 在(1，+∞)上存在零点，即方程 x x -∈x (-1，a ln x x 0=)0 在(1，+∞)上有解，设t =f (x (x t >)1) ，则方程可化为t x 2-∈t -(2a x ln 0t ,=+0(∞t > 1)) ，显然当a f (1=) =00 时，方程在(1，+∞)上无解；当 a f (x ≠) <00时，方程可化为 f ((a +1)2 )> 0 ，通过研究直线 (1，+∞) 与曲线x - x -a l n x =0的位置关系，易知t = x (t >1)，所以a > 1. 【解法 3】此题作为选择题，结合答案是有一些较为灵活的解题方法的，比如可以将问题转化为直线 t 2-t -2a ln t =0(t >1) 与a = 0 在 (1，+∞)上有交点，注意到 a ≠ 0和函数 h (x ) = + a l n x 的凹凸性以及 g (x ), h (x ) 均过点(1,1) ，故可研究h (x ) 在(1,1) 处的切线即可．二．填空题： 13． 414．115． 23 16． 2π316【解法 1】设 ∆A 'BD 的外接圆半径为 r ， ∠A 'DB = 2θ ，其中θ ∈(0, π) ．由正弦定理易得25nn n n * nnn4sin θ12r =，故r = ．由题意知 1+ r 2 = ．sin 2θ cos θ解得cos θ = 1 ，所以∠A 'DB =2θ = 2π．2 3【解法 2】设∆A 'BD 的外接圆半径为r ， ∠A 'DB = 2θ ，其中θ ∈(0, π) ，并设 A 'B 中点为2M ， DM = b ， A 'M = a ，则有 a 2 + (b - r )2 = r 2 ，由于 a 2 + b 2 = 4 ，由此可得br = 2 ，又因为1 + r2 =5 ，所以r =2 ，而cos θ = b = 1 = 1 ，所以∠A 'DB =2θ = 2π．2 r 2 3三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分 12 分）已知数列{a }满足a = 2 , a= a + 2n + 2 (n ∈ N * ) ．n1n +1n（1）判断数列{a n - 2 } 是否为等差数列，并说明理由；（2）记S n 为数列{a n }的前n 项和，求 S n ．【解析】(1) 设b = a - 2n，则b= a - 2n +1 ，……………………………2 分nnn +1n +1 则b - b = (a- 2n +1 ) - (a - 2n ) = a - a - 2n ， ……………………4 分n +1nn +1nn +1n= (a n + 2 + 2) - a - 2 = 2 (n ∈ N ) ， ……………………………5 分所以，数列{a n - 2 } 是首项为0 ，公差 d = 2 的等差数列．………………6 分 (2)由（1）可知a n - 2 = 0 + 2(n -1) ，…………………………………………8 分∴ a n = 2 + 2(n -1) ，………………………………………………………………9 分∴ S n = 2⨯ (1- 2n) + 1- 2 n [0 + (n -1)] 2= 2n +1 - 2 + n 2 - n . …………………………12 分【命题意图】本题主要考查数列的递推公式，等差数列的证明方法，分组求和法以及等差、等比数列的前n 项和公式等知识，重点考查等价转换思想，体现了数学运算、逻辑推理等核心素养．18．（本小题满分 12 分）某网店经销某商品，为了解该商品的月销量 y （单位：千件）与售价 x （单位：元/件）之间的关系，收集了5 组数据进行了初步处理，得到如下数表：x 5 6 7 8 9 y864.53.53（1）统计学中用相关系数r 来衡量两个变量之间线性相关关系的强弱，若 r ∈[0.75,1] ，则i ∑ n认为相关性很强；若 r ∈[0.3, 0.75) ，则认为相关性一般；若 r ∈[0, 0.25] ，则认为相关性较弱. 请计算相关系数r ，并说明 y 与 x 之间的线性相关关系的强弱（精确到0.01）；（2）求 y 关于 x 的线性回归方程；（3）根据（2）中的线性回归方程，应将售价 x 定为多少，可获取最大的月销售金额？解：(1)由表中数据和附注中的参考数据得，x = 7 ， y = 5 ，………………………………1 分55∑(xii =1 - x )2 = 10 ， ∑( y i =1- y )2= 16.5 ，……………………………………………2 分5(x - x )( y- y ) = -12.5 r ≈ -12.5 ≈ -0.97 ∑i i，i =1……………………………3 分因为r ≈ -0.97 ∈[0.75,1] ， ………………………4 分说明y 与 x 的线性相关关系很强．.……………………………………………………5 分 n∧ (x i - x )( y i - y )-12.5 （2）由（1）可知b = i =1= = -1.25 ………………………7 分 ∑ i =1(x i - x )210∧ ∧∴a = y - b x = 5 -（-1.25）⨯ 7 = 13.75 ，…………………………………………… 8 分∧∴ y = -1.25x +13.75 ……………………………………………………………………9 分∧∧（3）由题意可知，月销售额的预报值 z =1000⋅ y ⋅ x = -1250x 2 +13750x （元）∧∧或者 z = y ⋅ x = -1.25x 2 +13.75x （千元）………10 分∧则当 x = 5.5时， z 取到最大值，即该店主将售价定为5.5 元/件时，可使网店的月销售额最大.……12 分【命题意图】本题旨在考查概率统计在实际问题中的应用，以研究相关系数，线性回归，二次函数等知识为载体，考查了学生的数学运算、数学建模等数学核心素养． 19．（本小题满分 12 分）在边长为4 的正方形 ABCD 中，点 E 、 F 分别为边 AB 、 AD 的中点，以CE 和CF 为折痕把△ DFC 和△ BEC 折起，使点 B 、D 重合于点 P 位置，连结 PA ，得到如图所示的四棱锥P - AECF .（1）在线段 PC 上是否存在一点G ，使 PA 与平面 EFG 平行，若存在，求 PGGC若不存在，请说明理由.的值；2 E F ⊂平面A E C F 平面平面OC4 （2）求点 A 到平面 PEC 的距离．解：（1）线段 PC 上的点G 满足PG = 1时， PA 与平面EFG 平行． ………1 分证明如下：GC 3连结 EF ， EG ， FG ， AC ，记 AC 与 EF 的交点为O ，连结OG ．在正方形 ABCD 中，∵ E 、 F 分别为边 AB 、 AD 的中点，∴AO = 1，……………………2 分 OC 3故 AO = PG = 1 ， ……………………3 分 OC GC 3∴ PA // OG ． ……………………4 分∵ PA ⊄ 平面EFG ， OG ⊂ 平面EFG ,∴ PA / /平面EFG ． ……………………6 分（2）解法一：在正方形 ABCD 中， AB ⊥ BC ， AD ⊥ CD ，翻折后 PC ⊥ PE ， PC ⊥ PF ，又 PE PF = P ，∴PC ⊥ 平面 PEF ． ……………………8 分记 AC 与 EF 的交点为O ，连结 PO ，可知△ O PC 为直角三角形， O P = ， PC = 4 ， OC = 3 2 ，设 P 到直线 AC 的距离为h ， 4 2 = 3 2 ⋅ h ，∴h = ． (9)分 3OPC∴ EF ⊥ 平面PACEF ⊂ 平面AECF ,E F ⊥平面P A C∴ 平面PAC ⊥ 平面AECA平面平面∵ 平面PAC 平面AEC =AC∴ △ OPC 斜边OC 上的高 h 即为三棱锥 P -AEC 的高．……………………10 分∴V= 1⋅ S⋅ h = 1 ⨯ 1 ⨯ 2⨯ 4⨯ 4 = 16 ，P - AEC3 ∆AEC 3 2 3 9S ∆PCE= 1 ⋅ PC ⋅ PE = 4 ，设点 A 到平面 PCE 的距离为h ' ， 2PC ⊥ EF , AC ⊥ EF , AC PC = C ,D FOAEB2 8 23 2 2 2 PC ⊥ EF , AC ⊥ EF , AC PC = C ∴V A -PCE = 1 ⋅ S 3 ∆PCE⋅ h ' = 4⋅ h ' ， 3 ∴ 4 h ' = 16 ，解得h '= 4 ． …………………12 分3 9 3解法二：在正方形 ABCD 中， AB ⊥ BC ， AD ⊥ CD ，翻折后 PC ⊥ PE ， PC ⊥ PF ，又 PE PF = P ，∴PC ⊥ 平面 PEF ， ……………………8 分记 AC 与 EF 的交点为O ，连结 PO ，可知△ OPC 为直角三角形， OP = ， PC = 4 ， OC = 3 2 ， 4易得 P 到直线 AC 的距离为 3，……………………9 分P∴S ΔPAC = 1⋅ 4 2 2 ⋅ 4 = ， 3C∴ EF ⊥ 平面PAC ，1 1 8 16 ∴V P - AEC =V E -PAC = 3⋅ S ∆PAC ⋅ O E = ⨯ 2 ⨯ = ，又 S ∆PCE3 3 9= 1⋅ PC ⋅ PE = 4 ，设点 A 到平面 PCE 的距离为h ， 2 1 4 ∴V A -PCE = 3 ⋅ S ∆PCE ⋅ h = 3⋅ h ， ∴ 4 h = 16 ，解得h = 43 9 3． …………………12 分解法三：在正方形 ABCD 中， AB ⊥ BC ， AD ⊥ CD ，翻折后 PC ⊥ PE ， PC ⊥ PF ，又 PE PF = P ，∴PC ⊥ 平面 PEF ． ……………………8 分记 AC 与 EF 的交点为O ，连结 PO ，可知△ OPC 为直角三角形， OP = ， PC = 4 ， OC = 3 2 ，1易得 S ΔPOC = 2⋅ 4⋅ = 2 ．……………………9 分P，DC∴ EF ⊥ 平面PAC ，F∴V E-POC = 1⋅ 2 2 ⋅ 3 = 4 ， 3OAEBPC ⊥ EF , AC ⊥ E F , AC PC = C , 2 2∴V4= 4 ⋅ 4 = 16 ，E -PAC= 3 V E -POC 3 3 9 又 S ∆PCE= 1 ⋅ PC ⋅ PE = 4 ，设点 A 到平面 PCE 的距离为h ， 2 ∴V A -PCE = 1 ⋅ S 3 ∆PCE ⋅ h = 4 ⋅ h ， 3∴ 4 h = 16 ，解得h = 4．…………………12 分 3 9 3【说明】本题以翻折问题为载体考查空间中点，线，面的位置关系，线面平行的性质定理的应用，点到平面的距离等知识，意在考查考生的空间想象能力，逻辑推理能力以及运算求解能力． 20．（本小题满分 12 分）设点 P 是直线 y = -2 上一点，过点 P 分别作抛物线C : x 2 = 4y 的两条切线 PA 、 PB ，其中 A 、 B 为切点.1（1）若点 A 的坐标为(1, 4 ) ，求点 P 的横坐标；（2）当△ ABP 的面积为 27时，求 AB .2 【解析】（1）由 y = 1 x 2 ，所以 y ' = 1x ， ……………………………………1 分4 21因为 A (1, ) ，4由导数的几何意义知，切线 PA 的斜率k = 1 ⨯1= 1，……………………2 分PA2 2所以切线 PA 的方程为l : y - 1 = 1 (x -1) ，即 y = 1 x - 1，………………………3 分PA4 2 2 4又因为点 P 为直线 y = -2 与直线 y = 1 x - 1的公共点，2 4联立 y = -2 与 y = 1 x - 1 ，可得 P 点横坐标为- 7．.…………………………4 分2 4 2（2）法一：不妨设 A (x 1, y 1 ), B (x 2 , y 2 ) ， P (x 0 , -2) ，由（1）可知k= 1 x ，即直线 PA 的方程为 y - y = 1x (x - x ) ，PA 2 1 1 2 1 1即l : y = 1 x x - y ，同理可得l : y = 1x x - y ，…………………………5 分PA2 11 PB2 221+ 0 4x 2 4x 2 + 32 04x 2 + 32 0 5⎨ 00 x x x x ⎧ x 0x - y = -2因为切线 PA ， PB 均过点 P (x 0 , -2) ⎪ 2 11，所以⎨ x， ……………6 分⎪ 0 x - y = -2 ⎪⎩ 2 2 2所以(x , y ), (x , y ) 为方程x 0x - y = -2 的两组解，11222所以直线 AB 的方程为 x 0 x - y = -2 ，即l 2 AB : y = x0 x + 2 .…………………7 分2⎧y = x 0 x + 2 联立⎪ 2 ，可得 x 2 - 2x x - 8 = 0 ，显然∆＞0 ， ⎪⎩x 2 = 4 y 由韦达定理得， x 1 + x 2 = 2x 0 , x 1x 2 = -8 ， ……………………………………8 分所以 AB = = ， …………9 分又因为点 P 到直线 AB 的距离d ， …………………………10 分11 ⎛ x2 ⎫ 1 327 所以 S ∆ = AB ⋅ d = 0 + 4 ⎪ = (x 2 + 8)2 = ，………11 分ABP2 2 ⎝ 2 ⎭2 0 2x 2解得 x 2= 1，所以 AB =1+ 0 44x 2+ 32=3 . ………………………12 分2法二：不妨设 A (x 1, y 1 ), B (x 2 , y 2 ) ，由（1）可知直线 PA 的方程为 y = 1 x - 1 ， 2 42同理，直线 PB 的方程为 y = 2 x - 2，…………………………………………5 分2 4联立解得 P ( x 1 + x 2 , x 1x2 ) ，…………………………………………………………6 分2 4又点 P 在直线 y = -2 ，所以 x 1x2 = -2 ， x x = -8 ， …………………………7 分41 2⎧x 2= 4 y设直线 AB 的方程为 y = kx + m ，联立⎨ ⎩ y = kx + m由韦达定理得 x 1 + x 2 = 4k ， x 1x 2 = -4m = -8 ，，可得 x 2- 4kx - 4m = 0 ，可得m = 2 ， P (2k , -2) ，…………………………………………………………8 分1+ ( x0 )2 (2x )2 - 4⨯ (-8) 20 0+ 4x 22 1+ ( x 0 )2 21+ k 2所以| AB |= = 4 1+ k 2 k 2+ 2 ， …………………9 分| 2k 2 + 4 |又因为点 P 到直线 AB 的距离为 d =， ……………………………10 分1 2+ 4 | 3 27 所以 S = | AB | ⋅d = 2 1+ k 2 k 2 + 2 = 4(k 2 + 2)2= ，…11 分 ∆ABP 2 2解得k 2 = 1，所以| AB |= 4 1+ 1 ⨯ 2 + 1 =3 5 . ………………………12 分4 4 4【命题意图】本题以直线与抛物线为载体，及其几何关系为背景，利用方程思想解决几何问题，主要考查抛物线的切点弦，直线与抛物线的位置关系等知识，考查学生的逻辑推理，数学运算等数学核心素养及思辨能力. 21．（本小题满分 12 分）已知函数 f (x ) = a e x+2x -1，其中常数e = 2.71828...... ，是自然对数的底数．（1）讨论函数 f (x ) 的单调性；（2）证明：对任意的a ≥ 1，当 x > 0 时， f (x ) ≥ (x + a e)x ．【解析】（1） f '(x ) = a e x+ 2 ．…………………………1 分① 当a ≥ 0 时， f '(x ) > 0 ，函数 f (x ) 在R 上单调递增；………………………2 分 ② 当a < 0 时，由 f '(x ) > 0 解得 x < ln(- 2) ，由 f '(x ) < 0 解得 x > ln(- 2) ．aa故 f ( x ) 在⎛ -∞, ln(- 2 ) ⎫ 上单调递增，在⎛ ln(- 2 )，+ ∞ ⎫上单调递减．a ⎪ a ⎪ ⎝ ⎭ ⎝ ⎭…………………………4 分综上所述，当a ≥ 0 时， f (x ) 在 R 上单调递增；当 a < 0 时， f (x ) 在⎛-∞, ln(- 2 ) ⎫上单调递增，在⎛ln(- 2)，+ ∞ ⎫上单调递减．a ⎪ a⎪ ⎝⎭ex- x-1+ 2- ≥⎝⎭…………………………5 分（2）证法一：原不等式等价于x a ax ae 0 ．………………6 分e x x 1 2'(x -1)(a e x - x -1)令 g (x ) = - - + - e ，则 g (x ) =．…………………7 分x a ax aax21+ k 2 (4k )2 - 4⨯ (-8) 1+ k 2当a ≥ 1时，a e x -x -1 ≥ e x -x -1，…………………8 分令 h (x ) = e x - x -1，则当 x > 0 时， h '(x ) = e x-1 > 0 ，∴ 当 x > 0 时， h (x ) 单调递增，即h (x ) > h (0) = 0 ， ………………………10 分∴ 当0 < x < 1时， g '(x ) < 0 ；当 x = 1时， g '(x ) = 0 ；当 x > 1时， g '(x ) > 0 ，∴ g (x ) ≥ g (1) = 0 ． ………………………11 分e xx 12即 - - + - e ≥ 0 ，故 f (x ) ≥ (x + a e)x ．………………12 分x a ax a证法二：原不等式等价于 a (e x- e x )≥ (x -1)2．………………………6 分令 g (x ) = e x- e x ，则 g '(x ) = e x- e ．当 x < 1时， g '(x ) < 0 ；当 x > 1时， g '(x ) > 0 ．∴ g (x ) ≥ g (1) = 0 ，即e x- e x ≥ 0 ，当且仅当 x = 1时等号成立．…………………7 分当 x = 1时，a (e x- e x )≥ (x -1)2显然成立；当 x > 0 且 x ≠ 1时， e x- e x > 0 ．欲证对任意的a ≥ 1，a (e x- e x )≥ (x -1)2成立，只需证e x - e x ≥ (x -1)2．……9 分思路 1： ∵ x > 0 ，∴不等式e x - e x ≥ (x -1)2e x可化为 - x - 1- e + 2 ≥ 0 ，…………10 分令- - + - ≥ ，则 x a ax ax xf (x ) ≥ (x + a e)x ，易证当 x > 0 时， a (e x- e x )≥ (x -1)2，∴当g (x ) = e x -e x 时， g '(x ) = e x - e ，当 x < 1时， g '(x ) < 0 ，∴函数 x >1在g '(x ) > 0上单调递减，在g (x ) ≥ g (1) = 0上单调递增，∴ e x- e x ≥ 0 ，…………………11 分∴ x = 1 ，即 e x- x x - 1 - e + 2 ≥ 0 ， x从而，对任意的 x > 0 ，当 x ≠ 1时， e x - e x > 0 ． …………………………12 分(x -1) +e x a ⎪ a a (x -1)2+e x-(x -1)(x + e - 3)思路 2：令ϕ(x ) =，则ϕ'(x ) =．e xe xϕ'(x ) > 0 ⇒ 3 - e < x < 1，ϕ'(x ) < 0 ⇒ x >1或0 < x < 3- e ．∴ϕ (x ) 在(0, 3 - e) 上单调递减，在(3 - e ，1) 上单调递增，在(1，+∞) 上单调递减．…………………………11 分∵ ϕ (0)=ϕ(1) = 1，2∴ ϕ(x ) = ≤ 1，即(x -1)2 ≤ e x - e x ．e x从而，对任意的a ≥ 1，当 x > 0 时， f (x ) ≥ (x +a e)x ． …………………………12 分证法三：原不等式等价于a e x + 2x -1- x 2- a e x ≥ 0 ．令 g (x ) = a e x - x 2- (a e - 2)x -1 ，则 g '(x ) = a e x - 2x - (a e - 2) ． ……………6 分令 h (x ) = a e x - 2x - (a e - 2) ，则h '(x ) = a e x- 2 ，其中 x > 0 ．① 当a ≥ 2 时，h '(x ) > 0 ． h (x ) 在(0，+∞)上单调递增．注意到h (1) = 0 ，故当 x ∈ (0,1)时，g '(x )=h (x ) < 0 ；当 x ∈ (1，+∞) 时，g '(x )=h (x ) > 0 ．∴ g (x ) 在(0,1) 上单调递减，在(1, +∞) 上单调递增． ∴ g (x )min =g (1) = 0 ，即 f (x ) ≥ (x + a e)x ．…………………………7 分② 当1 ≤ a < 2时， 0 < ln⎛ 2 ⎫< 1． ⎝ ⎭当0 < x < ln⎛ 2 ⎫时，h '(x ) < 0 ，h (x ) 单调递减；当 x > ln⎛ 2 ⎫时，h '(x ) > 0 ，h (x ) 单调⎪⎪ ⎝ ⎭⎝ ⎭递增．②—（i ）：若 2e -1≤ a < 2 ，则h (0) = a (1- e )+2 ≤ 0 ．∵ h ⎛ ln 2 ⎫ < h (1) = 0a ⎪ ⎝ ⎭∴ 当 x ∈ (0,1)时， g '(x )=h (x ) < 0 ；当 x ∈ (1，+∞) 时， g '(x )=h (x ) > 0 ．与①同，不等式成立．…………………………9 分a ⎪⎩ π⎩2+ρθ y②—（ii）：若1≤a<2e -1，则h(0) =a (1- e)+2>0 ，∵ h ⎛ln2 ⎫<h(1) = 0 ，a ⎪ ⎝⎭∴∃x ∈⎛0, ln⎛2 ⎫⎫，使得h (x )= 0 ，且当x ∈(0, x )时，g'(x)=h(x) > 0 ；当x∈(x，1)0 ⎪0 0 0⎝⎝⎭⎭时，g'(x)=h(x) < 0 ；当x∈(1，+∞)时，g'(x)=h(x) > 0 ．∴g(x)在(0, x0 )上单调递增，在(x0，1)上单调递减，在(1, +∞)上单调递增．∵ g(0)=a -1 ≥ 0 ，g(1)=0∴ 此时，g(x) ≥ 0 ，即f (x) ≥ (x +a e)x ．综上所述，结论得证．…………………………12分【命题意图】本题旨在考查导数在研究函数时的应用，以研究单调性，证明不等式等为载体，综合考查学生的分类讨论、化归转化、数形结合等数学思想，考查了学生的数学运算、逻辑推理等数学核心素养．请考Th在第22、23 两题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做的第一题计分，作答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑．22．（本小题满分10 分）选修4－4：坐标系与参数方程在平面直角坐标系xOy 中，曲线C 的参数方程为⎧x = 2 cosα,（α为参数），圆C 的方程1 ⎨y = sinα,2为(x -2)2 +y2 =4，以原点O 为极点，x 轴正半轴为极轴建立极坐标系，射线l 的极坐标方程为θ=θ0 (ρ≥ 0) ．（1）求曲线C1 和圆C2 的极坐标方程；（2）当0 <θ0 <2时，若射线l 与曲线C1 和圆C2 分别交于异于点O 的M 、N 两点，且| ON |= 2 | OM | ，求△ MC2N 的面积．⎧x = 2 c osα,解：（1）由⎨y = sinα消去参数α可得C1 的普通方程为x2+24= 1，……………1 分把x =ρcosθ，y =ρsinθ代入，得(ρcosθ)2( sin )4= 1 ，6 3 2 3 6 2 2 1 2 22 2 22 即 ρ2= 4 cos 2θ + 4sin 2 θ = 4 ， 1+ 3sin 2θ所以C 的极坐标方程为 ρ 2= 4 1+ 3sin 2θ； ………………………3 分把 x = ρ cos θ ， y = ρ sin θ 代入(x - 2)2+ y 2= 4 ，得 ρ = 4 cos θ ，所以C 2 的极坐标方程为 ρ = 4 cos θ ．………………………5 分（2）把θ = θ0代入 ρ 2= 4 1+ 3sin 2θ，得 ρM = 4 ， 1+ 3sin 2 θ 把θ = θ0 代入 ρ = 4 cos θ ，得 ρN = 4cos θ0 ，………………………6 分由| ON |= 2 | OM | ，得 ρN = 2ρM ，即 ρN = 4ρM ，即(4 cos θ0 )2=161+ 3sin 2θ ， ………………………7 分∵ 0 < θ0< π ， 2∴ sin θ = ，cos θ = ， 03∴ ρM = 03= ， ρ 3N= 4 cos θ0=， …………………8 分3∴ △ MC 2 N 的面积 S ∆MC N = S ∆OC N - S ∆OC M= 1 | OC | (ρ - ρ ) ⋅ sin θ = 1 ⨯ 2⨯ 2 3⨯ = ．……………………10 分22 N M 02 3 3 3 【命题意图】本题主要考查了椭圆，圆的极坐标方程与直角坐标方程以及参数方程的互化、极径ρ 的几何意义与应用等知识点，重点考查数形结合思想，体现了数学运算、逻辑推理等核心素养．考察考生的化归与转化能力．23.（本小题满分 10 分）选修 4－5：不等式选讲1已知函数 f (x ) =| x - m | + | x +| (m > 1) ．m（1）当m = 2 时，求不等式 f (x ) > 3 的解集；（2）证明： f (x ) +1m (m -1)≥ 3 ．1解：（1）当m = 2 时， f (x ) =| x - 2 | + | x + | ，………………………1 分24 1+ 3sin 2 θ 0 4 3 0 0(m -1) ⋅(1 m -1①当x ≤-1时，原不等式等价于(2 -x) - (x +1) > 3 ，解得x <-3，……………2分2 2 4②当-1<x < 2 时，原不等式等价于5> 3 ，不等式无解，……………3分2 2③当x ≥ 2 时，原不等式等价于(x - 2)+ ⎛x +1 ⎫> 3 ，解得x >9，………………4 分2 ⎪4⎝⎭综上，不等式f (x) > 3 的解集为(-∞, -3) (9,4 4+∞) ；………………5分（2）由题f (x) =| x -m | +| x +1|≥|m +1| ，………………………6分m mm > 0 ，∴|m + 1|=m +1，m m∴f (x) ≥m +1，当且仅当x ∈⎡-1, m⎤时等号成立．………………7分∴f (x) +m1≥m +1+⎣⎢m1⎥⎦=m +1= (m -1) +1+1，m(m -1) m m(m -1) m -1 m -1m >1，∴m -1 >0 ，∴(m -1) +1m -1+1 ≥ 2 ) +1 = 3 ，…………9 分∴f (x) +1m(m -1)≥ 3 ，当m = 2 ，且x ∈[-1, 2] 时等号成立．……………………10 分2【说明】本题主要考查绝对值三角不等式以及不等式的解法，分段函数，基本不等式等知识点，重点考查分类讨论，数形结合的思想，体现了数学运算、逻辑推理等核心素养．。