八年级数学下册 解题技巧专题 勾股定理与面积问题 湘教版
湘教版八年级数学下册第2课时 勾股定理的实际应用课件

►Suffering is the most powerful teacher of life. 苦难是人生最伟大的老师。 ►For man is man and master of his fate. 人就是人,是自己命运的主人。 ►A man can't ride your back unless it is bent. 你的腰不弯,别人就不能骑在你的背上。 ►1Our destiny offers not the cup of despair, but the chalice of opportunity. ►So let us seize it, not in fear, but in gladness. · 命运给予我们的不是失望之酒,而是机会之杯。 因此,让我们毫无畏惧,满心愉悦地把握命运
几何画 板.gsp
课堂小结
1 说一说本节课的收获. 2 你还存在哪些疑惑?
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题.
►在有欢声笑语的校园里,满地都是雪,像一块大地毯。房檐上挂满了冰凌, 一根儿一根儿像水晶一样,真美啊!我们一个一个小脚印踩在大地毯上, 像画上了美丽的图画,踩一步,吱吱声就出来了,原来是雪在告我们:和 你们一起玩儿我感到真开心,是你们把我们这一片寂静变得热闹起来。对 了,还有树。树上挂满了树挂,有的树枝被压弯了腰,真是忽如一夜春风 来,千树万树梨花开。真好看呀! ►冬天,一层薄薄的白雪,像巨大的轻软的羊毛毯子,覆盖摘在这广漠的荒 原上,闪着寒冷的银光。
几何画 板.gsp
巩固练习
1.如图,一艘渔船以30海里/h的速度 由西向东追赶鱼群.在A处测得小岛C在船的 北偏东60°方向;40 min后,渔船行至B处, 此时测得小岛C在船的北偏东30°方向. 已 知以小岛C为中心,周围10海里以内有暗 礁,问这艘渔船继续向东追赶鱼群是否有 触礁的危险?
八年级数学下册1.2.2勾股定理二课件新版湘教版

4.长方形的一边长是5,对角线是13,则另一条边 是 12 .
5、若直角三角形两直角边分别为12,16,则此直
角三角形的周长为( D )
A. 28
B. 36 C. 32
D. 48
6、直角三角形的三边长分别为3,4,x,则x2等
于( D )
A. 5 B. 25
C. 7 D. 25或7
7、隔湖有两点A、B,从与BA方向成直角 的BC方
解:在△ABC中,AC=4,BC=1.5,
由勾股定理得:AB 421.52 13.753.71.
在 Rt△ABC 中,AC= 4 ,BC= 1 ,
故 AB= 42-12 = 15 3.87 ,
从而 A′A=3.87-3.71=0.16.
即梯子顶端A只向上移动了0.16m,
湘教版SHUXUE八年级下
本本节课内内容容
1.2.2
-----勾股定理的简单应用
勾股定理:如果直角三角形的两 A
直角边分别为a,b,斜边为c,那么
b
c
a2 b2 c2
Ca B
几何语言:在Rt△ABC中,∠ACB=90° 则:a2.+b2=c2
勾股定理作用:在直角三角形中已知两边。,求第三边。
∴x2+32=(10-x)2.
O3 B
∴OA=x=
91 20
(尺)
答:竹子折断处离地面有
2901 尺。
1.RtABC的两条直角边a=3, b=4,则斜边c是 5 .
2.已知直角三角形的两边长分别为3cm和5cm,
则第三边长为 √34 或4
cm。
3. 有一个边长为1米正方形的洞口,想用一个圆形 盖去盖住这个洞口,则圆形盖半径至少为 √2 米.
2020-2021学年湘教版(2012)初中数学八年级下册 1.2 勾 股 定 理 课件

探究发现
a b
ac b
b ca
cb a
证明: ∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形 =4× 1 ab+c2
2
=c2+2ab, ∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
探究发现
结论:
勾股定理: 直角三角形两直角边a、b的平
方和,等于斜边c的平方,即: a2+b2=c2.
谢谢聆听
Thank you for listening.
1.2勾股定理
探究发现
问题1 试问正方形A、B、C面 积之间有什么样的数量关系? (每个小正方形的面积为单位1)
S正方形A S正方形B S正方形C
猜想:
一直角边2 + 另一直角边2 = 斜边2
探究发现
如图,每个小正方形方格的边长为1. 求证: a2+b2=c2.
C Aa c
b
B
C A
B
探究发现
(3)若a:b=1:2 ,c=5,求a;
(4)若b=15,∠A=30°,求a,c. C
A
已知直角三角形两边关系和第三边的长求未知两 边时,要运用方程思想设未知数,根据勾股定理列方 程求解.
【变式题】 在Rt△ABC中,AB=4,AC=3,求BC的长.
当直角三角形中边时,其中一较长边可能是直角边,也可能是斜
小组活动
方法1:补形法
方法2:分割法
C Aa c
b
B
C A
B
C Aa c
b
B
C A
湘教版八年级下册数学第1章 直角三角形 阶段核心题型 勾股定理解题的十种常见题型

7.如图,某学校(A 点)到公路(直线 l)的距离为 300 m,到 公交站(D 点)的距离为 500 m.现要在公路边上建一个商 店(C 点),使之到学校及公交站的距离相等,求商店与 公交站之间的距离.
解:连接 AD,则 AD=500 m,过 A 作 AD 的垂直平分线交 l 于点 C,连接 AC,则 AC=CD,则点 C 就是商店的位置.过 A 作 AB⊥l 于点 B,则 AB= 300 m.在 Rt△ABD 中,AD2=AB2+BD2,AB=300 m,AD=500 m,∴BD =400 m.设 CD=AC=x m,则 BC=(400-x)m. 在 Rt△ABC 中,AC2=AB2+BC2,∴x2=3002+(400-x)2,解得 x=312.5. ∴商店与公交站之间的距离为 312.5 m.
10.如图,红星村 A 和幸福村 B 在河岸 CD 的同侧,它们到河 岸 CD 的距离 AC,BD 分别为 1 千米和 3 千米,又知道 CD 的长为 3 千米,现要在河岸 CD 上建一水厂向两村输送自来 水,铺设水管的工程费用为每千米 20 000 元. (1)请在 CD 上选取水厂的位置,使铺设水管的总费用最少; (2)求铺设水管的最少总费用. 【点拨】本题通过作点 A 关于 CD 的对称点,进一 步作辅助线构造直角三角形,利用勾股定理求解.
∵DF=DE,∠ADC=∠EDA,
∴EF=2EO=2.
2.如图,在四边形 ABFC 中,∠ABC=90°,CD⊥AD,AD2= 2AB2-CD2.求证:AB=BC.
【点拨】当已知条件中有线段的平方关系时,应选择用勾股定理 说明.应用勾股定理说明两条线段相等的一般步骤:①找出图中 说明结论所要用到的直角三角形;②根据勾股定理写出三边长的 平方关系;③联系已知,等量代换,求之即可.
湘教版八年级数学下册教学课件(XJ) 第1章 直角三角形 第2课时 勾股定理的实际应用

解:(1)在Rt△ ABC中,
A
别踩我,我怕疼!
C 根据勾股定理得
AB 32 42 5米,
∴这条“径路”的长为5米. (2)他们仅仅少走了
(3+4-5)×2=4(步). B
二 利用勾股定理求最短距离
问题 在A点的小狗,为了尽快吃到B点的香肠,它选择A 不选择A C B路线,难道小狗也懂数学?
问题 观看下面同一根长竹竿以三种不同的方式进门的情况,并结合曾 小贤和胡一菲的做法,对于长竹竿进门之类的问题你有什么启发?
这个跟我们学的勾股 定理有关,将实际问 题转化为数学问题
典例精析 例1 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能
否从门框内通过?为什么?
分析:可以看出木板横着,竖着都不能通过,
A A
B
解:台阶的展开图如图,连接AB.
在Rt△ABC中,根据勾股定理得
C
B
AB2=BC2+AC2=552+482=5329,
∴AB=73cm.
能力提升: 5. 为筹备迎新晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然 后缠绕红色油纸,如图.已知圆筒的高为108cm,其横截面周长为36cm, 如果在表面均匀缠绕油纸4圈,应裁剪多长的油纸?
例4 在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂, 树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗?
6 米
8米
A
6 米
C
8米
解:根据题意可以构建一直角三角
形模型,如图.
在Rt△ABC中,
AC=6米,BC=8米,
由勾股定理得
AB AC2 BC2
62 82
B
AB32= 62 +(10+8)2 =360, B2 ∴AB1<AB2<AB3.
最新数学湘教版初中八年级下册解题技巧勾股定理与面积问题
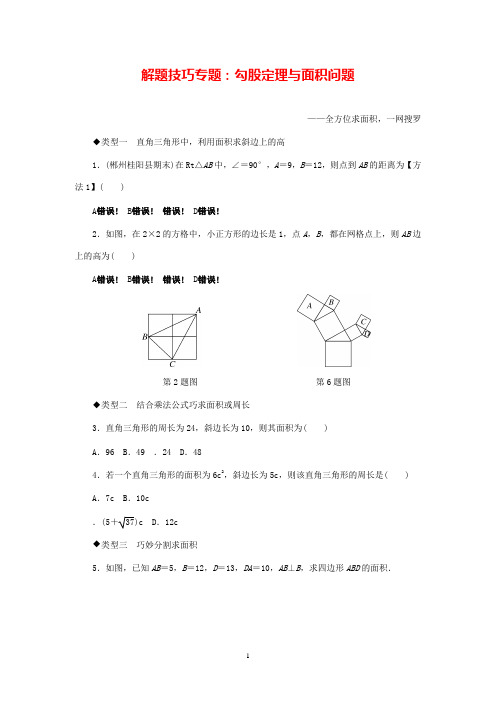
解题技巧专题:勾股定理与面积问题——全方位求面积,一网搜罗◆类型一直角三角形中,利用面积求斜边上的高1.(郴州桂阳县期末)在Rt△AB中,∠=90°,A=9,B=12,则点到AB的距离为【方法1】( )A错误! B错误!错误! D错误!2.如图,在2×2的方格中,小正方形的边长是1,点A,B,都在网格点上,则AB边上的高为( )A错误! B错误!错误! D错误!第2题图第6题图◆类型二结合乘法公式巧求面积或周长3.直角三角形的周长为24,斜边长为10,则其面积为( )A.96 B.49 .24 D.484.若一个直角三角形的面积为6c2,斜边长为5c,则该直角三角形的周长是( ) A.7c B.10c.(5+37)c D.12c◆类型三巧妙分割求面积5.如图,已知AB=5,B=12,D=13,DA=10,AB⊥B,求四边形ABD的面积.◆类型四“勾股树”及其拓展类型中有关面积的计算6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10c,正方形A的边长为6c,B的边长为5c,的边长为5c,则正方形D的边长为( )A14c B.4c 15c D.3c7.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )A.4 B.36 .16 D.55第7题图第8题图8.(青海中考)如图,正方形ABD的边长为2,其面积标记为S1,以D为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2……按照此规律继续下去,则S9的值为( )A错误!错误! B错误!错误!错误!错误! D错误!错误!◆类型五“赵爽弦图”中有关面积的计算9.“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是3和6,则大正方形与小正方形的面积差是( )A.9 B.36 .27 D.34第9题图第10题图10.(永州零陵区校级模拟)如图是4个全等的直角三角形与1个正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用,y表示直角三角形的两直角边(>y),下列四个说法:①2+y2=49;②-y=2;③2y+4=49;④+y=9其中说法正确的是( )A.①② B.①②③.①②④ D.①②③④参考答案与解析1.B2.A 解析:过点作D⊥AB于点D∵S△AB=22-错误!×1×2-错误!×1×1-错误!×1×2=错误!,又∵S△AB=错误!AB·D,∴错误!AB·D=错误!∵AB=错误!=错误!,∴D=错误!故选A3.解析:设该直角三角形的两直角边长分别为a,b,则有a+b=14①,a2+b2=102②①两边同时平方,得a2+b2+2ab=142,所以2ab=96,所以ab=48,错误!ab=24故选4.D5.解:连接A,过点作E⊥AD交AD于点E∵AB⊥B,∴∠BA=90°在Rt△AB中,由勾股定理得A=AB2+B2=52+122=13∵D=13,∴A=D,即△AD是等腰三角形.∵E⊥AD,∴AE=错误!AD=错误!×10=5在Rt△AE中,由勾股定理得E=错误!=错误!=12∴S四边形ABD=S△AB+S△AD=错误!AB·B+错误!AD·E=错误!(12×5+10×12)=906.A 78.A 解析:在图中标上字母E,如图所示.∵正方形ABD的边长为2,△DE为等腰直角三角形,∴DE2+E2=D2,DE=E,∴S2+S2=S1观察,发现规律:S1=22=4,S2=错误!S1=2,S3=错误!S2=1,S4=错误!S3=错误!,…,∴S n=错误!错误!当n=9时,S9=错误!错误!=错误!错误!故选A9.B 解析:大正方形的面积为32+62=45,小正方形的面积为(6-3)2=9,则面积差为45-9=36故选B10.B 解析:由题意得错误!①-②得2y=45③,∴2y+4=49,①+③得2+2y+y2=94,∴+y=94,∴①②③正确,④错误.故选B。
八年级数学下册 1_2 直角三角形的性质和判定(II)第1课时 勾股定理课件 (新版)湘教版

同理E,I,F在一条直线上;F,J,G在一条直线上,G,K,
D在一条直线上.
因此拼成的图形是正方形DEFG,它的边长为(1 a+b),
它的面积为(a+b)².
2
又正方形的DEFG的面积为c2+4· ab,
∴(a+b)²=c2+4· ab.
1
即a2+2ab+b2=c2+2ab,
2
∴a2+b2=c2.
S3 S2
S1
的面由积图,可再知减,去S4个1=小32,正S方2=形4的2,为面了积求,S得3,S我3=可52以. 先算出红色区域内大正方形 ∵32+42=52. ∴S1+S2=S3.
在上图中,S1+S2=S3, BC2+AC2=AB2,
那么是否对所有的直角三角形,都 有两
直角边的平方和等于斜边的平方呢?
关系,在直角三角形中,若已知直角三 角形
的任意两条边长,我们可以根据勾股定 理,
求出第三边的长.
例题
如图,在等腰三角形ABC中,已知AB=AC=13cm,
பைடு நூலகம்
BC=10cm,AD⊥BC于点D.你能算出BC边上的高AD的长
吗?
解 在△ABC中,
∵AB=AC=13,BC=10,AD⊥BC,
∴BD=
1 2
BC=5.
在Rt△ADB中,
由勾股定理得,AD2+BD2=AB2,
A D A 2 B B 2 D 1 2 3 5 21 8 8 1 . 2
故AD的长为12cm.
练习 1.在△ABC中, ∠C=90°,a=6,b=8,
则c=_1_0 __
八年级数学下册1.2直角三角形的性质和判定(Ⅱ)《勾股定理》方法学习素材湘教版(new)

《勾股定理》方法学习【例1】 在△ABC 中,已知∠B=90°,∠A、∠B、∠C 的对边分别是a 、b 、c ,且a=5,b=12,求c 2. 【分析】由∠B=90°,知b 才是斜边(如图),所以a 2+c 2= b 2,注意不要受思维定势(勾股定理的表达式:)的影响而误认为c 是斜边 【解答】由∠B=90°,则知b 是Rt△ABC 的斜边,由勾股定理,得c 2=22b a -=22125-=119.【总结】我们在运用勾股定理时,首先要正确识别哪个角是直角,从而确定哪条边是斜边,然后准确写出勾股定理表达式进行求解.【例2】如图,在△ABC 中,AB = 25,AC = 30,BC 边上的高AD = 24,求BC 的长。
【分析】本例不能直接求出BC 的长,但通过观察图形可以发现BC 边上的高AD 把△ABC 分成了两个直角三角形,可以分别在两个直角三角形中救出BD 、DC 的长,从而救出BC 的长。
【解答】在直角三角形ABD 中,由勾股定理,得 BD 2=AB 2-AD 2=252-242=49,所以BD=7 ; 在直角三角形ADC 中,由勾股定理,得 CD 2=AC 2-AD 2=302-242=324,所以CD=18。
所以,BC = BD + DC = 7 + 18 = 25.【总结】在直角三角形中已知两条边可以应用勾股定理救出第三条边,要注意发现题目中的直角三角形,从而找到解题的思路。
用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为“弦图",最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的.例1图例2图直角三角形中有关边的计数形结例1图观察,你能验证222c a b =+吗?把你的验证过程写下来,并与同伴进行交流.【分析】仔细观察图形,可以看出图中以c 为边的正方形面积有两种不同表示形式:即可以利用边长为C 来表示也可以用四个直角三角形的面积加上中间小正方形的面积来表示。
