逻辑代数习题作业及答案
第02章_逻辑代数习题答案

解: L( A, B, C , D) BC D BCD BC D ABD 2.2.3 用卡诺图化简下列个式 (1) ABCD ABCD AB AD ABC
-3-
新疆大学电气工程学院
解: ABCD ABCD AB AD ABC
ABCD ABCD AB (C C )( D D) AD( B B )(C C ) ABC ( D D)
A ACD CDE A CD CDE
A CD E
2.1.4 用代数法化简下列各式 (3) ABC ( B C ) 解: ABC ( B C )
( A B C )( B C )
AB AC BB BC CB C
AB C ( A B B 1)
ABCD ABCD ABC D ABCD ABC D ABC D ABC D
(6) L( A, B, C , D) 解:
m(0, 2, 4, 6,9,13) d (1,3,5, 7,11,15)
L A D
(7) L( A, B, C , D) 解:
新疆大学电气工程学院
第二章 逻辑代数 习题解答 2.1.1 用真值表证明下列恒等式 (3) A B AB AB (A⊕B)=AB+AB 解:真值表如下 A 0 0 1 1 B 0 1 0 1
A B
0 1 1 0
AB
1 0 0 0
AB 0 0 0 1
A B
1 0 0 1
AB +AB
1 0 0 1
3>由卡诺图,得逻辑表达式 L AB BC AC 用摩根定理将与或化为与非表达式
第2章-逻辑门与逻辑代数基础-习题与参考答案3-12
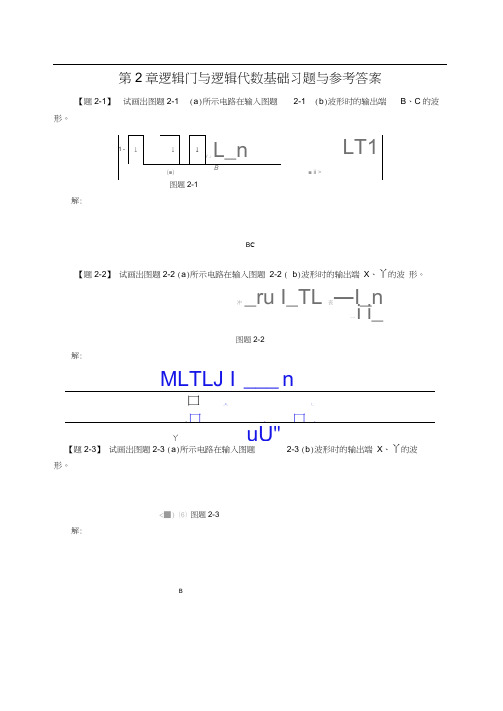
第2章逻辑门与逻辑代数基础习题与参考答案【题2-1】试画岀图题2-1 (a)所示电路在输入图题2-1 (b)波形时的输岀端B、C的波形。
解:B C【题2-2】试画岀图题2-2 (a)所示电路在输入图题2-2 ( b)波形时的输岀端X、丫的波形。
冲_ru I_TL 丧―I_n 一i i_图题2-2解:MLTLJ I ___ n口_n_ i_..x 口n 口n丫uU"【题2-3】试画岀图题2-3 (a)所示电路在输入图题2-3 (b)波形时的输岀端X、丫的波形。
<■) ⑹ 图题2-3解:B【题2-9】 如果如下乘积项的值为 1,试写岀该乘积项中每个逻辑变量的取值。
【题2-4】 试画岀图题2-4 (a )所示电路在输入图题 2-4 ( b )波形时的输岀端 X 、丫的波 形。
解:A J ~I _n ___ rvLB X.丫【题2-5】 试设计一逻辑电路,其信号 A 可以控制信号 B ,使输岀丫根据需要为 Y=B 或Y= B 。
解:可采用异或门实现,Y AB AB ,逻辑电路如下:【题2-6】某温度与压力检测装置在压力信号 A 或温度信号B 中有一个岀现高电平时, 输岀低电平的报警信号,试用门电路实现该检测装置。
解:压力信号、温度信号与报警信号之间的关系为: Y 「B ,有如下逻辑图。
【题2-7】某印刷裁纸机,只有操作工人的左右手同时按下开关 A 与B 时,才能进行裁纸操作,试用逻辑门实现该控制。
解:开关A 、B 与裁纸操作之间的关系为 丫 A B ,逻辑图如下:【题2-8】 某生产设备上有水压信号 A 与重量信号B ,当两信号同时为低电平时,检测电 路输出高电平信号报警,试用逻辑门实现该报警装置。
解:水压信号A 、重量信号B 与报警信号之间的关系为 Y 厂B ,逻辑图如下:A 「> 1(1) AB ; (2) ABC ; (3) ABC ; (4) ABC解:(1) A=1 , B=1(2)A=1、B=1、C=0(3)A=0, B=1, C=0(4)A=1, B=0 或C=1【题2-10】如果如下和项的值为0,试写岀该和项中每个逻辑变量的取值。
第二章 逻辑代数及其应用 习题参考答案

第二章 逻辑代数及其应用 习题解答【题2.21】给定逻辑函数的波形图如图 P2.21所示,试写出),,(C B A Y Y 的最小项之和形式的逻辑函数式。
解:根据逻辑函数),,(C B A Y ),,(C B A Y =C B A +C B A +C B A +【题2.23(1)BC C AB C B A C B A Y ++=),,(1解:BC C AB C B A C B A Y ++=),,(1 其波形图如右:【题2.25】用公式化简法将下列逻辑函数化为最简与或形式。
(3)BD A CD B A D C B A Y ++=),,,(3解:BD A CD B A D C B A Y ++=),,,(3=CD BD A C B B D A CD B BD A ++=++=++)( 【题2.26】用公式化简法将下列逻辑函数化为最简与或形式。
(1)C B C A BC A C B A Y ++=),,(1 (2))(),,(2C B A C B B A C B A Y +++= (3)D C A ABD CD B A D C B A Y ++=),,,(3解:(1)C B C A BC A C B A Y ++=),,(1=C A C B C A C A C B A C A C B B A ++=++=++)()( (2))(),,(2C B A C B B A C B A Y +++==)()(C A A B C B C B A C B B A ++=++C B A B B C B A C B B A C B C A B C B +=++=++=++=)()((3)D C A B C B AD D C B A Y ++=)(),,,(3=D C A C B AD ++)(=D C A ACD ABD ++=ABD+AD(C+AD B AD AD ABD C =+=+=)1()000001111111000CDAB 0001111000011011【题2.27】用卡诺图将下列逻辑函数化为最简与或形式。
逻辑代数基础习题

《逻辑代数基础》练习题及答案[1.1]将下列二进制数转为等值的十六进制数的等值的十进制数。
(1)(10010111)2 ;(2)(1101101)2 ;(3)(0.01011111)2 ;(4)(11.001)2 。
[解](1)(10010111)2 = (97)16 = (151)10,(2)(11011101)2 = (6D)16 = (109)10(3)(0.01011111)2 = (0.5F)16 = (0.37109375)10,(4)(11.001)2 = (3.2)16 = (3.125)10[1.2]将下列十六进制数化为等值的二进制数和等值的十进制数。
(1)(8C)16 ;(2)(3D.BE)16;(3)(8F.FF)16 ;(4)(10.00)16[解](1)(8C)16 = (10001100)2 = (140)10(2)(3D·BE)16 = (111101.1011111)2 = (61.7421875)10(3)(8F·FF)16 = (10001111.11111111)2 = (143.99609375)10(4)(10.00)16 = (10000.00000000)2 = (16.00000000)10[1.3]将下列十进制数转换成等效的二进制数和等效的十进制数。
要求二进制数保留小数点以后4位有效数字。
(1)(17)10 ;(2)(127 )10 ;(3)(0.39)10 ;(4)(25.7)10[解](1)(17)10 =(10001)2 =(11)16 ;(2)(127)10 = (1111111)2 = (7F)16(3)(0.39)10 = (0.0110)2 = (0.6)16;(4)(25.7)10 = (11001.1011)2 = (19.B)16[1.4]写出下列二进制数的原码和补码。
(1)(+1011)2 ;(2)(+00110)2 ;(3)(-1101)2 ;(4)(-00101)2 。
第3章 逻辑代数(习题)

CD
AB
00 01 11 10
00 1 1
1
01
1
(1) F1 m(0,1,2,4) d(5,6)
BC
11 1
1
10 1 1
1
(2) F2 m(3,5,6,7,10) d(0,1,2,4,8)
CD
AB
00 01 11 10
00 x x 1 x
(a)
BC
A
00 01 11 10
0 11
表 T3.4(3表)T3.4(3) A B CA FB C F 0 0 00 0 0 0 0 0 10 10 1 1 0 1 00 01 0 0 0 1 10 1 1 1 1 0 01 0 0 0 1 0 11 0 1 0 1 1 01 1 0 1 1 1 11 1 1 1
(3)
A
表 T3.4(1)
ABCD ABCD ABCD ABC D ABCD ABCD
3.2 答案
(1) 左边 AB B AB AB B A B 右边 (2) 左边 A B CCD (B C)(ABD BC)
(A B C) CD ABCD BC
A B C C D ABCD BC A B 1 D ABCD BC 1 右边
0 0 0X 0Y 1Z 1F
O 000 0
B
0 0 1 0 10 01 01
O
010 1
C
011 0
0 1 0 1 10 00 10
O
101 1
F 0 1 0 1 11 00 00
O
111 1
表 T3.4(2)
1 1A B C F t 000 0
1 10 0 1 1
0 1 0t 1
第三章 逻辑代数基础 作业题(参考答案)

第三章逻辑代数基础(Basis of Logic Algebra)1.知识要点逻辑代数(Logic Algebra)的公理、定理及其在逻辑代数化简时的作用;逻辑函数的表达形式及相互转换;最小项(Minterm)和最大项(Maxterm)的基本概念和性质;利用卡诺图(Karnaugh Maps)化简逻辑函数的方法。
重点:1.逻辑代数的公理(Axioms)、定理(Theorems),正负逻辑(Positive Logic, Negative Logic)的概念与对偶关系(Duality Theorems)、反演关系(Complement Theorems)、香农展开定理,及其在逻辑代数化简时的作用;2.逻辑函数的表达形式:积之和与和之积标准型、真值表(Truth Table)、卡诺图(Karnaugh Maps)、最小逻辑表达式之间的关系及相互转换;3.最小项(Minterm)和最大项(Maxterm)的基本概念和性质;4.利用卡诺图化简逻辑函数的方法。
难点:利用卡诺图对逻辑函数进行化简与运算的方法(1)正逻辑(Positive Logic)、负逻辑(Negative Logic)的概念以及两者之间的关系。
数字电路中用电压的高低表示逻辑值1和0,将代数中低电压(一般为参考地0V)附近的信号称为低电平,将代数中高电压(一般为电源电压)附近的信号称为高电平。
以高电平表示1,低电平表示0,实现的逻辑关系称为正逻辑(Positive Logic),相反,以高电平表示0,低电平表示1,实现的逻辑关系称为负逻辑(Negative Logic),两者之间的逻辑关系为对偶关系。
(2)逻辑函数的标准表达式积之和标准形式(又称为标准和、最小项和式):每个与项都是最小项的与或表达式。
和之积标准形式(又称为标准积、最大项积式):每个或项都是最大项的或与表达式。
逻辑函数的表达形式具有多样性,但标准形式是唯一的,它们和真值表之间有严格的对应关系。
第一章(数制、编码与逻辑代数)作业及答案

第一章(数制、编码与逻辑代数)作业及答案1、数制、编码转换题(1)(74.3 )8=( 60.375 )10=( 111100.011)2=( 0111 0100.0011 )8421BCD(2)(45.24 )10=(101101.001111 )2 精确到小数点后6位(3)(110101.11 )2=(35.C )16=( 65.6 )8(4)(71.45 )8=( 39.94 )16(5)(010********* )8421BCD =(1113)8=( 24B)162、求下列函数的反函数。
(1))(B D A C C B A F +++=(2)))()((B A D C C D A B F +++=3、写出下列函数的对偶式。
(1)(2)4、用公式法将下列各逻辑函数表达式化成最简“与—或”式,并继而将其转换成相应的“与非—与非”式、“或—与”式和“与或非”式。
(1))() (C B C B A C B BC A F +++=(2)ABD D C ABC C B A AC F ++++=D(3)BC C B A BC A A F ++++=)D ((4)C B C A AB F ++=(5)))()()()()((F E D F B F E C A D B C A B A A F +++++++++=答案:(1)A (2)D C AC +=D C AC ∙=(A+C )(C+D)=D C C A +(3)BC A +=BC A ∙=(A+B)(A+C)=C A B A +(4)C AB +=C AB ∙=(A+C)(B+C)=C B C A +(5)))((F B D B AC F ++==CD B A ABCF ∙=))((F B D B AC ++=F B C D B A +++5、写出下列逻辑函数的最小项表达式,并用卡诺图法将其化为最简“与—或”式。
(1)D C A D C A C B A D C AB ABC F +++++= D 解:C A AB D A ++(2)B C A BD F )(+= 解:D A D C B ++6、用卡诺图法将下列逻辑函数化为最简“与—或”式。
第三章 逻辑代数基础 作业题(参考答案)

第三章逻辑代数基础(Basis of Logic Algebra)1.知识要点逻辑代数(Logic Algebra)得公理、定理及其在逻辑代数化简时得作用;逻辑函数得表达形式及相互转换;最小项(Minterm)与最大项(Maxterm)得基本概念与性质;利用卡诺图(Karnaugh Maps)化简逻辑函数得方法。
重点:1.逻辑代数得公理(Axioms)、定理(Theorems),正负逻辑(Positive Logic, Negative Logic)得概念与对偶关系(Duality Theorems)、反演关系(plement Theorems)、香农展开定理,及其在逻辑代数化简时得作用;2.逻辑函数得表达形式:积之与与与之积标准型、真值表(Truth Table)、卡诺图(Karnaugh Maps)、最小逻辑表达式之间得关系及相互转换;3.最小项(Minterm)与最大项(Maxterm)得基本概念与性质;4.利用卡诺图化简逻辑函数得方法。
难点:利用卡诺图对逻辑函数进行化简与运算得方法(1)正逻辑(Positive Logic)、负逻辑(Negative Logic)得概念以及两者之间得关系。
数字电路中用电压得高低表示逻辑值1与0,将代数中低电压(一般为参考地0V)附近得信号称为低电平,将代数中高电压(一般为电源电压)附近得信号称为高电平。
以高电平表示1,低电平表示0,实现得逻辑关系称为正逻辑(Positive Logic),相反,以高电平表示0,低电平表示1,实现得逻辑关系称为负逻辑(Negative Logic),两者之间得逻辑关系为对偶关系。
(2)逻辑函数得标准表达式积之与标准形式(又称为标准与、最小项与式):每个与项都就是最小项得与或表达式。
与之积标准形式(又称为标准积、最大项积式):每个或项都就是最大项得或与表达式。
逻辑函数得表达形式具有多样性,但标准形式就是唯一得,它们与真值表之间有严格得对应关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 习题1.1. 数字信号与模拟信号的主要区别是什么?1.2. 完成下列数制或代码转换(1) (172)10=(?)2(2) (0.8123)10=(?)2(3) (10101101.0101)2=(?)10 (4) (3625)10=(?)8=(?)16 (5) (0.172)8=(?)16=(?)2 (6) (4CA)16=(?)2=(?)10解: (1) (172)10= (10101100)2(2) (0.8123)10 =(011001)2(3) (10101101.0101)2= (173.3125)10 (4) (3625)10= (7051)8=(E29)16(5) (0.172)8= (03D0)16=(0.00111101)2 (6) (4CA)16 =(10011001010)2=(1226)101.3. 用真值表证明下列等式1.))((C A B A BC A ++=+2.A C C B B A A C C B B A ++=++解: A B C BC A+BC A+B A+C (A+B)(A+C)0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 0 1 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 11111A B CA B CB AC B C A A C C B B A ++ B A C B A C A C C B B A ++0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 0 0 0 1 1 1 0 0 1 1 0 0 0 1 1 1 0 0 1 0 0 1 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 1 1 00 0 10 1 010 0 111 1 1 0 0 0 0 0 0 0 0 0 0 01.4. 求下列函数的对偶式和反函数式(1) D C B A D C A B Z +++++=)((1(2) C B AD D C B A Z +++=2解: (1) Z 1的对偶式为:D ABC D AC B Z ++=)('1Z 1的反函数式为:D C AB D C A B Z ++=1(2) Z 2的对偶式为:)('2C B D A D BC A Z ++++=Z 2的反函数式为:))((2C B D A D C B A Z ++++=1.5. 用逻辑代数证明下列等式(a)B A B A A +=+(b) AC AB C AB C B A ABC +=++(c)()E CD A E D C CD A C B A A ++=++++解:(a)B A B A A +=+由交换律 ))((C A B A BC A ++=+,得B A B A A A B A A +=++=+))(((b)AC AB C AB C B A ABC +=++ACAB B C A C B C A C B C B BC A C AB C B A ABC +=+=+=++=++)()()((c)()E CD A E D C CD A C B A A ++=++++()ECD A E CD CD A E D C CD A A E D C CD A C B A A ++=++=+++=++++_____)(1.6. 试从以下真值表写出L 的逻辑函数表达式A B C L A B C L 0 0 0 0 1 0 0 1 0 0 1 1 1 0 1 0 0 1 0 1 1 1 0 0 0 1 11 1 11解:ABC C B A C B A C B A C B A f L +++==),,(1.7. 已知逻辑电路图如图所示,试写出它的输出逻辑表达式,并列出真值表。
解: B A B A B A B A B A B A f L ⊕=++=+++==))((),(A B B A ⊕0 0 0 0 1 1 1 0 1 1 1 01.8. 求出下列函数的最小项表达式(1) C AB D AC D AB D C B A Z ++=),,,(1(2) BC C B D A D C A ACD D C B A Z ++++=),,,(2解:(1)∑=)14,13,12,10(1Z(2)∑=)10,8,2,0(2Z1.9. 用代数法将下列函数化简成为最简“与—或”表达式 (1) CD B A CD BCD A ++(2) EF B EF B A BD C A AB D A AD ++++++(3) )()(D A C B A D A C B A +++(4) ))()((E DE D C C B B C B A ++++++ (5) )(A BC AB +(6) C B BC C B A ABC A ++++(7)B A B A B A B A ++++(8) C E A E A E C A E B E C E B A ++++)((9) C AB C B CD ABC D A D A +++++)()((10) C B B A ⊕+⊕1.10. 利用与非门实现下列函数(a) L=AB+AC (b) _____________)(C A D L +=(c)____________________))((D C B A L ++=解: (a) L=AB+AC_______________________ACAB L ⋅=(b)_____________)(C A D L +=≥1≥1≥111A BL_____________________________)(CA D C A D L =+=(c)____________________))((D C B A L ++=__________________________________________))((DC B AD C B A L =++=1.11. 试用2输入与非门和反相器设计一个4位的奇偶校验器,即当4位数中有奇数个1时输出为0,否则输出为1。
解:D C B A L ⊕⊕⊕=_______________________BA B A B A B A L ⋅=+=1.12.用卡诺图法将下列函数化简成为最简“与-或”表达式(1) AB B A B A Z++=(2) C B A C B A +++(3) C AB C B CD ABC D A D A Z++++++=)()((4) E AC E A E C A E B E C E B A Z ++++=)( (5) )15,14,11,10,8,7,6,5,2,0(),,,(m D C B A Z ∑= (6) )13,12,11,10,9,8,7,6,5,3,2,1(),,,(m D C B A Z ∑= (7) C B C B C A C A D C B A Z +++=),,,((8) D C A C B A D C D C A ABD ABC D C B A Z +++++=),,,( (9) )14,11,10,9,8,6,4,3,2,1,0(),,,(m D C B A Z ∑= (10) D BD C A C BD B A D B A D C B A Z +++++=)()(),,,(解:(1) B A Z += (2) 12=ZB A10 1111 0 BCA 00 01 0 11111 1011 11 11 00 AB CD 00 01 01 11 11 10 10 0 00 0 0 0 0 0 0 00 01 1 1100ABCDE0000110111111100100010101101011 111 1 1 1 11 1 110 0 0 0 0 00 0 0 0 0 0 0 0 00 00 0C B =3 E A E B A =4(5) BDA DB BC B A Z +++=5 (6) BA C A C A D C +=6(7) C B B A C A Z ++=7或CB B AC A ++ D+8(9) D A D C B Z ++=9 (10)CA D AB Z ++=10BC A 00 01 0 1 1 1 11 10 0 1 0 1 1 1 00 AB CD00 01 01 11 11 1010 1 11 1 1 1 1 1 1 1 1 0 0 0 0 0 00 AB CD 00 01 01 11 11 1010 1 1 1 1 1 1 1 11 0 01 0 0 1 1 00 AB CD 00 01 01 11 11 1010 110 10 1 1 11 0 111 1 0 000 AB CD00 01 01 11 11 1010 111 11 1 1 10 1 1 1 10 0 0 00 AB CD00 01 01 11 11 10 10 1 1 11 111 1 1 1 1 1 0 0。
