基于EViews6的面板数据计量分析-白仲林
EVIEWS面板数据分析操作教程及实例解析

模型选择对分析结果影响
模型适用性
根据研究目的和数据特征选择合 适的面板数据模型,如固定效应 模型、随机效应模型等。
模型假设
确保所选模型满足基本假设,如 线性关系、误差项独立同分布等 ,否则可能导致结果不准确。
模型比较与选择
通过比较不同模型的拟合优度、 参数显著性等指标,选择最优模 型进行分析。
操作规范性与结果可靠性保障措施
操作步骤规范
结果验证与解读
对分析结果进行验证,确保结果的合理性和准确性 ;同时,正确解读分析结果,避免误导读者。
严格按照EVIEWS软件的操作步骤进行分析 ,避免操作失误或遗漏关键步骤。
数据分析报告
编写详细的数据分析报告,包括数据来源、 处理方法、模型选择、分析结果及解读等, 以便读者全面了解分析过程。
方和来估计模型参数。
广义最小二乘法(GLS)
02
当存在异方差性或自相关性时,采用广义最小二乘法进行参数
估计,以提高估计效率。
最大似然法(ML)
03
适用于随机效应模型等复杂面板数据模型,通过最大化似然函
数来估计模型参数。
模型诊断与检验
残差分析
检查残差是否满足独立同分布等假设条件, 以评估模型的拟合效果。
07 EVIEWS面板数 据分析操作注意 事项
数据质量对分析结果影响
数据来源
确保数据来自可靠、权威的来源,避免使用不准确或存在偏见的数 据。
数据完整性
检查数据是否存在缺失值、异常值或重复值,这些问题可能导致分 析结果失真。
数据处理
对数据进行适当的预处理,如清洗、转换和标准化,以提高数据质量 和一致性。
增强了解决实际问题的能力
通过实例解析和操作演示,学员们学会了如何运用所学知识解决实际问题,提高了分析 问题和解决问题的能力。
基于EViews 6的面板数据计量分析
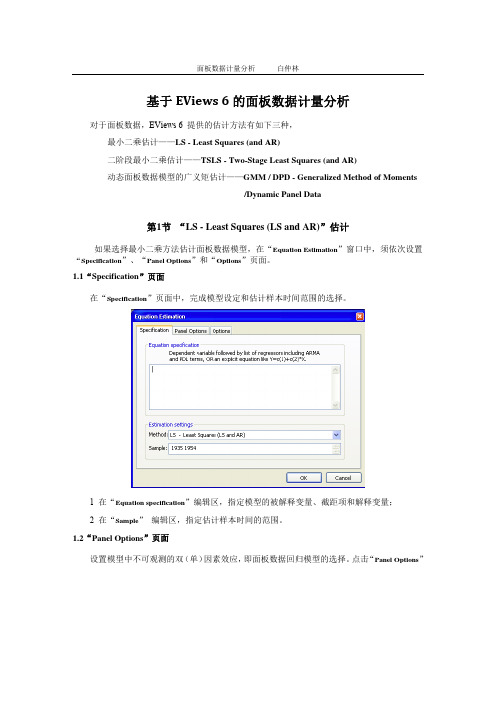
基于EViews 6的面板数据计量分析对于面板数据,EViews 6 提供的估计方法有如下三种,最小二乘估计——LS - Least Squares (and AR)二阶段最小二乘估计——TSLS - Two-Stage Least Squares (and AR)动态面板数据模型的广义矩估计——GMM / DPD - Generalized Method of Moments/Dynamic Panel Data第1节“LS - Least Squares (LS and AR)”估计如果选择最小二乘方法估计面板数据模型,在“Equation Estimation”窗口中,须依次设置“Specification”、“Panel Options”和“Options”页面。
1.1“Specification”页面在“Specification”页面中,完成模型设定和估计样本时间范围的选择。
1 在“Equation specification”编辑区,指定模型的被解释变量、截距项和解释变量;2 在“Sample”编辑区,指定估计样本时间的范围。
1.2“Panel Options”页面设置模型中不可观测的双(单)因素效应,即面板数据回归模型的选择。
点击“Panel Options”该页面包含三方面内容。
1 效应设置在“Effects specification”选择区,设定面板数据模型的个体效应和时间效应,可选择的选项有“None”、“Fixed”和“Random”,分别表示“无效应”、“固定效应”和“随机效应”。
如果选择了“Fixed”或“Random”,EViews在输出结果中自动添加一个共同常数,即截距项,以保证效应之和为零。
否则,截距项必要时,须在“Specification”页面的“Equation specification”编辑区设定模型截距项。
2 GLS加权设置“GLS Weights”可以在下拉框中选择如下选项之一。
eviews面板数据实例分析(包会)-

eviews面板数据实例分析(包会)-Eviews是一种流行的面板数据分析软件,广泛用于经济学及财务学领域。
本文将以一个面板数据实例为例,介绍Eviews的一些基本功能及应用。
数据说明本数据集为横截面面板数据,共包含11个国家(美国、加拿大、英国、法国、德国、意大利、荷兰、比利时、奥地利、瑞典、日本)在1970年至1986年间的年度数据。
变量说明如下:- gdpercap:人均GDP- invest:投资/GDP比率- consump:消费/GDP比率- inflation:通货膨胀率- popgrowth:人口增长率- literacy:成年人识字率- female:女性劳动力占比数据导入及面板设置首先,在Eviews中新建一个工作文件,并将数据导入。
打开数据文件后,我们可以看到数据已经被正确读入。
然后,我们需要将数据设为面板数据。
在Eviews中,选择“View”菜单下的“Structure of Workfile”选项,可以进入工作文件结构设置。
在弹出的窗口中,选择“Panel Data”选项,并按照数据的属性设置面板变量。
在本例中,我们选择“Country”作为单位维度,“Year”作为时间维度。
设置完成后,Eviews会自动进行面板数据检测。
检测结果显示,数据格式符合面板数据要求。
面板数据描述及汇总统计接下来,我们可以对数据进行初步的描述性统计和汇总统计。
选择“Quick”菜单下的“Descriptive Stats”选项,Eviews会自动生成数据的描述性统计报告,展示各变量在不同国家和不同年份的均值、标准差、最小值、最大值等基本信息。
我们也可以手动计算其他统计量。
例如,选择“Proc”菜单下的“Panel Data”选项,可以对选定的变量进行面板数据汇总统计。
下面是在Eviews中计算人均GDP和消费/GDP比率两个变量的面板均值统计结果:面板数据变量之间的相关性分析在分析面板数据时,我们通常需要考虑不同变量之间的相关性。
Eviews数据统计与分析教程12章-面板数据(Panel-Data)模型

EViews统计分析基础教程
二、Pool对象的基本操作
2.Pool对象数据的输入 (2)非堆积数据
在非堆积数据中,给定的截面数据和变量是放在一起的,但 同其他的截面成员和变量的数据是分开的。每一个截面成员 的观测值被放在一纵列中,每一列是截面成员不同时期的样 本观测值。 非堆积数据形式的导入方法与第三章所介绍的数据导入方法 相同。
EViews统计分析基础教程
二、Pool对象的基本操作
1.Pool对象的建立
在Pool对象的编辑窗口中输入截面成员的标识名称,例如做 中国省际面板数据分析时,选取中部五省份为截面成员,即 湖南、湖北、河南、江西和安徽,分布用字母HN,HB,HE, JX,AH表示。这些截面成员各名称之间可用空格隔开,也 可以通过回车键进行换行,即每一个名称占一行。需注意的 是,截面成员的标识名称的设定需简单,便于操作。通常可 以在截面成员标识名称前加下划线“_”。如下图所示。
EViews统计分析基础教程
三、Pool对象模型估计
通过Pool对象可以对固定影响、随机影响变截距模型和固定 影响变系数模型进行估计。常用的方法有最小二乘估计法、 加权最小二乘法等。
EViews统计分析基础教程
三、Pool对象模型估计
在EViews操作中,单击Pool对象工具栏中的“Estimate”或者 选择“Proc”|“Estimate”选项,将弹出下图所示的对话框。
EViews统计分析基础教程
第12章 面板数据(Panel Data)模型
重点内容: • Pool对象的建立 • Pool对象数据分析 • Pool对象模型估计
EViews统计分析基础教程
一、Panel Data模型原理
面板数据模型的基本形式是
eviews面板数据模型分析面板数据模型与应用数学

3.2 平均数(between)OLS 估计
平均数 OLS 估计法的步骤是首先对面板数据中的每个个体求平均数,共得到 N 个平均数(估计值)。然后利用 yit 和 Xit 的 N 组观测值估计参数。以个体固 定效应回归模型
yit = i + Xit &#t ' +it, i = 1, 2, …, N; t = 1, 2, …, T 如果模型是正确设定的,且解释变量与误差项不相关,即 Cov(Xit,it) = 0。
那么无论是 N,还是 T,模型参数的混合最小二乘估计量都具有 一致性。 对于经济序列每个个体 i 及其误差项来说通常是序列相关的。NT 个相关 观测值要比 NT 个相互独立的观测值包含的信息少。从而导致误差项的标 准差常常被低估,估计量的精度被虚假夸大。
• 可行GLS(feasible GLS)估计 (适用于随机效应模型)
3.面板数据模型估计方法
面板数据模型中的估计量既不同于截面数据估计量,也不同于时间序列
估计量,其性质随设定固定效应模型是否正确而变化。 3.1 混合最小二乘(Pooled OLS)估计 混合 OLS 估计方法是在时间上和截面上把 NT 个观测值混合在一起,然 后用 OLS 法估计模型参数。给定混合模型
yit = i + Xit' +it, i = 1, 2, …, N; t = 1, 2, …, T 如果i 为随机变量,其分布与 Xit 无关; Xit 为 k 1 阶回归变量列向 量(包括 k 个回归量),为 k 1 阶回归系数列向量,对于不同个体回 归系数相同,yit 为被回归变量(标量),it 为误差项(标量),这种模
截距项,zt 表示随不同截面(时点)变化,但不随个体变化的难以
eviews处理面板数据操作步骤
各种方法的结果(除Breitung检验 外)都接受原假设, I? 存在单位根,是非平稳的。
8
例10.4中I?的一阶差分变量的所有方法的单位根检验结果:
所有P值均小于 0.05,说明平稳
各种方法的结果都拒绝原假设,所以可 以得出结论: I?是I(1)的。
9
第三步 平稳性检验后分析路径选择
平稳性检验后若:
23
中部地区模型的Hausman Test结果: P值大于 0.05,所 以接受原 假设:应 建立随机 效应模型
由(10.3.68)式构造的中部地区模型的Hausman Test
统计量(W) 是0.29,p值是0.59,接受原假设:随机影响模
型中个体影响与解释变量不相关, 结论: 可以将模型设定为随机模型。
29
手工记下: 自由度为
N( T-K-1 )
手工记 下 S1
30
模型二:固定影响 (Fixed Effects) (i j,i =j )
yi m xi β ui
1.Pedroni检验 2.Kao检验 3.Johansen面板协整检验
13
协整检验操作
Pool序列的协整检验
※在EViews中打开pool对象,选
择Views/ Cointegration Test…,
则显示协整检验的对话框。
图10.6 面板数据的协整检验的对话框
14
Pedroni检验:
原假设:无协 整关系
若均为1阶单整,直接全取差分或全取对数,进行回归分析
12
协整检验 说 明
原:不存在协整
面板数据的协整检验方法可以分为两大类,一类是建立在Engle and Granger二
步法检验基础上的面板协整检验,具体方法主要有Pedroni检验和Kao检验;另
计量学教程及eviews实现面板数据模型的分析

二、一般面板数据模型介绍
符 号 介 绍 : yit — — 因 变 量 在 横 截 面 i 和 时 间 t 上 的 数 值 ;
x
j it
——第 j 个解释变量在横截面 i 和时间 t 上的数值;
假设:有 K 个解释变量,即 j 1,2,, K ;
有 N 个横截面,即i 1,2,, N ;
时间指标 t 1,2,,T 。
ˆ
2 ˆ w
s 2 ( X P D X ) 1
s2
ˆ
2 ˆ
i
s2 T
X iˆ ˆw X i
其中 是对误差项方差的估计量:
( y it ˆ i x it ˆ w ) 2
s2 i t
NT ቤተ መጻሕፍቲ ባይዱN K
注意:在对误差项方差的估计量中,分母(NT-N-K)反映了整个
模型的自由度。有了这些方差的估计量,就可以用传统的t-统计量 对估计系数的显著性进行检验。同时,还可以运用下列F-统计量对
;
(7
)
2
E
(
2 i
),
i
。
给定这些假设,随机效应面板数据模型也可同样写为:
其中
(In
i )
y=X β +μ
, α 的 向 量 形 式 与 以 前 相 同 。
是 Kronecker 乘法 符 号。
例 2 Kronecker 乘 法 :
I2
i 21
i
21
0
0 i 21
例 3 前 面 的 矩 阵 D 也 可 用 Kronecker 乘 法 表 示 : D I N iT 1
记第 i 个横截面的数据为
yi1
yi
yi2
张晓峒面板数据eviews

2.面板数据模型分类
对于个体固定效应模型,个体效应i 未知,E(i Xit)随 Xit 而变化,但不知
怎样与 Xit 变化,所以 E(yit Xit)不可识别。对于短期面板数据,个体固定效应
模型是正确设定的,的混合 OLS 估计量不具有一致性。
下面解释设定个体固定效应模型的原因。假定有面板数据模型
1.面板数据定义 面板数据分两种特征:(1)个体数少,时间长。(2)个体数多,时间短。
面板数据主要指后一种情形。 面板数据用双下标变量表示。例如
yi t, i = 1, 2, …, N; t = 1, 2, …, T i 对应面板数据中不同个体。N 表示面板数据中含有 N 个个体。t 对应面板数据 中不同时点。T 表示时间序列的最大长度。若固定 t 不变,yi ., ( i = 1, 2, …, N)是
横截面上的 N 个随机变量;若固定 i 不变,y. t, (t = 1, 2, …, T)是纵剖面上的一个
时间序列(个体)。 对于面板数据 yi t, i = 1, 2, …, N; t = 1, 2, …, T,如果每个个体在相同的时期
内都有观测值记录,则称此面板数据为平衡面板数据(balanced panel data)。 若面板数据中的个体在相同时期内缺失若干个观测值,则称此面板数据为非平 衡面板数据(unbalanced panel data)。
9.2
LOG(CP1999)
9.0
8.8
6000
8.6
5000
8.4
4000
8.2
3000 2000
IP
8.0
2000 4000 6000 8000 10000 12000 14000 7.8
IPCROSS
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于EViews 6的面板数据计量分析对于面板数据,EViews 6 提供的估计方法有如下三种,最小二乘估计——LS - Least Squares (and AR)二阶段最小二乘估计——TSLS - Two-Stage Least Squares (and AR)动态面板数据模型的广义矩估计——GMM / DPD - Generalized Method of Moments/Dynamic Panel Data第1节“LS - Least Squares (LS and AR)”估计如果选择最小二乘方法估计面板数据模型,在“Equation Estimation”窗口中,须依次设置“Specification”、“Panel Options”和“Options”页面。
1.1“Specification”页面在“Specification”页面中,完成模型设定和估计样本时间范围的选择。
1 在“Equation specification”编辑区,指定模型的被解释变量、截距项和解释变量;2 在“Sample”编辑区,指定估计样本时间的范围。
1.2“Panel Options”页面设置模型中不可观测的双(单)因素效应,即面板数据回归模型的选择。
点击“Panel Options”该页面包含三方面内容。
1 效应设置在“Effects specification”选择区,设定面板数据模型的个体效应和时间效应,可选择的选项有“None”、“Fixed”和“Random”,分别表示“无效应”、“固定效应”和“随机效应”。
如果选择了“Fixed”或“Random”,EViews在输出结果中自动添加一个共同常数,即截距项,以保证效应之和为零。
否则,截距项必要时,须在“Specification”页面的“Equation specification”编辑区设定模型截距项。
2 GLS加权设置“GLS Weights”可以在下拉框中选择如下选项之一。
其选择标准为:面板数据不存在异方差和自相关性时,选择“No weights”;面板数据在个体间存在异方差时,选择“Cross-section weights”;面板数据的个体间存在同期相关性和异方差时,选择“Cross-section SUR”;对于给定的个体,存在时间上的异方差时,选择“Period weights”。
对于给定的个体残差,存在时间上的序列相关性和异方差时,选择“Period SUR”;当选择了GLS加权(后四项),EViews采用FGLS估计模型。
特别,选择了两种SUR选项的FGLS估计也称为Parks估计。
3 系数协方差估计方法通过选择“Coef covariance method”选项,确定计算系数标准差的各种稳健估计方法。
可选择的选项有其选择标准为:对于不存在(个体间的和时间上的)异方差和时间上的序列相关性时,选择“Ordinary”;模型残差存在个体间的异方差和同期相关性时,可选择“White cross-section”;这时也可选择“Cross-section SUR”选项,最常见的选择是White的截面加权法(Whitecross-section)对于模型残差,只存在时间上的异方差时,选择“White Period”选项模型残差存在个体间的异方差时,可选择“White[Diagonal]”模型残差存在个体间的异方差和同期相关性时,可选择“Cross-section SUR”选项;对于模型残差,只存在个体间的异方差时,选择“Cross-section weights”选项;对于指定的个体,观测数据存在时间上的异方差和序列相关性时,选择“Period SUR”选项;对于模型残差,只存在时间上的异方差时,选择“Period weights”选项。
选择“No d.f. correction”,计算时不进行自由度修正。
注意:(1) 模型设定和估计方法的一些组合EViews 6不支持,例如,对于个体随机效应模型,设置AR项,或者,选择GLS加权,EViews 6不支持。
(2) 对于双因素随机效应模型,不支持非平衡面板数据。
1.3“Options”页面“Options”页面包括系数导数的计算方法选项“Derivatives”、GLS估计的加权选项“Weighting Options”、回归系数重命名“Coefficient Name”和迭代算法选项“Iteration Control”四方面的选项。
除回归系数重命名“Coefficient Name”编辑窗口外,该页面的其它选项依赖于“Panel Options”页面的设置。
对于随机效应模型,可选择“Weighting Options”确定随机效应方差的估计方法;对于固定效应模型,可选择“Iteration Control”确定迭代估计方法的收敛和迭代选择;如果“Panel Options”页面选择了GLS加权,在“Options”页面可选择“Weighting Options”、“Coefficient Name”和“Iteration Control”三方面的选项,1 系数导数的计算方法在EViews 6中,可以设置均值方程的(非线性)函数形式,并提供两种计算系数导数的计算方法。
选择“Use numeric only”,EViews 6采用有限差分法计算系数的数值导数。
否则,采用Newton-Raphson方法和Gauss-Newton/BHHH等方法对计算系数的解析导数。
对于线性模型,该选项无效。
2 加权选项在估计随机效应模型时,EViews 提供了计算随机效应方差的三种估计方法,分别是Swamy-Arora, Wallace-Hussain和Wansbeek-Kapteyn方法。
缺省选择是“Swamy-Arora”方法,详细内容参考Baltagi (2008).另外,“Keep GLS weights”选项决定是否保存该模型GLS估计的权重。
3 回归系数重命名缺省时,EViews 6使用向量C保存系数和效应的估计值。
如果使用其他变量名保存它们,在编辑栏输入变量名。
4 迭代算法选择“Max Iterations Convergence ”选项供选择系数和GLS 权重的迭代次数和收敛检验。
如果模型设定中含AR ,设置有AR 项模型系数的初始值,可分别选择无AR 项模型系数的OLS 估计分数、0或者用户自定义值。
“Display Settings ”决定在输出结果中是否显示收敛设置和系数的初始值。
最后的两个单项选择用于确定系数向量和加权矩阵收敛迭代设置,可选择“Simultaneous updating ”和“Sequential updating ”,选择前者EViews 同时对系数向量和GLS 加权矩阵迭代;如果选择“Sequential updating ”,系数向量迭代后,EViews 更新GLS 加权矩阵,再迭代系数向量。
但是对于无AR 项的GLS 模型,两种设置是相同的。
如果选择了“Update coefs to convergence ”和“ Update coefs once ”之一,GLS 加权矩阵只更新一次,前者对系数向量迭代计算直至收敛。
选择后者,系数向量也仅迭代一次。
同样,对于无AR 项的GLS 模型,两种设置也是相同的。
1.4“LS - Least Squares (LS and AR)”估计结果案例:Grunfeld(1958)建立了下面的投资方程:12it it it i t it I F C u αββξλ=+++++这里,I it 表示对第i 个企业在t 年的实际总投资,F it 表示企业的实际价值(即公开出售的股份),C it 表示资本存量的实际价值。
案例中的数据是来源于10个大型的美国制造业公司1935-1954共20年的面板数据。
利用EViews6 估计双因素固定效应和随机效应模型1 双因素固定效应模型的EViews6输出结果2 双因素随机效应模型的EViews6输出结果1.5 面板数据模型的检验1 固定效应的检验EViews 检验过程:View/Fixed/Random Effects Testing/Redundant Fixed Effects – Likelihood Ratio.检验结果:0表示估计值为负H02下有约束模型的估计H03下有约束模型的估计H01下有约束模型的估计2 随机效应 / 固定效应检验-Hausman检验EViews6的检验过程:View/Fixed/Random Effects Testing/Correlated Random Effects- Hausman Test检验结果:(1)基于双随机效应和双固定效应的Hausman 检验统计量 m 1 = 8.842,其p = 0.012,在5%的显著性水平下,Hausman 检验拒绝了零假设50H ;(2) EViews 还给报告了其他两种Hausman 检验。
最终,应选择个体随机时间固定的双因素效应模型。
第2节 “TSLS - Two-Stage Least Squares (and AR)”估计如果选择二阶段最小二乘估计方法(“TSLS - Two-Stage Least Squares (and AR)”)面板数据模型,在“Equation Estimation ”窗口中,须依次设置“Specification ”、“Panel Options ”、“Instruments ”和“Options ”页面。
其中,“Specification ”、“Panel Options ”和“Options ”页面的设置与最小二乘估计方法相同,下面主要介绍“Instruments ”页面设置。
在使用二阶段最小二乘估计方法时,需要设置“Instruments ”页面,以确定工具变量。
该页面有两部分。
在“Instrument list ”编辑框指定工具变量,列示所使用的工具变量序列。
“Instruments list ”页面缺省时,EViews6选择的工具变量是解释变量自身。
如果模型设定时,AR 项作为解释变量,可选择“Include lagged regressors for equations with AR terms ”选项,自动设定模型设定中的变量作为工具变量,并且,EViews6 采用非线性OLS 估计模型。
注意:在“Instruments ” 编辑框无需指定常数项。
第3节“GMM / DPD - Generalized Method of Moments/Dynamic Panel Data”估计在EViews6中,使用GMM方法估计面板数据模型,也需要设置“Specification”、“Panel Options”、“Instruments”和“Options”四个页面。
