空气动力学原理2
空气动力学前六章知识要点

空气动力学基础前六章总结第一章 空气动力学一些引述1、 空气动力学涉及到的物理量的定义及相应的单位①压强:是作用在单位面积上的正压力,该力是由于气体分子在单位时间内对面发生冲击(或穿过该面)而发生的动量变化,具有点属性。
0,lim →⎪⎭⎫ ⎝⎛=dA dA dF p 单位:Pa, kPa, MPa 一个标准大气压:101kPa②密度:定义为单位体积内的质量,具有点属性。
0,lim →=dv dvdm ρ 单位:kg/㎡ 空气密度:1.225Kg/㎡③温度:反应平均分子动能,在高速空气动力学中有重要作用。
单位:℃ ④流速:当一个非常小的流体微元通过空间某任意一点的速度。
单位:m/s ⑤剪切应力:dy dv μτ= μ:黏性系数 ⑥动压:212q v ρ∞∞∞= 2、 空气动力及力矩的定义、来源及计算方法空气动力及力矩的来源只有两个:①物体表面的压力分布 ②物体表面的剪应力分布。
气动力的描述有两种坐标系:风轴系(L,D )和体轴系(A,N)。
力矩与所选的点有关系,抬头为正,低头为负。
cos sin L N A αα=- , s i n c o s D N A αα=+3、 气动力系数的定义及其作用气动力系数是比空气动力及力矩更基本且反映本质的无量纲系数,在三维中的力系数与二维中有差别,如:升力系数S q L C L ∞=(3D ),cq L c l ∞='(2D )L L C q S ∞≡,D D C q S ∞≡,N N C q S ∞≡,A A C q S ∞≡,M M C q Sl ∞≡,p p p C q ∞∞-≡,f C q τ∞≡ 二维:S=C(1)=C4、 压力中心的定义压力中心,作用翼剖面上的空气动力,可简化为作用于弦上某参考点的升力L,阻力D 或法向力N ,轴向力A 及绕该点的力矩M 。
如果绕参考点的力矩为零,则该点称为压力中心,显然压力中心就是总空气动力的作用点,气动力矩为0。
第二章 空气动力学

2.1.3 流场、 定常流和非定常流
➢ 流场:流体流动所占据的空间称为流场。 ➢ 流场的选取可根据研究的需要进行确定。可大可小。
非定常流与定常流
➢ 非定常流与非定常流场:
在流场中的任何一点处,如果流体微团流过时的流动参 数——速度、压力、温度、密度等随时间变化,这种流动 就称为非定常流,这种流场被称为非定常流场。
的地方, 却流得比较快。 夏天乘凉时, 我们总喜欢坐在两座房屋之间的过道中, 因
为那里常有“ 穿堂风”。 在山区你可以看到山谷中的风经常比平原开阔的地方来得
大。
连续方程
质量守恒定律
➢ 质量守恒定律是自然界基本的定律之一, 它说明物质既不 会消失, 也不会凭空增加。
➢ 应用在流体的流动上: 在定常流动中,当流体低速、稳 定、连续不断地流动时, 流进任何一个截面的流体质量
➢ 只要相对气流速度相同 , 产生的空气动力也就相等。
(非定常流动转换为定常流动)
风洞实验
➢ 将飞机的飞行转换为空气的流动 ,使空气动力问题的研 究大大简化。
➢ 风洞实验就是根据这个原理建立起来的。
风洞应用
相对气流方向的判定
➢ 相对气流的方向与飞机运动的方向相反 。
平飞时:
相对气流方向 飞行速度方向
➢ 对于不可压缩的、理想的流体( 没有粘性) 表示为:
p1v2
2
p0
常数
静压
动压
总压
➢ 静压:单位体积流体具有的压力能。在静止的空气中, 静压等于大气压力。 ➢ 动压:单位体积流体具有的功能。 ➢ 总压:静压和动压之和。
p1v2
2
p0
常数
➢ 上式即为:不可压缩的、理想的流体( 没有粘性) 的伯努利 方程。
空气动力学数学知识点总结

空气动力学数学知识点总结1. 流体力学基础知识流体是一种连续的物质,可以流动并适应它所处的容器的形状。
在空气动力学中,我们关注的是气体流体,它遵循流体力学的基本原理。
这些原理包括连续方程、动量方程和能量方程。
这些方程描述了流体的运动和行为,并且可以通过数学模型来描述。
1.1 连续方程连续方程描述了流体中的质量守恒。
在欧拉描述中,连续方程可以用以下形式表示:∂ρ/∂t + ∇•(ρv) = 0其中ρ是流体的密度,t是时间,v是速度矢量。
这个方程表达了流体在空间和时间上的密度变化。
解决这种类型的偏微分方程需要深入的数学知识,如微分方程、变分法和复杂的数值计算技术。
1.2 动量方程动量方程描述了流体中的运动和力的作用。
在欧拉描述中,动量方程可以写成:∂(ρv)/∂t + ∇•(ρv⊗v) = -∇p + ∇•τ + ρg其中p是静压力,τ是应力张量,g是重力加速度。
这个方程描述了流体在外力下的运动。
解决这个方程需要运用向量微积分、非线性偏微分方程和数值方法等数学知识。
特别是应力张量的计算和解析是非常复杂的数学问题。
1.3 能量方程能量方程描述了流体内部的热力学过程。
在欧拉描述中,能量方程可以写成:∂(ρe)/∂t + ∇•(ρev) = ∇•(k∇T) + σ其中e是单位质量的内能,k是导热系数,T是温度,σ是能量源项。
解决这个方程需要运用热力学、热传导方程和数值计算技术等数学知识。
2. 边界层理论在空气动力学中,边界层理论是一个重要的概念。
边界层是指流体靠近固体物体表面的区域,流体在这里受到了物体表面的影响,速度变化很大。
边界层理论涉及到流体力学、热力学和数学物理等多个领域的知识。
2.1 边界层方程边界层方程描述了边界层中流体速度和温度的变化。
这些方程通常是非定常的、非线性的偏微分方程,包括动量方程、能量方程以及质量守恒方程。
解决这些方程需要运用复杂的数学方法和数值模拟技术。
2.2 边界层控制边界层控制是指通过改变固体表面的形状或表面条件,来控制边界层的性质,从而影响流体的运动。
空气动力学原理(经典)

如果在汽车行驶时,流过车体的气流可以紧贴在车体轮廓之上,我们称之为ATTECHED或者LAMINAR (即所谓的流线型)。而水滴的形状就是现今我们所知的最为流线的形状了。不过并非汽车非要设计成水滴的形状才能达到最好的LAMINAR ,其实传统的汽车形态也可以达到很好的LAMIAR的效果。常用的方法就是将后挡风玻璃的倾斜角控制在25度之内。FERRARI 360M和丰田的SUPRA就是有此特点的双门轿跑车。
其实仔细观察这类轿跑车的侧面,就不难发现从车头至车尾的线条会朝着车顶向上呈弧形,而车底则十分的平坦,其实这个形状类似机翼截面的形状。当气流流过这个机翼形状的物体时,从车体上方流过的气体一定较从车体下方流过的快,如此一来便会产生一股浮升力。随着速度的升高,下压力的损失会逐渐加大。
1
虽然车体上下方的压力差有可能只有一点点,但是由于车体上下的面积较大,微小的压力差便会造成明显的抓着力分别。一般而言,车尾更容易受到浮升力的影响,而车头部分也会因此造成操控稳定性的问题。
尾翼和扰流器的简史
早在上世纪30年代,各大车厂已经开始致力于降低气流拉力,而对于浮升力的研究,各车厂大致要到60年代才开始关注。FERRAR的赛车手RICHIE GINTHER于1961年发明了能产生下压力的车尾扰流器,他也因此闻名于世。随后的FERRARI战车也都使用此项设计。而第一部使用前扰流器(俗称气霸)的汽车应该是大名鼎鼎的FORD GT40。这部车在超越时速300KM/H时所产生的浮升力令其成为一部根本无法驾驭的汽车,据说在加装了前气霸之后, GT40在达到极速时前轮的下压力由原来的310磅激增至604磅! ! !至于第一部使用尾翼的汽车我没有准确的资料,不过据说时道奇于60年代末生产的CHARGER DAYTONA PLYMOUTH SUPERBIRD。
第2章-风力发电空气动力学基本原理-答案

第2章风力发电空气动力学基本原理1、在分析风电机组的空气动力学过程中,分别应用了一维动量理论、叶素—动量理论和涡流理论。
这些理论以及对气流流过风机叶轮时更复杂的运动状态的研究,本质上都是以气体的动量守恒为基础,来研究更接近气流真实流动状态下叶片转换能量的效率和作用在叶片上的载荷。
2、风是空气流动的现象。
流动的空气具有能量,在忽略化学能的情况下,这些能量包括机械能(动能、势能和压力能)和热能。
3、从动能到机械能的转化是通过叶片来实现的,而从机械能到电能则是通过发电机实现的。
4、风能的大小与气流密度和通过的面积成正比,与气流速度的立方成正比。
5、可压缩流体:在压力作用下体积发生明显变化的流体。
6、远低于音速的空气流动过程(风),气体的压力和温度的变化忽略不计,因而可以将空气作为不可压缩流体来研究。
7、黏性是流体的重要物理属性。
是流体抵抗剪切力变形的能力。
8、流体运动时,如果相邻层流体的运动速度不同,在他们的界面上会产生切应力。
速度快的流层对速度慢的流层产生拖动力,速度慢的对速度快的流层产生阻力。
这个切应力叫做流体内摩擦力,或黏性切应力。
9、在流动的物体都会受到相对于空气运动的所受的逆物体运动方向或沿空气来流速度方向的气体动力的分力。
这个力叫做流动阻力。
在低于音速的情况下,流动阻力分为摩擦阻力和压差阻力。
在物体表面产生的全部摩擦力的合力成为摩擦阻力。
与物体面相垂直的气流压力合成的阻力称压差阻力。
10、古老的风能利用使用的风车、现在使用的风杯式测风仪是利用压差阻力进行工作的。
11、流体运动分为层流和湍流两种状态。
12、层流和湍流传递动量、热量和质量的方式不同:层流的传递过程通过分子间相互作用,湍流的传递过程主要通过质点间的混掺。
13、雷诺数在物理上的本质是表征了流体运动的惯性力与粘性力的比值。
14、流体边界层是流体高雷诺数流过壁面时,在紧贴壁面的粘性力不可忽略的流动薄层。
15、伯努利方程是流体的机械能量守恒方程。
汽车空气动力学课件 第二章

8. 现代SONATA御翔:没查到? 9. 丰田锐志:0.28 10.丰田普锐斯:0.26 11.新Mazda6:没查到? 12.三菱戈蓝:0.32 13.上汽荣威750:没查到?
30万以上热点车型
1. 丰田皇冠:0.27 2. 奥迪 A4 :0.28 3. 奥迪 A6L:0.30 4. 华晨宝马新3系:0.28 5. 华晨宝马5系:0.28 6. 奔驰 E级:0.26 7. 凯迪拉克CTS:0.31 8. 现代Azera(雅尊):0.29 9. Acura讴歌RL:0.29
不考虑空气动力学的卡车流场
分离流的扩展区
考虑空气动力学的卡车流场
分离流的区域变小
摩擦阻力
由于空气的粘性作用使得空气与汽车车身
表面产生摩擦而形成的阻力。约占汽车总 气动阻力的6%~11%。
与车身表面面积和粗糙度有关
宾利
诱导阻力
诱导阻力由车身附着涡诱导而成,实际上是汽 车升力在水平方向的分力。约占汽车总气动阻 力的8%~15%。
汽车正投影面积A的测量
汽车的正投影面积A应 包括车身、轮胎、发动 机及底盘等零部件的前 视投影。其测量方法是 将汽车置于平行光源与 屏幕之间,此时其正投 影面积便既不放大也不 缩小地投在屏幕上。
气动阻力
D
=
1 2
ρv∞2
ACD
D取决于正面投影面积A和气动阻力系数CD;通
常正面投影面积A取决于汽车的外形尺寸,这是由
绕y轴的纵倾力矩MP
绕z轴的横摆力矩MY
阻力系数
CD
=
1 2
D ρυ∞2
⋅
A
升力系数
CL
=
1 2
L ρυ∞2
⋅
A
侧向力系数
空气动力学第二章第一部分分解
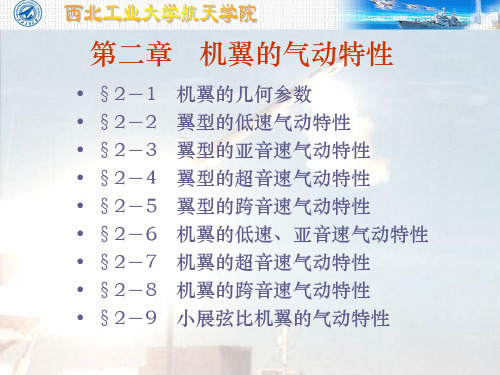
2.翼型的力矩特性
mz , L , E
1 4 Cy
1
4
( A2
A1)
mCy z
Cy
mz 0
mz , L, E
mz0
mCy y
n 1
2
( A0
A1 ) 2
升力和力矩特性(续)
mz
Mz qb2
1 qb2
b
P(x)xdx
0
mz
1 2
(
A0
A1
1 2
A2 )
Cy
2
( A0
A1 ) 2
1
mz 4 C y 4 ( A2 A1 )
A0
An
2
1 dy f (x) d 0 dx
dy f
(x)
cos n
d
0 dx
1.翼型的升力特性
x • y f (x)-弯度函数; f -最大弯度;
• b -翼弦
c -最大厚度位置
-最大弯度位置; f
•
-前缘内切圆半径; -后缘角
r l
翼面方程:
• 对于弯度、厚度不太大的翼型的形面是由弯度分布和厚度分布迭加 而成的,所以上下翼面的方程可写成 :
yu,l (x) y f (x) yc (x)
§2-1 机翼的几何参数
机翼的几何参数:翼型+平面形状 机翼的坐标系:
一、翼型的几何参数
• 翼型:平行于机翼纵向对称面的平面与机翼 相截所得到的外形。
①翼弦:
翼型前缘与后缘的连线。其长度叫弦长,用b表示。翼弦上部的机翼表面 为上翼面,翼弦下部机翼表面为下翼面。
②厚度特性:
• 厚度分布 yc (x) :上下翼面在垂直翼弦方向的距离叫翼型的厚度,
2-第2章-《风力发电空气动力学基本原理》

第二章一、填空:1、风的能量包括【机械能(动能、势能和压力能)】和【热能】。
2、黏性是流体的重要物理属性。
是流体【抵抗剪切变形】的能力。
3、在低于音速的情况下,流动阻力分为【摩擦阻力】和【压差阻力】。
4、流体运动分为【层流】和【湍流】两种状态。
5、层流和湍流传递【动量】、【热量】和【质量】的方式不同。
湍流的传递速率远大于层流传递速率。
6、雷诺数在物理上的本质是表征了流体运行的【惯性力】和【黏性力】的比值。
7、【轴向诱导因子】代表了风轮前来流速度和风轮处速度变化的比率。
8、风轮最多可以吸收59.3%的风的动能。
在风轮效率最高时,风轮后的速度是风轮前速度的【1/3】。
9、【切向诱导因子】的意义是气流切向旋转角速度与叶轮旋转角速度的比例。
10、【风轮的叶尖速比】是风轮的线速度与风轮上游来流速度的比值。
11、一维动量理论分析得到风轮的功率因数仅与【轴向诱导因子】有关;在考虑风轮尾流旋转后,影响功率因数的因素增加了【叶尖速比】;叶素-动量理论的结果中影响因素【气流迎角】,【叶尖速比】、【叶片数量】、【风轮实度】以及【叶片翼型的升力系数和阻力系数】。
12、所有以阻力原理作用的风力机的叶尖比都【小于1】,属于低叶尖速比风力机。
13、两叶片风电机组的尖速比在【9-10】之间,三叶片的风电机组尖速比在【6-8】之间。
14、风力发电机组实度大致在【5%-20%】。
15、通过对风轮的分析得到叶片的空气动力参数——【气流迎角】、【升力系数】、【阻力系数】等对风轮的效率有着重要影响。
16、只有当绕物体流动的气流中出现【环流】时才会产生升力。
17、边界层在翼型上的分离有薄翼分离(一般出现在相对厚度【小于6%】的薄翼型上)、前缘分离(一般出现在相对厚度【9%-12%】的翼型上)、后缘分离(一般出现在相对厚度【大于15%】的翼型上)、混合分离(是在翼型上同时发生前缘分离和后缘分离)。
18、当迎角超过一定数值时,通常为【10-16】度,翼面的边界层会在上翼面发生完全分离,翼型升力系数陡然下降。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
λ = λm = 5.5
u0 λ = = 5. 5 v1
u0 = 5.5 • v1 = 5.5 × 8 m s = 44 m s
u0 =
πDn
60
60u0 60 × 44 m s n= = = 300 r s πD 3.14 × 1.4m
nD = nm Dm
2
2
D2 nm = n • 2 = 500 r min × (4.7) 2 = 11045 r min Dm
D ∆ m1 = ≠ Dm ∆m
式中
∆ ——表面粗糙度。
然而,对于风力机来讲,表面粗糙度的相似与否影响 不大,所以一般情况下不考虑。
• 2.运动相似 2.运动相似 • 空气流经几何相似的模型与原型机时,其
对应点的速度方向相同、比值保持常数, 称为运动相似,即满足以下条件:
ω0 u0 v1 v2 v u = = = = = = mv v1m v m v 2 m ω 0 m u 0 m u m
叶片叶素: • 叶素理论的基本出发点是将风轮叶片沿展 向分成许多微段,称这些微段为叶素,如 前面所述,多个圆环,半径r,径向宽δr。 前面所述,多个圆环,半径r,径向宽δr。 在每个叶素上作用的气流相互之间没有干 扰,作用在叶片上的力可分解为升力和阻 力二维模型,作用在每个叶素单元的合成 流速与叶片平面的夹角为攻角。翼型特征 系数CL和CD随攻角的改变而改变。 系数CL和CD随攻角的改变而改变。
• 以下研究的是满足几何相似与运动相似的
惯性力以及黏性力是否也满足动力相似的 条件,以表示长度尺寸的量,由于加速度 的尺寸大小等同于:v 2 l • 根据理论力学能够得到惯性力:
dA = ma = ρv ldS l = ρv dS
2 2
• 根据牛顿内摩擦定律得到黏性力:
dv dF = µdS = µvdl dδ
0m
相对速度; u • u 0 ,0m ——叶尖气流的切向速度; ——叶尖气流的切向速度; u ——原型机和模型对应叶素上气流的 • u ,m ——原型机和模型对应叶素上气流的 切向速度。
上式表明了原型机和模型的叶尖速比 λ (风轮 外径圆周线速度与风轮前方气流速度的比)必须 相等。 模型和原型机空间对应点速度相似,则对 应叶素上对应点的速度三角形相似,对应的气 流倾角相等,对应叶素的安装角相等:
• 风力机的相似是指风轮与气体的能量传递
过程以及气体在风力机内流动过程相似, 它们在任一对应点的同名物理量之比保持 常数,这些常数叫相似常数(或比例常 数)。下面介绍一下风力机的相似条件以 及相似结果。
• 相似条件
• 根据相似理论,要保证气体流动过程相似,
必须满足几何相似、运动相似、动力相似。
• 1.几何相似 1.几何相似
φ = φm
θ = θm
• 冲角
是它们的差值( ),由于它们相等, φ −θ α 所以冲角也相等,所以对应的 CL 和 CD 也具有相 同的值。
• 动力相似
• 动力相似是指满足几何相似、运动相似的模型与
原型机上,作用于对应点力的方向相同、大小之 比保持常数。这里所讲的作用于气体的力除了因 压力分布形成的推理和切向力外,还包括惯性力 以及黏性力。
• 几何相似是指模型(以下用m代表)与原型 几何相似是指模型(以下用m
风力机的几何形状相同,对应的线性长度 为一定值
式中
Dh
——风轮轮毂直径。
• 理论上说,还应保证叶片表面的相对粗糙
度相似。相对粗糙度会影响流动损失的大 小,但是由于加工条件的限制,在尺寸小 的情况下粗糙度成比例缩小是难以保证的, 即要保证以下公式:
Pm P = ρv 3 D 2 ρ m v m 3 Dm 2
风轮的效率得:
MωTm v m Dωv m u 0 v1 η λ = = = = η m M mω mTv Dmω m v u 0 m v1m λm
• 上式表明,具有相同尖速比的相似模型和原型机,它们的
效率也对应相等,利用这一结论,可以从风洞试验中由试 验机的性能推断出原型机的效率。 由于风轮前方的速度不受外界干扰
1 பைடு நூலகம் 2
• 作用在叶素上轴向合力
dT = d FL cos φ + dF D sin φ
• 作用在叶素上引起转矩的合力
d FL sin φ − dF D cos φ
• 作用在叶素上的合力引起的转矩
dM = (dFL sin φ − dFD cos φ )r
• 叶素获得的有用功 dP = ω ⋅ dM • 风提供给叶素的功率为
翼型选取NACA4415,叶片数 尖速比
z =3
λ = 5.5
1m × 1m
试验风洞的大小为
• 根据几何相似,由已知条件得
m= D 1.4m = = 4.7 Dm 0.3m
v1 =m v1m
v1m = v1 • m = 8 m s × 4.7 = 37.6 m s
u0 v1 λ = =1 λm u0 m vm
ρv 2 D 2 ρ m v m 2 Dm 2
dM = dM m ×
ρv 2 rdS ρ m v m rm dS m
= dTm ×
dP = dPm ×
ρv 3 dS ρ m v m Dm
3 3
= dPm ×
ρv 3 D 2 ρ m v m 3 Dm 2
由于风轮的总推力、总功率以及总力矩分别是由它们各自 叶片的推力、功率和力矩相加所得,因此可以推出下列的 公式:
Pm P = 3 2 ρv D ρ m v m 3 Dm 2
Re ——雷诺数, ——雷诺数, 它表示作用于流 体上的惯性力与 黏性力之比; ——流体的运 ν ——流体的运 动黏度。
ν
=
lm vm
νm
= Re m
• 相似模型与原型机的雷诺数定性尺寸用它的直径,
速度以风轮前风速代表时,上式可以写成如下的 形式:
Re = v1 D
ν
=
v1m Dm
νm
= Re m
1 2 T = ρC T Sv1 2
1 2 M = ρC M RSv1 2
1 3 P = ρC P Sv1 2
30λv1 n= πR
• 计算例题
已知实际风力机的风轮直径为
D =1.4
m
P = 100w
选取模型的风轮直径为
,
n = 500 r min Dm = 0.3 m
实际风速
v1 = 8 m s
u
dP = V ⋅ dT
• 叶素的理论空气动力效率
dPu u (C L sin φ − C D cos φ ) η= = dP V (C L cos φ + C D sin φ )
• 升阻比
k=
CL CD
化简上式得
dPu 1 - 1 cot φ ) η= = k1 dP 1 + k tan φ
由上式可见翼型的升阻比k增大,空气动力效率增大 极限情况,阻力为0,k无穷大,空气动力效率为1 实际上,k的值取决与翼型的攻角α,参照前面介绍 的埃菲尔极线,要取得最大空气动力效率则攻角α应 该取升阻比最大的点对应的攻角α。
• 式中 v1 ——风力机、模型的前方风速; • v1 ,m ——风力机、模型的前方风速; v ——通过风轮时的气流速度; • v , m ——通过风轮时的气流速度; v ——风轮后方的气流速度; •v2 ,2m ——风轮后方的气流速度; ω ω 0 , ——原型机和模型对应叶素上气流的 • ——原型机和模型对应叶素上气流的
nD 2 = nm Dm
2
4.相似结果
因为风力机相似,所以它们对应叶素上的
θ α φ Cl Cd
的值都相等,那么由此可以知道,对于模型和原型机上 面所对应的叶素,它们满足下列关系式:
、
dT = dTm ×
ρv 2 dS ρ m v m dS m
2
2
= dTm
ρv 2 D 2 ρ m v m 2 Dm 2
'
式中
µ ——流体的动力黏度;
δ
dS '
——内摩擦力的面积; ——摩擦层的厚度; ——速度梯度。
dv dδ
• 假如模型与原型机的惯性力和黏性力相似,那么
可以得出以下结论:
dA dF = dAm dFm
• 由上式变换可以得到: • 即:
ρlv ρ m l m v m = µ µm
Re = lv
• 式中
由分析知道,雷诺数相等的条件在大型机模化 为实验风洞中的相似模型时,一般情况下是很 难实现的,实际上在风洞里的模型试验是在普 通大气压力和环境下进行的,因此模型和原型 机的运动黏度是相同的,即满足 ν = ν m ,因 此可以推出以下的结论:V1D = V1m Dm
uD = u m Dm
因为 u = πDn 60 ,所以上式可以写成:
• 风轮的推力、力矩、功率、效率 • N叶素数目 z叶片数 M总力矩
P = z ∑ VdT i = TV
1 N
Pu = z ∑ ω dM i = M ω
1
N
总推力T最终作用在塔架上
相似理论
• 相似理论主要应用于风力机的相似设计及
性能的换算。所谓的相似设计,即根据试 验研究出来 的性能良好、运行可靠的模型 来设计与模型相似的风力机。性能的相似 换算是用于试验条件不同于设计的现场条 件时,将试验条件下的性能利用相似原理 换算到设计条件下的性能。
• 叶素安装角
:在半径r :在半径r处翼型剖面的弦线 与叶轮旋转平面的夹角
θ
• 从图3.3可以看出,作用在叶素上的合成流速为: 从图3.3可以看出,作用在叶素上的合成流速为:
2π n ω= 60
W = V 2 + ω 2r 2
