概率模拟题(高考试题)
高考数学模拟复习试卷试题模拟卷第01节 随机事件的概率 2

高考模拟复习试卷试题模拟卷第01节 随机事件的概率A 基础巩固训练1.(·江西南昌检测)从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是()A .“至少有1个白球”和“都是红球”B .“至少有1个白球”和“至多有1个红球”C .“恰有1个白球”和“恰有2个白球”D .“至多有1个白球”和“都是红球”[答案]C[解析] 该试验有三种结果:“恰有1个白球”“恰有2个白球”“没有白球”,故“恰有1个白球”和“恰有2个白球”是互斥事件且不是对立事件.2.(文)(·滨州模拟)在区间[0,1]上任取两个数a ,b ,则函数f(x)=x2+ax +b2无零点的概率为( )A .12B .23C .34D .14[答案] C3. 甲、乙两人喊拳,每人可以用手出0,5,10三个数字,每人则可喊0,5,10,15,20五个数字,当两人所出数字之和等于某人所喊数字时喊该数字者获胜,若甲喊10,乙喊15时,则 ()A .甲胜的概率大B .乙胜的概率大C .甲、乙胜的概率一样大D .不能确定谁获胜的概率大【答案】A4.(·赤峰模拟)先后抛掷硬币三次,则至少一次正面朝上的概率是( ) A.18B.38C.58D.78【答案】D【解析】至少一次正面朝上的对立事件的概率为18,故P =1-18=78. 5.在一次随机试验中,彼此互斥的事件A ,B ,C ,D 的概率分别为0.2,0.2,0.3,0.3,则下列说法正确的是()A .A ∪B 与C 是互斥事件,也是对立事件 B .B ∪C 与D 是互斥事件,也是对立事件C .A ∪C 与B ∪D 是互斥事件,但不是对立事件 D .A 与B ∪C ∪D 是互斥事件,也是对立事件【答案】DB 能力提升训练1.(·济南调研)现釆用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出 0到9之间取整数值的随机数,指定0、1表示没有击中目标,2、3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:7527 0293 7140 9857 0347 4373 8636 6947 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )A . 0.852B . 0.8192C .0.8D . 0.75[答案] D[解析] 随机模拟产生的20组随机数,表示至少击中3次的组数为15,所以概率为P =1520=0.75. 2.从1,2,3,4,5中随机抽三个不同的数,则其和为奇数的概率为( )A.15B.25C.35D.45【答案】B3. (·浙江台州中学统练)甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a ,再由乙猜甲刚才所想的数字,把乙猜的数字记为b ,其中a 、b ∈{0,1,2,3,4,5},若|a -b|≤1,则称甲乙“心相近”.现任意找两人玩这个游戏,则他们“心相近”的概率为( )A .29B .718C .49D .19[答案] C4. (威海市高三3月模拟考试)从集合{2,3,4,5}中随机抽取一个数a ,从集合{1,3,5}中随机抽取一个数b ,则向量(,)m a b =与向量(1,1)n =-垂直的概率为(A )16(B )13(C )14(D )12【答案】A【解析】由题意可知(,)m a b =有:(2,1),(2,3),(2,5),(3,1),(3,3),(3,5),(4,1),(4,3),(4,5),(5,1),(5,3),(5,5).共12个.m n ⊥即0,m n ⋅=所以1(1)0,a b ⨯+⨯-=即a b =,有(3,3),(5,5)共2个满足条件.故所求概率为16. 5. 从一个三棱柱ABC -A1B1C1的六个顶点中任取四点,这四点不共面的概率是( ) A .15 B .25C .35D .45 [答案] D[解析] 从6个顶点中选4个,共有15种选法,其中共面的情况有三个侧面,∴概率P =15-315=45.C 思维扩展训练1.(·安庆一模)将一颗骰子投掷两次,第一次出现的点数记为a ,第二次出现的点数记为b ,设两条直线l1:ax +by =2与l2:x +2y =2平行的概率为P1,相交的概率为P2,则点P(36P1,36P2)与圆C :x2+y2=1 098的位置关系是()A .点P 在圆C 上B .点P 在圆C 外 C .点P 在圆C 内D .不能确定【答案】C2. 设集合A ={1,2},B ={1,2,3},分别从集合A 和B 中随机取一个数a 和b ,确定平面上的一个点P(a ,b),记“点P(a ,b)落在直线x +y =n 上”为事件Cn(2≤n ≤5,n ∈N),若事件Cn 的概率最大,则n 的所有可能值为()A .3B .4C .2和5D .3和4【答案】D【解析】P(a ,b)的个数为6个.落在直线x +y =2上的概率P(C2)=16,若在直线x +y =3上的概率P(C3)=26,落在直线x +y =4上的概率P(C4)=26,落在直线x +y =5上的概率P(C5)=16. 3. 某学校成立了数学、英语、音乐3个课外兴趣小组,3个小组分别有39、32、33个成员,一些成员参加了不止一个小组,具体情况如图所示.现随机选取一个成员,他属于至少2个小组的概率是________,他属于不超过2个小组的概率是________. 【答案】3513154. 已知某台纺纱机在1小时内发生0次、1次、2次断头的概率分别是0.8、0.12、0.05,则这台纺纱机在1小时内断头不超过两次的概率和断头超过两次的概率分别为__________,________.【答案】0.970.03【解析】断头不超过两次的概率P1=0.8+0.12+0.05=0.97.于是,断头超过两次的概率P2=1-P1=1-0.97=0.03.5. 【雅安中学高三下期3月月考数学】(本小题满分12分)某产品的三个质量指标分别为x, y, z, 用综合指标S = x + y + z 评价该产品的等级. 若S≤4, 则该产品为一等品. 先从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下: 产品编号A1 A2 A3 A4 A5 质量指标(x, y, z)(1,1,2) (2,1,1) (2,2,2) (1,1,1) (1,2,1) 产品编号A6 A7 A8 A9 A10 质量指标(x, y, z) (1,2,2) (2,1,1) (2,2,1) (1,1,1) (2,1,2)(Ⅰ) (Ⅱ) 在该样品的一等品中, 随机抽取两件产品,(1) 用产品编号列出所有可能的结果;(2) 设事件B 为 “在取出的2件产品中, 每件产品的综合指标S 都等于4”, 求事件B 发生的概率高考模拟复习试卷试题模拟卷第03节 二项式定理一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选择中,只有一个是符合题目要求的.)1.【“五个一名校联盟” 高三教学质量监测(一)5】在154)212(+x 的展开式中,系数是有理数的项共有 ( )A.4项B.5项C.6项D.7项2.【宝鸡市高三数学质量检测(一)】若)21(3x x n -的展开式中第四项为常数项,则=n ( ) A . 4 B. 5 C. 6 D. 73.【改编题】6(1)(1)x x +-展开式中3x 项系数为( )A.14 B .15 C .16 D .174.【金丽衢十二校高三第二次联考】二项式2111()x x -的展开式中,系数最大的项为( )A.第五项B.第六项C.第七项D.第六和第七项 5.【江西赣州市六校高三上学期期末联考】已知8a x x ⎛⎫- ⎪⎝⎭展开式中常数项为5670,其中a 是常数,则展开式中各项系数的和是( )A .28B .48C .28或48D .1或286.【高考陕西,理4】二项式(1)()n x n N ++∈的展开式中2x 的系数为15,则n =( ) A .4 B .5 C .6 D .77.【高考新课标1,理10】25()x x y ++的展开式中,52x y 的系数为( )(A )10 (B )20 (C )30(D )608.【高考湖北,理3】已知(1)n x +的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式 系数和为()A.122 B .112 C .102 D .92 9.【咸阳市高考模拟考试试题(三)】若n x x )2(3+展开式中存在常数项,则n 的值可以是( )A .8B .9C .10D .1210.【潍坊市高三3月模拟考试】设0(sin cos )k x x dx π=-⎰,若8280128(1)...kx a a x a x a x -=++++,则1238...a a a a ++++=( )(A) 1 (B)0 (C)l (D)256 11.【浙江高考第5题】在46)1()1(y x ++的展开式中,记nm y x 项的系数为),(n m f ,则=+++)3,0(2,1()1,2()0,3(f f f f ) ( )A.45B.60C.120D. 21012.【原创题】210(1)x x -+展开式中3x 项的系数为( ).A.210 B .120 C .90 D .210二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.)13.【大纲高考第13题】8x y y x ⎛⎫- ⎪ ⎪⎝⎭的展开式中22x y 的系数为. 14.【改编题】对任意实数x ,有423401234(1)(3)(3)(3)(3)x a a x a x a x a a -=+-+-+-+-,则3a 的值为.15.【高考四川,理11】在5(21)x -的展开式中,含2x 的项的系数是(用数字作答).16.【高考新课标2,理15】4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32,则a =__________.三、解答题 (本大题共4小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知在332n x x ⎛- ⎪⎭的展开式中,第6项为常数项. (1)求n ;(2)求含x2的项的系数;(3)求展开式中所有的有理项.18.已知223)n x x 的展开式的二项式系数和比(31)n x -的展开式的二项式系数和大992.求在212nx x ⎛⎫- ⎪⎝⎭的展开式中, (1)二项式系数最大的项;(2)系数的绝对值最大的项.19.设(1-2x)2 013=a0+a1x +a2x2+…+a2 013x2 013 (x ∈R).(1)求a0+a1+a2+…+a2 013的值;(2)求a1+a3+a5+…+a2 013的值;(3)求|a0|+|a1|+|a2|+…+|a2 013|的值.20.【第二次大联考数学江苏版】对于给定的函数()f x ,定义()n f x 如下:()0()C (1)n k k n k n n k k f x f x x n -==-∑,其中2n n ∈*N ≥,. (1)当()1f x =时,求证:()1n f x =;(2)当()f x x =时,比较2014(2013)f 与2013(2014)f 的大小;(3)当2()f x x =时,求()n f x 的不为0的零点.高考模拟复习试卷试题模拟卷第八章 直线与圆一.基础题组1.(重庆市巴蜀中学高三月考数学、文、1)若直线210ax y ++=与直线20x y +-=互相垂直,那么a 的值等于( )A .1B .13-C .23-D .2- 2.(文昌中学高三模拟考试、文、15)圆心在直线x -2y =0上的圆C 与y 轴的正半轴相切,圆C 截x 轴所得弦的长为23,则圆C 的标准方程为________________.3.(重庆市巴蜀中学高三月考数学、文、15)在平面直角坐标系xOy 中,以点)0,1(为圆心且与直线)(012R m m y mx ∈=---相切的所有圆中,半径最大的圆的标准方程为.4.(重庆市部分区县高三上学期入学考试、文、16)若实数c b a ,,成等差数列,点)0,1(-P 在动直线0:==+c by ax l 上的射影为M ,点)3,0(N ,则线段MN 长度的最小值是.二.能力题组1.(五校协作体高三上学期期初考试数学、文、9)曲线21y x =+在点(1,2)处的切线为l ,则直线l 上的任意点P 与圆22430x y x +++=上的任意点Q 之间的最近距离是( )A.4515-B.2515- C.51- D.2 2.(示范高中高三第一次联考、文、14)已知圆的方程为()2214x y +-=。
高考概率大题及答案

高考概率大题及答案【篇一:2015年高考数学概率与统计试题汇编】4.为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:??a??0.76,a? ,据此估计,??bx? ,其中b???根据上表可得回归直线方程y该社区一户收入为15万元家庭年支出为( )a.11.4万元 b.11.8万元c.12.0万元 d.12.2万元【答案】b考点:线性回归方程.13.如图,点a 的坐标为?1,0? ,点c 的坐标为?2,4? ,函数f?x??x2 ,若在矩形abcd 内随机取一点,则此点取自阴影部分的概率等于.【答案】5 12【解析】试题分析:由已知得阴影部分面积为4??x2dx?4?1275?.所以此点取自阴影3355部分的概率等于?. 412考点:几何概型.16.某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定,小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定. (Ⅰ)求当天小王的该银行卡被锁定的概率;(Ⅱ)设当天小王用该银行卡尝试密码次数为x,求x的分布列和数学期望.15【答案】(Ⅰ);(Ⅱ)分布列见解析,期望为. 22【解析】试题分析:(Ⅰ)首先记事件“当天小王的该银行卡被锁定”的事件为a.则银行3卡被锁死相当于三次尝试密码都错,基本事件总数为a6?6?5?4,事件a包含3的基本事件数为a5?5?4?3,代入古典概型的概率计算公式求解;(Ⅱ)列出随机变量x的所有可能取值,分别求取相应值的概率,写出分布列求期望即可.试题解析:(Ⅰ)设“当天小王的该银行卡被锁定”的事件为a,5431= 则p(a)=6542(Ⅱ)依题意得,x所有可能的取值是1,2,3151又p(x=1)=,p(x=2)=?6651542,p(x=3)=1=. 6653所以x的分布列为所以e(x)=1?1122?3?6635. 2考点:1、古典概型;2、离散型随机变量的分布列和期望.2015江苏理科5.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为________. 【答案】5. 6考点:古典概型概率2015年重庆理科17.(本小题满分13分,(1)小问5分,(2)小问8分)端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同,从中任意选取3个。
2025年新高考数学模拟试题二带解析

2025年新高考数学模拟试题(卷二)第I 卷(选择题)一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的。
1.已知集合{}2{Z14},40A x x B x x x =∈-≤<=-≤∣∣,则A B = ()A .{}1,2,3,4B .{}1,2,3C .{}0,1,2,3D .()0,42.已知复数z =z 的共轭复数为()A .22i-B .22i+C .11i44-+D .11i44--3.沙漏是我国古代的一种计时工具,是用两个完全相同的圆锥顶对顶叠放在一起组成的(如图).在一个圆锥中装满沙子,放在上方,沙子就从顶点处漏到另一个圆锥中,假定沙子漏下来的速度是恒定的.已知一个沙漏中沙子全部从一个圆锥中漏到另一个圆锥中需用时1小时.当上方圆锥中沙子的高度漏至一半时,所需时间为()A .12小时B .78小时C .34小时D .23小时4.若π13πtan sin123α⎛⎫-= ⎪⎝⎭,则πtan 4α⎛⎫-= ⎪⎝⎭()A B .5-C .9D .55.二项式210(1)(1)x x x ++-展开式中4x 的系数为()A .120B .135C .140D .1006.已知函数13x y m-=+(0m >且1m ≠)图像恒过的定点A 在直线()10,0x ya b a b+=>>上,若关于t 的不等式253a b t t +≥++恒成立,则实数t 的取值范围为()A .[]6,1-B .[]1,6-C .(][),16,-∞-⋃+∞D .(][),61,-∞-⋃+∞7.已知F 是双曲线E :()222210,0x y a b a b-=>>的右焦点,O 为坐标原点,A 是E 的右支上一点,若=AF a ,OA b =,则E 的离心率为()A .2B .2C D 8.设函数()f x 在R 上的导函数为()f x ',()()0f x f x +-=,对任意,()0x ∈+∞,都有()()f x f x x '>,且()12f =,则不等式22[(1)]24f x x x -<-+的解集为()A .(,0)(2,)-∞+∞ B .()0,2C .()1,3D .(,1)(3,)-∞+∞ 二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.函数()()2sin 2(0)f x x ωϕω=+>,以下正确的是()A .若()f x 的最小正周期为π,则2ω=B .若()()124f x f x -=,且12minπ2x x -=,则1ω=C .当0,N ϕω=∈时,()f x 在ππ,55⎡⎤-⎢⎥⎣⎦单调且在ππ,33⎡⎤-⎢⎥⎣⎦不单调,则1ω=.D .当π12ϕ=时,若对任意的x 有()π3f x f ⎛⎫≤ ⎪⎝⎭成立,则ω的最小值为5810.在棱长为2的正方体1111ABCD A B C D -中,点M ,N ,P 分别是线段11C D ,线段1C C ,线段1A B 上的动点,且110MC NC =≠.则下列说法正确的有()A .1⊥MN AB B .直线MN 与AP 所成的最大角为90°C .三棱锥1N D DP -的体积为定值D .当四棱锥11P D DBB -体积最大时,该四棱锥的外接球表面积为9π11.已知圆22:(1)(1)4M x y +++=,直线:20+-=l x y ,P 为直线l 上的动点,过P 点作圆M 的切线PA ,PB ,切点为A ,B ,则下列说法正确的是()A .四边形MAPB 面积的最小值为4B .线段AB 的最小值为C .当直线AB 的方程为0x y +=时,APB ∠最小D .若动直线1//l l ,1l 且交圆M 于C 、D 两点,且弦长CD ∈,则直线1l 横截距的取值范围为2,0)(4,2)⋃-第II 卷(非选择题)三、填空题:本题共3小题,每小题5分,共15分.12.盲盒,是指消费者不能提前得知具体产品款式的玩具盒子.已知某盲盒产品共有3种玩偶,小明共购买了5个盲盒,则他恰能在第5次集齐3种玩偶的概率为__________.13.过点()1,P a 作曲线ln y x x =的切线,若切线有且只有两条,则实数a 的取值范围是___________.14.已知函数()f x 定义域为(0,)+∞,(1)e f =,对任意的12,(0,)x x ∈+∞,当21x x >时,有()()21121212e e x xf x f x x x x x ->-(e 是自然对数的底).若(ln )2e ln f a a a >-,则实数a 的取值范围是______.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)已知数列{}n a 中,11a =,前n 项和23n n n S a +=.(1)求2a ,3a ,及{}n a 的通项公式;(2)证明:12311112na a a a ++++< .16.(15分)某加盟连锁店总部对旗下600个加盟店中每个店的日销售额(单位:百元)进行了调查,如图是随机抽取的50个加盟店的日销售额的频率分布直方图.若将日销售额在(]16,18的加盟店评定为“四星级”加盟店,日销售额在(]18,20的加盟店评定为“五星级”加盟店.(1)根据上述调查结果,估计这50个加盟店日销售额的平均数和中位数(同一组中的数据用该组区间的中点值为代表,结果精确到0.1);(2)若该加盟连锁店总部旗下所有加盟店的日销售额(),6.25X N μ ,其中μ近似为(1)中的样本平均数,根据X 的分布估计这600个加盟店中“五星级”加盟店的个数(结果精确到整数);(3)该加盟连锁店总部决定对样本中“四星级”及“五星级”加盟店进一步调研,现从这些加盟店中随机抽取3个,设Y 为抽取的“五星级"加盟店的个数,求Y 的概率分布列与数学期望.参考数据:若()2,X N μσ ,则()0.6827P X μσμσ-≤≤+≈,()220.9545P X μσμσ-≤≤+≈,()330.9973P X μσμσ-≤≤+≈.17.(15分)如图,直三棱柱111ABC A B C -的体积为12,A BC 的面积为2(1)求点1C 到平面1A BC 的距离;(2)设D 为1AC 的中点,1AAAB =,平面1A BC ⊥平面11A B BA ,求二面角A BD C --的正切值.18.(17分)已知椭圆()2222:10x y C a b a b+=>>,过C 的右焦点F 且垂直于长轴的弦AB 的长为1,焦点F 与短轴两端点构成等边三角形.(1)求椭圆C 的方程;(2)过点()P的直线l 与椭圆C 交于M ,N 两点,点E 在x 轴上且对任意直线l ,直线OE 都平分MEN ∠(O 为坐标原点).①求点E 的坐标;②求EMN 的面积的最大值.19.(17分)已知函数()e 1xf x x =-.(1)若直线e 1=--y kx 与曲线()y f x =相切,求k 的值;(2)若()0,x ∀∈+∞,()ln f x x ax >-,求a 的取值范围.2025年新高考数学模拟试题(卷二)(解析版)第I 卷(选择题)一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的。
高考数学《概率》综合复习练习题(含答案)
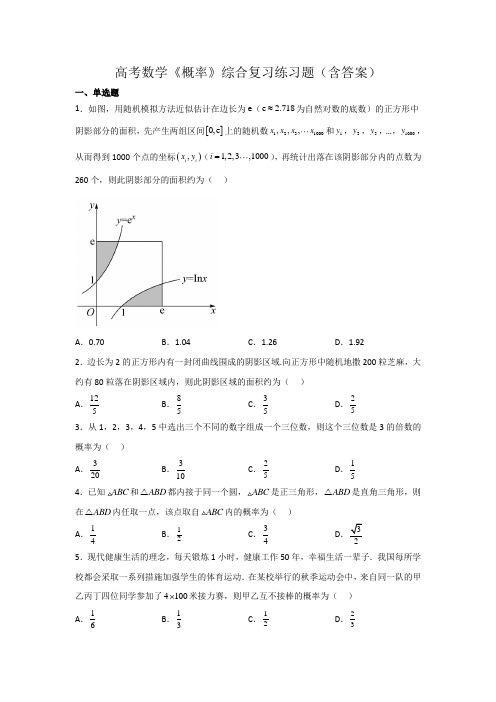
高考数学《概率》综合复习练习题(含答案)一、单选题1.如图,用随机模拟方法近似估计在边长为e (e 2.718≈为自然对数的底数)的正方形中阴影部分的面积,先产生两组区间[]0,e 上的随机数1231000,,,x x x x 和1y ,2y ,3y ,…,1000y ,从而得到1000个点的坐标(),i i x y (1,2,3,1000i =),再统计出落在该阴影部分内的点数为260个,则此阴影部分的面积约为( )A .0.70B .1.04C .1.26D .1.922.边长为2的正方形内有一封闭曲线围成的阴影区域.向正方形中随机地撒200粒芝麻,大约有80粒落在阴影区域内,则此阴影区域的面积约为( ) A .125 B .85C .35D .253.从1,2,3,4,5中选出三个不同的数字组成一个三位数,则这个三位数是3的倍数的概率为( ) A .320B .310 C .25D .154.已知ABC 和ABD △都内接于同一个圆,ABC 是正三角形,ABD △是直角三角形,则在ABD △内任取一点,该点取自ABC 内的概率为( )A .14B .12C .34D 35.现代健康生活的理念,每天锻炼1小时,健康工作50年,幸福生活一辈子.我国每所学校都会采取一系列措施加强学生的体育运动.在某校举行的秋季运动会中,来自同一队的甲乙丙丁四位同学参加了4100⨯米接力赛,则甲乙互不接棒的概率为( ) A .16B .13C .12D .236.某校对高一新生进行体能测试(满分100分),高一(1)班有40名同学成绩恰在[]60,90内,绘成频率分布直方图(如图所示),从[)60,70中任抽2人的测试成绩,恰有一人的成绩在[)60,65内的概率是()A.715B.815C.23D.137.我国拥有包括民俗、医药、文学、音乐等国家级非物质文化遗产3000多项,下图为民俗非遗数进前10名省份排名,现从这10个省份中任取2个,则这2个省份民俗非遗数量相差不超过1个的概率为()A.215B.15C.415D.258.观察下面数阵,则该数阵中第9行,从左往右数的第20个数是( ) A .545B .547C .549D .5519.在各不相同的10个球中有6个红球和4个白球,不放回地依次摸出两个球,第一次摸出红球的条件下,第二次也摸出红球的概率为 A .110 B .13C .25D .5910.有5把外形一样的钥匙,其中3把能开锁,2把不能开锁,现准备通过一一试开将其区分出来,每次随机抽出一把进行试开,试开后不放回,则恰好试开3次就将能开锁的和不能开锁的钥匙区分出来的概率是( )A .35B .310 C .45D .2511.从0,1,2,3这四个数中任取两个不同的数组成一个两位数,则这个两位数是偶数的概率为 A .27B .57C .29D .5912.关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请200名同学,每人随机写下一个都小于1的正实数对(),x y ,再统计x 、y 两数能与1构成钝角三角形时的数对(),x y 的个数m ,最后再根据m 来估计π的值.假如统计结果是60m =,那么π≈( )A .165 B .65C .7825D .14245二、填空题13.已知某人同时抛掷了两枚质地均匀的正方体骰子,记“两枚骰子的点数之和是6的倍数”为事件A ,则()P A =______________.14.如图,连接△ABC 的各边中点得到一个新的111A B C △,又连接111A B C △的各边中点得到222A B C △,如此无限继续下去,得到一系列三角形:ABC ,111A B C △,222A B C △,…,这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是______.15.某校有高一、高二、高三、三个年级,其人数之比为2:2:1,现用分层抽样的方法从总体中抽取一个容量为10的样本,现从所抽取样本中选两人做问卷调查,至少有一个是高一学生的概率为___________.16.一张储蓄卡的密码共有6位数字,每位数字都可以从0~9中任选一个,某人在银行自动提款机上取钱时,忘记了密码的最后一位,如果他记得密码的最后一位是奇数,则他不超过两次就按对密码的概率是________.三、解答题17.在第29届“希望杯”全国数学邀请赛培训活动中,甲、乙两名学生的6次培训成绩(单位:分)如茎叶图所示.(1)若从甲、乙两名学生中选择一人参加第29届“希望杯”全国数学邀请赛,你会选择哪一位?说明理由;(2)从甲的6次成绩中随机抽取2次,试求抽到119分的概率.18.甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8,甲、乙都中靶的概率为0.72,求下列事件的概率; (1)乙中靶; (2)恰有一人中靶; (3)至少有一人中靶.19.从0,1,2,3,4,5,6,7,8,9这10个自然数中,任取3个不同的数. (1)这3个数组成一个三位数,求这个三位数能够被5整除的概率; (2)设X 为所取的3个数中奇数的个数,求X 的可能取值及相应的概率.20.在全国防控疫情阻击战关键阶段,校文艺团排练了4个演唱节目,2个舞蹈节目参加社区慰问演出.(结果用数字作答)(1)若从6个节目中选3个参加市演出汇报,求3个节目中恰有1个舞蹈节目的选法种数; (2)现对6个节目安排演出顺序,求4个演唱节目接在一起的概率;(3)现对6个节目安排演出顺序,求节目甲不在第一个且不在最后一个演出的概率.21.为了调查某地区高中女生的日均消费情况,研究人员随机抽取了该地区5000名高中女生作出调查,所得数据统计如下图所示.(1)求a 的值以及这5000名高中女生的日均消费的平均数(同一组数据用该组区间的中间值代替);(2)在样本中,现按照分层抽样的方法从该地区消费在[)15,20与[)20,25的高中女生中随机抽取9人,若再从9人中随机抽取3人,记这3人中消费在[)15,20的人数为X ,求X 的分布列以及数学期望.22.为了研究性格和血型的关系,随机抽查了100个人的血型和性格,其情况如下表:(1)根据上面的22⨯列联表,判断是否有95%的把握认为性格与血型有关?(2)在“内向型”性格的人中,用分层抽样的方法抽取5人.若从5人中抽取3人进一步分析性格和血型的关系,求恰好抽到两名“O型或A型”人的概率.附表:其中22()()()()()n ad bcKa b c d a c b d-=++++,n a b c d=+++23.某科研机构为了研究喝酒与糖尿病是否有关,对该市30名成年男性进行了问卷调查,并得到了如下列联表,规定“”平均每天喝100mL以上的”为常喝.已知在所有的30人中随机抽取1人,患糖尿病的概率为4 .(1)请将上表补充完整,并判断是否有99.5%的把握认为糖尿病与喝酒有关?请说明理由;(2)已知常喝酒且有糖尿病的6人中恰有两名老年人,其余为中年人,现从常喝酒且有糖尿病的这6人中随机抽取2人,求恰好抽到一名老年人和一名中年人的概率.参考公式及数据:()()()()()22n ad bcKa b c d a c b d-=++++,n a b c d=+++.24.A,B,C三个班共有180名学生,为调查他们的上网情况,通过分层抽样获得了部分学生一周的上网时长,数据如下表(单位:小时):(Ⅰ)试估计B班的学生人数;(Ⅱ)从这180名学生中任选1名学生,估计这名学生一周上网时长超过15小时的概率; (Ⅲ)从A班抽出的6名学生中随机选取2人,从C班抽出的7名学生中随机选取1人,求这3人中恰有2人一周上网时长超过15小时的概率。
专题17 概率-2023年高考数学真题题源解密(新高考)(解析版)

专题17 概率目录一览2023真题展现考向一概率考向二离散型随机变量及其分布列真题考查解读近年真题对比考向一概率考向二离散型随机变量及其分布列考向三正太分布命题规律解密名校模拟探源易错易混速记/二级结论速记考向一概率1.(多选)(2023•新高考Ⅱ•第12题)在信道内传输0,1信号,信号的传输相互独立.发送0时,收到1的概率为α(0<α<1),收到0的概率为1﹣α;发送1时,收到0的概率为β(0<β<1),收到1的概率为1﹣β.考虑两种传输方案:单次传输和三次传输.单次传输是指每个信号只发送1次,三次传输是指每个信号重复发送3次.收到的信号需要译码,译码规则如下:单次传输时,收到的信号即为译码;三次传输时,收到的信号中出现次数多的即为译码(例如,若依次收到1,0,1,则译码为1)( )A.采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为(1﹣α)(1﹣β)2B.采用三次传输方案,若发送1,则依次收到1,0,1的概率为β(1﹣β)2C.采用三次传输方案,若发送1,则译码为1的概率为β(1﹣β)2+(1﹣β)3D.当0<α<0.5时,若发送0,则采用三次传输方案译码为0的概率大于采用单次传输方案译码为0的概率【答案】ABD解:采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为:(1﹣β)(1﹣α)(1﹣β)=(1﹣α)(1﹣β)2,故A正确;采用三次传输方案,若发送1,依次收到1,0,1的概率为:(1﹣β)β(1﹣β)=β(1﹣β)2,故B正确;采用三次传输方案,若发送1,则译码为1包含收到的信号为包含两个1或3个1,故所求概率为:C23β(2−β)2+(1−β)3,故C错误;三次传输方案发送0,译码为0的概率P1=C23α(1−α)2+(1−α)3,单次传输发送0译码为0的概率P2=1﹣α,P2−P1=(1−α)−C23α(1−α)2−(1﹣α)3=(1−α)[1−C23α(1−α)−(1−α)2]=(1﹣α)(2α2﹣α)=(1﹣α)α(2α﹣1),当0<α<0.5时,P2﹣P1<0,故P2<P1,故D正确.考向二离散型随机变量及其分布列2.(2023•新高考Ⅰ•第21题)甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若未命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8.由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5.(1)求第2次投篮的人是乙的概率;(2)求第i次投篮的人是甲的概率;(3)已知:若随机变量X i服从两点分布,且P(X i=1)=1﹣P(X i=0)=q i,i=1,2,⋯,n,则E(ni=1X i)=ni=1q i.记前n次(即从第1次到第n次投篮)中甲投篮的次数为Y,求E(Y).【解答】解:(1)设第2次投篮的人是乙的概率为P,由题意得P=0.5×0.4+0.5×0.8=0.6;(2)由题意设P n为第n次投篮的是甲,则P n+1=0.6P n+0.2(1﹣P n)=0.4P n+0.2,∴P n+1−13=0.4(P n−13),又P1−13=12−13=16≠0,则{P n−13}是首项为16,公比为0.4的等比数列,∴P n−13=16×(25)n﹣1,即P n=13+16×(25)n﹣1,∴第i次投篮的人是甲的概率为P i=13+16×(25)i﹣1;(3)由(2)得P i=13+16×(25)i﹣1,由题意得甲第i次投篮次数Y i服从两点分布,且P(Y i=1)=1﹣P(Y i=0)=P i,∴E(ni=1Y i)=E(Y)=ni=1P i,∴当n≥1时,E(Y)=ni=1P i=1(25)i−1+n3=16[1−(25)n]1−25+n3=518[1﹣(25)n]+n3;当n =0时,E (Y )=0=518[1﹣(25)0]+03,综上所述,E (Y )=518[1﹣(25)n ]+n3,n ∈N .【命题意图】概率、随机变量的分布列与数学期望.【考查要点】概率多为小题。
高考真题与模拟训练 专题26 计数原理与概率统计(解析版)

专题26 计数原理与概率统计第一部分 真题分类1.(2021·天津高考真题)甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局,已知每次活动中,甲、乙猜对的概率分别为56和15,且每次活动中甲、乙猜对与否互不影响,各次活动也互不影响,则一次活动中,甲获胜的概率为____________,3次活动中,甲至少获胜2次的概率为______________. 【答案】23 2027【解析】由题可得一次活动中,甲获胜的概率为564253⨯=;则在3次活动中,甲至少获胜2次的概率为23232122033327C ⎛⎫⎛⎫⨯⨯+= ⎪ ⎪⎝⎭⎝⎭.故答案为:23;2027.2.(2021·江苏高考真题)下图是某项工程的网络图(单位:天),则从开始节点①到终止节点⑧的路径共有( )A .14条B .12条C .9条D .7条【答案】B【解析】由图可知,由①→④有3条路径,由④→⑥有2条路径,由⑥→⑧有2条路径,根据分步乘法计算原理可得从①→⑧共有32212⨯⨯=条路径. 故选:B3.(2021·江苏高考真题)已知()12nx -的展开式中2x 的系数为40,则n 等于( ) A .5 B .6 C .7 D .8【答案】A【解析】()()222221n C x n n x -=-,所以()21405n n n -=⇒=.故选:A.4.(2021·天津高考真题)从某网络平台推荐的影视作品中抽取400部,统计其评分分数据,将所得400个评分数据分为8组:[)66,70、[)70,74、、[]94,98,并整理得到如下的费率分布直方图,则评分在区间[)82,86内的影视作品数量是( )A .20B .40C .64D .80【答案】D【解析】由频率分布直方图可知,评分在区间[)82,86内的影视作品数量为4000.05480⨯⨯=. 故选:D.5.(2020·天津高考真题)从一批零件中抽取80个,测量其直径(单位:mm ),将所得数据分为9组:[)[)[)[]5.31,5.33,5.33,5.35,,5.45,5.47,5.47,5.49,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间[5.43,5.47)内的个数为( )A .10B .18C .20D .36【答案】B【解析】根据直方图,直径落在区间[)5.43,5.47之间的零件频率为:()6.25 5.000.020.225+⨯=, 则区间[)5.43,5.47内零件的个数为:800.22518⨯=. 故选:B.6.(2020·北京高考真题)在5(2)x 的展开式中,2x 的系数为( ). A .5- B .5C .10-D .10【答案】C 【解析】)52x 展开式的通项公式为:()()55215522r rrrr r r T Cx C x--+=-=-,令522r -=可得:1r =,则2x 的系数为:()()11522510C -=-⨯=-.故选:C.7.(2020·海南高考真题)我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是A .这11天复工指数和复产指数均逐日增加;B .这11天期间,复产指数增量大于复工指数的增量;C .第3天至第11天复工复产指数均超过80%;D .第9天至第11天复产指数增量大于复工指数的增量; 【答案】CD【解析】由图可知,第1天到第2天复工指数减少,第7天到第8天复工指数减少,第10天到第11复工指数减少,第8天到第9天复产指数减少,故A 错误;由图可知,第一天的复产指标与复工指标的差大于第11天的复产指标与复工指标的差,所以这11天期间,复产指数增量小于复工指数的增量,故B 错误;由图可知,第3天至第11天复工复产指数均超过80%,故C 正确;由图可知,第9天至第11天复产指数增量大于复工指数的增量,故D 正确;8.(2021·江苏高考真题)已知关于x 的二次函数()24f x ax bx a =-+.(1)若{}1,1,2,3a ∈-,{}0,1,2b ∈,求事件(){A f x =在[)1,+∞上是增函数}的概率; (2)若[]1,2a ∈,[]0,2b ∈,求事件B =“方程()0f x =没有实数根”的概率. 【答案】(1)512;(2)38.【解析】(1)根据题意有:0a >,且对称轴21bx a=. 基本事件总数为114312C C ⋅=,满足事件A 的事件数为(1,0),(2,0),(2,1),(3,0),(3,1)共有5个,P ∴(A )512=; (2)方程240ax bx a -+=无实根,则22(4)40a b a ≠⎧⎨--<⎩,∴22040a ab ≠⎧⎨->⎩, 又[1a ∈,2],[0b ∈,2],20a b ∴->, 如图,∴11(1)1322()28P B +⨯==.9.(2021·全国高考真题)一种微生物群体可以经过自身繁殖不断生存下来,设一个这种微生物为第0代,经过一次繁殖后为第1代,再经过一次繁殖后为第2代……,该微生物每代繁殖的个数是相互独立的且有相同的分布列,设X 表示1个微生物个体繁殖下一代的个数,()(0,1,2,3)i P X i p i ===. (1)已知01230.4,0.3,0.2,0.1p p p p ====,求()E X ;(2)设p 表示该种微生物经过多代繁殖后临近灭绝的概率,p 是关于x 的方程:230123p p x p x p x x+++=的一个最小正实根,求证:当()1E X ≤时,1p =,当()1E X >时,1p <; (3)根据你的理解说明(2)问结论的实际含义. 【答案】(1)1;(2)见解析;(3)见解析. 【解析】(1)()00.410.320.230.11E X =⨯+⨯+⨯+⨯=.(2)设()()3232101f x p x p x p x p =++-+,因为32101p p p p +++=,故()()32322030f x p x p x p p p x p =+-+++,若()1E X ≤,则123231p p p ++≤,故2302p p p +≤.()()23220332f x p x p x p p p '=+-++,因为()()20300f p p p '=-++<,()230120f p p p '=+-≤, 故()f x '有两个不同零点12,x x ,且1201x x <<≤,且()()12,,x x x ∈-∞⋃+∞时,()0f x '>;()12,x x x ∈时,()0f x '<; 故()f x 在()1,x -∞,()2,x +∞上为增函数,在()12,x x 上为减函数, 若21x =,因为()f x 在()2,x +∞为增函数且()10f =,而当()20,x x ∈时,因为()f x 在()12,x x 上为减函数,故()()()210f x f x f >==,故1为230123p p x p x p x x +++=的一个最小正实根,若21>x ,因为()10f =且在()20,x 上为减函数,故1为230123p p x p x p x x +++=的一个最小正实根,综上,若()1E X ≤,则1p =.若()1E X >,则123231p p p ++>,故2302p p p +>. 此时()()20300f p p p '=-++<,()230120f p p p '=+->, 故()f x '有两个不同零点34,x x ,且3401x x <<<, 且()()34,,x x x ∈-∞+∞时,()0f x '>;()34,x x x ∈时,()0f x '<;故()f x 在()3,x -∞,()4,x +∞上为增函数,在()34,x x 上为减函数, 而()10f =,故()40f x <,又()000f p =>,故()f x 在()40,x 存在一个零点p ,且1p <.所以p 为230123p p x p x p x x +++=的一个最小正实根,此时1p <,故当()1E X >时,1p <.(3)意义:每一个该种微生物繁殖后代的平均数不超过1,则若干代必然灭绝,若繁殖后代的平均数超过1,则若干代后被灭绝的概率小于1.10.(2020·海南高考真题)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和2SO 浓度(单位:3μg/m ),得下表:(1)估计事件“该市一天空气中PM2.5浓度不超过75,且2SO 浓度不超过150”的概率; (2)根据所给数据,完成下面的22⨯列联表:(3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与2SO 浓度有关?附:22()()()()()n ad bc K a b c d a c b d -=++++,【答案】(1)0.64;(2)答案见解析;(3)有.【解析】(1)由表格可知,该市100天中,空气中的 2.5PM 浓度不超过75,且2SO 浓度不超过150的天数有32618864+++=天,所以该市一天中,空气中的 2.5PM 浓度不超过75,且2SO 浓度不超过150的概率为640.64100=; (2)由所给数据,可得22⨯列联表为:2SO2.5PM[]0,150(]150,475合计[]0,7564 16 80 (]75,11510 10 20 合计7426100222()100(64101610)()()()()80207426n ad bc K a b c d a c b d -⨯⨯-⨯==++++⨯⨯⨯36007.4844 6.635481=≈>,因为根据临界值表可知,有99%的把握认为该市一天空气中 2.5PM 浓度与2SO 浓度有关.第二部分 模拟训练1.三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用2⨯勾⨯股+(股-勾)2=4⨯朱实+黄实=弦实,化简,得勾2+股2=弦2,设勾股中勾股比为1:3,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在红(朱)色图形内的图钉数大约为()(参考数据:2 1.414,3 1.732≈≈)A.866 B.500 C.300 D.134【答案】A【解析】不妨设勾长13则朱色面积为1314232⨯=22132,面积为224=,所以落在红(朱)色图形内的图钉数大约为2310005003500 1.732866=≈⨯=.故选:A2.琵琶、二胡、编钟、箫、笛、瑟、琴、埙、笙和鼓这十种民族乐器被称为“中国古代十大乐器”.为弘扬中国传统文化,某校以这十种乐器为题材,在周末学生兴趣活动中开展了“中国古代乐器”知识讲座,共连续安排四节课,一节课只讲一种乐器,一种乐器最多安排一节课,则琵琶、二胡一定安排,且这两种乐器互不相邻的概率为()A.1360B.16C.115D.715【答案】C【解析】由题意得:10种乐器种任选4种,故总的可能性有410A种,琵琶、二胡一定安排且不相邻的可能性有2283A A种,所以两种乐器互不相邻的概率2283410115A APA==.故选:C3.造纸术、印刷术、指南针、火药被称为中国古代四大发明,这四种发明对中国古代的政治、经济、文化的发展产生了巨大的推动作用;2017年5月,来自“一带一路”沿线的20国青年评选出了“中国的新四大发明”:高铁、扫码支付、共享单车和网购.若从这8个发明中任取两个发明,则两个都是新四大发明的概率为( ) A .114B .17C .314D .14【答案】C【解析】从8个发明中任取两个发明共有28C 28=种, 两个都是新四大发明的有24C 6=种, ∴所求概率为632814P ==, 故选:C4.蟋蟀鸣叫可以说是大自然优美、和谐的音乐,殊不知蟋蟀鸣叫的频率x (每分钟鸣叫的次数)与气温y (单位:℃)存在着较强的线性相关关系.某地观测人员根据下表的观测数据,建立了y 关于x 的线性回归方程ˆ0.25yx k =+ x (次数/分钟)2030405060y (℃) 25 27.5 29 32.5 36则当蟋蟀每分钟鸣叫60次时,该地当时的气温预报值为( ) A .33℃ B .34℃C .35℃D .35.5℃【答案】C【解析】由题意,得40x=,30y =,则0.25300.254020k y x =-=-⨯=;当60x =时,35y =. 故选:C.5.将一线段AB 分为两线段AC ,CB ,使得其中较长的一段AC 是全长AB 与另一段CB 的比例中项,即满足AC AB =BC AC =512-≈0.618,后人把这个数称为黄金分割,把点C 称为线段AB 的黄金分割点.图中在ABC 中,若点P ,Q 为线段BC 的两个黄金分割点,在ABC 内任取一点M ,则点M 落在APQ 内的概率为( )A .512B 5-2C .514-D .522-【答案】B【解析】由几何概型公式知,所求概率为515112252 APQABCBC BCS PQ BQ BPS BC BC BC⎛⎫----⎪-⎝⎭====-.故选:B.6.在新冠疫情的持续影响下,全国各地电影院等密闭式文娱场所停业近半年,电影行业面临巨大损失.2011~2020年上半年的票房走势如下图所示,则下列说法正确的是()A.自2011年以来,每年上半年的票房收入逐年增加B.自2011年以来,每年上半年的票房收入增速为负的有5年C.2018年上半年的票房收入增速最大D.2020年上半年的票房收入增速最小【答案】D【解析】由图易知自2011年以来,每年上半年的票房收入相比前一年有增有减,增速为负的有3年,故A,B错误;2017年上半年的票房收入增速最大,故C错误;2020年上半年的票房收入增速最小,故D正确.故选:D7.某士特产超市为预估2021年元旦期间游客购买土特产的情况,对2020年元且期间的90位游客购买情况进行统计,得到如下人数分布表.购买金额(元)[0,15)[15,30)[30,45)[45,60)[60,75)[75,90)人数10 15 20 15 20 1060元与性别有关.不小于60元小于60元合计(23次,每次中奖概率为P (每次抽奖互不影响,且P 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元若游客甲计划购买80元的土特产,请列出实际付款数X (元)的分布列并求其数学期望. 参考公式及数据:22()()()()()n ad bc K a b c d a c b d -=++++,n a b c d =+++附表:【答案】(1)列联表见解析,有95%的把握认为购买金额是否少于60元与性别有关;(2)分布列见解析,75EX =.【解析】(1)22⨯列联表如下:2290(12204018)1440 5.830 3.84130605238247K ⨯⨯-⨯==≈>⨯⨯⨯,因此有95%的把握认为购买金额是否少于60元与性别有关. (2)X 可能取值为65,70,75,80,且10201903p +==. 由题意知:33311(65)327P X C ⎛⎫=== ⎪⎝⎭,223122(70)339P X C ⎛⎫==⨯= ⎪⎝⎭,213124(75)339P X C ⎛⎫==⨯⨯= ⎪⎝⎭,30328(80)327P X C ⎛⎫=== ⎪⎝⎭, 所以X 的分布列为1246570758075279927EX =⨯+⨯+⨯+⨯=. 8.一年一度的剁手狂欢节——“双十一”,使千万女性朋友们非常纠结.2020年双十一,淘宝点燃火炬瓜分2.5个亿,淘宝、京东、天猫等各大电商平台从10月20号就开始预订,进行了强大的销售攻势.天猫某知名服装经营店,在10月21号到10月27号一周内,每天销售预定服装的件数x (百件)与获得的纯利润y (单位:百元)之间的一组数据关系如下表:(1)若y 与x (2)试求y 与x 的线性回归方程;(3)该服装经营店打算11月2号结束双十一预定活动,预计在结束活动之前,每天销售服装的件数x (百件)与获得的纯利润y (单位:百元)之间的关系仍然服从(1)中的线性关系,若结束当天能销售服装14百件,估计这一天获得的纯利润与前一周的平均利润相差多少百元?(有关计算精确到小数点后两位)参考公式与数据:ˆˆˆybx a =+,()()()121ˆniii nii x x y y b x x ==--=-∑∑,ˆˆay bx =-.713487i ii x y==∑.【答案】(1)y 与x 是正相关;(2)ˆ 4.7551.36yx =+;(3)结束当天获得的纯利润比前一周的平均利润多38.00百元.【解析】解:(1)由题目中的数据表格可以看出,y 随着x 的增大而增大, ∴判断出y 与x 是正相关; (2)由题设知,721280ii x==∑,345678967x ++++++==,6669738189909155977y ++++++==,∴5593487761337ˆ 4.7528073628b -⨯⨯===-⨯, 则559ˆ6 4.7551.367a=-⨯≈, ∴线性回归直线方程为ˆ 4.7551.36yx =+; (3)由(1)知,当14x =时, 4.751451.361ˆ17.86y=⨯+=(百元), ∴11月2号这天估计可获得的纯利润大约为117.86百元; 由(1)知,前一周的平均利润为55979.867y =≈(百元), 故结束当天获得的纯利润比前一周的平均利润多38.00百元.。
《统计与概率》高考模拟

《统计与概率》高考模拟一、选择题(本大题共12小题,每小题5分,共60分)1.(2019·成都统考)某工厂生产,,A B C 三种不同型号的产品,产品数量之比为:5:3k ,现用分层抽样的方法抽出个容量为120的样本,已知A 型号产品抽取了24件,则C 型号产品抽取的件数为( ) A.24 B.30 C.36 D.402.(2019·菏泽模拟)在样本频率分布直方图中,共有9个小长方形,若某个小长方形的面积等于其他8个小长方形的面积和的25,且样本容量为140,则该组的频数为( ) A.28 B.40 C.56 D.603.(2019·河南八市高一联考)如图所示的茎叶图记录了甲、乙两名同学在10次英语听力比赛中的成绩(单位:分),已知甲得分的中位数为76分,乙得分的平均数是75分,则下列结论正确的是( )A.76x =甲B.甲数据中3x =,乙数据中6y =C.甲数据中6x =,乙数据中3y =D.乙同学成绩较为稳定4.在5件产品中,有4件正品,从中任取2件,2件都是正品的概率是( )A.4 5B.1 5C.3 5D.2 55.有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为()A.18B.36C.54D.726.(2019·辽宁实验中学月考)甲盒中有200个螺杆,其中有x个A型的,乙盒中有240个螺母,其中有y个A型的.今从甲、乙两盒中各任取一个,不能配成A型螺栓的概率为25,则恰可配成A型螺栓的概率为()A.1 20B.15 16C.3 5D.19 207.(2019·绵阳中学高一期末)口袋中有100个大小相同的红球、白球、黑球,其中红球45个,从口袋中摸出一个球,摸出白球的概率为0.23,则摸出黑球的概率为()A.0.45B.0.67C.0.64D.0.328.随机猜测“选择题”的答案,每道题猜对的概率为0.25,则两道选择题至少猜对一道的概率为()A.7 16B.1 16C.9 16D.3 89.(2019·绵阳中学高一期末)现有10道题,其中6道甲类题,4道乙类题,小明同学从中任取3道题解答.已知所取的3道题中有2道甲类题,1道乙类题.若小明同学答对每道甲类题的概率都是35,答对每道乙类题的概率都是45,且各题答对与否相互独立.则小明同学至少答对2道题的概率为()A.12 25B.57 125C.36 125D.93 12510.设矩形的长为a,宽为b,其比满足1:0.6182b a=≈,这种矩形给人以美感,称为黄金矩形.黄金矩形常应用于工艺品设计中,下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本甲批次:甲批次:0.598 0.625 0.628 0.595 0.639乙批次:0.618 0.613 0.592 0.622 0.620根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是()A.甲批次的总体平均数与标准值更接近B.乙批次的总体平均数与标准值更接近C.两个批次总体平均数与标准值接近程度相同D.两个批次总体平均数与标准值接近程度不能确定11.从甲、乙两个城市分布随机抽取14台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图),设甲、乙两组数据的平均数分别为,x x 甲乙,中位数分别为,m m 甲乙,则( )A.,x x m m <>甲乙甲乙B.,x x m m <<甲乙甲乙C.,x x m m >>甲乙甲乙D.,x x m m ><甲乙甲乙12.(2019·武昌模拟)学校要从甲、乙、丙三名同学中选取两名去参加物理竞赛,因为他们的水平相当,所以准备采取抽签的方式决定.学校制作了三个签,其中两个写有“参赛”,一个写有“不参赛”.抽签时,由甲先抽,然后乙抽,最后丙抽.记事件A :甲抽中“参赛”,事件B :乙抽中“参赛”,则( ) A.()()P A P B =且事件,A B 独立 B.()()P A P B =且事件,A B 不独立 C.()()P A P B >且事件,A B 独立 D.()()P A P B >且事件,A B 不独立二、填空题(本大题共4小题,每小题5分,共20分)13.(2019·南阳检测)为了调查某野生动物保护区内某种野生动物数量,调查人员逮到这种动物1200只,作过标记后放回,一星期后,调查人员再次逮到该种动物1000只,其中作过标记的有100只,估计保护区有这种动物______只. 14.(2019·郑州一中期末)用两种不同的颜色给图中三个矩形随机涂色,每个矩形只涂一种颜色,则相邻两个矩形涂不同颜色的概率是_________.15.(2019沈阳质检)某工厂生产,A B两种元件,先从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:由于表格被污损,数据,x y看不清,统计员只记得,A B两种元件的检测数据的平均数相等,方差也相等,则xy ________.16.两台机床同时生产直径为10的零件,为了检验产品质量,质量检验员从两台机床生产的产品中各抽出4件进行测量,结果如下:如果你是质量检验员,在收集到上述数据后,你将通过运算来判断哪台机床生产的零件质量更好、更符合要求,那么你的判断是_________.三、解答题(本大题共6小题,共70分)17.(2019·武汉二中月考)(10分)一个地区共有5个乡镇,人口3万人,其中人口比例为3:2:5:2:3.从3万人中抽取一个300人的样本,分析某种疾病的发病率,已知这种疾病与不同的地理位置及水土有关,问应采取什么样的抽样方法?并写出具体过程.18.(2019·海口一中质检)(12分)随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.(1)根据茎叶图判断哪个班的平均身高较高; (2)计算甲班的样本方差.19.(2019·育才中学期中)(12分)一个口袋内装有大小相同的1个白球和已编有号码的3个黑球,从中摸出2个球. (1)共有多少种不同的结果?(2)2个球均为黑球有多少种不同结果? (3)2个球均为黑球的概率是多少?20.(2019·北京十一中学期中)(12分)某校进入高中数学竞赛复赛的学生中,高一年级有6人,高二年级有12人,高三年级有24人,现采用分层抽样的方法从这些学生中抽取7人进行采访. (1)求应从各年级分别抽取的人数;(2)若从抽取的7人中再随机抽取2人做进一步了解(注高一学生记为i A ,高二学生记为i B ,高三学生记为1,2,3,i C i =⋅⋅⋅,). ①列出所有可能的抽取结果;②求抽取的2人均为高三年级学生的概率.21.(2019·济南模拟)(12分)现有甲、乙、丙三名学生参加某大学的自主招生考试,考试分两轮,第一轮笔试,第二轮面试,只有第一轮笔试通过才有资格进入第二轮面试,面试通过就可以在高考录取中获得该校的优惠加分,两轮考试相互独立.根据以往多次的模拟测试,甲、乙、丙三名学生能通过笔试的概率分别为0.4,0.8,0.5,能通过面试的概率分别为0.8,0.4,0.64.根据这些数据我们可以预测:(1)甲、乙、丙三名学生中至少有两名学生通过第一轮笔试的概率 (2)甲、乙、丙三名学生恰有2人获得该校优惠加分的概率.22.(2019·长沙八校联考)(12分)某医药公司研发一种新的保健产品,从生产的一批产品中抽取200盒作为样本,测量产品的一项质量指标值,该指标值越高越好,由测量结果得到如图所示的频率分布直方图:(1)求a,并试估计这200盒产品的该项指标的平均值;(2)国家有关部门规定每盒产品该项指标值不低于150均为合格,且按指标值的从低到高依次分为合格、优良、优秀三个等级,其中(185,215)为优良,不高于185为合格,不低于215为优秀.用样本的该项质量指标值的频率代替产品的该项质量指标值的概率.①求产品该项指标值的优秀率;②现从这批产品中随机抽取3盒,求其中至少有1盒该项质量指标值为优秀的概率.参考答案 1. 答案:C 解析:由2453120k k =++得2k =,故C 型号产品抽取的件数为312036253⨯=++.2.答案:B解析:设该小长方形的面积为x ,则2(1)5x x =-,解得27x =,即该组的频率为27,所以频数为2140407⨯=.3. 答案:C解析:因为甲得分的中位数为76分,所以6x =,所以75x =甲,故A 、B 错误;因为乙得分的平均数是75分,所以5668687072(70)808688897510y ++++++++++=,解得3y =,故C 正确;由茎叶图中甲、乙成绩的分布可知D 错误. 4. 答案:C 解析: 5. 答案:B解析:从左到右四个矩形的面积分别为0.04、0.1、0.3、0.38,所以第五个矩形的面积为10.040.10.30.380.18----=,即样本数据落在区间[10,12)内的频率为0.18,所以样本数据落在区间[10,12)内的频数为2000.1836⨯=. 6. 答案:C 解析: 7. 答案:D 解析:答案:A解析:每道题猜对的概率为10.254=,则猜错的概率为34,由独立事件概率的计算公式得:两道选择题都猜错的概率为3394416⨯=,所以至少猜对一道的概率为9711616-=.故选A. 9. 答案:D解析:设小明同学答对题的个数为X ,则23134257(2)255555125P X ⎛⎫==⨯+⨯⨯⨯= ⎪⎝⎭,23436(3)55125P X ⎛⎫==⨯=⎪⎝⎭,故93(2)(2)(3)125P X P X P X ==+==≥.则小明同学至少答对2道题的概率为93125.选D. 10. 答案:A 解析:0.5980.6250.6280.5950.6390.6175x ++++==甲,0.6180.6130.5920.6220.6200.6135x ++++==乙,故选A.11. 答案:A解析:由题中茎叶图可得56101014182225303038414348170147x +++++++++++++==甲, 88101220222323313234344243171147x +++++++++++++==乙, 23.5,23m m ==甲乙,故,x x m m <>甲乙甲乙,故选A. 12. 答案:B解析:因为221122(),()332323P A P B ==⨯+⨯=,所以()()P A P B =,但211()323P AB =⨯=,从而()()()P AB P A P B ≠,故,A B 相互不独立.答案:12000解析:设保护区内有这种动物x 只,每只动物被逮到的概率是相同的,所以12001001000x =,解得12000x =. 14. 答案:14解析:由于只有两种颜色,不妨将其标注为1和2.若只用一种颜色,则有111,222,共2种情况;若用两种颜色,则有122,212,221,211,121,112,共6种情况.所以基本事件共有8个,其中相邻两个矩形颜色不同的事件有2个,故所求概率2184P ==. 15. 答案:72解析:因为1(777.599.5)8,5A B x x =⨯++++==1(68.58.5)5x y ⨯++++,所以由A B x x =,得17x y +=.①因为21(110.251 2.25) 1.15A s =⨯++++=,22214(8)0.250.25(8)5B s x y ⎡⎤=⨯+-+++-⎣⎦,所以由22A B s s =,得22(8)(8)1x y -+-=.②由①②,解得72xy =. 16. 答案:乙解析:先计算平均直径:1(109.810 10. 2) 104x =+++=甲;1(10.1109.910)104z x =+++=.由于x x =甲乙,因此,平均直径不能反映两台机床生产的零件的质量优劣.再计算方差:222221(1010)(9.810)(1010)(10.210)0.024s ⎡⎤=-+-+-+-=⎣⎦甲; 222221(10.110)(1010)(9.910)(1010)0.0054s ⎡⎤=-+-+-+-=⎣⎦乙.由于22s s <乙甲,这说明乙机床生产出的零件直径波动小.因此,从产品质量稳定性的角度考虑,乙机床生产的零件质量更好、更符合要求.17.答案:见解析解析:因为疾病与地理位置和水土均有关系,所以不同乡镇的发病情况差异明显,因而采用分层抽样的方法,具体过程如下:①3万人分为5层,其中一个乡镇为一层.②按照样本容量的比例随机抽取各乡镇应抽取的样本.33006015⨯=(人),23004015⨯=(人),530010015⨯=(人),23004015⨯=(人),33006015⨯=(人),因此各乡镇抽取人数分别为60人、40人、100人、40人、60人.③将抽取的300人组到一起,即得到一个300人的样本.18.答案:见解析解析:(1)甲、乙两班同学的平均身高分别为:170,171.1x x ==甲乙,所以乙班同学的平均身高较高.(2)甲班的样本方差为:22221[(158170)(162170)(163170)10s =-+-+-+甲222222(168170)(168170)(170170)(171170)(179170)(179170)-+-+-+-+-+-2(182170)]57.2+-=.19.答案:见解析解析:(1)设已编号的3个黑球分别为黑1、黑2黑3,则从中摸出2个球,共有6种不同的结果,分别为(黑1,黑2)、(黑1,黑3)、(黑2,黑3)、(白,黑1)、(白,黑2)、(白,黑3).(2)由(1)知,2个球均为黑球有3种不同的结果.(3)由于6种结果是等可能的,其中2个球均为黑球(记为事件A )有3种不同的结果,31()62P A ∴==. 20.答案:见解析解析:(1)由分层抽样的特征,得61271;726122461224⨯=⨯=++++;247461224⨯=++,所以应从高一年级抽取1人,高二年级抽取2人,高三年级抽取4人.(2)由(1)知,高一年级有1人,记为1A ,高二年级有2人,记为12,B B ,高三年级有4人,记为1234,,,C C C C .①从中抽取2人,所有可能的结果为:11121112131412,,,,,,A B A B AC AC AC AC B B , 1112131421222324121314232434,,,,,,,,,,,,,B C B C B C B C B C B C B C B C C C C C C C C C C C C C ,共21种.②由①知,共有21种情况,抽取的2人均为高三年级学生的可能结果为:121314232434,,,,,C C C C C C C C C C C C ,共6种,所以抽取的2人均为高三年级学生的概率62217P ==. 21.答案:见解析解析:(1)记事件A :甲通过第一轮笔试,事件B :乙通过第一轮笔试,事件C :丙通过第一轮笔试,事件D :至少有两名学生通过第一轮笔试,则()0.4P A =,()0.8,()0.5P B P C ==.()()()()()()()()()()()P D P ABC P ABC P ABC P ABC P A P B P C P A P B P C =+++=+()()()()()()0.40.80.50.40.20.50.60.80.5P A P B P C P A P B P C ++=⨯⨯+⨯⨯+⨯⨯0.40.80.50.6+⨯⨯=,所以至少有两名学生通过第一轮笔试的概率为0.6.(2)因为甲、乙、丙三名学生中每个人获得优惠加分(两轮都通过)的概率均为0.32,故恰有2人获得优惠加分的概率为230.320.680.208896⨯⨯=. 22.答案:见解析解析:(1)由10(20.0020.0080.0090.0220.024)1a ⨯⨯+++++=,解得0.033a =. 设平均值为x ,则0.021700.091800.221900.332000.24x =⨯+⨯+⨯+⨯+⨯ 2100.082200.02230200+⨯+⨯=,即产品的该项指标的平均值为200.(2)①由直方图知该指标值不低于215包括直方图中的最后2个长方形区域,由互斥事件的概率公式可得该项指标值的优秀率10(0.0080.002)0.1P =⨯+=.②设抽取的3盒中恰好有X 盒该项质量指标值为优秀,由①可得随机抽取1盒不是优秀的概率为10.10.9-=,则由独立事件的概率可得,抽取的3盒该项质量指标值均不是优秀的概率为30.90.729=,由对立事件的概率可得,抽取的3盒中至少有1盒该项质量指标值为优秀的概率为10.7290.271-=.。
人教版高中数学必修三第三章概率选修2-3概率-高考题(3)

选修2-3概率-高考题 (3)一、选择题1.下列说法中,正确的是A .不可能事件发生的概率为B .随机事件发生的概率为21C .概率很小的事件不可能发生D .投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次【答案】A【逐步提示】本题考查了概率的意义和事件发生的概率,根据概率的意义和事件发生的概率,依次判断各个选项是否正确.【详细解答】解: A.不可能事件发生的概率为0,所以A 选项正确;B.随机事件发生的概率在0与1之间,所以B 选项错误;C.概率很小的事件不是不可能发生,而是发生的机会较小,所以C 选项错误;D.投掷一枚质地均匀的硬币100次,正面朝上的次数可能为50次,所以D 选项错误,故选择 A. 【解后反思】概率的意义:一般地,在大量重复实验中,如果事件A 发生的频率会稳定在某个常数p 附近,那么这个常数p 就叫做事件A 的概率,记为P (A )=p ;概率是频率(多个)的波动稳定值,是对事件发生可能性大小的量的表现.必然发生的事件的概率P (A )=1;不可能发生事件的概率P (A )=0.【关键词】不可能事件;随机事件;概率的意义;2.(2016甘肃省天水市,3,4分)下列事件中,必然事件是()A .抛掷1枚骰子,出现6点向上B .两条直线被第三条直线所截,同位角相等C .366人中至少有2个人的生日相同D .实数的绝对值是非负数【答案】D【逐步提示】本题考查事件的分类,解题的关键是认识到在一定条件下,有些事件必然会发生,这样的事件称为必然事件;在一定条件下,可能发生也可能不发生的事件称为随机事件,只有分清各种事件才能做出正确的判断.【详细解答】解:抛掷1枚骰子,可能出现6点向上,也可能出现其它点数向上,所以A 中事件是随机事件.只有两条平行直线被第三条直线所截,同位角才一定相等,所以B 中事件是随机事件.由于闰年有366天,有可能出现这366人的生日一人占一天的情况,所以C 中事件不是必然事件.对于D ,由于正实数的绝对值是正数,0的绝对值是0,负实数的绝对值是正数,所以实数的绝对值一定是非负数,属于必然事件.故选择D .【解后反思】对于B 中事件,由于阅读不细致、认真,易受思维定势的影响误认为是两条平行直线被第三条直线所截,从而认定同位角必定相等而错误地判断为必然事件.另外,本题难点在于对C 中事件的认识,可以按照“一个萝卜一个坑”的现实原理加强理解.【关键词】必然事件;随机事件.3.(2016广东省广州市,4,3分)某个密码锁的密码由三个数字组成,每个数字都是0-9这十个数字中的一个,只有当三个数字与所设定的密码及顺序完全相同时,才能将锁打开,如果仅忘记了所设密码的最后那个数字,那么一次就能打开该密码锁的概率是()A .101B .91C .31D .21【答案】A【逐步提示】所设密码最后那个数字是0-9这十个数字中的一个,即共有10种可能,密码数字只有1种,据此可根据概率的计算公式求解结果.【详细解答】解:根据题意可知,密码锁所设密码的最后那个数字是0-9这十个数字中的一个,因此,一次就能打开该密码锁的概率是101,故选择A .【解后反思】(1)一般地,如果在一次试验中,有n 种可能的结果,并且它们发生的可能性相等,事件A包含其中的m 种结果,那么事件A 发生的概率nm A P )(.(2)求较复杂随机事件的概率时,常用画树状图或列表法不重不漏地列出所有等可能结果.【关键词】概率的计算公式4.(2016广东茂名,4,3分)下列事件中,是必然事件的是()A.两条线段可以组成一个三角形B.400人中有两个人的生日在同一天C.早上的太阳从西方升起D.打开电视机,它正在播放动画片【答案】B【逐步提示】本题考查了必然事件的概念,解题的关键是正确区分必然事件与不可能事件、随机事件.事先能肯定它一定会发生的事件称为必然事件.事先能肯定它一定不会发生的事件称为不可能事件,必然事件和不可能事件都是确定的.而不确定事件(即随机事件)是在一定条件下,可能发生也可能不发生的事件.【详细解答】解:三角形是由三条不在同一直线上的线段首尾顺次相接组成的,两条线段不能组成一个三角形,选项A中的事件属于不可能事件;一年有365天或366天,由于400>365,400>366,因此400人中必有两个人的生日在同一天,选项B中的事件属于必然事件;根据自然规律,早上的太阳从东方升起,选项C中的事件属于不可能事件;打开电视机,它不一定正在播放动画片,选项D中的事件属于随机事件. 故选择 B .【解后反思】事件分为确定事件和不确定事件(随机事件),确定事件又分为必然事件和不可能事件,其中,①必然事件发生的概率为1,即P(必然事件)=1;②不可能事件发生的概率为0,即P(不可能事件)=0;③如果A为不确定事件(随机事件),那么0<P(A)<1.【关键词】不可能事件;必然事件;随机事件5.(2016湖北宜昌,6,3分)在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法来估算正面朝上的概率,其实验次数分别为10次,50次,100次,200次,其中实验相对科学的是()A.甲组B.乙组C.丙组D.丁组【答案】D【逐步提示】本题考查了用频率估计概率,解题的关键是根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.【详细解答】解:甲组实验了10次,乙组实验了50次,丙组实验了100次,丁组实验了200次,实验次数多的频率往往接近事件发生的概率,故选择 D .【解后反思】在一次试验中,若共有n次等可能的结果,其中事件A包含m个等可能的结果,则事件A的概率为P(A)=mn.随机事件的频率,指此事件发生的次数与试验总次数的比值,当试验次数很多时,它具有一定的稳定性,即稳定在某一常数附近,而偏离的它可能性很小.为了说明这种规律,我们把这个常数称为这个随机事件的概率.它从数量上反映了随机事件发生的可能性的大小,而频率在大量重复试验的前提下可近似地作为这个事件的概率.【关键词】概率公式;用频率估计概率6(2016湖南常德,5,3分)下列说法正确的是A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机取出一个球,一定是红球.B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨.C.某地发行一种福利彩票,中奖概率是千分之一.那么,买这种彩票1000张,一定会中奖.D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上.【答案】D【逐步提示】本题考查的是概率的含义.概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,机会大也不一定发生,机会小也有可能.【详细解答】解:选项A、“取到红球”是随机事件,且可能性较大,但不是必然事件,所以从中随机取出一个球,不一定是红球,所以A选项错误;选项B、“明天降水概率10%”,是指下雨的可能性为10%,而不是10%的时间会下雨,所以B选项错误;选项C、“中奖概率是千分之一”是指这批彩票总体平均每1000张有一张中奖,而不是买这种彩票1000张,一定会中奖,所以C选项错误;选项D、“投掷一枚质地均匀的硬币正面朝上”是随机事件,所以第六次仍然可能正面朝上,所以D选项正确.故选D.【解后反思】事件分为确定事件和不确定事件,确定事件分为必然事件和不可能事件;也就是说一定发生的事件是必然事件,一定不会发生的事件是不可能事件;可能发生,也可能不发生的事件是不确定事件;必然事件发生的概率是1,不可能发生的事件发生的概率是0,不确定事件发生的概率大于零小于1,偶然事件0到1之间【关键词】概率的含义;随机事件;7.(2016湖南湘西,15,4分)在一个不透明的口袋中装有6个红球,2个绿球,这些球除颜色外无其它差别,从这个袋子中随机摸出一个球,摸到红球的概率为A .43B .41C .21D .1【答案】A【逐步提示】本题考查了概率的定义,熟悉定义是解题的关键.口袋中共8个球,其中有6个红球,根据概率定义解题即可.【详细解答】解:P(摸到红球)=86=43,故答案为43.故选择 A .【解后反思】一般地,在试验中,如果各种结果发生的可能性都相同,那么一个事件A 发生的概率计算公式为P(A)=A 事件可能发生的结果数所有等可能结果的总数.【关键词】摸球;简单事件的概率二、填空题1.(2016福建福州,15,4分)已知四个点的坐标分别是(-1,1),(2,2),(32,23),(-5,-51),从中随机选取一个点,在反比例函数y =x1图象上的概率是.【答案】12【逐步提示】本题考查了概率的计算和反比例函数的性质,解题的关键是掌握等可能事件概率的计算公式.先判断四个点的坐标是否在反比例函数y =x1图象上,再用在反比例函数y =x1图象上点的个数除以点的总数即为在反比例函数y =x1图象上的概率.【详细解答】解:∵﹣1×1=﹣1,2×2=4,×=1,(﹣5)×(﹣)=1,∴2个点的坐标在反比例函数y =x1图象上,∴在反比例函数y =x1图象上的概率是2÷4=12,故答案为12.【解后反思】此类问题容易出错的地方是不能正确判断所关注事件可能出现的结果数,以及所有等可能出现的结果数.等可能性事件的概率的计算公式:P(A)=n m,其中m 是总的结果数,n 是该事件成立包含的结果数.【关键词】反比函数的图像;概率的计算公式;2.(2016贵州省毕节市,18,5分)掷两枚质地均匀的骰子,其点数之和大于10的概率为_________.【答案】112【逐步提示】本题考查了求简单随机事件的概率,解题的关键掌握用列表法或画树状图的方法进行计算.本题用列表法更方便,表中也可只用两种符号来表示点数之和大于10和不大于10,这样能一目了然,不易出错.【详细解答】解:设点数之和小于或等于10用○表示,大于10用√表示不,列表如下:1 2 3 4 5 6 1 ○○○○○○2 ○○○○○○3 ○○○○○○4 ○○○○○○5 ○○○○○√6○○○○√√由表可知,掷两枚骰子,共有36种等可能的情况出现,其中点数之和大于10的结果共有3种,所以P (点数之和大于10)=336=112,故答案为112.【解后反思】此类问题的易错点是没有列表或画树状图,只凭想象列举出所有可能的结果,造成丢掉一些情况,如把(1,2)和(2,1)当作一种情况,从而致错.【关键词】求概率的方法;3.(2016河南省,12,3分)在“阳光体育”活动期间,班主任将全班同学随机分成了4组进行活动,则该班小明和小亮被分在同一组的概率是_________.【答案】41【逐步提示】本题考查的是用列表法或画树状图法求概率,解题的关键是合理选择方法求概率.思路:选择树状图或列表法解题,通过分析看出,小明和小亮任意分在各组的可能情况为16种,两次抽出卡片所标数字不同占4种,则利用公式可求出事件的概率.【详细解答】解:列表得:设分A 、B 、C 、D 四个组AB C D A (A ,A )(A ,B )(A ,C )(A ,D )B (B ,A )(B ,B )(B ,C )(B ,D )C (C ,A )(C ,B )(C ,C )(C ,D )D(D ,A )(D ,B )(D ,C )(D ,D )所有等可能的情况有16种,其中小明和小亮分在同一组的情况有4种,则P=41164,故答案为41.【解后反思】此类问题容易出错的地方是抽象不出基本概型,事件发生的可能情况列举不出来.一般方法规律是用数值来刻画事件发生的可能性大小,这个数值就是概率.一般地,如果一个实验有n 个等可能的结果,而事件A 包含其中m 个结果,我们可计算概率P(A)=m n=A 事件包含的可能结果数所有可能结果数.运用列举法(包括列表、画树状图)计算简单事件发生的概率的能力,有利于提高学生的数学意识、应用数学的能力和数学素养.【关键词】求概率方法——树状图法和列表法4.(2016湖南省郴州市,13,3分)同时掷两枚均匀的硬币,则两枚都出现反面朝上的概率是.【答案】14【逐步提示】本题考查的是概率问题,解题的关键是弄清事件发生的所有可能的情况,然后看事件发生的概率.抛两枚硬币有四种情况:即(正正)(正反)(反反)(反正),然后判断两个反面朝上的概率就可以了.【详细解答】解:设两枚硬币分别为甲、乙:共有四种结果:(正正)(正反)(反正)(反反)∴14P 两个反面朝上=.反面硬币甲硬币乙开始正面反面正面正面反面【解后反思】此类问题容易出错的地方是列举所有可能性事件时重复或遗漏.(1)运用公式P(A)=nm 求简单事件发生的概率,在确定各种事件等可能性的基础上,关键是求事件所有可能的结果种数n 和使事件A 发生的结果种数m.(2)求简单随机事件的概率有两种方法.①在做了大量试验的基础上,可以用频率的近似地估计概率;②可以用列表或画树状图,列举出所有可能事件,再求概率.(3)列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.【关键词】概率;树状图;.6(2016湖南省怀化市,14,4分)一个不透明的袋子,装了除颜色不同,其它没有任何区别的红色球3个,绿色球4个,黑色球7个,黄色球2个,从袋子中随机摸出一个球,摸到黑色球的概率是______________.【答案】716【逐步提示】在等可能的条件下,袋共有球3+4+7+2=16个,其中黑色球7个,从袋子中随机摸出一个球,摸到黑色球的概率是黑色球数:总球数.【详细解答】解:P黑色球=73472=716,故答案为716.【解后反思】此题考查概率,难度不大,解题的关键是掌握概率的计算公式.【关键词】概率的计算公式7.(2016湖南省湘潭市,12,3分)从2015年12月26日起,一艘载满湘潭历史和文化的“航船——湘潭市规划展示馆、博物馆和党史馆(以下简称‘三馆’)”正式起航,市民可以免费到三馆参观.听说这个好消息,小张同学准备星期天去参观其中一个馆,假设参观者选择每一个馆参观的机会均等,则小张同学选择参观博物馆的概率为.【答案】13【逐步提示】本题考查了概率的计算,解题的关键是知道某事件发生的概率等于该事件出现的可能次数与所有可能次数之间的比.因此先确定参观博物馆的可能次数和参观三个馆总数,再根据概率公式计算即可.【详细解答】解:∵共有3个馆,参观博物馆的可能性为1,∴小张同学选择参观博物馆的概率为13,故答案为13.【解后反思】掌握此类问题,需熟练掌握以下知识:(1)公式法:P(A)=nm,其中n 为所有事件的总数,m 为事件A 发生的总次数;(2)列举(列表或画树状图)法的一般步骤为:①判断使用列表或画树状图方法:列表法一般适用于两步计算;画树状图法适合于两步及两步以上求概率;②不重不漏的列举出所有事件出现的可能结果,并判定每种事件发生的可能性是否相等;③确定所有可能出现的结果数n 及所求事件A 出现的结果m ;④用公式P(A)=nm ,求事件A 发生的概率.【关键词】概率初步8.(2016年湖南省湘潭市,12,3分)从2015年12月26日起,一艘载满湘潭历史和文化的“航船——湘潭市规划展示馆、博物馆和党史馆(以下简称‘三馆’)”正式起航,市民可以免费到三馆参观。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
