电路第九章(第26讲)(20091203) 正弦稳态电路分析习题课)
最全第九章(正弦稳态电路分析)习题解答打印版.doc
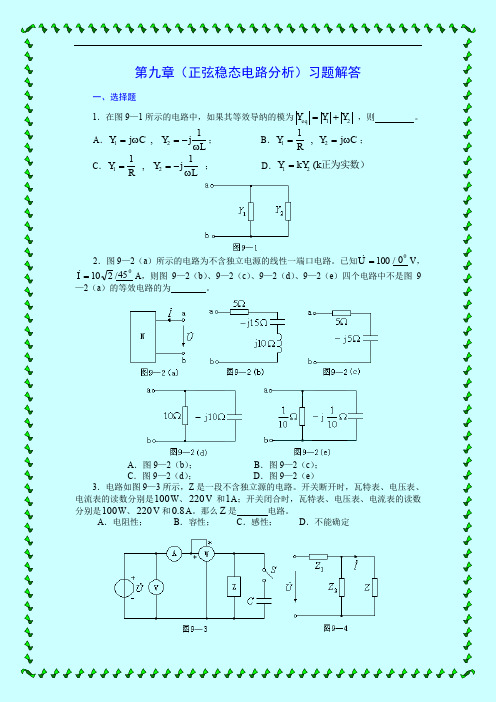
第九章（正弦稳态电路分析）习题解答一、选择题1．在图9—1所示的电路中，如果其等效导纳的模为21Y Y Y eq += ，则 。
A ．L Y C Y ω-=ω=1j, j 21； B ．C Y RY ω==j , 121；C ．L Y R Y ω-==1j , 121 ；D ．正为实数）k kY Y ( 21=2．图9—2（a ）所示的电路为不含独立电源的线性一端口电路。
已知00 /100=UV ，045 /210=I A ，则图9—2（b ）、9—2（c ）、9—2（d ）、9—2（e ）四个电路中不是图9—2（a ）的等效电路的为 。
A ．图9—2（b ）；B ．图9—2（c ）；C ．图9—2（d ）；D ．图9—2（e ）3．电路如图9—3所示，Z 是一段不含独立源的电路。
开关断开时，瓦特表、电压表、电流表的读数分别是100W 、220V 和1A ；开关闭合时，瓦特表、电压表、电流表的读数分别是100W 、220V 和8.0A 。
那么Z 是 电路。
A ．电阻性；B ．容性；C ．感性；D ．不能确定4．电路如图9—4所示，U固定不变。
如果 ，则改变Z （Z 不等于无限大）时，I不变。
A ．21Z Z =； B ．21Z Z -=； C ．21Z Z =； D ．)Arg()Arg(21Z Z =5．Ω=10R 的电阻，F 1μ=C 的电容与电感L 串联，接到频率1000Hz 的正弦电压源上。
为使电阻两端的电压达到最高，电感应取 。
A ．1H ；B ．π21Ｈ； C ．21H ； D ．241πＨ二、填空题1．若Ω=3R ，Ω=ω6L ，Ω=ω2011C ，Ω=ω2012C ，则图9—5所示电路的输入阻抗为 j4)3(-Ω。
.2．线性一端口电路如图9—6所示，A /02 V ,30/5000=-=I U。
则此一端口电路吸收的复功率，有功功率、无功功率分别为V A 30/1000、W 350、50Var 。
电路分析习题(第九章)答案
第九章 正弦稳态电路的分析计算下列各题，并说明电路的性质。
（1）??,55,30100==Ω+=∠=••P I j Z V U（2）???,1653,153000===-∠-=∠=••P X R A I V U（3）???,5,301000300====∠-=-••P X R A e I V U j在如图所示的各电路图中，除A 0和V 0外，其余电流表和电压表的读数在图上都已标出（都是正弦量的有效值），试求电流表A 0或电压表V 0的读数。
在RLC 串联电路中，已知，Ω=50R ，mH L 60=，F C μ100=s rad /1000=ω，V U C ︒∠=010&，试求：（1）电路的阻抗Z ；（2）电流•I 和电压•U 、•L U 及有功功率P 、Q 、S ；（3）绘电压、电流相量图。
在图示电路中，V )30314sin(23600+=t u ，R 1=32，R 2=60，X 1=48，X 2=80。
求总电流i ，总有功功率P 及总功率因数。
I.I .I .U .R R j j 1212XX 12+－在如图所示的电路中，,51A I =,252A I =,110V U =,5Ω=R ,2L X R =试求,I ,C X L X 2R 及。
在如图所示的电路中，i u V U A I I 与,100,1021===同相，试求L C X X R I 及,,。
单相交流电路如图所示，已知ο&60401∠=U V ，Ω=5C X ，Ω==4L X R 。
求：（1）电流I &及电压2U &、U &；（2）电路的P 、Q 、S 。
图示电路中，并联负载Z 1、Z 2的电流分别为I 1=10 A ，I 2=20 A ，其功率因数分别为)0(6.0cos ),0(8.0cos 222111>==<==ϕϕλϕϕλ，端电压U =100 V ，ω=1000 rad/s 。
电路原理：第9章 正弦稳态电路的分析
1000 166.99 52.3
0.652.3
A
I2
j
1 C
1 R1 j C
I1
j318.47 1049.5 17.7
0.652.3
0.181 20
A
I3
R1
R1 j 1
C
I1
1000 1049.5 17.7
0.652.3
0.5770
A
例2.
_
列写电路的回路电流方程和节点电压方程
Z Z1Z2 Z1 Z2
例 求图示电路的等效阻抗， ＝105rad/s 。
解 感抗和容抗为：
X L L 105 1103 100
1
1
XC C 105 0.1106 100
R1
30 1mH
R2 100 0.1F
Z
R1
jX L (R2 jX C ) jX L R2 jX C
U I
j
L
jX L
Z可以是实数，也可以是虚数
2. RLC串联电路
iR
L
+ + uR - + uL - +
u
C uC
-
-
.
IR
j L
+
+
.
U
-
R
+
.
U
L
-
.
1
U -
jω C
+. -U C
..
由KVL： U UR
[R j(L 1 C
.
U
)]
.
L UC
I [R
.
RI
j( X
.
jL I j
第9章 正弦稳态电路的分析(2010-2011第一学期 邱关源)
第九章 正弦稳态电路的分析
§9-3 正弦稳态电路的分析
第九章 正弦稳态电路的分析
§9-3 正弦稳态电路的分析
第九章 正弦稳态电路的分析
§9-3 正弦稳态电路的分析
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
无源单口网络N0任一时刻输入的瞬时功率为该时刻 电压和电流的乘积，即
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
3. 视在功率 由于变压器等电力设备的容量是由它们的额定电压 和额定电流（均指有效值）的乘积决定的，为此引入视 在功率的概念，用大写字母S来表示
S UI
显然有
S 2 P 2 Q 2 S P2 Q 2
P S cos
Q S sin
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
瞬时功率还可以表示为
p UI cos UI cos 2t UI cos UI cos cos 2t UI sin sin 2t UI cos 1 cos 2t UI sin sin 2t
式中Y的实部就是电路中的电阻G，虚部即电抗B为
B BC BL C
1 BC C 为电容的电纳，简称容纳；BL 为电感的电 L
1 L
纳，简称感纳。
第九章 正弦稳态电路的分析
§9-1 阻抗和导纳
当 时，容纳的作用大于感纳的作用， 电路呈容性，这时， Y ,电流的相位超前于电压的 0 相位。 当 时，感纳的作用大于容纳的作 用，电路呈感性，这时，Y 0 ,电压的相位超前于电 流的相位。 B<0，即 C
电路课件 第九章 正弦稳态电路的分析
u 0
2 G 2
பைடு நூலகம்
I L IC
I
I I I I (IC I L )
2 G 2 B
y
IB U
IG
注意
RLC并联电路会出现分电流大于总电流的现象
返 回 上 页 下 页
第 九 章
正 弦 稳 态 电 路 的 分 析
等效电路
+ I
IR
IB
U
R
-
1 jCeq
（3）C<1/L，B<0，y<0，电路为感性，
电流落后电压；
y
U
IG
I
I I I I (I L IC )
2 G 2 B 2 G
2
IC
IL
返 回 上 页 下 页
第 九 章
正 弦 稳 态 电 路 的 分 析
I
等效电路 +
U
IR
R
（4）C=1/L，B=0， y
j Leg
IB
=0，电路为电阻性，
电流与电压同相。
U -
UX
UC
返 回
上 页
下 页
第 九 章
正 弦 稳 态 电 路 的 分 析
例
已知：R=15, L=0.3mH, C=0.2F,
u 5 2cos( t ), f 3 10 Hz.4 60
求 i, uR , uL , uC . 解 画出相量模型
U 560 V j L j2π 3 104 0.3 103
邱关源《电路》第九章正弦稳态电路的分析1
BUCT
设备额定容量SN向负载送多少有功功率要由负载的阻抗角决定。
cosj = P/S
SN
负载 cosj = 1, P =S=75kW
75kVA
cosj = 0.7, P=0.7S=52.5kW
功率因数低带来的问题：
S
j2
Q2
(1) 设备不能充分利用，效率低； P2
S
j1
Q1
P1
(2) 当输出相同的有功功率时，线路上电流大 I=P/(Ucosj )，线路压降损耗大。
反映电气设备（如：发电机、变压器等）的容量。
BUCT
功率、电压、阻抗三角形
S
•
U
•
Q
Z
j
UX X
阻抗三角形 R
•
UR
电压三角形
P
功率三角形
S = P2 + Q2
+
U
R
_
º+ R +
U_
U_X
jX
º
9
交流电路功率的测量
i
*
W
*
+ u
Z
i1
-
i2 电压线圈
R 电流线圈
W1
A1
V1
*
* * 0.75A 3A 125V 500V 1.5A自动 250V U V W N
第九章 正弦稳态电路的分析
BUCT
9. 1 阻抗和导纳 9. 2 阻抗（导纳）的串联和并联 9. 3 电路的相量图 9. 4 正弦稳态电路的分析 9. 5 正弦稳态电路的功率 9. 6 电路的谐振
1
9. 3 电路的相量图
一、RL、RC串联电路
《电路》课件：第九章 正弦稳态电路的分析1-3
(4) 当 z 90 ~ 0或Y 0 ~ 90 时为容性
§9-2 阻抗(导纳)的串联和并联
1．串联：
Z Z1Z 2Z n
分压：
U k
Zk Z
U
2．并联：
1 1 1 1
Z Z1 Z2
Zn
Y Y1 Y2 Yn
分流：
Ik
Yk Y
I
例5-4-2 如图RLC串联电路。R= 2105 ，L= 152 mH，C= 150 F，
（2〕当ω =1 rad/s
Zac
1.5
1 2
j(2
1) 2
2
j1.5
（Ω
）
等效相量电路如图
ch9s1-7 例5-4-2 求如图RLC串联电路的阻抗
解：
Zi
R
j(L 1 ) C
X L 1 C
R jX
Zi R2 X2
Zi z
当
z
tg 1
X R
(1)L 1 C
即
＝
1 LC
时，Zi
端电压 u=141.4cos(5000t)V。
求：i、元件的电压相量。
解： 用相量法。
U 1000 (V ) 5000(rad / s)
Z R j L 1
1250
j(5000
j
1125
C
10 3
5000
1 15 0
10 6
)
I
U R
1250 U Z
IR
j2505 2558.52 5730.1.03 ()
R
(2)L 1 C
即
1 LC
时，感性Zi
(3)L 1 C
即
1 LC
最全第九章(正弦稳态电路分析)习题解答打印版.doc
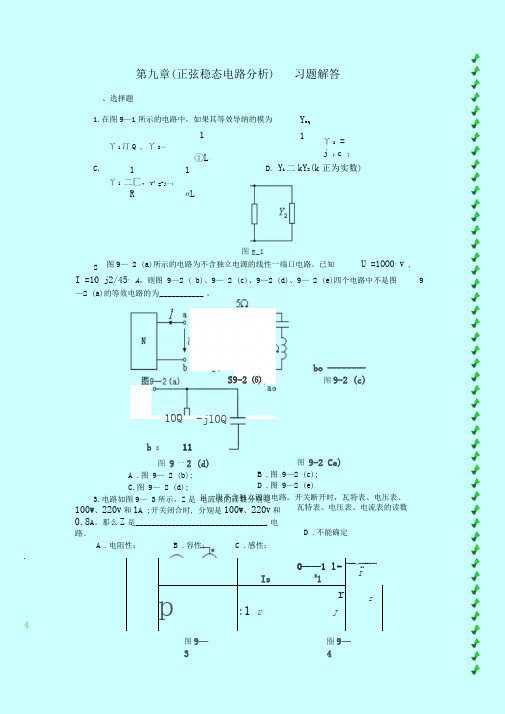
、选择题第九章(正弦稳态电路分析)习题解答1.在图9—1所示的电路中，如果其等效导纳的模为C .1丫1汀Q , 丫2…①L11 丫1 二匚，Y^ =-j —;R«LY eq1丫2 =j ,c ；D . Y i 二kY 2(k 正为实数)图g_i图9— 2 (a )所示的电路为不含独立电源的线性一端口电路。
已知U =1OO0°V ,I =10 j2/45° A ，则图 9—2 ( b )、9— 2 (c )、9—2 (d )、9— 2 (e )四个电路中不是图 9—2 (a )的等效电路的为 ___________ 。
2. S9-2 ⑹10Q -jlOQbo --------图9-2 (c)b D11图 9一2 (d)A .图 9— 2 (b );C .图 9— 2 (d );3.电路如图9— 3所示，Z 是 电流表的读数分别是100W 、220V 和1A ;开关闭合时, 分别是100W 、220V 和0.8A 。
那么Z 是 _________________________________ 电路。
A .电阻性；B .容性；C .感性；图 9-2 Ce)B .图 9—2 (c ); D .图 9—2 (e ) 旦一段不含独立源的电路。
开关断开时，瓦特表、电压表、 瓦特表、电压表、电流表的读数 D .不能确定%O ——1 l -IsZ1---------- ► -----------------■■I 4pr:1 UJTz图9—圏9—入阻抗为（3 - j4）门。
09-52 .线性一端口电路如图 9—6所示, 吸收的复功率，有功功率、无功功率分别为U - -50 /300V, I =2/0^A 。
则此一端口电路100/30°VA 、50 .. 3W 、50Var 。
4.在图9 — 8所示电路中，已知电流表 表V 2的读数为20 V ，则电压表V 的读数为A 的读数为2A ，电压表V 的读数10V ，电压V 。
第09章 正弦稳态电路的分析..
U
-
UR
UL
UR 60(53.13 )V
U L 24036.87 V UC 160(143.13 )V
0
U
I
5μF
UC -
UL
0
I
U
53.13
UC UC UR
UL
UR
（a）
（b）
例2：画出上节例2电路的相量图
I 10Ω
0.5H +
I 0.6052.30 A
U 1000 I 4(53.13 )A Z eq 2553.13
正弦电流 i 为
i 4 2 cos(5000t 53.13 )A
I 15Ω 12mH + + - + UR UL U 5μF
-
UC -
+
各元件电压相量为：
UR R I 60(53.13 )V
二、 绘制相量图的目的
1. 可以直观地显示各相量之间的关系，主要是各 元件之间的拓扑连接关系，即KCL和KVL关系；
2. 借助于相量图可以方便交流电路的分析和计算。
三、绘制相量图的一般方法
1. 如果绘制电路串联支路部分的相量图，则以电 流相量作为参考相量，根据支路元件的VCR确定 有关电压相量，然后再根据回路上的KVL方程， 用相量平移求和的法则，画出回路上各电压相量 所组成的多边形；
Yeq Y1 Y2 Yn
各个导纳的电流分配为：
Yk Ik I (k 1, 2, Yeq
电路课件第九章正弦稳态电路的分析
04
正弦稳态电路的谐振
串联谐振
串联谐振的定义
在串联电路中，当电路的感抗等 于容抗时，电路呈现纯电阻性质， 此时电路中的电流与电压同相位，
这种现象称为串联谐振。
串联谐振的特点
在串联谐振时，电路的阻抗最小， 电流最大；电感和电容上的电压大 小相等，方向相反，互相抵消。
串联谐振的应用
串联谐振在电子、通信、电力等领 域有广泛应用，如收音机的调谐电 路、无线电通信的滤波器等。
无功补偿作用
无功补偿能够提高电力系统的效率，减少能源浪费，并有助于维持电力系统的 稳定运行。
无功补偿的方法和实现
无功补偿方法
无功补偿的方法包括并联电容器、静止无功补偿器（SVC）、静止无功发生器 （SVG）等。
无功补偿实现
无功补偿的实现通常需要在电力系统中安装相应的无功补偿装置，并根据电力系 统的实际情况进行配置和控制。
分析的重要方法之一。
阻抗和导纳的概念
阻抗是表示电路对电流阻碍作用的物 理量，由电阻、电感和电容共同决定。
在正弦稳态电路中，阻抗和导纳都是 复数，可以用实部和虚部表示。
导纳是表示电路导通能力的物理量， 由电导和电纳共同决定。
阻抗和导纳是分析正弦稳态电路的重 要概念，对于理解电路的工作原理和 计算具有重要意义。
功率因数（Power Factor）是衡量电 力设备效率的指标，它表示了电力设 备在能量转换过程中，有功功率与视 在功率的比值。
功率因数计算
功率因数可以通过测量电压和电流的 波形，然后计算有功功率和视在功率 来实现。在实际应用中，功率因数通 常由电力表直接给出。
无功补偿的概念和作用
无功补偿概念
无功补偿（Reactive Power Compensation）是指在电力系统中，通过引入 无功电源，以改善电力系统的电压质量和稳定性，同时减少线路损耗和变压器 损耗。
电路(第五版)第九章 正弦稳态电路的分析12共52页文档
U . U .R U .L U .C R I . jL I . j1 C I .
[R j( L 1 C )I ] [R j(X L X C )I ]
(RjX)I
j Z R j(L 1 C ) R j( X L X C ) R jX Z
L 1 C
X0, j0
Z2
•
I
Z1 Z2
(分流公式)
并:联 Y Y k,
I•kY k
•
I
Y k
例：已知 Z1=10+j6.28, Z2=20-j31.9 , Z3=15+j15.7 。
a Z3
求 Zab。
Zab
Z2
Z1
b
ZabZ3Z Z 11 Z Z 22Z3Z ZZ 1Z 2 (1 0j6.2)8 2 ( 0j3.9 1 )
•
(Z1 Z2)I
•
Z
U
•
Z1
Z2
I
•
U1
Z1
•
I
Z1 Z
•
U
(分压公式)
串:联 Z Z k,
U •kZ k
•
U
Z k
•
I
•
•
Y
+
•
U
Y1
I1
Y2
I2
-
•
Y
I
•
Y1 Y2
U
•
I1
Y1U• YY1
•
I
•• •
I I1I2
•
•
Y1UY2U
•
(Y1 Y2)U
Z Z1Z 2 Z1 Z2
•
I1
（1）R：
•
•
第九章正弦交流稳态电路习题
第九章正弦交流稳态电路习题9—1 图9—25所示电路，当开关S 合上和断开时，电流表的读数不变，求：L X 和C X 的关系。
9—2 图9—26所示电路正弦交流电路，电压60=U V ，Ω=Ω=40,40C X R ，开 关S 于位置1时，电压表的读数○V =48V 。
求：开关S 于位置2时电压表的读数。
图9—25 图9—269—3图9—27所示电路，222L R U U U +=是否正确？试用相量图说明。
9—4 图9—28所示电路正弦交流电路中，已知Ω=10R ，Ω=101C ，bc ab U U =，U与I同相。
求：电路的阻抗Z 。
图9—27 图9—289—5 图9—29所示电路正弦交流电路中，已知Ω=71R ，Ω=12R ，2=L H ，1=C F ，4=ωrad/s 。
求：（1）输入阻抗；（2）用两个串联元件等效时，元件的参数值；（3）用两个并联元件等效时，元件的参数值。
9—6 为确定电感线圈的参数R 和L ，用一只Ω1000电阻1R 与线圈并联，如图9—30所示，另以一电流表依次测得各支路的电流为：04.0=I A ，035.01=I A ，01.02=I A 。
已知Hz f 50=，试计算R 和L 。
图9—29 图9—309—7 如图9—31所示的电感线圈接到120=U V 的直流电源上时，电流为20A ，接到50=f Hz ，220=U V 的交流电源上时，电流为25A 。
求：线圈的R 和L 。
9—8 图9—32所示电路中，已知Ω=100R ，Hz f 50=，要使1U 和2U 间相位差为︒60，则C 应为多大？图9—31 图9—329—9 阻抗为Ω+=1.01.0j Z l 的输电线末端，接上10=P kW ，9.0cos =φ的感性负载，如图9—33所示，负载两端电压2202=U V 。
求：线路输入端的电压1U 及功率因数φcos 。
9—10 图—34所示正弦交流电路中，1,121=Ω==L R R H ，C 可变，10=ωrad/s 。
第9章正弦稳态电路分析1
9.1 阻抗与导纳 . I = G + jB = | Y | Y Y= . U B = BL+ BC = 1 +ωC ωL B 2+B2 Y = arctg |Y| = G G
+ I U
.
.
I1 R . I3
.
I2 jωL 1 jωC
.
I3
.
. . I1 = I
. U
. I2
9.1 阻抗与导纳 3. 阻抗与导纳的相互等效 Z(jω) = R(ω) + jX(ω) Y(jω) = G(ω) + jB(ω) 一端口的阻抗和导纳可 以互换,等效互换的条 件为: Z(jω) Y(jω) =1 分开写 | Z | | Y | = 1 Z + Y = 0
. + I . U 含线性 无源元 件的一 端口N0
若已知 Z = 5 30ο 1 = 0.2 S 则 |Y| = |Z|
Y = z =30ο
所以 Y = 0.2 -30ο S
9.1 阻抗与导纳 若已知 Z=R+jX ,求等效的 Y=G+jB (R jX) 1 = 1 = Y 则: = Z R + jX (R + jX) (R jX) X = G + jB R = 2 2 +j 2 2 R +X R +X = R2 = X2 G B |Z| |Z| 若已知 Y = G + jB 等效成 Z = R + jX 则 R = G2 |Y| B X= 2 |Y|
.
I1
.
I2 1 jωC
.
I3
.
9.1 阻抗与导纳 . I = G + jB = | Y | Y Y= . U B = BL+ BC = 1 +ωC ωL B 2+B2 Y = arctg |Y| = G G 结论: 对于 RLC 并联电路
正弦电流电路-习题课
正弦稳态电路分析习题课正弦稳态电路分析习题课例1:i正弦稳态电路分析习题课例2:指出下列结果是否正确,若有错,试将其改正。
正弦稳态电路分析习题课i 正弦稳态电路分析习题课i s6正弦稳态电路分析习题课已知：电流表读数为1.5A(有效值)。
例5:正弦稳态电路分析习题课Ω40•I &正弦稳态电路分析习题课例6:已知:5ΩV )452sin(2)(o −=t t u 正弦稳态电路分析习题课I &Z 正弦稳态电路分析习题课例7：如图所示正弦稳态电路中，电流A 1、A 2的指示均为的读数。
满足KCL 的，相量满足o 01090j =o A o 452∠读数为14.1A正弦稳态电路分析习题课如图U =220V ，f =50H ，例8:•1I 正弦稳态电路分析习题课220U正弦稳态电路分析习题课例9:正弦稳态电路如图示，V1•正弦稳态电路分析习题课V1•正弦稳态电路分析习题课V1正弦稳态电路分析习题课例正弦稳态电路分析习题课正弦稳态电路分析习题课例12：设计RLC 带通滤波器电路，已知总电阻为正弦稳态电路分析习题课R L Cu s1u s2I&例11：如图所示电路，已知kHz 1210−Aμ142103106=×−正弦稳态电路分析习题课正弦稳态电路分析习题课例14：在串联谐振电路中电源内阻，电阻R代表线。
试求电阻R、电容C、。
Ω=1R 实际线圈模型正弦稳态电路分析习题课∴正弦稳态电路分析习题课设计电路，并计算互感线圈的各元件值。
当画耦合电感T型去耦等效电路时，若互感线圈两正弦稳态电路分析习题课据以上分析，所设计的互感电路(b)(a)正弦稳态电路分析习题课例16：P314 7-10求：i (t)和它的有效值I解：画出每一个频率分量的电路相量模型(0频率)(ω频率)50=I &)(&1⎟⎟⎞⎜⎜⎛正弦稳态电路分析习题课(3(9()()t t i ω6.17sin 74.135−+=o 正弦稳态电路分析习题课)V t ⎥⎦⎤ω2正弦稳态电路分析习题课0=I &0=∴U &。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
已知： u 已知： S = 2U cos(ωt +ψu )
应用三要素法： 应用三要素法： +
R L
+
iL(0− ) = iL(0+ ) = 0
用相量法求正弦稳态解
τ =L R
练习3. 练习
列写电路的回路电流方程和节点电压方程 & _ US _ us + + L R1 R4 R2 R3 C
is
jωL R1 ω
& I2 R4
& I1
R2
& I3
& I4
1 −j ωc
& IS
R3
解
回路法: 回路法
& & & & (R1 + R2 + jωL)I1 − (R1 + jωL)I2 − R2 I3 = US & & & (R1 + R3 + R4 + jωL)I2 − (R1 + jωL)I1 − R3 I3 = 0 1 & & −R I − j 1 I =0 & & (R2 + R3 − j )I3 − R2 I1 3 2 4 ωC ωC & &
I4 = −IS
& _ US
& Un1 +
R2
& IS
−j 1 ωc
jωL R1 ω
R4 节点法: 节点法
& Un2
R3
& Un3
& & Un1 = US 1 1 1 & 1 & 1 & ( + + )Un2 − Un1 − Un3 = 0 R1 + jωL R2 R3 R2 R3
1 1 & − 1 U − jωCU = −I & & & ( + + jωC)Un3 n2 n1 S R3 R4 R3
_
+ & U _
• I1 R & 1 + I 2 jX C UC •
& I2
& I1 & UL
I3
jXL
& UR1 & UC
R2
900
450
解 用相量图分析 & & & I1 = I2 + I3 = 10 2 + 10∠1350 = 10∠450 ⇒ I1 = 10A & & & U = UR1 + UC ⇒ 200 = 5×10 + UC ⇒UC = 150V
Z1
Z3
Zeq = Z1 // Z3 + Z2
•
= 15 − j45
& U0 84.86∠45o & I= = Z0 + Z 15 − j45 + 45 = 1.13∠81.9o A
Zeq + •
U0
I
Z
-
பைடு நூலகம்
练习5 求图示电路的戴维南等效电路。 练习 求图示电路的戴维南等效电路。
•
4I 1
＋
& 200I1 _
正弦稳态电路的 电路的分析 第9章 正弦稳态电路的分析
习题课） （习题课）
要点串讲： 要点串讲： 习题练习： 习题练习：
正弦交流电路分析的步骤：
1、画出对应的向量图，（包括：各电流、电压的向量， 、画出对应的向量图，（包括：各电流、电压的向量， ，（包括 电阻、电容、电感的阻抗）； 电阻、电容、电感的阻抗）； 2、按照稳态电路的方法分析和处理向量，得出所求 、按照稳态电路的方法分析和处理向量， 的向量。（注意是复数的运算）； 。（注意是复数的运算 的向量。（注意是复数的运算）； 3、按要求将所要求的向量写回正弦交流形式. 、按要求将所要求的向量写回正弦交流形式
R2 =| Z2 | cosθ2 = 19.6 L = X2 /(2 f ) = 0.133H π
| Z2 |= U2 / I = 80 / 1.73 = 46.2 X2 =| Z2 | sinθ 2 = 41.8
方法二、 方法二、
I R1
+ U _ & + 1 R 2 & U _ L2 +
•
& & & U = U1 + U2 = 55.4∠00 + 80∠ϕ = 115∠θ
I R1
+ U _ & + 1 R 2 & U _ L2
& U
•
练习9 练习
+
& U2 _ 解
已知： 已知：U=115V , U1=55.4V , U2=80V , R1=32Ω , f=50Hz Ω 线圈的电阻R 和电感L 求： 线圈的电阻 2和电感 2 。 方法－、 画相量图分析。 方法－、 画相量图分析。
•
& IS
解
•
•
US
(2) US 单独作用I S 开路 : ( )
US I2 = − Z2 + Z3
''
• •
•
•
(1) I S 单独作用US 短路 : ( )
Z3 I2 = I S Z2 + Z3 50∠30o = 4∠0o × 50∠ − 30o + 50∠30o 200∠30o = = 2.31∠30o A 50 3
Z1
解 平衡条件：Z1 Z3= Z2 Zx 得 平衡条件：
Z2
|Z1|∠ϕ1 •|Z3|∠ϕ3 = |Z2|∠ϕ2 •|Zx|∠ϕx ∠ ∠ ∠ ∠ |Z1| |Z3| = |Z2| |Zx|
Zx
Z3
∼
ϕ 1 +ϕ 3 = ϕ 2 +ϕ x
R1(R3+jωL3)=R2(Rx+j ωLx) ∴ Rx=R1R3 /R2 , Lx=L3 R1/R2
j4(15−j15) = 15−j15−j30+45
5.657∠45o = 1.13∠81.9o A = 5∠- 36.9o
方法二： 方法二：戴维南等效变换 Z2
求开路电压： 求开路电压：
& & U0 = IS (Z1 // Z3 )
& U0
& IS
= 84.86∠45o V
求等效电阻： 求等效电阻：
Ω Ω 练习8 已知： 练习 已知：Z=10+j50Ω , Z1=400+j1000Ω。 & & 等于多少时， I 90 β 问： 等于多少时，1和US相位差 o ? I Z
•
+
•
•
I1
•
US _
Z1
β I1
& 关系： & 分析： I U 分析：找出&1和US关系： & S = Z转I1， Z转实部为零 相位差为 o. , 90
解
& & & & US = ZI + Z1I1 = Z(1 +βI1 + Z1I1 )&
& US ) β β & = (1+βZ + Z1 = 410 + 10 + j(50 + 50 + 1000) I1
β 令 410 + 10 = 0 ，β −41 =
& US & = −j1000 I1 90 故电流领先电压 o.
Z2 = R2 + jωL = 10 + j157 Ω
Z = Z1 + Z2 = 92.11− j289.13 + 10 + j157 = 102.11− j132.13 = 166.99∠ − 52.3 Ω
o
& I1
+ & U _
& I2 R1
1 & I3 − j ωC
R2
jωL ω
Z1
Z2
& U 100∠0o & I1 = = = 0.6∠52.3o A Z 166.99∠− 52.3o
& I1
+ & U _
& I2 R1
& I3
−j
1 ωC
R2
jωL ω
Z1
Z2
解
画出电路的相量模型 R1(− j 1 ) 1000×(− j318.47) 318.47×103 ∠− 90o ωC = Z1 = = 1000 − j318.47 1049.5∠−17.7o R1 − j 1 ωC = 303.45∠ − 72.3o = 92.11− j289.13 Ω
练习4. 练习
Z2 Z1 Z3
已知：& 已知：IS = 4∠90o A , Z1 = Z2 = −j30
& IS
& I 求：I. & Z 解
Z3 = 30 , Z = 45
方法一： 方法一：电源变换
Z2 Z1// 3 //Z + & (Z1 // Z3 )IS
& I
Z
30(− j30) Z1 // Z3 = =15 − j15Ω 30 − j30 • & IS(Z1 // Z3 ) I= Z1 // Z3+Z2+Z