北理工07级第一学期信号与系统B类B卷
北理工《信号与系统》习题答案第2章答案(纯手写)

xt*)*?23 u.D
k,r*t-^ at+L (aN)
hLt-4nb)
)= qa)(4t*x t&xI
L tt-t1=Gt + z
=) l, 'xt = ({'- e-121 ) u,t*1
btl L ul = + (e-t- u-%) LtLt)
@) | ht ft) = a{m+ cyte
{) a=o
(I C, =l
\ lU Ur= C e-c atrr 7 C,ito;t
,
hnttl:
t
+
O-l) ,at
ht-r{*/-t)+--e "tr;t +e "C.rDt
) i, Lt) = 0o D i,,*t
)l =
dr (-b-A) ryz/L) clx = 1z Lt)x 4, th)
t Crto
-o) (D'-+?/D+zl!/ot=o t flr.o)=1, g'ttro)=z
; ; :t,r,il,Aln= co-m + cro''6 -J
) h,n*)= L'vt-o-'t-tzo
0, kl = d N bt) l,u*) = lw> u u,4,L) = ,f! U
= Lb, ct+t) _ 2 + g *-,., ] *, J -I r/" Lzr) al t -, I-t*r,ol,
-t,-ttt-itUt --;t,e---*rkt) = (+L-t-)tu-'+*wt ) t,LLt)
信号与系统2007-7B

2006-2007学年第2学期考试试题 (B )卷课程名称 《信号与系统》 任课教师签名 王龙海 出题教师签名 王龙海 审题教师签名考试方式 (闭 )卷 适用专业 通信工程考试时间 (120 )分钟(所有答案请写在答题纸上,注意:应给出详细的答题步骤)一、 分析判断题(2×10分)1、计算下列信号的能量与功率,判断信号是能量信号还是功率信号?(a) ()t e t f -=(b) ()()42cos 6k k f π=2、分析讨论下列系统的因果性、线性性、时变性。
(a)()()()224'+=-+t f t y t y(b) ()()at f t y 2= (c) ()()()52'+=-t f t y t y (d) ()()32+=k f k y (e) ()()()k f k y k k y k =+++12232二、利用傅立叶变换、拉氏变换的性质求解下列各题(2×10分)1、求信号()()()t t e t f t -=-12εε的傅立叶变换()ωj F 及频谱()()ωωωcos 8⎪⎭⎫ ⎝⎛=Sa j F的傅立叶反变换()t f 。
2、试求()()()12-=--t te t f t ε的拉氏变换()s F 及()()1123-=s s s F 的原函数()t f 。
3题图4、线性系统的特征方程为04223=+++K s s s ;求系统稳定时K 的取值范围。
5、将如图所示的系统框图改画为信号流图,并求系统函数()s H 。
5题图6、某线性非时变系统的差分方程为()()()()k k y k y k y k ε22213=-+-+,当初始状态为(),01=-y ()5.02=-y 时, 求零输入响应、零状态响应和全响应。
北京理工大学2019-2020-学年-第二学期《信号与系统》期末试题

北京理工大学 2019 - 2020 学年 第二学期
2017 级《信号与系统 B》期末试题 A 卷
班级
学号
姓名
成绩
答题说明: 1. 如无特别说明,试卷中的“系统”均为线性时不变系统; 2. 必须写出解题步骤和必要的文字说明,只写答案不给分。
一、(本题共 60 分,6 道小题,每小题 10 分) 1) 计算卷积 u(t) eatu(t) 。
F
2)已知函数 f t e-3tu(t) ,通过傅里叶变换得出其频谱函数
。
3)若信号
x(
t 2
)
最高角频率为
m
,求对
x(
t) 3
采样的最大时间间隔
Tmax
。
1
4) 线性时不变离散系统的单位抽样响应 hn 1 n u1 n,试判定系统的因果性和
2 稳定性。
5)已知因果序列 x[n] 的y(zt)变换 X (z)
2
5z2 1
1 ,试求 x[n] 的初值 x[0] 和
(z )(z )
32
终值 x[]。
6)知系统函数 Hs
s2 3s 2
,完整见172,7791,836,试判断系统的稳定性,并
8s4 2s3 3s2 s 5 说明是否有
位于 s 平面右半平面上的极点,有几个。 )
二、(本题 10 分)
7)已知某系统 S 由两个子系统 S1 并联而成,子系统 S1 在信号 x1 t cost ut 激 励下的零状态响应为 y1 t Asint ut 。
(a) 求系统 S 的单位冲激响应;
(b) 计算系统 S 在信号 x t ut ut 2 激励下的零状态响应 y t ;
07级1-2班《计算机组成原理》期末考试卷(B卷)

07级1-2班《计算机组成原理》期末考试卷(B卷)2009-2010学年第⼀学期计算机科学学院07级(1-2)班《计算机组成原理》期末考试卷(B 卷)2、此试卷适⽤于计算机科学与技术本科专业。
⼀、填空题(本题共10⼩题,每个空1分,共20分)1.计算机软件⼀般分为两⼤类:⼀类叫__系统软件____________ ,另⼀类叫____应⽤软件________ 。
操作系统属于__系统软件____________ 类。
2. BCD 码的含义是⼆进制编码的⼗进制数,最⼴泛使⽤的⼀种BCD 码是 8421BCD 码。
3.若浮点数的尾数⽤补码表⽰,当运算结果的两位符号位和⼩数点后的第⼀位是 00.1 或 11.0 时,表明结果是规格化的数。
4.每条指令由两部分组成,即操作码部分和地址码部分。
5.在补码⼀位乘法中,如果判断位Y i Y i-1=10,则下⼀步(但不是最后⼀步)的操作是将部分积加上 [-X]补,再向右移⼀位。
(设x 为被乘数,y 为乘数)6.静态 RAM 是利⽤触发器电路的两个稳定状态来表⽰信息——————————————装————————————————订————————————————线————————————————————————————————“0”和“1”,故在不断开电源时,可以长久保持信息;动态RAM利⽤电容器存储的电荷来表⽰信息“0”和“1”,因此需要不断进⾏刷新。
7.某半导体存储器的地址码为16位,因此该机由地址码计算出的主存最⼤容量为64K 个单元。
8.由于⼀个存储器芯⽚的容量和位数⼀般不能满⾜使⽤要求,所以通常将若⼲个芯⽚按串联(或地址串联)和并联(或位并联) 两种⽅式相连接。
9.根据⽬前常⽤的存储介质将存储器分为_____半导体存储器__ ____、_____磁表⾯存储器 ____和光盘存储器三种。
10.按数据传输格式来分,I/O接⼝类型可分并⾏接⼝和串⾏接⼝两种。
⼆、选择题(本题共10⼩题,每个空1分,共10分)1、若X=-0.1010,则其对应的[X]补为(A)。
北京理工大学信号与系统考研复习题

目录目录 (1)复习题一 (2)答案 (4)复习题二 (8)答案 (13)复习题三 (25)答案 (40)复习题四 (71)答案 (72)复习题五 (74)答案 (81)复习题六 (96)答案 (97)复习题七 (99)复习题八 (108)复习题一1.1 选择题(每小题可能有一个或几个正确答案,将正确的题号填入[ ]内) 1.f (5-2t )是如下运算的结果————————( ) (1)f (-2t )右移5 (2)f (-2t )左移5 (3)f (-2t )右移25 (4)f (-2t )左移251.2 是非题(下述结论若正确,则在括号内填入√,若错误则填入×) 1.偶函数加上直流后仍为偶函数。
( )2. 不同的系统具有不同的数学模型。
( )3. 任何信号都可以分解为偶分量与奇分量之和。
( ) 4.奇谐函数一定是奇函数。
( ) 5.线性系统一定满足微分特性 ( )1.3 填空题1.=⋅t t cos )(δ=+t t 0cos )1(ωδ=-⋅)(cos )(0τωδt t=--)2()cos 1(πδt t=--⎰∞∞-dt t t )2()cos 1(πδ ⎰+∞∞-=⋅tdt t cos )(δ⎰+∞∞-=tdt t 0cos )(ωδ ⎰∞-=td ττωτδ0cos )(⎰+∞∞-=+tdt t 0cos )1(ωδ⎰∞-=+td ττωτδ0cos )1(2.=⋅-at e t )(δ=⋅-t e t )(δ⎰∞--=td e ττδτ)(⎰∞∞--=--dt t e t t )1(][22δ⎰∞∞--=dt e t at )(δ1.4 简答题1.画出题图一所示信号f (t )的偶分量f e (t )与奇分量f o (t )。
图一2.)(t f 如图二所示,试画出)(t f 的偶分量)(t f e 和奇分量()o f t 的波形。
t图二3.某线性时不变系统在零状态条件下的输入e (t )与输出r (t )的波形如题图三所示,当输入波形为x (t )时,试画出输出波形y (t )。
北京理工大学信号与系统试题

1 .按照信号的能量或功率为有限值,信号可分为和。
2 .一个离散时间系统可由、、等基本部件组成。
3 .如图所示 LTIS ,若, , ,则系统的输出为。
4 .应用卷积积分的方法可以得到系统的。
5 .6 .试写出下列函数的频谱密度函数(a) , 所以(b) , 所以7. x(n) 的离散时间傅立叶变换为 X(e ), 则 y(n)= 的傅立叶变换为8. 果而稳定的 LTI 系统,单位冲击响应为 h(t) , 系统 H(s) 有一极点在s= -2, 则是9. 知一因果而稳定系统的单位脉冲响应为 h(n),H(z) 是有理的,且, 则10 .二、计算题1 .设三个因果 LTI 系统的级联如图 1 所示,其中冲激响应而总的冲激响应如图 2 所示,求(a)冲激响应(b) 整个系统对输入的响应2 .考虑一个 LTI 系统它对输入的响应为(a) 求该系统的频率响应(b) 确定该系统的冲激响应(c) 求出联系输入、输出的微分方程,并用积分器、相加器和系数相乘器实现该系统。
3 .如图所示,系统(1) 以为状态变量列出其状态方程与输出方程(2) 求状态转移矩阵4.的单边拉氏反变换5.已知信号 x(n) 的傅立叶变换, 求的傅立叶反变换试题一答案一. 填空题1 .答案:(能量信号,功率信号)2 .答案:(单位延时器、相加器、倍乘器)3 .4 .答案:(零状态响应)5 .答案:6 .答案:(a)7.8.9.10 .二、计算题1 .答案:2 .解 :(a)(b)(c)3 .解 :(1)(2)4.解:(分子阶次与分母阶次相同,降阶)(分母多项式带有重根的部分分式展开法)又因为求单边拉氏变换所得信号为因果信号5.解:(注:文档可能无法思考全面,请浏览后下载,供参考。
)。
10.北京理工大学信号与系统精品课程习题及答案.doc
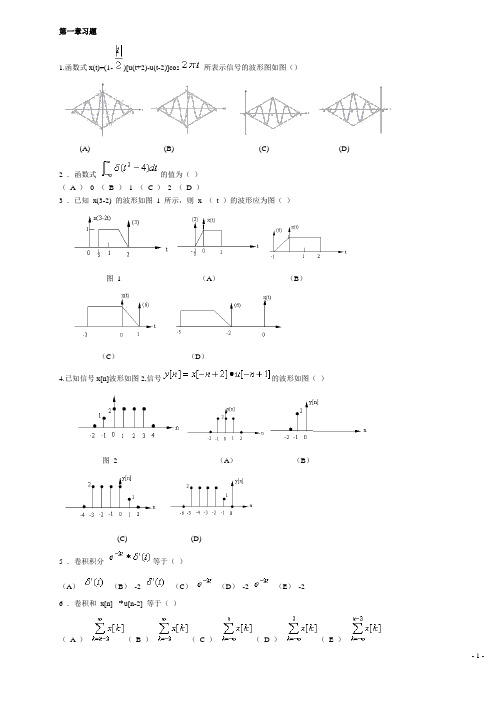
第一章习题1.函数式x(t)=(1-)[u(t+2)-u(t-2)]cos所表示信号的波形图如图()(A) (B) (C) (D)2 .函数式的值为()( A )0 (B )1 ( C ) 2 (D )3 .已知x(3-2) 的波形如图1 所示,则x (t )的波形应为图()图1 (A)(B)(C)(D)4.已知信号x[n]波形如图2,信号的波形如图()图2 (A)(B)(C) (D)5 .卷积积分等于()(A)(B)-2 (C)(D)-2 (E)-26 .卷积和x[n] u[n-2] 等于()( A )( B )( C )( D )( E )7 .计算卷积的结果为()( A )(B )( C )(D )8 .已知信号x(t) 的波形如图3 所示,则信号的波形如图()图3 (A)(B)(C) (D) 题九图9 .已知信号x (t )如图所示,其表达式为()(A) (B)(C) (D)10 .已知x(t)为原始信号,y(t)为变换后的信号,y(t) 的表达式为()( A )(B )( C )(D )11 .下列函数中()是周期信号( A )(B )( C )( D )( E )12 .函数的基波周期为()。
( A )8 (B )12 (C )16 ( D )2413 .某系统输入—输出关系可表示为,则该系统是()系统。
( A )线性( B )时不变( C )无记忆(D )因果( E )稳定14 .某系统输入—输出关系可表示为,则系统为()系统。
( A )线性( B )时不变( C )无记忆(D )因果( E )稳定15.某系统输入—输出关系可表示为,则系统为()系统。
( A )线性( B )时不变( C )无记忆(D )因果( E )稳定16.某系统输入—输出关系可表示为,则系统为()系统。
( A )线性( B )时不变( C )无记忆(D )因果( E )稳定17 .某系统输入—输出关系可表示为,则系统为()系统( A )线性( B )时不变( C )无记忆(D )因果()稳定18 .下列系统中,()是可逆系统(A)y[n]=nx[n] (B)y[n]=x[n]x[n-1] (C)y(t)=x(t-4) (D)y(t)=cos[x(t)] (E )y[n]=19 .如图系统的冲激响应为()( A )( B )( C )(D )20 .某系统的输入x (t )与输出y (t )之间有如下关系,则该系统为()(A)线性时变系统(B)线性非时变系统(C)非线性时变系统(D)非线性非时变系统21 .一个LTI 系统在零状态条件下激励与响应的波形如图,则对激励的响应的波形()(A) (B) (C) (D)22. 线形非时变系统的自然(固有)响应就是系统的()( A )零输入响应( B )原有的储能作用引起的响应( C )零状态响应(D )完全的响应中去掉受迫(强制)响应分量后剩余各项之和23 .零输入响应是()( A )全部自由响应( B )部分零状态响应( C )部分自由响应( D )全响应与强迫响应之差24 .下列叙述或等式正确的是()(A) (B)(C)若,则(D)x(t) 和h(t) 是奇函数,则是偶函数25.设是一离散信号,,,则下列说法( )是正确的(A) 若是周期的,则也是周期的(B) 若是周期的,则也是周期的(C) 若是周期的,则也是周期的(D) 若是周期的,则也是周期的26 .有限长序列经过一个单位序列响应为的离散系统,则零状态响应为()(A) (B)(C) (D)第二章习题1. 某LTI 连续时间系统具有一定的起始状态,已知激励为x (t )时全响应,t 0 ,起始状态不变,激励为时,全响应y (t )=7e +2e ,t 0 ,则系统的零输入响应为()( A )( B )( C )(D )2 .微分方程的解是连续时间系统的()(A) 零输入响应(B) 零状态响应(C) 自由响应(D) 瞬态响应(E)全响应3 .单位阶跃响应是()(A) 零状态响应(B) 瞬态响应(C) 稳态响应(D) 自由响应(E) 强迫响应4 .已知系统如图所示,其中h (t) 为积分器,为单位延时器,h (t) 为倒相器,则总系统的冲激响应h (t) 为()( A )( B )( C )(D )5 .如图所示电路以为响应,其冲激响应h (t) 为()(A) (B)(C) (D)6. 某LTI 系统如图所示,该系统的微分方程为()(A ) (B)(C) (D)7 .已知系统的微分方程, 则求系统单位冲激响应的边界条件h(0 ) 等于()(A) -1 (B) 0 (C) 2 (D) +18 .已知系统的微分方程则系统的单位冲激响应为()(A) (B) (C) (D)9 .已知描述系统的微分方程和初始状态0 值如下;y (0 ) =2 ,, , ,则初始条件0 值为()(A) (B)(C) (D)10 .已知描述系统的微分方程和初始状态0 值如y(t) +6 y (t) +8 y (t) =x (t) +2x (t) ,y (0 ) =1 ,y (0 ) =2 ,x (t) =(t )则初始条件0 值为()。
北京理工大学信号与系统考研真题2007

W ( ) ) ;
(2)当 w(t ) sin t cos 5t ,求出傅立叶变换 W () 和 H () ,画出二者的频域图形并注明主要
t
频率参数; (3)指明系统是何种滤波器?写出在 H () ~ 图形中,通带宽度、通带中心频率以及二者之 比的表达式;讨论参数 a 变化时,三者的变化情况。
3. 一个累加器系统 y(n) 并画出模拟框图。
n x(k ) , x( n) 为输入, y (n) 为输出,写出该系统的差分方程, k
4. 设一实序列 x(n) a n u(n) ,(其中 | a | 1 ) ,写出其离散时间傅立叶变化 X (e ) ,并证明其满 足共轭对称性。
s sk
j ( 1 2 2 k 1 ) 2N
, k 1,2,...N ;
Ak ,所有小数取小数点后 3 位。) 1 e skT z 1
六、 (20 分) 一个离散时间 LTI 系统,输入 x( n) ,输出为 y (n) 。已知下列情况: a.若对全部 n, x(n) (2) n ;则对全部 n,有 y (n) 0 ; b.若对全部 n, x(n) (1/ 2) n u(n) ;则对全部 n,有 y(n) (n) a(1/ 4) n u(n) ,其中 a 为一常 数。 (1)求常数 a 的值; (2)画出系统并联结构图; (3)当输入为 x(n) (1/ 3)
jw
5. 对于一个具有如下频率响应的理想滤波器,写出其单位脉冲响应 h( n) ,并指出它是什么类 型的滤波器。
e jwnd , wc | w | H (e jw ) 0, | w | wc
6. 已知一线性时不变系统,当其输入为图 1(a)时,其输出如图 1(b) ,求其单位冲激响应
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
该系统_________因果系统;_________线性系统; _________时不变系统(空格填 “是”或“不是” ) 。 2. (2 分)信号 x(t ) e j 2t (t ) 的傅里叶变换为
3.(2 分) x[n] 的 Z 变换 X ( z ) 为有理式,在 z 和, x 2 [n] ( ) x[ n] 不绝对可和,则 x[n] 是 4.(2分) X ( z ) 4 z 2 3 z 5.(3分)输入信号 x[n] sin 则输出 6.一个LTI系统对输入函数 x(t ) (e 则系统的频率响应(1分)
d2 d d y (t ) - 4 y (t ) 3 y (t ) x(t ) - 2 x(t ) 2 dt dt dt
试画出该系统的正准型模拟图。 三. 综合题(共 46 分)
x(t ) 的频谱 X ( ) 如图 (b)所示, 且已知 p (t ) 1. 如图.2 (a) 所示系统, 已知:
3t
。
10.(2 分)LTI 系统的单位冲激响应 h(t ) 3 ,则该系统
t
因果系统;
稳定系
统。 (空格填“是”或“不是” )
1 n X (e j ) d = 4 sin 3 t sin 2 t 2 12.(3 分)信号 x(t ) ] 的奈奎斯特抽样率为 [ t t
;单位冲激响应(2分)
7. (2 分)卷积和 {2,1, 1}*{1, 2,3} 的值为:
1 (3 分) 线性时不变系统的单位冲激响应为 h(t ) e 3t u (t ) , 若输入为 x(t ) e 2t , 8. 2
则其对应的输出 y (t )
9. (2 分)计算卷积积分 e u (t ) * u (t ) =
j
1 处有极点,在 2
1 4
n
)0
2.已知 x(5 2t ) 的波形如图 1 所示。试画出 x(t ) 的波形。
x(5 2t )
1 (2)
1 3/2 2 5/2 3
t
图1
3. 试求下面信号的拉普拉斯变换和 ROC.
x(t ) e2t u (t 1)
4. 已知 LTI 系统的微分方程描述为
1)求该系统的冲激响应表达式,该系统是因果系统吗? 2)求描述该系统的微分方程表达式; 3)若初始状态为 y (0 ) 1; y(0 ) 1; 求该系统的零输入响应 y0 (t )
21 n
3. 设 X (e
j
) 代表下图所示信号 x[n] 的傅里叶变换。
11.(3 分)已知 x[n] ( ) u[ n 1] ,则
。 rad/s。
二. 简答题(每小题 6 分)
1.已知一因果稳定系统的单位抽样响应为 h[ n] , H ( z ) 为有理式,且在 z 单位园某处有一个零点。判断下列说法正确性并陈述理由。 1) F {( ) h[n]} 收敛 2)存在某个 , H (e 3) h[n] 为有限长序列
n
(t nT ) ,
输出 y (t ) x(t ) , H1 ( j ) 和 H 2 ( j ) 分别如图 c)和 d)所示,若:
F x(t ) X ( j ) F x1 (t ) X 1 ( j ) F x2 (t ) X 2 ( j ) F x3 (t ) X 3 ( j ) F y (t ) Y ( j )
1)求 X (e ) 和 X (e ) 的值; 2)求 arg X (e 3)求值
j
j0
j
);
j
X (e
)d 。
t
。
1 n 1 处有一极点。 x1 [n] ( ) x[n] 绝对可 4 2
(左边,右边,双边)序列
1 8
n
2
1
, 0 z ,求 x[n]
n n sin n / 6 2 cos , h[n] , 8 4 n
e 3t )u (t ) 的响应为 y (t ) (2e t 2e 4t )u (t ) ,
2 T
1 -
2 T 6 T
-
(b) 1
6 T
H 2 ( j )
( c)
T
T
2 t
2. (15 分 ) 某 稳 定 的 LTI 系 统 , 当 输 入 为 x(t ) (t ) 3e (d)
u (t ) 时 , 其 对 应 的 输 出 为
y (t ) e t u (t ) e 2t u (t )
1) 根据已知条件求 0 ; 2) 画出 X 1 ( j ) ; 3) 画出 X 2 ( j ) ; 4) 画出 X 3 ( j ) 。
x(t )
x1 (t )
H1 ( j )
x2 (t ) cos 0t
( a)
x3 (t )
H 2 ( j )
y (t )
p (t )
H1 ( j )
课程编号:01500238
北京理工大学 2009 – 2010 学年第一学期
2007 级信号与系统 B 期末试题 B 卷
班级
第一部分:填空 题 题号 分数 1-12
学号
姓名
成绩
第二部分:计算题 1 2 3 4 1
第三部分:综合题 2 3
一 填空题(共 30 分)
1. (3 分)已知离散时间系统的输入输出关系为: y[n] x[n] x[n 2] ,则:
