北京理工大学信号与系统实验 实验2 LTI系统的时域分析
北京理工大学信号与系统实验实验报告

北京理工大学信号与系统实验实验报告信号与系统实验报告姓名:肖枫学号:1120111431班号:05611102专业:信息对抗技术学院:信息与电子学院12实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB表示及其可视化方法。
2. 掌握信号基本时域运算的MATLAB实现方法。
3. 利用MATLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB并不能处理连续时间信号,在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
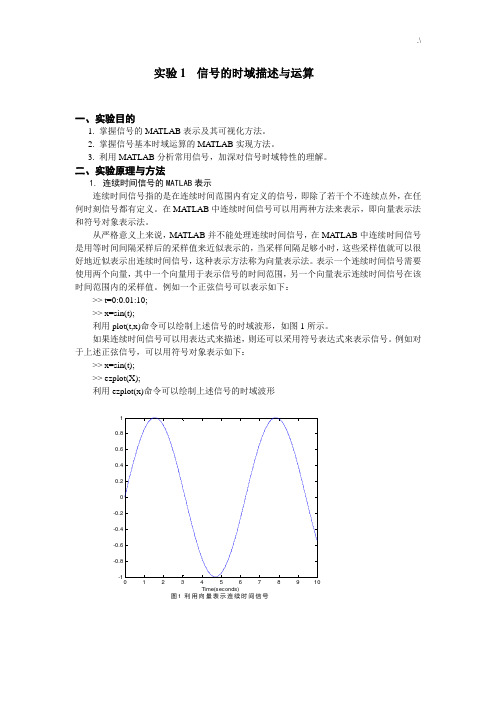
例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形10.80.60.40.2-0.2-0.4-0.6-0.8-1012345678910Time(seconds)图1 利用向量表示连续时间信号3sin(t)10.5-0.5-1-6-4-20246t图 2 利用符号对象表示连续时间信号常用的信号产生函数函数名功能函数名功能 heaviside 单位阶跃函数 rectpuls 门函数 sin 正弦函数 tripuls 三角脉冲函数 cos 余弦函数 square 周期方波 sinc sinc函数 sawtooth 周期锯齿波或三角波 exp 指数函数2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
北京理工大学信号与系统实验实验报告
实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB表示及其可视化方法。
2. 掌握信号基本时域运算的MA TLAB实现方法。
3. 利用MA TLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB并不能处理连续时间信号,在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形Time(seconds)图1 利用向量表示连续时间信号t图 2 利用符号对象表示连续时间信号sin(t)2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
1)相加和相乘信号相加和相乘指两信号对应时刻的值相加和相乘,对于两个采用向量表示的可以直接使用算术运算的运算符“+”和“*”来计算,此时要求表示两信号的向量时间范围和采样间隔相同。
采用符号对象表示的两个信号,可以直接根据符号对象的运算规则运算。
实验2离散时间LTI系统的时域分析

实验二 离散时间LTI 系统的时域分析一 实验目的(1) 学会运用MATLAB 求解离散时间系统的零状态响应;(2) 学会运用MATLAB 求解离散时间系统的单位取样响应;(3) 学会运用MATLAB 求解离散时间系统的卷积和。
二 实验原理及实例分析1、离散时间系统的响应离散时间LTI 系统可用线性常系数差分方程来描述,即∑∑==-=-Mj jN i i j n x b i n y a 00)()( (1) 其中,i a (0=i ,1,…,N )和j b (0=j ,1,…,M )为实常数。
MATLAB 中函数filter 可对式(1)的差分方程在指定时间范围内的输入序列所产生的响应进行求解。
函数filter 的语句格式为y = filter (b , a , x )其中,x 为输入的离散序列;y 为输出的离散序列;y 的长度与x 的长度一样;b 与a 分别为差分方程右端与左端的系数向量。
【实例1】 已知某LTI 系统的差分方程为)1(2)()2(2)1(4)(3-+=-+--n x n x n y n y n y试用MATLAB 命令绘出当激励信号为)()2/1()(n u n x n=时,该系统的零状态响应。
解:MATLAB 源程序为>>a=[3 -4 0 2];>>b=[1 2]; >>n=0:30;>>x=(1/2).^n;>>y=filter(b,a,x);>>stem(n,y,'fill'),grid on>>xlabel('n'),title('系统响应y(n)')程序运行结果如图1所示。
2、离散时间系统的单位取样响应系统的单位取样响应定义为系统在)(n δ激励下系统的零状态响应,用)(n h 表示。
MATLAB 求解单位取样响应可利用函数filter ,并将激励设为前面所定义的impDT 函数。
实验2-LTI系统的时域分析

一,实验目的作为基础性实验部分,实验2使我们了鮮和拿握利用MATLAB 对糸统进行时域分析的方法,拿握了连续时间糸统和离散时呵糸统下对零状态响应、单住抽样响应的方法,以及求卷积积分和卷积和的方冻O二,实验原理(\)连续肘间糸统肘域分析的MATLAB卖现。
(D连续时间糸统的MATLAB表示。
用糸统微分方程描述LTI连续糸统,然后症matlab中建立棋型:b=[bLb2,……]a=[al,a2. .......... ]$y$=tf(b,a)②连续时间糸统的零状态响应。
调用函数lsim(sys,x,t)绘出信号及响应的波形。
③连续时间糸统的冲击响应与阶跃响应。
描述糸统的单伐冲击响应调用impulse函救:impul$e(sy$)>4?k认肘间阖绘出糸统冲激响应的肘城波形。
impul$e(sys, T)绘出糸统在0~T谢冲激响应的肘城姝形。
impulse(sys, ts:tp:te)绘出糸统在ts~te国,以tp为肘间间隔取样的冲击响应欧形。
描述糸统的单伐阶販响应调用step函数:impulse(sys)impulsefsys, T)impul$e(sys, ts:tp:te)(2)需散时间糸统时域分析的MATLAB卖现。
Q)离散时间糸统的MATLAB表示。
用向量b=[b1,b2, ............ ], a=[al,a2, .......... ]可以裹示糸统。
②离散时间糸统对任意输入的响应。
可以调用函数filter fb,a,xj③离散时间糸统的单住抽样响应。
可以调用函数impz:impz fb,aj症默认肘间團绘出糸统单佞轴样响应的肘城欧形。
impz (b,a,N绘出糸统在0~N阖单伐.轴样响应的肘域波形。
impz(b.a,ns:ne)绘岀糸统淮.n$~ne囲的单伐轴样响应波形。
(3)卷积与卷积积分①离散时间序列的卷积和可以调用函数conv求得两个富散存列的巻积和。
②连续时间估号的卷积积分惟取样间隔足够小的情况下,由卷积和近似求得卷积积分。
实验二 离散时间LTI系统的时域分析

实验二离散时间LTI系统的时域分析1.实验目的通过本实验,要求学生学会运用MATLAB求解离散时间系统的零状态响应;学会运用MATLAB求解离散时间系统的单位冲激响应;学会运用MATLAB求解离散时间系统的卷积和。
2.实验原理MATLAB中函数filter可对上式的差分方程在指定时间范围内的输入序列所产生的响应进行求解。
函数filter的语句格式为 y=filter(b,a,x) 其中,x为输入的离散序列;y 为输出的离散序列;y的长度与x的长度一样;b与a分别为差分方程右端和左端的系数向量。
系统的单位冲激响应定义为系统在δ(n)激励下系统的零状态响应,用h(n)表示。
MATLAB求解单位冲激响应可利用函数filter,并设激励为δ(n)函数。
系统的单位阶跃响应定义为系统在u (n)激励下系统的零状态响应,用g(n)表示。
MATLAB 求解单位阶跃响应可利用函数filter,并设激励为u(n)函数。
系统的零状态响应是激励与系统的单位冲激响应的卷积。
离散时间信号的卷积运算是求和运算,因而常称为卷积和。
MATLAB求离散时间信号卷集和的命令为conv,其语句格式为 y=conv(x,h)。
例如,利用MATLAB的conv命令求两个长为4的矩形序列的卷积和,即g(n)=[u(n)- u(n-4)]*[ u(n)- u(n-4)],其结果应是长为7(4+4-1=7)的三角序列。
运行结果如图10-7所示。
图10-7 矩形序列3.实验内容(1) 已知x(n)=u(n-“学号后两位”)-u(n-(“学号后两位”+4))、h(n)=R5(n)。
(2) 编制程序求解下列两个系统的单位冲激响应和单位阶跃响应,并绘出其图形。
(3) 已知某系统的单位冲激响应为h(n)=0.5n[u(n)-u(n-4)],试分别利用MATLAB卷积和两种方法求当激励信号为x(n)=u(n)-u(n-4)时,系统的零状态响应。
4.实验设备计算机,MATLAB软件。
LTI系统的时域分析

实验二:LTI系统的时域分析一实验目的1.掌握利用计算机进行连续时间信号卷积运算和离散时间信号卷积运算的原理和方法;2.掌握用MATLAB求解LTI系统的时域响应。
二、涉及的MATLAB函数1、conv()函数2、filter()函数3、impulse()函数4、dsolve()函数三、实验内容与方法1、信号的卷积运算p=0.001; % 取样时间间隔nf=0:p:2; % f(t)对应的时间向量f=2*((nf>=0)-(nf>=2)); % 序列f(n)的值nh=0:p:5; % h(t)对应的时间向量h=exp(-nh); % 序列h(n)的值y=conv(f,h); % 计算序列f(n)与h(n)的卷积和y(n)y=y*p; % y(n)变成y(t)left=nf(1)+nh(1) % 计算序列y(n)非零样值的起点位置right=length(nf)+length(nh)-2 % 计算序列y(n)非零样值的终点位置k=p*(left:right);subplot(3,1,1),stairs(nf,f); % 绘制f(t)的波形title('f(t)');axis([0 3 0 2.1]);subplot(3,1,2),stairs(nh,h); % 绘制h(t)的波形title('h(t)');axis([0 3 0 2.1]);subplot(3,1,3),plot(k,y); % 绘制y(t)=f(t)*h(t)的波形title('y(t)=f(t)*h(t)');axis([0 3 0 3]);2、系统的时域分析f(k)=(k),b=[1 1];a=[1 -0.25 0.5]; % 差分方程的系数n=0:15; % 序列的个数fn=0.5.^n; % 输入序列y1=filter(b,a,fn); % 零状态响应y2=impz(b,a,16); % 单位响应subplot(1,2,1),stem(n,y1,'filled');title('零状态响应');grid onsubplot(1,2,2),stem(n,y2,'filled');title('单位响应');grid on五、实验报告要求1、实验目的概述;2、实验原理分析;3、将源代码及其运行结果附在报告中并加以分析说明;4、实验收获及体会;。
信号与系统实验二 连续LTI系统的时域研究分析

信号与系统实验二连续LTI 系统的时域分析————————————————————————————————作者:————————————————————————————————日期:2实验二 连续LTI 系统的时域分析一. 实验目的1. 加深对线性时不变系统中零状态响应概念的理解,掌握其求解方法;2. 掌握求解给定连续系统的冲激响应和阶跃响应的方法。
二. 实验原理1.连续系统零状态响应的数值解线性时不变 (LTI) 连续时间系统用常系数线性微分方程进行描述,系统的零状态响应就是在系统初始状态为零条件下微分方程的解。
MATLAB 控制系统工具箱提供了一个lism 函数来求解连续时间系统的零状态响应,其调用格式为y = lism(sys,f,t)其中t 表示计算系统响应的时间抽样点向量,f 是系统输入信号向量,sys 是LTI 系统模型,用来表示微分方程、状态方程。
在求解微分方程时,微分方程的LTI 系统模型sys 要借助MATLAB 中的tf 函数来获得,其调用格式为sys = tf(b,a)其中a 、b 分别为微分方程左端和右端各项的系统向量。
例如系统方程 (3)(2)(1)(2)(1)2210210()()()()()()()a y t a y t a y t a y t b f t b f t b f t +++=++该方程左边、右边的系数向量分别为3210[,,,]a a a a a =,210[,,]b b b b =。
例1:描述某线性时不变系统的方程为"()4'()4()'()3()y t y t y t f t f t ++=+试求:当()()tf t e t ε-=时,系统的零状态响应()zs y t 。
解:实现所要求运算的m 文件如下,a = [1 4 4]; %将y (t )各阶导数的系数放在向量a 中b = [1 3]; %将f (t )各阶导数的系数放在向量b 中sys = tf(b, a); %求系统模型systd = 0.01; %定义时间间隔t = 0 : td : 10; %定义时间向量f = exp(-t); %将f (t )表示出来y = lsim(sys, f, t); %求系统的零状态响应plot(t, y); %绘出零状态响应的波形xlabel('t(sec)'); %给出x 坐标的标签ylabel('y(t)'); %给出y 坐标的标签grid on %在图上显示方格程序运行结果见图1。
《信号与系统》第二章 北京理工大学

2.1 引言
时域分析方法:
输入信号(激励)
时域数学模型 输出信号(响应) (输入输出法)
LTI系统零输入和零状态的求取: ➢解微分方程法 ➢卷积积分法
2.2 LTI系统的微分方程表示及其响应
2 微分方程的求解 ▪微分方程的完全解:由齐次解 yh (t)和特解 yp (t)两部分 组成。 ▪齐次解的求法 表2-1 ▪特解的求法 表2-2 ▪完全解:其中齐次解中的待定系数应在完全解中由给 定的附加初始条件确定。
将x(t ) e t 代入方程的右端,得 e t ,其中a 1与1=-1相重,
故特解 y p (t ) A1te t
代入微分方程,得 A1=1,因此 y p (t ) te t
(3)完全解
y(t ) yh (t ) y p (t ) c1e t c2e 2t te t ,由初始条件
P47,例2-8
2.4 卷积积分
1 用冲激函数表示任意信号
u(t) 0 (t )d
2 卷积积分
x(t) x( ) (t )d
y(t) x( )h(t )d y(t) x(t) h(t)
卷积积分公式
LTI系统对于任意信号 x(t) 的零状态响应,可以由 该信号与系统的单位冲激响应的卷积积分得到。
y(0) 1, y(0) 3 得 y(0) c1 c2 0
解得c1 2,
y(0) c1 2c2 1 3
c2 2
y(t ) 2e t 2e 2t te t , t 0
2.3零输入响应和零状态响应
➢零输入响应( y0(t)):由微分方程的齐次解得到,齐次解中 的系数由给定的初始条件确定; ➢零状态响应 ( yx (t) ) :由方程的全解得到,其中齐次解的系 数应在全解中由初始条件确定(y(0)=y(1)(0)=…= y(n-1)(0)= 0。 ?完全解和完全响应 完全解=齐次解+特解 完全响应=零输入响应+零状态响应
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验2 LTI 系统的时域分析一、实验目的1.掌握利用MATLAB 对系统进行时域分析的方法。
2.掌握连续时间系统零状态响应、冲激响应和阶跃响应的求解方法。
3.掌握求解离散时间系统响应、单位抽样响应的方法。
4.加深对卷积积分和卷积和的理解。
掌握利用计算机进行卷积积分和卷积和计算的方法。
二、实验原理1、连续时间系统时域分析的MATLAB 实现1) 连续时间系统的MATLAB 表示设LTI 因果系统的微分方程一般式为:)()()()()()()()(0'1)1(1)(0'1)1(1)(t x b t x b t x b t x b t y a t y a t y a t y a m m m m n n n n ++++=++++----则在MATLAB 里,可以建立系统模型如下:b =[b M ,b M−1,…,b 0]; a =[a N ,a N−1,…,a 0] sys =tf(b,a);2)连续时间系统的零状态响应零状态响应指系统的初始状态为0,仅由输入信号所引起的响应。
MATLAB 提供了lsim(sys,x,t)表示求解零状态响应。
他不绘出波形,而是返回响应二等地数值向量。
3)连续时间系统的冲激响应与阶跃响应。
MATLAB 提供了impulse 函数来求指定时间范围内,由模型sys 描述的连续时间系统的单位冲击响应。
函数step 用于求解单位阶跃响应。
2、离散时间系统时域分析的MATLAB 实现1)离散时间系统的MATLAB 表示。
LTI 离散系统通常可以由系统差分方程描述;差分方程为:0101()(1)...()()(1)...()N M a y n a y n a y n M b x n b x n b x n N +-++-=+-++-则在MATLAB 里,可以建立系统模型如下:b =[b M ,b M−1,…,b 0]; a =[a N ,a N−1,…,a 0]2)离散时间系统对任意输入的响应。
Matlab 提供了求LTI 离散系统响应的专用函数filter ,该函数用于求取由差分方程所描述的离散时间系统在指定时间范围内对输入序列所产生的响应。
其基本调用格式为:y =filter(b,a,x)3)离散时间系统的单位抽样响应。
Matlab 提供impz 函数来求解指定时间范围内,由向量b 和a 描述的离散时间系统的单位抽样响应。
3、卷积和与卷积积分1)离散时间序列的卷积和:x 1(n )和x 2(n )的卷积和x(n)定义如下:x (n )=x 1(n )∗x 2(n )MATLAB 的conv 函数调用格式为x=conv(x1,x2); 2)连续时间信号的卷积积分连续时间信号x 1(t )和x 2(t )的卷积积分x (t )定义如下1212x()()*()()(t )t x t x t x x d τττ+∞-∞==⋅-⎰对一连续LTI 系统,设其输入信号为x (t ),单位冲激响应为ℎ(t ),其零状态响应为y (t ),则有()()*()y t x t h t =即连续LTI 系统的零状态响应可以表示成输入信号和单位冲激响应的卷积。
三、实验内容(1)采用MATLAB 绘出各系统的单位冲激响应和单位阶跃响应波形。
①)()()(2)(t x t y t y t y =+'+'' 程序如下: b=[1];a=[1 sqrt(2) 1]; sys=tf(b,a); subplot(121); impulse(sys); subplot(122); step(sys);程序运行结果如下:Impulse ResponseTime (seconds)A m p l i t u d eStep ResponseTime (seconds)A m p l i t u d e○2)()()(2)(t x t y t y t y ''=+'+''程序如下: b=[1 0 0];a=[1 sqrt(2) 1]; sys=tf(b,a); subplot(121); impulse(sys); subplot(122); step(sys);程序运行结果如下:③)()()()(t x t y t y t y '=+'+''程序如下: b=[1 0]; a=[1 1 1]; sys=tf(b,a); subplot(121); impulse(sys); subplot(122); step(sys);程序运行结果如下:02468-1.6-1.4-1.2-1-0.8-0.6-0.4-0.20.2Impulse ResponseTime (seconds)A m p l i t u d e0246-0.4-0.20.20.40.60.81Step ResponseTime (seconds)A m p l i t u d e○4)()()()()(t x t x t y t y t y +''=+'+''程序如下: b=[1 0 1]; a=[1 1 1]; sys=tf(b,a); subplot(121); impulse(sys); subplot(122); step(sys);程序运行结果如下:-0.4-0.200.20.40.60.81Impulse ResponseTime (seconds)A m p l i t u d eStep ResponseTime (seconds)A m p l i t u d e(2)已知某系统可以由如下微分方程描述 )()(6)()(t x t y t y t y =+'+''○1利用MATLAB 绘出该系统冲激响应和阶跃响应的时域波形。
程序如下: b=[1];a=[1 1 6]; sys=tf(b,a); subplot(121); impulse(sys); subplot(122); step(sys);程序运行结果如下:Impulse ResponseTime (seconds)A m p l i t u d eStep ResponseTime (seconds)A m p l i t u d e○2根据冲激响应的时域波形分析系统的稳定性 观察上面的波形,t 趋于无穷时,y(t)均趋于0。
函数在时域上收敛,绝对可积,所以系统稳定。
○3如果系统的输入为)()(t u e t x t-=,求系统的零状态响应。
程序如下: b=[1];a=[1 1 6]; sys=tf(b,a); t=0:0.01:10; x=exp(-1*t); lsim(sys,x,t); 程序运行结果如下:Impulse ResponseTime (seconds)A m p l i t u d eStep ResponseTime (seconds)A m p l i t u d eLinear Simulation ResultsTime (seconds)A m p l i t u d e(3)知描述离散系统的微分方程如下,用MATLAB 绘出各系统的单位抽样响应,根据单位抽样响应的时域波形分析系统的稳定性。
○1)()2(2)1(3)(n x n y n y n y =-+-+ 程序如下: b=[1];a=[1 3 2];impz(b,a,0:10);程序运行结果如下:系统的稳定性由图像可知,n 趋于无穷时,y(n)越来越大,所以y(n)发散,所以该系统是不稳定的。
○2)1(3)()2(8.0)1(5.0-)(--=-+-n x n x n y n y n y 程序如下: b=[1 -3];a=[1 -0.5 0.8]; impz(b,a,0:10); 程序运行结果如下:012345678910n (samples)A m p l i t u d eImpulse Response系统的稳定性由图像可知,n 趋于无穷时,y(n)越来越小且是有界的,即y(n)收敛,所以该系统是稳定的。
(4)已知系统可以由如下差分方程描述)()2(25.0)1()(n x n y n y n y =-+-+程序如下: b=[1];a=[1 1 0.25]; subplot(121); impz(b,a,0:10); n=0:20; x=(n>=0);y=filter(b,a,x); subplot(122);stem(n,y, 'filled' ); xlabel('n' ); 程序运行结果如下:n (samples)A m p l i t u d eImpulse Response(5)用MATLAB 计算如下两个序列的卷积,并绘出图形。
122(){1,2,1,1}-22,()1()0x n n x n x n =≤≤==其他,程序如下:x1=[1 2 1 1]; x2=[1 1 1 1 1];t=[-3 -2 -1 0 1 2 3 4]; x=conv(x1,x2); stem(t,x);程序运行结果如下:(6)已知某LTI 离散系统,其单位抽样响应0),5.0sin()(≥=n n n h ,系统的输入为0),2.0sin()(≥=n n n x ,计算当n=0,1,2,…,40时系统的零状态响应y(n),绘出x(n),h(n)和y(n)时域波形。
程序如下: n=0:40;h=sin(0.5*n); x=sin(0.2*n); n1=0:80;y=conv(x,h); subplot(311);stem(n,x, 'filled' );xlabel('n');ylabel('x(n)' ); subplot(312);stem(n,h, 'filled' );xlabel('n');ylabel('h(n)' ); subplot(313);stem(n1,y, 'filled' );xlabel('n');ylabel('y(n)' );程序运行结果如下:(7)已知两个连续时间信号,求两个信号的卷积。
程序如下: dt=0.01;t1=-1:dt:1;x1=2*ones(size(t1)); t2=-2:dt:2;x2=ones(size(t2));[x,t]=sconv(x1,x2,t1,t2,dt);plot(t,x);xlabel('t(s)' );title('x(t)=x_1(t)*x_2(t)\deltat=0.01' );编写函数文件:function [x,t]=sconv(x1,x2,t1,t2,dt)x=conv(x1,x2);x=x*dt;t0=t1(1)+t2(1);l=length(x1)+length(x2)-2;t=t0:dt:(t0+l*dt);end程序运行结果如下:四.实验心得体会经过这次实验,对MATLAB有了进一步的了解和应用,并且加深了对信号与系统这门课程的理解。
