北京交通大学信号与系统时域分析
第二章 信号与系统的时域分析

二 卷积积分(The convolution integral) 若 (t ) h(t ) 则 (t ) h(t ) = h (t )
x t x h t
x(t ) x( ) (t )d y(t ) x( )h (t )d
则 y(t ) ak yk (t )
k
4
信号与系统的时域分析:
一般的信号都可以表示为延迟冲激的线性组合。
结合系统的叠加性和时不变性,就能够用LTI的单位
冲激响应来完全表征任何一个LTI系统的特性。这样
一种表示在离散情况下称为卷积和;在连续时间情
况下称为卷积积分。
5
分析方法:
对信号分解可在时域进行,也可在频域或变换域 进行,相应地产生了对LTI系统的时域分析法、频 域分析法和变换域分析法。
h( n n kk n h ) uu (n k )k
1
1
k
0
...
0
k
n
12
运算过程:
k k) ,再随参变量 为 h(
点值累加,得到
将一个信号 xk 不动,另一个信号反转后成为
下,将 xk 与 hn k 对应点相乘,再把乘积的各
n
移位.在每个 n 值的情况
x( [ n] y x x[ (n n] )* [ (n) h2 (n n)] x ) y( n n) (h h1 ) 1 n h2 h (n ) h( n) h2 x(t ) 11 y(t ) x(t ) [h1 (t ) h2 (t )] h1 (t ) h2 (t )
0
16
对一般信号 x(t ) ,可以分成很多 宽度的区段, 用一个阶梯信号 x (t ) 近似表示 x(t ) .当 0 时,
信号与系统的分析方法有时域,变换域两种

§2-3 Z反变换
一.定义:
已知X(z)及其收敛域,反过来求序列x(n) 的变换称作Z反变换。
记作:x(n) Z [ X ( z )]
1
z变换公式:
正:X ( z )
n
x ( n) z n ,
R x z Rx
1 反:x(n) X ( z ) z n 1dz, c ( Rx , Rx ) 2j c
j Im[ z ]
z 收敛域: a
0
a
z
Re[ z ]
*收敛域一定在模最大的极点所在的圆外。
[例2-3]求序列 x(n) b u(n 1) 变换及收敛域。
n
x ( n)
n
b nu (n 1) z n
b 1 z (b 1 z ) 2 (b 1 z ) n
§2-1 引言
信号与系统的分析方法有时域、变换域两种。 一.时域分析法 1.连续时间信号与系统: 信号的时域运算,时域分解,经典时域 分析法,近代时域分析法,卷积积分。 2.离散时间信号与系统: 序列的变换与运算,卷积和,差分方程 的求解。
二.变换域分析法
1.连续时间信号与系统: 信号与系统的频域分析、复频域 分析。
2.离散时间信号与系统: Z变换,DFT(FFT)。 Z变换可将差分方程转化为代数方程。
§2-2 Z变换的定义及收敛域
一.Z变换定义: 序列的Z变换定义如下:
X ( z ) Z [ x(n)]
n
x ( n) z
n
*实际上,将x(n)展为z-1的幂级数。
ze ze
jT ST
[例2-5]利用部分分式法,求X ( z) 1 (1 2 z 1 ) (1 0.5z 1 ) , 的z反变换。 解:
信号与系统_北京交通大学中国大学mooc课后章节答案期末考试题库2023年

信号与系统_北京交通大学中国大学mooc课后章节答案期末考试题库2023年1.某连续周期信号如题1图所示,该信号的频谱成分有( )【图片】参考答案:直流、奇次谐波的余弦分量2.已知描述某连续时间LTI系统的状态方程的矩阵分别为【图片】【图片】【图片】【图片】则该系统的系统函数【图片】为参考答案:3行3列矩阵3.关于连续非周期信号的频域表示,正确的说法是( )参考答案:将信号表示为不同频率正弦信号的线性组合4.连续非周期信号频谱的特点是( )参考答案:连续、非周期5.已知某线性连续时间系统,其在初始状态为【图片】、输入激励为【图片】作用下产生的完全响应为【图片】【图片】;该系统在初始状态为【图片】、输入激励为【图片】作用下产生的完全响应为【图片】【图片】试求初始状态为【图片】,激励为【图片】时系统的完全响应【图片】=( )。
参考答案:,6.连续非周期信号频谱的特点是参考答案:连续、非周期7.已知信号【图片】,其频谱【图片】在【图片】的值【图片】参考答案:88.连续周期信号【图片】是功率信号,其傅里叶变换【图片】都不存在。
参考答案:错误9.已知信号【图片】的最高频率分量为【图片】 Hz,若抽样频率【图片】,则抽样后信号的频谱一定混叠。
参考答案:错误10.连续时间周期信号【图片】的平均功率为( )参考答案:1111.利用状态变量分析法分析连续时间LTI系统时,输出方程【图片】可能与哪些因素有关参考答案:与输入和状态变量有关12.关于连续周期信号频谱的特性,正确的说法是( )参考答案:同时具有离散特性和幅度衰减特性。
13.若描述离散时间系统的差分方程为【图片】,该系统为( )。
参考答案:因果、线性时不变系统14.连续周期信号在有效带宽内各谐波分量的平均功率之和占整个信号平均功率的很大一部分。
参考答案:正确15.连续时间信号在时域展宽后,其对应的频谱中高频分量将增加。
参考答案:错误16.信号时域时移,其对应的幅度频谱不变,相位频谱将发生相移。
信号与系统分析第二章 连续时间系统的时域分析

第二章 连续时间系统的时域分析
2.1.1
对系统进行分析时, 首先要建立系统的数学模型。 对于电的系统, 只要利用理想的电路元件, 根据基尔霍 夫定律, 就可以列出一个或一组描述电路特征的线性 微分方程。 现举例来说明微分方程的建立方法。
第二章 连续时间系统的时域分析
例2.1 图2.1所示为RLC串联电路, 求电路中电流i(t) 与激励e(t)之间的关系。
第二章 连续时间系统的时域分析
(3)
y(t) C 1 e t C 2 e 6 t5 2c 0 1o 2 t)s 5 3 (s0i2 n t) (
D(p)y(t)=N(p)f(t)
y(t) N(p) f (t) D(P)
式(2.15)中的 N ( p ) 定义为转移算子, 用H(p)表示,
D (P)
(2.14) (2.15)
H (p ) N D ( (P p ) ) b a m n p p m n a b n m 1 1 p p n m 1 1 a b 1 1 p p a b 0 0 (2.16)
t0
解 (1) 齐次解。 由例2.4 yh (t)=C1e-t+C2e-6t
第二章 连续时间系统的时域分析
(2) 特解。 查表2.2, yp(t)=B1cos (2t)+B2sin(2t)
-14B1+2B2-6=0 2B1+14B2=0
于是,
B15201,
B2530
yp(t)5 20 c 1o2ts) (530 si2 nt)(
第二章 连续时间系统的时域分析
3. 用算子符号表示微分方程, 不仅书写简便, 而且在建 立系统的数学模型时也很方便。 把电路中的基本元件R、 L、 C的伏安关系用微分算子形式来表示, 可以得到相应 的算子模型, 如表2.1所示。
01北交大数字信号处理研究性学习报告.

《数字信号处理》课程研究性学习报告DSP基本概念和技能的训练姓名张然学号13211074同组成员蔡逸飞13211078朱斌指导教师陈后金时间2015/6DSP 基本概念和技能研究性学习报告【目的】(1) 掌握离散信号和系统时域、频域和z 域分析中的基本方法和概念; (2) 学会用计算机进行离散信号和系统时域、频域和z 域分析。
(3) 培养学生自主学习能力,以及发现问题、分析问题和解决问题的能力。
【研讨内容】问题一(1)阅读教材1.9节及MATLAB 中的Help ,学会MA TLAB 函数filter 的使用方法;(2)利用filter 函数,求出下列系统的单位脉冲响应,并判断系统是否稳定。
讨论实验所获得的结果。
211850586.0845.111)(--+-=z z z H21285.085.111)(--+-=z z z H 【题目目的】 1. 掌握LTI 系统单位脉冲响应的基本概念、系统稳定性与单位脉冲响应的关系; 2. 学会filter 函数的使用方法及用filter 函数计算系统单位脉冲响应; 3. 体验有限字长对系统特性的影响。
【仿真结果】 极点10.9430 0.9020 极点21.0000 0.8500051015202530354045502468y 1[k ]051015202530354045502468y 2[k ]【结果分析】我们所使用的计算机的是有限字长的,当我们用计算机对系统的各项参数进行量化,计算离散时,这些量化误差会使实际系统的极点值偏离理论值,导致系统的特性发生变化,甚至会使稳定系统变为非稳定系统。
【问题探究】已知LTI 系统的系统函数)(z H ,有哪些计算系统单位脉冲响应方法,比较这些方法的优缺点。
Filter 函数,可计算出差分方程的零状态响应,既可以用来求y[k],也可以求出h[k]; Impulse 函数,只是用来实现冲击响应的;Conv 函数,是用来计算卷积的,可以用来求y[k] 【仿真程序】 b1=[1 0 0]; b2=[1 0 0];a1=[1 -1.845 0.850586]; a2=[1 -1.85 0.85]; x=0:50;y1=filter(b1,a1,x); subplot(2,1,1); stem(y1);axis([0 50 0 8])[r1,p1,m1]=residuez(b1,a1); disp('极点1'); disp(p1');y2=filter(b2,a2,x); subplot(2,1,2); stem(y2);axis([0 50 0 8])[r2,p2,m2]=residuez(b2,a2); disp('极点2'); disp(p2');b1=[1 0 0]; b2=[1 0 0];a1=[1 -1.845 0.850586]; a2=[1 -1.85 0.85]; n=0:512;x=[1 zeros(1,512)] y1=filter(b1,a1,x); subplot(2,1,1); stem(n,y1); axis([0 50 0 8]) axis([0 50 0 8]) ylabel('y1[k]')[r1,p1,m1]=residuez(b1,a1); disp('极点1'); disp(p1');y2=filter(b2,a2,x); subplot(2,1,2); stem(n,y2); axis([0 50 0 8]) ylabel('y2[k]')[r2,p2,m2]=residuez(b2,a2); disp('极点2'); disp(p2');当取下列值时a1=[1 -1.8506 0.850586]; a2=[1 -1.85 0.906];极点11.0001 0.8505 极点20.9250 - 0.2244i 0.9250 + 0.2244i051015202530354045502468y 1[k ]5101520253035404550-505y 2[k ]问题二(1)阅读教材1.9节及MATLAB 中的Help ,学会MA TLAB 函数freqz 的使用方法; (2)利用MATLAB 语句x=firls(511,[0 0.4 0.404 1],[1 1 0 0]产生一个长度为512的序列x [k ],用plot 函数画出序列x [k ]的波形,用freqz 函数画出该序列的幅度频谱。
信号与系统-陈后金-北京交通大学-全

Ä ¿ Ð µ
Ó Õ ¼ Ê è · É ±
« Ð ´ · ð Å
Ð Â Ä ¢ Ó Ó Ð Ï
ç Ó ã ¥ ¨Ä µ ³ î » µ Ê ¸ ² Í Ð Ï Í ¾ Í
ä è Ê È f(t)
¿ ì ó ·º µ Ë ¨ð Á ² Å
A/D
ý Ö ¦ Ê ×´ í µ ³ ¿ Ï Í
D/A
¼ ¬ Ë Å º Á ¨ð ² Å
2.线性系统与非线性系统 • 线性系统:具有线性特性的系统。线性特性包括
均匀特性与叠加特性。 (1)均匀特性:
若f1 (t ) y1 (t )
则Kf1 (t ) Ky1 (t )
(2)叠加特性:
若f1 (t ) y1 (t ), f 2 (t ) y2 (t )
数学解析式或图形
• 2. 表示
语音信号:空气压力随时间变化的函数
0
0.1
0.2
语音信号“你好”的波
0.3
0.4
静止的单色图象: 亮度随空间位置变化的信号f(x,y)。
静止的彩色图象: 三基色红(R)、绿(G)、蓝(B)随空间位置变化的信号。
I R ( x, y ) I ( x, y ) I G ( x, y ) I B ( x, y )
[例2] 试判断下列系统是否为时不变系统
(1)y(t)=sin[f(t)]
时不变系统
(2)y(t)=cost· f(t)
(3)y(t)=4f 2(t) +3f(t)
时变系统
时不变系统
(4)y(t)=2t· f(t)
时变系统
分析: 判断系统是否为时不变系统,只需判断当输入激励f(t) 变为f(t-t0)时,相应的输出响应y(t)是否变为 y(t-t0)。 注意:时不变特性只考虑系统的零状态响应,因此在判 断系统的时不变特性时,不涉及系统的初始状态。
信号与系统实验报告
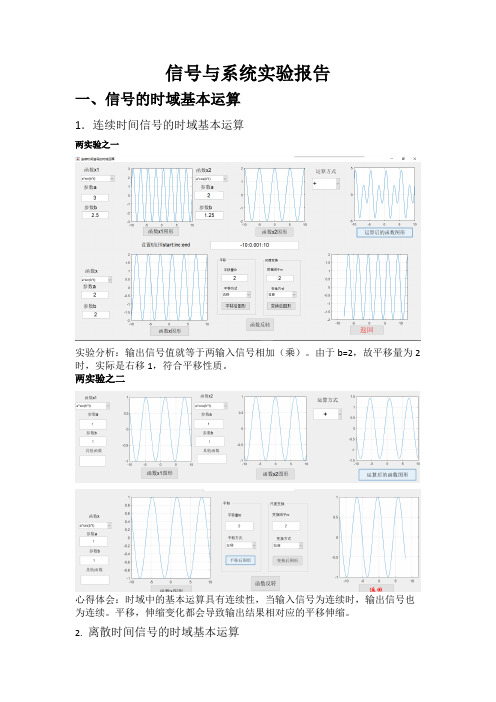
信号与系统实验报告一、信号的时域基本运算1.连续时间信号的时域基本运算两实验之一实验分析:输出信号值就等于两输入信号相加(乘)。
由于b=2,故平移量为2时,实际是右移1,符合平移性质。
两实验之二心得体会:时域中的基本运算具有连续性,当输入信号为连续时,输出信号也为连续。
平移,伸缩变化都会导致输出结果相对应的平移伸缩。
2.离散时间信号的时域基本运算两实验之一实验分析:输出信号的值是对应输入信号在每个n值所对应的运算值,当进行拉伸变化后,n值数量不会变,但范围会拉伸所输入的拉伸系数。
两实验之二心得体会:离散时间信号可以看做对连续时间信号的采样,而得到的输出信号值,也可以看成是连续信号所得之后的采样值。
二、连续信号卷积与系统的时域分析1.连续信号卷积积分两实验之一实验分析:当两相互卷积函数为冲激函数时,所卷积得到的也是一个冲激函数,且该函数的冲激t值为函数x,函数y冲激t值之和。
两实验之二心得体会:连续卷积函数每个t值所对应的卷积和可以看成其中一个在k值取得的函数与另外一个函数相乘得到的一个分量函数,并一直移动k值直至最后,最后累和出来的最终函数便是所得到的卷积函数。
3.RC电路时域积分两实验之一实验分析:全响应结果正好等于零状态响应与零输入响应之和。
两实验之二心得体会:具体学习了零状态,零输入,全响应过程的状态及变化,与之前所学的电路知识联系在一起了。
三、离散信号卷积与系统的时域分析1.离散信号卷积求和两实验之一实验分析:输出结果的n值是输入结果的k号与另一个n-k的累和两实验之二心得体会:直观地观察到卷积和的产生,可以看成连续卷积的采样形式,从这个方面去想,更能深入地理解卷积以及采样的知识。
2.离散差分方程求解两实验之一实验分析:其零状态响应序列为0 0 4 5 7.5,零输入响应序列为2 4 5 5.5 5.75,全状态响应序列为2 4 9 10.5 13.25,即全状态=零输入+零状态。
两实验之二心得体会:求差分方程时,可以根据全状态响应是由零输入输入以及零状态相加所得,分开来求,同时也加深了自己对差分方程的求解问题的理解。
北京交通大学信号与系统第四章典型例题讲解

第四章 典型例题【例4-1-1】写出下图所示周期矩形脉冲信号的Fourier 级数。
t周期矩形信号分析:周期矩形信号)(~t x 是实信号,其在一个周期[-T 0/2,T 0/2]内的定义为⎩⎨⎧>≤=2/02/ )(~ττt t A t x满足Dirichlet 条件,可分别用指数形式和三角形式Fourier 级数表示。
解:根据Fourier 级数系数C n 的计算公式,有t t x T C t n T T n d e )(~1000j 2/2/0ω--⎰===--⎰t A T t n d e 10j 2/2/0ωττ 2/2/j 000e )j (ττωω=-=--t t t n n T A 2/)2/sin(00τωτωτTn n A =)2(Sa 00τωτn T A =故周期矩形信号)(~t x 的指数形式Fourier 级数表示式为t n n t n n n n T A C t x 00j 00j e )2(Sa )(e )(~ωωτωτ∑∑∞-∞=∞-∞===利用欧拉公式2e e )cos(00j j 0tn t n t n ωωω-+=可由指数形式Fourier 级数写出三角形式的Fourier 级数,其为()t n n T A T A t x n 00010cos )2(Sa )2()(~ωτωττ∑∞=+=结论:实偶对称的周期矩形信号)(~t x 中只含有余弦信号分量。
【例4-1-2】写出下图所示周期三角波信号的Fourier 级数。
t周期三角波信号分析:周期矩形信号)(~t x 是实信号,其在一个周期 [-1/2,3/2]的表达式为⎪⎩⎪⎨⎧≤<-≤=2321 )1(221 2)(~t t A t At t x满足Dirichlet 条件,可分别用指数形式和三角形式Fourier 级数表示。
解:由于该三角波信号)(~t x 的周期T 0=2,所以ππ200==T ω。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京交通大学信号与系统时域分析【研讨题目2】 信号与系统时域分析专题研讨【目的】1.研究用离散方法近似计算连续信号的卷积积分;2.通过分析近似计算卷积积分过程中出现的问题,锻炼学生分析问题和解决问题的能力; 【知识点】信号时域分析,卷积积分,卷积和 【研讨题目】连续信号卷积积分的数值近似计算 两个连续信号的卷积积分定义为τττd )()()(-=⎰∞∞-t h x t y为了能用数值方法进行计算,需对连续信号进行抽样。
记x [k ]=x (k), h [k ]=h (k ),为进行数值计算所选定的抽样间隔,可以证明连续信号卷积积分可近似的表示为(Δ)Δ([][])y k x k h k ≈⨯*(1)由式(1)可知,可以利用Matlab 提供的conv 函数近似计算连续信号的卷积积分。
一、(*)理论分析为了对近似计算的结果进行分析,用解析的方法计算下列卷积积分,推出卷积积分的解析表达式; (1) 时限信号卷积积分x 1(t )=u (t )-u (t -1),y 1(t )=x 1(t )*x 1(t );卷积结果为:y1(t)= x 1(t )*x 1(t )=r(t)-2*r(t-1)+r(t-2) (2) 分段常数信号卷积积分x 2(t )= x 1(t )+2 x 1(t -1)+ x 1(t -2),h 2(t )= x 1(t )- x 1(t -1), y 2(t )=x 2(t )*h 2(t );卷积结果为:y2(t)= x 2(t )*h 2(t )=y1(t)+y1(t-1)-y1(t-2)-y1(t-3)=r(t)-r(t-1)-2*r(t-2)+2*r(t-3)+r(t-4)-r(t-5) (3) 非时限信号卷积积分x 3(t )=u (t ),h 3(t )=e -t u (t ), y 3(t )=x 3(t )*h 3(t )卷积结果为:y3= x 3(t )*h 3(t ) =[1-exp(-t)]*u(t) 二、(*)时限信号卷积积分的近似计算取不同的△值,用Matlab 函数conv 近似计算卷积积分y 1(t )并画出其波形,讨论的取值对计算结果的影响。
上图中,绿线为间隔0.01的结果,蓝线是间隔0.1结果,红线为实际结果,由此可见:时间间隔越小,与实际结果越接近。
附程序代码:t1=[0:0.01:5];t2=[0:0.1:5];t=[0:0.1:5];x1=1.*(t1>=0)-1.*(t1>=1);x2=1.*(t2>=0)-1.*(t2>=1);y1=convn(x1,x1);y2=convn(x2,x2);y=t.*[t>=0]-2*(t-1).*[t>=1]+(t-2).*[t>=2]N1=length(y1); %length函数取y1的长度%N2=length(y2);plot(t,y,'r');hold on;plot(0:0.01:(N1-1).*0.01,y1*0.01,'g');plot(0:0.1:(N2-1).*0.1,y2*0.1,'b');axis([0 5 0 1])三、(**)分段常数信号卷积积分的Matlab计算(1)若x2[k]={1,2 ,1,0; k=0,1,2}, h2[k]= {1,1 ; k=0,1},计算离散卷积y2[k]=x2[k]*h2[k];y2[k]=x2[k]*h2[k]结果如下:附程序代码:x2=[1,2,1,0];h2=[1,-1];y2=conv(x2,h2);N=length(y2);stem(0:N-1,y2);axis([0 8 -1 1])(2)比较y2(t)和y2[k],你发现了什么?y(t)的图像如下:2附程序代码:t=[0:0.1:5];y=t.*[t>=0]-(t-1).*[t>=1]-2*(t-2).*[t>=2]+2*(t-3).*[t>=3]+(t-4).*[t>=4]-(t -5).*[t>=5]plot(t,y);hold on;axis([0 8 -1 1])y2(t)和y2[k]图像比较:附程序代码:x2=[1,2,1,0];h2=[1,-1];y2=conv(x2,h2);t=[0:0.1:5];y=t.*[t>=0]-(t-1).*[t>=1]-2*(t-2).*[t>=2]+2*(t-3).*[t>=3]+(t-4).*[t>=4]-(t -5).*[t>=5]N=length(y2);stem(0:N-1,y2);hold on;axis([0 8 -1 1])plot(t,y);hold on;axis([0 8 -1 1])比较两图可知,y2(t)与y2[t]的卷积积分相似,将y2[t]向右平移一个单位后,两图像波形重合,若在y2[t]最前面补零,或缩小抽样间隔,即可由y2[t]的卷积积分近似地求解y2(t)地卷积积分。
(3)对(2)中发现象进行理论分析,根据理论分析的结果,给出用Matlab函数conv计算卷积积分y2(t) 的方法并画出卷积积分y2(t)的波形;x2(t)=u(t)+u(t-1)-u(t-2)-u(t-3),h2(t)=u(t)-2u(t-1)+u(t-2)x2[k]={1, 2 ,1, 0; k=0,1,2}, h2[k]= {1,1;k=0,1}当抽样间隔为0.1时,y2[t]比y2(t)超前一个单位,故在y2[t]最前面补零,采用plot即可画出y2(t)的正确波形。
另外,由二题研讨可知,将抽样间隔缩小(例如抽样间隔取0.01),采用plot画图也可以得到y2(t)的正确波形。
采用补零的方法画出y2(t)的波形为:附程序代码:x2=[0,1,2,1,0];h2=[1,-1]; %在x2最前面补零y2=conv(x2,h2);N=length(y2);plot(0:N-1,y2);axis([0 8 -1 1](4)若分段常数的区间宽度不是1,应如何修改算法?如图,若间隔为0.5时,图像及代码如下:附程序代码:x2=[1,2,1,0];h2=[1,-1];y2=conv(x2,h2);N=length(y2);stem(0:0.5:(N-1).*0.5,y2); %红体为相比间隔为1的函数修改的部分axis([0 8 -1 1])(5)完成了分段常数信号卷积积分的分析和计算后,你对y1(t)的近似计算方法有无新的认识?可以由离散的卷积来近似的计算连续函数的卷积,但是要根据实际函数在0右边的积分的值,来确定离散函数向右偏移的格数,如可以取y1(t)的边界值先进行离散序列的卷积,如在用y2[t]来近似计算y2(t)时,由于y2(t)在0~1时,存在卷积积分的由0逐渐增长,到1时,存在着积分的变化,所以应将离散的图形向右平移一个单位。
同时由于连续序列卷积后也是连续的可以将相邻的离散点相连。
这样可以较快的计算出y1(t)的近似。
四、(**)非时限信号卷积积分的近似计算近似计算若卷积积分y3(t)。
若出现问题请分析出现问题的原因,并给出一种解决问题的方案;根据提出的方案完成近似计算卷积分的程序;用近似方法计算y3(t)的代码及结果如下。
当区间长度为20时:附程序代码:N=0.01;t=0:0.01:20;x=1*(t>=0);y=exp(-t).*(t>=0);yt=conv(x,y);subplot(211);n=0:0.01:40;plot(n,N*yt);axis([0 20 0 2]);xlabel('时间(s)'); ylabel('近似值yt(t)'); subplot(212);yt1=(1-exp(-t)).*(t>=0); plot(t,yt1);axis([0 inf 0 2]);xlabel('时间(s)'); ylabel('真实值yt(t)');当区间长度为40时:附程序代码:N=0.01;t=0:0.01:20;x=1*(t>=0);y=exp(-t).*(t>=0);yt=conv(x,y);subplot(211);n=0:0.01:40;plot(n,N*yt);axis([0 40 0 2]);xlabel('时间(s)');ylabel('近似值yt(t)');subplot(212);yt1=(1-exp(-t)).*(t>=0);plot(t,yt1);axis([0 inf 0 2]);xlabel('时间(s)');ylabel('真实值yt(t)');出现这种情况的原因:因为conv函数无法计算一个无穷的卷积,题目中虽然是算了exp(-t)的卷积,但是实际取的是(0,20)这个区间内的值,在做卷积的计算过程中,使用matlab对t进行了赋值,在赋值以外的点,被认为时0,所以在t>=0&t<=20这个区间内是没有问题的,但是t一但大于20两者的卷积就会有缺失,计算值就不在准确,t>20的部分就相当于是错误的,没有任何意义。
解决方法:在绘制图形时,将绘制图形的坐标范围限定在t的取值范围之内,或绘制图形后去掉无效值。
五、(***)卷积函数conv函数选项的定义与应用研究在新版MATLAB中,卷积函数conv提供了选项conv(A, B,’valid’ ),下面将研究conv(A, B,’valid’ )的定义及应用。
(1)读MATLAB提供的关于conv的Help,给出卷积函数conv(A, B,’valid’ )的定义。
设计一些简单的实验,验证你给出的定义。
你认为这样定义的卷积有何优缺点?键入“help conv”可知matlab对于valid的定义:C = CONV(A, B, SHAPE) returns a subsection of the convolution with sizespecified by SHAPE:'valid' - returns only those parts of the convolutionthat are computed without the zero-padded edges.LENGTH(C)is MAX(LENGTH(A)-MAX(0,LENGTH(B)-1),0).【只返回那些卷积计算无零填充的边缘部分】接下来利用A=[1 2 3 4 5]和B=[1 2 3]对valid进行研究。
