数学百大经典例题
数学百大经典例题
例1 已知p：x1，x2是方程x2＋5x－6＝0的两根，q：x1＋x2＝－5，则p是q的[ ] A．充分但不必要条件B．必要但不充分条件C．充要条件D．既不充分也不必要条件分析利用韦达定理转换．解∵x1，x2是方程x2＋5x－6＝0的两根，∴x1，x2的值分别为1，－6，∴x1＋x2＝1－6＝－5．因此选A．说明：判断命题为假命题可以通过举反例．例2 p是q的充要条件的是[ ] A．p：3x＋2＞5，q：－2x－3＞－5B．p：a＞2，b＜2，q：a＞bC．p：四边形的两条对角线互相垂直平分，q：四边形是正方形D．p：a≠0，q：关于x的方程ax＝1有惟一解分析逐个验证命题是否等价．解对A．p：x＞1，q：x＜1，所以，p是q的既不充分也不必要条件；对B．p q但q p，p是q的充分非必要条件；对C．p q且q p，p是q的必要非充分条件；⇒⇒⇔D p q q p p q p q D对．且，即，是的充要条件．选．说明：当a＝0时，ax＝0有无数个解．例3 若A是B成立的充分条件，D是C成立的必要条件，C是B成立的充要条件，则D是A成立的[ ] A．充分条件B．必要条件C．充要条件D．既不充分也不必要条件分析通过B、C作为桥梁联系A、D．解∵A是B的充分条件，∴A B①∵D是C成立的必要条件，∴C D②∵是成立的充要条件，∴③⇔C B C B由①③得A C④由②④得A D．∴D 是A 成立的必要条件．选B ．说明：要注意利用推出符号的传递性．例4 设命题甲为：0＜x ＜5，命题乙为|x －2|＜3，那么甲是乙的[ ]A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 分析 先解不等式再判定．解 解不等式|x －2|＜3得－1＜x ＜5．∵0＜x ＜5－1＜x ＜5，但－1＜x ＜50＜x ＜5 ∴甲是乙的充分不必要条件，选A ．说明：一般情况下，如果条件甲为x ∈A ，条件乙为x ∈B ．当且仅当时，甲为乙的充分条件；当且仅当时，甲为乙的必要条件；A B A B ⊆⊇当且仅当A ＝B 时，甲为乙的充要条件． 例5 设A 、B 、C 三个集合，为使A(B ∪C)，条件AB 是[ ]A ．充分条件B ．必要条件C ．充要条件D ．既不充分也不必要条件 分析 可以结合图形分析．请同学们自己画图．∴A(B ∪C)．但是，当B ＝N ，C ＝R ，A ＝Z 时， 显然A(B ∪C)，但AB 不成立， 综上所述：“A B ”“A (B ∪C)”，而“A (B ∪C)”“AB ”．即“AB ”是“A (B ∪C)”的充分条件(不必要)．选A ．说明：画图分析时要画一般形式的图，特殊形式的图会掩盖真实情况． 例6 给出下列各组条件：(1)p ：ab ＝0，q ：a 2＋b 2＝0；(2)p ：xy ≥0，q ：|x|＋|y|＝|x ＋y|；(3)p ：m ＞0，q ：方程x 2－x －m ＝0有实根； (4)p ：|x －1|＞2，q ：x ＜－1． 其中p 是q 的充要条件的有[ ]A ．1组B ．2组C ．3组D ．4组分析 使用方程理论和不等式性质． 解 (1)p 是q 的必要条件 (2)p 是q 充要条件 (3)p 是q 的充分条件 (4)p 是q 的必要条件．选A ．说明：ab ＝0指其中至少有一个为零，而a 2＋b 2＝0指两个都为零． 例＞＞是＞＞的条件．7x 3x 3x x x 12112⎧⎨⎩+⎧⎨⎩x 269分析 将前后两个不等式组分别作等价变形，观察两者之间的关系．解＞且＞＋＞且＞，但当取＝，＝时，＞＞成立，而＞＞不成立＝与＞矛盾，所以填“充分不必要”．x 3x 3x x 6x x 9x 10x 2(x 2x 3)1212121222⇒+⎧⎨⎩⎧⎨⎩x x x x x x 1212126933 说明：＞＞－＞－＞x 3x 3 x 30x 301212⎧⎨⎩⇔⎧⎨⎩ ⇔⎧⎨⎩⇔⎧⎨⎩(x 3)(x 3)0(x 3)(x 3)0x x 6x x 3(x x )901212121212－＋－＞－－＞＋＞－＋＋＞这一等价变形方法有时会用得上．例8 已知真命题“a ≥bc ＞d ”和“a ＜be ≤f ”，则“c ≤d ”是“e ≤f ”的________条件．分析 ∵a ≥b c ＞d(原命题)， ∴c ≤d a ＜b(逆否命题)． 而a ＜b e ≤f ，∴c ≤de ≤f 即c ≤d 是e ≤f 的充分条件．答 填写“充分”．说明：充分利用原命题与其逆否命题的等价性是常见的思想方法． 例9 ax 2＋2x ＋1＝0至少有一个负实根的充要条件是[ ]A ．0＜a ≤1B ．a ＜1C ．a ≤1D ．0＜a ≤1或a ＜0分析 此题若采用普通方法推导较为复杂，可通过选项提供的信息，用排除法解之．当a ＝1时，方程有负根x ＝－1，当a ＝0时，x ＝－．故排除、、选．12A B D C 解常规方法：当＝时，＝－． a 0x 12当a ≠0时1a 0ax 2x 10021a 0a 12．＞，则＋＋＝至少有一个负实根＜－＜＜≤．⇔---⇔-⇔24422a a2a 0ax 2x 100221a 21a 1a 02．＜，则＋＋＝至少有一个负实根＜＞－＞－＞＜．⇔-+-⇔⇔⇔2442a a综上所述a ≤1．即ax 2＋2x ＋1＝0至少有一个负实根的充要条件是a ≤1． 说明：特殊值法、排除法都是解选择题的好方法．例10 已知p 、q 都是r 的必要条件，s 是r 的充分条件，q 是s 的充分条件，那么s ，r ，p 分别是q 的什么条件？分析 画出关系图1－21，观察求解．解 s 是q 的充要条件；(s r q ，q s)r 是q 的充要条件；(r q ，q s r) p 是q 的必要条件；(q s r p)说明：图可以画的随意一些，关键要体现各个条件、命题之间的逻辑关系．例11 关于x 的不等式 |x |x 3(a 1)x 2(3a 1)0AB A B 1a 3a 12－≤与－＋＋＋≤的解集依次为与，问“”是“≤≤或＝－”的充要条件吗？()()a a +-⊆121222分析 化简A 和B ，结合数轴，构造不等式(组)，求出a ． 解 A ＝{x|2a ≤x ≤a 2＋1}，B ＝{x|(x －2)[x －(3a ＋1)]≤0}当≤＋即≥时，23a 1a 13B ＝{x|2≤x ≤3a ＋1}．A B 2a 2a +13a +11a 323a 1a 2⊆⇔⎧⎨⎩⇔≥≤≤≤当＞＋即＜时，13 B ＝{x|3a ＋1≤x ≤2}A B 2a 3a +1a +12a 1A B a 11a 3A B 1a 3a 12⊆⇔⎧⎨⎩⇔⊆⇔⊆≥≤＝－．综上所述：＝－或≤≤．∴“”是“≤≤或＝－”的充要条件．说明：集合的包含关系、命题的真假往往与解不等式密切相关．在解题时要理清思路，表达准确，推理无误．例＞，＞是＜的必要条件还是充分条件，还是充12 x y xy 011x y要条件？分析 将充要条件和不等式同解变形相联系． 解．当＜时，可得－＜即＜ 1001111x yx y y x xy-则－＞＜或－＜＞，即＜＜或＞＞，y x 0xy 0y x 0xy 0 x y xy 0x 0⎧⎨⎩⎧⎨⎩⎧⎨⎩⎧⎨⎩y xy故＜不能推得＞且＞有可能得到＜＜，即＞且＞并非＜的必要条件．1111x y x yxy x yx y xy 0()x y xy0⎧⎨⎩2x y xy 0x y x 0y 0x yx 0y 0x y xy 0．当＞且＞则分成两种情况讨论：＞＞＞或＞＜＜不论哪一种情况均可化为＜．∴＞且＞是＜的充分条件．⎧⎨⎪⎩⎪⎧⎨⎪⎩⎪1111x y x y说明：分类讨论要做到不重不漏．例13 设α，β是方程x 2－ax ＋b ＝0的两个实根，试分析a ＞2且b ＞1是两根α，β均大于1的什么条件？分析 把充要条件和方程中根与系数的关系问题相联系，解题时需 要搞清楚条件与结论分别指什么．然后再验证是还是还是．p q p q q p p q ⇒⇒⇔解据韦达定理得：＝α＋β，＝αβ，判定的条件是：＞＞结论是：α＞β＞还要注意条件中，，需要满足大前提Δ＝－≥ a b p q (p a b a 4b 0)2a b 2111⎧⎨⎩⎧⎨⎩(1)1a2b1由α＞β＞得＝α＋β＞，＝αβ＞，1⎧⎨⎩∴q p．上述讨论可知：a＞2，b＞1是α＞1，β＞1的必要但不充分条件．说明：本题中的讨论内容在二次方程的根的分布理论中常被使用．例14 (1991年全国高考题)设甲、乙、丙是三个命题，如果甲是乙的必要条件，丙是乙的充分条件，但不是乙的必要条件，那么[ ] A．丙是甲的充分条件，但不是甲的必要条件B．丙是甲的必要条件，但不是甲的充分条件C．丙是甲的充要条件D．丙不是甲的充分条件，也不是甲的必要条件分析1：由丙乙甲且乙丙，即丙是甲的充分不必要条件．分析2：画图观察之．答：选A．说明：抽象命题之间的逻辑关系通常靠画图观察比较方便。
数学百大经典例
数学百大经典例————————————————————————————————作者：————————————————————————————————日期：例1 简述下列问题的结论，并画图说明：（1）直线⊂a 平面α，直线A a b =I ，则b 和α的位置关系如何？ （2）直线α⊂a ，直线a b //，则直线b 和α的位置关系如何？ 分析：（1）由图（1）可知：α⊂b 或A b =αI ； （2）由图（2）可知：α//b 或α⊂b ．说明：此题是考查直线与平面位置关系的例题，要注意各种位置关系的画法与表示方法．典型例题二例2 P 是平行四边形ABCD 所在平面外一点，Q 是PA 的中点，求证：//PC 平面BDQ ． 分析：要证明平面外的一条直线和该平面平行，只要在该平面内找到一条直线和已知直线平行就可以了．证明：如图所示，连结AC ，交BD 于点O ， ∵四边形ABCD 是平行四边形∴CO AO =，连结OQ ，则OQ 在平面BDQ 内，且OQ 是APC ∆的中位线，∴OQ PC //． ∵PC 在平面BDQ 外， ∴//PC 平面BDQ ．说明：应用线面平行的判定定理证明线面平行时，关键是在平面内找一条直线与已知直线平行，怎样找这一直线呢？由于两条直线首先要保证共面，因此常常设法过已知直线作一平面与已知平面相交，如果能证明已知直线和交线平行，那么就能够马上得到结论．这一个证明线面平行的步骤可以总结为：过直线作平面，得交线，若线线平行，则线面平行．例3 经过两条异面直线a ，b 之外的一点P ，可以作几个平面都与a ，b 平行？并证明你的结论．分析：可考虑P 点的不同位置分两种情况讨论． 解：（1）当P 点所在位置使得a ，P （或b ，P ）本身确定的平面平行于b （或a ）时，过P 点再作不出与a ，b 都平行的平面；（2）当P 点所在位置a ，P （或b ，P ）本身确定的平面与b （或a ）不平行时，可过点P 作a a '//，b b //'．由于a ，b 异面，则a '，b '不重合且相交于P ．由于P b a =''I ，a '，b '确定的平面α，则由线面平行判定定理知：α//a ，α//b ．可作一个平面都与a ，b 平行．故应作“0个或1个”平面．说明：本题解答容易忽视对P 点的不同位置的讨论，漏掉第（1）种情况而得出可作一个平面的错误结论．可见，考虑问题必须全面，应区别不同情形分别进行分类讨论．典型例题四例4 平面外的两条平行直线中的一条平行于这个平面，那么另一条直线也平行于这个平面．已知：直线b a //，//a 平面α，α⊄b ． 求证：α//b ．证明：如图所示，过a 及平面α内一点A 作平面β． 设c =βαI ，∵α//a ， ∴c a //． 又∵b a //， ∴c b //．∵α⊄b ，α⊂c ， ∴α//b ．说明：根据判定定理，只要在α内找一条直线b c //，根据条件α//a ，为了利用直线和平面平行的性质定理，可以过a 作平面β与α相交，我们常把平面β称为辅助平面，它可以起到桥梁作用，把空间问题向平面问题转化．和平面几何中添置辅助线一样，在构造辅助平面时，首先要确认这个平面是存在的，例如，本例中就是以“直线及直线外一点确定一个平面”为依据来做出辅助平面的．典型例题五例5 已知四面体ABC S -的所有棱长均为a ．求：（1）异面直线AB SC 、的公垂线段EF 及EF 的长； （2）异面直线EF 和SA 所成的角．分析：依异面直线的公垂线的概念求作异面直线AB SC 、的公垂线段，进而求出其距离；对于异面直线所成的角可采取平移构造法求解．解：（1）如图，分别取AB SC 、的中点F E 、，连结CF SF 、．由已知，得SAB ∆≌CAB ∆． ∴CF SF =，E 是SC 的中点， ∴SC EF ⊥．同理可证AB EF ⊥∴EF 是AB SC 、的公垂线段．在SEF Rt ∆中，a SF 23=，a SE 21=． ∴22SE SF EF -=a a a 22414322=-． （2）取AC 的中点G ，连结EG ，则SA EG //．∴EF 和GE 所成的锐角或直角就是异面直线EF 和SA 所成的角． 连结FG ，在EFG Rt ∆中，a EG 21=，a GF 21=，a EF 22=． 由余弦定理，得22222124142412cos 222222=⋅⋅-+=⋅⋅-+=∠a a aa a EF EG GF EF EG GEF ． ∴ο45=∠GEF ．故异面直线EF 和SA 所成的角为ο45．说明：对于立体几何问题要注意转化为平面问题来解决，同时要将转化过程简要地写出来，然后再求值．典型例题六例6 如果一条直线与一个平面平行，那么过这个平面内的一点且与这条直线平行的直线必在这个平面内．已知：直线α//a ，α∈B ，b B ∈，a b //．求证：α⊂b ．分析：由于过点B 与a 平行的直线是惟一存在的，因此，本题就是要证明，在平面α外，不存在过B 与a 平行的直线，这是否定性命题，所以使用反证法．证明：如图所示，设α⊄b ，过直线a 和点B 作平面β，且'b =αβI ． ∵α//a ，∴α//'b ．这样过B 点就有两条直线b 和'b 同时平行于直线a ，与平行公理矛盾． ∴b 必在α内．说明：(1)本例的结论可以直接作为证明问题的依据． (2)本例还可以用同一法来证明，只要改变一下叙述方式．如上图，过直线a 及点B 作平面β，设'b =αβI ．∵α//a ，∴α//'b ．这样，'b 与b 都是过B 点平行于a 的直线，根据平行公理，这样的直线只有一条， ∴b 与'b 重合．∵α⊂'b ，∴α⊂b ．典型例题七例7 下列命题正确的个数是（ ）．(1)若直线l 上有无数个点不在平面α内，则α//l ； (2)若直线l 平行于平面α内的无数条直线，则α//l ；(3)若直线l 与平面α平行，则l 与平面α内的任一直线平行； (4)若直线l 在平面α外，则α//l ．A ．0个B ．1个C ．2个D ．3个分析：本题考查的是空间直线与平面的位置关系．对三种位置关系定义的准确理解是解本题的关键．要注意直线和平面的位置关系除了按照直线和平面公共点的个数来分类，还可以按照直线是否在平面内来分类．解：(1)直线l 上有无数个点不在平面α内，并没有说明是所在点都不在平面α内，因而直线可能与平面平行亦有可能与直线相交．解题时要注意“无数”并非“所有”．(2)直线l 虽与α内无数条直线平行，但l 有可能在平面α内，所以直线l 不一定平行α．(3)这是初学直线与平面平行的性质时常见错误，借助教具我们很容易看到．当α//l 时，若α⊂m 且l m //，则在平面α内，除了与m 平行的直线以外的每一条直线与l 都是异面直线．(4)直线l 在平面α外，应包括两种情况：α//l 和l 与α相交，所以l 与α不一定平行． 故选A ．说明：如果题中判断两条直线与一平面之间的位置关系，解题时更要注意分类要完整，考虑要全面．如直线l 、m 都平行于α，则l 与m 的位置关系可能平行，可能相交也有可能异面；再如直线m l //、α//l ，则m 与α的位置关系可能是平行，可能是m 在α内．典型例题八例8 如图，求证：两条平行线中的一条和已知平面相交，则另一条也与该平面相交． 已知：直线b a //，P a =α平面I ．求证：直线b 与平面α相交．分析：利用b a //转化为平面问题来解决，由b a //可确定一辅助平面β，这样可以把题中相关元素集中使用，既创造了新的线面关系，又将三维降至二维，使得平几知识能够运用．解：∵b a //，∴a 和b 可确定平面β． ∵P a =αI，∴平面α和平面β相交于过点P 的直线l ．∵在平面β内l 与两条平行直线a 、b 中一条直线a 相交，∴l 必定与直线b 也相交，不妨设Q l b =I ，又因为b 不在平面α内（若b 在平面α内，则α和β都过相交直线b 和l ，因此α与β重合，a 在α内，和已知矛盾）．所以直线b 和平面α相交．说明：证明直线和平面相交的常用方法有：证明直线和平面只有一个公共点；否定直线在平面内以及直线和平面平行；用此结论：一条直线如果经过平面内一点，又经过平面外一点，则此直线必与平面相交（此结论可用反证法证明）．典型例题九例9 如图，求证：经过两条异面直线中的一条，有且仅有一个平面与另一条直线平行．已知：a 与b 是异面直线．求证：过b 且与a 平行的平面有且只有一个．分析：本题考查存在性与唯一性命题的证明方法．解题时要理解“有且只有”的含义．“有”就是要证明过直线b 存在一个平面α，且α//a ，“只有”就是要证满足这样条件的平面是唯一的．存在性常用构造法找出（或作出）平面，唯一性常借助于反证法或其它唯一性的结论．证明：(1)在直线b 上任取一点A ，由点A 和直线a 可确定平面β． 在平面β内过点A 作直线'a ，使a a //'，则'a 和b 为两相交直线， 所以过'a 和b 可确定一平面α． ∵α⊂b ，a 与b 为异面直线，∴α⊄a ．又∵'//a a ，α⊂'a ，∴α//a ．故经过b 存在一个平面α与a 平行．(2)如果平面γ也是经过b 且与a 平行的另一个平面， 由上面的推导过程可知γ也是经过相交直线b 和'a 的．由经过两相交直线有且仅有一个平面的性质可知，平面α与γ重合， 即满足条件的平面是唯一的．说明：对于两异面直线a 和b ，过b 存在一平面α且与a 平行，同样过a 也存在一平面β且与b 平行．而且这两个平面也是平行的（以后可证）．对于异面直线a 和b 的距离，也可转化为直线a 到平面α的距离，这也是求异面直线的距离的一种方法．典型例题十例10 如图，求证：如果一条直线和两个相交平面都平行，那么这条直线和它们的交线平行．已知：l =βαI ，α//a ，β//a ，求证：l a //．分析：本题考查综合运用线面平行的判定定理和性质定理的能力．利用线面平行的性质定理，可以先证明直线a 分别和两平面的某些直线平行，即线面平行可得线线平行．然后再用线面平行的判定定理和性质定理来证明a 与l 平行．证明：在平面α内取点P ，使l P ∉，过P 和直线a 作平面γ交α于b ． ∵α//a ，γ⊂a ，b =αγI ， ∴b a //．同理过a 作平面δ交β于c ． ∵β//a ，δ⊂a ，c =βδI ， ∴c a //． ∴c b //．∵β⊄b ，β⊂c ， ∴β//b ．又∵α⊂b ，l =βαI ， ∴l b //． 又∵b a //， ∴l a //．另证：如图，在直线l 上取点M ，过M 点和直线a 作平面和α相交于直线1l ，和β相交于直线2l ．∵α//a ，∴1//l a ， ∵β//a ，∴2//l a ，但过一点只能作一条直线与另一直线平行． ∴直线1l 和2l 重合．又∵α⊂1l ，β⊂2l ， ∴直线1l 、2l 都重合于直线l ，∴l a //． 说明：“线线平行”与“线面平行”在一定条件下是可以相互转化的，这种转化的思想在立体几何中非常重要．典型例题十一例11 正方形ABCD 与正方形ABEF 所在平面相交于AB ，在AE 、BD 上各取一点P 、Q ，且DQ AP =．求证：//PQ 面BCE ．分析：要证线面平行，可以根据判定定理，转化为证明线线平行．关键是在平面BCE 中如何找一直线与PQ 平行．可考察过PQ 的平面与平面BCE 的交线，这样的平面位置不同，所找的交线也不同．证明一：如图，在平面ABEF 内过P 作AB PM //交BE 于M ，在平面ABCD 内过Q 作AB QN //交BC 于N ，连结MN ．∵AB PM //，∴AEPEAB PM =． 又∵CD AB QN ////，∴BD BQ DC QN =，即BDBQAB QN =． ∵正方形ABEF 与ABCD 有公共边AB ， ∴DB AE =．∵DQ AP =，∴BQ PE =． ∴QN PM =．又∵AB PM //，AB QN //， ∴QN PM //．∴四边形PQNM 为平行四边形．∴MN PQ //．又∵⊂MN 面BCE ，∴//PQ 面BCE ．证明二：如图，连结AQ 并延长交BC 于S ，连结ES ．∵AD BS //，∴QBDQ QS AQ =． 又∵正方形ABEF 与正方形ABCD 有公共边AB ，∴DB AE =，∵DQ AP =，∴QB PE =．∴QSAQ QB DQ PE AP ==． ∴ES PQ //，又∵⊂ES 面BEC ，∴//PQ 面BEC ．说明：从本题中我们可以看出，证线面平行的根本问题是要在平面内找一直线与已知直线平行，此时常用中位线定理、成比例线段、射影法、平行移动、补形等方法，具体用何种方法要视条件而定．此题中我们可以把“两个有公共边的正方形”这一条件改为“两个全等的矩形”，那么题中的结论是否仍然成立？典型例题十二例12 三个平面两两相交于三条交线，证明这三条交线或平行、或相交于一点．已知：a =βαI ，b =γβI ，c =αγI ．求证：a 、b 、c 互相平行或相交于一点．分析：本题考查的是空间三直线的位置关系，我们可以先从熟悉的两条交线的位置关系入手，根据共面的两条直线平行或相交来推论三条交线的位置关系．证明：∵a =βαI ，b =γβI ，∴β⊂b a 、．∴a 与b 平行或相交．①若b a //，如图∵γ⊂b ，γ⊄a ，∴γ//a ．又∵c =αγI ，α⊂a ，∴c a //．∴c b a ////．②若a 与b 相交，如图，设O b a =I ，∴a O ∈，b O ∈．又∵βαI =a ，γβI =b ．∴α∈O ，γ∈O又∵c =γαI ，∴c O ∈．∴直线a 、b 、c 交于同一点O ．说明：这一结论常用于求一个几何体的截面与各面交线问题，如正方体ABCD 中， M 、N 分别是1CC 、11B A 的中点，画出点D 、M 、N 的平面与正方体各面的交线，并说明截面多边形是几边形？典型例题十三例13 已知空间四边形ABCD ，AC AB ≠，AE 是ABC ∆的BC 边上的高，DF 是BCD ∆的BC 边上的中线，求证：AE 和DF 是异面直线．证法一：（定理法）如图由题设条件可知点E 、F 不重合，设BCD ∆所在平面α．∴⇒⎪⎪⎩⎪⎪⎨⎧∉∈∉⊂DFEEADFαααAE和DF是异面直线．证法二：（反证法）若AE和DF不是异面直线，则AE和DF共面，设过AE、DF的平面为β．(1)若E、F重合，则E是BC的中点，这与题设ACAB≠相矛盾．(2)若E、F不重合，∵EFB∈，EFC∈，β⊂EF，∴β⊂BC．∵β∈A，β∈D，∴A、B、C、D四点共面，这与题设ABCD是空间四边形相矛盾．综上，假设不成立．故AE和DF是异面直线．说明：反证法不仅应用于有关数学问题的证明，在其他方面也有广泛的应用．首先看一个有趣的实际问题：“三十六口缸，九条船来装，只准装单，不准装双，你说怎么装？”对于这个问题，同学们可试验做一做．也许你在试验几次后却无法成功时，觉得这种装法的可能性是不存在的．那么你怎样才能清楚地从理论上解释这种装法是不可能呢？用反证法可以轻易地解决这个问题．假设这种装法是可行的，每条船装缸数为单数，则9个单数之和仍为单数，与36这个双数矛盾．只须两句话就解决了这个问题．典型例题十四例14已知AB、BC、CD是不在同一平面内的三条线段，E、F、G分别是AB、BC、CD的中点，求证：平面EFG和AC平行，也和BD平行．分析：欲证明AC//平面EFG，根据直线和平面平等的判定定理只须证明AC平行平面EFG内的一条直线，由图可知，只须证明EFAC//．证明：如图，连结AE、EG、EF、GF．在ABC∆中，E、F分别是AB、BC的中点．∴EFAC//．于是AC//平面EFG．同理可证，BD//平面EFG．说明：到目前为止，判定直线和平面平行有以下两种方法：(1)根据直线和平面平行定义；(2)根据直线和平面平行的判定定理．典型例题十五例15 已知空间四边形ABCD ，P 、Q 分别是ABC ∆和BCD ∆的重心，求证：ACD PQ 平面//．分析：欲证线面平行，须证线线平行，即要证明PQ 与平面ACD 中的某条直线平行，根据条件，此直线为AD ，如图．证明：取BC 的中点E ．∵P 是ABC ∆的重心，连结AE ，则1∶3=PE AE ∶，连结DE ，∵Q 为BCD ∆的重心，∴1∶3=QE DE ∶，∴在AED ∆中，AD PQ //．又ACD AD 平面⊂，ACD PQ 平面⊄，∴ACD PQ 平面//．说明：(1)本例中构造直线AD 与PQ 平行，是充分借助于题目的条件：P 、Q 分别是ABC ∆和BCD ∆的重心，借助于比例的性质证明AD PQ //，该种方法经常使用，望注意把握．(2)“欲证线面平行，只须证线线平行”．判定定理给我们提供了一种证明线面平等的方法．根据问题具体情况要熟练运用．典型例题十六例16 正方体1111D C B A ABCD -中，E 、G 分别是BC 、11D C 的中点如下图． 求证：D D BB EG 11//平面．分析：要证明D D BB EG 11//平面，根据线面平等的判定定理，需要在平面D D BB 11内找到与EG 平行的直线，要充分借助于E 、G 为中点这一条件．证明：取BD 的中点F ，连结EF 、F D 1．∵E 为BC 的中点，∴EF 为BCD ∆的中位线，则DC EF //，且CD EF 21=． ∵G 为11D C 的中点，∴CD G D //1且CD G D 211=， ∴G D EF 1//且G D EF 1=，∴四边形G EFD 1为平行四边形，∴EG F D //1，而111B BDD F D 平面⊂，11B BDD EG 平面⊄，∴11//B BDD EG 平面．典型例题十七例17 如果直线α平面//a ，那么直线a 与平面α内的（ ）．A ．一条直线不相交B ．两条相交直线不相交C ．无数条直线不相交D ．任意一条直线都不相交解：根据直线和平面平行定义，易知排除A 、B ．对于C ，无数条直线可能是一组平行线，也可能是共点线，∴C 也不正确，应排除C ．与平面α内任意一条直线都不相交，才能保证直线a 与平面α平行，∴D 正确． ∴应选D ．说明：本题主要考查直线与平面平行的定义．典型例题十八例18 分别和两条异面直线平行的两条直线的位置关系是（ ）．A ．一定平行B ．一定相交C ．一定异面D ．相交或异面解：如图中的甲图，分别与异面直线a 、b 平行的两条直线c 、d 是相交关系； 如图中的乙图，分别与异面直线a 、b 平行的两条直线c 、d 是相交关系．综上，可知应选D ．说明：本题主要考查有关平面、线面平行等基础知识以及空间想象能力．典型例题十九例19 a 、b 是两条异面直线，下列结论正确的是（ ）．A ．过不在a 、b 上的任一点，可作一个平面与a 、b 平行B ．过不在a 、b 上的任一点，可作一个直线与a 、b 相交C ．过不在a 、b 上的任一点，可作一个直线与a 、b 都平行D ．过a 可以并且只可以作一平面与b 平行解：A 错，若点与a 所确定的平面与b 平行时，就不能使这个平面与α平行了． B 错，若点与a 所确定的平面与b 平等时，就不能作一条直线与a ，b 相交．C 错，假如这样的直线存在，根据公理4就可有b a //，这与a ，b 异面矛盾．D 正确，在a 上任取一点A ，过A 点做直线b c //，则c 与a 确定一个平面与b 平行，这个平面是惟一的．∴应选Ｄ．说明：本题主要考查异面直线、线线平行、线面平行等基本概念．典型例题二十例20 (1)直线b a //，α平面//a ，则b 与平面α的位置关系是_____________．(2)A 是两异面直线a 、b 外的一点，过A 最多可作___________个平面同时与a 、b 平行．解：(1)当直线b 在平面α外时，α//b ；当直线b 在平面α内时，α⊂b ．∴应填：α//b 或α⊂b ．(2)因为过A 点分别作a ，b 的平行线只能作一条，（分别称'a ，'b ）经过'a ，'b 的平面也是惟一的．所以只能作一个平面；还有不能作的可能，当这个平面经过a 或b 时，这个平面就不满足条件了．∴应填：1．说明：考虑问题要全面，各种可能性都要想到，是解答本题的关键．典型例题二十一例21 如图，α//a ，A 是α的另一侧的点，a D C B ∈,,，线段AB ，AC ，AD 交α于E ，F ，G ，若4=BD ，4=CF ，5=AF ，则EG =___________．解：∵α//a ，ABD EG 平面I α=．∴EG a //，即EG BD //， ∴FCAF AF BD EG CD BC FG EF AC AF CD FG BC EF +==++===． 则9204545=+⨯=+⋅=FC AF BD AF EG ． ∴应填：920． 说明：本题是一道综合题，考查知识主要有：直线与平面平行性质定理、相似三角形、比例性质等．同时也考查了综合运用知识，分析和解决问题的能力．。
高考数学百大经典例题 算术平均数与几何平均数
典型例题一例1 已知R c b a ∈,,，求证.222ca bc ab c b a ++≥++ 证明：∵ ab b a 222≥+， bc c b 222≥+，ca a c 222≥+， 三式相加，得)(2)(2222ca bc ab c b a ++≥++，即.222ca bc ab c b a ++≥++说明：这是一个重要的不等式，要熟练掌握．典型例题二例2 已知c b a 、、是互不相等的正数，求证：abc b a c c a b c b a 6)()()(222222>+++++ 证明：∵0222>>+a bc c b ，， ∴abc c b a 2)(22>+同理可得：abc b a c abc c a b 2)(2)(2222>+>+，． 三个同向不等式相加，得abc b a c c a b c b a 6)()()(222222>+++++ ①说明：此题中c b a 、、互不相等，故应用基本不等式时，等号不成立．特别地，b a =，c b ≠时，所得不等式①仍不取等号．典型例题三例3 求证)(2222222c b a a c c b b a ++≥+++++．分析：此问题的关键是“灵活运用重要基本不等式ab b a 222≥+，并能由)(2c b a ++这一特征，思索如何将ab b a 222≥+进行变形，进行创造”．证明：∵ab b a 222≥+，两边同加22b a +得222)()(2b a b a +≥+．即2)(222b a b a +≥+．∴)(222122b a b a b a +≥+≥+．同理可得：)(2222c b c b +≥+，)(2222a c a c +≥+． 三式相加即得)(2222222c b a a c c b b a ++≥+++++．典型例题四例4 若正数a 、b 满足3++=b a ab ，则ab 的取值范围是 ． 解：∵+∈R b a ,， ∴323+≥++=ab b a ab ，令ab y =，得0322≥--y y ，∴3≥y ，或1-≤y （舍去）．∴92≥=ab y ，∴ ab 的取值范围是[).,9+∞说明：本题的常见错误有二．一是没有舍去1-≤y ；二是忘了还原，得出[)+∞∈,3ab ．前者和后者的问题根源都是对ab 的理解，前者忽视了.0≥ab 后者错误地将2y 视为ab ．因此，解题过程中若用换元法，一定要对所设“元”的取值范围有所了解，并注意还原之．典型例题五例5 （1）求41622++=x x y 的最大值． （2）求函数1422++=x x y 的最小值，并求出取得最小值时的x 值． （3）若0,0>>y x ，且2=+y x ，求22y x +的最小值．解：（1）41622++=x x y 13163)1(162222+++=+++=x x x x .3326=≤即y 的最大值为.3当且仅当13122+=+x x 时，即22=x 2±=x 时，取得此最大值．（2）1141142222-+++=++=x x x x y 3142=-⋅≥ ∴ y 的最小值为3，当且仅当11422+=+x x ，即4)1(22=+x ，212=+x ，1±=x 时取得此最小值．（3）∴ xy y x 222≥+ ∴222)()(2y x y x +≥+即2)(222y x y x +≥+∵2=+y x ∴222≥+y x 即22y x +的最小值为2． 当且仅当4==y x 时取得此最小值．说明：解这类最值，要选好常用不等式，特别注意等号成立的条件．典型例题六例6 求函数xx y 321--=的最值． 分析：本例的各小题都可用最值定理求函数的最值，但是应注意满足相应条件．如：0≠x ，应分别对0,0<>x x 两种情况讨论，如果忽视+∈R x 的条件，就会发生如下错误：∵ 6213221)32(1321-=⋅-≤+-=--=xx x x x x y ，.621max -=y 解：当0>x 时，03,02>>x x ，又632=⋅xx ， 当且仅当x x 32=，即26=x 时，函数x x 32+有最小值.62 ∴ .621max -=y 当0<x 时，03,02>->-x x ，又6)3()2(=-⋅-xx ， 当且仅当x x 32-=-，即26+=x 时，函数)32(x x +-最小值.62 ∴ .621min +=y典型例题七例7 求函数91022++=x x y 的最值．分析：291991)9(2222≥+++=+++=x x x x y ．但等号成立时82-=x ，这是矛盾的！于是我们运用函数xx y 1+=在1≥x 时单调递增这一性质，求函数)3(1≥+=t tt y 的最值．解：设392≥+=x t ，∴t t x x y 191022+=++=．当3≥t 时，函数tt y 1+=递增． 故原函数的最小值为310313=+，无最大值．典型例题八例8 求函数4522++=x x y 的最小值．分析：用换元法，设242≥+=x t ，原函数变形为)2(1≥+=t tt y ，再利用函数)2(1≥+=t tt y 的单调性可得结果．或用函数方程思想求解．解：解法一： 设242≥+=x t ，故).2(14522≥+=++=t t t x x y212121212121121)()11()(2t t t t t t t t t t y y t t --=-+-=-≥>，设． 由202121><-t t t t ，，得：0121>-t t ，故：21y y <． ∴函数)2(1≥+=t t t y 为增函数，从而25212=+≥y ． 解法二： 设242≥=+t x ，知)2(1≥+=t tt y ，可得关于t 的二次方程012=+-yt t ，由根与系数的关系，得：121=t t ．又2≥t ，故有一个根大于或等于2，设函数1)(2+-=yt t t f ，则0)2(≤f ，即0124≤+-y ，故25≥y ．说明：本题易出现如下错解：2414452222≥+++=++=x x x x y ．要知道，41422+=+x x 无实数解，即2≠y ，所以原函数的最小值不是2．错误原因是忽视了等号成立的条件．当a 、b 为常数，且ab 为定值，b a ≠时，ab ba >+2，不能直接求最大（小）值，可以利用恒等变形ab b a b a 4)(2+-=+，当b a -之差最小时，再求原函数的最大（小）值．典型例题九例9 ,4,0,0=+>>b a b a 求2211⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+b b a a 的最小值．分析：此题出现加的形式和平方，考虑利用重要不等式求最小值． 解：由,4=+b a ，得.2162)(222ab ab b a b a -=-+=+ 又,222ab b a ≥+得ab ab 2216≥-，即4≤ab ．21111222⎪⎭⎫ ⎝⎛+++≥⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+∴b b a a b b a a .225244444422=⎪⎭⎫ ⎝⎛+≥⎪⎭⎫ ⎝⎛+=ab 故2211⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+b b a a 的最小值是225．说明：本题易出现如下错解：8441212112222=+=⎪⎪⎭⎫ ⎝⎛⋅+⎪⎪⎭⎫ ⎝⎛⋅≥⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+∴b b a a b b a a ，故2211⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+b b a a 的最小值是8．错误的原因是，在两次用到重要不等式当等号成立时，有1=a 和1=b ，但在4=+b a 的条件下，这两个式子不会同时取等号（31==b a 时，）．排除错误的办法是看都取等号时，与题设是否有矛盾．典型例题十例10 已知：+∈R c b a ,,，求证：c b a cab b ac a bc ++≥++． 分析：根据题设，可想到利用重要不等式进行证明．证明：.2,222c bac a bc c ab abc b ac a bc ≥+=≥+即同理：a cab b ac b c ab a bc 2,2≥+≥+ ).(22c b a c ab b ac a bc ++≥⎪⎭⎫⎝⎛++∴.c b a cab b ac a bc ++≥++∴说明：证明本题易出现的思维障碍是：(1)想利用三元重要不等式解决问题；(2)不会利用重要不等式ab ba ≥+2的变式；(3)不熟练证明轮换对称不等式的常用方法．因此，在证明不等式时，应根据求证式两边的结构，合理地选择重要不等式．另外，本题的证明方法在证轮换对称不等式时具有一定的普遍性．典型例题十一例11设R e d c b a ∈、、、、，且8=++++e d c b a ，1622222=++++e d c b a ，求e 的最大值．分析：如何将22b a +与b a +用不等式的形式联系起来，是本题获解的关键．算术平均数与几何平均数定理ab b a 222≥+两边同加22b a +之后得222)(21b a b a +≥+． 解：由222)(21b a b a +≥+，则有 ,)(41])()[(212222222d c b a d c b a d c b a +++≥+++≥+++.5160)8(411622≤≤⇒-≥-∴e e e.51656＝时，当最大值e d c b a ====说明：常有以下错解：abcd cd ab d c b a e 4)(21622222≥+≥+++=-， 448abcd d c b a e ≥+++=-．故abcd e abcd e ≥-≥-4222)48(,4)16(． 两式相除且开方得516014)8(1622≤≤⇒≥--e e e ．错因是两不等式相除，如211,12>>，相除则有22>． 不等式222)(21b a b a +≥+是解决从“和”到“积”的形式．从“和”到“积”怎么办呢？有以下变形：222)(21b a b a +≥+或)(21222b a b a +≥+．典型例题十二例12 已知：0>y x ＞，且：1=xy ，求证：2222≥-+yx y x ，并且求等号成立的条件．分析：由已知条件+∈R y x ，，可以考虑使用均值不等式，但所求证的式子中有y x -，无法利用xy y x 2≥+，故猜想先将所求证的式子进行变形，看能否出现)(1)(y x y x -+-型，再行论证．证明：,1.0,0=>-∴>>xy y x y x 又yx xyy x y x y x -+-=-+∴2)(222 yx y x -+-=2)( .22)(2)(2=-⋅-≥y x y x等号成立，当且仅当)(2)(y x y x -=-时．.4,2,2)(222=+=-=-∴y x y x y x ,6)(,12=+∴=y x xy.6=+∴y x由以上得226,226-=+=y x 即当226,226-=+=y x 时等号成立．说明：本题是基本题型的变形题．在基本题型中，大量的是整式中直接使用的均值不等式，这容易形成思维定式．本题中是利用条件将所求证的式子化成分式后再使用均值不等式．要注意灵活运用均值不等式．典型例题十三例13 已知00>>y x ，，且302=++xy y x ，求xy 的最大值． 分析：由302=++xy y x ，可得，)300(230<<+-=x xxy ， 故)300(2302<<+-=x x x x xy ，令xx x t +-=2302．利用判别式法可求得t （即xy ）的最大值，但因为x 有范围300<<x 的限制，还必须综合韦达定理展开讨论．仅用判别式是不够的，因而有一定的麻烦，下面转用基本不等式求解．解法一：由302=++xy y x ，可得，)300(230<<+-=x xxy ． xx x x x x xy +-+++-=+-=264)2(34)2(23022⎥⎦⎤⎢⎣⎡+++-=264)2(34x x 注意到16264)2(2264)2(=+⋅+≥+++x x x x ． 可得，18≤xy ． 当且仅当2642+=+x x ，即6=x 时等号成立，代入302=++xy y x 中得3=y ，故xy 的最大值为18．解法二：+∈R y x , ，xy xy y x ⋅=≥+∴22222， 代入302=++xy y x 中得：3022≤+⋅xy xy 解此不等式得180≤≤xy ．下面解法见解法一，下略．说明：解法一的变形是具有通用效能的方法，值得注意：而解法二则是抓住了问题的本质，所以解得更为简捷．典型例题十四例14 若+∈R c b a 、、，且1=++c b a ，求证：8111111≥⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-c b a ．分析：不等式右边的数字“8”使我们联想到可能是左边三个因式分别使用基本不等式所得三个“2”连乘而来，而abca cb a a a 2111≥+=-=-． 证明：acb a a a +=-=-111，又0>a ，0>b ，0>c ， a bc a c b 2≥+∴，即a bca a 21≥-． 同理b ca b 211≥-，cab c 211≥-， 8111111≥⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-∴c b a ．当且仅当31===c b a 时，等号成立． 说明：本题巧妙利用1=++c b a 的条件，同时要注意此不等式是关于c b a 、、的轮换式．典型例题十五例15 设+∈R c b a 、、，求证：)(2222222c b a a c c b b a ++≥+++++．分析：本题的难点在于222222a c c b b a +++、、不易处理，如能找出22b a +与b a +之间的关系，问题可得到解决，注意到：b a b a b a b a ab b a +≥+⇒+≥+⇒≥+)(2)()(222222222，则容易得到证明．证明：2222222)(2)(22b a ab b a b a ab b a +≥++≥+∴≥+， ，于是．)(222222b a b a b a +=+≥+ 同理：)(2222c b c b +≥+，)(2222a c a c +≥+． 三式相加即得：)(2222222c b a a c c b b a ++≥+++++．说明：注意观察所给不等式的结构，此不等式是关于c b a 、、的轮换式．因此只需抓住一个根号进行研究，其余同理可得，然后利用同向不等式的可加性．典型例题十六例16 已知：+∈R b a 、（其中+R 表示正实数）求证：．ba ab b a b a b a 112222222+≥≥⎪⎪⎭⎫ ⎝⎛+≥+≥+ 分析：要证明的这一串不等式非常重要，222b a +称为平方根，2b a +称为算术平均数，ab 称为几何平均数，ba 112+称为调和平均数．证明：()．0412222222≥-=⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫⎝⎛+b a b a b a ．222222⎪⎭⎫ ⎝⎛+≥⎪⎪⎭⎫ ⎝⎛+∴b a b a +∈R b a 、∴2222ba b a +≥+，当且仅当“b a =”时等号成立． ．0)(412222≥-=⎪⎪⎭⎫ ⎝⎛+-+b a b a b a ∴222⎪⎪⎭⎫⎝⎛+≥+b a b a ，等号成立条件是“b a =” ，0)(41222≥-=-⎪⎪⎭⎫ ⎝⎛+b a ab b a ∴ab b a ≥⎪⎪⎭⎫⎝⎛+22，等号成立条件是“b a =”．ba abab b a b a ab ab ba ab +-+=+-=+-2)(2112 ．0)()2(2≥+-=+-+=ba b a ab b a ab b a ab∴ba ab 112+≥，等号成立条件是“b a =”．说明：本题可以作为均值不等式推论，熟记以上结论有利于处理某些复杂不等式的证明问题．本例证明过程说明，不等式性质中的比较法是证明不等式的最基本、最重要的方法．典型例题十七例17 设实数1a ，1b ，1c ，2a ，2b ，2c 满足021>a a ，2111b c a ≥，2222b c a ≥，求证2212121)())((b b c c a a +≥++．分析：由条件可得到1a ，2a ，1c ， 2c 同号．为方便，不妨都设为正．将求证式子的左边展开后可看出有交叉项21c a 和12c a 无法利用条件，但使用均值不等式变成乘积后，重新搭配，可利用条件求证．证明：同号．2121,,0a a a a ∴>同理，由22222111b c a b c a ≥≥，知1a 与1c 同号，2a 与2c 同号∴1a ，1c ，2a ，2c 同号．不妨都设为正． 122122112121))((c a c a c a c a c c a a +++=++∴122122212c a c a b b ⋅++≥221122212c a c a b b ⋅++= 222122212b b b b ⋅++≥ ||2212221b b b b ++=221212221)(2b b b b b b +=++≥，即2212121)())((b b c c a a +≥++．说明：本题是根据题意分析得1a ，1c ，2a ，2c 同号，然后利用均值不等式变形得证．换一个角度，由条件的特点我们还会联想到使用二次方程根的判别式，可能会有另一类证法．实际上，由条件可知1a ，1c ，2a ，2c 为同号，不妨设同为正．又∵2111b c a ≥，2222b c a ≥，∴211144b c a ≥，222244b c a ≥．不等式021121≥++c x b x a ，022222≥++c x b x a 对任意实数x 恒成立（根据二次三项式恒为正的充要条件），两式相加得0)()(2)(2121221≥+++++c c x b b x a a ，它对任意实数x 恒成立．同上可得：2212121)())((b b c c a a +≥++．典型例题十八例18 如下图所示，某畜牧基地要围成相同面积的羊圈4间，一面可利用原有的墙壁，其余各面用篱笆围成，篱笆总长为36m ．问每间羊圈的长和宽各为多少时，羊圈面积最大？分析：可先设出羊圈的长和宽分别为x ，y ，即求xy 的最大值．注意条件3664=+y x 的利用．解：设每间羊圈的长、宽分别为x ，y ，则有3664=+y x ，即1832=+y x ．设xy S = ,623223218xy y x y x =⋅≥+=227,227≤≤∴S xy 即 上式当且仅当y x 32=时取“＝”．此时⎩⎨⎧===,1832,32y x y x ⎪⎩⎪⎨⎧==∴.3,29y x ∴羊圈长、宽分别为29m ，3m 时面积最大． 说明：(1)首先应设出变量（此处是长和宽），将题中条件数学化（即建立数学模型）才能利用数学知识求解；(2)注意在条件1832=+y x 之下求积xy 的最大值的方法：直接用不等式y x y x 3223218⋅≥+=，即可出现积xy ．当然，也可用“减少变量”的方法：22218261)218(261)218(31)218(31⎪⎭⎫ ⎝⎛-+⋅≤-⋅⋅=-⋅==→-=x x x x x x xy S x y ，当且仅当x x 2182-=时取“=”．典型例题十九例19 某单位建造一间地面面积为12m 2的背面靠墙的矩形小房，房屋正面的造价为1200元/m 2，房屋侧面的造价为800 元/m 2，屋顶的造价为5800元．如果墙高为3m ，且不计房屋背面的费用，问怎样设计房屋能使总造价最低，最低总造价是多少元？分析：这是一个求函数最小值的问题，关键的问题是设未知数，建立函数关系．从已知条件看，矩形地面面积为12m 2，但长和宽不知道，故考虑设宽为x m ，则长为x 12m ，再设总造价为y ．由题意就可以建立函数关系了．解：设矩形地面的正面宽为x m ，则长为x12m ；设房屋的总造价为y ．根据题意，可得： 5800280012312003+⨯⋅⋅+⋅=xx y 5800576003600++=xx 580016236005800)16(3600+⋅⨯≥++=xx x x )(34600580028800元=+= 当xx 16=，即4=x 时，y 有最小值34600元． 因此，当矩形地面宽为4m 时，房屋的总造价最低，最低总造价是34600元．说明：本题是函数最小值的应用题，这类题在我们的日常生活中经常遇到，有求最小值的问题，也有求最大值的问题，这类题都是利用函数式搭桥，用均值不等式解决，解决的关键是等号是否成立，因此，在解这类题时，要注意验证等号的成立．典型例题二十例20 某单位决定投资3200元建一仓库（长方体状），高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每1m 长造价40元，两侧墙砌砖，每1m 长造价45元，顶部每1m 2造价20元．计算：(1)仓库底面积Ｓ的最大允许值是多少？(2)为使Ｓ达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？ 分析：用字母分别表示铁栅长和一堵砖墙长，再由题意翻译数量关系．解：设铁栅长为x m ，一堵砖墙长为y m ，则有xy S =.由题意得(*).32002045240=+⨯+xy y x应用算术平均数与几何平均数定理，得 ,201202012020904023200S S xyxy xyy x +=+=+⋅≥,1606≤+∴S S 即：.0)10)(10(≤--S S,010,016≤-∴>+S S从而：.100≤S因此S 的最大允许值是2100m ，取得此最大值的条件是y x 9040=，而100=xy ，由此求得15=x ，即铁栅的长应是m 15．说明：本题也可将xS y =代入（*）式，导出关于x 的二次方程，利用判别式法求解． 典型例题二十一例21 甲、乙两地相距km s ，汽车从甲地匀速行驶到乙地，速度不超过km/h c ，已知汽车每小时的运输成本．．．．．．．．（以元为单位）由可变部分和固定部分组成：可变部分与速度km/h v 的平方成正比，且比例系数为b ；固定部分为a 元．（1）把全程运输成本y 元表示为速度km/h v 的函数，并指出这个函数的定义域；（2）为了使全程运输成本最小，汽车应以多大速度行驶？分析：这是1997年的全国高考试题，主要考查建立函数关系式、不等式性质（公式）的应用．也是综合应用数学知识、思想和方法解决实际问题的一道优秀试题．解：（1）依题意知汽车从甲地匀速行驶到乙地所用的时间为h vs ，全程运输成本为 )(2bv va s v s bv v s a y +=⋅+⋅=． 故所求函数为)(bv ba s y +=，定义域为)0(c v ，∈． （2）由于vb a s 、、、都为正数， 故有bv ba s bv v as ⋅⋅≥+2)(， 即ab s bv vas 2)(≥+． 当且仅当bv v a =，即ba v =时上式中等号成立． 若cb a ≤时，则ba v =时，全程运输成本y 最小； 当c b a ≤，易证c v <<0，函数)()(bv v a s v f y +==单调递减，即c v =时，)(m i n bc ca s y +=． 综上可知，为使全程运输成本y 最小，在c b a ≤时，行驶速度应为b av =； 在c b a ≤时，行驶速度应为c v =．。
数学百大经典例题
调查学生如何进行简单随机抽样例、某校有学生1200人，为了调查某种情况打算抽取一个样本容量为50的样本，问此样本若采用简单随机抽样将如何获得？分析：简单随机抽样分两种：抽签法和随机数表法．尽管此题的总体中的个体数不一定算“较少”，但依题意其操作过程却是保障等概率的．解：法一：首先，把该校学生都编上号码：0001，0002，0003，…，1200．如用抽签法，则作1200个形状、大小相同的号签（号签可以用小球、卡片、纸条等制作），然后将这些号签放在同一个箱子里，进行均匀搅拌．抽签时，每次从中抽出1个号签，连续抽取50次，就得到一个容量为50的样本．法二：首先，把该校学生都编上号码：0001，0002，0003，…，1200如用随机数表法，则可在数表上随机选定一个起始位置（例如，随意投一针，针尖所指数字可作起始位置）．假如起始位置是表中的第5行第9列的数字6，从6开始向右连续取数字，以4个数为一组，碰到右边线时向下错一行向左继续取，所得数字如下：6438，5482，4622，3162，4309，9006，1844，3253，2383，0130，3046，1943，6248，3469，0253，7887，3239，7371，28的，3445，9493，4977，2261，8442，……所取录的4位数字如果小于或等于1200，则对应此号的学生就是被抽取的个体；如果所取录的4位数字大于1200而小于或等于2400，则减去1200剩余数即是被抽取的号码；如果大于2400而小于3600，则减去2 400；依些类推．如果遇到相同的号码，则只留第一次取录的数字，其余的舍去．经过这样处理，被抽取的学生所对应的号码分别是：0438，0682，1022，0762，0709，0606，0644，0853，1183，013O，0646，0743，0248，1069，0253，0687，0839，0171，0445，1045，1093，0177，1061，0042，…一直取够50人为止．说明：规范的，不带主观意向的随机抽样，才能保证公平性、客观性、准确性和可信性．故此，抽样的过程，也反映科学的工作态度和求实的工作作风．判断抽牌方法是否为简单随机抽样例人们打桥牌时，将洗好的扑克牌（52张）随机确定一张为起始牌，这时，开始按次序搬牌，对任何一家来说，都是从52张总体中抽取一个13张的样本．问这种抽样方法是否为简单随机抽样？分析：简单随机抽样的实质是逐个地从总体中随机抽取．而这里只是随机确定了起始张，这时其他各张虽然是逐张起牌的，其实各张在谁手里已被确定，所以，不是简单随机抽样，据其等距起牌的特点，应将其定位在系统抽样．解：是简单随机抽样，是系统抽样．说明：逐张随机抽取与逐张起牌不是一回事，其实抓住其“等距”的特点不难发现，属于哪类抽样．判断是不是系统抽样例下列抽样中不是系统抽样的是（）i，A．从标有1－15号的15个球中，任选3个作样本，按从小号到大号排序，随机选起点以后10,500++i i （超过15则从1再数起）号入样B ．工厂生产的产品，用传送带将产品送入包装车间前，检验人员从传送带上每隔五分钟抽一件产品进行检验C ．搞某一市场调查，规定在商场门口随机抽一个人进行询问，直到调查到事先规定调查人数为止D ．电影院调查观众的某一指标，通知每排（每排人数相等）座位号为14的观众留下来座谈分析：本题考查系统抽样的有关概念，系统抽样适用于个体较多但均衡的总体．判断是否为系统抽样（简单随机抽样和分层抽样也是这样），应首先看是否在抽样前知道总体是由什么构成的，抽样的方法能否保证每个个体按事先规定的概率入样（即等可能抽样），再看是否将总体分成几个均衡的部分，每个部分中进行简单随机抽样．解： C ．不是系统抽样，因事先不知道总体，抽样方法不能保证每个个体按事先规定的概率入样．答案是C说明：抽样方法的实质是：抽样过程中，每个个体被抽取的概率相等，并且抽样前对总体的构成必须心中有数，比如起码知道总体中个体有多少．用系统抽样调查工人到单位的时间例 某单位共有在岗职工人数为624人，为了调查工人上班时，从离开家到来到单位的路上平均所用时间，决定抽取10％的工人调查这一情况，如何采用系统抽样方法完成这一抽样？ 分析：总体中的每个个体，都必须等和能地入样，为了实现“等距”入样，且又等概率，因此，应先剔除，再“分段”，后定起始化解：首先，将在岗的工人624人，用随机方式编号（如按出生年月日顺思维诊断序），000，001，002，…，623。
数学百大经典例题
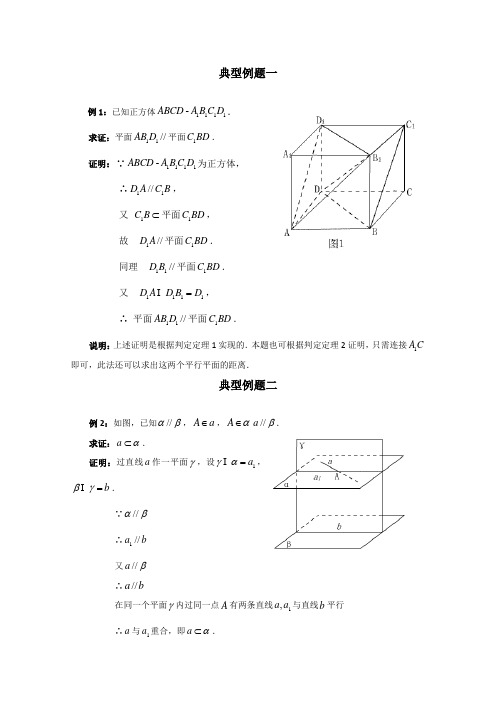
典型例题一例1：已知正方体1111-D C B A ABCD ． 求证：平面//11D AB 平面BD C 1． 证明：∵1111-D C B A ABCD 为正方体，∴B C A D 11//， 又 ⊂B C 1平面BD C 1， 故 //1A D 平面BD C 1． 同理 //11B D 平面BD C 1． 又 1111D B D A D = ， ∴ 平面//11D AB 平面BD C 1．说明：上述证明是根据判定定理1实现的．本题也可根据判定定理2证明，只需连接C A 1即可，此法还可以求出这两个平行平面的距离．典型例题二例2：如图，已知βα//，a A ∈，α∈A β//a ．求证：α⊂a ．证明：过直线a 作一平面γ，设1a =αγ ，b =γβ ． ∵βα// ∴b a //1又β//a∴b a //在同一个平面γ内过同一点A 有两条直线1,a a 与直线b 平行∴a 与1a 重合，即α⊂a ．说明：本题也可以用反证法进行证明．典型例题三例3：如果一条直线与两个平行平面中的一个相交，那么它和另一个也相交． 已知：如图，βα//，A l =α ． 求证：l 与β相交．证明：在β上取一点B ，过l 和B 作平面γ，由于γ与α有公共点A ，γ与β有公共点B ．∴γ与α、β都相交． 设a =αγ ，b =γβ ． ∵βα// ∴b a //又l 、a 、b 都在平面γ内，且l 和a 交于A ． ∵l 与b 相交． 所以l 与β相交．典型例题四例4：已知平面βα//，AB ，CD 为夹在a ，β间的异面线段，E 、F 分别为AB 、CD 的中点．求证： α//EF ，β//EF ．证明：连接AF 并延长交β于G ． ∵F CD AG =∴ AG ，CD 确定平面γ，且AC =αγ ，DG =βγ ．∵βα//，所以 DG AC //， ∴ GDF ACF ∠=∠，又 DFG AFC ∠=∠，DF CF =， ∴ △ACF ≌△DFG ． ∴ FG AF =． 又 BE AE =，∴ BG EF //，β⊂BG ． 故 β//EF ．同理α//EF说明：本题还有其它证法，要点是对异面直线的处理．典型例题六例6 如图，已知矩形ABCD 的四个顶点在平面上的射影分别为1A 、1B 、1C 、1D ，且1A 、1B 、1C 、1D 互不重合，也无三点共线．求证：四边形1111D C B A 是平行四边形． 证明：∵α⊥1AA ， α⊥1DD∴11//DD AA不妨设1AA 和1DD 确定平面β． 同理1BB 和1CC 确定平面γ． 又11//BB AA ，且γ⊂1BB ∴γ//1AA 同理γ//AD 又A AD AA = 1∴γβ//又11D A =βα ，11C B =γα∴1111//C B D A ． 同理1111//D C B A ．∴四边形1111D C B A 是平行四边形．典型例题七例7 设直线l 、m ，平面α、β，下列条件能得出βα//的是（ ）． A ．α⊂l ，α⊂m ，且β//l ，β//m B ．α⊂l ，β⊂m ，且m l // C ．α⊥l ，β⊥m ，且m l // D ．α//l ，β//m ，且m l //分析：选项A 是错误的，因为当m l //时，α与β可能相交．选项B 是错误的，理由同A ．选项C 是正确的，因为α⊥l ，l m //，所以α⊥m ，又∵β⊥m ，∴βα//．选项D 也是错误的，满足条件的α可能与β相交．答案：C说明：此题极易选A ，原因是对平面平行的判定定理掌握不准确所致．本例这样的选择题是常见题目，要正确得出选择，需要有较好的作图能力和对定理、公理的准确掌握、深刻理解，同时要考虑到各种情况．典型例题八例8 设平面α⊥平面γ，平面β⊥平面γ，且α、β分别与γ相交于a 、b ，b a //．求证：平面α//平面β．分析：要证明两平面平行，只要设法在平面α上找到两条相交直线，或作出相交直线，它们分别与β平行（如图）．证明：在平面α内作直线PQ ⊥直线a ，在平面β内作直线MN ⊥直线b ． ∵平面α⊥平面γ，∴PQ ⊥平面γ，MN ⊥平面γ， ∴MN PQ //．又∵p a //，Q a PQ = ，N b MN = ， ∴平面α//平面β．说明：如果在α、β内分别作γ⊥PQ ，γ⊥MN ，这样就走了弯路，还需证明PQ 、MN 在α、β内，如果直接在α、β内作a 、b 的垂线，就可推出MN PQ //．由面面垂直的性质推出“线面垂直”，进而推出“线线平行”、“线面平行”，最后得到“面面平行”，最后得到“面面平行”．其核心是要形成应用性质定理的意识，在立体几何证明中非常重要．典型例题九例9 如图所示，平面α//平面β，点A 、C α∈，点β∈D B 、，a AB =是α、β的公垂线，CD 是斜线．若b BD AC ==，c CD =，M 、N 分别是AB 和CD 的中点，(1)求证：β//MN ； (2)求MN 的长．分析：（1）要证β//MN ，取AD 的中点P ，只要证明MN 所在的平面β//PMN ．为此证明β//PM ，β//PN 即可．(2)要求MN 之长，在CMA ∆中，CM 、CN 的长度易知，关键在于证明CD MN ⊥，从而由勾股定理可以求解．证明：(1)连结AD ，设P 是AD 的中点，分别连结PM 、PN ． ∵M 是AB 的中点，∴BD PM //． 又β⊂BD ，∴β//PM ．同理∵N 是CD 的中点，∴AC PN //． ∵α⊂AC ，∴α//PN ．∵βα//，P PM PN = ，∴平面β//PMN ． ∵MN ⊂平面PMN ，∴β//MN ． (2)分别连结MC 、MD ． ∵b BD AC ==，a BM AM 21==，又∵AB 是α、β的公垂线，∴︒=∠=∠90DBM CAM ， ∴ACM Rt ∆≌BDM Rt ∆，∴DM CM =， ∴DMC ∆是等腰三角形．又N 是CD 的中点，∴CD MN ⊥． 在CMN Rt ∆中，22222421c a b CNCMMN -+=-=．说明：(1)证“线面平行”也可以先证“面面平行”，然后利用面面平行的性质，推证“线面平行”，这是一种以退为进的解题策略．(2)空间线段的长度，一般通过构造三角形、然后利用余弦定理或勾股定理来求解． (3)面面平行的性质：①面面平行，则线面平行；②面面平行，则被第三个平面所截得的交线平行．典型例题十例10 如果平面α内的两条相交直线与平面β所成的角相等，那么这两个平面的位置关系是__________．分析：按直线和平面的三种位置关系分类予以研究． 解：设a 、b 是平面α内两条相交直线．(1)若a 、b 都在平面β内，a 、b 与平面β所成的角都为︒0，这时α与β重合，根据教材中规定，此种情况不予考虑．(2)若a 、b 都与平面β相交成等角，且所成角在)90,0(︒︒内； ∵a 、b 与β有公共点，这时α与β相交．若a 、b 都与平面β成︒90角，则b a //，与已知矛盾．此种情况不可能．(3)若a 、b 都与平面β平行，则a 、b 与平面β所成的角都为︒0，α内有两条直线与平面β平行，这时βα//．综上，平面α、β的位置关系是相交或平行．典型例题十一例11 试证经过平面外一点有且只有一个平面和已知平面平行． 已知：α平面∉A ，求证：过A 有且只有一个平面αβ//．分析：“有且只有”要准确理解，要先证这样的平面是存在的，再证它是惟一的，缺一不可．证明：在平面α内任作两条相交直线a 和b ，则由α∉A 知，a A ∉，b A ∉． 点A 和直线a 可确定一个平面M ，点A 和直线b 可确定一个平面N ． 在平面M 、N 内过A 分别作直线a a //'、b b //'， 故'a 、'b 是两条相交直线，可确定一个平面β． ∵α⊄'a ，α⊂a ，a a //'，∴α//'a ． 同理α//'b ．又β⊂'a ，β⊂'b ，A b a =''，∴αβ//． 所以过点A 有一个平面αβ//．假设过A 点还有一个平面αγ//，则在平面α内取一直线c ，c A ∉，点A 、直线c 确定一个平面ρ，由公理2知：m =ρβ ，n =ργ ， ∴c m //，c n //，又m A ∈，n A ∈，这与过一点有且只有一条直线与已知直线平行相矛盾，因此假设不成立， 所以平面β只有一个．所以过平面外一点有且只有一个平面与已知平面平行．典型例题十二例12 已知点S 是正三角形ABC 所在平面外的一点，且SC SB SA ==，SG 为SAB ∆上的高，D 、E 、F 分别是AC 、BC 、SC 的中点，试判断SG 与平面DEF 内的位置关系，并给予证明分析1：如图，观察图形，即可判定//SG 平面DEF ，要证明结论成立，只需证明SG 与平面DEF 内的一条直线平行．观察图形可以看出：连结CG 与DE 相交于H ，连结FH ，FH 就是适合题意的直线． 怎样证明FH SG //？只需证明H 是CG 的中点．证法1：连结CG 交DE 于点H ， ∵DE 是ABC ∆的中位线，∴AB DE //．在ACG ∆中，D 是AC 的中点，且AG DH //， ∴H 为CG 的中点．∵FH 是SCG ∆的中位线，∴SG FH //． 又SG ⊄平面DEF ，FH ⊂平面DEF ， ∴//SG 平面DEF ．分析2：要证明//SG 平面DEF ，只需证明平面SAB //平面DEF ，要证明平面DEF //平面SAB ，只需证明DF SA //，EF SB //而DF SA //，EF SB //可由题设直接推出． 证法2：∵EF 为SBC ∆的中位线， ∴SB EF //．∵⊄EF 平面SAB ，⊂SB 平面SAB ，∴//EF 平面SAB ．同理：//DF 平面SAB ，F DF EF = ， ∴平面SAB //平面DEF ，又∵⊂SG 平面SAB ， ∴//SG 平面DEF ．典型例题十三例13 如图，线段PQ 分别交两个平行平面α、β于A 、B 两点，线段PD 分别交α、β于C 、D 两点，线段QF 分别交α、β于F 、E 两点，若9=PA ，12=AB ，12=BQ ，ACF ∆的面积为72，求BDE ∆的面积．分析：求BDE ∆的面积，看起来似乎与本节内容无关，事实上，已知ACF ∆的面积，若BDE ∆与ACF ∆的对应边有联系的话，可以利用ACF ∆的面积求出BDE ∆的面积．解：∵平面AF QAF =α ，平面BE QAF =β ， 又∵βα//，∴BE AF //．同理可证：BD AC //，∴FAC ∠与EBD ∠相等或互补，即EBD FAC ∠=∠sin sin ． 由BE FA //，得212412∶∶∶∶===QA QB AF BE ， ∴AF BE 21=由AC BD //，得：73219∶∶∶∶===PB PA BD AC ，∴AC BD 37=．又∵ACF ∆的面积为72，即72sin 21=∠⋅⋅FAC AC AF ．∴EBD BD BE S DBE ∠⋅⋅=∆sin 21FAC AC AF ∠⋅⋅⋅=sin 372121 FAC AC AF ∠⋅⋅⋅=sin 2167 847267=⨯=．∴BDE ∆的面积为84平方单位．说明：应用两个平行的性质一是可以证明直线与直线的平行，二是可以解决线面平行的问题．注意使用性质定理证明线线平行时，一定第三个平面与两个平行平面相交，其交线互相平行．典型例题十四例14 在棱长为a 的正方体中，求异面直线BD 和C B 1之间的距离．分析：通过前面的学习，我们解决了如下的问题：若a 和b 是两条异面直线，则过a 且平行于b 的平面必平行于过b 且平行于a 的平面．我们知道，空间两条异面直线，总分别存在于两个平行平面内．因此，求两条异面直线的距离，有时可以通过求这两个平行平面之间的距离来解决．具体解法可按如下几步来求：①分别经过BD 和C B 1找到两个互相平等的平面；②作出两个平行平面的公垂线；③计算公垂线夹在两个平等平面间的长度．解：如图，根据正方体的性质，易证：1111111//////D CB BD A C D B A D B BD 平面平面⇒⎭⎬⎫连结1AC ，分别交平面BD A 1和平面11D CB 于M 和N因为1CC 和1AC 分别是平面ABCD 的垂线和斜线，AC 在平面ABCD 内，BD AC ⊥ 由三垂线定理：BD AC ⊥1，同理：D A AC 11⊥ ∴⊥1AC 平面BD A 1，同理可证：⊥1AC 平面11D CB ∴平面BD A 1和平面11D CB 间的距离为线段MN 长度． 如图所示：在对角面1AC 中，1O 为11C A 的中点，O 为AC 的中点∴a AC NC MN AM 333111====．∴BD 和C B 1的距离等于两平行平面BD A 1和11D CB 的距离为a 33．说明：关于异面直线之间的距离的计算，有两种基本的转移方法：①转化为线面距．设a 、b 是两条异面直线，作出经过b 而和a 平行的平面α，通过计算a 和α的距离，得出a 和b 距离，这样又回到点面距离的计算；②转化为面面距，设a 、b 是两条异面直线，作出经过b 而和a 平行的平面α，再作出经过a 和b 平行的平面β，通过计算α、β之间的距离得出a 和b 之间的距离．典型例题十五例15 正方体1111D C B A ABCD -棱长为a ，求异面直线AC 与1BC 的距离． 解法1：（直接法）如图：取BC 的中点P ，连结PD 、1PB 分别交AC 、1BC 于M 、N 两点， 易证：MN DB //1，AC DB ⊥1，11BC DB ⊥．∴MN 为异面直线AC 与1BC 的公垂线段，易证：a DB MN 33311==．小结：此法也称定义法，这种解法是作出异面直线的公垂线段来解．但通常寻找公垂线段时，难度较大． 解法2：（转化法）如图：∵//AC 平面B C A 11，∴AC 与1BC 的距离等于AC 与平面B C A 11的距离， 在1OBO Rt ∆中，作斜边上的高OE ，则OE 长为所求距离，∵a OB 22=，a OO =1，∴a B O 231=，∴a BO OB OO OE 3311=⋅=．小结：这种解法是将线线距离转化为线面距离．解法3：（转化法）如图：∵平面1ACD //平面B C A 11，∴AC 与1BC 的距离等于平面1ACD 与平面B C A 11的距离． ∵⊥1DB 平面1ACD ，且被平面1ACD 和平面B C A 11三等分；∴所求距离为a D B 33311=．小结：这种解法是线线距离转化为面面距离． 解法4：（构造函数法）如图：任取点1BC Q ∈，作BC QR ⊥于R 点，作AC PK ⊥于K 点，设x RC =，则x a QR BR -==，KR CK =，且222CR CKKR =+∴2222121x CRKR ==．则222)(21x a x QK-+= 2223131)32(23a a a x ≥+-=，故QK 的最小值，即AC 与1BC 的距离等于a 33．小结：这种解法是恰当的选择未知量，构造一个目标函数，通过求这个函数的最小值来得到二异面直线之间的距离．解法5：（体积桥法）如图：当求AC 与1BC 的距离转化为求AC 与平面B C A 11的距离后，设C 点到平面B C A 11的距离为h ，则1111BCC A BCA C V V --=．∵222131)2(4331a a a h ⋅⋅=⋅，∴a h33．即AC 与1BC 的距离等于a 33．小结：本解法是将线线距离转化为线面距离，再将线面距离转化为锥体化为锥体的高，然后用体积公式求之．这种方法在后面将要学到．说明：求异面直线距离的方法有：(1)（直接法）当公垂线段能直接作出时，直接求．此时，作出并证明异面直线的公垂线段，是求异面直线距离的关键．(2)（转化法）把线线距离转化为线面距离，如求异面直线a 、b 距离，先作出过a 且平行于b 的平面α，则b 与α距离就是a 、b 距离．（线面转化法）．也可以转化为过a 平行b 的平面和过b 平行于a 的平面，两平行平面的距离就是两条异面直线距离．（面面转化法）．(3)（体积桥法）利用线面距再转化为锥体的高用何种公式来求．(4)（构造函数法）常常利用距离最短原理构造二次函数，利用求二次函数最值来解． 两条异面直线间距离问题，教科书要求不高（要求会计算已给出公垂线时的距离），这方面的问题的其他解法，要适度接触，以开阔思路，供学有余力的同学探求．典型例题十六例16 如果βα//，AB 和AC 是夹在平面α与β之间的两条线段，AC AB ⊥，且2=AB ，直线AB 与平面α所成的角为︒30，求线段AC 长的取值范围．解法1：如图所示：作β⊥AD 于D ，连结BD 、CD 、BC∵BD AB >，DC AC >，222BC AC AB =+， ∴在BDC ∆中，由余弦定理，得： 022cos 222222=⋅-+<⋅-+=∠CDBD BCACAB CDBD BCCDBD BDC ．∵β⊥AD ，∴ABD ∠是AB 与β所在的角． 又∵βα//，∴ABD ∠也就等于AB 与α所成的角，即︒=∠30ABD ． ∵2=AB ， ∴1=AD ，3=BD ，12-=AC DC ，24ACBC +=，∴01324131222<-⋅---+≤-ACAC AC，即：31102≤-<AC．∴332≥AC ，即AC 长的取值范围为⎪⎪⎭⎫⎢⎣⎡∞+,332．解法2：如图：∵AC AB ⊥∴AC 必在过点A 且与直线AB 垂直的平面γ内设l =βγ ，则在γ内，当l AC ⊥时，AC 的长最短，且此时ABC AB AC ∠⋅=tan33230tan =︒⋅AB而在γ内，C 点在l 上移动，远离垂足时，AC 的长将变大，从而332≥AC ，即AC 长的取值范围是⎪⎪⎭⎫⎢⎣⎡∞+,332．说明：(1)本题考查直线和直线、直线和平面、平面和平面的位置关系，对于运算能力和空间想象能力有较高的要求，供学有余力的同学学习．(2)解法1利用余弦定理，采用放缩的方法构造出关于AC 长的不等式，再通过解不等式得到AC 长的范围，此方法以运算为主．(3)解法2从几何性质角度加以解释说明，避免了繁杂的运算推导，但对空间想象能力要求很高，根据此解法可知线段AC 是连结异面直线AB 和l 上两点间的线段，所以AC 是AB 与l 的公垂线段时，其长最短．典型例题十七例17 如果两个平面分别平行于第三个平面，那么这两个平面互相平行． 已知：γα//，γβ//，求证：βα//．分析：本题考查面面平行的判定和性质定理以及逻辑推理能力．由于两个平面没有公共点称两平面平行，带有否定性结论的命题常用反证法来证明，因此本题可用反证法证明．另外也可以利用平行平面的性质定理分别在三个平面内构造平行且相交的两条直线，利用线线平行来推理证明面面平行，或者也可以证明这两个平面同时垂直于某一直线．证明一：如图，假设α、β不平行，则α和β相交．∴α和β至少有一个公共点A ，即α∈A ，β∈A ． ∵γα//，γβ//， ∴γ∉A ．于是，过平面γ外一点A 有两个平面α、β都和平面γ平行，这和“经过平面外一点有且只有一个平面与已知平面平行”相矛盾，假设不成立。
百个著名初等数学问题
第01题阿基米德分牛问题Archimedes' Problema Bovinum 太阳神有一牛群，由白、黑、花、棕四种颜色的公、母牛组成.在公牛中，白牛数多于棕牛数，多出之数相当于黑牛数的1/2+1/3；黑牛数多于棕牛数，多出之数相当于花牛数的1/4+1/5；花牛数多于棕牛数，多出之数相当于白牛数的1/6+1/7.在母牛中，白牛数是全体黑牛数的1/3+1/4；黑牛数是全体花牛数1/4+1/5；花牛数是全体棕牛数的1/5+1/6；棕牛数是全体白牛数的1/6+1/7.问这牛群是怎样组成的？第02题德·梅齐里亚克的法码问题The Weight Problem of Bachet de Meziriac 一位商人有一个40磅的砝码，由于跌落在地而碎成4块.后来，称得每块碎片的重量都是整磅数，而且可以用这4块来称从1至40磅之间的任意整数磅的重物.问这4块砝码碎片各重多少？第03题牛顿的草地与母牛问题Newton's Problem of the Fields and Cows a头母牛将b块地上的牧草在c天内吃完了；a'头母牛将b'块地上的牧草在c'天内吃完了；a"头母牛将b"块地上的牧草在c"天内吃完了；求出从a到c"9个数量之间的关系？第04题贝韦克的七个7的问题Berwick's Problem of the Seven Sevens 在下面除法例题中，被除数被除数除尽：* * 7 * * * * * * * ÷ * * * * 7 * = * * 7 * ** * * * * ** * * * * 7 ** * * * * * ** 7 * * * ** 7 * * * ** * * * * * ** * * * 7 * * * * * * * ** * * * * *用星号（*）标出的那些数位上的数字偶然被擦掉了，那些不见了的是些什么数字呢？第05题柯克曼的女学生问题Kirkman's Schoolgirl Problem 某寄宿学校有十五名女生，她们经常每天三人一行地散步，问要怎样安排才能使每个女生同其他每个女生同一行中散步，并恰好每周一次？第06题伯努利-欧拉关于装错信封的问题The Bernoulli-Euler Problem of the Misaddressed letters 求n个元素的排列，要求在排列中没有一个元素处于它应当占有的位置.第07题欧拉关于多边形的剖分问题Euler's Problem of Polygon Division 可以有多少种方法用对角线把一个n边多边形（平面凸多边形）剖分成三角形？第08题鲁卡斯的配偶夫妇问题Lucas' Problem of the Married Couples n对夫妇围圆桌而坐，其座次是两个妇人之间坐一个男人，而没有一个男人和自己的妻子并坐，问有多少种坐法？第09题卡亚姆的二项展开式Omar Khayyam's Binomial Expansion 当n是任意正整数时，求以a和b的幂表示的二项式a+b的n次幂.第10题柯西的平均值定理Cauchy's Mean Theorem 求证n个正数的几何平均值不大于这些数的算术平均值.第11题伯努利幂之和的问题Bernoulli's Power Sum Problem 确定指数p为正整数时最初n个自然数的p次幂的和S=1p+2p+3p+…+n p.第12题欧拉数The Euler Number 求函数φ(x)=(1+1/x)x及Φ(x)=(1+1/x)x+1当x 无限增大时的极限值.第13题牛顿指数级数Newton's Exponential Series 将指数函数e x变换成各项为x的幂的级数.第14题麦凯特尔对数级数Nicolaus Mercator's Logarithmic Series 不用对数表，计算一个给定数的对数.第15题牛顿正弦及余弦级数Newton's Sine and Cosine Series 不用查表计算已知角的正弦及余弦三角函数.第16题正割与正切级数的安德烈推导法Andre's Derivation of the Secant and Tangent Series 在n个数1，2，3，…,n的一个排列c1，c2，…，c n中，如果没有一个元素c i 的值介于两个邻近的值c i-1和c i+1之间，则称c1，c2，…，c n为1，2，3，…,n的一个屈折排列. 试利用屈折排列推导正割与正切的级数.第17题格雷戈里的反正切级数Gregory's Arc Tangent Series 已知三条边，不用查表求三角形的各角.第18题德布封的针问题Buffon's Needle Problem 在台面上画出一组间距为d 的平行线，把长度为l（小于d）的一根针任意投掷在台面上，问针触及两平行线之一的概率如何？第19题费马-欧拉素数定理The Fermat-Euler Prime Number Theorem 每个可表示为4n+1形式的素数，只能用一种两数平方和的形式来表示.第20题费马方程The Fermat Equation 求方程x2－dy2=1的整数解，其中d为非二次正整数.第21题费马-高斯不可能性定理The Fermat-Gauss Impossibility Theorem 证明两个立方数的和不可能为一立方数.第22题二次互反律The Quadratic Reciprocity Law （欧拉-勒让德-高斯定理）奇素数p与q的勒让德互反符号取决于公式（p/q）·（q/p）=（－1）[(p-1)/2]·[(q-1)/2].第23题高斯的代数基本定理Gauss' Fundamental Theorem of Algebra 每一个n 次的方程z n+c1z n-1+c2z n-2+…+c n=0具有n个根.第24题斯图谟的根的个数问题Sturm's Problem of the Number of Roots 求实系数代数方程在已知区间上的实根的个数.第25题阿贝尔不可能性定理Abel's Impossibility Theorem 高于四次的方程一般不可能有代数解法.第26题赫米特-林德曼超越性定理The Hermite-Lindemann TranscedenceTheorem 系数A不等于零，指数α为互不相等的代数数的表达式A1eα1+A2eα2+A3eα3+…不可能等于零.第27题欧拉直线Euler's Straight Line 在所有三角形中，外接圆的圆心，各中线的交点和各高的交点在一直线—欧拉线上，而且三点的分隔为：各高线的交点（垂心）至各中线的交点（重心）的距离两倍于外接圆的圆心至各中线的交点的距离.第28题费尔巴哈圆The Feuerbach Circle 三角形中三边的三个中点、三个高的垂足和高的交点到各顶点的线段的三个中点在一个圆上.第29题卡斯蒂朗问题Castillon's Problem 将各边通过三个已知点的一个三角形内接于一个已知圆.第30题马尔法蒂问题Malfatti's Problem 在一个已知三角形内画三个圆，每个圆与其他两个圆以及三角形的两边相切.第31题蒙日问题Monge's Problem 画一个圆，使其与三已知圆正交.第32题阿波洛尼斯相切问题The Tangency Problem of Apollonius. 画一个与三个已知圆相切的圆.第33题马索若尼圆规问题Macheroni's Compass Problem. 证明任何可用圆规和直尺所作的图均可只用圆规作出.第34题斯坦纳直尺问题Steiner's Straight-edge Problem 证明任何一个可以用圆规和直尺作出的图，如果在平面内给出一个定圆，只用直尺便可作出.第35题德里安倍立方问题The Deliaii Cube-doubling Problem 画出体积为一已知立方体两倍的立方体的一边.第36题三等分一个角Trisection of an Angle 把一个角分成三个相等的角.第37题正十七边形The Regular Heptadecagon 画一正十七边形.第38题阿基米德π值确定法Archimedes' Determination of the Number Pi 设圆的外切和内接正2v n边形的周长分别为a v和b v，便依次得到多边形周长的阿基米德数列：a0，b0，a1，b1，a2，b2，…其中a v+1是a v、b v的调和中项，b v+1是b v、a v+1的等比中项. 假如已知初始两项，利用这个规则便能计算出数列的所有项. 这个方法叫作阿基米德算法.第39题富斯弦切四边形问题Fuss' Problem of the Chord-TangentQuadrilateral 找出半径与双心四边形的外接圆和内切圆连心线之间的关系.（注：一个双心或弦切四边形的定义是既内接于一个圆而同时又外切于另一个圆的四边形）第40题测量附题Annex to a Survey 利用已知点的方位来确定地球表面未知但可到达的点的位置.第41题阿尔哈森弹子问题Alhazen's Billiard Problem 在一个已知圆内，作出一个其两腰通过圆内两个已知点的等腰三角形.第42题由共轭半径作椭圆An Ellipse from Conjugate Radii 已知两个共轭半径的大小和位置，作椭圆.第43题在平行四边形内作椭圆An Ellipse in a Parallelogram, 在规定的平行四边形内作一内切椭圆，它与该平行四边形切于一边界点.第44题由四条切线作抛物线A Parabola from Four Tangents 已知抛物线的四条切线，作抛物线.第45题由四点作抛物线A Parabola from Four Points. 过四个已知点作抛物线.第46题由四点作双曲线A Hyperbola from Four Points. 已知直角（等轴）双曲线上四点，作出这条双曲线.第47题范·施古登轨迹题Van Schooten's Locus Problem 平面上的固定三角形的两个顶点沿平面上一个角的两个边滑动，第三个顶点的轨迹是什么？第48题卡丹旋轮问题Cardan's Spur Wheel Problem. 一个圆盘沿着半径为其两倍的另一个圆盘的内缘滚动时，这个圆盘上标定的一点所描出的轨迹是什么？第49题牛顿椭圆问题Newton's Ellipse Problem. 确定内切于一个已知（凸）四边形的所有椭圆的中心的轨迹.第50题彭赛列-布里昂匈双曲线问题The Poncelet-Brianchon HyperbolaProblem 确定内接于直角（等边）双曲线的所有三角形的顶垂线交点的轨迹.第51题作为包络的抛物线A Parabola as Envelope 从角的顶点，在角的一条边上连续n次截取任意线段e，在另一条边上连续n次截取线段f，并将线段的端点注以数字，从顶点开始，分别为0，1，2，…，n和n，n－1，…，2，1，0.求证具有相同数字的点的连线的包络为一条抛物线.第52题星形线The Astroid 直线上两个标定的点沿着两条固定的互相垂直的轴滑动，求这条直线的包络.第53题斯坦纳的三点内摆线Steiner's Three-pointed Hypocycloid 确定一个三角形的华莱士（Wallace）线的包络.第54题一个四边形的最接近圆的外接椭圆The Most Nearly Circular Ellipse Circumscribing a Quadrilateral 一个已知四边形的所有外接椭圆中，哪一个与圆的偏差最小？第55题圆锥曲线的曲率The Curvature of Conic Sections 确定一个圆锥曲线的曲率.第56题阿基米德对抛物线面积的推算Archimedes' Squaring of a Parabola 确定包含在抛物线内的面积.第57题推算双曲线的面积Squaring a Hyperbola 确定双曲线被截得的部分所含的面积.第58题求抛物线的长Rectification of a Parabola 确定抛物线弧的长度.第59题笛沙格同调定理（同调三角形定理）Desargues' Homology Theorem (Theorem of Homologous Triangles) 如果两个三角形的对应顶点连线通过一点，则这两个三角形的对应边交点位于一条直线上.反之，如果两个三角形的对应边交点位于一条直线上，则这两个三角形的对应顶点连线通过一点.第60题斯坦纳的二重元素作图法Steiner's Double Element Construction 由三对对应元素所给定的重迭射影形，作出它的二重元素.第61题帕斯卡六边形定理Pascal's Hexagon Theorem 求证内接于圆锥曲线的六边形中，三双对边的交点在一直线上.第62题布里昂匈六线形定理Brianchon's Hexagram Theorem 求证外切于圆锥曲线的六线形中，三条对顶线通过一点.第63题笛沙格对合定理Desargues' Involution Theorem 一条直线与一个完全四点形*的三双对边的交点与外接于该四点形的圆锥曲线构成一个对合的四个点偶. 一个点与一个完全四线形*的三双对顶点的连线和从该点向内切于该四线形的圆锥曲线所引的切线构成一个对合的四个射线偶.*一个完全四点形（四线形）实际上含有四点（线）1，2，3，4和它们的六条连线交点23，14，31，24，12，34；其中23与14、31与24、12与34称为对边（对顶点）.第64题由五个元素得到的圆锥曲线A Conic Section from Five Elements 求作一个圆锥曲线，它的五个元素——点和切线——是已知的.第65题一条圆锥曲线和一条直线A Conic Section and a Straight Line 一条已知直线与一条具有五个已知元素——点和切线——的圆锥曲线相交，求作它们的交点.第66题一条圆锥曲线和一定点A Conic Section and a Point 已知一点及一条具有五个已知元素——点和切线——的圆锥曲线，作出从该点列到该曲线的切线.第67题斯坦纳的用平面分割空间Steiner's Division of Space by Planes n个平面最多可将整个空间分割成多少份？第68题欧拉四面体问题Euler's Tetrahedron Problem 以六条棱表示四面体的体积.第69题偏斜直线之间的最短距离The Shortest Distance Between Skew Lines 计算两条已知偏斜直线之间的角和距离.第70题四面体的外接球The Sphere Circumscribing a Tetrahedron 确定一个已知所有六条棱的四面体的外接球的半径.第71题五种正则体The Five Regular Solids 将一个球面分成全等的球面正多边形.第72题正方形作为四边形的一个映象The Square as an Image of aQuadrilateral 证明每个四边形都可以看作是一个正方形的透视映象.第73题波尔凯-许瓦尔兹定理The Pohlke-Schwartz Theorem 一个平面上不全在同一条直线上的四个任意点，可认为是与一个已知四面体相似的四面体的各隅角的斜映射.第74题高斯轴测法基本定理Gauss' Fundamental Theorem of Axonometry 正轴测法的高斯基本定理：如果在一个三面角的正投影中，把映象平面作为复平面，三面角顶点的投影作为零点，边的各端点的投影作为平面的复数，那么这些数的平方和等于零.第75题希帕查斯球极平面射影Hipparchus' Stereographic Projection 试举出一种把地球上的圆转换为地图上圆的保形地图射影法.第76题麦卡托投影The Mercator Projection 画一个保形地理地图，其坐标方格是由直角方格组成的.第77题航海斜驶线问题The Problem of the Loxodrome 确定地球表面两点间斜驶线的经度.第78题海上船位置的确定Determining the Position of a Ship at Sea 利用天文经线推算法确定船在海上的位置.第79题高斯双高度问题Gauss' Two-Altitude Problem 根据已知两星球的高度以确定时间及位置.第80题高斯三高度问题Gauss' Three-Altitude Problem 从在已知三星球获得同高度瞬间的时间间隔，确定观察瞬间，观察点的纬度及星球的高度.第81题刻卜勒方程The Kepler Equation 根据行星的平均近点角，计算偏心及真近点角.第82题星落Star Setting 对给定地点和日期，计算一已知星落的时间和方位角.第83题日晷问题The Problem of the Sundial 制作一个日晷.第84题日影曲线The Shadow Curve 当直杆置于纬度φ的地点及该日太阳的赤纬有δ值时，确定在一天过程中由杆的一点投影所描绘的曲线.第85题日食和月食Solar and Lunar Eclipses 如果对于充分接近日食时间的两个瞬间太阳和月亮的赤经、赤纬以及其半径均为已知，确定日食的开始和结束，以及太阳表面被隐蔽部分的最大值.第86题恒星及会合运转周期Sidereal and Synodic Revolution Periods 确定已知恒星运转周期的两共面旋转射线的会合运转周期.第87题行星的顺向和逆向运动Progressive and Retrograde Motion ofPlanets 行星什么时候从顺向转为逆向运动（或反过来，从逆向转为顺向运动）？第88题兰伯特慧星问题Lambert's Comet Prolem 借助焦半径及连接弧端点的弦，来表示慧星描绘抛物线轨道的一段弧所需的时间.第89题与欧拉数有关的斯坦纳问题Steiner's Problem Concerning the Euler Number 如果x为正变数，x取何值时，x的x次方根为最大？第90题法格乃诺关于高的基点的问题Fagnano's Altitude Base PointProblem 在已知锐角三角形中，作周长最小的内接三角形.第91题费马对托里拆利提出的问题Fermat's Problem for Torricelli 试求一点，使它到已知三角形的三个顶点距离之和为最小.第92题逆风变换航向Tacking Under a Headwind 帆船如何能顶着北风以最快的速度向正北航行？第93题蜂巢（雷阿乌姆尔问题）The Honeybee Cell (Problem by Reaumur) 试采用由三个全等的菱形作成的顶盖来封闭一个正六棱柱，使所得的这一个立体有预定的容积，而其表面积为最小.第94题雷奇奥莫塔努斯的极大值问题Regiomontanus' Maximum Problem 在地球表面的什么部位，一根垂直的悬杆呈现最长？（即在什么部位，可见角为最大？）第95题金星的最大亮度The Maximum Brightness of Venus 在什么位置金星有最大亮度？第96题地球轨道内的慧星A Comet Inside the Earth's Orbit慧星在地球的轨道内最多能停留多少天？第97题最短晨昏蒙影问题The Problem of the Shortest Twilight 在已知纬度的地方，一年之中的哪一天晨昏蒙影最短？第98题斯坦纳的椭圆问题Steiner's Ellipse Problem 在所有能外接（内切）于一个已知三角形的椭圆中，哪一个椭圆有最小（最大）的面积？第99题斯坦纳的圆问题Steiner's Circle Problem 在所有等周的（即有相等周长的）平面图形中，圆有最大的面积.反之：在有相等面积的所有平面图形中，圆有最小的周长.第100题斯坦纳的球问题Steiner's Sphere Problem 在表面积相等的所有立体中，球具有最大体积.在体积相等的所有立体中，球具有最小的表面.。
数学百大经典例题
数学百大经典例题数学是一门严谨而又充满挑战的学科，它包含着无尽的智慧和美妙的逻辑。
在数学学习的过程中，例题是必不可少的一部分。
下面，我将为大家介绍数学领域中的百大经典例题，希望能够对大家的数学学习有所帮助。
1. 平行线与三角形试题描述：已知三角形ABC，其中AB // CD，AD = BD，角A = 40°，角C = 70°，求角A的大小。
解答：由于AB // CD，因此角A与角C是对应角，它们的大小相等。
由题意，可以得出角C = 70°，那么角A也等于70°。
2. 直角三角形的边长关系试题描述：在直角三角形ABC中，已知角A = 90°，且BC = 6，AC = 8，求AB的长度。
解答：根据勾股定理，直角三角形的两个直角边的平方和等于斜边的平方。
代入已知条件，得到 6^2 + AB^2 = 8^2，即 36 + AB^2 = 64。
解方程可得 AB = 2。
3. 点到直线的距离试题描述：已知平面上一直线L的方程为3x - 4y + 5 = 0，求点A(2,3)到直线L的距离。
解答：点A到直线L的距离公式为：d = |Ax + By + C| /√(A^2 +B^2)。
将已知数据代入公式，得到 d = |3*2 - 4*3 + 5| / √(3^2 + (-4)^2) = 7 / 5。
4. 平面与平面的交线试题描述：已知平面α过点A(1,2,3)，直线L通过点B(2,-1,1)，求平面α与直线L的交线。
解答：首先，求直线L的方程。
根据两点式公式可得直线L的方程为 x - 2 = y + 1 = z - 1。
然后，将直线L的方程代入平面α的方程中，得到 1*(x-1) + 2*(y-2) + 3*(z-3) = 0。
整理化简后可得平面α与直线L的交线方程。
5. 不等式的解集试题描述：求不等式2x - 3 > 5的解集。
解答：将不等式中的x系数移到左边，得到 2x - 3 - 5 > 0，即 2x - 8 > 0。
数学百大经典例题
开锁次数的数学期望和方差例 有n 把看上去样子相同的钥匙，其中只有一把能把大门上的锁打开．用它们去试开门上的锁．设抽取钥匙是相互独立且等可能的．每把钥匙试开后不能放回．求试开次数ξ的数学期望和方差．分析：求)(k P =ξ时，由题知前1-k 次没打开，恰第k 次打开．不过，一般我们应从简单的地方入手，如3,2,1=ξ，发现规律后，推广到一般．解：ξ的可能取值为1，2，3，…，n ．;12112121)111()11()3(;111111)11()2(,1)1(nn n n n n n n n P nn n n n n P nP =-⋅--⋅-=-⋅--⋅-===-⋅-=-⋅-====ξξξ nk n k n k n n n n n n n k n k n n n n k P 111212312111)211()211()111()11()(=+-⋅+-+---⋅--⋅-=+-⋅+----⋅--⋅-== ξ；所以ξ的分布列为：2131211=⋅++⋅+⋅+⋅=n n n n n E ξ； n n n n n k n n n n n n D 1)21(1)21(1)213(1)212(1)211(22222⋅+-++⋅+-++⋅+-+⋅+-+⋅+-= ξ ⎥⎦⎤⎢⎣⎡⋅+++++++-++++=n n n n n n 22222)21()321)(1()321(1 1214)1(2)1()12)(1(611222-=⎥⎦⎤⎢⎣⎡+++-++=n n n n n n n n n 说明：复杂问题的简化处理，即从个数较小的看起，找出规律所在，进而推广到一般，方差的公式正确使用后，涉及一个数列求和问题，合理拆项，转化成熟悉的公式，是解决的关键．次品个数的期望例 某批数量较大的商品的次品率是5％，从中任意地连续取出10件，ξ为所含次品的个数，求ξE ．分析：数量较大，意味着每次抽取时出现次品的概率都是0.05，ξ可能取值是：0，1，2，…，10．10次抽取看成10次独立重复试验，所以抽到次品数ξ服从二项分布，由公式np E =ξ可得解．解：由题，()05.0,10~B ξ，所以5.005.010=⨯=ξE ．说明：随机变量ξ的概率分布，是求其数学期望的关键．因此，入手时，决定ξ取哪些值及其相应的概率，是重要的突破点．此题k k k C k P --⋅==1010)05.01()05.0()(ξ，应觉察到这是()05.0,10~B ξ．根据分布列求期望和方差例 设ξ 是一个离散型随机变量，其分布列如下表，求q 值，并求ξ ξ D E、．分析：根据分布列的两个性质，先确定q 的值，当分布列确定时，ξ ξ D E、只须按定义代公式即可．解： 离散型随机变量的分布满足（1）,,3,2,1,0 =≥i P i （2）.1321=+++P P P 所以有⎪⎪⎩⎪⎪⎨⎧≤≤-≤=+-+.1,1210,1212122q q q q 解得 .211-=q 故ξ 的分布列为⎪⎭⎫ ⎝⎛-⨯+-⨯+⨯-=∴2231)12(021)1(ξ E .2122321 -=-+-= ⎪⎭⎫ ⎝⎛-⨯--+-⨯-+⨯---=223)]21(1[)12()21(21)]21(1[ 222ξ D ⎪⎭⎫ ⎝⎛-+-+⨯-=2232)12(21)22( 32 .12223123622223 -=-+-+-+-=小结：解题时不能忽视条件i i p k P ==)(ξ时，10≤≤i p ，⋅⋅⋅=,2,1i 否则取了1>q 的值后，辛辛苦苦计算得到的是两个毫无用处的计算．产品中次品数分布列与期望值例 一批产品共100件，其中有10件是次品，为了检验其质量，从中以随机的方式选取5件，求在抽取的这5件产品中次品数分布列与期望值，并说明5件中有3件以上（包括3件）为次品的概率．（精确到0．001）分析：根据题意确定随机变量及其取值，对于次品在3件以上的概率是3，4，5三种情况的和．解：抽取的次品数是一个随机变量，设为ξ ，显然ξ 可以取从0到5的6个整数．抽样中，如果恰巧有k 个（5,4,3,2,1,0=k ）次品，则其概率为510059010)(C C C k P k k -⋅==ξ按照这个公式计算，并要求精确到0．001，则有.0)5( ,0)4( ,07.0)3( ,070.0)2( ,340.0)1( ,583.0)0(============ξ ξ ξ ξ ξ ξ P P P P P P 故ξ 的分布列为.501.00504007.03070.02340.01583.00=⨯+⨯+⨯+⨯+⨯+⨯=ξ E由分布列可知，.007.0)3( ,00007.0)3( =≥∴++=≥ξ ξ P P 这就是说，所抽取的5件品中3件以上为次品的可能性很小，只有7％．评定两保护区的管理水平例 甲、乙两个野生动物保护区有相同的自然环境，且野生动物的种类和数量也大致相等．而两个保护区内每个季度发现违反保护条例的事件次数的分布列分别为：甲保护区：乙保护区：分析：一是要比较一下甲、乙两个保护区内每季度发生的违规事件的次数的均值，即数学期望；二是要看发生违规事件次数的波动情况，即方差值的大小．（当然，亦可计算其标准差，同样说明道理．）解：甲保护区的违规次数1ξ的数学期望和方差为：;3.12.032.023.013.001=⨯+⨯+⨯+⨯=ξE;21.12.0)3.13(2.0)3.12(3.0)3.11(3.0)3.10(22221=⨯-+⨯-+⨯-+⨯-=ξD乙保护区的违规次数2ξ的数学期望和方差为：;3.14.025.011.002=⨯+⨯+⨯=ξE41.04.0)3.12(5.0)3.11(1.0)3.10(2222=⨯-+⨯-+⨯-=ξD ；因为2121,ξξξξD D E E >=，所以两个保护区内每季度发生的违规平均次数是相同的，但乙保护区内的违规事件次数更集中和稳定，而甲保护区的违规事件次数相对分散和波动．（标准差64.0,1.12211≈===ξσξξσξD D 这两个值在科学计算器上容易获得，显然，σξσξ>1）说明：数学期望仅体现了随机变量取值的平均大小，但有时仅知道均值大小还是不够的，比如：两个随机变量的均值相等了（即数学期望值相等），这就还需要知道随机变量的取值如何在均值周期变化，即计算其方差（或是标准差）．方差大说明随机变量取值分散性大；方差小说明取值分散性小或者说取值比较集中、稳定．射击练习中耗用子弹数的分布列、期望及方差例 某射手进行射击练习，每射击5发子弹算一组，一旦命中就停止射击，并进入下一组的练习，否则一直打完5发子弹后才能进入下一组练习，若该射手在某组练习中射击命中一次，并且已知他射击一次的命中率为0.8，求在这一组练习中耗用子弹数ξ 的分布列，并求出ξ 的期望ξ E 与方差ξ D （保留两位小数）． 分析：根据随机变量不同的取值确定对应的概率，在利用期望和方差的定义求解． 解： 该组练习耗用的子弹数ξ 为随机变量，ξ 可以取值为1，2，3，4，5．ξ ＝1，表示一发即中，故概率为;8.0)1(==ξ Pξ ＝2，表示第一发未中，第二发命中，故;16.08.02.08.0)8.01()2(=⨯=⨯-==ξ Pξ ＝3，表示第一、二发未中，第三发命中，故;032.08.02.08.0)8.01()3(22=⨯=⨯-==ξ Pξ ＝4，表示第一、二、三发未中，第四发命中，故0064.08.02.08.0)8.01()4(33=⨯=⨯-==ξ Pξ ＝5，表示第五发命中，故.0016.02.01)8.01()5(44==⋅-==ξ P因此，ξ 的分布列为0016.050064.04032.0316.028.01⨯+⨯+⨯+⨯+⨯=ξ E,25.1008.00256.0096.032.08.0 =++++=0016.0)25.15(0064.0)25.14(032.0)25.13(16.0)25.12(8.0)25.11(22222⨯-+⨯-+⨯-+⨯-+⨯-=ξ D .31.00225.00484.0098.009.005.0 =++++=说明：解决这类问题首先要确定随机变量的所有可能取值，然后再根据概率的知识求解对应的概率．准备礼品的个数例 某寻呼台共有客户3000人，若寻呼台准备了100份小礼品，邀请客户在指定时间来领取．假设任一客户去领奖的概率为4％．问：寻呼台能否向每一位顾客都发出奖邀请？若能使每一位领奖人都得到礼品，寻呼台至少应准备多少礼品？分析：可能来多少人，是一个随机变量ξ．而ξ显然是服从二项分布的，用数学期望来反映平均来领奖人数，即能说明是否可行．解：设来领奖的人数)3000,,2,1,0(, ==k k ξ，所以k k k C k P --⋅==300003000)04.01()04.0()(ξ，可见()04.0,30000~B ξ，所以，12004.03000=⨯=ξE （人）100>（人）．答：不能，寻呼台至少应准备120份礼品．说明：“能”与“不能”是实际问题转到数学中来，即用数字来说明问题．数字期望反映了随机变量取值的平均水平．用它来刻画、比较和描述取值的平均情况，在一些实际问题中有重要的价值．因此，要想到用期望来解决这一问题．。
高考数学 百大经典例题——绝对值不等式
典型例题一绝对值不等式例1 解不等式2321-->+x x分析：解含有绝对值的不等式，通常是利用绝对值概念⎩⎨⎧<-≥=)0()0(a a a a a ，将不等式中的绝对符号去掉，转化成与之同解的不含绝对值的不等式（组），再去求解．去绝对值符号的关键是找零点（使绝对值等于零的那个数所对应的点），将数轴分成若干段，然后从左向右逐段讨论．解：令01=+x ，∴ 1-=x ，令032=-x ，∴23=x ，如图所示． （1）当1-≤x 时原不等式化为2)32()1(--->+-x x∴2>x 与条件矛盾，无解．（2）当231≤<-x 时，原不等式化为2)32(1--->+x x ． ∴ 0>x ，故230≤<x ． （3）当23>x 时，原不等式化为 2321-->+x x ．∴6<x ，故623<<x ． 综上，原不等式的解为{}60<<x x ．说明：要注意找零点去绝对值符号最好画数轴，零点分段，然后从左向右逐段讨论，这样做条理分明、不重不漏．典型例题二例2 求使不等式a x x <-+-34有解的a 的取值范围．分析：此题若用讨论法，可以求解，但过程较繁；用绝对值的几何意义去求解十分简便．解法一：将数轴分为(]),4(],4,3[,3,+∞∞-三个区间当3<x 时，原不等式变为27,)3()4(a x a x x -><-+-有解的条件为327<-a ，即1>a ；当43≤≤x 时，得a x x <-+-)3()4(，即1>a ；当4>x 时，得a x x <-+-)3()4(，即27+<a x ，有解的条件为427>+a ∴1>a ． 以上三种情况中任一个均可满足题目要求，故求它们的并集，即仍为1>a ．解法二：设数x ，3，4在数轴上对应的点分别为P ，A ，B ，如图，由绝对值的几何定义，原不等式a PB PA <+的意义是P 到A 、B 的距离之和小于a ． 因为1=AB ，故数轴上任一点到A 、B 距离之和大于（等于1），即134≥-+-x x ，故当1>a 时，a x x <-+-34有解．典型例题三例3 已知),0(,20,2M y ab y M a x ∈ε<-<ε<-，求证ε<-ab xy ． 分析：根据条件凑b y a x --,． 证明：ab ya ya xy ab xy -+-=-ε=ε⋅+ε⋅<-⋅+-≤-+-=aa M Mb y a a x y b y a a x y 22)()(． 说明：这是为学习极限证明作的准备，要习惯用凑的方法．典型例题四例4 求证 b a a b a -≥-22分析：使用分析法证明 ∵0>a ，∴只需证明b a a b a -≥-222，两边同除2b ，即只需证明 ba b a b b a -≥-22222，即 ba b a b a -≥-22)(1)( 当1≥b a 时，b a b a b a b a -≥-=-222)(1)(1)(；当1<ba 时， 0<-b a ，原不等式显然成立．∴原不等式成立．说明：在绝对值不等式的证明，常用分析法．本例也可以一开始就用定理：b a b a a b a a b a ⋅-=-≥-2222 （1）如果1≥ba ，则0≤-b a ，原不等式显然成立． （2）如果1<a b ，则b a b ->-，利用不等式的传递性知a b a -，b a b ->，∴原不等式也成立．典型例题五例5 求证b ba ab a ba +++≤+++111．分析：本题的证法很多，下面给出一种证法：比较要证明的不等式左右两边的形式完全相同，使我们联想利用构造函数的方法，再用单调性去证明．证明：设xx x x x x f +-=+-+=+=1111111)(． 定义域为｛R x x ∈，且1-≠x ｝，)(x f 分别在区间)1,(--∞，区间),1(∞+-上是增函数． 又b a b a +≤+≤0， ∴)()(b a f b a f +≤+ 即b a ba b a ba +++≤+++11b ba ab a bb a a+++≤+++++=1111∴原不等式成立．说明：在利用放缩法时常常会产生如下错误： ∵b a b a +≤+，01>++b a ， ∴b a b b a a b a b a b a b a +++++=+++≤+++1111bb a a +++≤11． 错误在不能保证a b a +≥++11，b b a +≥++11．绝对值不等式b a b a +≤±在运用放缩法证明不等式时有非常重要的作用，其形式转化比较灵活．放缩要适度，要根据题目的要求，及时调整放缩的形式结构．典型例题六例6 关于实数x 的不等式2)1(2)1(22-≤+-a a x 与0)13(2)1(32≤+++-a x a x )(R a ∈的解集依次为A 与B ，求使B A ⊆的a 的取值范围．分析：分别求出集合A 、B ，然后再分类讨论．解：解不等式2)1(2)1(22-≤+-a a x ， 2)1(2)1(2)1(222-≤+-≤--a a x a ， ∴{}R a a x a x A ∈+≤≤=,122．解不等式0)13(2)1(32≤+++-a x a x ，0)2)](13([≤-+-x a x ． 当31>a 时（即213>+a 时），得⎭⎬⎫⎩⎨⎧>+≤≤=31,132a a x x B ． 当31≤a 时（即213≤+a 时），得⎭⎬⎫⎩⎨⎧≤≤≤+=31,213a x a x B ． 当31>a 时，要满足B A ⊆，必须⎩⎨⎧+≤+≥,131,222a a a 故31≤≤a ； 当31≤a 时，要满足B A ⊆，必须⎩⎨⎧+≥+≥;12,1322a a a ⎩⎨⎧≤≤--≤,11,1a a ∴1-=a ．所以a 的取值范围是{}311≤≤-=∈a a R a 或．说明：在求满足条件B A ⊆的a 时，要注意关于a 的不等式组中有没有等号，否则会导致误解．典型例题七例6 已知数列通项公式nn na a a a a 2sin 23sin 22sin 2sin 32++++= 对于正整数m 、n ，当n m >时，求证：nn m a a 21<-． 分析：已知数列的通项公式是数列的前n 项和，它的任意两项差还是某个数列的和，再利用不等式n n a a a a a a +++≤+++ 2121，问题便可解决．证明：∵n m >∴m n n n m ma a n a n a a 2sin 2)2sin(2)1sin(21+++++=-++ mn n ma a n a n 2sin 2)2sin(2)1sin(21+++++≤++ 211)211(2121212121--=+++≤++m n n)12110(21)211(21<-<<-=--nm n n m n ． 说明：m n n 21212121+++++ 是以121+n 为首项，以21为公比，共有n m -项的等比数列的和，误认为共有1--n m 项是常见错误． 正余弦函数的值域，即1sin ≤α，1cos ≤α，是解本题的关键．本题把不等式、三角函数、数列、n 个变量的绝对值不等式问题连在一起，是一个较为典型的综合题目．如果将本题中的正弦改为余弦，不等式同样成立．典型例题八例8 已知13)(2+-=x x x f ，1<-a x ，求证：)1(2)()(+<-a a f x f分析：本题中给定函数)(x f 和条件1<-a x ，注意到要证的式子右边不含x ，因此对条件1<-a x 的使用可有几种选择：(1)直接用；(2)打开绝对值用11+<<-a x a ，替出x ；(3)用绝对值的性质11+<⇒<-≤-a x a x a x 进行替换．证明：∵13)(2+-=x x x f ，∴13)(2+-=a a a f ， ∵1<-a x ，∴1<-≤-a x a x ． ∴1+<a x ， ∴x a a x a f x f -+-=-22)()()())((a x a x a x --+-=)1)((-+-=a x a x1-+⋅-=a x a x)1(21111+=+++<++<-+<a a a a x a x ，即)1(2)()(+<-a a f x f ．说明：这是绝对值和函数的综合题，这类题通常要涉及绝对值及绝对值不等式的性质等综合知识的运用．分析中对条件1<-a x 使用时出现的三种可能是经常碰到的，要结合求证，灵活选用．典型例题九例9 不等式组⎪⎩⎪⎨⎧+->+->x x x x x 22330的解集是（ ）． A ．{}20<<x x B ．{}5.20<<x xC ．{}60<<x xD ．{}30<<x x 分析：本题是考查含有绝对值不等式的解法，由x x x x +->+-2233，知033>+-xx ，∴33<<-x ，又0>x ，∴30<<x ，解原不等式组实为解不等式x x x x +->+-2233（30<<x ）． 解法一：不等式两边平方得：2222)2()3()2()3(x x x x -+>+-．∴2222)6()6(-+>--x x x x ，即0)66)(66(2222>+-----++--x x x x x x x x ， ∴0)6(2>-x x ，又30<<x ．∴⎩⎨⎧<<<-30062x x ∴60<<x ．选C ．解法二：∵0>x ，∴可分成两种情况讨论：(1)当20≤<x 时，不等式组化为x x x x +->+-2233（20≤<x ）． 解得20≤<x ．(2)当2>x 时，不等式组可化为xx x x +->+-2233（2>x ）， 解得62≤<x ．综合(1)、(2)得，原不等式组的解为60<<x ，选C ．说明：本题是在0>x 的条件下，解一个含绝对值的分式不等式，如何去绝对值是本题的关键所在，必须注意，只有在保证两边均为非负数时，才能将不等式两边同时平方．另一种方法则是分区间讨论，从而去掉绝对值符号．当然本题还可用特殊值排除法求解．典型例题十例10 设二次函数c bx ax x f ++=2)((0>a ，且0≠b )，已知a b ≤，1)0(≤f ，1)1(≤-f ，1)1(≤f ，当1≤x 时，证明45)(≤x f ． 分析：从0>a 知，二次函数的图像是开口向上的抛物线；从1≤x 且1)1(≤-f ，1)1(≤f 知，要求证的是45)(≤x f ，所以抛物线的顶点一定在x 轴下方，取绝对值后，图像翻到x 轴上方．因此抛物线的顶点的取值非常重要，也是解这道题的关键所在．证明：∵)()(2c b a c b a b +--++=c b a c b a +-+++≤11)1()1(+≤-+=f f2=， ∴1≤b ． 又∵a b ≤，∴1≤ab ． ∴1212<≤-a b ． 又1)0(≤=f c ，ab c a b ac a b f 444)2(22-=-=-， ∴ab c a b c a b f 44)2(22+≤-=- 451141141=⋅⋅+≤⋅⋅+=b a b c ． 而)(x f 的图像为开口向上的抛物线，且1≤x ，11≤≤-x ， ∴)(x f 的最大值应在1=x ，1-=x 或a b x 2-=处取得． ∵1)1(≤f ，1)1(≤-f ，45)2(≤-a b f ， ∴45)(≤x f ．说明：本题考查了绝对值不等式的性质、二次函数的最值及分类讨论的思想和逻辑思维的能力，关键是通过对参数a ，b ，c 的分析，确定抛物线顶点的取值范围，然后通过比较求出函数在1 x 范围内的最大值．。
数学百大经典例题——四种命题(新课标)
例命题“若＝，则与成反比例关系”的否命题是 1 y x y k x［ ］A y x yB y kx x yC x y y ．若≠，则与成正比例关系．若≠，则与成反比例关系．若与不成反比例关系，则≠k xk xD y x y ．若≠，则与不成反比例关系k x分析 条件及结论同时否定，位置不变．答 选D ．例2 设原命题为：“对顶角相等”，把它写成“若p 则q ”形式为________．它的逆命题为________,否命题为________，逆否命题为________．分析 只要确定了“p"和“q ”，则四种命题形式都好写了． 解 若两个角是对顶角，则两个角相等；若两个角相等，则这两个角是对顶角；若两个角不是对顶点，则这两个角不相等;若两个角不相等，则这两个角不是对顶角．例 3 “若P ＝{x ｜x|＜1｝，则0∈P"的等价命题是________．分析 等价命题可以是多个，我们这里是确定命题的逆否命题．解原命题的等价命题可以是其逆否命题，所以填“若，则 0P p≠｛x||x ｜＜1}”例4 分别写出命题“若x 2＋y 2＝0,则x 、y 全为0”的逆命题、否命题和逆否命题．分析根据命题的四种形式的结构确定．解逆命题：若x、y全为0，则x2＋y2＝0;否命题：若x2＋y2≠0，则x，y不全为0；逆否命题:若x、y不全为0，则x2＋y2≠0．说明：“x、y全为0"的否定不要写成“x、y全不为0"，应当是“x，y不全为0"，这要特别小心．例5有下列四个命题：①“若xy＝1，则x、y互为倒数”的逆命题；②“相似三角形的周长相等"的否命题；③“若b≤－1，则方程x2－2bx＋b2＋b＝0有实根”的逆否命题；④“若∪＝，则”的逆否命题，其中真命题是A B B A B[ ］A．①② B．②③C．①③ D．③④分析应用相应知识分别验证．解写出相应命题并判定真假①“若x，y互为倒数,则xy＝1”为真命题;②“不相似三角形周长不相等"为假命题；③“若方程x2－2bx＋b2＋b＝0没有实根,则b＞－1”为真命题；选C．例6 以下列命题为原命题，分别写出它们的逆命题，否命题和逆否命题．①内接于圆的四边形的对角互补;②已知a、b、c、d是实数，若a＝b，c＝d，则a＋c＝b＋d；分析首先应当把原命题改写成“若p则q”形式，再设法构造其余的三种形式命题．解对①：原命题：“若四边形内接于圆，则它的对角互补”;逆命题：“若四边形对角互补，则它必内接于某圆”；否命题:“若四边形不内接于圆，则它的对角不互补";逆否命题：“若四边形的对角不互补,则它不内接于圆”．对②:原命题:“已知a、b、c、d是实数，若a＝b，c＝d，则a＋c＝b＋d”，其中“已知a、b、c、d是实数"是大前提，“a＝b,c＝d”是条件，“a＋c＝b＋d”是结论．所以：逆命题:“已知a、b、c、d是实数，若a＋c＝b＋d，则a＝b，c＝d”；否命题：“已知a、b、c、d是实数，若a≠b或c≠d,则a＋c ≠b＋d”(注意“a＝b,c＝d”的否定是“a≠b或c≠d”只需要至少有一个不等即可）；逆否命题：“已知a、b、c、d是实数，若a＋c≠b＋d则a ≠b或c≠d”．逆否命题还可以写成：“已知a、b、c、d是实数，若a＋c ≠b＋d则a＝b，c＝d两个等式至少有一个不成立"说明：要注意大前题的处理．试一试:写出命题“当c＞0时，若a ＞b,则ac ＞bc ”的逆命题，否命题,逆否命题,并分别判定其真假．例7 已知下列三个方程：x 2＋4ax －4a ＋3＝0，x 2＋(a －1）x ＋a 2＝0，x 2＋2ax －2a ＝0至少有一个方程有实根，求实数a 的取值范围．分析 如果从正面分类讨论情况要复杂的多，而利用补集的思想（也含有反证法的思想)来求三个方程都没有实根的a 范围比较简单．解由－－＜－－＜＋＜得 16a 4(34a)0(a 1)4a 04a 8a 02222⎧⎨⎪⎩⎪说明：利用补集思想，体现了思维的逆向性．例8 分别写出下列命题的逆命题、否命题、逆否命题，并判断它们的真假．①＞时，－＋＝无实根；m mx x 10214②当abc ＝0时，a ＝0或b ＝0或c ＝0．分析 改造原命题成“若p 则q 形式”再分别写出其逆命题、否命题、逆否命题．在判定各种形式命题的真假时要注意利用等价命题的原理和规律．解①原命题：“若＞，则－＋＝无实根”，是真 m mx x 10214命题；逆命题：“若－＋＝无实根，则＞”，是真命题；否命题：“若≤，则－＋＝有实根”，是真命题；逆否命题：“若－＋＝有实根，则≤”，是真命题．mx x 10m m mx x 10mx x 10m 222141414②原命题;“若abc ＝0,则a ＝0或b ＝0或c ＝0”，是真命题； 逆命题：“若a ＝0或b ＝0或c ＝0，则abc ＝0”是真命题； 否命题：“若abc ≠0，则a ≠0且b ≠0且c ≠0"，是真命题；（注意:“a ＝0或b ＝0或c ＝0”的否定形式是“a ≠0且b ≠0且c ≠0"逆否命题:“若a ≠0且b ≠0且c ≠0,则abc ≠0",是真命题． 说明：判定四种形式命题的真假可以借助互为逆否命题的等价性．例若、、均为实数，且＝－＋π，＝－＋π，＝－＋π，求证：、、中至少有一个大于．9 a b c a x 2y b y 2z c z 2x a b c 0222236分析 如果直接从条件推证，方向不明,过程不可预测，较难，可以使用反证法．解 设a 、b 、c 都不大于0，即a ≤0，b ≤0，c ≤0,则有a ＋b ＋c ≤0,而a b c (x 2y )(y 2z )(z 2x )222＋＋＝－＋π＋－＋π＋－＋π236＝(x 2－2x ）＋(y 2－2y ）＋(z 2－2z)＋π＝（x －1）2＋(y －1)2＋（z －1）2＋（π－3）∴ a ＋b ＋c ＞0这与a ＋b ＋c ≤0矛盾．因此a 、b 、c 中至少有一个大于0．说明：如下表,我们给出一些常见词语的否定．。
数学百大经典例题
例用符号∈或填空1 ∉1________N ， 0________N ， －3________N ，0.5N N ，；21________Z ， 0________Z ， －3________Z ，0.5Z Z ，；21________Q ， 0________Q ， －3________Q ，0.5Q Q ，；21________R ， 0________R ， －3________R ，0.5R R ，；2分析元素在集合内用符号∈，而元素不在集合内时用符号． ∉解∈，∈，－，，；1N 0N 3N 0.5N N ∉∉∉2 1Z 0Z 3Z 0.5Z Z 1Q 0Q 3Q ∈，∈，－∈，，；∈，∈，－∈，∉∉20.5Q Q 1R 0R 3R 0.5R R ∈，；∈，∈，－∈，∈，；22∉∉说明：要注意符号的规范书写．例2 (1)用列举法表示不超过10的非负偶数的集合，并用另一种方法表示出来；(2)设集合A ＝{(x ，y)|x ＋y ＝6，x ∈N ，y ∈N}，试用列举法表示集合A ；分析 (1)中集合含的元素为0、2、4、6、8、10；(2)中集合所含的元素是点(0，6)，(1，5)，(2，4)，(3，3)，(4，2)，(5，1)，(6，0)．解 (1){0，2，4，6，8，10｝；用描述法表示为{不超过10的非负偶数}，或|x|x ＝2n ，n ∈N ，n ＜6}．(2)A ＝{(0，6)，(1，5)，(2，4)，(3，3)，(4，2)，(5，1)，(6，0)}．说明：注意(2)中集合A 的元素是点的坐标．例由实数，－，，及－所组成的集合，最多含有3 x x |x|x x 233[ ]A ．2个元素B ．3个元素C ．4个元素D ．5个元素分析 当x 等于零时只有一个元素，当x 不等于零时有两个元素．答 A ．说明：问题转化为对具有相同结果的不同表达式的识别．例4 试用适当的方式表示：被3整除余1的自然数集合．分析 被3整除余1的自然数可以表示为3n ＋1(n 为自然数)．解 集合可以表示为{x|x ＝3n ＋1，n ∈N}．说明：虽然这一集合是无限集，但也可以用列举法来表示：{1，4，7，…，3n ＋1，…}．例5 下列四个集合中，表示空集的是[ ]A ．{0}B ．{(x ，y)|y 2＝－x 2，x ∈R ，y ∈R}C {x||x|5x Z x N}．＝，∈，∉D ．{x|2x 2＋3x －2＝0，x ∈N}分析 {0}是含有元素0蹬集合．{(x ，y)|y 2＝－x 2，x ∈R ，y∈含有元素，．＝，∈，含有元素－．虽然方R}(00){x||x|5x Z x N}5∉ 程2x 2＋3x －2＝0的解是0.5和－2，但都不是自然数．答 选D ．说明：注意集合元素的限制条件．例试用适当的符号把－＋＋和＋，∈连结6 {|a b 6a b R|}2323 起来．分析 这是元素与集合的关系问题，它们之间有从属或不从属的关系．注意到： (2323)(2)(2)2(2362－＋＋＝－＋＋＋－＋＝，3323)()根据所给集合的元素特征，该元素属于集合．解－＋＋∈＋，∈． 23{|a b 6a b R|}23说明：元素是否在集合内，有时需要仔细变形、验证．例年全国理改编题设，都是非零实数，＝＋＋7 (1990)a b y a a b b ab ab ||||||可能取的值组成的集合是 [ ]A ．{3}B ．{3，2，1}C ．{3，1，－1}D ．{3，－1}分析 根据两个字母的符号分类讨论．答 选D ．说明：本题考查的是实数的符号运算、绝对值等。
数学百大经典例题
典型例题一例1 已知)3,0(A ，)0,1(-B ，)0,3(C ，求D 点的坐标，使四边形ABCD 为等腰梯形． 分析：利用等腰梯形所具备的性质“两底互相平行且两腰长相等”进行解题． 解：如图，设),(y x D ，若CD AB //，则CD AB k k =，BC AD =，即⎪⎩⎪⎨⎧=+=-+--=+-②①.1613)3(,301003222y x x y由①、②解得)53,516(D ．若BC AD //，则⎪⎩⎪⎨⎧==,,BC AD k k BC AD即⎪⎩⎪⎨⎧+=+-=--④③.31)3(,0032222y x x y由③、④式解得)3,2(D ． 故D 点的坐标为)53,516(或)3,2(．说明：(1)把哪两条边作为梯形的底是讨论的标准，解此题时注意不要漏解．(2)在遇到两直线平行问题时，一定要注意直线斜率不存在的情况．此题中AB 、BC 的斜率都存在，故不可能出现斜率不存在的情况．典型例题二例2当a 为何值时，直线01)1()2(1=--++y a x a l ：与直线02)32()1(2=+++-y a x a l ：互相垂直？分析：分类讨论，利用两直线垂直的充要条件进行求解．或利用结论“设直线1l 和2l 的方程分别是01111=++C y B x A l ：，02222=++C y B x A l ：，则21l l ⊥的充要条件是02121=+B B A A ”（其证明可借助向量知识完成）解题．解法一：由题意，直线21l l ⊥．(1)若01=-a ，即1=a ，此时直线0131=-x l ：，0252=+y l ：显然垂直； (2)若032=+a ，即23-=a 时，直线0251=-+y x l ：与直线0452=-x l ：不垂直；(3)若01≠-a ，且032≠+a ，则直线1l 、2l 斜率1k 、2k 存在，aa k -+-=121，3212+--=a a k ．当21l l ⊥时，121-=⋅k k ，即1)321()12(-=+--⋅-+-a a aa ，∴1-=a .综上可知，当1=a 或1-=a 时，直线21l l ⊥．解法二：由于直线21l l ⊥，所以0)32)(1()1)(2(=+-+-+a a a a ，解得1±=a ． 故当1=a 或1-=a 时，直线21l l ⊥．说明：对于本题，容易出现忽视斜率存在性而引发的解题错误，如先认可两直线1l 、2l 的斜率分别为1k 、2k ，则aa k -+-=121，3212+--=a a k ．由21l l ⊥，得121-=⋅k k ，即1)321()12(-=+--⋅-+-a a aa ．解上述方程为1-=a ．从而得到当1-=a 时，直线1l 与2l 互相垂直．上述解题的失误在于机械地套用两直线垂直（斜率形式）的充要条件，忽视了斜率存在的大前提，因而失去对另一种斜率不存在时两直线垂直的考虑，出现了以偏概全的错误．典型例题三例3 已知直线l 经过点)1,3(P ，且被两平行直线011=++y x l ：和062=++y x l ：截得的线段之长为5，求直线l 的方程．分析：(1)如图，利用点斜式方程，分别与1l 、2l 联立，求得两交点A 、B 的坐标（用k 表示），再利用5=AB 可求出k 的值，从而求得l 的方程．(2)利用1l 、2l 之间的距离及l 与1l 夹角的关系求解．(3)设直线l 与1l 、2l 分别相交于),(11y x A 、),(22y x B ，则可通过求出21y y -、21x x -的值，确定直线l 的斜率（或倾斜角），从而求得直线l 的方程．解法一：若直线l 的斜率不存在，则直线l 的方程为3=x ，此时与1l 、2l 的交点分别为)4,3('-A 和)9,3('-B ，截得的线段AB 的长594=+-=AB ，符合题意，若直线l 的斜率存在，则设直线l 的方程为1)3(+-=x k y ． 解方程组⎩⎨⎧=+++-=,01,1)3(y x x k y 得⎪⎭⎫⎝⎛+--+-114,123k k k k A ， 解方程组⎩⎨⎧=+++-=,06,1)3(y x x k y 得⎪⎭⎫⎝⎛+--+-119,173k k k k B ． 由5=AB ，得2225119114173123=⎪⎭⎫ ⎝⎛+-++--+⎪⎭⎫ ⎝⎛+--+-k k k k k k k k ． 解之，得0=k ，即欲求的直线方程为1=y ．综上可知，所求l 的方程为3=x 或1=y ． 解法二：由题意，直线1l 、2l 之间的距离为125261=-=d ，且直线l 被平等直线1l 、2l 所截得的线段AB 的长为5（如上图），设直线l 与直线1l 的夹角为θ，则225225sin ==θ，故∴︒=45θ．由直线011=++y x l ：的倾斜角为135°，知直线l 的倾斜角为0°或90°，又由直线l 过点)1,3(P ，故直线l 的方程为3=x 或1=y ．解法三：设直线l 与1l 、2l 分别相交),(11y x A 、),(22y x B ，则：0111=++y x ，0622=++y x ．两式相减，得5)()(2121=-+-y y x x ． ① 又25)()(221221=-+-y y x x ②联立①、②，可得⎩⎨⎧=-=-052121y y x x 或⎩⎨⎧=-=-502121y y x x由上可知，直线l 的倾斜角分别为0°或90°． 故所求直线方程为3=x 或1=y ．说明：本题容易产生的误解是默认直线l 的斜率存在，这样由解法一就只能得到0=k ，从而遗漏了斜率不存在的情形．一般地，求过一定点，且被两已知平行直线截得的线段为定长a 的直线，当a 小于两平行直线之间距离d 时无解；当d a =时有唯一解；当d a >时，有且只有两解．另外，本题的三种解法中，解法二采取先求出夹角θ后，再求直线l 的斜率或倾斜角，从方法上看较为简单；而解法三注意了利用整体思想处理问题，在一定程度上也简化了运算过程．典型例题四例4 已知点()31，-A ，()13，B ，点C 在坐标轴上，且90=∠ACB ，则满足条件的点C的个数是（ ）．（A ）1 （B ）2 （C ）3 （D ）4解：点C 在坐标轴上，可有两种情况，即在x 轴或y 轴上，点C 的坐标可设为()0，x 或()0，y ．由题意， 90=∠ACB ，直线AC 与直线BC 垂直，其斜率乘积为－1，可分别求得0=x 或2，0=y 或4，所以满足条件的点的坐标为（0，0），（2，0），（0，4）．说明：①本题还可以有另外两种解法：一种是利用勾股定理，另一种是直角三角形斜边AB 与y 轴交点D 恰为斜边AB 中点，则由D 到A 、B 距离相等的性质可解．②本题易错，可能只解一个坐标轴；可能解方程时漏解；也可能看到x 、y 各有两解而误以为有四点．典型例题五例5 已知ABC ∆的一个定点是()13-，A ，B ∠、C ∠的平分线分别是0=x ，x y =，求直线BC 的方程．分析：利用角平分线的轴对称性质，求出A 关于0=x ，x y =的对称点，它们显然在直线BC 上．解：()13-，A 关于0=x ，x y =的对称点分别是()13--，和()31，-，且这两点都在直线BC 上，由两点式求得直线BC 方程为052=+-y x ．典型例题六例 6 求经过两条直线0132=++y x 和043=+-y x 的交点，并且垂直于直线0743=-+y x 的直线的方程．解一：解得两直线0132=++y x 和043=+-y x 的交点为（35-，97），由已知垂直关系可求得所求直线的斜率为34，进而所求直线方程为0934=+-y x ．解二：设所求直线方程为034=+-m y x ，将所求交点坐标（35-，97）代入方程得9=m ，所以所求直线方程为0934=+-y x ．解三：所求直线过点（35-，97），且与直线0743=-+y x 垂直，所以，所求直线方程为0973354=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+y x 即 0934=+-y x ． 解四：设所求直线得方程为()()043132=+-+++y x m y x即 ()()041132=++-++m y m x m （1）由于该直线与已知直线0743=-+y x 垂直 则 ()()013423=-⋅++m m 解得 2=m 代入（1）得所求直线方程为0934=+-y x ．典型例题七例7 已知定点A （3，1），在直线x y =和0=y 上分别求点M 和点N ，使AMN ∆的周长最短，并求出最短周长．分析：由连接两点的线中，直线段最短，利用对称，把折线转化为直线，即转化为求两点间的距离．解：如图1，设点A 关于直线x y =和0=y 的对称点分别为()31，B ，()13-，C ∵MN CN BM MN AN AM ++=++又BC MN CN BM ≥++ 周长最小值是： 52=BC 由两点式可得BC 方程为： 052=-+y x ． 而且易求得：M （35，35），N （25，0），此时，周长最短，周长为52．典型例题八例8 已知实数a ，b 满足1=+b a ，求证：()()2252222≥+++b a ．解：本题的几何意义是：直线1=+b a 上的点（a ，b ）与定点()22--，的距离的平方不小于225．因为直线外一点与直线上任一点连线中，垂线段距离最短，而垂线段的长度即距离251112222=+---=d ，所以25)2()2(22≥+++b a ，即()()2252222≥+++b a ．说明：本题应为不等式的题目，难度较大，证明方法也较多，但用解析几何的方法解决显得轻松简捷，深刻地体现了数形结合的思想．典型例题九例9 在平面直角坐标系中，α=∠xOA ，παπ<<2，点B 在OA 上a OA =，b OB =，()0>>b a ，试在x 轴的正半周上求一点C，使ACB ∠取得最大值．分析：要使最大，只需最大，而是直线到直线的角（此处即为夹角），利用公式可以解决问题．解：如图2，设点()()00>x x C ，∵α=∠xOA ，a OA =，b OB =， ∴()ααsin cos a a A ，， ()ααsin cos b b B ，，于是直线CA 、CB 的斜率分别为：x a a xCA k CA -=∠=ααcos cos tan ， xa a xCB k CB -=∠=ααcos cos tan ∴CACB CA CB k k k k ACB +-=∠1tan ＝)cos )(cos (sin 1cos sin cos sin 2x a x b ab x a a x b b --+---ααααααα＝α+-α-α-αα--αα2sin )cos )(cos ()cos (sin )cos (sin ab x a x b x b a x a b＝2cos )(sin )(xx b a ab x b a +α+-α-＝α+-+α-cos )(sin )(b a x xab b a∵ab x xab 2≥+∴()()α+-α-≤∠cos 2sin tan b a ab b a ACB当且仅当x xab =即ab x =，C 点的坐标为（ab ，0），由παπ<<2可知ACB ∠为锐角，所以此时ACB ∠有最大值arctanααcos )(2sin )(b a ab b a +--．说明：本题综合性强，是三角、不等式和解析几何知识的交汇点．另外本题也是足球射门最大角问题的推广．为了更好地理解问题，可以演示用“几何画板”制作的课件.典型例题十例10 直线0421=-+y x l ：，求1l 关于直线0143=-+y x l ：对称的直线2l 的方程．分析：本题可有多种不同的解法，给出多种解法的途径是：一类利用直线方程的不同形式求解；另一类采用消元思想进行求解．解法一：由⎩⎨⎧=-+=-+0143042y x y x 得1l 与l 的交点为)2,3(-P ，显见P 也在2l 上．设2l 的斜率为k ，又1l 的斜率为-2，l 的斜率为43-，则kk )43(1)43()2)(43(1)2(43-+--=--+---，解得112-=k ． 故2l 的直线方程为)3(1122--=+x y ．即016112=++y x ．解法二：在直线1l 上取一点)0,2(A ，又设点A 关于直线l 的对称点为),(00y x B ，则⎪⎪⎩⎪⎪⎨⎧=-+⋅++⋅=--.01204223,3420000y x x y 解得)58,54(-B 故由两点式可求得直线2l 的方程为016112=++y x ．解法三：设直线2l 上一动点),(y x M 关于直线l 的对称点为),('''y x M ，则⎪⎪⎩⎪⎪⎨⎧=-+⋅++⋅=--.012423,34''''y y xx x x y y 解得256247'+-=y x x ，258724'+--=y x y ．显然),('''y x M 在1l 上，即042587242562472=-+--++-⋅y x y x ，也即016112=++y x ．这便是所求的直线2l 的方程．解法四：设直线2l 上一动点),(y x M ，则M 关于l 的对称点'M 在直线1l 上，可设'M 的坐标为)24,(00x x -，则⎪⎪⎩⎪⎪⎨⎧=-----+=-+,34)24(,51)24(4351430000x x x y x x y x即⎪⎪⎩⎪⎪⎨⎧=-----+=-+-.34)24(,51)24(435)143(0000x x x y x x y x消去0x ，得016112=++y x ，即此所求的直线2l 的方程．说明：在解法一中，应注意正确运用“到角公式”，明确由哪条直线到哪条直线的角．在具体解题时，最好能准确画出图形，直观地得出关系式．在解法四中，脱去绝对值符号时，运用了平面区域的知识．否则，若从表面上可得到两种结果，这显然很难准确地得出直线2l 的方程．本题的四种不同的解法，体现了求直线方程的不同的思想方法，具有一定的综合性．除此之外，从本题的不同解法中可以看出，只有对坐标法有了充分的理解与认识，并具有较强的数形结合意识，才有可能驾驭本题，从而在解法选择的空间上，真正做到游刃有余，左右逢源．典型例题十一例11 不论m 取什么实数，直线0)11()3()12(=--++-m y m x m 都经过一个定点，并求出这个定点．分析：题目所给的直线方程的系数含有字母m ，给m 任何一个实数值，就可以得到一条确定的直线，因此所给的方程是以m 为参数的直线系方程．要证明这个直线系的直线都过一定点，就是证明它是一个共点的直线系，我们可以给出m 的两个特殊值，得到直线系中的两条直线，它们的交点即是直线系中任何直线都过的定点．另一思路是由于方程对任意的m 都成立，那么就以m 为未知数，整理为关于m 的一元一次方程，再由一元一次方程有无数个解的条件求得定点的坐标．解法一：对于方程0)11()3()12(=--++-m y m x m ，令0=m ，得0113=--y x ；令1=m ，得0104=++y x ．解方程组⎩⎨⎧=++=--01040113y x y x 得两直线的交点为)3,2(-．将点)3,2(-代入已知直线方程左边，得：)11()3()3(2)12(---⨯++⨯-m m m 0119324=+----=m m m ．这表明不论m 为什么实数，所给直线均经过定点)3,2(-． 解法二：将已知方程以m 为未知数，整理为： 0)113()12(=++-+-+y x m y x ． 由于m 取值的任意性，有⎩⎨⎧=++-=-+0113012y x y x ，解得2=x ，3-=y ． 所以所给的直线不论m 取什么实数，都经过一个定点)3,2(-．说明：(1)曲线过定点，即与参数无关，则参数的同次幂的系数为0，从而求出定点． (2)分别令参数为两个特殊值，得方程组求出点的坐标，代入原方程满足，则此点为定点．典型例题十二例12 一年级为配合素质教育，利用一间教室作为学生绘画成果展览室．为节约经费，他们利用课桌作为展台，将装画的镜框旋置桌上，斜靠展出．已知镜框对桌面的倾角为α(︒<≤︒18090α)镜框中，画的上、下边缘与镜框下边缘分别相距a m 、b m (b a >)，学生距离镜框下缘多远看画的效果最佳？分析：建立如图所示的直角坐标系，AO 为镜框边，AB 为画的宽度，O 为下边缘上的一点，则可将问题转化为：已知α=∠xOA ，a OA =，b OB =，在x 轴的正方向向上求一点C ，使A C B ∠取最大值． 因为视角最大时，从理论上讲，看画的效果最佳（不考虑其他因素）．解：设C 点坐标为)0,(x (0>x )，从三角函数定义知A 、B 两点坐标分别为)sin ,cos (ααa a 、)sin ,cos (ααb b ，于是直线AC 、BC 的斜率分别为xa a xCA k AC -=∠=ααcos sin tan ，xb b xCB k BC -=∠=ααcos sin tan ．于是2cos )(sin )(1tan xx b a ab x b a k k k k ACB ACBC AC BC ++--=⋅+-=∠αα，即ααcos )(sin )(tan b a x xab b a ACB +-+-=∠．由于ACB ∠是锐角，且在)2,0(π上，则：ααcos )(2sin )(tan b a ab b a ACB +--≤∠，当且仅当x xab =，即ab x =时，等号成立，此时ACB ∠取最大值，对应的点为)0,(ab C ，因此，学生距离镜框下缘m ab 处时，视角最大，即看画效果最佳．说明：解决本题有两点至关重要：一是建立恰当的坐标系，使问题转化成解析几何问题求解；二是把问题进一步转化成求ACB ∠tan 的最大值．如果坐标系选择不当，或选择求ACB ∠sin 的最大值，都将使问题变得复杂起来．本题是一个非常实际的数学应用问题，它不仅考查了直线的有关概念以及三角知识的结合运用，而且更重要的是考查了把实际问题转化为数学问题的能力．典型例题十三例13 知实数x ，y 满足04=-+y x ，求22)1()1(-+-y x 的最小值．分析：本题可使用减少变量法和数形结合法两种方法：22)1()1(-+-y x 可看成点),(y x 与)1,1(之间的距离．解：(法1)由04=-+y x 得x y -=4(R x ∈)， 则2222)14()1()1()1(--+-=-+-x x y x 961222+-++-=x x x x 10822+-=x x 2)2(22+-=x ， ∴22)1()1(-+-y x 的最小值是2. (法2)∵实数x ，y 满足04=-+y x ， ∴点),(y x P 在直线04=-+y x 上．而22)1()1(-+-y x 可看成点),(y x P 与点)1,1(A 之间的距离(如图所示)显然22)1()1(-+-y x 的最小值就是点)1,1(A 到直线04=-+y x 的距离：21141122=+-+=d ，∴22)1()1(-+-y x 的最小值为2．说明：利用几何意义，可以使复杂问题简单化．形如22)()(b y a x -+-的式子即可看成是两点间的距离，从而结合图形解决．典型例题十四例14直线x y 2=是ABC ∆中C ∠的平分线所在的直线，且A ，B 的坐标分别为)2,4(-A ，)1,3(B ，求顶点C 的坐标并判断ABC ∆的形状．分析：“角平分线”就意味着角相等，故可考虑使用直线的“到角”公式将“角相等”列成一个表达式．解：(法1)由题意画出草图（如图所示）．∵点C 在直线x y 2=上，∴设)2,(a a C ， 则422+-=a a k AC ，312--=a a k BC ，2=l k ．由图易知AC 到l 的角等于l 到BC 的角，因此这两个角的正切也相等． ∴lBC l BC lAC AC l k k k k k k k k +-=⋅+-11，∴231212312242214222⋅--+---=⋅+-++--a a a a a a a a ． 解得2=a ．∴C 的坐标为)4,2(， ∴31=AC k ，3-=BC k ， ∴BC AC ⊥．∴ABC ∆是直角三角形．(法2)设点)2,4(-A 关于直线x y l 2=：的对称点为),('b a A ，则'A 必在直线BC 上．以下先求),('b a A ．由对称性可得⎪⎪⎩⎪⎪⎨⎧-⋅=+-=+-,24222,2142a b a b解得⎩⎨⎧-==24b a ，∴)2,4('-A ．∴直线BC 的方程为343121--=---x y ，即0103=-+y x ．由⎩⎨⎧=-+=01032y x x y 得)4,2(C ．∴31=AC k ，3-=BC k ，∴BC AC ⊥．∴ABC ∆是直角三角形．说明：(1)在解法1中设点C 坐标时，由于C 在直线x y 2=上，故可设)2,(a a ，而不设),(b a ，这样可减少未知数的个数．(2)注意解法2中求点)2,4(-A 关于l 的对称点),('b a A 的求法：原理是线段'AA 被直线l 垂直平分．典型例题十五例15 两条直线m y x m l 352)3(1-=++：，16)5(42=++y m x l ：，求分别满足下列条件的m 的值．(1) 1l 与2l 相交； (2) 1l 与2l 平行； (3) 1l 与2l 重合； (4) 1l 与2l 垂直； (5) 1l 与2l 夹角为︒45． 分析：可先从平行的条件2121b b a a =(化为1221b a b a =)着手．解：由mm +=+5243得0782=++m m ，解得11-=m ，72-=m ．由163543m m -=+得1-=m ．(1)当1-≠m 且7-≠m 时，2121b b a a ≠，1l 与2l 相交；(2)当7-=m 时，212121c c b b a a ≠=．21//l l ；(3)当1-=m 时，212121c c b b a a ==，1l 与2l 重合；(4)当02121=+b b a a ，即0)5(24)3(=+⋅+⋅+m m ，311-=m 时，21l l ⊥；(5) 231+-=m k ，mk +-=542．由条件有145tan 11212=︒=+-k k k k ．将1k ，2k 代入上式并化简得029142=++m m ，527±-=m ；01522=-+m m ，35或-=m ．∴当527±-=m 或-5或3时1l 与2l 夹角为︒45． 说明：由mm +=+5243解得1-=m 或7-=m ，此时两直线可能平行也可能重合，可将m 的值代入原方程中验证是平行还是重合．当mm +≠+5243时两直线一定相交，此时应是1-≠m 且7-≠m ．典型例题十六例16点)3,2(1P ，)5,4(2-P 和)2,1(-A ，求过点A 且与点1P ，2P 距离相等的直线方程．分析：可以用待定系数法先设出直线方程，再求之；也可从几何意义上考察这样的直线具有的特征．解：(法1)设所求直线方程为)1(2+=-x k y ，即02=++-k y kx ，由点1P 、2P 到直线的距离相等得：1254123222+++--=+++-k k k k k k ．化简得3313--=-k k ，则有：3313--=-k k 或3313+=-k k ， 即31-=k 或方程无解．方程无解表明这样的k 不存在，但过点A ，所以直线方程为1-=x ，它与1P ，2P 的距离都是3．∴所求直线方程为)1(312+-=-x y 或1-=x ．(法2)设所求直线为l ，由于l 过点A 且与1P ，2P 距离相等，所以l 有两种情况，如下图：(1)当1P ，2P 在l 同侧时，有21//P P l ，此时可求得l 的方程为)1(24352+---=-x y ，即)1(312+-=-x y ；(2)当1P ，2P 在l 异侧时，l 必过21P P 中点)4,1(-，此时l 的方程为1-=x ． ∴所求直线的方程为)1(312+-=-x y 或1-=x ．说明：该题如果用待定系数法解易漏掉1-=x ，即斜率不存在的情况．所以无论解什么题目，只要图形容易画出，就应结合图形，用代数法、几何法配合来解．典型例题十七例17 经过点)1,2(-P 且与直线0623=--y x 平行的直线l 的方程．分析：已知直线l 与直线0623=--y x 平行，故l 的斜率可求，又l 过已知点P ，利用点斜式可得到l 的方程．另外由于l 与已知直线平行，利用平行直线系方程，再由已知点P ，也可确定l 的方程．解法一：由已知直线0623=--y x ，知其斜率23=k ．又由l 与直线0623=--y x 平行，所以直线l 的斜率23=l k ．又由直线l 经过已知点)1,2(-P ，所以利用点斜式得到直线l 的方程为：)2(231-=+x y ，即0823=--y x ．解法二：因为直线l 平行于直线0623=--y x ，所以可设直线l 的方程为023=+-C y x ．又点)1,2(-P 在直线l 上，所以0)1(223=+-⨯-⨯C ，解得8-=C ． 故直线l 的方程为0823=--y x ．说明：解法二使用的是平行直线系，并用了待定系数法来解．典型例题十八例18 过点)1,1(-P 且与直线0132=++y x 垂直的直线l 的方程．分析：已知直线l 与直线0132=++y x 垂直，故l 的斜率可求，又l 过已知点P ，利用点斜式可得到l 的方程．另外由于l 与已知直线垂直，利用垂直直线系方程，再由已知点P ，也可确定l 的方程．解法一：由直线0132=++y x ，知其斜率32-=k ．又由l 与直线0132=++y x 垂直，所以直线l 的斜率231=-=k k l ．又因l 过已知点)1,1(-P ，利用点斜式得到直线l 的方程为)1(231-=+x y ，即0523=--y x ．解法二：由直线l 与直线0132=++y x 垂直，可设直线l 的方程为：023=+-C y x ．又由直线l 经过已知点)1,1(-P ，有0)1(213=+-⨯-⨯C ． 解得5-=C ．因此直线l 的方程为0523=--y x ．说明：此题的解二中使用垂直直线系方程，并使用了待定系数法．典型例题十九例19知直线l 经过两条直线021=+y x l ：与010432=--y x l ：的交点，且与直线03253=+-y x l ：的夹角为4π，求直线l 的方程．分析：先求1l 与2l 的交点，再列两条直线夹角公式，利用l 与3l 夹角为4π，求得l 的斜率．也可使用过两直线交点的直线系方程的方法省去求交点的过程，直接利用夹角公式求解．解法一：由方程组⎩⎨⎧=--=+0104302y x y x 解得直线1l 与2l 的交点)1,2(-．于是，所求直线l 的方程为)2(1-=+x k y ．又由已知直线03253=+-y x l ：的斜率253=k ，而且l 与3l 的夹角为4π，故由两直线夹角正切公式，得3314tankk k k +-=π，即kk 251254tan+-=π． 有125125±=+-kk ，15252±=+-k k ， 当15252=+-k k 时，解得37-=k ；当15252-=+-kk 时，解得73=k ．故所求的直线l 的方程为)2(731-=+x y 或)2(371--=+x y ，即01373=--y x 或01137=-+y x ．解法二：由已知直线l 经过两条直线1l 与2l 的交点，则可设直线l 的方程为0)2()1043(=++--y x y x λ， （*）即010)42()3(=--++y x λλ． 又由l 与3l 的夹角为4π，3l 的方程为0325=+-y x ，有212112214tanB B A A B A B A +-=π，即)42)(2()3(55)42()2)(3(1--++⨯---+=λλλλ，也即λλ+-=2312141，从而1231214=+-λλ，1231214-=+-λλ．解得139-=λ，1137=λ．代入（*）式，可得直线l 的方程为01373=--y x 或01137=-+y x ．说明：此题用到两直线的夹角公式，注意夹角公式与到角公式的区别。
高考数学 百大经典例题——空间直线(新课标)
典型例题一空间直结例1 若b a //，A c b = ，则a ，c 的位置关系是（ ）．A ．异面直线B ．相交直线C ．平行直线D ．相交直线或异面直线 分析：判断两条直线的位置关系，可以通过观察满足已知条件的模型或图形而得出正确结论．解：如图所示，在正方体1111D C B A ABCD -中，设a B A =11，b AB =，则b a //． 若设c B B =1，则a 与c 相交．若设c BC =，则a 与c 异面．故选D ．说明：利用具体模型或图形解决问题的方法既直观又易于理解．一般以正方体、四面体等为具体模型．例如，a ，b 相交，b ，c 相交，则a ，c 的位置关系是相交、平行或异面．类似地；a ，b 异面，b ，c 异面，则a ，c 的位置关系是平行、相交或异面．这些都可以用正方体模型来判断．典型例题二例2 已知直线a 和点A ，α∉A ，求证：过点A 有且只有一条直线和a 平行．分析：“有且只有”的含义表明既有又惟一，因而这里要证明的有两个方面，即存在性和惟一性．存在性，即证明满足条件的对象是存在的，它常用构造法（即找到满足条件的对象来证明）；惟一性，即证明满足条件的对象只有．．一个，换句话说，说是不存在第二个满足条件的对象．因此，这是否定性．．．命题，常用反证法． 证明：（1）存在性．∵ a A ∉，∴ a 和A 可确定一个平面α，由平面几何知识知，在α内存在着过点A 和a 平行的直线． （2）惟一性假设在空间过点A 有两条直线b 和c 满足a b //和a c //．根据公理4，必有c b //与A c b = 矛盾，∴ 过点A 有一条且只有一条直线和a 平行．说明：对于证明“有且只有”这类问题，一定要注意证明它的存在性和惟一性．典型例题三例3 如图所示，设E ，F ，G ，H 分别是空间四边形ABCD 的边AB ，BC ，CD ，DA 上的点，且λ==AD AH AB AE ，μ==CDCGCB CF ，求证： （1）当μλ=时，四边形EFGH 是平行四边形； （2）当μλ≠时，四边形EFGH 是梯形． 分析：只需利用空间等角定理证明FG EH //即可．证明：连结BD ，在ABD ∆中，λ==AD AHAB AE ，∴ BD EH //，且BD EH λ=． 在CBD ∆中，μ==CDCGCB CF ，∴ BD FG //，且BD FG μ=． ∴ FG EH //，∴ 顶点E ，F ，G ，H 在由EH 和FG 确定的平面内．（1）当μλ=时，FG EH =，故四边形EFGH 为平行四边形； （2）当μλ≠时，FG EH ≠，故四边形EFGH 是梯形． 说明：显然，课本第11页的例题就是本题（2）的特殊情况． 特别地，当21==μλ时，E ，F ，G ，H 是空间四边形各边中点，以它们为顶点的四边形是平行四边形．如果再加上条件BD AC =，这时，平行四边形EFGH 是菱形．典型例题四例4 已知b a 、是两条异面直线，直线a 上的两点B A 、的距离为6，直线b 上的两点D C 、的距离为8，BD AC 、的中点分别为N M 、且5=MN ，求异面直线b a 、所成的角．分析：解题的关键在于依据异面直线所成角的定义构造成和异面直线b a 、平行的两条相交直线，然后把它们归纳到某一三角形中求解．解：如图，连结BC ，并取BC 的中点O ，连结ON OM 、，∵ON OM 、分别是ABC ∆和BCD ∆的中位线， ∴AB OM //，CD ON //，即 a OM //，b ON //．∴ON OM 、所成的锐角或直角是异面直线b a 、所成的角． 又∵ 6=AB ，8=CD ， ∴3=OM ，4=ON ．在OMN ∆中，又∵5=MN ，∴222MN ON M =+， ∴90=∠MON ．故异面直线b a 、所成的角是90．说明：在求两条异面直线所成的角时，一般要依据已知条件，找出与两条异面直线分别平行并且相交于一点的两条直线．但是，异面直线所成角的定义中的点O 一般是在图形中存在着的，需要认真观察分析图形的性质，从而找出这一点和过这一点与两异面直线平行的直线，以得到两条异面直线所成的角，在求这个角的大小时，一般是根据平面图形中解三角形的知识求解的．典型例题五例5 已知四面体ABC S -的所有棱长均为a ．求： （1）异面直线AB SC 、的公垂线段EF 及EF 的长； （2）异面直线EF 和SA 所成的角．分析：依异面直线的公垂线的概念求作异面直线AB SC 、的公垂线段，进而求出其距离；对于异面直线所成的角可采取平移构造法求解．解：（1）如图，分别取AB SC 、的中点F E 、，连结CF SF 、．由已知，得SAB ∆≌CAB ∆． ∴CF SF =，E 是SC 的中点， ∴SC EF ⊥．同理可证AB EF ⊥∴EF 是AB SC 、的公垂线段．在SEF Rt ∆中，a SF 23=，a SE 21=．∴22SE SF EF -=a a a 22414322=-． （2）取AC 的中点G ，连结EG ，则SA EG //．∴EF 和GE 所成的锐角或直角就是异面直线EF 和SA 所成的角． 连结FG ，在EFG ∆中，a EG 21=，a GF 21=，a EF 22=． 由余弦定理，得22222124142412cos 222222=⋅⋅-+=⋅⋅-+=∠a a aa a EF EG GF EF EG GEF ． ∴45=∠GEF ．故异面直线EF 和SA 所成的角为45．说明：对于立体几何问题要注意转化为平面问题来解决，同时要将转化过程简要地写出来，然后再求值．典型例题六例6 如图所示，两个三角形ABC ∆和'''C B A ∆的对应顶点的连线'AA 、'BB 、'CC 交于同一点O ，且32'''===O C CO O B BO O A AO ． (1)证明：''//B A AB ，''//C A AC ，''//C B BC ； (2)求'''C B A ABCS S ∆∆的值．分析：证两线平等当然可用平面几何的方法．而求面积之比则需证两个三角形相似，由于三角形是平面图形，故也可用平面几何的方法证明．证明：(1)当ABC ∆和'''C B A ∆在O 点两侧时，如图甲 ∵'AA 与'BB 相交于O 点，且OB BOO A AO ''=， ∴''//B A AB （因为'AA 、'BB 共面）． 同理''//C A AC ，''//C B BC ．(2)∵''//B A AB ，且''//C A AC ，AB 和''B A ，AC 和''C A 的方向相反，∴'''C A B BAC ∠=∠，同理'''C B A ABC ∠=∠．因此，ABC ∆∽'''C B A ∆．又32'''==O A AO B A AB ，∴94322'''=⎪⎭⎫⎝⎛=∆∆C B A ABC S S ． 当ABC ∆和'''C B A ∆在O 点的同侧时，如图乙所示，同理可得(1)(2)．说明：此题ABC ∆与'''C B A ∆是否共面并不重要，因为等角定理对各种位置已作说明．典型例题七例7 S 是矩形ABCD 所在平面外一点，BC SA ⊥，CD SB ⊥，SA 与CD 成︒60角，SD 与BC 成︒30角，a SA =，求：(1)直线SA 与CD 的距离； (2)求直线SB 与AD 的距离．分析：要求出SA 与CD 、SB 与AD 的距离，必须找到它们的公垂线段，公垂线段的长度即为异面直线间的距离．解：如图所示，在矩形ABCD 中，AD BC //． ∵BC SA ⊥，∴AD SA ⊥．又AD CD ⊥，∴AD 是异面直线SA 、CD 的公垂线段， 其长度为异面直线SA 、CD 的距离．在SAD Rt ∆中，∵SDA ∠是SD 与BC 所成的角， ∴︒=∠30SDA ．又a SA =，∴a AD 3=．(2)在矩形ABCD 中，CD AB //，AD SB ⊥， ∴AB SB ⊥，又AD AB ⊥，∴AB 是直线SB 、AD 的公垂线段，其长度为异面直线SB 、AD 的距离． 在SAB Rt ∆中，SAB ∠是异面直线SA 与CD 所成的角，∴︒=∠60SAB ． 又a SA =，∴260cos a a AB =︒=， ∴直线SB 与AD 的距离为2a ． 说明：(1)求异面直线之间距离的步骤是：①找（作）线段；②证线段是公垂线段；③求公垂线段的长度．(2)求异面直线间的距离的问题，高考中一般会给出公垂线段．典型例题八例8 a 、b 、c 是三条直线，若a 与b 异面，b 与c 异面，判断a 与c 的位置关系，并画图说明．分析：这是一道考查异面直线概念及空间直线位置关系的问题，同时也考查了图形语言的表达能力．解：直线a 与c 的位置关系有以下三种情形如图：∴直线a 与c 的位置关系可能平行（图中的(1)）；可能相交（如图中的(2)）； 可能异面（图中的(3)）．说明：本题也考查了空间想象能力和逻辑划分、分类讨论的能力．典型例题九例9 如果两条异面直线称作“一对”，那么在正方体的十二条棱中，共有几对异面直线（ ）．A ．12对B ．24对C ．36对D ．48对分析：一般地，立体几何中的计数问题，是由所数的量的性质，确定一规律，然后按此规律进行计数．正方体的各棱具有相同的位置关系．所以以一条棱为基量，考察与其异面的几对，问题可解．解：如图，正方体中与AB 异面有C C 1，D D 1，11C B ，11D A ，∵各棱具有相同的位置关系，且正方体有12条棱，排除两棱的重复计算成本， ∴异面直线共有242412=⨯对． 说明：分析清楚几何体特点是避免重复计数的关键．计数问题必须避免盲目乱数，做到“不重不漏”．典型例题十例10 如图，已知不共面的直线a ，b ，c 相交于O 点，M 、P 是直线a 上两点，N 、Q 分别是b ，c 上一点．求证：MN 和PQ 是异面直线．证法1：假设MN 和PQ 不是异面直线， 则MN 与PQ 在同一平面内，设为α∵a P M ∈、，α∈P M 、 ∴α⊂a ．又a O ∈，∴α∈O ．∵α∈N 且b O ∈，b N ∈， ∴α⊂b ． 同理：α⊂C∴a ，b ，c 共面于α，与已知a ，b ，c 不共面相矛盾， ∴MN 、PQ 是异面直线．证法2：∵O c a = ，∴直线a ，c 确定一平面设为β． ∵a P ∈，c Q ∈，∴β∈P ，β∈Q ， ∴β⊂PQ 且β∈M ，PQ M ∉． 又a ，b ，c 不共面，b N ∈，∴β∉N ， ∴MN 与PQ 为异面直线．说明：证明两条直线异面的方法有两种． (1)用定义证明（即定义法）：此时需借反证法，假设两条直线不异面，根据空间两条直线的位置关系，这两条直线一定共面，即这两条直线可能相交也可能平行，然后，推导出矛盾即可．(2)用定理证明（即定理法）：用该法证明时，必须阐述出定理满足的条件：α⊂a ，α∉A ，a B ∉，然后可以推导出直线a 与AB 是异面直线．典型例题十一例11 已知平面α与平面β相交于直线l ，A ，B 为直线l 上的两点．在α内作直线AC ，在β内作直线BD ．求证AC 和BD 是异面直线．已知：平面α 平面β=l ，l A ∈，l B ∈，α⊂AC ，β⊂BD ，如图． 求证：AC 、BD 是异面直线．证明：假设AC ，BD 不是异面直线，则它们必共面． ∴A 、B 、C 、D 在同一平面内．即A 、B 、C 所确定的平面α与A 、B 、D 确定的平面β重合 这与平面α 平面β=l 矛盾∴AC 、BD 是异面直线．说明：证明两条直线为异面直线，用反证法往往比较简单．典型例题十二例12 已知空间四边形ABCD ，求证它的对角线AC 和BD 是异面直线． 证法一：（反证法）如图假设AC 和BD 不是异面直线，则AC 和BD 在同一平面内．∴A 、B 、C 、D 在同一平面内，即四边形ABCD 是平面四边形， 这与已知条件矛盾，所以假设不成立． 因此AC 和BD 是异面直线． 证法二：（定理法）过BC 和CD 作一平面α，则对角线BD 在平面α内．对角线AC 与平面α交于BD 外的一点C ，即点C 不在直线BD 上， 且A 点在平面α外．∴根据异面直线判定定理知：AC 和BD 是异面直线．说明：判定两条直线是异面直线的证明问题常用这两种方法，即(1)反证法，(2)用判定定理．典型例题十三例13 已知空间四边形ABCD ，AC AB ≠，AE 是ABC ∆的BC 边上的高，DF 是BCD ∆的BC 边上的中线，求证：AE 和DF 是异面直线．证法一：（定理法）如图由题设条件可知点E 、F 不重合，设BCD ∆所在平面α．∴⇒⎪⎪⎩⎪⎪⎨⎧∉∈∉⊂DFE E A DF αααAE 和DF 是异面直线． 证法二：（反证法）若AE 和DF 不是异面直线，则AE 和DF 共面，设过AE 、DF 的平面为β． (1)若E 、F 重合，则E 是BC 的中点，这与题设AC AB ≠相矛盾． (2)若E 、F 不重合，∵EF B ∈，EF C ∈，β⊂EF ，∴β⊂BC ． ∵β∈A ，β∈D ，∴A 、B 、C 、D 四点共面，这与题设ABCD 是空间四边形相矛盾． 综上，假设不成立．故AE 和DF 是异面直线．说明：反证法不仅应用于有关数学问题的证明，在其他方面也有广泛的应用． 首先看一个有趣的实际问题：“三十六口缸，九条船来装，只准装单，不准装双，你说怎么装？” 对于这个问题，同学们可试验做一做． 也许你在试验几次后却无法成功时，觉得这种装法的可能性是不存在的．那么你怎样才能清楚地从理论上解释这种装法是不可能呢？用反证法可以轻易地解决这个问题．假设这种装法是可行的，每条船装缸数为单数，则9个单数之和仍为单数，与36这个双数矛盾．只须两句话就解决了这个问题．典型例题十四例14 已知E 、1E 分别是正方体1111D C B A ABCD -的棱AD 、11D A 的中点． 求证：111C E B BEC ∠=∠．分析：欲证两个角相等，可通过等角定理或其推论来实现． 证明：如图，连结1EE∵1E ，E 分别为11D A ，AD 中点，∴11E A AE ，∴EA E A 11为平行四边形．∴A A 1E E 1．又∵A A 1B B 1，∴EE 1B B 1，∴四边形11EBB E 是平行四边形．∴EB B E //11．同理EC C E //11．又111B E C ∠与CEB ∠方向相同． ∴CEB B E C ∠=∠111．说明：有关证明角相等问题，一般采用下面三种途径：(1)利用等角定理及其推论；(2)利用证三角形相似；(3)利用证三角形全等．本例是通过第一种途径来实现．请同学们再利用第三种途径给予证明．典型例题十五例15 由四个全等的等边三角形的封面几何体称为正四面体，如图，正四面体ABCD 中，E 、F 分别是棱BC 、AD 的中点，CF 与DE 是一对异面直线，在图形中适当的选取一点作出异面直线CF 、DE 的平行线，找出异面直线CF 与DE 成的角．分析1：选取平面ACD ，该平面有以下两个特点，(1)该平面包含直线CF ，(2)该平面与DE 相交于点D ，伸展平面ACD ，在该平面中，过点D 作CF DM //交AC 的延长线于M ，连结EM ．可以看出：DE 与DM 所成的角，即为异面直线DE 与CF 所成的角．如图．分析2：选取平面BCF ，该平面有以下两个特点：(1)该平面包含直线CF ，(2)该平面与DE 相交于点E ．在平面BCF 中，过点E 作CF 的平行线交BF 于点N ，连结ND ，可以看出：EN 与ED 所成的角，即为异面直线FC 与ED 所成的角．如图．分析3：选取平面ADE ，该平面有如下两个特点：(1)该平面包含直线DE ，(2)该平面与CF 相交于点F ．在平面ADE 中，过点F 作DE FG //，与AE 相交于点G ，连结CG ，可以看出：FG 与FC 所成的角，即为异面直线CF 与DE 所成的角．分析4：选取平面BCD ，该平面有如下特点：(1)该平面包含直线DE ，(2)该平面与CF 相交于点C ，伸展平面BCD ，在该平面内过点C 作DE CK //与BD 的延长线交于点K ，且BD DK =，连结FK ，则CF 与CK 所成的角，即为异面直线CF 与DE 所成的角．如图．说明：(1)两条异面直线所成的角是非常重要的知识点，是每年高考的必考内容，要求牢固掌握两条异面直线所成的角的定义和两条异面直线互相垂直的概念，两条异面直线所成的角是刻划两条异面直线相对位置的一个量，是通过转化为相交直线成角来解决的，这里我们要注意：两条异面直线所成的角θ的范围是︒≤<︒900θ，当︒=90θ时，这两条异面直线互相垂直．求两条异面直线所成角的关键是作出这两条异面直线所成的角，作两条异面直线所成的角的方法是：将其中一条平移到某个位置使其与另一条相交或是将两条异面直线同时平移到某个位置使它们相交，然后在同一平面内求相交直线所成的角．值得注意的是：平移后相交所得的角必须容易算出，因此平移时要求选择恰当位置．一般提倡像思考2，那样作角，因为此角在几何体内部，易求．(2)本例题多方位、多角度思考问题，思路开阔、运用知识灵活，对我们解决异面直线所成角问题大有裨益，要认真理解．典型例题十六例16 如图，等腰直角三角形ABC 中，︒=∠90A ，2=BC ，AC DA ⊥，AB DA ⊥，若1=DA ，且E 为DA 的中点．求异面直线BE 与CD 所成角的余弦值．分析：根据异面直线所成角的定义，我们可以选择适当的点，分别引BE 与DC 的平行线，换句话说，平移BE （或CD ）．设想平移CD ，沿着DA 的方向，使D 移向E ，则C 移向AC 的中点F ，这样BE 与CD 所成的角即为BEF ∠或其补角，解EFB ∆即可获解．解：取AC 的中点F ，连结EF ，在ACD ∆中，E 、F 分别是AD 、AC 的中点， ∴CD EF //，∴BEF ∠即为所求的异面直线BE 与CD 所成的角或其补角．在EAB Rt ∆中，1=AB ，2121==AD AE ，∴25=BE ． 在AEF Rt ∆中，1=AC ，21=AE ，∴22=EF ． 在ABF Rt ∆中，1=AB ，21=AE ，∴25=BF ． 在等腰三角形EBF 中，1010254221cos ===∠BE EF FEB ， ∴异面直线BE 与CD 所成角的余弦值为1010． 说明：求角或求角的三角函数值的一般步骤是：①找（或作出）角，适合题意，②求角或求角的三角函数值，往往是化归成一个三角形的内角，通过解三角形求得．典型例题十七例17 在正四面体ABCD 中，已知E 是棱BC 的中点，求异面直线AE 和BD 所成角的余弦值．分析：可在平面BCD 内过E 作BD 平行线，可在AEF ∆中求得所成角的余弦值．解：如图，取CD 的中点F ，连结EF ，AF ，∵E 为BC 的中点，∴EF 为CBD ∆的中位线，∴BD EF //，∴AE 与EF 所成的锐角或直角就是异面直线AE 和BD 所成的角．设正四面体的棱长为a ，由正三角形的性质知，a AF AE 23==，a EF 21=．在AEF ∆中， 6321cos ==∠AE EF AEF ，即异面直线AE 和BD 所成角的余弦值为63． 说明：本题是利用三角形中位线达到平移的目的．这种作异面直线所成角的方法称为中位线平移法．典型例题十八例18 在正方体1111D C B A ABCD -中，求正方体对角线1BD 和面对角线AC 所成角的大小．解：如图．取D D 1上中点N ，则有：DN N D =1，连结BD ．令O AC BD = ，则DO BO =，连结NO ，NA ，NC∵N ，O 分别为D D 1，BD 的中点，∴NO 121BD ，∴NOA ∠(或NOC ∠)是异面直线1BD 和AC 所成的角．在NAD Rt ∆及NCD Rt ∆中，∵CD AD =，ND ND =，∴NAD Rt ∆≌NCD Rt ∆，∴NC NA =，∴ANC ∆为等腰三角形．又O 为AC 中点，∴AC NO ⊥，∴异面直线1BD 和AC 所成角为︒90．说明：(1)由于异面直线所成角最大为直角，所以，在把异面直线平移得到的两个夹角中，必须选取其中较小的角为异面直线的所成角．(2)实际上，正方体的体对角线与任意一条面对角线所成角均为直角．典型例题十九例19 在正方体1111D C B A ABCD -中，E 、F 分别为1BB 、1CC 的中点，求AE 、BF 所成角的余弦值．分析1：可平移BF 至1EC ，可得到角1AEC ，再解三角形即可．但要注意到1AEC ∠为钝角．解法1：如图，连结1EC ，则BF EC //1，由AE 与1EC 所成的锐角或直角，就是AE 与BF 所成的角，连1AC ，令正方体的棱长为a ， 有a EC AE 251==，a AC 31= 在1AEC ∆中，515612122cos 22122121-=-=-=-=∠AE AC AE AC AE AEC ， ∴1AEC ∠的补角为异面直线AE 与BF 所成角．∴AE 、BF 所成角的余弦值是51． 分析2：连结DB 、FD ，可得DFB ∠即为异面直线AE 和BF 所成的角．进而求其余弦值．解法2：连结DB 、FD ，可证得AE FD //．(∵EF AD )DFB ∠(或其补角)即为异面直线AE 、BF 所成的角．a BF DF 25==，a BD 2=． 由余弦定理，有 ()512245452525222525cos 222=-+=⋅⋅-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=∠a a aa a DFB ， ∴AE 、BF 所成角的余弦值是51． 说明：异面直线所成角的范围是]90,0(︒︒，当求得某角的余弦值为负值时，则此角的补角是异面直线所成角．典型例题二十例20 在空间四边形ABCD 中：CD AB =，BD AC =，E ，F 分别是AD ，BC 的中点．求证：线段EF 是异面直线AD ，BC 的公垂线．证明：如图．连结AF 、DF 、BE 、CE ．在ABD ∆和ACD ∆中，CD AB =，BD AC =，AD 公用∴ABD ∆≌ACD ∆．又E 是AD 中点，∴CE BE =．在BEC ∆中，F 是BC 的中点，∴BC EF ⊥．同理AD EF ⊥，∴EF 是异面直线AD 、BC 的公垂线．说明：证明某一条直线是两条异面直线的公垂线，须证明以下两点：(1)与两条异面直线都垂直；(2)与两条异面直线都相交．典型例题二十一例21 如图，空间四边形ABCD 中，四边AB 、BC 、CD 、DA 和对角线AC 、BD 都等于a ，E 、F 分别为AB 、CD 的中点．(1)求证：EF 是异面直线AB 、CD 的公垂线．(2)求异面直线AB 和CD 的距离．分析：要证明EF 是异面直线AB 与CD 的公垂线，必须说明两个方面的问题，一个方面EF 与AB 、CD 都相交，另一个方面AB 、CD 与EF 都垂直．(1)证明：连结AF 、BF ，由已知BCD ∆和ACD ∆均为正三角形，E 、F 分别为AB 、CD 的中点，∴BF AF =，AB EF ⊥．同理CD EF ⊥，又EF 与AB 、CD 都相交，∴EF 为异面直线AB 、CD 的公垂线．(2)解：∵空间四边形各边及对角线AC 、BD 的长均为a ， ∴a BF AF 23==，而a AE 21=， ∴在AEF Rt ∆中，a AE AF EF 2222=-=． ∴异面直线AB 和CD 之间的距离为a 22． 说明：(1)求线段的长度一般地要把该线段放到一个三角形中去求解，尤其是放到特殊三角形中去求解，如直角三角形、等腰三角形等．(2)满足条件的该空间四边形其实质是空间正四面体，该问题实质上是求正四面体对棱之间的距离．典型例题二十二例22 已知a 、b 是异面直线，直线c //直线a ，那么c 与b （ ）．A ．一定是异面直线B ．一定是相交直线C ．不可能是平行直线D ．不可能是相交直线解：由已知a 、b 是异面直线，直线c //直线a ，所以直线c 直线b ，否则若b c //，则有b a //与已知矛盾．所以c b ．∴应选C ．说明：本题考察两直线位置关系和公理4的应用及异面直线定义．典型例题二十三例23 两条异面直线指的是（ ）．A ．在空间内不相交的两条直线B ．分别位于两个不同平面内的两条直线C ．某平面内的一条直线和这个平面外的一条直线D ．不在同一平面内的两条直线解：对于A,在空间内不相交的两条直线也可能是平行，应排除A ．对于B ，分别位于两个不同平面内的两条直线可能是异面直线，也可能是相交直线或平行直线，应排除B ．对于C ，某平面内的一条直线和这个平面外的一条直线可能是异面直线，也可能是平行直线，应排除C ．∴应选D ．说明：本题主要考查对异面直线定义的掌握，特别是对“不同在任何一个平面内的两条直线”含义的理解．典型例题二十四例24 如图，在棱长为1的正方体1111D C B A ABCD -中，M 、N 分别为11B A 和1BB 的中点，那么直线AM 与CN 所成的角的余弦值是（ ）．A ．23B ．1010 C ．53 D ．52 解：在平面11A ABB 中，过N 点作AM NP //，交AB 于P ，连结PC ，如图，PNC ∠(或其补角)就是AM 与CN 所成的角．设AB 的中点为Q ，则P 是BQ 中点． 可求得45=NP ，417=CP ，25=NC ． 在PNC ∆中，由余弦定理得522cos 222=⋅-+=∠PN NC PC PN NC PNC ． ∴应选D ．说明：作出平行线PN ，进而在PNC ∆中利用余弦定理求出直线AM 与CN 所成角的余弦值．典型例题二十五例25 如图，1111D C B A ABCD -是正方体，4111111B A F D E B ==，则1BE 与1DF 所成的角的余弦值是（ ）．A ．1715B ．21C ．178D ．23解：过A 点在平面11A ABB 内作1//DF AF ，再过1E 在平面11A ABB 内作FA E E //1， 则E BE 1∠(或其补角)即是1BE 与1DF 所成的角． 由已知4111111B A F D E B ==， 1111D C B A ABCD -是正方体，所以可求得a BE 4171=(a 为正方体的棱长)， 又E E AF DF 11==，而11BE DF =， ∴a E E 4171=，显然a EB 21=． 在E BE 1∆中，由余弦定理，得171541722141722cos 2211221211=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=⋅-+=∠a a a E E BE EB E E BE E BE ． ∴应选A ．说明：(1)解答本题的关键是作平行线AF 、E E 1．进而在E BE 1∆中解出E BE 1∠的余弦值；(2)考查历届高考试题，求异面直线所成角的题常以正方体和正四面体为载体，在正方体和正四面体中命题．典型例题二十六例26 在棱长都相等的四面体BCD A -中，E 、F 分别是棱AD 、BC 的中点，连结AF 、CE ，如图所示，求异面直线AF 、CE 所成角的余弦值．解：连结DF ，取DF 的中点G ，连结EG ，CG ，又E 是AD 的中点，故AF EG //，所以GEC ∠是异面直线AF 、CE 所成角． ∵AF 是正三角形ABC 的高， ∴AB AF 23=，∴AB EG 43=． 在FCG Rt ∆中，AB AB FD FG 43232121=⋅==，AB CF 21=，则 AB AB AB FC FG CG 4721432222=⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=． 在EGC ∆中，AB CE 23=，AB EG 43=，AB CG 47=， 用余弦定理可得32cos =∠GEC ． ∴异面直线AF 、CE 所成角的余弦值是32． 说明：求两条异面直线所成角或求所成角的函数值，关键是作出异面直线所成的角． 作两条异面直线所成角的方法一般是：将其中一条平移到某个位置使其也另一条相交也或者将两条异面直线同时平移到某个位置使它们相交，使得这个角在某一个平面的三角形内，进而求出．但要注意：平移后相交所得的角必须容易算出，因此平移时应选择恰当的位置．。
数学百大经典例题-算术平均数与几何平均数
典型例题一例1已知，求证证明：∵，，，三式相加，得，即说明：这是一个重要的不等式，要熟练掌握．典型例题二例2已知是互不相等的正数，求证：证明：∵，∴同理可得：．三个同向不等式相加，得①说明：此题中互不相等，故应用基本不等式时，等号不成立．特别地，，时，所得不等式①仍不取等号．典型例题三例3求证．分析：此问题的关键是“灵活运用重要基本不等式，并能由这一特征，思索如何将进行变形，进行创造”．证明：∵，两边同加得．即．∴．同理可得：，．三式相加即得．典型例题四例4若正数、满足，则的取值范围是．解：∵，∴，令，得，∴，或（舍去）．∴，∴的取值范围是说明：本题的常见错误有二．一是没有舍去；二是忘了还原，得出．前者和后者的问题根源都是对的理解，前者忽视了后者错误地将视为．因此，解题过程中若用换元法，一定要对所设“元”的取值范围有所了解，并注意还原之．典型例题五例5 （1）求的最大值．（2）求函数的最小值，并求出取得最小值时的值．（3）若，且，求的最小值．解：（1）即的最大值为当且仅当时，即时，取得此最大值．（2）∴的最小值为3，当且仅当，即，，时取得此最小值．（3）∴∴即∵∴即的最小值为2．当且仅当时取得此最小值．说明：解这类最值，要选好常用不等式，特别注意等号成立的条件．典型例题六例6求函数的最值．分析：本例的各小题都可用最值定理求函数的最值，但是应注意满足相应条件．如：，应分别对两种情况讨论，如果忽视的条件，就会发生如下错误：∵，解：当时，，又，当且仅当，即时，函数有最小值∴当时，，又，当且仅当，即时，函数最小值∴典型例题七例7求函数的最值．分析：．但等号成立时，这是矛盾的！于是我们运用函数在时单调递增这一性质，求函数的最值．解：设，∴．当时，函数递增．故原函数的最小值为，无最大值．典型例题八例8求函数的最小值．分析：用换元法，设，原函数变形为，再利用函数的单调性可得结果．或用函数方程思想求解．解：解法一：设，故．由，得：，故：．∴函数为增函数，从而．解法二：设，知，可得关于的二次方程，由根与系数的关系，得：．又，故有一个根大于或等于2，设函数，则，即，故．说明：本题易出现如下错解：．要知道，无实数解，即，所以原函数的最小值不是2．错误原因是忽视了等号成立的条件．当、为常数，且为定值，时，，不能直接求最大（小）值，可以利用恒等变形，当之差最小时，再求原函数的最大（小）值．典型例题九例9求的最小值．分析：此题出现加的形式和平方，考虑利用重要不等式求最小值．解：由，得又得，即．故的最小值是．说明：本题易出现如下错解：，故的最小值是8．错误的原因是，在两次用到重要不等式当等号成立时，有和，但在的条件下，这两个式子不会同时取等号（）．排除错误的办法是看都取等号时，与题设是否有矛盾．典型例题十例10已知：，求证：．分析：根据题设，可想到利用重要不等式进行证明．证明：同理：说明：证明本题易出现的思维障碍是：(1)想利用三元重要不等式解决问题；(2)不会利用重要不等式的变式；(3)不熟练证明轮换对称不等式的常用方法．因此，在证明不等式时，应根据求证式两边的结构，合理地选择重要不等式．另外，本题的证明方法在证轮换对称不等式时具有一定的普遍性．典型例题十一例11设，且，，求的最大值．分析：如何将与用不等式的形式联系起来，是本题获解的关键．算术平均数与几何平均数定理两边同加之后得．解：由，则有说明：常有以下错解：，．故．两式相除且开方得．错因是两不等式相除，如，相除则有．不等式是解决从“和”到“积”的形式．从“和”到“积”怎么办呢？有以下变形：或．典型例题十二例12已知：，且：，求证：，并且求等号成立的条件．分析：由已知条件，可以考虑使用均值不等式，但所求证的式子中有，无法利用，故猜想先将所求证的式子进行变形，看能否出现型，再行论证．证明：等号成立，当且仅当时．由以上得即当时等号成立．说明：本题是基本题型的变形题．在基本题型中，大量的是整式中直接使用的均值不等式，这容易形成思维定式．本题中是利用条件将所求证的式子化成分式后再使用均值不等式．要注意灵活运用均值不等式．典型例题十三例13已知，且，求的最大值．分析：由，可得，故，令．利用判别式法可求得（即）的最大值，但因为有范围的限制，还必须综合韦达定理展开讨论．仅用判别式是不够的，因而有一定的麻烦，下面转用基本不等式求解．解法一：由，可得，．注意到．可得，．当且仅当，即时等号成立，代入中得，故的最大值为18．解法二：，，代入中得：解此不等式得．下面解法见解法一，下略．说明：解法一的变形是具有通用效能的方法，值得注意：而解法二则是抓住了问题的本质，所以解得更为简捷．典型例题十四例14 若，且，求证：．分析：不等式右边的数字“8”使我们联想到可能是左边三个因式分别使用基本不等式所得三个“2”连乘而来，而．证明：，又，，，，即．同理，，．当且仅当时，等号成立．说明：本题巧妙利用的条件，同时要注意此不等式是关于的轮换式．典型例题十五例15 设，求证：．分析：本题的难点在于不易处理，如能找出与之间的关系，问题可得到解决，注意到：，则容易得到证明．证明：，于是同理：，．三式相加即得：．说明：注意观察所给不等式的结构，此不等式是关于的轮换式．因此只需抓住一个根号进行研究，其余同理可得，然后利用同向不等式的可加性．典型例题十六例16 已知：（其中表示正实数）求证：分析：要证明的这一串不等式非常重要，称为平方根，称为算术平均数，称为几何平均数，称为调和平均数．证明：∴，当且仅当“”时等号成立．∴，等号成立条件是“”∴，等号成立条件是“”．∴，等号成立条件是“”．说明：本题可以作为均值不等式推论，熟记以上结论有利于处理某些复杂不等式的证明问题．本例证明过程说明，不等式性质中的比较法是证明不等式的最基本、最重要的方法．典型例题十七例17设实数，，，，，满足，，，求证．分析：由条件可得到，，，同号．为方便，不妨都设为正．将求证式子的左边展开后可看出有交叉项和无法利用条件，但使用均值不等式变成乘积后，重新搭配，可利用条件求证．证明：同理，由知与同号，与同号∴，，，同号．不妨都设为正．，即．说明：本题是根据题意分析得，，，同号，然后利用均值不等式变形得证．换一个角度，由条件的特点我们还会联想到使用二次方程根的判别式，可能会有另一类证法．实际上，由条件可知，，，为同号，不妨设同为正．又∵，，∴，．不等式，对任意实数恒成立（根据二次三项式恒为正的充要条件），两式相加得，它对任意实数恒成立．同上可得：．典型例题十八例18 如下图所示，某畜牧基地要围成相同面积的羊圈4间，一面可利用原有的墙壁，其余各面用篱笆围成，篱笆总长为36m．问每间羊圈的长和宽各为多少时，羊圈面积最大？分析：可先设出羊圈的长和宽分别为，，即求的最大值．注意条件的利用．解：设每间羊圈的长、宽分别为，，则有，即．设上式当且仅当时取“＝”．此时∴羊圈长、宽分别为m，3m时面积最大．说明：(1)首先应设出变量（此处是长和宽），将题中条件数学化（即建立数学模型）才能利用数学知识求解；(2)注意在条件之下求积的最大值的方法：直接用不等式，即可出现积．当然，也可用“减少变量”的方法：，当且仅当时取“=”．典型例题十九例19 某单位建造一间地面面积为12m2的背面靠墙的矩形小房，房屋正面的造价为1200元/m2，房屋侧面的造价为800 元/m2，屋顶的造价为5800元．如果墙高为3m，且不计房屋背面的费用，问怎样设计房屋能使总造价最低，最低总造价是多少元？分析：这是一个求函数最小值的问题，关键的问题是设未知数，建立函数关系．从已知条件看，矩形地面面积为12m2，但长和宽不知道，故考虑设宽为m，则长为m，再设总造价为．由题意就可以建立函数关系了．解：设矩形地面的正面宽为m，则长为m；设房屋的总造价为．根据题意，可得：当，即时，有最小值34600元．因此，当矩形地面宽为4m时，房屋的总造价最低，最低总造价是34600元．说明：本题是函数最小值的应用题，这类题在我们的日常生活中经常遇到，有求最小值的问题，也有求最大值的问题，这类题都是利用函数式搭桥，用均值不等式解决，解决的关键是等号是否成立，因此，在解这类题时，要注意验证等号的成立．典型例题二十例20某单位决定投资3200元建一仓库（长方体状），高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每1m长造价40元，两侧墙砌砖，每1m长造价45元，顶部每1m2造价20元．计算：(1)仓库底面积Ｓ的最大允许值是多少？(2)为使Ｓ达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？分析：用字母分别表示铁栅长和一堵砖墙长，再由题意翻译数量关系．解：设铁栅长为m，一堵砖墙长为m，则有.由题意得应用算术平均数与几何平均数定理，得即：从而：因此的最大允许值是，取得此最大值的条件是，而，由此求得，即铁栅的长应是．说明：本题也可将代入（*）式，导出关于的二次方程，利用判别式法求解．典型例题二十一例21甲、乙两地相距，汽车从甲地匀速行驶到乙地，速度不超过，已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度的平方成正比，且比例系数为；固定部分为元．（1）把全程运输成本元表示为速度的函数，并指出这个函数的定义域；（2）为了使全程运输成本最小，汽车应以多大速度行驶？分析：这是1997年的全国高考试题，主要考查建立函数关系式、不等式性质（公式）的应用．也是综合应用数学知识、思想和方法解决实际问题的一道优秀试题．解：（1）依题意知汽车从甲地匀速行驶到乙地所用的时间为，全程运输成本为．故所求函数为，定义域为．（2）由于都为正数，故有，即．当且仅当，即时上式中等号成立．若时，则时，全程运输成本最小；当，易证，函数单调递减，即时，．综上可知，为使全程运输成本最小，在时，行驶速度应为；在时，行驶速度应为．。
数学百大经典例题——球
典型例题一例1．已知地球的半径为R ，球面上B A ,两点都在北纬45圈上，它们的球面距离为R 3π，A 点在东经30上，求B 点的位置及B A ,两点所在其纬线圈上所对应的劣弧的长度．分析：求点B 的位置，如图就是求B AO 1∠的大小，只需求出弦AB 的长度．对于AB 应把它放在OAB ∆中求解，根据球面距离概念计算即可．解：如图，设球心为O ，北纬45圈的中心为1O ， 由B A ,两点的球面距离为R 3π，所以AOB ∠=3π， ∴OAB ∆为等边三角形．于是R AB =．由R R B O A O 2245cos 11=⋅==， 22121AB B O A O =+∴．即B AO 1∠=2π． 又A 点在东经30上，故B 的位置在东经120，北纬45或者西经60，北纬45．B A ,∴两点在其纬线圈上所对应的劣弧R A O ππ4221=⋅． 说明：此题主要目的在于明确经度和纬度概念，及利用球的截面的性质和圆的有关性质设计计算方案．典型例题二例2．用两个平行平面去截半径为R 的球面，两个截面圆的半径为cm r 241=，cm r 152=．两截面间的距离为cm d 27=，求球的表面积．分析：此类题目的求解是首先做出截面图，再根据条件和截面性质做出与球的半径有关的三角形等图形，利用方程思想计算可得．解：设垂直于截面的大圆面交两截面圆于2211,B A B A ，上述大圆的垂直于11B A 的直径交2211,B A B A 于21,O O ，如图2．设2211,d OO d OO ==，则⎪⎩⎪⎨⎧=+=+=+2222222121152427R d R d d d ，解得25=R ．)(2500422cm R S ππ==∴圆．说明：通过此类题目，明确球的有关计算问题需先将立体问题转化为平面问题，进一步熟悉有关圆的基础知识，熟练使用方程思想，合理设元，列式，求解．典型例题三例3．自半径为R 的球面上一点M ，引球的三条两两垂直的弦MC MB MA ,,，求222MCMB MA ++的值．分析：此题欲计算所求值，应首先把它们放在一个封闭的图形内进行计算，所以应引导学生构造熟悉的几何体并与球有密切的关系，便于将球的条件与之相联．解：以MC MB MA ,,为从一个顶点出发的三条棱，将三棱锥ABC M -补成一个长方体，则另外四个顶点必在球面上，故长方体是球的内接长方体，则长方体的对角线长是球的直径．∴222MC MB MA ++=224)2(R R =．说明：此题突出构造法的使用，以及渗透利用分割补形的方法解决立体几何中体积计算．典型例题四例4．试比较等体积的球与正方体的表面积的大小．分析：首先抓好球与正方体的基本量半径和棱长，找出等量关系，再转化为其面积的大小关系． 解：设球的半径为r ，正方体的棱长为a ，它们的体积均为V ，则由ππ43,3433V r V r ==，343πV r =，由,3V a =得3V a =． 322324)43(44V V r S ππππ===球． 32322322166)(66V V V a S ====正方体． ∴<2164π <324V π32216V ，即正方体球S S <．说明：突出相关的面积与体积公式的准确使用，注意比较大小时运算上的设计．典型例题五例5．如图1所示，在棱长为1的正方体内有两个球相外切且又分别与正方体内切．（1）求两球半径之和；（2）球的半径为多少时，两球体积之和最小．分析：此题的关键在于作截面，一个球在正方体内，学生一般知道作对角面，而两个球的球心连线也应在正方体的体对角线上，故仍需作正方体的对角面 ，得如图2的截面图，在图2中，观察R 与r 和棱长间的关系即可．解：如图2，球心1O 和2O 在AC 上，过1O ，2O 分别作BC AD ,的垂线交于F E ,．则由3,1==AC AB 得R CO r AO 3,321==．3)(3=+++∴R r R r ， 233133-=+=+∴r R ． （1）设两球体积之和为V ， 则))((34)(342233r Rr R R r r R V +-+=+=ππ =[]=-+rR r R 3)(233342π⎥⎦⎤⎢⎣⎡--)233(3)233(233342R R π=⎥⎦⎤⎢⎣⎡-+--22)233(2)33(3323334R R π 当433-=R 时，V 有最小值．∴当433-==r R 时，体积之和有最小值．典型例题六例6．设正四面体中，第一个球是它的内切球，第二个球是它的外接球，求这两个球的表面积之比及体积之比．分析：此题求解的第一个关键是搞清两个球的半径与正四面体的关系，第二个关键是两个球的半径之间的关系，依靠体积分割的方法来解决的．解：如图，正四面体ABCD 的中心为O ，BCD ∆的中心为1O ，则第一个球半径为正四面体的中心到各面的距离，第二个球的半径为正四面体中心到顶点的距离．图 1图2设R OA r OO ==,1，正四面体的一个面的面积为S ．依题意得)(31r R S V BCD A +=-， 又S r V V BCD O BCD A ⋅⨯==--3144r r R 4=+∴即r R 3=．所以914422==R r ππ外接球的表面积内切球的表面积．271343433==R rππ外接球的体积内切球的体积． 说明：正四面体与球的接切问题，可通过线面关系证出，内切球和外接球的两个球心是重合的，为正四面体高的四等分点，即定有内切球的半径h r 41=(h 为正四面体的高)，且外接球的半径r R 3=．典型例题七例7．把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离．分析：关键在于能根据要求构造出相应的几何体，由于四个球半径相等，故四个球一定组成正四面体的四个顶点且正四面体的棱长为两球半径之和2．解：由题意，四球心组成棱长为2的正四面体的四个顶点，则正四面体的高362)332(222=⋅-=h ． 而第四个球的最高点到第四个球的球心距离为求的半径1，且三个球心到桌面的距离都为1，故第四个球的最高点与桌面的距离为3622+． 说明：此类型题目对培养学生空间想象能力，并根据题意构造熟悉几何体都非常有帮助，且还可以适当增加一点实际背景，加强应用意识．典型例题八例8 过球面上两点作球的大圆，可能的个数是（ ）． A ．有且只有一个 B ．一个或无穷多个 C ．无数个 D ．以上均不正确分析：对球面上两点及球心这三点的位置关系进行讨论．当三点不共线时，可以作一个大圆；当三点共线时，可作无数个大圆，故选B ．答案：B说明：解此易选出错误判断A ．其原因是忽视球心的位置．典型例题九例9 球面上有3个点，其中任意两点的球面距离都等于大圆周长的61，经过3个点的小圆的周长为π4，那么这个球的半径为（ ）．A ．34B ．32C ．2D ．3分析：利用球的概念性质和球面距离的知识求解．设球的半径为R ，小圆的半径为r ，则ππ42=r ，∴2=r ．如图所示，设三点A 、B 、C ，O 为球心，362ππ==∠=∠=∠COA BOC AOB ．又∵OB OA =，∴AOB ∆是等边三角形，同样，BOC ∆、COA ∆都是等边三角形，得ABC ∆为等边三角形，边长等于球半径R ．r 为ABC ∆的外接圆半径，R AB r 3333==，3233==r R ．答案：B说明：本题是近年来球这部分所出的最为综合全面的一道题，除了考查常规的与多面体综合外，还考查了球面距离，几乎涵盖了球这部分所有的主要知识点，是一道不可多得的好题．典型例题十例10 半径为R 的球内接一个各棱长都相等的四棱锥．求该四棱锥的体积．分析：四棱锥的体积由它的底面积和高确定，只需找到底面、高与球半径的关系即可，解决这个问题的关键是如何选取截面，如图所示．解：∵棱锥底面各边相等， ∴底面是菱形． ∵棱锥侧棱都相等，∴侧棱在底面上射影都相等，即底面有外接圆．∴底面是正方形，且顶点在底面上的射影是底面中心，此棱锥是正棱锥．过该棱锥对角面作截面，设棱长为a ，则底面对角线a AC 2=，故截面SAC 是等腰直角三角形．又因为SAC 是球的大圆的内接三角形，所以R AC 2=，即R a 2=．∴高R SO =，体积33231R SO S V =⋅=底． 说明：在作四棱锥的截面时，容易误认为截面是正三角形，如果作平等于底面一边的对称截面（过棱锥顶点，底面中心，且与底面一边平行），可得一个腰长为斜高、底为底面边长的等腰三角形，但这一等腰三角形并不是外接球大圆的内接三角形．可见，解决有关几何体接切的问题，如何选取截面是个关键．解决此类问题的方法通常是先确定多面体的棱长（或高或某个截面内的元素）与球半径的关系，再进一步求解．典型例题十一例11 在球面上有四个点P 、A 、B 、C ，如果PA 、PB 、PC 两两互相垂直，且a PC PB PA ===．求这个球的表面积．分析：24R S π=球面，因而求球的表面关键在于求出球的半径R ． 解：设过A 、B 、C 三点的球的截面半径为r ， 球心到该圆面的距离为d ， 则222d r R +=．由题意知P 、A 、B 、C 四点不共面，因而是以这四个点为顶点的三棱锥ABC P -（如图所示）．ABC ∆的外接圆是球的截面圆．由PA 、PB 、PC 互相垂直知，P 在ABC 面上的射影'O 是ABC ∆的垂心，又a PC PB PA ===，所以'O 也是ABC ∆的外心，所以ABC ∆为等边三角形， 且边长为a 2，'O 是其中心， 从而也是截面圆的圆心．据球的截面的性质，有'OO 垂直于⊙'O 所在平面，因此P 、'O 、O 共线，三棱锥ABC P -是高为'PO 的球内接正三棱锥，从而'PO R d -=．由已知得a r 36=，a PO 33'=，所以2'2222)(PO R r d r R -+=+=，可求得a R 23=，∴2234a R S ππ==球面．说明：涉及到球与圆柱、圆锥、圆台切接问题，一般作其轴截面；涉及到球与棱柱、棱锥、棱台的切接问题，一般过球心及多面体中特殊点或线作截面，把空间问题化为平面问题，进而利用平面几何的知识寻找几何体元素间的关系．典型例题十二例12 已知棱长为3的正四面体ABCD ，E 、F 是棱AB 、AC 上的点，且FC AF 2=，AE BE 2=．求四面体AEFD 的内切球半径和外接球半径．分析：可用何种法求内切球半径，把AEF D V -分成4个小体积(如图)．解：设四面体AEFD 内切球半径为r ，球心N ，外接球半径R ，球心M ，连结NA 、NE 、NF 、ND ，则EFD N AD E N AFD N AEF N AEFD V V V V V ----+++=．四面体AEFD 各面的面积为2392==∆∆ABC AEF S S ，23332==∆∆ABC AFD S S ，43331==∆∆ABC AED S S ． DEF ∆各边边长分别为3=EF ，7==DE DF ，∴345=∆DEF S ． ∵2292==ABCD ADEF V V ， )(31DEF AED AFD AEF AEFD S S S S r V ∆∆∆∆+++=，∴)43543323323(3122+++=r ，∴86=r ． 如图，AEF ∆是直角三角形，其个心是斜边AF 的中点G ．设ABC ∆中心为1O ，连结1DO ，过G 作平面AEF 的垂线，M 必在此垂线上， 连结1GO 、MD ．∵ABC MG 平面⊥，ABC DO 平面⊥1， ∴1//DO MG ，1GO MG ⊥．在直角梯形DM GO 1中，11=GO ，61=DO ，R MD =，1222-=-=R AG AM MG ，又∵22121)(MD GO MG DO =+-，∴2221)16(R R =+--， 解得：210=R ． 综上，四面体AEFD 的内切球半径为86，外接球半径为210． 说明：求四面体外接半径的关键是确定其球心．对此多数同学束手无策，而这主要是因本题图形的背景较复杂．若把该四面体单独移出，则不参发现其球心在过各面三角形外心且与该三角形所在平面垂直的直线上，另还须注意其球心不一定在四面体内部．本题在求四面体内切球半径时，将该四面体分割为以球心为顶点，各面为底面的四个三棱锥，通过其体积关系求得半径．这样分割的思想方法应给予重视．典型例题十三例13 一个倒圆锥形容器，它的轴截面是正三角形，在容器内注入水，并放入一个半径为r 的铁球，这时水面恰好和球面相切．问将球从圆锥内取出后，圆锥内水平面的高是多少？分析：先作出轴截面，弄清楚圆锥和球相切时的位置特征，利用铁球取出后，锥内下降部分(圆台)的体积等于球的体积，列式求解．解：如图，作轴截面，设球未取出时，水面高h PC =，球取出后，水面高x PH =． ∵r AC 3=，r PC 3=， 则以AB 为底面直径的圆锥容积为PC AC V ⋅⋅=231π圆锥3233)3(31r r r ππ=⋅=， 334r V π=球．球取出后，水面下降到EF ，水的体积为32291)30tan (3131x PH PH PH EH V πππ=︒=⋅⋅=水．又球圆锥水V V V -=，则33334391r r x πππ-=，解得r x 315=．答：球取出后，圆锥内水平面高为r 315．说明：抓住水的何种不变这个关键，本题迅速获解．典型例题十四例14 球面上有三点A 、B 、C 组成这个球的一个截面的内接三角形三个顶点，其中18=AB ，24=BC 、30=AC ，球心到这个截面的距离为球半径的一半，求球的表面积．分析：求球的表面积的关键是求球的半径，本题的条件涉及球的截面，ABC ∆是截面的内接三角形，由此可利用三角形求截面圆的半径，球心到截面的距离为球半径的一半，从而可由关系式222d R r -=求出球半径R ．解：∵18=AB ，24=BC ，30=AC ，∴222AC BC AB =+，ABC ∆是以AC 为斜边的直角三角形． ∴ABC ∆的外接圆的半径为15，即截面圆的半径15=r ，又球心到截面的距离为R d 21=， ∴22215)21(=-R R ，得310=R ．∴球的表面积为πππ1200)310(4422===R S ． 说明：涉及到球的截面的问题，总是使用关系式22d R r -=解题，我们可以通过两个量求第三个量，也可能是抓三个量之间的其它关系，求三个量．例如，过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ，且两两夹角都为︒60，若球半径为R ，求弦AB 的长度．由条件可抓住BCD A -是正四面体，A 、B 、C 、D 为球上四点，则球心在正四面体中心，设a AB =，则截面BCD 与球心的距离R a d -=36，过点B 、C 、D 的截面圆半径a r 33=，所以222)36()33(R a R a --=得R a 362=． 典型例题十五例15 A 、B 是半径为R 的球O 的球面上两点，它们的球面距离为R 2π，求过A 、B 的平面中，与球心的最大距离是多少？分析：A 、B 是球面上两点，球面距离为R 2π，转化为球心角2π=∠AOB ，从而R AB 2=，由关系式222d R r -=，r 越小，d 越大，r 是过A 、B 的球的截面圆的半径，所以AB 为圆的直径，r 最小．解：∵球面上A 、B 两点的球面的距离为R 2π．∴2π=∠AOB ，∴R AB 2=．当AB 成为圆的直径时，r 取最小值，此时R AB r 2221==，d 取最大值， R r R d 2222=-=， 即球心与过A 、B 的截面圆距离最大值为R 22． 说明：利用关系式222d R r -=不仅可以知二求一，而且可以借此分析截面的半径r 与球心到截面的距离d 之间的变化规律．此外本题还涉及到球面距离的使用，球面距离直接与两点的球心角AOB ∠有关，而球心角AOB ∠又直接与AB 长度发生联系，这是使用或者求球面距离的一条基本线索，继续看下面的例子．典型例题十六例16 正三棱锥的高为1，底面边长为62，正三棱锥内有一个球与其四个面相切．求球的表面积与体积．分析：球与正三棱锥四个面相切，实际上，球是正三棱锥的内切球，球心到正三棱锥的四个面的距离相等，都为球半径R ．这样求球的半径可转化为球球心到三棱锥面的距离，而点面距离常可以用等体积法解决．解：如图，球O 是正三棱锥ABC P -的内切球，O 到正三棱锥四个面的距离都是球的半径R ．PH 是正三棱锥的高，即1=PH ．E 是BC 边中点，H 在AE 上，ABC ∆的边长为62，∴26263=⨯=HE ． ∴3=PE 可以得到2321=⋅===∆∆∆PE BC S S S PBC PAC PAB ． 36)62(432==∆ABC S 由等体积法，ABC O PBC O PAC O PAB O ABC P V V V V V -----+++= ∴R R ⨯⨯+⨯⨯⨯=⨯⨯363132********得：2633232-=+=R ， ∴πππ)625(8)26(4422-=-==R S 球． ∴33)26(3434-==ππR V 球． 说明：球心是决定球的位置关键点，本题利用球心到正三棱锥四个面的距离相等且为球半径R 来求出R ，以球心的位置特点来抓球的基本量，这是解决球有关问题常用的方法．比如：四个半径为R 的球两两外切，其中三个放在桌面上，第四个球放在这三个球之上，则第四个球离开桌面的高度为多少？这里，四个球的球心这间的距离都是R 2，四个球心构成一个棱长为R 2的正四面体，可以计算正四面体的高为R R 362236=⨯，从而上面球离开桌面的高度为R R 3622+． 典型例题十七例17 求球与它的外切圆柱、外切等边圆锥的体积之比．分析：首先画出球及它的外切圆柱、等边圆锥，它们公共的轴截面，然后寻找几何体与几何体之间元素的关系．解：如图，等边SAB ∆为圆锥的轴截面，此截面截圆柱得正方形11CDD C ，截球面得球的大圆圆1O ． 设球的半径R OO =1，则它的外切圆柱的高为R 2，底面半径为R ；R O O OB 330cot 1=︒⋅=，R R OB SO 33360tan =⋅=︒⋅=， ∴334R V π=球，3222R R R V ππ=⋅=柱， 3233)3(31R R R V ππ=⋅⋅=锥， ∴964∶∶∶∶锥柱球=V V V ．典型例题十八例18 正三棱锥ABC P -的侧棱长为l ，两侧棱的夹角为α2，求它的外接球的体积．分析：求球半径，是解本题的关键．解：如图，作⊥PD 底面ABC 于D ，则D 为正ABC ∆的中心．∵⊥OD 底面ABC ，∴O 、P 、D 三点共线．∵l PC PB PA ===，α2=∠APB ． ∴ααsin 22cos 2222l l l AB =-=． ∴αsin 33233==AB AD ， 设β=∠APD ，作PA OE ⊥于E ，在APD Rt ∆中， ∵αβsin 332sin ==PA AD ， 又R OA OP ==，∴l PA PE 2121==． 在POE Rt ∆中，∵αβ2sin 3412cos -===lPE PO R ， ∴)sin 43(2sin 433sin 34123422332ααπαπ--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=l l V 球． 说明：解决与球有关的接、切问题时，一般作一个适当的截面，将问题转化为平面问题解决，这类截面通常指圆锥的轴截面、球的大圆、多面体的对角面等，在这个截面中应包括每个几何体的主要元素，且这个截面必须能反映出体和体之间的主要位置关系和数量关系． 典型例题十九例19 在球心同侧有相距cm 9的两个平行截面，它们的面积分别为249cm π和2400cm π．求球的表面积．分析：可画出球的轴截面，利用球的截面性质，求球的半径．解：如图为球的轴截面，由球的截面性质知，21//BO AO ，且若1O 、2O 分别为两截面圆的圆心，则11AO OO ⊥，22BO OO ⊥．设球的半径为R ．∵ππ4922=⋅B O ，∴)(72cm B O =同理ππ40021=⋅A O ，∴)(201cm A O =设xcm OO =1，则cm x OO )9(2+=．在A OO Rt 1∆中，22220+=x R ；在B OO Rt 2∆中，2227)9(++=x R ，∴222)9(720++=+x x ，解得15=x ，∴22222520=+=x R ，∴25=R ∴)(2500422cm R S ππ==球．∴球的表面积为22500cm π．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
典型例题一例1 三条直线两两相交，由这三条直线所确定平面的个数是（ ）． A ．1 B ．2 C ．3 D ．1或3分析：本题显然是要应用推论2判断所能确定平面的个数，需要在空间想象出这三条直线所有不同位置的图形，有如下图的三种情况（如图）：答案：D ．说明：本题启发我们考虑问题不要只局限于平面图形，应养成在三维空间考虑问题的习惯．典型例题二例2 一条直线与三条平行直线都相交，求证这四条直线共面．分析：先将已知和求证改写成符号语言．证明诸线共面，可先由其中的两条直线确定一个平面，然后证明其余的直线均在此平面内．也可先由其中两条确定一个平面α，另两条确定平面β，再证平面α，β重合．已知：c b a ////，A a l = ，B b l = ，C c l = ． 求证：直线a ，b ，c ，l 共面． 证明： ∵ b a //，∴ a ，b 确定一个平面α． ∵ A a l = ，B b l = ， ∴ α∈A ，α∈B ，故α⊂l ．又 ∵ c a //， ∴ a ，c 确定一个平面β． 同理可证β⊂l ．∴ a =βα ，且l =βα ．∵ 过两条相交直线a ，l 有且只有一个平面，故α与β重合即直线a ，b ，c ，l 共面．说明：本例是新教材第9页第9题的一个简单推广，还可推广到更一般的情形．本例证明既采用了归一法，同时又采用了同一法．这两种方法是证明线共面问题的常用方法．在证明α⊂c 时，也可以用如下反证法证明：假设直线α⊄c ，则c 一定与α相交，此时直线c 与a 内的所有直线都不会平行，这显然与c a //矛盾．故α⊂c ．典型例题三例3 已知ABC ∆在平面α外，它的三边所在的直线分别交平面α于P ，Q ，R 三点，证明P ，Q ，R 三点在同一条直线上．分析：如图所示，欲证P ，Q ，R 三点共线，只须证P ，Q ，R 在平面α和平面ABC ∆的交线上，由P ，Q ，R 都是两平面的公共点而得证．证明：∵ P AB =α ，Q BC =α ， ∴ PQ 是平面α与平面ABC 的交线． 又 ∵ R AC =α ，∴ α∈R 且∈R 平面ABC ， ∴ PQ R ∈，∴ P ，Q ，R 三点共线．说明：证明点共线的一般方法是证明这些点是某两个平面的公共点，由公理2，这些点都在这两平面的交线上．典型例题四例4 如图所示，ABC ∆与111C B A ∆不在同一个平面内，如果三直线1AA 、1BB 、1CC 两两相交，证明：三直线1AA 、1BB 、1CC 交于一点． 分析：证明三线共点的一般思路是：先证明两条直线交于一点，再证明该点在第三条直线上即可．证明：由推论2，可设1BB 与1CC ，1CC 与1AA ，1AA 与1BB 分别确定平面α，β，γ．取P BB AA =11 ，则1AA P ∈，1BB P ∈． 又因1CC =βα ，则1CC P ∈（公理2）， 于是P CC BB AA =111 ，故三直线1AA 、1BB 、1CC 共点．说明：空间中证三线共点有如下两种方法：（1）先确定两直线交于一点，再证该点是这两条直线所在两个平面的公共点，第三条直线是这两个平面的交线，由公理2，该点在它们的交线上，从而得三线共点．（2）先将其中一条直线看做是某两个平面的交线，证明该交线与另两直线分别交于两点，再证这两点重合．从而得三线共点．典型例题五（1）不共面的四点可以确定几个平面？（2）三条直线两两平行但不共面，它们可以确定几个平面？ （3）共点的三条直线可以确定几个平面？ 分析：（1）可利用公里3判定。
（2）可利用公里3的推论3判定。
（3）需进行分类讨论判定。
解：（1）不共面的四点可以确定四个平面。
（2）三条直线两两平行但不共面，它们可以确定3个平面。
（3）共点的三条直线可以确定1个或3个平面。
说明：判定平面的个数问题关键是要紧紧地抓住已知条件，要做到不重不漏。
平面的确定问题主要是根据已知条件和公里3及其3个推论来判定平面的个数。
典型例题六例6 A 、B 、C 为空间三点，经过这三点：A ．能确定一个平面B ．能确定无数个平面C ．能确定一个或无数个平面D ．能确定一个平面或不能确定平面 分析：本题考查空间确定平面的方法，解题的主要依据是公理3及三个推论． 解：由于题设中所给的三点A 、B 、C 并没有指明这三点之间的位置关系， 所以在应用公理3时要注意条件“不共线的三点”．当A 、B 、C 三点共线时，经过这三点就不能确定平面，当A 、B 、C 三点不共线时，经过这三点就可以确定一个平面，故选D ．说明：空间确定一平面的方法有多种，既可以根据不共线的三点来确定一个平面，又可以根据空间两相交直线或两平行直线来确定一个平面．典型例题七例7 判断题（答案正确的在括号内打“√”号，不正确的在括号内打“×”号）．(1)两条直线确定一个平面；（ ）(2)经过一点的三条直线可以确定一个平面；（ ） (3)两两相交的三条直线不共面；（ ）(4)不共面的四点中，任何三点不共线．（ ）分析：(1)两条直线能否确定平面，应注意这两条直线的位置关系，不给出位置关系则要分情况讨论，才可得出结论．两条相交直线可确定一个平面，两条平行直线可确定一个平面，除此以外的任何两条直线不能确定平面；(2)经过一点的两条直线可确定一个平面，三条直线不一定能确定平面； (3)三条直线两两相交，若不共点时这三条直线必共面；(4)如果有三点共线，则此三点所在直线与第四点必同在某一平面内，即四点共面． 解：(1)× (2)× (3)× (4)√．说明：由(3)题的分析过程可知：两两相交的三条直线有时共面有时不共面．那么对于空间四条直线何时共面何时不共面呢？典型例题八例8 如图，在正方体1111D C B A ABCD 中，点E 、F 分别是棱1AA 、1CC 的中点，试画出过点1D 、E 、F 三点的截面．分析：本题考查作多面体截面的能力，主要依据是公理1和公理2欲画出所要求的截面与正方体各个侧面的交线．解：连F D 1并延长F D 1与DC 的延长线交于点H ，连结E D 1与DA 的延长线交于点G ，连结GH 与AB 、BC 两条棱交于点B ，连结BE 、BF ，则F BED 1就是过点1D 、E 、F 三点的截面．说明：本题亦可以证明点B 、E 、1D 、F 四点共面．若E 、F 不是棱A A 1与C C 1的中点，则作图过程中GH 不一定过点B ，所画的截面多边形可能是五边形．典型例题九例9 判断下列说法是否正确？并说明理由．(1)平行四边形是一个平面．(2)任何一个平面图形都是一个平面．(3)空间图形中先画的线是实线，后画的线是虚线．解：(1)不正确．平行四边形它仅是平面上四条线段构成的图形，它是不能无限延伸的． 说明：在立体几何中，我们通常用平行四边形表示平面，但绝不是说平行四边形就是平面．(2)不正确．平面图形和平面是完全不同的两个概念，平面图形是有大小，它是不可能无限延展的．说明：要严格区分“平面图形”和“平面”这两个概念．(3)不正确．在空间图形中，我们一般是把能够看得见的线画成实线，把被平面遮住看不见的线画成虚线（无论是题中原有的，还是后引的辅助线）．说明：在平面几何中，凡是后引的辅助线都画成虚线；在立体几何中却不然．有的同学在学习立体几何时，对此点没有认识，必将影响空间立体感的形成，削弱或阻断空间想象能力的培养．典型例题十例10按照给出的要求，完成下面两个相交平面的作图，如下图的(1)、(2)、(3)、(4)、(5)、(6)中的线段AB，分别是两个平面的交线．解：由两个相交平面的画法：本题只须过线段的端点画出与交线AB平行且相等的线段，即可得到相关的平行四边形，注意被平面遮住的部分应画成虚线或者不画，然后在相关的平面上标上表示平面的字母即可如下图所示．说明：(1)画好两个相交平面的图形，是画好一切立体图形的基础．(2)画空间图形的过程，是培养我们空间想象能力的过程，一定要认真对待，决不可以掉以轻心．典型例题十一例11(1)一个平面将空间分成几部分？(2)两个平面将空间分成几部分？(3)三个平面将空间分成几部分？画出图形，（要求：至少有两种情况有画法过程） 解：(1)一个平面将空间分成两部分．(2)两个平面平行时，将空间分成三部分，两个平面相交时，将空间分成四部分．(3)本小题情况比较复杂，须分类予以处理．情况1：当平面α、平面β、平面γ互相平行（即γβα////），将空间分成四个部分，其图形如右图．情况2：当平面α与平面β平行，平面γ与它们相交（即βα//，γ与其相交），将空间分成六部分，其图形如下图． 画法是：情况3：当平面α、平面β、平面γ都相交，且三条交线重合（即l =βα 且l =γα ） 将空间分成六部分，其图形如下图．说明：本种情况给出两种图形，一种是将交线画成水平状态，一种是将交线画成竖直状态．情况4：平面α、平面β、平面γ都相交且三条交线共点，但互不重合．（即l =γα ，且γ与α、β都相交，三条交线共点）．将空间分成八部分，其图形如下图． 画法是：情况5：平面α、平面β、平面γ两两相交且三条交线平行（即l =βα ，γ与α、β都相交且三条交线平行）．将空间分成七部分，其图形如下图．说明：1．本小题(3)，在解答过程中，采用了简单到复杂递进的处理方法，首先对两个平面在空间的位置分类讨论，再让第三个平面以不同情况介入，然后分类解决．2．通过此题的解答，要学会处理问题的思维方法，注意逻辑思维能力的培养与提高．3．本题是一个基础性很强的问题，无论是对立体图形的画法以及空间想象能力的形成都大有裨益．典型例题十二例12下图中表示两个相交平面，其中画法正确的是（）．解：对于A，图中没有画出平面α与平面β的交线，另外图中的实、虚线也没有按照画法原则去画，因此A的画法不正确．同样的道理，也可知B、C图形的画法不正确．D的图形画法正确．∴应选D．说明：对空间图形的准确辨识，是培养空间想象能力的重要组成部分，一定要注意这方面能力的锻炼．典型例题十三例13观察下图，说明图形中的不同之处．解：上面的图形都是由九条线段构成的图形、外形似乎相似．仔细观察，由于图中的实、虚线的画法不同，则反映了不同的几何体．A图是一个簸箕形图形；B图是体，是三棱柱；C图也是体，也是三棱柱．B图如果看作是从三棱柱的正面观察，C图则可看作是从三棱柱的后面观察．说明：在立体几何中，一定要明确画图过程中哪条线画实线，哪条线画虚线．要记住：能够看得到的线一定画成实线，被挡住的看不到的线画成虚线．下面再给出两组图形如下图所示，请同学们予以辨识，指出它们有什么不同．典型例题十四例14 若点Q 在直线b 上，b 在平面β内，则Q 、b 、β之间的关系可记作（ ）．A ．β∈∈b QB ．β⊂∈b QC ．β⊂⊂b QD ．β∈⊂b Q 解法1：（直接法）∵点Q 在直线b 上，∴b Q ∈， ∵直线b 在平面β内，∴β⊂b ， ∴β⊂∈b Q ． ∴应选B ． 解法2：（排除法）∵点Q 与直线b 之间的关系是元素与集合之间的关系， ∴只能用符号“∈”或“∉”表示， ∴C 、D 应予排除．∵直线b 与平面β之间是集合与集合之间的关系， ∴只能用符号“⊂”或“⊄”表示， ∴A 应予以排除．综上可知应选B ．说明：要能正确地使用点、直线、平面之间关系的符号语言．典型例题十五例15 用符号语言表示下列语句(1)点A 在平面α内，但在平面β外； (2)直线a 经过平面α外一点M ；(3)直线a 在平面α内，又在平面β内，即平面α和β相交于直线a ． 解：(1)α∈A 但β∉A ．(2)α∉M ，a M ∈．(3)α⊂a 且β⊂a ，即a =βα ．说明：符号语言比较简洁、严谨，可大大的缩短文字语言表达的长度，有利于推理、计算．典型例题十六例16 将下面用符号语言表示的关系改用文字语言予以叙述，并用用图形语言予以表示．βαβα⊂⊂∈=AC AB l A l ,,, ．分析：本题实质是数学三种语言——符号语言、文字语言、图形语言的互译． 解：文字语言叙述为：点A 在平面α与平面β的交线l 上，AB 、AC 分别在α、β内． 图形语言表示为如图：说明：文字语言比较自然、生动，它能将问题所研究的对象的含义更加明白地叙述出来，我们教科书上的概念、定理等多以文字语言叙述．图形语言，易引起清晰的视觉形象，它能直观地表达概念、定理的本质以及相互关系，在抽象的数学思维面前起着具体化和加深理解的作用．各种数学语言间的互译可为我们在更广阔的思维领域里寻找问题解决的途径提供方便．有利于培养我们思维的广阔性．典型例题十七例17 如下图中ABC ∆，若AB 、BC 在平面α内，判断AC 是否在平面α内．解：∵AB 在平面α内， ∴A 点一定在平面α内． ∵BC 在平面α内，∴C 点一定在平面α内．∴点A 、点C 都在平面α内． ∴直线AC 在平面内（公理1）．说明：公理1可以用来判断直线是否在平面内．典型例题十八例18 如下图，在正方体1111D C B A ABCD -中，E 、F 分别为1CC 和1AA 上的中点，画出平面F BED 1与平面ABCD 的交线．分析：可根据公理2，如果两个平面有一个公共点，它们就有过这点的一条直线，也只有这一条直线；这条直线的位置还须借助于另一个条件来确定．解：在平面D D AA 11内，延长F D 1， ∵F D 1与DA 不平行，因此F D 1与DA 必相交于一点，设为P 则1FD P ∈，DA P ∈．又∵⊂1FD 平面F BED 1，⊂AD 平面ABCD 内， ∴∈P 平面F BED 1，∈P 平面ABCD ． 又B 为平面ABCD 与平面F BED 1的公共点，∴连结PB ，PB 即为平面F BED 1与平面ABCD 的交线．说明：公理2是两个平面相交的性质，它说明两个平面相交，交线是一条直线．要注意理解两个平面不存在只有一个公共点的情形，如果有一个公共点，那么必定有无数多个公共点，且这些点恰好组成一条直线．同时要注意，找到两个平面的一个公共点，交线的具体位置还无法判定，只有找到两个公共点，才确定这两个平面的交线．这是做几何体截面时确定交线经常用到的方法．典型例题十九例19 已知E 、F 、G 、H 分别是空间四边形ABCD （四条线段首尾相接，且连接点不在同一平面内．所组成的空间图形叫空间四边形．）各边AB 、AD 、CB 、CD 上的点，且直线EF 和HG 交于点P ，如下图，求证：点B 、D 、P 在同一条直线上．证明：如图∵直线EF 直线PHG=，∴P∈直线EF，而EF⊂平面ABD，∴P∈平面ABD．同理，P∈平面CBD，即点P是平面ABD和平面CBD的公共点．显然，点B、D也是平面ABD和平面CBD的公共点，由公理2知，点B、D、P都在平面ABD和平面CBD的交线上，即点B、D、P在同一条直线上．说明：证明三点共线通常采用如下方法：方法1是首先找出两个平面，然后证明这三点都是这两个平面的公共点，根据公理2知，这些点都在交线上．方法2是选择其中两点确定一条直线，然后证明另一点在其上．。