电磁波测距三角高程测量
三角高程测量

中铁七局集团武汉工程有限公司测绘分公司
专业、专注、专心
勇于跨越 追求卓越
1、基本要求
1.1布设原则: 1.1.1以高程导线布设测区的基本高程控制,其等级应与测区范围相适 应,满足加密需要,一般应与国家水准点连测。 1.1.2导线水准点的高程,采用正常高系统和“1985国家高程基准”。 1.1.3各等级高程导线网的最弱点相对于高等级点(或起始点)的高程 中误差不超过0.05m。 1.1.4高程导线一般应在高级点间布设成附合路线或高程导线网。当测 区远离国家水准点时,也可布设支线引测国家水准点高程,作为测区的 高程起算点。 1.1.5当采用支线引测高程时,引测路线的等级不应低于测区基本高程 控制等级。引测高程的起算点必须进行检测。引测支线的长度可按表1 的规定放宽0.5倍。 1.1.6高程导线测量可与同等级水准测量混合使用,但在同一测段中只 能使用一种方法。
专业、专注、专心
勇于跨越 追求卓越
两点距离D>300m时,考虑地球曲率和大气折光的影响
地球曲率的影响:
c D2 2R
大气折光的影响: 综合两项的影响:
r k D2 2R
f c - r (1 k)D2 2R
当D=300m,K取0.14时,f≈5.9mm
中铁七局集团武汉工程有限公司测绘分公司
1、边长误差 边长误差决定于距离丈量方法。用普通视距法测定距离,精度只有
1/300;用电磁波测距仪测距,精度很高,边长误差一般为几万分之一到 几十万分之一。边长误差对三角高程的影响与垂直角大小有关,垂直角愈 大,其影响也愈大。因此,尽可能利用短边传算高程。
2、垂直角误差 垂直角观测误差包括仪器误差、观测误差和外界环境的影响。垂直
环线或附合路线闭合差
电磁波测距三角高程测量

6.4.1 解算原理和计算公式
3、由电磁波实测斜距和单向垂直角计算两点间高差 、
h12 = S sin α12 + I1 V2 + CS 2 cos 2 α12 NC = S sin α12
若顾及ε角,用正弦定理计算:
ε2 S sin α12 NC = = S sin α12 (1 + ) sin(90 + ε ) 2 δh = S sin α12 ε2
2 S 02 (1 + tg 2 β ) + 2tgβ (m n + p ) S 0 + (m n + p ) 2 S12 = 0
6.4.1 解算原理和计算公式
解得,平距为:
S0 =
2 S12 (1 + tg 2 β ) (m n + p ) 2 tgβ (m n + p ) 1 + tg 2 β
2
该公式误差很小。
S = 10km, α12 = 30 , 求得:δh = 0.0006m S = 10km, α12 = 50 , 求得:δh = 0.0010m
6.4.1 解算原理和计算公式
PC = S cos α12
ε2 ε2 S sin(90 α12 ε ) PC = = S[cos α12 (1 ) ε sin α12 ](1 + ) sin(90 + ε ) 2 2 = S cos α12 Sε sin α12 δS = Sε sin α12
ε2
2
= P C tgα12 (1 + tgα12ε +
ε2
2
) = P C tgα12 + δh
近似公式引入的误差为: δh = P C tgα12 (tgα12ε + 当 PC = 10km, α12 = 30 , 求得:δh = 0.043m
三角高程测量有关问题

jiaoshi三角高程随全站仪使用越来越普及,三角高程广泛用于工程测量的各个阶段.它的精度在一定情况下是可以代替水准高程的.大家做过什么样的三角高程呢?在测量过程中我们要注意些什么呢?使用不同的仪器进行三角高程测量的计算不完全一样,为什么呢?这主是测距仪与十字丝是否同轴的原因引起的。
在用徕卡系列的仪器进行三角高程测量时,由于仪器测距仪的中心与十字丝中心是同轴的,所以计算的角度和距离都不用进行测距仪与十字丝中心的改正!其它的测量距仪就要进行类似的改正。
FZFZFZ1968三角高程的高差计算原理公式,(不考虑球差改正)h=S*tgα+i-v其误差计算公式mh=√( ms*sinα)^2+(S*mα*cosα/ρ)^2+ mi^2+mv^2 2楼从中我们可以看出三角高程的误差主要是垂直角的大小、垂直角的测量误差、距离的长短在实地测量时一定要注意垂直角的观测精度,他对高差精度的影响最大,如果是用全站仪观测,更要注意,多观测几个回合是非常有必要的三角高程测量示意图jiaoshi水电水利工程施工测量规范(DL/T5173-2003)中的误差公式与你的公式略有不同,公式如下:m h=√( ms*sinα)^2+(S*mα*cosα/ρ)^2+ mi^2+mv^2+D^4/4R^2*mk^2增加了一个大气折光系统测量误差。
考虑球差高差计算公式是:h=S*cosZ+i-v+(1-K)S^2/2/R*SIN^2Z上式中:Z:归算到测距时的天顶距(度)K:大气折光系数(0.08至0.14)R:平均曲率半径6369000M另:在三角高程的计算时一定要考虑地球曲率和大气折光对高差的改正!下面两个点是我们做过的两个导线点,观测数据如下:站A测B:S=1187.98米,天顶距:95度58分18秒站B测A:S=1187.9768米,天顶距:84度02分8秒棱镜与仪器同高,如果按2楼的公式计算往返高差相差14.9厘米.FZFZFZ1968在三角高程的计算时要考虑地球曲率和大气折光对高差的改正是对的,但不是一定,至于你说的你所测的一对数据按我写的公式计算往返高差相差14.9厘米,我认为这绝不是因为没有经过两差改正的原因,那你按经过两差改正的高差分别又是多少呢,请你把完整的计算过程写出来,让看看到底经过改正和没有经过改正的高差分别相差jiaoshi站A测B:S=1187.98米,天顶距:95度58分18秒站B测A:S=1187.9768米,天顶距:84度02分8秒棱镜高与仪器高均相同高度一、用公式:h=S*tgα+i-v计算站A测B:GC=-123.5935米站B测A:GC=123.4444米相差:-0.1491米二、用公式:h=S*cosZ+i-v+(1-K)S^2/2/R*SIN^2Z站A测B:GC=-123.4981米站B测A:GC=123.4824米相差:-0.0157米计算说明:1、天顶距及斜距均采用TCR702进行测量,天顶距无需进行归算,斜距的温度与气压改正由全站仪完成;2、表中K值取0.13。
电磁波测距三角高程测量在水文测量中的应用

电磁波测距三角高程测量在水文测量中的应用发布时间:2021-07-26T10:26:05.647Z 来源:《科学与技术》2021年第9期作者:王泽群李国强[导读] 本文重点探究电磁波测距和三角高程测量在水文测量中的具体应用,进一步分析其测量精度,以供参考。
王泽群李国强黄河水利委员会西峰水文水资源勘测局甘肃省庆阳市西峰区 745000摘要:水文测量是一项关乎社会经济发展的重要工作,但由于测量工作往往在山区进行,会受到山区地形、地势等因素影响,导致测量速度较慢,工作效率较低。
随着科学技术的不断进步与发展,水文测量中所应用的技术及方式也更加先进,有研究和相关实践表明,将电磁波测距应用于水文测量中,能够大大降低测量人员的工作强度,提高工作效率,基于此,本文重点探究电磁波测距和三角高程测量在水文测量中的具体应用,进一步分析其测量精度,以供参考。
关键字:电磁波测距;三角高程测量;水文测量;应用在水文测量中,水准测量是最重要的工作内容,利用水平视线来进行几何水准测量,需要大量的测量仪器与设备,不仅工作强度大,工作效率也较为低下。
加上当今时代水文站网的不断发展,站点逐渐增多,使得水准测量工作日渐繁重,对此,相关单位及工作人员需要不断提高自身专业知识与技能水平的掌握程度,大力学习先进技术与设备使用,以期能够逐步降低工作强度,提高工作效率。
一、电磁波测距仪的工作原理近年来,电磁波测距在诸多测量工作中应用广泛,像是城市规划测量、建筑测量等,测距仪精度也受到社会各界的关注。
根据电磁波载波的不同,测距仪主要分为微波测距仪和光电测距仪两种,而根据电磁波传播方式的不同,光电测距仪又可以分为相位式、脉冲式、脉冲-相位比较法三种,且就目前的电磁波测距仪测量精度而言,能够提高到1公分上下,基本上能够满足当下大部分需要精密测距的测量要求。
其中,脉冲-相位比较法是最新的测距技术,具有测程远、测距精度较高的应用优势,也是近几年众多研究专家与学者眼中的宠儿,但与此同时,该测距仪也存在生产成本较高,技术难度较大的不足,实际应用仍十分受限。
电磁波测距三角高程测量施澜的主要技术要求应符合下列规定

电磁波测距三角高程测量施澜的主要技术要求应符合下列规定:
1 三角高程测量边长的测定,应采用符合本规范表4.7.1规定的相应精度等级的电磁波测距仪往返观测各2测回。
当采取中间设站观测方式时,前,后视各观测2测回。
测距的各项限差和要求应符合本规范第4.7节的要求;
2 垂直角观测应采用觇牌为照准目标,按表4.5.4的要求采用中丝双照准法观测。
当采用中间设站观测方式分两组观测时,垂直角观测的顺序宜为:
第一组:后视一前视一前视—后视(照准上目标);
第二组:前视一后视一后视—前视(照准下目标)。
每次照准后视或前视时,一次正倒镜完成该分组测回数的1/2。
中间设站观测方式的垂直角总测回数应等于每点设站、往返观测方式的垂直角总测回数;
3 垂直角观测宜在日出后2h至日落前2h的期间内目标成像清晰稳定时进行。
阴天和多云天气可全天观测;
4 仪器高、觇标高应在观测前后用经过检验的量杆或钢尺各量测一次,精确读至0.5mm,当较差不大于1mm时取用中数。
采用中间设站观测方式时可不量测仪器高;
5 测定边长和垂直角时,当测距仪光轴和经纬仪照准轴不共轴,或在不同觇牌高度上分两组观测垂直角时,必须进行边长和垂直角归算后才能计算和比较两组高差。
工程测量规范GB50026-2007高程控制测量
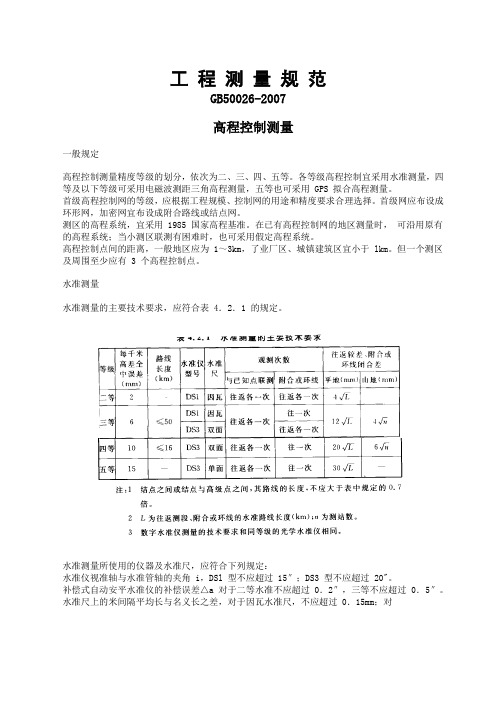
工程测量规范GB50026-2007高程控制测量一般规定高程控制测量精度等级的划分,依次为二、三、四、五等。
各等级高程控制宜采用水准测量,四等及以下等级可采用电磁波测距三角高程测量,五等也可采用 GPS 拟合高程测量。
首级高程控制网的等级,应根据工程规模、控制网的用途和精度要求合理选择。
首级网应布设成环形网,加密网宜布设成附合路线或结点网。
测区的高程系统,宜采用 1985 国家高程基准。
在已有高程控制网的地区测量时,可沿用原有的高程系统;当小测区联测有困难时,也可采用假定高程系统。
高程控制点间的距离,一般地区应为 1~3km,了业厂区、城镇建筑区宜小于 lkm。
但一个测区及周围至少应有 3 个高程控制点。
水准测量水准测量的主要技术要求,应符合表 4.2.1 的规定。
水准测量所使用的仪器及水准尺,应符合下列规定:水准仪视准轴与水准管轴的夹角 i,DSl 型不应超过15″;DS3 型不应超过 20"。
补偿式自动安平水准仪的补偿误差△a 对于二等水准不应超过 0.2″,三等不应超过 0.5″。
水准尺上的米间隔平均长与名义长之差,对于因瓦水准尺,不应超过 0.15mm;对于条形码尺,不应超过 0.10mm;对于木质双面水准尺,不应超过 0.5mm。
水准点的布设与埋石,除满足 4.1.4 条外还应符合下列规定:应将点位选在土质坚实、稳固可靠的地方或稳定的建筑物上,且便于寻找、保存和引测;当采用数字水准仪作业时,水准路线还应避开电磁场的干扰。
宜采用水准标石,也可采用墙水准点。
标志及标石的埋设应符合附录 D 的规定。
埋设完成后,二、三等点应绘制点之记,其他控制点可视需要而定。
必要时还应设置指示桩。
水准观测,应在标石埋设稳定后进行。
各等级水准观测的主要技术要求,应符合表 4.2.4 的规定。
两次观测高差较差超限时应重测。
重测后,对于二等水准应选取两次异向观测的合格结果,其他等级则应将重测结果与原测结果分别比较,较差均不超过限值时,取三次结果的平均数。
电磁波测距三角高程测量在航道高程测量中的应用

电磁波测距三角高程测量在航道高程测量中的应用引言高程测量是航道基本测量的重要内容,它包括高程控制测量、跨河水准测量、水面比降观测等。
用水准测量测定两点间的高差,其精度较高,是高程测量中常用的方法,但是,对于山区河流的高程测量却又十分困难。
山区河流地面起伏大、沟壑多,其高程测量通常采用电磁波测距三角高程测量的方法来实现。
随着测量仪器的发展,测距和测角精度的提高,三角高程测量代替水准测量的技术已发展成熟,而且也完全可行。
三角高程测量代替水准测量的依据和技术指标《水运工程测量规范》(JTJ(203-2001))和《工程测量规范》,对电磁波测距三角高程测量代替水准测量的等级、适用范围和精度评定方法做了规定,这是我们进行三角高程测量的依据。
规范规定: “4.3.1三角高程测量分为电磁波测距三角高程测量和经纬仪三角高程测量。
电磁波测距三角高程测量可代替四等水准测量和图根水准测量。
经纬仪三角高程测量只适用于图根水准测量。
”三角高程测量主要技术指标如下:注:①表中D为高程传递边的水平距离(km)三角高程测量的原理和精度分析三角高程测量的原理是用全站仪测定两点间的斜距和垂直角,把距离测量和角度测量结合起来,计算两点间的高差和点的高程。
如图所示,当测距较近时,根据全站仪测定的倾斜距离和竖直角,用三角函数,计算水平距离D、垂直距离V和高差h,再量取仪器高i和目标高L,计算出A、B两点间的高差,这种方法称为三角高程测量。
其计算高差的公式为:hAB=V+i-l。
然后,再根据A点高程和两点间的高差,计算B点的高程。
计算公式为HB=HA+hAB。
三角高程测量示意图当测距较大时,还需要加入球、气两差改正值。
首先是地球曲率影响的改正。
当测距在300米以上,对于工程测量,地球曲率对高程的影响已不容忽视,应进行改正,用f1=D2/(2R)计算改正值。
第其次是大气垂直折光影响改正。
地面大气层受重力影响,低层空气密度大于高层空气的密度,观测垂直角时,视线穿过密度不均匀的介质,成为一条向上凸的曲线,使视线的切线方向向上抬高,测得垂直角偏大,应进行气差改正,用f2=-kD2/(2R)计算改正值。
三角高程测量的计算公式

三角高程测量的计算公式如图6.27所示,已知A点的高程H A,要测定B点的高程 H B,可安置经纬仪于A点,量取仪器高i A;在B点竖立标杆,量取其高度称为觇 B 标高v B;用经纬仪中丝瞄准其顶端,测定竖直角α。
如果已知AB两点间的水平距离D (如全站仪可直接测量平距),则AB两点间的高差计算式为:如果当场用电磁波测距仪测定两点间的斜距D′,则AB两点间的高差计算式为:以上两式中,α为仰角时tanα或sinα为正,俯角时为负。
求得高差h AB以后,按下式计算B 点的高程:以上三角高程测量公式(6.27)、(6.28)中,设大地水准面和通过A、B点的水平面为相互平行的平面,在较近的距离(例如200米)内可以认为是这样的。
但事实上高程的起算面——大地水准面是一曲面,在第一章1.4中已介绍了水准面曲率对高差测量的影响,因此由三角高程测量公式(6.27)、(6.28)计算的高差应进行地球曲率影响的改正,称为球差改正f1,如图6.28(见课本)所示。
按(1.4)式:式中:R为地球平均曲率半径,一般取R=6371km。
另外,由于视线受大气垂直折光影响而成为一条向上凸的曲线,使视线的切线方向向上抬高,测得竖直角偏大,如图6.28所示。
因此还应进行大气折光影响的改正,称为气差改正f2,f2恒为负值。
图6.23 三角高程测量图6.24 地球曲率及大气折光影响设大气垂直折光使视线形成曲率大约为地球表面曲率K倍的圆曲线(K称为大气垂直折光系数),因此仿照(6.30)式,气差改正计算公式为:球差改正和气差改正合在一起称为球气差改正f,则f应为:大气垂直折光系数K随气温、气压、日照、时间、地面情况和视线高度等因素而改变,一般取其平均值,令K=0.14。
在表6.16中列出水平距离D=100m-200m的球气差改正值f,由于f1>f2,故f恒为正值。
考虑球气差改正时,三角高程测量的高差计算公式为:或由于折光系数的不定性,使球气差改正中的气差改正具有较大的误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Wi h12 h21
m2 Wi
2mh2i
Wi 2mWi 2 2mhi
mhi 2M hi Wi 4M hi Wi 0.1Si (m)
6.4.2 三角高程测量的精度和限差
3、环线高差闭合差的限差
W h1 hn
mW2
M
2 h1
M
2 h2
M
2 h2
M
2 hn
6.4 电磁波测距三角高程测量 6.4.1 解算原理和计算公式
1、由单向垂直角和平距计算两点间的高差
h12
S0tg12
1 2R
S0i
i1
1 2R
S02
v2
h12
S0tg12
i1
v2
1 k 2R
S02
S0tg12
i1
v2
CS
2 0
C称为球气差系数
6.4.1 解算原理和计算公式
因PCM并非直角,上式有误差,即关系: S0 MC PC tg12 是近似的。 严密公式应该按正弦定理计算:
将第二式代入第一式,得:
S
2 0
(1
tg 2
)
2tg
(m
n
p)S0
(m
n
p)2
S122
0
6.4.1 解算原理和计算公式
解得,平距为:
S0
S122 (1 tg2 ) (m n p)2 tg (m n p) 1 tg2
代入第二式,得高差。
若观测了返测距离,可得平距的计算公式:
S0 S21 (h12 V2 I1)2
S122 (h12 I2 V1)2 S122 (S0tg m n q)2
平距为:
S0
S122 (1 tg 2 ) (m n p)2 tg (m n p) 1 tg2
6.4.2 三角高程测量的精度和限差
1、高差测定误差
M hi 0.025 Si (m)
2、对向高差闭合差的限差
S
sin12 (1
2
2
)
h
S
s in 12
2
2
该公式误差很小。
S 10km, 12 30,求得:h 0.0006m
S 10km, 12 50,求得:h 0.0010m
6.4.1 解算原理和计算公式
PC S cos12
PC
S
sin(90 12 ) sin(90 )
S[cos12 (1
h12 S12 sin12 I1 V2 C12S122 cos2 12
h21 S21 sin212 I2 V1 C21S212 cos2 21
h12
1 2
(S12
s in 12
S21 sin121)
1 2
(I1
V1)
1 2
(I2
V2 )
消除了球气差项的影响。
6.4.1 解算原理和计算公式
tg12
Hmd R
tg12
6.4.1 解算原理和计算公式
2、由对向垂直角和平距计算两点间的高差
h12
dtg12
i1
v2
CS
2 0
h12
h21 dtg121 i2 v1 CS02 h21
h12
1 2
d (tg12
tg 21 )
1 2
(i1
v1 )
1 2
(i2
v2 )
h12
h12
dtg
1 2
(12
21 )
1 2
(i1
v1 )
1 2
(i2
v2 )
h12
6.4.1 解算原理和计算公式
3、由电磁波实测斜距和单向垂直角计算两点间高差
h12 S sin12 I1 V2 CS 2 cos2 12 NC S sin12
若顾及角,用正弦定理计算:
NC
S sin12 sin(90 )
5、用分别测定的斜距和垂直角计算高差和水平距离
观测斜距S12,仪高I,目标高V,则平距S0为:
S0 S122 (h12 V2 I1)2 S122 (h12 p)2 , p V2 I1
高差为:
h12
H2
H1
S0tg
1 2
(12
21 )
1 2
(i1
v1 )
1 2
(i2
v2 )
S0tg m n
MC
PC
s in 12 sin(90 12
)
PC
s in 12 cos(12 )
PC
c os12
s in 12 sin12 cos12
2
2
PC tg12
(1
tg12
2
2
)
PC tg12
h
近似公式引入的误差为:
h
PC tg12 (tg12
2
2
)
____
当 PC 10km, 12 30 ,求得:h 0.043 m
____
PC 10km, 12 50 ,求得:h 0.121m
6.4.1 解算原理和计算公式
若采用平均高程面上的距离计算,则有
S0
S0 (1
Hm R
)
d (1
ym2 2Rm2
)(1
Hm R
)
d (1
ym2 2Rm2
Hm R
)
h12
dtg12
i1
v2
CS
2 0
h12
h12
ym2 d 2Rm2
n
W 0.05
(
M
2 h1
M
2 h2
M
2 hn
)
j 1
2
2
)
sin12 ](1
2
2
)
S cos12 S sin12
S S sin12
NN
S
sin(90 12 sin(90 )
)
S[cos12 (1
2
2
)
sin12 ](1
2
2
)
S cos12 S sin12
则有: NN PC 2S cos12
6.4.1 解算原理和计算公式
4、电磁波往返实测斜距和往返实测垂直角计算两点间高差
